Scalable Model Selection for Spatial Additive Mixed Modeling: Application to Crime Analysis
Abstract
:1. Introduction
2. Spatial Additive Mixed Model
2.1. Model
2.2. Estimation
- (I)
- Replace the data matrices {}, whose dimensions are dependent on N, with their inner products, whose dimensions are independent of N.
- (II)
- Using the inner products, iterate the following calculations sequentially for :
- (II–1)
- Estimate by maximizing with .
- (II–2)
- Go to (III) if the likelihood value converges. Else, return to (II-1).
- (III)
- Output the final model.
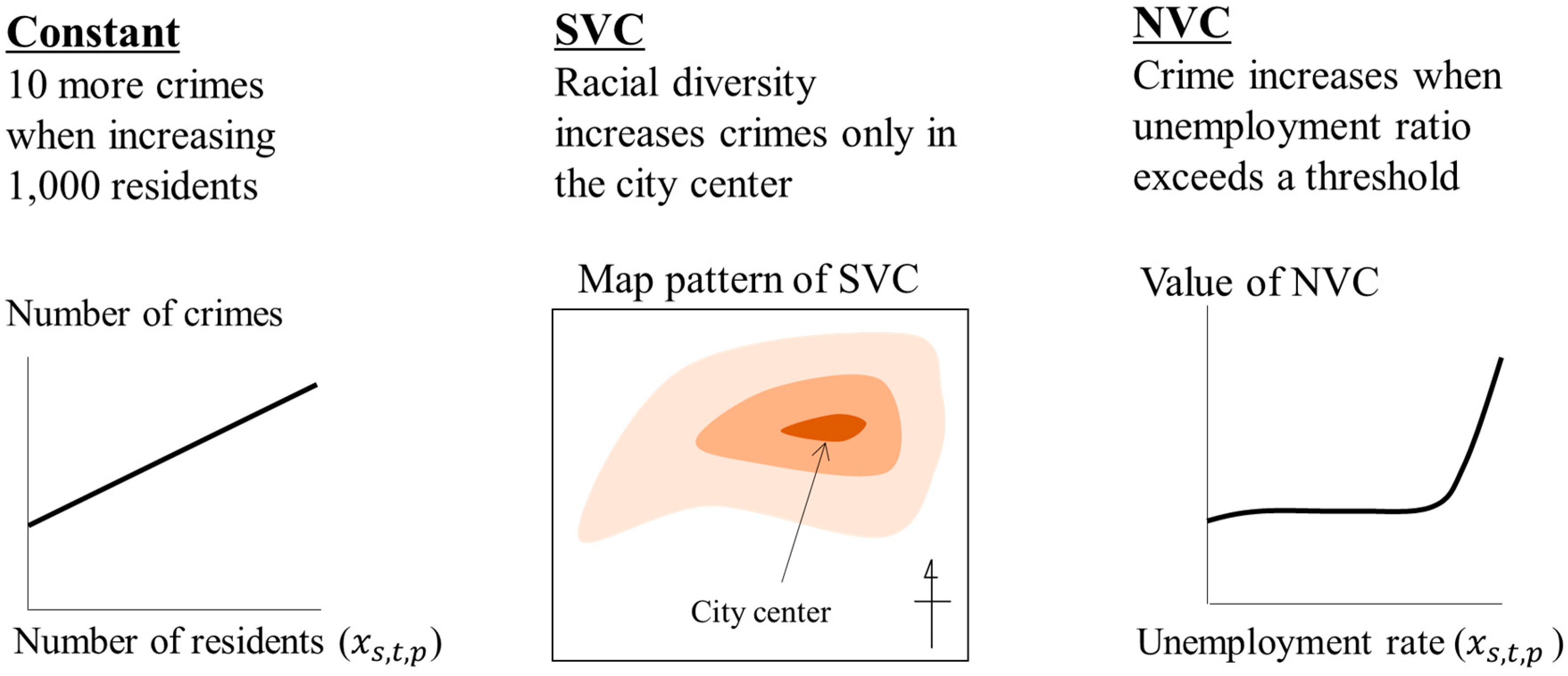
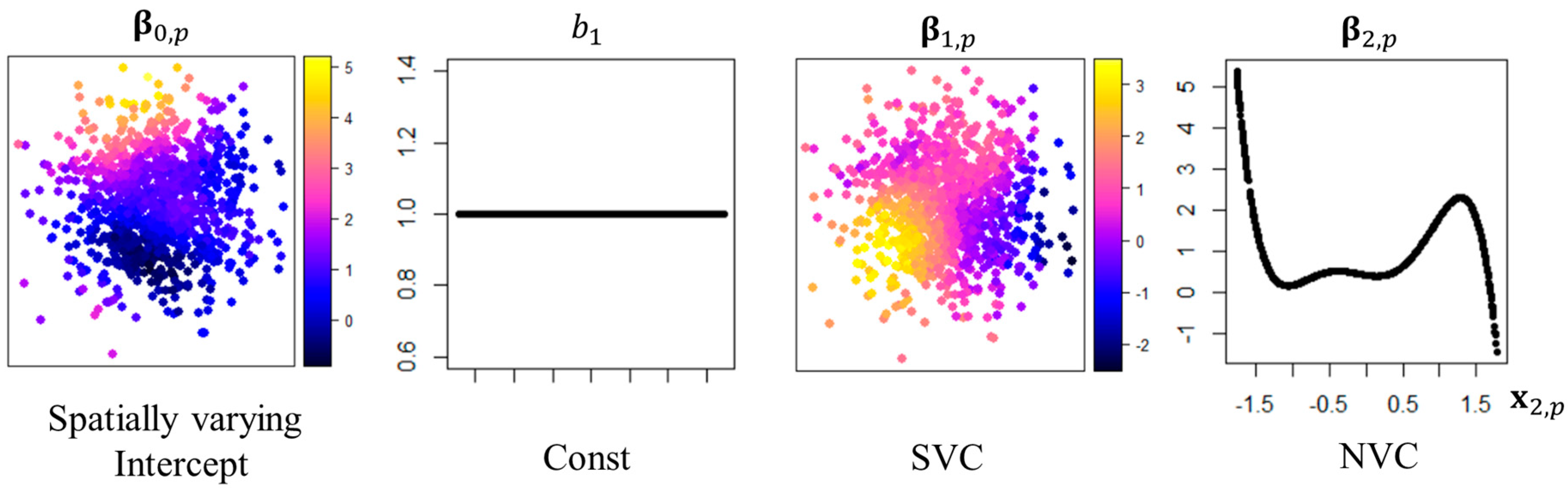
3. Model Selection
3.1. Introduction
- It is the most common specification for linear mixed effects models [30], including spatial additive mixed models.
- Although the marginal specification suffers from a theoretical bias, [32] showed that the influence of the bias on model selection result is quite small.
3.2. Model Selection Procedures
3.2.1. Simple Selection Method
- (a)
- Replace the data matrices {} with the inner products as processed in step (II) in Section 2.2.
- (b)
- Perform the following calculation sequentially for each :
- (b–1)
- Estimate the p-th SVC by maximizing with respect to , which is a subset of characterizing the SVC, and represents the set of variance parameters excluding from .
- (b–2)
- Select the SVC if it improves the cost function value (e.g., BIC). Otherwise, replace it with a constant.
- (b–3)
- Estimate the p-th NVC by maximizing with respect to , which is a subset of characterizing the NVC, and represents the set of variance parameters excluding from .
- (b–4)
- The NVC is selected if it improves the cost function value (e.g., BIC). Otherwise, it is replaced with a constant.
- (c)
- Go to (d) if the cost function converges. Otherwise, go back to (b).
- (d)
- Output the final model.
3.2.2. Monte Carlo (MC) Selection Method
- (A)
- Replace the data matrices {} with the inner products.
- (B)
- Iterate the following calculation G times using the inner products:
- (B–1)
- Randomly sample the g-th sequence without replacement.
- (B–2)
- Perform the following calculation sequentially for each :
- (B–2a)
- Estimate the -th SVC by maximizing , where are defined similarly as .
- (B–2b)
- Select the SVC if it improves the cost function value (e.g., BIC). Otherwise, replace it with a constant.
- (B–2c)
- Estimate the -th NVC by maximizing , where are defined similarly as .
- (B–2d)
- The NVC is selected if it improves the cost function value (e.g., BIC). Otherwise, it is replaced with a constant.
- (B–3)
- Go to (B–4) if the cost function converges. Otherwise, go back to (B–2).
- (B–4)
- Calculate the cost function value of the selected model.
- (C)
- Output the best model in the selected G models in terms of the lowest cost function.
4. Numerical Experiments
4.1. Computational Details
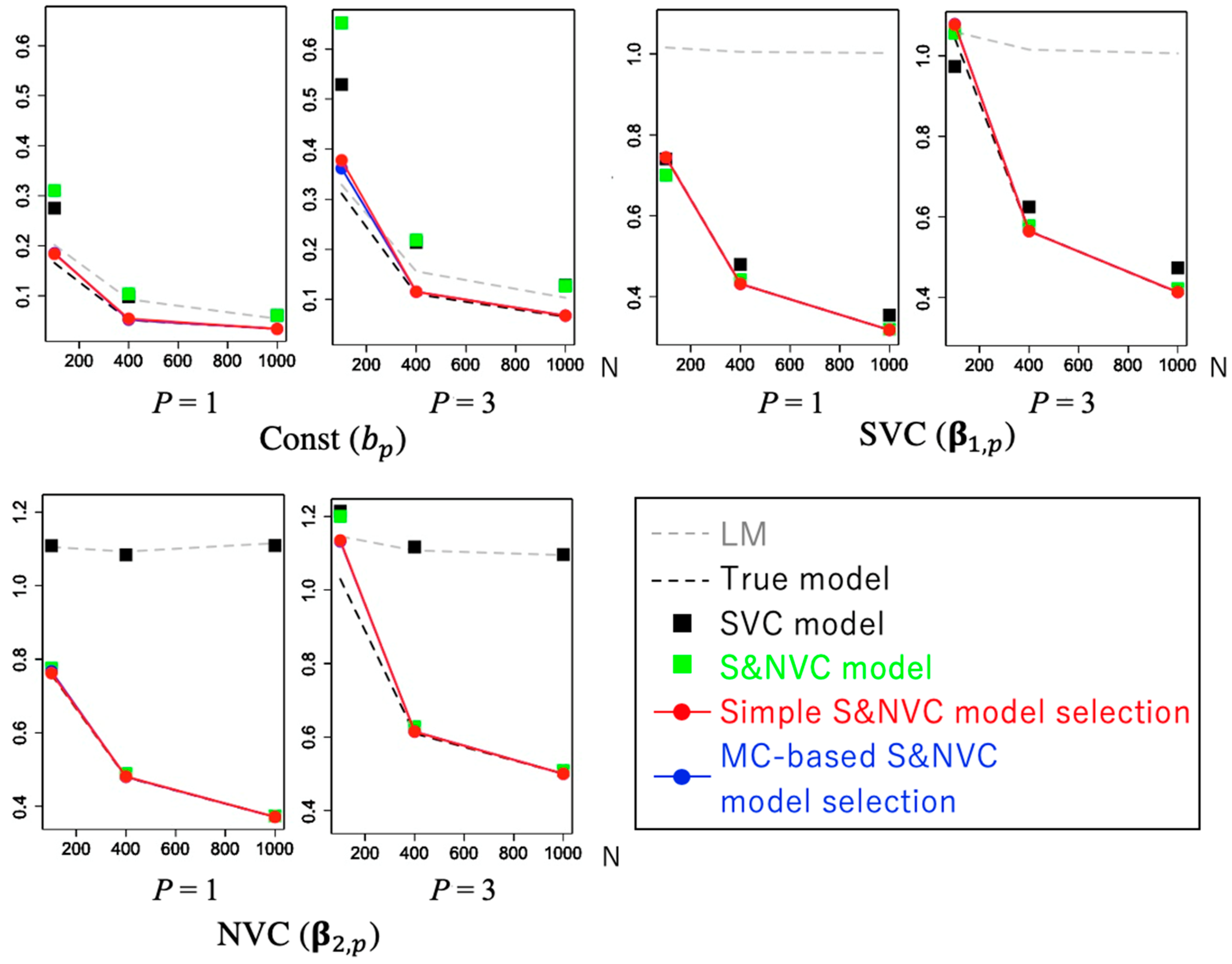
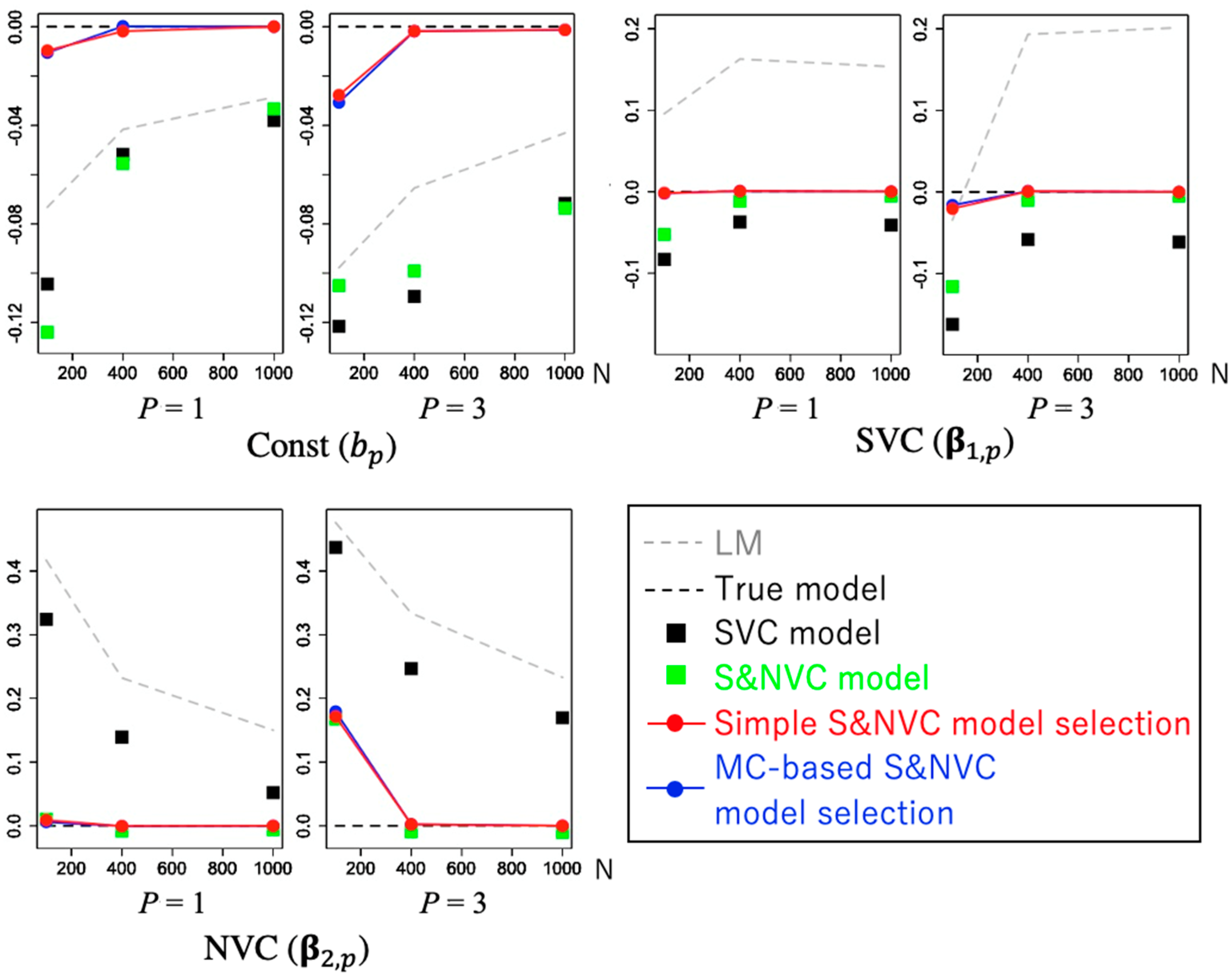
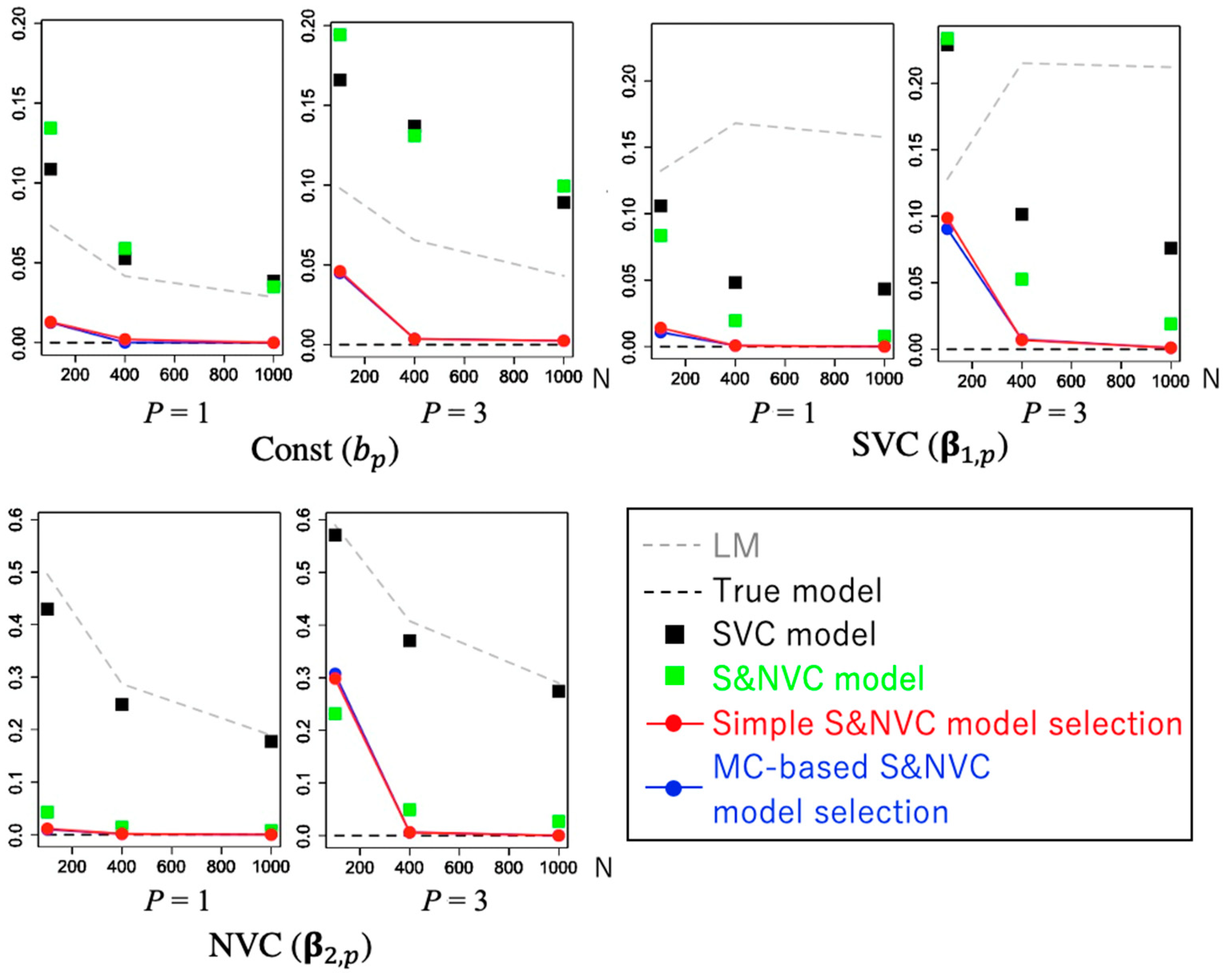
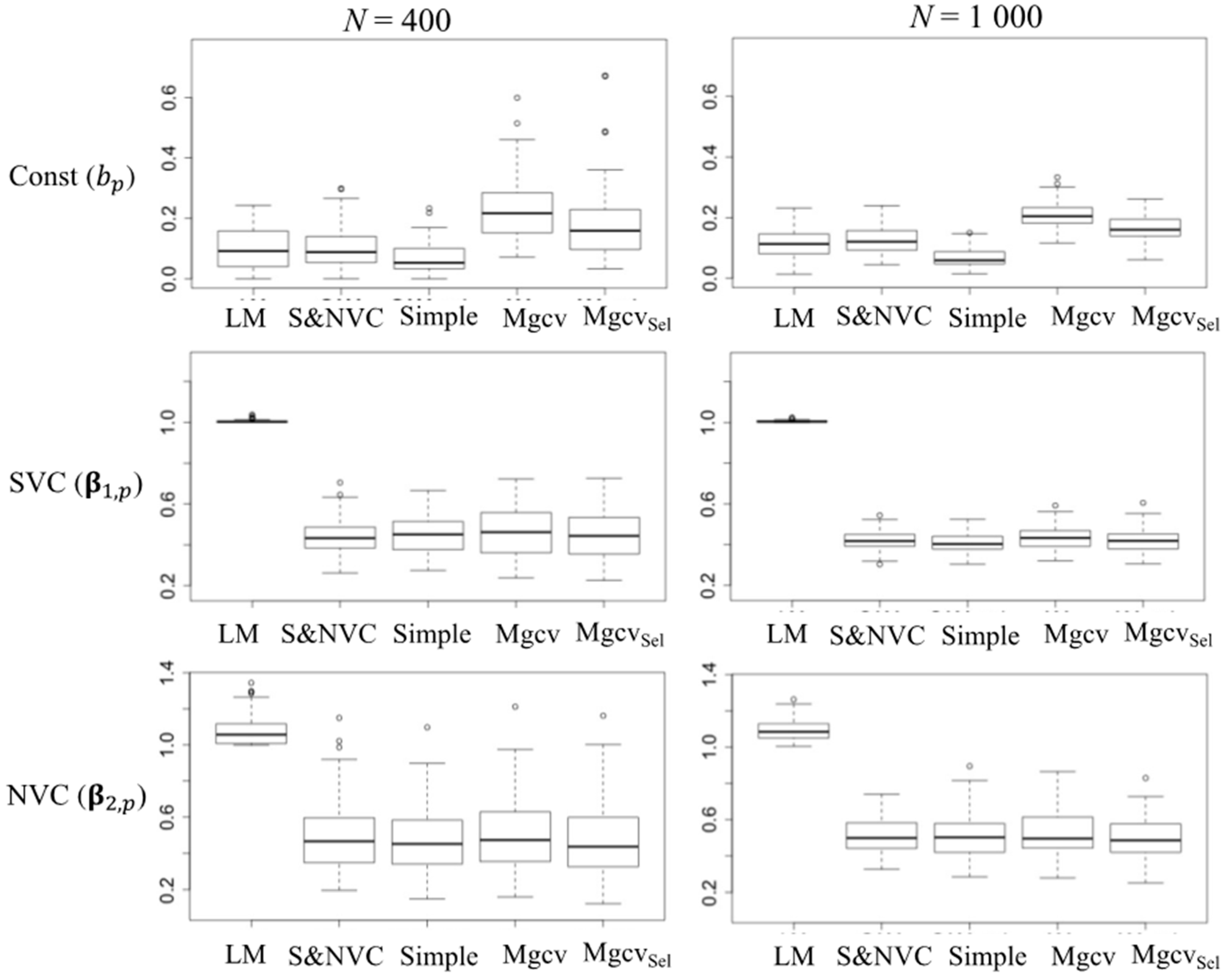
4.2. Performance of Model Selection
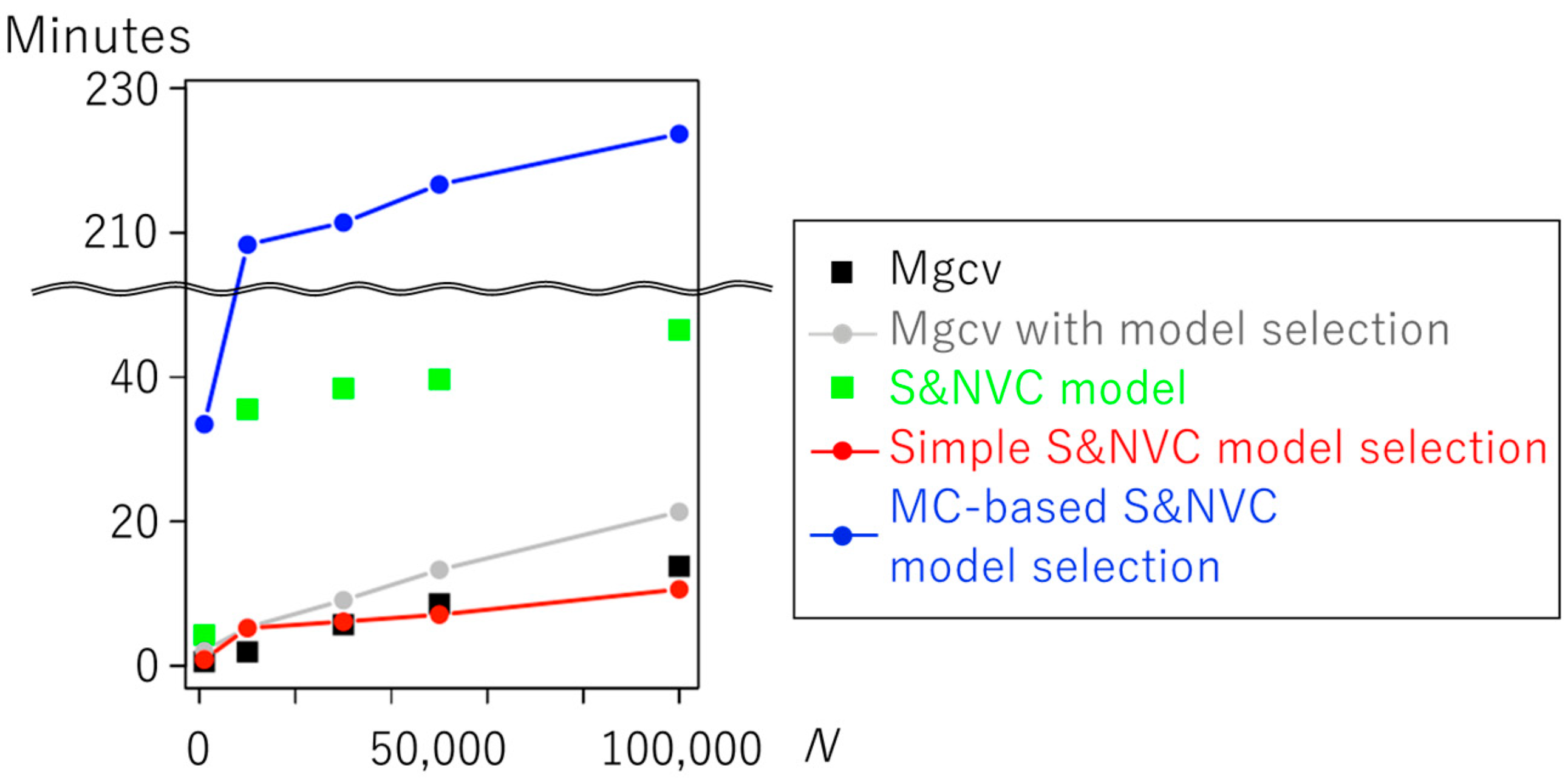
4.3. Benchmark Comparison of Model Selection Methods
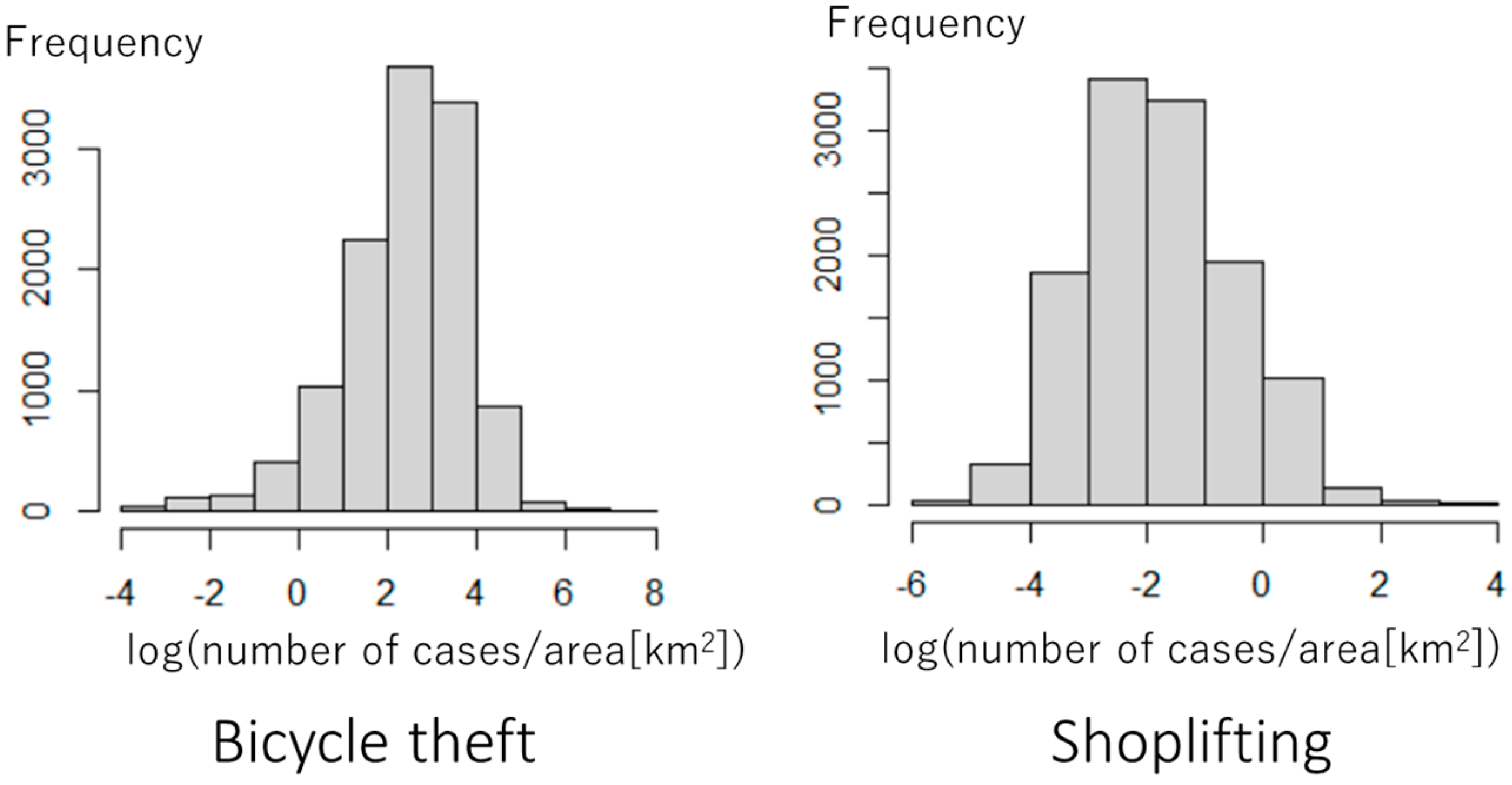
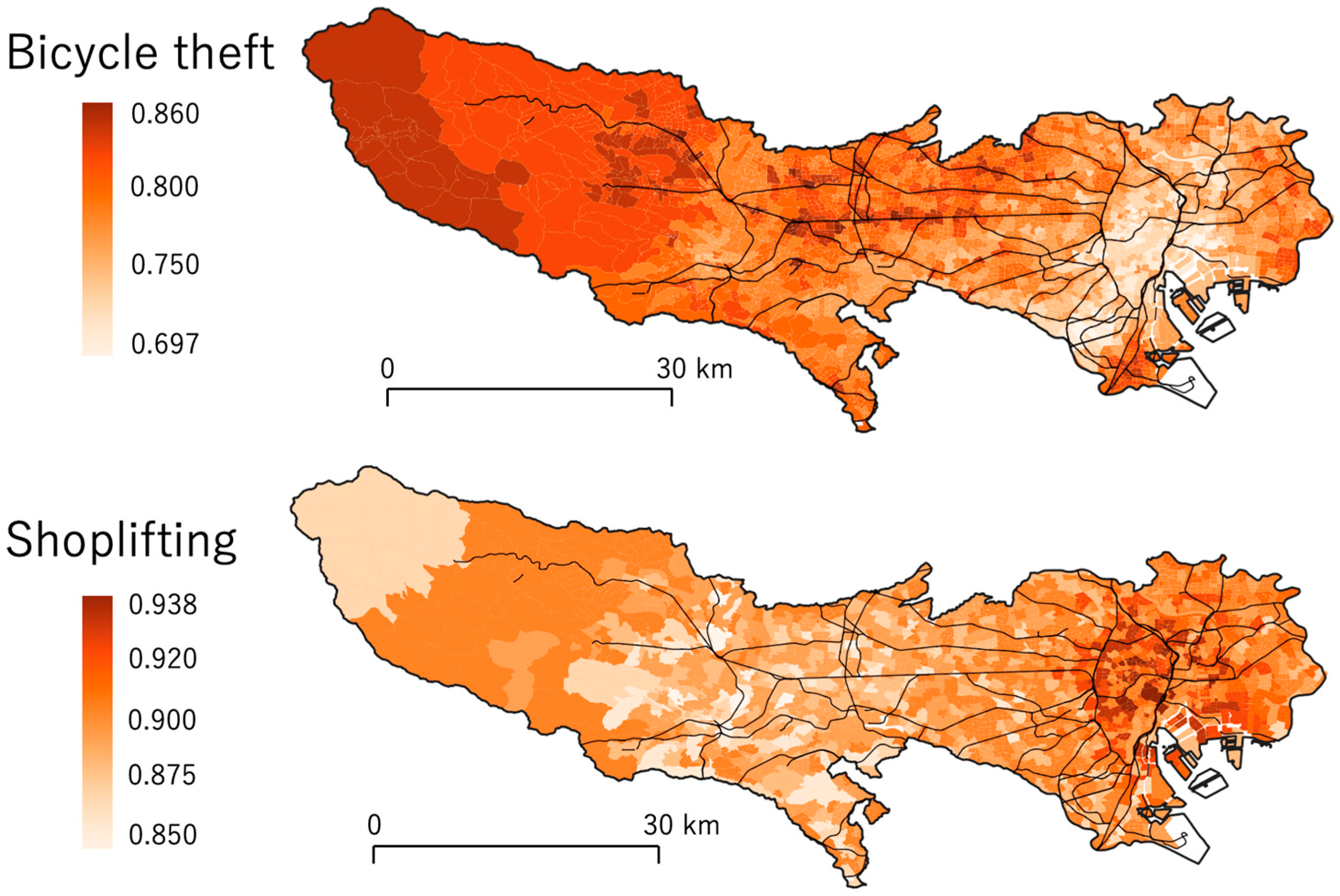
5. Application to Crime Modeling
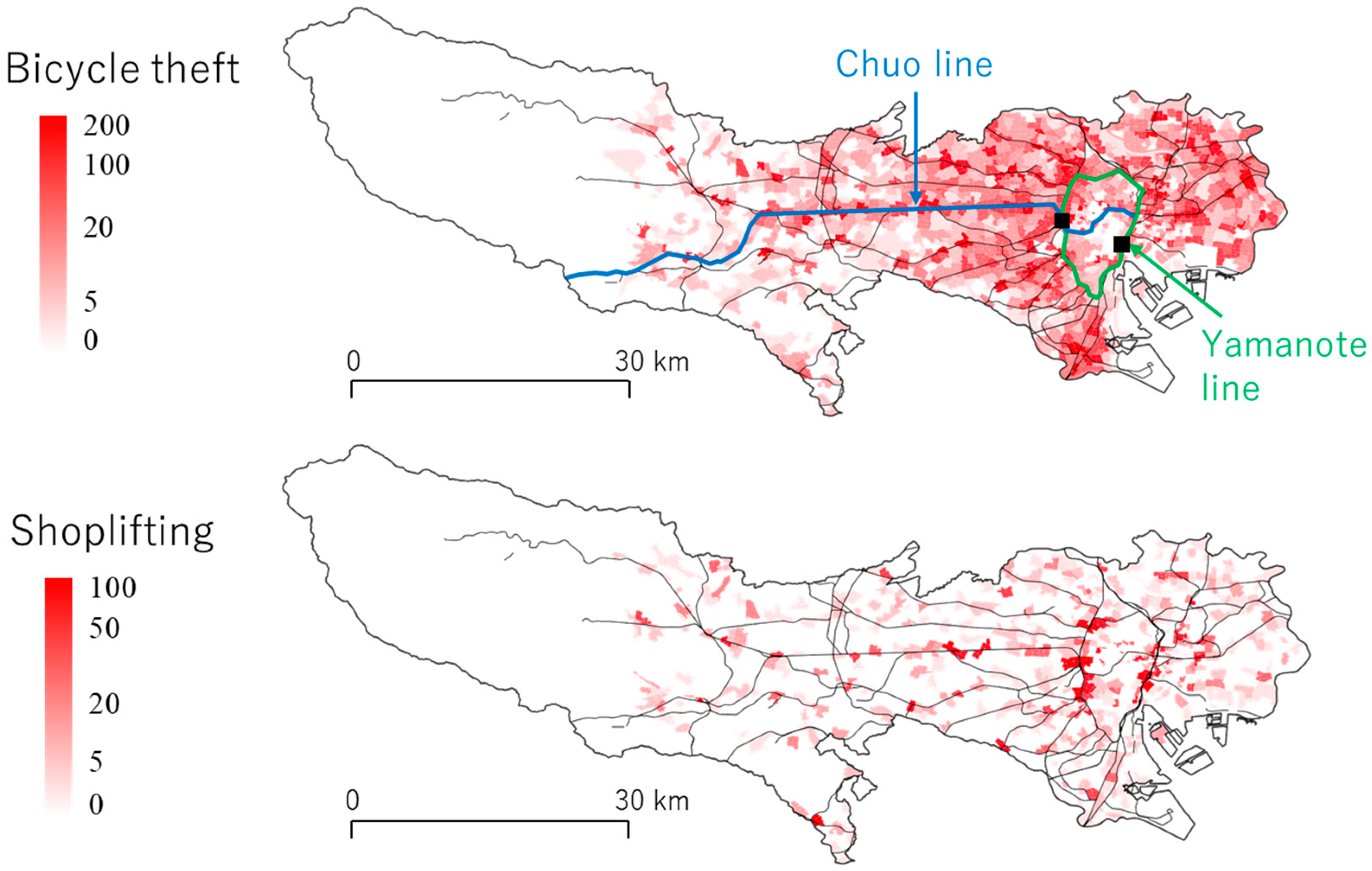
5.1. Outline
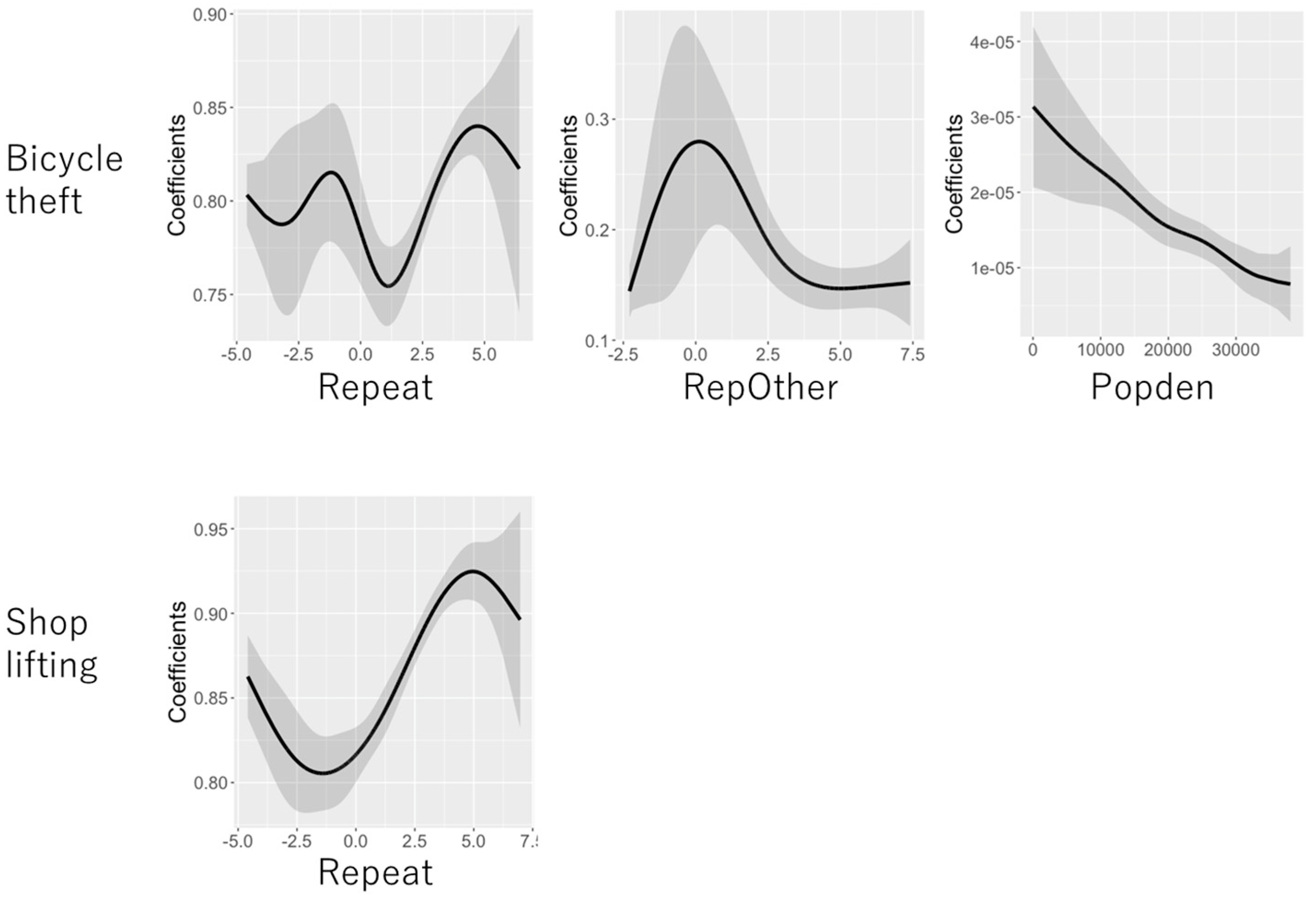
5.2. Coefficient Estimation Results
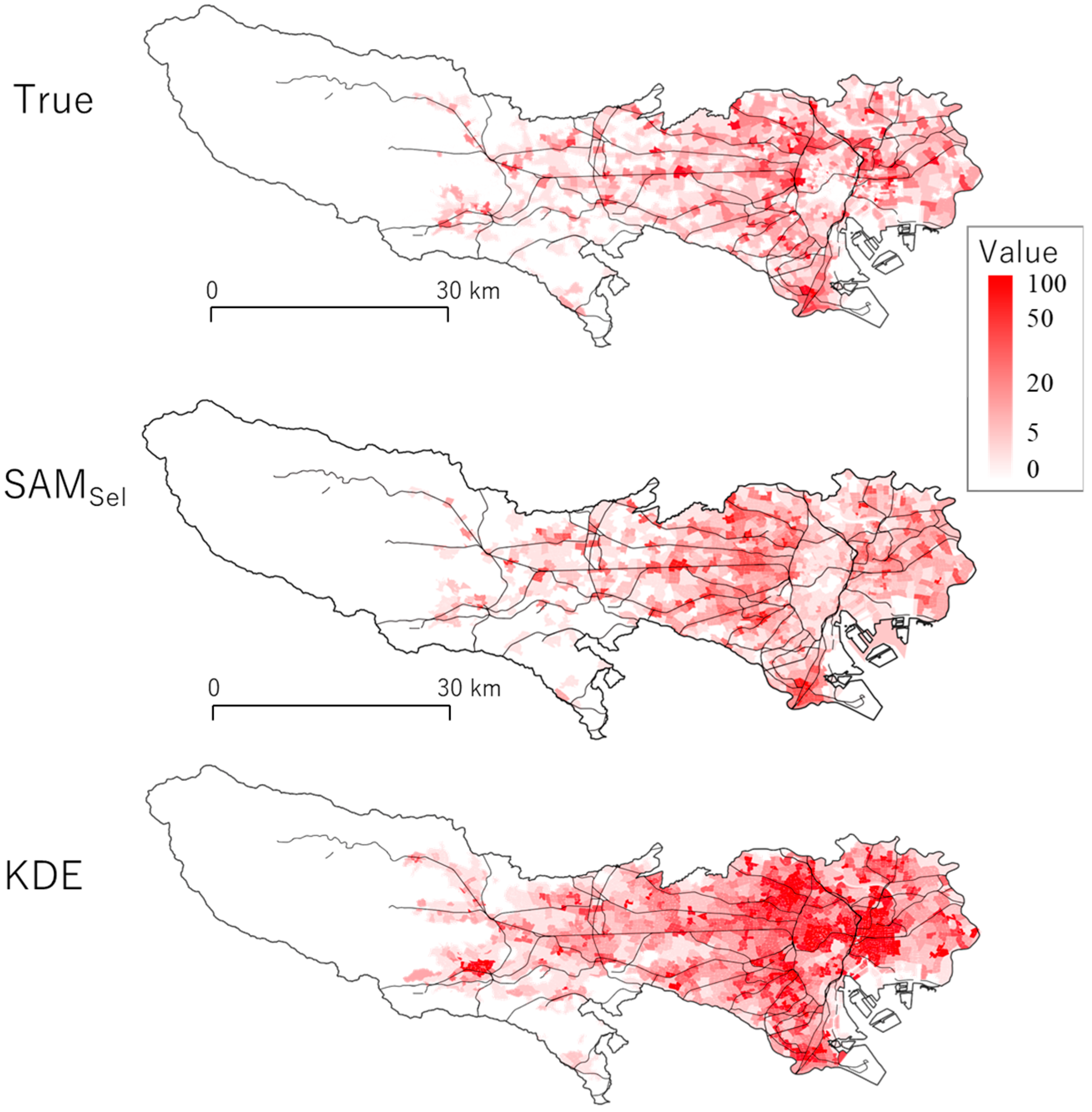
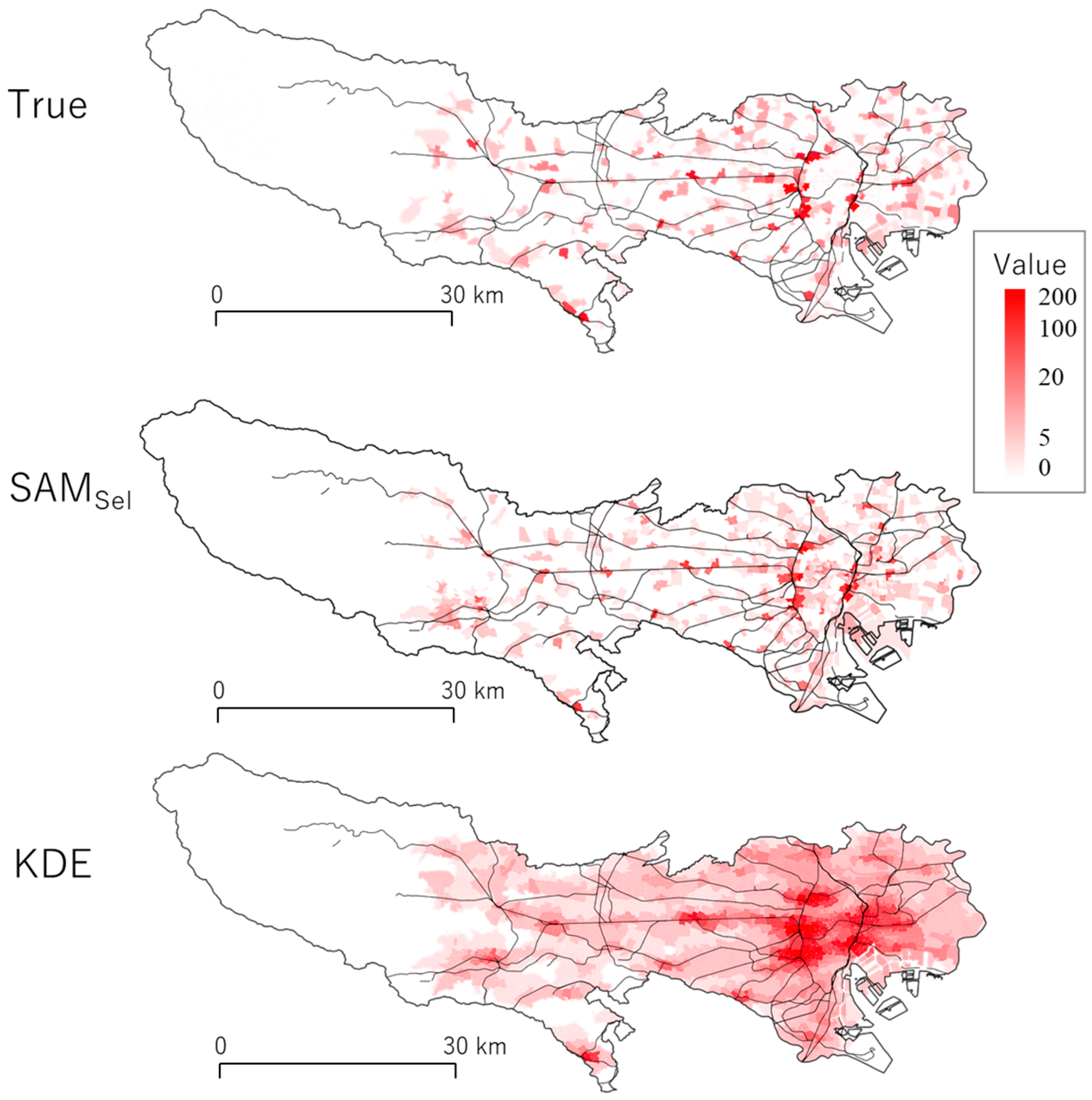
5.3. Application to Crime Prediction
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A. Restricted Log-Likelihood Function of The Spatial Additive Mixed Model
Appendix B. Details of Model Selection Approaches
References
- Osgood, D.W. Poisson-based regression analysis of aggregate crime rates. J. Quant. Criminol. 2000, 16, 21–43. [Google Scholar] [CrossRef]
- Cahill, M.; Mulligan, G. Using geographically weighted regression to explore local crime patterns. Soc. Sci. Comput. Rev. 2007, 25, 174–193. [Google Scholar] [CrossRef]
- Bernasco, W.; Block, R. Robberies in Chicago: A block-level analysis of the influence of crime generators, crime attractors, and offender anchor points. J. Res. Crime Delinq. 2011, 48, 33–57. [Google Scholar] [CrossRef]
- Maguire, M.; McVie, S. Crime data and criminal statistics: A critical reflection. In The Oxford Handbook of Criminology; Maruna, S., McAra, L., Eds.; Oxford University Press: Oxford, UK, 2017; pp. 163–189. [Google Scholar]
- LeSage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationship; John Wiley & Sons: West Sussex, UK, 2002. [Google Scholar]
- Lee, S.; Kang, D.; Kim, M. Determinants of crime incidence in Korea: A mixed GWR approach. In Proceedings of the World Conference of the Spatial Econometrics Association, Barcelona, Spain, 8–10 July 2009; pp. 8–10. [Google Scholar]
- Arnio, A.N.; Baumer, E.P. Demography, foreclosure, and crime: Assessing spatial heterogeneity in contemporary models of neighborhood crime rates. Demogr. Res. 2012, 26, 449–486. [Google Scholar] [CrossRef] [Green Version]
- Umlauf, N.; Adler, D.; Kneib, T.; Lang, S.; Zeileis, A. Structured additive regression models: An R interface to BayesX. J. Stat. Softw. 2015, 21, 63. [Google Scholar]
- Nakaya, T.; Fotheringham, S.; Charlton, M.; Brunsdon, C. Semiparametric geographically weighted generalised linear modelling in GWR 4.0. In Proceedings of the 10th International Conference on GeoComputation, Sydney, Australia, 30 November–2 December 2009. [Google Scholar]
- Wheeler, D.C. Simultaneous coefficient penalization and model selection in geographically weighted regression: The geographically weighted lasso. Environ. Plan. A 2009, 41, 722–742. [Google Scholar] [CrossRef] [Green Version]
- Comber, A.; Brunsdon, C.; Charlton, M.; Dong, G.; Harris, R.; Lu, B.; Lu, Y.; Murakami, D.; Nakaya, T.; Wang, Y.; et al. The GWR route map: A guide to the informed application of Geographically Weighted Regression. arXiv 2020, arXiv:2004.06070. [Google Scholar]
- Huang, J.; Horowitz, J.L.; Wei, F. Variable selection in nonparametric additive models. Ann. Stat. 2010, 38, 2282. [Google Scholar] [CrossRef] [Green Version]
- Amato, U.; Antoniadis, A.; De Feis, I. Additive model selection. Stat. Methods Appl. 2016, 25, 519–654. [Google Scholar] [CrossRef]
- Mei, C.L.; He, S.Y.; Fang, K.T. A note on the mixed geographically weighted regression model. J. Reg. Sci. 2004, 44, 143–157. [Google Scholar] [CrossRef]
- Li, Z.; Fotheringham, A.S.; Li, W.; Oshan, T. Fast Geographically Weighted Regression (FastGWR): A scalable algorithm to investigate spatial process heterogeneity in millions of observations. Int. J. Geogr. Inf. Sci. 2019, 33, 155–175. [Google Scholar] [CrossRef]
- Murakami, D.; Griffith, D.A. Spatially varying coefficient modeling for large datasets: Eliminating N from spatial regressions. Spat. Stat. 2019, 30, 39–64. [Google Scholar] [CrossRef] [Green Version]
- Murakami, D.; Griffith, D.A. A memory-free spatial additive mixed modeling for big spatial data. Jpn. J. Stat. Data Sci. 2020, 3, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Murakami, D.; Yoshida, T.; Seya, H.; Griffith, D.A.; Yamagata, Y. A Moran coefficient-based mixed effects approach to investigate spatially varying relationships. Spat. Stat. 2017, 19, 68–89. [Google Scholar] [CrossRef] [Green Version]
- Griffith, D.A. Spatial Autocorrelation and Spatial Filtering: Gaining Understanding through Theory and Scientific Visualization; Springer Science & Business Media: Berlin, Germany, 2003. [Google Scholar]
- Tiefelsdorf, M.; Griffith, D.A. Semiparametric filtering of spatial autocorrelation: The eigenvector approach. Environ. Plan. A 2007, 39, 1193–1221. [Google Scholar] [CrossRef]
- Murakami, D.; Griffith, D.A. Balancing spatial and non-spatial variation in varying coefficient modeling: A remedy for spurious correlation. arXiv 2020, arXiv:2005.09981. [Google Scholar]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. arXiv 2014, arXiv:1406.5823. [Google Scholar]
- Winter, B.; Wieling, M. How to analyze linguistic change using mixed models: Growth Curve Analysis and Generalized Additive Modeling. J. Lang. Evol. 2016, 1, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Baayen, H.; Vasishth, S.; Kliegl, R.; Bates, D. The cave of shadows: Addressing the human factor with generalized additive mixed models. J. Mem. Lang. 2017, 94, 206–234. [Google Scholar] [CrossRef] [Green Version]
- Gurka, M.J. Selecting the best linear mixed model under REML. Am. Stat. 2006, 60, 19–26. [Google Scholar] [CrossRef]
- Müller, S.; Scealy, J.L.; Welsh, A.H. Model selection in linear mixed models. Stat. Sci. 2013, 28, 135–167. [Google Scholar] [CrossRef] [Green Version]
- Dimova, R.B.; Markatou, M.; Talal, A.H. Information methods for model selection in linear mixed effects models with application to HCV data. Comput. Stat. Data Anal. 2011, 55, 2677–2697. [Google Scholar] [CrossRef]
- Sakamoto, W. Bias-reduced marginal Akaike information criteria based on a Monte Carlo method for linear mixed-effects models. Scand. J. Stat. 2019, 46, 87–115. [Google Scholar] [CrossRef]
- Greven, S.; Kneib, T. On the behaviour of marginal and conditional AIC in linear mixed models. Biometrika 2010, 97, 773–789. [Google Scholar] [CrossRef]
- Belitz, C.; Lang, S. Simultaneous selection of variables and smoothing parameters in structured additive regression models. Comput. Stat. Data Anal. 2008, 53, 61–81. [Google Scholar] [CrossRef]
- Reiss, P.T.; Todd Ogden, R. Smoothing parameter selection for a class of semiparametric linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009, 71, 505–523. [Google Scholar] [CrossRef]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 3–36. [Google Scholar] [CrossRef] [Green Version]
- Marra, G.; Wood, S.N. Practical variable selection for generalized additive models. Comput. Stat. Data Anal. 2011, 55, 2372–2387. [Google Scholar] [CrossRef]
- Wood, S.N.; Li, Z.; Shaddick, G.; Augustin, N.H. Generalized additive models for gigadata: Modeling the UK black smoke network daily data. J. Am. Stat. Assoc. 2017, 112, 1199–1210. [Google Scholar] [CrossRef] [Green Version]
- Felson, M. Crime and Everyday Life: Insights and Implications for Society (The Pine Forge Press Social Science Library); Pine Forge: Berks, PA, USA, 1994. [Google Scholar]
- Farrell, G. Preventing repeat victimization. Crime Justice 1995, 19, 469–534. [Google Scholar] [CrossRef]
- Johnson, S.D. Repeat burglary victimisation: A tale of two theories. J. Exp. Criminol. 2008, 4, 215–240. [Google Scholar] [CrossRef]
- Caplan, J.M.; Kennedy, L.W.; Miller, J. Risk terrain modeling: Brokering criminological theory and GIS methods for crime forecasting. Justice Q. 2011, 28, 360–381. [Google Scholar] [CrossRef]
- Ranson, M. Crime, weather, and climate change. J. Environ. Econ. Manag. 2014, 67, 274–302. [Google Scholar] [CrossRef]
- Harada, Y.; Shimada, T. Examining the impact of the precision of address geocoding on estimated density of crime locations. Comput. Geosci. 2006, 32, 1096–1107. [Google Scholar] [CrossRef]
- Wand, M.P.; Jones, M.C. Multivariate plug-in bandwidth selection. Comput. Stat. 1994, 9, 97–116. [Google Scholar]
- Yu, O.; Zhang, L. The under-recording of crime by police in China: A case study. Police Int. J. 1999, 22, 252–264. [Google Scholar] [CrossRef]
- Tabarrok, A.; Heaton, P.; Helland, E. The measure of vice and sin: A review of the uses, limitations, and implications of crime data. Handb. Econ. Crime 2010, 3, 53–81. [Google Scholar]
- Farrell, G.; Phillips, C.; Pease, K. Like taking candy-why does repeat victimization occur. Br. J. Criminol. 1995, 35, 384–399. [Google Scholar] [CrossRef]
- Farrell, G.; Pease, K. Repeat Victimization; Criminal Justice Press: New York, NY, USA, 2001. [Google Scholar]
- Gelfand, A.E.; Kim, H.J.; Sirmans, C.F.; Banerjee, S. Spatial modeling with spatially varying coefficient processes. J. Am. Stat. Assoc. 2003, 98, 387–396. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and temporal weighted regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef] [Green Version]
- Mohler, G. Modeling and estimation of multi-source clustering in crime and security data. Ann. Appl. Stat. 2013, 7, 1525–1539. [Google Scholar] [CrossRef] [Green Version]
- Kajita, M.; Kajita, S. Crime prediction by data-driven Green’s function method. Int. J. Forecast. 2020, 36, 480–488. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Cooley, D. Extreme value analysis and the study of climate change. Clim. Chang. 2009, 97, 77. [Google Scholar] [CrossRef]
| Model Type | |||
|---|---|---|---|
| Constant | 0 | 0 | N.A. |
| SVC | |||
| NVC | |||
| S&NVC |
| Bicycle Theft | ||||||||
| Coefficients | Intercept | Repeat | RepOther | Popden | Retail | Fpopden | UnEmp | Univ |
| Minimum | −0.469 | 0.702 | 0.144 | 0.008 | 0.014 | −0.015 | 0.028 | −0.035 |
| 1st quantile | −0.387 | 0.765 | 0.160 | 0.017 | ||||
| Median | −0.313 | 0.787 | 0.188 | 0.021 | ||||
| 3rd quantile | −0.283 | 0.805 | 0.208 | 0.025 | ||||
| Maximum | −0.208 | 0.872 | 0.279 | 0.031 | ||||
| Shoplifting | ||||||||
| Coefficients | Intercept | Repeat | RepOther | Dpopden | Retail | Fpopden | UnEmp | Univ |
| Minimum | −0.312 | 0.854 | 0.125 | 8.18×10−5 | 5.83×10−4 | −0.027 | 0.135 | 0.035 |
| 1st quantile | −0.295 | 0.886 | ||||||
| Median | −0.286 | 0.894 | ||||||
| 3rd quantile | −0.261 | 0.903 | ||||||
| Maximum | −0.226 | 0.934 | ||||||
| Bicycle theft | ||||||||
| Significance | Intercept | Repeat | RepOther | Popden | Retail | Fpopden | UnEmp | Univ |
| 10% level | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5% level | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 1% level | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| Shoplifting | ||||||||
| Significance | Intercept | Repeat | RepOther | Dpopden | Retail | Fpopden | UnEmp | Univ |
| 10% level | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5% level | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| 1% level | 1.000 | 1.000 | 1.000 | 1.000 | ||||
| Bicycle Theft | |||
|---|---|---|---|
| Estimate | Standard Error | t-Value | |
| January–March | −0.104 | 0.058 | −1.812 |
| April–June | 0.075 | 0.058 | 1.292 |
| July–September | 0.028 | 0.057 | 0.493 |
| October–December | 0.001 | NA | NA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, D.; Kajita, M.; Kajita, S. Scalable Model Selection for Spatial Additive Mixed Modeling: Application to Crime Analysis. ISPRS Int. J. Geo-Inf. 2020, 9, 577. https://doi.org/10.3390/ijgi9100577
Murakami D, Kajita M, Kajita S. Scalable Model Selection for Spatial Additive Mixed Modeling: Application to Crime Analysis. ISPRS International Journal of Geo-Information. 2020; 9(10):577. https://doi.org/10.3390/ijgi9100577
Chicago/Turabian StyleMurakami, Daisuke, Mami Kajita, and Seiji Kajita. 2020. "Scalable Model Selection for Spatial Additive Mixed Modeling: Application to Crime Analysis" ISPRS International Journal of Geo-Information 9, no. 10: 577. https://doi.org/10.3390/ijgi9100577
APA StyleMurakami, D., Kajita, M., & Kajita, S. (2020). Scalable Model Selection for Spatial Additive Mixed Modeling: Application to Crime Analysis. ISPRS International Journal of Geo-Information, 9(10), 577. https://doi.org/10.3390/ijgi9100577




