TOST: A Topological Semantic Model for GPS Trajectories Inside Road Networks
Abstract
1. Introduction
2. Related Work
3. Basic Concepts
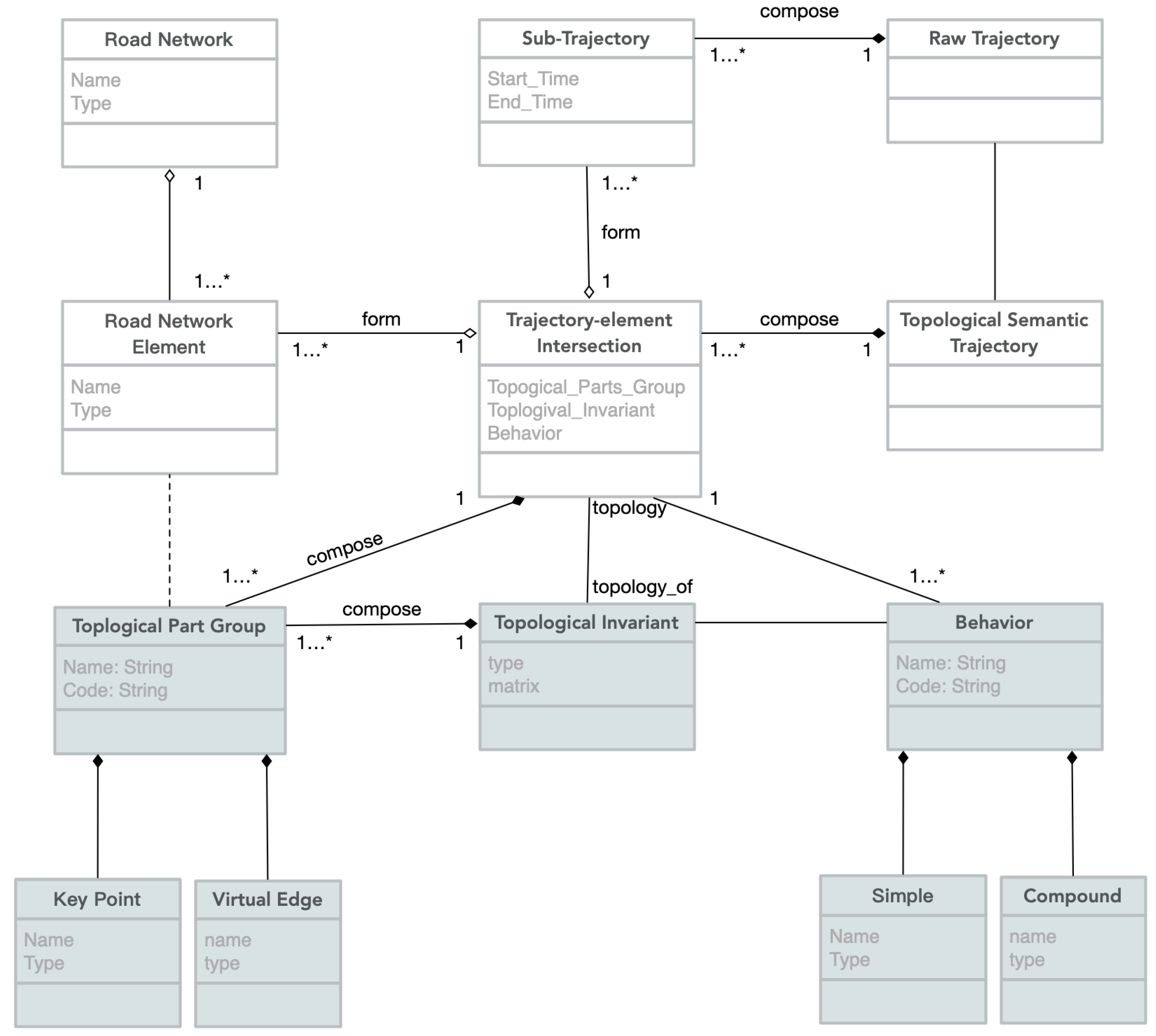
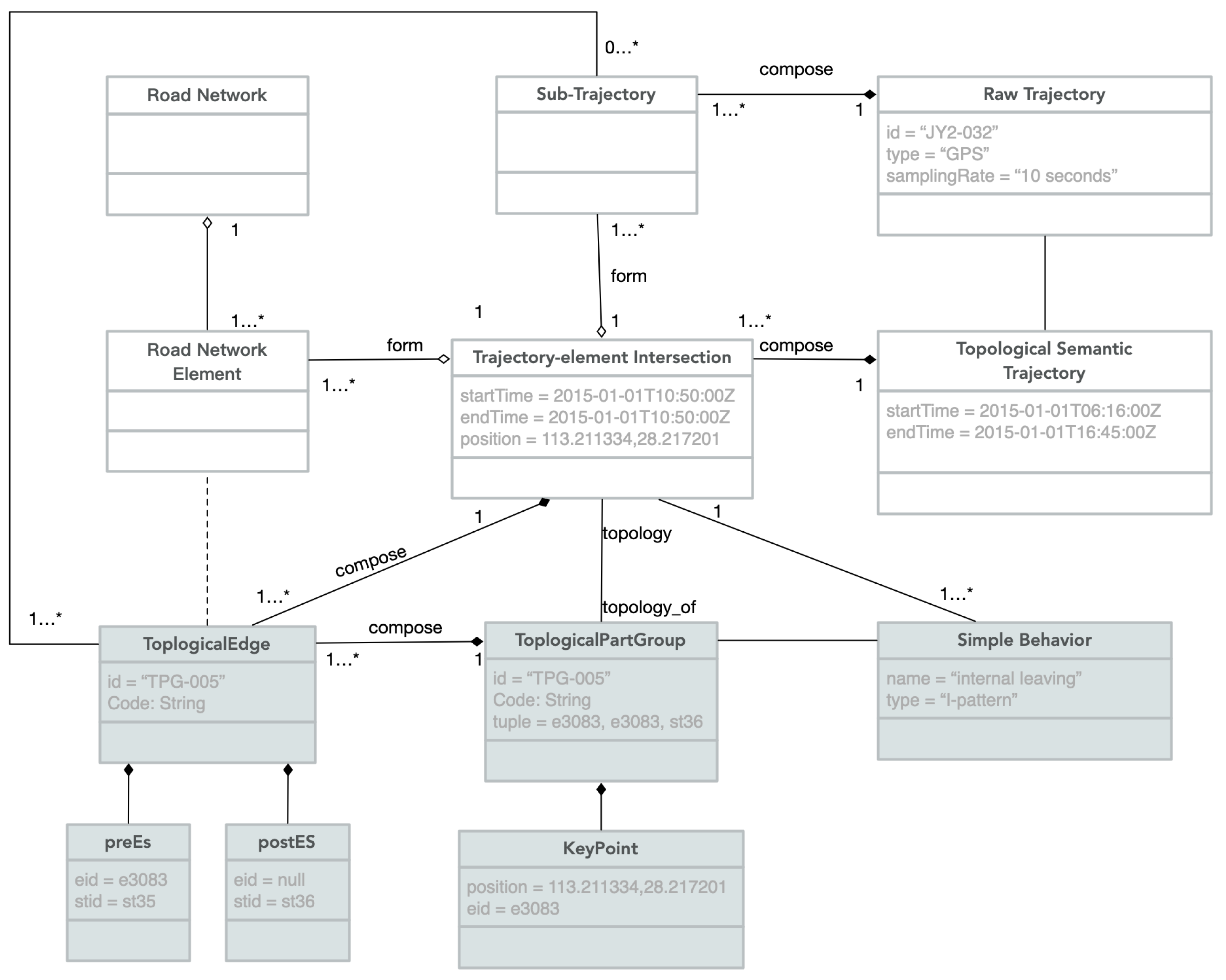
4. A Topological Semantic Model for Trajectories inside Road Networks
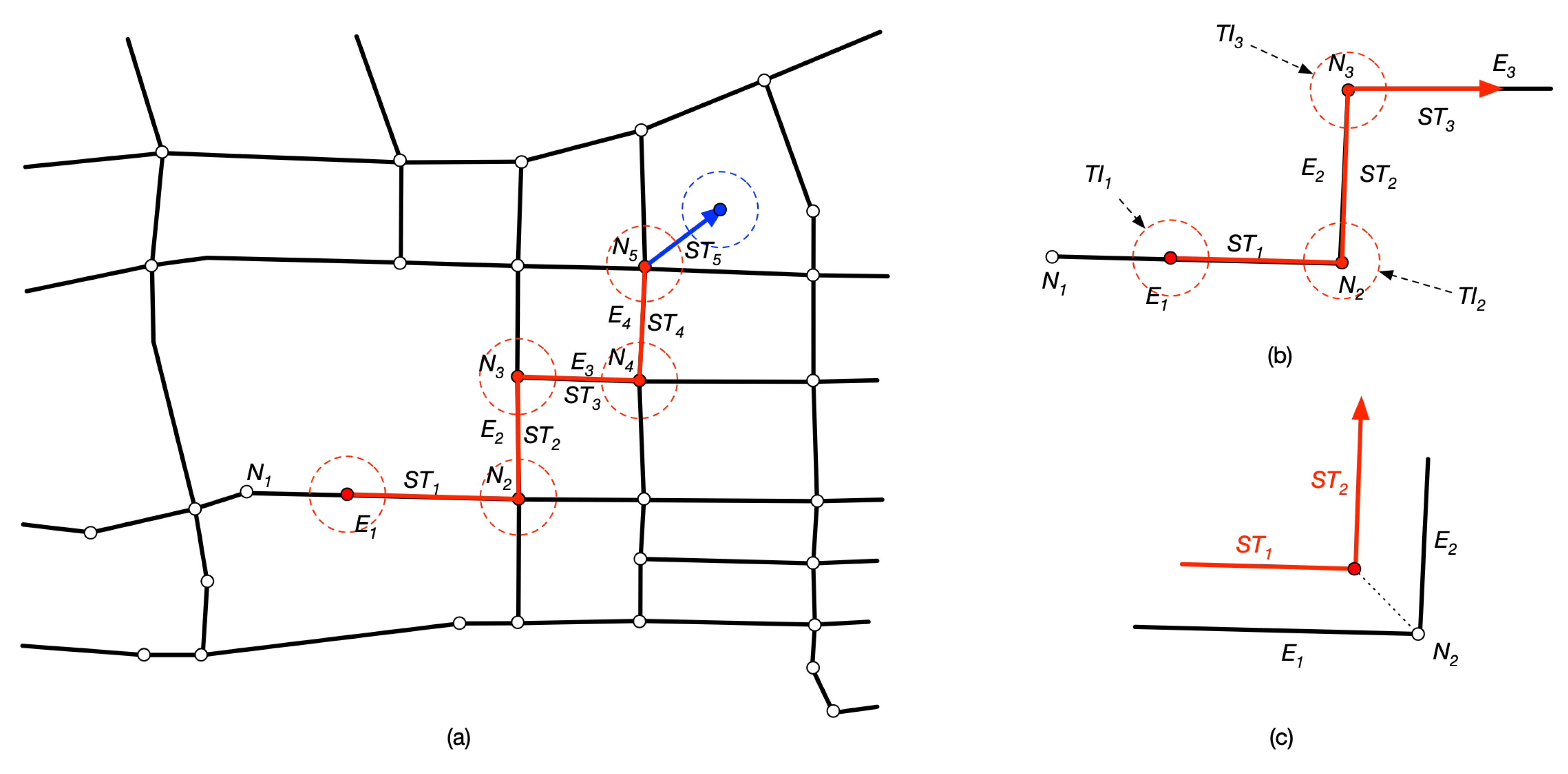
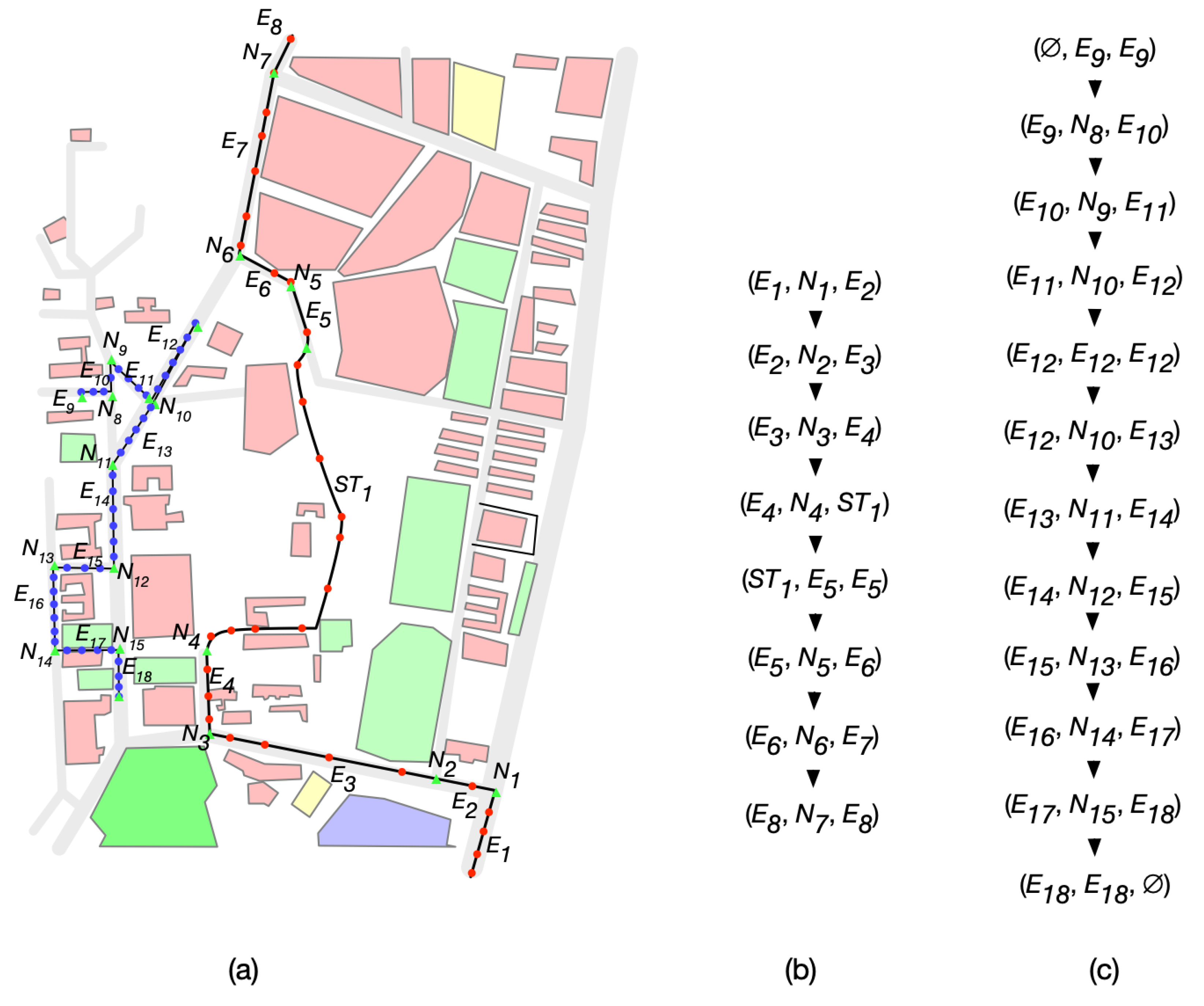
4.1. Representations for Trajectories inside Road Network
4.2. Topological Sematnics Related to Trajectory-element Intersections
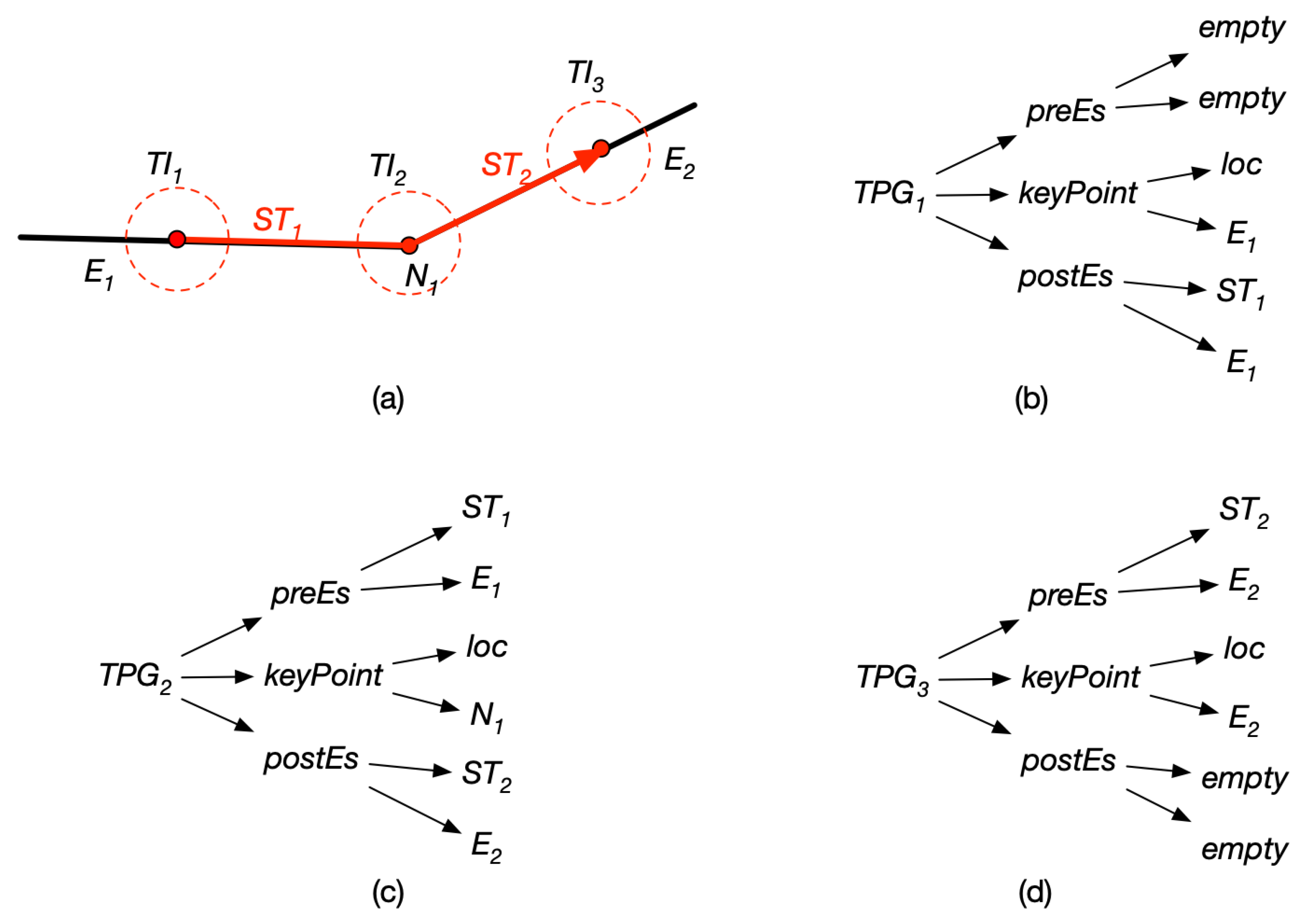
4.2.1. Topological Part Group
4.2.2. Intersection Topological Invariant
- and
- and
- and
- .
4.2.3. Behavior
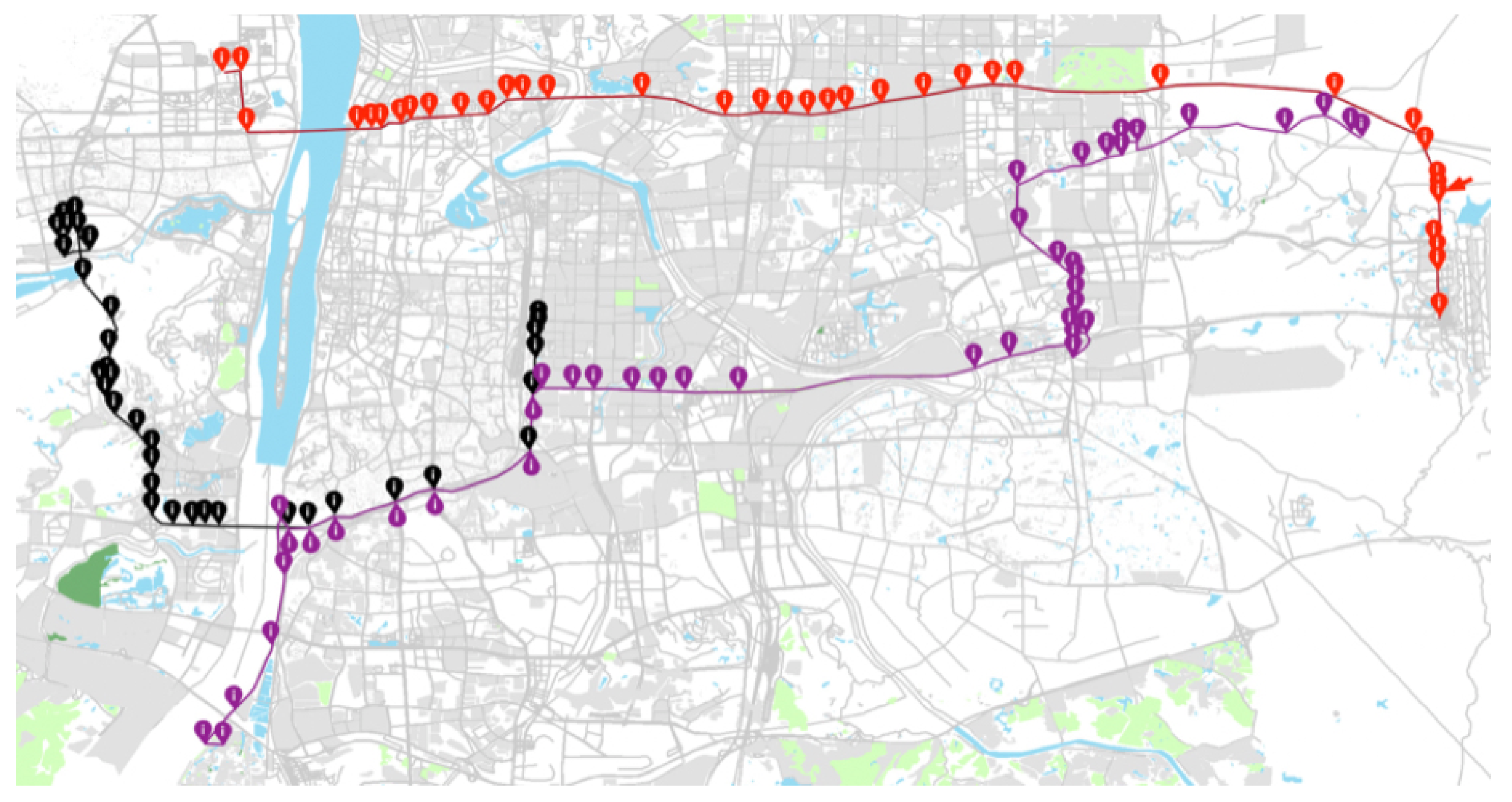
5. Experimenting in an Application Example
5.1. Experimental Setting
5.2. Semantic Trajectory Queries
SELECT distinct ve.eid FROM Trajectory-element Intersection ti JOIN TopologicalSemanticTrajectory tst, Trajectory-element Intersection ti JOIN TopologicalPartGroup tpg, TopologicalPartGroup tpg JOIN VirtualEdge ve WHERE tst.tid = “T1” AND ti.startTime between ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’ AND ti.endTime between ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’
SELECT distinct kp.eid FROM Trajectory-element Intersection ti JOIN TopologicalSemanticTrajectory tst, Trajectory-element Intersection ti JOIN TopologicalPartGroup tpg, Trajectory-element Intersection ti JOIN SimpleBehavior sb, TopologicalPartGroup tpg JOIN KeyPoint kp WHERE tst.tid = “T1” AND ti.startTime ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’ AND ti.endTime between ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’ AND sb.name = “internal turning-around”
SELECT pre.stid FROM Trajectory-element Intersection ti JOIN TopologicalSemanticTrajectory tst, Trajectory-element Intersection ti JOIN TopologicalPartGroup tpg, TopologicalPartGroup tpg JOIN preEs pre WHERE tst.tid = “T1” AND pre.eid = “null” AND pre.stid <> “null” UNION SELECT pte.stid FROM Trajectory-element Intersection ti JOIN TopologicalSemanticTrajectory tst, Trajectory-element Intersection ti JOIN TopologicalPartGroup tpg, TopologicalPartGroup tpg JOIN preEs pre WHERE tst.tid = “T1” AND pte.eid = “null” AND pte.stid <> “null”
SELECT tst.tid FROM Trajectory-element Intersection ti JOIN TopologicalSemanticTrajectory tst, Trajectory-element Intersection ti JOIN TopologicalPartGroup tpg, Trajectory-element Intersection ti JOIN SimpleBehavior sb, TopologicalPartGroup tpg JOIN VirtualEdge ve, VirtualEdge ve JOIN RoadNetworkElement rne WHERE ti.startTime ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’ AND ti.endTime between ‘2015-01-01 09:30:00’ and ‘2015-01-01 10:00:00’ AND rne.ename = “Xiang-Fu Road” AND sb.name = “driving-through”
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Chakraborty, D.; Parent, C.; Spaccapietra, S.; Aberer, K. Semantic trajectories: Mobility Data Computation and Annotation. ACM Trans. Intell. Syst. Technol. 2013, 4, 1–38. [Google Scholar] [CrossRef]
- Issa, H. Spatio-textual trajectories: Models and Applications. Ph.D. Thesis, University of Milan, Milan, Italy, 2017. [Google Scholar]
- Spaccapietra, S.; Parent, C.; Damiani, M.L.; de Macedo, J.A.; Porto, F.; Vangenot, C. A Conceptual View on Trajectories. Data Knowl. Eng. 2008, 65, 126–146. [Google Scholar] [CrossRef]
- Damiani, M.L.; Guting, R.H.; Valdés, F.; Issa, H. Moving Objects Beyond Raw and Semantic Trajectories. Int. Workshop Inf. Manag. Mob. Appl. 2013. [Google Scholar] [CrossRef]
- Schmid, F.; Richer, K.F.; Laube, P. Semantic Trajectory Compression. Int. Symp. Spat. Temporal Databases 2009, 5644, 411–416. [Google Scholar] [CrossRef]
- Li, X.; Lin, H. Indexing network-constrained trajectories for connectivity-based queries. Int. J. Geogr. Inf. Sci. 2006, 20, 303–328. [Google Scholar] [CrossRef]
- Macedo, J.; Vangenot, C.; Othman, W.; Pelekis, N.; Frentzos, E.; Kuijpers, B.; Ntoutsi, I.; Spaccapietra, S.; Theodoridis, Y. Trajectory Data Models. In Mobility Data Mining and Privacy; Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin, Germany, 2009; pp. 123–150. [Google Scholar]
- Khatri, V.; Ram, S.; Snodgrass, R.T. Augmenting a conceptual model with geospatiotemporal annotations. IEEE Trans. Knowl. Data Eng. 2004, 16, 1324–1338. [Google Scholar] [CrossRef]
- Tryfona, N.; Price, R.; Jensen, C.S. Conceptual Models for Spatio-temporal Applications. In Spatio-Temporal Databases; Springer: Berlin, Germany, 2003. [Google Scholar]
- Camossi, E.; Bertolotto, M.; Bertino, E.; Guerrini, G. A multigranular spatiotemporal data model. In Proceedings of the ACM International Symposium on Advances in Geographic Information Systems, New Orleans, LA, USA, 7–8 November 2003; pp. 94–101. [Google Scholar] [CrossRef]
- Pelekis, N.; Theodoridis, Y. An Oracle Data Cartridge for Moving Objects; CiteSeerX: University Park, PA, USA, 2007. [Google Scholar]
- Hajari, H.; Hakimpour, F. A Spatial Data Model for Moving Object Databases. Int. J. Database Manag. Syst. 2014, 6, 1–20. [Google Scholar] [CrossRef]
- Zheng, Y. Trajectory Data Mining. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Bogorny, V.; Renso, C.; de Aquino, A.R.; de Lucca Siqueira, F.; Alvares, L.O. CONSTAnT-A Conceptual Data Model for Semantic Trajectories of Moving Objects. Trans. GIS 2013, 18, 66–88. [Google Scholar] [CrossRef]
- Damiani, M.L.; Güting, R.H. Semantic Trajectories and Beyond. In Proceedings of the IEEE 15th International Conference on Mobile Data Management, Brisbane, Australia, 14–18 July 2014. [Google Scholar]
- Spaccapietra, S.; Parent, C. Adding Meaning to Your Steps. In Proceedings of the International Conference on Conceptual Modeling, Brussels, Belgium, 31 October–3 November 2011; Volume 6998, pp. 13–31. [Google Scholar] [CrossRef]
- Yan, Z. Semantic Trajectories: Computing and Understanding Mobility Data. Ph.D. Thesis, Verlag nicht ermittelbar. 2011. [Google Scholar]
- Parent, C.; Spaccapietra, S.; Renso, C.; Andrienko, G.; Andrienko, N.; Bogorny, V.; Damiani, M.L. Semantic Trajectories Modeling and Analysis. ACM Comput. Surv. 2013, 45, 1–37. [Google Scholar] [CrossRef]
- Renso, C.; Baglioni, M.; de Macedo, J.A.F.; Trasarti, R.; Wachowicz, M. How you move reveals who you are: Understanding human behavior by analyzing trajectory data. Knowl. Inf. Syst. 2012, 37, 331–362. [Google Scholar] [CrossRef]
- Güting, R.H.; Valdés, F.; Damiani, M.L. Symbolic Trajectories. ACM Trans. Spat. Algorithms Syst. 2015, 1, 1–58. [Google Scholar] [CrossRef]
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. The Effects of Navigation Sensors and Spatial Road Network Data Quality on the Performance of Map Matching Algorithms. Geoinformatica 2009, 13, 85–108. [Google Scholar] [CrossRef]
- Greenfeld, J. Matching GPS Observations to Locations on a Digital Map. In Proceedings of the Annual Meeting of the Transportation Research Board, Washington, DC, USA, 12–16 January 2002; pp. 164–173. [Google Scholar]
- Quddus, M.A. High Integrity Map Matching Algorithms for Advanced Transport Telematics Applications. Ph.D. Thesis, University of London, London, UK, 2006. [Google Scholar]
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. A High Accuracy Fuzzy Logic Based Map Matching Algorithm for Road Transport. J. Intell. Transp. Syst. 2007, 10, 103–115. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, C.; Zheng, Y.; Xie, X.; Wang, W.; Huang, Y. Map-Matching for Low-Sampling-Rate GPS Trajectories. In Proceedings of the ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2009; pp. 352–361. [Google Scholar] [CrossRef]
- Fileto, R.; Bogorny, V.; May, C.; Klein, D. Semantic Enrichment and Analysis of Movement Data: Probably it is just Starting! SIGSPATIAL Spec. 2015, 7, 11–18. [Google Scholar] [CrossRef]
- Wu, F.; Li, Z. Where did you go: Personalized annotation of mobility records. In Proceedings of the ACM 25th International on Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; pp. 589–598. [Google Scholar] [CrossRef]
- Xiang, L.; Wu, T.; Ettema, D. An intersection-based trajectory-region movement study. Trans. GIS 2016, 21, 701–721. [Google Scholar] [CrossRef]
- Tiesyte, D.; Jensen, C.S. Similarity-Based Prediction of Travel Times for Vehicles Traveling on Known Routes. In Proceedings of the ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008. [Google Scholar] [CrossRef]
- Richter, K.F.; Schmid, F.; Laube, P. Semantic trajectory compression: Representing urban movement in a nutshell. J. Spat. Inf. Sci. 2012, 4, 3–30. [Google Scholar] [CrossRef]
- Li, Z. Semantic Understanding of Spatial Trajectories. Adv. Spat. Temporal Databases 2017, 10411, 398–401. [Google Scholar] [CrossRef]
- Spinsanti, L.; Celli, F.; Renso, C. Where You Stop is Who You are: Understanding People’s Activities by Places Visited. Behav. Monit. Interpret. 2010, 678. [Google Scholar]
- Schussler, N.; Axhausen, K.W. Processing Raw Data from Global Positioning Systems without Additional Information. Transp. Res. Rec. J. Transp. Res. Board 2009, 2105, 28–36. [Google Scholar] [CrossRef]
- Kuijpers, B.; Othman, W. Trajectory databases: Data models, uncertainty and complete query languages. J. Comput. Syst. Sci. 2010, 76, 538–560. [Google Scholar] [CrossRef]
- Pelekis, N.; Kopanakis, I.; Kotsifakos, E.E.; Frentzos, E.; Theodoridis, Y. Clustering uncertain trajectories. Knowl. Inf. Syst. 2011, 28, 117–147. [Google Scholar] [CrossRef]
- Openstreetmap. 2015. Available online: http://www.openstreetmap.org (accessed on 1 January 2015).
- Wu, T.; Xiang, L.; Gong, J. Updating Road Networks by Local Renewal from GPS Trajectories. ISPRS Int. J. Geo-Inf. 2016, 5, 163. [Google Scholar] [CrossRef]
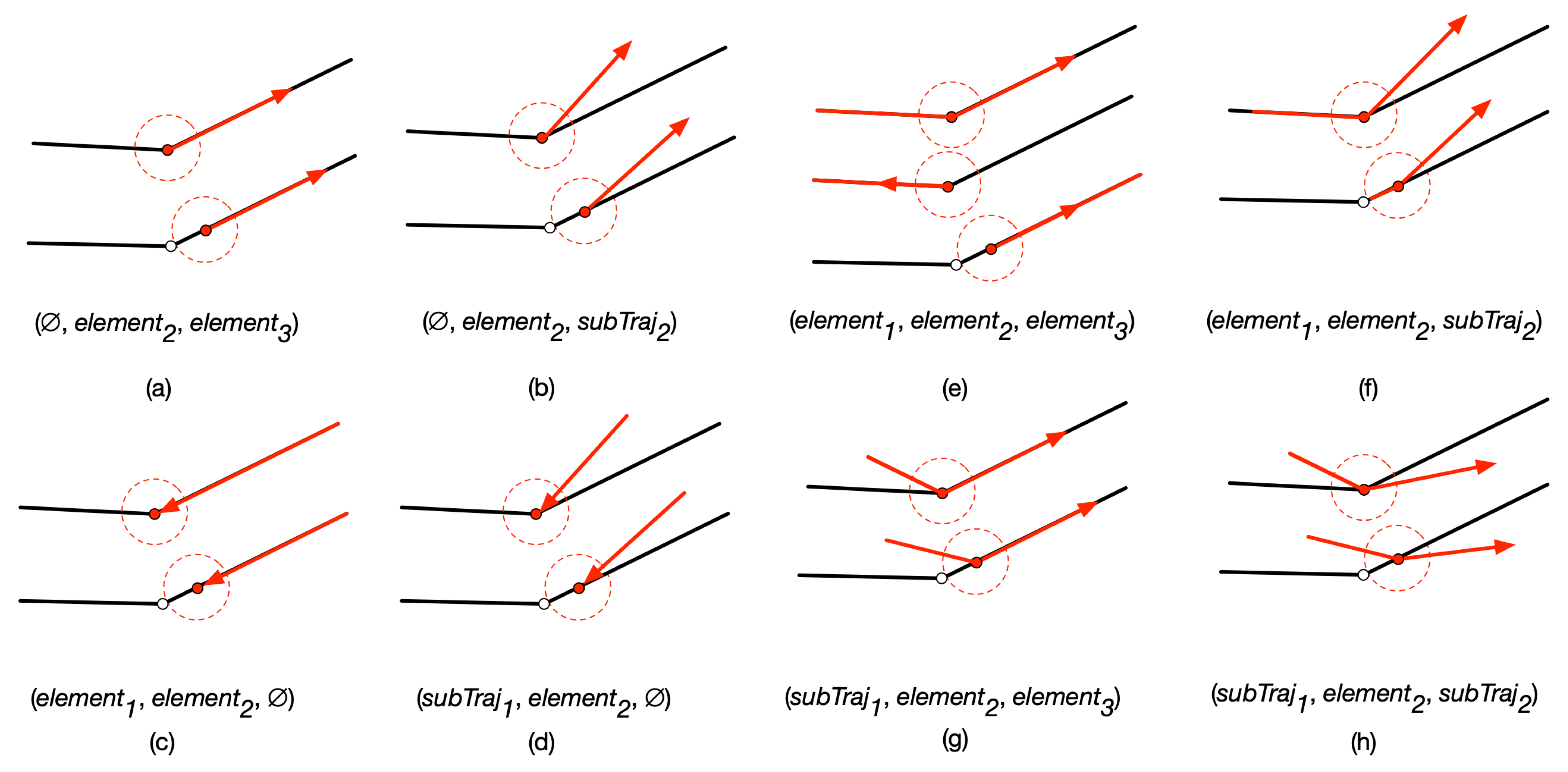
| Pattern | Tuple initiation | Situation |
|---|---|---|
| start from a node and enter into an edge | ||
| start from an edge and move along it | ||
| start from a node and go off roads | ||
| start from an edge and go off roads | ||
| move along an edge and end at the next node | ||
| move along an edge and end at it | ||
| move into a node from outside of network and end at it | ||
| move into an edge from outside of network and end at it | ||
| move into the from by a node | ||
| move along an edge and turn back after reaching a node | ||
| move along an edge and turn back at a position inside the edge | ||
| move along an edge and leave road network space at a node | ||
| move along an edge and leave road network space at position inside the edge | ||
| move into an edge from outside of network at a node and move along the edge | ||
| move into an edge from outside of network at a position inside the edge and move along it | ||
| pass a node without entering other elements | ||
| pass a position inside an edge without entering other elements |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Qin, J.; Wan, Y. TOST: A Topological Semantic Model for GPS Trajectories Inside Road Networks. ISPRS Int. J. Geo-Inf. 2019, 8, 410. https://doi.org/10.3390/ijgi8090410
Wu T, Qin J, Wan Y. TOST: A Topological Semantic Model for GPS Trajectories Inside Road Networks. ISPRS International Journal of Geo-Information. 2019; 8(9):410. https://doi.org/10.3390/ijgi8090410
Chicago/Turabian StyleWu, Tao, Jianxin Qin, and Yiliang Wan. 2019. "TOST: A Topological Semantic Model for GPS Trajectories Inside Road Networks" ISPRS International Journal of Geo-Information 8, no. 9: 410. https://doi.org/10.3390/ijgi8090410
APA StyleWu, T., Qin, J., & Wan, Y. (2019). TOST: A Topological Semantic Model for GPS Trajectories Inside Road Networks. ISPRS International Journal of Geo-Information, 8(9), 410. https://doi.org/10.3390/ijgi8090410





