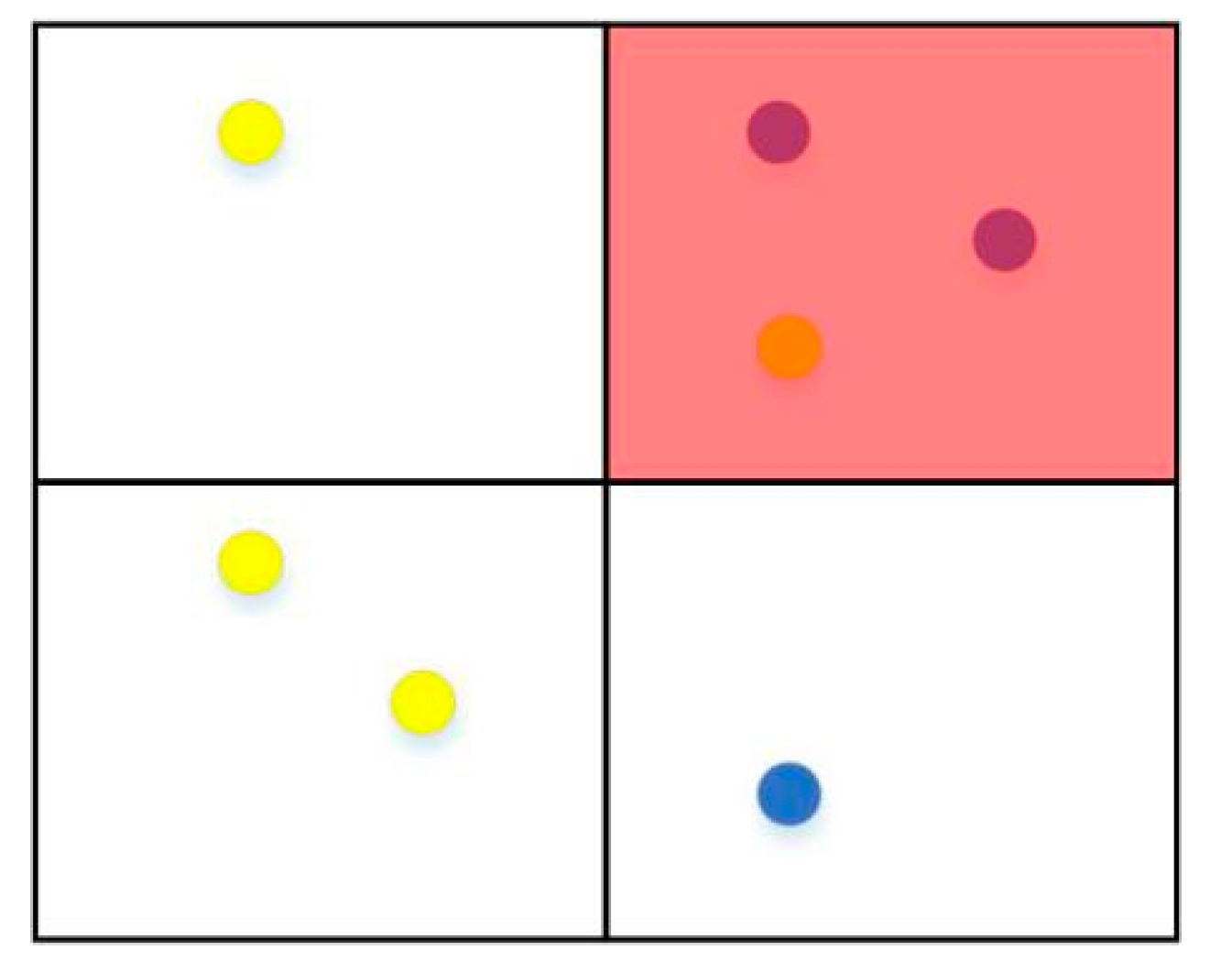
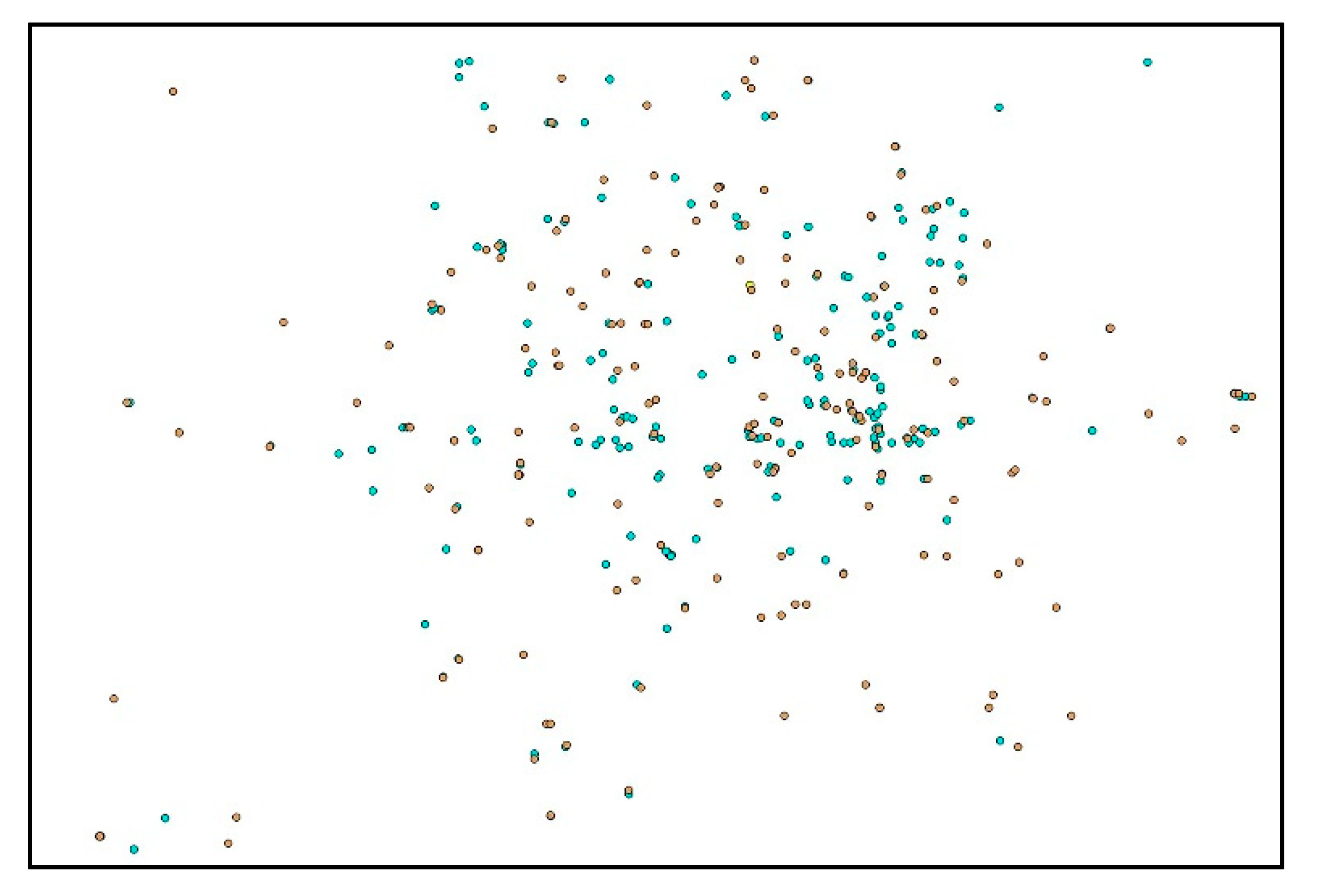
Figure 1.
The blue points represent the buildings with type label “school” and the yellow points indicate the buildings with type label “residential buildings”. As a result, the red region is returned as the result of our top-1 query by matching the environmental information of each candidate Region-Of-Interest (ROI) for the query.
Figure 1.
The blue points represent the buildings with type label “school” and the yellow points indicate the buildings with type label “residential buildings”. As a result, the red region is returned as the result of our top-1 query by matching the environmental information of each candidate Region-Of-Interest (ROI) for the query.
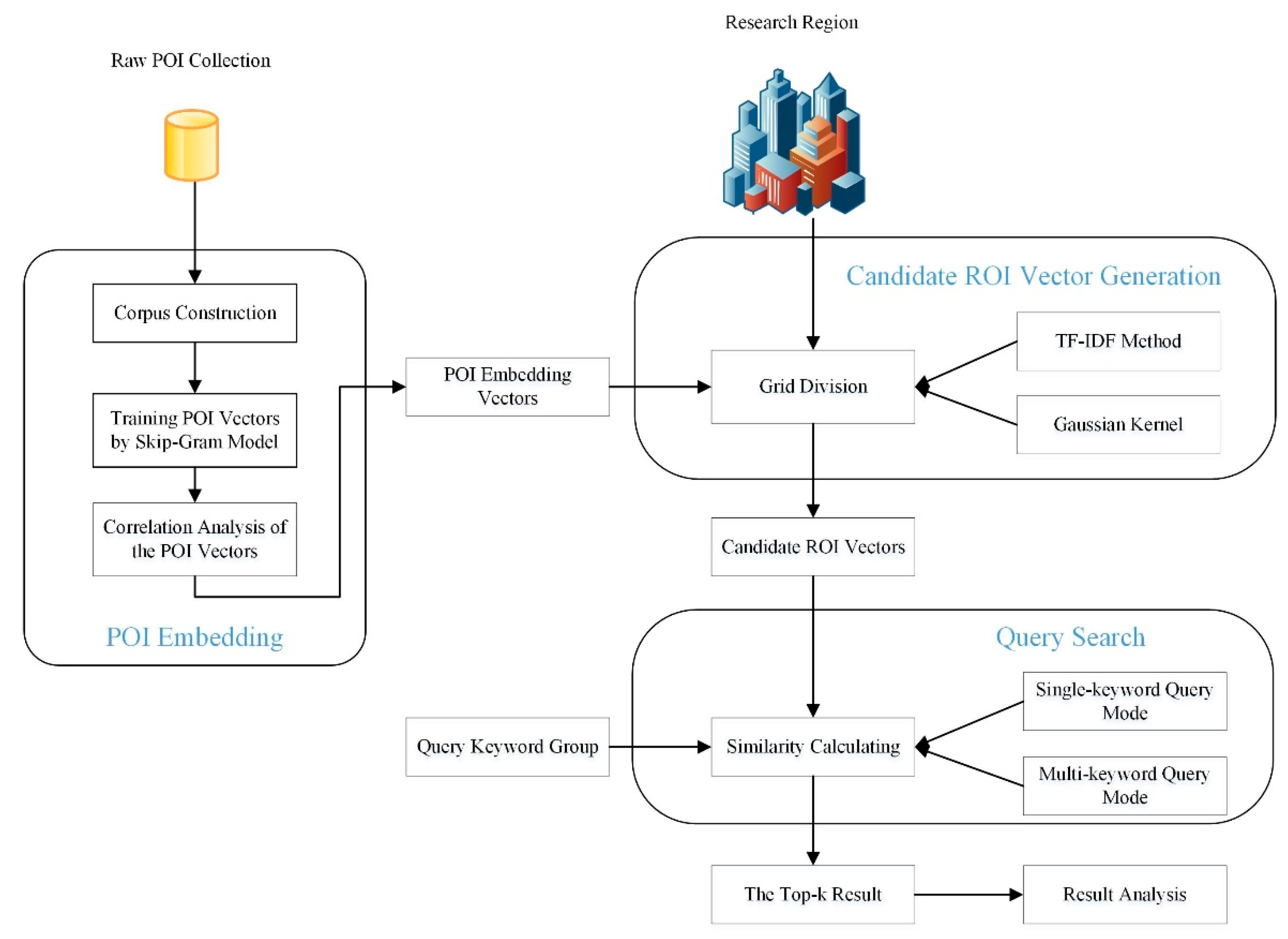
Figure 2.
Workflow of the spatial keyword query of the ROI with the distributed representation of Point-Of-Interest (POI)s. TF-IDF, term frequency-inverse document frequency.
Figure 2.
Workflow of the spatial keyword query of the ROI with the distributed representation of Point-Of-Interest (POI)s. TF-IDF, term frequency-inverse document frequency.
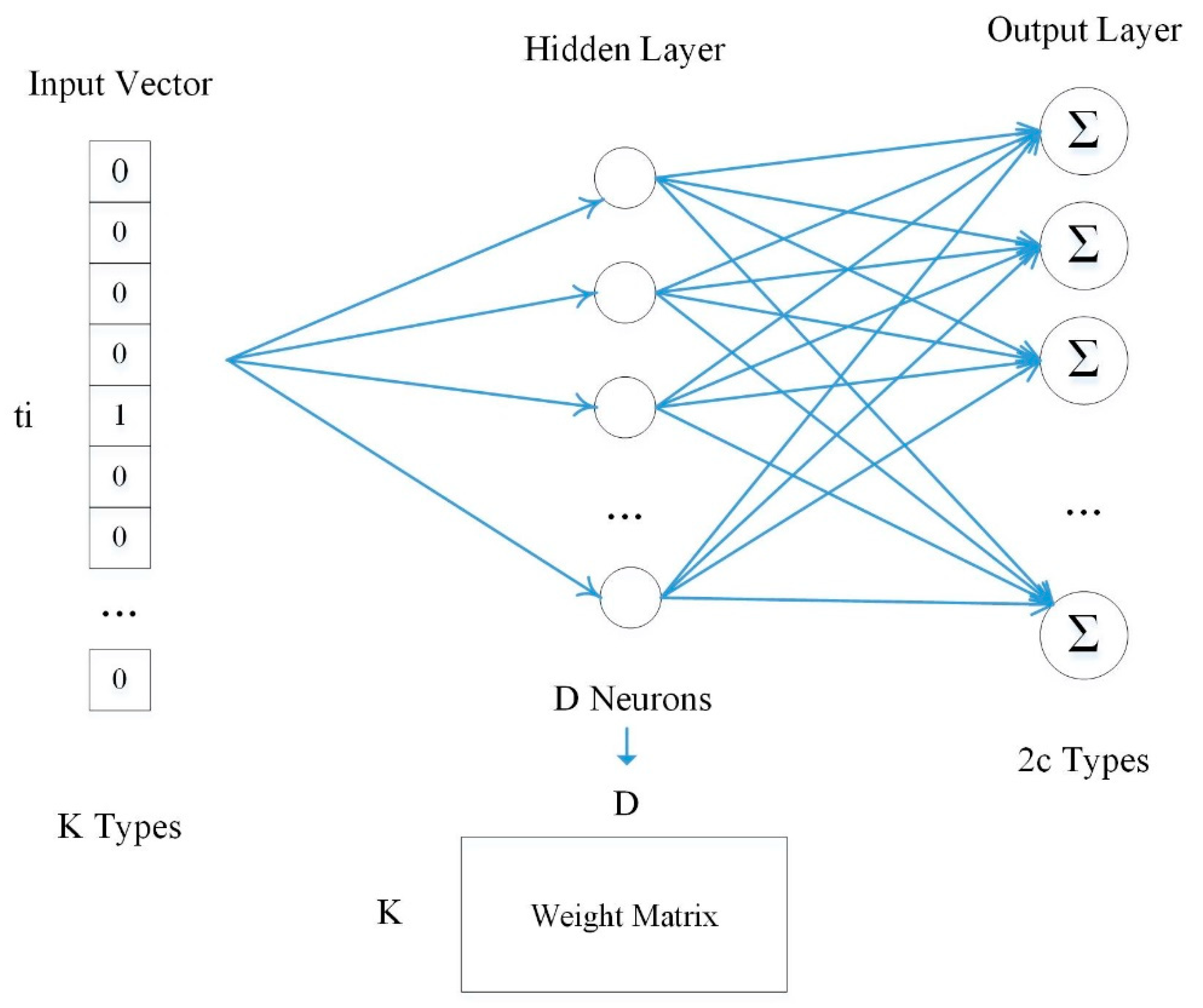
Figure 3.
The Skip-Gram model. In the output layer, the input vector is the one-hot form where “1” represents the occupied position of the input type in the K types. In the hidden layer, D linear neurons are adopted and the D×K weight matrix of the neurons is the POI vector matrix. In the output layer, each output neuron uses a softmax classifier to predict the conditional probability of its context POI types, and the target is to minimize the loss.
Figure 3.
The Skip-Gram model. In the output layer, the input vector is the one-hot form where “1” represents the occupied position of the input type in the K types. In the hidden layer, D linear neurons are adopted and the D×K weight matrix of the neurons is the POI vector matrix. In the output layer, each output neuron uses a softmax classifier to predict the conditional probability of its context POI types, and the target is to minimize the loss.
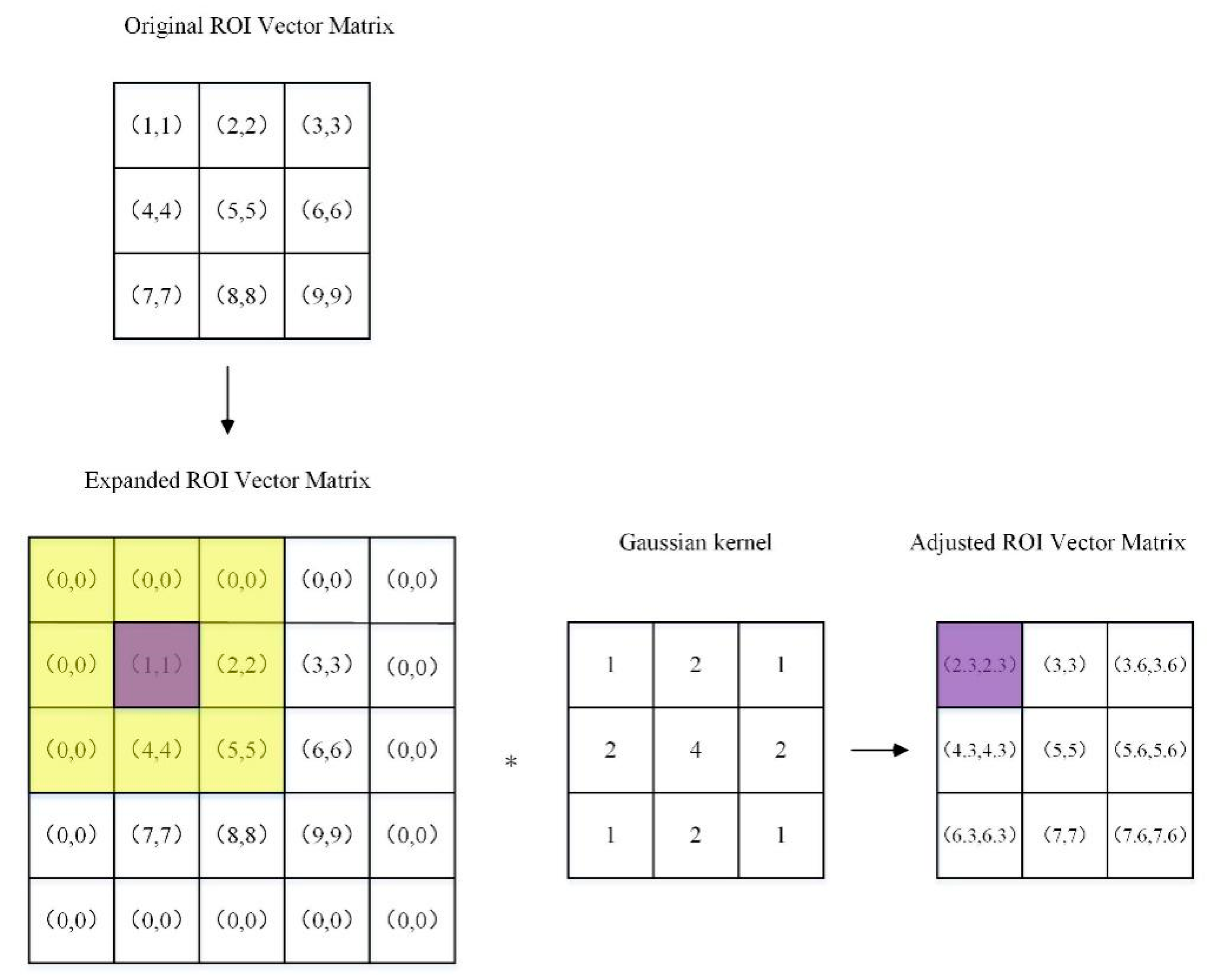
Figure 4.
Gaussian kernel computing. The figure reveals that the first step of computing is to expand the original ROI vector matrix R(a,b) to the size of R(a+2, b+2), where the extended part is filled by the 0 vector. Meanwhile, with the convolution kernel weight corresponding to the 0 vector region set as zeros, the ROI vector in the edge of the original matrix can also be computed.
Figure 4.
Gaussian kernel computing. The figure reveals that the first step of computing is to expand the original ROI vector matrix R(a,b) to the size of R(a+2, b+2), where the extended part is filled by the 0 vector. Meanwhile, with the convolution kernel weight corresponding to the 0 vector region set as zeros, the ROI vector in the edge of the original matrix can also be computed.
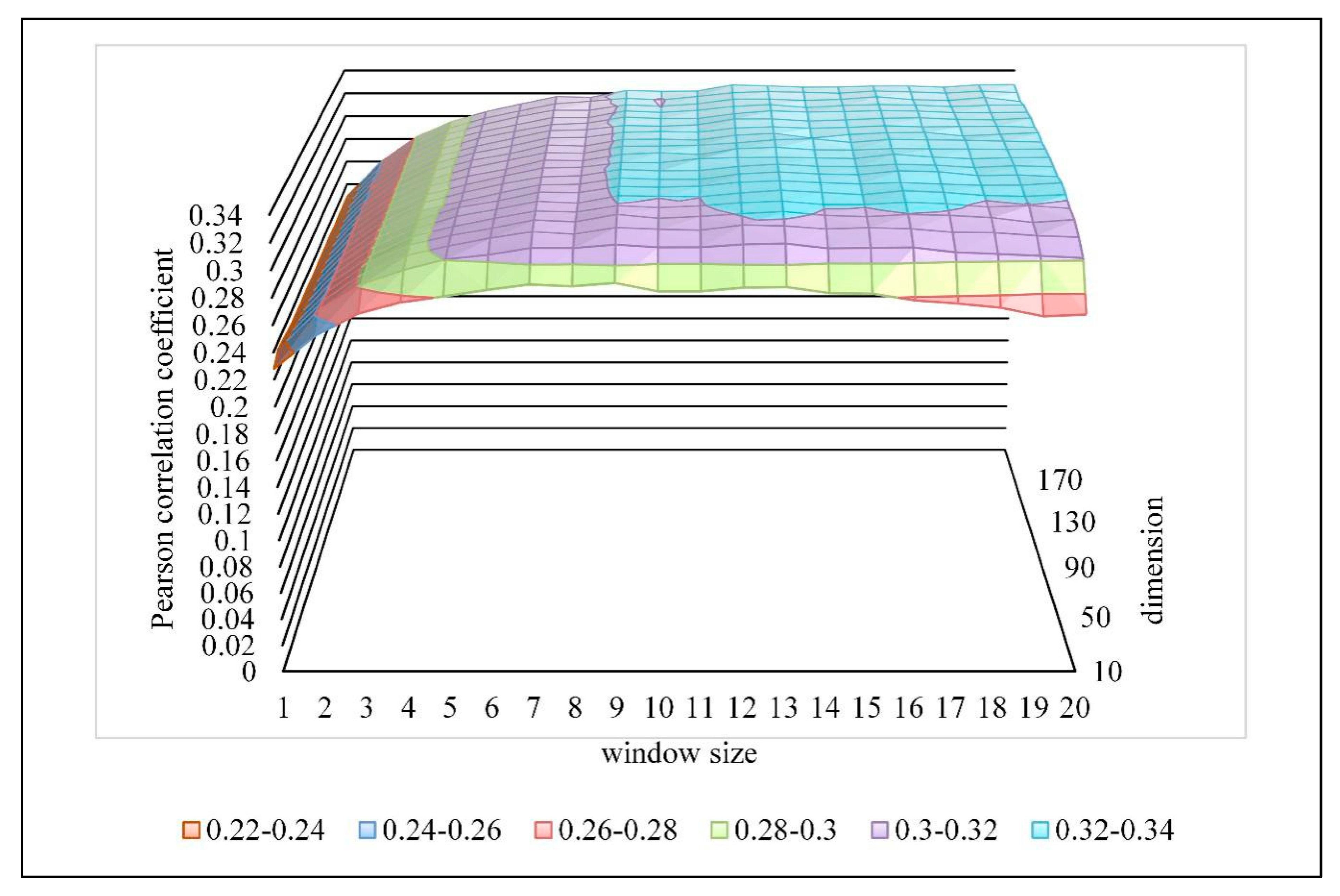
Figure 5.
Parameter selection of the distributed representation of POIs. The X-axis is the window size, the Y-axis is the dimension, and the z-axis is the Pearson correlation coefficient corresponding to the first two. The different colors indicate the magnitude of the Pearson correlation coefficient.
Figure 5.
Parameter selection of the distributed representation of POIs. The X-axis is the window size, the Y-axis is the dimension, and the z-axis is the Pearson correlation coefficient corresponding to the first two. The different colors indicate the magnitude of the Pearson correlation coefficient.
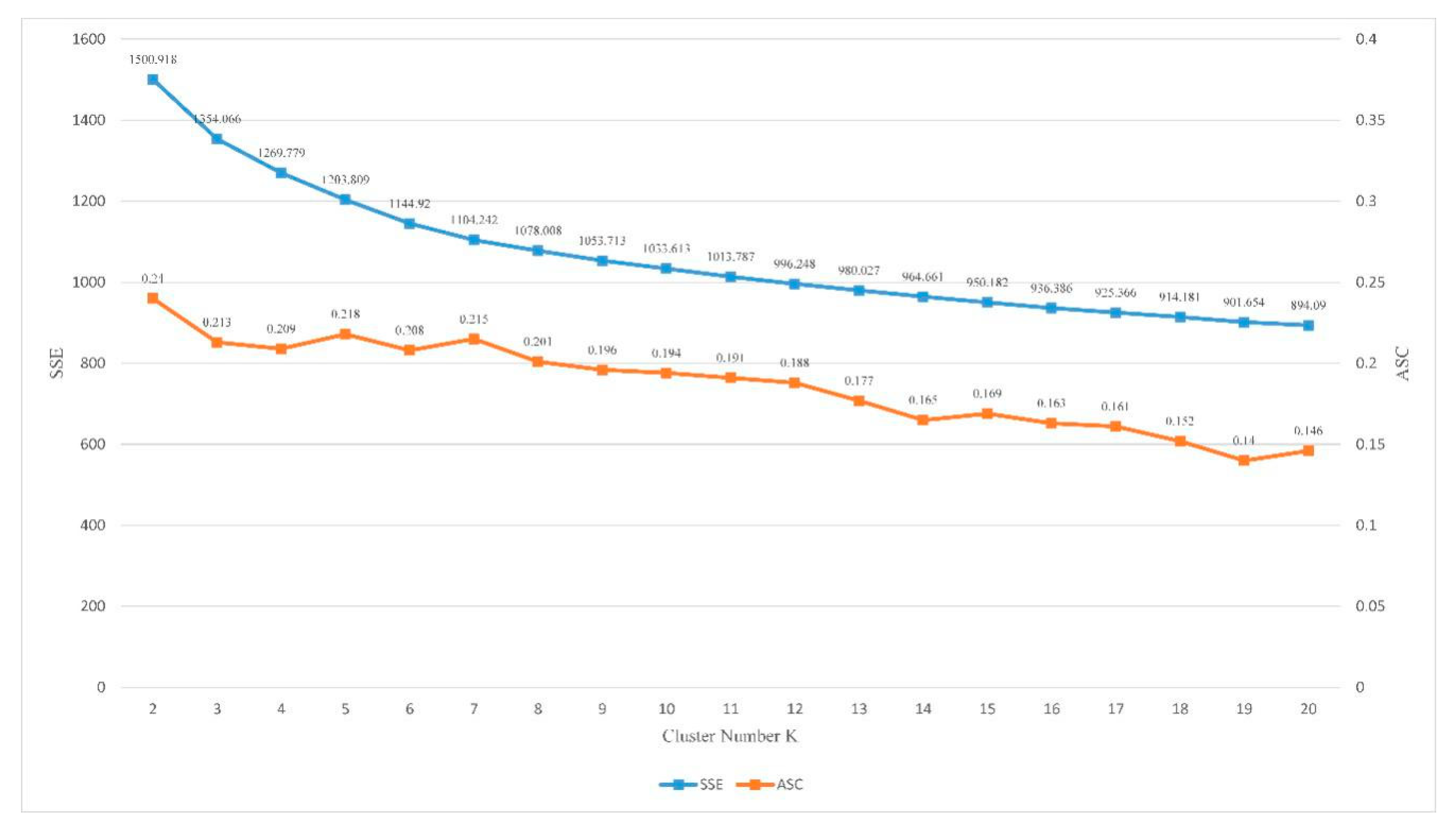
Figure 6.
Change of average silhouette value (left y-axis) and error square sum (right y-axis) of clustering results (POI vectors) with increases of K value (x-axis).
Figure 6.
Change of average silhouette value (left y-axis) and error square sum (right y-axis) of clustering results (POI vectors) with increases of K value (x-axis).
Figure 7.
Research region. Yellow lines in the figure denote the main road data of Beijing and the small black dots indicate the POIs of Beijing.
Figure 7.
Research region. Yellow lines in the figure denote the main road data of Beijing and the small black dots indicate the POIs of Beijing.
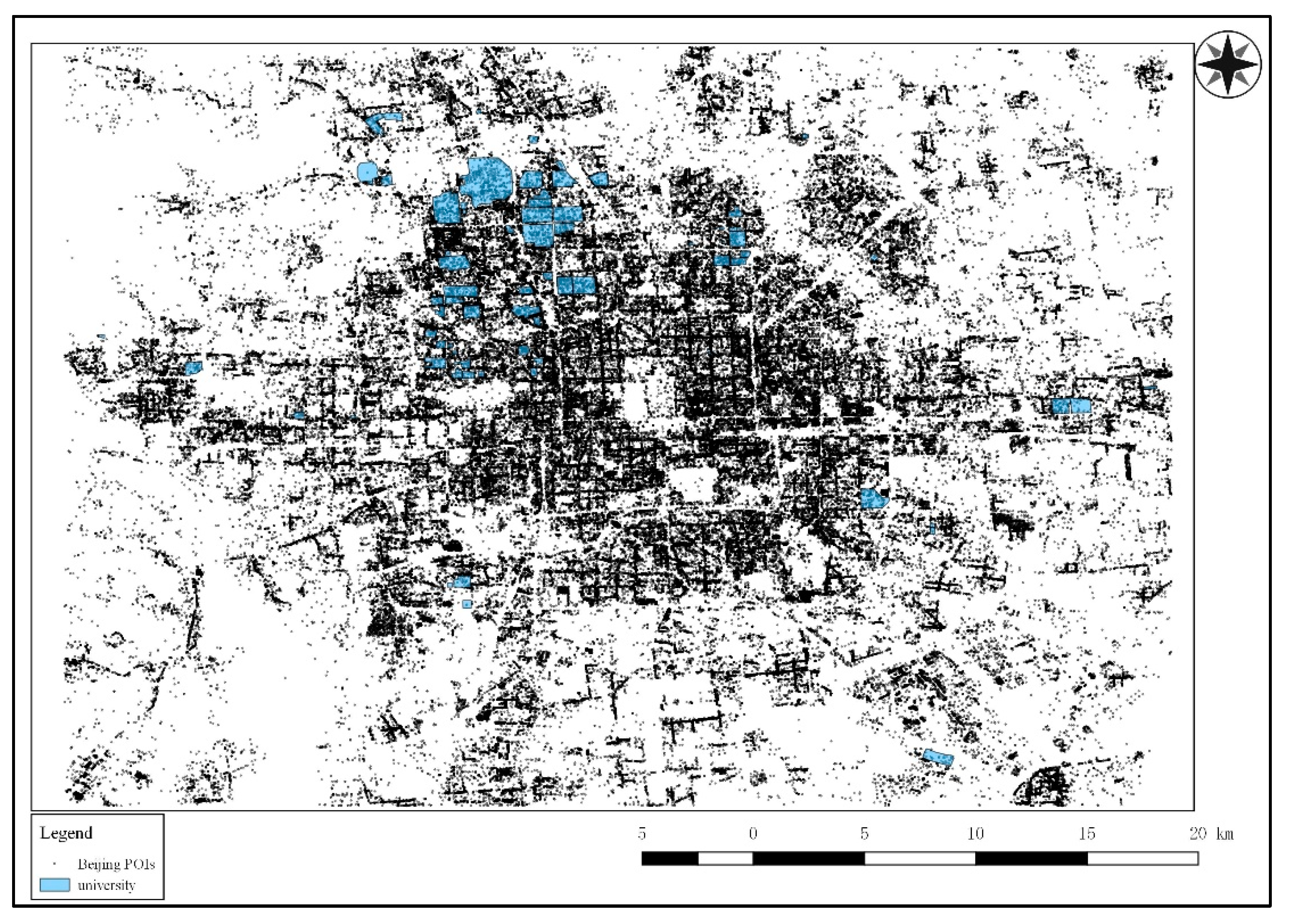
Figure 8.
ROI validation set. The figure shows the distribution of the ROIs labeled “university”, represented by the blue regions in the research region. These were utilized to verify the effectiveness of the keyword query for the ROI of the corresponding label.
Figure 8.
ROI validation set. The figure shows the distribution of the ROIs labeled “university”, represented by the blue regions in the research region. These were utilized to verify the effectiveness of the keyword query for the ROI of the corresponding label.
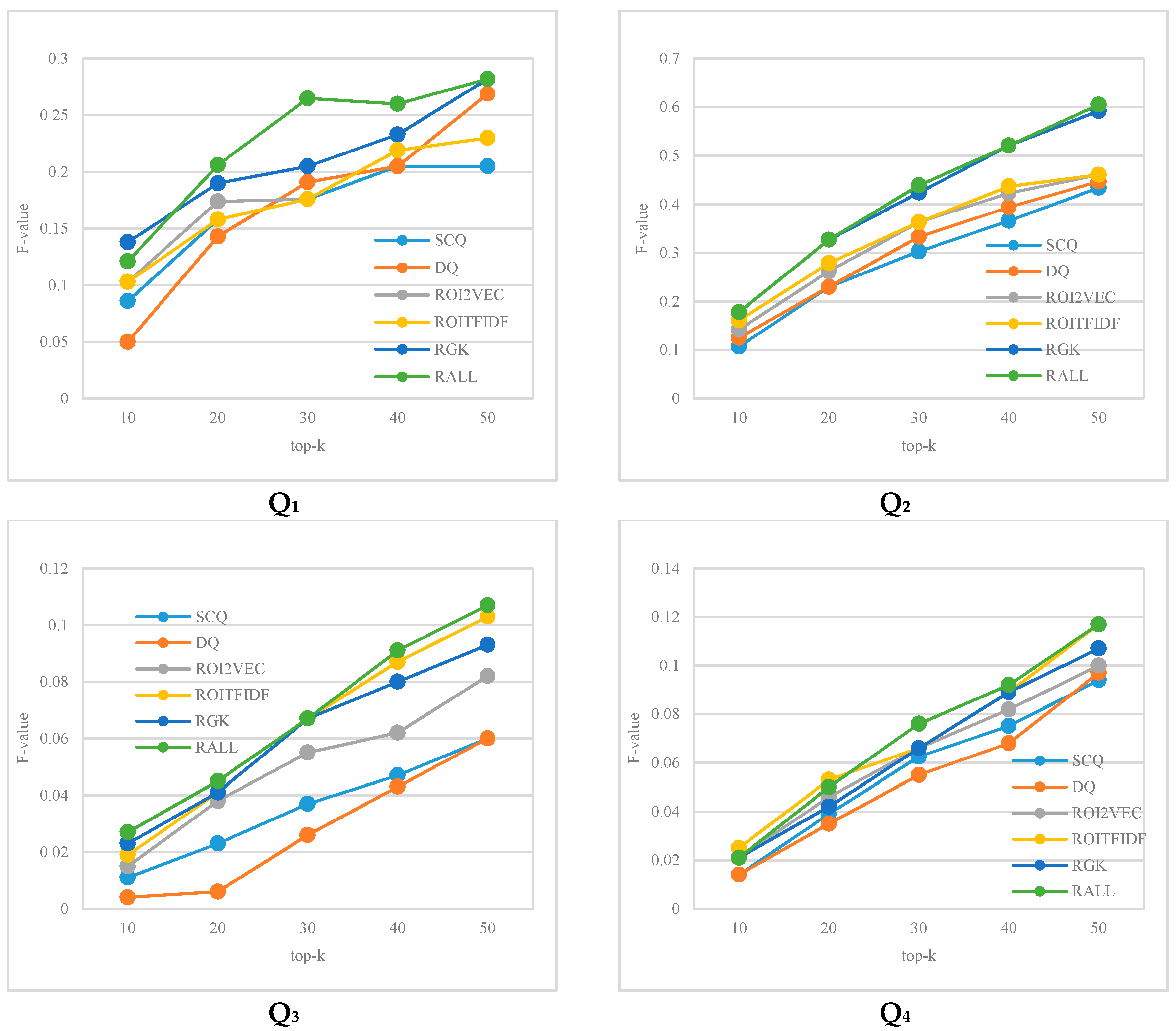
Figure 9.
The performance comparison of the methods in Q1~Q4, which shows the change of the F-values (y-axis) of the query results with increases in the K value of the top-K query (x-axis).
Figure 9.
The performance comparison of the methods in Q1~Q4, which shows the change of the F-values (y-axis) of the query results with increases in the K value of the top-K query (x-axis).
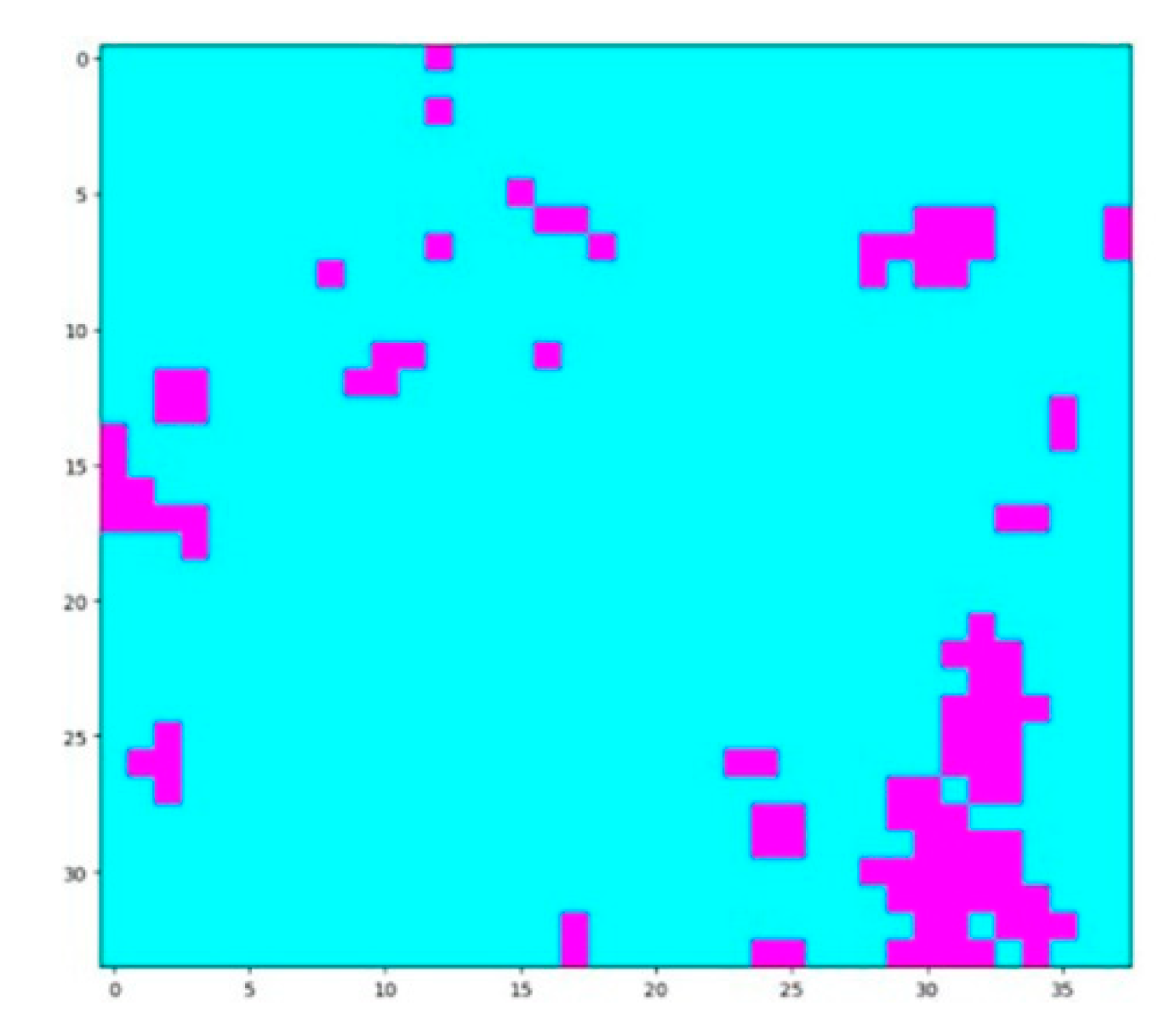
Figure 10.
Original ROI rasterization. The labeled ROI occupied 106 grids in total in the research region (38 × 34 grids). The purple grids indicate the labelled regions.
Figure 10.
Original ROI rasterization. The labeled ROI occupied 106 grids in total in the research region (38 × 34 grids). The purple grids indicate the labelled regions.
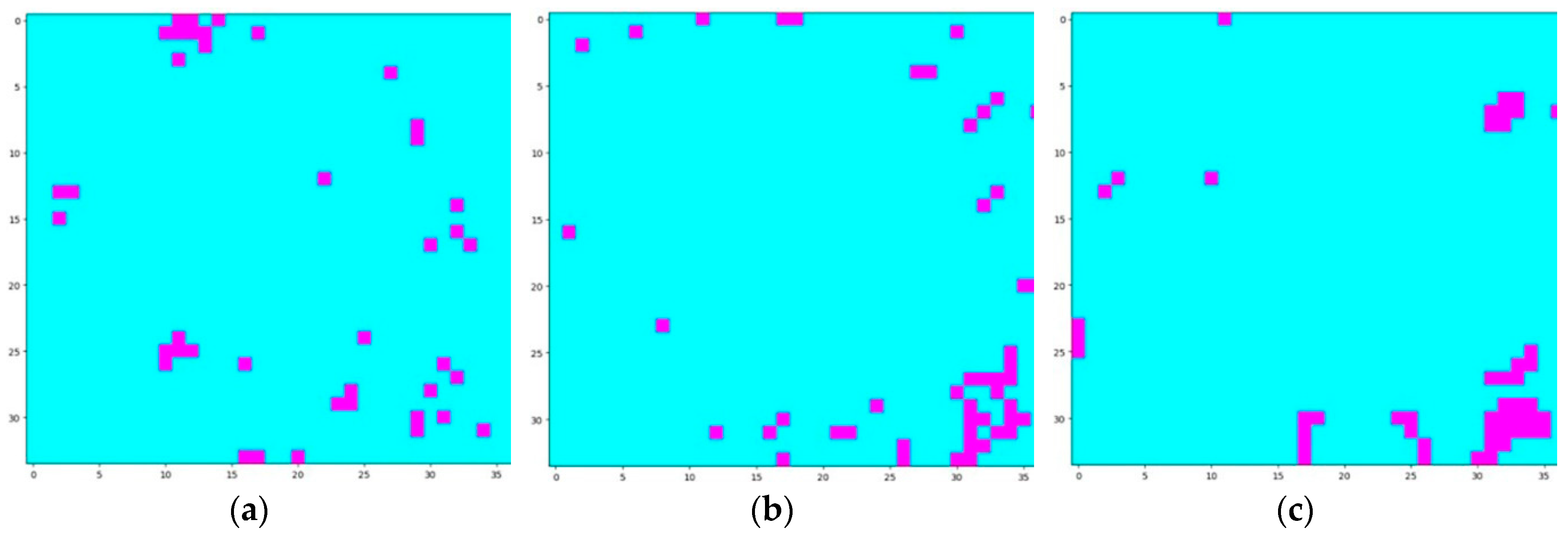
Figure 11.
(a) Simple count query (SCQ) result of the top-50 ROI queries. (b) ROI vector (ROI2VEC) result of the top-50 ROI queries. (c) ROI2VEC + TF-IDF + Gaussian kernel (RALL) result of the top-50 ROI queries.
Figure 11.
(a) Simple count query (SCQ) result of the top-50 ROI queries. (b) ROI vector (ROI2VEC) result of the top-50 ROI queries. (c) ROI2VEC + TF-IDF + Gaussian kernel (RALL) result of the top-50 ROI queries.
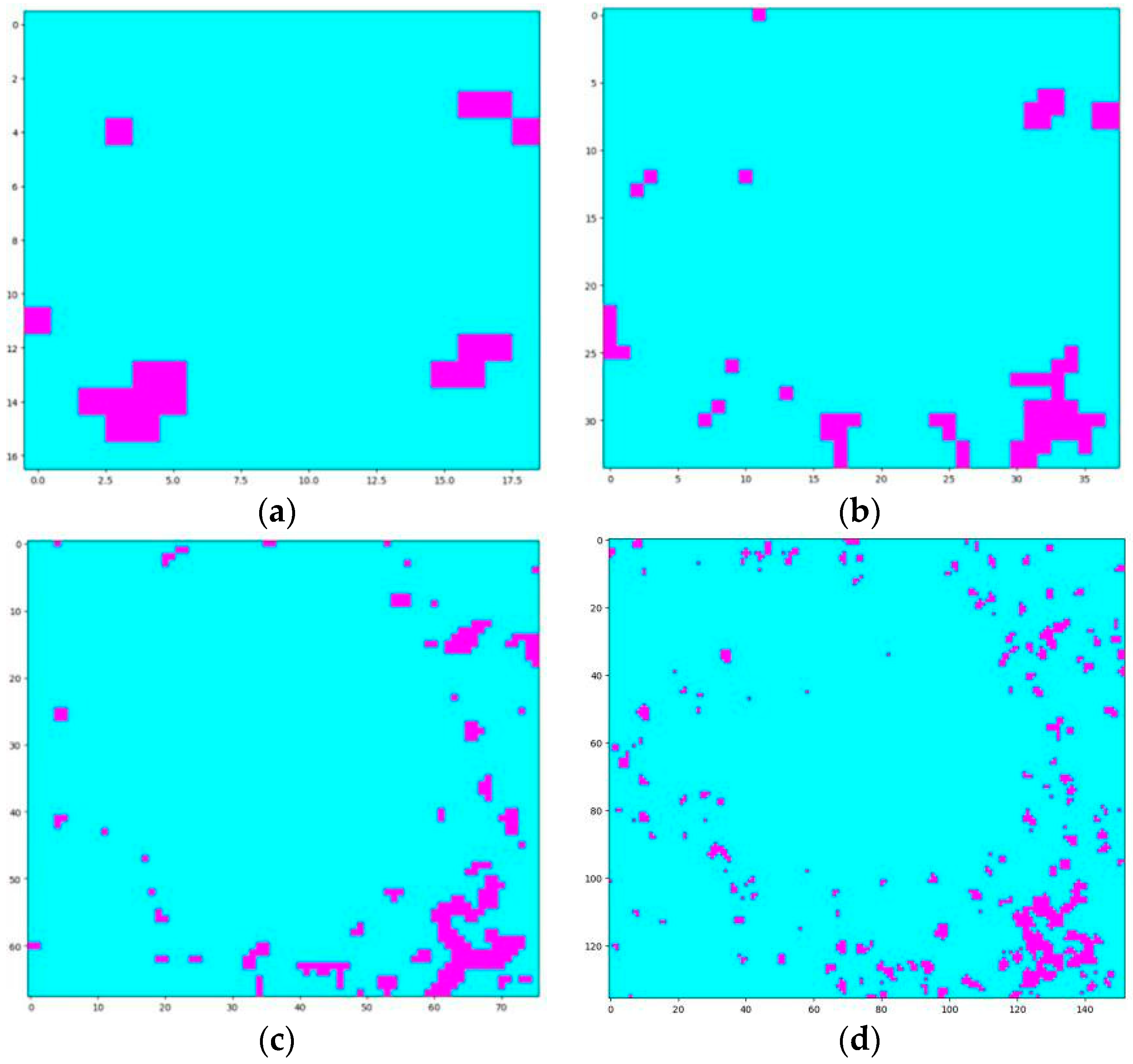
Figure 12.
Q1 query results by RALL for the different sizes of the grids. (a) The 4 km2 size of the grid. (b) The 1 km2 size of the grid. (c) The 0.25 km2 size of the grid. (d) The 0.0625 km2 size of the grid. With the same query area ratio set for different tasks, the corresponding F-values were: (a) 0.141, (b) 0.339, (c) 0.297, and (d) 0.215.
Figure 12.
Q1 query results by RALL for the different sizes of the grids. (a) The 4 km2 size of the grid. (b) The 1 km2 size of the grid. (c) The 0.25 km2 size of the grid. (d) The 0.0625 km2 size of the grid. With the same query area ratio set for different tasks, the corresponding F-values were: (a) 0.141, (b) 0.339, (c) 0.297, and (d) 0.215.
Figure 13.
In our research region, the blue POIs represent Starbucks while the yellow POIs represent the cinema. This figure shows their spatial distribution characteristics.
Figure 13.
In our research region, the blue POIs represent Starbucks while the yellow POIs represent the cinema. This figure shows their spatial distribution characteristics.
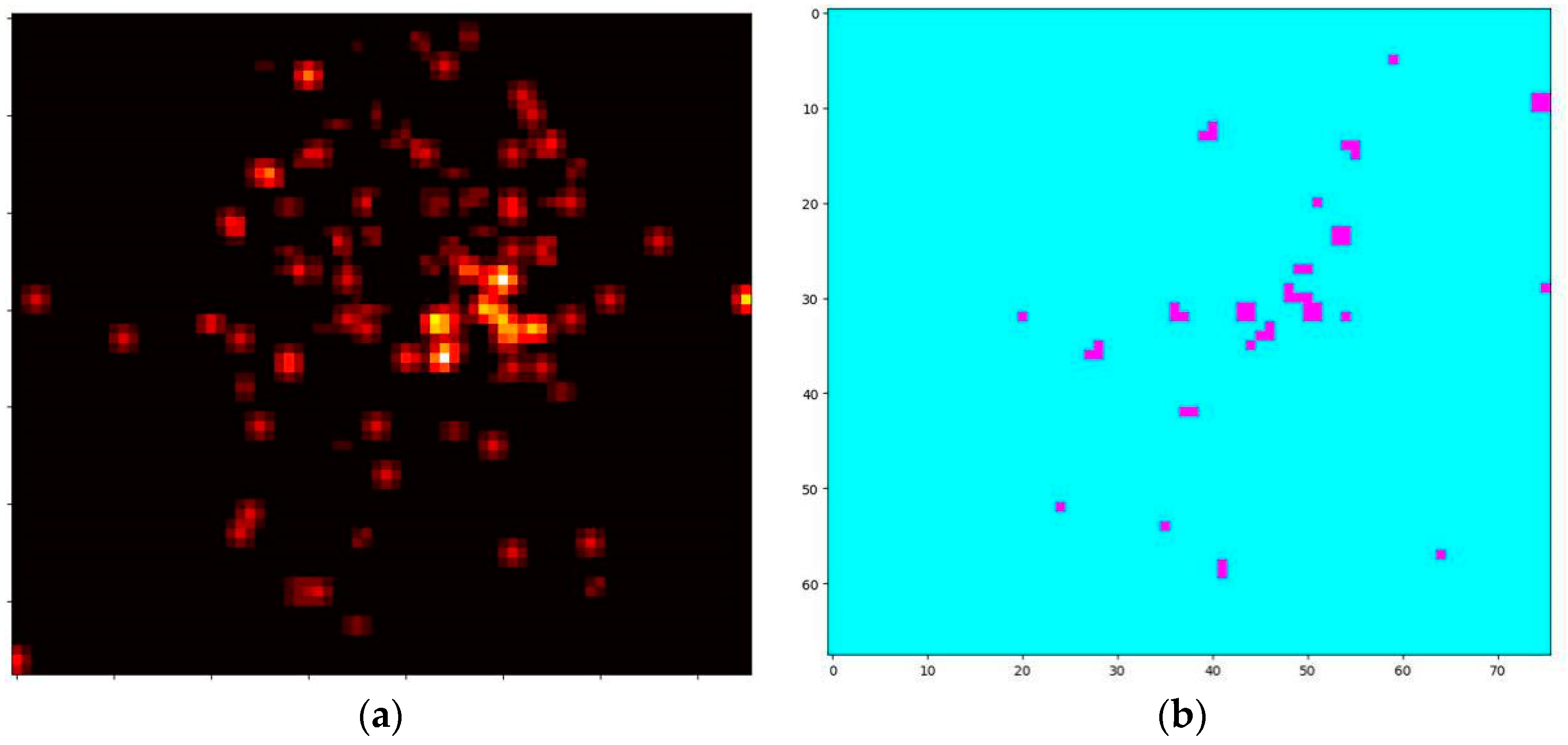
Figure 14.
(a) The heat map of the POIs. It intends to reflect a combined relevance of the POIs of the type of Starbucks and cinema. Brighter grids denote a higher value of their combined relevance, i.e. both are densely distributed in this ROI, while the dark ones are the opposite. It is worth noting that the grids populated by only one type of POI do not show a very high correlation. (b) The top-50 query results by RALL. The top-50 query results are basically consistent with the brighter grids in (a), reflecting that our method can achieve good performance in the task of multi-keyword queries.
Figure 14.
(a) The heat map of the POIs. It intends to reflect a combined relevance of the POIs of the type of Starbucks and cinema. Brighter grids denote a higher value of their combined relevance, i.e. both are densely distributed in this ROI, while the dark ones are the opposite. It is worth noting that the grids populated by only one type of POI do not show a very high correlation. (b) The top-50 query results by RALL. The top-50 query results are basically consistent with the brighter grids in (a), reflecting that our method can achieve good performance in the task of multi-keyword queries.
Table 1.
Example of raw dataset P.
Table 1.
Example of raw dataset P.
| ID | Location | Type Label | Other Attributes |
|---|
| 1 | (116.30, 40.41) | library | … |
| 2 | (116.43, 39.95) | newsstand | … |
| 3 | (116.46, 39.96) | Starbucks | … |
| 4 | (116.41, 39.98) | clinic | … |
Table 2.
Symbols list.
| Symbol | Meaning |
|---|
| P | a collection of POI |
| pi | i-th POI |
| ti | i-th type label |
| Q | a keyword query group |
| qi | i-th keyword in query |
| R | an ROI |
Table 3.
Type and count of top-level POI categories.
Table 3.
Type and count of top-level POI categories.
| Top-level Type | ID | Count | Top-level Type | ID | Count |
|---|
| Shopping Service | 1 | 76,038 | Financial Insurance Service | 11 | 11,503 |
| Life Service | 2 | 57,178 | Car Service | 12 | 10,866 |
| Transportation Facility | 3 | 37,404 | Accommodation Service | 13 | 7487 |
| Catering Services | 4 | 36,001 | Public Facility | 14 | 5376 |
| Government Agency | 5 | 30,484 | Car Maintenance Station | 15 | 2196 |
| Science and Education Service | 6 | 26,726 | Road Auxiliary Facilities | 16 | 2189 |
| Company | 7 | 21,011 | Famous Tourist Sites | 17 | 2090 |
| Residence | 8 | 19,137 | Car Sales | 18 | 649 |
| Healthcare Service | 9 | 16,893 | Motorcycle Service | 19 | 352 |
| Sports and Leisure Service | 10 | 16,210 | | | |
Table 4.
Clustering results. A higher percentage value means that the cluster has a higher proportion in top-level types, that is, it is more similar to this type. The numbers denote the type IDs of the top-level types, for example, “1” represents the “Shopping Service”.
Table 4.
Clustering results. A higher percentage value means that the cluster has a higher proportion in top-level types, that is, it is more similar to this type. The numbers denote the type IDs of the top-level types, for example, “1” represents the “Shopping Service”.
| K | Cluster | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|
| 5 | C1 | 0.0% | 2.1% | 1.1% | 0.0% | 3.2% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 2.1% | 10.5% | 0.0% | 0.0% | 36.8% | 3.2% | 0.0% | 41.1% | 0.0% |
| C2 | 7.1% | 7.1% | 4.0% | 9.1% | 6.1% | 5.1% | 5.1% | 2.0% | 1.0% | 4.0% | 47.5% | 0.0% | 2.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| C3 | 0.0% | 6.8% | 6.8% | 0.0% | 0.0% | 8.5% | 11.9% | 3.4% | 0.0% | 39.0% | 0.0% | 0.0% | 1.7% | 0.0% | 0.0% | 0.0% | 22.0% | 0.0% | 0.0% |
| C4 | 39.5% | 2.3% | 15.1% | 31.4% | 0.0% | 1.2% | 0.0% | 0.0% | 0.0% | 2.3% | 2.3% | 0.0% | 0.0% | 5.8% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| C5 | 14.3% | 13.2% | 2.7% | 10.4% | 14.3% | 8.2% | 3.8% | 2.2% | 10.4% | 6.0% | 4.9% | 2.7% | 2.7% | 1.1% | 0.0% | 0.5% | 0.5% | 0.5% | 1.1% |
| 7 | C1 | 0.0% | 0.0% | 0.0% | 0.0% | 2.3% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 2.3% | 11.4% | 0.0% | 0.0% | 39.8% | 0.0% | 0.0% | 44.3% | 0.0% |
| C2 | 5.0% | 5.0% | 5.0% | 7.5% | 3.7% | 1.3% | 6.2% | 2.5% | 1.3% | 3.7% | 56.2% | 0.0% | 2.5% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| C3 | 0.0% | 9.3% | 9.3% | 0.0% | 1.9% | 3.7% | 14.8% | 1.9% | 0.0% | 29.6% | 0.0% | 1.9% | 1.9% | 0.0% | 0.0% | 5.6% | 20.4% | 0.0% | 0.0% |
| C4 | 49.3% | 1.4% | 0.0% | 39.1% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 5.8% | 0.0% | 0.0% | 0.0% | 4.3% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| C5 | 22.3% | 18.2% | 1.7% | 17.4% | 0.8% | 2.5% | 4.1% | 0.8% | 7.4% | 6.6% | 9.1% | 2.5% | 3.3% | 0.8% | 0.0% | 0.0% | 0.8% | 0.0% | 1.7% |
| C6 | 9.1% | 9.1% | 59.1% | 4.5% | 0.0% | 4.5% | 0.0% | 0.0% | 0.0% | 0.0% | 4.5% | 0.0% | 0.0% | 9.1% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| C7 | 0.0% | 5.7% | 3.4% | 0.0% | 32.2% | 21.8% | 1.1% | 4.6% | 11.5% | 10.3% | 1.1% | 1.1% | 1.1% | 1.1% | 0.0% | 1.1% | 2.3% | 1.1% | 0.0% |