Top-Bounded Spaces Formed by the Built Environment for Navigation Systems
Abstract
1. Introduction
2. Related Work
3. Top-Bounded Spaces Formed by Built Structures
3.1. Definitions
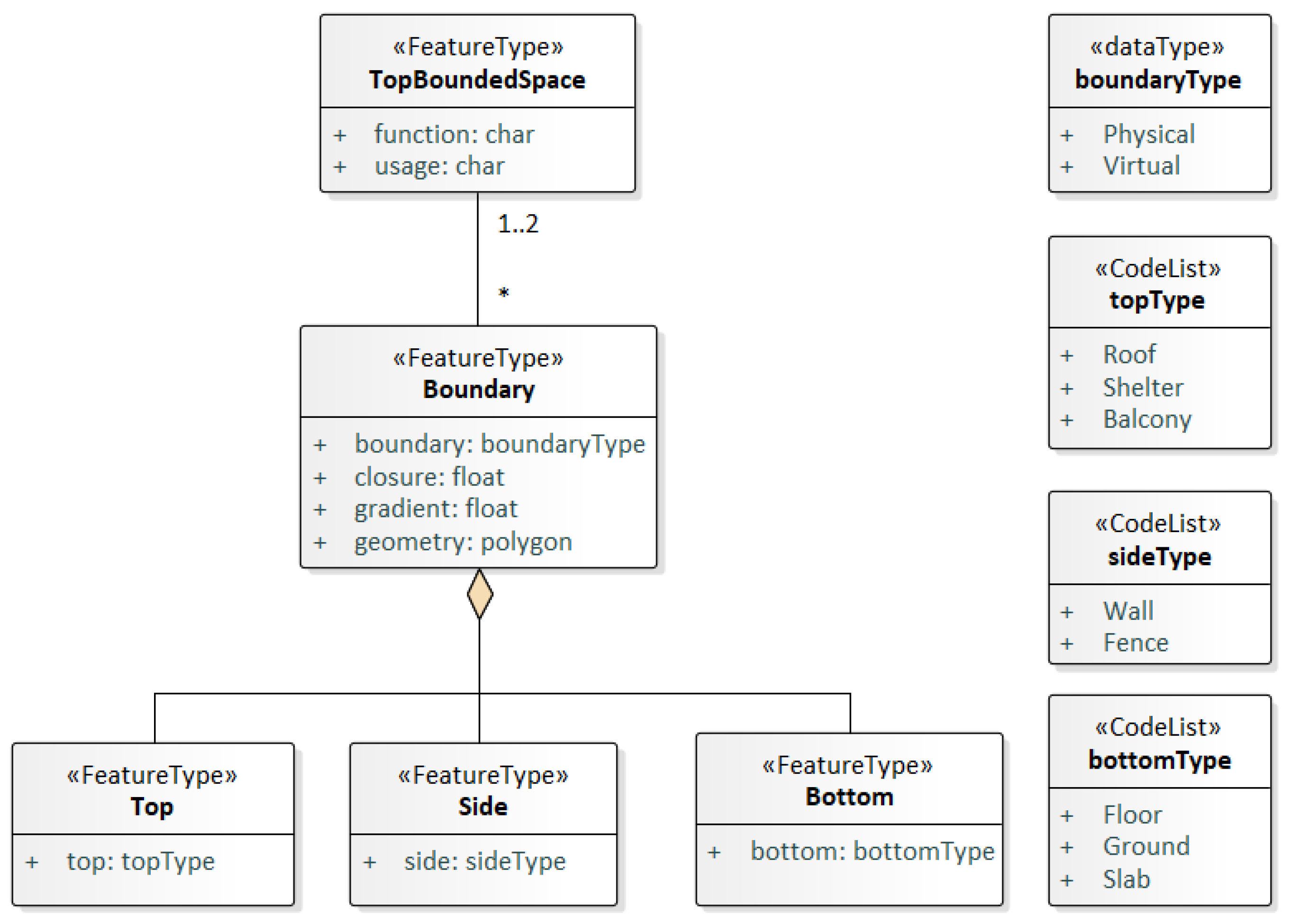
3.2. Space UML Model
3.2.1. TopBoundedSpace
3.2.2. Boundary
Boundary
Closure
Gradient
Geometry
3.2.3. Top, Side, and Bottom
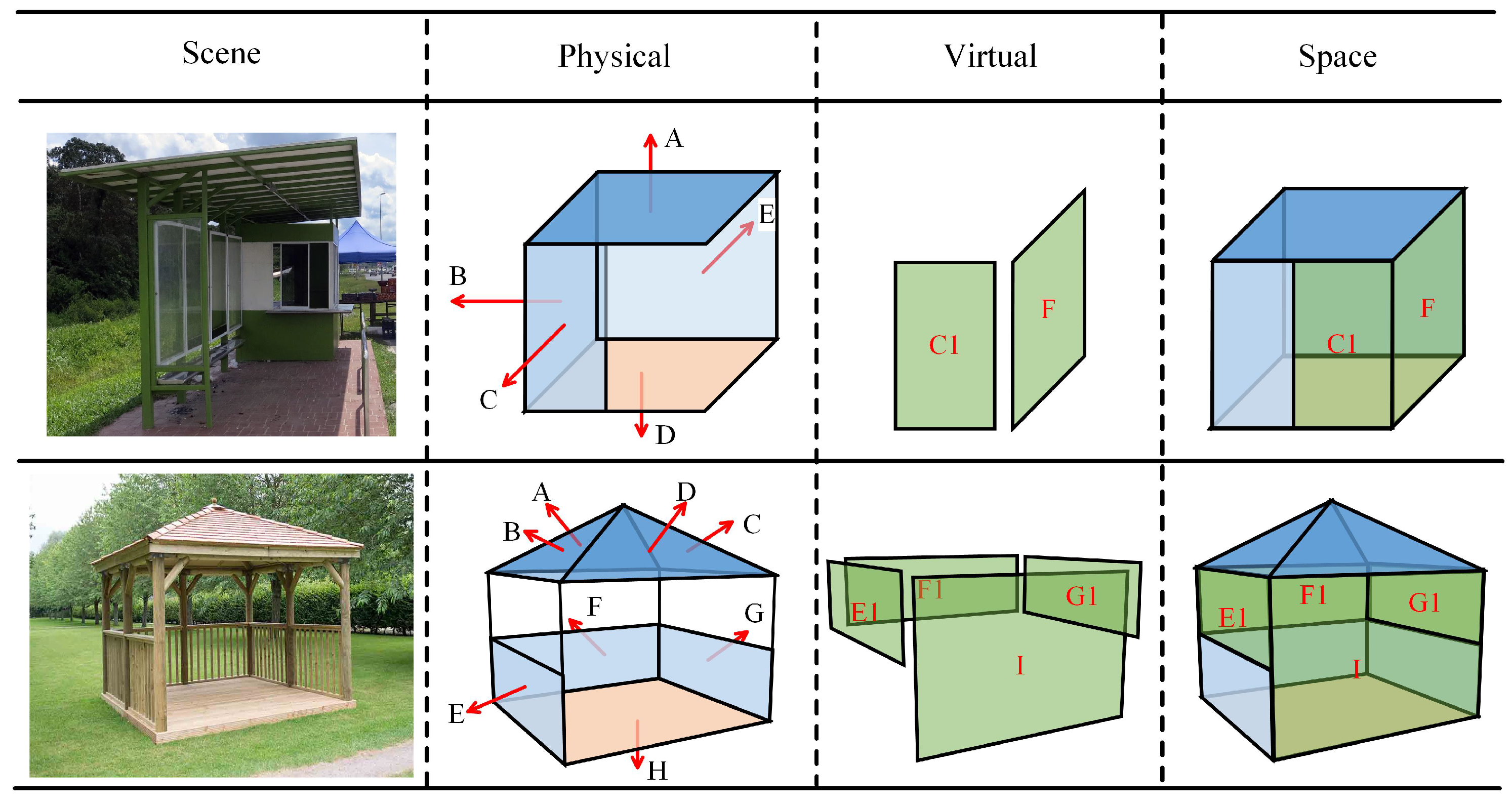
3.3. Examples
4. Top-Bounded Space Creation Approach
- (a)
- Identify and order construction objects.
- (b)
- Determine top/bottom and generate spaces.
- (c)
- Trim spaces.
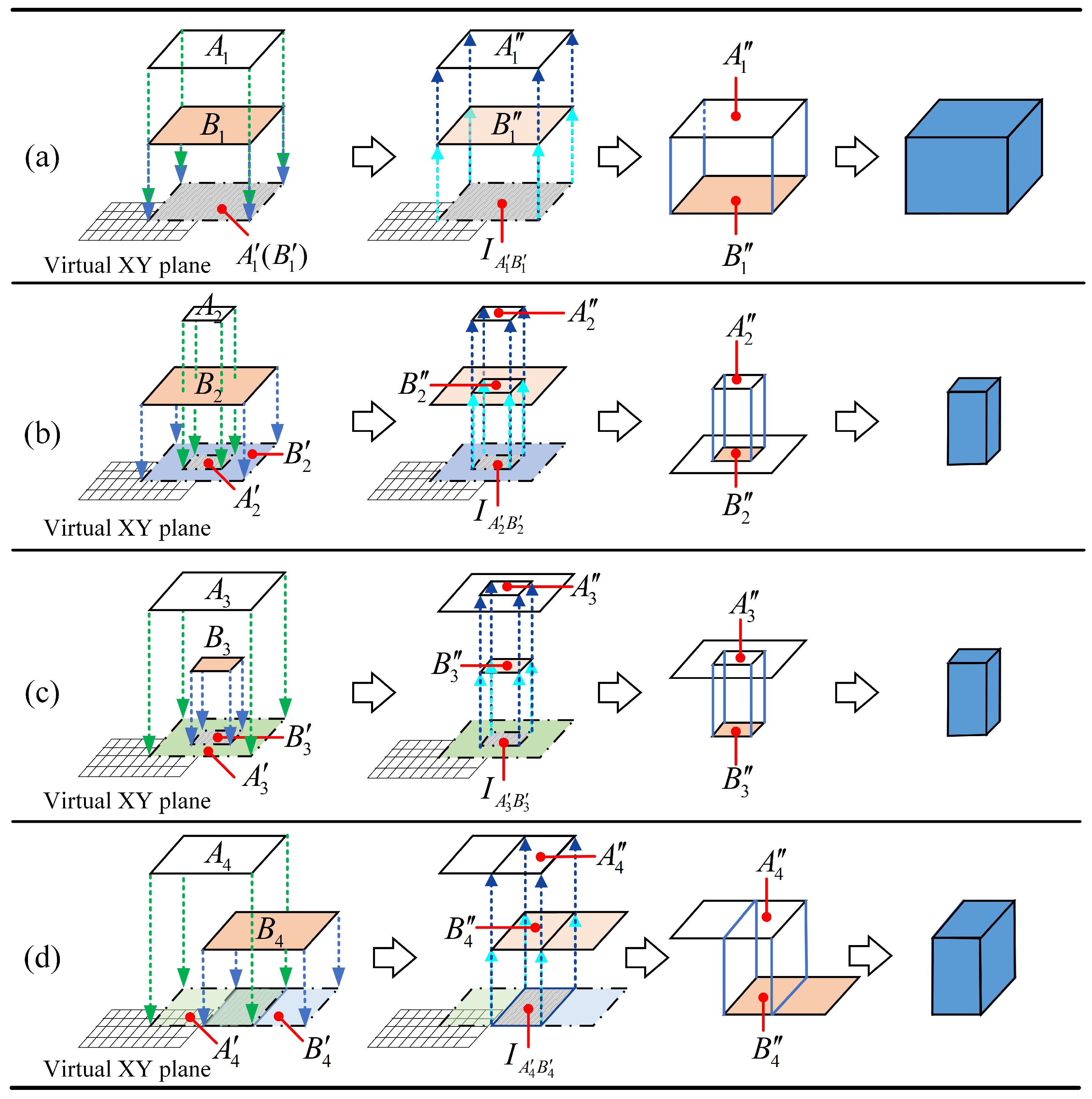
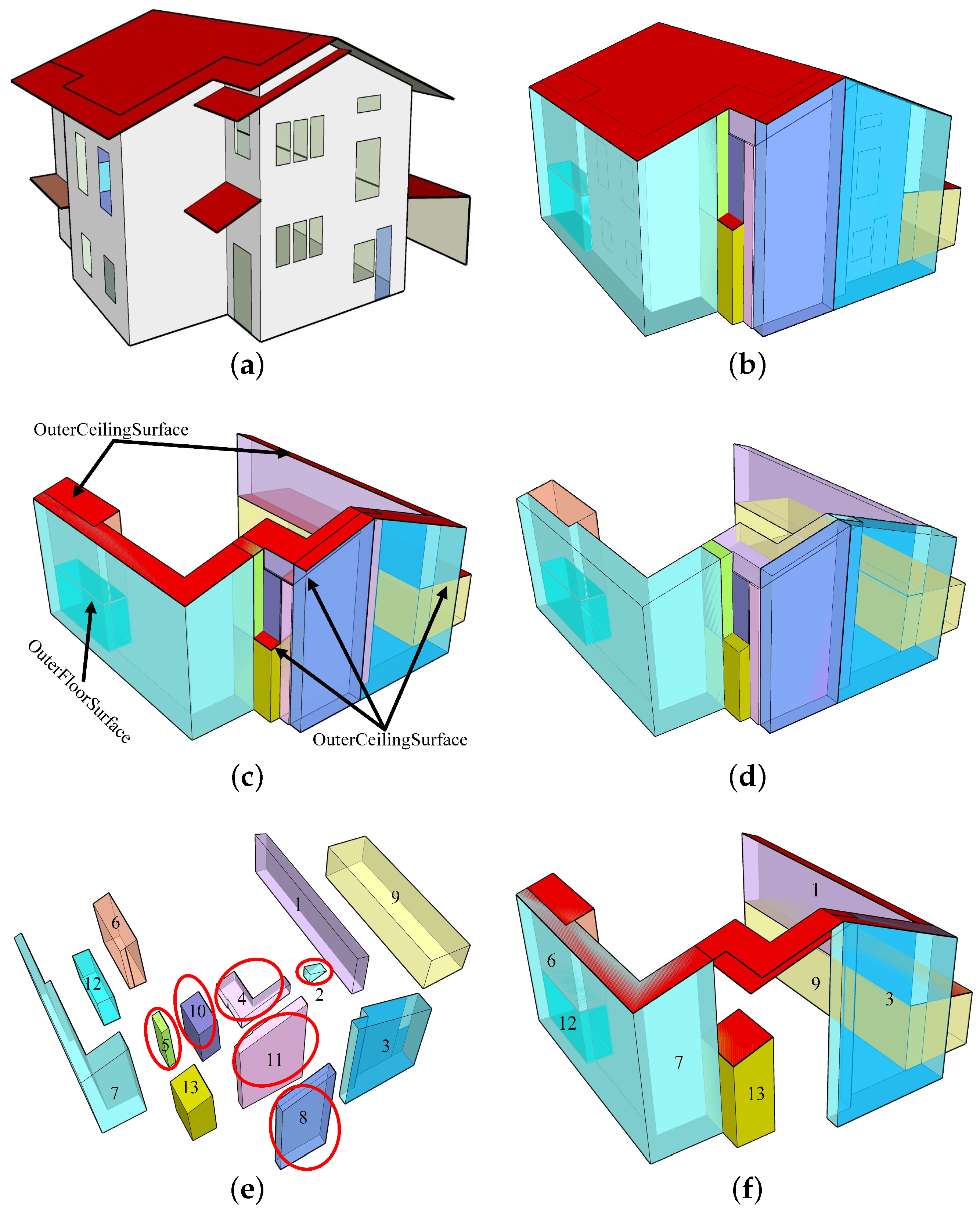
4.1. Identification and Ordering of Construction Objects
4.2. Determination of Boundaries and Space Generation
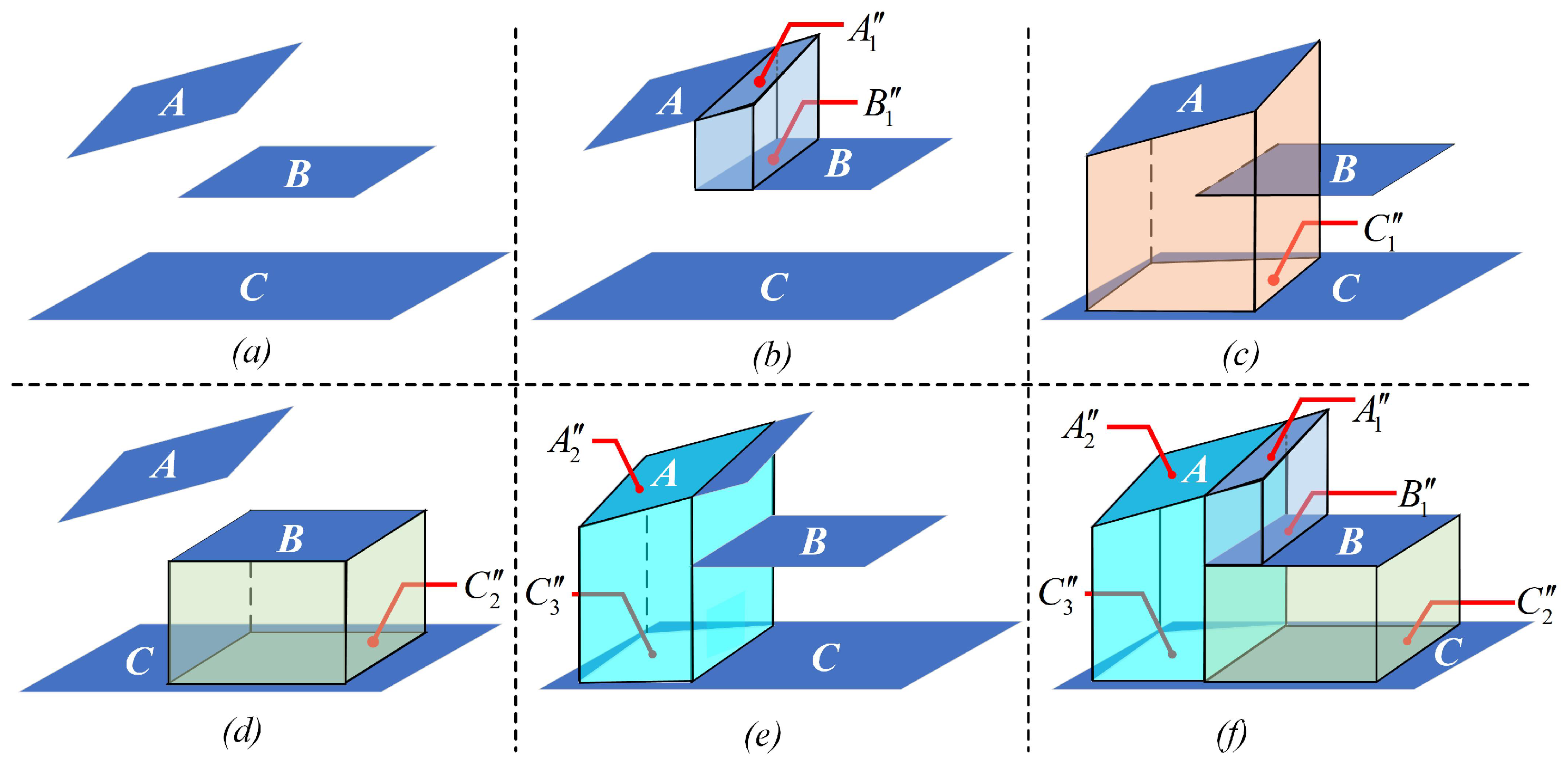
4.3. Space Trimming
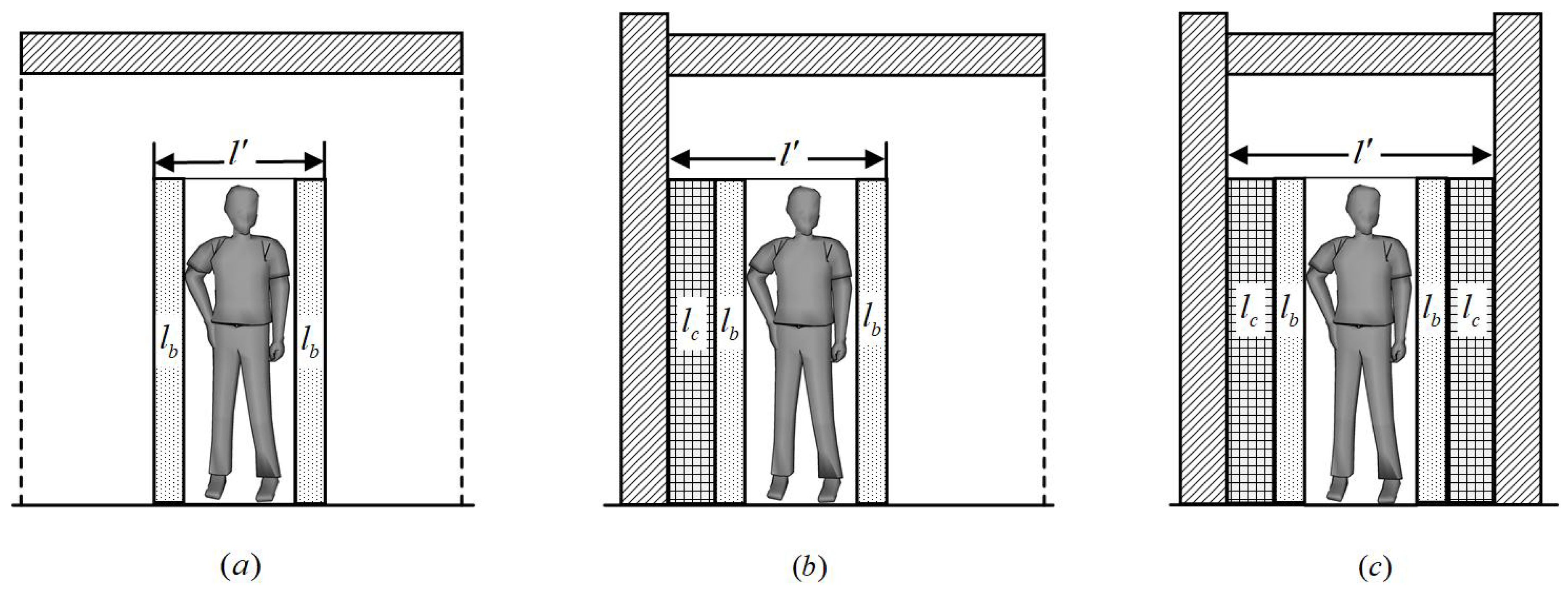
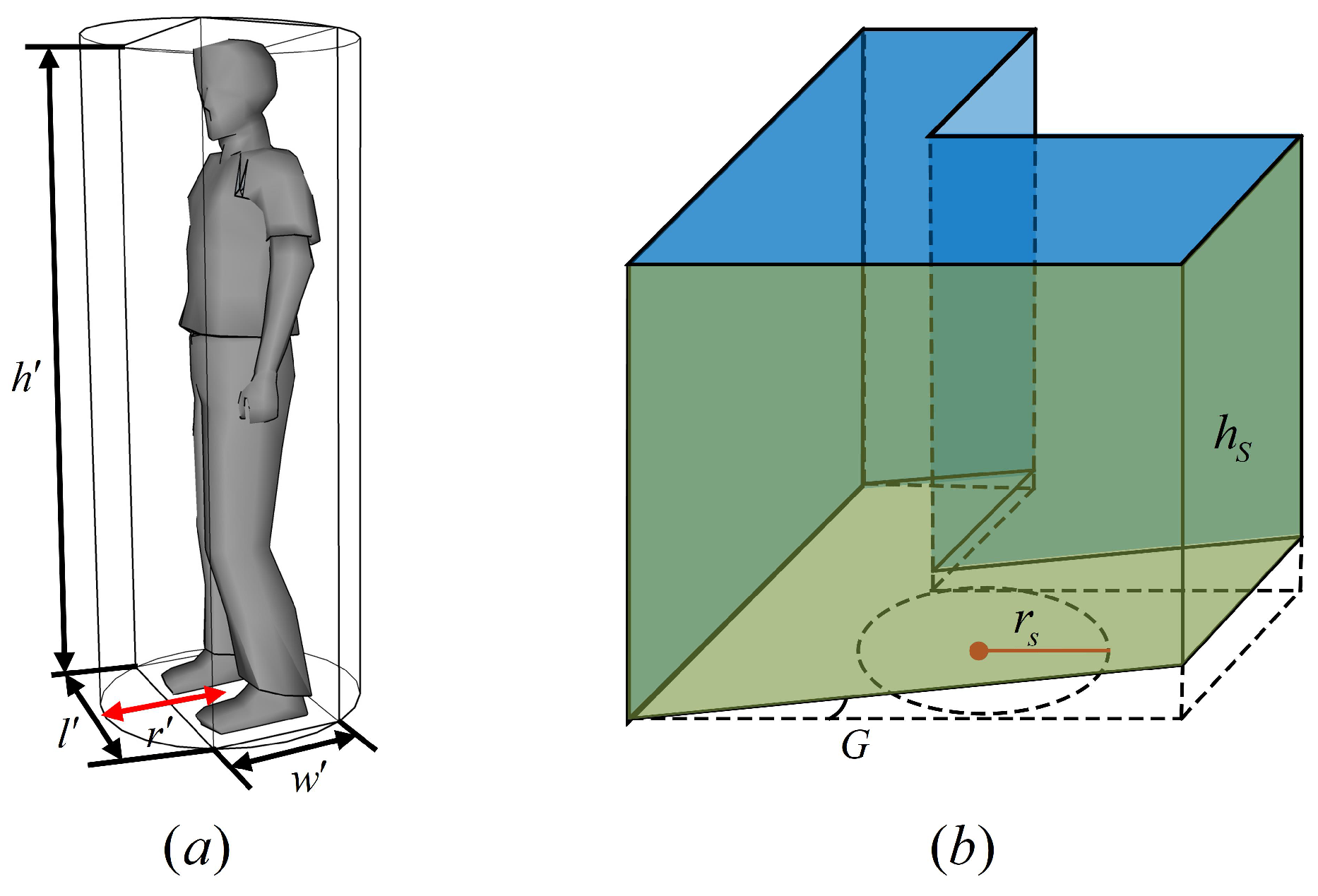
5. Space Requirements and Space Selection for Specific Agent
5.1. Space Requirements
5.2. Space Selection
5.3. Space Accessibility
6. Experiments
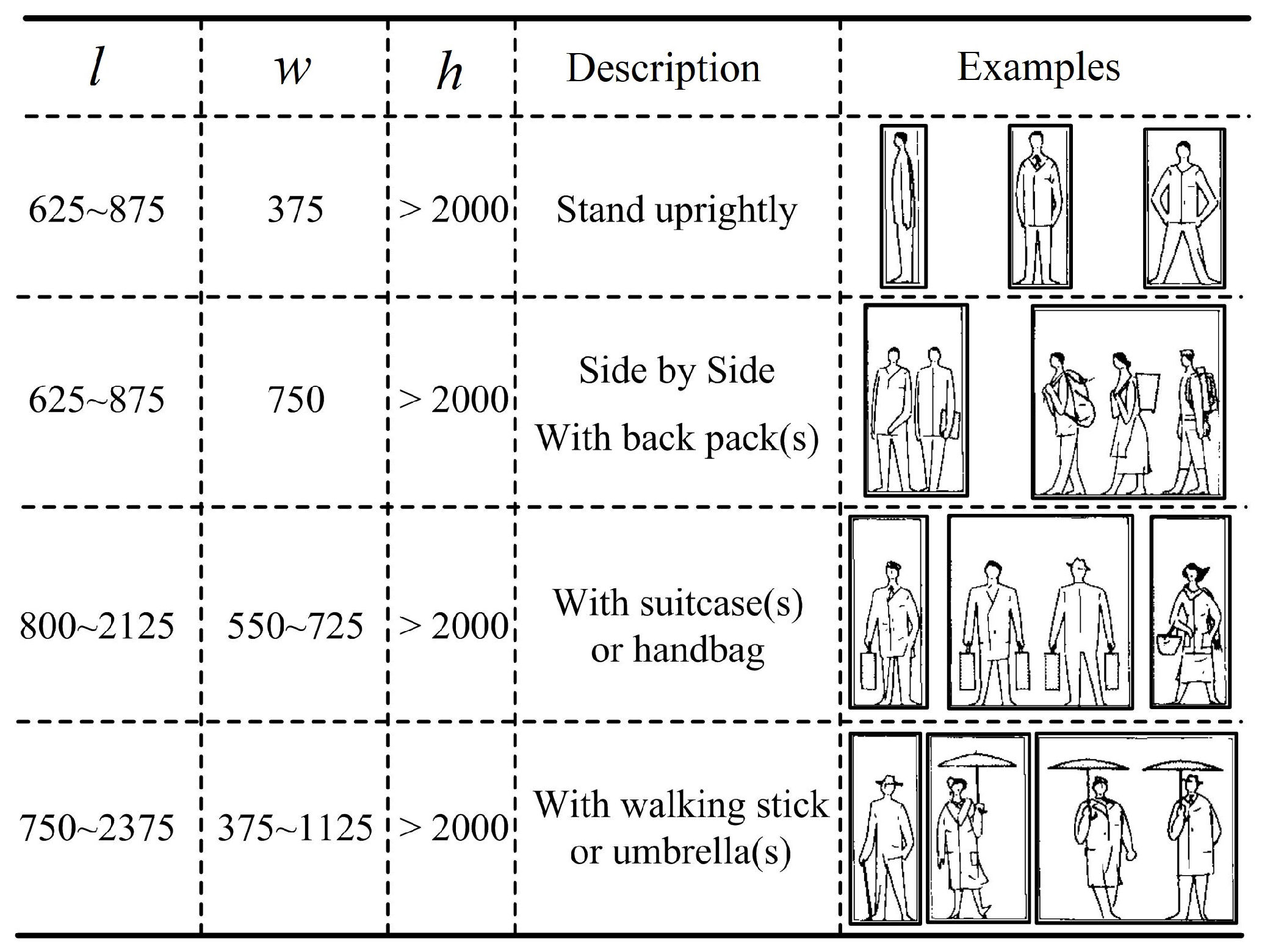
6.1. Pedestrian Definition and Size
6.2. Requirements of Top-Bounded Spaces
6.3. Use Case
7. Conclusions and Future Work
- (a)
- (b)
- (c)
- Investigating when satisfaction level of users, achieved with proposed approach, would have higher impact of their decisions compared to time- or distance-based routes that are currently in use.
- (d)
- Investigating more top-bounded spaces formed by other objects (e.g., trees) and trying to include them in the navigation system.
Author Contributions
Funding
Conflicts of Interest
References
- May, A.J.; Ross, T.; Bayer, S.H.; Tarkiainen, M.J. Pedestrian navigation aids: information requirements and design implications. Pers. Ubiquitous Comput. 2003, 7, 331–338. [Google Scholar] [CrossRef]
- Krūminaitė, M.; Zlatanova, S. Indoor space subdivision for indoor navigation. In Proceedings of the sixth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Dallas/Fort Worth, TX, USA, 4 November 2004; ACM: New York, NY, USA, 2014; pp. 25–31. [Google Scholar]
- Liu, L.; Zlatanova, S. A two-level path-finding strategy for indoor navigation. In Intelligent Systems for Crisis Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 31–42. [Google Scholar]
- Millonig, A.; Schechtner, K. Decision loads and route qualities for pedestrians—Key requirements for the design of pedestrian navigation services. In Pedestrian and Evacuation Dynamics 2005; Springer: Berlin/Heidelberg, Germany, 2007; pp. 109–118. [Google Scholar]
- Lee, J.; Li, K.J.; Zlatanova, S.; Kolbe, T.; Nagel, C.; Becker, T. OGC IndoorGML. OGC 14-005r1. 2014. Available online: http://docs.opengeospatial.org/is/14-005r5/14-005r5.html (accessed on 12 May 2018).
- Vanclooster, A.; Van de Weghe, N.; De Maeyer, P. Integrating indoor and outdoor spaces for pedestrian navigation guidance: A review. Trans. GIS 2016, 20, 491–525. [Google Scholar] [CrossRef]
- Becker, T.; Nagel, C.; Kolbe, T.H. A multilayered space-event model for navigation in indoor spaces. In 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2009; pp. 61–77. [Google Scholar]
- Boguslawski, P.; Gold, C. Construction operators for modelling 3D objects and dual navigation structures. In 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2009; pp. 47–59. [Google Scholar]
- Zlatanova, S.; Liu, L.; Sithole, G. A conceptual framework of space subdivision for indoor navigation. In Proceedings of the Fifth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Orlando, FL, USA, 5 November 2013; ACM: New York, NY, USA, 2013; pp. 37–41. [Google Scholar]
- Diakité, A.A.; Zlatanova, S. Spatial subdivision of complex indoor environments for 3D indoor navigation. Int. J. Geogr. Inf. Sci. 2018, 32, 213–235. [Google Scholar] [CrossRef]
- Isikdag, U.; Zlatanova, S.; Underwood, J. A BIM-Oriented Model for supporting indoor navigation requirements. Comput. Environ. Urban Syst. 2013, 41, 112–123. [Google Scholar] [CrossRef]
- Yan, J.; Diakite, A.; Zlatanova, S. An extraction approach of the top-bounded space formed by buildings for pedestrian navigation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 247–254. [Google Scholar] [CrossRef]
- Afyouni, I.; Ray, C.; Claramunt, C. A fine-grained context-dependent model for indoor spaces. In Proceedings of the 2nd ACM Sigspatial International Workshop on Indoor Spatial Awareness, San Jose, CA, USA, 2 November 2010; ACM: New York, NY, USA, 2010; pp. 33–38. [Google Scholar]
- Yang, L.; Worboys, M. A navigation ontology for outdoor-indoor space:(work-in-progress). In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Chicago, IL, USA, 1 November 2011; ACM: New York, NY, USA, 2011; pp. 31–34. [Google Scholar]
- Zhu, Q.; Li, Y.; Xiong, Q.; Zlatanova, S.; Ding, Y.; Zhang, Y.; Zhou, Y. Indoor multi-dimensional location gml and its application for ubiquitous indoor location services. ISPRS Int. J. Geo-Inf. 2016, 5, 220. [Google Scholar] [CrossRef]
- Corbetta, A.; Lee, C.M.; Muntean, A.; Toschi, F. Asymmetric pedestrian dynamics on a staircase landing from continuous measurements. In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 49–56. [Google Scholar]
- Ziemer, V.; Seyfried, A.; Schadschneider, A. Congestion dynamics in pedestrian single-file motion. In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 89–96. [Google Scholar]
- Liu, L.; Zlatanova, S. An Approach for Indoor Path Computation among Obstacles that Considers User Dimension. ISPRS Int. J. Geo-Inf. 2015, 4, 2821–2841. [Google Scholar] [CrossRef]
- Gaisbauer, C.; Frank, A.U. Wayfinding model for pedestrian navigation. In Proceedings of the AGILE 2008 Conference-Taking Geo-information Science One Step Further, University of Girona, Girona, Spain, 5–8 May 2008; Volume 9. [Google Scholar]
- Hughes, R.L. A continuum theory for the flow of pedestrians. Transp. Res. Part B Methodol. 2002, 36, 507–535. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P.; Bovy, P.H. Pedestrian route-choice and activity scheduling theory and models. Transp. Res. Part B Methodol. 2004, 38, 169–190. [Google Scholar] [CrossRef]
- Köster, G.; Lehmberg, D.; Dietrich, F. Is Slowing Down Enough to Model Movement on Stairs? In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 35–42. [Google Scholar]
- Daamen, W.; Bovy, P.H.; Hoogendoorn, S.P.; Van de Reijt, A. Passenger route choice concerning level changes in railway stations. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 9–13 January 2005; Volume 1930, pp. 12–20. [Google Scholar]
- Winter, S. Indoor spatial information. Int. J. 3-D Inf. Model. (IJ3DIM) 2012, 1, 25–42. [Google Scholar] [CrossRef]
- Kray, C.; Fritze, H.; Fechner, T.; Schwering, A.; Li, R.; Anacta, V.J. Transitional spaces: Between indoor and outdoor spaces. In Proceedings of the International Conference on Spatial Information Theory, Scarborough, UK, 2–6 September 2013; Springer: Cham, Switzerland, 2013; pp. 14–32. [Google Scholar]
- Kim, J.; Kim, T.; Leigh, S.B. Double window system with ventilation slits to prevent window surface condensation in residential buildings. Energy Build. 2011, 43, 3120–3130. [Google Scholar] [CrossRef]
- Du, X.; Bokel, R.; van den Dobbelsteen, A. Building microclimate and summer thermal comfort in free-running buildings with diverse spaces: A Chinese vernacular house case. Build. Environ. 2014, 82, 215–227. [Google Scholar] [CrossRef]
- Pagliarini, G.; Rainieri, S. Thermal environment characterisation of a glass-covered semi-outdoor space subjected to natural climate mitigation. Energy Build. 2011, 43, 1609–1617. [Google Scholar] [CrossRef]
- Nasir, N.H.M.; Salim, F.; Yaman, M. The potential of outdoor space utilization for learning interaction. In Proceedings of the UMRAN2014, Fostering Ecosphere in Built Environment, International Islamic University Malaysia, Selangor, Malaysia, 29 April 2014; pp. 1–17. [Google Scholar]
- Lin, T.P. Thermal perception, adaptation and attendance in a public square in hot and humid regions. Build. Environ. 2009, 44, 2017–2026. [Google Scholar] [CrossRef]
- He, J.; Hoyano, A. Measurement and evaluation of the summer microclimate in the semi-enclosed space under a membrane structure. Build. Environ. 2010, 45, 230–242. [Google Scholar] [CrossRef]
- Kim, K.; Park, S.; Kim, B.S. Survey and numerical effect analyses of the market structure and arcade form on the indoor environment of enclosed-arcade markets during summer. Sol. Energy 2008, 82, 940–955. [Google Scholar] [CrossRef]
- Turrin, M.; Kilian, A.; Stouffs, R.; Sariyildiz, S. Digital design exploration of structural morphologies integrating adaptable modules: A design process based on parametric modeling. In Proceedings of the Joining Languages, Cultures and Visions, CAAD Futures 2009 International Conference, Montreal, QC, Canada, 15–16 June 2009; pp. 17–19. [Google Scholar]
- Chengappa, C.; Edwards, R.; Bajpai, R.; Shields, K.N.; Smith, K.R. Impact of improved cookstoves on indoor air quality in the Bundelkhand region in India. Energy Sustain. Dev. 2007, 11, 33–44. [Google Scholar] [CrossRef]
- Tyson, G.M.; Schuler, R.M.; Leonhardt, M.P. In-Grade Lighting System. U.S. Patent 8,313,208, 5 October 2012. [Google Scholar]
- Amutha, B.; Nanmaran, K. Development of a ZigBee based virtual eye for visually impaired persons. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 564–574. [Google Scholar]
- Liu, X.H.; Chen, Q.Y.; Liu, H.; Yu, H.; Bie, F.Y. Urban Solar Updraft Tower Integrated with Hi-Rise Building–Case Study of Wuhan New Energy Institute Headquarter. Appl. Mech. Mater. 2013, 283, 67–71. [Google Scholar] [CrossRef]
- Monteiro, L.M.; Alucci, M.P. Transitional spaces in São Paulo, Brazil: mathematical modeling and empirical calibration for thermal comfort assessment. In Proceedings of the Building Simulation, Beijing, China, 3–6 September 2007; pp. 737–744. [Google Scholar]
- Hwang, R.L.; Lin, T.P. Thermal comfort requirements for occupants of semi-outdoor and outdoor environments in hot-humid regions. Archit. Sci. Rev. 2007, 50, 357–364. [Google Scholar] [CrossRef]
- Lin, T.P.; Andrade, H.; Hwang, R.; Oliveira, S.; Matzarakis, A. The comparison of thermal sensation and acceptable range for outdoor occupants between Mediterranean and subtropical climates. In Proceedings of the 18th International Congress on Biometeorology, Tokyo, Japan, 22–26 September 2008. [Google Scholar]
- Indraganti, M. Adaptive use of natural ventilation for thermal comfort in Indian apartments. Build. Environ. 2010, 45, 1490–1507. [Google Scholar] [CrossRef]
- Cao, B.; Luo, M.; Li, M.; Zhu, Y. Thermal comfort in semi-outdoor spaces within an office building in Shenzhen: A case study in a hot climate region of China. Indoor Built Environ. 2017. [Google Scholar] [CrossRef]
- Kim, T.; Kato, S.; Murakami, S. Indoor cooling/heating load analysis based on coupled simulation of convection, radiation and HVAC control. Build. Environ. 2001, 36, 901–908. [Google Scholar] [CrossRef]
- Lamia, K.; Rafik, B.; Djaffar, S. Thermal and Airflow Characteristics of Transitional Spaces in a Traditional Urban Fabric Case Study of a Covered Walkway in Timimoun (South West of Algeria). VFAST Trans. Math. 2015, 7, 1–9. [Google Scholar] [CrossRef][Green Version]
- Philokyprou, M.; Michael, A.; Thravalou, S.; Ioannou, I. Thermal performance assessment of vernacular residential semi-open spaces in Mediterranean climate. Indoor Built Environ. 2017. [Google Scholar] [CrossRef]
- Gröger, G.; Kolbe, T.H.; Czerwinski, A.; Nagel, C. OpenGIS City Geography Markup Language (CityGML) Encoding Standard, Version 2.0.0. 2012. Available online: http://www.opengis.net/spec/citygml/2.0 (accessed on 30 January 2019).
- Neufert, E.; Jones, V.; Thackara, J.; Miles, R. Architects’ Data; Granada: St Albans, UK, 1980. [Google Scholar]
- Bosina, E.; Meeder, M.; Büchel, B.; Weidmann, U. Avoiding Walls: What Distance Do Pedestrians Keep from Walls and Obstacles? In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 19–26. [Google Scholar]
- Alattas, A.; Zlatanova, S.; Van Oosterom, P.; Chatzinikolaou, E.; Lemmen, C.; Li, K.J. Supporting Indoor Navigation Using Access Rights to Spaces Based on Combined Use of IndoorGML and LADM Models. ISPRS Int. J. Geo-Inf. 2017, 6, 384. [Google Scholar] [CrossRef]
- Diakité, A.A.; Zlatanova, S. Extraction of the 3D free space from building models for indoor navigation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 4. [Google Scholar] [CrossRef]
- Munkres, J.R. Elements of Algebraic Topology; Addison-Wesley: Menlo Park, CA, USA, 1984; Volume 2. [Google Scholar]
- Becker, T.; Nagel, C.; Kolbe, T.H. Supporting contexts for indoor navigation using a multilayered space model. In Proceedings of the 2009 Tenth International Conference on Mobile Data Management: Systems, Services and Middleware, Taipei, Taiwan, 18–20 May 2009; pp. 680–685. [Google Scholar]
- Worboys, M. Modeling indoor space. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Chicago, IL, USA, 1 November 2011; pp. 1–6. [Google Scholar]


| No. | (°) | Qualified | ||
|---|---|---|---|---|
| 485.30 | 8.34 | 3504.03 | √ | |
| 333.08 | 18.17 | 3.594 | × | |
| 680.13 | 0 | 6602.51 | √ | |
| 638.44 | 18.17 | 862.34 | × | |
| 245.51 | 19.39 | 3789.22 | × | |
| 705.29 | 0 | 4004.33 | √ | |
| 640.08 | 0 | 6433.40 | √ | |
| 345.77 | 0 | 7664.48 | × | |
| 1911.08 | 0 | 2680.58 | √ | |
| 638.40 | 19.39 | 2892.37 | × | |
| 337.41 | 0 | 6777.85 | × | |
| 640.09 | 0 | 3682.28 | √ | |
| 883.89 | 0 | 2607.80 | √ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Diakité, A.A.; Zlatanova, S.; Aleksandrov, M. Top-Bounded Spaces Formed by the Built Environment for Navigation Systems. ISPRS Int. J. Geo-Inf. 2019, 8, 224. https://doi.org/10.3390/ijgi8050224
Yan J, Diakité AA, Zlatanova S, Aleksandrov M. Top-Bounded Spaces Formed by the Built Environment for Navigation Systems. ISPRS International Journal of Geo-Information. 2019; 8(5):224. https://doi.org/10.3390/ijgi8050224
Chicago/Turabian StyleYan, Jinjin, Abdoulaye A. Diakité, Sisi Zlatanova, and Mitko Aleksandrov. 2019. "Top-Bounded Spaces Formed by the Built Environment for Navigation Systems" ISPRS International Journal of Geo-Information 8, no. 5: 224. https://doi.org/10.3390/ijgi8050224
APA StyleYan, J., Diakité, A. A., Zlatanova, S., & Aleksandrov, M. (2019). Top-Bounded Spaces Formed by the Built Environment for Navigation Systems. ISPRS International Journal of Geo-Information, 8(5), 224. https://doi.org/10.3390/ijgi8050224








