NS-DBSCAN: A Density-Based Clustering Algorithm in Network Space
Abstract
1. Introduction
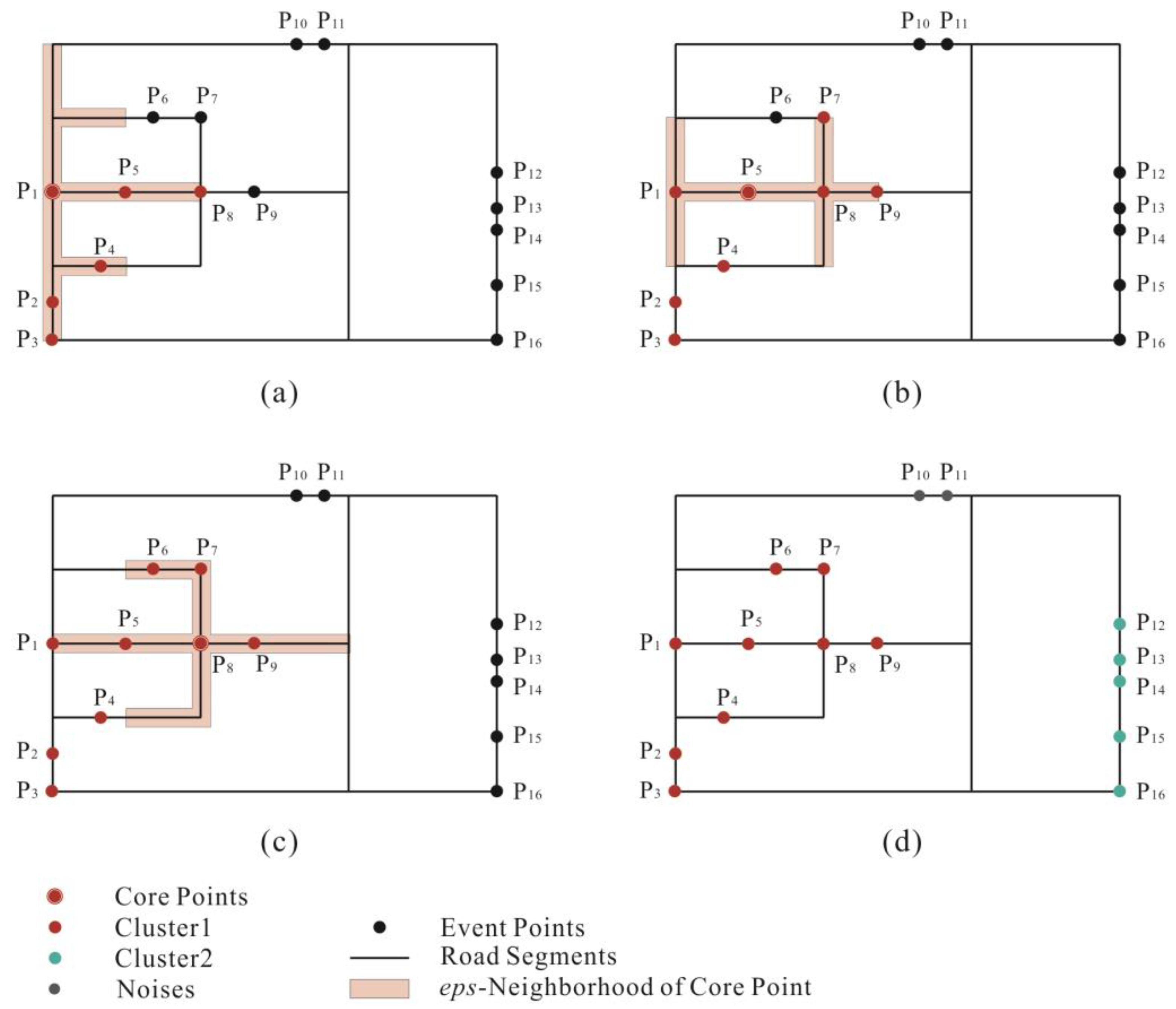
2. Basic Idea
3. NS-DBSCAN Algorithm
3.1. Generating Density Ordering
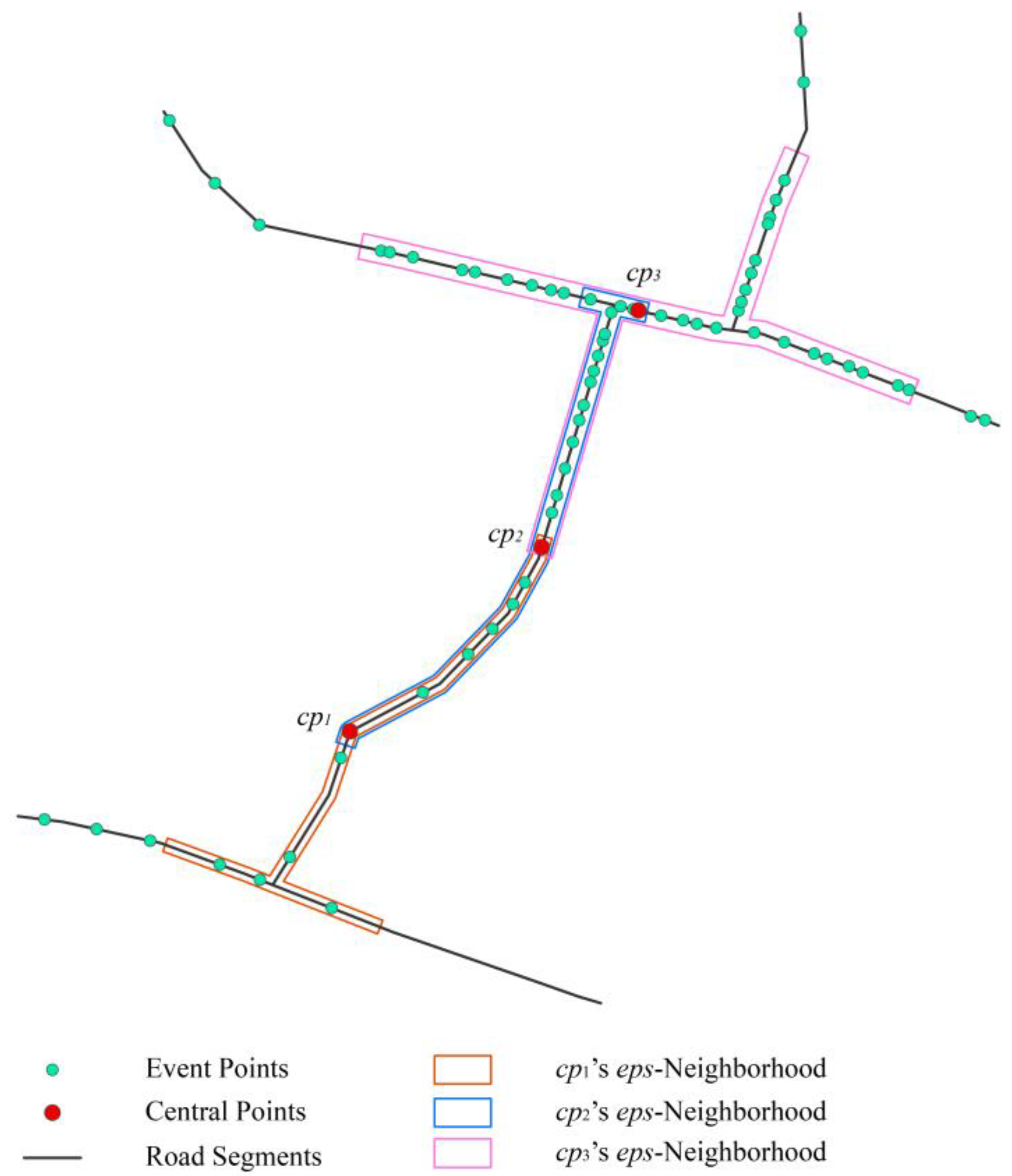
3.1.1. Obtaining Eps-Neighbors
- (1)
- Setting CDCV of central vertex to 0 and that of other vertices to ∞.
- (2)
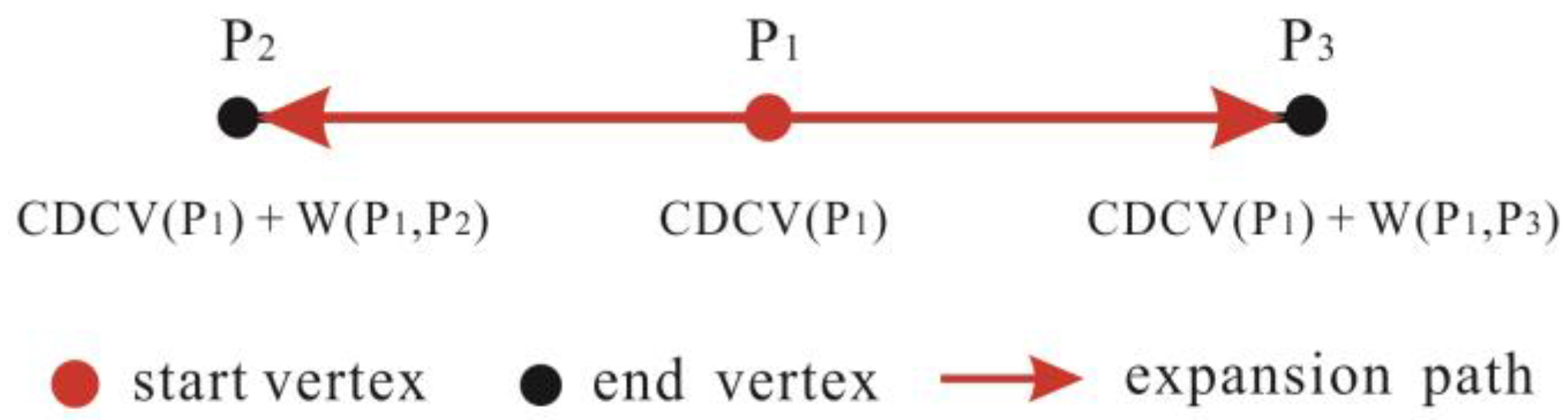
- Performing a basic expansion with the central vertex as the start vertex.
- (3)
- Continuing the expansion from the new vertices, which are actually the end vertices of the last expansion.
- (4)
- Repeating step 3 until all expansion paths are blocked. The vertices whose CDCV are neither ∞ nor 0 consist of eps-neighbors of the central vertex.
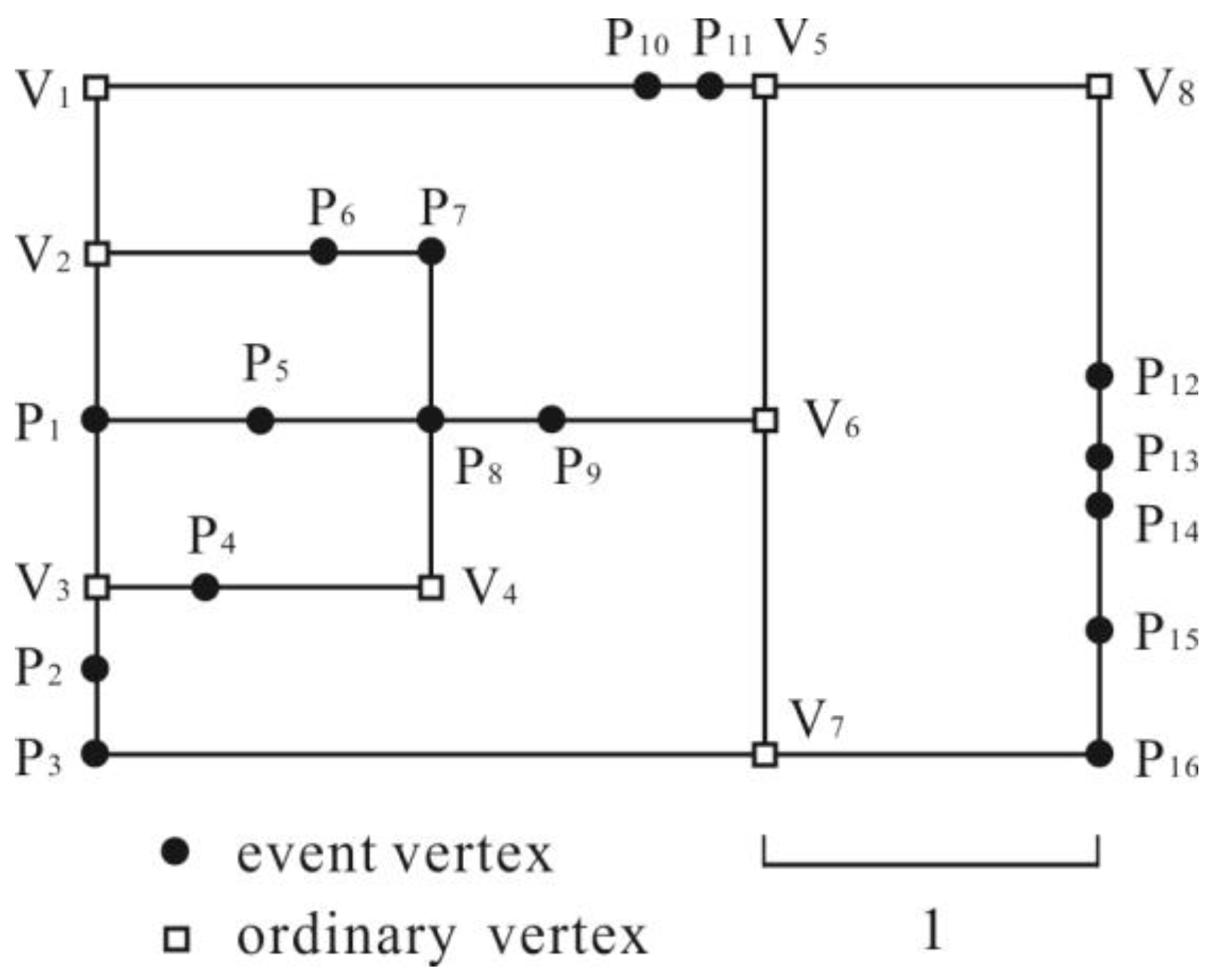
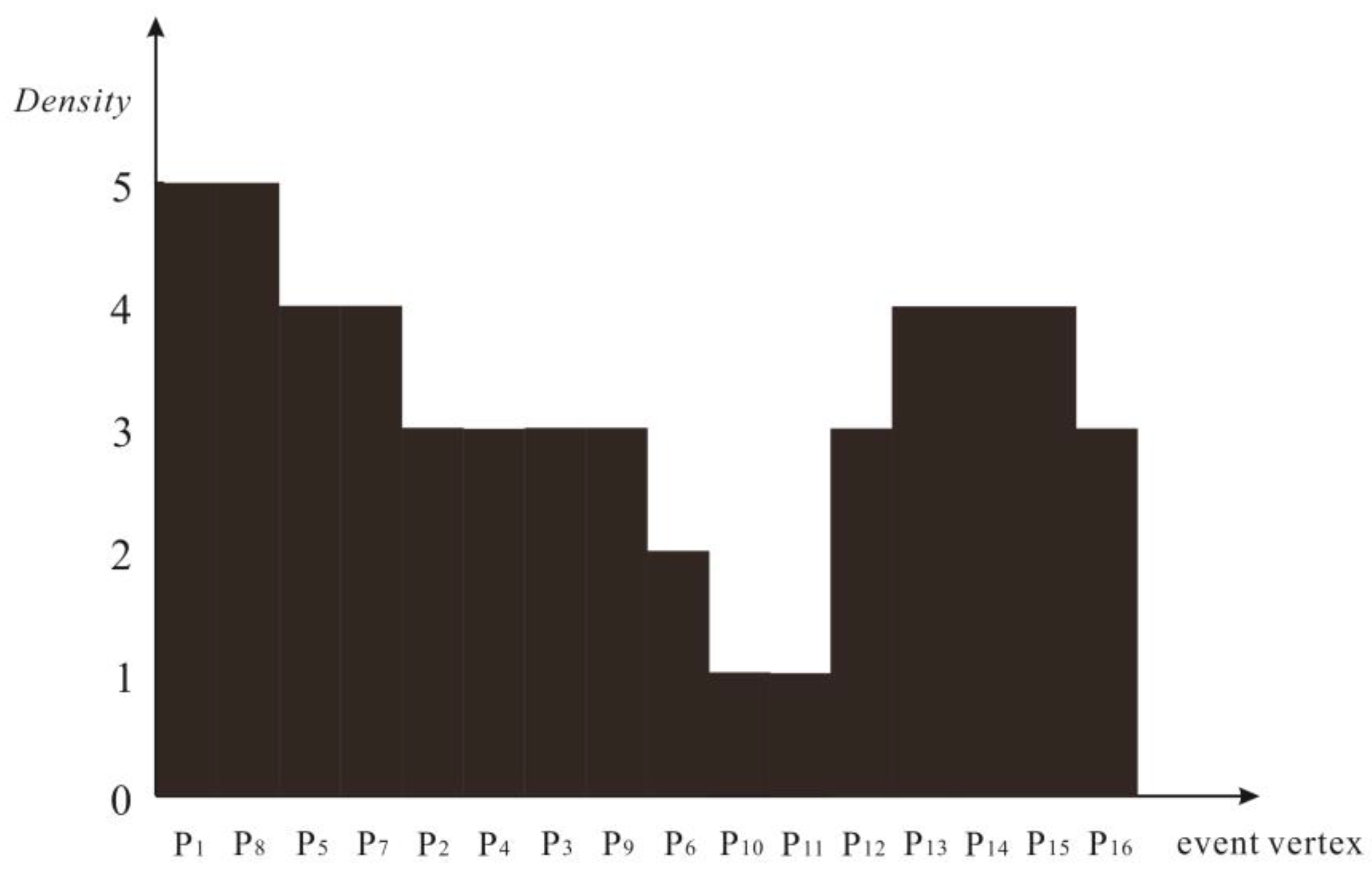
3.1.2. Generating the Density Ordering Table and Graph
3.2. Forming Clusters
4. Experiment
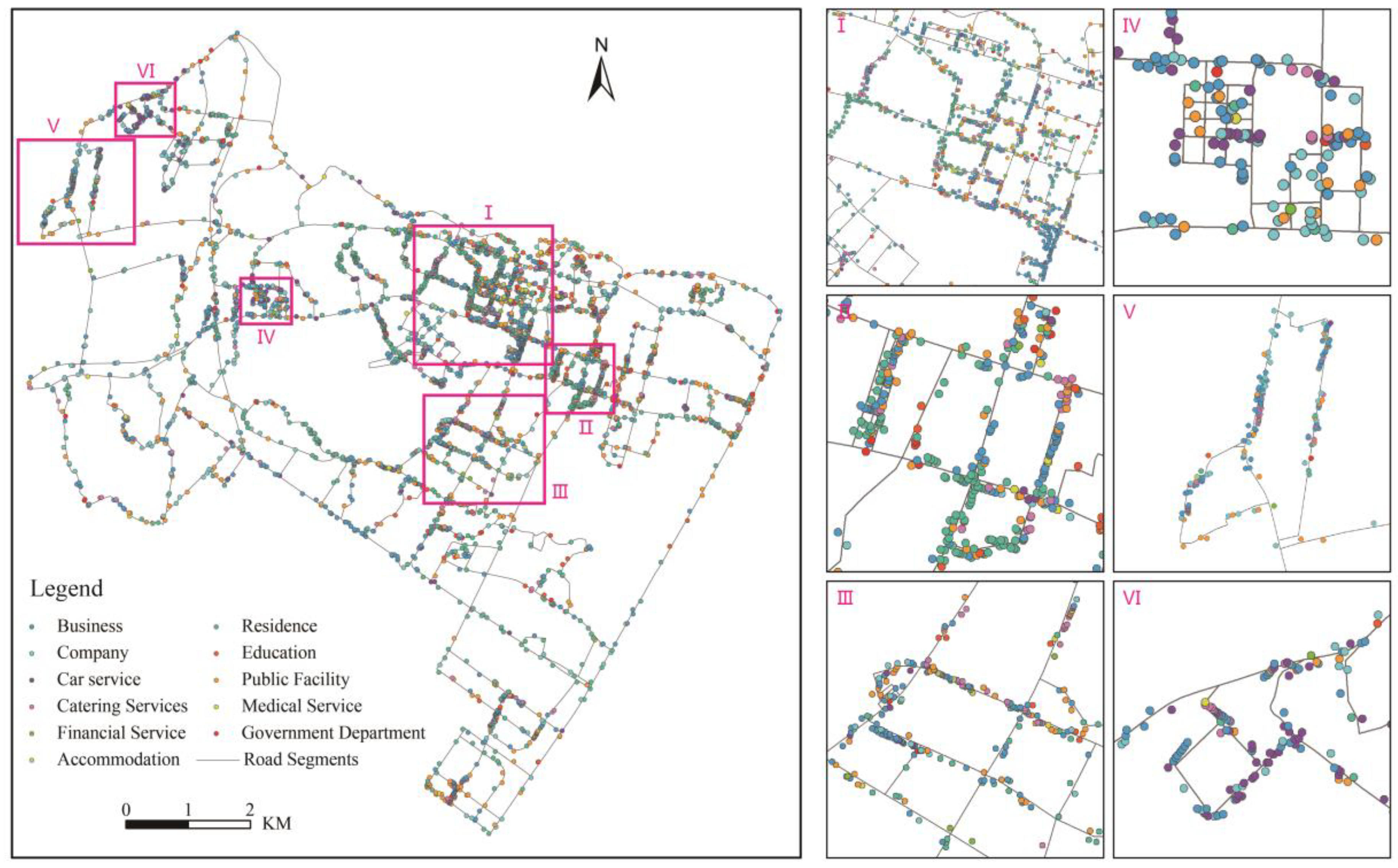
4.1. Dataset
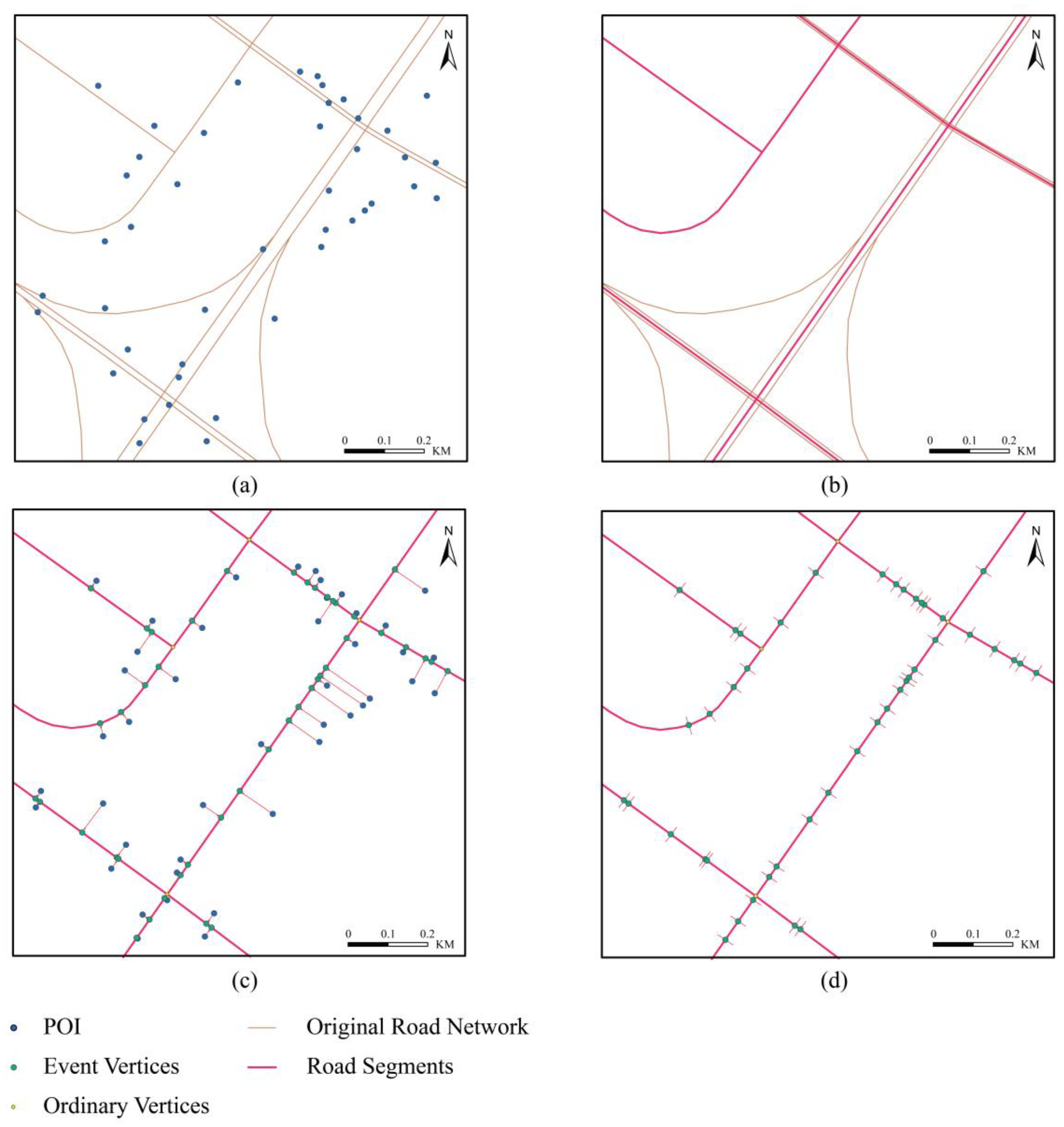
4.2. Preprocessing
- (1)
- Deleting all flyovers and tunnels to make the road network planar.
- (2)
- Extracting the skeletons of divided highways and splitting the road segments where they intersect (Figure 8b).
- (3)
- Moving the point alongside roads to its nearest road segment to create event vertices and establish a correspondence between event vertices and point, followed by creating ordinary vertices where road segments intersect (Figure 8c).
- (4)
- Splitting road segments at event vertices (Figure 8d).
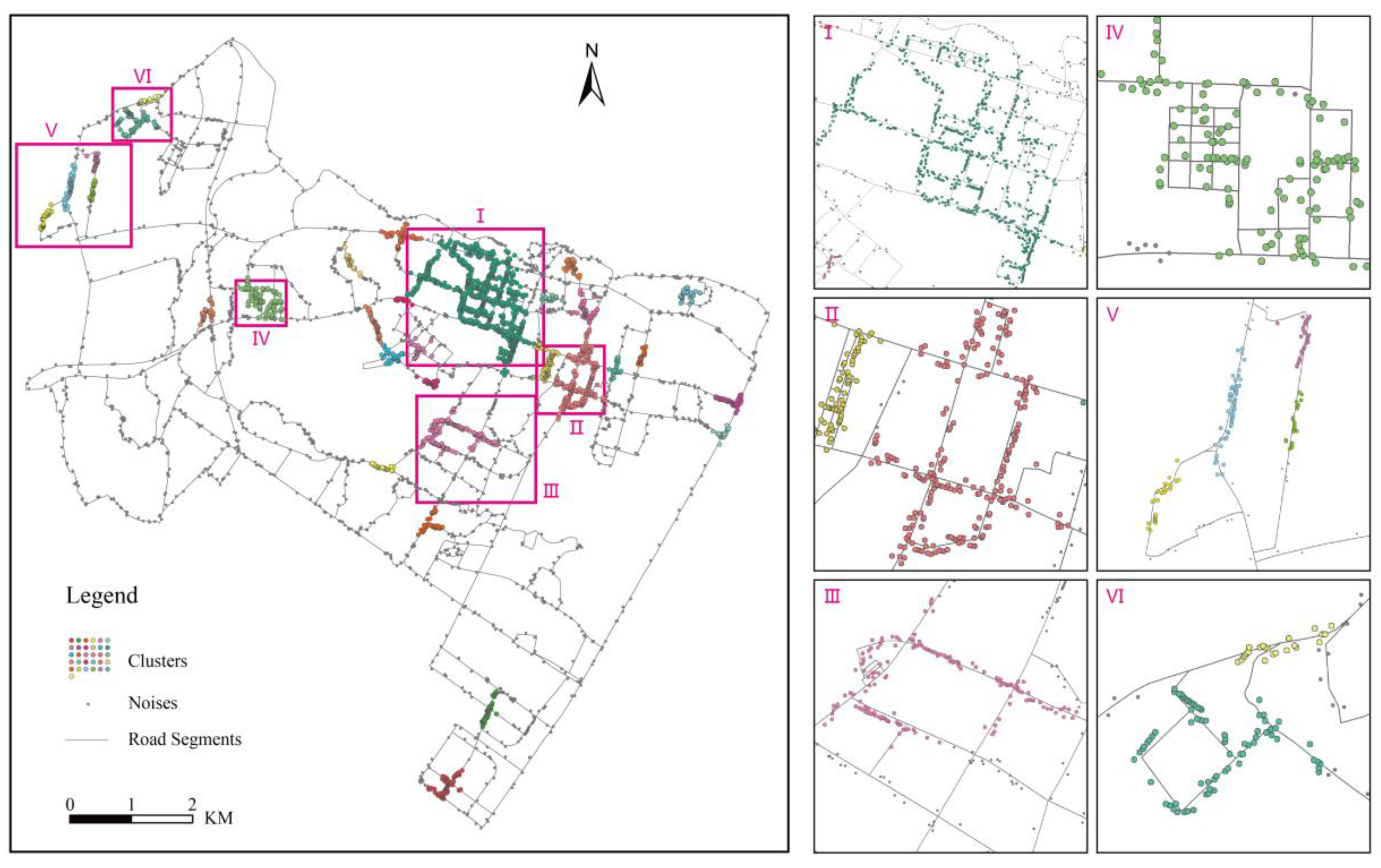
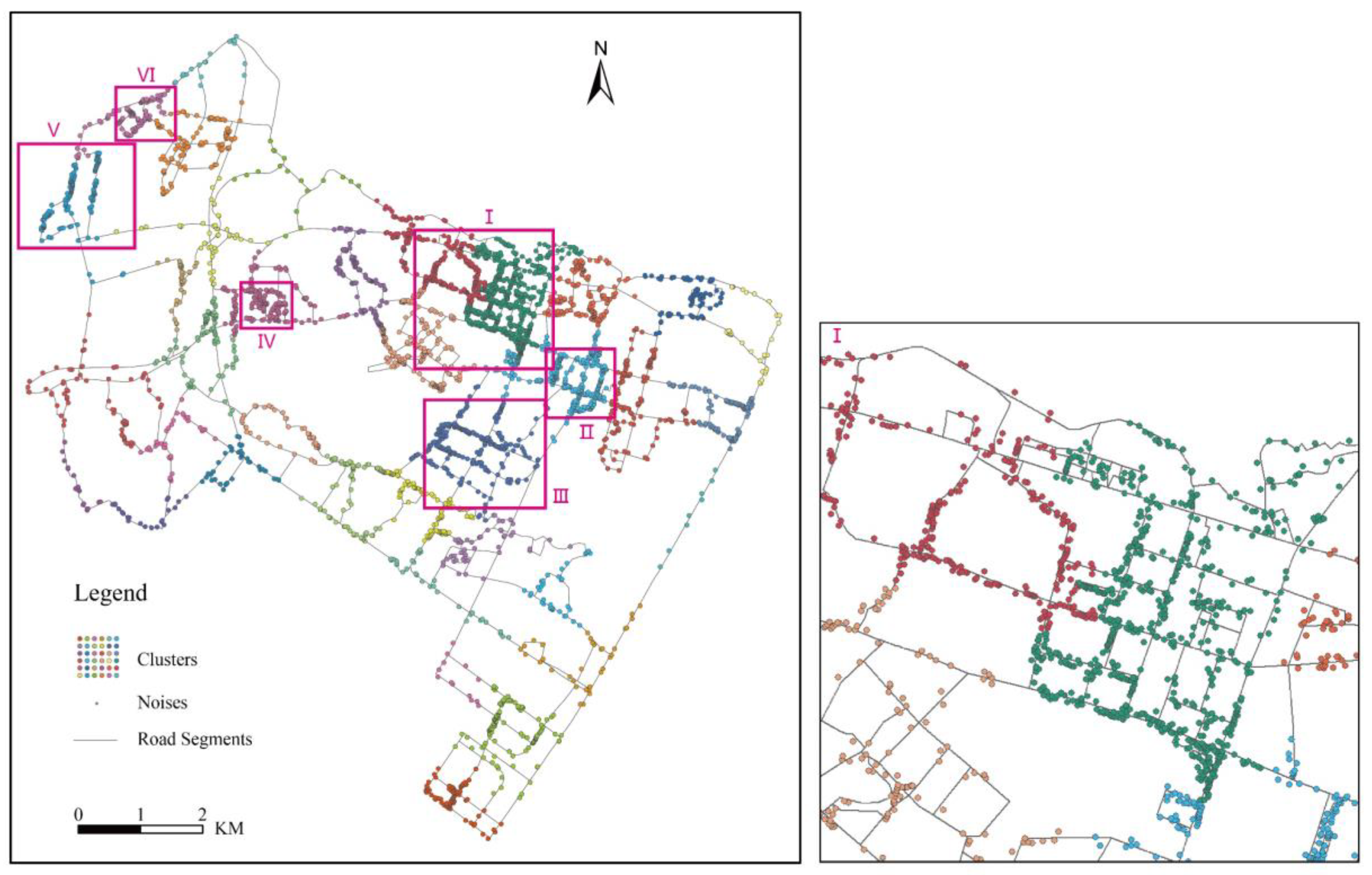
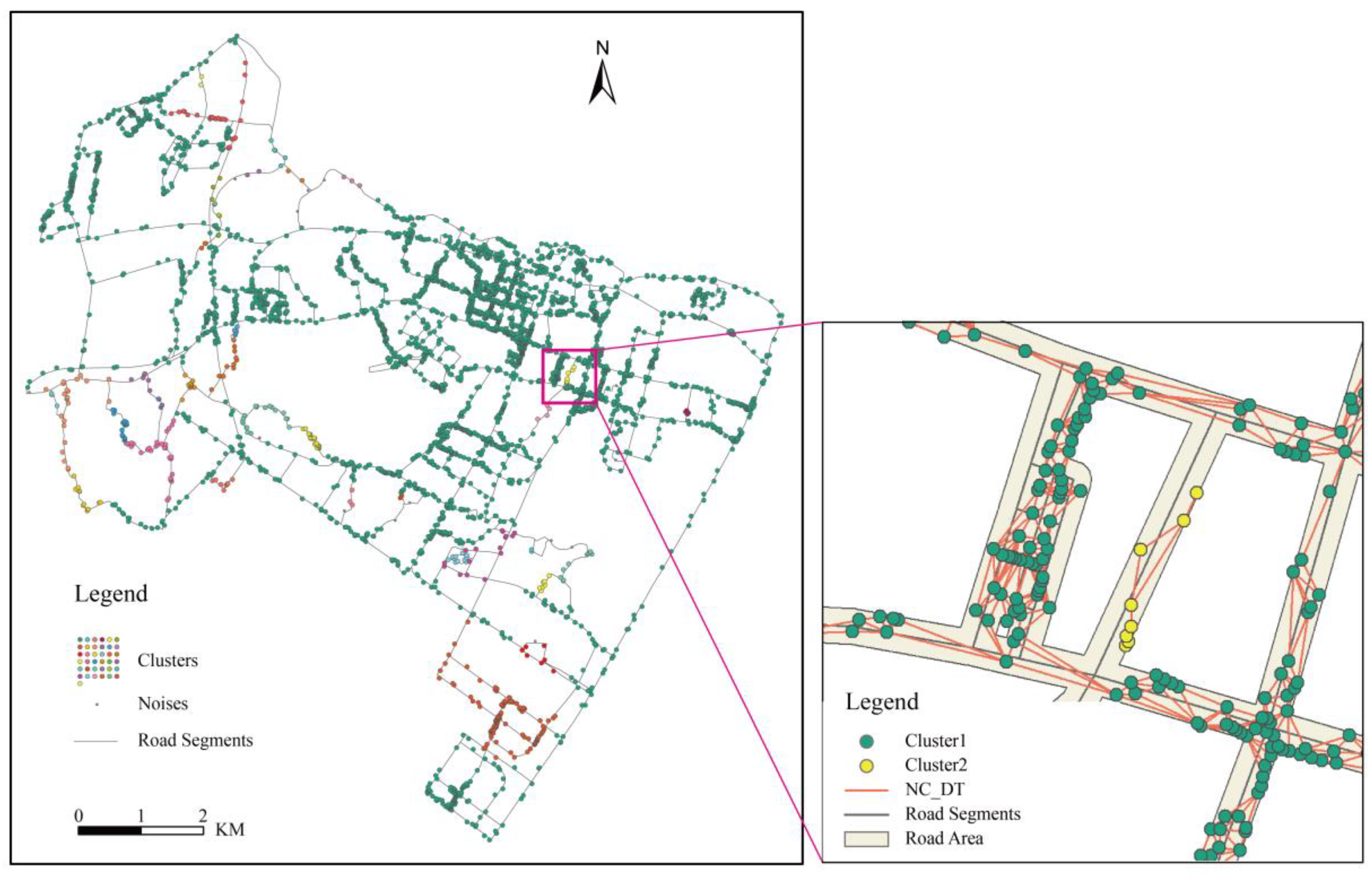
4.3. Results
5. Discussion
5.1. Parameterization
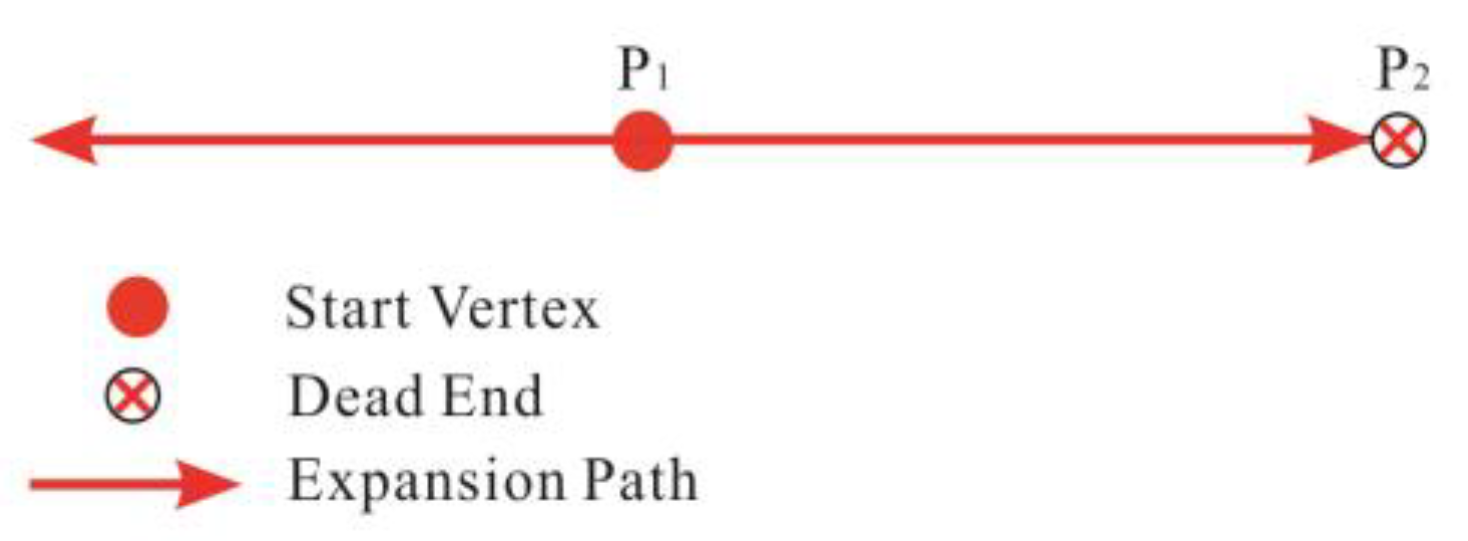
5.2. One-way and Dead-End Cases
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Waller, L.A. Detection of clustering in spatial data. In The SAGE Handbook of Spatial Analysis; SAGE Publications: Thousand Oaks, CA, USA, 2009; pp. 299–320. [Google Scholar]
- Estivill-Castro, V.; Lee, I. Multi-level clustering and its visualization for exploratory spatial analysis. Geoinformatica 2002, 6, 123–152. [Google Scholar] [CrossRef]
- Shiode, S. Street-level Spatial Scan Statistic and STAC for Analysing Street Crime Concentrations. Trans. GIS 2011, 15, 365–383. [Google Scholar] [CrossRef]
- He, L.; Páez, A.; Liu, D. Persistence of Crime Hot Spots: An Ordered Probit Analysis. Geogr. Anal. 2017, 49, 3–22. [Google Scholar] [CrossRef]
- Guo, D.; Zhu, X.; Jin, H.; Gao, P.; Andris, C. Discovering Spatial Patterns in Origin-Destination Mobility Data. Trans. GIS 2012, 16, 411–429. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, K.; Wang, Y.; Zhao, P.; Ye, X. A trajectory clustering approach based on decision graph and data field for detecting hotspots. Int. J. Geogr. Inf. Sci. 2016, 31, 1101–1127. [Google Scholar] [CrossRef]
- Pei, T.; Wang, W.; Zhang, H.; Ma, T.; Du, Y.; Zhou, C. Density-based clustering for data containing two types of points. Int. J. Geogr. Inf. Sci. 2015, 29, 175–193. [Google Scholar] [CrossRef]
- Yamada, I.; Thill, J.C. Local Indicators of Network—Constrained Clusters in Spatial Point Patterns. Geogr. Anal. 2007, 39, 268–292. [Google Scholar] [CrossRef]
- Nie, K.; Wang, Z.; Du, Q.; Ren, F.; Tian, Q. A network-constrained integrated method for detecting spatial cluster and risk location of traffic crash: A case study from Wuhan, China. Sustainability 2015, 7, 2662–2677. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, M.; Shi, Y.; Wang, J. A density-based spatial clustering algorithm considering both spatial proximity and attribute similarity. Comput. Geosci. 2012, 46, 296–309. [Google Scholar] [CrossRef]
- Nojarov, P. Genetic climatic regionalization of the Balkan Peninsula using cluster analysis. J. Geogr. Sci. 2017, 27, 43–61. [Google Scholar] [CrossRef]
- Pei, T.; Jasra, A.; Hand, D.J.; Zhu, A.X.; Zhou, C. DECODE: A new method for discovering clusters of different densities in spatial data. Data Min. Knowl. Discov. 2009, 18, 337–369. [Google Scholar] [CrossRef]
- Deng, M.; Liu, Q.; Cheng, T.; Shi, Y. An adaptive spatial clustering algorithm based on delaunay triangulation. Comput. Environ. Urban Syst. 2011, 35, 320–332. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, J.; Deng, M.; Shi, Y. An iterative detection and removal method for detecting spatial clusters of different densities. Trans. GIS 2015, 19, 82–106. [Google Scholar] [CrossRef]
- Deng, M.; Yang, X.; Shi, Y.; Gong, J.; Liu, Y.; Liu, H. A density-based approach for detecting network-constrained clusters in spatial point events. Int. J. Geogr. Inf. Sci. 2018, 33, 466–488. [Google Scholar] [CrossRef]
- Okabe, A.; Yamada, I. The K-Function Method on a Network and its computational implementation. Geogr. Anal. 2001, 33, 270–290. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, J.; Deng, M.; Shi, Y.; Li, Z.; Liu, Q.; Tang, J.; Deng, M. An adaptive method for clustering spatio-temporal events. Trans. GIS 2018, 22, 82–106. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial analysis—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Jackson, M.C.; Huang, L.; Xie, Q.; Tiwari, R.C. A modified version of Moran’s I. Int. J. Health Geogr. 2010, 9. [Google Scholar] [CrossRef] [PubMed]
- Martin, K.; Neville, N. Spatial disease clusters: Detection and inference. Stat. Med. 2018, 14, 799–810. [Google Scholar] [CrossRef]
- Rey, S.J. Space-time patterns of rank concordance: Local indicators of mobility association with application to spatial income inequality dynamics. Ann. Am. Assoc. Geogr. 2016, 106, 788–803. [Google Scholar] [CrossRef]
- Fan, Y.; Zhu, X.; She, B.; Guo, W.; Guo, T. Network-constrained spatio-temporal clustering analysis of traffic collisions in Jianghan District of Wuhan, China. PLoS ONE 2018, 13, e0195093. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concept and Techniques, 2nd ed.; Elsevier Pte Ltd.: Singapore, 2012. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An. Introduction to Cluster Anaalysis; Wiley: London, UK, 1990. [Google Scholar]
- Ng, R.T.; Han, J. Efficient and effective clustering methods for spatial data mining. In Proceedings of the VLDB Conference, Santiago, Chile, 12–15 September 1994. [Google Scholar]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data culatering method for very large databases. In Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data, Montreal, QC, Canada, 4 –6 June 1996; Volume 1, pp. 103–114. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. CURE: An Efficient Clustering Algorithm for Large Databases. In ACM SIGMOD Record; Elsevier: Seattle, WA, USA, 1998; Volume 27, pp. 73–84. [Google Scholar]
- Karypis, G.; Han, E.H.; Kumar, V. Chameleon: Hierarchical clustering using dynamic modeling. Computer 1999, 32, 68–75. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure. In ACM SIGMOD’99 International Conference on Management of Data; ACM: New York, NY, USA, 1999; pp. 49–60. [Google Scholar]
- Mai, G.; Janowicz, K.; Hu, Y.; Gao, S. ADCN: An anisotropic density-based clustering algorithm for discovering spatial point patterns with noise. Trans. GIS 2018, 22, 348–369. [Google Scholar] [CrossRef]
- Deng, M.; Liu, Q.; Li, G.; Cheng, T. Field-theory based spatial clustering method. J. Remote Sens. 2010, 14, 694–709. [Google Scholar]
- Marek, L.; Pászto, V.; Tucek, P. Using clustering in geosciences: Examples and case studies. In Proceedings of the 15th International Multidisciplinary Scientific GeoConference-SGEM, Albena, Bulgaria, 18–24 June 2015. [Google Scholar]
- Park, H.S.; Jun, C.H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Lucasius, C.B.; Dane, A.D.; Kateman, G. On k-medoid clustering of large data sets with the aid of a genetic algorithm: Background, feasiblity and comparison. Anal. Chim. Acta 1993, 282, 647–669. [Google Scholar] [CrossRef]
- van der Laan, M.J.; Pollard, K.S. A New Partitioning Around Medoids Algorithm. Biostatistics 2002, 73, 575–584. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, M.; Shi, Y. Adaptive spatial clustering in the presence of obstacles and facilitators. Comput. Geosci. 2013, 56, 104–118. [Google Scholar] [CrossRef]
- Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. Density-based clustering in spatial databases: The algorithm GDBSCAN and its applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Wang, X.; Hamilton, H.J. DBRS: A Density-Based Spatial Clustering Method with Random Sampling. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2637, pp. 563–575. [Google Scholar]
- Wang, B.; Wang, X. Spatial entropy-based clustering for mining data with spatial correlation. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Yamada, I.; Thill, J.C. Comparison of planar and network K-functions in traffic accident analysis. J. Transp. Geogr. 2004, 12, 149–158. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K. Nearest neighbourhood operations with generalized voronoi diagrams: A review. Int. J. Geogr. Inf. Syst. 1994, 8, 43–71. [Google Scholar] [CrossRef]
- Erwig, M. The graph Voronoi diagram with applications. Networks 2000, 36, 156–163. [Google Scholar] [CrossRef]
- Okabe, A.; Yomono, H.; Kitamura, M. Statistical Analysis of the Distribution of Points on a Network. Geogr. Anal. 1995, 27, 152–175. [Google Scholar] [CrossRef]
- Flahaut, B.; Mouchart, M.; Martin, E.S.; Thomas, I. The local spatial autocorrelation and the kernel method for identifying black zones: A comparative approach. Accid. Anal. Prev. 2003, 35, 991–1004. [Google Scholar] [CrossRef]
- Whiteaker, T.L.; Maidment, D.R.; Gopalan, H.; Patino, C.; McKinney, D.C. Raster-network regionalization for watershed data processing. Int. J. Geogr. Inf. Sci. 2007. [CrossRef]
- Tong, D.; Murray, A.T. Spatial Optimization in Geography. Ann. Assoc. Am. Geogr. 2012, 102, 1290–1309. [Google Scholar] [CrossRef]
- Yiu, M.L.; Mamoulis, N. Clustering Objects on a Spatial Network. In SIGMOD Conference; ACM: Paris, France, 2004; pp. 443–454. [Google Scholar]
- Sugihara, K.; Okabe, A.; Satoh, T. Computational method for the point cluster analysis on networks. Geoinformatica 2011, 15, 167–189. [Google Scholar] [CrossRef]
- Okabe, A.; Okunuki, K.; Shiode, S. A Toolbox for Spatial Analysis on a Network. GIS Based Stud. 2005, 38, 57–66. [Google Scholar] [CrossRef]
- Stefanakis, E. NET-DBSCAN: Clustering the nodes of a dynamic linear network. Int. J. Geogr. Inf. Sci. 2007, 21, 427–442. [Google Scholar] [CrossRef]
- Chen, J.; Lai, C.; Meng, X.; Xu, J.; Hu, H. Clustering Moving Objects in Spatial Networks. In Proceedings of the 12th International Conference on Database Systems for Advanced Applications, Bangkok, Thailand, 9–12 April 2007; pp. 611–623. [Google Scholar]
- Shi, Y.; Deng, M.; Gong, J.; Lu, C.-T.; Yang, X.; Liu, H. Detection of clusters in traffic networks based on spatio-temporal flow modeling. Trans. GIS 2019, 23, 312–333. [Google Scholar] [CrossRef]
- Oliveira, D.; Garrett, J.; Soibelman, L. Spatial clustering analysis of water main break events. In Proceedings of the International Workshop on Computing in Civil Engineering 2009, Austin, TX, USA, 24–27 June 2009; pp. 338–347. [Google Scholar] [CrossRef]
- Oliveira, D.; Garrett, J.; Soibelman, L. A density-based spatial clustering approach for defining local indicators of drinking water distribution pipe breakage. Adv. Eng. Inform. 2011, 25, 380–389. [Google Scholar] [CrossRef]
- Smaltschinski, T.; Seeling, U.; Becker, G. Clustering forest harvest stands on spatial networks for optimised harvest scheduling. Ann. For. Sci. 2012, 69, 651–657. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Cluster Validity Methods: Part I. SIGMOD Rec. 2002, 31, 40–45. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Halkidi, M.; Vazirgiannis, M.; Batistakis, Y.; Ri, H.S.W.; Wkhqv, Q.; Frqrplfv, R.I.; Hoodv, W.U.; Pyd, P.; Dqqlv, L.U.J.; Ju, D. Quality scheme assessment in the clustering process. In Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2000; pp. 265–276. [Google Scholar]


| Algorithm1: Local Shortest Path Distance Algorithm Input: undirected planar graph N, central vertex cp, radius eps Output: cp’s eps-neighbors N_eps(cp)
|
| Algorithm2: Generating Density Ordering Input: undirected planar graph N, radius eps Output: density ordering table, density ordering graph
|
| Algorithm3: Forming Clusters Input: density ordering table, density threshold MinPts Output: density-based clusters
|
| Clustering Algorithms | Parameters | Cluster Number | silhouette | RS | DB | SD |
|---|---|---|---|---|---|---|
| NC_DT Algorithm | 37 | −0.5054 | 0.2215 | 0.8167 | 0.0364 | |
| Heirarchical Algorithm | closest-pair distance | 10 | 0.0164 | 0.5517 | 0.4878 | 0.0887 |
| farthest-pair distance | 36 | 0.3949 | 0.9739 | 0.9251 | 0.0264 | |
| average-pair distance | 10 | 0.4466 | 0.9031 | 0.7822 | 0.0866 | |
| median-pair distance | 23 | 0.3420 | 0.9446 | 0.8121 | 0.0393 | |
| radius distance | 16 | 0.4292 | 0.9426 | 0.6821 | 0.0518 | |
| NS-DBSCAN Algorithm | eps = 100, MinPts = 10 | 60 | 0.4470 | 0.9968 | 0.4047 | 0.0131 |
| eps = 100, MinPts = 15 | 38 | 0.4296 | 0.9978 | 0.5004 | 0.0166 | |
| eps = 100, MinPts = 20 | 21 | 0.6740 | 0.9999 | 0.3605 | 0.0180 | |
| eps = 200, MinPts = 15 | 38 | 0.2002 | 0.9719 | 0.5375 | 0.0095 | |
| eps = 200, MinPts = 20 | 31 | 0.4187 | 0.9913 | 0.4407 | 0.0088 | |
| eps = 200, MinPts = 25 | 28 | 0.4703 | 0.9952 | 0.4456 | 0.0113 | |
| eps = 300, MinPts = 20 | 24 | 0.2902 | 0.9628 | 0.5473 | 0.0145 | |
| eps = 300, MinPts = 25 | 23 | 0.2608 | 0.9666 | 0.5213 | 0.0121 | |
| eps = 300, MinPts = 30 | 20 | 0.3220 | 0.9681 | 0.4860 | 0.0119 | |
| eps = 400, MinPts = 25 | 14 | 0.3424 | 0.9307 | 0.5812 | 0.0262 | |
| eps = 400, MinPts = 30 | 16 | 0.3560 | 0.9564 | 0.5610 | 0.0194 | |
| eps = 400, MinPts = 35 | 17 | 0.3777 | 0.9625 | 0.5098 | 0.0158 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Ren, C.; Luo, Y.; Tian, J. NS-DBSCAN: A Density-Based Clustering Algorithm in Network Space. ISPRS Int. J. Geo-Inf. 2019, 8, 218. https://doi.org/10.3390/ijgi8050218
Wang T, Ren C, Luo Y, Tian J. NS-DBSCAN: A Density-Based Clustering Algorithm in Network Space. ISPRS International Journal of Geo-Information. 2019; 8(5):218. https://doi.org/10.3390/ijgi8050218
Chicago/Turabian StyleWang, Tianfu, Chang Ren, Yun Luo, and Jing Tian. 2019. "NS-DBSCAN: A Density-Based Clustering Algorithm in Network Space" ISPRS International Journal of Geo-Information 8, no. 5: 218. https://doi.org/10.3390/ijgi8050218
APA StyleWang, T., Ren, C., Luo, Y., & Tian, J. (2019). NS-DBSCAN: A Density-Based Clustering Algorithm in Network Space. ISPRS International Journal of Geo-Information, 8(5), 218. https://doi.org/10.3390/ijgi8050218





