Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan
Abstract
:1. Introduction
- We proposed a new group movement pattern mining method based on similarity that can identify groups from a huge amount of mobile trajectory data;
- We designed an algorithm to calculate trajectory similarity of objects with low accuracy data;
- We explored different travel behaviors of group and individual tourists.
2. Related Works
2.1. Group Movement Mining
2.2. Trajectory Similarity
2.3. Travel Behaviors
2.4. Application of Group-Level Analysis
3. Materials and Methods
3.1. Problems and Framework
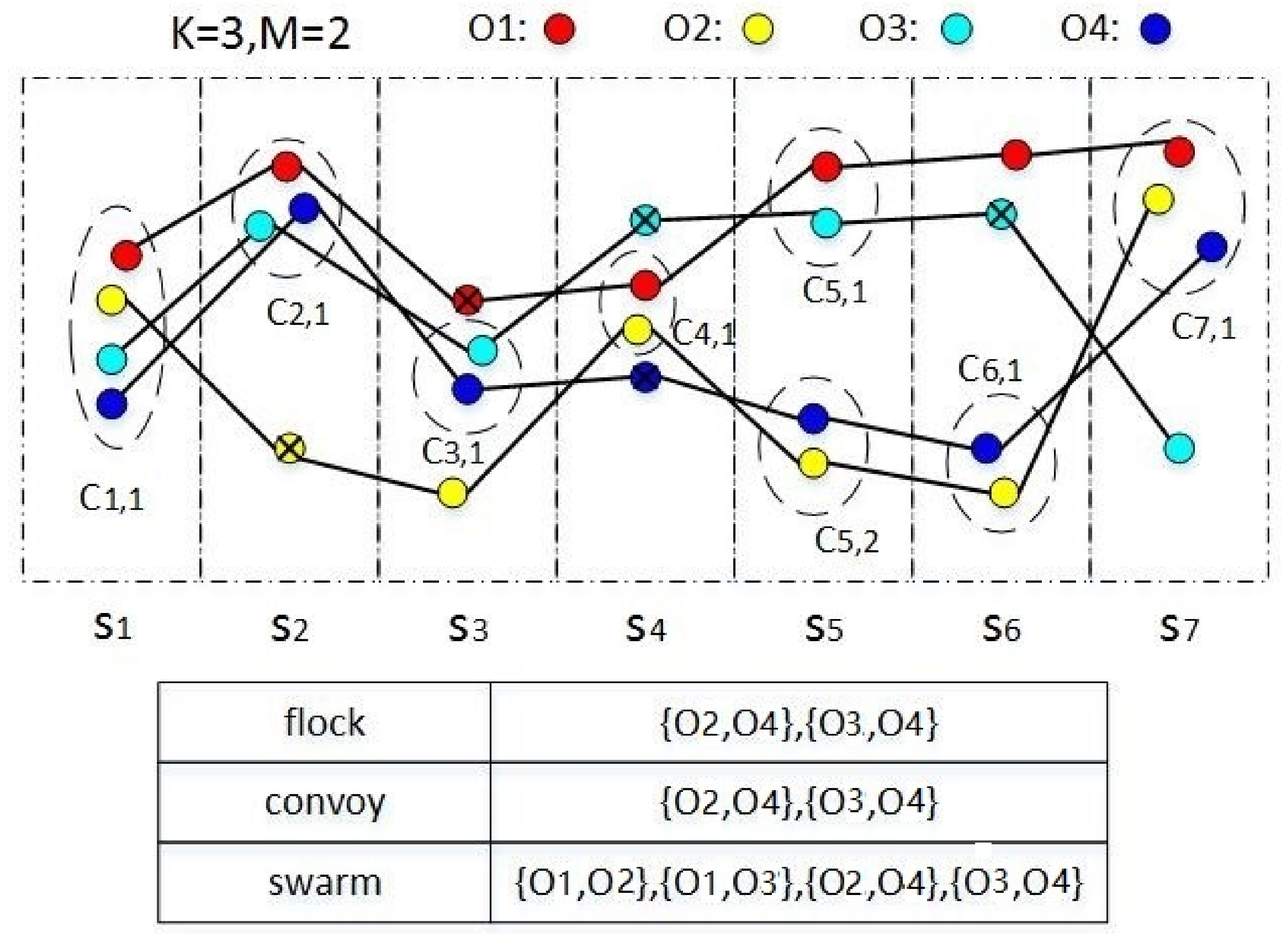
3.1.1. Problem Definition
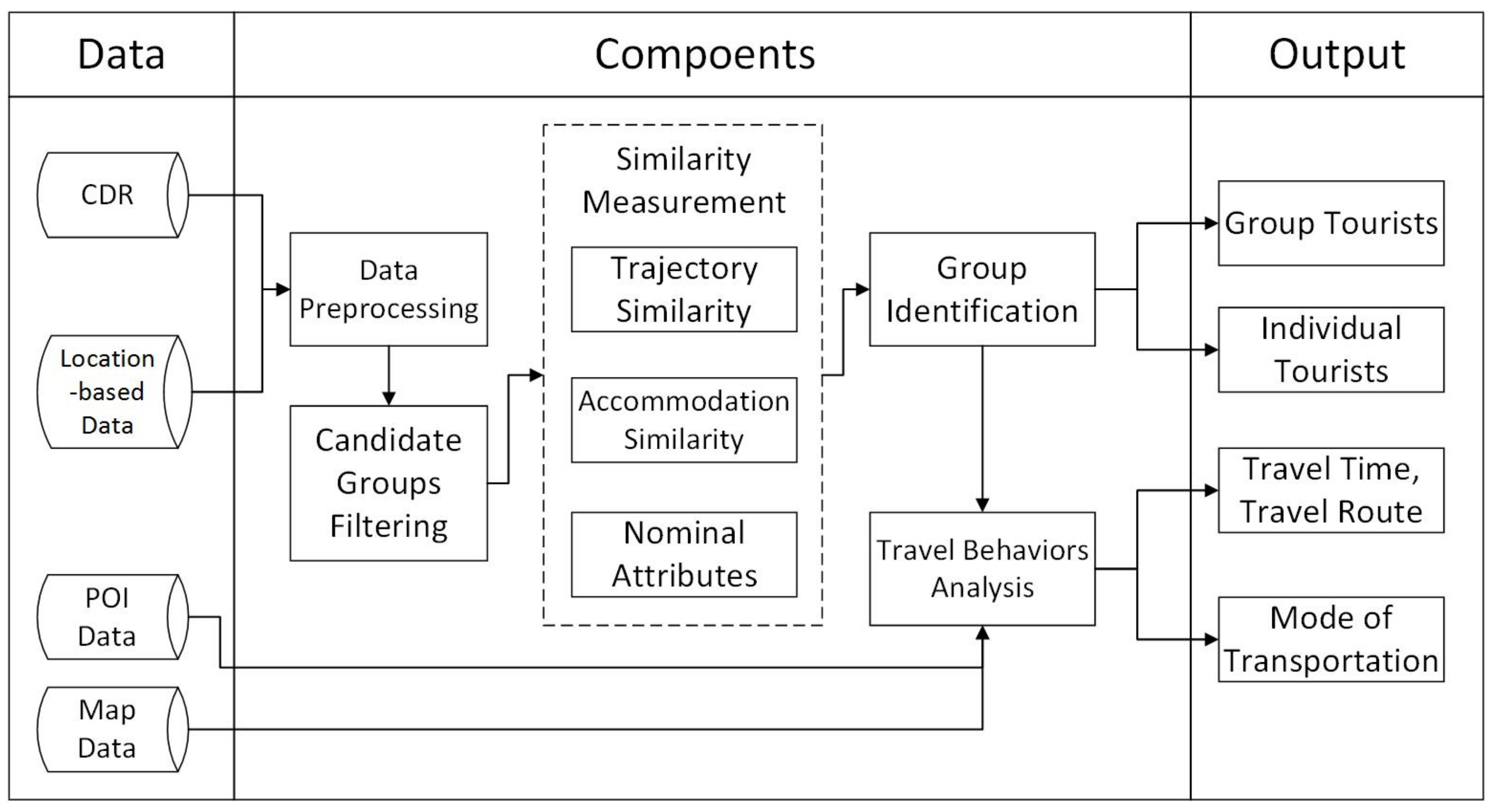
3.1.2. Framework
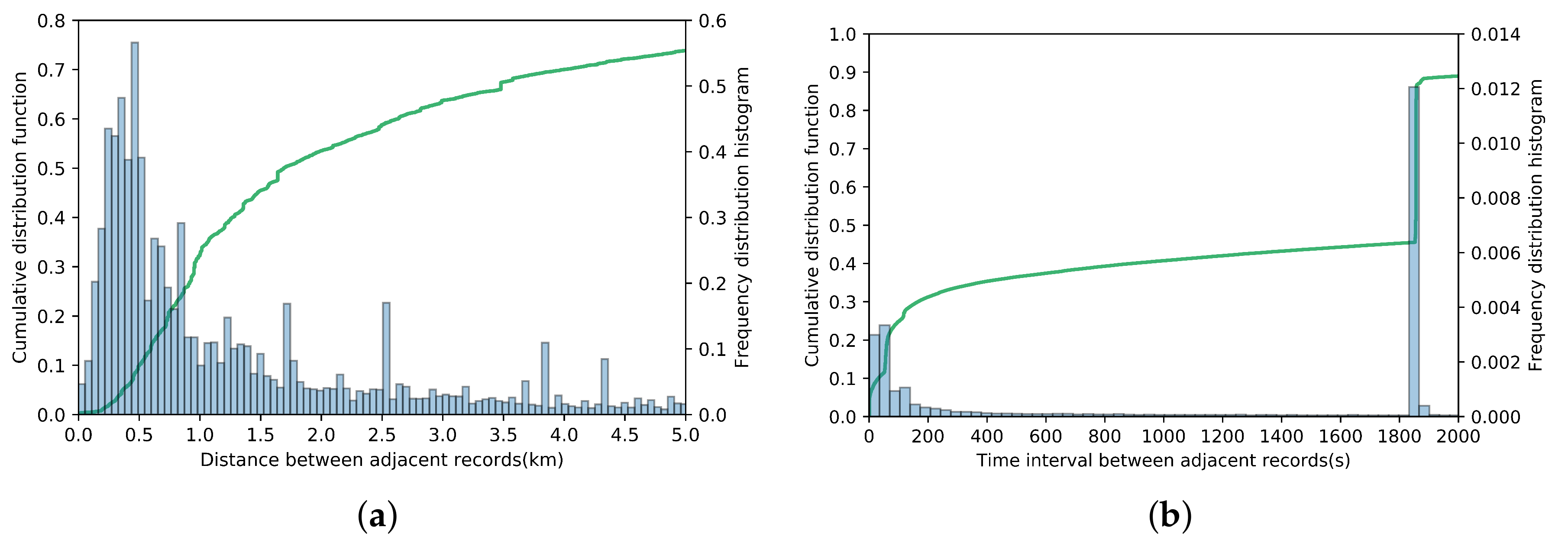
3.2. Data Preprocessing
3.3. Candidate Groups Filtering
3.4. Similarity Measurement
3.4.1. Trajectory Similarity
| Algorithm 1: Trajectory Similarity |
| Input: Output:  |
- (1)
- (2)
3.4.2. Accommodation Similarity
3.4.3. The Similarity of other Features
3.5. Identify Group Tourists
4. Experiment and Results
4.1. Data Set and Experiment
4.2. Tourists Group Identification Results and Validation
4.3. Travel Behaviors Analysis
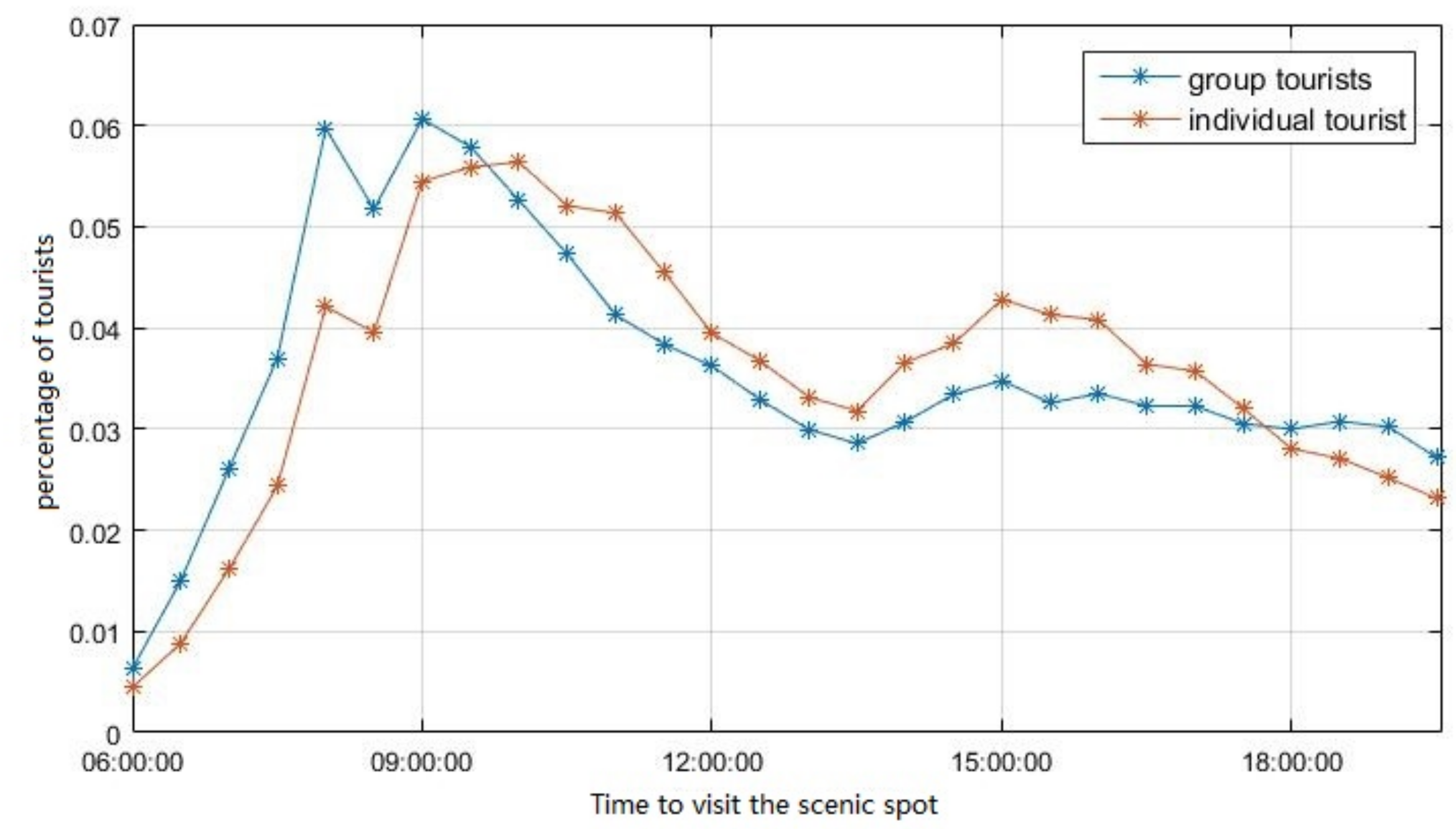
4.3.1. Time to Visit the Scenic Spot
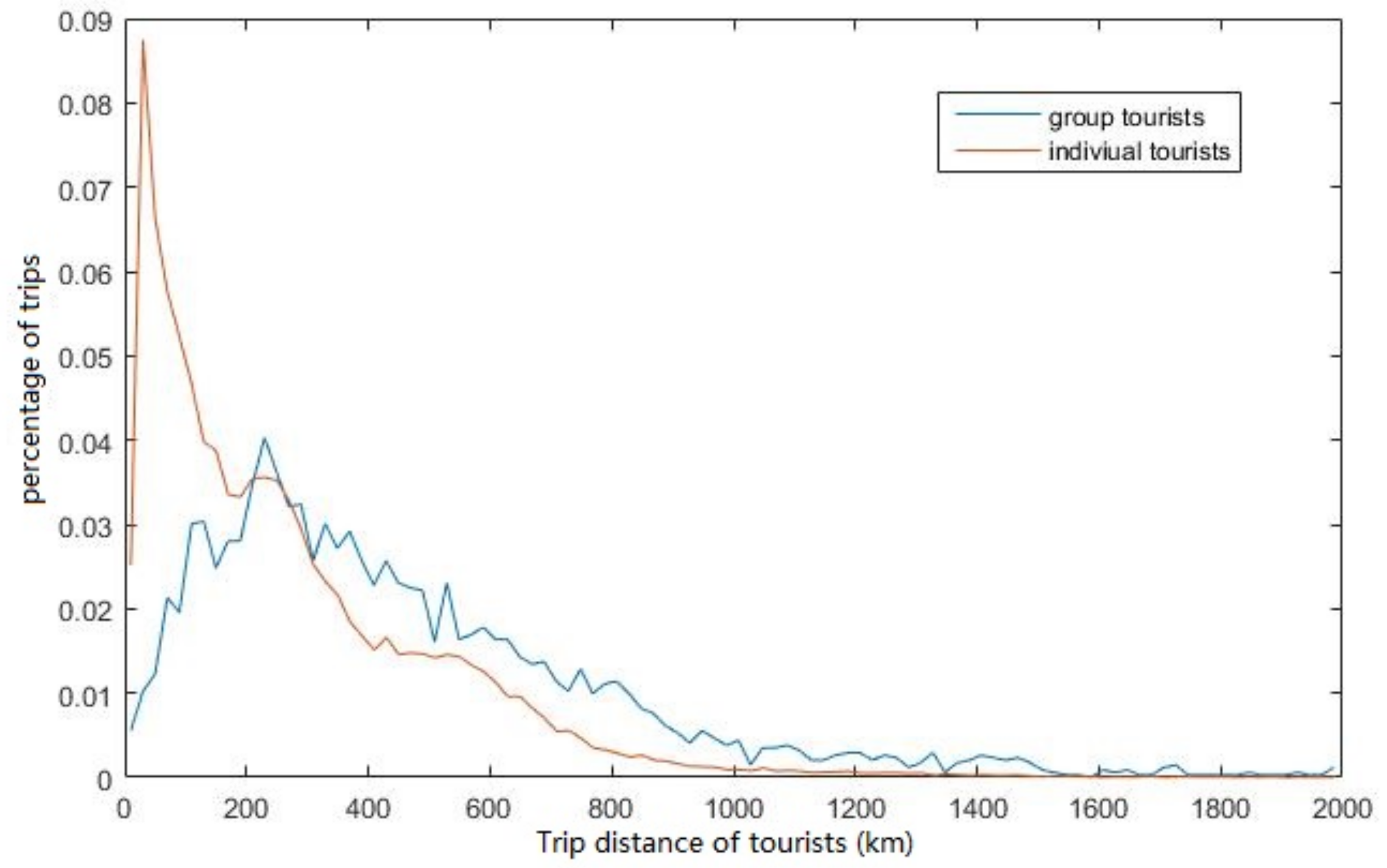
4.3.2. Trip Distance
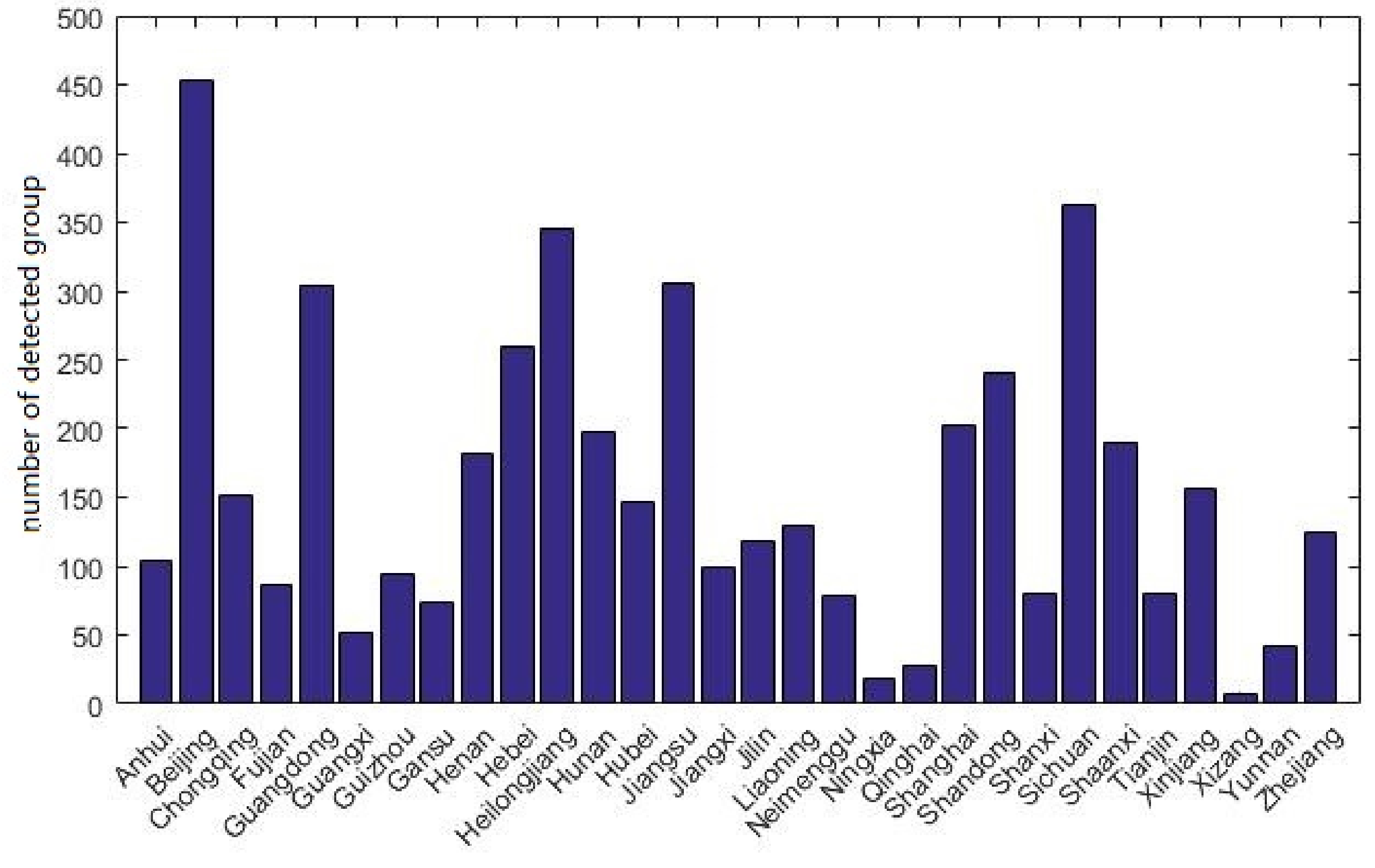
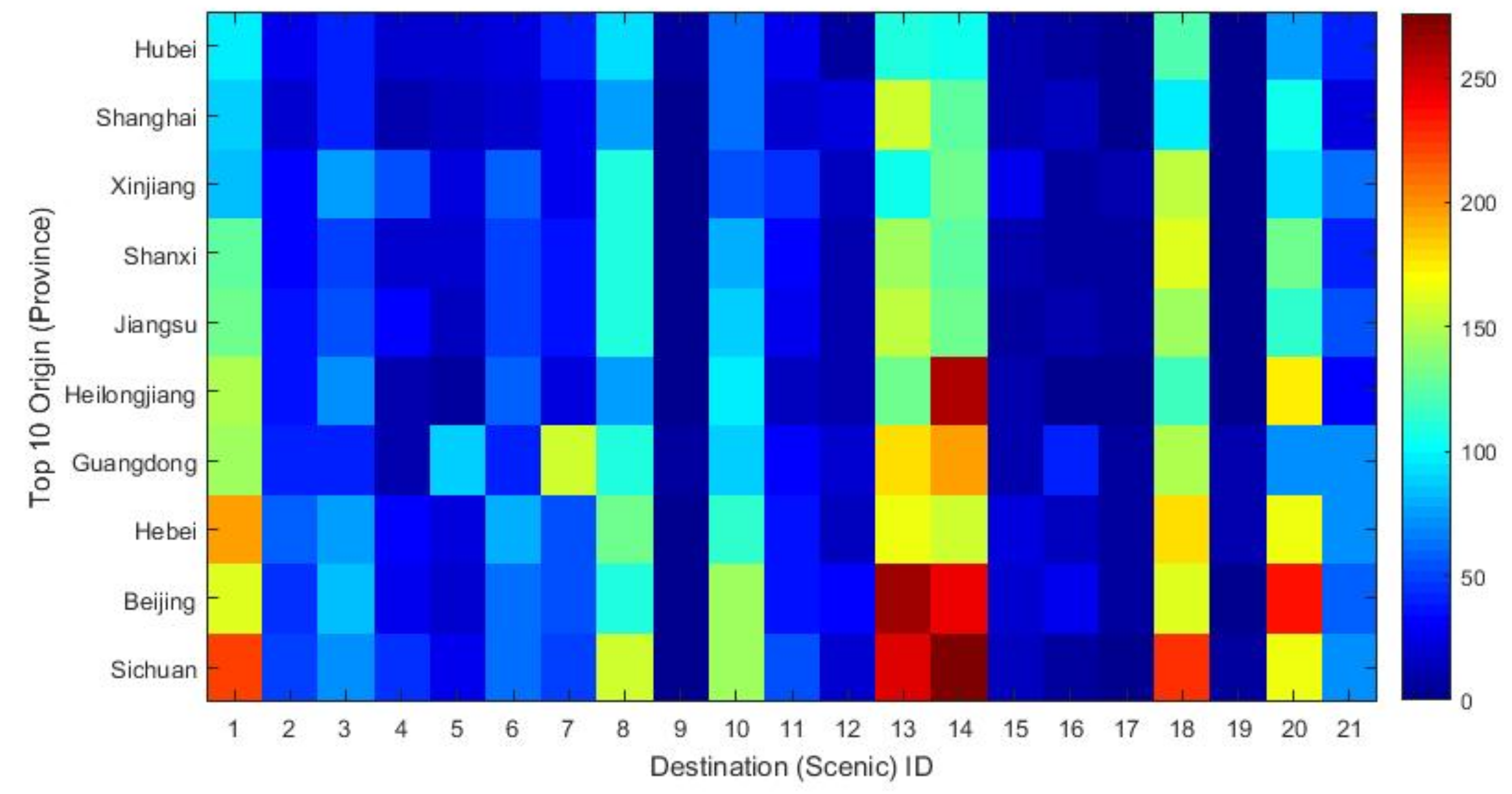
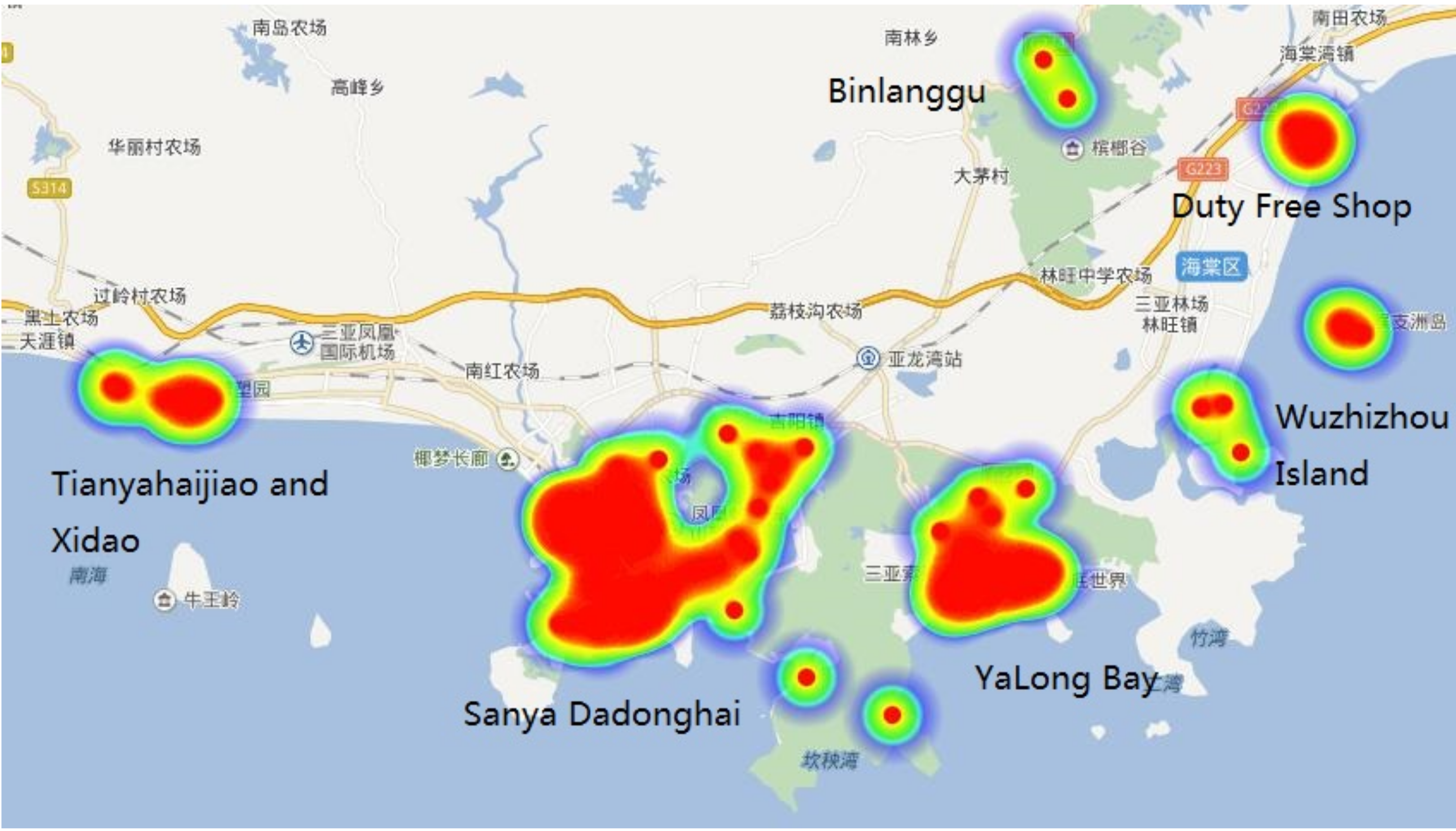
4.3.3. Origin and Destination
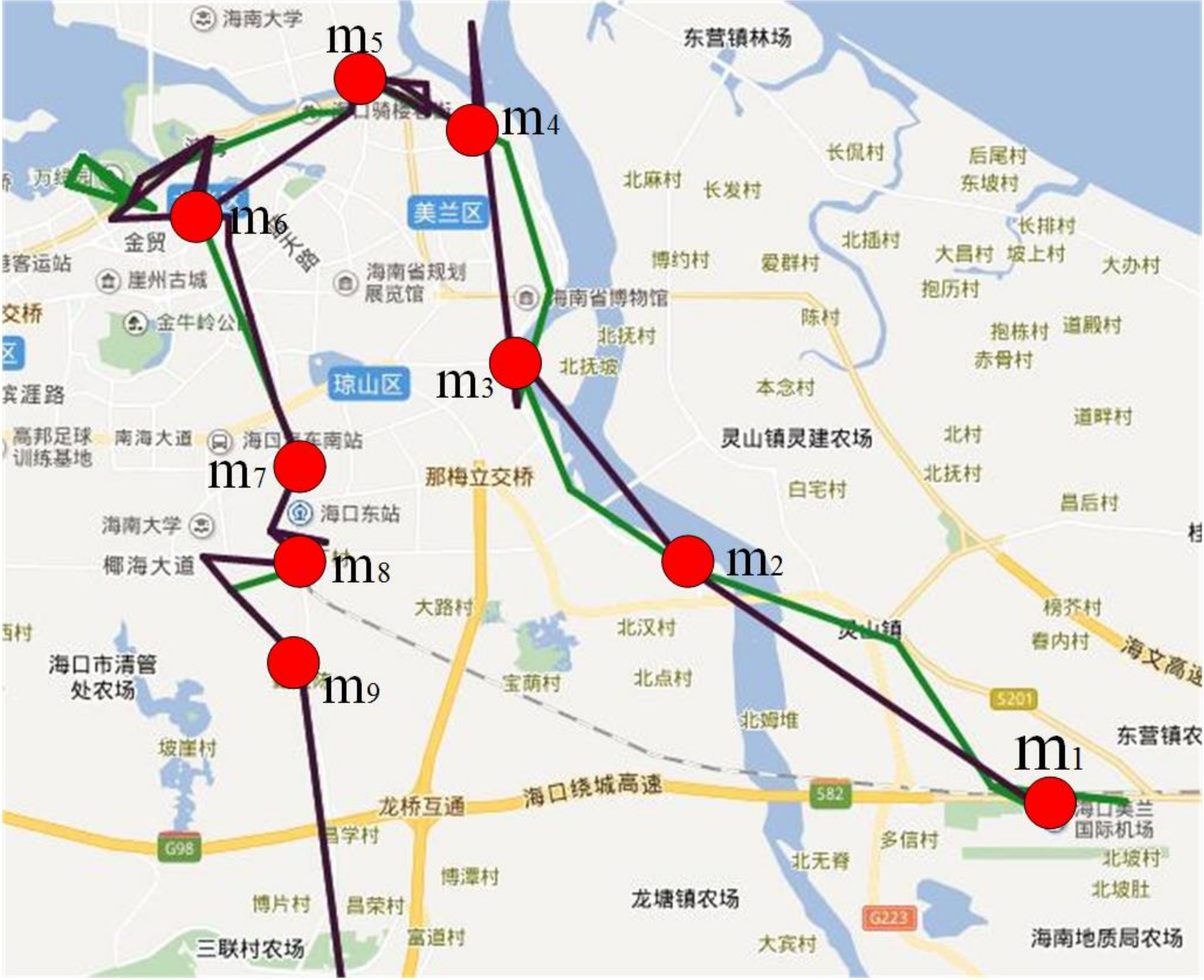
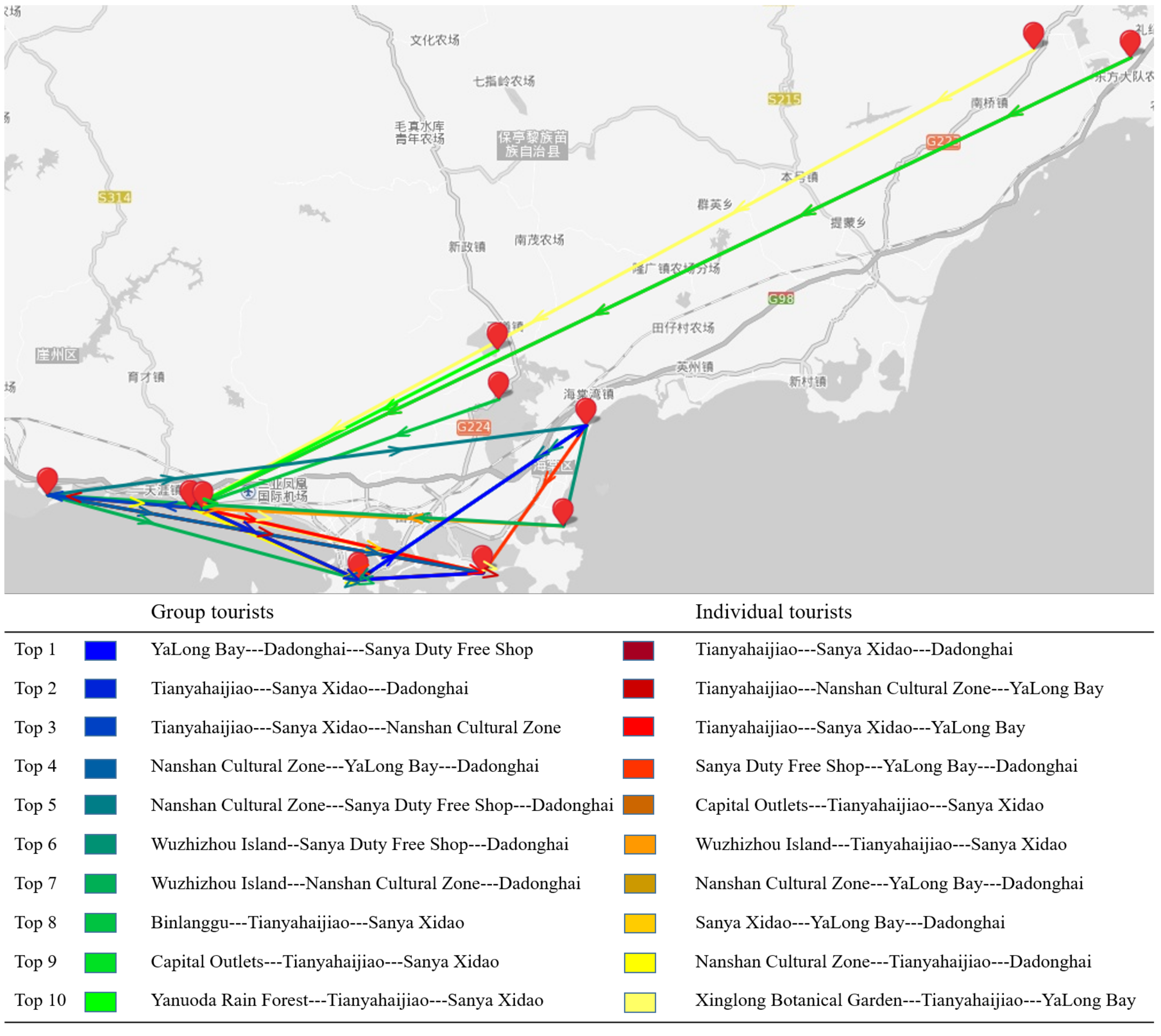
4.3.4. Popular Tourist Routes
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tsai, H.P.; Yang, D.N.; Chen, M.S. Mining group movement patterns for tracking moving objects efficiently. IEEE Trans. Knowl. Data Eng. 2011, 23, 266–281. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Ge, Y.; Xue, Z.; Fu, Y.; Guo, D.; Shao, J.; Zhu, T.; Wang, X.; Li, J. An efficient data processing framework for mining the massive trajectory of moving objects. Comput. Environ. Urban Syst. 2017, 61, 129–140. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Van Kreveld, M. Computing longest duration flocks in trajectory data. In Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, ACM-GIS’06, Arlington, VA, USA, 6–11 November 2006; Association for Computing Machinery: Arlington, VA, USA; pp. 35–42. [Google Scholar]
- Jeung, H.; Yiu, M.L.; Zhou, X.; Jensen, C.S.; Shen, H.T. Discovery of convoys in trajectory databases. Proc. VLDB Endow. 2008, 1, 1068–1080. [Google Scholar] [CrossRef]
- Li, Z.; Ding, B.; Han, J.; Kays, R. Swarm: Mining relaxed temporal moving object clusters. Proc. VLDB Endow. 2010, 3, 723–734. [Google Scholar] [CrossRef]
- Naserian, E.; Wang, X.; Xu, X.; Dong, Y. A framework of loose travelling companion discovery from human trajectories. IEEE Trans. Mobile Comput. 2018, 17, 2497–2511. [Google Scholar] [CrossRef]
- Liu, S.; Wang, S. Trajectory community discovery and recommendation by multi-source diffusion modeling. IEEE Trans. Knowl. Data Eng. 2017, 29, 898–911. [Google Scholar] [CrossRef]
- Tang, L.-A.; Zheng, Y.; Yuan, J.; Han, J.; Leung, A.; Hung, C.-C.; Peng, W.-C. On discovery of traveling companions from streaming trajectories. In Proceedings of the IEEE 28th International Conference on Data Engineering, ICDE 2012, Arlington, VA, USA, 1–5 April 2012; IEEE Computer Society: Arlington, VA, USA; pp. 186–197. [Google Scholar]
- Zheng, K.; Zheng, Y.; Yuan, N.J.; Shang, S.; Zhou, X. Online discovery of gathering patterns over trajectories. IEEE T. Knowl. Data Eng. 2014, 26, 1974–1988. [Google Scholar] [CrossRef]
- Zheng, Y. Trajectory data mining: An overview. ACM Trans Intell. Syst. Technol. 2015, 6, 29. [Google Scholar] [CrossRef]
- Sanches, D.E.; Alvares, L.O.; Bogorny, V.; Vieira, M.R.; Kaster, D.S. A top-down algorithm with free distance parameter for mining top-k flock patterns. In Proceedings of the Annual International Conference on Geographic Information Science, San Jose, CA, USA, 3–5 November 2018; pp. 233–249. [Google Scholar]
- Tang, L.-A.; Zheng, Y.; Yuan, J.; Han, J.; Leung, A.; Peng, W.-C.; Porta, T.L. A framework of traveling companion discovery on trajectory data streams. ACM Trans. Intell. Syst. Technol. 2013, 5, 3. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Xiong, Y.; Prosser, D.J.; Newman, S.H.; Takekawa, J.Y.; Yan, B. Discovering loose group movement patterns from animal trajectories. In Proceedings of the 11th IEEE International Conference on eScience, eScience 2015, Munich, Germany, 31 August–4 September 2015; Institute of Electrical and Electronics Engineers Inc.: Munich, Germany; pp. 196–206. [Google Scholar]
- Zhang, C.; Zhang, K.; Yuan, Q.; Zhang, L.; Hanratty, T.; Han, J. Gmove: Group-level mobility modeling using geo-tagged social media. In Proceedings of the Acm Sigkdd International Conference on Knowledge Discovery & Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1305–1314. [Google Scholar]
- Phan, N.; Poncelet, P.; Teisseire, M. All in one: Mining multiple movement patterns. Int. J. Inf. Techol. Decis. Mak. 2016, 15, 1115–1156. [Google Scholar] [CrossRef]
- Lee, J.-G.; Han, J.; Li, X. A unifying framework of mining trajectory patterns of various temporal tightness. IEEE Trans. Knowl. Data Eng. 2015, 27, 1478–1490. [Google Scholar] [CrossRef]
- Vlachos, M.; Hadjieleftheriou, M.; Gunopulos, D.; Keogh, E. Indexing multi-dimensional time-series with support for multiple distance measures. In Proceedings of the Acm Sigkdd International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2003; pp. 216–225. [Google Scholar]
- Vlachos, M.; Gunopoulos, D.; Kollios, G. Discovering similar multidimensional trajectories. In Proceedings of the Proceedings of the 18th International Conference on Data Engineering (ICDE’02), San Jose, CA, USA, 26 February–1 March 2002; pp. 673–684. [Google Scholar]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Know. Informat. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Lei, C.; Ng, R. On the marriage of lp-norms and edit distance. In Proceedings of the 30th International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 792–803. [Google Scholar]
- Lei, C.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the Acm Sigmod International Conference on Management of Data, Baltimore, MD, USA, 13–17 June 2005; pp. 491–502. [Google Scholar]
- Pierre-François, M. Time warp edit distance with stiffness adjustment for time series matching. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 306–318. [Google Scholar]
- Toohey, K.; Duckham, M. Trajectory similarity measures. Sigspatial Spec. 2015, 7, 43–50. [Google Scholar] [CrossRef]
- Magdy, N.; Sakr, M.A.; Mostafa, T.; El-Bahnasy, K. Review on trajectory similarity measures. In Proceedings of the 7th IEEE International Conference on Intelligent Computing and Information Systems, ICICIS 2015, Cairo, Egypt, 12–14 December 2015; Institute of Electrical and Electronics Engineers Inc.: Cairo, Egypt, 2015; pp. 613–619. [Google Scholar]
- Nakamura, T.; Taki, K.; Nomiya, H.; Seki, K.; Uehara, K. A shape-based similarity measure for time series data with ensemble learning. Pattern Ana. Appl. 2013, 16, 535–548. [Google Scholar] [CrossRef]
- Liu, H.; Schneider, M. Similarity measurement of moving object trajectories. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on GeoStreaming, IWGS 2012, Redondo Beach, CA, USA, 6 November 2012; Association for Computing Machinery: Redondo Beach, CA, USA, 2012; pp. 19–22. [Google Scholar]
- Wang, F.; Zhu, X.; Miao, J. Semantic trajectories-based social relationships discovery using wifi monitors. Pers. Ubiquitous Comput. 2017, 21, 85–96. [Google Scholar] [CrossRef]
- Ra, M.; Lim, C.; Yong, H.S.; Jung, J.; Kim, W.Y. Effective trajectory similarity measure for moving objects in real-world scene. In Information Science and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 641–648. [Google Scholar]
- Xue, M.; Wu, H.; Chen, W.; Ng, W.S.; Goh, G.H. Identifying tourists from public transport commuters. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD 2014, New York, NY, USA, 24–27 August 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 1779–1788. [Google Scholar]
- Vu, H.Q.; Li, G.; Law, R.; Ye, B.H. Exploring the travel behaviors of inbound tourists to hong kong using geotagged photos. Tourism Manag. 2015, 46, 222–232. [Google Scholar] [CrossRef]
- Yang, L.; Wu, L.; Liu, Y.; Kang, C. Quantifying tourist behavior patterns by travel motifs and geo-tagged photos from flickr. Pervasive Mobile Comput. 2015, 18, 18–39. [Google Scholar] [CrossRef]
- Önder, I.; Koerbitz, W.; Hubmannhaidvogel, A. Tracing tourists by their digital footprints: The case of Austria. J. Travel Res. 2016, 55, 566–573. [Google Scholar] [CrossRef]
- Maeda, T.N.; Yoshida, M.; Toriumi, F.; Ohashi, H. Decision tree analysis of tourists’ preferences regarding tourist attractions using geotag data from social media. In Proceedings of the International Conference on IoT in Urban Space, Urb-IoT 2016, Tokyo, Japan, 24–25 May 2016; pp. 61–64. [Google Scholar]
- Maeda, T.N.; Yoshida, M.; Toriumi, F.; Ohashi, H. Extraction of tourist destinations and comparative analysis of preferences between foreign tourists and domestic tourists on the basis of geotagged social media data. ISPRS Int. J. Geo-Inf. 2018, 7, 99. [Google Scholar] [CrossRef]
- Sun, Y.; Li, M. Investigation of travel and activity patterns using location-based social network data: A case study of active mobile social media users. ISPRS Int. J. Geo-Inf. 2015, 4, 1512. [Google Scholar] [CrossRef]
- Phithakkitnukoon, S.; Horanont, T.; Witayangkurn, A.; Siri, R.; Sekimoto, Y.; Shibasaki, R. Understanding tourist behavior using large-scale mobile sensing approach: A case study of mobile phone users in Japan. Pervasive Mobile Comput. 2015, 18, 18–39. [Google Scholar] [CrossRef]
- Barkhordari, R.; Yusof, A.; Sohkim, G. Understanding tourists’ motives for visiting malaysia’s national park. J. Phys. Educ. Sport 2014, 14, 599. [Google Scholar]
- Caughey, D.; Warshaw, C. Dynamic estimation of latent opinion using a hierarchical group-level irt model. Political Anal. 2015, 23, 197–211. [Google Scholar] [CrossRef]
- Bos, E.H.; Wanders, R.B. Group-level symptom networks in depression. JAMA Psychiatr. 2016, 73, 411. [Google Scholar] [CrossRef] [PubMed]
- Nagin, D.S.; Odgers, C.L. Group-based trajectory modeling in clinical research. Annu. Rev. Clin. Psychol. 2010, 6, 109–138. [Google Scholar] [CrossRef] [PubMed]
- Man, A.; Davidyock, T.; Ferguson, L.T.; Ieong, M.; Zhang, Y.; Simms, R.W. Changes in forced vital capacity over time in systemic sclerosis: Application of group-based trajectory modelling. Rheumatology 2015, 54, 1464. [Google Scholar] [CrossRef] [PubMed]
- Moore-Russo, D.; Radosta, M.; Martin, K.; Hamilton, S. Content in context: Analyzing interactions in a graduate-level academic facebook group. Int. J. Educ. Tech. Higher Educ. 2017, 14, 19. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Y.; Gomes, J.B.; Anh, D.T.; Antonatos, S.; Xue, M.; Yang, P.; Yap, G.E.; Li, X.; Krishnaswamy, S.; et al. Oscillation resolution for mobile phone cellular tower data to enable mobility modelling. In Proceedings of the 15th IEEE International Conference on Mobile Data Management, IEEE MDM 2014, Brisbane, QLD, Australia, 15–18 July 2014; Institute of Electrical and Electronics Engineers Inc.: Brisbane, QLD, Australia; pp. 317–324. [Google Scholar]
- Han, J.; Pei, J.; Yin, Y. Mining frequent patterns without candidate generation. In Proceedings of the 2000 ACM SIGMOD—International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 1–12. [Google Scholar]
- Li, Y.-F.; Zhou, Z.-H. Towards making unlabeled data never hurt. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 175–188. [Google Scholar]
- Yin, M.; Sheehan, M.; Feygin, S.; Paiement, J.F.; Pozdnoukhov, A. A generative model of urban activities from cellular data. IEEE Trans. Intell. Transport. Syst. 2018, 19, 1–15. [Google Scholar] [CrossRef]
- Tu, W.; Cao, J.; Yue, Y.; Shaw, S.-L.; Zhou, M.; Wang, Z.; Chang, X.; Xu, Y.; Li, Q. Coupling mobile phone and social media data: A new approach to understanding urban functions and diurnal patterns. Int. J. Geogr. Inf. Sci. 2017, 31, 2331–2358. [Google Scholar] [CrossRef]
- Widhalm, P.; Yang, Y.; Ulm, M.; Athavale, S.; González, M.C. Discovering urban activity patterns in cell phone data. Transportation 2015, 42, 597–623. [Google Scholar] [CrossRef]
- Jiang, S.; Fiore, G.A.; Yang, Y.; Ferreira, J., Jr.; Frazzoli, E.; Gonzalez, M.C. A review of urban computing for mobile phone traces. In Proceedings of the Acm Sigkdd International Workshop on Urban Computing, Chicago, IL, USA, 11–14 August 2013; p. 2. [Google Scholar]
| Notation | Description | Notation | Description |
|---|---|---|---|
| the moving object set | the snapshot | ||
| the moving object i | C | the collection set | |
| the trajectory set | the collection | ||
| the trajectory of moving object i | the distance threshold in collections | ||
| the distance threshold of stay points | M | the minimum size of groups | |
| the time threshold of stay points | K | the minimum snapshots for the occurrence of groups | |
| the stay points set | G | the candidate group set | |
| the stay points | the candidate group | ||
| the timestamp of the stay point | the time threshold of matching point | ||
| the time interval of snapshots | the distance threshold of center of mass | ||
| S | the snapshot set | the similarity threshold |
| User ID | Timestamp | Location ID | Latitude | Longitude | Province |
|---|---|---|---|---|---|
| 0DBFBD46FC7085B9C9C6850C2F02EFBE | 20151207163314 | 38812 | 18.XXXX6179 | 109.XXXX665 | 303 |
| Group Size | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Total Number of Groups | ||
|---|---|---|---|---|---|---|---|---|---|---|
| threshold-based method | weight1 = {0.5, 0.25, 0.25} | 0.60 | 0.684 | 0.123 | 0.073 | 0.061 | 0.040 | 0.016 | 0.003 | 1134 |
| 0.55 | 0.700 | 0.126 | 0.073 | 0.057 | 0.031 | 0.011 | 0.002 | 1683 | ||
| 0.50 | 0.738 | 0.119 | 0.064 | 0.045 | 0.023 | 0.008 | 0.003 | 2326 | ||
| 0.45 | 0.777 | 0.106 | 0.053 | 0.037 | 0.019 | 0.006 | 0.002 | 2987 | ||
| weight2 = {0.25, 0.5, 0.25} | 0.60 | 0.663 | 0.134 | 0.066 | 0.064 | 0.048 | 0.026 | 0 | 682 | |
| 0.55 | 0.668 | 0.130 | 0.075 | 0.066 | 0.041 | 0.017 | 0.003 | 1047 | ||
| 0.50 | 0.669 | 0.132 | 0.085 | 0.065 | 0.035 | 0.012 | 0.002 | 1459 | ||
| 0.45 | 0.723 | 0.121 | 0.068 | 0.051 | 0.026 | 0.009 | 0.002 | 2003 | ||
| weight3 = {0.25, 0.25, 0.5} | 0.60 | 0.695 | 0.130 | 0.076 | 0.057 | 0.031 | 0.010 | 0.002 | 1843 | |
| 0.55 | 0.712 | 0.124 | 0.071 | 0.053 | 0.029 | 0.009 | 0.002 | 2000 | ||
| 0.50 | 0.738 | 0.118 | 0.063 | 0.046 | 0.025 | 0.008 | 0.002 | 2332 | ||
| 0.45 | 0.780 | 0.105 | 0.052 | 0.036 | 0.019 | 0.006 | 0.002 | 3042 | ||
| weight4 ={0.33, 0.33, 0.33} | 0.60 | 0.659 | 0.133 | 0.079 | 0.070 | 0.041 | 0.016 | 0.003 | 1101 | |
| 0.55 | 0.676 | 0.136 | 0.080 | 0.062 | 0.032 | 0.011 | 0.002 | 1601 | ||
| 0.50 | 0.720 | 0.124 | 0.069 | 0.050 | 0.027 | 0.009 | 0.002 | 2129 | ||
| 0.45 | 0.765 | 0.110 | 0.056 | 0.040 | 0.020 | 0.007 | 0.003 | 2761 | ||
| S4VMs | 0.800 | 0.099 | 0.046 | 0.032 | 0.016 | 0.005 | 0.002 | 3509 | ||
| Group Size | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|
| threshold-based method | weight1 = {0.5, 0.25, 0.25} | 0.60 | 0.86 | 0.96 | 1.00 | 0.86 | 1.00 | 1.00 | 1.00 |
| 0.55 | 0.81 | 0.93 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.50 | 0.75 | 0.89 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.45 | 0.61 | 0.83 | 0.94 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| weight2 = {0.25, 0.5, 0.25} | 0.60 | 0.92 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0 | |
| 0.55 | 0.86 | 1.00 | 1.00 | 0.86 | 1.00 | 1.00 | 1.00 | ||
| 0.50 | 0.83 | 0.95 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.45 | 0.75 | 0.88 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| weight3 = {0.25, 0.25, 0.5} | 0.60 | 0.81 | 0.89 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | |
| 0.55 | 0.74 | 0.83 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.50 | 0.67 | 0.80 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.45 | 0.60 | 0.75 | 0.94 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| >weight4 = {0.33, 0.33, 0.33} | 0.60 | 0.87 | 0.96 | 1.00 | 0.86 | 1.00 | 1.00 | 1.00 | |
| 0.55 | 0.81 | 0.96 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.50 | 0.78 | 0.90 | 1.00 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| 0.45 | 0.64 | 0.85 | 0.94 | 0.88 | 1.00 | 1.00 | 1.00 | ||
| S4VMs | 0.91 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||
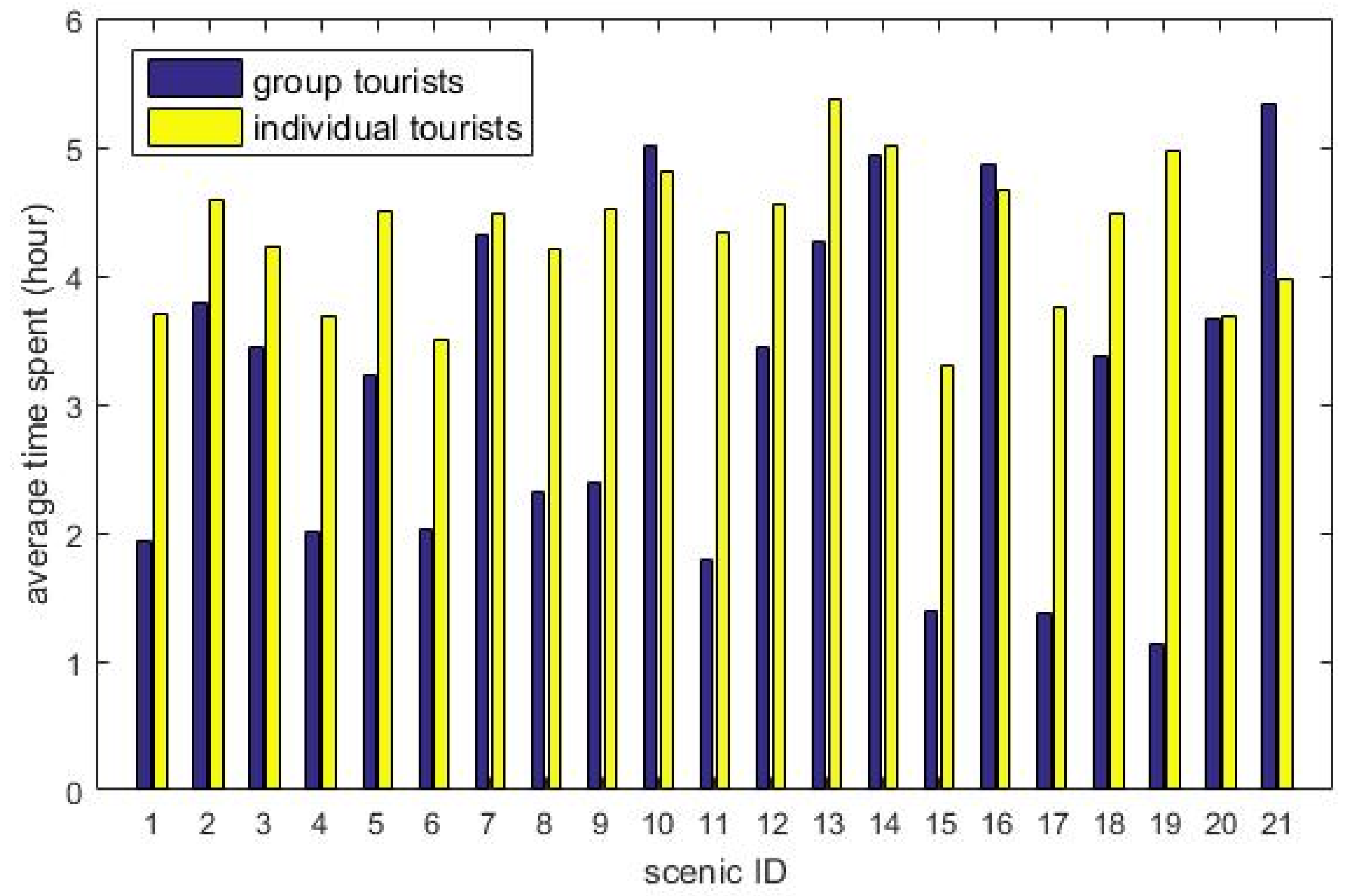
| Id | Scenic Area | Id | Scenic Area |
|---|---|---|---|
| 1 | Nanshan Cultural Zone | 12 | Permanent Site of Boao |
| 2 | Daxiaodongtian | 13 | YaLong Bay |
| 3 | Yanuoda Rain Forest | 14 | Dadonghai |
| 4 | Fenjiezhou Island | 15 | Nanwan Houdao Island |
| 5 | Volcanic Cluster Geopark | 16 | Mission Hills Haikou |
| 6 | Binlanggu | 17 | Hainan Wenbi Mountain |
| 7 | Holiday Beachside Resort | 18 | Sanya Xidao |
| 8 | Tianyahaijiao | 19 | Dongshan Ridge |
| 9 | Tropical Garden of Fauna | 20 | Sanya Duty Free Shop |
| 10 | Wuzhizhou Island | 21 | Capital Outlets |
| 11 | Xinglong Botanical Garden |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Sun, T.; Yuan, H.; Hu, Z.; Miao, J. Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan. ISPRS Int. J. Geo-Inf. 2019, 8, 74. https://doi.org/10.3390/ijgi8020074
Zhu X, Sun T, Yuan H, Hu Z, Miao J. Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan. ISPRS International Journal of Geo-Information. 2019; 8(2):74. https://doi.org/10.3390/ijgi8020074
Chicago/Turabian StyleZhu, Xinning, Tianyue Sun, Hao Yuan, Zheng Hu, and Jiansong Miao. 2019. "Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan" ISPRS International Journal of Geo-Information 8, no. 2: 74. https://doi.org/10.3390/ijgi8020074
APA StyleZhu, X., Sun, T., Yuan, H., Hu, Z., & Miao, J. (2019). Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan. ISPRS International Journal of Geo-Information, 8(2), 74. https://doi.org/10.3390/ijgi8020074





