Studies on Three-Dimensional (3D) Modeling of UAV Oblique Imagery with the Aid of Loop-Shooting
Abstract
1. Introduction
2. Study Area and Data
2.1. Experimental Equipment
2.2. Description of the Experimental Data
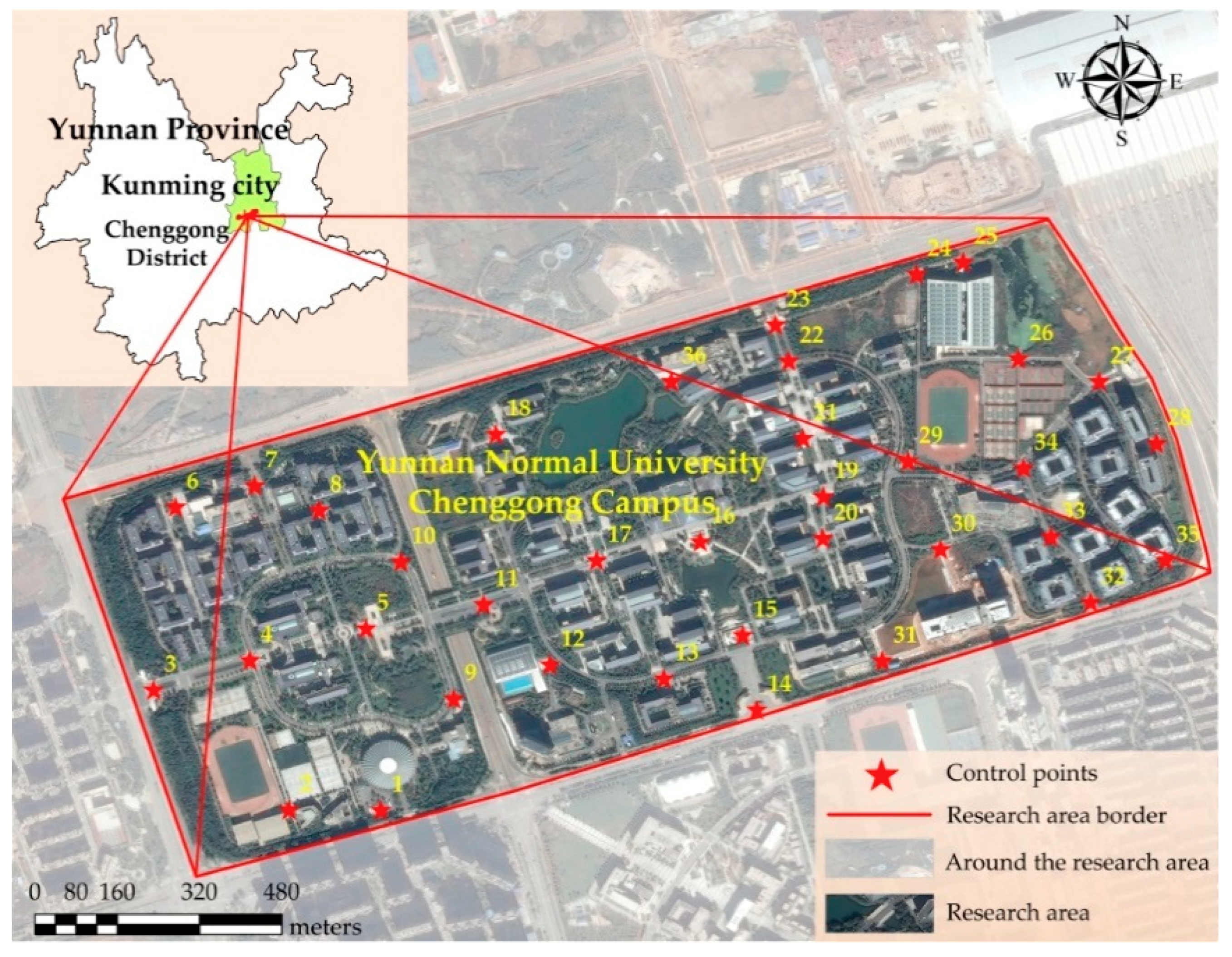
2.2.1. Selection of the Research Area
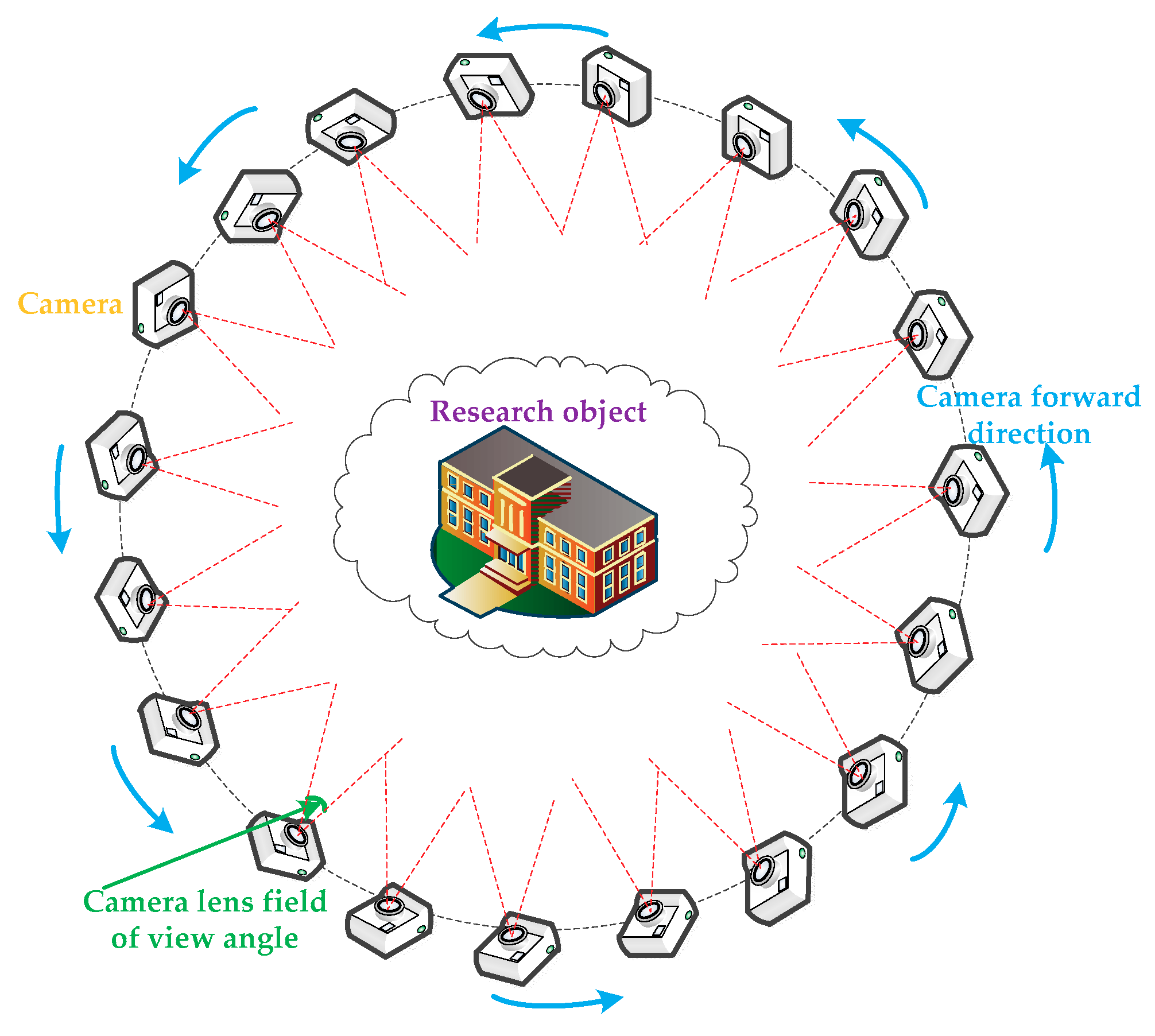
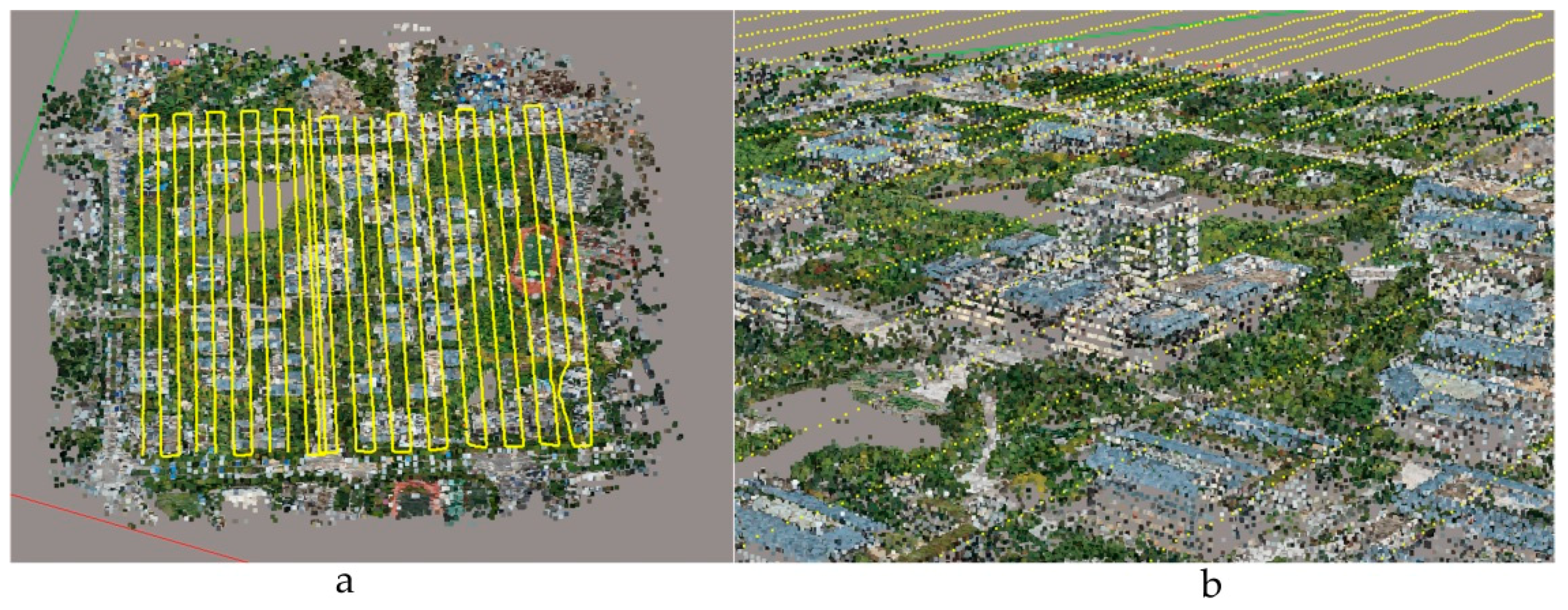
2.2.2. Acquisition of Experimental Data
3. Methods
3.1. The 3D Modeling Process
3.1.1. Data Preprocessing
3.1.2. POS-Aided Aerotriangulation
3.1.3. Construction of the 3D Model
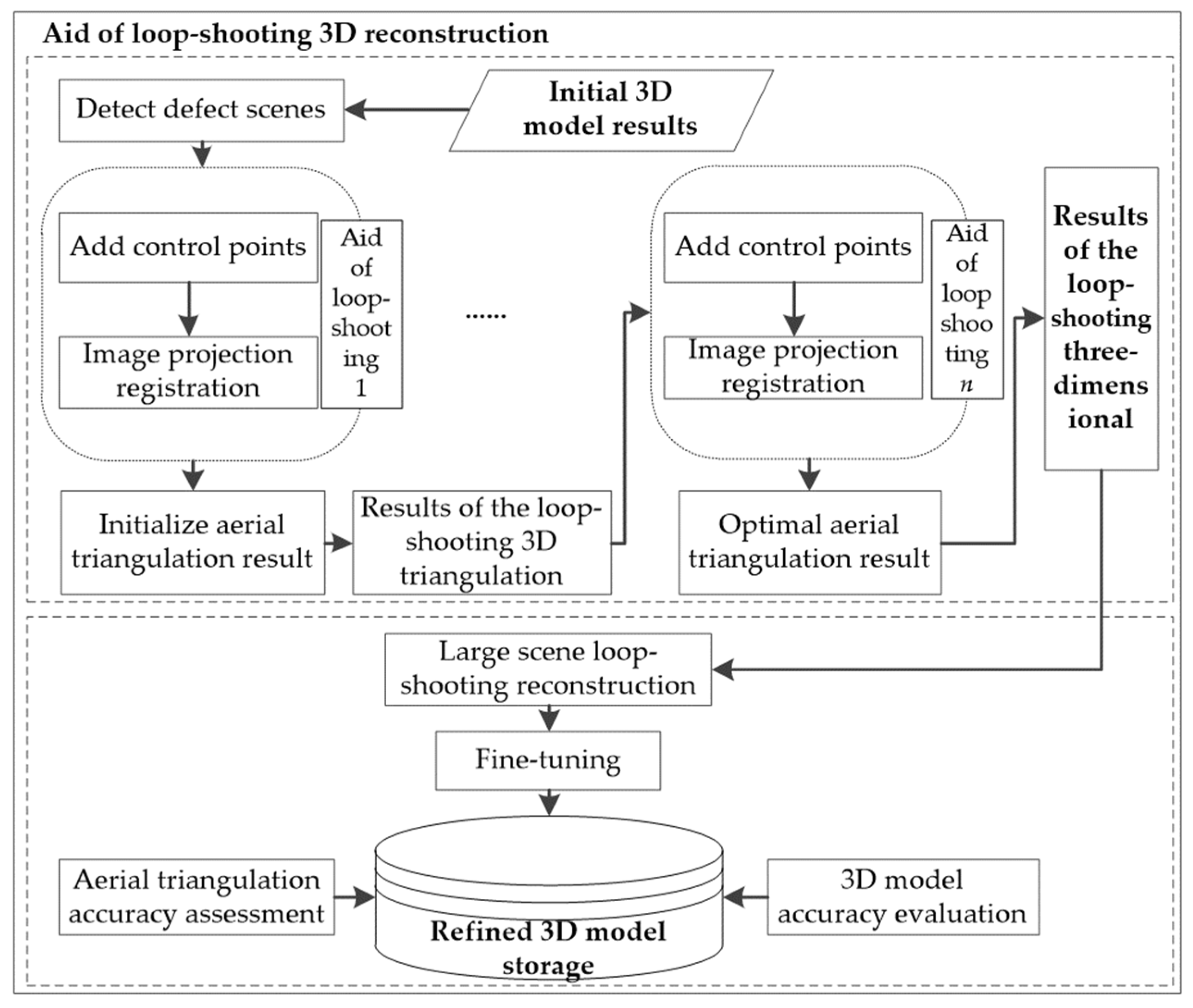
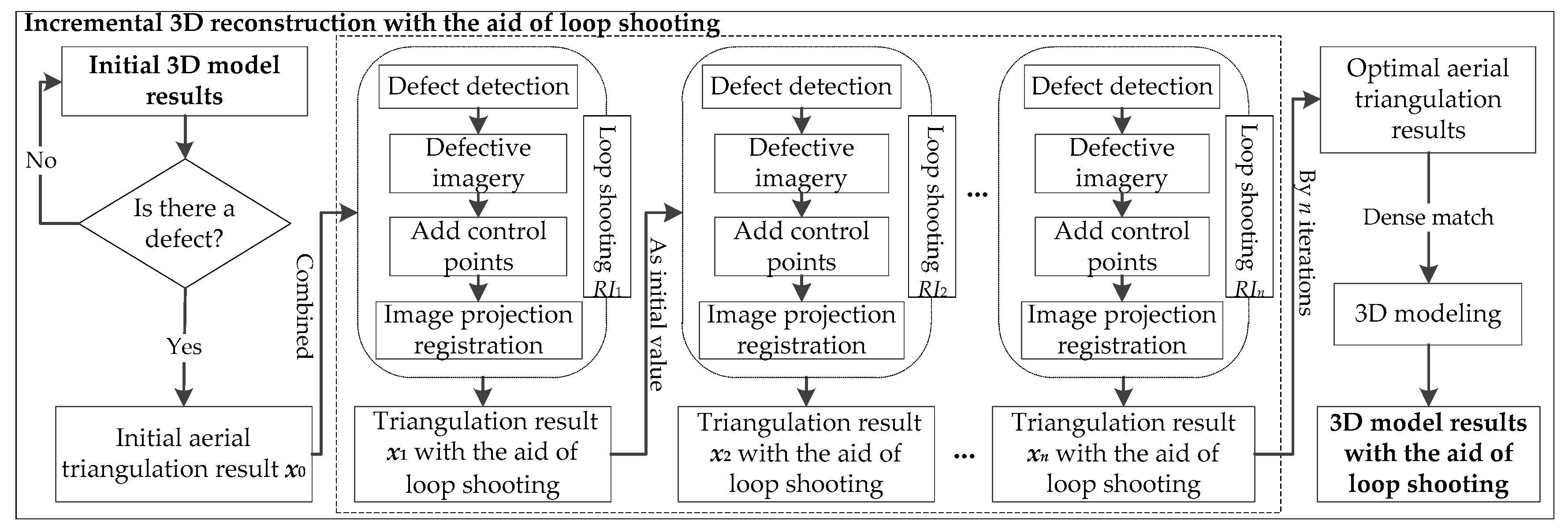
3.2. Incremental 3D Modeling with the Aid of Loop-Shooting
3.2.1. Incremental Modeling with the Aid of Loop-Shooting
3.2.2. Precision Verification and Model Refinement
4. Experimental Results
4.1. POS-Aided Aerotriangulation Results
4.2. Initial 3D Modeling Results
4.3. Incremental Modeling with the Aid of Loop-Shooting
4.4. Refined 3D Modeling
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Obanawa, H.; Hayakawa, Y.; Gomez, C. 3D Modelling of Inaccessible Areas using UAV-based Aerial Photography and Structure from Motion. Trans. Jpn. Geomorphol. Union 2014, 35, 283–294. [Google Scholar]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tuncer, A. UAV-Enabled Intelligent Transportation Systems for the Smart City: Applications and Challenges. IEEE Commun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Cunningham, K.; Walker, G.; Stahlke, E.; Wilson, R. Cadastral Audit and Assessments Using Unmanned Aerial Systems. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 3822, 213–216. [Google Scholar] [CrossRef]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual monitoring of civil infrastructure systems via camera-equipped Unmanned Aerial Vehicles (UAVs): A review of related works. Vis. Eng. 2016, 4, 1. [Google Scholar] [CrossRef]
- Kakooei, M.; Baleghi, Y. Fusion of satellite, aircraft, and UAV data for automatic disaster damage assessment. Int. J. Remote Sens. 2017, 38, 2511–2534. [Google Scholar] [CrossRef]
- Brutto, M.L.; Borruso, A.; D’argenio, A. UAV systems for photogrammetric data acquisition of archaeological sites. Int. J. Herit. Digit. Era 2012, 1, 7–13. [Google Scholar] [CrossRef]
- Room, M.H.M.; Ahmad, A. Mapping of river model using close range photogrammetry technique and unmanned aerial vehicle system. In Proceedings of the 8th International Symposium on Digital Earth, Sarawak, Malaysia, 26–29 August 2013. [Google Scholar]
- Xu, Z.; Wu, L.; Chen, S.; Wang, R.; Li, F.; Wang, Q. Extraction of Image Topological Graph for Recovering the Scene Geometry from UAV Collections. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 319–323. [Google Scholar] [CrossRef]
- Gui, D.Z.; Lin, Z.J.; Zhang, C.C.; Zhi, X.D. Automated texture mapping of 3D city models with images of wide-angle and light small combined digital camera system for UAV. In Proceedings of the SPIE-The International Society for Optical Engineering, Yichang, China, 30 October–1 November 2009; pp. 74982A-1–74982A-8. [Google Scholar]
- Shang, Y.; Sun, X.; Yang, X.; Wang, X.; Yu, Q. A camera calibration method for large field optical measurement. Optik Int. J. Light Electron Opt. 2013, 124, 6553–6558. [Google Scholar] [CrossRef]
- Yusoff, A.R.; Ariff, M.F.M.; Idris, K.M.; Majid, Z.; Chong, A.K. Camera Calibration Accuracy at Different Uav Flying Heights. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 595–600. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W. On-Board GNSS/IMU Assisted Feature Extraction and Matching for Oblique UAV Images. Remote Sens. 2017, 9, 813. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, L.; Gerke, M.; Wang, R.; Yang, H. Skeletal camera network embedded structure-from-motion for 3D scene reconstruction from UAV images. ISPRS J. Photogramm. Remote Sens. 2016, 121, 113–127. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Chen, P.; Liu, S.; Luan, K.; Li, L.; Liu, S.; Liu, X.; Xie, H.; Jin, Y.; et al. Integration of UAV-Based Photogrammetry and Terrestrial Laser Scanning for the Three-Dimensional Mapping and Monitoring of Open-Pit Mine Areas. Remote Sens. 2015, 7, 6635–6662. [Google Scholar] [CrossRef]
- Jutzi, B.; Weinmann, M.; Meidow, J. Weighted data fusion for UAV-borne 3D mapping with camera and line laser scanner. Int. J. Image Data Fusion 2014, 5, 226–243. [Google Scholar] [CrossRef]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef]
- Rhee, S.; Kim, T. Dense 3D Point Cloud Generation from Uav Images from Image Matching and Global Optimazation. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1005–1009. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Remondino, F.; Fraser, C. Digital camera calibration methods: Considerations and comparisons. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 266–272. [Google Scholar]
- Ackermann, F. Application of GPS for aerial triangulation. Photogramm. Eng. Remote Sens. 1993, 59, 1625–1632. [Google Scholar]
- Beck, A.; Pauwels, E.; Sabach, S. The Cyclic Block Conditional Gradient Method for Convex Optimization Problems. SIAM J. Optim. 2015, 25, 2024–2049. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- Xiao, X.; Guo, B.; Li, D.; Li, L.; Yang, N.; Liu, J.; Zhang, P.; Peng, Z. Multi-View Stereo Matching Based on Self-Adaptive Patch and Image Grouping for Multiple Unmanned Aerial Vehicle Imagery. Remote Sens. 2016, 8, 89. [Google Scholar] [CrossRef]
- Vacca, G.; Dessì, A.; Sacco, A. The Use of Nadir and Oblique UAV Images for Building Knowledge. ISPRS Int. J. Geo-Inf. 2017, 6, 393. [Google Scholar] [CrossRef]
- Papakonstantinou, A.; Topouzelis, K.; Pavlogeorgatos, G. Coastline zones identification and 3D coastal mapping using UAV spatial data. ISPRS Int. J. Geo-Inf. 2016, 5, 75. [Google Scholar] [CrossRef]
- Saeedi, S.; Liang, S.; Graham, D.; Lokuta, M.F.; Mostafavi, M.A. Overview of the OGC CDB Standard for 3D Synthetic Environment Modeling and Simulation. ISPRS Int. J. Geo-Inf. 2017, 6, 306. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Fang, Y.; Chen, S. UAV low altitude photogrammetry for power line inspection. ISPRS Int. J. Geo-Inf. 2017, 6, 14. [Google Scholar] [CrossRef]
- Djuknic, G.M.; Richton, R.E. Geolocation and assisted GPS. Computer 2001, 34, 123–125. [Google Scholar] [CrossRef]
- Easa, S.M. Space resection in photogrammetry using collinearity condition without linearisation. Emp. Surv. Rev. 2010, 42, 40–49. [Google Scholar] [CrossRef]
- Přibyl, B.; Zemčík, P.; Čadík, M. Absolute Pose Estimation from Line Correspondences using Direct Linear Transformation. Comput. Vis. Image Underst. 2017, 161, 130–144. [Google Scholar] [CrossRef]
- El-Manadili, Y.; Novak, K. Precision rectification of SPOT imagery using the direct linear transformation model. Photogramm. Eng. Remote Sens. 1996, 62, 67–72. [Google Scholar]
- Yan, L.; Gou, Z.Y.; Zhao, S.H.; Su, M.D. Geometric and automatic mosaic method with collinear equation for aviation twice-imaging data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 585–588. [Google Scholar]
- Zhang, Z.; Zhu, L.; Huang, X.; Lai, H.; Zhao, T. Five-Point Relative Orientation Based on Forward Intersection. Acta Opt. Sin. 2015, 35, 231–238. [Google Scholar] [CrossRef]





| Flight Platform | UAV Configuration |
|---|---|
| Focal length | 16 mm |
| Image pixels | 4000 × 6000 |
| Main point (x, y) | (2999.5, 1999.5) |
| Pixel size | 4 μm |
| Camera sensor | CCD |
| Number of shots | 4 tilted lenses, 1 vertical lens |
| Lens tilt angle | 45° |
| Camera | Parameters Symbol | Value |
|---|---|---|
| Focal length (mm) | F | 16 |
| Radial distortion (mm) | K1 | −2.93279097580502 × 10−10 |
| Radial distortion (mm) | K2 | 2.71144019108787 × 10−17 |
| Radial distortion (mm) | K3 | −7.632447492096 × 10−26 |
| Tangential distortion (mm) | P1 | −1.0747635629201 × 10−10 |
| Tangential distortion (mm) | P2 | −5.08835248657514 × 10−11 |
| Type | Prj (px) | Dis (m) | 3D (m) | X (m) | Y (m) | ∆Prj (px) | ∆Dis (m) | ∆3D (m) | ∆x (m) | ∆y (m) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Original | 0.1 | 0.002 | 0.004 | 0.002 | −0.004 | −0.16 | −0.001 | −0.002 | 0 | −0.001 |
| 1 | Loop-shooting | 0.26 | 0.003 | 0.006 | 0.002 | −0.005 | |||||
| 2 | Original | 0.5 | 0.014 | 0.017 | 0.014 | 0.01 | 0.05 | 0.005 | 0.003 | 0.005 | 0 |
| 2 | Loop-shooting | 0.45 | 0.009 | 0.014 | 0.009 | 0.01 | |||||
| 3 | Original | 0.88 | 0.021 | 0.021 | 0.005 | −0.021 | 0.08 | 0.01 | 0.009 | −0.004 | 0.013 |
| 3 | Loop-shooting | 0.8 | 0.011 | 0.012 | 0.009 | −0.008 | |||||
| 4 | Original | 0.67 | 0.012 | 0.016 | 0.003 | 0.016 | 0.2 | 0.004 | 0.006 | −0.006 | 0.012 |
| 4 | Loop-shooting | 0.47 | 0.008 | 0.01 | 0.009 | 0.004 | |||||
| 5 | Original | 0.07 | 0.002 | 0.002 | 0.002 | 0 | −0.34 | −0.003 | −0.005 | 0.001 | 0.005 |
| 5 | Loop-shooting | 0.41 | 0.005 | 0.007 | 0.001 | −0.007 | |||||
| 6 | Original | 0.27 | 0.007 | 0.008 | 0.007 | 0.002 | −0.49 | 0.001 | 0.002 | 0.003 | −0.003 |
| 6 | Loop-shooting | 0.76 | 0.006 | 0.006 | 0.004 | 0.005 | |||||
| 7 | Original | 0.49 | 0.012 | 0.013 | 0.011 | −0.006 | 0.22 | 0.008 | 0.007 | 0.006 | 0.003 |
| 7 | Loop-shooting | 0.27 | 0.004 | 0.006 | 0.005 | −0.003 |
| Number | ALL_P | Med_P | All_Prj (px) | All_Dis (m) |
|---|---|---|---|---|
| 1 | 24,477 | 1,069 | 0.71 | 0.018 |
| 2 | 67,442 | 1,060 | 0.69 | 0.019 |
| 3 | 86,204 | 1,170 | 0.68 | 0.017 |
| 4 | 161,145 | 1,371 | 0.69 | 0.016 |
| 10 (m) | 20 (m) | 30 (m) | 40 (m) | 50 (m) | 100 (m) | 200 (m) | |
|---|---|---|---|---|---|---|---|
| Observation distance (m) after mending (m) | 10.02 | 20.3 | 30.09 | 40.04 | 50.03 | 100.07 | 200.12 |
| Error value (m) | 0.02 | 0.03 | 0.09 | 0.04 | 0.03 | 0.07 | 0.12 |
| Relative accuracy (%) | 99.80 | 99.85 | 99.70 | 99.90 | 99.94 | 99.93 | 99.94 |
| Small Window | Front Door | Footstep | Back Door | French Window | Stone Pillar | Side Door | |
|---|---|---|---|---|---|---|---|
| Field observation distance (m) | 2.75 | 15.38 | 15.93 | 4.23 | 6.39 | 1.32 | 6.41 |
| Observation distance before mending (m) | 2.65 | 15.22 | 15.86 | 4.11 | 6.14 | 1.22 | 6.52 |
| Observation distance after mending (m) | 2.73 | 15.34 | 15.91 | 4.20 | 6.26 | 1.30 | 6.37 |
| Error value before mending (m) | 0.10 | 0.16 | 0.07 | 0.12 | 0.25 | 0.10 | 0.11 |
| Error value after mending (m) | 0.02 | 0.04 | 0.02 | 0.03 | 0.13 | 0.02 | 0.04 |
| Relative accuracy (%) | 99.27 | 99.74 | 99.87 | 99.29 | 97.97 | 98.48 | 99.38 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yao, Y.; Duan, P.; Chen, Y.; Li, S.; Zhang, C. Studies on Three-Dimensional (3D) Modeling of UAV Oblique Imagery with the Aid of Loop-Shooting. ISPRS Int. J. Geo-Inf. 2018, 7, 356. https://doi.org/10.3390/ijgi7090356
Li J, Yao Y, Duan P, Chen Y, Li S, Zhang C. Studies on Three-Dimensional (3D) Modeling of UAV Oblique Imagery with the Aid of Loop-Shooting. ISPRS International Journal of Geo-Information. 2018; 7(9):356. https://doi.org/10.3390/ijgi7090356
Chicago/Turabian StyleLi, Jia, Yongxiang Yao, Ping Duan, Yun Chen, Shuang Li, and Chi Zhang. 2018. "Studies on Three-Dimensional (3D) Modeling of UAV Oblique Imagery with the Aid of Loop-Shooting" ISPRS International Journal of Geo-Information 7, no. 9: 356. https://doi.org/10.3390/ijgi7090356
APA StyleLi, J., Yao, Y., Duan, P., Chen, Y., Li, S., & Zhang, C. (2018). Studies on Three-Dimensional (3D) Modeling of UAV Oblique Imagery with the Aid of Loop-Shooting. ISPRS International Journal of Geo-Information, 7(9), 356. https://doi.org/10.3390/ijgi7090356





