1. Introduction
Remotely sensed hyperspectral data which is collected by hyperspectral sensors consist of hundreds of contiguous spectral bands with high resolutions [
1,
2]. Recent studies in remote sensing have shown that hyperspectral images (HSIs) have been successfully applied in precision agriculture, urban planning, environmental monitoring and various other fields [
3,
4,
5,
6]. One of the typical characteristics of an HSI is that it cannot only obtain the scene information in the two-dimensional space of the target image but can also acquire one-dimensional spectral information with a high resolution to characterize the physical property. However, the superiority of HSIs with high resolution occurs at the expense of their vast amount of data and their high-dimensionality property (often including hundreds of bands). Furthermore, the great deal of information can also deteriorate the accuracy of classification, due to the redundant and noisy bands [
7,
8]. Therefore, it is of great importance to introduce new dimensionality-reduction methods that readily utilize the information resources of HSIs.
A large number of dimensionality reduction (DR) approaches have been developed in the past decades [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. The existing dimensionality reduction methods can be commonly partitioned into the two branches of feature/band extraction and feature/band selection. The former projects the original high-dimensional HSIs data into a lower-dimensional space to reduce the number of dimensions through various transformations [
16]. Typical algorithms include locally linear embedding (LLE) [
17], principal component analysis (PCA) [
12,
18], and locality preserving projection (LPP) [
19]. A powerful moment distance method was proposed for hyperspectral analysis by using all bands or a subset of bands to detect the shape of the curve in vegetation studies [
14]. Despite the favorable results that can be provided by these methods, the critical information is sometimes damaged after the destruction of the band correlation in the transformation of HSIs data [
20]. Therefore, compared with the band selection approaches, these methods are not always the most optimal choices for dimensionality reduction.
As for the band selection method, the most informative and distinctive band subset is automatically selected from the original band space of the HSIs [
21,
22,
23]. Briefly, band selection technology contains two key elements: the search strategy and the evaluation criterion function [
24]. The former seeks the most discriminative band subset among all feasible subsets through an impactful search strategy, while the latter evaluates a score for each band subset that was selected from the original bands by a suitable criterion function.
The search strategy for the optimal subset is a crucial issue in band selection. One can traverse all combinations of band subsets to generate the optimal subset by an exhaustive search [
25]. However, this method is inapplicable after considering the high dimensionality of hyperspectral data. To randomly select
m bands out of the
n original bands, there are
n!/(n − m)!m! possible results. An extremely high computational cost could be paid for selecting the optimal band combination from all band combinations. Another method is to randomly search for the minimal reduction by metaheuristics [
26].
The inspiration for the metaheuristics usually comes from nature. It is mainly reflected in three types [
27]: physics-based (simulated annealing [
28]), evolutionary-based (genetic algorithm [
29]), and swarm-based (GWO [
30], artificial bee colony [
31], particle swarm optimization [
32],). Notably, the swarm-based technique has been extensively investigated in order to seek out the global optimal band combination by using stochastic and bio-inspired optimization techniques. The GWO algorithm advocated by Mirjalili [
30] is a novel evolutionary-based method and is capable of offering competitive results, in contrast with the other state-of-the-art metaheuristics algorithms. It has the advantages of a broader range of pre-search, simple operation and fast convergence [
30]. It is advantageous for approximating the global optimal solution [
33,
34,
35,
36]. Medjahed et al. [
33] first applied the GWO algorithm to search for the optimal band combination for HSIs classification. It can be seen from their work that the classification result was not satisfied.
With regards to evaluation criteria, each candidate band subset could be assessed by two different techniques: wrapper and filter [
27]. In the wrapper-based method [
27,
37,
38,
39], the learning algorithm, as a predictor wrapped on the search algorithm, participates in the evaluation of the band subset during its search procedure, and the classification results are used as the evaluation criteria for the band subset. In Ma et al. [
39], the three indices of classification accuracy, computing time and stability were used to construct the criteria for evaluation. Despite the attractive performance of the wrapper-based approach, unfortunately, an enormous computational burden would be triggered because a new model is invariably established to evaluate the current band subset at every turn during the search procedures [
40].
The filter-based method evaluates a score for each band or band subset by measuring their inherent attributes that are associated with their class separability rather than a learning method (classification algorithm) [
41]. Often, correlation criteria, distance or information entropy are taken as measurements [
42]. As a direct criterion for similarity comparison, linear prediction (LP) jointly evaluates the similarity between a single band and multiple bands [
43]. The Laplacian score (Lscore) criterion has been utilized to rank bands in order to reduce the search space and obtain the optimal band subset [
44]. Mutual information (MI) has been extensively used over the years as the measurement criterion due to its nonlinear and nonparametric characteristics [
20,
23]. Trivariate mutual information (TMI) is different from the traditional MI-based criterion and takes the correlation among three variables (the class label and two bands) into account concurrently [
45]. The semi-supervised band selection approach based on TMI and graph regulation (STMIGR) used a graph regulation term to select the informative features by unlabeled samples [
45]. Based on Ward’s linkage and MI, a hierarchical clustering method was introduced to reduce the original bands [
20]. This approach was termed WaLuMI. Maximum information and minimum redundancy (MIMR) defines a criterion that maximizes the amount of information for the selected band combination while removing redundant information [
23]. The bands with low redundancy were selected by MI for HSIs classification in these methods. However, choosing a certain number of bands to minimize the correlation among them is a time-consuming optimization issue [
46]. Information gain (IG), also known as the Kullback–Leibler divergence, can measure how much information the features could contribute to the classification. In a previous study [
47], IG was applied to rank the text features to achieve text recognition. Intuitively, the features with larger IG values are considered informative and momentous contributions to classification. Koonsanit [
48] proposed an integrated PCA and IG method for hyperspectral band selection that significantly reduced the computational complexity. Qian et al. [
15] used IG as the similarity function to measure the similarity between the two bands, and then an AP clustering algorithm was used to cluster the initial band to select the optimal band subset.
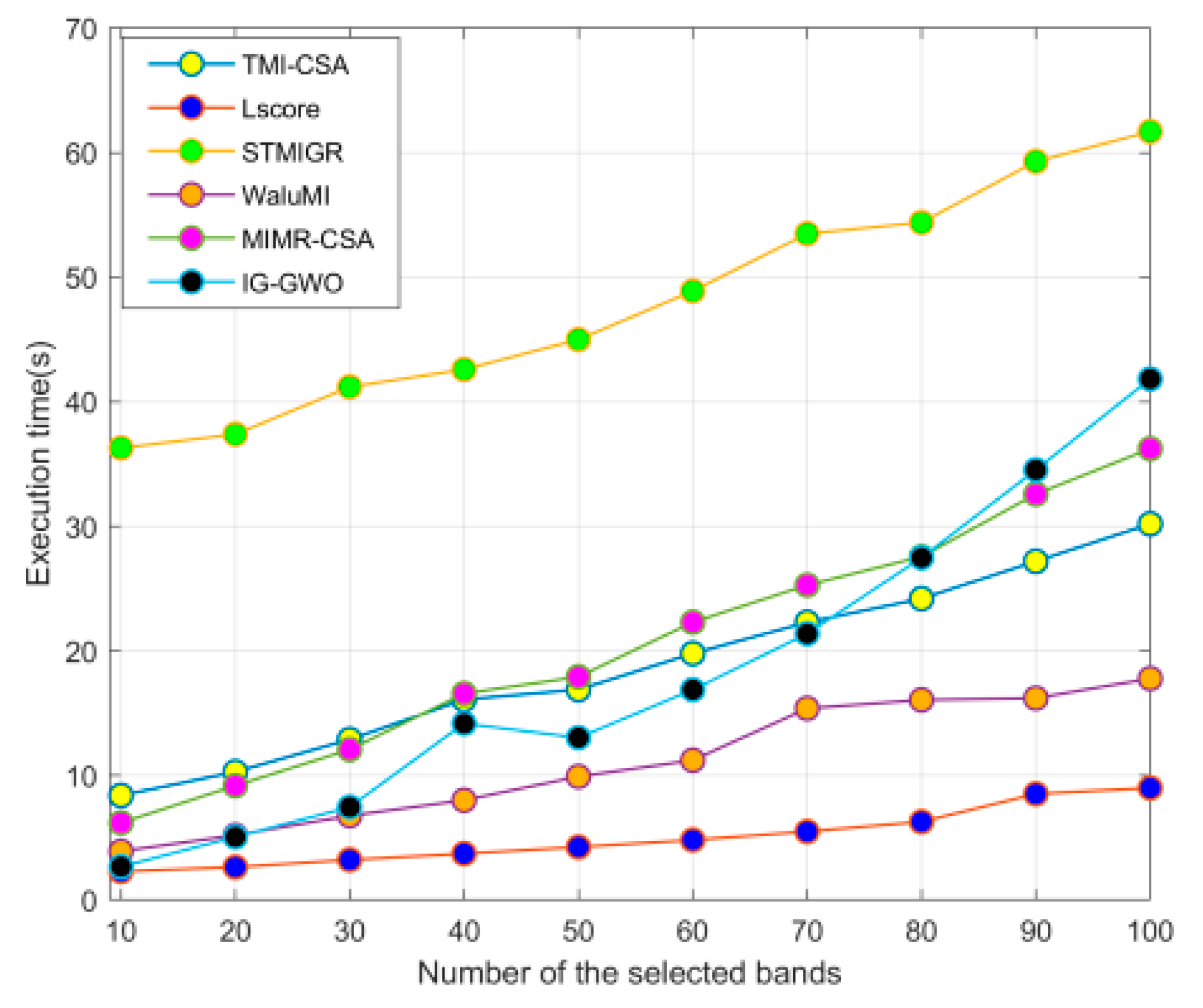
Compared with the wrapper method, the filter-based method is independent of the subsequent learning algorithms during the band selection process and has the advantages of a low computational complexity and strong generalization capability [
40,
41]. However, there are still two issues that need to be addressed: (1) the representative bands can be quickly obtained in terms of the score of each band in the filter-based method, but the correlation between the selected bands may be high; (2) some bands show a significant and indispensable effect on HSIs classification when combined with other bands. However, their score may not be high, so they may be abandoned in error.
On the basis of the above analysis, it is highly necessary to develop a hybrid filter–wrapper feature selection method. In this paper, the filter method based on IG is designed to replace the predictor wrapped on the search algorithm in the wrapped method. The experimental results show that this attempt achieves a reasonable compromise between efficiency (computing time) and effectiveness (classification accuracy actualized by the selected bands).
Furthermore, inspired by the concept of the adaptive subspace decomposition approach (ASD) [
49], an improved subspace decomposition approach has been newly defined. As described previously [
49], the entire spectral bands were first partitioned into band subsets in line with the correlation coefficient of adjacent bands. Then, bands were selected from each subset according to the quantity of information or class separability. Nevertheless, ASD did not overcome the limitations of the traditional subspace decomposition method, which only used correlation coefficients to partition the band space. This leads to the problem that subspaces are difficult to partition because of their multiple minimum points. Thus, we suggest an improved subspace decomposition technique in which band space is decomposed by calculating the value of IG along with the visualization result of the HSIs spectral curve. Moreover, the selection of the same number of bands from each band subset ensures that each band subset makes the same contribution to the final classification results.
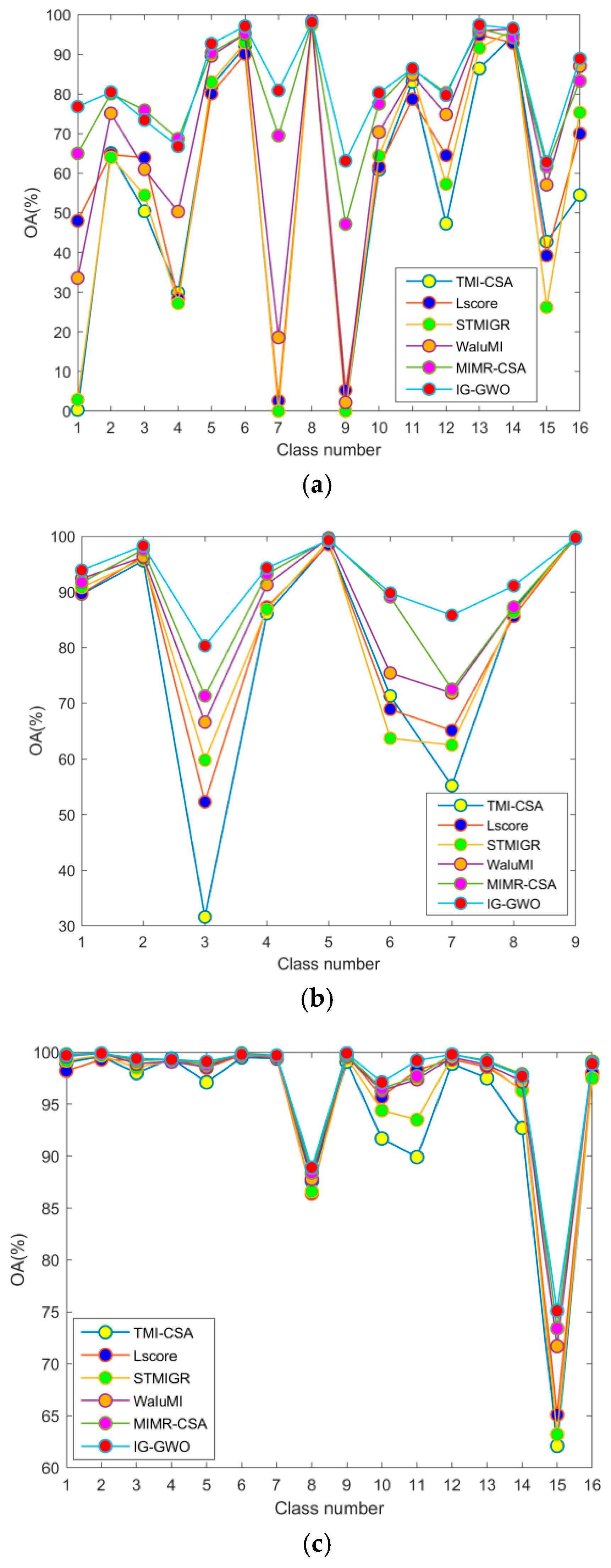
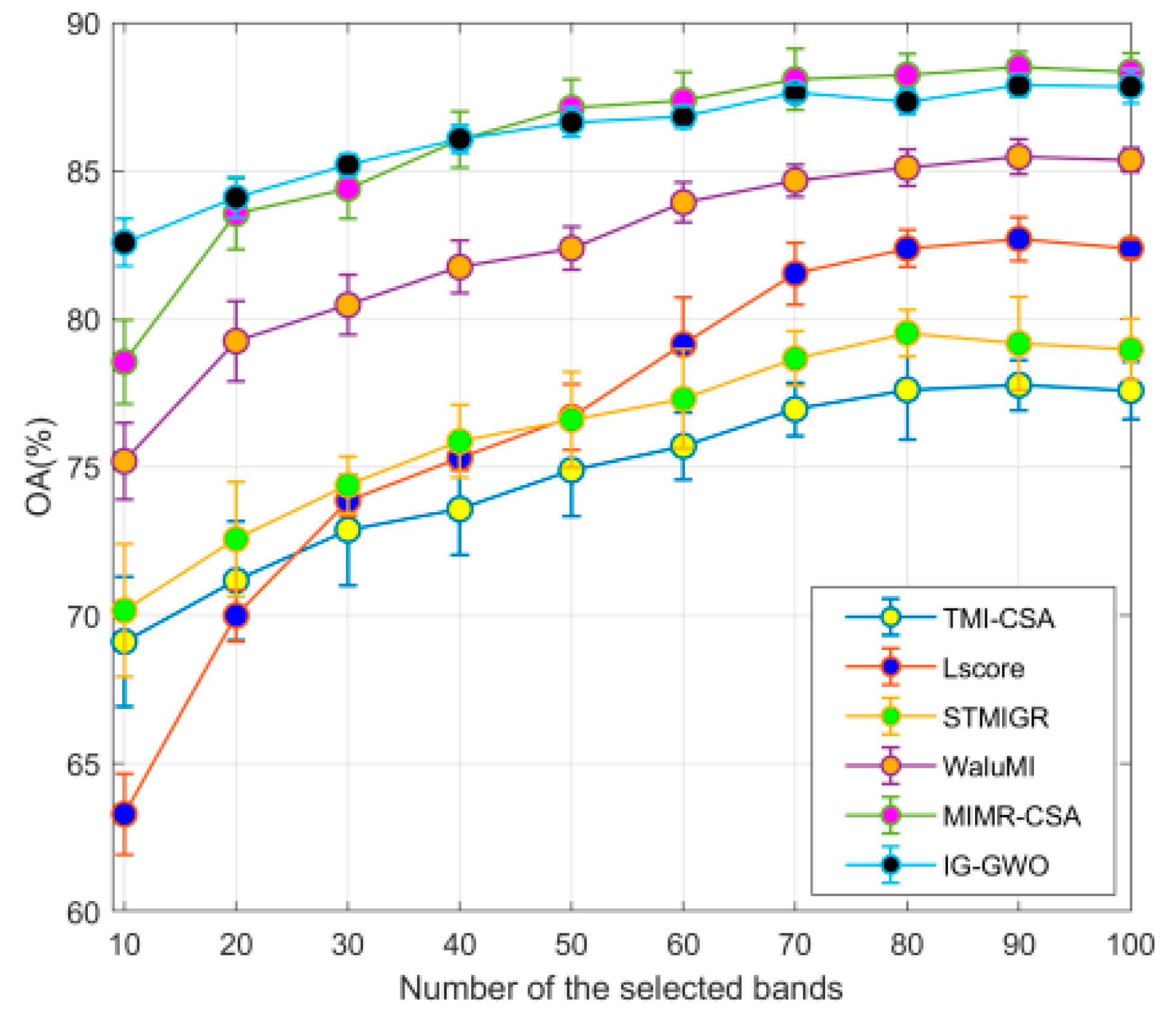
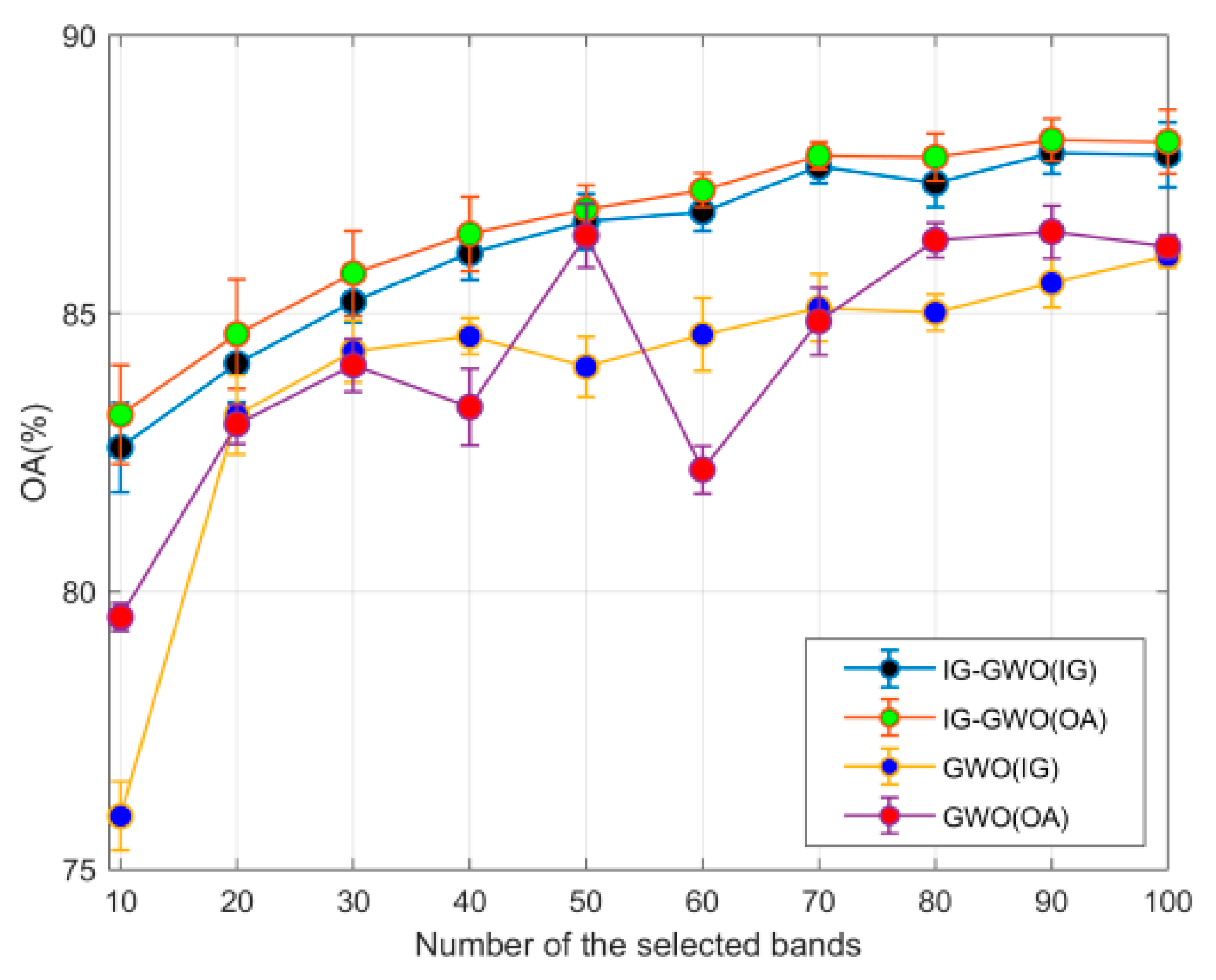
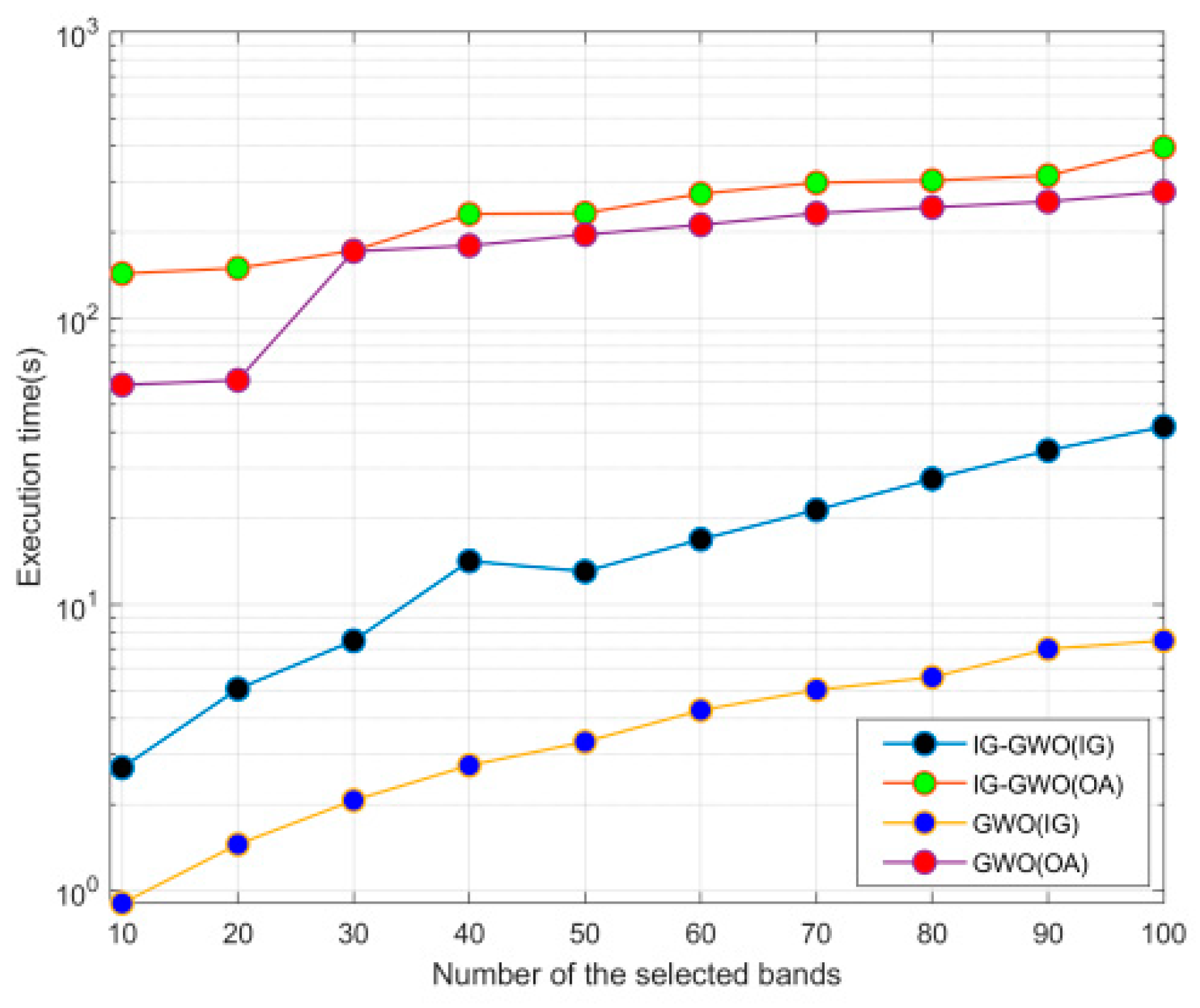
In this study, a novel hybrid filter-wrapper band selection method is introduced based on an improved subspace decomposition method and GWO optimization algorithm, and it is implemented through a three-step strategy: decomposition, selection and optimization. Extensive experimental results over the three hyperspectral datasets presented here clearly prove the effectiveness of the proposed method (IG-GWO), offering a solution to the aforementioned limitations and excelling compared to the other state-of-the-art band selection methods.
2. Materials and Methods
2.1. Information Gain (IG)
In machine learning and information theory, IG is a synonym for Kullback—Leibler divergence, which was introduced by Kullback and Leibler [
47]. As a feature selection technique, IG has been widely applied to select a slice of important features for text classification. The larger the IG of a feature is, the more information it contains [
48]. The computation of IG is based on entropy and conditional entropy.
Given a hyperspectral dataset
with
l bands
and
q classes {
C1,
C2,
…, Cq}, the
IG of band
Bi can be mathematically defined as below:
where
E(
C) denotes the entropy of dataset
HD, and
E(
C|
B) is the conditional entropy.
E(
C) and
E(
C|
Bi) are expressed as follows:
where
denotes the cardinality of the set, and
NBm indicates the number of pixels in the
m-th set that was obtained by using the band
Bi to partition the hyperspectral dataset into
k different sets via their intensity value
G. Assuming a hyperspectral image with a radiometric resolution of 8 bits, the intensity value
G of pixels in the image will have 256 gray levels;
is the number of pixels belonging to the
j-th class in the
m-th set.
The band with the highest IG value is characterized by better classification performance. However, it is possible that the bands with high IG values will concentrate on a band subinterval. In this case, a flawed classification result will be obtained because the adjacent bands generally have a strong correlation. In addition, we do not know how to properly pre-assign the threshold to select them. Consequently, it is difficult to directly select such bands from the original bands to reduce the dimension of the hyperspectral dataset by using IG values only.
2.2. Gray Wolf Optimizer (GWO)
Very recently, a more powerful optimization method, the gray wolf optimizer, was proposed by Mirjalili [
30]. This algorithm simulated the living and hunting behavior of a group of gray wolves. All gray wolves were divided hierarchically into four groups, denoted in turn as alpha wolf, beta wolf, delta wolf and omega wolf. In the first group, there was only a gray wolf, the alpha wolf, which was the leader of the others and controlled the whole wolf pack. The beta wolf only obeyed the alpha wolf in the second group and helped the alpha wolf to make some decisions and commanded the rest of the wolves in the two lower levels. The alpha wolf would be replaced by the beta wolf if the alpha wolf passed away. The gray wolves in the fourth group were named omega wolves and were responsible for collecting useful information to submit to the alpha wolf and beta wolf. The remainders were called delta wolves. The hunting procedure of gray wolves was carried out in three steps: tracking, pursuing and attacking the prey.
The social hierarchy and hunting procedure can be mathematically described as follows:
: The fittest solution;
: The second-best solution;
: The third-best solution;
: The remaining candidate solutions.
The mathematical model of encircling the prey can be described as
where
t denotes the current iteration;
represents the distance between the gray wolf and the prey;
and
are coefficient vectors;
is the position vector of the prey and
the position vector of a gray wolf. The symbol. represents the corresponding multiplication of each component of two vectors.
The coefficient vectors
A and
C can be obtained by
where components of
linearly decrease from 2 to 0 over the course of iterations;
and
are random vectors.
The mathematical model of hunting is
Repeating Equations (4)–(10), one can eventually compute the best solution .
It should be noted that this theory is valid in a continuous case. If we slightly revise Equation (10) by rounding the operation, this algorithm can be used in a discrete case.
The GWO algorithm is summarized by the following steps:
- Step 1
Initialize the gray wolf population GWi (= 1, 2, …, N); parameters ; maximum iterations;
- Step 2
Select the alpha, beta and delta wolves from the population by calculating fitness;
- Step 3
Update the position of each wolf by Equation (10);
- Step 4
Compute Equations (4)–(9) and go to step 2;
- Step 5
Output alpha until the iterations reach their maximum or the choice of the same alpha wolf twice in succession is satisfied.
To select the most distinguished band combination for increasing classification accuracy, it is important to choose/define the fitness function in step 2. The information gain (IG) is adopted as the fitness function in this study. Unlike the adoption of overall accuracy (OA) as fitness, one of the advantages of adopting IG as fitness is to effectively reduce the computation time of the GWO method since the computation of IG has nothing to do with the classification results.
Provided that there are s bands in a band combination (gray wolf), the
IG value can be computed by Equation (11):
where
is the information gain value of
i-th band obtained from Equations (1)–(3).
2.3. The Proposed Band Selection Method
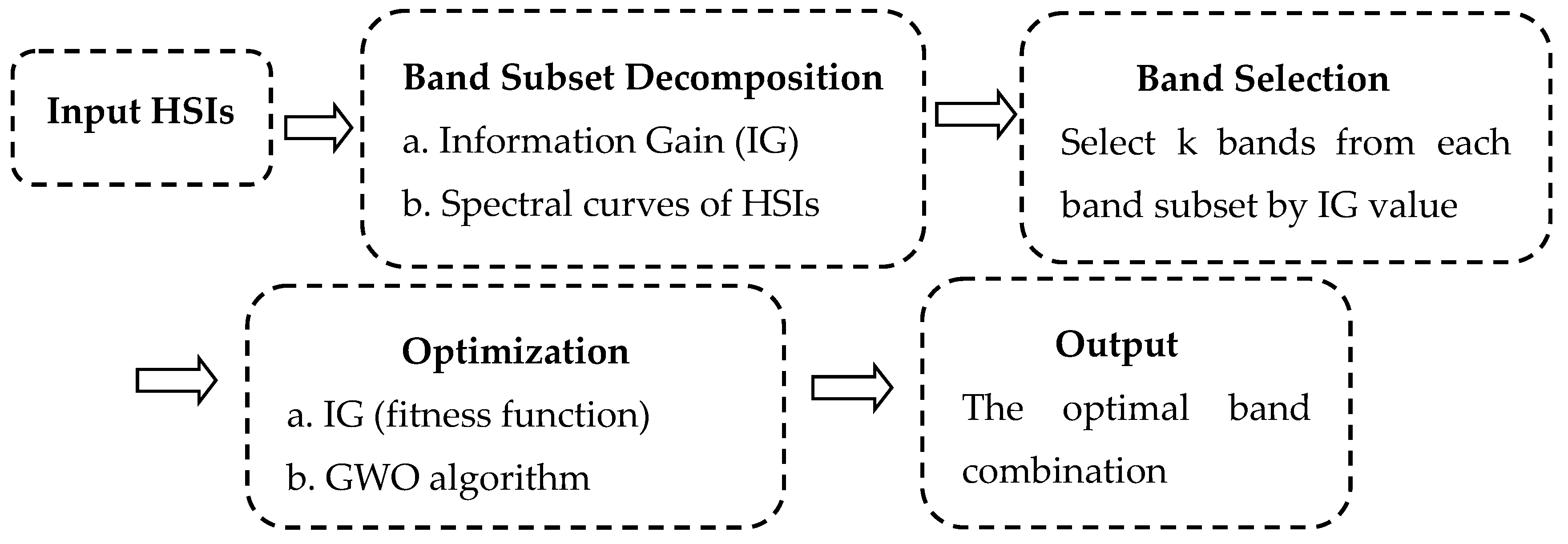
In this study, we integrate band subset decomposition, band selection and a GWO optimization algorithm to select the optimal band combination. The framework of the proposal is described in
Figure 1.
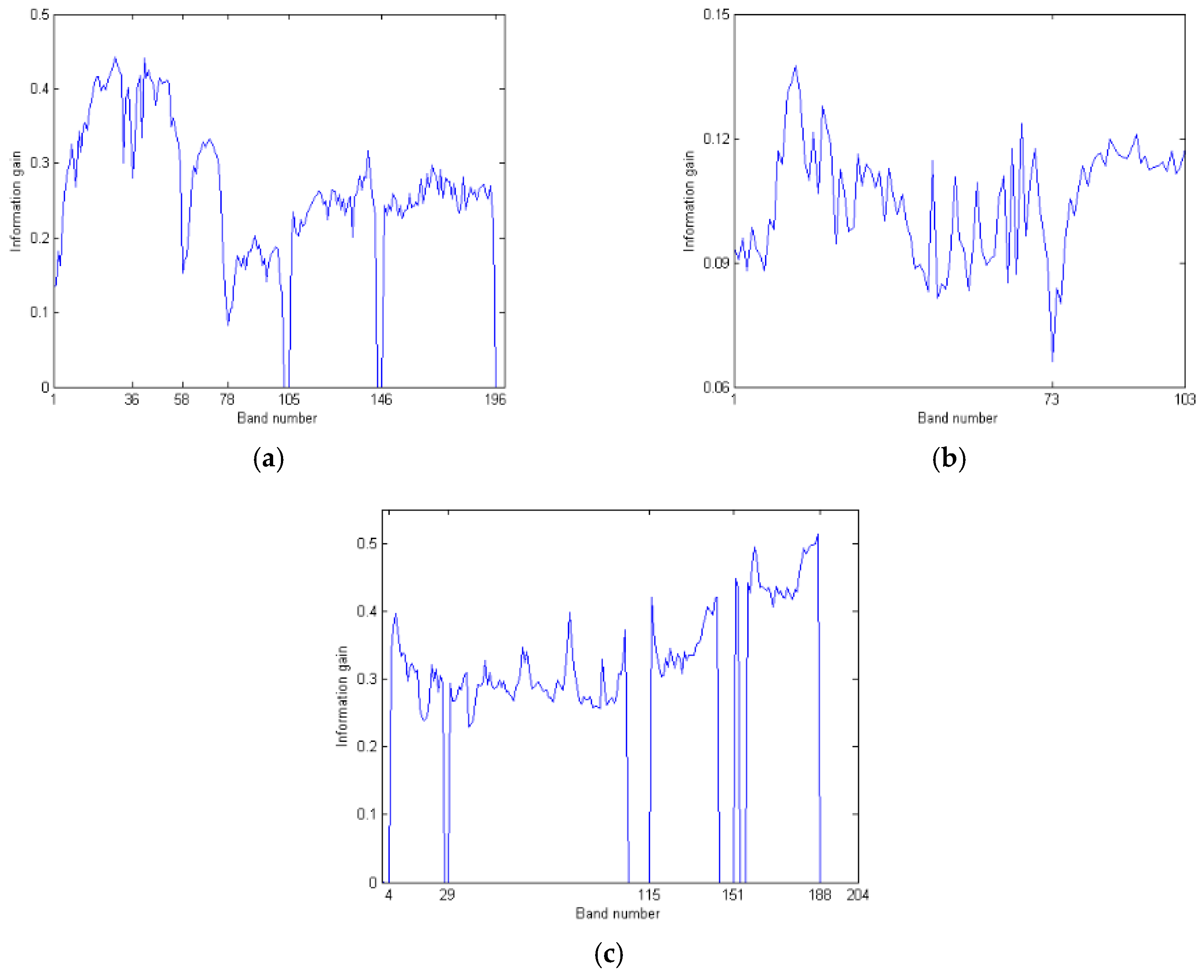
Band subset decomposition is the partitioning of the original bands into different subsets so that bands in the same subset are similar to each other, and bands from different subsets are dissimilar. With this process, bands in different subsets enjoy different classification performances. Obviously, it is arduous to actualize band subset decomposition by only using the IG value. Therefore, in this work, we introduce an improved subset decomposition technique by simultaneously considering the spectral curve of the hyperspectral dataset and local minimal value method.
Specifically, for a given HSI, the information gain of each band is first calculated by Equations (1)–(3). The number c of band subsets is determined by the line chart of information gain in the spectral curve of the HSI. Finally, one can properly partition all bands into c different band subsets.
Regarding band selection, the spectral curve of the hyperspectral data set implies that the spectral curves of each pixel in a certain interval are similar in shape and only different from each other in radiance. This means that bands that are located in the same interval have a similar distinguishing capacity for different land surface features. Consequently, it is logical to replace all bands in the same subset with several selected bands in an attempt to maintain similar classification results. This process implies that some of the redundant bands are abandoned.
On the basis of
c different subsets, one can obviously select the bands with high IG values from each subset. However, this may lead to the loss of substantial information. Alternately, we randomly select
k different bands from each band subset to constitute a band combination in a process that is also known as gray wolf, (
). The component
in gray wolf denotes the selected
j-th band from
i-th subset. This ensures that each band subset has the same contribution to the classification result. It is notable that the acquired band combination has less band redundancy, but this does not mean that it has good classification performance. Thus, the GWO algorithm is employed to optimize it to provide a satisfactory classification performance. The GWO algorithm is chosen as the optimization method because the GWO algorithm shows very good performance in exploration, local minima avoidance, and exploitation, simultaneously [
30].
Regarding optimization: suppose that there are N gray wolves in the initial population. The IG value of each gray wolf in the initial population is computed by using Equations (1)–(3) and (11). One then performs a descending sort of the IG values, with the largest in front. The wolves that correspond to the three largest IG values are called the alpha wolf, beta wolf and delta wolf, one after the other. The rest are designated as omega wolves. In the absence of information about the location of the prey, the position vector of the prey is replaced approximately by the position of the alpha wolf. The following supposes that each of the gray wolves knows the location of prey and encircles it [
30,
33].
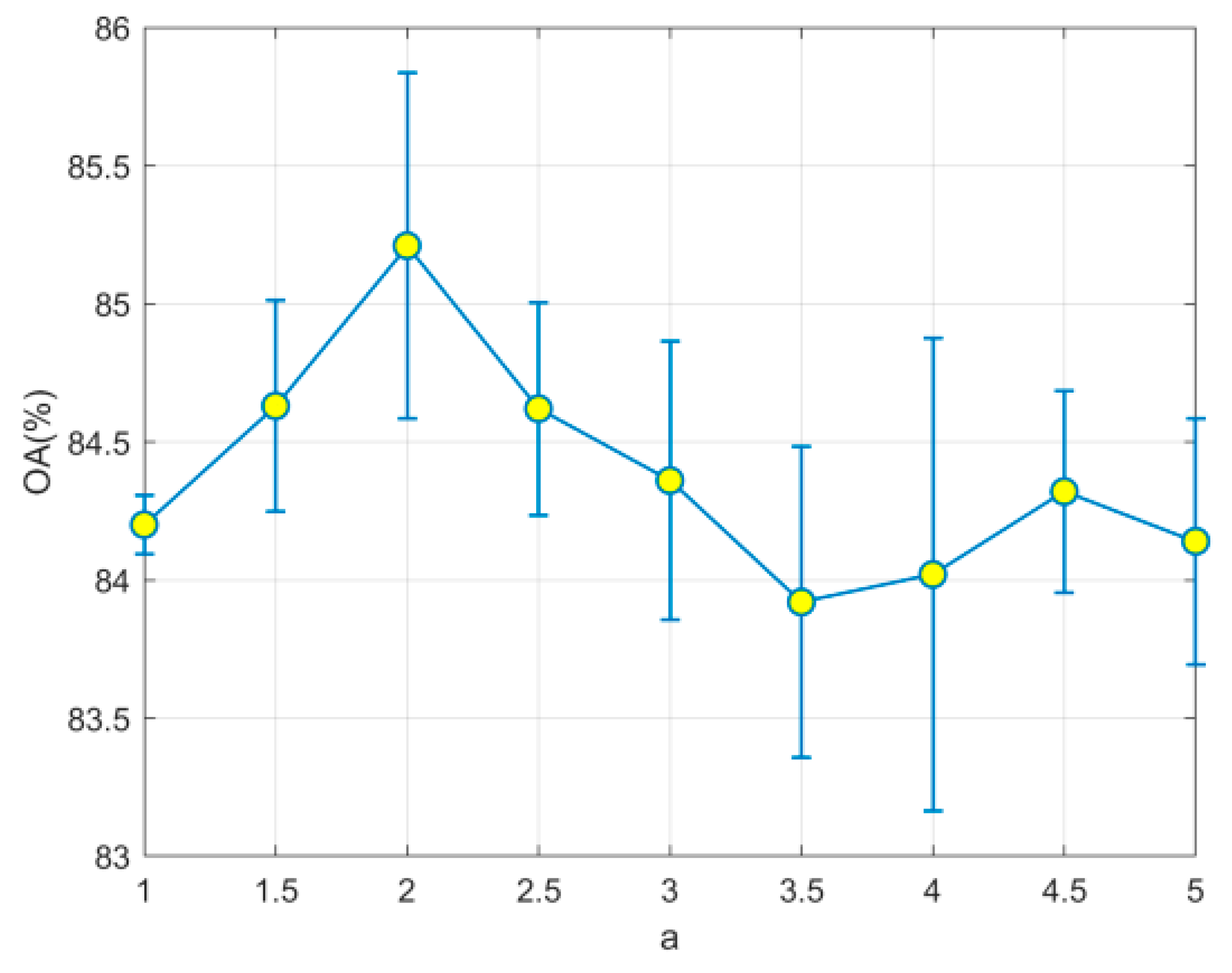
Encircling the prey during the hunt can be performed by Equations (4)–(7) and setting a = 2.
After encircling the prey, each wolf should quickly update its position relative to the locations of the alpha, beta and delta wolves in order to enclose the prey. The hunting process is accomplished by computing Equations (8)–(10).
The proposed band selection algorithm IG-GWO can be summarized as follows:
Input: Hyperspectral dataset; parameters and maximum iterations.
Output: The most informative feature, subset .
Step 1: Divide the initial bands into c subsets by their IG value and the spectral curve of the hyperspectral dataset.
Step 2: Randomly select k different bands from each subset to constitute a gray wolf.
Step 3: Initialize the population in GWO by repeatedly performing step 2 N times.
Step 4: Call the GWO algorithm mentioned in
Section 2.2.