Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy
Abstract
:1. Introduction
- In pre-processing and post-processing, the DPR strategy combined with the Roberts cross operator is adopted to denoise the original hyperspectral data and improve the classification accuracy, respectively.
- A new classifier combination for the pre-classification process of HSIs is proposed, which addresses the problem of automatically labeling samples based on a small training set. Two classifiers, MLRsub and LMPNN, are used together to perform the pre-classification of automatically predicting more labeled samples in terms of a few labeled instances per class.
- A novel semi-supervised classification scheme is built by four steps: pre-processing, pre-classification, classification, and post-processing.
2. The Proposed Semi-Supervised Classification Method
2.1. Relaxation Method
2.2. Multinomial Logistic Regression (MLR)
2.3. Local Mean-Based Pseudo Nearest Neighbor (LMPNN)
2.4. The Proposed Method
3. Experimental Results
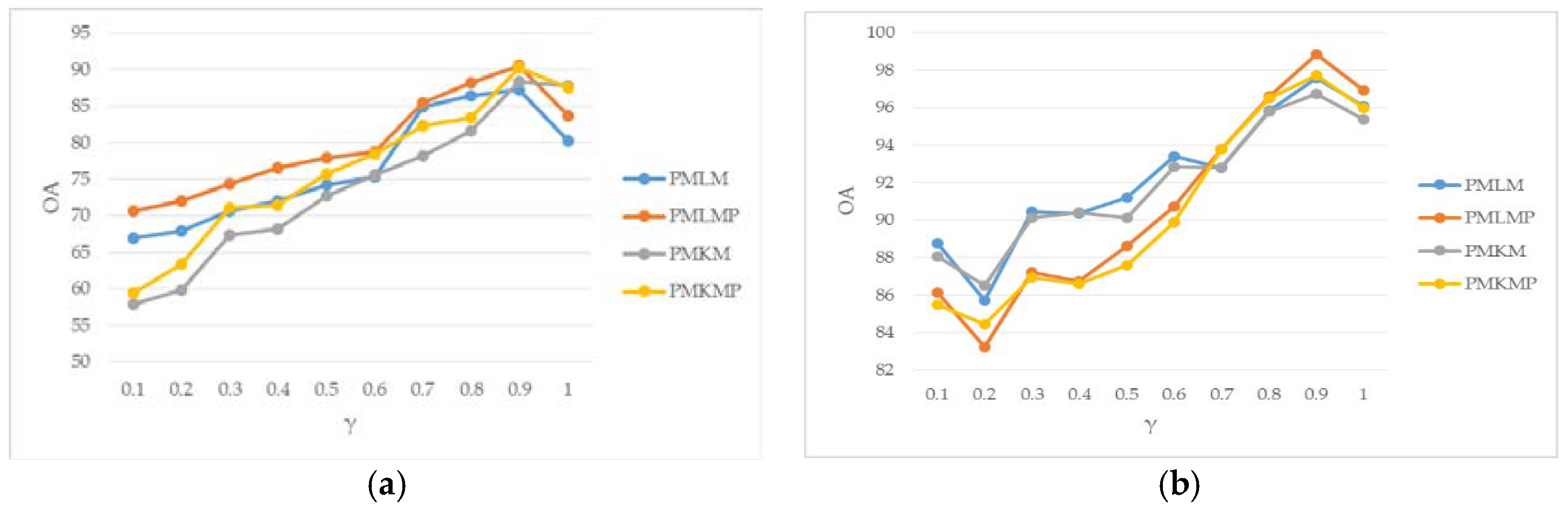
- PMKM: Pre-processing + MLRsub + KNN + MLRsub.
- PMLM: Pre-processing + MLRsub + LMPNN + MLRsub.
- PMKMP: Pre-processing + MLRsub + KNN + MLRsub + Post-processing.
- PMLMP: Pre-processing + MLRsub + LMPNN + MLRsub + Post-processing.
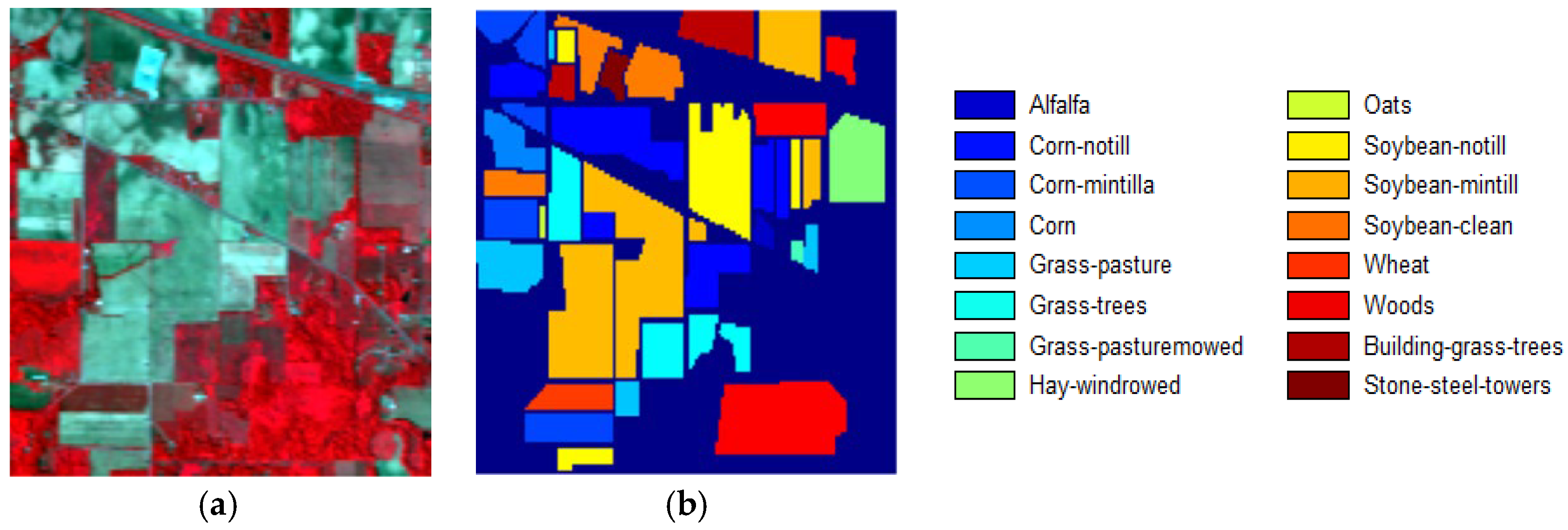
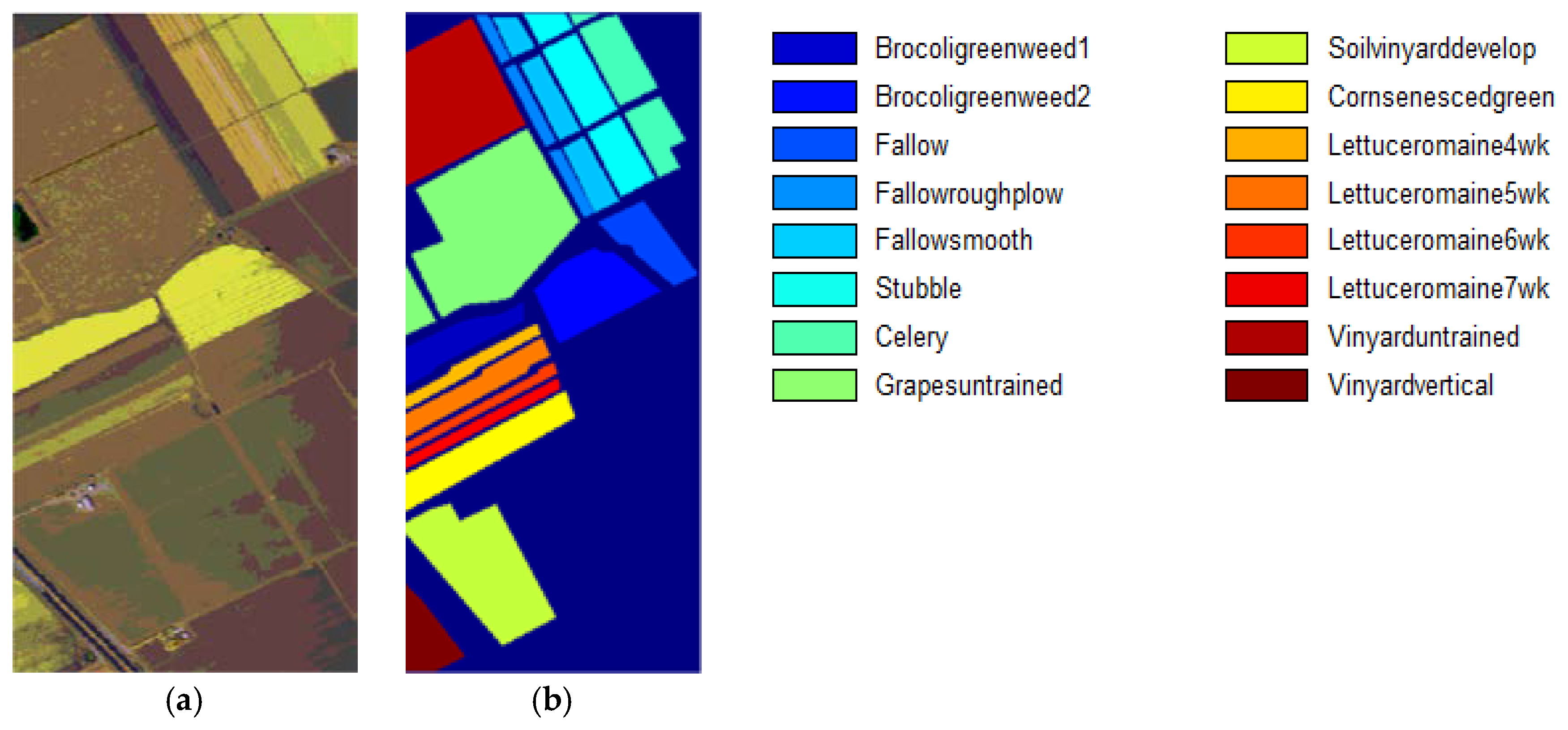
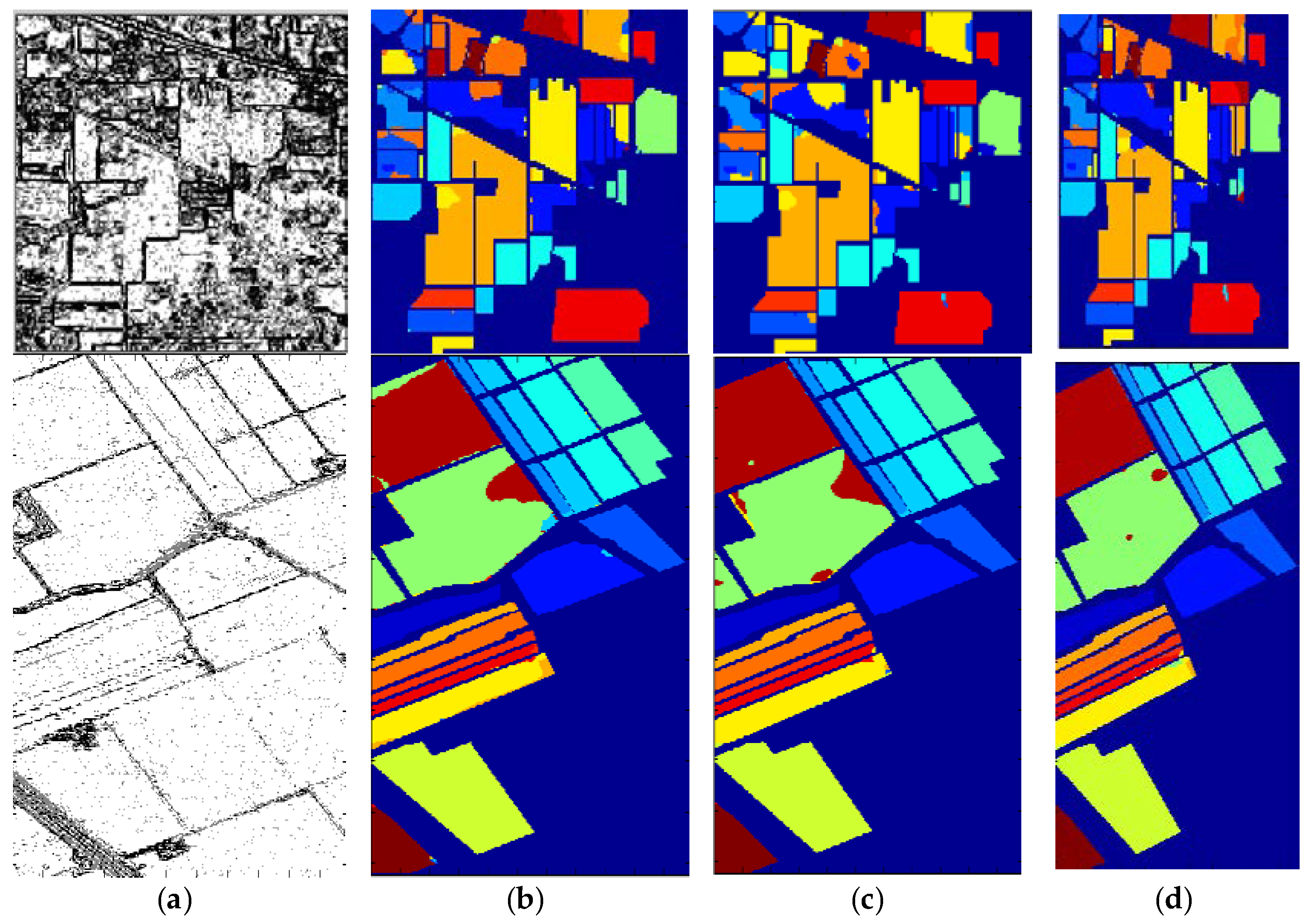
3.1. Datasets and Classification Results
3.2. Comparative Tests
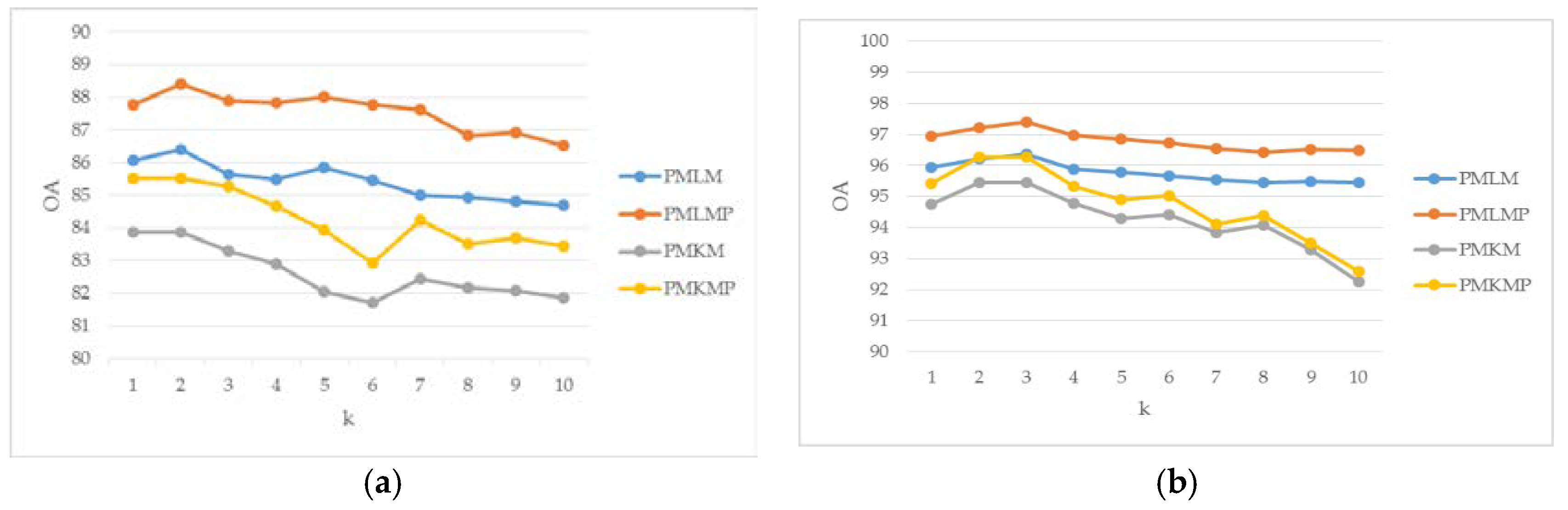
3.3. Parameter Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, T.; Felt, R. Hyperspectral remote sensing technology (HRST) program. In Proceedings of the 1998 IEEE Aerospace Conference, Snowmass at Aspen, CO, USA, 28 March 1998; pp. 193–200. [Google Scholar]
- Tan, K.; Hua, J.; Li, J.; Du, P. A novel semi-supervised hyperspectral image classification approach based on spatial neighborhood information and classifier combination. ISPRS J. Photogramm. Remote Sens. 2015, 105, 19–29. [Google Scholar] [CrossRef]
- Paoli, A.; Melgani, F.; Pasolli, E. Clustering of hyperspectral images based on multi-objective particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4175–4188. [Google Scholar] [CrossRef]
- Wu, J. Unsupervised intrusion feature selection based genetic algorithm and FCM. In Lecture Notes in Electrical Engineering; Springer: London, UK, 2012; Volume 154, pp. 1005–1012. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Rojo-Alvare, J.L.; Martinez-Ramon, M. Kernel-based framework for multitemporal and multisource remote sensing data classification and change detection. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1822–1835. [Google Scholar] [CrossRef] [Green Version]
- Bioucas-Dias, J.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Ghamisi, P.; Hofle, B. LiDAR Data Classification using Extinction prolfies and a composite kernel support vector machine. IEEE Geosci. Remote Sens. Lett. 2017, 14, 659–663. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.C.; Zhang, X.; Sun, T. Hyperspectral band selection based on trivariate mutual information and clonal selection. IEEE Trans. Geosci. Remote Sens. 2014, 57, 4092–4105. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Unsupervised feature selection based on maximum information and minimum redundancy for hyperspectral images. Pattern Recognit. 2016, 51, 295–309. [Google Scholar] [CrossRef]
- Tobler, W. Computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Heras, D.; Argüello, F.; Quesada-Barriuso, P. Exploring ELM-based spatial–spectral classification of hyperspectral images. Int. J. Remote Sens. 2014, 35, 401–423. [Google Scholar] [CrossRef]
- Franchi, G.; Angulo, J. Morphological principal component analysis for hyperspectral image analysis. ISPRS Int. J. Geo-Inf. 2016, 5, 83. [Google Scholar] [CrossRef]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J. A Survey on Spectral-spatial classification techniques based on attribute profiles. IEEE Trans. Geos. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, Z.; Chen, Y.; Yang, J. Spatial-spectral graph regularized kernel sparse representation for hyperspectral image classification. ISPRS Int. J. Geo-Inf. 2017, 6, 258. [Google Scholar] [CrossRef]
- Paul, S.; Nagesh Kumar, D. Spectral-spatial classification of hyperspectral data with mutual information based segmented stacked autoencoder approach. ISPRS J. Photogramm. Remote Sens. 2018, 138, 265–280. [Google Scholar] [CrossRef]
- Li, J.; Khodadadzadeh, M.; Plaza, A.; Jia, X.; Bioucas-Dias, J.M. A discontinuity preserving relaxation scheme for spectral–spatial hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 9, 625–639. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Li, J.; Li, S.S.; Zhang, B.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification using subspace-based support vector machines and adaptive Markov random fields. Remote Sens. 2016, 8, 355. [Google Scholar] [CrossRef]
- Li, H.; Zheng, H.; Han, C.; Wang, H.; Miao, M. Onboard spectral and spatial cloud detection for hyperspectral remote sensing images. Remote Sens. 2018, 10, 152. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Ulfarsson, M.O. Spectral–spatial classification of hyperspectral images based on hidden Markov random fields. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2565–2574. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Hyperspectral image classification using gaussian mixture models and Markov random fields. IEEE Geosci. Remote Sens. Lett. 2013, 11, 153–157. [Google Scholar] [CrossRef]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral–spatial hyperspectral image classification with weighted Markov random fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1490–1503. [Google Scholar] [CrossRef]
- Deng, W.; Iyengar, S.S. A New Probabilistic Relaxation Scheme and Its Application to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 432–437. [Google Scholar] [CrossRef]
- Wang, L.; Dai, Q.; Huang, X. spatial regularization of pixel-based classification maps by a two-step MRF method. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2407–2410. [Google Scholar]
- Gao, Q.; Lim, S.; Jia, X. Hyperspectral image classification using joint sparse model and discontinuity preserving relaxation. IEEE Geosci. Remote Sens. Lett. 2017, 99, 78–82. [Google Scholar] [CrossRef]
- Lin, Z.; Yan, L. A support vector machine classifier based on a new kernel function model for hyperspectral data. Mapp. Sci. Remote Sens. 2016, 53, 85–101. [Google Scholar] [CrossRef]
- Prabhakar, T.V.N.; Xavier, G.; Geetha, P.; Soman, K.P. Spatial preprocessing based multinomial logistic regression for hyperspectral image classification. Procedia Comput. Sci. 2015, 46, 1817–1826. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A subspace-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Denoeux, T. A k-nearest neighbor classification rule based on Dempster-Shafer theory. IEEE Trans. Syst. Man Cybern. 2008, 25, 804–813. [Google Scholar] [CrossRef]
- Gou, J.; Zhan, Y.; Rao, Y.; Shen, X.; Wang, X.; He, W. Improved pseudo nearest neighbor classification. Knowl.-Based Syst. 2014, 70, 361–375. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, W.; Sun, Y.; Hu, P.; Tu, K. Detection of cold injury in peaches by hyperspectral reflectance imaging and artificial neural network. Food Chem. 2016, 192, 134–141. [Google Scholar]
- Ahmed, A.; Duran, O.; Zweiri, Y.; Smith, M. Hybrid spectral unmixing: Using artificial neural networks for linear/non-linear switching. Remote Sens. 2017, 9, 775. [Google Scholar] [CrossRef]
- Mitani, Y.; Hamamoto, Y. A local mean-based nonparametric classifier. Pattern Recognit. Lett. 2006, 27, 1151–1159. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, Y.; Zhao, L. Pseudo nearest neighbor rule for pattern classification. Expert Syst. Appl. 2009, 36, 3587–3595. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM and MRF-based method for accurate classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Spectral–spatial hyperspectral image segmentation using subspace multinomial logistic regression and markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–814. [Google Scholar] [CrossRef]
- Roberts, L.G. Machine Perception of Three-Dimensional Solids; Outstanding Dissertations in the Computer Sciences; Garland Publishing: New York, NY, USA, 1963. [Google Scholar]
- Böning, D. Multinomial logistic regression algorithm. Annu. Inst. Stat. Math. 1992, 44, 197–200. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Spectral–spatial classification of hyperspectral data using loopy belief propagation and active learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Dudani, S.A. The distance-weighted k-nearest neighbor rule. IEEE Trans. Syst. Man Cybern. 1976, 6, 325–327. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Semi-supervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar]
| Dataset | Method | 5 | 10 | 15 | |||
|---|---|---|---|---|---|---|---|
| OA (%) | KC (%) | OA (%) | KC (%) | OA (%) | KC (%) | ||
| Indian Pines | PMKM | 74.85 ± 1.10 | 71.55 ± 1.43 | 84.53 ± 1.69 | 82.48 ± 2.13 | 88.73 ± 3.99 | 87.22 ± 4.91 |
| PMLM | 75.05 ± 3.57 | 71.87 ± 4.48 | 84.57 ± 2.12 | 82.55 ± 2.67 | 88.95 ± 1.25 | 87.48 ± 1.59 | |
| PMKMP | 76.89 ± 1.36 | 73.80 ± 1.56 | 86.45 ± 1.08 | 84.64 ± 1.36 | 90.46 ± 4.10 | 89.17 ± 5.14 | |
| PMLMP | 77.23 ± 2.85 | 74.27 ± 3.71 | 86.69 ± 1.39 | 84.92 ± 1.72 | 91.18 ± 2.30 | 89.98 ± 3.90 | |
| Salinas | PMKM | 92.16 ± 1.06 | 91.30 ± 1.28 | 95.11 ± 5.76 | 94.58 ± 7.08 | 96.77 ± 1.29 | 96.41 ± 1.59 |
| PMLM | 95.22 ± 3.65 | 94.69 ± 4.48 | 96.02 ± 6.84 | 95.58 ± 8.45 | 97.12 ± 2.50 | 96.80 ± 3.08 | |
| PMKMP | 93.05 ± 1.68 | 92.28 ± 2.04 | 95.90 ± 4.02 | 95.45 ± 4.93 | 97.42 ± 5.30 | 97.13 ± 6.55 | |
| PMLMP | 96.00 ± 2.98 | 95.56 ± 3.66 | 96.82 ± 4.00 | 96.46 ± 4.99 | 97.96 ± 3.83 | 97.74 ± 4.73 | |
| 5 | 10 | 15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PMKM | PMLM | PMKMP | PMLMP | PMKM | PMLM | PMKMP | PMLMP | PMKM | PMLM | PMKMP | PMLMP | |
| Alfalfa (46) | 93.70 ± 1.90 | 95.22 ± 2.00 | 93.48 ± 1.77 | 92.39 ± 1.85 | 94.35 ± 2.34 | 94.35 ± 2.93 | 94.13 ± 1.47 | 94.35 ± 2.06 | 97.61 ± 2.16 | 96.09 ± 1.71 | 95.00 ± 2.24 | 93.91 ± 1.05 |
| Corn-no till (1428) | 43.10 ± 10.25 | 48.40 ± 11.81 | 45.87 ± 13.45 | 51.23 ± 12.04 | 72.25 ± 4.22 | 68.93 ± 6.29 | 68.12 ± 10.32 | 68.93 ± 5.26 | 76.67 ± 5.45 | 80.08 ± 5.36 | 80.86 ± 5.90 | 84.46 ± 7.66 |
| Corn-min till (830) | 60.18 ± 12.57 | 60.80 ± 13.36 | 63.00 ± 16.62 | 68.82 ± 13.69 | 81.14 ± 8.86 | 78.88 ± 5.72 | 85.70 ± 8.58 | 78.88 ± 5.81 | 80.48 ± 9.82 | 83.94 ± 7.43 | 85.11 ± 8.12 | 85.16 ± 9.20 |
| Corn (237) | 85.15 ± 8.05 | 75.61 ± 17.69 | 84.51 ± 8.77 | 78.99 ± 19.81 | 83.88 ± 11.39 | 88.44 ± 9.43 | 84.94 ± 11.38 | 88.44 ± 7.78 | 90.89 ± 4.53 | 90.55 ± 4.36 | 90.51 ± 4.85 | 89.79 ± 6.37 |
| Grass-pasture (483) | 75.01 ± 8.56 | 79.05 ± 9.36 | 76.87 ± 11.00 | 73.31 ± 19.42 | 89.65 ± 3.62 | 87.74 ± 4.98 | 91.78 ± 3.85 | 87.74 ± 4.24 | 91.16 ± 4.07 | 89.23 ± 9.05 | 92.63 ± 3.79 | 91.93 ± 4.33 |
| Grass-trees (730) | 99.74 ± 0.56 | 99.49 ± 0.50 | 99.96 ± 0.10 | 98.59 ± 2.88 | 99.62 ± 0.64 | 98.84 ± 2.03 | 99.82 ± 0.35 | 98.84 ± 0.59 | 99.62 ± 0.61 | 99.71 ± 0.46 | 99.99 ± 0.00 | 99.99 ± 0.00 |
| Grass-pasture-mowed (28) | 99.64 ± 1.13 | 100.00 ± 0.00 | 98.21 ± 3.86 | 100.00 ± 0.00 | 100.00 ± 0.00 | 98.57 ± 4.52 | 87.14 ± 16.43 | 98.57 ± 14.60 | 99.29 ± 2.26 | 100.00 ± 0.00 | 92.50 ± 10.13 | 94.29 ± 12.42 |
| Hay-windrowed (478) | 93.39 ± 3.91 | 93.77 ± 3.65 | 95.31 ± 2.64 | 95.42 ± 3.52 | 94.85 ± 4.26 | 92.76 ± 12.51 | 95.77 ± 3.67 | 92.76 ± 12.85 | 96.51 ± 4.81 | 96.99 ± 3.18 | 94.21 ± 0.81 | 98.37 ± 7.93 |
| Oats (20) | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Soybean-no till (972) | 78.77 ± 11.50 | 82.35 ± 8.19 | 80.94 ± 12.01 | 83.08 ± 9.77 | 89.87 ± 7.02 | 86.77 ± 5.39 | 91.97 ± 6.61 | 86.77 ± 4.64 | 92.12 ± 5.74 | 91.87 ± 5.16 | 92.87 ± 5.13 | 93.55 ± 5.62 |
| Soybean-min till (2455) | 75.82 ± 3.87 | 71.60 ± 5.59 | 77.30 ± 5.31 | 73.57 ± 5.33 | 78.37 ± 4.98 | 79.97 ± 4.25 | 82.65 ± 2.62 | 79.97 ± 5.07 | 85.62 ± 3.13 | 85.92 ± 2.96 | 88.47 ± 3.58 | 88.21 ± 3.29 |
| Soybean-clean (593) | 69.12 ± 8.33 | 59.98 ± 15.99 | 66.31 ± 16.11 | 66.58 ± 7.46 | 67.93 ± 14.29 | 80.12 ± 10.21 | 73.66 ± 14.83 | 80.12 ± 10.32 | 87.74 ± 7.74 | 82.56 ± 9.52 | 83.93 ± 6.89 | 84.65 ± 10.30 |
| Wheat (205) | 99.27 ± 0.81 | 99.32 ± 0.57 | 99.66 ± 0.33 | 99.61 ± 0.20 | 99.46 ± 0.96 | 99.46 ± 0.74 | 99.80 ± 0.24 | 99.46 ± 0.20 | 99.80 ± 0.35 | 99.46 ± 0.71 | 99.66 ± 0.20 | 99.61 ± 0.24 |
| Woods (1265) | 90.84 ± 10.19 | 92.51 ± 4.89 | 94.33 ± 7.55 | 94.96 ± 5.29 | 98.09 ± 3.12 | 97.64 ± 3.70 | 97.95 ± 3.28 | 97.64 ± 3.10 | 97.33 ± 2.82 | 96.93 ± 2.81 | 98.58 ± 2.17 | 98.63 ± 2.17 |
| Buildings-Grass-Trees-Drives (386) | 73.76 ± 13.78 | 79.72 ± 7.94 | 75.67 ± 14.74 | 79.27 ± 13.67 | 91.01 ± 6.32 | 90.78 ± 7.99 | 95.13 ± 7.83 | 90.78 ± 8.95 | 94.84 ± 4.16 | 97.98 ± 1.02 | 95.39 ± 4.17 | 97.93 ± 6.57 |
| Stone-Steel-Towers (93) | 96.24 ± 2.83 | 93.87 ± 4.97 | 95.16 ± 4.19 | 91.72 ± 4.51 | 96.67 ± 3.53 | 94.84 ± 2.57 | 93.01 ± 5.27 | 94.84 ± 4.18 | 95.59 ± 2.97 | 93.66 ± 4.10 | 93.44 ± 3.50 | 92.69 ± 3.77 |
| 5 | 10 | 15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PMKM | PMLM | PMKMP | PMLMP | PMKM | PMLM | PMKMP | PMLMP | PMKM | PMLM | PMKMP | PMLMP | |
| Brocoli_green_weeds_1 (2009) | 99.67 ± 0.56 | 99.27 ± 1.87 | 99.78 ± 0.44 | 99.40 ± 1.75 | 99.76 ± 0.28 | 99.54 ± 0.69 | 99.93 ± 0.22 | 99.69 ± 0.51 | 99.72 ± 0.42 | 99.79 ± 0.37 | 99.67 ± 0.48 | 99.92 ± 0.26 |
| Brocoli_green_weeds_2 (3726) | 99.90 ± 0.17 | 99.81 ± 0.30 | 100.00 ± 0.00 | 99.97 ± 0.00 | 99.82 ± 0.44 | 99.92 ± 0.14 | 99.97 ± 0.10 | 100.00 ± 0.00 | 99.98 ± 0.00 | 99.92 ± 0.17 | 100.00 ± 0.00 | 99.99 ± 0.00 |
| Fallow (1976) | 93.84 ± 9.67 | 97.02 ± 3.54 | 95.29 ± 9.86 | 98.07 ± 3.02 | 99.89 ± 0.22 | 99.35 ± 1.15 | 99.61 ± 1.20 | 99.72 ± 0.57 | 99.89 ± 0.22 | 99.92 ± 0.14 | 99.98 ± 0.00 | 99.98 ± 0.00 |
| Fallow-rough-plow (1394) | 98.27 ± 0.83 | 97.70 ± 1.71 | 98.21 ± 1.20 | 97.67 ± 2.52 | 98.42 ± 0.32 | 98.01 ± 0.63 | 98.68 ± 0.72 | 97.96 ± 1.16 | 97.77 ± 0.84 | 98.14 ± 0.54 | 97.71 ± 1.47 | 98.12 ± 1.01 |
| Fallow-smooth (2678) | 95.81 ± 4.48 | 96.52 ± 2.36 | 97.68 ± 3.66 | 97.45 ± 2.03 | 97.98 ± 1.08 | 98.85 ± 1.21 | 99.01 ± 0.82 | 99.19 ± 0.83 | 98.69 ± 0.77 | 97.66 ± 1.66 | 99.28 ± 0.47 | 98.41 ± 1.57 |
| Stubble (3959) | 99.74 ± 0.22 | 99.78 ± 0.20 | 99.96 ± 0.00 | 99.96 ± 0.00 | 99.78 ± 0.24 | 99.73 ± 0.24 | 99.97 ± 0.00 | 99.96 ± 0.00 | 99.88 ± 0.00 | 99.86 ± 0.10 | 99.96 ± 0.00 | 99.97 ± 0.00 |
| Celery (3579) | 99.79 ± 0.10 | 99.80 ± 0.10 | 99.94 ± 0.00 | 99.96 ± 0.00 | 99.84 ± 0.10 | 99.80 ± 0.10 | 99.95 ± 0.00 | 99.95 ± 0.00 | 99.82 ± 0.14 | 99.81 ± 0.14 | 99.95 ± 0.00 | 99.94 ± 0.00 |
| Grapes-untrained (11271) | 78.22 ± 8.09 | 86.79 ± 2.82 | 79.95 ± 8.33 | 88.78 ± 2.48 | 82.72 ± 3.00 | 87.91 ± 1.29 | 85.02 ± 2.89 | 90.20 ± 0.81 | 89.55 ± 1.62 | 84.54 ± 5.18 | 91.46 ± 1.16 | 86.69 ± 5.73 |
| Soil-vineyard-develop (6203) | 99.49 ± 0.74 | 99.65 ± 0.67 | 99.76 ± 0.55 | 99.84 ± 0.39 | 99.99 ± 0.00 | 99.95 ± 0.14 | 100.00 ± 0.00 | 99.99 ± 0.00 | 99.99 ± 0.00 | 99.98 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Corn-senesced-green-weeds (3278) | 85.61 ± 5.28 | 89.99 ± 2.94 | 87.30 ± 5.68 | 91.35 ± 2.74 | 92.30 ± 3.68 | 92.72 ± 2.51 | 94.29 ± 2.79 | 93.49 ± 2.25 | 94.47 ± 1.65 | 92.46 ± 6.59 | 94.96 ± 1.60 | 92.13 ± 7.74 |
| Lettuce_romaine_4weeks (1068) | 99.30 ± 0.62 | 99.56 ± 0.56 | 99.65 ± 0.90 | 99.78 ± 0.44 | 99.12 ± 0.88 | 99.64 ± 0.35 | 99.50 ± 0.86 | 99.87 ± 0.35 | 98.90 ± 1.15 | 99.54 ± 0.69 | 99.77 ± 0.36 | 100 ± 0.00 |
| Lettuce_romaine_5weeks (1927) | 97.37 ± 4.58 | 98.83 ± 2.14 | 97.25 ± 5.06 | 98.94 ± 1.83 | 98.52 ± 2.32 | 99.69 ± 0.33 | 99.24 ± 1.50 | 99.77 ± 0.26 | 99.75 ± 0.37 | 99.91 ± 0.14 | 99.68 ± 0.37 | 99.83 ± 0.24 |
| Lettuce_romaine_6weeks (916) | 98.84 ± 1.36 | 97.67 ± 1.79 | 98.12 ± 1.85 | 96.62 ± 2.32 | 99.34 ± 0.47 | 99.04 ± 0.96 | 98.40 ± 0.99 | 98.22 ± 1.46 | 99.42 ± 0.49 | 98.89 ± 1.14 | 98.58 ± 1.24 | 98.72 ± 1.34 |
| Lettuce_romaine_7weeks (1070) | 97.83 ± 1.27 | 97.10 ± 3.47 | 97.54 ± 1.98 | 96.02 ± 4.97 | 98.63 ± 0.63 | 98.30 ± 1.10 | 97.88 ± 1.18 | 98.57 ± 1.11 | 98.47 ± 0.89 | 98.76 ± 0.89 | 98.11 ± 1.32 | 97.84 ± 2.33 |
| Vineyard-untrained (7268) | 89.43 ± 7.66 | 94.72 ± 2.14 | 90.83 ± 7.50 | 95.72 ± 1.93 | 96.62 ± 2.54 | 94.94 ± 1.85 | 97.16 ± 2.07 | 96.11 ± 2.22 | 97.26 ± 1.66 | 95.15 ± 5.37 | 98.16 ± 1.76 | 96.12 ± 4.9 |
| Vineyard-vertical-trellis (1807) | 92.40 ± 5.64 | 96.44 ± 3.59 | 93.56 ± 5.19 | 97.60 ± 3.07 | 98.17 ± 1.09 | 98.57 ± 0.98 | 98.97 ± 0.85 | 99.13 ± 0.71 | 97.75 ± 3.12 | 97.20 ± 2.94 | 98.38 ± 2.86 | 98.38 ± 2.6 |
| Method | Indian Pine | Salinas | ||
|---|---|---|---|---|
| OA (%) | KC (%) | OA (%) | KC (%) | |
| MLR | 64.30 ± 2.29 | 60.03 ± 2.45 | 85.28 ± 1.51 | 83.67 ± 1.66 |
| MLR-MLL | 75.09 ± 2.86 | 72.03 ± 3.10 | 89.02 ± 6.54 | 87.80 ± 7.28 |
| ppMLR | 88.36 ± 1.67 | 86.88 ± 1.86 | 93.30 ± 1.70 | 92.56 ± 1.89 |
| ppMLRpr | 91.05 ± 1.87 | 89.87 ± 2.09 | 93.79 ± 4.46 | 93.11 ± 4.91 |
| PMKM | 88.73 ± 3.99 | 87.22 ± 4.91 | 96.77 ± 1.29 | 96.41 ± 1.59 |
| PMLM | 88.95 ± 1.25 | 87.48 ± 1.59 | 97.12 ± 2.50 | 96.80 ± 3.08 |
| PMKMP | 90.46 ± 4.10 | 89.17 ± 5.14 | 97.42 ± 5.30 | 97.13 ± 6.55 |
| PMLMP | 91.18 ± 2.30 | 89.98 ± 3.90 | 97.96 ± 3.83 | 97.74 ± 4.73 |
| Method | Operator | Indian Pine | Salinas | ||
|---|---|---|---|---|---|
| OA (%) | KC (%) | OA (%) | KC (%) | ||
| PMKM | Sobel | 85.15 ± 0.81 | 83.23 ± 0.96 | 95.70 ± 0.84 | 95.23 ± 1.03 |
| Roberts | 88.73 ± 2.00 | 87.22 ± 2.46 | 96.77 ± 0.65 | 96.41 ± 0.80 | |
| PMKMP | Sobel | 86.95 ± 0.49 | 85.23 ± 0.59 | 96.60 ± 3.55 | 96.22 ± 4.39 |
| Roberts | 90.46 ± 2.05 | 89.17 ± 2.57 | 97.42 ± 2.65 | 97.13 ± 3.28 | |
| PMLM | Sobel | 84.74 ± 0.77 | 82.78 ± 0.93 | 96.04 ± 1.25 | 95.60 ± 1.54 |
| Roberts | 88.95 ± 0.63 | 87.48 ± 0.80 | 97.12 ± 1.25 | 96.80 ± 1.54 | |
| PMLMP | Sobel | 86.33 ± 0.84 | 84.54 ± 1.02 | 96.90 ± 0.83 | 96.56 ± 1.00 |
| Roberts | 91.18 ± 1.15 | 89.98 ± 1.95 | 97.96 ± 1.92 | 97.74 ± 2.37 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; Hu, D.; Li, F.; Yang, J.; Liu, D. Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy. ISPRS Int. J. Geo-Inf. 2018, 7, 284. https://doi.org/10.3390/ijgi7070284
Xie F, Hu D, Li F, Yang J, Liu D. Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy. ISPRS International Journal of Geo-Information. 2018; 7(7):284. https://doi.org/10.3390/ijgi7070284
Chicago/Turabian StyleXie, Fuding, Dongcui Hu, Fangfei Li, Jun Yang, and Deshan Liu. 2018. "Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy" ISPRS International Journal of Geo-Information 7, no. 7: 284. https://doi.org/10.3390/ijgi7070284
APA StyleXie, F., Hu, D., Li, F., Yang, J., & Liu, D. (2018). Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy. ISPRS International Journal of Geo-Information, 7(7), 284. https://doi.org/10.3390/ijgi7070284






