Abstract
Determining the positions of facilities, and allocating demands to them, is a vitally important problem. Location-allocation problems are optimization NP-hard procedures. This article evaluates the ordered capacitated multi-objective location-allocation problem for fire stations, using simulated annealing and a genetic algorithm, with goals such as minimizing the distance and time as well as maximizing the coverage. After tuning the parameters of the algorithms using sensitivity analysis, they were used separately to process data for Region 11, Tehran. The results showed that the genetic algorithm was more efficient than simulated annealing, and therefore, the genetic algorithm was used in later steps. Next, we increased the number of stations. Results showed that the model can successfully provide seven optimal locations and allocate high demands (280,000) to stations in a discrete space in a GIS, assuming that the stations’ capacities are known. Following this, we used a weighting program so that in each repetition, we could allot weights to each target randomly. Finally, by repeating the model over 10 independent executions, a set of solutions with the least sum and the highest number of non-dominated solutions was selected from among many non-dominated solutions as the best set of optimal solutions.
1. Introduction
Optimal location of facilities and allocation of demands to them are important issues, since the costs of construction are considerable. Fire station location for the purpose of easy response and recovery is a significant problem today. However, it is important to give emergency assistance properly and on time, so as to save the lives of the wounded [1]. If they are not well positioned, they cannot satisfy the needs of, or offer some services to, the customers. In crowded cities where there is insufficient space for positioning these facilities, the issue becomes even more important. Different conditions and goals can be considered in location-allocation problems, further complicating the problem. The location-allocation problem includes some common models. There has been much previous research on different models for the location-allocation optimization problem [2,3,4,5,6] using GIS technologies [7]. Location-allocation problems are NP-hard optimization procedures and the problem becomes very complex if it involves a combination of location-allocation models [8].
Nonetheless, few studies include a combination of such models. The present work considers two common models for this problem, (i.e., coverage and p-median), taking various goals and conditions into account. Much research has been conducted on the location-allocation problem using metaheuristic methods for emergency services [9,10,11], but capacity conditions or multiple objectives were not considered in these studies. Liu et al. applied simulated annealing to solve large-scale location-allocation problems with rectilinear distances. The results showed high solution quality and acceptable computation times [12], but they considered only a single objective, and the capacity constraint was also ignored. Furthermore, ordered demands were omitted. Gonzalez–Monroy and Cordoba compared simulated annealing with a genetic algorithm for optimization of energy supply systems. The results showed that for small problems. The genetic algorithm was more efficient than simulated annealing, but for large problems, the reverse was true [13]. In that research, they considered only a single objective, and the capacity constraint was also ignored. Furthermore, ordered demands were omitted.
A genetic algorithm was applied for solving the location-allocation problem for parks and open spaces optimization, but the capacity of facilities and the order of demands were not considered, and the problem space was continuous [14]. Bashiri and Bakhtiarifar used simulated annealing for a problem with one objective, but the present study has three objectives, which complicates the problem space [15]. In the former study, the capacity constraint and ordered demands were also omitted. Yu and Solvang used multi-objective location-allocation for the management of municipal solid waste, but the capacity constraint was omitted, and their results showed that the CPU running time increased significantly with an increase in the size of the problem. For future development, they proposed using an efficient algorithm such as a genetic algorithm [16]. Ma and Zhao used a multi-objective artificial immune optimization model in land use allocation. However, they did not integrate their model into a GIS environment and the capacities of facilities and the order of demands were not considered [17].
In this research, the ordered capacitated multi-objective location-allocation problem for fire stations is presented with some incompatible objectives, such as minimizing the distance between the demand and the station, minimizing the arrival time from the station, and maximizing the station’s coverage. When the demands are ordered according to their objective functions, this causes the nearer demands to be allocated to a station where it locates a closer distance to the demands. To this end, a demand with a shorter distance or time takes a higher priority to be allocated to a fire station. Selecting ranked or ordered demands can make an optimal solution possible to access the fire stations in a shorter time. The problem space is considered as a discrete space and distances are measured on a network. The demands are ordered based on goals and allocated to the facilities. For solving this ordered capacitated location-allocation model, two efficient algorithms are applied and their results are compared. The outcomes of the ordered capacitated location-allocation problem are presented in a GIS environment. Solving the ordered capacitated multi-objective location-allocation problem has not previously been investigated. Furthermore, integration of the problem into a GIS environment for fire stations using a genetic algorithm and simulated annealing has not previously been investigated.
2. Materials and Methods
The generic goal of this research is solving the location-allocation problem with a large number of demand points, using chosen algorithms and non-dominated solutions. The following objectives have been considered. Firefighters must attend incident sites in less than five minutes. Therefore, routes must be selected so that they can arrive at the accident site in the shortest time. Distance and time are important factors that include parameters such as congestion, maximum speed of road, and so on. In addition, the best possible service should be provided with a minimum number of fire stations, and therefore the coverage of the fire stations should be maximized. The studied space is a discrete space, but the calculations are also performed on the road network. The general objective of this research is optimizing locations for fire stations in Region 11, Tehran, in a GIS, with regard to the three above-mentioned objectives. The sum of these objectives and conditions, which considerably complicate the calculations, distinguishes this research from previous research.
First, the data are entered into a GIS environment. The suggested model can be implemented in a GIS environment [18]. Then, the model’s parameters were regulated by a sensitivity analysis for each algorithm, and the data were processed, searching for optimal locations for fire stations via fitness rating, in accordance with the problem’s objectives. The results of each of the two algorithms with the same initial point were evaluated, to determine which algorithm should be selected to solve this problem. The chosen algorithm was used for the case study (Figure 1). To find optimal locations for fire stations, three objectives have been taken into consideration. In order to combine them and turn them into an objective function, a weighted objective function was employed, as shown below:
where is the normalized rate of f, T is the transposed matrix and W is the weight of each objective function. There are two strategies for allocating a weight to each objective function. Strategy I is a fixed-weight approach that determines the weights from prior knowledge of the objectives, and the weights do not change during the entire evolutionary process. Strategy II represents a random weight approach where weights are randomly reset at each step of the evolutionary process to consider all possible combinations of solutions. This strategy explores the entire solution space [19].
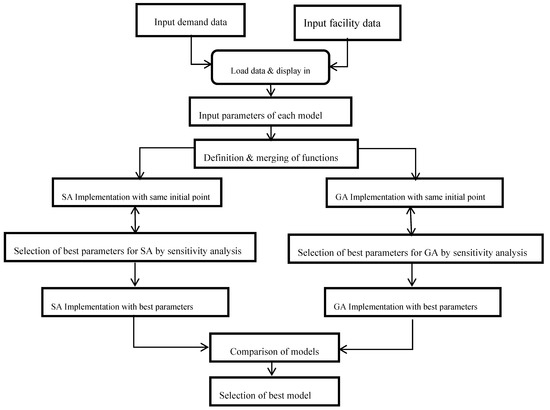
Figure 1.
Methodological procedure.
It is often not possible to find a single solution that achieves the best values for all objectives, given the constraints. In an optimization problem with D objectives, a solution x is said to dominate another solution (denoted x ) only if:
where is the objective function value of objective i for a solution x. This formulation has assumed a maximization problem, but the modifications necessary for a minimization problem are clear [20].
To obtain Pareto-optimal solutions, a random weighting schedule was employed. The random weights were derived as follows:
where is a random number between 0 and 1 generated for the th objective function, h = 1, 2, …, k [21]. Since this study has taken three objective functions into consideration, h = 3. In this schedule, the weight vector is (W1, W2, W3) in each repetition and the algorithm is produced by a random non-dominated method in order to produce all non-dominated solutions. In this research, the described method and the second strategy are chosen from among the various available weighting methods, for utilization in the problem under consideration.
Since the objectives of the present research have different units, they cannot be aggregated [22]; therefore, each function must be normalized before aggregation. In this research, the method described below is used to normalize each function [23].
The general goal of this research is to minimize the ordered capacitated multi-objective function, but among the objectives there is one which should be maximized. Multiplying all maximization objective functions by −1, we obtain the multi-objective minimization model [24].
2.1. Minimizing the Distance between the Demand and the Fire Station
Assuming demands are allocated to the nearest station, the objective function will be:
This constrain maintains that partial sum of the kth rank should be less than or equal to the partial sum at the next rank.
where r is the number of facilities, m is the number of demands, is the network-based distance between the facility point j and demand point i based upon Dijkstra’s algorithm, is the weight of demand point i, is the maximum capacity of facility j (= 50,000), is the allocated demand at facility j, and is the weight of the kth rank of service [25].
2.2. Minimizing the Time for Reaching the Demand from the Fire Station
The minimizing function for the time is as shown below:
where is the travel time between demand point i and facility point j. This research considers the road direction and road width to measure the distance and time respectively. Road width, average road congestion, and direction are descriptive items of information about the road, held in the table relating to the road in the GIS (roads with lesser widths, higher road congestion average, and contrary directions of movement are assigned lesser weights). These two items have an effect on both the time and distance functions.
2.3. Maximizing the Fire Station’s Coverage
Based on Maliszewski et al. [26], the maximizing function of each fire station’s coverage is as below:
The total coverage of all stations can be obtained from the function below:
Here, the number of related demands to each station is calculated if capacity of each station is full, any demand point cannot assign to that station.
: weight of demand in point i.
where P is the population or demand in each district, TP is the total population, F is the number of existing fire stations in each district, and TF is the total number of fires. Since there are four areas in this region, four values are obtained. Each point is given a coefficient according to the area in which it is located. Furthermore, in this research, the operation radius for the coverage model is considered to be five minutes [27].
This research seeks to establish appropriate locations for fire stations such that these stations can cover an area with the greatest population (up to 50,000).
3. Proposed Solution Approaches
3.1. Genetic Optimization
Genetic algorithms (GAs) are the search technique to find optimal or nearly optimal solutions invented by John Holland in the 1960s [28]. Its attempt is to mimic the natural evolution processed by the use of genetic operators such as selection, crossover, and mutation [29]. In this GA, a chromosome or solution is given as a string of location variants of x and y (as is also the case in this research). The algorithm starts with a set of solutions (individuals). These initial solutions, which are the coordinates of the facilities, were obtained by service area analysis with a radius of five minutes in ArcGIS. This accelerates the process of reaching optimal solutions. In the first step, it starts with an initial population. Next, the fitness of each individual is measured by means of an objective function (1) and each member that cannot dominate another is stored in the archive (in accordance with a non-dominated function).
In the third step, the parents are selected from the stored individuals using the rank method. Crossover is a recombination operator that combines parts of two parent chromosomes to produce offspring that contain some parts of each of the parent genes. The two-point crossover operator was used in this study. A point on two selected parents is randomly selected, and portions of the two chromosomes beyond this point are exchanged to form the offspring. Reproduction and mutation is performed so that a new population is established and the algorithm is prevented from falling into local optima. The process of mutation is performed to switch a few randomly chosen genes. The produced individuals are added to the population and the fitness of each is measured. To obtain balance in the population size, some of the individuals are omitted based on fitness values, so that individuals with poor fitness are removed. This process is repeated until the final condition (the algorithm’s solutions remain unchanged for 10 iterations) is achieved. Eventually, the non-dominated function is implemented for the individuals stored in each step. The values of x and y are the spatial coordinates of the fire stations.
3.2. Simulated Annealing (SA) Optimization
The simulated annealing concept is inspired by crystal formation during cooling. The slower the cooling, the more perfect the obtained crystal. The parameters of SA are cooling rate, initial temperature, and absolute temperature. These parameters will be set in Section 5.1.
The steps of the multi-objective SA to produce non-dominated solutions are as follows:
Step 1: Initialization
Select the initial solutions s (the same as the initial genetic solutions) from S (the set of all possible solutions). The same solutions are obtained by service area analysis for the genetic algorithm.
Select an initial temperature , set the absolute temperature , and set the cooling rate ( can be any fraction between 0 and 1).
Step 2: Improving the solution
Set the repetition counter n = 0
Repeat the following operations until
Randomly produce a solution s’ in the vicinity of each N(s). We created a 1 km buffer around each gene (fire station), and randomly selected a fire station within this buffer to produce a chromosome or vicinity solution.
Calculate for each solution and each function (f(s) is the fitness of each function). If L for all functions (in the case of appropriate neighbour solutions), then s = s′.
If L for all functions (no fitting in neighbourhood solutions) x is randomly selected from U(0,1). If , then s = s′, otherwise generate a new neighborhood
Otherwise (improvement in one function and no improvement in other functions) save both s and s′
Remove the dominated solutions to the set of saved solutions in the archive
Set n = n + 1, T = T × δT and t = t + 1
Stop if the stopping condition is met or go to step 2.
Initialized solutions create a string or chromosome. Then, another string called a neighborhood string is created. The fitness value for both strings is calculated according to Equation (1). If the neighborhood solution is better than the previous solution, it will be saved, and the process will continue, otherwise a new neighborhood string will be produced. At this time, the temperature is reduced, and the operations continue until the optimum solution is obtained. The algorithm ends when the same results are obtained 10 times consecutively. When the multi-objective SA uses the weights in step 1, it produces only one random solution, while at this stage GA produces several solutions, based on the population size.
4. Study Area and Data
4.1. Study Area
Region 11 is one of the most crowded regions of Tehran, being located in the central part of the city. It contains four areas, and the sum of the populations of these four areas is about 280,000. There are only four fire stations in this region; therefore, the number of fire stations in this region is insufficient based on world standards (according to world standards, the capacity of each station is equal to 50,000 persons per station). The total area of the region is 12.6 km2. Figure 2a shows the populations of each census zone in this region. Figure 2b shows the distributed demand points (created and distributed randomly in each census zone in accordance with the population of each census zone and field observations). There are some areas in this figure 2b which are shown in white, indicating military areas where people cannot settle and live.
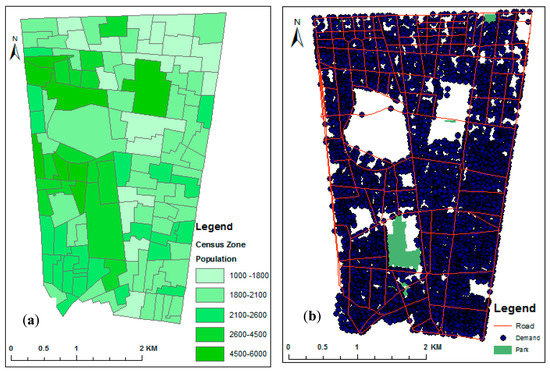
Figure 2.
(a) The populations of each census zone in region 11, Tehran; (b) The distributed demand points.
4.2. Data
To solve the ordered capacitated multi-objective location-allocation problem, some facilities and demands are needed. The former includes potential and existing fire stations, while the latter is the customer or the population using the facilities. The data are entered into a GIS environment in shapefile format. The number of fire accidents reported to each station in 2016, the number of fire stations in each area, and other pieces of required information were obtained from the firefighting organization. In accordance with the standards, a capacity of 50,000 people was considered for each station in the case study and it was assumed that all stations have similar features.
The demands originate from the people dwelling in the four areas of Region 11, whose populations were obtained from both existing statistics and from the municipality. Following this, 280,000 distributed demand points were created in ArcGIS, based on statistics from the population of each census zone and on field visits. The total number of these points is equal to the region’s population. Figure 3 shows 23 potential and four existing fire stations. Since there is no expert view on introducing new stations, the 23 potential fire stations were generated with a 1 km grid in ArcGIS [30]. Investigations revealed that the distance between one fire station and its nearest-neighbor fire station must be within 1–9 km [31].
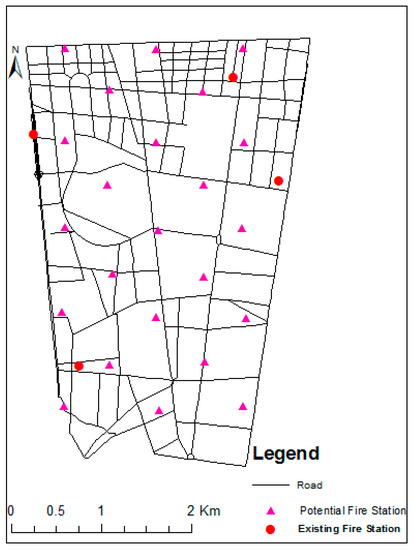
Figure 3.
Potential and existing fire station locations.
Since the location-allocation problem only searches for the best locations for fire stations from predefined points, the 1 km distance helps in producing more stations so that we can select the optimal stations from them in accordance with our goals. Though potential points have been created on a grid, and there is no expert view of price, area, and so on, the authors tried to avoid placing potential points on prohibited areas such as rivers or private buildings by undertaking a field visit. The field visit also allowed some points to be deliberately placed on worn-out, state-owned, or military areas which had enough space for the station and were located adjacent to main streets. For this reason, the potential points are partially displaced from the grid, and the distance between the potential points is not exactly equal to 1 km.
Our calculations are performed on the main road network of this region, with each road having its own attributes such as legal speed limit in that segment, road width, etc. Since we wanted to establish optimal stations, and considering the existing population of the region, the minimum number of stations required is six, our goal was to select six stations from 27 potential stations. GA and SA solutions were exploited in order to solve this combinatorial capacitated multi-objective location-allocation problem. It should be added that both of these algorithms have been implemented by MATLAB 2012, and so MATLAB was modified to implement multi-objective algorithms. The calculation results, as well as the final processing and vectors, are given in the ArcGIS environment or presented as tables.
5. Results and Discussion
5.1. Sensitivity Analysis and Tuning the Model Parameters
Initially, the GA and SA models are validated by means of distributed demand points with a number equal to the population of each area of Region 11, Tehran. The considered weights for each function were as follows:. Simultaneously, the best values of the model parameters were determined by sensitivity analysis to produce high-quality solutions. This study has practical importance for the solution of real-world problems when the optimal solutions are completely unknown [32]. After some preliminary evaluations, the sensitivity analysis was performed for different values in the GA for crossover (0.4 to 0.9), population size (10 to 20), and mutation probabilities (0.1 to 0.4). For SA, the values were initial temperature (50 to 300), absolute temperature (0.01), and cooling rate (0.8 to 0.95). These rates are taken from previous research in the literature [19,20,33].
The stopping condition for each run of the algorithms was 150 generations. Each set of factors generated for the analysis was used for five runs and the result is the average of the fitness over those five runs. The sensitivity analysis therefore considers all the algorithm parameter combinations. Sensitivity analysis was performed on the algorithms. It is necessary to use the best parameters for the GA and SA in order to achieve acceptable results. Table 1 gives the results of the parameter sensitivity analysis for the genetic model, with fixed weights .

Table 1.
Effect of crossover, mutation rate, and population size on objective function in genetic algorithms (GA) by sensitivity analysis.
From Table 1, it can be observed that for population size the objective function values do not follow any pattern, but for crossover = 0.4 and mutation = 0.3 to 0.4, the objective function values follow a consistent pattern. Small population size values, small crossover values, and higher mutation values, (e.g., 0.3, 0.4) are preferred by the analysis. Therefore, the preferred parameter combination for solving the problem in this paper is: population size = 10, crossover = 0.4, and mutation = 0.4.
The model results with the best parameters, selecting six stations out of 27, show that the fitness of the final solutions has decreased, while the convergence of the fitness graph demonstrates that these facts ensure the model’s verification. Figure 4 illustrates the locations of the optimal fire stations, their capacity, and their allocations for f1, f2, and f3 in ArcGIS by means of the best GA parameters with fixed weights . The output graph shows the convergence of the fitness values. The sum of all demands for f1 and f2 is equal to the considered demands for this region, but in f3, it is not equal to the number of considered demands in the region. This shows that all the points have not been covered, and the time between some demand points and the optimal stations was more than five minutes.
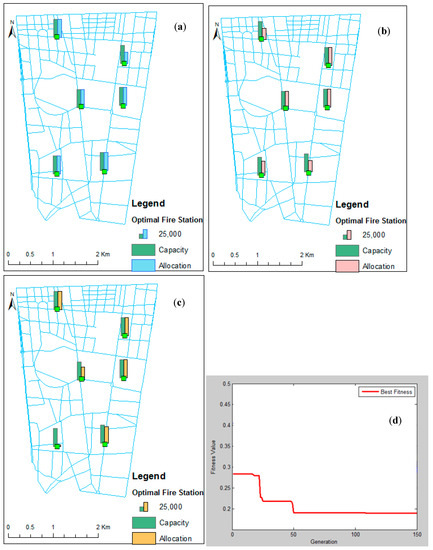
Figure 4.
Optimal location of fire stations, their capacity, and allocations in ArcGIS by means of best GA parameters with fixed weights for functions (a) f1, (b) f2, (c), f3, and (d) fitness output graph.
Results of the sensitivity analysis for the SA model with fixed weights are given in Table 2. These rates are close to those obtained by Murray and Church [34]. From Table 2, it can be observed that fitness values decrease with increasing initial temperature. However, cooling rates do not follow any particular pattern, except for the case of initial temperature = 300 and cooling rates of, e.g., 0.8, 0.9, and 0.95, where the objective function values follow a consistent pattern, with the smallest objective function value obtained for initial temperature = 300 and cooling rate = 0.95. Therefore, these parameters are selected by the sensitivity analysis for this problem.

Table 2.
Best initial temperature for simulated annealing (SA).
Figure 5 illustrates the locations of the optimal fire stations, their capacity, and their allocations for f1, f2, and f3 in ArcGIS by means of the best SA parameters with fixed weights . The output graph shows the convergence of the fitness value. Furthermore, Figure 5, like Figure 4, shows that the sum of the demand allocation for f1 and f2 is equal to the demands present in this region. However, the sum of demands allocated to f3 is not equal to the demands in this region, showing that some points have not been covered. Thus, to cover all demand points, it is necessary to increase the number of optimal locations in the case study. Therefore, the goal is to choose seven fire stations from 27 existing and potential stations, using the algorithm selected as the best model in the algorithm evaluation step.
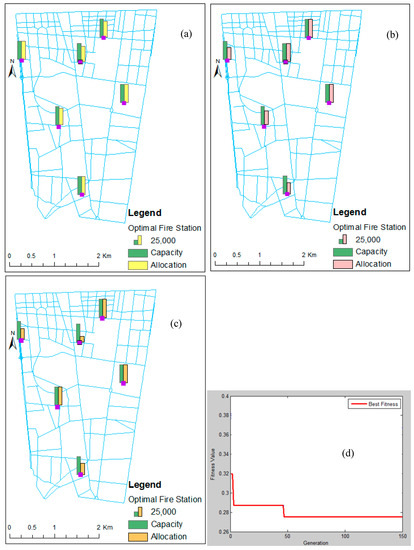
Figure 5.
Optimal location of fire stations, their capacity, and allocations in ArcGIS by means of the best SA parameters with fixed weights for functions (a) f1, (b) f2, (c) f3 and (d) fitness output graph.
Table 3 compares the computation times for SA and GA, using their best parameters. Both algorithms were used as multi-objective algorithms with fixed weights . The computer used to run the algorithms was an Intel(R) Core (TM) i7 760 @ 2.93 GHz with 8.00 GB of RAM, 1 TB hard disk, and Windows 7. The SA algorithm could achieve the results of the GA algorithm in approximately twice the number of iterations in this problem.

Table 3.
The comparison of GA and SA over 150 iterations with the same initial solution.
We wish to estimate the differences between the means with a 95% degree of confidence. According to Freund, if and are the values of the means of independent random samples of sizes and from normal populations with known variances and , then:
is a (1 − ) confidence interval for the difference between the population means.
For a 95% confidence interval, (1 − ∝) = 0.95 so and . From the z_tables for standard normal distribution (Table III in Freund [35]), [35]. In this study, index 1 refers to the genetic algorithm, while index 2 refers to the simulated annealing method. Table 4 shows the results of the comparison of the genetic algorithm with simulated annealing for data sets 1 and 2, which are used to calculate the confidence intervals.

Table 4.
Table of results.
Since both limits are negative, we can conclude with 95% confidence that the genetic algorithm produces a solution with a smaller average than simulated annealing in each data set.
5.2. Evaluation of the Algorithms
We compare the implementation of GA and SA in the ordered capacitated multi-objective location-allocation problem, solving for fire stations with the criteria of fitness rate and calculation time [8]. The results of two heuristic algorithms are compared. The best algorithm is selected for the final implementation in the case study. SA is a simple and effective method that can produce a good solution for combined and difficult problems. However, the disadvantage of this algorithm is its need for a large amount of CPU time for producing the solutions.
It is understood from Table 3 that the fitness value of GA is better than SA, since GA uses the elite individuals in each repetition, whereas SA only studies random solutions and their neighborhoods. With 95% confidence, we can state that the GA can produce better results than SA. SA with many repetitions can produce the same optimal locations as GA, but the convergence time and the number of repetitions in GA is less than for SA. The slowest part of these algorithms is the allocation of demands or customers to the stations, where the algorithms must analyze and then order all the distances between the demands and the chosen stations in each step, in order to find the best demand allocation for each station.
These calculations require a lot of memory resources. With respect to computational resources, GA showed better efficiency. After 150 repetitions, it was clear that the computational time for achieving optimal solutions for SA is about twice as long as for GA. As a result, GA is selected for the final implementation in the case study. In summary, GA produced better results than SA in this problem with a large number of allocations (280,000 demands) for time and fitness values for fire stations.
5.3. Implementation of Genetic Model in Case Study
5.3.1. Increasing the Number of Fire Stations While Retaining Existing Fire Stations
In this section, we increase the number of fire stations (as mentioned in Section 5.1) so that all 280,000 demand points are covered. Therefore, our aim is to select seven fire stations. We retain the existing stations, and therefore our goal becomes the selection of only three new optimal stations out of 23 potential stations. In this case, the ordered capacitated multi-objective function is obtained from function (1) with fixed weights . The GA parameters are in accordance with the best parameters mentioned previously, and the number of repetitions is 150. Figure 6 shows the locations of three optimal stations, obtained from the ordered capacitated multi-objective function with fixed weights together with the four existing stations (considered to be fixed), and the output fitness (in this case, since the weights in each step of the algorithm’s repetition are fixed, the algorithm can eventually achieve a general optimization).
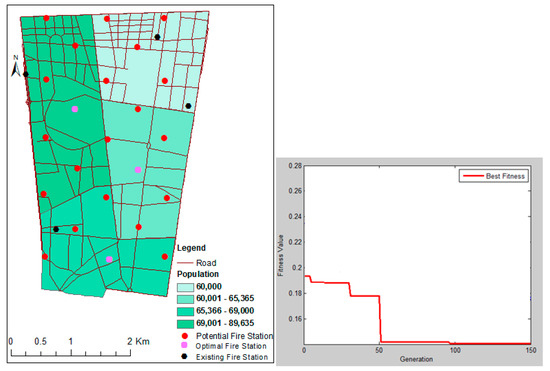
Figure 6.
Optimal locations of fire stations, obtained from ordered capacitated multi-objective function with fixed weights ( and output fitness.
The three stations are located near crowded areas, and the four fixed stations participate in the demand allocation step. Figure 7 shows the optimal location of fire stations with fixed weights and the demand allocation to each function. Since the locations of optimal stations result from function (1), the location of optimal stations is the same in all maps, as indicated by Figure 7. Here, only the allocation capacity of each station is given by each function.
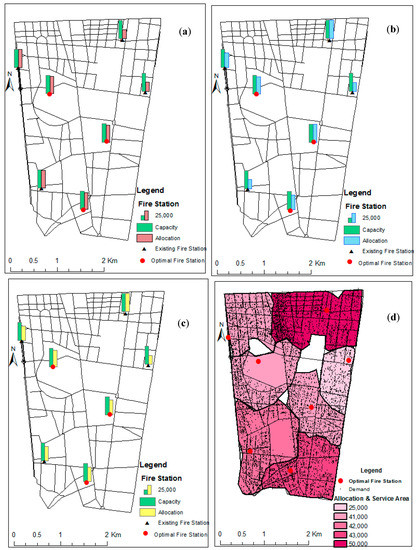
Figure 7.
Optimal locations of the fire stations, obtained from capacitated multi-objective function with fixed weights and demand allocations of (a) f1, (b) f2, and (c) f3; (d) the service areas of the individual fire stations.
The sum of demand allocations for f1, f2, and f3 is equal to the existing demands of the region, which indicates that all demand points have been covered and that the number of fire stations in this region is sufficient. The radius of demand coverage on the road network is considered to be five minutes; therefore, this number of facilities can meet the demands.
5.3.2. Non-Dominated Solutions Retaining the Existing Fire Stations
In practical ordered capacitated multi-objective optimization problems, finding a unique solution that optimizes all objectives simultaneously is very difficult or impossible. A set of non-dominated solutions representing a compromise between objectives is obtained and forms the optimal Pareto front [29]. In this case, since the weights differ with each algorithm’s repetition, the algorithm seeks local optimizations each time among the produced solutions of the same step, and our general aim here is not to achieve the general optimization, but to find all optimizations, even the local ones. This is so that each decision maker can find a desired optimization based on his own criteria, among the set of produced solutions, taking into account the utilized weights.
By retaining the four existing stations, this paper seeks non-dominated solutions. Thus, the produced non-dominated solutions that include four existing stations, along with three others, contain different weights and demand allocations. Here, the ordered capacitated multi-objective function is derived from function (1) and the weights from a random weighting program (function (2)). Model parameters are regulated as follows: the number of generations is 150 repetitions of the model and the population size is 10 individuals or chromosomes.
Table 5 shows the solutions of several independent implementations of the model with 150 repetitions, including the total number of non-dominated solutions in each implementation of the model, the given weights for each objective function, the minimum and maximum distances between adjacent stations, the demand allocations of f3, and the sum. In this table, for purposes of generalization, some solutions have been removed. Consequently, the decision makers can select their desired solutions (Pareto optima) based on these weights.

Table 5.
Non-dominated solutions of 10 independent implementations with 150 iterations.
Among the independent implementations of the model, the best implementation or run is run 5, as it has the lowest value of the sum and the highest number of non-dominated solutions compared to the other runs [14]. Figure 8 shows the non-dominated solutions in 150 repetitions of each model’s run. These solutions cannot dominate one another. Maximum and minimum values are found in the Pareto-optimal sets presented in Table 6. Repeated runs of the model can lead to the generation of different solutions with various weights. Given the information in Table 5 and Table 6, the decision makers can easily select solutions in accordance with the importance of different objectives, as well as in accordance with budget constraints. Furthermore, Using GIS in management is considered to be more significant when the manager must make important decisions in complicated conditions [36].
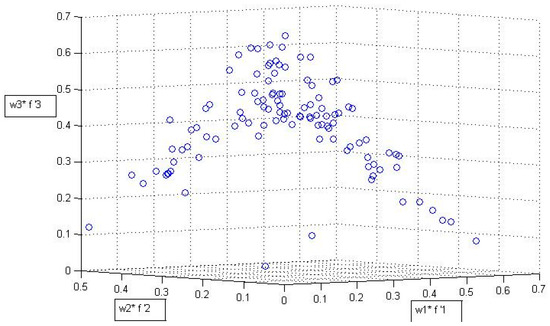
Figure 8.
Non-dominated Pareto-front solutions.

Table 6.
Maximum and minimum values are found in the Pareto-optimal sets.
6. Conclusions
In this paper, three objective functions were taken into consideration in order to solve the ordered capacitated multi-objective location-allocation problem for fire stations. Initially, the parameters of SA and GA were tuned for this problem by sensitivity analysis. While tuning the parameters, the algorithms’ verification was determined via demand data. Then, both algorithms were implemented using the best parameters, for fire stations located in Region 11, Tehran. All our calculations took place on the road network. The implementation of both algorithms showed that the number of optimal stations was not enough to cover all demand points. Furthermore, results from the algorithms’ evaluation, based on the output fitness of both algorithms, as well as the computational time, showed that the GA is more efficient than SA at the 95% confidence level for solving this optimization problem with large sizes. Thus, GA was selected for the final implementation of the model in the case study.
To solve the ordered capacitated multi-objective problem in the case study, we increased the number of optimal stations, retaining the existing stations in our processing, and used the fixed weight vector in the ordered capacitated multi-objective function. The model’s output showed that GA could successfully provide optimal locations for fire stations in Region 11, while considering a capacity of 50,000 individuals for each station. Following this, to generate non-dominated solutions, we used a weighting program to allocate weights to each objective in each run of the program. Here, too, we retained the existing stations in our processing. Eventually, after several independent runs of the model with 150 repetitions, we selected the best set of solutions from among the set of non-dominated solutions. More repetitions of the model, as well as increasing the number of independent runs, leads to the generation of more weights and non-dominated solutions, with the result that the decision makers are offered more alternatives.
Ordered capacitated multi-objective location-allocation problems are complicated problems that can include several conditions and incompatible objectives. This paper proposes implementation of an efficient facility ranking method for output solutions based on other criteria, such as cost, accessibility indicator, and so on, in future. The authors suggest using other weighting schemes and comparing the results in future work.
Acknowledgments
I would like to thank my supervisors and my family for their support and guidance throughout this work.
Author Contributions
Samira Bolouri, Alireza Vafaeinejad, Aliasghar Alesheikh and Hossein Aghamohammadi summarized the contributions and wrote the editorial. All authors read and edited drafts, and approved the final manuscript.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Macit, I. Solving fire department station location problem using modified binary genetic algorithm: A case study of Samsun in Turkey. Eur. Sci. J. 2015, 11, 10–25. [Google Scholar]
- Aghamohammadi, H.; Mesgari, M.; Molaei, D.; Aghamohammadi, H. Development a heuristic method to locate and allocate the medical centers to minimize the earthquake relief operation time. Iran. J. Public Health 2013, 42, 63–71. [Google Scholar] [PubMed]
- Saeedi Mehrabad, M.; Aazami, A.; Goli, A. A location-allocation model in the multi-level supply chain with multi-objective evolutionary approach. J. Ind. Syst. Eng. 2017, 10, 140–160. [Google Scholar]
- Storme, T.; Witlox, F. Location-Allocation models. In The International Encyclopedia of Geography; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Xie, Y.; Runck, B.; Shekhar, S.; Kne, L.; Mulla, D.; Jordan, N.; Wiringa, P. Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation. ISPRS Int. J. Geo-Inf. 2017, 6, 226. [Google Scholar] [CrossRef]
- Zhu, Y.; Du, Q.; Tian, F.; Ren, F.; Liang, S.; Chen, Y. Location Optimization Using a Hierarchical Location-Allocation Model for Trauma Centers in Shenzhen, China. ISPRS Int. J. Geo-Inf. 2016, 5, 190. [Google Scholar] [CrossRef]
- Zuidgeest, M.; Brussel, M.; van Maarseveen, M. GIS for Sustainable Urban Transport. ISPRS Int. J. Geo-Inf. 2015, 4, 2583–2585. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A. Integration of genetic algorithms and GIS for optimal location search. Int. J. Geogr. Inf. Sci. 2005, 19, 581–601. [Google Scholar] [CrossRef]
- Murray, A.; Tong, D. GIS and Spatial analysis in the media. Appl. Geogr. 2009, 29, 250–259. [Google Scholar] [CrossRef]
- Tsai, Y.; Chow-In Ko, P.; Huang, C.; Wen, T. Optimizing locations for the installation of automated external defibrillators (AEDs) in urban public streets through the use of spatial and temporal weighting schemes. Appl. Geogr. 2012, 35, 394–404. [Google Scholar] [CrossRef]
- Yin, P.; Mu, L. Modular capacitated maximal covering location problem for the optimal siting of emergency vehicles. Appl. Geogr. 2012, 34, 247–254. [Google Scholar] [CrossRef]
- Liu, C.M.; Kao, R.L.; Wang, A.H. Solving Location-Allocation problems with rectilinear distances by Simulated Annealing. J. Oper. Res. Soc. 1994, 45, 1304–1315. [Google Scholar] [CrossRef]
- Gonzalez-Monroy, L.I.; Cordoba, A. Optimization of energy supply systems: Simulated Annealing versus Genetic Algorithm. Int. J. Mod. Phys. C 2000, 11, 675–690. [Google Scholar] [CrossRef]
- Neema, M.N.; Ohgai, A. Multi-objective location modeling of urban parks and open spaces: Continuous optimization. Comput. Environ. Urban Syst. 2010, 34, 359–376. [Google Scholar] [CrossRef]
- Bashiri, M.; Bakhtiarifar, M.H. Finding the optimal location in a one-median network problem with correlated demands using simulated annealing. Sci. Iran. 2013, 20, 793–800. [Google Scholar]
- Yu, H.; Solvang, W. A multi-objective location-allocation optimization for sustainable management of municipal solid waste. Environ. Syst. Decis. 2017, 37, 289–308. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, X. Land use allocation based on a multi-objective artificial immune optimization model: An application in Anlu County, China. Sustainability 2015, 7, 15632–15651. [Google Scholar] [CrossRef]
- Vafaeinezhad, A.; Alesheikh, A.; Nouri, J. Developing a spatio-temporal model of risk management for earthquake life detection rescue team. Int. J. Environ. Sci. Technol. 2010, 7, 243–250. [Google Scholar] [CrossRef]
- Zhou, G.; Min, H.; Gen, M. A genetic algorithm approach to the bi-criteria allocation of customers to warehouses. Int. J. Prod. Econ. 2003, 86, 35–45. [Google Scholar] [CrossRef]
- Duh, J.; Brown, D. Knowledge-informed pareto simulated annealing for multi-objective spatial allocation. Comput. Environ. Urban Syst. 2007, 31, 253–281. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H.; Tanaka, H. Multi-objective genetic algorithm and its applications to flow shop scheduling. Comput. Ind. Eng. 1996, 30, 957–968. [Google Scholar] [CrossRef]
- Rakas, J.; Teodorović, D.; Kim, T. Multi-objective modeling for determining location of undesirable facilities. Transp. Res. Part D Transp. Environ. 2004, 9, 125–138. [Google Scholar] [CrossRef]
- Özcan, T.; Çelebi, N.; Esnaf, Ş. Comparative analysis of multi-criteria decision making methodologies and implementation of a warehouse location selection problem. Expert Syst. Appl. 2011, 38, 9773–9779. [Google Scholar] [CrossRef]
- Erkut, E.; Karagiannidis, A.; Perkoulidis, G.; Tjandra, S.A. A multicriteria facility location model for municipal solid waste management in North Greece. Eur. J. Oper. Res. 2008, 182, 1402–1421. [Google Scholar] [CrossRef]
- Lei, T.; Church, R. Vector assignment ordered median problem: A unified median problem. Int. Reg. Sci. Rev. 2012, 37, 194–224. [Google Scholar] [CrossRef]
- Maliszewski, P.; Kuby, M.; Horner, M. A comparison of multi-objective spatial dispersion models for managing critical assets in urban areas. Comput. Environ. Urban Syst. 2012, 36, 331–341. [Google Scholar] [CrossRef]
- Erden, T.; Coskun, M.Z. Multi criteria site selection for fire services: The interaction with analytic hierarchy process and geographic information systems. Nat. Hazards Earth Syst. Sci. 2010, 10, 2127–2134. [Google Scholar] [CrossRef]
- Melanie, M. An Introduction to Genetic Algorithms; Fifth Printing; MIT Press: Cambridge, MA, USA; London, UK, 1999. [Google Scholar]
- Didier Lins, I.; López Droguett, E. Redundancy allocation problems considering systems with imperfect repairs using multi-objective genetic algorithms and discrete event simulation. Simul. Model. Pract. Theory 2011, 19, 362–381. [Google Scholar] [CrossRef]
- Shamsul Arifin, M.D. Location Allocation Problem Using Genetic Algorithm and Simulated Annealing: A Case Study Based on School in Enschede. Master’s Thesis, Department of Geo-information Science and Earth Observation, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Liu, N.; Huang, B.; Chandramouli, M. Optimal Siting of Fire Stations Using GIS and ANT Algorithm. J. Comput. Civ. Eng. 2006, 20, 361–369. [Google Scholar] [CrossRef]
- Srinivas, C.; Ramgopal Reddy, B.; Ramji, K.; Naveen, R. Sensitivity analysis to determine the Parameters of genetic algorithm for machine layout. Procedia Mater. Sci. 2014, 6, 866–876. [Google Scholar] [CrossRef]
- Wang, K.; Makond, B.; Liu, S.Y. Location and Allocation decisions in a two-echelon supply chain with stochastic demand-A Genetic-Algorithm based solution. Expert Syst. Appl. 2011, 38, 6125–6131. [Google Scholar] [CrossRef]
- Murray, A.; Church, R. Applying simulated annealing to location-planning models. J. Heuristics 1996, 2, 31–53. [Google Scholar] [CrossRef]
- Manikas, T.; Cain, J. Genetic Algorithms vs. Simulated Annealing: A Comparison of Approaches for Solving the Circuit Partitioning Problem; Technical Report: 96-101; Computer Science and Engineering, University of Pittsburg: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Vafaeinezhad, A.; Alesheikh, A.; Hamrah, M.; Nourjou, R.; Shad, R. Using GIS to develop an efficient Spatio-temporal task allocation algorithm to human groups in an entirely dynamic environment case study: Earthquake rescue teams. In Proceedings of the Computational Science and Its Applications ICCSA 2009, Seoul, Korea, 29 June–2 July 2009; pp. 66–78. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).