Incrementally Detecting Change Types of Spatial Area Object: A Hierarchical Matching Method Considering Change Process
Abstract
:1. Introduction
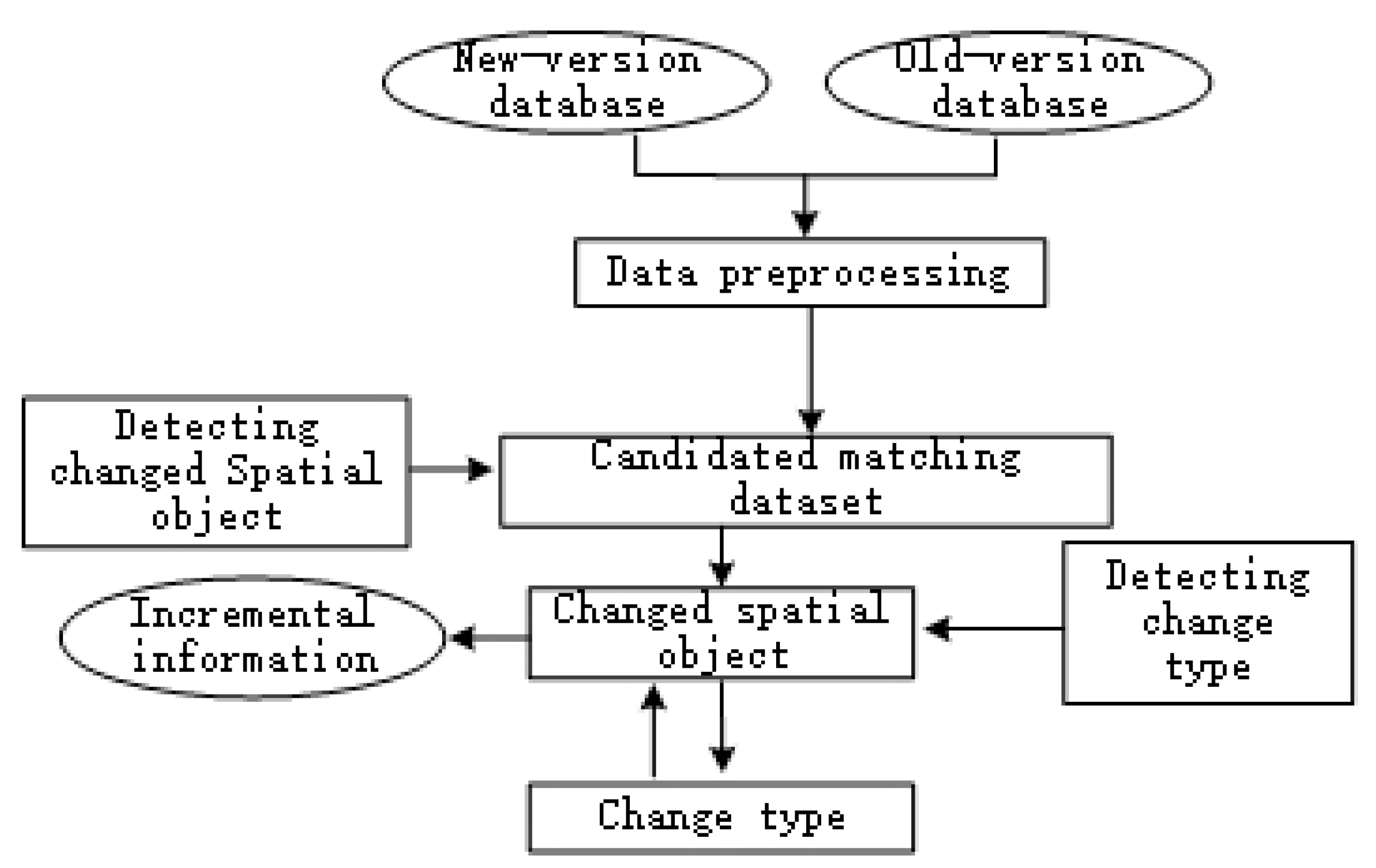
2. Incremental Detection of Change Information of Area Objects
2.1. Basic Idea
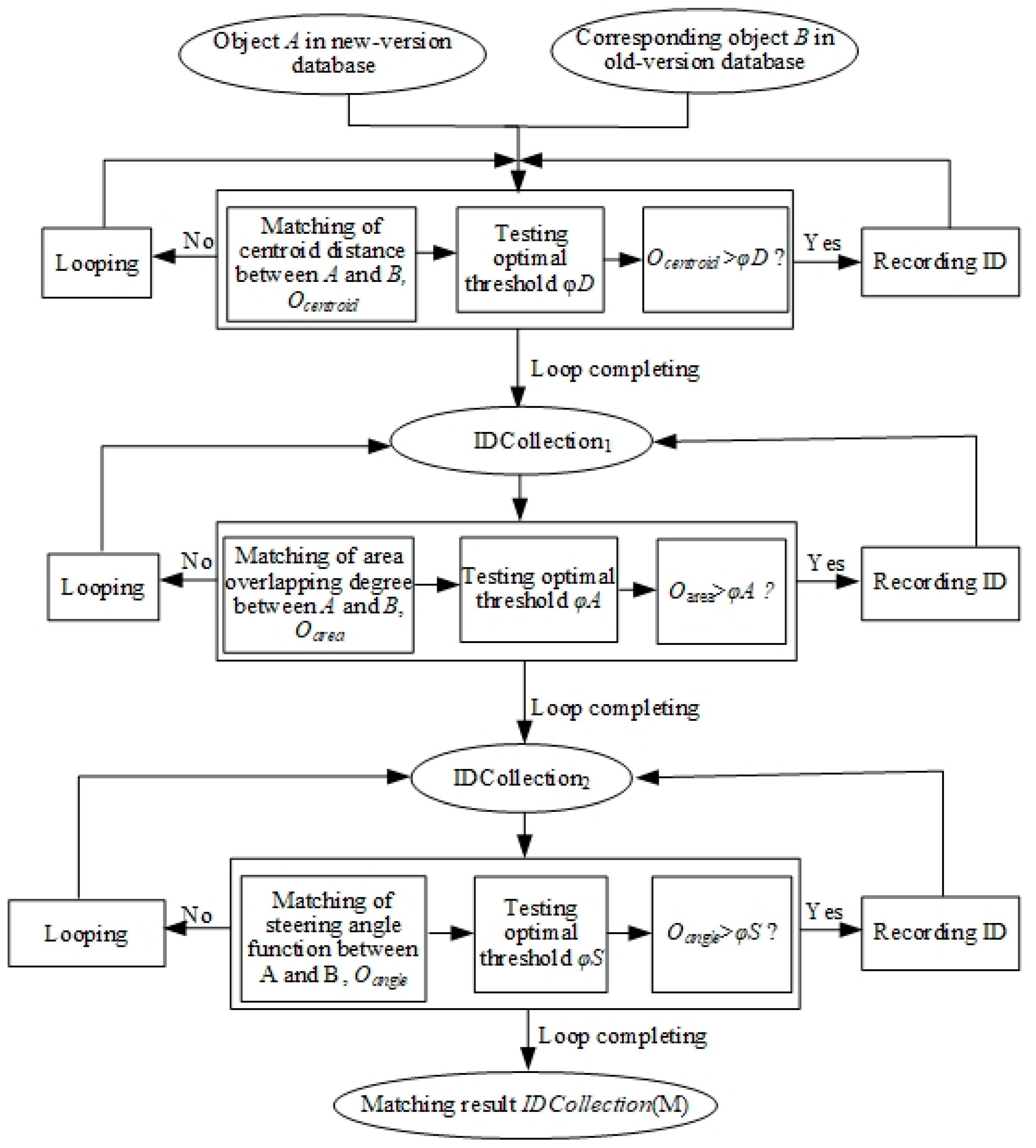
2.2. Selection of Hierarchical Matching Operators
2.3. Extraction of Incremental Information Based on Hierarchical Matching
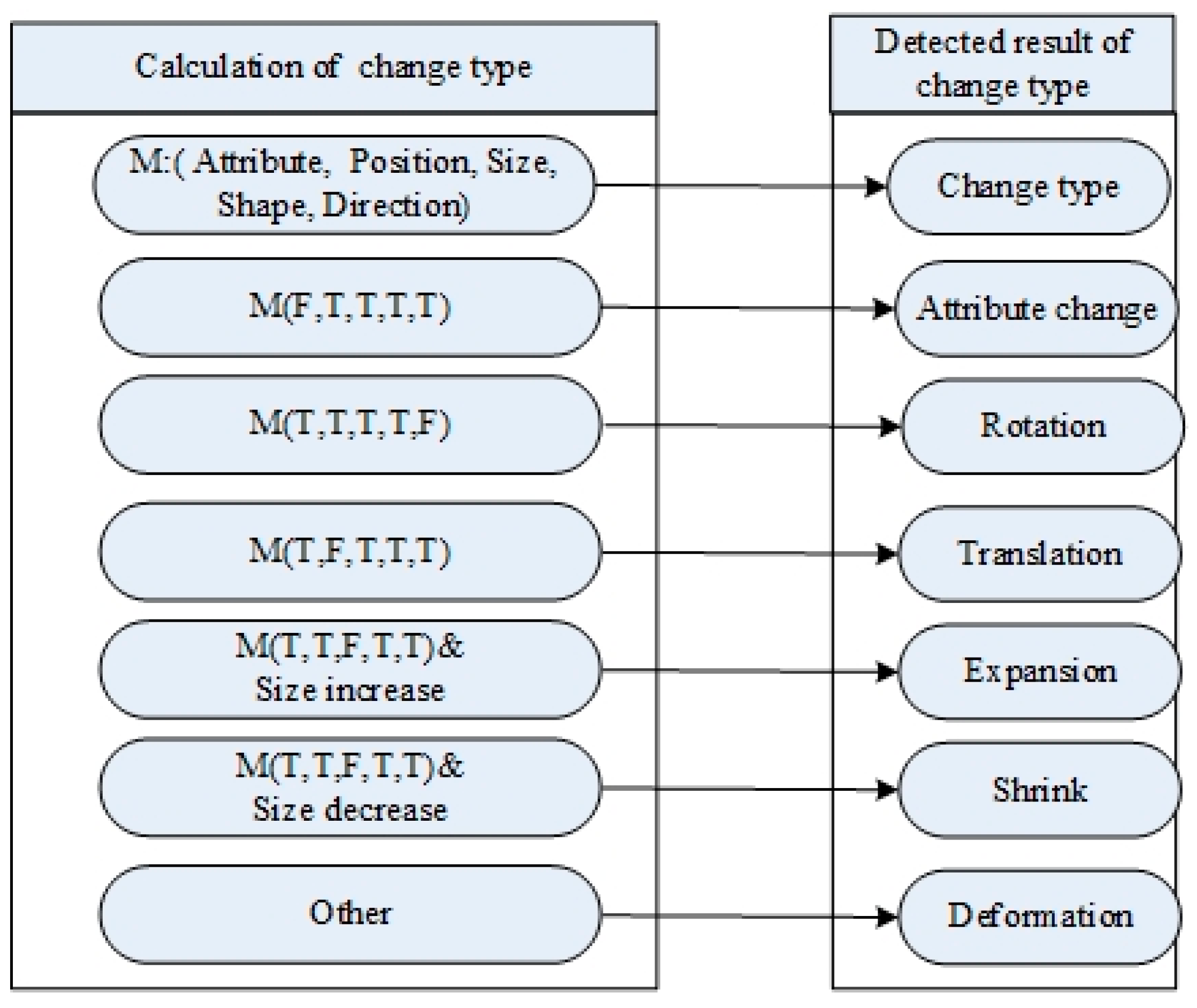
2.4. Detection of Change Types Based on Matching Operators
- Rule 1: If there is no intersection between the area object Fo and any object Fn within the same geographical theme, the change of Fo is classified as Vanish.∀Fn ∈ ChangeCollection (N), ∃Fo ∈ ChangeCollection (O), if (Fo∩Fn = Ø) then ChangeType (Fo) ← Vanish.
- Rule 2: If there is no intersection between the area object Fn and any object Fo within the same geographical theme, the change of Fo is classified as Vanish.∀Fo ∈ ChangeCollection (O), ∃Fn ∈ ChangeCollection (N), if (Fn∩Fo = Ø) then ChangeType (F0) ← Vanish.
- Rule 3: If Fp and Fn are matched, and the types of changes of Fp and Fn are Vanish and Appearance, then the change of Fn is classified as Reappearance.if ((Matching (Fo, Fn) = Ture)and (ChangeType (Fo) = Vanish) and (ChangeType (Fn) = Appearance)) then ChangeType (Fn) ← Reappearance.
- Rule 4: If geometrical features of Fo and Fn are determined to be unchanged and the attribute information has changed, then the change of the object is classified as AttributeChange.if ((IsAttributeMatch = False) and (PositionResult ≥ φ1) and (AreaResult ≥ φ2) and (ShapeDirectionResult ≥ φ3)) then ChangeType (Fo → Fn) ← AttributeChange.
- Rule 5: If area geometrical features of Fn and Fo are determined to be unchanged and the area of Fn decreases from that of Fo, while the other discriminant indexes are unchanged, then the change of the object is classified as Shrink.if ((IsAttributeMatch = True) and (PositionResult ≥ φ1) and (AreaResult < φ2) and (ShapeDirectionResult ≥ φ3) and (S(Fn) < S(Fo))) then ChangeType (Fo → Fn) ← Shrink.
- Rule 6: If geometrical features of the areas of Fn and Fo are determined to be changed and the area of Fn increases from that of Fo, while the other discriminant indexes are unchanged, then the change of the object is classified as Expansion.if ((IsAttributeMatch = True) and (PositionResult ≥ φ1) and (AreaResult < φ2) and (ShapeDirectionResult ≥ φ3) and (S(Fn) > S(Fo))) then ChangeType (Fo → Fn) ← Expansion.
- Rule 7: If geometrical features of the positions of Fn and Fo are determined to be changed while the other discriminant indexes are unchanged, then the change of the object is classified as Translation.if ((IsAttributeMatch = True) and (PositionResult < φ1) and (AreaResult ≥ φ2) and (ShapeDirectionResult ≥ φ3)) then ChangeType (Fo → Fn) ← Translation.
- Rule 8: If geometrical features of the directions of Fn and Fo are determined to be changed while the other discriminant indexes are deemed as unchanged, then the types of changes of the object is classified as Rotation.if ((IsAttributeMatch = True) and (PositionResult ≥ φ1) and (AreaResult ≥ φ2) and (ShapeDirectionResult < φ3) and (AssistResult ≥ φ4)) then ChangeType (Fo → Fn) ← Rotation.
- Rule 9: The types of changes other than the types of changes stated in Rule 1–Rule 8 are defined as Deformation.∀E1 ∈ ChangeCollection (O), Fn ∈ ChangeCollection (N), if ((ChangeType ∉ (Rule 1∪Rule 2∪Rule 3∪Rule 4∪Rule 5∪Rule 6∪Rule 7∪Rule 8)) then ChangeType (Fo → Fn) ← Deformation.
3. Experimental Test
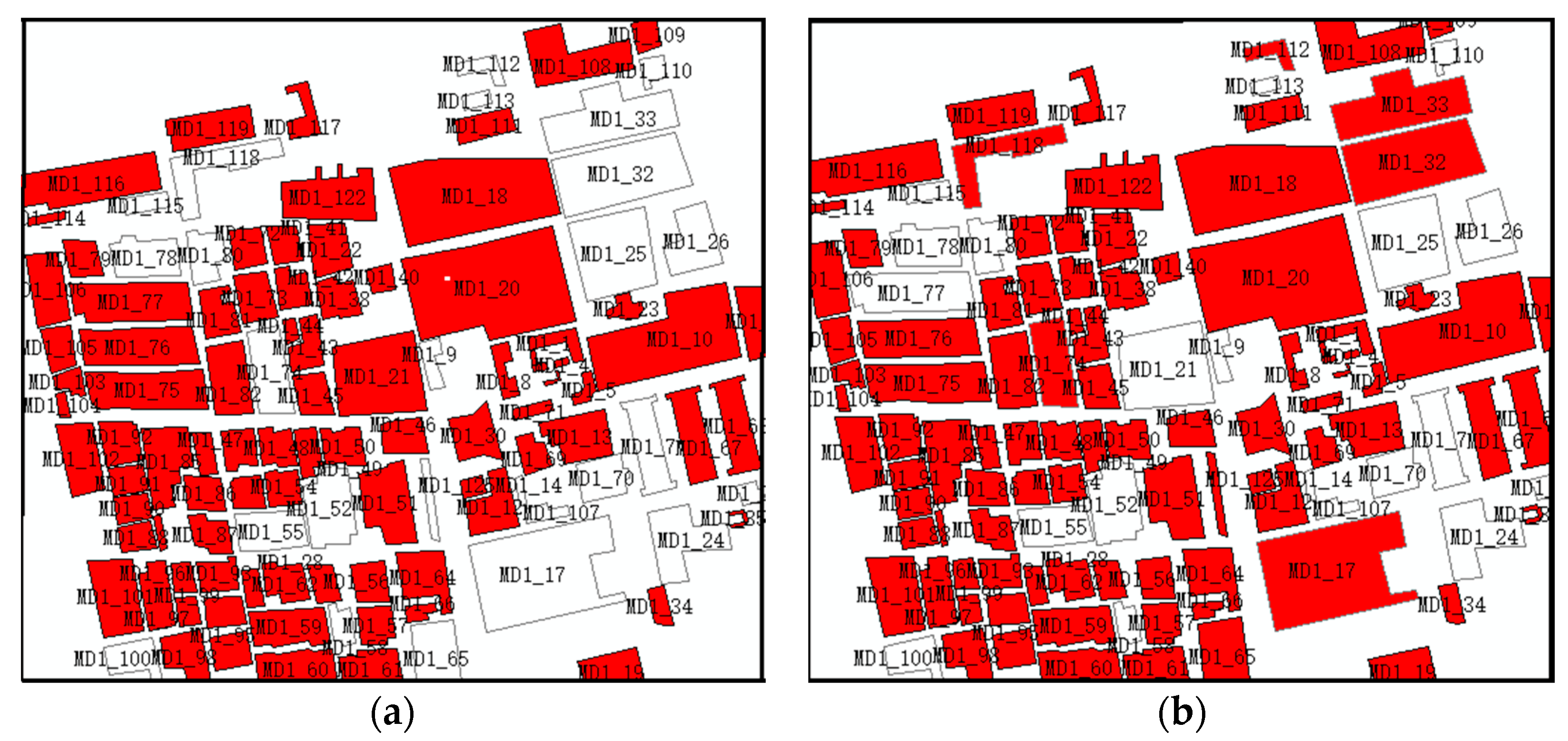
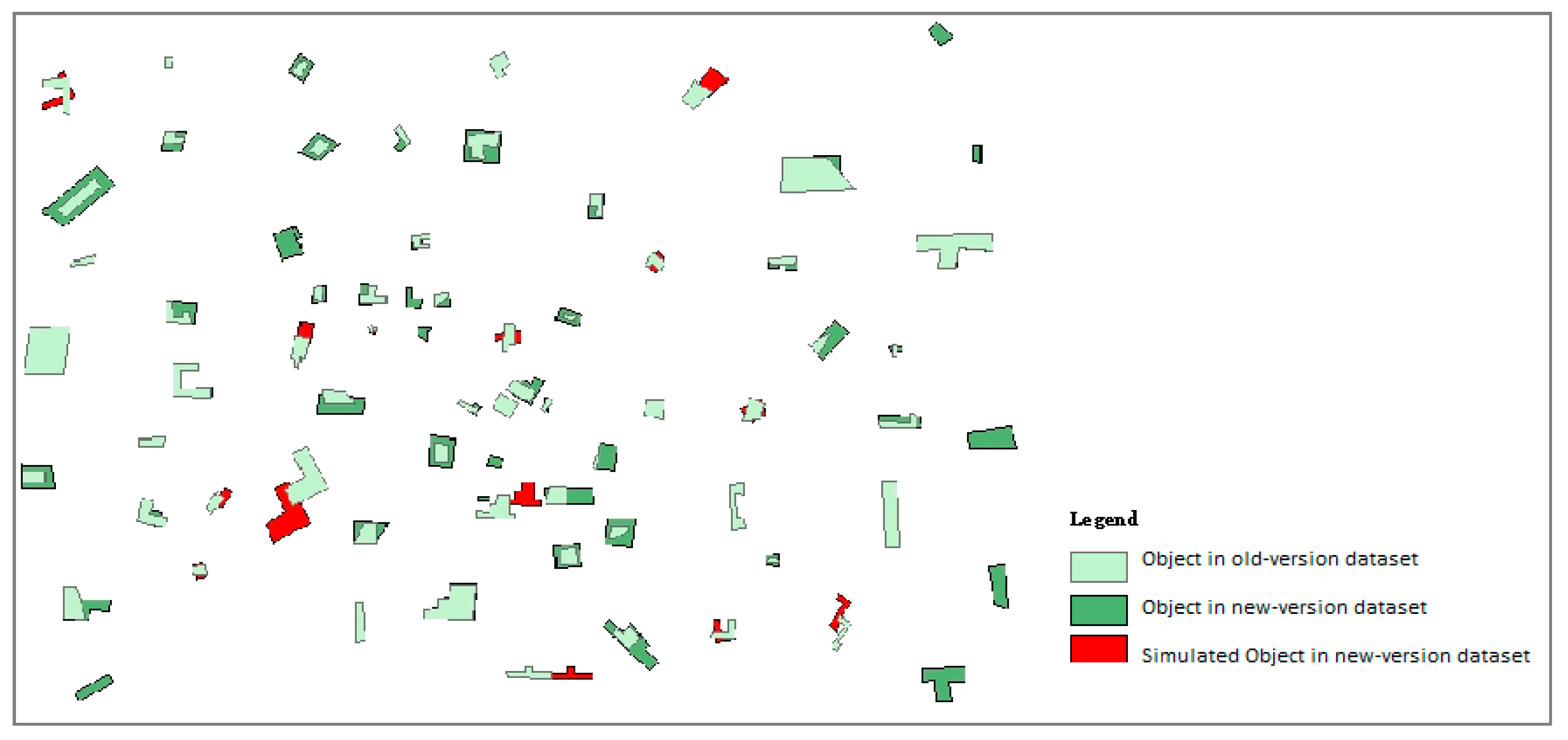
3.1. Incremental Information Extraction
3.2. Detection of Change Types
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ye, Y.; Chen, B.; Wan, B. MMS-IU Model for Incremental Update of Spatial Database. Commun. Comput. Inf. Sci. 2013, 398, 359–370. [Google Scholar]
- Zhou, X.; Zeng, L.; Jiang, Y.; Zhou, K.; Zhao, Y. Dynamically Integrating OSM Data into a Borderland Database. ISPRS Int. J. Geo-Inf. 2015, 3, 1707–1728. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, C.; Ding, Y. Multi-scale Extraction for the Road Network Incremental Information in Navigation Electronic Map. J. Southwest Jiaotong Univ. 2015, 4, 590–596. [Google Scholar] [CrossRef]
- Harrie, L. Generalisation Methods for Propagating Updates between Cartographic Data Sets; Surveying Lund Institute of Technology, Lund University: Lund, Sweden, 1998. [Google Scholar]
- Zhang, X.; Guo, T.; Tang, T. An Adaptive Method for Incremental Updating of Vector Data. Acta Geod. Cartogr. Sin. 2012, 4, 613–619. [Google Scholar]
- Badard, T.; Richard, D. Using XML for the Exchange of Updating Information between Geographical Information Systems. Comput. Environ. Urban. Syst. 2001, 25, 17–31. [Google Scholar] [CrossRef]
- Briatm, O.; Monnot, J.L.; Kressmann, T. Incremental Update of Cartographic Data in a Versioned Enviroment. In Proceedings of the 22nd International Cartographic Conference, Coruna, Spain, 11–16 July 2005; pp. 1–9. [Google Scholar]
- Zhang, Q.; Wang, Y. Automatic Detection Method for Change Type in Incremental Information Extraction Process of the Area Entities. Geogr. Geogr. Inf. Sci. 2016, 2, 11–16. [Google Scholar]
- Spery, L.; Claramunt, C.; Libourel, T. A Spatio-Temporal Model for the Manipulation of Lineage Metadata. Geoinformatica 2001, 1, 51–70. [Google Scholar] [CrossRef]
- Gombosˇi, M.; Zˇalik, B.; Krivograd, S. Comparing Two Sets of Polygons. Int. J. Geogr. Inf. Sci. 2003, 5, 431–443. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, X.; Qi, L. An Incremental Updating Method of Spatial Data Considering the Geographic Features Change Process. Acta Sci. Nat. Univ. Sunyatseni 2014, 4, 131–141. [Google Scholar]
- Zhang, Q.; Wang, Y. The Research of Polygon Geometric Matching Method Based on Hierarchical Matching. Geogr. Geogr. Inf. Sci. 2016, 3, 298–306. [Google Scholar]
- Chen, J.; Wang, D.; Shang, Y. Master Design And Technical Development For National 1: 50,000 Topographic Database Updating Engineering in China. Acta Geod. Cartogr. Sin. 2010, 1, 7–10. [Google Scholar]
- Safra, E.; Kanza, Y.; Sagiv, Y.; Beeri, C.; Doytsher, Y. Location-Based Algorithms For finding Sets of Corresponding Objects over Several Geo-Spatial Data sets. Int. J. Geogr. Inf. Sci. 2010, 1, 69–106. [Google Scholar] [CrossRef]
- Zhai, R.J. Research on Automated Matching Methods for Multi-Scale Vector Spatial Data Based on Global Consistency Evaluation; PLA Information Engineering University: Zhengzhou, China, 2011. (In Chinese) [Google Scholar]
- Shin, K. Comparative Study on the Measures of Similarity for the Location Template Matching (LTM) Method. Trans. Korean Soc. Noise Vib. Eng. 2014, 4, 310–316. [Google Scholar] [CrossRef]
- Kim, I.; Feng, C.; Wang, Y. A Simplified Linear Feature Matching Method Using Decision Tree Analysis, Weighted Linear Directional Mean, and Topological Relationships. Int. J. Geogr. Inf. Sci. 2017, 5, 1042–1060. [Google Scholar] [CrossRef]
- Armiti, A.; Gertz, M. Efficient Geometric Graph Matching Using Vertex Embedding. In Proceedings of the ACM Sigspatial International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 224–233. [Google Scholar] [CrossRef]
- Xing, H.; Chen, J. Parametric Approach to Classification of Spatial Object Change. J. Cent. South Univ. (Sci. Technol.) 2014, 2, 495–500. [Google Scholar]
- Zhang, J.; Wang, Y.; Zhao, W. An Improved Probabilistic Relaxation Method for Matching Multi-Scale Road Networks. Int. J. Digit. Earth 2017. [Google Scholar] [CrossRef]
- Claramunt, C.; Thériault, M. Managing Time in GIS: An Event-Oriented Approach. In Proceedings of the International Workshop on Temporal Databases, Zürich, Switzerland, 17–18 September 1995; pp. 23–42. [Google Scholar] [CrossRef]
- Hornsby, K.; Egenhofer, M.J. Identity-based Change: A Foundation for Spatio-Temporal Knowledge Representation. Int. J. Geogr. Inf. Sci. 2000, 3, 207–224. [Google Scholar] [CrossRef]
- Bhatt, M.; Wallgruen, J.O. Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning For High-Level Analyses In Geographic Information Systems. ISPRS Int. J. Geo-Inf. 2014, 1, 80–95. [Google Scholar] [CrossRef]
- Wang, S.; Liu, D.; Gu, F. Identity Change Based Spatio-Temporal Reasoning. Chin. J. Comput. 2012, 2, 210–217. [Google Scholar] [CrossRef]
- Klippel, A.; Worboys, M.; Duckham, M. Identifying Factors of Geographic Event Conceptualisation. Int. J. Geogr. Inf. Sci. 2008, 2, 183–204. [Google Scholar] [CrossRef]
- Kane, J.; Naumov, P. The Semantics of Similarity in Geographic Information Retrieval. J. Spat. Inf. Sci. 2011, 2, 29–57. [Google Scholar] [CrossRef]
- Fan, Y.T.; Yang, J.Y.; Zhu, D.H. An Event-Based Change Detection Method of Cadastral Database Incremental Updating. Math. Comput. Model. 2011, 11–12, 1343–1350. [Google Scholar] [CrossRef]
- Pan, L.; Wang, H. Using Topological Relation Model to Automatically Detect the Change Types of Residential Land. Geomat. Inf. Sci. Wuhan Univ. 2009, 3, 301–304. [Google Scholar]
- Zhu, H.; Wu, H.; Ma, S. Description and Representation Model of Spatial Object Incremental Update. J. Spat. Sci. 2014, 1, 49–61. [Google Scholar] [CrossRef]
- Chen, J.; Lin, Y.; Liu, W. Formal Classification of Spatial Incremental Changes for Updating. Acta Geod. Cartogr. Sin. 2012, 1, 108–114. [Google Scholar]
- Li, J. Spatial Conflict Detection and Processing Method for Incremental Change of Residential Land. Master’s Thesis, PLA Information Engineering University, Zhengzhou, China, 2015. (In Chinese). [Google Scholar]
- Zhao, Z.; Stough, R.; Song, D. Measuring Congruence of Spatial Objects. Int. J. Geogr. Inf. Sci. 2011, 1, 113–130. [Google Scholar] [CrossRef]
- Arjun, P.; Mirnalinee, T.T.; Tamilarasan, M. Compact Centroid Distance Shape Descriptor Based on Object Area Normalization. In Proceedings of the International Conference on Advanced Communication Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2015; pp. 1650–1655. [Google Scholar] [CrossRef]
- Moreira, D.; Wang, L. Hausdorff Measure Estimates and Lipschitz Regularity in Inhomogeneous Nonlinear Free Boundary Problems. Arch. Ration. Mech. Anal. 2014, 2, 527–559. [Google Scholar] [CrossRef]
- Yin, C.; Wang, Y. Target Geometry Matching Threshold in Incremental Updating of Road Network Based on OSTU. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 1061–1067. [Google Scholar]
| Algorithm | Calculation Times of | Calculation Times of | Calculation Times of |
|---|---|---|---|
| Weighted matching algorithm | m*n | m*n | m*n |
| Hierarchical matching algorithm | m*n | k1 | k2 |
| Matching Method | Number of Samples | R | t | T | Ri | Ra |
|---|---|---|---|---|---|---|
| Hierarchical matching | 487 | 409 | 384 | 424 | 90.6% | 93.9% |
| Weighted matching | 487 | 432 | 363 | 424 | 85.6% | 84.0% |
| Corresponding ID | Weight of Weighted Matching Method | Hierarchical Matching Detection | Weighted Matching Detection | |||
|---|---|---|---|---|---|---|
| MD1_32/MD2_30 | 0.999 | 0.979 | 0.513 | 0.830 | No | Yes |
| MD1_33/MD2_32 | 0.998 | 0.965 | 0.495 | 0.819 | No | Yes |
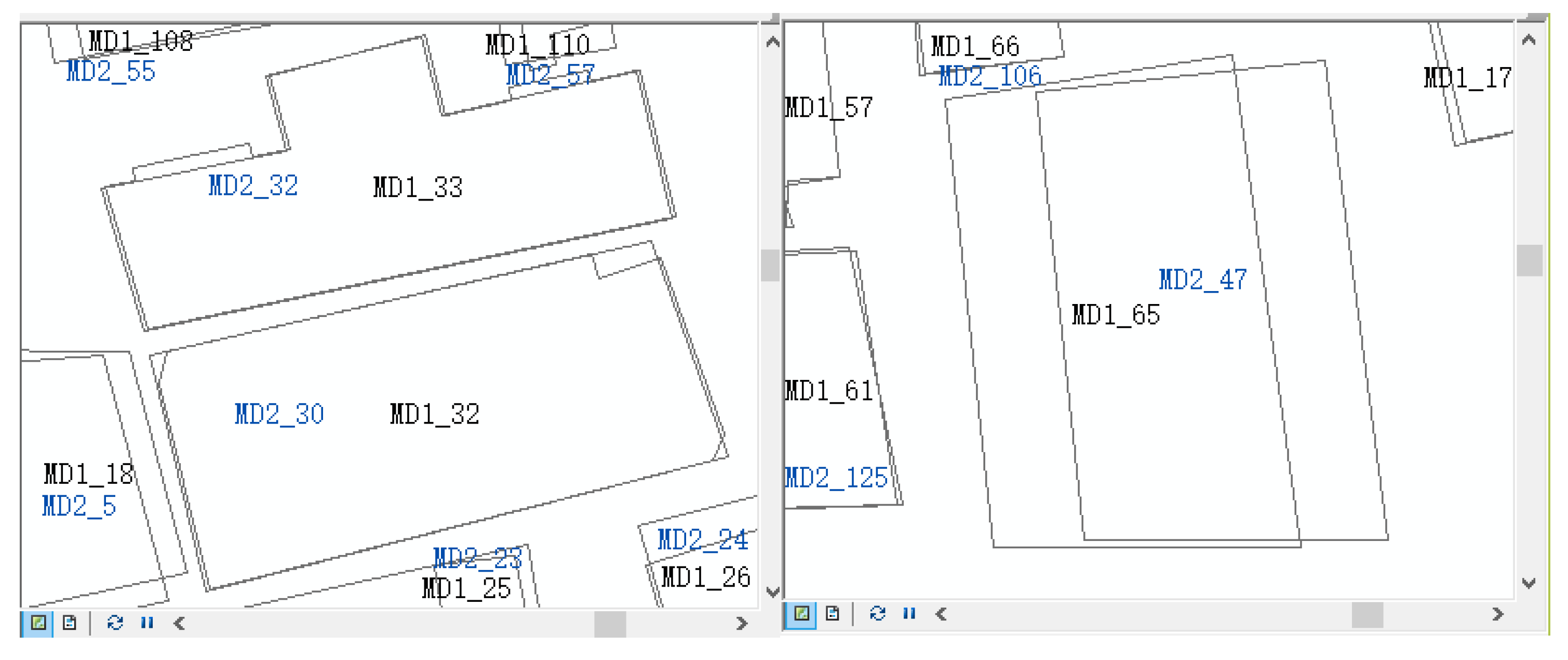
| MD1_65/MD2_47 | 0.781 | 0.753 | 0.986 | 0.840 | No | Yes |
| No. of Study Area | Number of Samples | Hierarchical Matching | Weighted Matching | ||
|---|---|---|---|---|---|
| Ri (%) | Ra (%) | Ri (%) | Ra (%) | ||
| 1 | 313 | 91.7 | 97.6 | 87.2 | 88.9 |
| 2 | 696 | 94.2 | 94.3 | 84.7 | 86.3 |
| 3 | 1092 | 92.9 | 95.1 | 82.9 | 87.4 |
| 4 | 1721 | 93.4 | 95.6 | 86.1 | 86.7 |
| Overall | 3822 | 93.3 | 95.3 | 85.0 | 87.2 |
| Change Type | R | t | T | Ra | Ri |
|---|---|---|---|---|---|
| Vanish | 24 | 24 | 24 | 100% | 100% |
| Appearance | 37 | 37 | 37 | 100% | 100% |
| Reappearance | - | - | - | 100% | 100% |
| AttributeChange | 21 | 21 | 21 | 100% | 100% |
| Shrink | 11 | 11 | 11 | 100% | 100% |
| Expansion | 46 | 46 | 46 | 100% | 100% |
| Translation | 4 | 4 | 4 | 100% | 100% |
| Rotation | 27 | 25 | 28 | 92.6% | 89.3% |
| Deformation | 43 | 39 | 44 | 90.7% | 88.6% |
| Overall | 213 | 207 | 215 | 97.2% | 96.2% |
| No. of Study Area | R | t | T | Ra (%) | Ri (%) |
|---|---|---|---|---|---|
| 1 | 230 | 209 | 224 | 90.9 | 93.3 |
| 2 | 613 | 584 | 621 | 95.3 | 94.0 |
| 3 | 874 | 809 | 863 | 92.6 | 93.7 |
| 4 | 1203 | 1136 | 1178 | 94.4 | 96.4 |
| Overall | 2920 | 2738 | 2886 | 93.8 | 94.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Q.; Guan, H. Incrementally Detecting Change Types of Spatial Area Object: A Hierarchical Matching Method Considering Change Process. ISPRS Int. J. Geo-Inf. 2018, 7, 42. https://doi.org/10.3390/ijgi7020042
Wang Y, Zhang Q, Guan H. Incrementally Detecting Change Types of Spatial Area Object: A Hierarchical Matching Method Considering Change Process. ISPRS International Journal of Geo-Information. 2018; 7(2):42. https://doi.org/10.3390/ijgi7020042
Chicago/Turabian StyleWang, Yanhui, Qisheng Zhang, and Hongliang Guan. 2018. "Incrementally Detecting Change Types of Spatial Area Object: A Hierarchical Matching Method Considering Change Process" ISPRS International Journal of Geo-Information 7, no. 2: 42. https://doi.org/10.3390/ijgi7020042
APA StyleWang, Y., Zhang, Q., & Guan, H. (2018). Incrementally Detecting Change Types of Spatial Area Object: A Hierarchical Matching Method Considering Change Process. ISPRS International Journal of Geo-Information, 7(2), 42. https://doi.org/10.3390/ijgi7020042




