A Space-Time Periodic Task Model for Recommendation of Remote Sensing Images
Abstract
1. Introduction
2. Related Work
2.1. General Recommendation System
2.2. Recommendation for Spatial Data
2.3. Space and Time Recommendation Based on Topic Model
3. Methodology
3.1. LDA Model
3.2. Problem Description
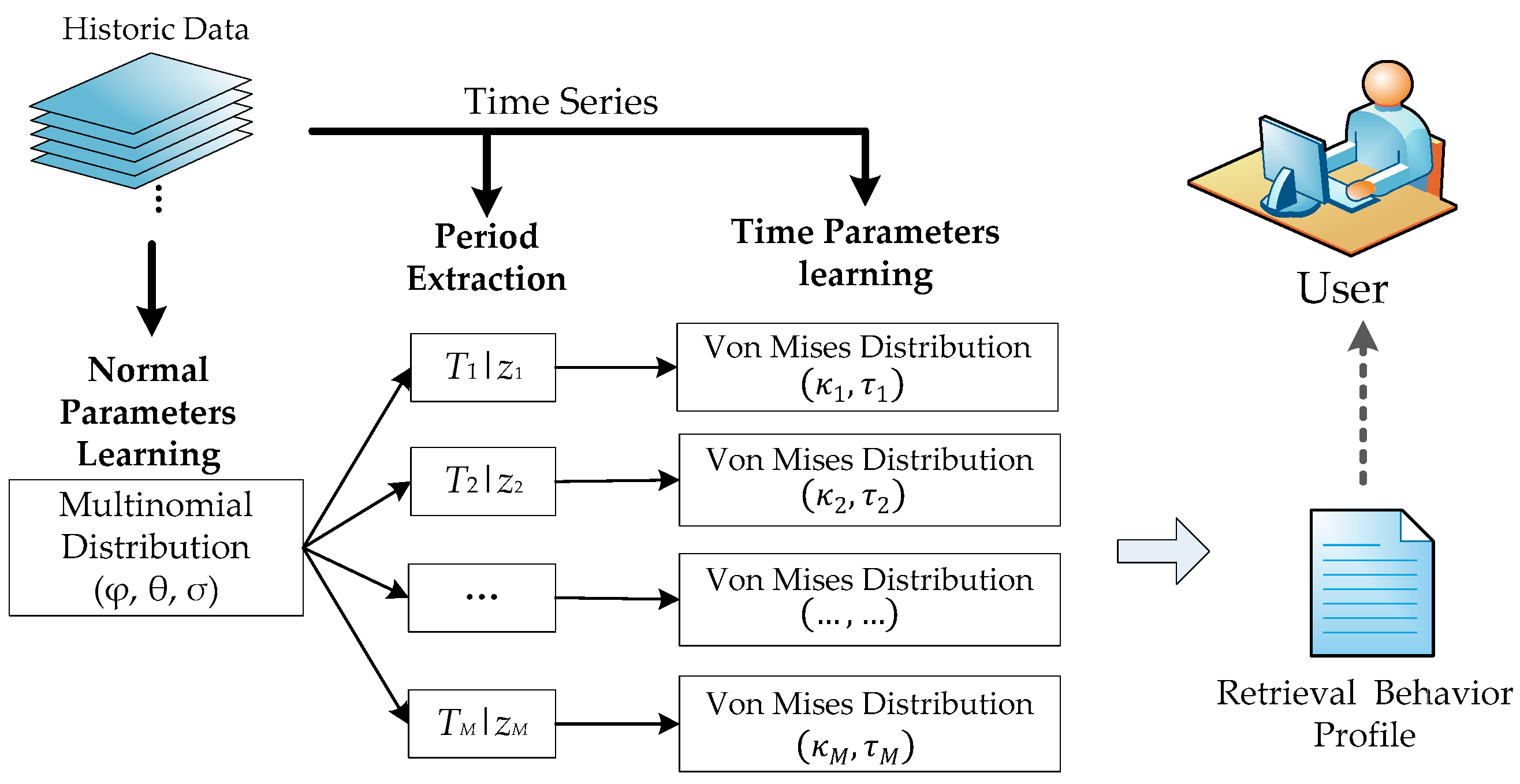
3.3. Space-Time Periodic Task Model
3.3.1. Model Structure
| Algorithm 1: Generative process |
| Input: a set of retrieval behavior documents D |
| Output: estimated parameters θ, ϕ, σ; |
| for each task z do |
| Draw ϕz ~ Dirichlet (β); |
| Draw σz ~ Dirichlet (γ); |
| Assign a task period Tz; |
| end for |
| for each retrieval behavior profile Dr do |
| Draw θr from Dirichlet (α); |
| Draw a task zri from multinomial zri ~ Multi(zri|θr); |
| Draw an image element ez from multinomial ez ~ Multi(e|σzri); |
| Draw a spatial grid sz from multinomial sz ~ Multi(s|ϕzri); |
| end for |
| for each task z do |
| for each period Tz do |
| Draw a timestamp tzw ~ P(t|κz, τz, Tz) from tzw ~ specific von Mises distribution; |
| end for |
| end for |
3.3.2. Parameter Learning
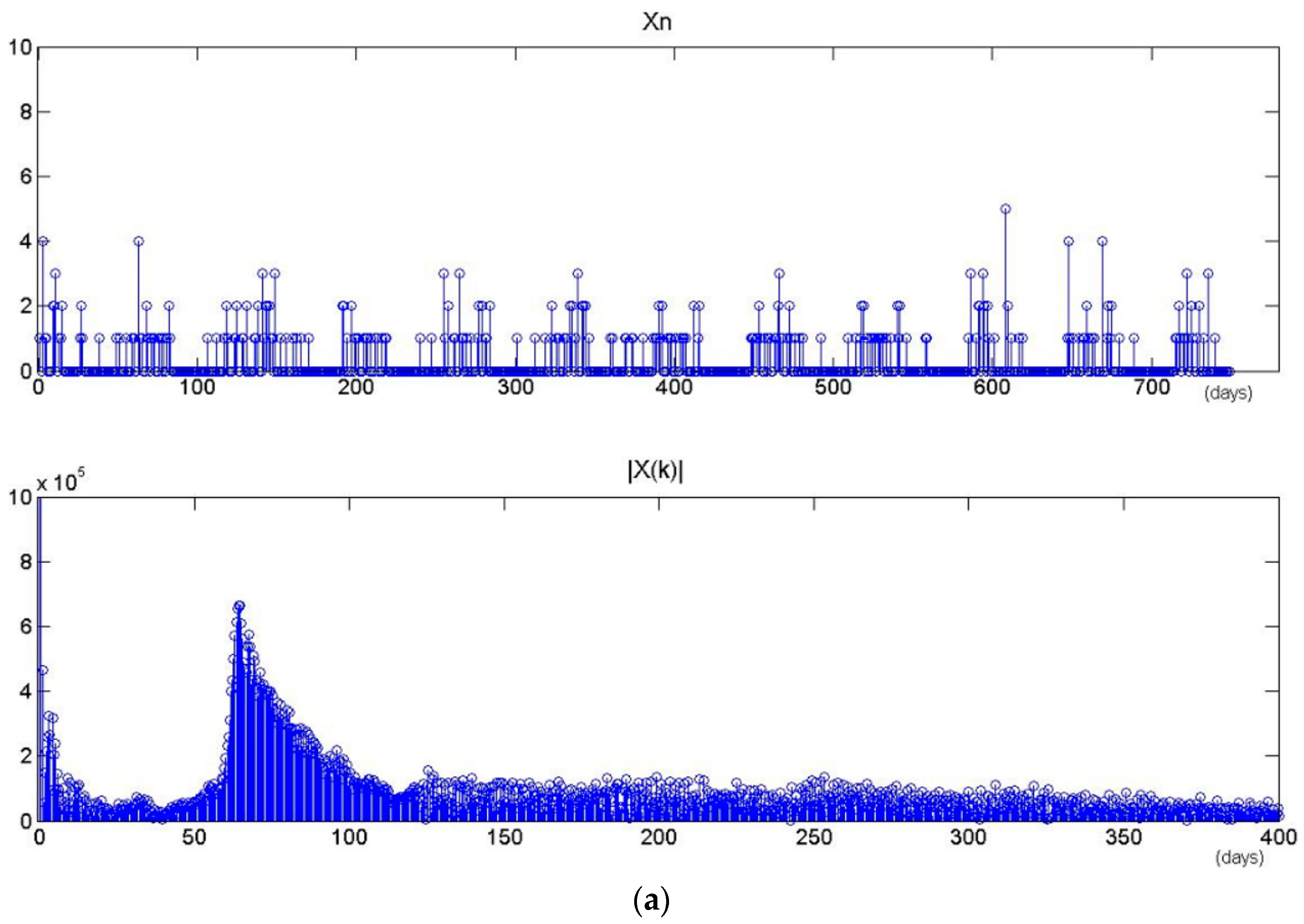
| Algorithm 2: Period Extraction |
| input: time series for task z, Qz = {t1, t2, …, tw}; |
| output: the period Tz of task z; |
| step 1: Normalization |
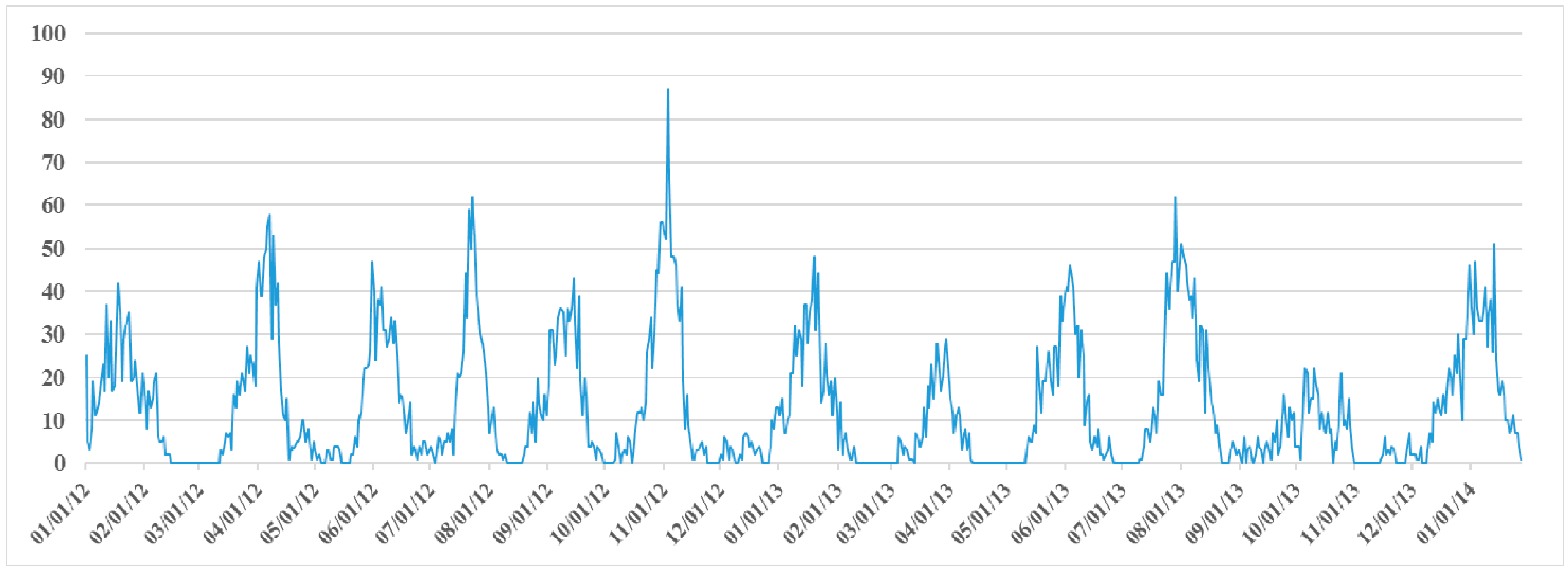
| The time series is mapped to one dimension axis: according to the time at which the user accesses each image, the time items in the series are sorted by time intervals on the time axis, and the earliest point is taken as zero time. |
| Then computes the first order difference of Qz. |
| A new one series is obtained to denote Qz’ = {t’1, t’2, …, t’h} where h = w(w − 1)/2. |
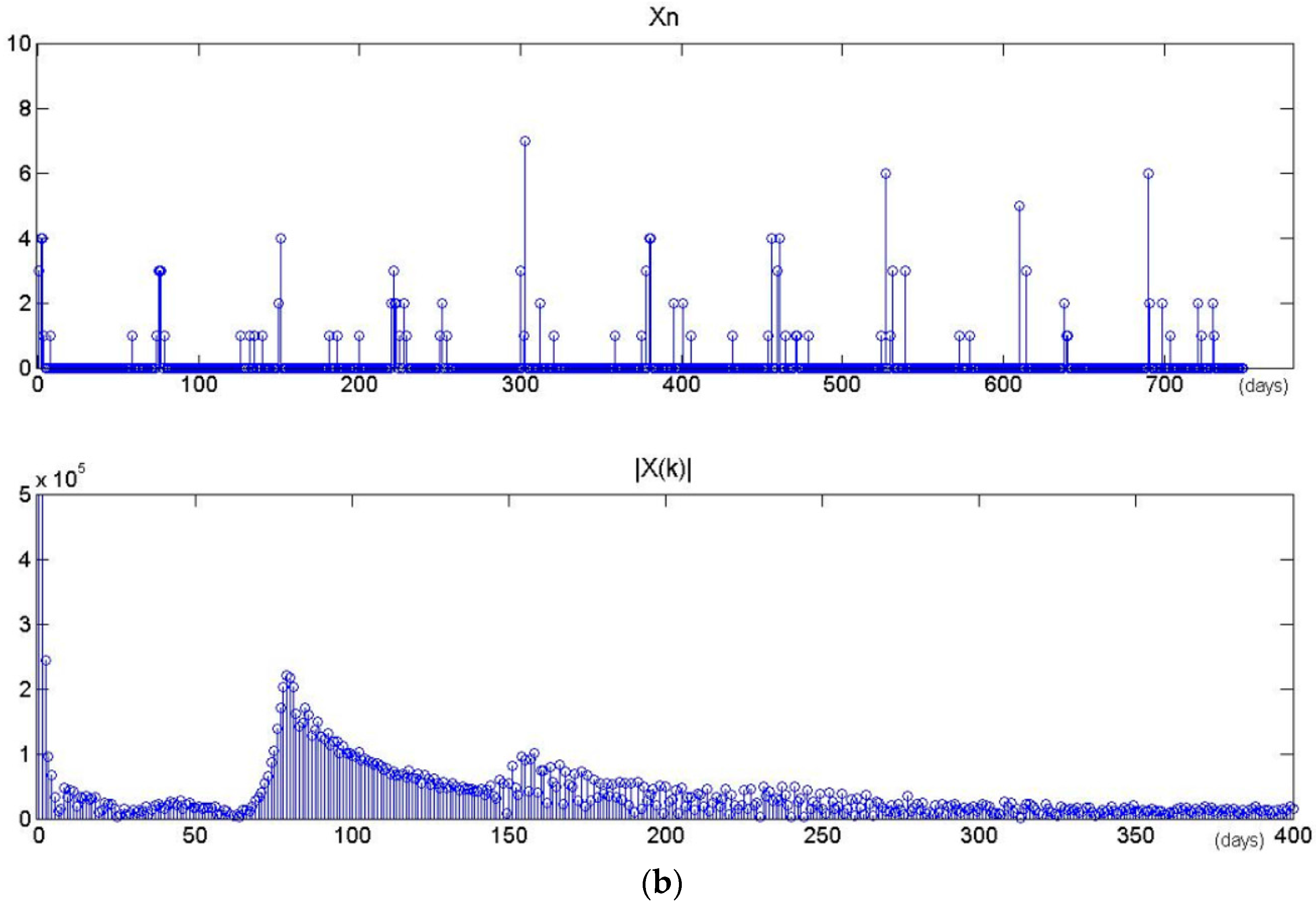
| step 2: Discrete Fourier Transform |
| Perform Fourier transform on the new time series. |
| step 3: Spectral Analysis |
| Calculate spectral density using Equation (7). As it meets the frequency threshold, the period of time series is . |
| return the period value Tz at the spot of maximal Ak; |
3.3.3. Inference Framework
| Algorithm 3: Inference Framework of STPT model |
| input: user retrieval behavior document D, Limitation of Iteration Npl, Priors α, β, γ; |
| output: estimated parameter θ, ϕ, σ and {κz, τz}; |
| for each document Dr ∈ D do |
| Assign task randomly; |
| end for |
| Initialize task mode parameters θ, ϕ and σ; |
| for iteration = 1 to Npl do |
| for each document Dr ∈ D do |
| Update task assignment using Equation (5); |
| Update model parameter θrz, ϕzs and σze as follows |
| end for |
| end for |
| for each task z do |
| Fetch the time series Qz and extracted the period Tz with Algorithm 2; |
| Initialize the κz and τz; |
| for iteration = 1 to Npl do |
| for each item <e, s, t> ∈ z do |
| Update parameters κz and τz using Equation (8); |
| end for |
| end for |
| end for |
| Return estimated model parameters θ, ϕ, σ and {κz, τz}; |
4. Experimental Evaluations
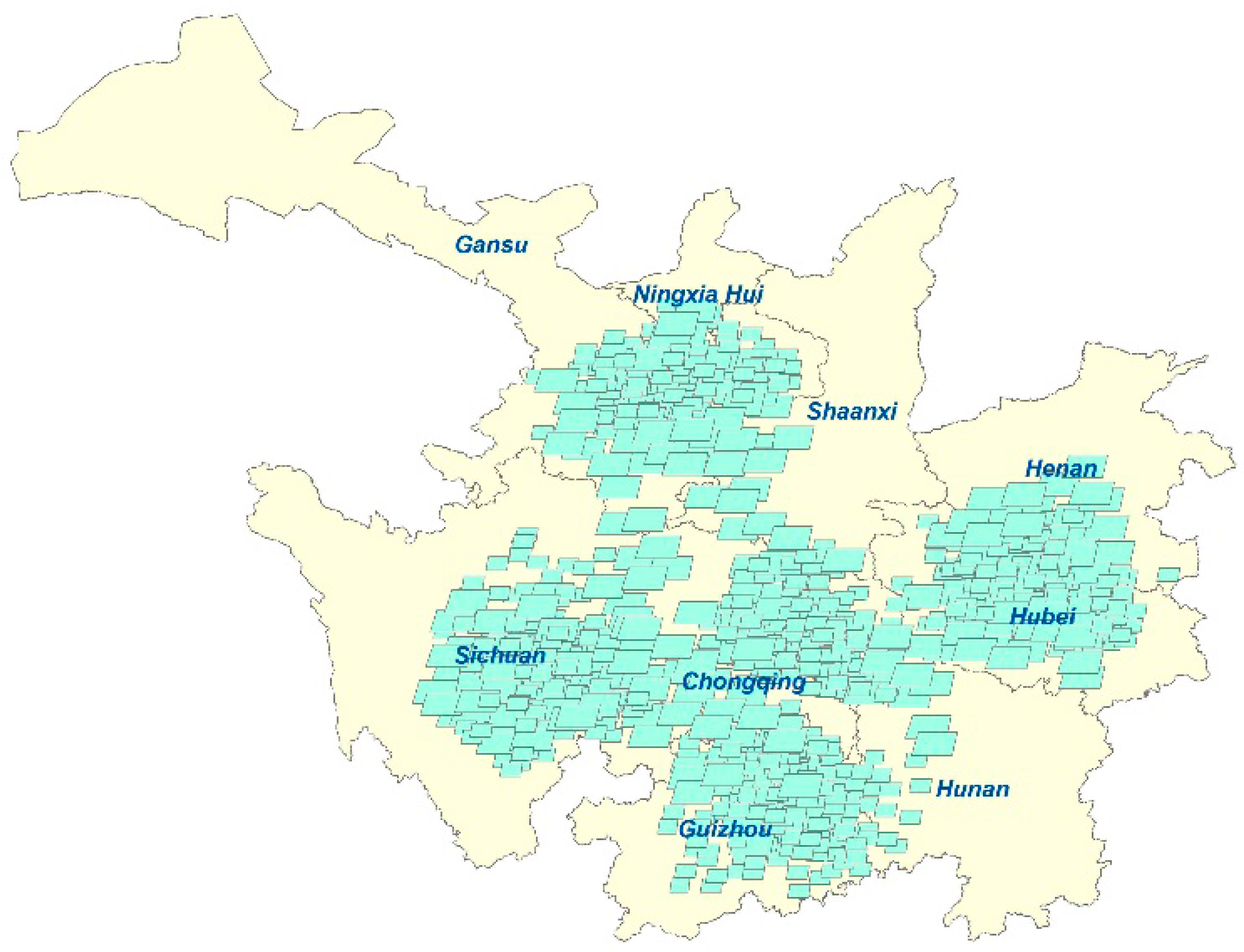
4.1. Dataset
4.2. Comparison Approaches
4.3. Experimental Evaluations
- (1)
- Generate randomly a batch dataset from the remaining single subsample as test case |Stest|.
- (2)
- For each RS image, compute the probability P(e, t, s) with the STPT model, and generate a top-k recommendation list RSISTPT based on P(e, t, s).
- (3)
- Given the relevance scores of RSISTPT, generate the ideal ranking list RSIGT which is the ground truth list. In addition, calculate the NDCG@k using Equation (16).
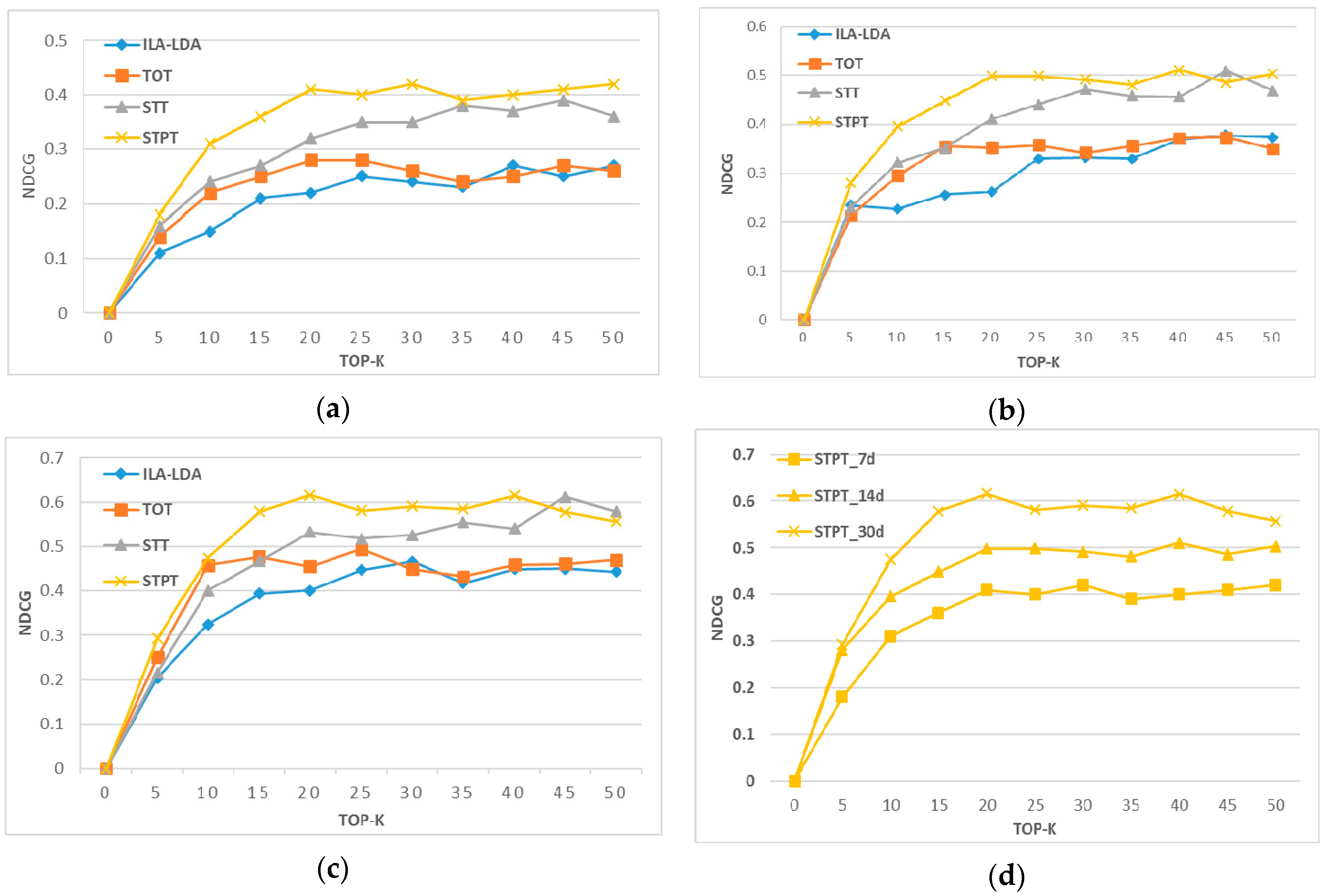
4.3.1. Top-k Recommendation
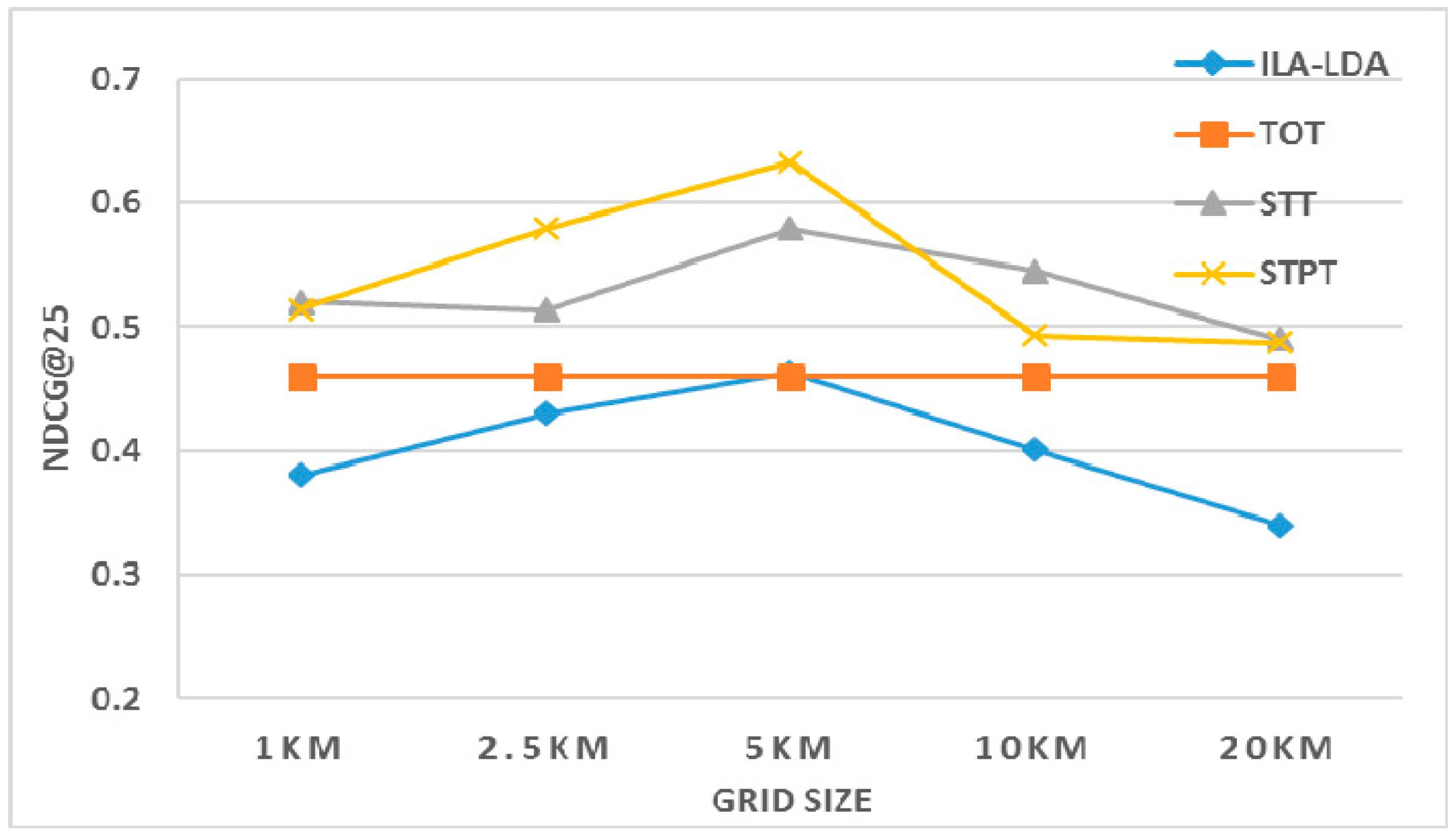
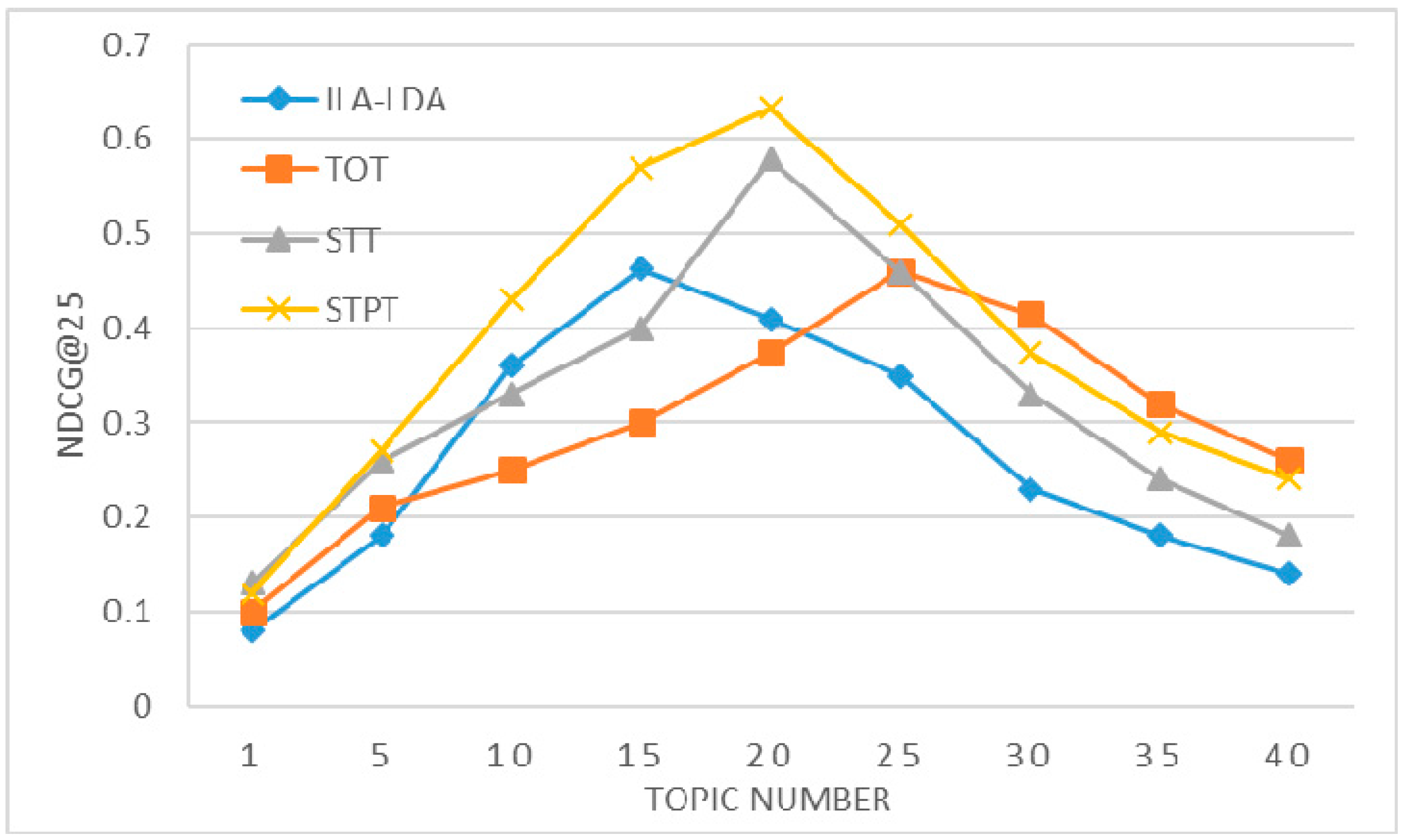
4.3.2. Effect of Spatial Granularity and Number of Tasks
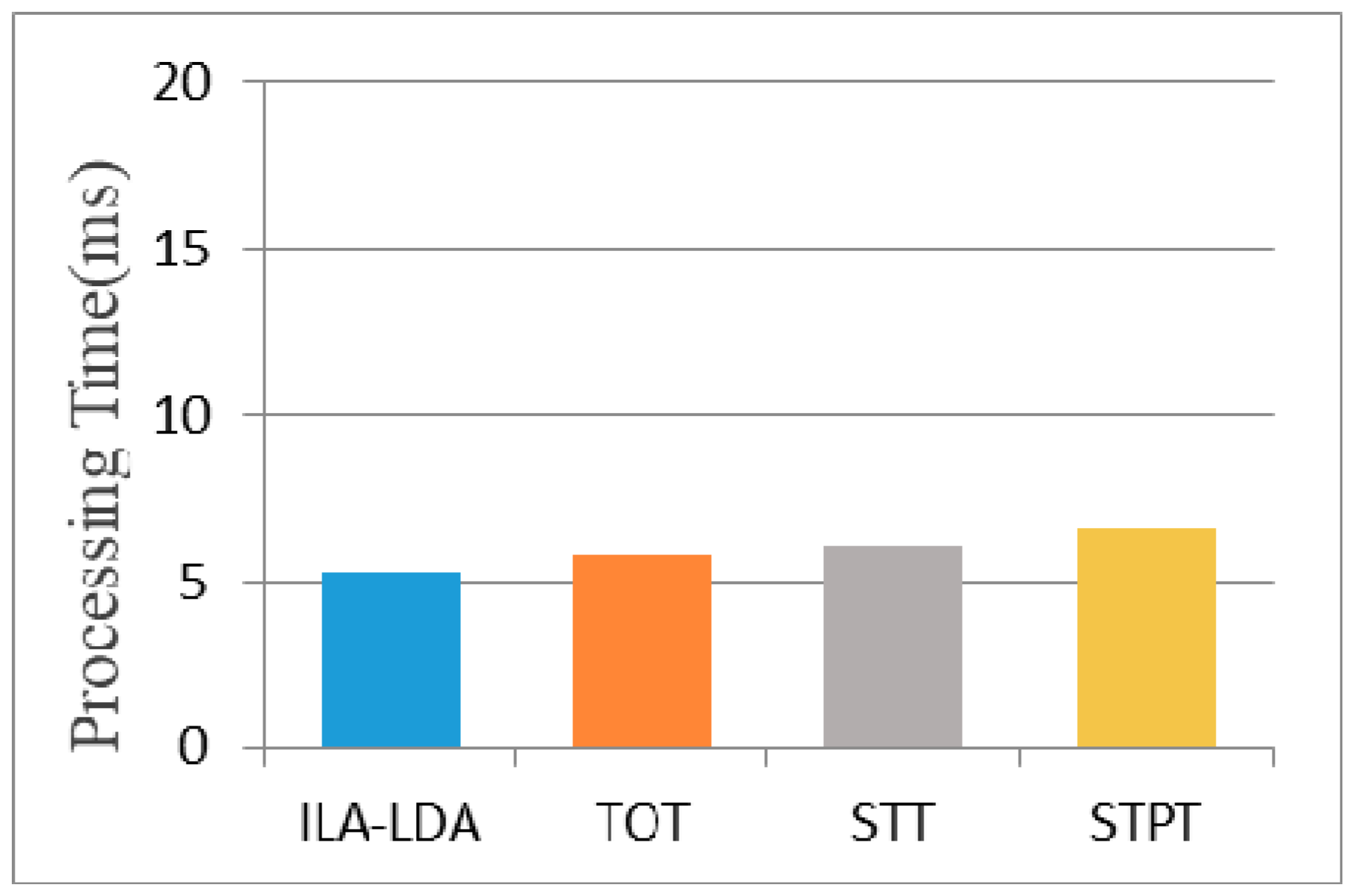
4.3.3. Training and Online Recommendation Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Gibbs Sampling Derivation for STPT
References
- Fang, C.Y.; Lin, H.; Xu, Q.; Tang, D.L.; Wang, W.C.; Zhang, J.X.; Pang, Y.C. Online generation and dissemination of disaster information based on satellite remote sensing data. In Proceedings of the Web and Wireless Geographical Information Systems, Shanghai, China, 11–12 December 2008; pp. 63–74. [Google Scholar]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 2011. [Google Scholar]
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, L.; Liu, P.; Ranjan, R. Towards building a data-intensive index for big data computing—A case study of Remote Sensing data processing. Inf. Sci. 2015, 319, 171–188. [Google Scholar] [CrossRef]
- Wu, L.; Liu, L.; Li, J.; Li, Z. Modeling user multiple interests by an improved GCS approach. Expert Syst. Appl. 2005, 29, 757–767. [Google Scholar]
- Ferecatu, M.; Boujemaa, N. Interactive remote-sensing image retrieval using active relevance feedback. IEEE Trans. Geosci. Remote Sens. 2007, 45, 818–826. [Google Scholar] [CrossRef]
- Roy, D.P.; Trigg, S.; Bhima, R.; Brockett, B.H.; Dube, O.P.; Frost, P.; Govender, N.; Le Roux, J.; Neo-Mahupeleng, G.; Norman, M. Utility of satellite fire product accuracy information—Perspectives and recommendations from the Southern Africa fire network. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1928–1930. [Google Scholar] [CrossRef]
- Matyas, C.; Schlieder, C. A spatial user similarity measure for geographic recommender systems. In GeoSpatial Semantics; Springer: New York, NY, USA, 2009; pp. 122–139. [Google Scholar]
- Ivánová, I.; Morales, J.; de By, R.; Beshe, T.; Gebresilassie, M. Searching for spatial data resources by fitness for use. J. Spat. Sci. 2013, 58, 15–28. [Google Scholar] [CrossRef]
- Beshe, T. Turning Spatial Data Search Engine to Spatial Data Recommendation Engine. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2012. [Google Scholar]
- O’Sullivan, D.; McLoughlin, E.; Bertolotto, M.; Wilson, D. Adaptive presentation and navigation for geospatial imagery tasks. In Proceedings of the Adaptive Hypermedia and Adaptive Web-Based Systems, Eindhoven, The Netherlands, 23–26 August 2004; pp. 688–698. [Google Scholar]
- Wilson, D.C.; Bertolotto, M.; McLoughlin, E.; O’Sullivan, D. Knowledge capture and reuse for geo-spatial imagery tasks. In Proceedings of the 5th International Conference on Case-Based Reasoning: Research and Development, Trondheim, Norway, 23–26 June 2003; pp. 622–636. [Google Scholar]
- McLoughlin, E.; O Sullivan, D.; Bertolotto, M.; Wilson, D. A knowledge management system for intelligent retrieval of geo-spatial imagery. Lect. Notes Comput. Sci. 2004, 535–544. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Wang, X.; McCallum, A. Topics over time: A non-Markov continuous-time model of topical trends. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 424–433. [Google Scholar]
- Bo, H.; Jamali, M.; Ester, M. Spatio-Temporal Topic Modeling in Mobile Social Media for Location Recommendation. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining (ICDM), Dallas, TX, USA, 7–10 December 2013; pp. 1073–1078. [Google Scholar]
- Xia, Y.; Zhu, X.; Li, D.; Zhan, Q. A user profile model for intelligent delivery of spatial information. In Proceedings of the Geoinformatics 2008 and Joint Conference on GIS and Built Environment: Geo-Simulation and Virtual GIS Environments, Guangzhou, China, 28–29 June 2008. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Schafer, J.B.; Konstan, J.A.; Riedl, J. E-commerce recommendation applications. In Applications of Data Mining to Electronic Commerce; Springer: New York, NY, USA, 2001; pp. 115–153. [Google Scholar]
- Pirasteh, P.; Jung, J.J.; Hwang, D. Item-Based Collaborative Filtering with Attribute Correlation: A Case Study on Movie Recommendation; Springer: New York, NY, USA, 2014; pp. 245–252. [Google Scholar]
- Xia, J.B. E-Commerce Product Recommendation Method Based on Collaborative Filtering Technology. In Proceedings of the International Conference on Smart Grid and Electrical Automation, Zhangjiajie, China, 11–12 August 2016. [Google Scholar]
- Foster, J. Collaborative information seeking and retrieval. Ann. Rev. Inf. Sci. Technol. 2006, 40, 329–356. [Google Scholar] [CrossRef]
- Rebollo-Monedero, D.; Forné, J.; Solanas, A.; Martínez-Ballesté, A. Private location-based information retrieval through user collaboration. Comput. Commun. 2010, 33, 762–774. [Google Scholar] [CrossRef]
- Bellogín, A.; Wang, J.; Castells, P. Text Retrieval Methods for Item Ranking in Collaborative Filtering. In Proceedings of the European Conference on Advances in Information Retrieval, Dublin, Ireland, 18–21 April 2011; pp. 301–306. [Google Scholar]
- Melville, P.; Mooney, R.J.; Nagarajan, R. Content-boosted collaborative filtering for improved recommendations. In Proceedings of the Eighteenth National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 187–192. [Google Scholar]
- Barragáns-Martínez, A.B.; Costa-Montenegro, E.; Burguillo, J.C.; Rey-López, M.; Mikic-Fonte, F.A.; Peleteiro, A. A hybrid content-based and item-based collaborative filtering approach to recommend TV programs enhanced with singular value decomposition. Inf. Sci. 2010, 180, 4290–4311. [Google Scholar] [CrossRef]
- Yao, L.; Sheng, Q.Z.; Ngu, A.H.H.; Yu, J. Unified Collaborative and Content-Based Web Service Recommendation. IEEE Trans. Serv. Comput. 2015, 8, 453–466. [Google Scholar] [CrossRef]
- Mathew, P.; Kuriakose, B.; Hegde, V. Book Recommendation System through content based and collaborative filtering method. In Proceedings of the International Conference on Data Mining and Advanced Computing, Ernakulam, India, 16–18 March 2016; pp. 47–52. [Google Scholar]
- Lee, B.-H.; Kim, H.-N.; Jung, J.-G.; Jo, G. Location-based service with context data for a restaurant recommendation. In Proceedings of the Database and Expert Systems Applications, Kraków, Poland, 4–8 September 2006; pp. 430–438. [Google Scholar]
- Gupta, G.; Lee, W.C. Collaborative Spatial Object Recommendation in Location Based Services. In Proceedings of the 39th International Conference on Parallel Processing Workshops, San Diego, CA, USA, 13–16 September 2010; pp. 24–33. [Google Scholar]
- Wang, H.; Terrovitis, M.; Mamoulis, N. Location recommendation in location-based social networks using user check-in data. In Proceedings of the ACM Sigspatial International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 374–383. [Google Scholar]
- Li, H.; Hong, R.; Zhu, S.; Ge, Y. Point-of-Interest Recommender Systems: A Separate-Space Perspective. In Proceedings of the IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 231–240. [Google Scholar]
- Kosmides, P.; Demestichas, K.; Adamopoulou, E.; Remoundou, C.; Loumiotis, I.; Theologou, M.; Anagnostou, M. Providing recommendations on location-based social networks. J. Ambient Intell. Humaniz. Comput. 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Wang, W.; Yin, H.; Sadiq, S.; Chen, L.; Xie, M.; Zhou, X. SPORE: A sequential personalized spatial item recommender system. In Proceedings of the IEEE 32nd International Conference on Data Engineering, Helsinki, Finland, 16–20 May 2016; pp. 954–965. [Google Scholar]
- Yin, H.; Cui, B.; Sun, Y.; Hu, Z.; Chen, L. LCARS: A spatial item recommender system. ACM Trans. Inf. Syst. 2014, 32, 11. [Google Scholar] [CrossRef]
- Wang, W.; Yin, H.; Chen, L.; Sun, Y.; Sadiq, S.; Zhou, X. Geo-SAGE: A Geographical Sparse Additive Generative Model for Spatial Item Recommendation. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 1255–1264. [Google Scholar]
- Oku, K.; Kotera, R.; Sumiya, K. Geographical recommender system based on interaction between map operation and category selection. In Proceedings of the 1st International Workshop on Information Heterogeneity and Fusion in Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 71–74. [Google Scholar]
- Hong, J.-H.; Su, Z.L.-T.; Lu, E.H.-C. A recommendation framework for remote sensing images by spatial relation analysis. J. Syst. Softw. 2014, 90, 151–166. [Google Scholar] [CrossRef]
- Zhang, J.D.; Chow, C.Y. CoRe: Exploiting the personalized influence of two-dimensional geographic coordinates for location recommendations. Inf. Sci. 2015, 293, 163–181. [Google Scholar] [CrossRef]
- Krestel, R.; Fankhauser, P.; Nejdl, W. Latent dirichlet allocation for tag recommendation. In Proceedings of the Third ACM Conference on Recommender Systems, New York, New York, USA, 23–25 October 2009; pp. 61–68. [Google Scholar]
- Guo, Y.; Joshi, J.B.D. Topic-based personalized recommendation for collaborative tagging system. In Proceedings of the 21st ACM Conference on Hypertext and Hypermedia, Toronto, ON, Canada, 13–16 June 2010; pp. 61–66. [Google Scholar]
- Hong, L.; Ahmed, A.; Gurumurthy, S.; Smola, A.J.; Tsioutsiouliklis, K. Discovering geographical topics in the twitter stream. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 769–778. [Google Scholar]
- Ference, G.; Ye, M.; Lee, W.C. Location recommendation for out-of-town users in location-based social networks. In Proceedings of the ACM International Conference on Information & Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 721–726. [Google Scholar]
- Yin, H.; Cui, B.; Chen, L.; Hu, Z.; Zhang, C. Modeling Location-Based User Rating Profiles for Personalized Recommendation. ACM Trans. Knowl. Discov. Data 2015, 9, 1–41. [Google Scholar] [CrossRef]
- Yuan, Q.; Cong, G.; Ma, Z.; Sun, A.; Thalmann, N.M. Time-aware point-of-interest recommendation. In Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 28 July–1 August 2013; pp. 363–372. [Google Scholar]
- Zhang, J.D.; Chow, C.Y. Spatiotemporal Sequential Influence Modeling for Location Recommendations: A Gravity-based Approach. ACM Trans. Intell. Syst. Technol. 2015, 7, 1–25. [Google Scholar] [CrossRef]
- Zhang, J.D.; Chow, C.Y. Point-of-interest recommendations in location-based social networks. Sigspat. Spec. 2016, 7, 26–33. [Google Scholar] [CrossRef]
- Oetter, D.R.; Cohen, W.B.; Berterretche, M.; Maiersperger, T.K.; Kennedy, R.E. Land cover mapping in an agricultural setting using multiseasonal Thematic Mapper data. Remote Sens. Environ. 2001, 76, 139–155. [Google Scholar] [CrossRef]
- Hughes, G. Multivariate and Time Series Models for Circular Data with Applications to Protein Conformational Angles. Ph.D. Thesis, University of Leeds, Leeds, UK, 2007. [Google Scholar]
- Levine, R.A.; Casella, G. Implementations of the Monte Carlo EM algorithm. J. Comput. Graph. Stat. 2001, 10, 422–439. [Google Scholar] [CrossRef]
- Razavian, N.S.; Kamisetty, H.; Langmead, C.J. The Von Mises Graphical Model: Structure Learning. Carnegie Mellon University School of Computer Science Technical Report; Carnegie Mellon University: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Li, Q.; Wang, S.; Chen, B. Remote sensing image distribute system supported by metadata. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005; p. 4. [Google Scholar]
- Zhu, X.; Li, M.; Guo, W.; Zhang, X. Semantic-based user demand modeling for remote sensing images retrieval. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 2902–2905. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval: Boolean Retrieval; Cambridge University Press: Cambridge, UK, 2008; pp. 824–825. [Google Scholar]
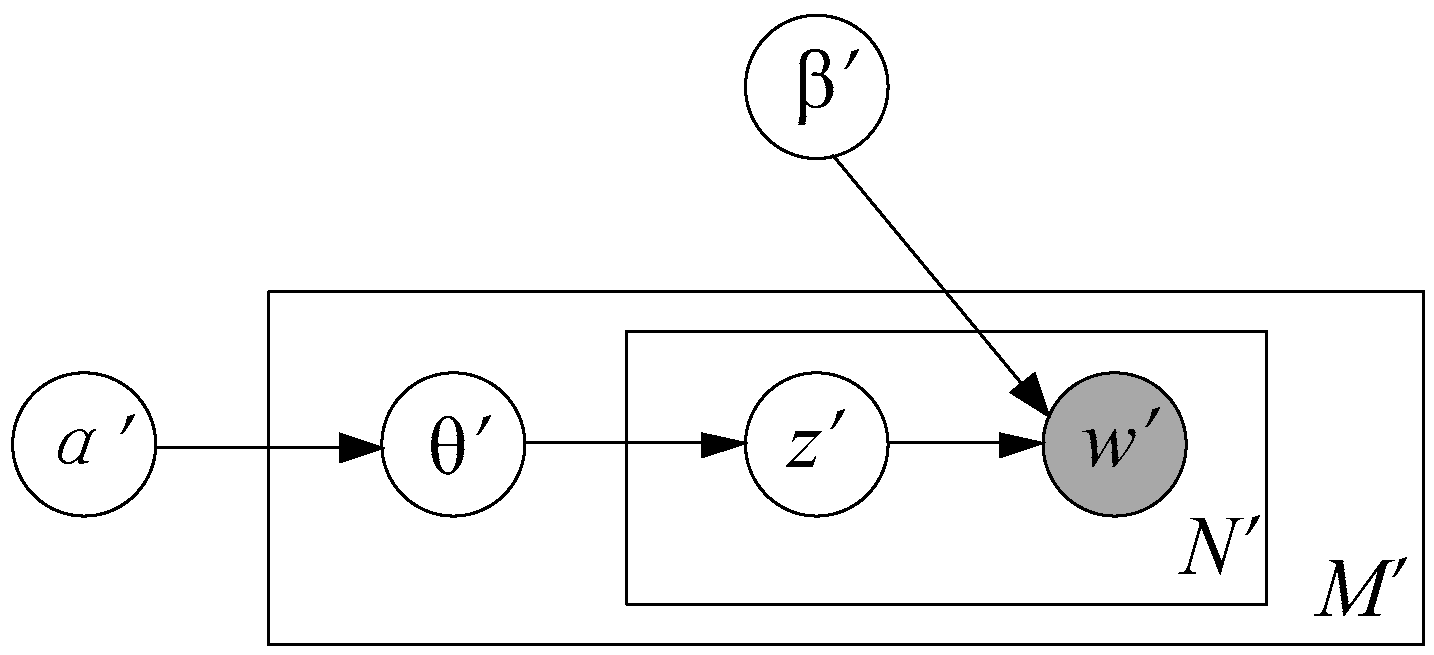
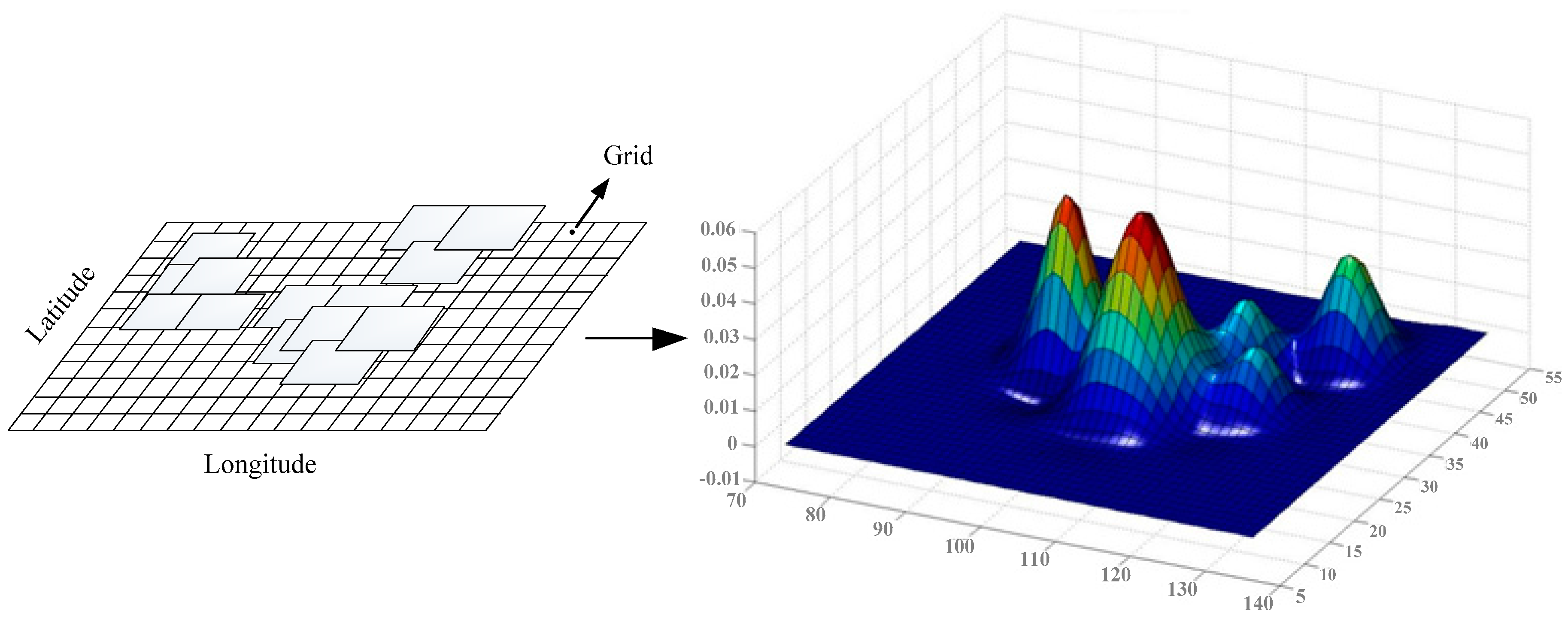
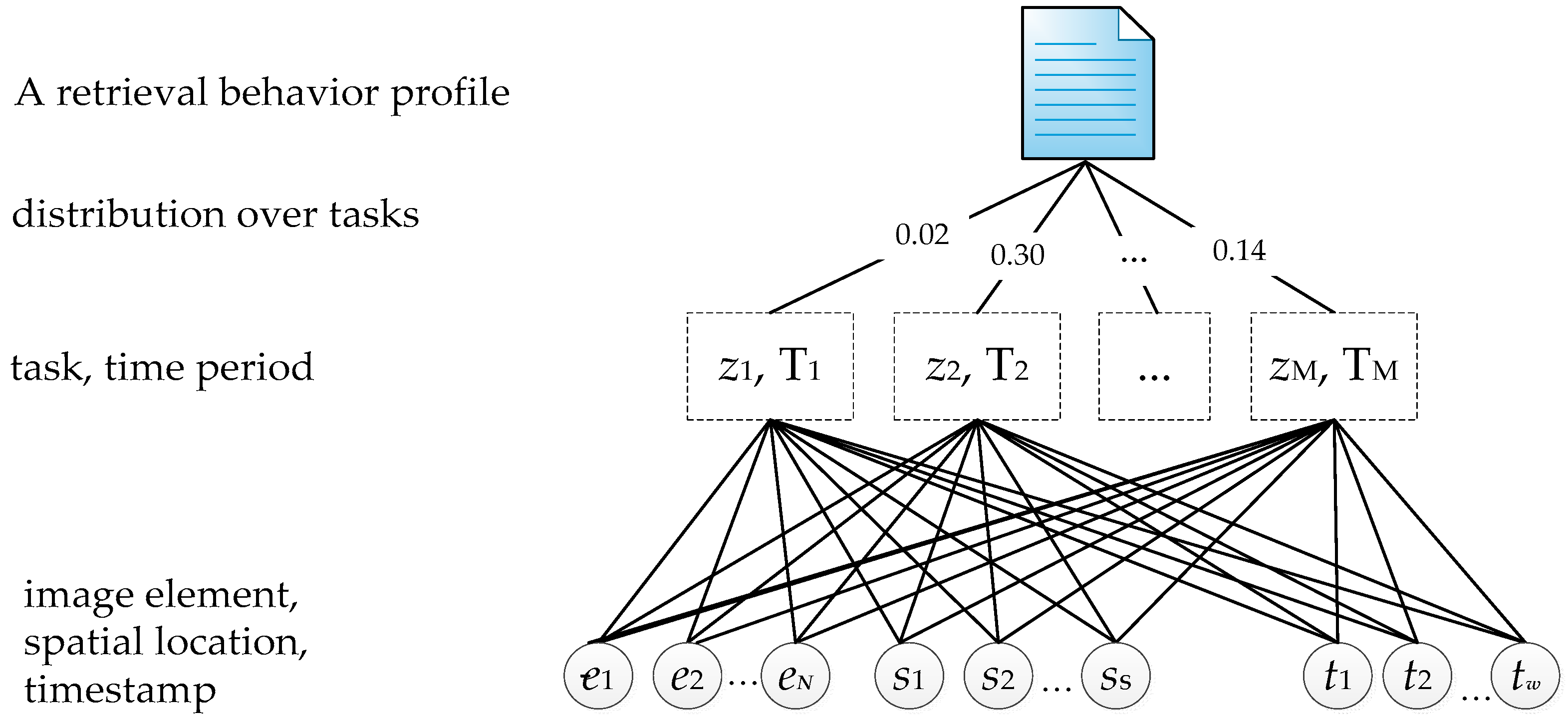
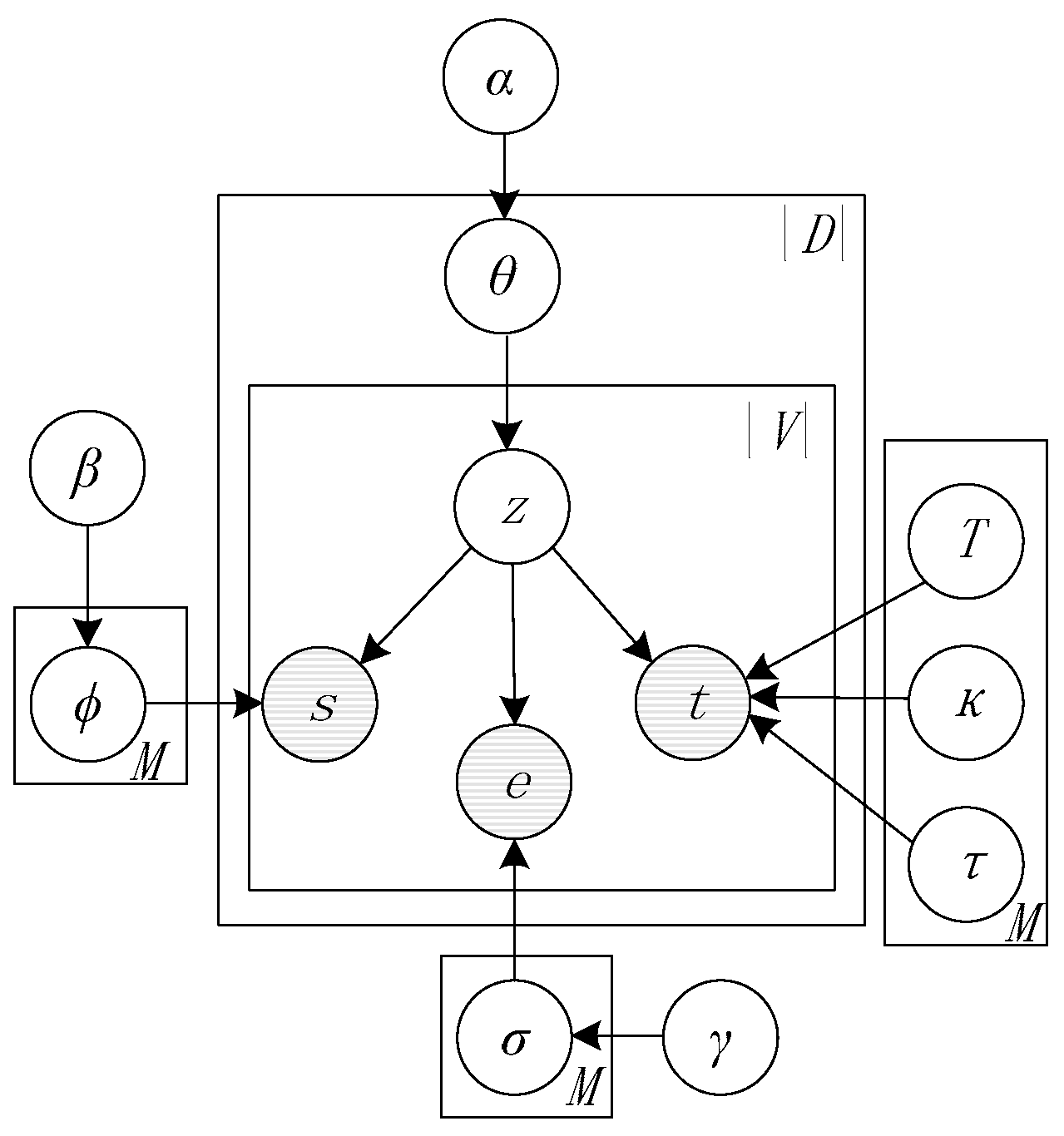

| Variable | Meaning |
|---|---|
| Dr, D | a retrieval behavior document, the set of retrieval behavior documents |
| |D| | the number of retrieval behavior documents |
| S, N | the number of spatial grids and the number of image elements of RS images in the retrieval results, respectively |
| |V| | the number of RS images retrieved by each retrieval behavior |
| M | the number of tasks |
| z | latent task |
| s | the collection of spatial location grids for each RS image |
| T | the time period of task z |
| t | retrieval timestamp of remote sensing image |
| e | the sequence of image elements for each RS image |
| θ | the multinomial distributions of tasks specific to the retrieval behavior document Dr |
| ϕ | the multinomial distributions of spatial grid specific to task z: S × M matrix |
| σ | the multinomial distributions of image elements s specific to task z: N × M matrix |
| α, β, γ | the hyper parameters of the Dirichlet priors for multinomial distributions θ, ϕ, σ, respectively |
| κ | a reciprocal measure of dispersion (for the von Mises distribution) |
| τ | the initial phase point of task z (for the von Mises distribution) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, D.; Liu, J. A Space-Time Periodic Task Model for Recommendation of Remote Sensing Images. ISPRS Int. J. Geo-Inf. 2018, 7, 40. https://doi.org/10.3390/ijgi7020040
Zhang X, Chen D, Liu J. A Space-Time Periodic Task Model for Recommendation of Remote Sensing Images. ISPRS International Journal of Geo-Information. 2018; 7(2):40. https://doi.org/10.3390/ijgi7020040
Chicago/Turabian StyleZhang, Xiuhong, Di Chen, and Jiping Liu. 2018. "A Space-Time Periodic Task Model for Recommendation of Remote Sensing Images" ISPRS International Journal of Geo-Information 7, no. 2: 40. https://doi.org/10.3390/ijgi7020040
APA StyleZhang, X., Chen, D., & Liu, J. (2018). A Space-Time Periodic Task Model for Recommendation of Remote Sensing Images. ISPRS International Journal of Geo-Information, 7(2), 40. https://doi.org/10.3390/ijgi7020040




