Multilevel Visualization of Travelogue Trajectory Data
Abstract
:1. Introduction
- We propose a visual analytic framework for trajectory data with large volume and variety, by considering the characteristics of the travelogue.
- We propose a multilevel visualization method to explore individual movement patterns and population movement patterns in travelogues.
- We propose an adaptive plotting scale for choosing the cutoff point in multilevel visualizations to help find movement patterns.
2. Related Work
3. Data Processing
4. Design Consideration
4.1. Data Characteristic
- Trajectory with semantic information: When people travel to a place, they always choose a region and wander around this region. Then, they take a coach or train to the next region. The semantic information in a trajectory is very important to show the movement patterns of a trajectory.
- Intensive region of interest: The primary data characteristic is that the trajectory graph is scattered and sparse in general, but dense in some center area. This feature leads to comparatively large numbers of lines in the intensive area. When the intensive area holds over twenty sites, the trajectory in this area in too dense to explore. This characteristic arises because people always choose some key or famous spot in a region to constitute the skeleton of their trajectory, and these main tourist attractions are far away. On arriving, people always choose small tourist sites around the primary tourist site.
- Large amount of trajectory data and wide geographic coverage: The number of travelogues is large. Every traveler has his/her own interests and considerations. It is a big challenge to visualize the large numbers of trajectories and keep the geographic information to explore the movement patterns or help travel route planning.
- Many types of sites and messy trajectory: Trajectory data in a travelogue might include tourist attractions, restaurants, shopping destinations and other locations. Therefore, it is not a good idea to visualize the trajectory directly. At the same time, the number of sites in a trajectory is very variable. It is not appropriate to compare the movement patterns between a trip that lasts two days and a trip that lasts two weeks.
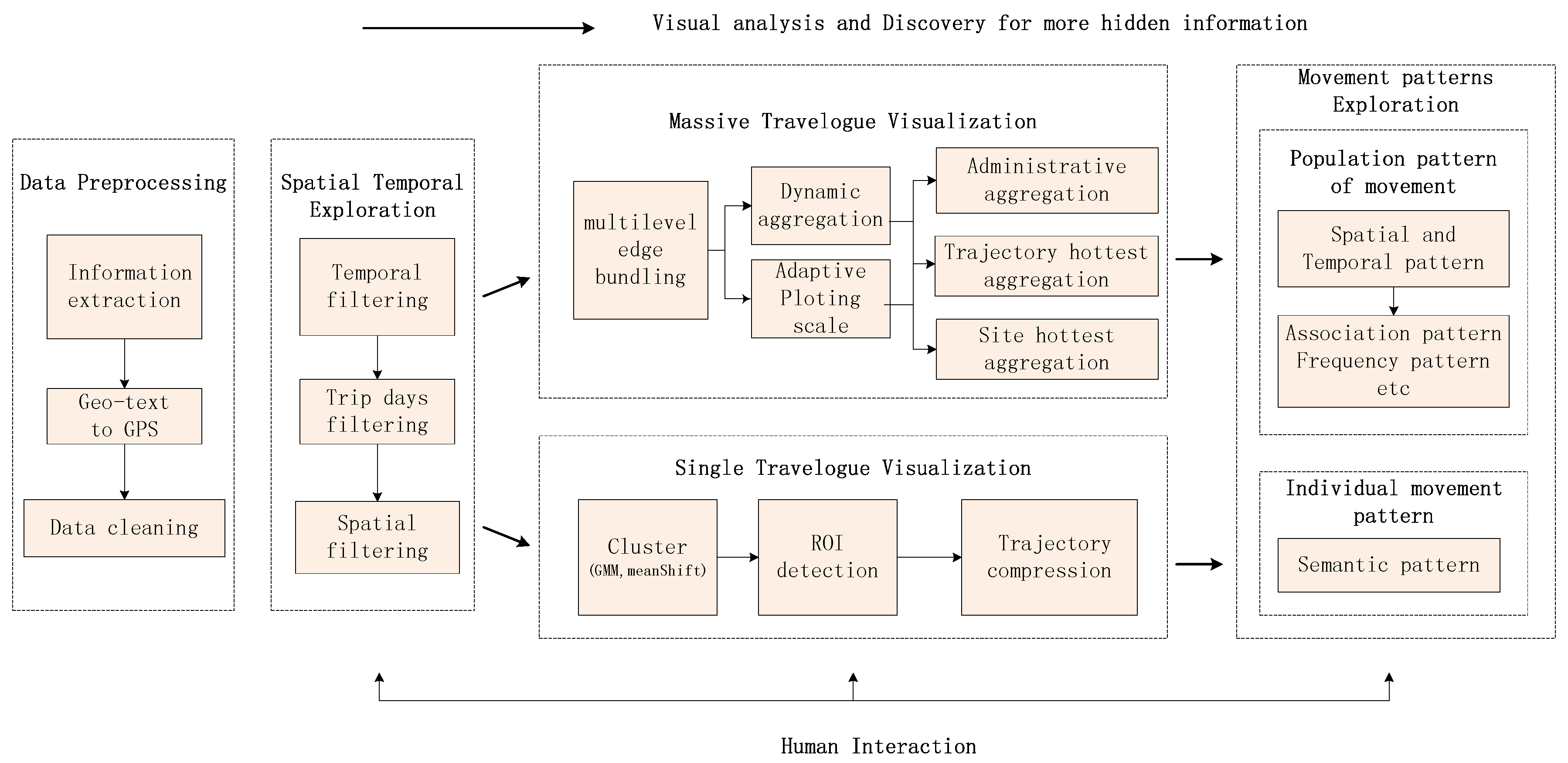
4.2. Visual Analytical Framework
- For trajectories in a single travelogue, the trajectory lines are dense in detail, but sparse in in general. Firstly, for the semantic movement pattern, we clustered the trajectory data to get the region of interest, which is the main area. Although there are many machine learning methods to mine the semantic information, the information in a trajectory only uses GPS. It is better to use the cluster method to get the clustering area. Secondly, for exploring the hidden information after ROI detection, we used the trajectory compression algorithm to reduce visual confusion of regions of interest. Besides, for detailed information, we obtained the scale from the compression algorithm, then used the multilevel trajectory compression method to visualize the single travelogue trajectory data in multilevel views.
- For trajectories in a vast travelogue, the trajectory lines are dense, not only in general, but also in detail. At the same time, the trajectory lines always cross each other. It is hard to explore these data using direct visualization. For the density and line intersection problems, we used an edge bundling algorithm. Furthermore, we applied data filtering through temporal filtering or spatial filtering to reduce visual confusion about volume. Next, we applied the aggregation method to solve the problem of messy trajectories. We designed three aggregation visualization methods to explore population movement patterns. For an administrative view of all kinds of location, we firstly aggregated the trajectories at the administrative level to identify which two cities were the most popular trajectory. This method categorizes the messy trajectories into administrative regions. Next, we designed a multilevel method to explore the pattern in the view of the hottest site. Finally, we developed a multilevel method to view the hottest trajectory.
- Data preprocessing: In this step, we use information extraction techniques to extract related information about a travelogue, then parse the geographic text into GPS location and clean the data to put it into a formatted structure.
- Spatial temporal visualization: In this step, the user can apply interactions to filter according to some attributes like trips days, trip time and trip site. For example, they can choose the trips in September to filter the travelogues.
- Massive travelogue visualization: In this step, we first use multilevel edge bounding to simplify the massive travelogue. Next, we propose an adaptive plotting scale according to the data distribution to choose the plotting scale in multilevel dynamic aggregation. Finally, we develop three aggregation methods to explore the movement patterns. These three aggregation methods can also help travel route planning.
- Single travelogue visualization: In this step, we first use the cluster method to cluster the trajectory to several interest regions. Then, for solving the problem of many lines in the dense regions, we use the trajectory compression method to simplify these trajectories. We also extract the scale in the trajectory compression to show the trajectory in a multilevel way.
- Movement pattern exploration: In this step, we can use the methods like filtering and data aggregation to interact with travelogues and explore movement patterns. For example, we can know which trajectory between two districts is the hottest in October.
5. Single Travelogue Visualization
5.1. Region of Interest Detection
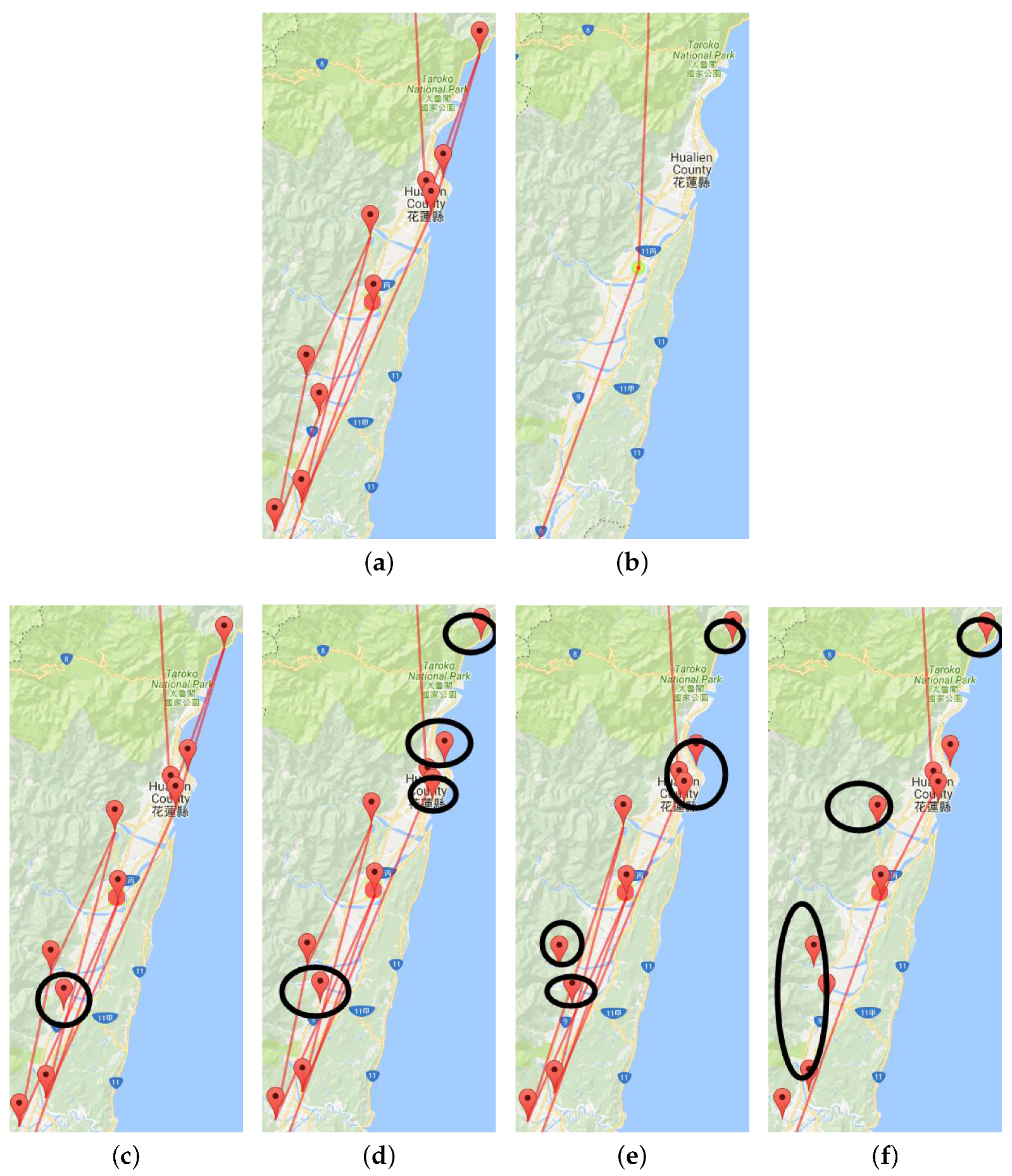
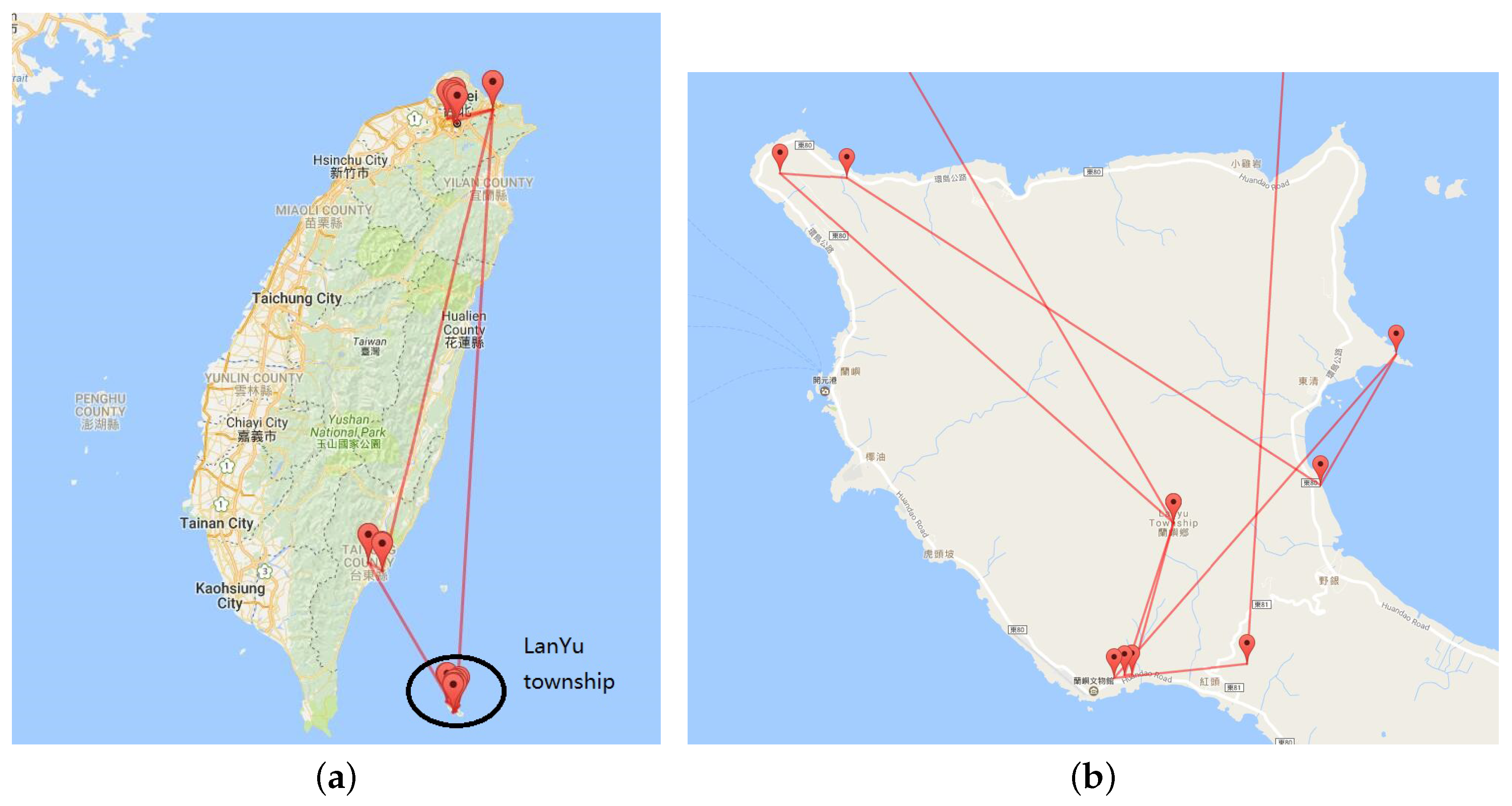
5.2. Multilevel Trajectory Compression
6. Vast Travelogue Visualization
| Algorithm 1 Scale Douglas–Peucker. |
|
6.1. Edge Bundling
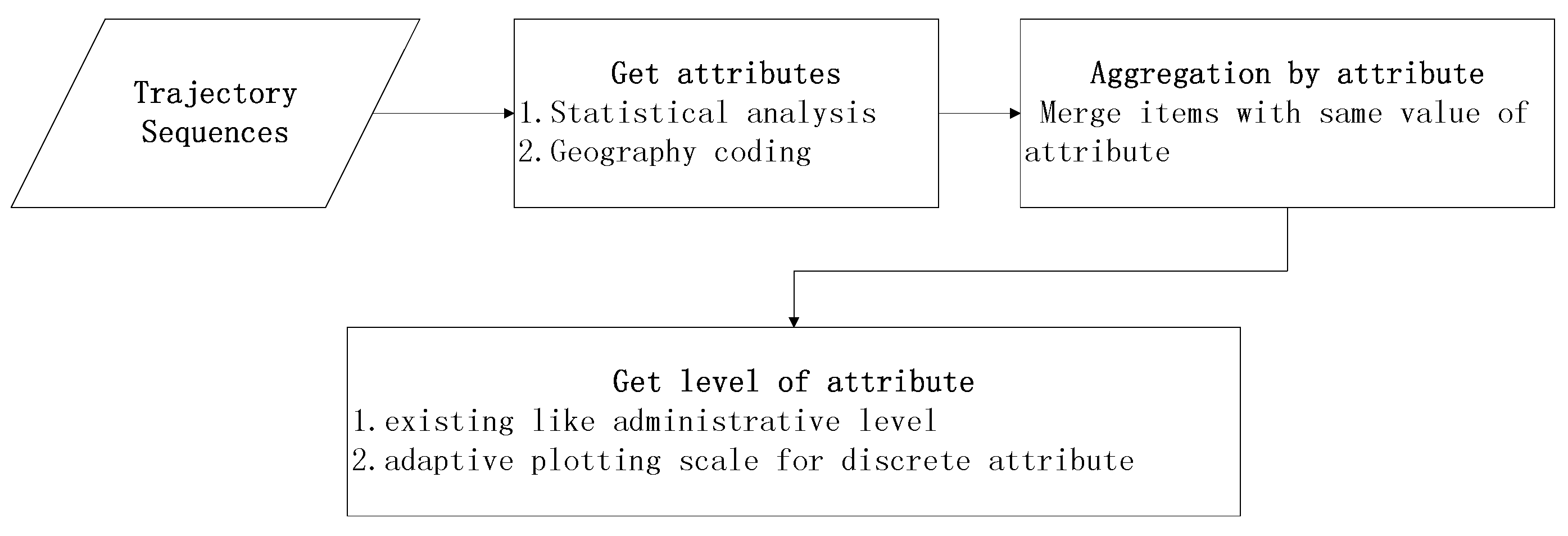
6.2. Multilevel Aggregation Procedure and Adaptive Plotting Scale
6.3. Aggregation in the Time Dimension
6.4. Aggregation in the Space Dimension
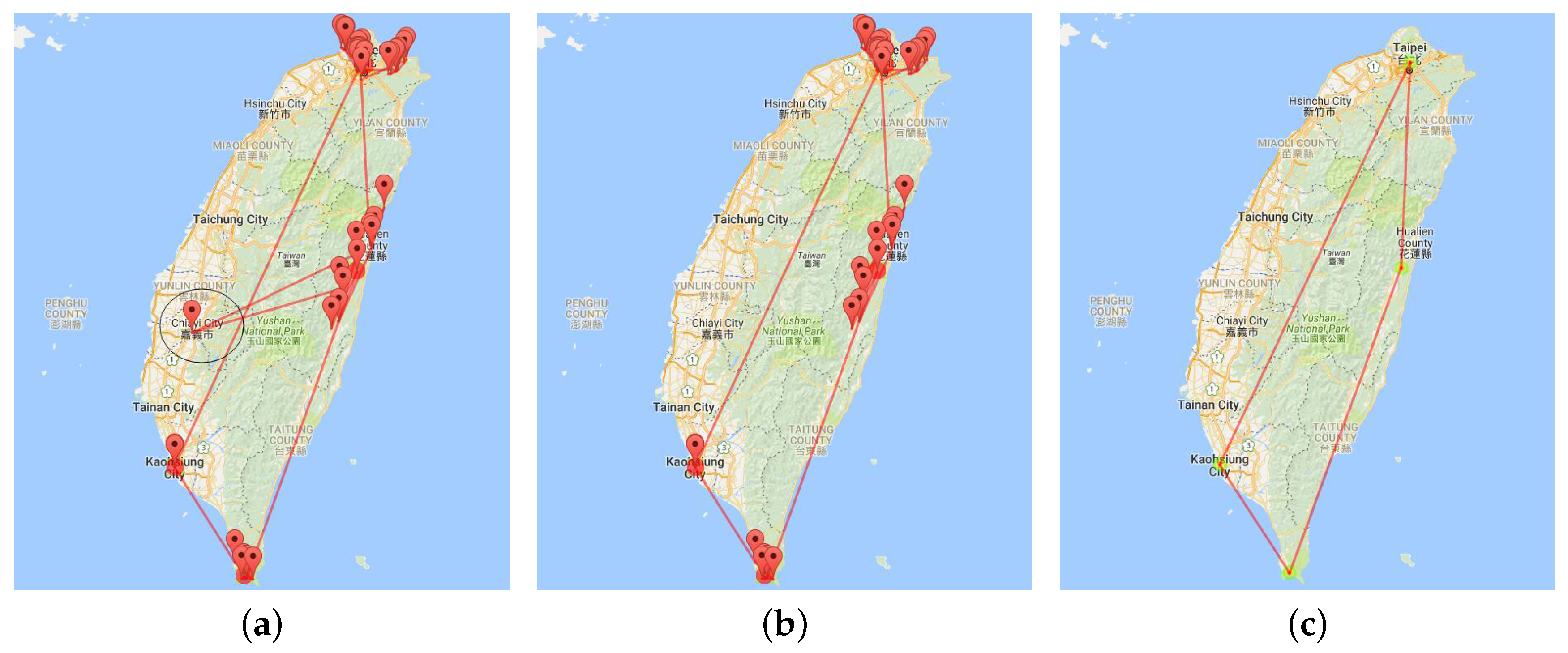
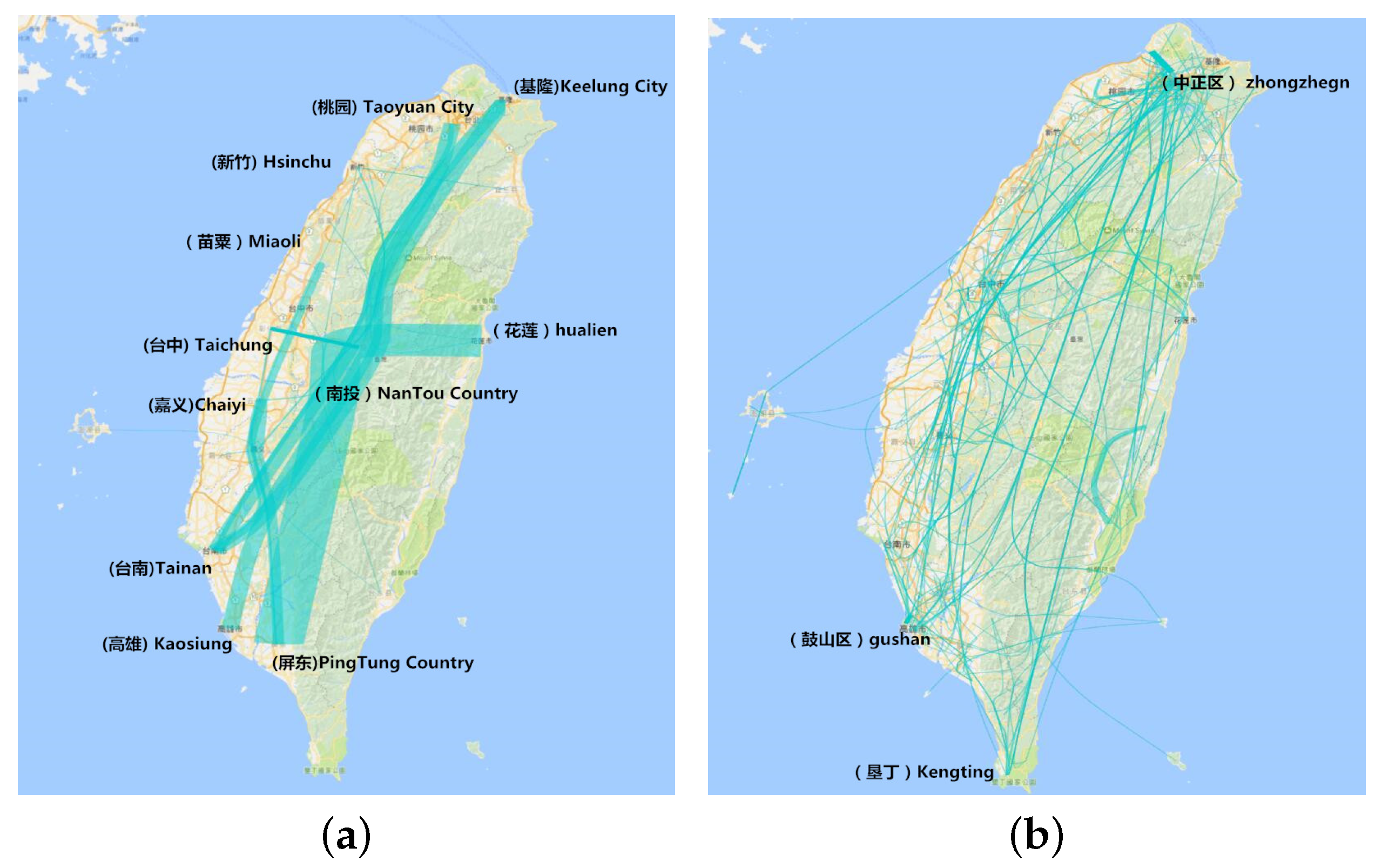
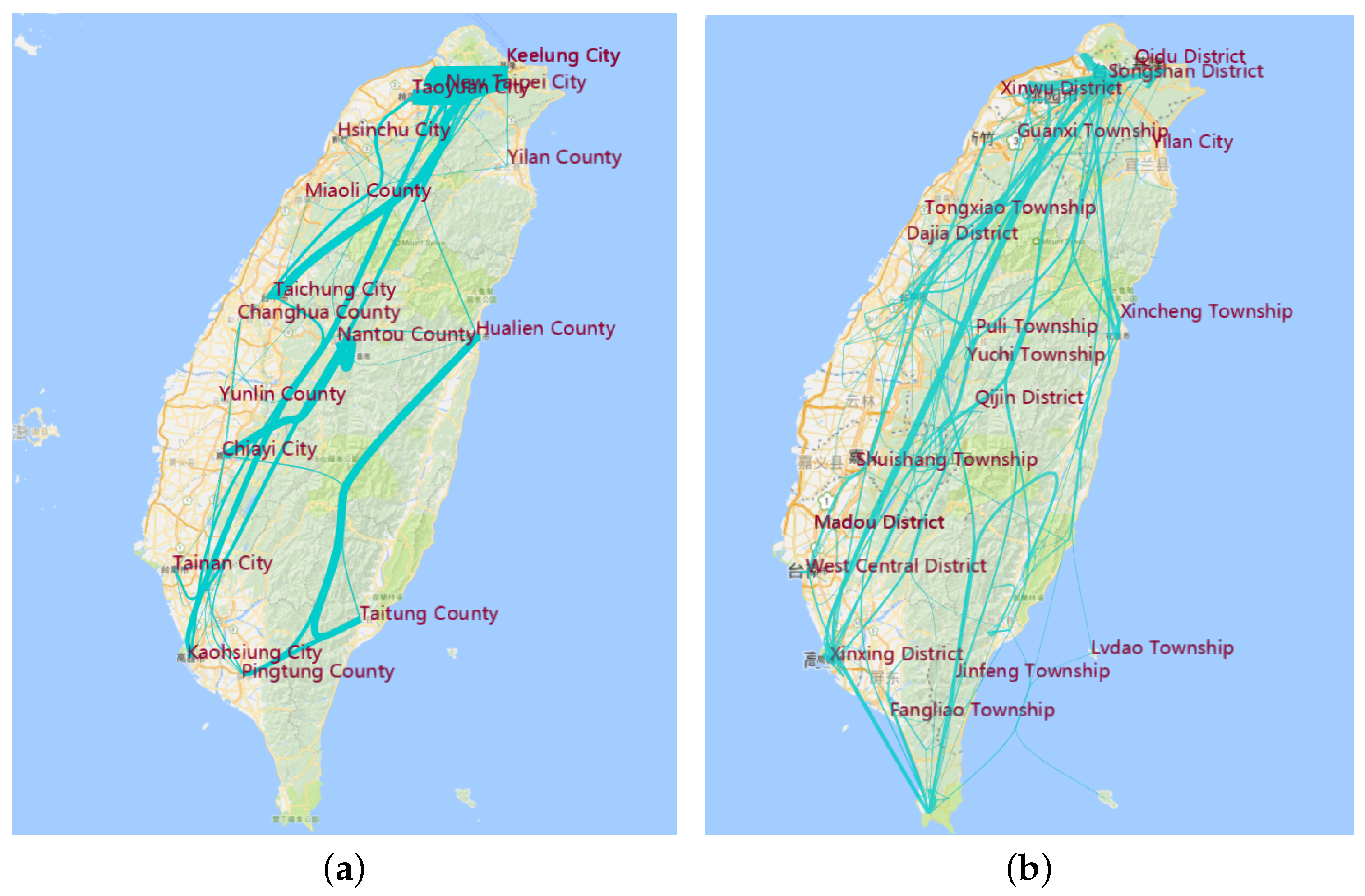
6.4.1. Aggregation by Administrative Region
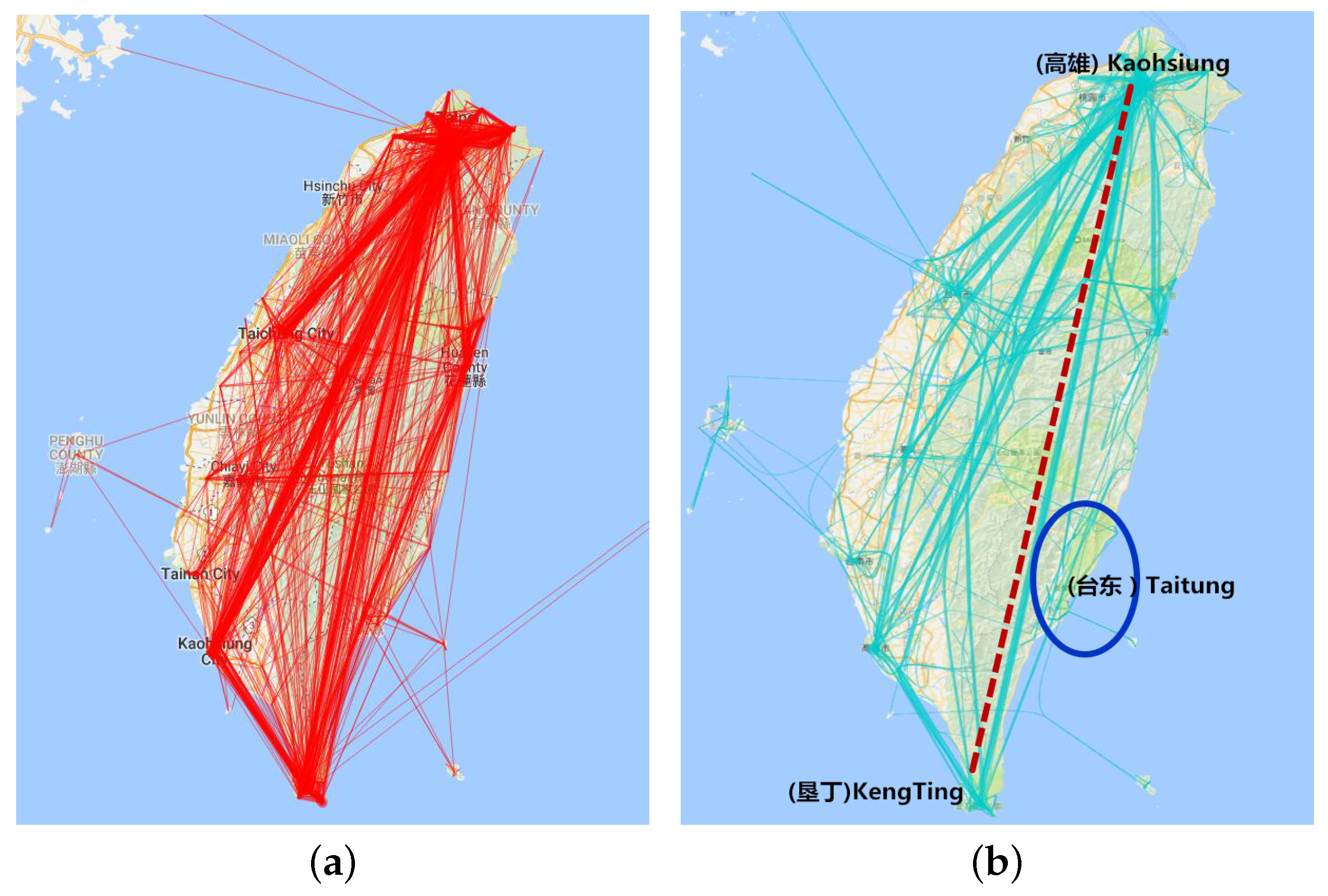
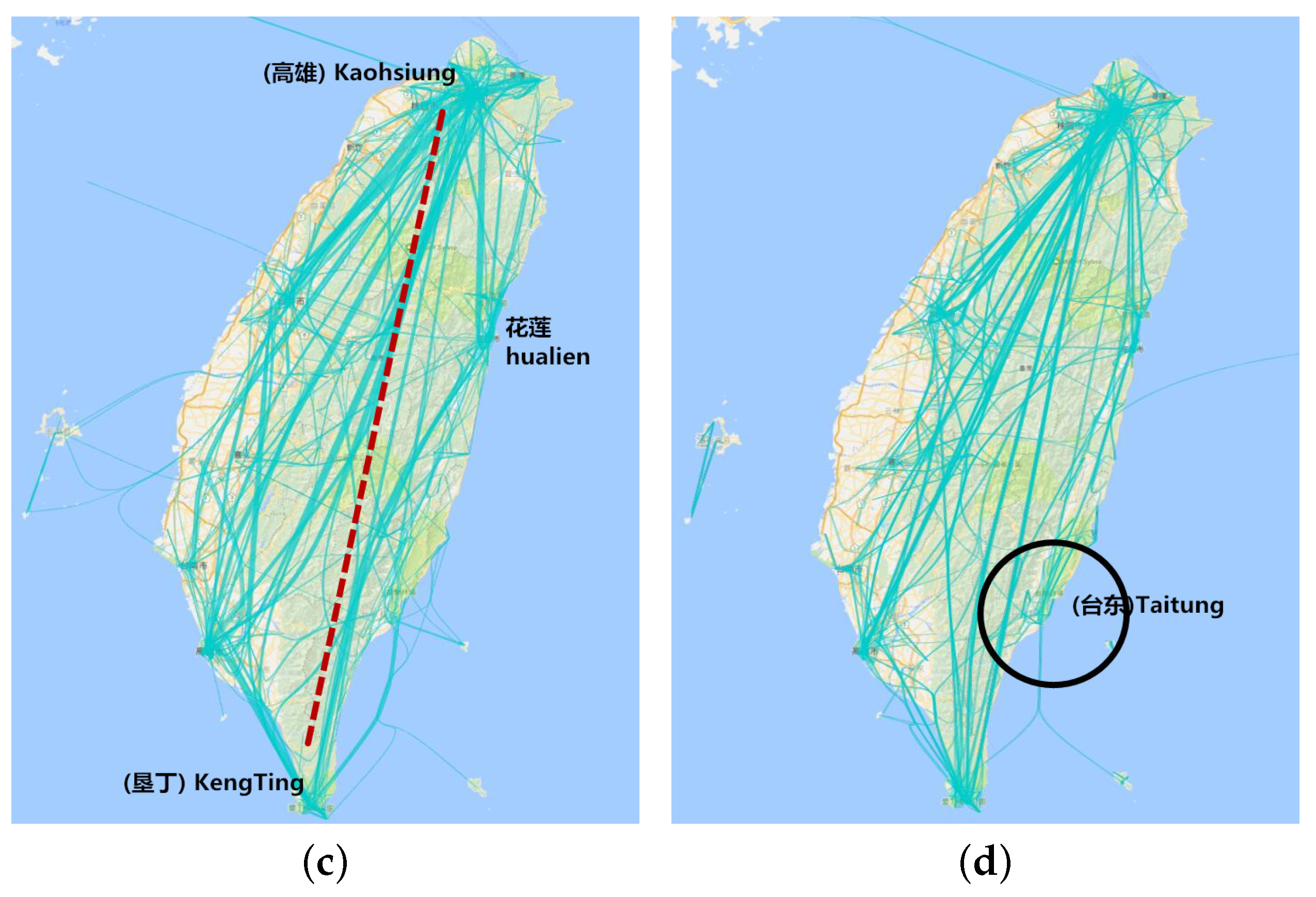
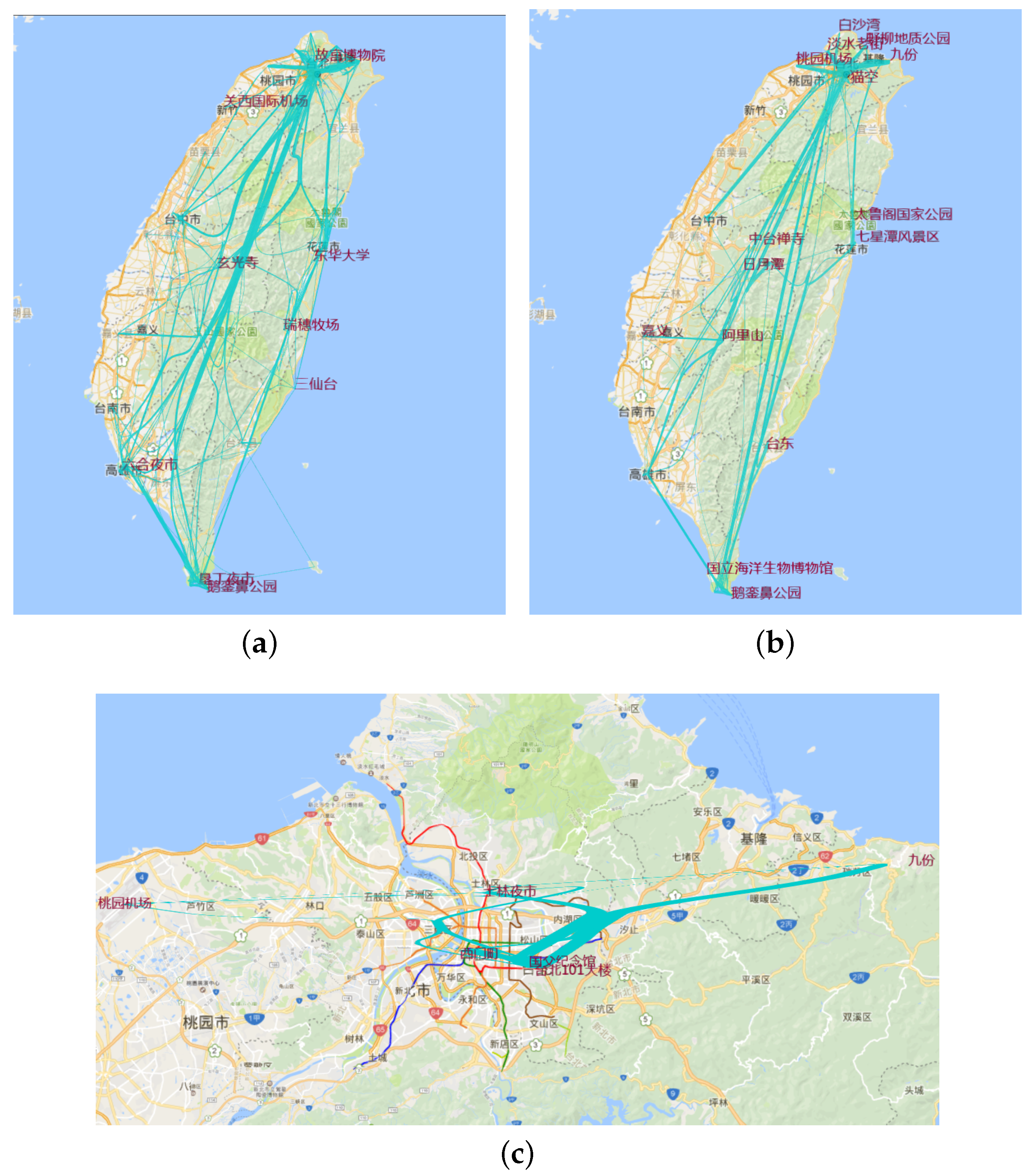
6.4.2. Aggregation by Hottest Site
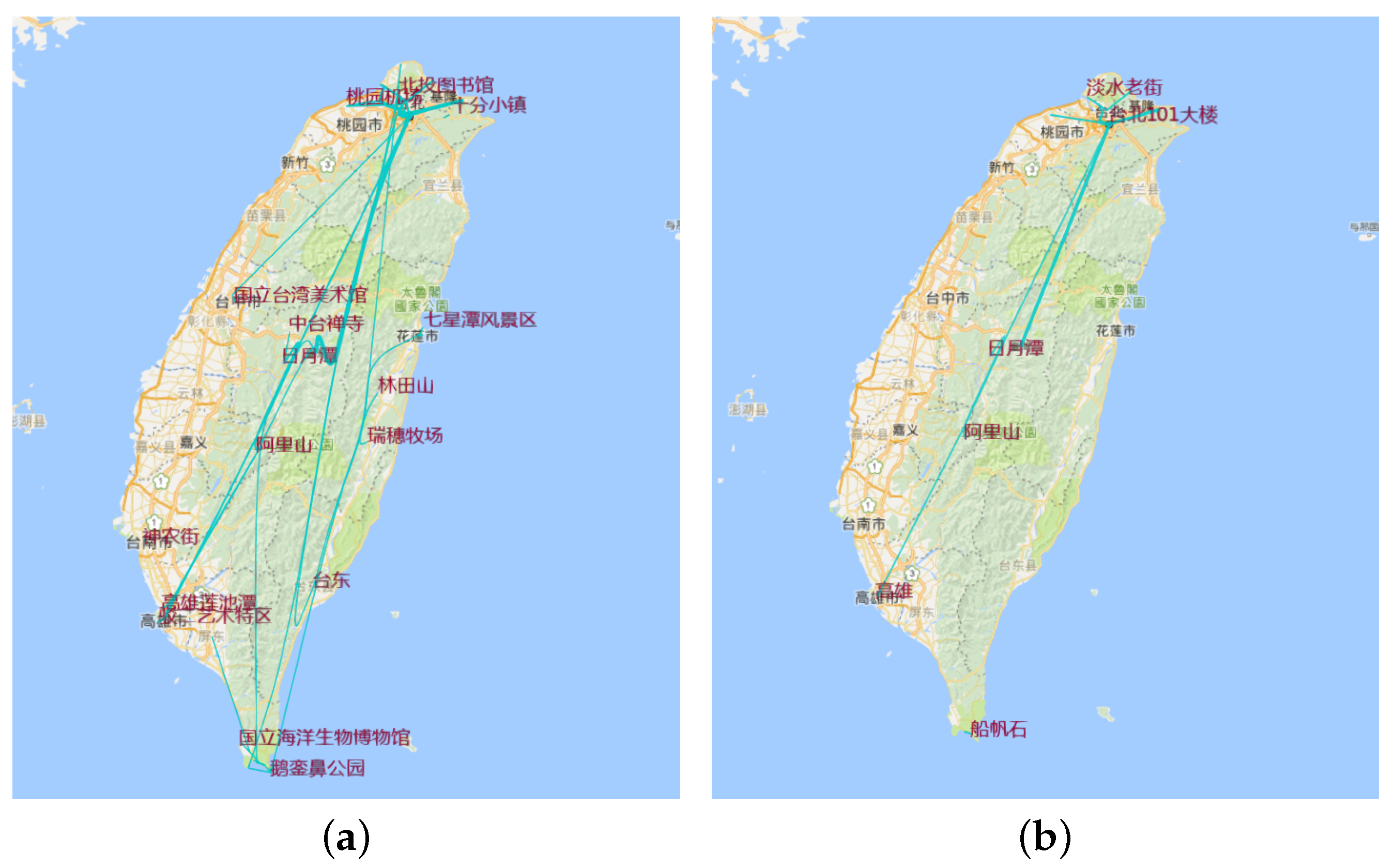
6.4.3. Aggregation in Hottest Trajectory
7. Interaction
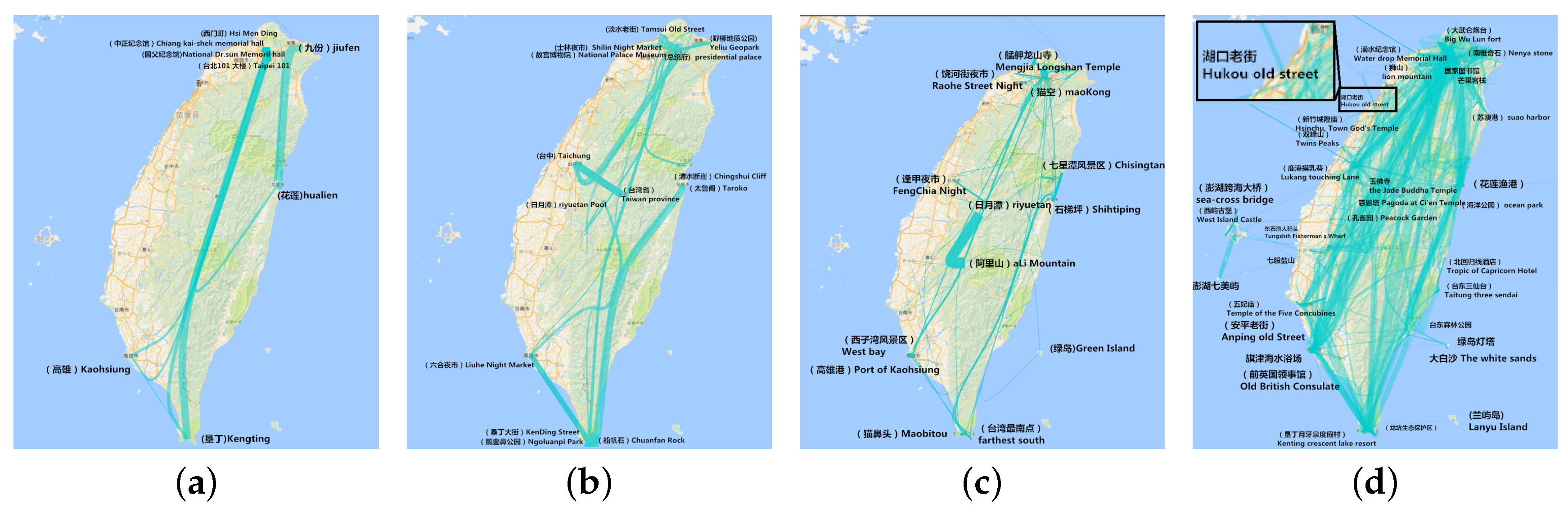
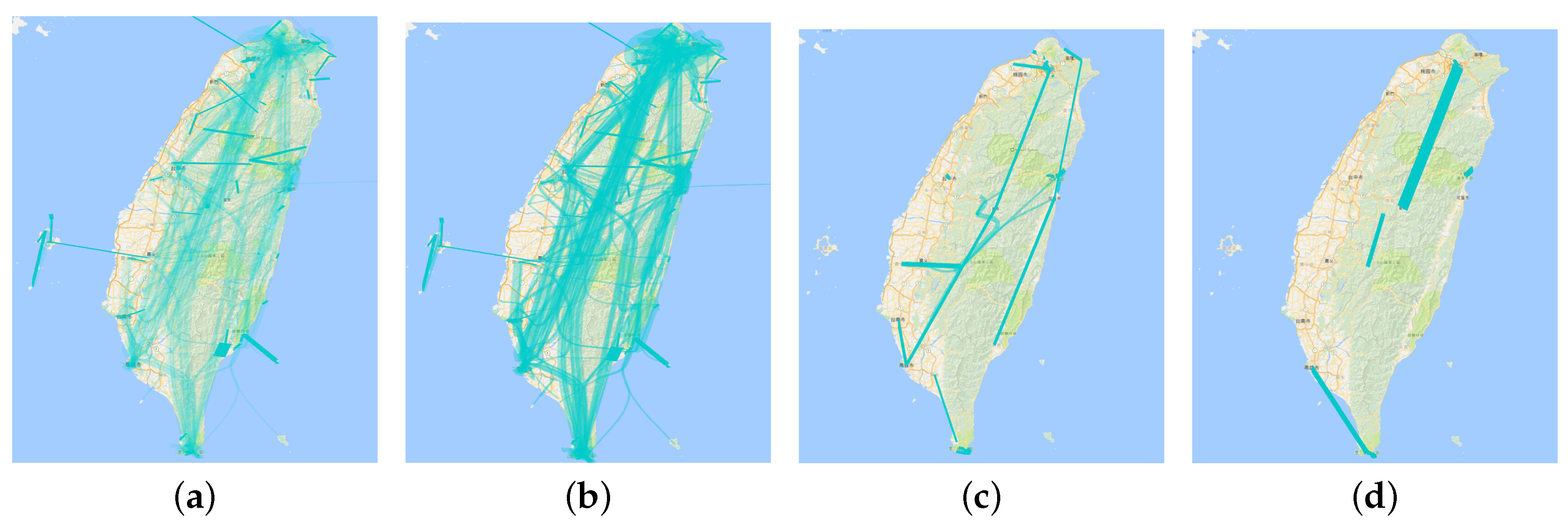
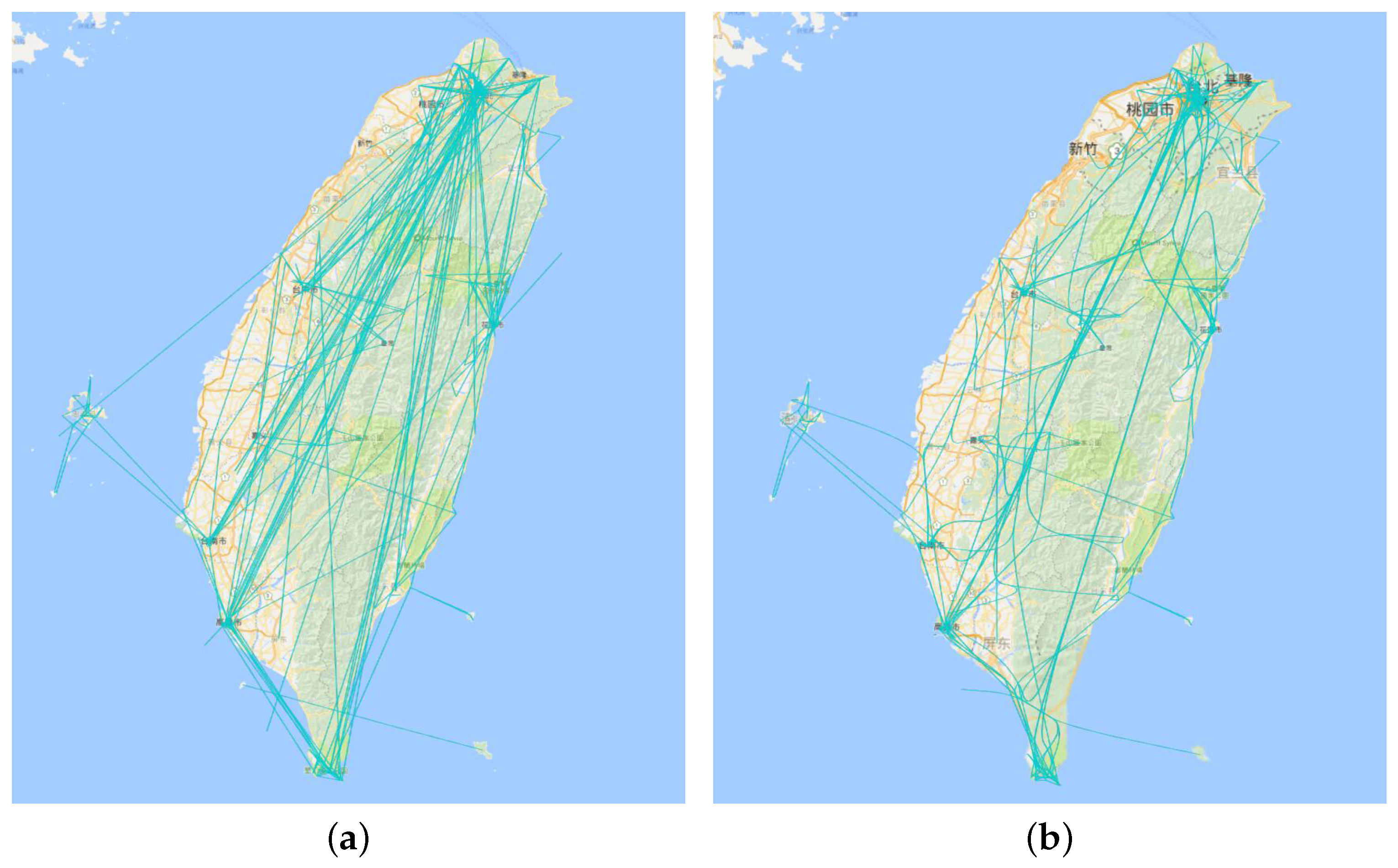
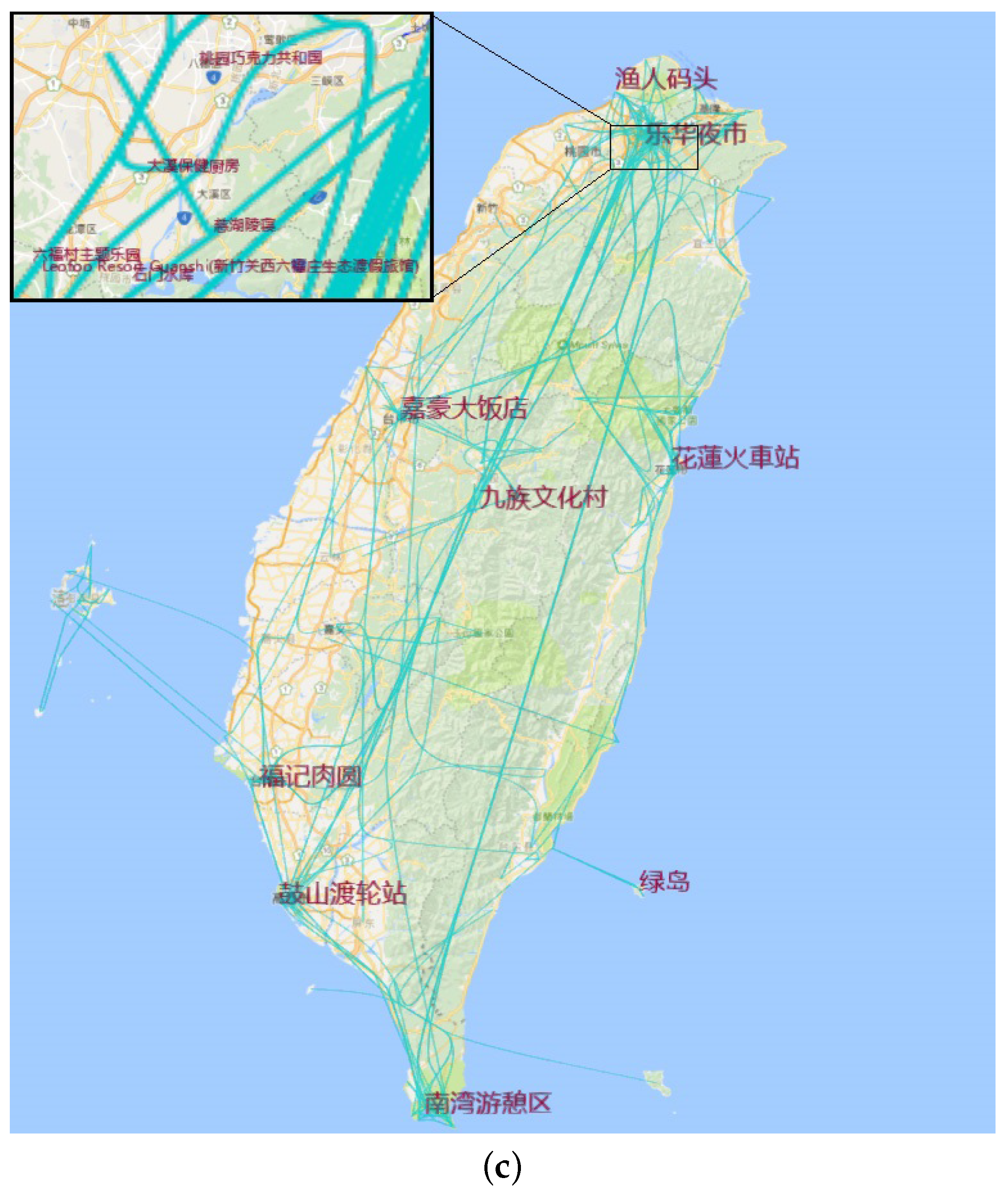
8. Experiment
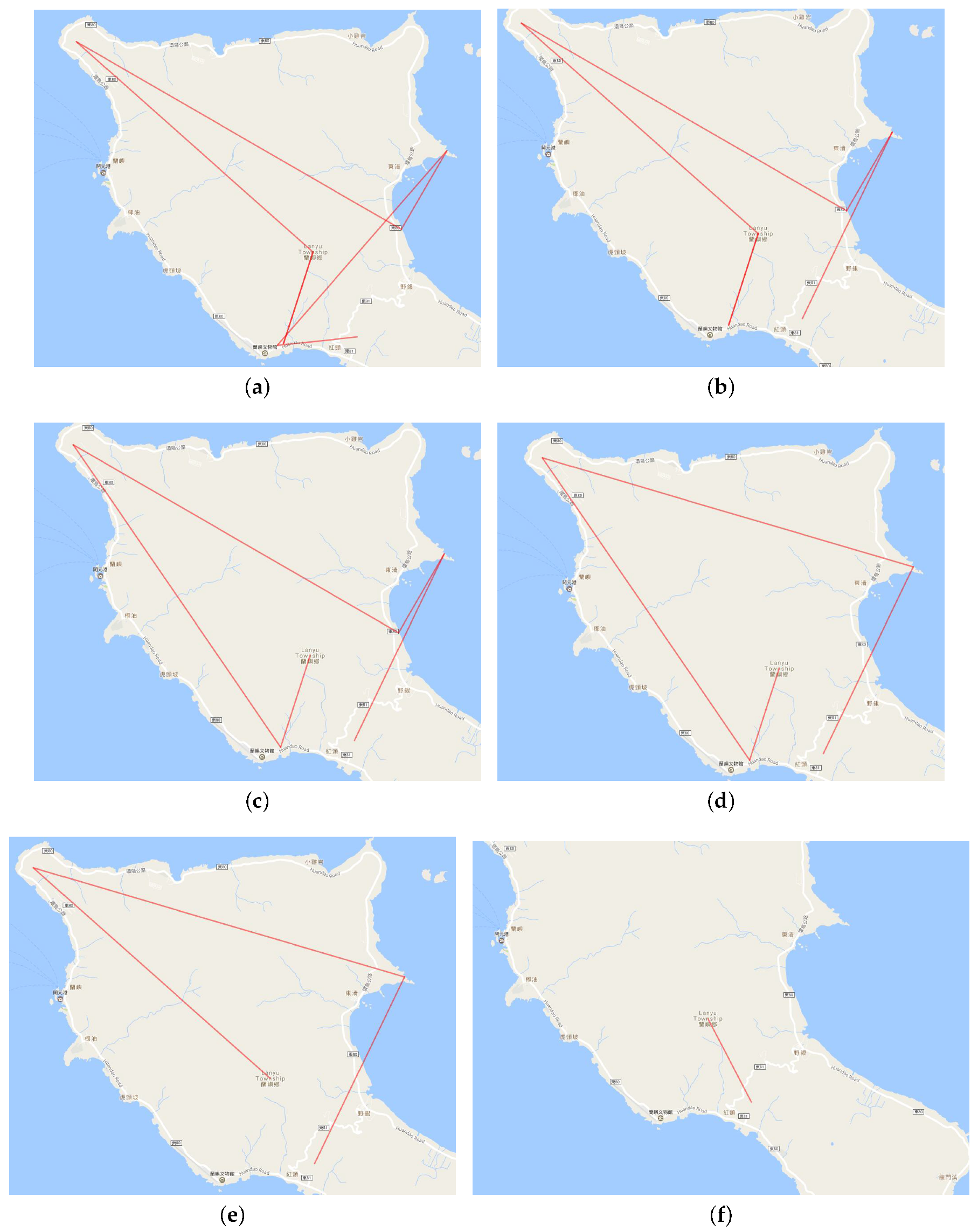
8.1. Multilevel Trajectory Compression
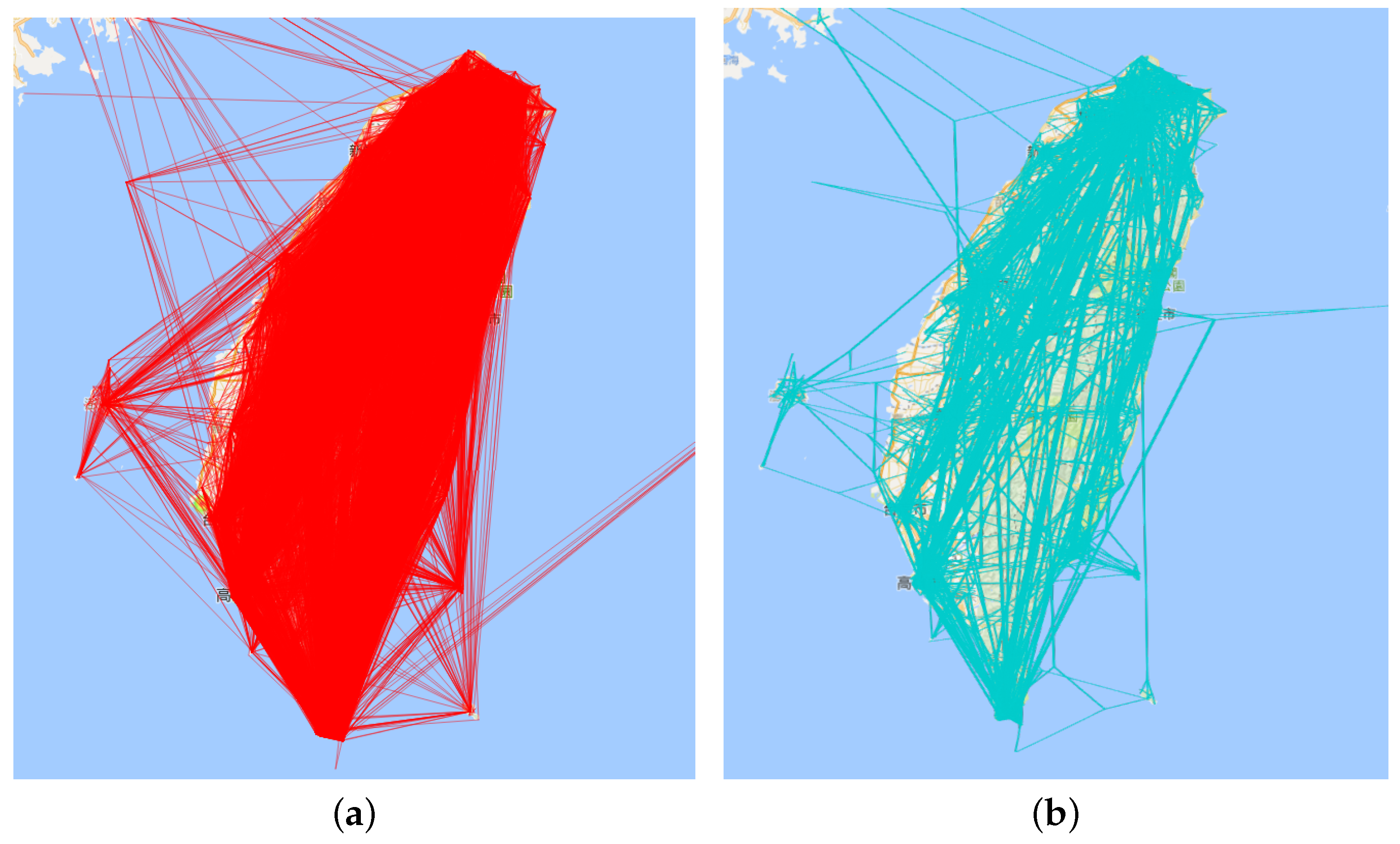
8.2. Edge Bundling
8.3. Aggregation in the Time Dimension
8.4. Aggregation in the Administrative Region
8.5. Aggregation by Hottest Site
8.6. Aggregation by Hottest Trajectory
9. Discussion
9.1. Adaptive Plotting Scale
9.2. Movement Patterns Exploration
10. Application on Travel Route Planning
11. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andrienko, G.; Andrienko, N.; Dykes, J.; Fabrikant, S.I.; Wachowicz, M. Geovisualization of dynamics, movement and changKeye: Issues and developing approaches in visualization research. Inf. Vis. 2008, 7, 173–180. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure; ACM Sigmod Record; ACM: New York, NY, USA, 1999; Volume 28, pp. 49–60. [Google Scholar]
- Wan, Y.; Zhou, C.; Pei, T. Semantic-geographic trajectory pattern mining based on a new similarity measurement. ISPRS Int. J. Geo-Inf. 2017, 6, 212. [Google Scholar] [CrossRef]
- Surhone, L.M.; Tennoe, M.T.; Henssonow, S.F.; Model, S.; Projection, M.; Map, S. Scale (Ratio). Comput. Sci. 2010, 12, 795–801. [Google Scholar]
- Thompson, R.J. Generalisation of spatial information. Spatial data—The final frontier: To boldly go into 3, 4 or more dimensions. Otb Res. Inst. 2009, 36, 150–151. [Google Scholar]
- Eades, P.; Feng, Q.W. Multilevel visualization of clustered graphs. In Proceedings of the Symposium on Graph Drawing, Berkeley, CA, USA, 18–20 September 1996; pp. 101–112. [Google Scholar]
- Wang, C.; Wang, J.; Xie, X.; Ma, W.Y. Mining geographic knowledge using location aware topic model. In Proceedings of the 4th ACM Workshop on Geographical Information Retrieval, Lisbon, Portugal, 9 November 2007; pp. 65–70. [Google Scholar]
- Pang, Y.; Hao, Q.; Yuan, Y.; Hu, T.; Cai, R.; Zhang, L. Summarizing tourist destinations by mining user-generated travelogues and photos. Comput. Vis. Image Underst. 2011, 115, 352–363. [Google Scholar] [CrossRef]
- Zhu, Z.; Shou, L.; Chen, K. Get into the spirit of a location by mining user-generated travelogues. Neurocomputing 2016, 204, 61–69. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, X. Computing with Spatial Trajectories; Springer Science & Business Media: New York, NY, USA, 2011; pp. 1–31. [Google Scholar]
- Lee, J.G.; Han, J.; Li, X. Trajectory outlier detection: A partition-and-detect framework. In Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; pp. 140–149. [Google Scholar]
- Patel, D.; Sheng, C.; Hsu, W.; Lee, M.L. Incorporating duration information for trajectory classification. In Proceedings of the 2012 IEEE 28th International Conference on Data Engineering (ICDE), Arlington, VA, USA, 1–5 April 2012; pp. 1132–1143. [Google Scholar]
- Bakshev, S.; Spisanti, L.; Fernández de Macedo, J.; Vidal, V.; Casanova, M. Semantic visualization of trajectories. In Proceedings of the 13th International Conference on Enterprise Information Systems, Beijing, China, 8–11 June 2011. [Google Scholar]
- Krueger, R.; Thom, D.; Ertl, T. Visual analysis of movement behavior using web data for context enrichment. In Proceedings of the 2014 IEEE Pacific Visualization Symposium (PacificVis), Yokohama, Japan, 4–7 March 2014; pp. 193–200. [Google Scholar]
- Wood, J.; Dykes, J.; Slingsby, A. Visualisation of origins, destinations and flows with OD maps. Cartogr. J. 2010, 47, 117–129. [Google Scholar] [CrossRef]
- Guo, D. Flow mapping and multivariate visualization of large spatial interaction data. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1041–1048. [Google Scholar] [PubMed]
- Ashok, K.; Ben-Akiva, M.E. Dynamic origin-destination matrix estimation and prediction for real-time traffic management systems. In Proceedings of the 12th International Symposium on the Theory of Traffic Flow and Transportation, Berkeley, CA, USA, 21–23 July 1993. [Google Scholar]
- Cui, W.; Zhou, H.; Qu, H.; Wong, P.C.; Li, X. Geometry-based edge clustering for graph visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1277–1284. [Google Scholar] [CrossRef] [PubMed]
- Holten, D.; Van Wijk, J.J. Force-Directed Edge Bundling for Graph Visualization; Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2009; Volume 28, pp. 983–990. [Google Scholar]
- Gansner, E.R.; Hu, Y.; North, S.; Scheidegger, C. Multilevel agglomerative edge bundling for visualizing large graphs. In Proceedings of the 2011 IEEE Pacific Visualization Symposium (PacificVis), Hong Kong, China, 1–4 March 2011; pp. 187–194. [Google Scholar]
- Visvalingam, M.; Whyatt, J.D. The Douglas-Peucker Algorithm for Line Simplification: Re-Evaluation through Visualization. Comput. Graph. Forum 1990, 9, 213–225. [Google Scholar] [CrossRef]
- Chen, M.; Xu, M.; Franti, P. A fast o(n) multiresolution polygonal approximation algorithm for GPS trajectory simplification. IEEE Trans. Image Process. 2012, 21, 2770–2785. [Google Scholar] [CrossRef] [PubMed]
- Klein, T.; Van Der Zwan, M.; Telea, A. Dynamic multiscale visualization of flight data. In Proceedings of the 2014 International Conference on Computer Vision Theory and Applications (VISAPP), Lisbon, Portugal, 5–8 January 2014; Volume 1, pp. 104–114. [Google Scholar]
- XieCheng website. Available online: http://you.ctrip.com/travels/ (accessed on 2 June 2017).
- Chen, S.; Yuan, X.; Wang, Z.; Guo, C.; Liang, J.; Wang, Z.; Zhang, X.L.; Zhang, J. Interactive visual discovering of movement patterns from sparsely sampled geo-tagged social media data. IEEE Trans. Vis. Comput. Graph. 2016, 22, 270–279. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Kurashima, T.; Iwata, T.; Irie, G.; Fujimura, K. Travel route recommendation using geotags in photo sharing sites. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management, Toronto, ON, Canada, 26–30 October 2010; pp. 579–588. [Google Scholar]




| Method | Time Spent | Data Size |
|---|---|---|
| ROI detection with mean-shift | 2.3 s | trajectory with 28 edges |
| Trajectory compression with Douglas-Peucker | 0.8 s | trajectory with 11 edges |
| Edge bundling with MINGLE | 6 s | trajectory with 53,240 edges |
| Adaptive scale with K-means | 2.8 s | trajectory with 53,240 edges |
| K-th Cut-off Point | Line Number | Line Weight Value Range |
|---|---|---|
| 0 | 53,240 | 1–504 |
| 1 (again cutoff) | 10,319 | 6–504 |
| 2 | 1275 | 11–504 |
| 3 | 200 | 47–504 |
| 4 | 17 | 136–504 |
| K-th Cut-off Point | Line Number | Line Weight Value Range |
|---|---|---|
| 0 | 53,240 | 1–504 |
| 1 | 50 | 101–504 |
| 2 | 5 | 201–504 |
| 3 | 2 | 300–504 |
| 4 | 1 | 400–504 |
| K-th Cut-off Point | Line Number | Line Weight Value Range |
|---|---|---|
| 0 | 53,240 | 1–504 |
| 1 | 3546 | 4–504 |
| 2 | 1156 | 13–504 |
| 3 | 246 | 42–504 |
| 4 | 15 | 146–504 |
| K-th Cut-off Point | Line Number | Line Weight Value Range |
|---|---|---|
| 0 | 10,000 | 1–200 |
| 1 | 7473 | 52–200 |
| 2 | 5003 | 102–200 |
| 3 | 2547 | 151–200 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Wang, Y.; Xu, G.; Tai, X. Multilevel Visualization of Travelogue Trajectory Data. ISPRS Int. J. Geo-Inf. 2018, 7, 12. https://doi.org/10.3390/ijgi7010012
Ma Y, Wang Y, Xu G, Tai X. Multilevel Visualization of Travelogue Trajectory Data. ISPRS International Journal of Geo-Information. 2018; 7(1):12. https://doi.org/10.3390/ijgi7010012
Chicago/Turabian StyleMa, Yongsai, Yang Wang, Guangluan Xu, and Xianqing Tai. 2018. "Multilevel Visualization of Travelogue Trajectory Data" ISPRS International Journal of Geo-Information 7, no. 1: 12. https://doi.org/10.3390/ijgi7010012
APA StyleMa, Y., Wang, Y., Xu, G., & Tai, X. (2018). Multilevel Visualization of Travelogue Trajectory Data. ISPRS International Journal of Geo-Information, 7(1), 12. https://doi.org/10.3390/ijgi7010012




