Abstract
Human development has far-reaching impacts on the surface of the globe. The transformation of natural land cover occurs in different forms, and urban growth is one of the most eminent transformative processes. We analyze global land cover data and extract cities as defined by maximally connected urban clusters. The analysis of the city size distribution for all cities on the globe confirms Zipf’s law. Moreover, by investigating the percolation properties of the clustering of urban areas we assess the closeness to criticality for various countries. At the critical thresholds, the urban land cover of the countries undergoes a transition from separated clusters to a gigantic component on the country scale. We study the Zipf-exponents as a function of the closeness to percolation and find a systematic dependence, which could be the reason for deviating exponents reported in the literature. Moreover, we investigate the average size of the clusters as a function of the proximity to percolation and find country specific behavior. By relating the standard deviation and the average of cluster sizes—analogous to Taylor’s law—we suggest an alternative way to identify the percolation transition. We calculate spatial correlations of the urban land cover and find long-range correlations. Finally, by relating the areas of cities with population figures we address the global aspect of the allometry of cities, finding an exponent δ ≈ 0.85, i.e., large cities have lower densities.
1. Introduction
In the beginning of the last century, F. Auerbach [1] claimed “The law of population concentration”. In various phases [2], the seemingly scale-invariant character of city size distributions is most often described in terms of a power-law
where p denotes the probability density of observing within a scoped region a city sample of size X. For this expression empirical estimations of the exponent ζ closely deviate around 2—so called Zipf’s law for cities, after G. K. Zipf’s [3].
While several city growth models have been proven successful in reconstructing power-law city size distributions [4,5,6,7,8], statistical tests have also assigned a great plausibility to alternative functional forms, as in the case of log-normal distributions [9].
In this work we estimate the global city size distribution, based on both, urban land cover and population. For this purpose we apply an orthodromic version [10] of the recently proposed City Clustering Algorithm (CCA) [11], to account for a more accurate estimation of the areas of all urban settlements of the world (approximately 250, 000). We find that Zipf’s law approximately holds to a great extent for city areas and to a lesser extent for urban population.
As a matter of fact, characterization of the spatial organization and scaling properties of urban clusters depends on the definition of a city boundary. In particular, defining a city boundary by means of the CCA requires to specifying a distance below which adjacent urban areas are considered to be part of the same cluster. The variation of this parameter involves a problem similar to percolation transition; beyond a critical clustering distance value, a giant cluster component emerges. We explore further the influence of the choice of the clustering parameter on the spatial organization and scaling properties of urban land cover clusters, for several European countries.
This paper is organized as follows: In Section 2 we provide a brief description of the CCA algorithm and of the land cover and population databases. Section 3 reports on the global city size distribution for city area and population. In Section 4 we present the country scale results; Section 4.1 addresses the CCA percolation transition; Section 4.2 elaborates on the connection between the scaling properties of city size distributions and the CCA percolation transition; in Section 4.3 we discuss the scaling of the average size of city clusters, approaching the percolation transition; in Section 4.4 we show that the variability of city cluster sizes also exhibits scaling, in the form of the so called Taylor’s law; regarding the spatial organization of city clusters, in Section 4.5 we present results on the scaling of spatial correlations. Finally, in Section 5 we explore the global aspect of the city allometry relationship, i.e., the power-law relation between population and area for approximately 70,000 cities under scope. The main results of this work are summarized and discussed in Section 6.
2. City Clustering and Land Cover Data
It is convenient to define cities as connected clusters of neighboring populated sites. This idea has been recently implemented in the so called City Clustering Algorithm (CCA) [11], which is an adapted version of the Burning Algorithm [12].
Basically, CCA identifies any pair of urban spatial units (either by population or land cover) as belonging to the same urban cluster if these are located within a distance l from each other. This distance beyond nearest neighbors is motivated by the observation that a city might include natural gaps, such as the River Thames in London or other topographic obstacles. Thus, when applied to an entire region, CCA provides a means to determine the areas and boundaries of the cities contained within, according to the parameter l, which represents a degree of coarse-graining.
At the global scale, data on the spatial distribution of population is only available for administrative boundaries or as raster data with a rather coarse resolution. Therefore, we opted for determining the extent of cities using a remote sensing based classification of land cover data, as provided by the GlobCover 2009 land cover map [13] at a grid resolution of approx. 0.308 km (at the Equator). From the 23 land cover classes, we select the class #190 (artificial surfaces and associated areas) and considered it as urban and aggregated all other classes to non-urban.
For the sake of illustration, Figure 1 exhibits the application of the CCA to the land cover data for Paris and its surroundings. A satellite image of the region is displayed in Figure 1a, the corresponding aggregated land cover classes in Figure 1b, and the urban clusters identified after application of the CCA in panel Figure 1c.
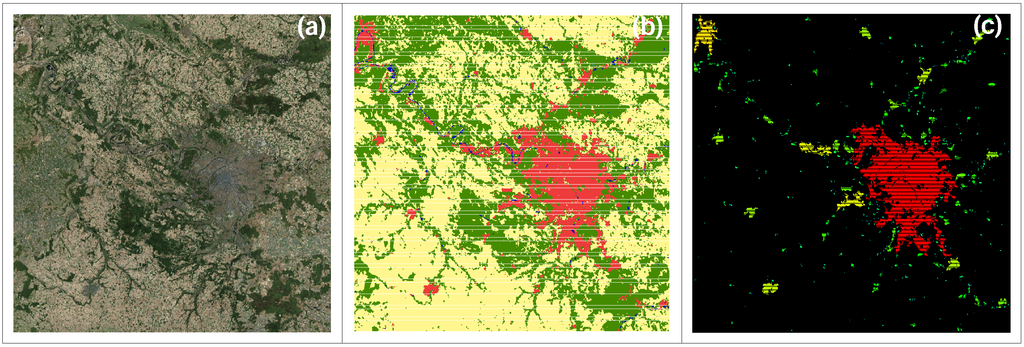
Figure 1.
Application of city clustering to urban land cover data. The following panels illustrate different aspects of the city of Paris and its surroundings: (a) Remote sensing image as extracted from the ArcGIS 10 component ArcMap; (b) Urban land cover data as obtained from the GlobCover 2009 land cover map. The colors indicate urban (red, class 190), water bodies (blue, class 210), forests and grasslands (green, classes 20-110), and rainfed croplands (yellow, class 14); (c) From the urban land cover and by taking l = 4 km, the identified clusters are color coded according to the logarithm of their size: from small (light blue) via medium (green) to large (red). The cutout has the approximate area of (215 km)2.
Since the raster cell size decreases from the Equator to the poles, the use of the Euclidian metric is not suitable for the application of CCA at the global scale. Accordingly, orthodromic distances were considered in a new implementation of the CCA [10] in order to provide a more accurate representation of distances and areas across different latitudes on a sphere. In the orthodromic representation, a distance between two cells is determined with respect to their latitudes and longitudes according to where with the radius of the terrestrial sphere km.
In terms of population, the global probability density, was obtained using population data from the Global Rural Urban Mapping Project (GRUMP) [14], which comprises coordinates, names, and population figures of 67, 935 administrative units (estimated data for the year 2000). From this sample we found 16, 908 urban settlement points which are located inside an urban cluster or within a distance of l = 0.4 km (following a similar approach as in [15]).
Figure 2 shows the clusters that can be associated to a population number for the entire world. Due to Zipf’s law, we represents each city cluster as a dot and the size by the color. The insets (a) and (b) display maps of Austria and France together with the identified urban clusters. Some remarkable things can be seen. For example, while the west of the USA is largely covered by many small urban clusters, Central and Western Europe exhibits a mixed pattern of small and large cities.
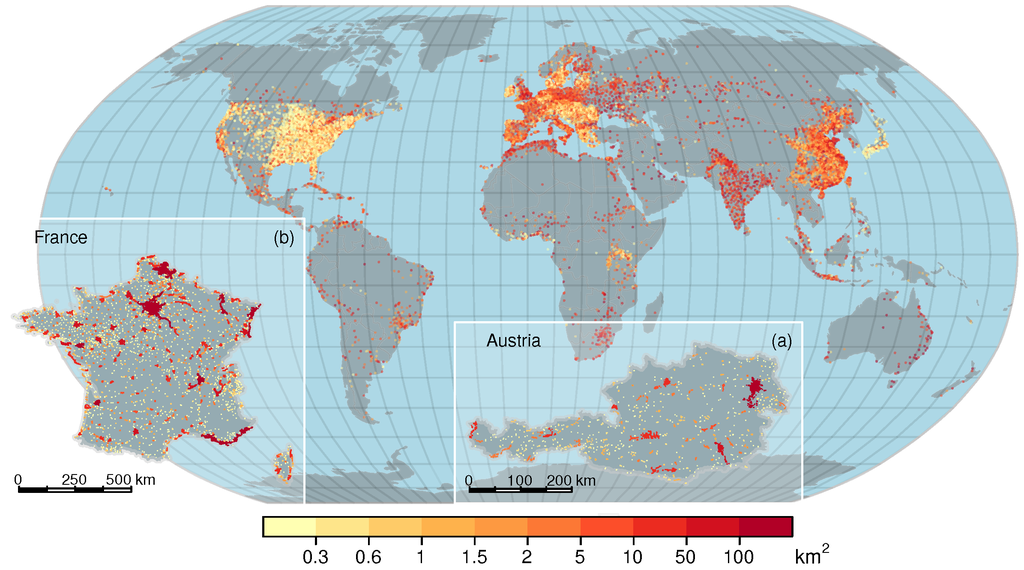
Figure 2.
Global map of cluster area in km2 for l = 4 km. For better visibility all clusters (15,640) are plotted as single dots, instead of spatial extent. Notice that only clusters with associated population information are displayed. Exemplary the spatial extent is shown for (a) Austria (460 clusters) and (b) France (1907 clusters). Due to the fact that small clusters are much more often than big ones, they are more present in the global dotted map compared to the spatial explicit country examples. Furthermore noticeable is the highly sprawled small urban clusters in the US compared with the concentrated dens urban hot spots in India.
3. Global City Size Distribution
With the aim of addressing the global city size distribution, we applied CCA with a clustering distance of l = 0.4 km to the entire global land cover database described in Section 2, from which we extracted 249, 512 urban clusters.
The resulting area probability density is shown in Figure 3a. Besides deviations for small sizes—which are mainly due to the discreteness of the grid cells—we find a fair power-law relation in agreement with Equation (1), with and for km2.
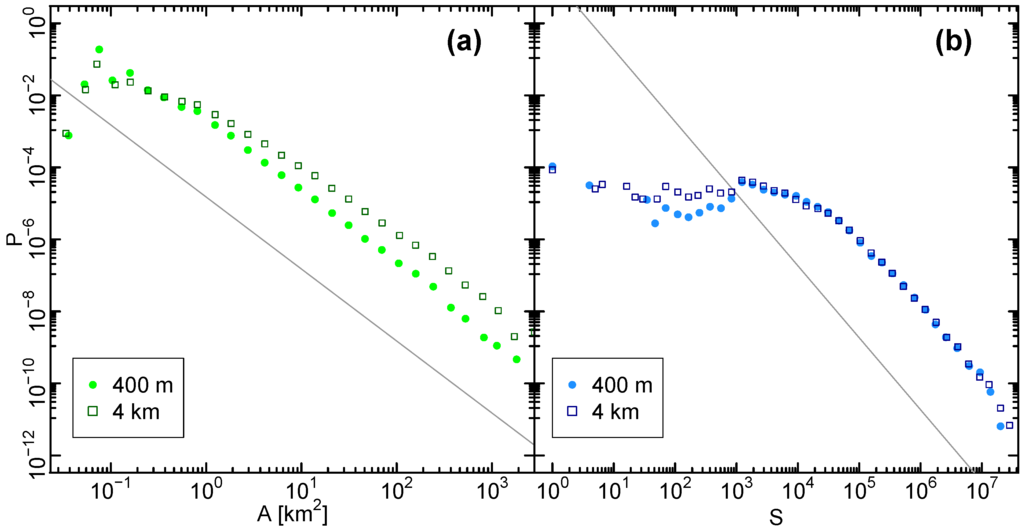
Figure 3.
Probability density of city size in terms of area and population. (a) Cluster area distribution p(A), as obtained by applying the City Clustering Algorithm (CCA) to global land cover data and extracting all urban clusters on the globe. For A > 0.1 km2 we estimate for l = 0.4 km (249,512 clusters) and for l = 4 km (46,754 clusters); (b) Cluster population distribution p(S), as obtained from associating population settlement points with the urban clusters identified by means of CCA. For we estimate for l = 0.4 km and for l = 4 km. In both panels: l = 0.4 km (circles), l = 4 km (squares). The solid grey lines have slope −2.
Figure 3b shows the population probability density . The city population values have been obtained by summing up those GRUMP population values which coordinates are within the corresponding urban land cover clusters. Since small populations are more likely to be missing in the GRUMP dataset, the number of values which could be assigned to a small cluster is reduced and we observe in Figure 3b deviations from the power-law distribution Equation (1) at the lower end. Therefore, the power-law fitting is carried out for urban clusters above 104 inhabitants, resulting in an exponent . Accordingly, we observe that Zipf’s law approximately holds for the cities on the global scale, whereas the actual exponent is smaller than 2. We explore also l = 4 km and similar power-law size distributions, however with a different exponent in the case of the areas (Figure 3a).
Studies of global population city size distributions were reported in [16,17], for a reduced subset of cities, e.g., the 2, 700 largest clusters in the case of the former. Distributions of city size in terms of area has been considered previously, e.g., in [6,15,18,19,20] at the regional and country scale. More recently, a global analysis has positively tested Zipf’s law by considering temporally stable night lights as a proxy indicator for human habitation and anthropogenic land use [21].
4. Percolation Transition and Size Distribution on the Country Scale
4.1. Percolation Transition
It is worth noting that when the clustering parameter l is set to a very small value the CCA does not take any effect, in the sense that the urban clusters thereby identified correspond trivially to the grid cells from the input land cover map. In the opposite limit of very large l, most of the urban area under scope are assigned to the same giant cluster component. Accordingly, when applied to a large area, for intermediate values of l it is expectable to observe a percolation transition of the urban clusters. As it turns out, it becomes natural to inquire into this possibility and to eventually address the spatial properties drawn from application of the CCA in the light of concepts and methods stemming from percolation theory [12,22].
At the country scale, let us address the possible percolation transition that may occur at the level of the urban patch clustering when changing the parameter l in a typical application of the CCA—which, more in general, constitutes a problem inherent to the ambiguous character of the definition of city boundaries [11,20,23]. It is in order to mention that the scale defined by the clustering parameter l determines the type of percolation transition under scope—for small l, the transition resembles the one occurring in site percolation on a square lattice, while for large l it can be further assimilated to the one observed in continuum percolation problems [22]. Here, we are interested in the value lc at which the giant cluster component spans within a country territory. The critical value lc is analogous to the critical occupation probability Pc, which constitutes the control parameter in most of lattice percolation formulations [22]. Both quantities are approximately related by with .
In real world data, however, it can be difficult to identify such an lc percolation threshold. We find that the average cluster size excluding the largest cluster, , constitutes a sensitive indicator of the transition. In infinite systems, diverges at Pc [22] whereas for finite systems, a (finite) peak occurs. Similarly, one can in principle detect the presence of a peak in around a value lc when applying CCA to the urban land cover of different countries. Since in the limit of small l the urban clusters identified by the CCA approximate the cells of urban land cover, we conjecture that a small lc value constitutes a proxy indicator of the percolation threshold of the urban land cover.
For illustrative purposes, let us consider the case of Austria. Figure 4a depicts the plot of vs. l. In the case of Austria we find that the peak occurs at lc = 15 km. As it can be observed, for l < lc the average cluster size increases strongly with l, yet gradually, and it drops sharply for l > lc.
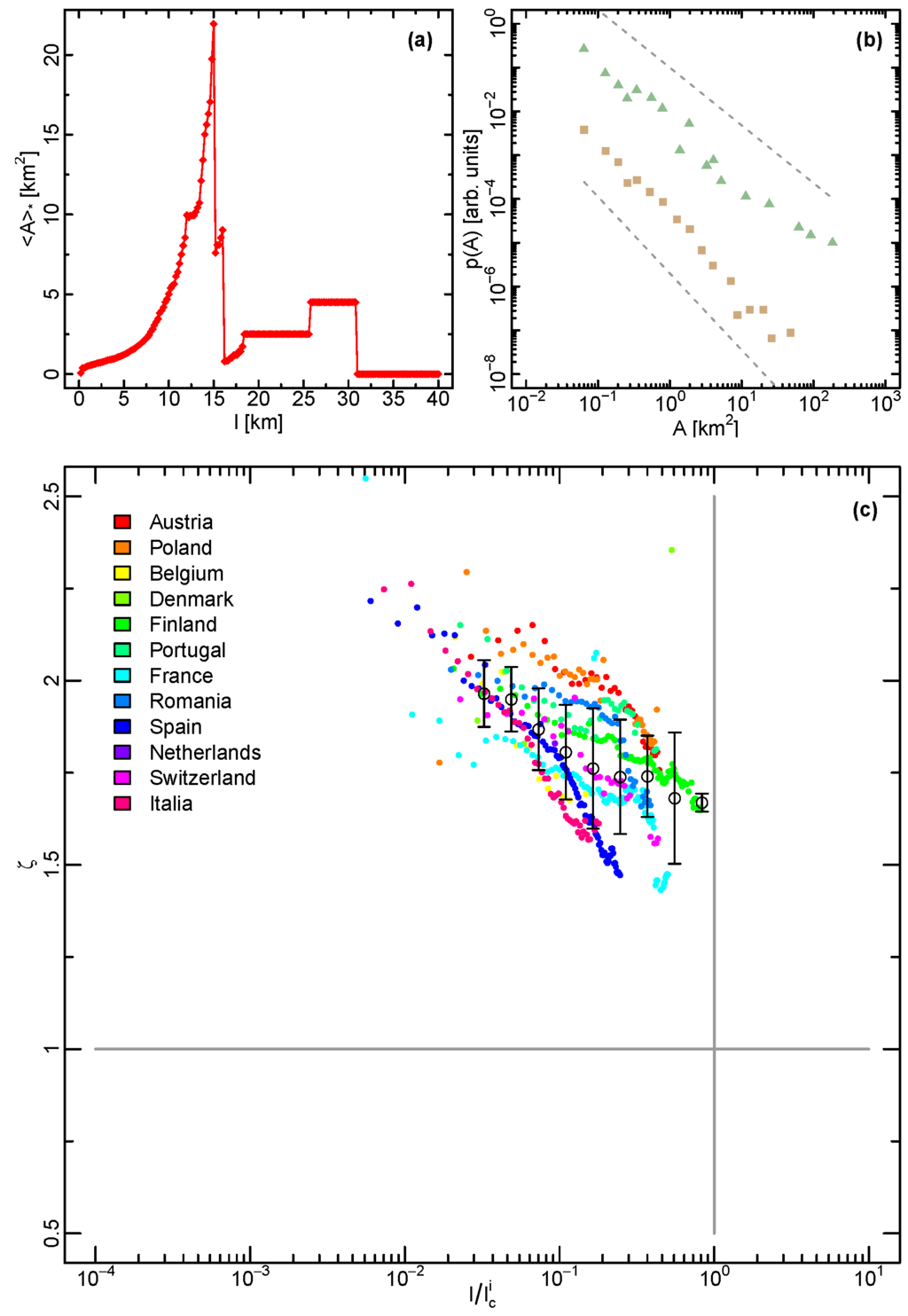
Figure 4.
Percolation and Zipf’s law. (a) Average cluster size excluding the largest component as a function of the clustering parameter l for Austria. The maximum is located at the percolation transition, which in this example is km; (b) Probability density of cluster areas for Austria and for (370 clusters, green triangles) as well as (87 clusters, brown squares). The dotted grey lines have the slopes −1.71 and −1.27; (c) Estimated power-law distribution exponent as a function of the rescaled clustering parameter for various countries as indicated by colored dots. Since we found out that the method proposed in [28] has a significant deviation from the real value for input with less than 100 entries, we estimated the power-law distribution exponents for each country just for those l with at least 100 clusters remaining. The open circles represent averages in logarithmic bins and their error bars the corresponding standard deviations. The exponent decreases with increasing and takes values between for and for .
In a model based on correlated gradient percolation [6,24] the urban/non-urban structure is formed from spatial correlations, i.e., the probabilities of two sites being urban/non-urban are more similar the closer they are. Furthermore, a radial decay of density around the city center is assumed. A similar approach has been recently applied to reproduce the scaling properties observed in urban land parcels [25]. The dynamics and characteristics of the percolation transition of the urban land cover has been investigated also by means of diffusion limited [26] and gravity based [8] stochastic aggregation models of city growth. Hierarchical percolation and fractal dimensions for the case of Britain are studied in [27].
4.2. City Size Distribution
Let us now consider the influence of the coarse-graining used in defining a city cluster, i.e., parameter l in the CCA, on the scaling of the city size distributions. At this stage, we stress the fact that for many countries lc cannot be identified unambiguously, as in the presence of multiple peaks—often a signature of large clusters being disconnected by vastly extended topographic heterogeneities. Therefore, we focus on a selected set of countries exhibiting (i) a clear percolation threshold and (ii) a large number of urban areas.
For a given l value we extract all city cluster areas and estimate the corresponding exponent by applying the method proposed in [28] while testing power-law against log-normal. Thus, we first quantify the pointwise log-likelihood ratios between the fitted power-law and fitted log-normal distributions and then apply the Voung test for non-nested models [29]. This test essentially consists in testing the hypothesis that both distributions are equally far away from the true distribution, against the two alternative cases where either of each distributions is closer to the true distribution than the other one. Consequently, we account only for those cases where the fitted -values results in positive Voung test and where the associated one-sided p-value exceeded 0.9 (which corresponds to a significance level of 10%). For this procedure we used the corresponding R code (available at http://tuvalu.santafe.edu/~aaronc/powerlaws/). We vary l and repeat the procedure to obtain .
Figure 4b shows the probability density , as obtained for the same country as in Figure 4a for two different values of l (for illustrative purposes, normalized histograms with logarithmic binning are shown). The fitting results in and , for km and km, respectively. Similar decreases in ζ are also found for other countries (see Figure 4c). From these findings, we conjecture an approximately logarithmic dependence on the ratio , with for and for . We cannot determine the exact value for , since the sample sizes become small and the estimated ζ unreliable. Note that the curves in Figure 4c do not fully collapse [30], i.e., the curves do not fall on the identical line. Hence, there must be other influences beyond our analysis, such as heterogeneities in the urban land cover. Another possible explanation for this could be measurement errors in the estimation of and . We stress the fact that the size distributions of urban land cover clusters appear to agree with the functional form in Equation (1), independently of the distance to the percolation threshold .
Decreasing ζ with increasing l has also been reported for the USA [15]. Moreover, a recent study of a “gravity” based urban growth model [8] has shown that , where P represents the site occupation probability. Depending on the values of a, b, and c, this expression leads to a similar decay as in Figure 4c. This similarity suggests a generic influence of the proximity to the percolation threshold on the power-law size distribution of urban land cover.
4.3. Average Size Scaling
According to percolation theory, the average cluster size of finite clusters, , i.e., disregarding the largest cluster, scales with the proximity of the occupation probability to the critical probability, , where the exponent γ is universal and only depends on the dimension [22]. It is of our interest to explore whether the percolation of the urban land cover clustering exhibits a similar scaling. Since in our analysis only few clusters remain above the percolation transition, we omit the case and study as a function of .
Figure 5 shows the results for Austria and Denmark. Due to the finite size of the countries, does not diverge for and we see a plateau. In the other limit, for large small l. In between we find a regime approximately following a power-law
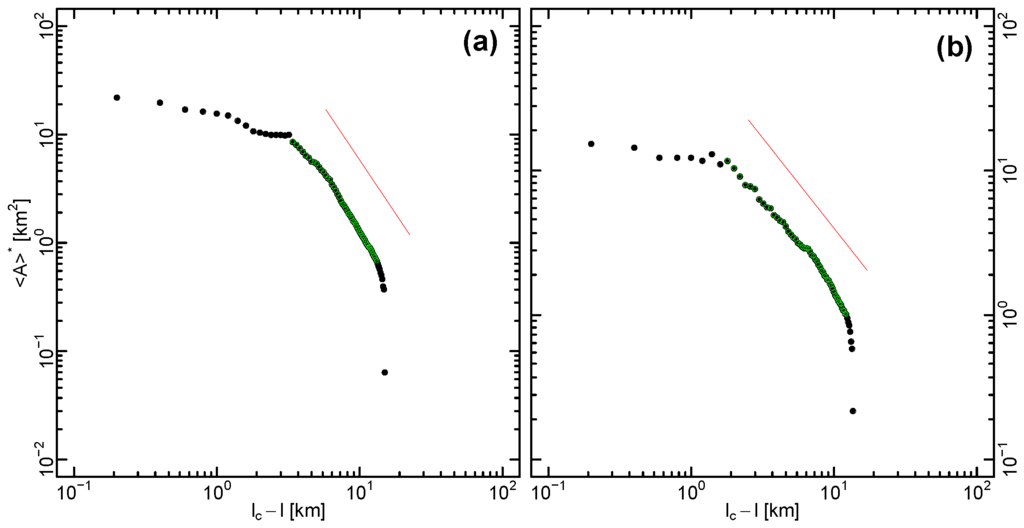
Figure 5.
Fitting of the average size scaling for Austria (a) and Denmark (b). In both cases we have a unique clear peak in the curve of against l. The red lines represent the exponents of the function fitted to the green highlighted parts. Fittings yields the parameter for Austria and for Denmark.
In general, we did not find a universal behavior as in random percolation, in the sense that the values obtained for γ can strongly differ among countries. For Austria, least squares fitting provides and for Denmark . Such a variability in the γ values can result from measurement errors in the identification of (as discussed in Section 4.1) or due to systematic structural influences occurring at larger scale, such as the presence of spatial correlations or an accidented topography. Moreover, in some countries the plot of vs. l does not exhibit a clear power-law relation. The log-log plot of vs l can appear as composed by various linear segments, or, furthermore, the presence of a power-law-like segment cannot even be adequately prescribed over a substantial range of l-values.
4.4. Taylor’s Law For City Size Distribution
Beyond the behavior of the average size with respect to l, characterizing the scaling properties of urban clusters requires also to attend to statistical regularities occurring at the level of the variability of the cluster sizes. For this purpose we elaborate on an empirical relation first established in the context of ecology, the so called Taylor’s law [31,32]. In systems satisfying Taylor’s law, the standard deviation and the average of a quantity are related by a power-law. Both quantities are either temporal or over ensembles. According to de Menezes and Barabasi [33], in the case of temporal variability it follows either a linear or square-root scaling. For a recent review on this topic we refer to Eisler et al. [34].
In the case of cities, we consider the standard deviations and average of cluster sizes for a given l, whereas we omit the largest cluster. This is necessary since at least for the largest cluster is an outlier. By varying l, the ensemble of cluster sizes and the hypothesized power-law can be investigated.
In Figure 6 we show the results for two example countries (Austria and Spain). While the major panels display vs. , the corresponding l can be inferred from the color-coded insets. For Austria (Figure 6a), a power-law regime is found for small l, i.e., km with . The slope seems to hold up to km but separated by jumps in the standard deviation. In contrast, for Spain (Figure 6b), two different power-law regimes can be seen, the first up to km with and the second one up to km with . For other countries we obtained similar results.
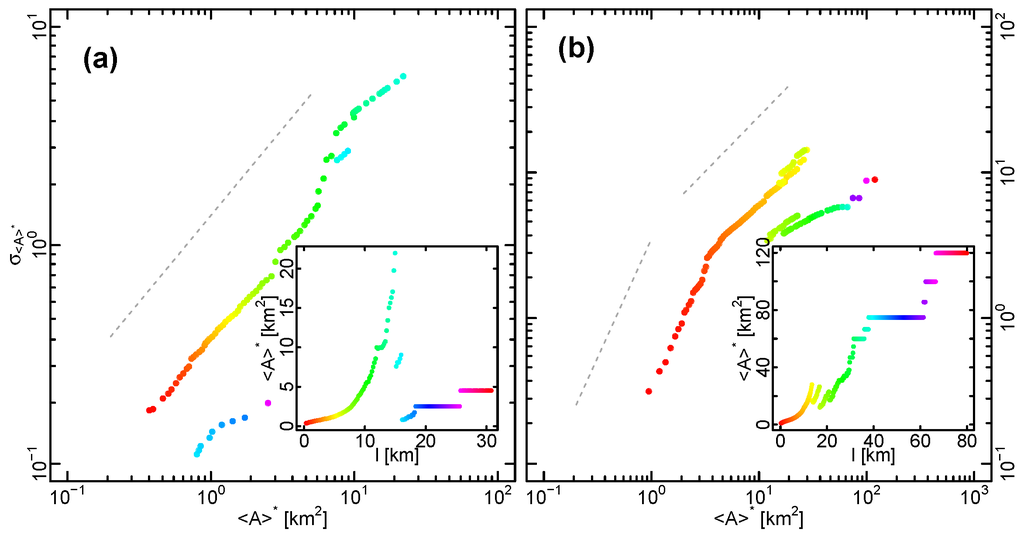
Figure 6.
Taylor’s law for city sizes. The standard deviation of cluster sizes disregarding the largest cluster is plotted as a function of for various values of l. The panels show the results for (a) Austria and (b) Spain. The insets depict the corresponding curve of against l (see also Figure 4a). In the panels and insets corresponding coloring is used in order to enable comparison. For Austria, the standard deviation reaches its maximum at km (light-blue) and for Spain it is located at km (yellow). In the former case this maximum corresponds to the percolation point. In the latter case the maximum corresponds to the first peak one can identify in the curve of against l.
We conclude that Taylor’s law holds to some extent for city sizes but there is no unique exponent and the scaling regimes are country specific. Nevertheless, we observe a characteristic maximum in the plot of vs. . In the case of Austria, this maximum matches with the percolation threshold . In the case of Spain, the maximum standard deviation is located at the similar position as a small peak in the representation of vs. l (inset of Figure 6b). This suggests a relation between the percolation threshold and Taylor’s law, where the presence of a maximum of the latter could constitute a mean to identify the former.
4.5. Spatial Correlations
In the context of the analysis of the scaling properties of city clusters, it is worth stressing the role dynamic processes underlying city growth play. As shown by Makse et al. [6,24], city cluster size distributions are influenced by the presence of spatial correlations. The above mentioned gravity based model of urban growth [8] has illustrated the relation between the degree of compactness of urban clusters and the exponent ζ of the cluster size distribution Equation (1).
With the aim of addressing the spatial organization of real urban clusters we calculate the auto-covariance function
Here, , represent the land cover of sites i, j, respectively, i.e., for urban and otherwise. The indices i, j run over all land cells and the average (denoted by ) is taken on those cells at an approximate distance d, which is predefined by logarithmic bins.
In Figure 7 we show for Austria and the Netherlands as illustrative cases. As can be observed, remains positive for scales at least up 100 km and it decays with distance, approximately following a power-law
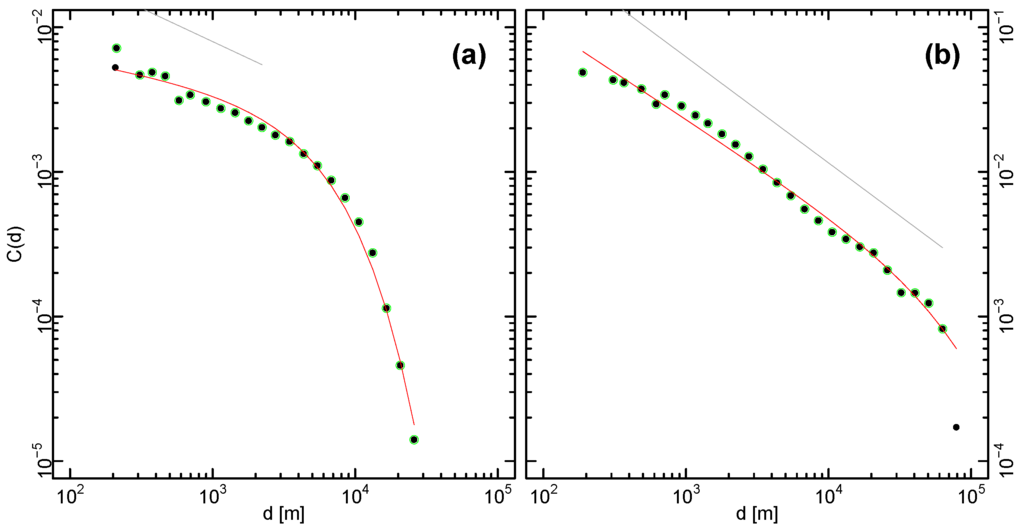
Figure 7.
Spatial correlation computations for Austria (a) and Netherlands (b). The fitted curve (red) on the green-highlighted points which follows the function (power-law with exponential cut-off) has the values for Austria and for the Netherlands . The grey lines (fitted on the corresponding points below the displayed part) have slopes for Austria and for the Netherlands. Beyond the shown range, fluctuates around zero.
Note however that at large distances, the decay exhibits a cut-off where drops considerably. In order to take the cut-off into account, we elaborate further on the fit
as used, e.g., by Clauset et al. [28] in different contexts.
We fit Equation (5) to the approximately linear regime of vs. by means of least squares and Equation (6) by employing non-linear curve-fitting applying the Gauss-Newton-Algorithm (cf. [35]). While both approaches, Equations (5) and (6), lead to different exponents ξ and , these are both lower than 2, thereby indicating the presence of long-range correlations.
Regarding the relation between the correlation decay and the percolation threshold, it has been shown that long-range correlations can influence the percolation properties [36]. However, according to [37], the influence of correlations on the threshold value is only minor. For site percolation on a square lattice [37], the site occupation probability threshold has been shown to vary slightly between for the case of no long-range correlation effect ( in Equation (5)) and for the case of strong long-range correlations ( in Equation (5)). As mentioned in Section 4.2, spatial inhomogeneities can hinder unambiguous identification of the clustering threshold . Since long-range spatial correlations can entail spatial inhomogeneities, quantification the weak influence of correlations on the value of cannot be achieved in many cases.
5. Fundamental Urban Allometry—Relating Area and Population
An important aspect in the analysis of cities is their allometry properties, i.e., the relation between the city sizes (e.g., given by population) and their socio-economic “functions” [38] and structure. Of particular interest in this context is the fundamental allometry, i.e., the relation between city size and area [39]. Thus, we last address the relation between urban cluster population and area. For this purpose, we combine urban land cover data, as provided by GlobCover, with the pointwise population numbers of the 67, 935 administrative cities included in the GRUMP database. We match population and area of clusters by summing up for each cluster those population numbers that are located within the distance l to the considered cluster (similar to the procedure used by Rozenfeld et al. [15]).
Figure 8a depicts the obtained relation between area and population. Most clusters are spread around , except clusters with small population which exhibit discreteness (stemming from the land cover resolution) and deviate from the power-law. In order to overcome this difficulty, we remove a fraction q of clusters with low values for both S and A, as indicated by blue lines in Figure 8a. It is also necessary to consider that a direct fitting of vs. and vs. statistically leads to different results. Therefore, we assimilate δ to the slope of the longitudinal principal axis of rotation of the cloud of points in the vs. plot, as obtained from the eigenvector analysis of the corresponding tensor of “inertia”.
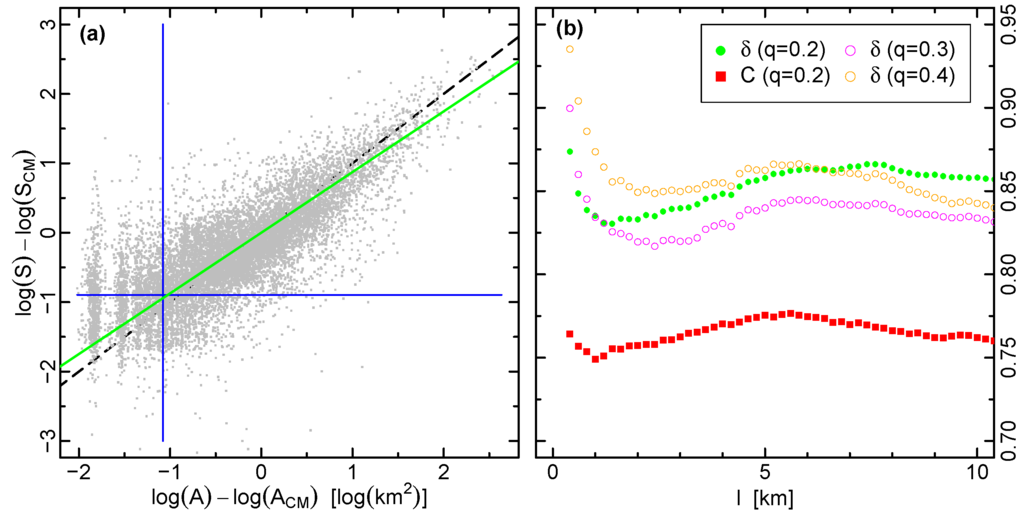
Figure 8.
Correlations between area and population. (a) vs. for l = 0.4 km and of all land cover clusters that could be matched with population figures (grey dots). The blue vertical and horizontal lines truncate the fraction q = 0.2 along both axis in order to avoid the discreteness at small A. The green solid line corresponds to the main axis around which the momentum of inertia of the truncated cloud is minimal. In this case, 8786 out of 12321 clusters remain. It’s slope δ is smaller than the diagonal (black dashed line, background); (b) Slope δ (circles) and Pearson correlation coefficients C (squares) vs. clustering parameter l for the cut-off q = 0.2 (green, red), q = 0.3 (magenta), q = 0.4 (orange). The exponent δ is found roughly between 0.82 and 0.87 except for small l where δ up to 0.87 and 0.93 are achieved but always below 1. For q = 0.2 the correlations exhibit a maximum around 5 km.
In order to address the dependency of the correlations between area and population on the observational scale, i.e., on the clustering parameter l, in Figure 8b we plot for the Pearson correlation values as a function of l and consistently find values above 0.85 with a maximum of approx. 0.88 at approx. 5 km. Figure 8b also shows the values of δ. For very small l, highest values are found between for and for . For other values of l, the slope fluctuates but generally δ is roughly within 0.82 and 0.87. As it turns out, the results show a sublinear population to area relation, i.e., . That is, doubling the area typically comes along with an increase of the population by factor smaller than two.
While the values collected by Batty [39] suggest an evolution of δ, i.e., that estimations of δ are decreasing since the 1940s (see also [40]), our results indicate a dependence of δ on l, i.e. that the value depends on the observational scale, but generally in the lower range of those listed by Batty [39]. This is a relevant aspect, since, as mentioned before, allometry could be responsible for the scaling of socio-economic quantities with the population of cities. A systematic assessment of the scaling between cluster area and cluster population has first been performed by means of night-time satellite imagery [41]. On the global scale the authors find linearity, i.e., , in contrast to our results.
6. Summary and Discussion
In this paper we have elaborated on the influence exerted by the degree of coarsening resolution that is inherent to the definition of city boundaries, on a set of indicators of the scaling, spatial organization, and allometry aspects of urban clusters. For this purpose we implemented a version of the City Clustering Algorithm that takes the curvature of the globe into account and apply it to global satellite based information on the global urban land cover, in combination with pointwise information of populated units worldwide.
Our results show that, at the global scale, Zipf’s law is found to approximately hold to a great extent for the areas of urban clusters and to a lesser extent for the corresponding population. A shortcoming are inaccuracies stemming from automatized identification of urban areas from satellite imagines as inherent in the land cover data used in this study [42]. As a matter of fact, the climatological, vegetational and structural variety of urban clusters on the globe can hinder their classification, e.g., in GlobCover2009 Kabul city, with an area of around 275 km2 and a population of around 3.7 million, is classified as bare area.
At the country scale, we addressed the percolation transition that may occur, at the level of the urban cluster definition, when coarsening the resolution considered to identify urban clusters. This information is relevant as a proxy indicator for detecting the proximity to the percolation transition occurring eventually on the real land cover of large urbanized areas—which in turn could exert influence on important factors of the sustainability, such as Urban Heat Island effect (see, e.g., [43]), landscape fragmentation, water surface run-off and floods control, among others. As a matter, identifying an urban clustering percolation threshold can become a cumbersome task, due to spatial inhomogeneities in the distribution of urban clusters at the large country scale.
The concept of percolation may also shed light on phenomena like primate cities [44,45], dragon-kings [45,46], and largest city allometry [40,47]. Primate Cities are considerably bigger than the second largest one in the considered country. Similarly, a Dragon-King city is understood as largest unit and deviating from Zipf’s law, i.e., a significant outlier. Interestingly, for , i.e., l slightly larger than , the largest cluster dominates in size and certainly deviates from the remaining power-law distribution.
In this work we used as an indicator the behavior of the average cluster size, excluding the largest one, which itself provides a suitable characterization of urban clusters, for different levels of coarsening-resolution. This analysis was applied to selected country cases, for which we addressed the linkage between the scaling of urban cluster sizes and the degree of resolution used for their definition. Our results appear to be at a certain degree consistent with recent results obtained numerically in a simple gravity-based urban growth model. Beyond the scaling and average size, characterization of urban clusters requires addressing the scaling of deviations of cluster sizes around the average. In particular, for the selected country cases, we illustrate the validity of Taylor’s law between average urban cluster sizes and their standard deviations. Moreover, we show that strong deviations from Taylor’s law can be readily used to identify threshold values in proxy indicators of the percolation transition of urban clustering, in cases where the average cluster size fails.
Regarding the spatial organization of urban clusters in selected country cases, we find the presence of long-range correlations decaying as a power-law with exponential cut-off. However, for densely urbanized areas we find that a power-law decay is further significative, as compared to the fitting of a power-law with exponential cut-off.
Finally, our results on the relation of area to population indicate that for a given increase in population, the associated increase in area is greater for large cities than for small ones. A shortcoming in our analysis of city allometry is the minor time period discrepancy between the population and land cover databases—that actually represent the most updated and accurate publicly available global databases.
The work in hand is limited by a few issues which also open a perspective for future research. Most importantly, the data quality in arid regions hinders a percolation understanding of the urban fabric in those countries. Thus, it would be important to repeat the percolation study with new and better land cover products. Moreover, it needs to be noted that not in all countries unique percolation thresholds could be identified. Whether or not this is related to the data quality needs to remain an open question at this moment.
Acknowledgments
Diego Rybski acknowledges Elsa Arcaute and A. Paolo Masucci for useful discussions. The research leading to these results has received funding from the European Community’s Seventh Framework Programme under Grant Agreement No. 308497 (Project RAMSES). This work has been funded by the Federal Ministry of Education and Research (BMBF) through the program “Spitzenforschung und Innovation in den Neuen Länden” (contract “Potsdam Research Cluster for Georisk Analysis, Environmental Change and Sustainability” D.1.1). The publication of this article was funded by the Open Access Fund of the Leibniz Association.
Author Contributions
Till Fluschnik, Anselmo García Cantú Ros, Jürgen P. Kropp, and Diego Rybski conceived and designed the experiments; Till Fluschnik and Steffen Kriewald performed the experiments; Till Fluschnik and Steffen Kriewald analyzed the data; Steffen Kriewald, Bin Zhou, and Dominik E. Reusser contributed reagents/materials/analysis tools; Anselmo García Cantú Ros and Diego Rybski wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Auerbach, F. Das gesetz der bevölkerungskonzentration. Petermanns Geogr. Mitt. 1913, 59, 73–76. [Google Scholar]
- Rybski, D. Auerbach’s legacy. Environ. Plan. A 2013, 45, 1266–1268. [Google Scholar] [CrossRef]
- Zipf, G.K. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology (Reprint of 1949 Edition); Martino Publishing: Mansfield, CT, USA, 2012. [Google Scholar]
- Gibrat, R. Les Inégalités Économiques; Libraire du Recueil Sierey: Paris, France, 1931. [Google Scholar]
- Simon, H.A. On a class of skew distribution functions. Biometrika 1955, 42, 425–440. [Google Scholar] [CrossRef]
- Makse, H.A.; Andrade, J.S.; Batty, M.; Havlin, S.; Stanley, H.E. Modeling urban growth patterns with correlated percolation. Phys. Rev. E 1998, 58, 7054–7062. [Google Scholar] [CrossRef]
- Gabaix, X. Zipf’s law for cities: An explanation. Q. J. Econ. 1999, 114, 739–767. [Google Scholar] [CrossRef]
- Rybski, D.; Ros, A.G.C.; Kropp, J.P. Distance weighted city growth. Phys. Rev. E 2013, 87, 042114. [Google Scholar] [CrossRef] [PubMed]
- Eeckhout, J. Gibrat’s law for (All) cities. Am. Econ. Rev. 2004, 94, 1429–1451. [Google Scholar] [CrossRef]
- Kriewald, S.; Fluschnik, T.; Reusser, D.; Rybski, D. OSC: Orthodromic Spatial Clustering, R package version 1.0.0. Available online: https://CRAN.R-project.org/package=osc (accessed on 7 April 2011).
- Rozenfeld, H.D.; Rybski, D.; Andrade, J.S., Jr.; Batty, M.; Stanley, H.E.; Makse, H.A. Laws of population growth. Proc. Nat. Acad. Sci. USA 2008, 105, 18702–18707. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, D.; Aharony, A. Introduction To Percolation Theory; Taylor & Francis: London, UK, 1994. [Google Scholar]
- ESA (European Space Agency). The Ionia GlobCover Project. GlobCover Land Cover 2009 v2.3. Available online: http://ionia1.esrin.esa.int (accessed on 21 August 2011).
- Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IFPRI), The World Bank; Centro Internacional de Agricultura Tropical (CIAT). Global Rural-Urban Mapping Project, Version 1 (GRUMPv1): Settlement Points. Website. 2011. Available online: http://sedac.ciesin.columbia.edu/data/dataset/grump-v1-settlement-points (accessed on 26 November 2011).
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The area and population of cities: New insights from a different perspective on cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Zanette, D.H.; Manrubia, S.C. Role of intermittency in urban development: A model of large-scale city formation. Phys. Rev. Lett. 1997, 79, 523–526. [Google Scholar] [CrossRef]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, F.; Steinbrink, J. Estimation of megacity growth—Simple rules versus complex phenomena. Appl. Geogr. 1998, 18, 69–81. [Google Scholar] [CrossRef]
- Kinoshita, T.; Kato, E.; Iwao, K.; Yamagata, Y. Investigating the rank-size relationship of urban areas using land cover maps. Geophys. Res. Lett. 2008, 35, L17405. [Google Scholar] [CrossRef]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2014, 12, 20140745. [Google Scholar] [CrossRef] [PubMed]
- Small, C.; Elvidge, C.D.; Balk, D.; Montgomery, M. Spatial scaling of stable night lights. Remote Sens. Environ. 2011, 115, 269–280. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. (Eds.) Fractals and Disordered Systems; Springer-Verlag: New York, NY, USA, 1991.
- Berry, B.J.L.; Okulicz-Kozaryn, A. The city size distribution debate: Resolution for US urban regions and megalopolitan areas. Cities 2012, 29, S17–S23. [Google Scholar] [CrossRef]
- Makse, H.A.; Havlin, S.; Stanley, H.E. Modeling urban-growth patterns. Nature 1995, 377, 608–612. [Google Scholar] [CrossRef]
- Bitner, A.; Holyst, R.; Fialkowski, M. From complex structures to complex processes: Percolation theory applied to the formation of a city. Phys. Rev. E 2009, 80, 037102. [Google Scholar] [CrossRef] [PubMed]
- Murcio, R.; Sosa-Herrera, A.; Rodriguez-Romo, S. Second-order metropolitan urban phase transitions. Chaos Soliton Fract. 2013, 48, 22–31. [Google Scholar] [CrossRef]
- Arcaute, E.; Molinero, C.; Hatna, E.; Murcio, R.; Vargas-Ruiz, C.; Masucci, P.; Batty, M. Regions and Cities in Britain through Hierarchical Percolation. Available online: http://arxiv.org/abs/1504.08318v2 (accessed on 10 July 2016).
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Vuong, Q.H. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Stanley, H.E. Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 1999, 71, S358–S366. [Google Scholar] [CrossRef]
- Taylor, L.R. Aggregation, variance and mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Smith, H.F. An empirical law describing heterogeneity in the yields of agricultural crops, Part: 1. J. Agric. Sci. 1938, 28, 1–23. [Google Scholar] [CrossRef]
- de Menezes, M.A.; Barabasi, A.L. Fluctuations in network dynamics. Phys. Rev. Lett. 2004, 92, 028701. [Google Scholar] [CrossRef] [PubMed]
- Eisler, Z.; Bartos, I.; Kertész, J. Fluctuation scaling in complex systems: Taylor’s law and beyond. Adv. Phys. 2008, 57, 89–142. [Google Scholar] [CrossRef]
- Bates, D.M.; DebRoy, S. R-Documentation: Nonlinear Least Squares. Available online: http://stat.ethz.ch/R-manual/R-patched/library/stats/html/nls.html (accessed on 7 April 2011).
- Weinrib, A. Long-range correlated percolation. Phys. Rev. B 1984, 29, 387–395. [Google Scholar] [CrossRef]
- Prakash, S.; Havlin, S.; Schwartz, M.; Stanley, H.E. Structural and dynamic properties of long-range correlated percolation. Phys. Rev. A 1992, 46, R1724–R1727. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Batty, M. Defining city size. Environ. Plan. B-Plan. Des. 2011, 38, 753–756. [Google Scholar] [CrossRef]
- Rybski, D.; Reusser, D.E.; Winz, A.L.; Fichtner, C.; Sterzel, T.; Kropp, J.P. Cities as nuclei of sustainability? Environ. Plan. B 2016. [Google Scholar] [CrossRef]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from Heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens. 2001, 22, 3061–3076. [Google Scholar] [CrossRef]
- Potere, D.; Schneider, A.; Angel, S.; Civco, D.L. Mapping urban areas on a global scale: which of the eight maps now available is more accurate? Int. J. Remote Sens. 2009, 30, 6531–6558. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. On the statistics of urban heat island intensity. Geophys. Res. Lett. 2013, 40, 5486–5491. [Google Scholar] [CrossRef]
- Jefferson, M. The law of the primate city. Geogr. Rev. 1939, 29, 226–232. [Google Scholar] [CrossRef]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2014, 12, 20140745. [Google Scholar] [CrossRef] [PubMed]
- Pisarenko, V.F.; Sornette, D. Robust statistical tests of Dragon-Kings beyond power law distributions. Eur. Phys. J. Spec. Top. 2012, 205, 95–115. [Google Scholar] [CrossRef]
- Pumain, D.; Moriconi-Ebrard, F. City size distributions and metropolisation. GeoJournal 1997, 43, 307–314. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).