Retrieval of Remote Sensing Images with Pattern Spectra Descriptors
Abstract
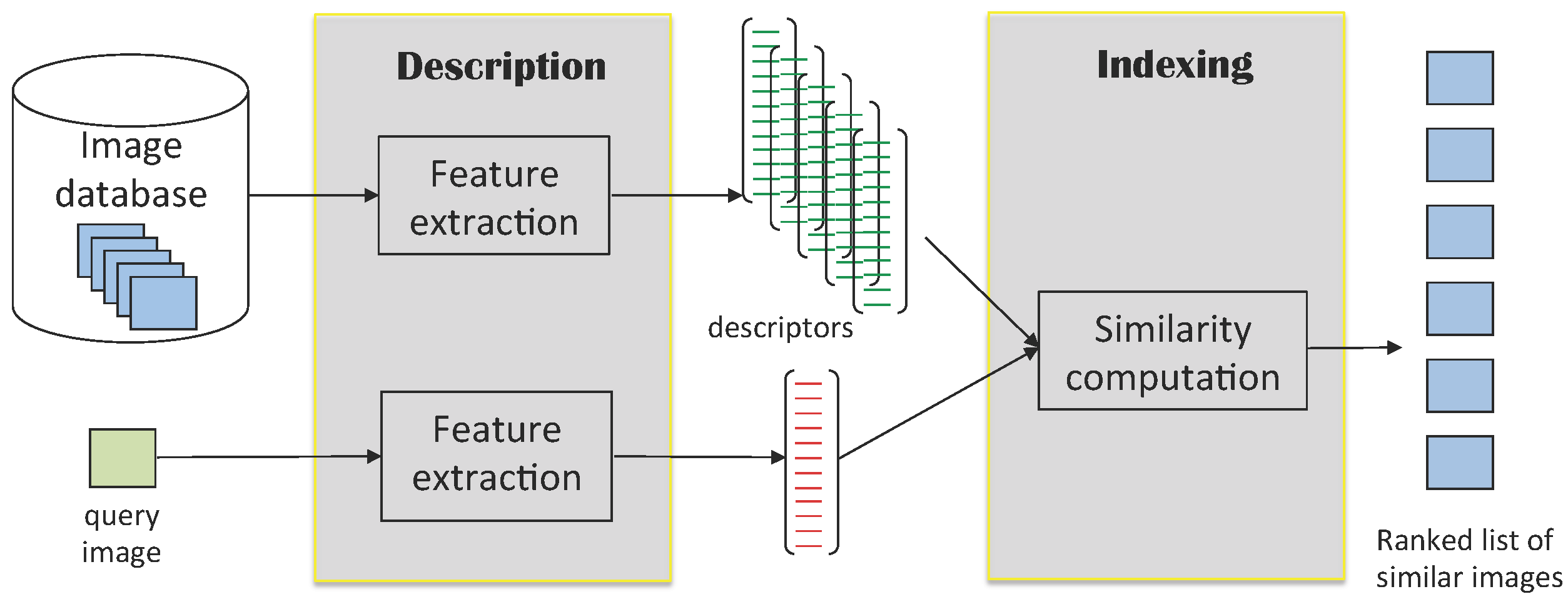
:1. Introduction
2. Previous Work
2.1. Related Work
2.2. Our Contributions
3. Pattern Spectra
3.1. Min- and Max-Trees
3.2. Filtering and Granulometries
3.3. Global Pattern Spectra
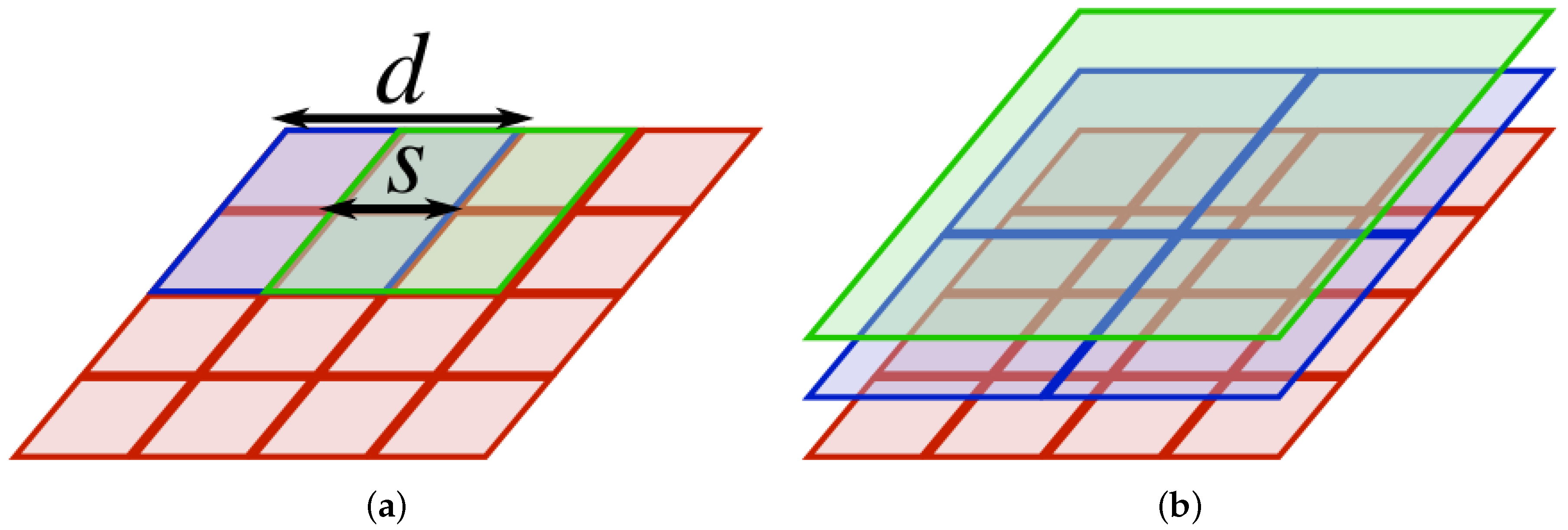
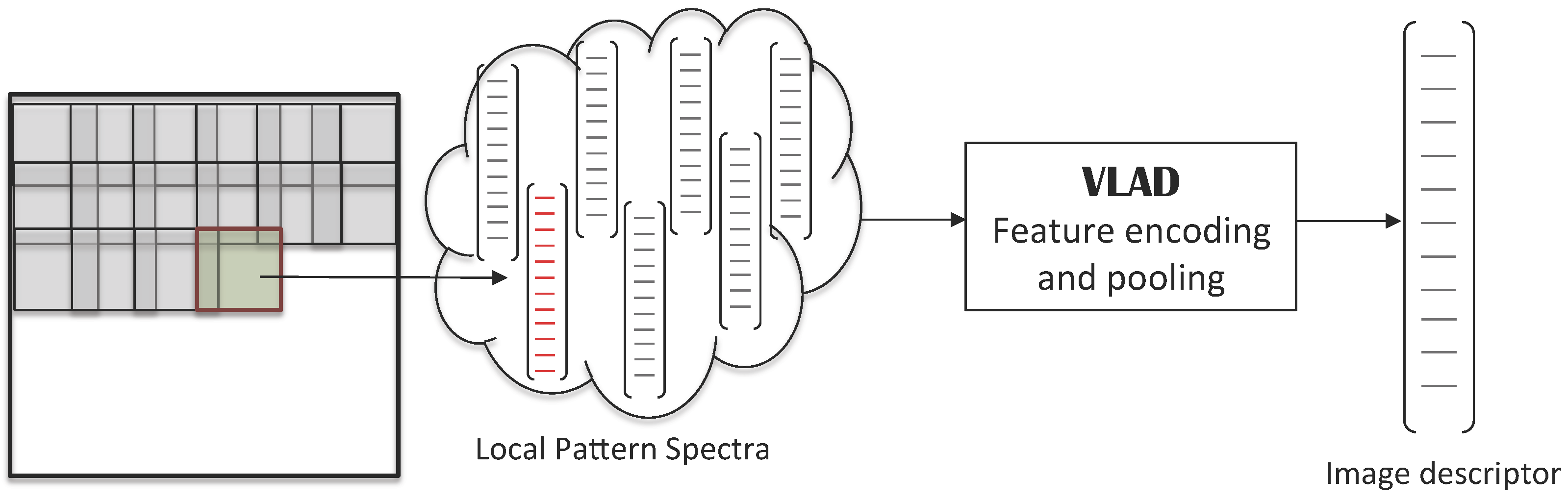
3.4. Local Pattern Spectra
4. Experimental Set-Up
4.1. Dataset and Evaluation Metrics
4.2. Settings of Pattern Spectra Approaches
4.2.1. Global Pattern Spectra
4.2.2. Local Pattern Spectra
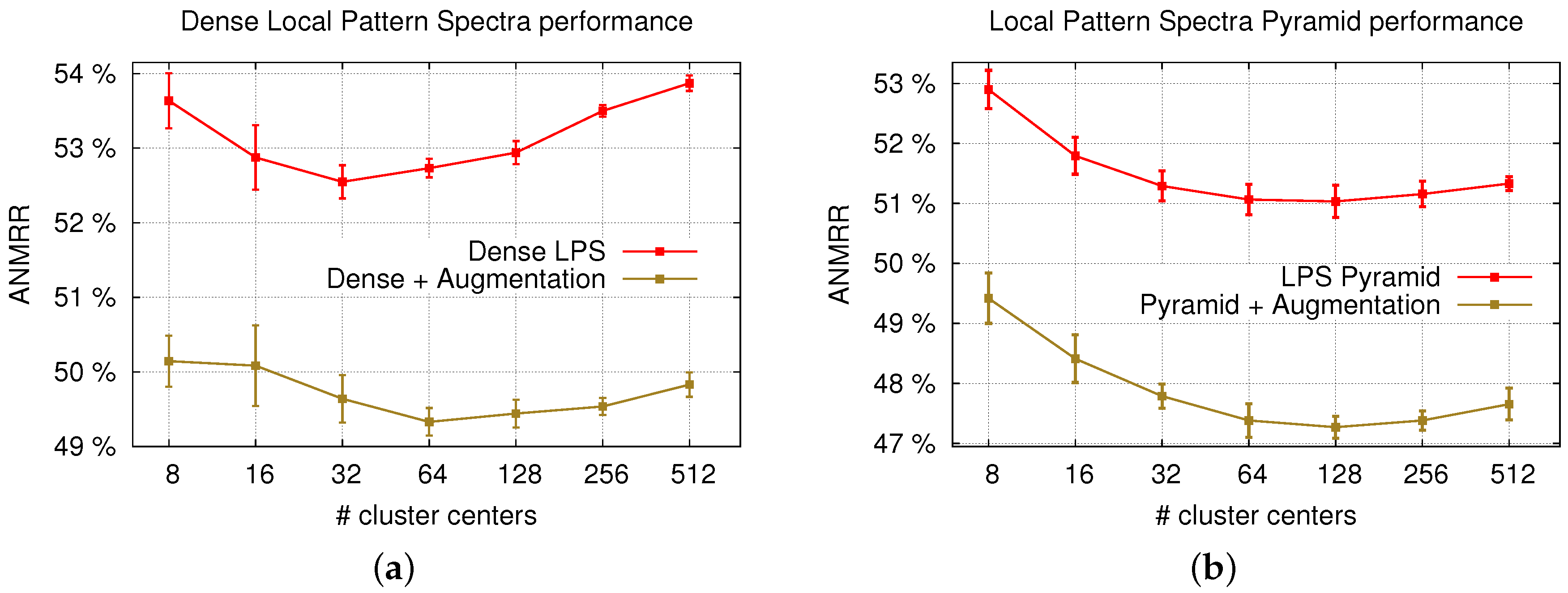
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. A fast local descriptor for dense matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Alahi, A.; Ortiz, R.; Vandergheynst, P. Freak: Fast retina keypoint. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 510–517.
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Datta, R.; Joshi, D.; Li, J.; Wang, J.Z. Image retrieval: Ideas, influences, and trends of the new age. ACM Comput. Surv. 2008, 40. [Google Scholar] [CrossRef]
- Tushabe, F.; Wilkinson, M.H.F. Content-based image retrieval using combined 2D attribute pattern spectra. In Advances in Multilingual and Multimodal Information Retrieval; Springer: Budapest, Hungary, 2008; pp. 554–561. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. An affine invariant interest point detector. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 128–142.
- Ozkan, S.; Ates, T.; Tola, E.; Soysal, M.; Esen, E. Performance analysis of state-of-the-art representation methods for geographical image retrieval and categorization. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1996–2000. [Google Scholar] [CrossRef]
- Iscen, A.; Tolias, G.; Gosselin, P.H.; Jégou, H. A comparison of dense region detectors for image search and fine-grained classification. IEEE Trans. Image Process. 2015, 24, 2369–2381. [Google Scholar] [CrossRef] [PubMed]
- Jégou, H.; Douze, M.; Schmid, C.; Pérez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3304–3311.
- Sivic, J.; Zisserman, A. Video Google: Efficient visual search of videos. In Toward Category-Level Object Recognition; Ponce, J., Hebert, M., Schmid, C., Zisserman, A., Eds.; Springer: Budapest, Hungary, 2006; pp. 127–144. [Google Scholar]
- Wang, M.; Wan, Q.M.; Gu, L.B.; Song, T.Y. Remote-sensing image retrieval by combining image visual and semantic features. Int. J. Remote Sens. 2013, 34, 4200–4223. [Google Scholar] [CrossRef]
- Espinoza-Molina, D.; Datcu, M. Earth-Observation image retrieval based on content, semantics, and metadata. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5145–5159. [Google Scholar] [CrossRef]
- Bahmanyar, R.; Cui, S.; Datcu, M. A comparative study of bag-of-words and bag-of-topics models of EO image patches. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1357–1361. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Benediktsson, J.; Waske, B.; Bruzzone, L. Morphological attribute profiles for the analysis of very high resolution images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. A survey on spectral-spatial classification techniques based on attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Aptoula, E. Hyperspectral image classification with multi-dimensional attribute profiles. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2031–2035. [Google Scholar] [CrossRef]
- Aptoula, E.; Dalla Mura, M.; Lefèvre, S. Vector attribute profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3208–3220. [Google Scholar] [CrossRef]
- Aptoula, E. Remote sensing image retrieval with global morphological texture descriptors. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3023–3034. [Google Scholar] [CrossRef]
- Aptoula, E. Bag of morphological words for content-based geographical retrieval. In Proceedings of the International Workshop on Content-Based Multimedia Indexing, Klagenfurt, Austria, 18–20 June 2014.
- Maragos, P. Pattern spectrum and multiscale shape representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 701–716. [Google Scholar] [CrossRef]
- Bosilj, P.; Wilkinson, M.H.F.; Kijak, E.; Lefèvre, S. Local 2D pattern spectra as connected region descriptors. In Proceedings of the International Symposium on Mathematical Morphology, Reykjavik, Iceland, 27–29 May 2015; pp. 182–193.
- Bosilj, P.; Kijak, E.; Wilkinson, M.H.F.; Lefèvre, S. Short local descriptors from 2D connected pattern spectra. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015.
- Bosilj, P.; Wilkinson, M.H.F.; Kijak, E.; Lefèvre, S. Local 2D pattern spectra as connected region descriptors. Math. Morphol. Theory Appl. 2016, 1, 203–215. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Lu, G.; Ma, W.Y. A survey of content-based image retrieval with high-level semantics. Pattern Recognit. 2007, 40, 262–282. [Google Scholar] [CrossRef]
- Bretschneider, T.; Cavet, R.; Kao, O. Retrieval of remotely sensed imagery using spectral information content. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 2253–2255.
- Scott, G.; Klaric, M.; Davis, C.; Shyu, C. Entropy-balanced bitmap tree for shape-based object retrieval from large-scale satellite imagery databases. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1603–1616. [Google Scholar] [CrossRef]
- Yao, H.; Li, B.; Cao, W. Remote sensing imagery retrieval based-on Gabor texture feature classification. In Proceedings of the International Conference on Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 733–736.
- Tobin, K.W.; Bhaduri, B.L.; Bright, E.A.; Cheriyadat, A.; Karnowski, T.P.; Palathingal, P.J.; Potok, T.E.; Price, J.R. Large-scale geospatial indexing for image-based retrieval and analysis. In Proceedings of the International Symposium on Visual Computing, Lake Tahoe, NV, USA, 5–7 December 2005; pp. 543–552.
- Xu, S.; Fang, T.; Li, D.; Wang, S. Object classification of aerial images with bag-of-visual words. IEEE Geosci. Remote Sens. Lett. 2010, 7, 366–370. [Google Scholar]
- Chen, L.; Yang, W.; Xu, K.; Xu, T. Evaluation of local features for scene classification using VHR satellite images. In Proceedings of the Joint Urban Remote Sensing Event, Munich, Germany, 10–13 April 2011; pp. 385–388.
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Ozdemir, B.; Aksoy, S. Image classification using subgraph histogram representation. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1112–1115.
- Negrel, R.; Picard, D.; Gosselin, P.H. Evaluation of second-order visual features for land-use classification. In Proceedings of the International Workshop on Content-Based Multimedia Indexing, Klagenfurt, Austria, 18–20 June 2014.
- Zhao, L.J.; Tang, P.; Huo, L.Z. Land-use scene classification using a concentric circle-structured multiscale bag-of-visual-words model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4620–4631. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Saliency-guided unsupervised feature learning for scene classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2175–2184. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhu, Q.; Zhang, L. Scene classification based on the multifeature fusion probabilistic topic model for high spatial resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6207–6222. [Google Scholar] [CrossRef]
- Gueguen, L. Classifying compound structures in satellite images: A compressed representation for fast queries. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1803–1818. [Google Scholar] [CrossRef]
- Fan, J.; Tan, H.L.; Lu, S. Multipath sparse coding for scene classification in very high resolution satellite imagery. SPIE Remote Sens. 2015, 9643, 96430S. [Google Scholar]
- Song, Q.; Huang, R.; Wang, K. Remote sensing image retrieval based on attribute profiles. In Proceedings of the International Conference on Computer Science and Mechanical Automation, Hangzhou, China, 23–25 October 2015; pp. 231–234.
- Zhou, W.; Shao, Z.; Diao, C.; Cheng, Q. High-resolution remote-sensing imagery retrieval using sparse features by auto-encoder. Remote Sens. Lett. 2015, 6, 775–783. [Google Scholar] [CrossRef]
- Napoletano, P. Visual descriptors for content-based retrieval of remote sensing images. arXiv, 2016; arXiv:1602.00970. [Google Scholar]
- Wang, Y.; Zhang, L.; Tong, X.; Zhang, L.; Zhang, Z.; Liu, H.; Xing, X.; Mathiopoulos, P.T. A three-layered graph-based learning approach for remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6020–6034. [Google Scholar] [CrossRef]
- Demir, B.; Bruzzone, L. A novel active learning method in relevance feedback for content based remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2323–2334. [Google Scholar] [CrossRef]
- Urbach, E.R.; Roerdink, J.B.T.M.; Wilkinson, M.H.F. Connected shape-size pattern spectra for rotation and scale-invariant classification of gray-scale images. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Breen, E.J.; Jones, R. Attribute openings, thinnings, and granulometries. Comput. Vis. Image Underst. 1996, 64, 377–389. [Google Scholar] [CrossRef]
- Urbach, E.R.; Wilkinson, M.H.F. Shape-only granulometries and grey-scale shape filters. In Proceedings of the International Symposium on Mathematical Morphology, Sydney, Australia, 3–5 April 2002; pp. 305–314.
- Salembier, P.; Oliveras, A.; Garrido, L. Antiextensive connected operators for image and sequence processing. IEEE Trans. Image Process. 1998, 7, 555–570. [Google Scholar] [CrossRef] [PubMed]
- Jones, R. Component trees for image filtering and segmentation. In Proceedings of the IEEE Workshop on Nonlinear Signal and Image Processing, Mackinac Island, MI, USA, 8–10 September 1997.
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Westenberg, M.A.; Roerdink, J.B.T.M.; Wilkinson, M.H.F. Volumetric attribute filtering and interactive visualization using the Max-Tree representation. IEEE Trans. Image Process. 2007, 16, 2943–2952. [Google Scholar] [CrossRef] [PubMed]
- Lantuéjoul, C.; Maisonneuve, F. Geodesic methods in quantitative image analysis. Pattern Recognit. 1984, 17, 177–187. [Google Scholar] [CrossRef]
- Morard, V.; Decenciere, E.; Dokládal, P. Efficient geodesic attribute thinnings based on the barycentric diameter. J. Math. Imaging Vis. 2013, 46, 128–142. [Google Scholar] [CrossRef]
- Salembier, P.; Wilkinson, M.H.F. Connected operators. IEEE Signal Process. Mag. 2009, 26, 136–157. [Google Scholar] [CrossRef]
- Soille, P. On genuine connectivity relations based on logical predicates. In Proceedings of the International Conference on Image Analysis and Processing, Modena, Italy, 10–14 September 2007; pp. 487–492.
- Lefèvre, S. Beyond morphological size distribution. J. Electron. Imaging 2009, 18, 013010. [Google Scholar] [CrossRef]
- Manjunath, B.S.; Ohm, J.R.; Vasudevan, V.V.; Yamada, A. Color and texture descriptors. IEEE Trans. Circuits Syst. Video Technol. 2001, 11, 703–715. [Google Scholar] [CrossRef]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 1–42. [Google Scholar] [CrossRef]



| Approach | ANMRR | mAP |
|---|---|---|
| SIFT (on keypoints, [34]) | 0.601 | |
| dense SIFT [9] | 0.4604 | |
| (using VLAD, ) | ||
| global texture descriptors ([21]) | 0.575 | |
| local texture descriptors [22] | 0.585 | |
| (Bag of Words, ) | ||
| GPS—Area + | 0.579 | 0.304 |
| GPS—Area + | 0.670 | 0.221 |
| GPS—both shape attributes ( + ) | 0.557 | 0.325 |
| dense LPS | 0.525 | 0.380 |
| (using VLAD, ) | ||
| dense LPS-augmentation | 0.494 | 0.411 |
| (using VLAD, ) | ||
| pyramid LPS | 0.510 | 0.396 |
| (using VLAD, ) | ||
| pyramid LPS-augmentation | 0.472 | 0.437 |
| (using VLAD, ) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosilj, P.; Aptoula, E.; Lefèvre, S.; Kijak, E. Retrieval of Remote Sensing Images with Pattern Spectra Descriptors. ISPRS Int. J. Geo-Inf. 2016, 5, 228. https://doi.org/10.3390/ijgi5120228
Bosilj P, Aptoula E, Lefèvre S, Kijak E. Retrieval of Remote Sensing Images with Pattern Spectra Descriptors. ISPRS International Journal of Geo-Information. 2016; 5(12):228. https://doi.org/10.3390/ijgi5120228
Chicago/Turabian StyleBosilj, Petra, Erchan Aptoula, Sébastien Lefèvre, and Ewa Kijak. 2016. "Retrieval of Remote Sensing Images with Pattern Spectra Descriptors" ISPRS International Journal of Geo-Information 5, no. 12: 228. https://doi.org/10.3390/ijgi5120228
APA StyleBosilj, P., Aptoula, E., Lefèvre, S., & Kijak, E. (2016). Retrieval of Remote Sensing Images with Pattern Spectra Descriptors. ISPRS International Journal of Geo-Information, 5(12), 228. https://doi.org/10.3390/ijgi5120228







