GPS-Aided Video Tracking
Abstract
:1. Introduction
2. Data Acquisition and Processing Methods
2.1. The Approach

2.2. Input Data from Sensors
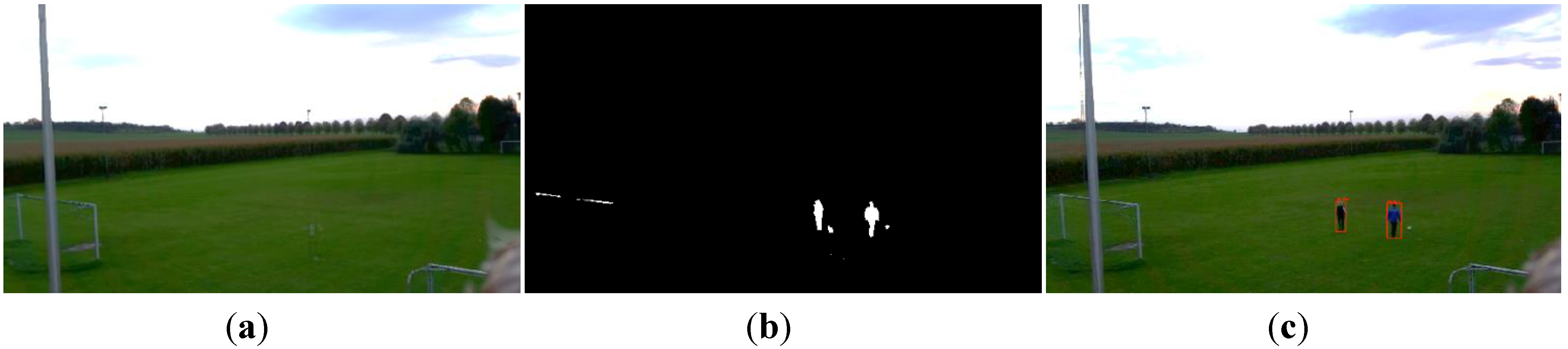
2.3. Preprocessing the Data
2.4. Data Fusion
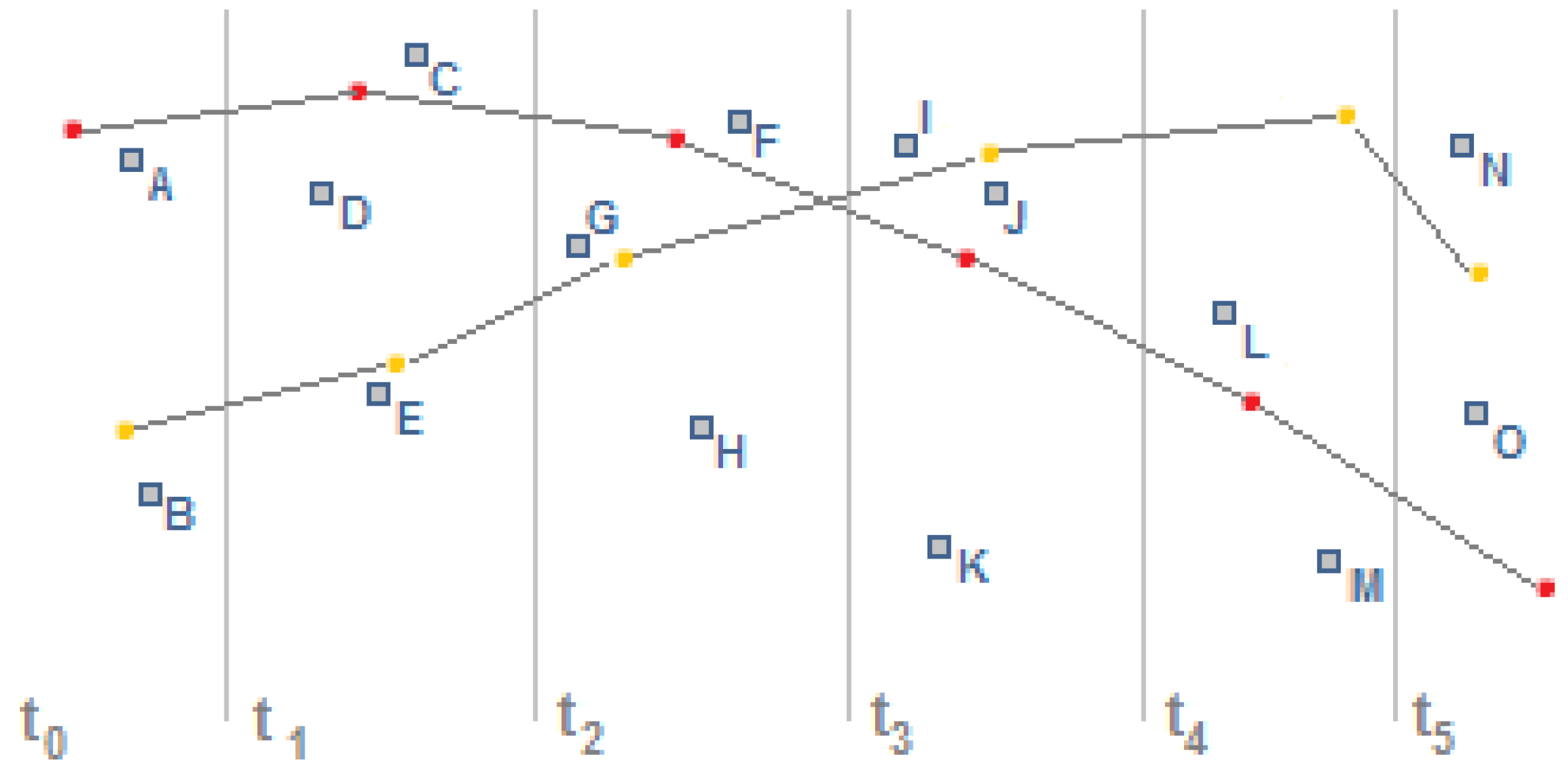
2.4.1. Hidden Markov Models
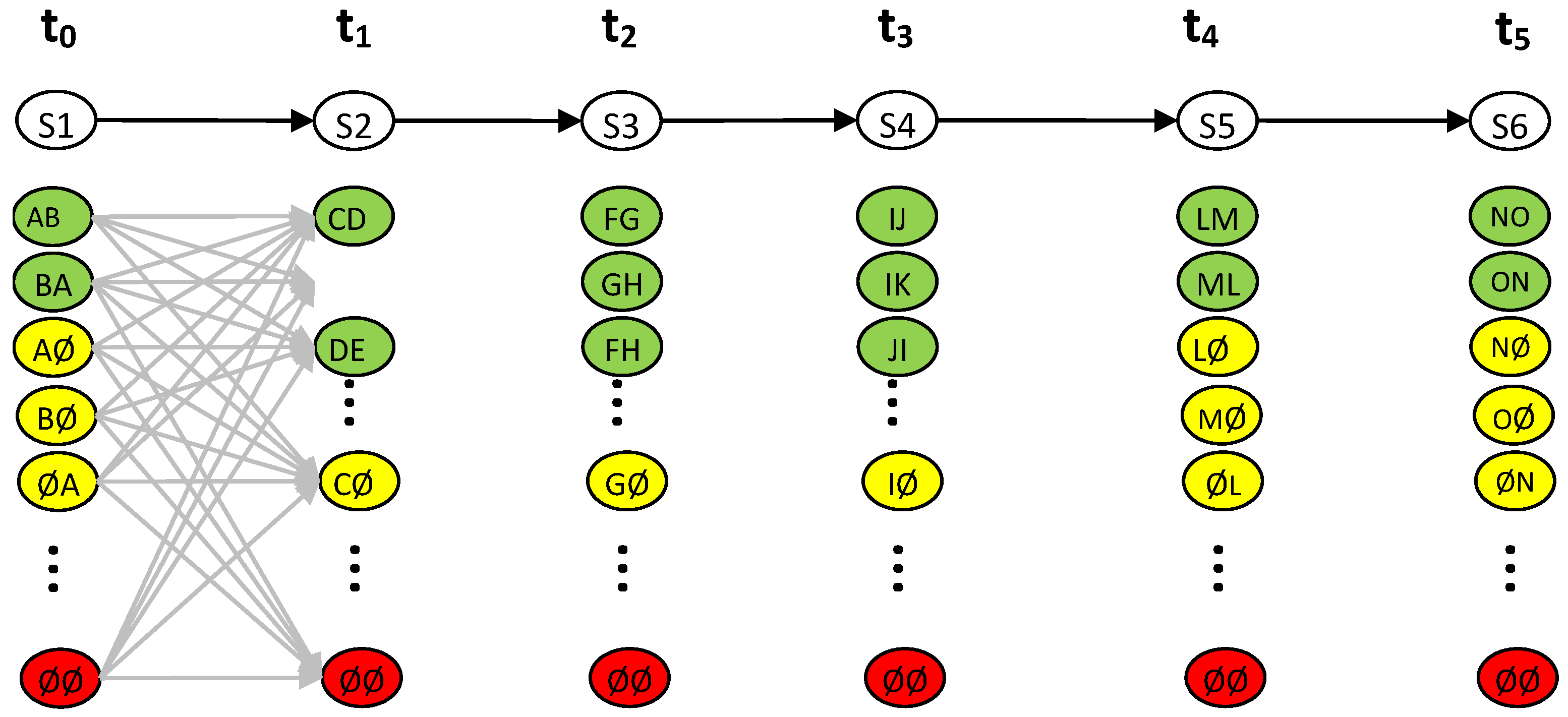
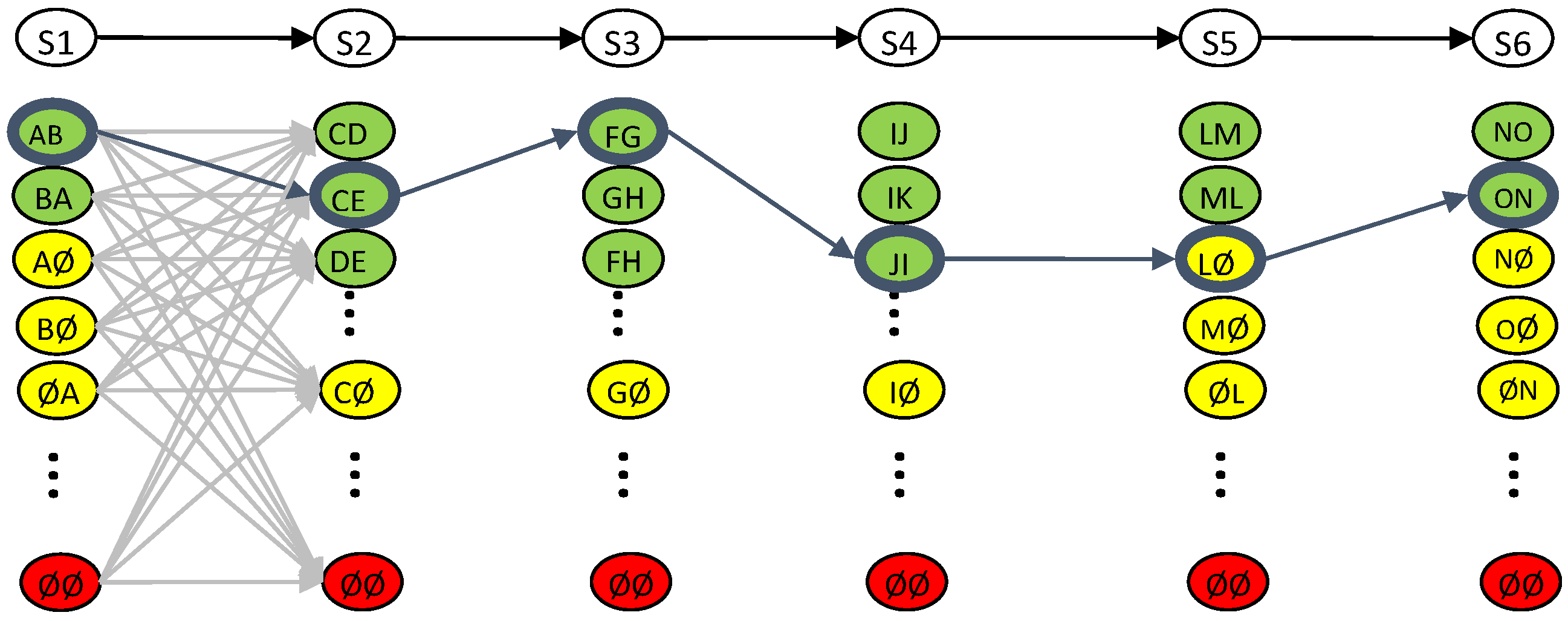
2.4.2. The Viterbi Algorithm
2.5. Output Trajectories
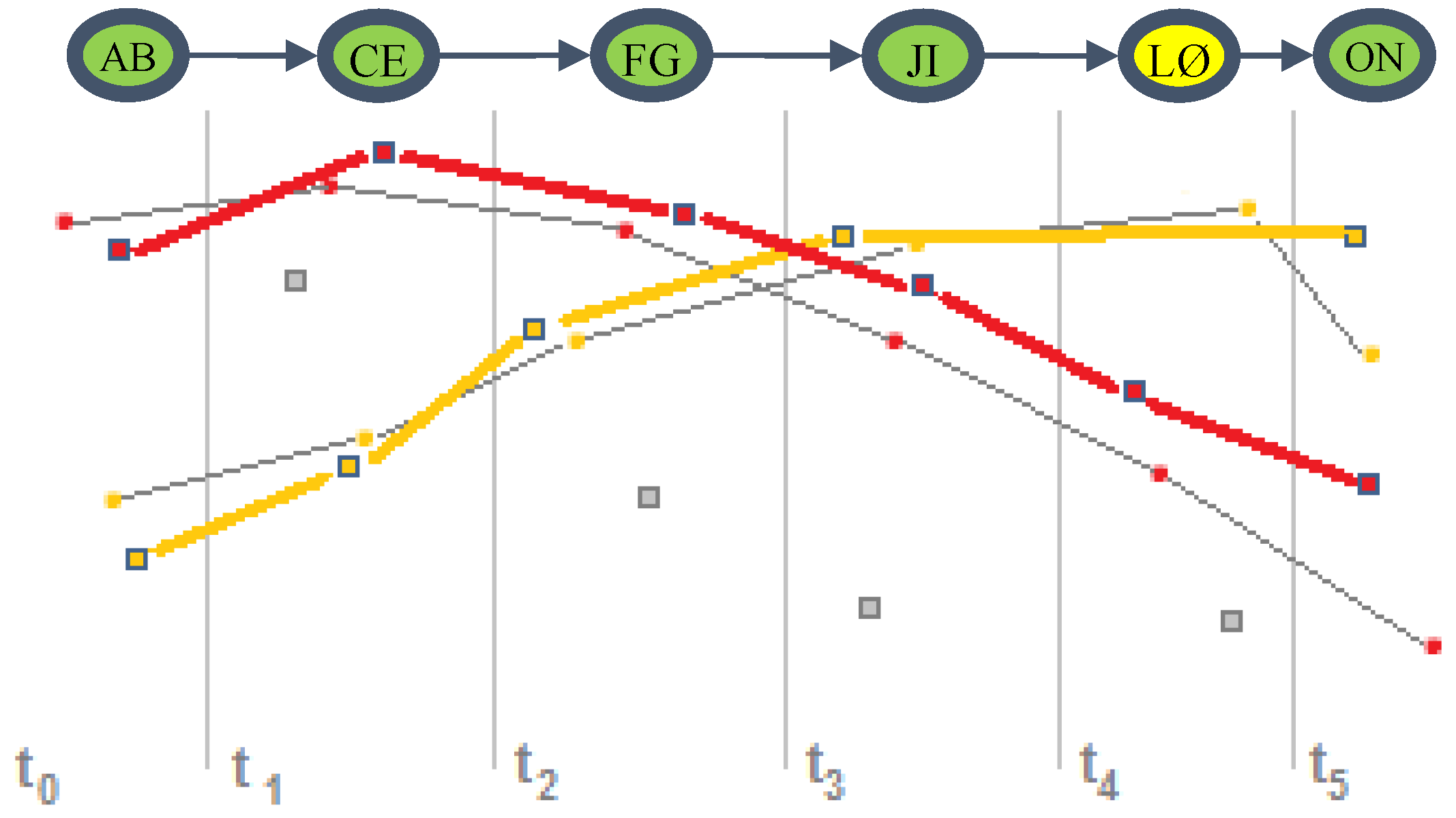
2.6. Performance of the Algorithm
3. Experimental Section
3.1. Experiments
3.2. Experimental Setup
3.2.1. Experiment 1—Accuracy
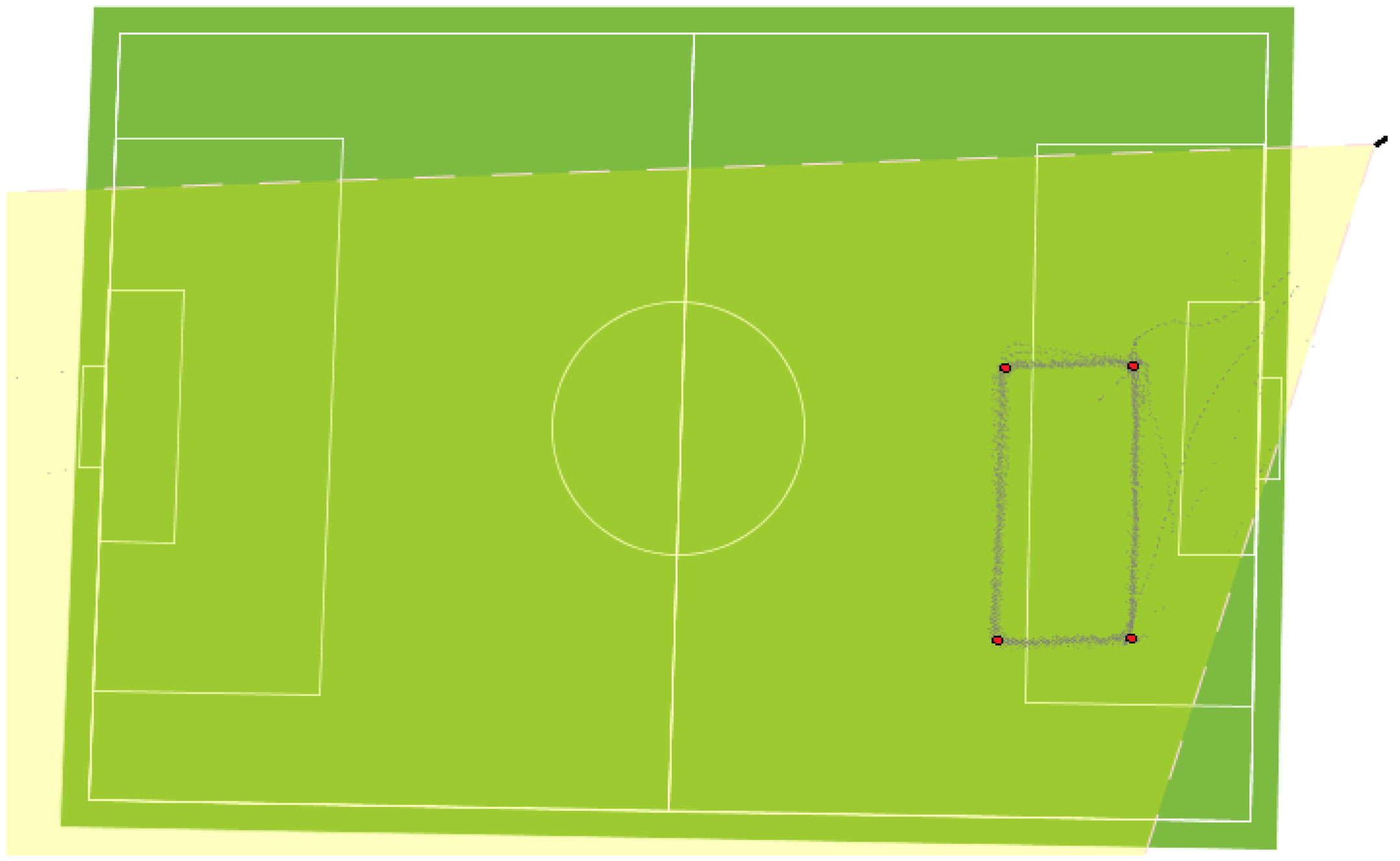
3.2.2. Experiment 2—Completeness and Correctness
3.2.3. Experiment 3—Multiple Object Tracking
4. Results
4.1. Experiment 1—Accuracy
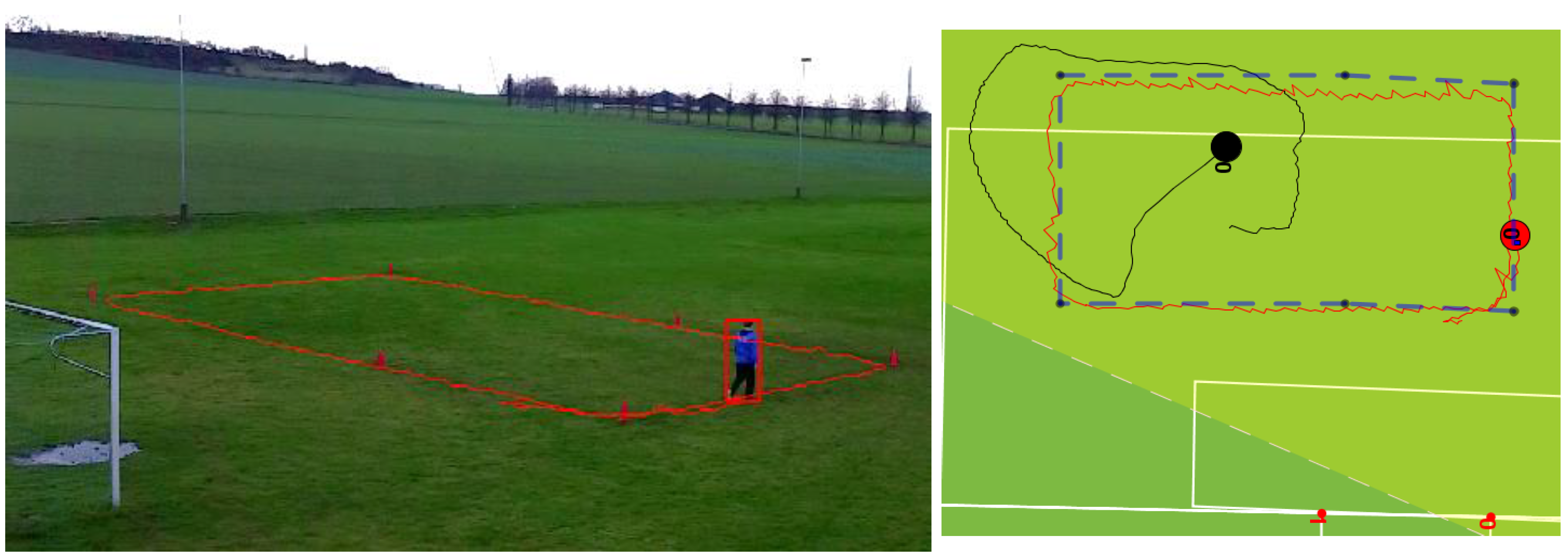
4.2. Experiment 2—Correctness of Assignments
| With GPS | Without GPS | |
|---|---|---|
| Total (objects/unassignable) | 2238 (2030/208) | 2238 (2030/208) |
| Recall (%) | 2109 (94.2%) | 2013 (89.9%) |
| Misses (%) | 129 (5.8%) | 225 (10.1%) |
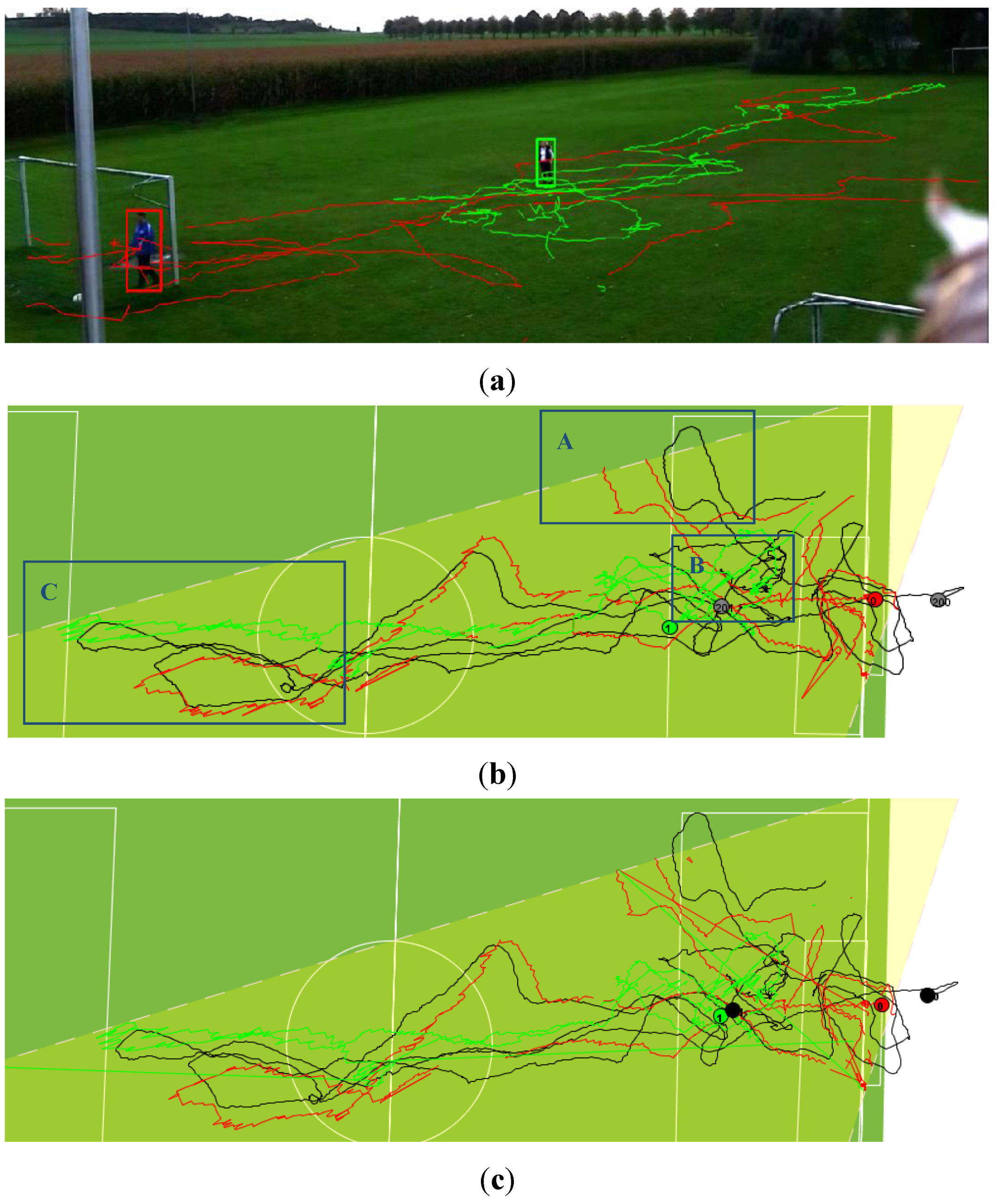

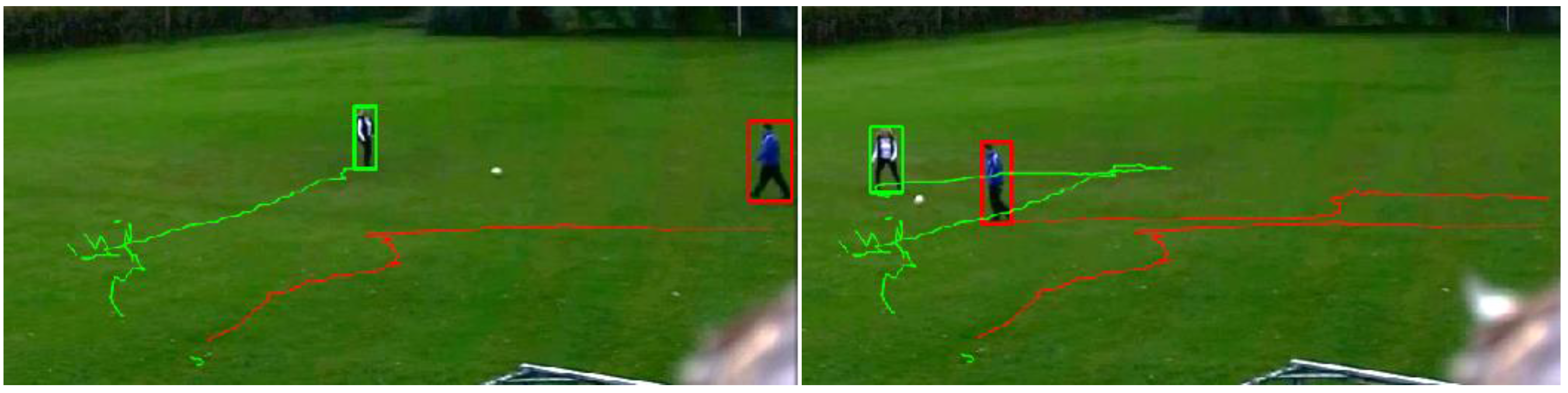
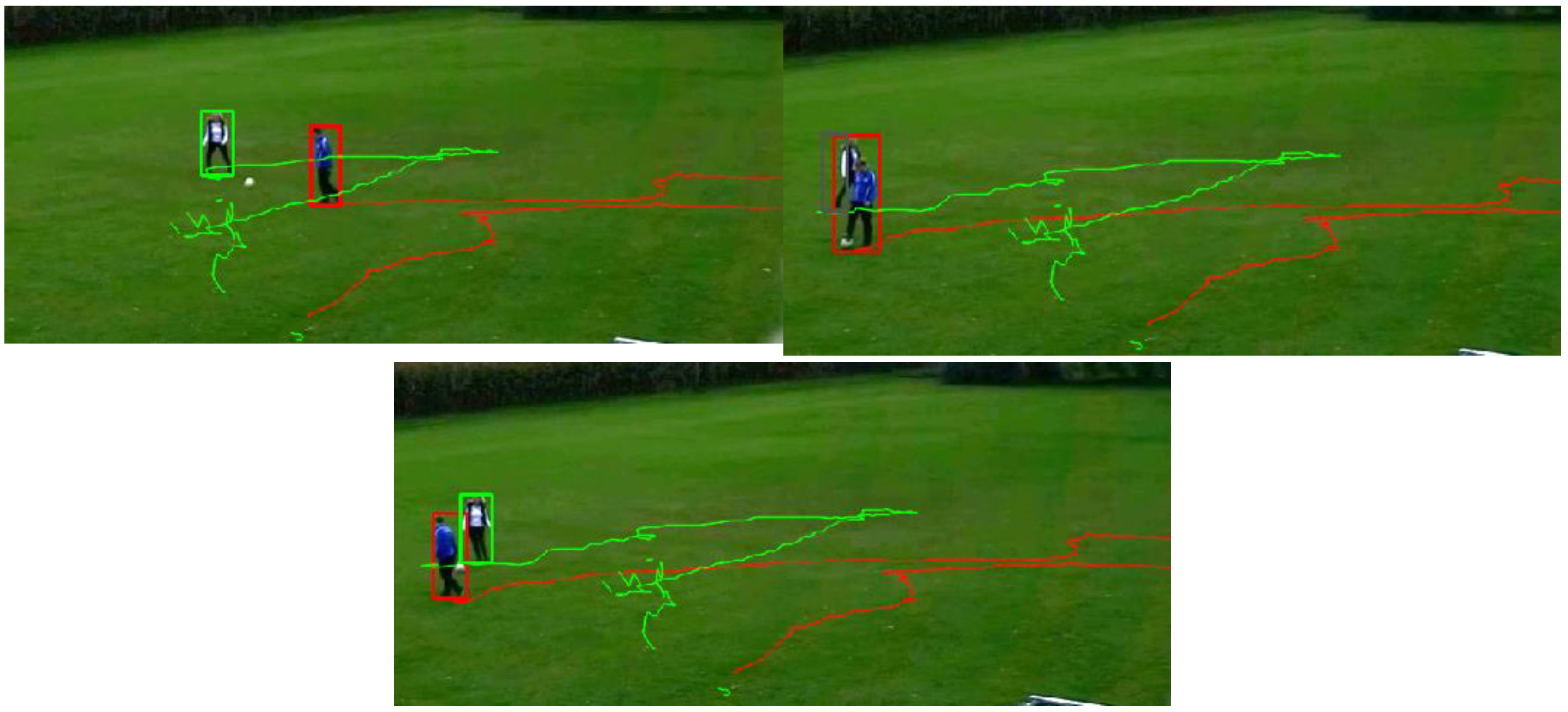
4.3. Experiment 3—Multiple Object Tracking

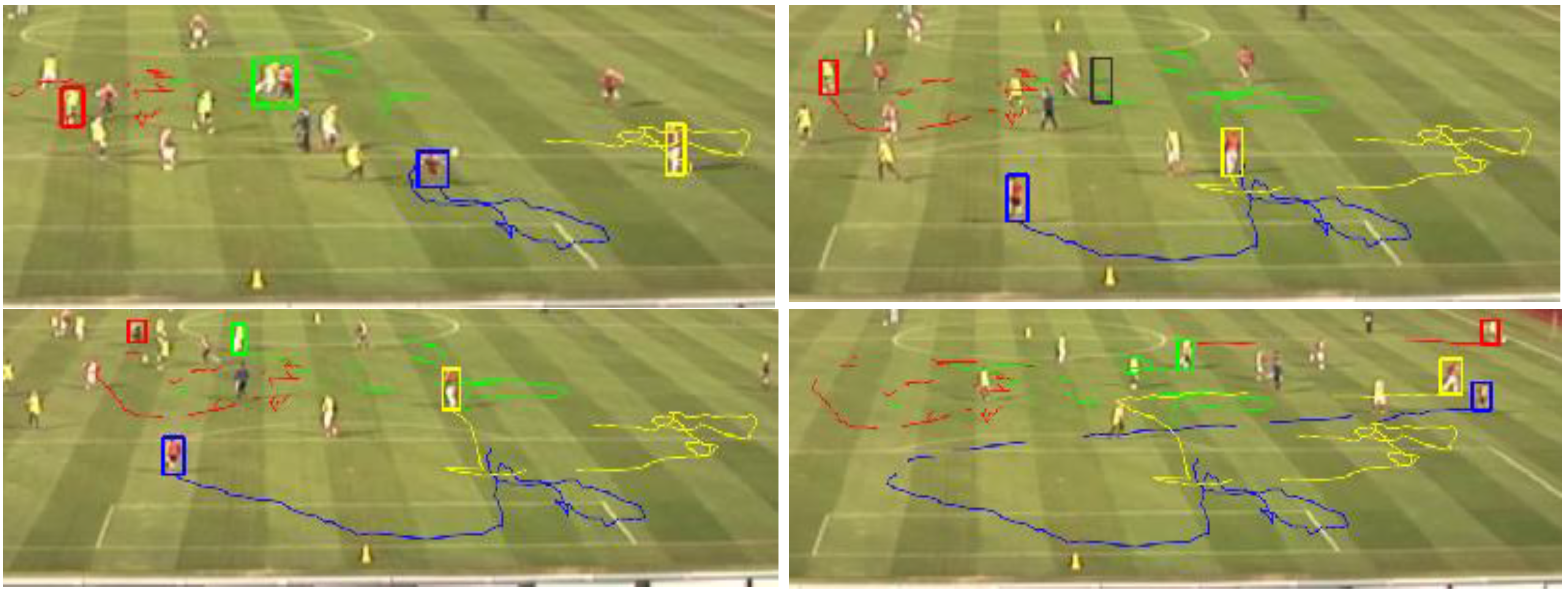
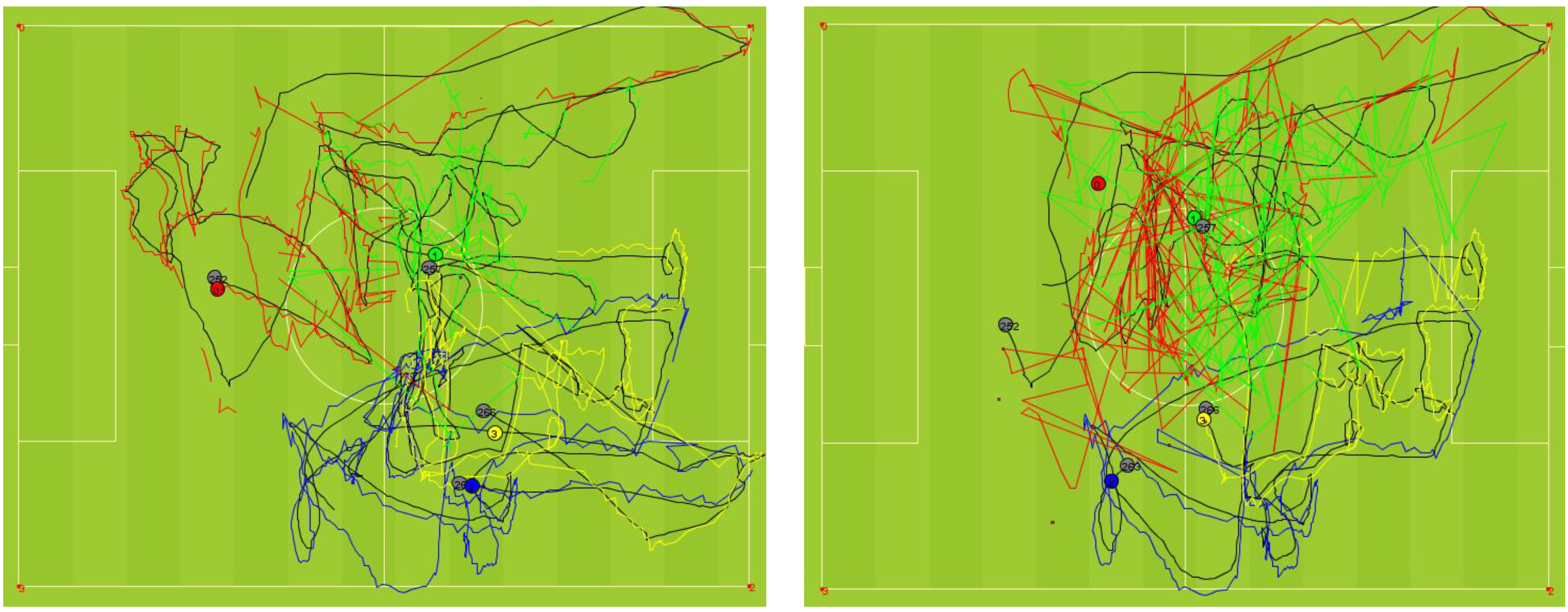
5. Conclusions and Outlook
Acknowledgments
Author Contributions
- Udo Feuerhake: Literature review, modeling, programming, data acquisition, analysis, writing.
- Claus Brenner: Modeling, revisions.
- Monika Sester: Basic concept, revisions.
Conflicts of Interest
References
- Home: Hawk-Eye. Available online: http://www.hawkeyeinnovations.co.uk/?page_id=1011 (accessed on 9 January 2015).
- Coutts, A.J.; Duffield, R. Validity and reliability of GPS devices for measuring movement demands of team sports. J. Sci. Med. Sport 2010, 13, 133–135. [Google Scholar] [CrossRef] [PubMed]
- Gray, A.J.; Jenkins, D.; Andrews, M.H.; Taaffe, D.R.; Glover, M.L. Validity and reliability of GPS for measuring distance travelled in field-based team sports. J. Sports Sci. 2010, 28, 1319–1325. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.J.; Watsford, M.L.; Kelly, S.J.; Pine, M.J.; Spurrs, R.W. The Validity and reliability of 10 Hz and 15 Hz GPS units for assessing athlete movement demands. J. Strength Cond. Res. 2013. [CrossRef] [PubMed]
- Randers, M.B.; Mujika, I.; Hewitt, A.; Santisteban, J.; Bischoff, R.; Solano, R.; Zubillaga, A.; Peltola, E.; Krustrup, P.; Mohr, M. Application of four different football match analysis systems: A comparative study. J. Sports Sci. 2010, 28, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Varley, M.C.; Fairweather, I.H.; Aughey, R.J. Validity and reliability of GPS for measuring instantaneous velocity during acceleration, deceleration, and constant motion. J. Sports Sci. 2012, 30, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Barris, S.; Button, C. A review of vision-based motion analysis in sport. Sports Med. 2008, 38, 1025–1043. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.; Ai, H.; Liu, L.; Lao, S. Multiple player tracking in sports video: A dual-mode two-way bayesian inference approach with progressive observation modeling. IEEE Trans. Image Process. 2011, 20, 1652–1667. [Google Scholar] [CrossRef] [PubMed]
- Iwase, S.; Saito, H. Parallel tracking of all soccer players by integrating detected positions in multiple view images. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004.
- Barros, R.M.L.; Misuta, M.S.; Menezes, R.P.; Figueroa, P.J.; Moura, F.A.; Cunha, S.A.; Anido, R.; Leite, N.J. Analysis of the distances covered by first division brazilian soccer players obtained with an automatic tracking method. J. Sports Sci. Med. 2007, 6, 233–242. [Google Scholar] [PubMed]
- Yang, T.; Pan, Q.; Li, J.; Li, S.Z. Real-time multiple objects tracking with occlusion handling in dynamic scenes. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005.
- Sugimura, D.; Kitani, K.M.; Okabe, T.; Sato, Y.; Sugimoto, A. Using individuality to track individuals: Clustering individual trajectories in crowds using local appearance and frequency trait. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009.
- Yang, C.; Duraiswami, R.; Davis, L. Fast multiple object tracking via a hierarchical particle filter. In Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–21 October 2005.
- Rabiner, L.; Juang, B.H. An introduction to hidden Markov models. IEEE ASSP Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Forney, J.G.D. The viterbi algorithm. IEEE Proc. 1973, 61, 268–278. [Google Scholar] [CrossRef]
- Martinerie, F. Data fusion and tracking using HMMs in a distributed sensor network. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 11–28. [Google Scholar] [CrossRef]
- Zen, H.; Tokuda, K.; Kitamura, T. A Viterbi algorithm for a trajectory model derived from HMM with explicit relationship between static and dynamic features. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004.
- Duckham, M. Decentralized Spatial Computing: Foundations of Geosensor Networks; Springer: Berlin, Germany, 2012. [Google Scholar]
- Yilmaz, A.; Javed, O.; Shah, M. Object tracking: A survey. ACM Comput. Surv. 2006, 38, 1–45. [Google Scholar] [CrossRef]
- Zivkovic, Z. Improved adaptive Gaussian mixture model for background subtraction. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004.
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. IEEE Proc. 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Dugad, R.; Desai, U.B. A Tutorial on Hidden Markov Models; Signal Processing and Artificial Neural Networks Laboratory Department of Electrical Engineering Indian Institute of Technology: Bombay, India, 1996. [Google Scholar]
- Xie, X.; Evans, R. Multiple target tracking using hidden Markov models. In Proceedings of the Record of the IEEE 1990 International Radar Conference, Arlington, VA, USA, 7–10 May 1990.
- DEBS 2013. Available online: http://www.orgs.ttu.edu/debs2013/index.php?goto=cfchallengedetails (accessed on 4 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feuerhake, U.; Brenner, C.; Sester, M. GPS-Aided Video Tracking. ISPRS Int. J. Geo-Inf. 2015, 4, 1317-1335. https://doi.org/10.3390/ijgi4031317
Feuerhake U, Brenner C, Sester M. GPS-Aided Video Tracking. ISPRS International Journal of Geo-Information. 2015; 4(3):1317-1335. https://doi.org/10.3390/ijgi4031317
Chicago/Turabian StyleFeuerhake, Udo, Claus Brenner, and Monika Sester. 2015. "GPS-Aided Video Tracking" ISPRS International Journal of Geo-Information 4, no. 3: 1317-1335. https://doi.org/10.3390/ijgi4031317
APA StyleFeuerhake, U., Brenner, C., & Sester, M. (2015). GPS-Aided Video Tracking. ISPRS International Journal of Geo-Information, 4(3), 1317-1335. https://doi.org/10.3390/ijgi4031317







