Abstract
The objective of this paper is to devise a strategy for developing a flexible tool to efficiently install a marine energy farm in a suitable area. The current methodology is applied to marine tidal current, although it can be extended to other energy contexts with some adaptations. We introduce a three-step approach that searches for marine farm sites and technological solutions. The methodology applied is based on a combination of Geographic Information Systems (GIS), multi-criteria analysis (MCA) and an optimization algorithm. The integration of GIS and MCA is at the core of the search process for the best-suited marine areas, taking into account geographical constraints, such as human activity, pressure on the environment and technological opportunities. The optimization step of the approach evaluates the most appropriate technologies and farm configurations in order to maximize the quantity of energy produced while minimizing the cost of the farm. Three main criteria are applied to finally characterize a location for a marine energy farm: the global cost of the project, the quantity of energy produced and social acceptance. The social acceptance criterion is evaluated by the MCA method, Electre III, while the optimization of the energy cost is approximated by a genetic algorithm. The whole approach is illustrated by a case study applied to a maritime area in North-West France.
1. Introduction
Marine renewable energy has recently been a subject of increasing interest, as oceans have a tremendous amount of energy available close to many population areas [1]. The main principle behind a marine current energy converter (e.g., marine current turbine) is that the energy is captured by a mechanical device that extracts kinetic energy from the flow and imparts this into a mechanical motion of a rotor or foil. When the installation of a marine converter farm is planned, the objective is to extract the maximum energy from the resource, while minimizing additional costs, environmental and social impacts. Even if the technological and market evolution are likely to lead to a small number of operational solutions [2], the many options available for the turbine design and the spatial constraints of a potential farm site offer many possible configurations to evaluate. In order to maximize the extracted energy, the choice of the most appropriate technology for a given farm site is essential, as well as finding the best site for a given technology. Moreover, the resource exploitation should be done in reasonable cost conditions. Indeed, the choice of a technical option (e.g., generator, turbine, drive train) may affect the quantity of produced energy, as well as the cost of the energy production. Furthermore, such a choice must also be adapted to the specific characteristics of a given site. In the specific case of marine current turbines, which is the context of this study, several viable technologies have arisen over the past few years [3,4], and some turbines have even already been tested in situ in some specific areas in the west of France, Canada and Scotland, to mention a few examples.
Despite rapid technological progress in the development of marine energy technologies, the implementation of successful marine farms is still a non-straightforward issue, as many parameters should be considered: technological, spatial, economic and social. In particular, the selection of an experimental test area, as well as future farm locations is a complex geographical and multi-criteria decision problem. The selection of the best implantation site is a tricky task, due to the huge amount of constraints to take into consideration. In addition to the technical and economic constraints, the sea is a regulated space where an important number of human activities take place, especially near the coasts. We believe that the combination of GIS capabilities with multi-criteria analysis can provide a flexible approach to identify several solutions and facilitate expertise between stakeholders. The objective of the research presented in this paper is to develop such a methodology in order to find an optimal location for a marine converter farm and to choose the harnessing systems in terms of technology choice, size, power rating and the number of machines. The current approach is applied to marine current energy, but the principles of the methodology can be extended to other marine energies (e.g., wind, swell).
The problem to consider can be split into two parts. The first step is to identify the best location: implementation of an offshore tidal energy farm that can be treated as a geographical problem. Geographical constraints arise from the technological/cost limits and/or from the selected marine area. The selection process should manage the conflicting nature of these constraints, as well as quantitative and qualitative ones (particularly for societal aspects). The combination of GIS and multi-criteria analysis should help users evaluate various possibilities, taking into account multiple and conflicting criteria and objectives. The second step aims to find the optimal farm configuration and the most adequate technologies. In order to find the optimal configurations among the various technologies available, a genetic algorithm has been applied to optimize the process. This optimization evaluates the system’s cost and quantity of energy produced for a given area and suggests the optimal farm configurations and the technological solution.
The methodology developed hereafter includes three criteria: the global cost of the project, the quantity of energy produced and social acceptance; but, the principles of this approach can be extended to take into account additional criteria (Figure 1). The multi-criteria analysis (MCA) retained, named Electre III [5], is first applied to measure the degree of social acceptance of a given marine area. This method has been successfully used in several engineering studies and is adapted to a ranking process [6,7,8]. The application of Electre III allows one to rank different regions according to their ability to reduce potential conflicts. Moreover, Electre III takes into account a degree of uncertainty in the decision process. It allows one to integrate human sensitivity that is inherent to most decision evaluations [9]. The MCA method is applied again after the optimization process, to consider the cost and energy criteria that result from the optimization process.
The rest of the paper is organized as follows. Section 2 presents the three parts of the methodology. Section 3 describes the spatial and technological criteria that have been used in the approach. A case study illustrates the potential of the methodology in Section 4. Finally, Section 5 concludes the paper and outlines further work.
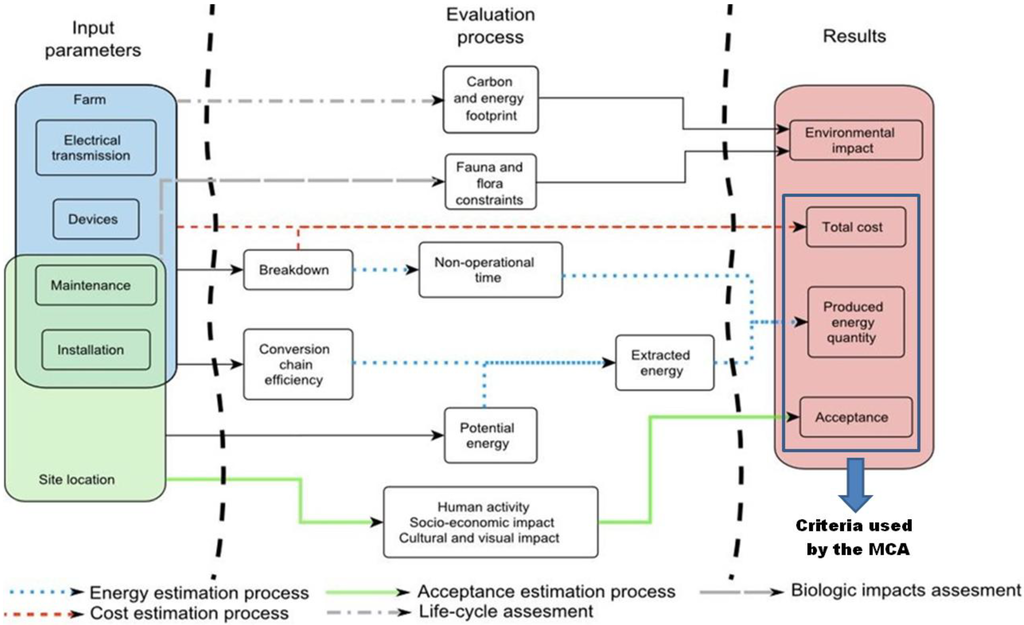
Figure 1.
Multi-criteria approach: principles.
2. Methodology Principles
Over the past few years, several decision-making and multi-criteria approaches have been applied for renewable energy planning and to take into account different socio-economic scenarios [10]. The problem can be considered as part of a marine spatial planning (MSP) task. The goal is to evaluate the potential of a given marine region for the development of marine technologies, especially in areas where important conflicts among users and the environment are possible [11]. This can also be considered as a framework for understanding the different tasks of the decision process, thus facilitating the participation of the stakeholders [12]. The aim of the proposed approach is not only to find the best implantation site for marine energy farms, but also to suggest the most appropriate technologies in terms of cost and efficiency, as well as to minimize the social impact. In order to create such a framework, the proposed approach combines GIS, MCA and an optimization algorithm. The methodology principles and the different dimensions of the approach are introduced in Figure 2.
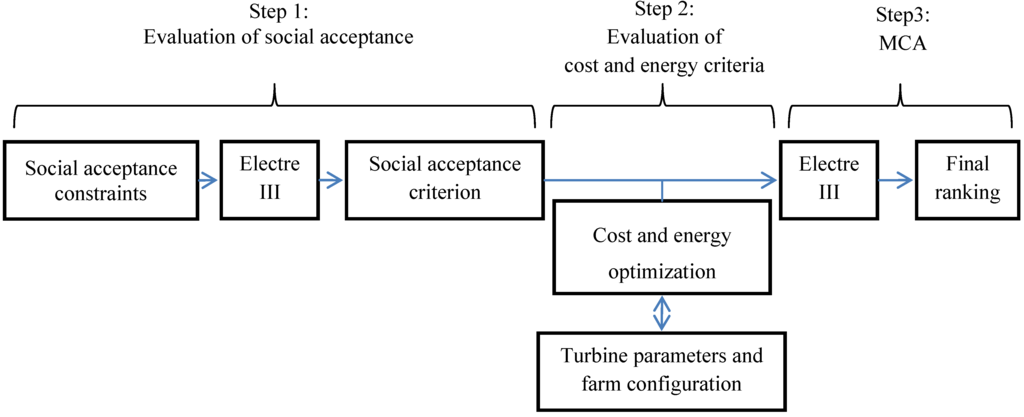
Figure 2.
Methodology principles.
The first step of the methodology is similar to the one suggested in [13] with the generation of a multi-criteria map. This scored area map reflects the degree of conformability of the project according to some decision-makers’ preferences (these preferences being considered as parameters by Electre III) and, overall, evaluates the social acceptance criterion. This allows one to spatially organize the marine area into sub-areas and to derive a value describing the degree of social acceptance for each of these sub-areas (note that the social acceptance criteria applied in the following steps are those considered in our case study; additional social acceptance criteria can be considered under similar principles). The generation of such a map is derived from the following four steps (numbered 1.1 to 1.4 in Figure 3):
- -
- Step 1.1: Generate a series of constraint maps. Each map represents a geographical area with a specific conflict source. Each constraints map is respectively divided into a number (n, m, k in Figure 3) of spatial units, ui, having an attribute, ai, describing the activities. With respect to the example presented in Figure 3, these maps are C1 for fishing area, C2 for buried cables and C3 for military activities and have n, m and k spatial units, respectively.C1 : [u1, …, un] → [a1, …, an]C2 : [u1, …, um] → [a1, …, am]C3 : [u1, …, uk] → [a1, …, ak]
- -
- Step 1.2: Derive the multi-criteria map. The generation of this intermediate map, Cm, is obtained by the overlay of constraint maps. This intermediate map is composed of a set of p spatial units uʹ1, …, uʹp. This means that each spatial unit, uʹi, is derived from the intersection of spatial units from C1 and C2 and C3 and is valued by three attributes a(C1), a(C2) and a(C3).Cm : [uʹ1, …, uʹi, …, uʹp] → [aʹ1, …, aʹi, …, aʹp] with uʹi → aʹi = {ai(C1), ai(C2), ai(C3)}
- -
- Step 1.3: Apply the MCA method. The goal of this step is to reduce the dimension of uʹi to a single attribute, A, applying the aggregation method of Electre III.
- -
- Step 1.4: Generate the decision-based map. The p spatial unit, uʹ, of this final map, Cd, is the same as the multi-criteria map. However, each of these units has a single attribute. The unique value assigned to each spatial unit reflects the final social acceptance ranking of each sub-area.Cd : [uʹ1, …, uʹp] → [A1, …, Ap]
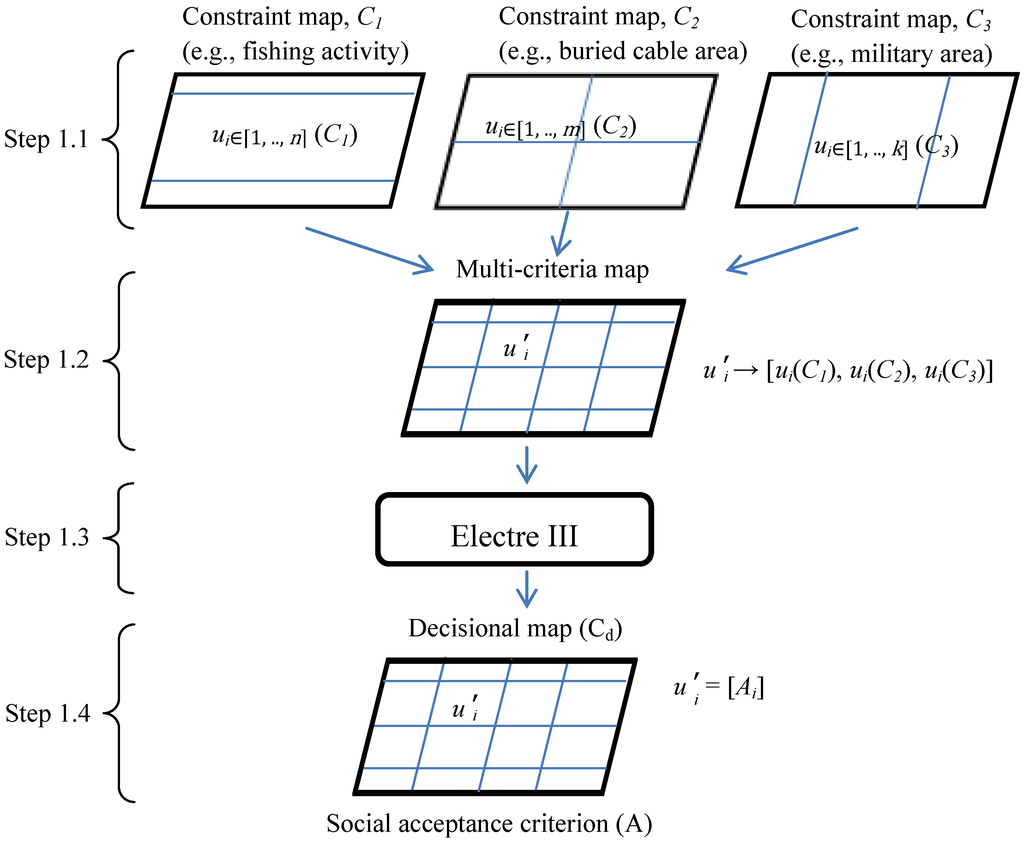
Figure 3.
First step of the methodology.
The maritime area is then divided into several zones according to the social acceptance criterion. The second step of the methodology is dedicated to the evaluation and optimization of the cost and energy production; it is divided into three internal steps (cf. 2.1 to 2.3 in Figure 4).
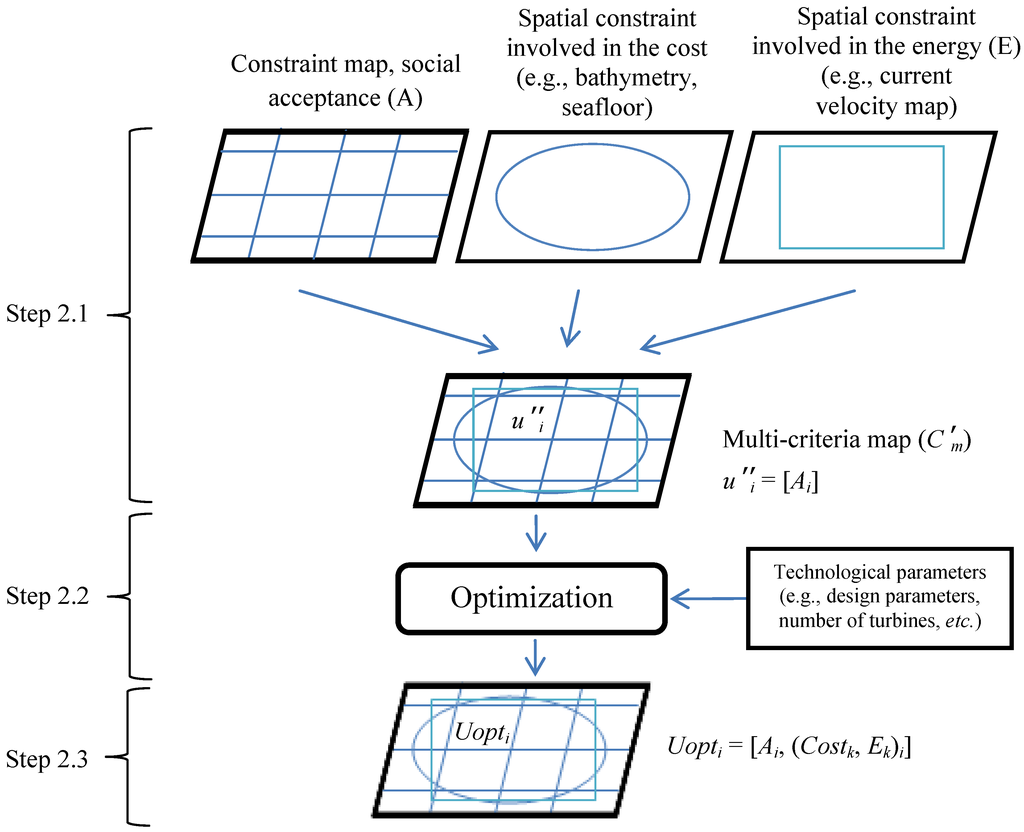
Figure 4.
Second step of the methodology.
- -
- Step 2.1: Generate a map (as Step 1.2) derived from an overlay of the social acceptance map with geographical constraints involved in the estimation of the cost and energy. The geographical maps considered here are the bathymetry, marine currents and seafloor geological characteristics. This derived map, Cʹm, is split into q spatial units, uʹʹ, having only one attribute: the value of social acceptability. This step generates a map of the study area segmented into homogeneous sub-areas. Values, such as the depth, are the parameters used in the appraisal of the cost.Cʹm : [uʹʹ1, …, uʹʹq] → [A1, … Aq]
- -
- Step 2.2: Optimize and evaluate the possible solutions using a genetic algorithm. For each spatial unit, uʹʹi, the optimization process searches, among all the possible configurations of the farm (number of machines, design choices, individual rating of the machines, etc.), for those that maximize the energy produced while minimizing the cost. The genetic algorithm is used to define a Pareto frontier that takes into account these two objectives. This Pareto frontier denotes the optimal solutions (i.e., solutions that minimize the cost for a set of given values of produced energy), as it exhibits a set of solutions that dominate the others (i.e., a solution, A, dominates a solution, B, if A is better than B regarding all dimensions considered). The optimal solutions exhibited by this Pareto frontier are ordered. This process provides the p best solutions for the cost-energy couple, (Costj=1, ... ,p, Ej=1, ... ,p) for each defined spatial unit (uʹʹi).
- -
- Step 2.3: Project the optimization solutions to each spatial unit of the multi-criteria map, Cʹm, as new attributes (cost and energy). Therefore, each spatial unit, Uopt, is characterized by three criteria. The social acceptance, A, and the p pairs of values related to the optimal cost and an energy corresponding to the optimal farm configurations, which have been found in the previous step.Cʹm : [uʹʹ1, …, uʹʹi, …,uʹʹq] with uʹʹi = Uopti → [Ai, (Costj=1, ... , p, Ej=1, ... , p)i]
The third step of the methodology is to apply an MCA to find the best solutions. Electre III ranks the different alternatives. The possibility offered by the Electre III method is to affect specific weights for each criterion and to reduce the choice of farm configurations proposed by the optimization algorithm. The principles of this approach are described in the next section.
3. Multi-Criteria Approach
3.1. Social Acceptance
The insertion of a new maritime activity should take into account socio-ecological constraints that are complex, heterogeneous, dynamic and prone to nonlinear and often abrupt changes [14]. Indeed, developing a new marine farm in a regulated space can generate a spatial/temporal overlap of human activities (Figure 5), restricted, protected and regulated areas, causing conflicts. These possible sources of conflict are grouped under the criteria of social acceptance. For marine renewable energy planning, conflicts of interest are restricted to areas already referenced that principally concern maritime traffic, defense and fishing interests. Some areas, such as major maritime routes, pipelines and cable routes can be excluded from consideration [15] and can act like a preliminary filter of the site search. Other areas may be more flexible in the sense that degrees of freedom exist for a potential overlap. The aggregation method, Electre III, helps to rank the overlapped areas according to the social acceptance criteria.
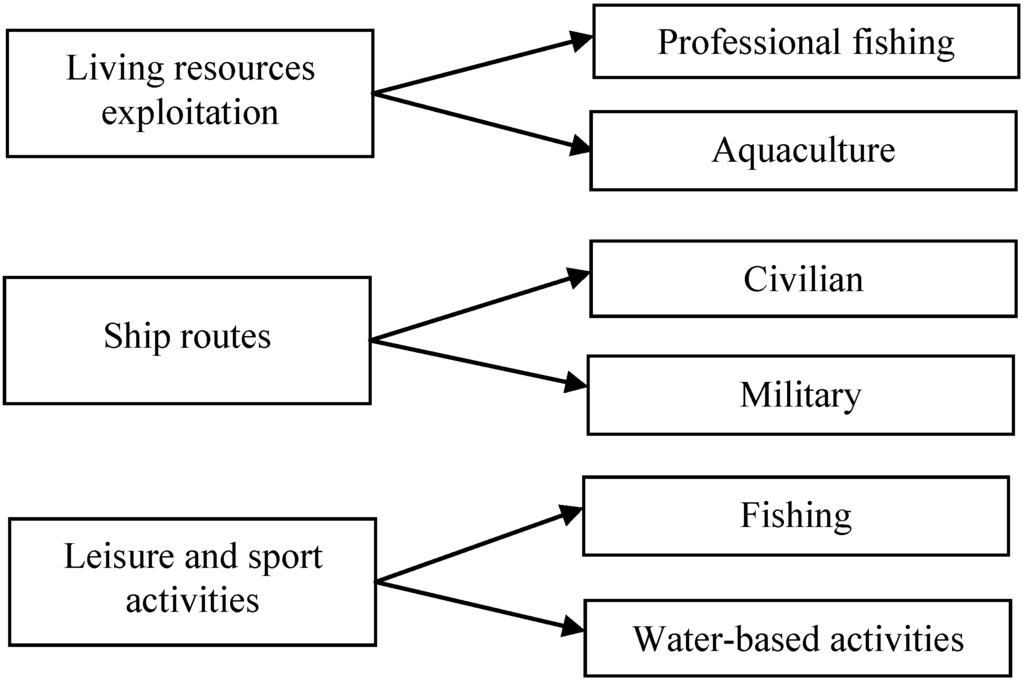
Figure 5.
Sea activities (adapted from [16]).
3.2. Energy Assessment
The estimation of the produced electricity is based on the available resource, the performance of the extracting system and the running time. In the approach developed, the performance basically depends on the following components: turbine, gearbox, generator, power converter and transmission elements. The non-operational time is integrated in this estimation and is calculated using the downtime statistical rates of each component.
In the case of a marine current turbine, the resource is estimated with the tidal current velocity, which can be predicted for each hour using a model developed by the French National Hydrography and Oceanographic Service (SHOM) [17]. The tidal current velocity in one place can be estimated by a relation function of the tidal coefficient and the hourly velocity at neap and spring tides. The possibility offered to choose between different technologies for the resource extraction allows one to introduce a compromise between efficiency, cost and the power rating of the converter.
For the turbine, three solutions are considered:
- -
- vertical axis turbine;
- -
- horizontal axis turbine with yaw;
- -
- horizontal axis turbine without yaw.
The vertical axis (VA) turbine harnesses the current from all directions, but the efficiency is lower than the horizontal axis (HA) turbine. The HA turbine is characterized by a capture angle (20°). Currents whose orientation is higher than 10° of the turbine’s axis are considered not harnessed. The current is also modified inside the capture cone, modelled with a cosines law [18]. One constraint is to find the best orientation when the turbine is installed. In order to solve this problem, a solution is to equip the turbine with a yaw system, as in conventional wind turbines, this allowing one to extract the energy from the current from all orientations with no attenuation. This implies raising the cost of the system (component cost and O&M cost), this potentially leading to an increase of the failure rate. Depending on the current characteristics (i.e., velocity and orientation), the maximization of the energy extracted leads to favoring one of these three turbine solutions.
For the generator/converter/drive train associations, two solutions are considered:
- -
- three-stage gearbox with DFIG (double-fed induction generator),
- -
- direct drive with PMSG (permanent magnet synchronous generator).
These different associations are proposed in order to illustrate the compromise between an expensive generator/power electronics system (PMSG) and the DFIG, where the cost of the power electronics is significantly reduced, but that requires a very failure-prone gearbox with a high level of maintenance [17].
3.3. Marine Farm System Cost
The global cost of the project should include the farm’s initial cost, installation/dismantling and maintenance operations’ costs. A farm is generally composed of the following components: a set of turbines, a transformer station located at sea or on land (depending on the distance to the coast and the total power of the farm), a network of submarine inter-turbines cables (buried or not, depending on the seafloor type), a network of submarine cables for transmitting the energy from the offshore substation to the shore station and a connection cable to the electric distribution grid. Accordingly, the cost of the farm depends on two main elements. The first one is that which rests on the technological characteristics (design, layout/configuration), while the second one depends on the parameters, including the geographical position of the farm. For instance, the cost of a turbine depends on the technologies and components used. Some cost components, such as the foundation of the system, also depend on the location (in relation with depth and seabed geological properties).
The installation/dismantling cost is estimated by a parameter that includes the distance to the harbor, the vessel’s characteristics and the number of turbines, as suggested in [19]. For maintenance operations, the cost is influenced by similar parameters, but the number of operations is evaluated by the technological choice (based on the statistical failure rates of each component).
4. Case Study
The case study considers a scenario of marine current turbine implantation in the Iroise Sea located in the north-west of France, where areas with high marine current velocity have been identified. Two areas are particularly well-known: the “Raz de Sein area” near Sein Island and the Fromveur pass area near Ouessant Island. Figure 6 shows the locations where several current velocity surveys were performed and the velocity is higher than 1 ms−1 at least during 30% of the time for a year. Our study is focused on “Raz de Sein”, which is also a high-density human activity area and particularly for fishery. In order to find the place generating the fewest conflicts between sea users, the first step consists of classifying the study area in different zones according to the social acceptance criteria.
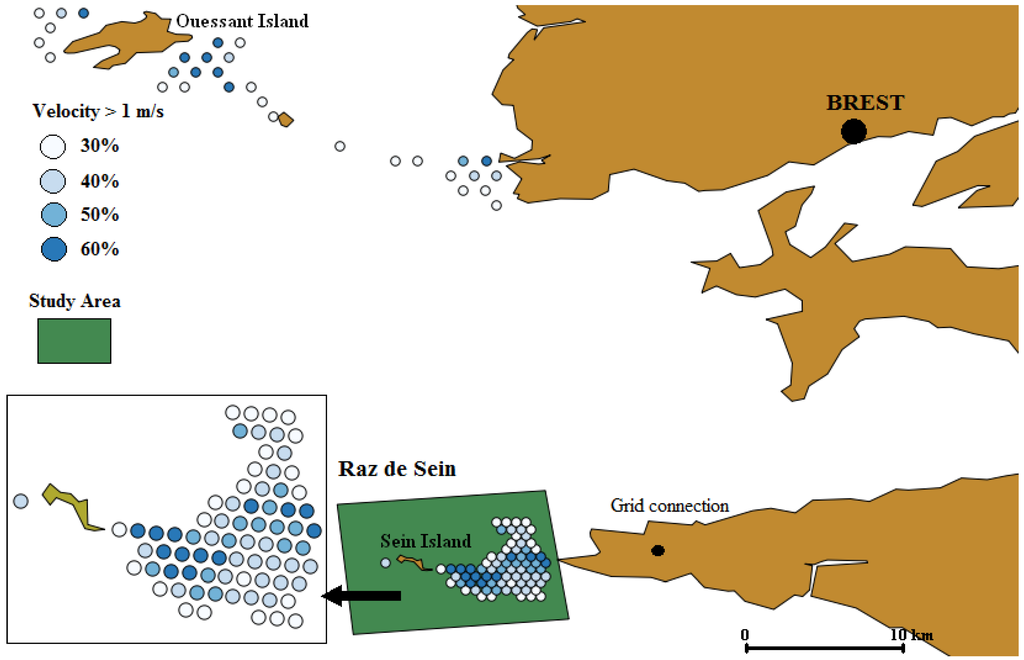
Figure 6.
Study area.
4.1. Social Acceptance Evaluation Using Electre III
Let us apply the strategy described by Step 1 of the methodology in order to evaluate the social acceptance criteria. The Electre III outranking MCA method has been applied. In this example, the demonstration is restricted to professional fishery activities, which are the principal human activity nearby the Sein area. Different kinds of fishery practices are identified in the study area. The knowledge of the location of the fishery activities comes from the regulation and seabed properties [20]. These locations are approximated, as they do not take into account the time/seasonal dimension for the fishery activities, but nevertheless, they give some useful information on the practice geographical breakdown. The fishery activities in the study area are grouped into four categories, which constitute four constraints. The first constraint groups floating longlines and floating lines (Figure 7). The derived map shows potential overlapping areas. This means that, if two activities overlap in a given location, conflicts may arise. The three other constraints are derived under the same principles. They group net, trawling and dredge and ground line areas, which are respectively shown by Figure 8, Figure 9 and Figure 10 (on top of the map of currents exhibited in Figure 6).
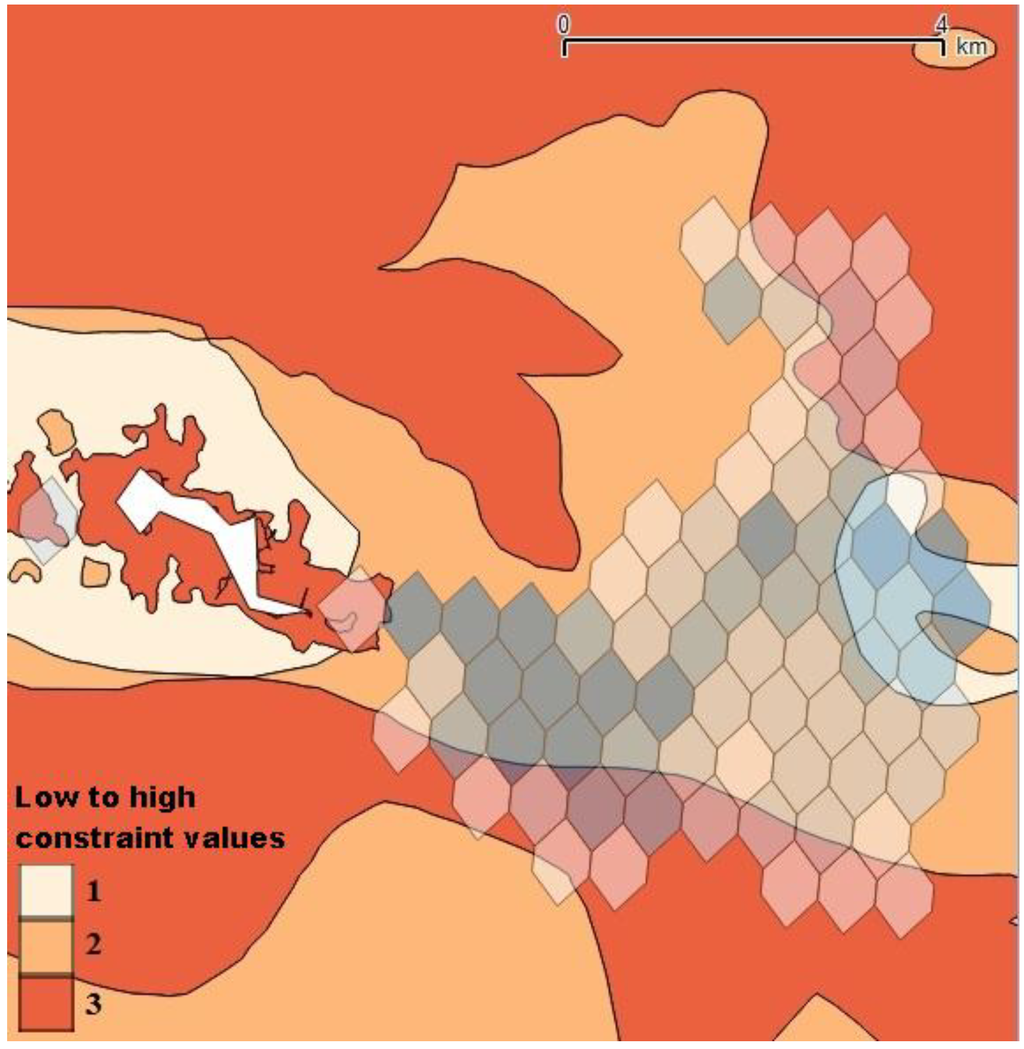
Figure 7.
Floating line fishing areas.
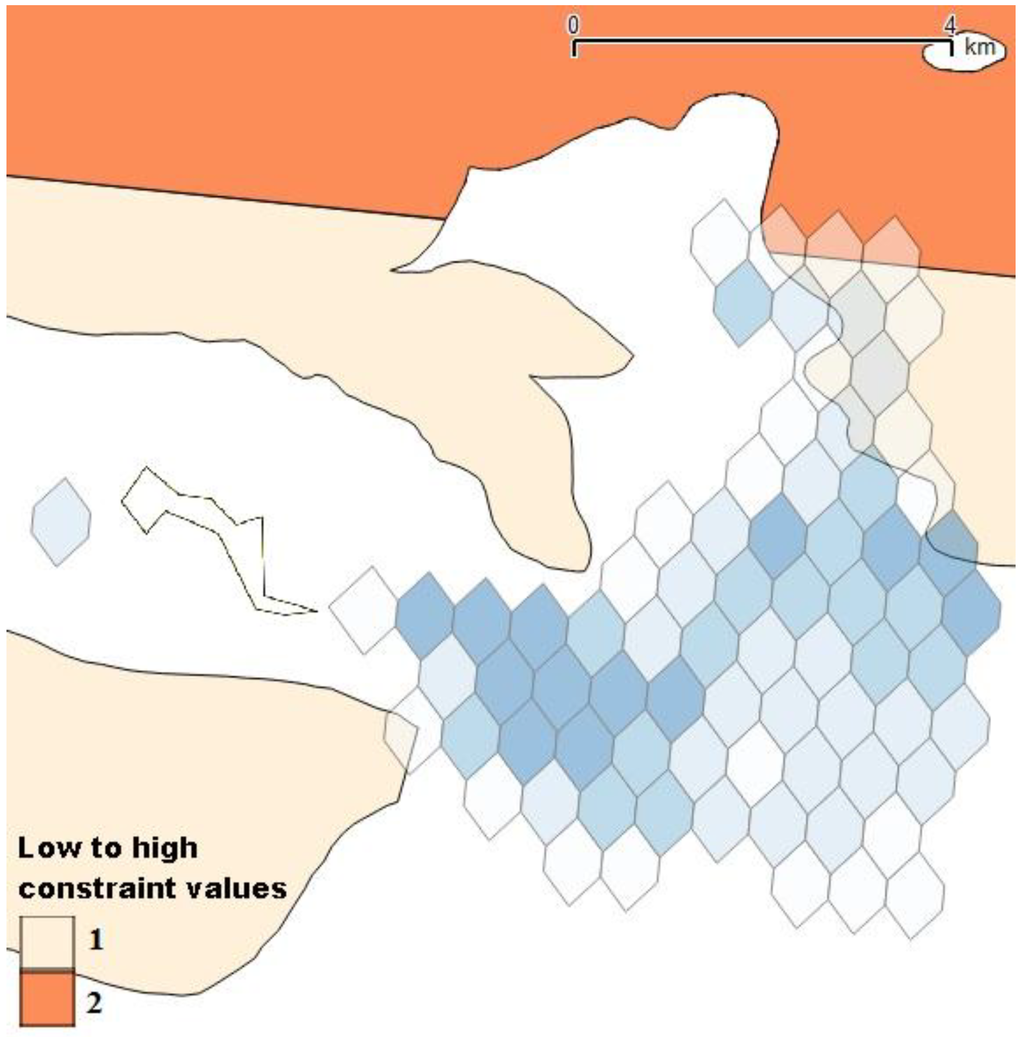
Figure 8.
Net fishing areas.
Electre III also incorporates the fuzzy dimension of a decision-based process. The outranking relation, S, is derived for each pair of alternatives (a, b) of a set of solutions, A. The assertion, a outranks b, aSb, is based on two indexes. The concordance index evaluates if a majority of criteria is in favor of aSb, and the discordance index evaluates if in the minority of criteria; none of them is strongly opposed to aSb. The fuzzy value is introduced using different thresholds (indifference, q, preference, p and veto, v) in the outranking relation [5]. The outranking is then defined as follows:
where g(x) is the performance of the alternative, x, regarding a given constraint.
aPb (a is strongly preferred to b): g(a) − g(b) > p
aQb (a is weakly preferred to b): q < g(a) − g(b) ≤ p
aIb (a is indifferent to b; and b to a): |g(a) − g(b)| ≤ q
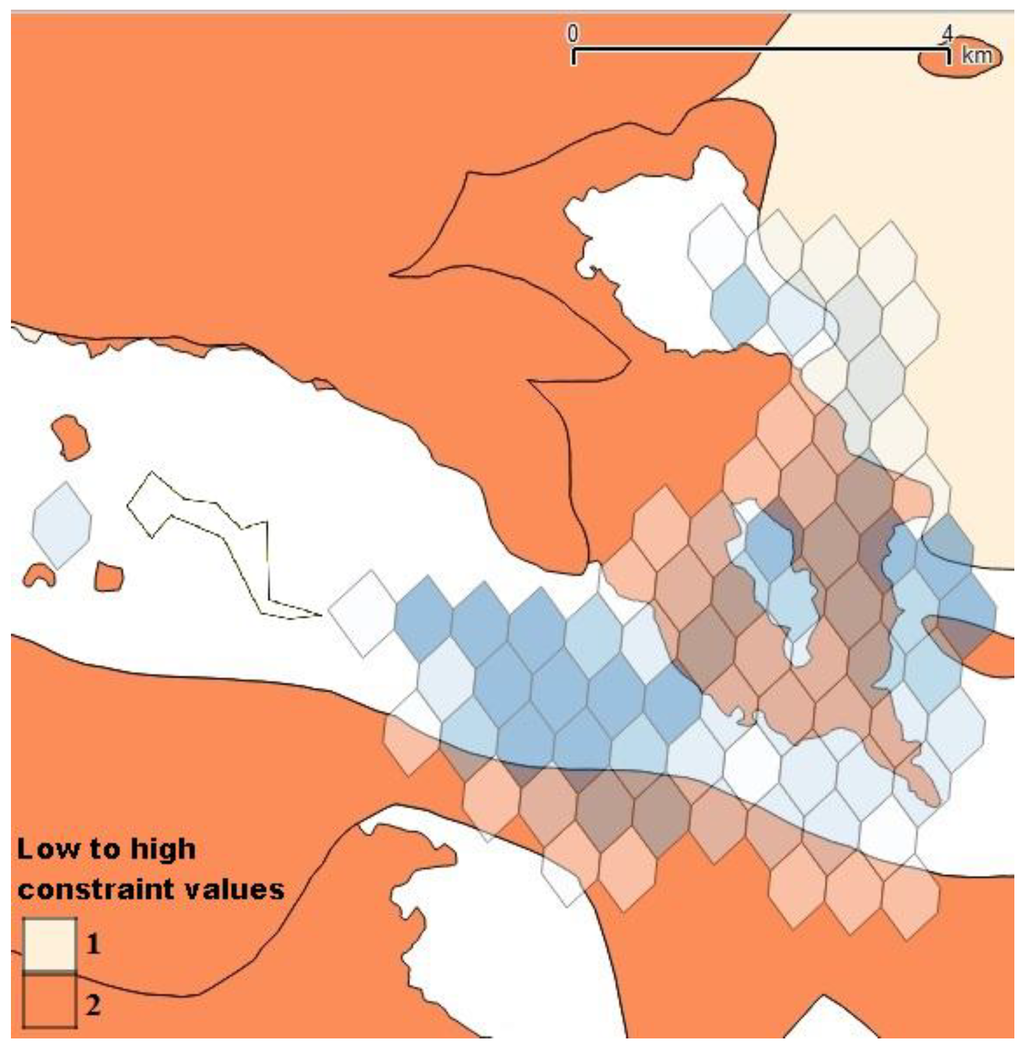
Figure 9.
Dredge and trawling areas.
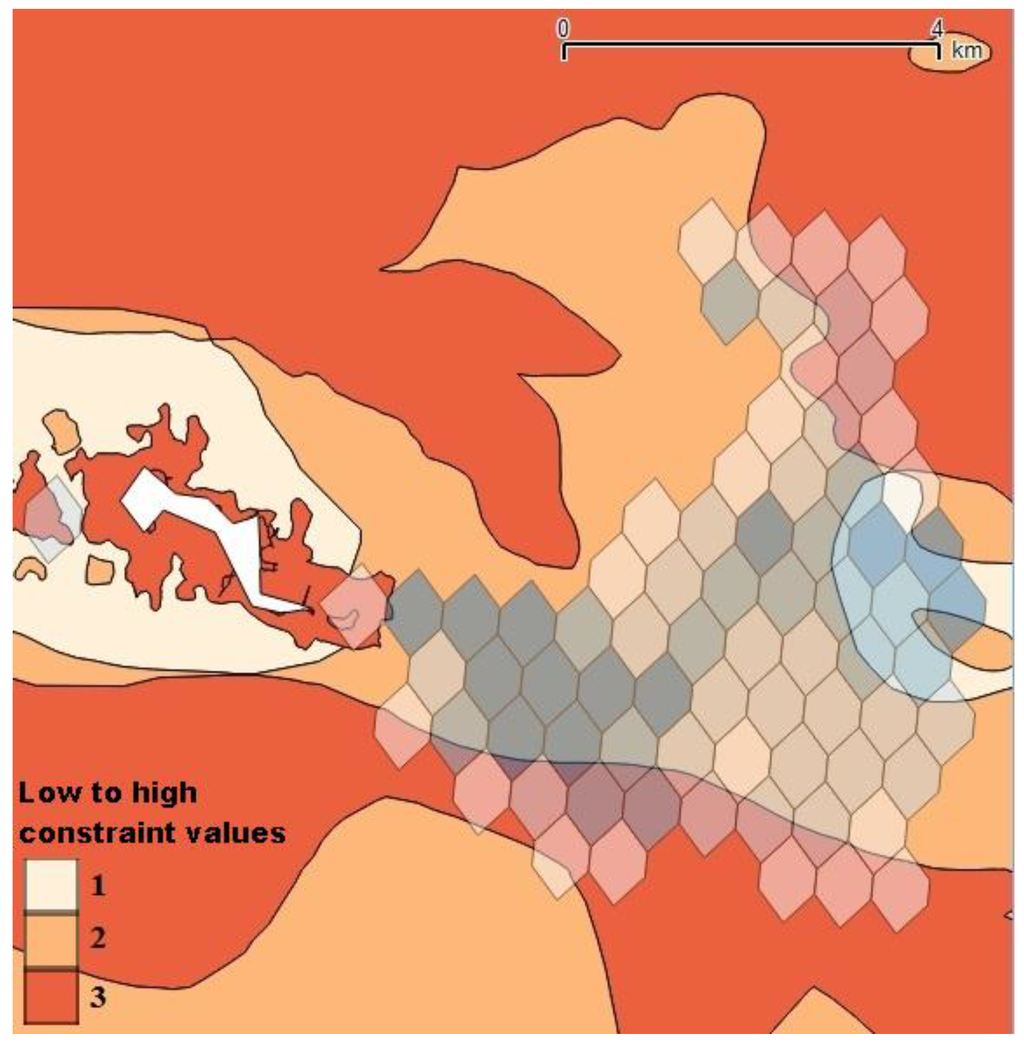
Figure 10.
Ground line fishing areas.
The veto threshold, v, is used in the discordance index calculation and defines the case where the performance of b regarding a given criteria is so high that it constitutes a veto for the assertion aSb. The threshold values and constraint weight used for the four constraints related to fishing activities are shown in Table 1. The weight of the floating line has been defined as the lowest, as we assume that this activity has a lesser impact on the potential location of a marine current turbine. Conversely, we assume that trawling and dredge activities are the most-conflicting activities, so those are valued with the highest weights. Indeed, and as part of a real marine spatial planning process, these values should be confirmed by experts and stakeholders. As previously introduced in Step 1 (Figure 3), before running the MCA, a multi-criteria map is derived. Accordingly, the four constraint maps are overlapped in order to create a new subdivision of the study area made by the intersection of the maps related to the different fishing activities. Electre III allows one to classify all subareas into six categories: the first one denotes the least-impacting areas, while the sixth one denotes the most important conflicting areas (Figure 11). Therefore, the whole region considered is classified according to the social acceptance criteria. The next step of the methodology develops the cost evaluation.

Table 1.
Threshold values and weights.
| Constraints | Weight (k) | Indifference Threshold (q) | Preference Threshold (p) | Veto Threshold (v) |
|---|---|---|---|---|
| Trawling/dredge | 3 | 0 | 1 | 3 |
| Nets | 2 | 0 | 1 | 3 |
| Floating lines | 1 | 0 | 1 | 3 |
| Ground lines | 2 | 0 | 1 | 3 |
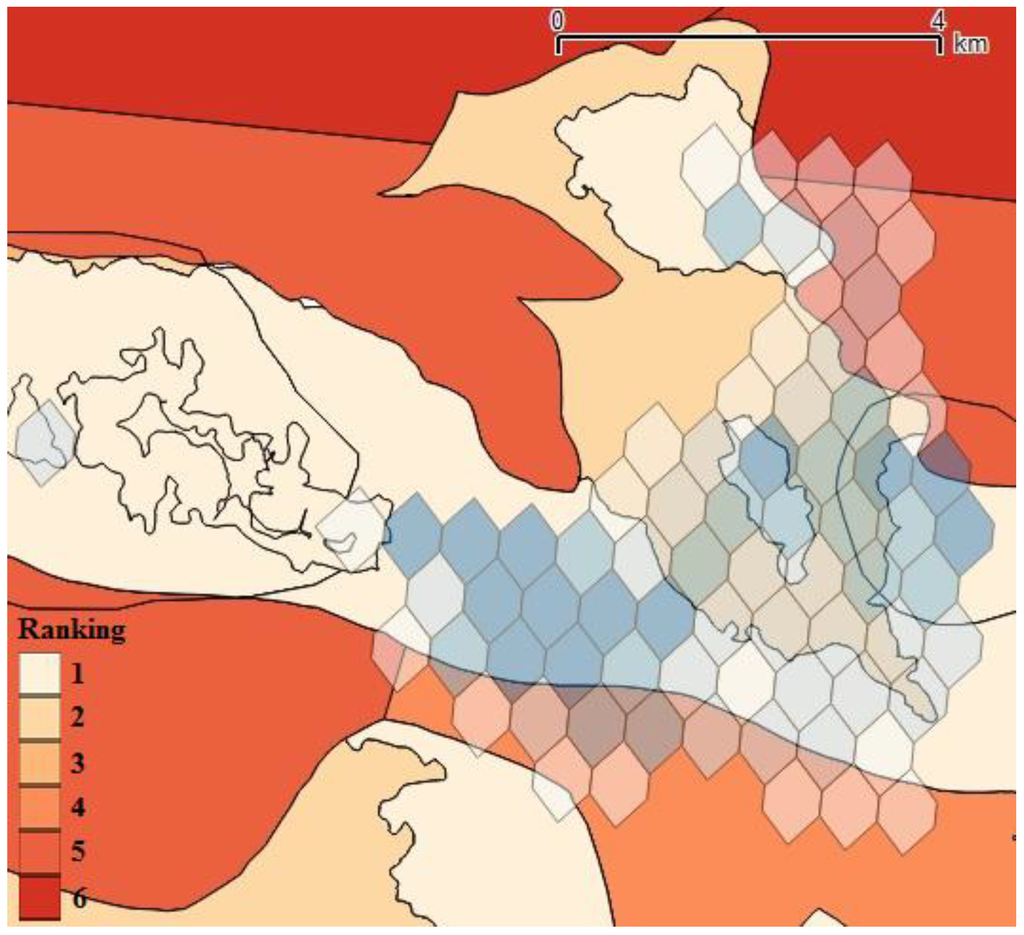
Figure 11.
Classification of the study area according to fishery activities.
4.2. Cost and Energy: Evaluation Using a Genetic Algorithm
As for the previous steps and before applying the optimization algorithm, a multi-criteria map has to be built by taking into account the geographical constraints involved in the estimation of the cost and energy. These constraints modify the suitability resources map. The new map is generated by an overlay of bathymetry, current resource and social acceptance. Figure 12 shows the current map overlapped by these constraints and where 180 spatial units are obtained. Firstly, locations where the depth is too low have been removed (i.e., under 15 m). Secondly, spatial units with small areas (i.e., less than 2600 m2) are spatially aggregated when they have similar current characteristics. Each spatial unit is, at this step, a homogenous part of the study area according to the social acceptance criteria and the two parameters involved in the estimation of the cost and energy produced. In order to estimate these two parameters, other attributes are added to each of these spatial units: their area, distance to the harbor and distance to the electric grid. The area allows one to define the maximum number of turbines, NTmax, which can be installed in the spatial unit (NTmax is at least equal to one, as the installation of a single turbine does not need a large area). This number depends on a minimum distance between two devices, which also depends on the turbine radius, R. The turbines are supposed to be placed as a patchwork with a device spacing approximated to seven times its diameter, D. NTmax is defined as follows:
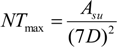 where Asu is the area of the spatial unit.
where Asu is the area of the spatial unit.
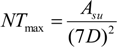
The maximum radius allowed for a specific spatial unit is denoted as Rmax and is evaluated as a function of the water depth in the area and surface and bottom margins:
2Rmax ≤ depth-margins
Next, the installation and maintenance costs depend on the harbor distance. For the considered case study, this harbor is that of Brest, which is planned to house a complete set of specific marine energy maintenance and installation devices.
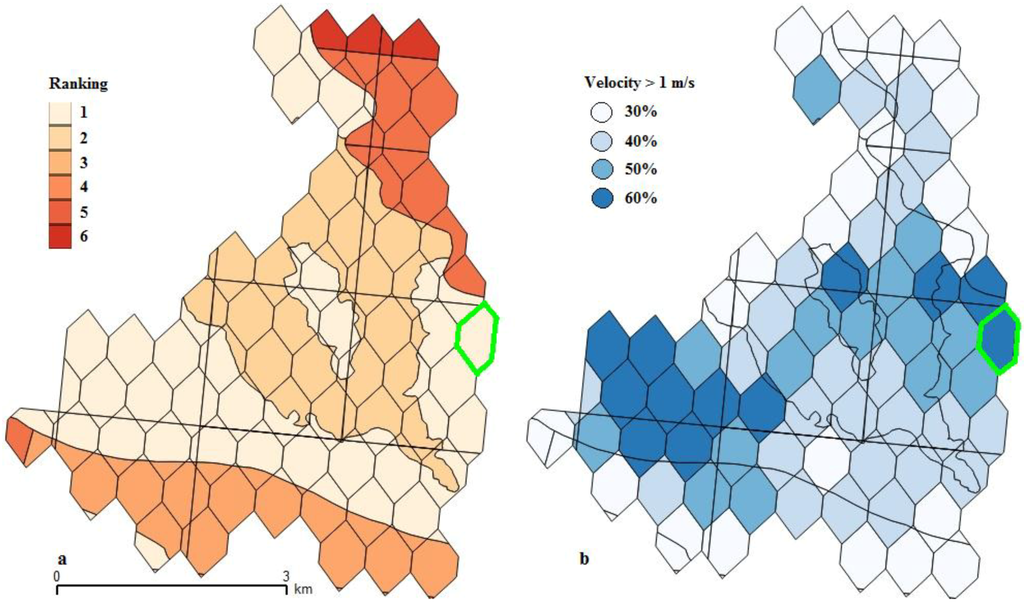
Figure 12.
(a) Multi-criteria map social acceptance ranking visualization. (b) Multi-criteria map current resource visualization.
In fact, the design of a marine current turbine cannot be treated by a classic and deterministic optimization method. Due to the non-linearity of the variables considered and the high number of possible combinations, stochastic methods, such as inductive learning, neural networks and genetic algorithms, should be preferred [21]. In particular, genetic algorithms perform very well at optimizing a search process with a relatively high number of variables and combinations, and those have been already used for the design of wind turbines [22]. We retain the solution of a genetic algorithm to best adapt a marine current turbine farm to a specific site according to the technical feasibility and economic viability. The parameters retained for the optimization process are presented hereafter with their corresponding variation domain and variation step (note that the approach is flexible enough to be extended towards some additional parameters):
- -
- the turbine type (TT): VA or HA without yaw or HA + yaw
- -
- the rotor radius (R): 2.5 m to Rmax with a step of 0.5 m
- -
- the drive train configuration (DT): Direct-drive PMSG or DFIG + gearbox
- -
- the rating power (Pn) of DT: 0.1 to 3MW with a step of 0.1 MW
- -
- the number of turbines (NT) one to NTmax
In the case of a VA turbine, the rotor radius corresponds to half the turbine’s height. The width of the VA turbine is calculated in such a way that its area is the same as that of an HA turbine with an equivalent radius.
In order to illustrate the solution exhibited by the application of the optimization algorithm, let us consider a spatial unit (green contour in Figure 12). This spatial unit is characterized by an area of 310,000 m2 and a mean depth of 24 m. The distance of this unit from Brest harbor and from the fictive grid connection point are, respectively, 48 km and 10 km. The marine current distribution is described by Figure 13. A surface of (7D)2 is reserved for one turbine. A top margin of 5 m is suggested to allow small boat navigation and to minimize turbulence and swell effects. Moreover, a five-meter bottom clearance is recommended as a minimum distance to avoid damage by materials moving at the seabed and to minimize the hydrodynamic effects related to the boundary layer [23]; as the minimum radius considered is 2.5 m and 10 m are allocated for bottom and top clearance (this explains why depths under 15 m have been previously removed).
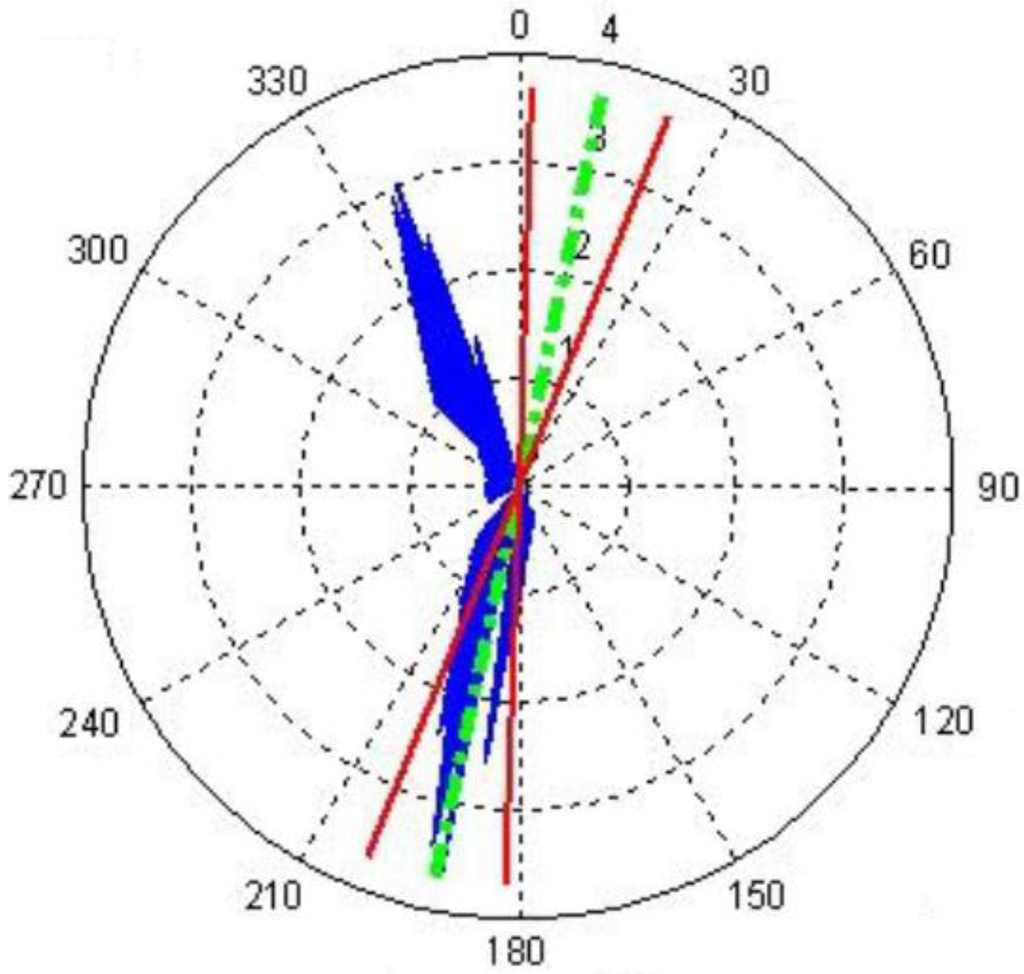
Figure 13.
Distribution of current.
For the spatial unit considered, the current is characterized by a dissymmetric distribution. Figure 13 shows the ideal orientation and the cone of extraction in the case where an HA turbine (without yaw) is taken. In this particular case, various current orientations are hence not harnessed efficiently. The optimization applied to that spatial unit characteristics and algorithm parameters presented previously gives the results shown in Table 2. As expected, solutions that allow one to harness the current in all directions are selected by the optimization algorithm. No solution with a VA turbine is found; however, a VA solution with the same design of the lowest cost solution (Alternative 1) should be considered by the Pareto optimum, but with a lower value of the produced energy (due to a lower power coefficient). Another observation is that the rotor radius tends to take the entire place that is allocated to it (24 m depth with 10 m of top/bottom clearance that leads to a 7-m turbine radius). In this case, the maximal number of turbines is NTmax = 32. It can also be noticed that the cost of the energy decreases when the number of turbines increases, due to equipment sharing effects.
4.3. Final Ranking
The genetic algorithm, applied with the same parameters, is performed for all spatial units (Figure 12). This process generates a set of turbine solutions for each spatial unit (as in Table 2). This results in 2265 possible solutions overall (alternatives) for 180 spatial units. Each of these alternatives is characterized by the energy produced, its cost and the social acceptance of the area to which it belongs (determined by Step 1). Electre III is applied to these alternatives. The weight and threshold values used in the MCA are shown in Table 3. In this example, a preference for low-cost alternatives grading the highest weight is chosen. The energy indifference threshold is set to 10 MWh; this roughly corresponds to the annual energy needed by a 70-m2 house. That means that if, for two alternatives, the difference of the energy is less than 10 MWh, these two alternatives are considered as equivalent under this criterion. When the difference lies between the indifference and preference thresholds, a linear interpolation is performed. This allows one to derive a fuzzy outranking relation that permits one to state how an action weakly outranks another one. The cost preference threshold is set to 100 k€ (this being the lowest value that can be attributed, due to the cost approximation). The 2265 possible solutions are sorted into 1376 ranks for each spatial unit. The best alternative for a given spatial unit is having the lowest rank among the alternatives belonging to that unit. Figure 14 gives the classification of the study area, according to the best alternative of the spatial unit, based on the three criteria considered.
In Figure 14, the four most suitable spatial units are qualified from A to D (A being the best one). The characteristics of the best alternatives and their ranks are given in Table 4. A has its alternative ranked as one, but the second spatial unit, B, has its alternative ranked as three. This means that the alternative, which belongs to A, has a better ranking than the alternative related to B. A similar observation can be seen for C. A gap of three ranks exists between B and C. There are two alternatives of A or B that can be taken into consideration before considering the spatial unit, C.
The results show that a majority of the most suitable spatial units have currents, whose velocities are superior to 1 ms−1 during at least 50% or 60% of the time, except for C, for instance. The two first spatial units considered (A and B) are located in the lowest fishery area and correspond to a low cost.

Table 2.
Results of the genetic algorithm optimization. PMSG, permanent magnet synchronous generator; TT, turbine type; NT, number of turbines; DT, direct-drive turbine.
| Alternatives | Energy (MWh/year) | Cost (M€) | Pn (MW) | R (m) | TT | NT | DT | €/MWh (20 years) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1068 | 5.7 | 0.3 | 7 | HA + yaw | 1 | PMSG | 267 |
| 2 | 1210 | 5.8 | 0.4 | 7 | HA + yaw | 1 | PMSG | 240 |
| 3 | 1469 | 6.2 | 1 | 7 | HA + yaw | 1 | PMSG | 211 |
| 4 | 1478 | 6.3 | 1.1 | 7 | HA + yaw | 1 | PMSG | 213 |
| 5 | 1493 | 6.4 | 1.4 | 7 | HA + yaw | 1 | PMSG | 214 |
| 6 | 1496 | 6.9 | 2.1 | 7 | HA + yaw | 1 | PMSG | 231 |
| 7 | 2137 | 8.3 | 0.3 | 7 | HA + yaw | 2 | PMSG | 194 |
| 8 | 2420 | 8.4 | 0.4 | 7 | HA + yaw | 2 | PMSG | 174 |
| 9 | 2956 | 9.3 | 1.1 | 7 | HA + yaw | 2 | PMSG | 157 |
| 10 | 2985 | 9.7 | 1.4 | 7 | HA + yaw | 2 | PMSG | 162 |
| 11 | 2993 | 10.2 | 1.8 | 7 | HA + yaw | 2 | PMSG | 170 |
| 12 | 3205 | 10.8 | 0.3 | 7 | HA + yaw | 3 | PMSG | 168 |
| 13 | 3630 | 11 | 0.4 | 7 | HA + yaw | 3 | PMSG | 152 |
| 14 | 4407 | 12.2 | 1 | 7 | HA + yaw | 3 | PMSG | 138 |
| 15 | 4433 | 12.4 | 1.1 | 7 | HA + yaw | 3 | PMSG | 140 |
| 16 | 4478 | 13 | 1.4 | 7 | HA + yaw | 3 | PMSG | 145 |
| 17 | 4489 | 13.8 | 1.8 | 7 | HA + yaw | 3 | PMSG | 154 |
| 18 | 8867 | 21.6 | 1.1 | 7 | HA + yaw | 6 | PMSG | 122 |

Table 3.
Threshold values and weights.
| Constraints | Weight (k) | Indifference Threshold (q) | Preference Threshold (p) | Veto Threshold (v) |
|---|---|---|---|---|
| Energy | 1 | 10 (MWh) | 300 (MWh) | 3000 (MWh) |
| Cost | 3 | 0 | 0.1 (M€) | 1 (M€) |
| Social acceptance | 1 | 0 | 1 | 3 |
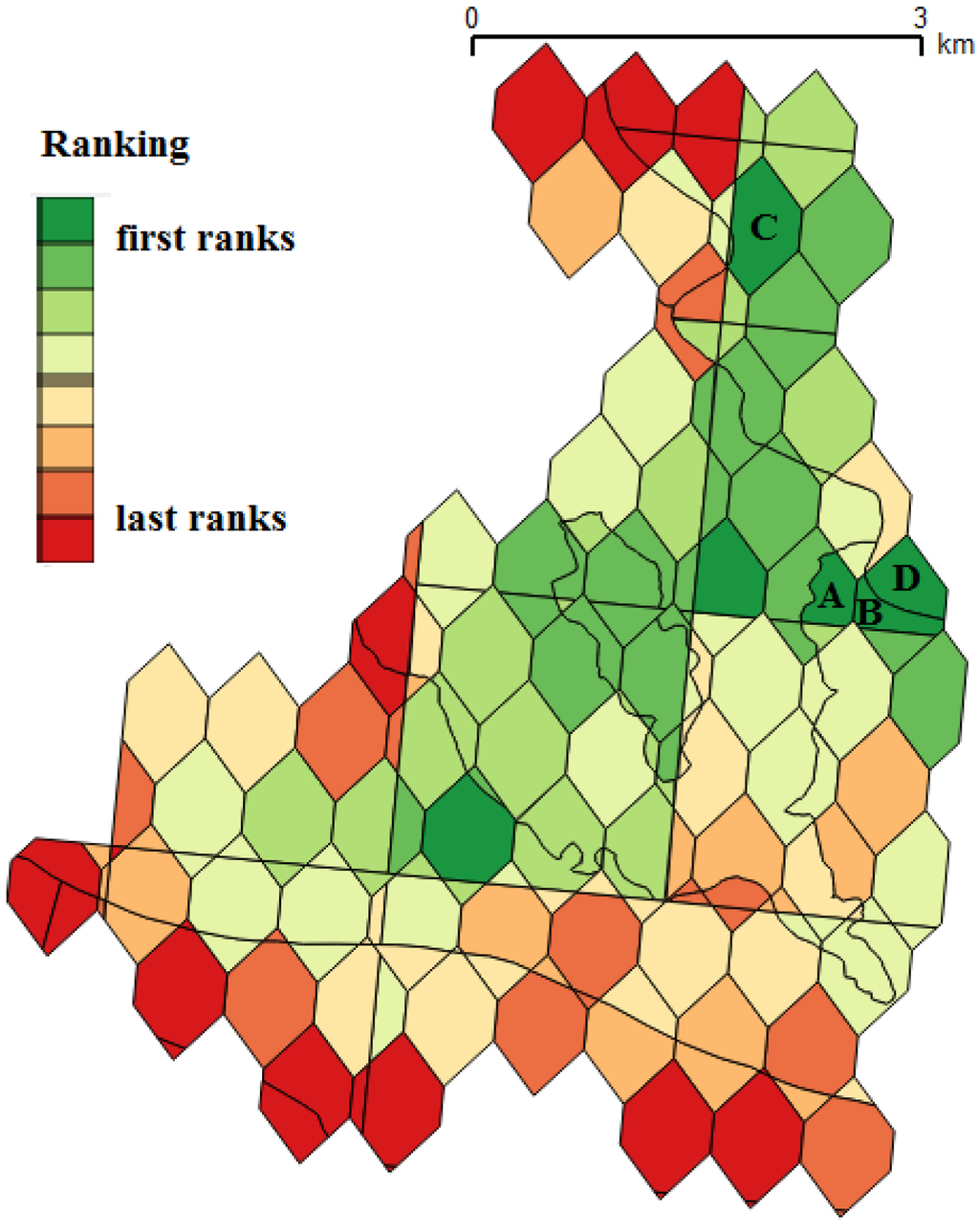
Figure 14.
Areas ranked considering energy, cost and acceptance.
In the case study, no information about the budget allocated for the marine current turbine has been considered so far. As the cost is a minimized criterion with the highest weight, the alternatives generated as best solutions tend to be low-cost projects (i.e., including a single turbine). When and if a budget is allocated, one might search in the project ranking for which one has the best corresponding cost. This actually shows the role of the decision aid component of our approach: the final ranking provides an ordered classification of possible solutions, the final decision being in the hands of the decision-maker. Another method to consider if the budget is given as a straight constraint is to apply the value, project cost-budget, as a minimized criterion.

Table 4.
Spatial unit ranking and turbine characteristics.
| Spatial Unit | Rank | Energy (MWh/year) | Cost (M€) | Pn (MW) | R (m) | TT | NT | NTmax | DT | €/MWh (20 years) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 2710 | 6.3 | 0.5 | 11 | HA | 1 | 5 | PMSG | 116.2 |
| B | 3 | 2860 | 6.5 | 1.1 | 11 | HA + yaw | 1 | 4 | PMSG | 113. 6 |
| C | 6 | 7426 | 11.9 | 0.6 | 12 | HA | 3 | 10 | PMSG | 80.1 |
| D | 7 | 3221 | 7.3 | 2.1 | 11 | HA + yaw | 1 | 7 | PMSG | 113.3 |
5. Conclusions
The research presented in this paper introduces an approach whose objective is to find the most suitable sites and marine farm preliminary design. The method developed integrates and combines GIS, multi-criteria analysis and an optimization algorithm. A first spatial structuring and ranking of the study area according to some social acceptance criteria has been applied using Electre III. For each part of the study area, several types of marine current turbines have been evaluated using a genetic-based optimization process based on cost and energy. A final ranking has been applied re-using Electre III for the three criteria, that is, social acceptance, cost and energy produced. A classification of the areas and the turbine characteristics for each spatial subdivision has been performed. The whole approach is illustrated in a context in which the project manager has to give priority to a low-cost project rather than a project based on social or energy criteria, but the principles behind the decision-based process can be adapted to different scenarios and criteria depending on user choices.
Three criteria have been taken into consideration by our modelling approach. The social acceptance has been limited in this work to fishery areas, but additional geographical constraints can be taken into account with some minor adaptations of our approach. The methodology can also be enriched by some seasonal characteristics of the different activities considered. Cost estimation has been essentially based on the extrapolation of offshore wind turbine current technological knowledge; the parameters used in the model proposed can also be modified as soon as additional feedback on marine current turbines is available.
In further work, a more precise subdivision of the study area will be explored, also taking into account other activities, such as water-based activities or ship corridors and refining the granularity of the temporal dimension. Indeed, the integration of additional spatial criteria is likely to increase the number of spatial subdivisions and decrease the area of the resulting spatial units in the study area, thus potentially reducing the number of turbines that can be installed. We plan to apply some spatial clustering and aggregation techniques, as well as to explore the idea of sharing different technologies at neighboring places. A more precise location of the turbines into the respective spatial units is also a track to explore to increase the efficiency of the marine farm. Other criteria, such as environmental constraints, will be also considered in further work.
Acknowledgments
The authors thank the reviewers for their useful and constructive comments and suggestions. Nicolas Maslov’s research has been founded by the Brittany Region. The authors also thank the SHOM for providing the marine current data.
Author Contributions
Nicolas Maslov is the main contributor of this paper which presents some of the main results of his doctoral research that has been developed under the join supervision of David Brosset, Christophe Claramunt and Jean-Frédéric Charpentier. Jean-Frédéric Charpentier has been particularly involved in the supervision of the marine energy components, while David Brosset and Christophe Claramunt have been guiding Nicolas Maslov for the GIS and genetic algorithm developments. All the computed results and data processing presented in this paper are Nicolas Maslov’s own work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Multon, B. Marine Renewable Energy Handbook; Wiley-ISTE: Hoboken, NJ, USA, 2011. [Google Scholar]
- O’Sullivan, D.L.; Lewis, A.W. Generator selection and comparative performance in offshore oscillating water column ocean wave energy converters. IEEE Trans. Energy Convers. 2011, 26, 603–614. [Google Scholar] [CrossRef]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Marine Tidal Current Electric Power Generation Technology: State of the Art and Current Status. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC ’07), Antalya, Turkey, 3–5 May 2007.
- Roy, B. ELECTRE III: Un algorithme de classements fondé sur une représentation floue des préférences en présence de criteres multiples. Cahiers du CERO 1978, 20, 3–24. [Google Scholar]
- Beccali, M.; Cellura, M.; Mistretta, M. Decision-making in energy planning. Application of the electre method at regional level for the diffusion of renewable energy technology. Renew. Energy 2003, 13, 2063–2087. [Google Scholar]
- Barda, O.H.; Dupuis, J.; Lencioni, P. Multicriteria location of thermal power plants. Eur. J. Oper. Res. 1990, 45, 332–346. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Lalas, D.; Papagiannakis, L. A multicriteria decision aid approach for energy: The case of renewable energy option. Eur. J. Oper. Res. 1997, 103, 38–54. [Google Scholar] [CrossRef]
- Rogers, M.; Bruen, M. Choosing realistic values of indifference, preference and veto thresholds for use with environmental criteria within ELECTRE. Eur. J. Oper. Res. 1998, 107, 542–551. [Google Scholar] [CrossRef]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar]
- Douvere, F. The importance of marine spatial planning in advancing ecosystem-based sea use management. Mar. Policy 2008, 32, 762–771. [Google Scholar]
- Ehler, C.; Douvere, F. Marine Spatial Planning, a Step-by-Step Approach towards Ecosystem-Based Management; Intergovernmental Oceanographic Commission and Man and the Biosphere Programme: Paris, France, 2009. [Google Scholar]
- Chakhar, S. Cartographie Décisionnelle Multicritère: Formalisation et Implémentation Informatique. Ph.D. Thesis, University of Paris Dauphine, Paris, France, 2006. [Google Scholar]
- Young, O.R.; Osherenko, G.; Ekstrom, J.; Crowder, L.B.; Ogden, J.; Wilson, J.A.; Day, J.C.; Douvere, F.; Ehler, C.N.; McLeod, K.L.; et al. Solving the crisis in ocean governance: Place-based management of marine ecosystems. Environ. Sci. Policy Sustain. Dev. 2007, 49, 20–32. [Google Scholar]
- Henderson, A. Offshore Wind Energy—Ready to Power a Sustainable Europe. EU Concerted Action on Offshore Wind Energy in Europe. 2001. Available online: http://www.offshorecenter.dk/log/bibliotek/offshore%20wind%20energy%20ready%20to%20power.PDF (accessed on 12 March 2014).
- Le Guyader, D. Modélisation des Activités Humaines en Mer Côtière. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2012. [Google Scholar]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Comparison of PMSG and DFIG for Marine Current Turbine Applications. In Proceedings of the 2010 XIX International Conference on Electrical Machines (ICEM); Rome, Italy: 6–8 September 2010.
- Suzuki, M. Numerical analysis of horizontal-axis wind turbine characteristics in yawed conditions. Open J. Fluid Dyn. 2012, 2, 331–336. [Google Scholar] [CrossRef]
- Gonzalez, J.S.; Payan, B.M.; Santos, J.R. An Improved Evolutive Algorithm for Large Offshore Wind Farm Optimum Turbines Layout. In Proceedings of the 2011 IEEE Trondheim PowerTech; Trondheim, Norway: 19–23 June 2011.
- Le Tixerant, M.; Gourmelon, F.; Tissot, C.; Brosset, D. Modelling of human activity development in coastal sea areas. J. Coast. Conserv. 2011, 15, 407–416. [Google Scholar] [CrossRef]
- Pham, D.T.; Pham, P.T.N. Artificial intelligence in engineering. Int. J. Mach. Tools Manuf. 1999, 39, 937–949. [Google Scholar] [CrossRef]
- Diveux, T.; Sebastian, P.; Bernard, D.; Puiggali, J.R.; Grandidier, J.Y. Horizontal axis wind turbine systems: Optimization using genetic algorithms. Wind Energy 2001, 4, 151–171. [Google Scholar] [CrossRef]
- Legrand, C. Assessment of Tidal Energy Resource: Marine Renewable Energy Guides; European Marine Energy Centre: London, UK, 2009. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).