Abstract
With the rapid advancement of urbanization in China, the demand for community-based elderly care facilities (CECFs) has been increasing. One pressing challenge is the question of how to provide CECFs that not only meet the health needs of the elderly but also make efficient use of limited urban land resources. This study addresses this issue by adopting an integrated multi-method research framework that combines multi-objective optimization (MOO) algorithms, Spearman rank correlation analysis, ensemble learning methods (Random Forest combined with SHapley Additive exPlanations (SHAP), where SHAP enhances the interpretability of ensemble models), and Self-Organizing Map (SOM) neural networks. This framework is employed to identify optimal building configurations and to examine how different architectural parameters influence key daylight performance indicators—Useful Daylight Illuminance (UDI) and Daylight Factor (DF). Results indicate that when UDI and DF meet the comfort thresholds for elderly users, the minimum building area can be controlled to as little as 351 m2 and can achieve a balance between natural lighting and spatial efficiency. This ensures sufficient indoor daylight while mitigating excessive glare that could impair elderly vision. Significant correlations are observed between spatial form and daylight performance, with factors such as window-to-wall ratio (WWR) and wall thickness (WT) playing crucial roles. Specifically, wall thickness affects indoor daylight distribution by altering window depth and shading. Moreover, the ensemble learning models combined with SHAP analysis uncover nonlinear relationships between various architectural parameters and daylight performance. In addition, a decision support method based on SOM is proposed to replace the subjective decision-making process commonly found in traditional optimization frameworks. This method enables the visualization of a large Pareto solution set in a two-dimensional space, facilitating more informed and rational design decisions. Finally, the findings are translated into a set of practical design strategies for application in real-world projects.
1. Introduction
The world is facing an increasingly severe problem of population aging. Researchers predict that by 2050, the proportion of the population aged 60 and above will reach 21.8%, and by 2100, this proportion could rise to 32.2% [1]. The aging trend in China is particularly significant, with the elderly population expected to account for 34.9% of the total by 2050 [2]. Against this backdrop, improvements in the quality of life of the elderly have become an important goal, and the Chinese government has formulated corresponding strategic measures [3,4]. By the end of 2024, China built 369,000 community elderly care service institutions and facilities, a 1.2-fold increase from 2019 [5]. However, the process of urbanization raised the issue of land availability, with the contradiction between supply and demand becoming increasingly prominent [6,7]. As early as 2008, the building density in the core area of Beijing had already exceeded 20% (building density refers to the ratio of the building footprint area to the total land area) [8], and more than 85% of the permanent population resided there, indirectly reflecting the high-density characteristics of the city center [9]. This phenomenon affects land economics, environmental quality, and spatial structure [10], which in turn impact the internal environment of elderly care buildings [11].
Although related policies have attempted to alleviate land pressure, the imbalance between supply and demand is still one of land scarcity and rising costs [12]. The trend toward architectural intensification further exacerbates issues such as lighting and ventilation, reducing the comfort of elderly residents [13]. The renovation of existing buildings into elderly care facilities has become one practical option, but it faces challenges such as mismatched functional areas, fixed spatial layouts, structural limitations, difficulty in expansion, and insufficient environmental comfort [14,15,16]. Additionally, factors such as small window-to-wall ratios, fixed orientations, and high density tend to result in poor lighting, dampness, and even mold issues [17,18]. Existing research has also highlighted the importance of indoor environments for the health of the elderly [19,20,21], covering aspects such as air quality [22,23,24], lighting [25], thermal comfort [26], and natural daylight [27]. Good daylighting not only enhances thermal comfort [28] but also has a positive impact on mental health [29] and plays an active role in medical rehabilitation [30]. To optimize daylight, some studies have proposed the use of optical devices [31], light tubes [32], and atrium designs [33].
In summary, optimizing indoor daylight is not only an important strategy for enhancing the quality of life for the elderly but also an effective means of addressing urbanization and aging trends. However, in high-density urban environments, there remains a research gap regarding how to optimize daylight within limited building spaces. Therefore, this study uses MOO methods, combining parametric modeling, performance simulation, and machine learning techniques to explore optimal daylight design solutions within the limited space of community elderly care facilities. We aim to identify key design indicators, optimize the internal spatial layout of elderly care service facilities, and provide theoretical support and practical pathways for improving daylight quality in elderly care facilities in high-density urban areas.
2. Literature Review
2.1. The Impact of Indoor Natural Lighting on the Elderly
The indoor lighting performance of a building is commonly evaluated using several key indicators, among which Daylight Factor (DF) and Useful Daylight Illuminance (UDI) are widely used [34,35]. DF refers to the ratio of the indoor illuminance at a certain point under overcast conditions to the simultaneous outdoor horizontal illuminance, which is influenced by factors such as the window-to-wall ratio, glass transparency, and spatial layout, and it reflects the overall natural lighting intensity of a building [36]. For elderly activity areas, experts recommend that the DF be maintained at ≥2% to meet basic visual requirements [37,38], as light exposure significantly affects sleep quality and visual health [39,40]. Studies also suggest that considering the decline in visual sensitivity due to physiological aging, an appropriate DF range is 3–5% [38,41,42]. When DF is below 3%, artificial lighting is required, which not only increases energy consumption but may also lead to visual fatigue, and when DF exceeds 5%, glare and fall risks may occur [43,44].
Therefore, combining DF with UDI in lighting evaluations can provide a more comprehensive perspective—DF captures the stability of daylight under overcast conditions, while UDI reflects dynamic daylight availability throughout the year. This complementary approach supports a more balanced consideration of safety, comfort, energy efficiency, and the specific needs of elderly-friendly design [44]. However, this combination should not be regarded as inherently superior in all contexts, but rather as offering distinct and complementary insights.
UDI is a time-based metric used to assess the effectiveness of natural daylighting by measuring the percentage of time during which the illuminance at a specific point inside a building falls within a predefined range—typically between 100 and 2000 lux—throughout the year [45,46,47]. Studies have shown that for elderly individuals engaged in reading activities, the optimal UDI range is 600–800 lux, with 700 lux being the most effective in alleviating visual fatigue [25,46]. In addition, appropriate natural lighting optimization strategies have been shown to improve both daylight performance and residential comfort, thereby enhancing the overall living environment for older adults [48]. Compared to static DF, UDI can dynamically reflect the availability of light at different times of the year [49,50]. For elderly living spaces, experts recommend that UDI remain within the 100–2000 lx range for over 70% of the year to support visual function and circadian rhythms [25]. When UDI falls below 100 lx, it may disrupt these rhythms and lead to depression, and exceeding 2000 lx may cause glare and eye diseases [46,51]. Using MOO methods can more precisely define appropriate UDI thresholds for the elderly population, thereby improving the quality of the lighting environment [52].
In conclusion, optimizing lighting is not only a functional requirement for buildings but also a key element for ensuring healthy aging. Under the constraints of high urban density and limited land resources, creating a good lighting environment for the elderly remains an important challenge in architectural design.
2.2. Research on Building Performance Based on Multi-Objective Optimization
Amid accelerating global urbanization, the increasing scarcity of construction land has intensified the conflict between land’s economic value and its development intensity [53,54,55]. Therefore, achieving multi-objective collaborative optimization of building functionality and environmental performance under limited-land conditions has become a major challenge in modern architectural design [55,56]. One study in Nanjing demonstrated that a block morphology optimization model based on GA revealed a nonlinear conflict between floor area ratio and lighting performance [57]. Similarly, in high-density urban areas of the Netherlands, insufficient building spacing caused some indoor areas to fail to meet both visual and nonvisual daylighting standards, highlighting the tension between land use intensity and residential quality [53]. Another study, in Mendoza, Argentina, also pointed out that building morphology limits daylight potential, thus requiring the use of solar simulation tools to find a balance between land efficiency and daylight demand [55].
Other studies have shown that combining MOO with parametric modeling can enhance building performance and environmental adaptability [58,59,60], but MOO’s robustness in handling nonlinear and uncertain problems remains limited [61,62]. For example, a study in the temperate region of Australia proposed a window–wall ratio optimization method based on coupled heat transfer and daylighting models to improve daylight efficiency, but its applicability, variable selection, and modeling tools had limitations [63]. Another study introduced MOO for daylight optimization based on the window-to-wall ratio (WWR), but its scope and depth of analysis were relatively limited [64]. A studies have also used parametric design and MOO methods to adjust structural parameters dynamically in order to find an optimal balance between maximizing building area and seasonal daylight performance (UDI) [65]. Many studies have likewise explored factors such as building density, window-to-wall ratio, and spatial area on indoor daylight, emphasizing the resolution of conflicts through façade design to achieve multi-objective collaborative optimization [66,67,68,69].
In the early stages of technological development, multi-objective optimization (MOO) methods faced significant challenges in practical application due to their high algorithmic complexity and limited operability [70]. In recent years, with the continuous advancement of parametric design tools, mainstream platforms such as Rhino/Grasshopper and Revit/Dynamo have gradually integrated evolutionary algorithms like genetic algorithms and simulated annealing. These have been further combined with performance evaluation plugins such as Octopus and Wallacei, significantly enhancing the efficiency and flexibility of MOO applications [54,56,71]. For example, a study conducted in rural residential buildings in cold regions of China employed these integrated tools to optimize daylight performance and thermal comfort, demonstrating the notable advantages of MOO methods in improving building performance [72]. Another study applied a genetic algorithm-based MOO approach to systematically analyze the impact of skylight design on indoor daylight performance [73]. These studies not only validate the applicability of such algorithms in addressing complex design challenges but also provide effective design strategies and methodological support for resolving the conflict between compact spatial layouts and high-quality lighting environments [74,75].
2.3. Decision Support Methods for Optimal Solutions
MOO methods have been widely applied in architectural design and energy efficiency optimization, commonly using genetic algorithms (GAs) [75], Multi-Objective Particle Swarm Optimization (MOPSO) [76], and Nondominated Sorting Genetic Algorithm II (NSGA-II) [77], for example, to generate Pareto fronts for supporting trade-offs between conflicting objectives [78,79]. However, MOO does not directly provide a single optimal solution for all objectives but instead outputs a set of nondominated solutions, where each solution excels in some aspects but may be weaker in others [76]. Therefore, designers need to identify the most feasible solutions from these sets, a process that is still complex and challenging. The main difficulties include the following: (1) the “curse of dimensionality” in high-dimensional objective spaces significantly reduces algorithm convergence efficiency [80]; (2) traditional parameter-sensitive methods, working with prior knowledge, struggle to capture implicit correlations in nonlinear design spaces [81,82]; and (3) the complex topology of Pareto solution sets makes it difficult for existing methods to analyze them effectively in multi-dimensional-parameter contexts [83,84].
To address the difficulty of selecting Pareto solutions, clustering methods such as K-means or hierarchical clustering (e.g., DIANA) are commonly used, but these methods have technical limitations. The K-means algorithm requires pre-setting the number of clusters using the elbow method and is sensitive to outliers due to its reliance on global means during iteration, making data preprocessing complexity grow exponentially, making it infeasible for high-dimensional spaces [85,86,87]. The DIANA algorithm, however, constructs a tree-like structure by progressively partitioning the data, but its reliance on global distance matrix updates can lead to “dimensional distortion” in high-dimensional spaces, reducing the interpretability of clustering results [86,87]. More critically, both methods assume Euclidean distance, which makes them unsuitable for characterizing the intrinsic features of many high-dimensional nonlinear data manifolds, particularly in architectural performance optimization, where nonuniform distribution and multi-peak solution sets are common, leading to clustering distortions. Hence, efficient decision support tools are urgently needed to improve solution selection efficiency and the operability of optimization solutions [88].
SOM, a type of unsupervised neural network model, can map high-dimensional data to a two-dimensional topological grid, and it excels in data classification and visualization [89,90]. SOM does not require pre-setting target weights and can identify potential patterns in complex data, making it especially suitable for feature extraction in high-dimensional nonlinear systems [91,92,93]. In practical analysis, SOM supports dimensionality reduction to identify key influencing factors, and its dynamic learning mechanism adapts to data changes. Studies have shown that SOM can significantly simplify the complexity of high-dimensional solution sets and enhance the diversity and interpretability of solutions in constrained optimization problems [94,95,96,97].
In summary, combining MOO methods with SOM neural networks provides a clear decision-making basis for trade-offs in architectural design.
2.4. Research Innovation and Objectives
This study focuses on key bottleneck issues in the architectural optimization process for elderly communities in high-density urban contexts. The current research faces three main limitations: (1) Due to the high technical threshold of performance simulations, research on lighting requirements for elderly populations remains scarce. (2) Traditional statistical methods (such as multiple linear regression and Pearson correlation coefficients) have limited ability to reveal the nonlinear relationships between building morphology and performance. (3) In MOO, there is a lack of effective decision support mechanisms when dealing with high-dimensional Pareto solution sets, especially when more than three objectives are involved, as conventional K-means and hierarchical clustering methods struggle to handle complex interactions between variables.
To address these issues, we propose the following three research objectives.
- (1)
- This study proposes an optimization framework for CECF in land-constrained urban environments. The framework integrates natural daylight performance simulation with a SOM neural network. It is applied to elderly residential communities in Beijing to verify its practicality and adaptability, providing a reference for future applications in similar urban contexts.
- (2)
- The study innovatively combines Spearman rank correlation analysis with interpretable machine learning models (Random Forest + SHAP) to overcome the limitations of traditional linear models. This approach effectively reveals the nonlinear coupling mechanisms between design parameters and daylighting performance. The SHAP values quantify the contribution of each parameter to overall performance, offering theoretical support for designing elderly care facilities in densely built urban environments.
- (3)
- The study introduces a SOM neural network to construct a topology-preserving mapping model, which projects high-dimensional optimization objectives onto a two-dimensional feature plane. This enables intuitive pattern recognition within the solution set and addresses the “curse of dimensionality” commonly encountered in MOO.
3. Research Methods
3.1. Research Framework
In this study, we propose a cross-platform collaborative optimization framework for designing CECFs (Community Elderly Care Facilities) in high-density urban environments that innovatively integrates parametric modeling, ensemble learning, and MOO techniques to create a “morphology–performance–decision”-integrated intelligent design system. The framework is designed to address the challenges of designing elderly-friendly facilities in central urban areas with limited land and focuses on optimizing spatial efficiency and daylight quality simultaneously, thereby enhancing the decision-making process in the early stages of design. This study also develops a decision support system based on the SOM neural network.
As shown in Figure 1, the framework consists of five core modules: morphology abstraction and parameter modeling, performance simulation, MOO, ensemble learning and correlation analysis, and decision support for the high-dimensional solution space.
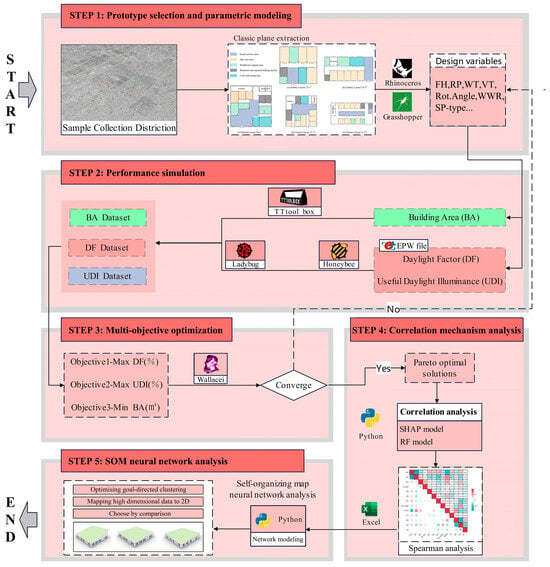
Figure 1.
The research framework.
First, we collect building and spatial morphology data through field surveys of actual CECFs. Based on these surveys, five typical prototypes are identified that represent common design scenarios, and dynamic parametric models are built using Rhino 7/Grasshopper [98]. The models include nine adjustable design variables (orientation, roof pitch, wall thickness, etc.) that can generate thousands of morphological combinations.
In the second phase, performance simulations are conducted. We use Ladybug v1.8.0 [99] and Honeybee v1.8.0 [100] plugins to build a multi-physics simulation platform. Ladybug is used to analyze EPW weather data, and Honeybee integrates the EnergyPlus v24.1.0 [101] energy consumption simulation engine and Radiance/Daysim v6.0 [102] lighting simulation core to achieve simultaneous thermal and optical performance simulations. Then, Latin Hypercube Sampling (LHS) was performed on the design samples using the DSE (Design Space Exploration) plugin in Rhino v7.33 + Grasshopper v1.0.0007. Compared with random sampling, LHS stratifies the input probability distributions to ensure comprehensive coverage of the design space. Through this method, a dataset comprising design parameters and their corresponding performance indicators was constructed. Finally, the sampled data was documented using the TT Toolbox v2.0.7 [103].
To address the conflict between CECF area and daylight performance in high-density urban environments, we also construct a MOO system with UDI and DF as daylight indicators and building area (BA) as a spatial efficiency indicator. Field surveys show that elderly care facilities often suffer from poor daylighting due to high land coverage, intense development, and significant environmental obstruction. Therefore, in this research, we aim to achieve an optimal balance between spatial efficiency and daylight performance by maximizing UDI/DF and minimizing BA and seeking the best design under high-density constraints. The NSGA-II multi-objective genetic algorithm is employed, with the Wallacei X v2.7 [104] plugin to implement a parameter modeling–lighting simulation–optimization–evaluation closed-loop process. The initial population is generated in Grasshopper, and nondominated sorting is used to select dominant individuals. Through crossover and mutation operations, the population is iterated and evolved to obtain the Pareto solution set.
In the fourth stage, the correlation between spatial morphology and performance is analyzed. Two complementary methods are used. First, Spearman’s rank correlation coefficient is used to reveal the linear relationship between key parameters (window-wall ratio, building spacing, etc.) and daylighting indicators. Second, the Random Forest + SHAP interpretability model is implemented in Python v3.13.0 to identify potential nonlinear patterns that traditional methods may overlook [105]. These two methods are then cross-validated: if the key parameters identified by machine learning and Spearman’s correlation are consistent, it indicates that the parameter influence is stable. If discrepancies arise, it may suggest the existence of nonlinear relationships or interactions. This approach both validates statistical patterns and unravels the “black box” of machine learning to provide deeper logical explanations.
Finally, to address the decision-making dilemma of high-dimensional Pareto solution sets, SOM neural network technology is introduced to construct a decision support mechanism for multi-objective spatial–environmental performance optimization in Matlab, which we use to identify superior solutions from the optimization results.
3.2. Study Area
We selected Beijing, China, as the research area and focused on investigating typical CECF architectural forms (see Figure 2). Beijing serves as a representative case for the study for several reasons. First, Beijing has a large and widely distributed elderly population. As of 2023, the population aged 60 and above accounted for 22.6% of the total, which is 1.5 percentage points higher than the national average [106], making the optimization of CECF daylight environments more urgent there. Second, in response to the challenges brought about by population aging, the Beijing municipal government has actively introduced various policies and measures aimed at improving the quality of life for the elderly. Currently, there are 476 community elderly care service stations in Beijing that serve over 1.55 million elderly people [107], providing a rich sample base for this study. In Beijing, community CECFs are commonly referred to as Community Elderly Care Stations (CECSs).
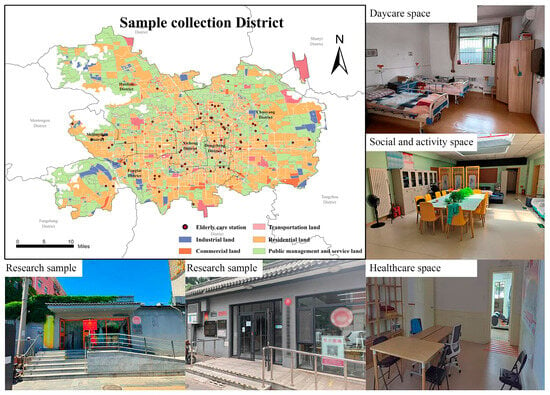
Figure 2.
Study area and distribution of selected samples.
In the previous stage of this research [108], the research team conducted field surveys of 256 CECSs within Beijing’s core functional areas. After excluding closed facilities, 201 samples remained. These facilities were divided into two categories based on their building area and overall scale. We chose to focus on large stations with building areas that exceed 310 square meters. After excluding nonoperational facilities, 72 stations met this research criterion. The representative case samples used in this study all derived from the field survey data of these 72 operational CECSs (see Figure 2).
3.3. Typology Abstraction and Variable Setting
3.3.1. Sample Selection and Typology Abstraction
To address the conflict between “limited land area” and “high daylight demand” faced by CECSs in the high-density development context of Beijing’s central urban areas, we constructed a “MOO framework” with the core goal of “maximizing indoor daylighting performance while minimizing building area.” and conducted a systematic investigation around two key dimensions: “building characteristics” and “site environment characteristics.” In terms of building characteristics, the research emphasizes building form classification, collecting data on floor layout and functional space composition through on-site measurements, and in terms of site environment characteristics, GIS technology was used to extract parameters within a 150 m radius around each station, including road network scale, building spacing, building type composition, interface height distribution, and urban block texture.
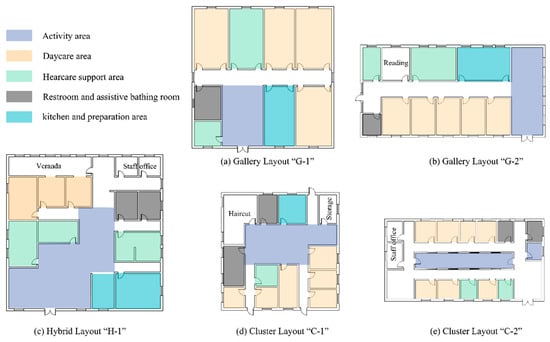
The survey results show that more than 90% of the facilities use a single-story structure, which can be classified into two basic building types based on their forms: point-type buildings and slab-type buildings. According to their spatial organization logic, these two forms are further subdivided into five typical subtypes:
In these two layouts, functional units are arranged along one or both sides of a linear corridor to form a continuous spatial sequence structure.
- (3)
- Point-type building—cluster layout (see Figure 3d);
- (4)
- Slab-type building—cluster layout (see Figure 3e).
These two layouts consist of multiple independent volumes surrounding a central public activity space.
- (5)
- Point-type building—hybrid layout (see Figure 3c). This is a combination of the above two layout features, possessing characteristics of both linear and centralized organization.
Based on statistical analysis results from earlier work [109], five representative building prototypes were selected, labeled as C-1, C-2, G-1, G-2, and H-1, to serve as the basic prototypes for the subsequent parametric modeling phase. The building areas of the five selected prototypes are shown in Table 1.

Table 1.
Classification and area table of building prototypes.
3.3.2. Constraint Conditions and Generation Mechanism Design
Based on the field survey data, we first reconstructed each site’s environmental model, focusing on restoring the narrow streets, low-rise building clusters, and their high-density three-dimensional spatial features in the central urban area of Beijing (see Figure 4). To focus on the interaction between the buildings and the urban interface, the influence of surrounding vegetation on the buildings was excluded during the modeling process. This was carried out to enhance computational efficiency while ensuring the accuracy of daylight simulation results.
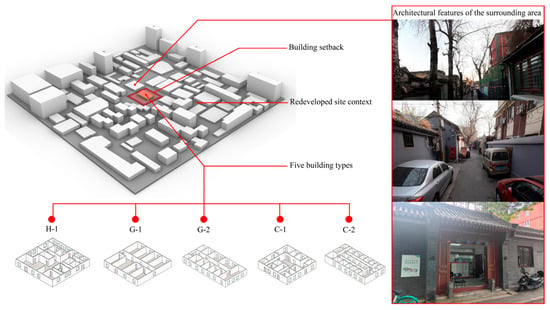
Figure 4.
Site environment modeling and surrounding architectural features.
At the same time, based on the on-site investigation data as well as the Technical Specification for Application of Architectural Glass [109], the Technical Requirements for the Ancillary Frames of Architectural Doors and Windows [110], and The Standard for the design of care facilities for older people [111], this study constructed a two-dimensional variable system of “morphological control–functional constraints” through a parametric platform. In the dimension of morphological control, core design variables such as the window-to-wall ratio (0.2–0.6) and the roof slope (15–20°) were set. Figure 5 explains the 3D visualization of these variables when generating the model, where all the variables and their value ranges are detailed in Table 2. The value ranges of these variables strictly refer to the requirements of the specifications and the measured data.
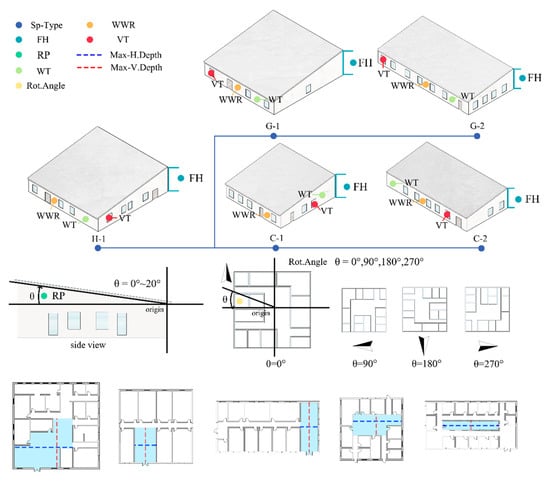
Figure 5.
Visualization of design variable settings.

Table 2.
Design variable settings.
In the “functional constraints” dimension, the focus was on parameters related to the activity room. Two variables were defined, the vertical depth ratio and the horizontal depth ratio, each with a value range of ±15%. This means that, under the premise of a fixed overall building outline, the vertical or horizontal depth of the activity room could be dynamically adjusted within ±15% of the total vertical or horizontal depth. In order to maintain the appropriate scale of the activity space, the dimensions of other functional spaces would be correspondingly reduced or expanded. Under this “dual constraint” framework, we randomly generated a morphological sample library corresponding to the five building prototypes (C-1, C-2, G-1, G-2, H-1) within the fixed site boundary conditions. Each time the form changed during subsequent daylight simulations, a new simulation was conducted.
To evaluate the effectiveness of the optimization results, a baseline model was first established. This model utilized prior analysis to determine the morphological parameter distribution trends for each of the five prototypes statistically. More than seven variables exhibited a positively skewed normal distribution. Therefore, the baseline model adopted the median values for each parameter and shared the same surrounding environment and site conditions as these generated models. The detailed parameter settings are shown in Table 2.
3.3.3. Definition of Core Functional Spaces
Based on previous work [108], we set the activity, daycare, and healthcare support rooms (which, based on field surveys, often include the infirmary, rehabilitation therapy room, and counseling room) as the three core functional spaces most closely associated with elderly individuals’ daily activities in (Community Elderly Care Facilities). Moreover, in most CECFs, the activity room and dining room are combined into a large semi-open space, and these spaces, along with the daycare room, healthcare support room, and other smaller rooms, all have significant lighting needs. In terms of quantifying indicators, we used space ratio coefficients as core evaluation parameters: the activity room ratio (AR), daycare room ratio (DR), and healthcare room ratio (IR). These indicators are represented by the ratio of the effective usable area of each functional space to the total building area, and the mathematical equations for these coefficients are shown in Table 3.

Table 3.
Equation for core functional spaces.
In order to strike a balance between the quantitative nature and practical operability of the research variables, key dimensions of spatial morphology were parameterized during the early design phase. Special attention was given to the dynamic range settings for the horizontal (X-axis) and vertical (Y-axis) depths of the activity spaces. These settings not only provide a basis for variables in the subsequent MOO but also ensure that the calculation of space ratio coefficients have clear physical meaning and comparability.
3.4. Simulation and Calculation of Optimization Objectives
3.4.1. Evaluation Indicators for Optimization Objectives
- 1.
- UDI
UDI is a dynamic evaluation indicator that quantifies the percentage of time throughout the year during which indoor illuminance falls within a specified range. It systematically assesses the availability of natural light within a space from both temporal and spatial perspectives [41]. A higher UDI value indicates longer durations where daylight meets the required illuminance levels while also minimizing glare.
For elderly-friendly environments, the threshold for UDI must be adjusted according to the physiological needs of older adults. A UDI range of 100–2000 lux that covers more than 70% of annual daylight hours is considered appropriate for maintaining visual function and reducing eye fatigue [43,44,45,46,47]. Studies have shown that UDI < 100 lux may disrupt circadian rhythms and increase the risk of depression, and UDI > 2000 lux may lead to glare and worsen visual conditions such as cataracts [25]. MOO methods such as GA can help precisely determine UDI thresholds for caregiving spaces, aligning them with the daily physiological needs of the elderly [51]. Given the dynamic nature of our present study, we adopt UDI as a core metric to evaluate the daylight availability within elderly service stations. UDI is calculated as shown in Equation (4):
- 2.
- DF: Daylight Factor
The Daylight Factor (DF) is a static indicator that measures the ratio between indoor illuminance at a specific point and outdoor illuminance on a horizontal surface under overcast sky conditions, and it is typically expressed as a percentage [34]. DF reflects the efficiency of daylight penetration and the quality of window design by linking the interior light environment to outdoor natural light. Although DF ≥ 2% is generally considered sufficient for basic visual tasks, this threshold must be increased for elderly populations due to their reduced light sensitivity [35,37]. Research suggests that a DF range of 3–6% is more suitable for elderly care environments, effectively compensating for the age-related decline in visual acuity [38]. When DF < 3%, older adults may rely heavily on artificial lighting, increasing energy consumption and causing visual fatigue [37]. DF > 6% can result in uneven lighting and excessive brightness contrast, potentially leading to glare and an increased risk of falls [39]. Due to its simplicity and static nature, DF requires elevated thresholds for elderly spaces. In this study, DF simulation results are integrated with dynamic analysis methods to achieve a balanced and comfortable daylight environment. The formula for DF is given in Equation (5):
- 3.
- BA: Building Area
BA (building area) is the core indicator for measuring spatial efficiency. It refers to the total horizontal projection area of the building above ground level, enclosed by external structures such as exterior walls, and includes the area occupied by structural components. In this study, we aim to address the urgent need for land-intensive use in high-density urban areas and to explore optimization strategies for compact CECSs.
By establishing a multi-objective collaborative optimization model, we optimize building morphology and the area of core functional spaces under the constraint of meeting the above daylight performance benchmarks (a Daylight Factor (DF) controlled between 3% and 6%, and a UDI above 70%). The performance-driven refined design approach advocated in this study seeks to achieve a Pareto optimal balance between lighting quality and spatial efficiency under strict land use limitations, thus providing quantitative decision support for the land-saving design of CECFs in high-density urban areas. The formula for BA is shown in Equation (6):
3.4.2. Simulation Parameters and Calculation Steps
- 1.
- UDI and DF Simulation
The simulation of DF and UDI involves the use of meteorological data, and local meteorological data from the study area must be collected in order to ensure the accuracy of the simulation results. EPW climate data from the Beijing Meteorological Station (Station ID: 545110) was obtained through EnergyPlus for this purpose. The DF simulation was carried out using the Honeybee-Radiance simulation engine. First, a unified analysis grid with a resolution of 0.5 × 0.5 m was established on the primary activity plane for elderly people (at a height of 0.75 m from the ground) in accordance with the “Design Standards for Elderly Residential Buildings” [111]. The reflectance parameters for walls, ceilings, and floors were set as shown in Table 4. Using the Honeybee component, the optical properties of the building surfaces were precisely mapped. The Perez sky model was used to simulate static sky conditions, and the direct adaptive subdivision (DAS) algorithm in Radiance’s ray-tracing engine was employed. The DF value for each analysis point was then calculated using distributed parallel computation, and the final output included both point values and spatial averages, ensuring the continuity of the daylight distribution assessment.

Table 4.
Simulation parameter settings.
To overcome the limitations of static daylight metrics, the UDI simulation was completed using the Daysim engine. The simulation time was set according to the actual operating hours of the CECSs, from 8:00 a.m. to 5:00 p.m. In the standardized analysis grid, the activity plane height was still set at 0.75 m, and the surface reflectance parameters were consistent with those used in the DF simulation. This “DF + UDI” dual-metric verification system effectively combines static daylight quality evaluation with dynamic temporal performance analysis, thus providing a multidimensional data foundation for the subsequent MOO. Before the simulation began, this study compared the simulated results of five building prototypes with field measurement data to verify the accuracy of the generative model. The comparison showed that the error between the two was within 4.5%, meeting the required level of precision and ensuring the reliability of subsequent simulation results.
- 2.
- BA Calculation
The calculation of BA only involves geometric analysis of a building. This process does not include nongeometric variables such as meteorological data or optical material properties. In this study, the floor plan outlines of the five building prototypes were fixed. Thus, the BA was extracted from the building design solutions generated using parametric modeling techniques in Section 3.4, and the area data was calculated using the input formula in (6) in the Colibri geometry calculation module in the TT toolbox plugin.
3.5. MOO
Multi-objective genetic optimization (MOGO) is a method used to enhance overall performance under multiple conflicting objectives by comprehensively analyzing the interactions between various parameters. It simulates the mechanism of natural selection to resolve conflicts between different optimization goals. When multiple conflicting objectives are involved, the solutions typically appear as a set, ultimately forming a nondominated solution set, also known as a Pareto optimal set, that represents the best trade-offs between objectives [112]. Therefore, solving a MOO problem essentially involves finding this set of optimal solutions. The general mathematical expression for the problem is as follows:
In the above mathematical expression, (1 ≤ ≤ k) represents the objective functions, and represents the corresponding constraints. Hence, the set of optimal solutions includes k objective functions and h constraints.
We employ the Nondominated Sorting Genetic Algorithm II (NSGA-II) to generate the Pareto solution set, thereby achieving genetic optimization across multiple objectives. NSGA-II offers several notable advantages: (a) high computational efficiency; (b) algorithmic flexibility; (c) good diversity and distribution of solution sets; and (d) effective constraint-handling capabilities [112,113].
We define three optimization objectives across two main dimensions, building area and daylighting performance, as shown in Table 4. To construct the MOO model and carry out genetic optimization, the design variables listed in Table 2 were used as input data. The mathematical expressions of the optimization objectives are defined by Equations (8)–(10).
, , and represent the three optimization objectives, where denotes the k dimensional design variable vector. The design variables used in this study are listed in Table 2, such as RP, WT, etc. The function represents the constraint functions.
Since the optimization tool by default minimizes objective functions, but both DF and UDI require maximization, we transform these two objectives by taking their negative values. The operational parameters of the NSGA-II algorithm are detailed in Table 5.

Table 5.
NSGA-II algorithm parameter settings.
3.6. Ensemble Learning Method and Spearman Correlation Coefficient
Following MOO, the second generation of solutions generated by the genetic algorithm forms the optimal solution set for prediction. This set comprises two components: one contains building form parameters (including design variables and the defined spatial indicators of the three core functional areas), and the other includes the three optimized performance indicators simulated based on variations in the design variables.
First, the Spearman correlation coefficient was employed to analyze the linear association mechanism between design variables and daylighting indicators [114]. The Spearman rank correlation coefficient is a non-parametric statistical method used to assess the monotonic relationship between two variables, regardless of whether the relationship is linear. Its advantage lies in not requiring the data to follow a normal distribution, making it well suited for evaluating the correlation trends between various environmental parameters and building form features. This statistic quantifies the strength of association within the range of [−1, 1], where values closer to ±1 indicate a stronger correlation; a positive value suggests a promoting effect, while a negative value indicates a suppressing influence [115]. The analysis not only identified key design parameters affecting visual comfort but also generated a heatmap of variable sensitivity rankings, providing a quantitative basis for optimizing indoor daylighting environments in elderly care facilities.
To enhance accuracy, we also integrate Random Forest and the SHAP (SHapley Additive exPlanations) models from interpretable machine learning, to explore nonlinear relationships between form variables and lighting performance. Ensemble learning models are developed using UDI and DF datasets that are split into training and testing sets at a 70:30 ratio. After cross-validation, the system records the coefficient of determination (R2) for both models in the training and testing phases. Specific values are shown in Table 6. The closer the R2 value is to 1, the better the model explains the variance in the data and the higher the goodness-of-fit between predictions and actual observations.

Table 6.
Evaluation parameters of model performance for UDI and DF in training and testing sets.
3.7. SOM Neural Network
In Section 2.3, we highlight a key challenge in existing MOO studies: although MOO algorithms yield many Pareto solutions, architects struggle to efficiently select from high-dimensional results due to complex inter-objective relationships. Traditional clustering methods, such as K-means and hierarchical clustering, often rely on subjective decisions (e.g., preset cluster numbers or manual cuts) and are sensitive to outliers, limiting their effectiveness. To address this, we introduce a Self-Organizing Map (SOM) neural network as a decision support tool. Unlike traditional methods, SOM does not require predefined cluster numbers and updates based on local neighborhood values, reducing clustering errors. Moreover, SOM maintains high-dimensional data integrity while projecting it onto a two-dimensional space, enabling intuitive pattern recognition and improved interpretability of solution sets.
The topological structure used in this study is a hexagonal cell array, which provides better visual interpretability and accuracy than a rectangular matrix. Each cell represents a neuron, and the arrangement and adjacency of cells reflect the neural network structure. Visual elements such as colors, symbols, text, numbers, charts, and images can be overlaid on the cells, further demonstrating the data characteristics of various nondominated solutions. This enables designers to make decisions through a visual exploration process. Although the final results can compress the solution set by more than 33%, there are still limitations. The screening results are influenced by specific threshold constraints on indicators and the number of case data points.
4. Research Results
4.1. MOO Results
After 40 generations of genetic optimization, a total of 214 optimized solutions were generated, and after further excluding 27 duplicate solutions, 187 solutions were finalized as Pareto solutions. A parallel coordinate plot was created for these 187 Pareto-optimized results in which the first three vertical axes on the far left (from left to right) correspond to the results of the three optimization objectives; the three vertical axes on the far right (from right to left) represent the spatial characteristic parameters of the three core functional spaces in the Pareto solutions; and the seven vertical axes in the middle correspond to seven variable design parameters. In this study, these three spatial characteristic parameters and seven design variables were defined as building characteristic parameters. Each line in the plot represents a different Pareto solution.
Figure 6 shows that the distribution range of parameters that describe building characteristics, such as RP, WWR, VT, DR, and IR, is quite broad, and the distribution within each variable’s range is relatively uniform. However, AR is concentrated in the lower end of its range.
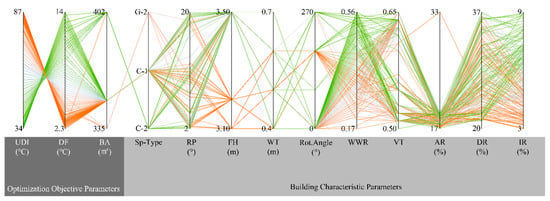
Figure 6.
Parallel coordinate plot of Pareto solutions from MOO. Each complete broken line from left to right represents the number of iterations.
In the Pareto solution set, only three building types were retained: G-2, C-1, and C-2. This indicates that these three building types can achieve a balanced optimization of natural lighting performance while also minimizing building area. Specifically, the performance range of UDI in the Pareto solution set is between 34% and 87%, and the performance range of DF is between 2.3% and 14%.
In order to further determine the effectiveness of the optimization algorithm, three-dimensional line plots of all solutions (Figure 7a) and Pareto solutions (Figure 7b) were created to display the distribution of the three optimization objectives. Figure 7a shows the distribution of lighting performance for different building types in all solutions. The C-1 type has the best overall lighting conditions, with UDI values ranging from 20% to 87% and DF values ranging from 2% to 14.7%. The next best is C-2, with UDI values ranging from 10% to 84% and DF values ranging from 0.4% to 7%. The worst lighting performance is observed in the G-2 type, with UDI values ranging from 15% to 68% and DF values ranging from 0.3% to 5%. Furthermore, it is evident that in the Pareto solutions, the optimization algorithm has excluded the H-1 and G-1 types of elderly building design proposals. The remaining three building types have more concentrated and evenly distributed UDI and DF data. For example, for the G-2 type, the algorithm only retained solutions where the UDI ranged from 36% to 50% and the DF ranged from 2.3% to 4.5%, focusing on solutions with balanced performance for the two lighting metrics. In addition, the threshold performance of the three indicators in the Pareto solution set is superior to that in the unoptimized all-solution set, further confirming that the Pareto solutions selected by the optimization algorithm offer better optimization outcomes.
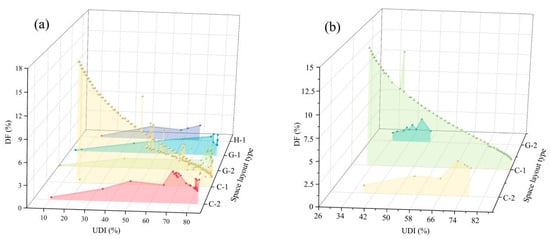
Figure 7.
Three-dimensional polyline plots of all solutions and Pareto solutions. (a) Three-dimensional polyline plot of all solutions; (b) three-dimensional polyline plot of Pareto solutions.
4.2. Spearman Correlation Analysis Results
We use Spearman correlation analysis to quantify the relationship between building characteristic parameters and lighting performance indicators. Figure 8 displays the correlation coefficient matrix between the variables. UDI is significantly positively correlated with WT (0.36) and weakly positively correlated with RP (0.32), but significantly negatively correlated with WWR (−0.53). In contrast, DF is significantly positively correlated with WWR (0.57), significantly negatively correlated with WT (−0.41), and weakly negatively correlated with AR (−0.31). Additionally, there is a very strong negative correlation between the two core lighting evaluation indicators, UDI and DF (−0.93), which is consistent with previous research findings.
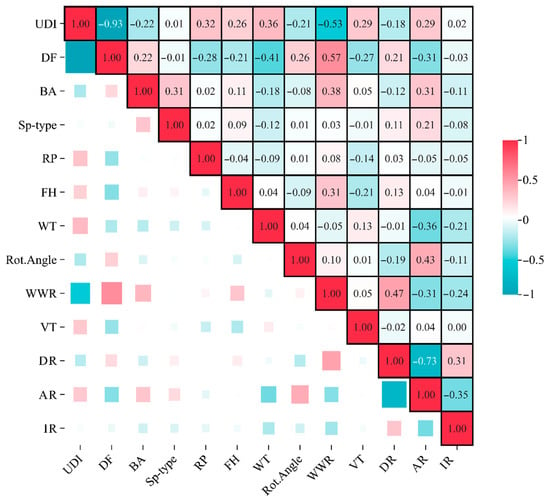
Figure 8.
Spearman correlation coefficient matrix.
These results reveal the interactions between building form parameters and daylight performance indicators. A strong negative correlation was observed between UDI and DF, which is consistent with findings from previous studies. The primary reason for this inverse relationship lies in the differing spatial and temporal characteristics of the two metrics: UDI emphasizes the temporal stability of daylight within a space, whereas DF reflects the total amount of daylight entering the space across its spatial dimensions. This difference is particularly prominent in the opposite effects caused by WWR: although increasing the window-to-wall ratio can improve DF by expanding the lighting area, it also increases direct sunlight penetration, which leads to glare and increased heat load, thus weakening UDI performance. However, thicker walls form deeper window openings, enhancing the entry of diffuse light and thereby extending the effective daylighting duration, but the complex light paths reduce the DF in the deeper areas of the space.
Among the secondary parameters, the weak positive correlation between a small-angle-sloped roof and UDI can likely be attributed to the eaves’ shading effect on direct sunlight. In the core functional spaces, the weak negative correlation between AR and DF suggests that natural light needs to cover a larger floor area, leading to a reduction in light intensity per unit area. Future studies could further isolate the interaction effects between parameters through controlled variable experiments in order to provide more precise data support for more refined CECF lighting environment optimization.
4.3. Ensemble Learning and SHAP Model Results
Although the Spearman correlation analysis revealed linear trends between building characteristic parameters and lighting indicators, due to the limitations of statistical methods in explaining nonlinear relationships and higher-order interaction effects, we also employ the Random Forest algorithm to construct predictive models. Using the SHAP (SHapley Additive exPlanations) interpretability framework further allows us to analyze the nonlinear dependencies and feature contributions between parameters quantitatively after constructing ensemble learning models for annual UDI and DF.
Figure 9a and Figure 10a show the SHAP bar plots for the UDI and DF models, respectively, and Figure 9b and Figure 10b display the corresponding summary plots. SHAP values represent the contribution of each variable to the model’s predictions, and each bar in the bar plot represents a variable, with its length reflecting the average absolute SHAP value for that variable across all samples, indicating the extent of its influence on the prediction result. Bars are arranged in descending order of importance. The summary plot maintains the same variable order, where each point represents a sample, and the color of the point indicates the variable value for that sample. By observing the distribution of points around SHAP = 0, one can determine the positive or negative influence of a variable on the model.
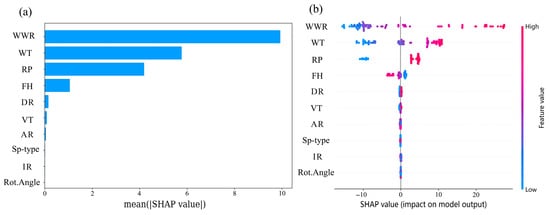
Figure 9.
Bar plot and summary plot of UDI. (a) UDI bar plot; (b) UDI summary plot.
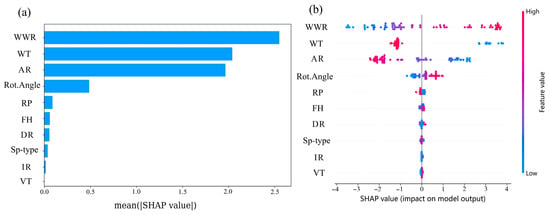
Figure 10.
Bar plot and summary plot of DF. (a) DF bar plot; (b) DF summary plot.
The most significant variables that positively influence UDI are WWR, WT, and RP, and the most notable variables that negatively influence them is FH, with no significant correlation between FH and other indicators. A comparison between the ensemble learning method and the Spearman method reveals that the effects of RP and WWR are opposite, indicating the presence of a complex nonlinear relationship between them and UDI. Additionally, the variable FH was not captured by the Spearman method but was emphasized by ensemble learning methods, further confirming the existence of a complex nonlinear mechanism.
Figure 10a,b show that the variables with the most positive impact on DF are WWR and Rot. Angle. The influence of WWR is consistent with the explanation from the Spearman method, whereas the Rot. Angle is emphasized by the Random Forest and SHAP methods, which can be considered complements to the Spearman method. The variables with the most negative impact are WT and AR, which do align with the results from the Spearman method. Compared to the linear correlation coefficients and statistical significance levels of the Spearman analysis, the results obtained from the machine learning methods show high similarity, which can be viewed as further validation of the linear correlation model. However, results that do differ indicate that certain architectural feature variables and lighting performance indicators may be influenced by nonlinear relationships.
4.4. SOM Neural Network Screening Results
4.4.1. Selection of Building Types
Before building the SOM neural network, we first conducted a comparative analysis of the lighting performance parameters of different building types to select a Pareto solution set that meets the lighting needs of elderly people. First, box plots of DF and UDI for three building types (G-2, C-1, C-2) within the Pareto solution set were plotted (see Figure 10) to visualize their data distribution characteristics. As shown in Figure 11a, the UDI values for the G-2 building type range from 36% to 50%, with a median of 46.7%, which is significantly below the 70% threshold of the elderly building standard and indicates insufficient daylighting performance. The UDI distribution for the C-1 building type is the broadest (34–87%), with a median of 55.3%. Its upper quartile and maximum values outperform those of the other types and show the best uniformity of daylight. The UDI values for the C-2 building type range from 39% to 75%, with a median of 53%, still below the standard line for elderly-friendly environments.
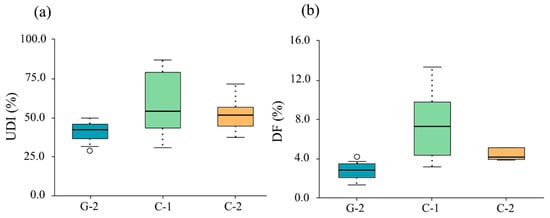
Figure 11.
Box plots of UDI and DF for three building types in Pareto solutions. (a) Box plot of UDI; (b) Box plot of DF.
Further analysis of the DF value distributions (see Figure 11b) reveals that the DF values for the G-2 type range from only 2.3% to 3.9%, far below the 3% supplementary lighting threshold required for elderly people and therefore necessitating increased reliance on artificial lighting and potentially causing visual fatigue. The DF values for the C-1 type have a larger range (3–14%), with a median of 5.8%, which is close to the ideal range, but its extreme values reach 14% and thus exceed the glare risk limit (6%). In contrast, the DF values for the C-2 type strictly range from 3.4% to 5.2%, generally meeting the safe range for indoor lighting environments for the elderly (3–6%).
Based on the above analysis, we selected subsets of the Pareto solution set in which the C-1 type performed well in terms of UDI, while the C-2 type exhibited excellent performance in DF. These two subsets—C-1 with superior UDI and C-2 with better DF—were chosen as the basis for the subsequent SOM analysis.
4.4.2. Daylighting Performance-Oriented SOM Clustering
Based on the 149 Pareto solutions selected in Section 4.4.1, we next constructed a 5 × 9-sized SOM neural network. The normalized optimization objective data were used to train the SOM neural network iteratively until convergence, which resulted in the final SOM model for building optimization objectives. As shown in Figure 12, the neural network displays the distribution characteristics of high-dimensional data in a two-dimensional plane and captures the topological structure of the data.
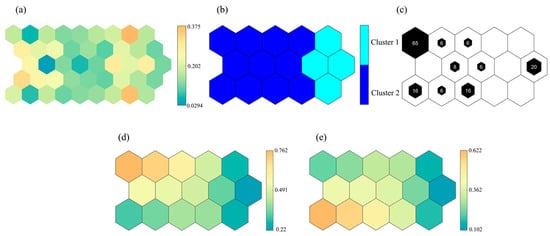
Figure 12.
Two-dimensional SOM mapping results of Pareto solutions. (a) SOM U-matrix; (b) SOM clustering matrix; (c) Number of solutions per neuron; (d) UDI weight matrix; (e) DF weight matrix.
Figure 12a shows the U-matrix of the neural network model, where hexagons in odd rows and odd columns represent the positions of competitive layer neurons. The gradient from blue to yellow indicates the increasing distance between neurons, where the closer the colors of odd rows are to yellow, the greater the average distance between those neurons and their adjacent neurons. Hexagons in even rows and even columns represent the distance between two adjacent neurons, where the closer these colors are to yellow, the sparser the data distribution between two adjacent neurons. The closer to blue they are, the denser the distribution. Neurons with sparse distributions can be thought of as transition boundary values between different clusters.
Because the number of neurons is large, making direct comparison difficult, we mapped the samples onto a two-dimensional plane and performed hierarchical clustering. Different colors represent different clustering categories, as shown in Figure 12b. In Figure 12a,b, we can see that the SOM neural network roughly divides the samples into two categories. In Cluster 1, the average distance between neurons and their adjacent neurons is smaller, indicating that the sample distribution is denser. In contrast, Cluster 2 has a more scattered distribution, suggesting that Cluster 1 has a more compact data distribution than Cluster 2, which may be more suitable for subsequent selection. Similarly, Figure 12c shows the number of samples aggregated by each hexagonal neuron. In Figure 12b,c, we can see that the neurons corresponding to Cluster 1 aggregate the largest number of Pareto solutions and that Cluster 2 aggregates fewer solutions. This further indicates that Cluster 1 may contain more representative data patterns.
Figure 12d,e are the weight matrix plots for the two lighting performance indicators (UDI and DF) used to observe the similarity of optimization objectives between the competitive layer neurons and analyze the relationship between the two objectives. The color gradient from yellow to blue reflects the distribution of the neuron weights from large to small, respectively. The hexagonal distribution patterns in Figure 12d,e are similar, but the neurons on the left side of the matrix exhibit opposite color gradients, indicating a significant negative correlation between the two objectives. Specific numerical analysis shows that neurons with a color closer to yellow have larger weight values and that the corresponding optimization objective values are higher.
By comparing Figure 12b with the UDI weight matrix in Figure 12d, we can see that Cluster 1 generally exhibits better UDI performance (when UDI exceeds 70%, the natural daylighting environment for the elderly is more comfortable). Similarly, by comparing Figure 12b with the DF weight matrix in Figure 12e, it is evident that Cluster 1 also performs better in DF (when DF is in the 3–6% range, it helps reduce the fall risk for the elderly).
The data in Cluster 1 and Cluster 2 were plotted as box plots to quantitatively verify the results of the SOM method and ensure the accuracy of the findings. As shown in Figure 13a, the median DF values of Cluster 1 and Cluster 2 are 4.7 and 9, respectively. Comparing the two, the DF threshold for Cluster 1 ranges from 3.5 to 7, indicating that the light environment in these buildings is the most comfortable, significantly reducing the probability of falls among the elderly. When comparing the UDI indicators of the two clusters, as shown in Figure 13b, the median of Cluster 1 is located near the top of the box, indicating a higher proportion of larger values in the data. This box (representing the main values) is distributed between 67 and 87, indicating that the natural lighting environment in the buildings within Cluster 1 is the most comfortable, with a longer duration of reduced glare, and this finding is consistent with the results of the SOM method. Importantly, this decision support process has certain limitations, as the results are constrained by specific threshold values for the indicators and the number of case data. However, compared to the vast scale of the original solution set (which usually includes hundreds of potential solutions), it is still possible to reduce the solution set size to a manageable range (usually by more than 33%).
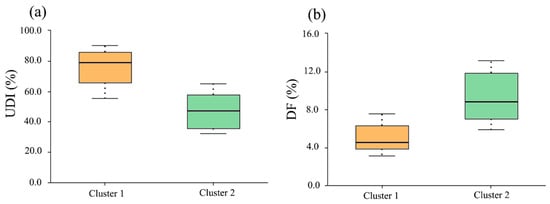
Figure 13.
Box plots of different SOM clusters of Pareto solutions. (a) UDI Pareto solution of different self-organising maps (SOM) clustering box plots; (b) DF Pareto solution of different self-organising maps (SOM) clustering box plots.
After selection, we chose three representative solutions from Cluster 1 for further analysis (as shown in Figure 14). This cluster category exhibits excellent balance among the three key performance indicators of UDI, DF, and BA. For example, the solution for sample Gen.19 Indv.23, with a UDI value of 83%, is well above the 70% threshold required for maintaining normal visual function in the elderly (this level effectively mitigates visual fatigue), and the DF value remains stable at 3.7%, falling precisely within the 3–6% glare control standard range suitable for the elderly (this range helps compensate for the reduced visual sensitivity due to weakened pupil adjustment ability). Moreover, the BA is optimized to 351 m2, fully meeting the minimum building area requirement.
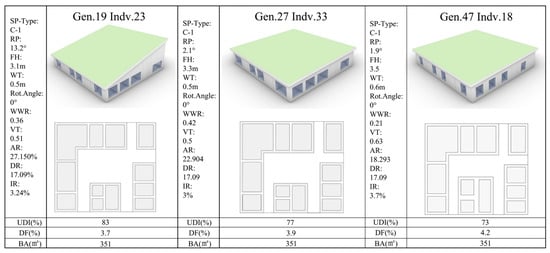
Figure 14.
Selected reference solutions from Cluster 1 and related performance indicators for the three cases.
The large number of Pareto solutions obtained in the earlier stages poses significant challenges for architects during the decision-making process. By refining the decision-making process based on the SOM method, however, we effectively reduced the size of the solution set and compressed the decision space. This enabled designers to make more precise choices within a smaller range, improving the optimization process compared to earlier approaches that mainly rely on K-means or hierarchical clustering methods. Furthermore, the solutions in Cluster 1 have already reached an optimal balance in the three-dimensional objective space. Any further optimization of a single objective would come at the expense of other objectives’ performance.
5. Conclusions
This study focused on exploring ways to maximize natural light performance while minimizing building area in the design of CECFs in the context of urban land resource constraints. Through MOO algorithms, we sought to identify the configuration of the minimum building area that still meets health lighting environment requirements. We systematically analyzed the influence mechanisms of different building characteristic parameters on two core lighting performance indicators, UDI and DF, using two different approaches: Spearman rank correlation analysis and ensemble learning methods (Random Forest + SHAP). Finally, we introduced SOM neural networks to replace traditional optimization frameworks based on subjective decisions or clustering decision methods, successfully reducing the vast solution set and minimizing the decision-making difficulties faced by architects when faced with otherwise large Pareto solution sets. The main findings of the study are enumerated below.
- (1)
- When both UDI and DF meet the comfort standards for the elderly, a minimum building area of 351 square meters is sufficient to balance both. This area ensures adequate natural lighting indoors and avoid excessive glare that could damage the elderly’s eyesight, thereby improving the quality and safety of the indoor lighting environment.
- (2)
- There is a linear relationship between building characteristic parameters and lighting indicators. UDI shows a significant negative correlation with WWR (−0.53), and positive correlations with WT (0.36) and RP (0.32), but DF shows a significant positive correlation with WWR (0.57) and negative correlations with WT, AR, and RP. UDI and DF also exhibit a significant negative correlation with each other (−0.93), indicating a trade-off between the two in the optimization process.
- (3)
- Ensemble learning and SHAP interpretability analysis reveal nonlinear relationships between WWR, WT, RP, FH, UDI, and DF. In particular, a negative correlation between FH and UDI was discovered using ensemble learning methods, suggesting that adjusting building floor heights has the potential to regulate the lighting environment. This also validates the complementary advantages of nonlinear methods and Spearman methods in building performance analysis.
- (4)
- The SOM neural network introduced in this study replaces the clustering methods or subjective decisions typically used in traditional optimization frameworks, helping to pinpoint the optimal building solutions. After mapping 149 Pareto solutions to a two-dimensional neural network space, two clusters were identified. solutions in Cluster 1 performed excellently in both UDI and DF dimensions (UDI: 67% to 87%; DF: 3.5% to 7%), showing good sunlight duration and controllable glare risks, and better meeting the elderly’s demand for a comfortable natural lighting environment. The final three representative solutions were selected for reference.
Based on the above results, we propose the following design strategies.
- (1)
- Recommended Building Type:
In the design of future community-based energy-efficient facilities, point-block building layouts with superior natural daylighting performance should be prioritized—particularly the C-1 type configuration identified in this study. The C-1 type demonstrated outstanding performance within Cluster 1, characterized by high sample concentration and strong design regularity. It effectively balances daylighting quality with building compactness. Therefore, the C-1 configuration is recommended not only as a prototype for newly constructed CECF projects but also as a preferred model for the renovation of existing buildings. Its scalability and adaptability make it especially suitable for urban renewal and the development of age-friendly communities.
- (2)
- Window-to-Wall Ratio (WWR) Control:
The window-to-wall ratio (WWR) affects both Useful Daylight Illuminance (UDI) and Daylight Factor (DF), thus necessitating a careful balance in design. We recommend a WWR of approximately 0.42 for new buildings and a WWR of no less than 0.21 for renovation projects. If the WWR is relatively high, shading devices should be installed to mitigate glare and control sunlight exposure.
- (3)
- Optimization of Building Orientation and Roof Slope:
Building corners should be adjusted to enhance the uniformity of daylight distribution, avoiding problems of overexposure or insufficient lighting caused by excessively uniform north–south orientations. A thoughtful combination of building orientation and roof slope can significantly improve indoor lighting comfort.
- (4)
- Proportion Control of Large Activity Rooms:
Based on our analysis, in cases with limited building area, the proportion of large activity spaces should be controlled within the range of 18% to 27%. This strategy not only fulfills the spatial needs for elderly residents’ daily activities but also ensures adequate daylighting comfort, thereby creating a more balanced indoor environment and enhancing the overall quality of life for older adults.
Additionally, it is important to acknowledge certain limitations of this study. First, the selected base prototype is limited to a CECF located in the Beijing region, which may not fully represent the diversity of other regions. Future studies could extend the validation to CECFs in different climatic zones and at various spatial scales. Moreover, some building form variables did not exhibit significant correlations with performance indicators, which may be due to potential interaction effects. Future research could apply variable isolation techniques for sensitivity analysis to further explore the underlying mechanisms behind these variables.
Author Contributions
Fang Wen and Lu Zhang: conceptualization, methodology, writing—review and editing, data curation, formal analysis, investigation, software, visualization, and writing—original draft; Ling Jiang, Wenqi Sun and Tong Jin: methodology, writing—review and editing, data curation, formal analysis, investigation, software, visualization, and writing—original draft; Fang Wen and Bo Zhang: funding acquisition, project administration, supervision, and writing—review and editing; All authors have read and agreed to the published version of the manuscript.
Funding
Beijing Municipal Social Science Foundation (Grant No. 21SRC024).
Informed Consent Statement
This study did not involve humans.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors thank the Yuxiu Innovation Project of NCUT (Project No. 2024NCUTYXCX214) and Academic Services (www.aimieditor.com).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CECF | Community-Based Elderly Care Facilities |
| SHAP | SHapley Additive exPlanations |
| SOM | Self-Organizing Map |
| MOO | Multi-Objective Optimization |
| WWR | Window-To-Wall Ratio |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| GA | Genetic Algorithms |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| DIANA | Divisive Analysis |
| CECSs | Community Elderly Care Stations |
| GIS | Geographic Information System |
| DAS | Direct Adaptive Subdivision |
| AM | Ante Meridiem |
| PM | Post Meridiem |
| MOGO | Multi-Objective Genetic optimization |
| AR | Activity Room Ratio |
| DR | Daycare Room Ratio |
| IR | Healthcare Support Room Ratio |
| UDI | Useful Daylight Illuminance |
| DF | Daylight Factor |
| BA | Building Area |
References
- World Population Prospects 2024: Summary of Results. Available online: https://desapublications.un.org/publications/world-population-prospects-2024-summary-results (accessed on 21 February 2025).
- Lutz, W.; Sanderson, W.; Scherbov, S. The Coming Acceleration of Global Population Ageing. Nature 2008, 451, 716–719. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, H.; Li, C. Study on the Development Characteristics and Spatial and Temporal Patterns of Population Ageing in 31 Central Cities in China. Front. Public Health 2024, 12, 1341455. [Google Scholar] [CrossRef]
- Ning, J. Analysis of the Impact of Population Aging on the Economy and Countermeasures—Take China as an Example. Highlights Sci. Eng. Technol. 2024, 94, 70–75. [Google Scholar] [CrossRef]
- The Number of Various Elderly Care Institutions and Facilities in China Has Reached 410,000, Doubling Compared to 2019. China News Service, 22 October 2024. Available online: https://www.mca.gov.cn/zt/n2892/n2896/c1662004999980001961/content.html (accessed on 21 February 2025).
- Colantoni, A.; Grigoriadis, E.; Sateriano, A.; Venanzoni, G.; Salvati, L. Cities as Selective Land Predators? A Lesson on Urban Growth, Deregulated Planning and Sprawl Containment. Sci. Total Environ. 2016, 545–546, 329–339. [Google Scholar] [CrossRef]
- Seto, K.C.; Sánchez-Rodríguez, R.; Fragkias, M. The New Geography of Contemporary Urbanization and the Environment. Annu. Rev. Environ. Resour. 2010, 35, 167–194. [Google Scholar] [CrossRef]
- Li, L.H.; Zheng, X.Q.; Xiang, W.N. Research on the Spatial Distribution Law of Building Density in Beijing Based on GIS. China Popul. Resour. Environ. 2008, 18, 122–127. [Google Scholar]
- Achieving the targets set out in the 14th Five-Year Plan ahead of schedule—Over 65%, urbanisation enters the “second half”. Xinhua News Agency, 29 March 2023. Available online: https://www.xinhuanet.com/politics/2023-03/29/c_1129473788.htm (accessed on 5 July 2025).
- Chen, H.; Jia, B.; Lau, S.S.Y. Sustainable Urban Form for Chinese Compact Cities: Challenges of a Rapid Urbanized Economy. Habitat Int. 2008, 32, 28–40. [Google Scholar] [CrossRef]
- Zhang, X.Q. The Trends, Promises and Challenges of Urbanisation in the World. Habitat Int. 2016, 54, 241–252. [Google Scholar] [CrossRef]
- Guan, X.; Wei, H.; Lu, S.; Dai, Q.; Su, H. Assessment on the Urbanization Strategy in China: Achievements, Challenges and Reflections. Habitat Int. 2018, 71, 97–109. [Google Scholar] [CrossRef]
- Han, J.; Fontanos, P.; Fukushi, K.; Herath, S.; Heeren, N.; Naso, V.; Cecchi, C.; Edwards, P.; Takeuchi, K. Innovation for Sustainability: Toward a Sustainable Urban Future in Industrialized Cities. Sustain. Sci. 2012, 7, 91–100. [Google Scholar] [CrossRef]
- Langston, C.; Wong, F.K.W.; Hui, E.C.M.; Shen, L.-Y. Strategic Assessment of Building Adaptive Reuse Opportunities in Hong Kong. Build. Environ. 2008, 43, 1709–1718. [Google Scholar] [CrossRef]
- Xiang, L.; Yu, A.T.W.; Tan, Y.; Shan, X.; Shen, Q. Senior Citizens’ Requirements of Services Provided by Community-Based Care Facilities: A China Study. Facilities 2019, 38, 52–71. [Google Scholar] [CrossRef]
- Ravetz, J. State of the Stock—What Do We Know about Existing Buildings and Their Future Prospects? Energy Policy 2008, 36, 4462–4470. [Google Scholar] [CrossRef]
- Wu, J.; Li, Z.; Yang, T.; Xie, L.; Liu, J. Daylighting Enhancement in Traditional Military Settlement Dwellings of Xiangxi, China: A Study on Cost-Effective and Heritage-Consistent Renovation Approaches. Energy Build. 2024, 316, 114356. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Dong, Z.; Li, L.; Li, W.; Li, S. More Urban Elderly Care Facilities Should Be Placed in Densely Populated Areas for an Aging Wuhan of China. Land 2023, 12, 220. [Google Scholar] [CrossRef]
- Wu, H.-W.; Kumar, P.; Cao, S.-J. Implementation of Green Infrastructure for Improving the Building Environment of Elderly Care Centres. J. Build. Eng. 2022, 54, 104682. [Google Scholar] [CrossRef]
- Mendes, A.; Bonassi, S.; Aguiar, L.; Pereira, C.; Neves, P.; Silva, S.; Mendes, D.; Guimarães, L.; Moroni, R.; Teixeira, J.P. Indoor Air Quality and Thermal Comfort in Elderly Care Centers. Urban Clim. 2015, 14, 486–501. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, Y.; Yu, H.; Wang, F. The Impact of Thermal Environment of Transition Spaces in Elderly-Care Buildings on Thermal Adaptation and Thermal Behavior of the Elderly. Build. Environ. 2023, 228, 109871. [Google Scholar] [CrossRef]
- Rodríguez, M.; Seseña, S.; Valiente, N.; Palop, M.L.; Rodríguez, A. Indoor Air Quality in Elderly Care Centers: A Multidisciplinary Approach. Build. Environ. 2024, 262, 111832. [Google Scholar] [CrossRef]
- Chenari, B.; Dias Carrilho, J.; Gameiro Da Silva, M. Towards Sustainable, Energy-Efficient and Healthy Ventilation Strategies in Buildings: A Review. Renew. Sustain. Energy Rev. 2016, 59, 1426–1447. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, X.; Gao, J.; Cao, G.; Zhou, X.; Su, X. Indoor Air Pollutants, Ventilation Rate Determinants and Potential Control Strategies in Chinese Dwellings: A Literature Review. Sci. Total Environ. 2017, 586, 696–729. [Google Scholar] [CrossRef]
- Mazurek, K.A.; Li, L.; Klein, R.J.; Rong, S.; Mullan, A.F.; Jones, D.T.; St. Louis, E.K.; Worrell, G.A.; Chen, C.Y. Investigating the Effects of Indoor Lighting on Measures of Brain Health in Older Adults: Protocol for a Cross-over Randomized Controlled Trial. BMC Geriatr. 2024, 24, 816. [Google Scholar] [CrossRef]
- Su, Y.; Gong, A.; Wang, C.; Han, Y.; Gao, W. Exploring Thermal Comfort for the Older Adults: A Comparative Study in Dalian City’s Diverse Living Environments. Front. Archit. Res. 2025, 14, 812–824. [Google Scholar] [CrossRef]
- Morales-Bravo, J.; Navarrete-Hernandez, P. Enlightening Wellbeing in the Home: The Impact of Natural Light Design on Perceived Happiness and Sadness in Residential Spaces. Build. Environ. 2022, 223, 109317. [Google Scholar] [CrossRef]
- Du, X.; Zhang, Y.; Zhao, S. Research on Interaction Effect of Thermal, Light and Acoustic Environment on Human Comfort in Waiting Hall of High-Speed Railway Station. Build. Environ. 2022, 207, 108494. [Google Scholar] [CrossRef]
- Hwang, T.; Kim, J.T. Effects of Indoor Lighting on Occupants’ Visual Comfort and Eye Health in a Green Building. Indoor Built Environ. 2011, 20, 75–90. [Google Scholar] [CrossRef]
- Zeng, X.; Luo, P.; Wang, T.; Wang, H.; Shen, X. Screening Visual Environment Impact Factors and the Restorative Effect of Four Visual Environment Components in Large-Space Alternative Care Facilities. Build. Environ. 2023, 235, 110221. [Google Scholar] [CrossRef]
- Jong-Woei Whang, A.; Wang, C.-C.; Chen, Y.-Y. Design of Cascadable Optical Unit to Compress Light for Light Transmission Used for Indoor Illumination. Renew. Energy 2009, 34, 2280–2295. [Google Scholar] [CrossRef]
- Li, D.H.W.; Tsang, E.K.W.; Cheung, K.L.; Tam, C.O. An Analysis of Light-Pipe System via Full-Scale Measurements. Appl. Energy 2010, 87, 799–805. [Google Scholar] [CrossRef]
- Samant, S. A Critical Review of Articles Published on Atrium Geometry and Surface Reflectances on Daylighting in an Atrium and Its Adjoining Spaces. Archit. Sci. Rev. 2010, 53, 145–156. [Google Scholar] [CrossRef]
- Ngarambe, J.; Adilkhanova, I.; Uwiragiye, B.; Yun, G.Y. A Review on the Current Usage of Machine Learning Tools for Daylighting Design and Control. Build. Environ. 2022, 223, 109507. [Google Scholar] [CrossRef]
- Ma, J.; Inoue, T.; Fang, Q.; Li, K.; Li, M. A Study on Optimal Opening Configuration for Art Museum Exhibition Space Considering Daylight Performance, Indoor Thermal Comfort, and Energy Consumption. Sustainability 2023, 15, 16431. [Google Scholar] [CrossRef]
- Li, D.H.W.; Tsang, E.K.W. An Analysis of Daylighting Performance for Office Buildings in Hong Kong. Build. Environ. 2008, 43, 1446–1458. [Google Scholar] [CrossRef]
- Sinoo, M.M.; Van Hoof, J.; Kort, H.S.M. Light Conditions for Older Adults in the Nursing Home: Assessment of Environmental Illuminances and Colour Temperature. Build. Environ. 2011, 46, 1917–1927. [Google Scholar] [CrossRef]
- Yang, H.; Guo, B.; Shi, Y.; Jia, C.; Li, X.; Liu, F. Interior Daylight Environment of an Elderly Nursing Home in Beijing. Build. Environ. 2021, 200, 107915. [Google Scholar] [CrossRef]
- Yang, E.; Ismail, A.; Kim, Y.; Erdogmus, E.; Boron, J.; Goldstein, F.; DuBose, J.; Zimring, C. Multidimensional Environmental Factors and Sleep Health for Aging Adults: A Focused Narrative Review. Int. J. Environ. Res. Public Health 2022, 19, 15481. [Google Scholar] [CrossRef]
- Maksoud, A.; Hussien, A.; Mushtaha, E.; Alawneh, S.I.A.-R. Computational Design and Virtual Reality Tools as an Effective Approach for Designing Optimization, Enhancement, and Validation of Islamic Parametric Elevation. Buildings 2023, 13, 1204. [Google Scholar] [CrossRef]
- Gerhardsson, K.M.; Hassan, M.; Tornberg, Å.B.; Schmidt, S.M. Usability and Feasibility of an Online Intervention for Older Adults to Support Changes to Routines and the Home (‘Light, Activity and Sleep in My Daily Life’). BMC Public Health. 2024, 24, 2808. [Google Scholar] [CrossRef]
- Kumar, S.; Underwood, S.H.; Masters, J.L.; Manley, N.A.; Konstantzos, I.; Lau, J.; Haller, R.; Wang, L.M. Ten Questions Concerning Smart and Healthy Built Environments for Older Adults. Build. Environ. 2023, 244, 110720. [Google Scholar] [CrossRef]
- Ashe, M.C. Indoor Environments and Promoting Physical Activity Among Older People. In The Palgrave Handbook of Ageing and Physical Activity Promotion; Nyman, S.R., Barker, A., Haines, T., Horton, K., Musselwhite, C., Peeters, G., Victor, C.R., Wolff, J.K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 467–483. ISBN 978-3-319-71290-1. [Google Scholar]
- Cilasun Kunduraci, A.; Karagözler, S.; SeviNç Karci, Z. Indoor Environmental Quality in Residential Care Facilities: A Scoping Review with Design Focus. Mimar. Bilim. Ve Uygulamaları Derg. MBUD 2023, 8, 123–145. [Google Scholar] [CrossRef]
- Nabil, A.; Mardaljevic, J. Useful Daylight Illuminances: A Replacement for Daylight Factors. Energy Build. 2006, 38, 905–913. [Google Scholar] [CrossRef]
- Cubukcuoglu, C.; Cilasun Kunduraci, A.; Asadollahi Asl Zarkhah, S. Indoor Environmental Quality Optimisation Model for Institutional Care Rooms of Elderly People. Buildings 2023, 13, 2625. [Google Scholar] [CrossRef]
- Tao, Y.; Gou, Z.; Yu, Z.; Fu, J.; Chen, X. The Challenge of Creating Age-Friendly Indoor Environments in a High-Density City: Case Study of Hong Kong’s Care and Attention Homes. J. Build. Eng. 2020, 30, 101280. [Google Scholar] [CrossRef]
- Juda, M.; Liu-Ambrose, T.; Feldman, F.; Suvagau, C.; Mistlberger, R.E. Light in the Senior Home: Effects of Dynamic and Individual Light Exposure on Sleep, Cognition, and Well-Being. Clocks Sleep 2020, 2, 557–576. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Gao, X.; Du, J. The Association between Perceived Housing Environment and Health and Satisfaction among the Older Adults during the COVID-19 Pandemic: A Cross-Sectional Survey in Northern China. Buildings 2023, 13, 2875. [Google Scholar] [CrossRef]
- Gábrová, L. Comparison between Dynamic and Static Metrics for Daylight Evaluation in the Case of Obstructed Buildings. AMM 2016, 861, 477–484. [Google Scholar] [CrossRef]
- Van Hoof, J.; Kort, H.S.M.; Duijnstee, M.S.H.; Rutten, P.G.S.; Hensen, J.L.M. The Indoor Environment and the Integrated Design of Homes for Older People with Dementia. Build. Environ. 2010, 45, 1244–1261. [Google Scholar] [CrossRef]
- Falkenberg, H.K.; Kvikstad, T.M.; Eilertsen, G. Improved Indoor Lighting Improved Healthy Aging at Home – an Intervention Study in 77-Year-Old Norwegians. J. Multidiscip. Healthc. 2019, 12, 315–324. [Google Scholar] [CrossRef]
- Koster, D.; Rafiee, A.; Brembilla, E. The Effect of Urban Density on Compliance with Indoor Visual and Non-Visual Daylight Targets: A Dutch Case Study. Sustain. Cities Soc. 2025, 120, 106149. [Google Scholar] [CrossRef]
- Mesa, N.A.; Corica, L.; Pattini, A. Evaluation of the Potential of Natural Light to Illuminate Buildings in Dense Urban Environment. A Study in Mendoza, Argentina. Renew. Energy 2011, 36, 2414–2423. [Google Scholar] [CrossRef]
- Steemers, K. Energy and the City: Density, Buildings and Transport. Energy Build. 2003, 35, 3–14. [Google Scholar] [CrossRef]
- Tan, P.Y.; Ismail, M.R.B. Building Shade Affects Light Environment and Urban Greenery in High-Density Residential Estates in Singapore. Urban For. Urban Green. 2014, 13, 771–784. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Xia, Y.; Song, Y.; Xie, H. Optimization of Urban Block Form by Adding New Volumes for Capacity Improvement and Solar Performance Using a Multi-Objective Genetic Algorithm: A Case Study of Nanjing. Buildings 2022, 12, 1710. [Google Scholar] [CrossRef]
- Wang, L.; Janssen, P.; Chen, K.W.; Tong, Z.; Ji, G. Subtractive Building Massing for Performance-Based Architectural Design Exploration: A Case Study of Daylighting Optimization. Sustainability 2019, 11, 6965. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, J.; Zheng, R. Multi-Objective Optimization of Building Energy Saving Based on the Randomness of Energy-Related Occupant Behavior. Sustainability 2024, 16, 1935. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, K.; Ni, E.; Deng, Q. Optimizing Classroom Modularity and Combinations to Enhance Daylighting Performance and Outdoor Platform through ANN Acceleration in the Post-Epidemic Era. Heliyon 2023, 9, e21598. [Google Scholar] [CrossRef]
- Besbas, S.; Nocera, F.; Zemmouri, N.; Khadraoui, M.A.; Besbas, A. Parametric-Based Multi-Objective Optimization Workflow: Daylight and Energy Performance Study of Hospital Building in Algeria. Sustainability 2022, 14, 12652. [Google Scholar] [CrossRef]
- Budaiwi, I.M.; Abdul Fasi, M. Assessing the Energy-Saving Potential and Visual Comfort of Electrochromic Smart Windows in Office Buildings: A Case Study in Dhahran, Saudi Arabia. Sustainability 2023, 15, 9632. [Google Scholar] [CrossRef]
- Chen, Z.; Hammad, A.; Kamardeen, I.; Haddad, A. Optimising Window Design on Residential Building Facades by Considering Heat Transfer and Natural Lighting in Nontropical Regions of Australia. Buildings 2020, 10, 206. [Google Scholar] [CrossRef]
- Society for Research on Education, Design, and Architecture (SEDARCH), Ottawa, Canada; Kharvari, F. A Field-Validated Multi-Objective Optimization of the Shape and Size of Windows Based on Daylighting Metrics in Hot-Summer Mediterranean and Dry Summer Continental Climates. J. Daylighting 2020, 7, 222–237. [Google Scholar] [CrossRef]
- Khidmat, R.P.; Fukuda, H.; Kustiani. Design Optimization of Hyperboloid Wooden House Concerning Structural, Cost, and Daylight Performance. Buildings 2022, 12, 110. [Google Scholar] [CrossRef]
- Lu, Y.; Wolf, T.; Kang, J. Optimization of Facade Design Based on the Impact of Interior Obstructions to Daylighting. Build. Simul. 2016, 9, 1–14. [Google Scholar] [CrossRef]
- Ghamari, M.; Sundaram, S. Solar Window Innovations: Enhancing Building Performance through Advanced Technologies. Energies 2024, 17, 3369. [Google Scholar] [CrossRef]
- Rezaei, F.; Sangin, H.; Heiranipour, M.; Attia, S. Multi-Objective Optimization of Window and Light Shelf Design in Office Buildings to Improve Occupants’ Thermal and Visual Comfort. J. Daylighting 2024, 11, 55–68. [Google Scholar] [CrossRef]
- Ciardiello, A.; Rosso, F.; Dell’Olmo, J.; Ciancio, V.; Ferrero, M.; Salata, F. Multi-Objective Approach to the Optimization of Shape and Envelope in Building Energy Design. Appl. Energy 2020, 280, 115984. [Google Scholar] [CrossRef]
- Kabiri, E.; Maftouni, N. Multiple Objective Energy Optimization of a Trade Center Building Based on Genetic Algorithm Using Ecological Materials. Sci. Rep. 2024, 14, 9366. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Zhong, Q.; Wu, J.; Xie, L. Multi-Objective Optimization of Daylighting Performance and Energy Consumption of Educational Buildings in Different Climatic Zones of China. J. Build. Eng. 2024, 95, 110322. [Google Scholar] [CrossRef]
- Fang, Y.; Cho, S.; Wang, Y.; He, L. Sensitivity Analysis and Multi-Objective Optimization of Skylight Design in the Early Design Stage. Energies 2023, 17, 219. [Google Scholar] [CrossRef]
- Gassar, A.A.A.; Koo, C.; Kim, T.W.; Cha, S.H. Performance Optimization Studies on Heating, Cooling and Lighting Energy Systems of Buildings during the Design Stage: A Review. Sustainability 2021, 13, 9815. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, W.; Wang, W. BIM-Based Multi-Objective Optimization of Low-Carbon and Energy-Saving Buildings. Sustainability 2022, 14, 13064. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-Objective Optimization Using Genetic Algorithms: A Tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-Objective Optimization of the Building Energy Performance: A Simulation-Based Approach by Means of Particle Swarm Optimization (PSO). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-Objective Optimization of Energy Performance for a Detached Residential Building with a Sunspace Using the NSGA-II Genetic Algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of Multi-Objective Genetic Algorithm to Optimize Energy Efficiency and Thermal Comfort in Building Design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Bre, F.; Fachinotti, V.D. A Computational Multi-Objective Optimization Method to Improve Energy Efficiency and Thermal Comfort in Dwellings. Energy Build. 2017, 154, 283–294. [Google Scholar] [CrossRef]
- Bandaru, S.; Ng, A.H.C.; Deb, K. Data Mining Methods for Knowledge Discovery in Multi-Objective Optimization: Part A—Survey. Expert Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
- Hakimi-Asiabar, M.; Ghodsypour, S.H.; Kerachian, R. Deriving Operating Policies for Multi-Objective Reservoir Systems: Application of Self-Learning Genetic Algorithm. Appl. Soft Comput. 2010, 10, 1151–1163. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Fleming, P.J. Methods for Multi-Objective Optimization: An Analysis. Inf. Sci. 2015, 293, 338–350. [Google Scholar] [CrossRef]
- Suga, K.; Kato, S.; Hiyama, K. Structural Analysis of Pareto-Optimal Solution Sets for Multi-Objective Optimization: An Application to Outer Window Design Problems Using Multiple Objective Genetic Algorithms. Build. Environ. 2010, 45, 1144–1152. [Google Scholar] [CrossRef]
- Okabe, T.; Oya, Y.; Yamamoto, G.; Sato, J.; Matsumiya, T.; Matsuzaki, R.; Yashiro, S.; Obayashi, S. Multi-Objective Optimization for Resin Transfer Molding Process. Compos. Part Appl. Sci. Manuf. 2017, 92, 1–9. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H. A Clustering Method Based on K-Means Algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar] [CrossRef]
- Li, T.; Rezaeipanah, A.; Tag El Din, E.M. An Ensemble Agglomerative Hierarchical Clustering Algorithm Based on Clusters Clustering Technique and the Novel Similarity Measurement. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 3828–3842. [Google Scholar] [CrossRef]
- Shahidinejad, A.; Ghobaei-Arani, M.; Masdari, M. Resource Provisioning Using Workload Clustering in Cloud Computing Environment: A Hybrid Approach. Clust. Comput. 2021, 24, 319–342. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A Review on Building Energy Efficient Design Optimization Rom the Perspective of Architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Bre, F.; Roman, N.; Fachinotti, V.D. An Efficient Metamodel-Based Method to Carry out Multi-Objective Building Performance Optimizations. Energy Build. 2020, 206, 109576. [Google Scholar] [CrossRef]
- Astudillo, C.A.; Oommen, B.J. Topology-Oriented Self-Organizing Maps: A Survey. Pattern Anal. Appl. 2014, 17, 223–248. [Google Scholar] [CrossRef]
- Delgado, S.; Higuera, C.; Calle-Espinosa, J.; Morán, F.; Montero, F. A SOM Prototype-Based Cluster Analysis Methodology. Expert Syst. Appl. 2017, 88, 14–28. [Google Scholar] [CrossRef]
- Palomo, E.J.; North, J.; Elizondo, D.; Luque, R.M.; Watson, T. Application of Growing Hierarchical SOM for Visualisation of Network Forensics Traffic Data. Neural Netw. 2012, 32, 275–284. [Google Scholar] [CrossRef]
- Ramírez-Alonso, G.; Chacón-Murguía, M.I. Auto-Adaptive Parallel SOM Architecture with a Modular Analysis for Dynamic Object Segmentation in Videos. Neurocomputing 2016, 175, 990–1000. [Google Scholar] [CrossRef]
- He, C.; Li, M.; Zhang, C.; Chen, H.; Zhong, P.; Li, Z.; Li, J. A Self-Organizing Map Approach for Constrained Multi-Objective Optimization Problems. Complex Intell. Syst. 2022, 8, 5355–5375. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yue, C.; Yu, K.; Qu, B.; Xu, R.; Li, Z.; Hu, Y. A Clustering-Based Differential Evolution Algorithm for Solving Multimodal Multi-Objective Optimization Problems. Swarm Evol. Comput. 2021, 60, 100788. [Google Scholar] [CrossRef]
- Yi, Y.K. Building Facade Multi-Objective Optimization for Daylight and Aesthetical Perception. Build. Environ. 2019, 156, 178–190. [Google Scholar] [CrossRef]
- Zawidzki, M.; Szklarski, J. Multi-Objective Optimization of the Floor Plan of a Single Story Family House Considering Position and Orientation. Adv. Eng. Softw. 2020, 141, 102766. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. Multi-objective Optimal Power Flow Using Grasshopper Optimization Algorithm. Optim. Control Appl. Methods 2024, 45, 623–645. [Google Scholar] [CrossRef]
- Ladybug, version 1.8.0. Software for Technical Computation. Ladybug Tools: Fairfax, VA, USA, 2024.
- Honeybee, version 1.8.0. Software for Technical Computation. Ladybug Tools: Fairfax, VA, USA, 2024.
- EnergyPlus, version 24.1.0. Software for Technical Computation. Department of Energy: Washington DC, USA, 2024.
- Radiance, version 6.0a. Software for Technical Computation. Radsite: Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2025.
- TT Toolbox, version 2.0.7. Software for Technical Computation. Thornton Tomasetti: New York, NY, USA, 2024.
- Evolutionary Engine for Grasshopper3D, version 2.7. Software for Technical Computation. Wallacei Team: London, UK, 2022.
- Python, version 3.13.0. Software for Technical Computation. Python Software Foundation: Beaverton, OR, USA, 2024.
- Beijing Elderly Career Development Report; Beijing Municipal Civil Affairs Bureau: Beijing, China, 2024. Available online: https://mzj.beijing.gov.cn/art/2024/10/21/art_4490_735482.html (accessed on 21 February 2025).
- Statistics of the Civil Affairs Bureau; Beijing Municipal Civil Affairs Bureau: Beijing, China, 2025. Available online: https://mzj.beijing.gov.cn/art/2025/1/2/art_10834_684684.html (accessed on 21 February 2025).
- Wen, F.; Zhang, Y.; Du, P.; Zhang, Z.; Zhang, B.; Zhang, Y. Factors Influencing the Usage Frequency of Community Elderly Care Facilities and Their Functional Spaces: A Multilevel Based Study. Buildings 2024, 14, 1827. [Google Scholar] [CrossRef]
- JGJ 113-2015; Technical Specification for Application of Architectural Glass. Ministry of Housing and Urban-Rural Development of People’s Republic of China: Beijing, China, 2015.
- GB/T 39866-2012; Technical Requirements for the Ancillary Frames of Architectural Doors and Windows. State Administtation for Market Regulation: Beijing, China, 2012.
- JGJ 450-2018; Standard for Design of Care Facilities for the Aged. Ministry of Housing and Urban-Rural Development of People’s Republic of China: Beijing, China, 2018.
- Harkouss, F.; Fardoun, F.; Biwole, P.H. Multi-Objective Optimization Methodology for Net Zero Energy Buildings. J. Build. Eng. 2018, 16, 57–71. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; De Stasio, C.; Mauro, G.M.; Vanoli, G.P. Multi-Objective Optimization of the Renewable Energy Mix for a Building. Appl. Therm. Eng. 2016, 101, 612–621. [Google Scholar] [CrossRef]
- Ieva, F.; Ronzulli, M.; Romo, J.; Paganoni, A.M. A Spearman Dependence Matrix for Multivariate Functional Data. J. Nonparametric Stat. 2025, 37, 82–104. [Google Scholar] [CrossRef]
- Zhang, W.-Y.; Wei, Z.-W.; Wang, B.-H.; Han, X.-P. Measuring Mixing Patterns in Complex Networks by Spearman Rank Correlation Coefficient. Phys. A Stat. Mech. Its Appl. 2016, 451, 440–450. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).