Submarine Terrain Generalization in Nautical Charts: A Survey of Traditional Methods and Graph Neural Network Solutions
Abstract
1. Introduction
- The basic theory and methodology of chart generalization and GNN;
- A review of the generalization of various types of submarine terrain data;
- Discussion of the limitations of the classical methods in cartographic generalization, with case studies to illustrate how GNN can effectively deal with these challenges, especially in terms of geographic feature representation, data processing, and the generalization process;
- Introduction to the advantages and challenges of GNN. By comparing different GNN architectures vertically and comparing them horizontally with other popular architectures. The advantages of GNN in cartographic generalization are shown. The challenges of developing GNN in the context of submarine geomorphology generalization are presented;
- The concluding remarks are presented.
2. Fundamental Knowledge on Chart Generalization and GNN
2.1. Main Operators for Chart Generalization
2.2. Traditional Methods of Chart Generalization
2.3. Graph Neural Network
3. Generalization of Various Types of Submarine Terrain Data
3.1. Generalization of Soundings
- Taking the shallow soundings and leaving the deeper soundings so as to ensure navigational safety.
- Focusing on the selection of important soundings that can reflect the channel and other negative seabed topography.
- Rational distribution of soundings should be in the form of a diamond as far as possible. The ratio of the rhombus should be adjusted according to the requirements.
- The selection of soundings should be harmonized with other elements such as coastlines and depth contours.
3.1.1. Sounding Generalization of Cartographic Products
3.1.2. Sounding Generalization of Bathymetry Survey Results
3.1.3. Sounding Generalization of the Digital Bathymetric Model
3.2. Generalization of Depth Contours
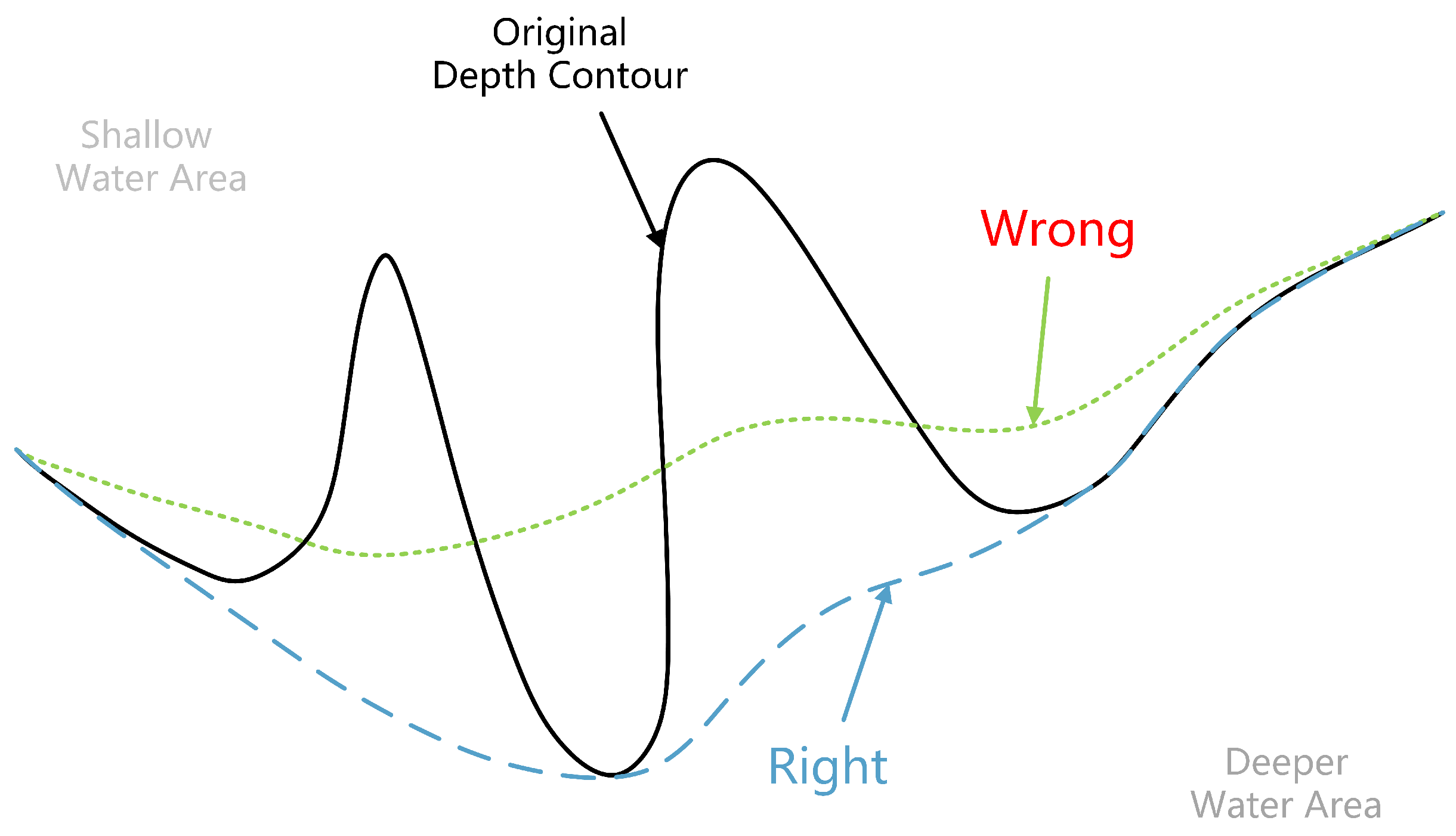
- The trend of depth contours before and after generalization must remain consistent with the primary characteristics of the seabed topography.
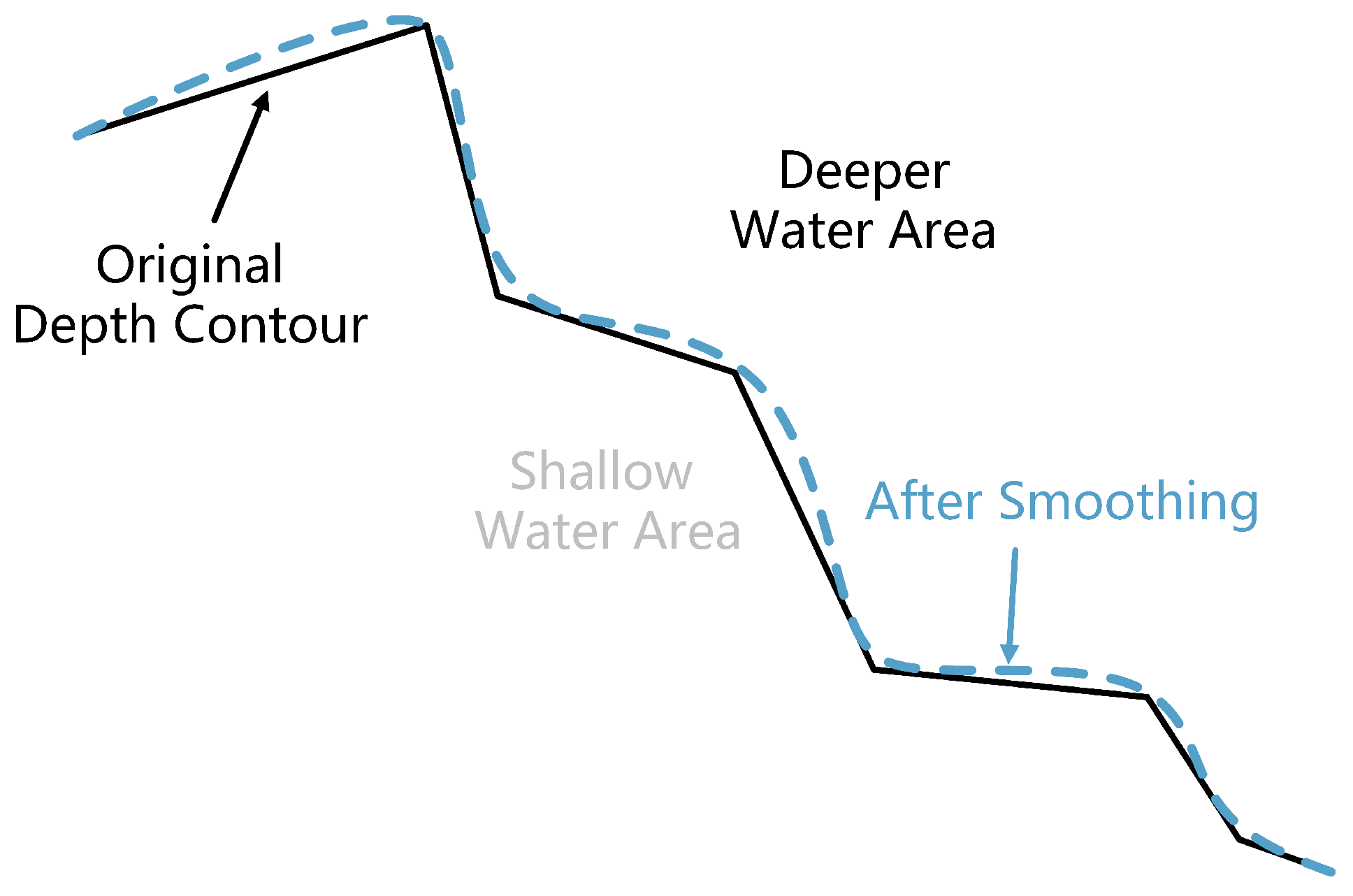
- In the process of generalization, it is necessary to make the area of shallow water larger than that before generalization and the area of deep water smaller than that before generalization, i.e., “expansion of shallow water and reduction of deep water” (Figure 11), in order to ensure the safety of navigation.
- Topological errors such as intersections, self-intersections, and mutual overlapping of depth contours should not occur.
- Only essential information should be retained and presented in a clear and understandable manner.
3.2.1. Generalization Based on Geometric Elements
3.2.2. Generalization Based on Submarine Terrain
3.3. Generalization of Coastlines
- It should be ensured that the position of the connection point of the polyline is accurate because they are the skeleton of the coastlines.
- Shape maintenance: Coastlines should maintain the curved shape and outer contours of the graphic.
- “Expanding the land and reducing the sea”: Priority should be given to retaining important headlands and discarding smaller bays. In some special cases, they can be appropriately exaggerated. It is particularly important in the production of large-scale nautical charts and must be strictly observed.
3.4. Generalization of Islands and Reefs
- No isolated islands are allowed to be discarded at any scale, regardless of size.
- If it is not possible to accurately plot small islands clustered together or close to the coast at the scale, they may be represented by black dots of a certain diameter.
4. Critical Problems and Graph Neural Networks as Solutions
- GNN is capable of learning multiple features of non-Euclidean data.
- Geometric elements in a chart can be conceptualized as graph structures to address the unique challenges associated with cartographic generalization.
4.1. Geographic Feature Representation
4.2. Data Processing
4.3. Generalization Process
5. Advantages and Challenges of Graph Neural Networks
5.1. Different Architectures of GNN
5.2. Advantages of GNN
5.3. Experimental Verification
5.3.1. Establishment of a Simple Graph Structure
5.3.2. Simple Model Settings
5.3.3. Comparison with Traditional Methods
5.4. Challenges
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Hongbo, C.; Wenxuan, F.U.; Mengya, C. A Brief Analysis on the Data Differences between Topographic Map and Electronic Chart. Geomat. Spat. Inf. Technol. 2018, 41, 243–245. [Google Scholar]
- Zhao, W.; Hui, Z.; Center, T.H. Reviewon Nautical Chart Automatic Generalization. Hydrogr. Surv. Charting 2017, 37, 51–54. [Google Scholar]
- Brassel, K.E.; Weibel, R. A review and conceptual framework of automated map generalization. Int. J. Geogr. Inf. Syst. 1988, 2, 229–244. [Google Scholar] [CrossRef]
- Oraas, S. Automated sounding selection. In The International Hydrographic Review; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Tsoulos, L.; Stefanakis, K. Sounding selection for nautical charts: An expert system approach. In Proceedings of the 18th International Cartographic Conference, Stockholm, Sweden, 23–27 June 1997; pp. 23–27. [Google Scholar]
- Nada, T.; Kastrisios, C.; Calder, B.; Ence, C.; Greene, C.; Bethell, A. Towards automating the nautical chart generalization workflow. Geo-Spat. Inf. Sci. 2024, 27, 1–26. [Google Scholar] [CrossRef]
- Woodlief, M. Unlock insights from hydrographic data with GeoAI. Int. Hydrogr. Rev 2024, 30, 144–149. [Google Scholar] [CrossRef]
- Wang, J.Y.; Tian, Z. The cartographic generalization of soundings on chart by artificial neural network techniques. Acta Geod. Cartogr. Sin. 1999, 28, 335–339. [Google Scholar]
- Jia, S.; Song, Z.; Zhang, L.; Liang, Z. A Case-Based Reasoning Method for Generalizing Depth Contours considering Both Navigational Safety Assurance and Line Shape Preservation. Mar. Geod. 2024, 47, 1–22. [Google Scholar] [CrossRef]
- Song, Z.; Jia, S.; Liang, Z.; Zhang, L.; Liang, C. A reinforcement learning method for collaborative generalization of soundings and depth contours. Acta Geod. Cartogr. Sin. 2024, 53, 1345. [Google Scholar]
- Wu, F.; Du, J.; Qian, H.; Zhai, R. Overview of research progress and reflections in intelligent map generalization. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1675–1687. [Google Scholar]
- Yu, W. Automatic sounding generalization in nautical chart considering bathymetry complexity variations. Mar. Geod. 2018, 41, 68–85. [Google Scholar] [CrossRef]
- Lu, Y.; Zhai, J.; Du, J. Sounding selection based on recognition of submarine topography features. J. Inst. Surv. Mapp. 2000, 17, 296–300. [Google Scholar]
- Zhai, J.; Lu, Y. Recognition and measurement of marine topography for sounding generalization in digital nautical chart. Mar. Geod. 2005, 28, 167–174. [Google Scholar]
- Jinghan, L.I.; Fang, W.U.; Ruixing, X.; Jiawei, D.U.; Qingguang, D.; University, I.E. Recognition of Complex Seabed Regions for Nautical Chart Generalization. J. Geomat. Sci. Technol. 2018, 35, 524–528. [Google Scholar]
- Wang, M.; Zhang, L.; Yu, C.; Liu, T. Distilling Feature Shallow Points from Soundings Based on the Slope-Relationship. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 208–213. [Google Scholar]
- Liu, Y.; Zhai, J.; Lu, Y.; Wang, M. Automatic generalization of sounding in digital chart. Acta Geod. et Cartogr. Sin. 2005, 34, 179–184. [Google Scholar]
- Li, J. Research on Automated Cartographic Generalization of Submarine Relief. Ph.D. Thesis, PLA Strategic Support Force Information Engineering University, Zhengzhou, China, 2018. [Google Scholar]
- Li, J.; Wu, F.; Du, J.; Gong, X.; Xing, R. Chart Depth Contour Simplification Based on Delaunay Triangulation. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 778–783. [Google Scholar]
- Li, J.; Wu, F.; Du, J.; Xing, R. Study on Automated Aggregation of Depth Contour on Nautical Charts. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1484–1490. [Google Scholar]
- Ai, T.; Zhou, Q.; Zhang, X.; Huang, Y.; Zhou, M. A simplification of ria coastline with geomorphologic characteristics preserved. Mar. Geod. 2014, 37, 167–186. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, L.; Dong, J.; Wei, H.; Wei, S. An Adaptive Simplification Method for Coastlines Using a Skeleton Line “Bridge” Double Direction Buffering Algorithm. ISPRS Int. J. Geo-Inf. 2024, 13, 155. [Google Scholar] [CrossRef]
- Lu, Y.; Zhai, J.; Du, J.; Li, S. Recognition, measurement and generalization for point cluster features in digital nautical chart. Geomat. Inf. Sci. Wuhan Univ. 2001, 26, 133–139. [Google Scholar]
- Huang, Y.; Ai, T.; Liu, Y.; Zhang, H. Geographic-feature oriented ria coastline simplification. Acta Geod. Cartogr. Sin. 2013, 42, 595–601. [Google Scholar]
- Huang, Y. Research on Supporting Data Models and Methods for Maritime Feature Generalization; Wuhan University: Wuhan, China, 2011. [Google Scholar]
- Yafeng, H.; Tinghua, A.I.; Hangfeng, Z. Automatic selection of soundings based on Voronoi diagram. Sci. Surv. Mapp. 2016, 41, 28–33. [Google Scholar] [CrossRef]
- Peters, R.; Ledoux, H.; Meijers, M. A Voronoi-based approach to generating depth-contours for hydrographic charts. Mar. Geod. 2014, 37, 145–166. [Google Scholar] [CrossRef][Green Version]
- Yan, H.; Weibel, R. An algorithm for point cluster generalization based on the Voronoi diagram. Comput. Geosci. 2008, 34, 939–954. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, Y. An Automatic Selecting Model of Islands in Chart. Hydrogr. Surv. Charting 2005, 25, 23–25. [Google Scholar]
- Tang, L.; Zhang, L.; Xu, W.; Jia, S.; Dong, J. A Composite Influence Domain Model for Automatically Selecting Islands in Nautical Charts. Mar. Geod. 2020, 43, 189–212. [Google Scholar] [CrossRef]
- Zhu, J.; Lu, Y. A New Method of Island Cartography Generalization. Hydrogr. Surv. Charting 2004, 17–19. [Google Scholar]
- Fei, L.; He, J. A three-dimensional Douglas–Peucker algorithm and its application to automated generalization of DEMs. Int. J. Geogr. Inf. Sci. 2009, 23, 703–718. [Google Scholar] [CrossRef]
- Shuaidong, J.; Lihua, Z.; Rencan, P. Method for automatic selection of water depth harmonizing with a depth contour. J. Harbin Eng. Univ. 2016, 37, 59–64. [Google Scholar]
- Guimin, H.; Jinhua, G.; Lin, L. Research on Depth Contour Generalization Method Based on Curve Characteristic. Hydrogr. Surv. Charting 2014, 34, 38–41. [Google Scholar]
- Haisen, L.; Dan, L.; Yukuo, W.; Bin, Y. Fast algorithm of contour generation for a multibeam seafloor terrain. J. Harbin Eng. Univ. 2012, 33, 622–628. [Google Scholar]
- Yang, H.; Li, L.; Hu, H.; Wu, Y.; Xia, H.; Liu, Y.; Tan, S. A coastline generalization method that considers buffer consistency. PLoS ONE 2018, 13, e0206565. [Google Scholar] [CrossRef] [PubMed]
- Qi, Q.; Liu, Y. An Automated Solution to the Graphic Generalization of Discontinuous Area Phenomena. Geogr. Res. 1996, 15, 1–10. [Google Scholar]
- Sui, H.; Zhu, X.; Zhang, A. A system for fast cartographic sounding selection. Mar. Geod. 2005, 28, 159–165. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, L.; Jia, S. A method for selecting islands based on their influence domains. Hydrogr. Surv. Charting 2018, 38, 67–70. [Google Scholar]
- Tang, L.; Zhang, L.; Jia, S.; Li, B. A Method for Islands Automatic Selection Based on Buffer Dynamic Growing Model. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1874–1882. [Google Scholar]
- Tang, L.; Zhang, L.; Jia, S.; Liu, X. Line Element Synthesis Method Based on Rolling-circle. Hydrogr. Surv. Charting 2019, 39, 16–19. [Google Scholar]
- Tang, L.; Zhang, L.; Dong, J.; Jia, S. Automatic simplification and merging algorithm of isobaths based on surface simplification. In Proceedings of the International Conference on Geographic Information and Remote Sensing Technology (GIRST 2022), Kunming, China, 16–18 September 2022; Volume 12552, pp. 898–903. [Google Scholar]
- Guilbert, E.; Saux, E. Cartographic generalisation of lines based on a B-spline snake model. Int. J. Geogr. Inf. Sci. 2008, 22, 847–870. [Google Scholar] [CrossRef]
- Miao, D. Gradual Generalization of Nautical Chart Contours with a B-Spline Snake Method. Master’s Thesis, University of New Hampshire, Durham, NH, USA, 2014. [Google Scholar]
- Miao, D.; Calder, B. Gradual generalization of nautical chart contours with a cubic B-spline snake model. In Proceedings of the 2013 OCEANS-San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–7. [Google Scholar]
- Wu, F.; Zhu, K. Geometric accuracy assessment of linear features’ simplification algorithms. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 600–603. [Google Scholar]
- Fang, W.; Jiawei, D.; Fanghua, W. A survey of the research progress in automated generalization of submarine terrain data. Acta Geod. Cartogr. Sin. 2022, 51, 1588. [Google Scholar]
- Tang, Q. A study on automated generalization of submarine relief. Acta Geod. Cartogr. Sin. 1987, 16, 314–320. [Google Scholar]
- Zhu, M.; Yang, B.; Wang, M.; You, B.; Liu, G. The present situation and analysis of the comprehensive study of water depth in digital chart. Hydrogr. Surv. Charting 2018, 38, 11. [Google Scholar]
- Zoraster, S.; Bayer, S. Automated cartographic sounding selection. Int. Hydrogr. Rev. 1992, 69, 57–61. [Google Scholar]
- Dyer, N.; Kastrisios, C.; De Floriani, L. Label-based generalization of bathymetry data for hydrographic sounding selection. Cartogr. Geogr. Inf. Sci. 2022, 49, 338–353. [Google Scholar] [CrossRef]
- Dyer, N.; Kastrisios, C.; De Floriani, L. Chart features, data quality, and scale in cartographic sounding selection from composite bathymetric data. Geo-Spat. Inf. Sci. 2024, 27, 1542–1567. [Google Scholar] [CrossRef]
- Stateczny, A.; Gronska-Sledz, D.; Motyl, W. Precise bathymetry as a step towards producing bathymetric electronic navigational charts for comparative (terrain reference) navigation. J. Navig. 2019, 72, 1623–1632. [Google Scholar] [CrossRef]
- Smith, S.M.; Alexander, L.; Armstrong, A.A. The navigation surface: A new database approach to creating multiple products from high-density surveys. Int. Hydrogr. Rev. 2002, 3, 12–16. [Google Scholar]
- Maleika, W. The Effect of the Density of Measurement Points Collected from a Multibeam Echosounder on the Selection of IDW Interpolation Points in the Process of Creating Seabed Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 7292–7304. [Google Scholar] [CrossRef]
- Wen, J.; Li, J.; Xing, R.; Du, J.; Liu, X. A thinning algorithm of multibeam sounding data considering the complexity of seabed terrain. J. Geomat. Sci. Technol. 2018, 35, 435–440. [Google Scholar]
- Mo, W.; He-Yuan, L.I.; Xiao-Nan, Z. A sounding-generalization method based on the rhomb box-counting fractal dimension estimate. Eng. Surv. Mapp. 2015, 24, 17–21. [Google Scholar] [CrossRef]
- Skopeliti, A.; Stamou, L.; Tsoulos, L.; Pe’eri, S. Generalization of soundings across scales: From DTM to harbour and approach nautical charts. ISPRS Int. J. Geo-Inf. 2020, 9, 693. [Google Scholar] [CrossRef]
- Li, M.; Zhang, A.; Zhang, D.; Di, M.; Liu, Q. Automatic Sounding Generalization Maintaining the Characteristics of Submarine Topography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10278–10286. [Google Scholar] [CrossRef]
- Yu, L.; Du, J.; Zhai, R.; Wu, F.; Qian, H. A fast generalization method of multibeam echo soundings for nautical charting. J. Geovis. Spat. Anal. 2022, 6, 1–12. [Google Scholar] [CrossRef]
- Tsai, V.J. Delaunay triangulations in TIN creation: An overview and a linear-time algorithm. Int. J. Geogr. Inf. Sci. 1993, 7, 501–524. [Google Scholar] [CrossRef]
- Ying, Z.; Yi, L.U.; Hong-Yan, J.; Ming, S.; Zhong-Dong, Z.; Ying, C.; Yan, L.U. Research on Automatic Generalization of Digital Soundings. Hydrogr. Surv. Charting 2008, 48–51. [Google Scholar]
- Kastrisios, C.; Calder, B.; Masetti, G.; Holmberg, P. Towards automated validation of charted soundings: Existing tests and limitations. Geo-Spat. Inf. Sci. 2019, 22, 290–303. [Google Scholar] [CrossRef]
- Zhang, L.; Jia, S.; Wu, C.; Yin, X. A method for interpolating digital depth model considering uncertainty. Acta Geod. Cartogr. Sin. 2011, 40, 359–365. [Google Scholar]
- Jia, S.; Zhang, L.; Dong, J.; Peng, R. A method for constructing DDM serving for navigation using pre-constructed model surface to control and adjust the selection of DDM nodes. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1715–1722. [Google Scholar]
- Alcaras, E.; Amoroso, P.P.; Figliomeni, F.G.; Parente, C.; Vallario, A. Using Electronic Navigational Chart for 3D bathymetric model of the port of Naples. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 7–13. [Google Scholar] [CrossRef]
- Guilbert, E.; Zhang, X. Generalisation of submarine features on nautical charts. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 13–18. [Google Scholar] [CrossRef]
- Saux, E. B-spline functions and wavelets for cartographic line generalization. Cartogr. Geogr. Inf. Sci. 2003, 30, 33–50. [Google Scholar] [CrossRef]
- Xing, R.; Wu, F.; Li, J.; Gong, X. A fast algorithm of contour generation considering ambiguity. J. Comput.-Aided Des. Comput. Graph. 2017, 29, 1705–1712. [Google Scholar]
- Lida, W.; Xiaodong, Y.; Lihua, Z. Efficient Algorithm to Tracing Nodes of Equivalent Depth Based on Topology of Triangles. Port Waterw. Eng. 2007, 13–16. [Google Scholar]
- Wang, Z.; Müller, J.C. Line generalization based on analysis of shape characteristics. Cartogr. Geogr. Inf. Syst. 1998, 25, 3–15. [Google Scholar] [CrossRef]
- Hongcheng, W.; Lihua, Z.; Lulu, T.; Jian, D.; Gaixiao, L.; Hao, Y. Complexity measurement of line element on nautical chart considering local difference. Acta Geod. Cartogr. Sin. 2022, 51, 1959. [Google Scholar]
- Li, J.; Wu, F.; Gong, X.; Du, J.; Xing, R. Depth contour smoothing based on the fitting of multi-segment bezier curves. Mar. Geod. 2018, 41, 382–404. [Google Scholar] [CrossRef]
- Lianfa, W.; Lihua, Z.; Shuaidong, J. Application of Snake Model in Auto Simplification of a Depth-Contour. Hydrogr. Surv. Charting 2016, 36, 15–18. [Google Scholar]
- Kim, Y.J.; Lee, J.S.; Kong, G.Y.; Cho, I.S. A study on the creation of high density depth contours in coastal waters using spatial analysis based on depth and AIS data. J. Coast. Disaster Prev. 2022, 9, 157–165. [Google Scholar] [CrossRef]
- Skopeliti, A.; Tsoulos, L.; Pe’eri, S. Depth contours and coastline generalization for harbour and approach nautical charts. ISPRS Int. J. Geo-Inf. 2021, 10, 197. [Google Scholar] [CrossRef]
- Ning, Z.; Jiang, C.; Chen, J.; Wu, Z.; Yao, Z.; Ma, Y.; Deng, T.; Chen, Y. Long-term spatiotemporal analysis of coastline morphological evolutions and their underlying mechanisms in the Pearl River Delta region of China. Ocean Coast. Manag. 2024, 258, 107426. [Google Scholar] [CrossRef]
- Liu, H.; Xie, S.; Wang, F. Study on the Method of Automatic Cartographic Generalization of Coastline. J. Geomat. Sci. Technol 2010, 27, 225–228. [Google Scholar]
- Christensen, A.H. Cartographic line generalization with waterlines and medial-axes. Cartogr. Geogr. Inf. Sci. 1999, 26, 19–32. [Google Scholar] [CrossRef]
- Lewin, S.; Jiang, X.; Clausing, A. Perceptually motivated shape evolution with shape-preserving property. Pattern Recognit. Lett. 2010, 31, 447–453. [Google Scholar] [CrossRef]
- Visvalingam, M.; Whyatt, J.D. Line generalization by repeated elimination of points. In Landmarks in Mapping; Routledge: London, UK, 2017; pp. 144–155. [Google Scholar]
- Chen, H.; Peng, R.; Zheng, Y.; Li, S. Coastline generalization based on skeleton line of curve bends. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1418–1422. [Google Scholar]
- Ai, T. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Liu, Y.; Zhai, J. The research on pattern presentation and automatic generalization of coastlines. Geomat. Spat. Inf. Technol 2005, 28, 78–81. [Google Scholar]
- Wang, L.; Wu, Y.; Tang, J. A coastline generalization method for marine delimitation. Sci. Surv. Mapp 2015, 40, 18–21. [Google Scholar] [CrossRef]
- Töpfer, F.; Pillewizer, W. The principles of selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Steiniger, S.; Burghardt, D.; Weibel, R. Recognition of island structures for map generalization. In Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, Hamburg, Germany, 13–16 November 2006; pp. 67–74. [Google Scholar]
- Anderson-Tarver, C.; Leyk, S.; Buttenfield, B.P. Fuzzy modeling of geometric textures for identifying archipelagos in area-patch generalization. Cartogr. Geogr. Inf. Sci. 2011, 38, 137–145. [Google Scholar] [CrossRef]
- Müller, J.; Zeshen, W. Area-patch generalisation: A competitive approach. Cartogr. J. 1992, 29, 137–144. [Google Scholar] [CrossRef]
- Qiao, W.; Hehai, W. The research on fractal method of automatic generalization of map polygons. Geomat. Inf. Sci. Wuhan Univ. 1996, 21, 59–63. [Google Scholar]
- McBrearty, I.W.; Beroza, G.C. Earthquake location and magnitude estimation with graph neural networks. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 3858–3862. [Google Scholar]
- Zhang, F.; Sun, Q.; Huang, W.; Su, Y.; Ma, J.; Xing, R. Enhancing the Recognition of Collinear Building Patterns by Shape Cognition Based on Graph Neural Networks. Appl. Artif. Intell. 2024, 38, 2439611. [Google Scholar] [CrossRef]
- Rampášek, L.; Galkin, M.; Dwivedi, V.P.; Luu, A.T.; Wolf, G.; Beaini, D. Recipe for a general, powerful, scalable graph transformer. Adv. Neural Inf. Process. Syst. 2022, 35, 14501–14515. [Google Scholar]
- Shi, Y.; Li, Q.; Zhu, X.X. Building segmentation through a gated graph convolutional neural network with deep structured feature embedding. ISPRS J. Photogramm. Remote Sens. 2020, 159, 184–197. [Google Scholar] [CrossRef]
- Pan, Z.; Xu, L.; Chen, N. Combining graph neural network and convolutional LSTM network for multistep soil moisture spatiotemporal prediction. J. Hydrol. 2025, 651, 132572. [Google Scholar] [CrossRef]
- Yu, D.; Bai, G.; Li, Y.; Zhao, L. Deep spatial domain generalization. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Orlando, FL, USA, 28 November–1 December 2022; pp. 1293–1298. [Google Scholar]
- Li, Y.; Lu, X.; Yan, H.; Wang, W.; Li, P. A skeleton-line-based graph convolutional neural network for areal settlements’ shape classification. Appl. Sci. 2022, 12, 10001. [Google Scholar] [CrossRef]
- Tianyuan, X.; Tinghua, A.; Huafei, Y.; Min, Y.; Pengcheng, L. A point cluster simplification approach of graph convolutional neural network for map generalization. Acta Geod. Cartogr. Sin. 2024, 53, 158. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Li, W.; Fu, Y.; Fan, S.; Xin, M.; Bai, H. DCI-PGCN: Dual-channel interaction portable graph convolutional network for landslide detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, J.; Li, H.; Wang, G.; Guo, J.; Wang, J. Road Network Intelligent Selection Method Based on Heterogeneous Graph Attention Neural Network. ISPRS Int. J. Geo-Inf. 2024, 13, 300. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Geng, X.; Jin, B.; Xu, L. Time series prediction of sea surface temperature based on an adaptive graph learning neural model. Future Internet 2022, 14, 171. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Z.; Yu, J.; Xu, L. Global spatiotemporal graph attention network for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Haigang, S.; Penggen, C.; Anming, Z.; Jianya, G. An algorithm for automatic cartographic sounding selection. Geo-Spat. Inf. Sci. 1999, 2, 96–99. [Google Scholar] [CrossRef]
- He, L.; Nan, J.; Chen, L.; Ye, X.; Ji, S.; Chen, Z.; Zhang, Y.; Wu, F.; Liu, B.; Ge, Z.; et al. Spatiotemporal graph convolutional network using sparse monitoring data for accurate water-level reconstruction in urban drainage systems. J. Hydrol. 2025, 652, 132681. [Google Scholar] [CrossRef]
- Shi, Z.; Liang, X.; Wang, J. LMC: Fast training of GNNs via subgraph sampling with provable convergence. arXiv 2023, arXiv:2302.00924. [Google Scholar]
- Chiang, W.L.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C.J. Cluster-gcn: An efficient algorithm for training deep and large graph convolutional networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 257–266. [Google Scholar]
- Elmore, P.; Calder, B.; Petry, F.; Masetti, G.; Yager, R. Aggregation Methods Using Bathymetry Sources of Differing Subjective Reliabilities for Navigation Mapping. Mar. Geod. 2023, 46, 99–128. [Google Scholar] [CrossRef]
- Zeng, H.; Zhu, Q.; Ding, Y.; Hu, H.; Chen, L.; Xie, X.; Chen, M.; Yao, Y. Graph neural networks with constraints of environmental consistency for landslide susceptibility evaluation. Int. J. Geogr. Inf. Sci. 2022, 36, 2270–2295. [Google Scholar] [CrossRef]
- Shi, N.; Xu, J.; Wurster, S.W.; Guo, H.; Woodring, J.; Van Roekel, L.P.; Shen, H.W. Gnn-surrogate: A hierarchical and adaptive graph neural network for parameter space exploration of unstructured-mesh ocean simulations. IEEE Trans. Vis. Comput. Graph. 2022, 28, 2301–2313. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Tong, X. Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps. Int. J. Geogr. Inf. Sci. 2021, 35, 490–512. [Google Scholar] [CrossRef]
- Yangyang, Y.; Kangjie, H.; Fang, W.; Junkui, X. Graph convolution neural network method for shape classification of areal settlements. Acta Geod. Cartogr. Sin. 2022, 51, 2390. [Google Scholar]
- Xiao, T.; Ai, T.; Burghardt, D.; Liu, P.; Yang, M.; Gao, A.; Kong, B.; Yu, H. A road generalization method using graph convolutional network based on mesh-line structure unit. Geocarto Int. 2024, 39, 2413549. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Du, J.; Zhang, S.; Wu, G.; Moura, J.M.; Kar, S. Topology adaptive graph convolutional networks. arXiv 2017, arXiv:1710.10370. [Google Scholar]
- Zhang, H.; He, B.; Xing, J.; Lu, M. Deep spatial and temporal graph convolutional network for rice planthopper population dynamic forecasting. Comput. Electron. Agric. 2023, 210, 107868. [Google Scholar] [CrossRef]
- Huang, Z.; Derin, Y.; Kirstetter, P.E.; Li, Y. Multigraph convolutional networks for rainfall estimation in complex terrain. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1506005. [Google Scholar] [CrossRef]
- Maurya, S.K.; Liu, X.; Murata, T. Improving graph neural networks with simple architecture design. arXiv 2021, arXiv:2105.07634. [Google Scholar]
- Wang, L.; Dai, M.; He, J.; Huang, J. Regularized primitive graph learning for unified vector mapping. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 16817–16826. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Liu, B.; Gao, K.; Yu, A.; Guo, W.; Wang, R.; Zuo, X. Semisupervised graph convolutional network for hyperspectral image classification. J. Appl. Remote Sens. 2020, 14, 026516. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Spatio-temporal graph deep neural network for short-term wind speed forecasting. IEEE Trans. Sustain. Energy 2018, 10, 670–681. [Google Scholar] [CrossRef]
- Li, P.; Hao, H.; Zhang, Z.; Mao, X.; Xu, J.; Lv, Y.; Chen, W.; Ge, D. A field study to estimate heavy metal concentrations in a soil-rice system: Application of graph neural networks. Sci. Total Environ. 2022, 832, 155099. [Google Scholar] [CrossRef]
- Cachay, S.R.; Erickson, E.; Bucker, A.F.C.; Pokropek, E.; Potosnak, W.; Bire, S.; Osei, S.; Lütjens, B. The World as a Graph: Improving El Ni∖˜ no Forecasts with Graph Neural Networks. arXiv 2021, arXiv:2104.05089. [Google Scholar]
- Shi, Y.; Li, Q.; Zhu, X. Building footprint extraction with graph convolutional network. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5136–5139. [Google Scholar]
- Niu, X.; Qian, H.; Wang, X.; Xie, L.; Cui, L. Determining the optimal generalization operators for building footprints using an improved graph neural network model. Geocarto Int. 2024, 39, 2306265. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, Z.; Ma, J.; Shen, J.; Zhang, K. Deep graph convolutional networks for accurate automatic road network selection. ISPRS Int. J. Geo-Inf. 2021, 10, 768. [Google Scholar] [CrossRef]
- Karsznia, I.; Sielicka, K. When traditional selection fails: How to improve settlement selection for small-scale maps using machine learning. ISPRS Int. J. Geo-Inf. 2020, 9, 230. [Google Scholar] [CrossRef]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale dynamic graph convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Q.; Du, B.; Zhang, L. Weighted feature fusion of convolutional neural network and graph attention network for hyperspectral image classification. IEEE Trans. Image Process. 2022, 31, 1559–1572. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Dai, H.; Li, H.; Tian, T.; Huang, X.; Wang, L.; Zhu, J.; Song, L. Adversarial attack on graph structured data. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1115–1124. [Google Scholar]
- Gasteiger, J.; Weißenberger, S.; Günnemann, S. Diffusion improves graph learning. Adv. Neural Inf. Process. Syst. 2019, 32, 13366–13378. [Google Scholar]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N.V. Heterogeneous graph neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 793–803. [Google Scholar]
- Manessi, F.; Rozza, A.; Manzo, M. Dynamic graph convolutional networks. Pattern Recognit. 2020, 97, 107000. [Google Scholar] [CrossRef]
- Skarding, J.; Gabrys, B.; Musial, K. Foundations and modeling of dynamic networks using dynamic graph neural networks: A survey. IEEE Access 2021, 9, 79143–79168. [Google Scholar] [CrossRef]
- Shehzad, A.; Xia, F.; Abid, S.; Peng, C.; Yu, S.; Zhang, D.; Verspoor, K. Graph transformers: A survey. arXiv 2024, arXiv:2407.09777. [Google Scholar]
- Yuan, H.; Yu, H.; Gui, S.; Ji, S. Explainability in graph neural networks: A taxonomic survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5782–5799. [Google Scholar] [CrossRef]
- Wang, C.; Tsepa, O.; Ma, J.; Wang, B. Graph-mamba: Towards long-range graph sequence modeling with selective state spaces. arXiv 2024, arXiv:2402.00789. [Google Scholar]
- Touya, G.; Zhang, X.; Lokhat, I. Is deep learning the new agent for map generalization? Int. J. Cartogr. 2019, 5, 142–157. [Google Scholar] [CrossRef]
- Kang, Y.; Gao, S.; Roth, R.E. Artificial intelligence studies in cartography: A review and synthesis of methods, applications, and ethics. Cartogr. Geogr. Inf. Sci. 2024, 51, 599–630. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Z. A comparative study of various supervised learning approaches to selective omission in a road network. Cartogr. J. 2017, 54, 254–264. [Google Scholar] [CrossRef]
- Kang, Y. Integrating Artificial Intelligence in Cartography: Using Deep Learning for Map Style Transfer and Map Generalization. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2020. [Google Scholar]
- Liu, C.; Hu, Y.; Li, Z.; Xu, J.; Han, Z.; Guo, J. TriangleConv: A deep point convolutional network for recognizing building shapes in map space. ISPRS Int. J. Geo-Inf. 2021, 10, 687. [Google Scholar] [CrossRef]
- Yang, M.; Yuan, T.; Yan, X.; Ai, T.; Jiang, C. A hybrid approach to building simplification with an evaluator from a backpropagation neural network. Int. J. Geogr. Inf. Sci. 2022, 36, 280–309. [Google Scholar] [CrossRef]
- Courtial, A.; Touya, G.; Zhang, X. Deriving map images of generalised mountain roads with generative adversarial networks. Int. J. Geogr. Inf. Sci. 2023, 37, 499–528. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Tong, X.; Liu, Q. A graph deep learning approach for urban building grouping. Geocarto Int. 2022, 37, 2944–2966. [Google Scholar] [CrossRef]
- Zhou, Z.; Fu, C.; Weibel, R. Move and remove: Multi-task learning for building simplification in vector maps with a graph convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2023, 202, 205–218. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Z.; Xiong, Z.; Shi, Y.; Saha, S.; Zhu, X.X. Beyond Grid Data: Exploring graph neural networks for Earth observation. IEEE Geosci. Remote Sens. Mag. 2024, 13, 175–208. [Google Scholar] [CrossRef]
- Tinghua, A. Some thoughts on deep learning enabling cartography. Acta Geod. Cartogr. Sin. 2021, 50, 1170. [Google Scholar]
- Zhang, K.; Zheng, J.; Shen, J.; Ma, J. Application of the graph convolution network in the selection of road network. Sci. Surv. Mapp 2021, 46, 165–170. [Google Scholar]
- Xiaoya, A.; Yude, Z.; Xiongfeng, Y. A building selection method supported by graph convolutional network. Acta Geod. Cartogr. Sin. 2023, 52, 1574. [Google Scholar]
- Zhanlong, C.; Xiechun, L.; Yongyang, X. A building aggregation method based on deep clustering of graph vertices. Acta Geod. Et Cartogr. Sin. 2024, 53, 736. [Google Scholar]
- Zhang, L.; Wen, L.; Jia, S. Indices and methods for evaluating quantificationally the quality of simplification of a depth-contour in nautical chart. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 496–501. [Google Scholar]
- Courtial, A.; Touya, G.; Zhang, X. Constraint-based evaluation of map images generalized by deep learning. J. Geovisualiz. Spat. Anal. 2022, 6, 13. [Google Scholar] [CrossRef]
- Karsznia, I.; Weibel, R. Improving settlement selection for small-scale maps using data enrichment and machine learning. Cartogr. Geogr. Inf. Sci. 2018, 45, 111–127. [Google Scholar] [CrossRef]
- Fu, C.; Zhou, Z.; Xin, Y.; Weibel, R. Reasoning cartographic knowledge in deep learning-based map generalization with explainable AI. Int. J. Geogr. Inf. Sci. 2024, 38, 2061–2082. [Google Scholar] [CrossRef]
- Ke, E.; Zhao, J.; Zhao, Y. Investigating the influence of nonlinear spatial heterogeneity in urban flooding factors using geographic explainable artificial intelligence. J. Hydrol. 2025, 648, 132398. [Google Scholar] [CrossRef]
- Johnson, S.Y.; Cochrane, G.R.; Golden, N.E.; Dartnell, P.; Hartwell, S.R.; Cochran, S.A.; Watt, J.T. The California seafloor and coastal mapping program–Providing science and geospatial data for California’s state waters. Ocean Coast. Manag. 2017, 140, 88–104. [Google Scholar] [CrossRef]
- Milli, M. Nautical cartography as a tool of international maritime cooperation: Some Italian cases in the Mediterranean Sea. Ocean Coast. Manag. 2021, 213, 105876. [Google Scholar] [CrossRef]
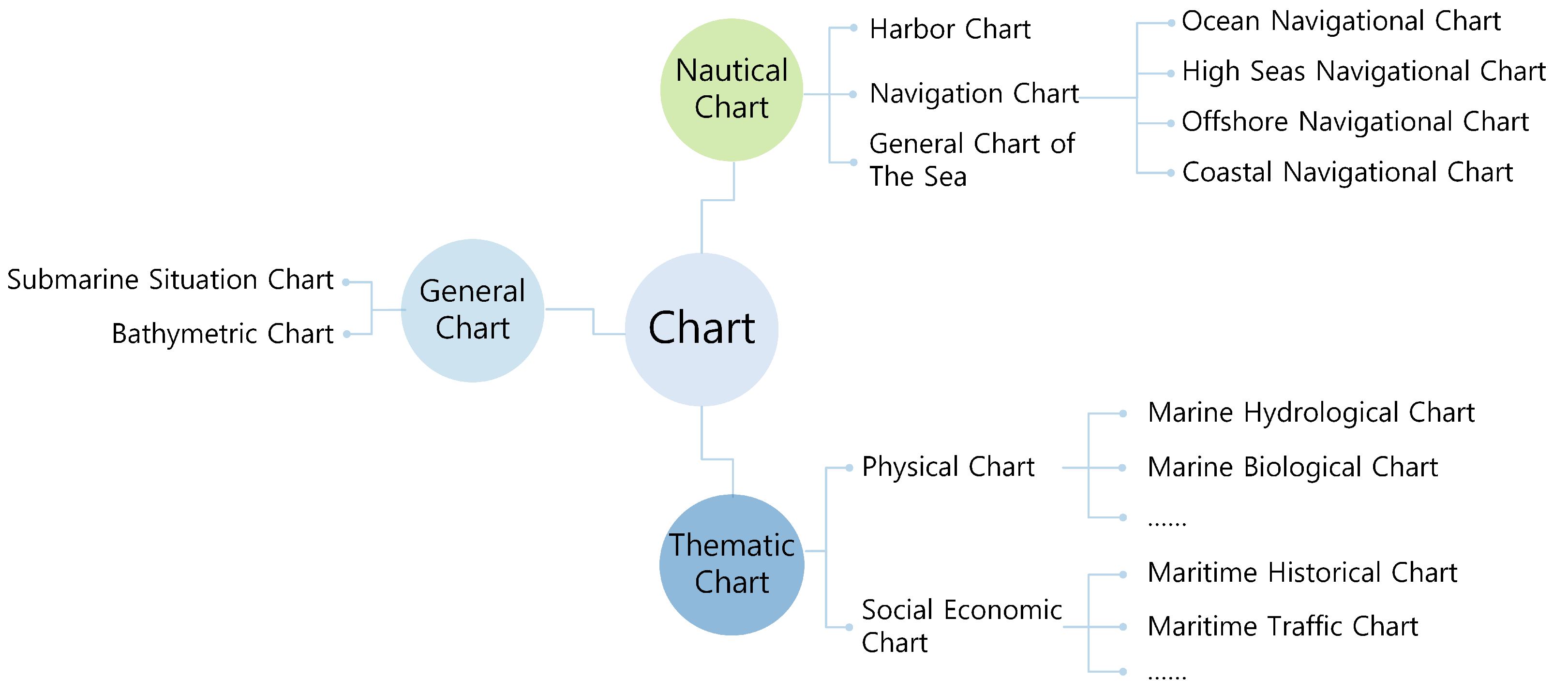
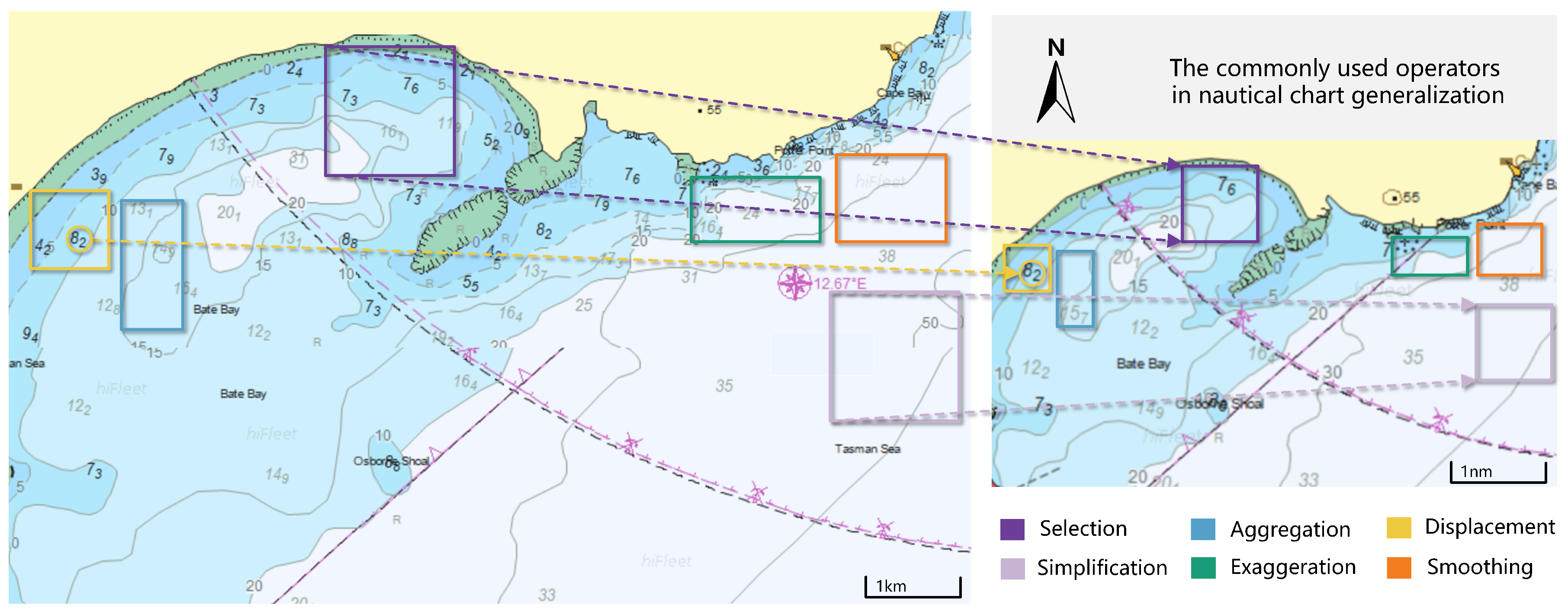
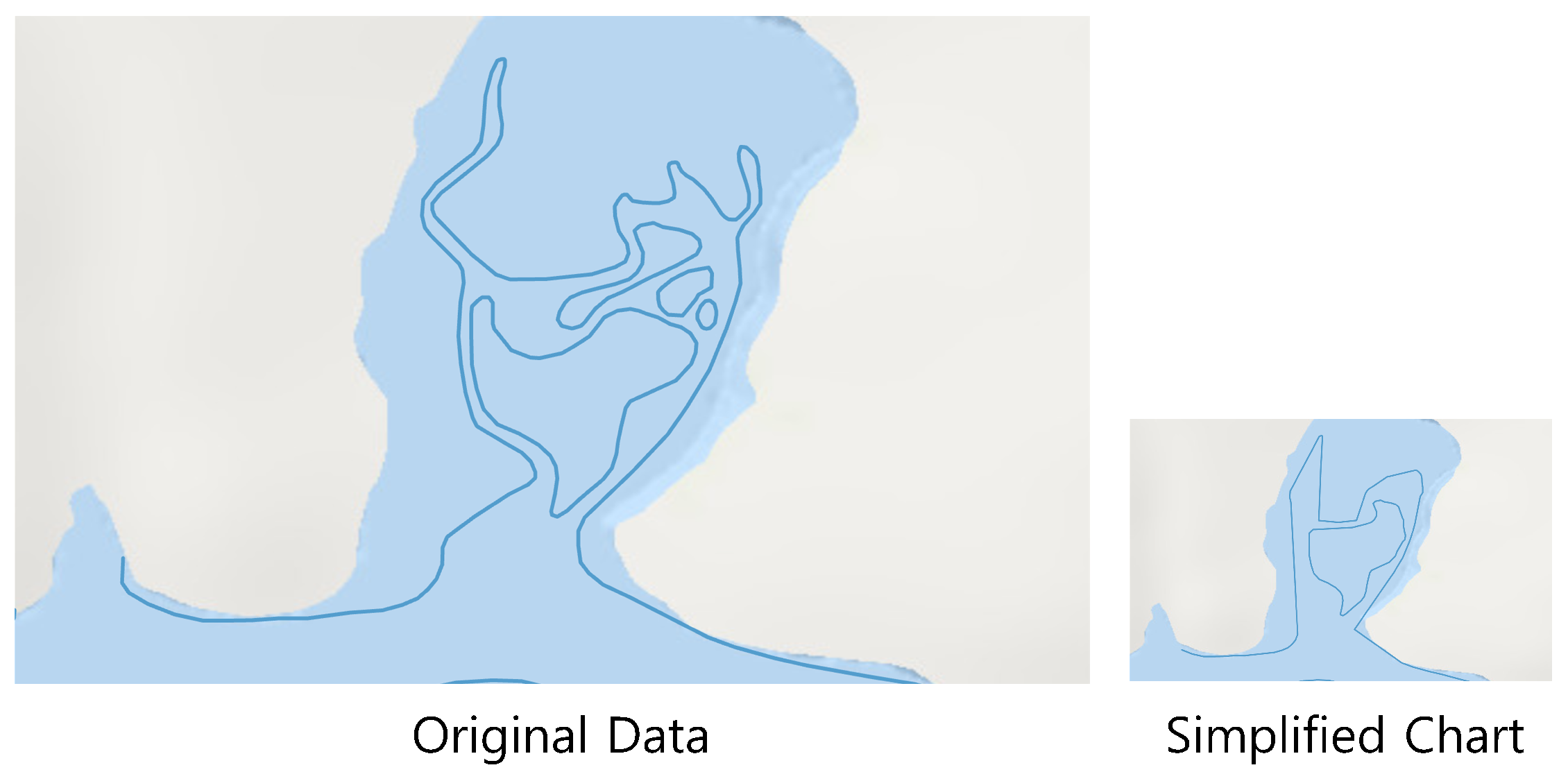
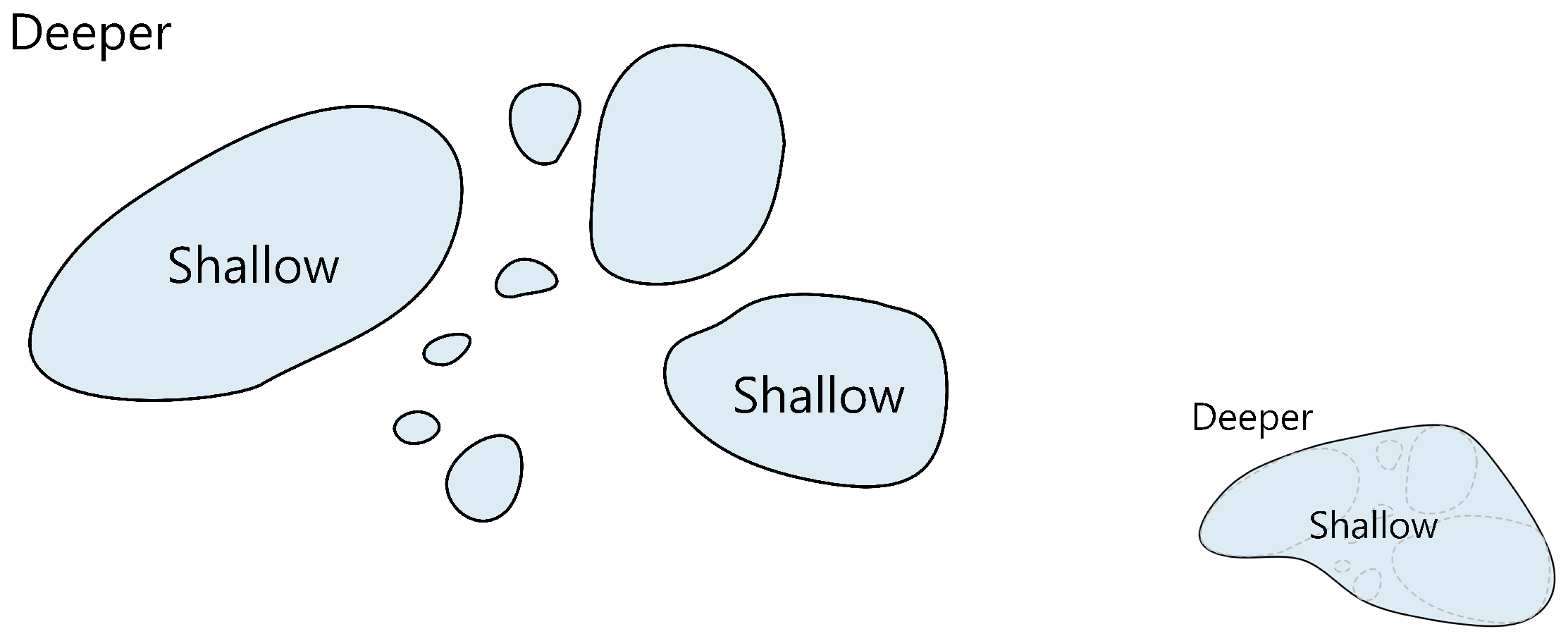




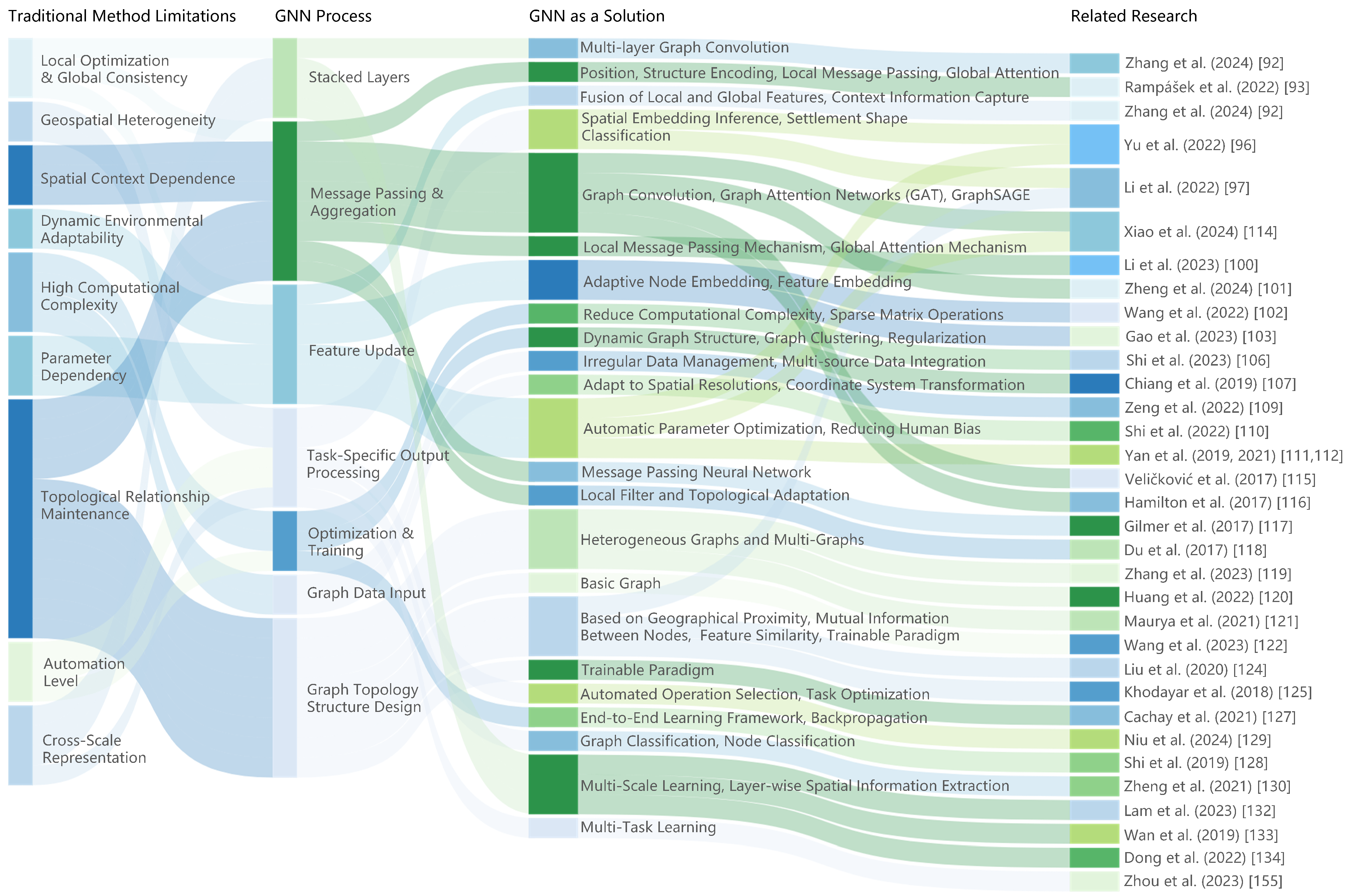
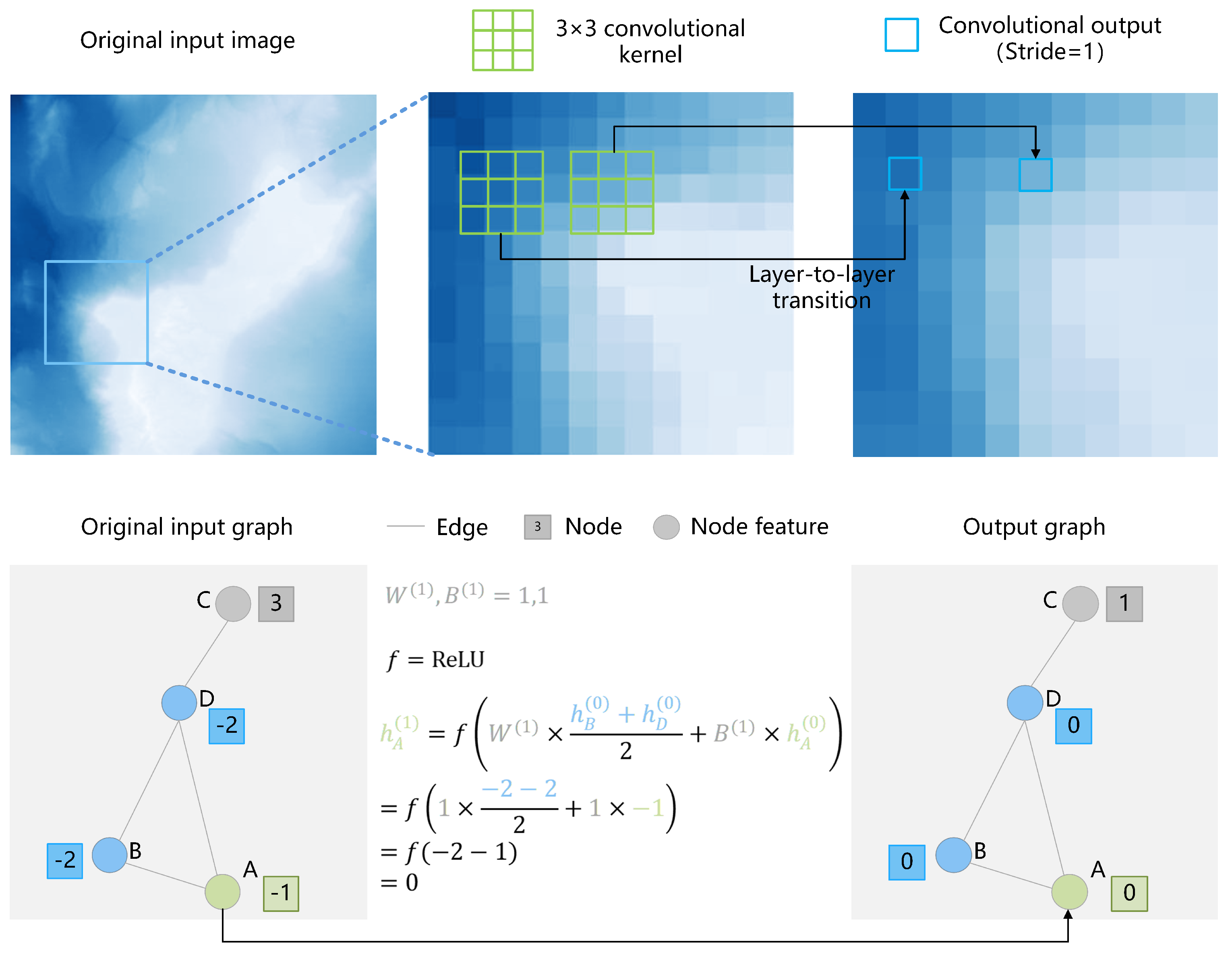


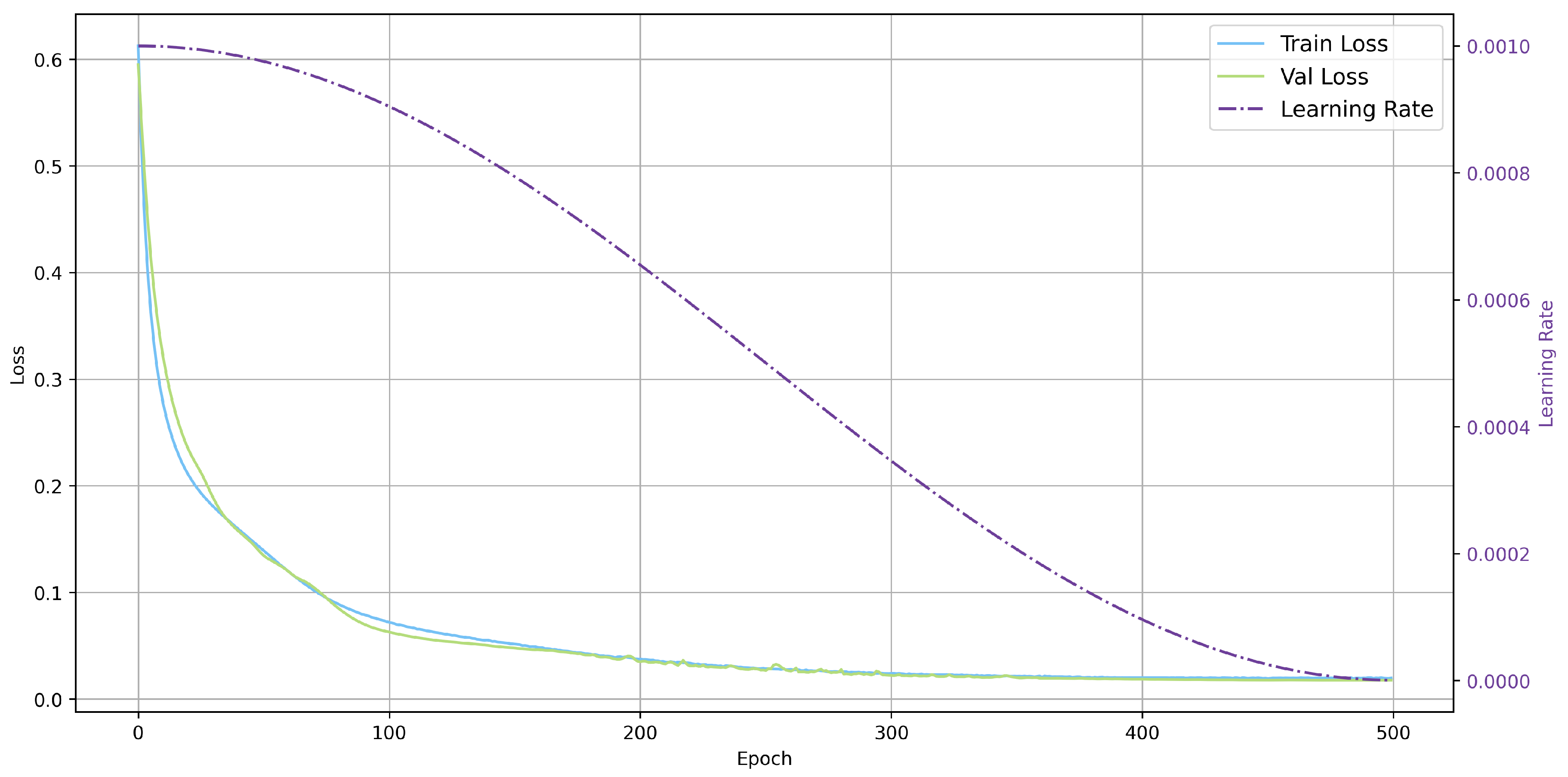
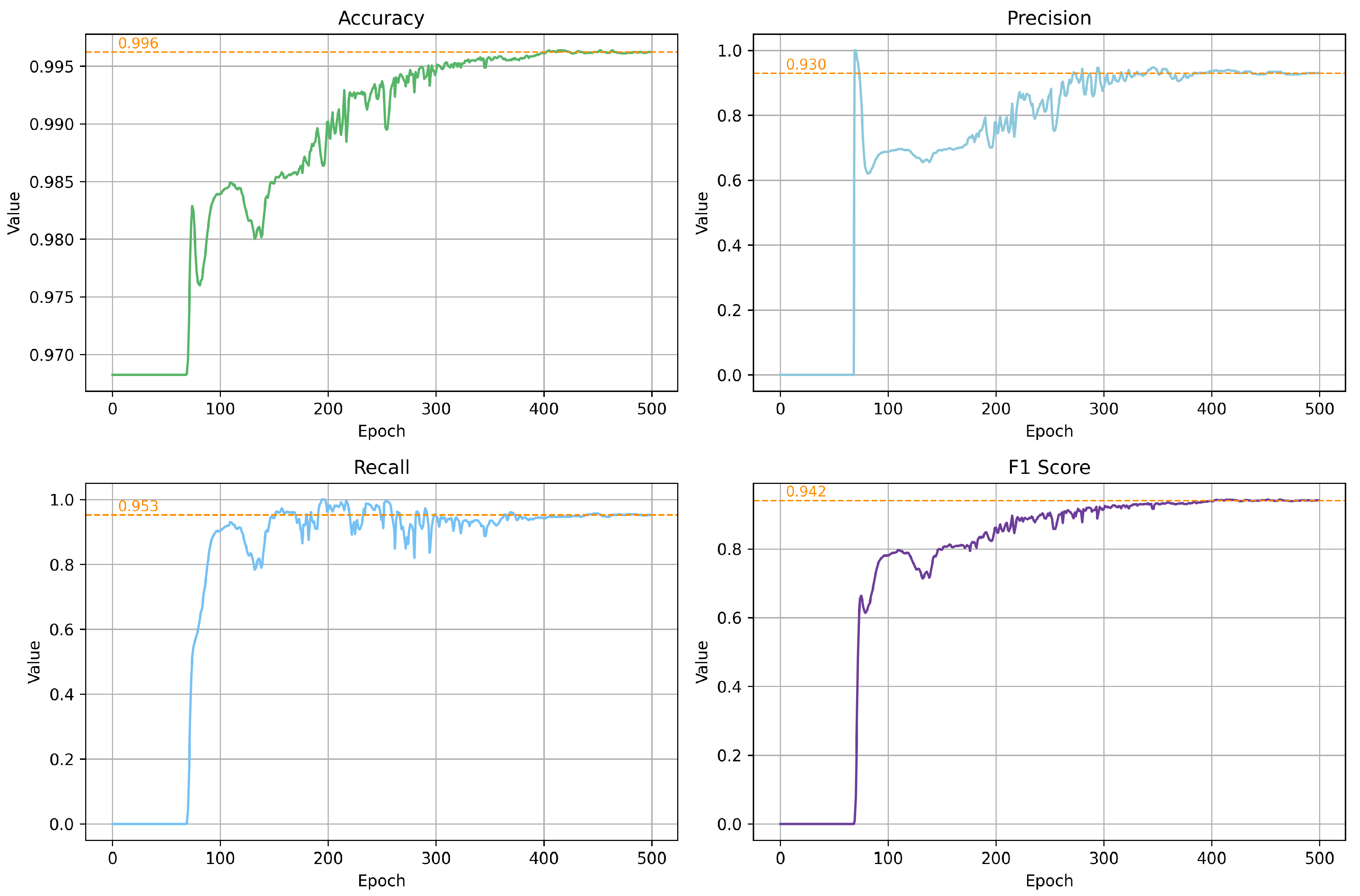

| Aspects | Charts | General Topographic Maps |
|---|---|---|
| Mathematical Foundation | Uses geocentric systems (e.g., WGS-84/CGCS2000), with depth referenced to the lowest tidal level. | Uses geocentric and projection systems (e.g., WGS-84, UTM), with elevation referenced to mean sea level. |
| Data Source | Marine survey. | Terrestrial survey. |
| Representation Content | Focuses on navigation and hydrographic features: coasts, reefs, depths, aids to navigation, shipping lanes, etc. | Focuses on land features: water systems, settlements, transport, terrain, soil and vegetation, and boundaries. Marine content is minimal. |
| Representation Methods | Mainly uses Mercator projection; scale not fixed. | Uses various projections, with fixed scales. |
| Symbol and Encoding | Codes follow international standards (e.g., S-57). | Codes based on national standards; symbols follow unified design rules. |
| Accuracy Requirements | High for position and depth, ensuring navigational safety. | Varies by scale and terrain, focusing on landform accuracy. |
| Correction | Frequently updated for safety. | Longer revision cycles, fewer updates. |
| Traditional Methods | Operators | Advantages | Limitations of Traditional Methods | Related Research |
|---|---|---|---|---|
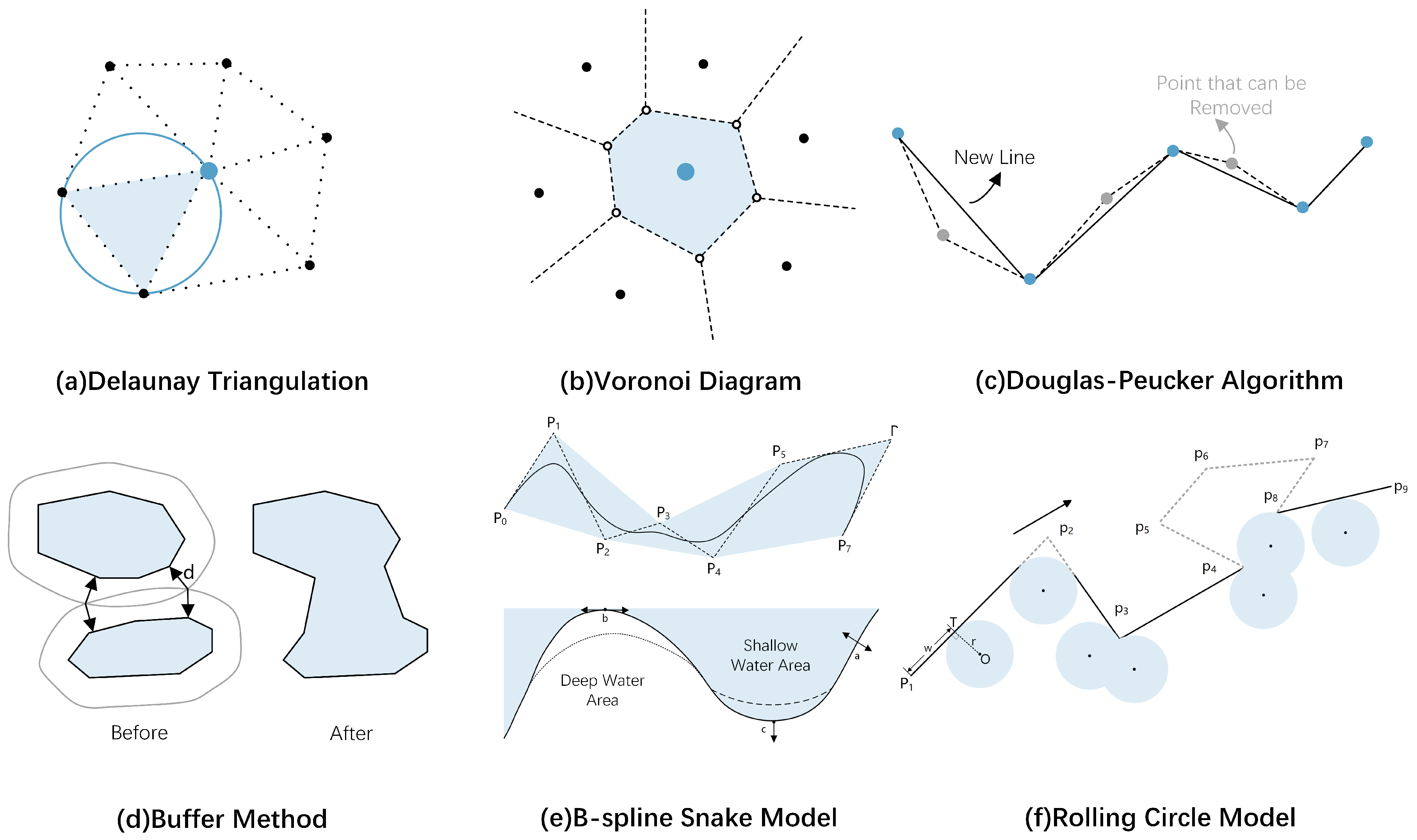
| Delaunay Triangulation | Selection Simplification Exaggeration Aggregation Displacement | Effectively maintain geographic element proximity. Construct uniqueness. Stability and clear hierarchical structure. | Local optimization limitations. High computational complexity. Difficult to express dynamic information. | Soundings [12,13,14,15,16,17]. Depth contours [18,19,20]. Coastlines [21,22]. Islands [23,24,25]. |
| Voronoi Diagram | Selection Simplification Smoothing | Captures neighbor relations. Supports density analysis. Enables pairwise combination. | High computational complexity. Inadequate representation of dynamic information. Data redundancy | Soundings [14,25,26]. Depth contours [27]. Islands [28,29,30,31]. |
| Douglas–Peucker Algorithm | Simplification Exaggeration Aggregation Displacement | Reduction in data volume. Significant features retained. Cannot be used directly for 3D terrain simplification. | Starting point dependency. Prone to topology errors. Sensitive to data distribution. Limited spatial context | DBM [32]. Depth contours [33,34,35]. Coastlines [22,36]. Islands [37]. |
| Buffer Method | Selection Simplification Exaggeration Aggregation Displacement | Reduces redundancy and noise. Easy to implement and compute. | Parameter-dependent. Limited in dense areas. Poor with dynamic features. Inconsistent globally. | Soundings [38]. Depth contours [35]. Coastlines [22,36]. Islands [39,40]. |
| Rolling Circle Model | Selection Simplification Displacement | Applicable to directional constraints. Algorithm commonality. | Parameter dependency. High computational complexity. | Depth contours [9,41,42]. |
| B-Spline Snake Model | Simplification Exaggeration Aggregation Displacement Smoothing | High degree of automation. Highly adaptable. | Parameter dependency. High computational complexity. Limited spatial context. | Depth contours [43,44,45]. |
| Models | Applicability Scenarios | Key Features | Advantages | Limitations |
|---|---|---|---|---|
| GCN | Node classification. Graph classification. Link prediction. | Weighted aggregation of node features and neighbor features based on spectral graph theory. | Global information capture. Simple and efficient. Widely applicable. Low computational complexity. | Consumes memory and graphics memory. No large graphs. Transductive learning only. No new nodes embedding. |
| Graph SAGE | Large-scale graph. Dynamic graph. | Sample a fixed number (order K) of neighbors, with flexible feature aggregation (mean, max, etc., LSTM). | Overcoming GCN Memory and Graphics Limitations. Inductive Learning. Shared parameters. Incremental learning support. Supervised and unsupervised tasks support. | No weighted graphs support. Equal neighbor weights. Unstable embeddings. High gradient variance. |
| GAT | Node classification. Graph classification. Heterogeneous graph analysis. | Dynamically assigning importance weights to neighboring nodes based on attention mechanism. | Flexible attention mechanism. Fast computation and parallel computation. Transductive learning and Inductive Learning support. Highly scalable. | High parameter count. No dynamic graph handling. Limited efficiency of large-scale graphs. |
| GAE | Graph embedding. Graph reconstruction. Link prediction. | Auto-encoder framework for low-dimensional embeddings. | Unsupervised learning. Highly capable of capturing graph structure. Flexible encoder choice. | Sparse graph sensitivity. Poor performance in heterogeneous and dynamic graphs. Limited generation capability. |
| Graph Transformer | Node classification. Graph prediction. | Combining Transformer’s Global Attention with Graph Structure Embedding. | Greater characterization capabilities. Capture of long-range dependencies. Graph data efficiency. Over-smoothing and over-squeezing mitigations. | Weak local focus. Higher computational complexity. Large-scale data dependency. |
| Graph Diffusion | Weakly connected graphs. Sparse graphs. Graph clustering. Homogeneous graphs. | The original adjacency matrix is replaced by the sparsified graph diffusion matrix. | Strong global information capture. Suitable for sparse and noisy graphs. Enhanced clustering. | Reliance on the assumption of homogeneity. Insufficient support for complex graph structures. Diffusion matrix preprocessing is computationally inefficient. |
| Graph Mamba | Dynamic graphs. Long-range dependency modeling. Spatio-temporal data prediction | An efficient graph learning model combining state space models and selective scanning mechanisms. | Capturing long-range dependencies. Highly adaptable in non-sequential graph. Reduced memory consumption. | Strong reliance on high-quality graph data. |
| Models | Key Features | Advantages | Limitations | Applications |
|---|---|---|---|---|
| GNN | Message passing Non-Euclidean space modeling Graph topology adaptation | Handles non-Euclidean data. Captures complex relations. Supports semi-supervised learning. | Requires graph input. High cost for large graphs. | Social networks. Molecular modeling. Traffic prediction. Vector map learning. |
| CNN | Translation invariance Local receptive fields Parameter sharing | Efficient and shift-invariant. Optimizes local patterns. | Weak in global context. Sensitive to scale/rotation. Fixed input size. | Image tasks. Object detection. Medical segmentation. Action recognition. |
| GAN | Generative adversarial training Minimax game | Realistic image generation. Learns complex distributions. | Unstable training. Mode collapse. Hard to evaluate. | Image synthesis. Data augmentation. Text-to-image. Domain transfer. |
| Transformers | Self-attention Positional encoding Global modeling | Captures long-range context. Supports parallelism. Handles varied input length. | High computation. Data hungry. | NLP tasks. Speech recognition. Time series. Multimodal fusion. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, T.; Wang, R.; Chen, P.; Sun, C.; Gan, C.; Liu, J.; Zhang, A. Submarine Terrain Generalization in Nautical Charts: A Survey of Traditional Methods and Graph Neural Network Solutions. ISPRS Int. J. Geo-Inf. 2025, 14, 257. https://doi.org/10.3390/ijgi14070257
Dong T, Wang R, Chen P, Sun C, Gan C, Liu J, Zhang A. Submarine Terrain Generalization in Nautical Charts: A Survey of Traditional Methods and Graph Neural Network Solutions. ISPRS International Journal of Geo-Information. 2025; 14(7):257. https://doi.org/10.3390/ijgi14070257
Chicago/Turabian StyleDong, Taoning, Ruifu Wang, Pengxv Chen, Chenyue Sun, Chaohua Gan, Jiayi Liu, and Anmin Zhang. 2025. "Submarine Terrain Generalization in Nautical Charts: A Survey of Traditional Methods and Graph Neural Network Solutions" ISPRS International Journal of Geo-Information 14, no. 7: 257. https://doi.org/10.3390/ijgi14070257
APA StyleDong, T., Wang, R., Chen, P., Sun, C., Gan, C., Liu, J., & Zhang, A. (2025). Submarine Terrain Generalization in Nautical Charts: A Survey of Traditional Methods and Graph Neural Network Solutions. ISPRS International Journal of Geo-Information, 14(7), 257. https://doi.org/10.3390/ijgi14070257






