Monte Carlo-Based Spatial Optimization of Simulation Plots for Forest Growth Modeling
Abstract
1. Introduction
2. Methods
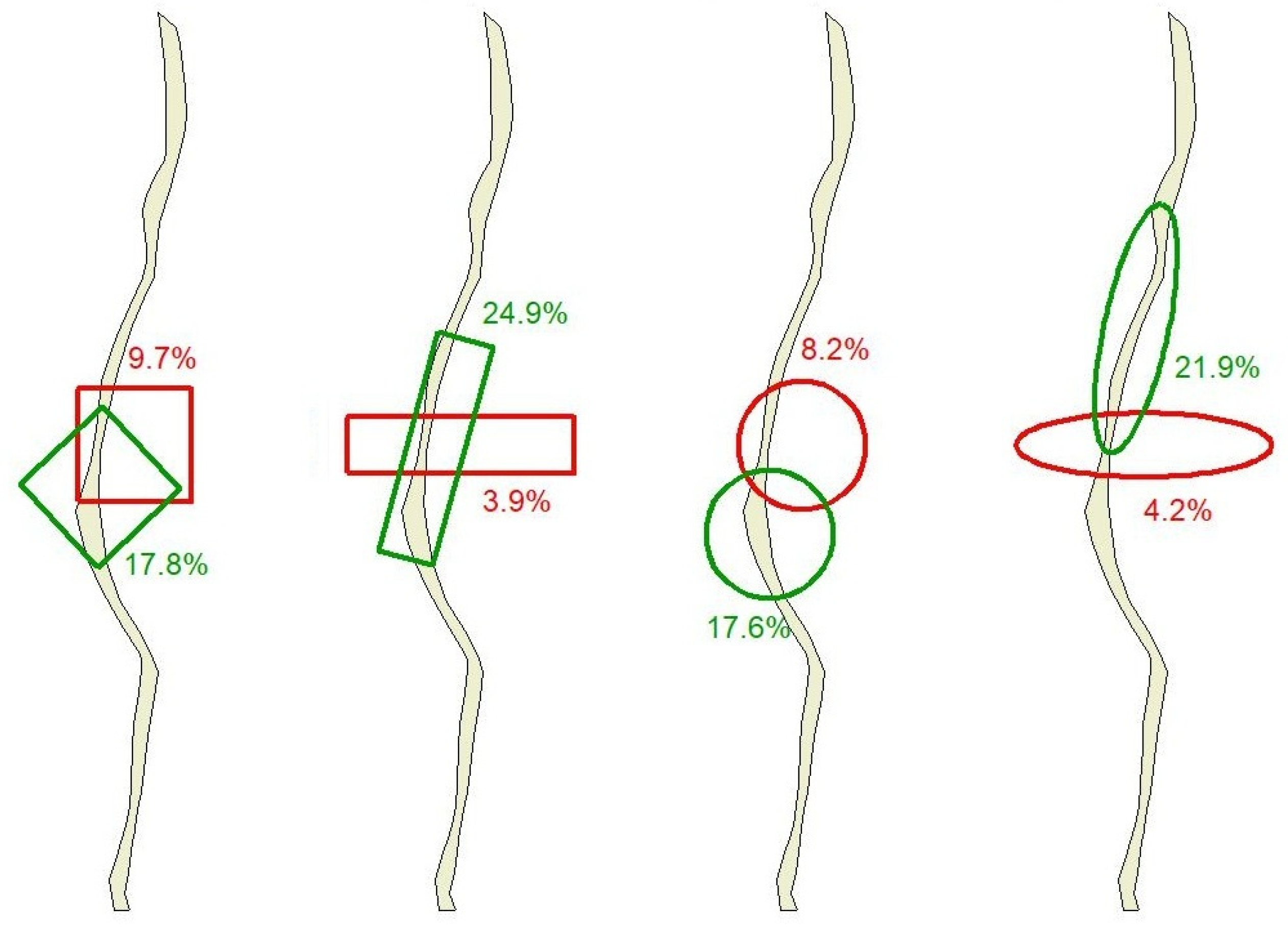
2.1. Construction of Simulation Plot Geometries
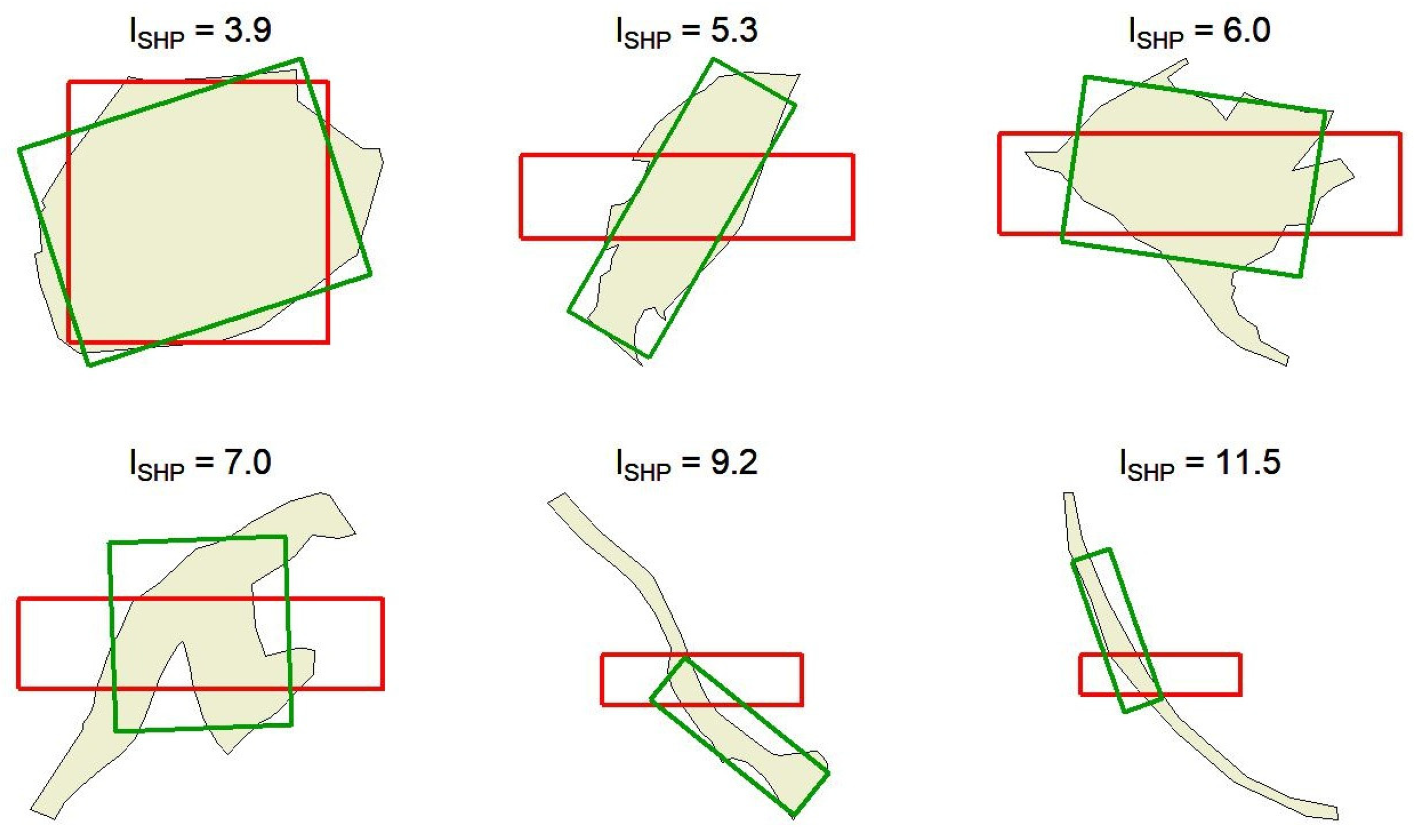
2.2. Refinement of Plot Shape and Position Using the Monte Carlo Method
- Number of iterations: The number of random proposals evaluated for each simulation plot. Larger values tend to improve solution quality but increase computation time.
- Maximum translation: The upper bound (as a percentage of plot size) on random shifts in the x and y directions.
- Maximum rotation: The upper bound (in degrees) on random rotations applied to the plot geometry.
- Maximum resize: The upper bound (as a percentage) on area-preserving shape adjustments used to modify aspect ratio; not applicable to square or circular plots. The adjusted plot must also respect the side-ratio limit below.
- Maximum side ratio: The upper bound on elongation, defined as the ratio of the longer to the shorter side of the bounding rectangle.
2.3. Extraction of Terrain and Environmental Variables
2.4. Tuning of Monte Carlo Hyperparameters
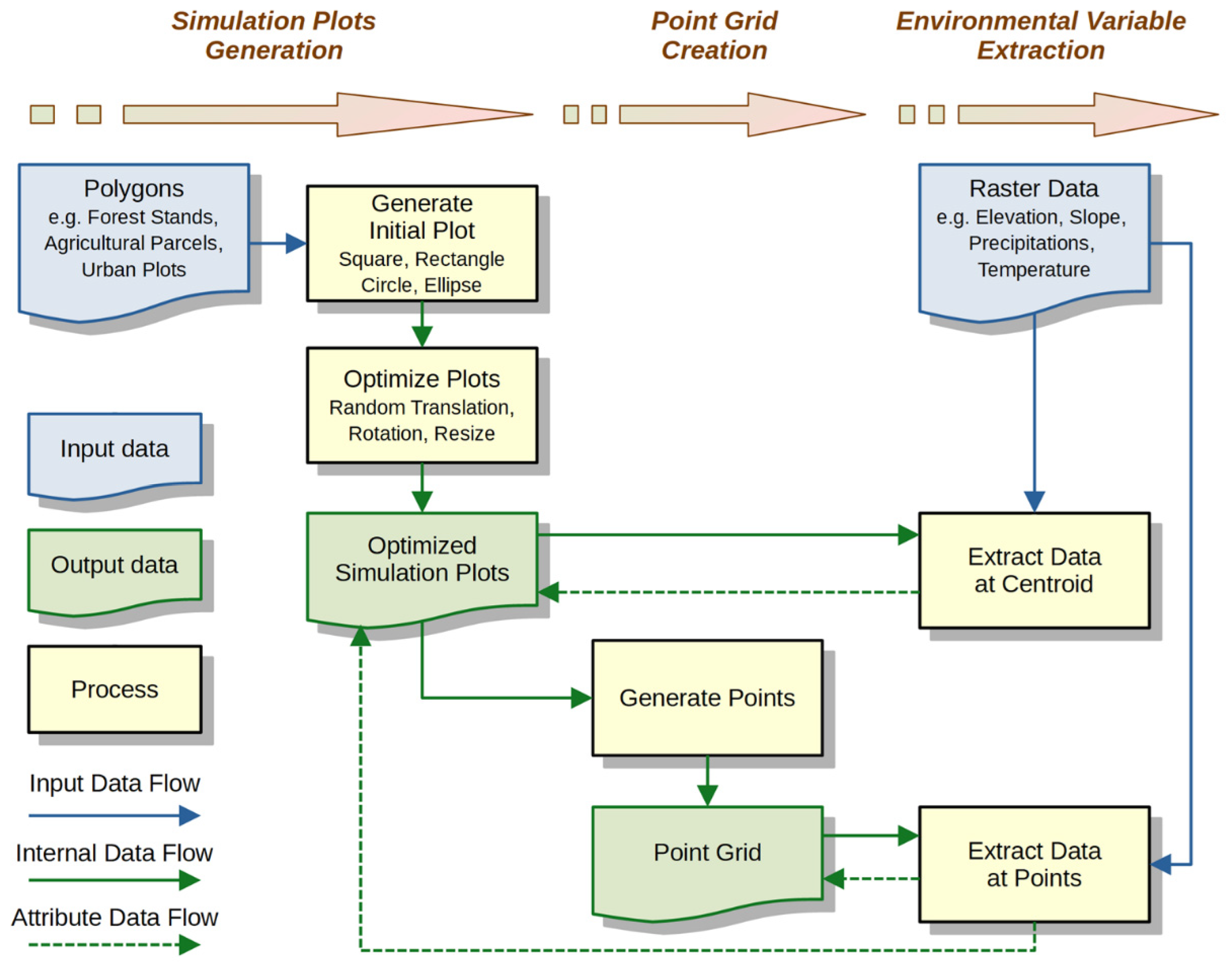
2.5. Plugin Architecture
- Simulation Plot Generation: Functions that manage plot geometry, size, shape, and spatial alignment, ensuring that generated plots accurately capture the properties of the target landscape or forest stand.
- Point Grid Creation: Tools for generating a regular point grid within each simulation plot. These points may be used to extract elevation and other environmental variables, thereby representing local features. Such detailed grids support improved visualization and modeling (e.g., tree competition).
- Environmental Variable Extraction: Utilities for retrieving terrain and environmental attributes from raster layers. These data are essential for comprehensive forest growth models and other simulation-based analyses.
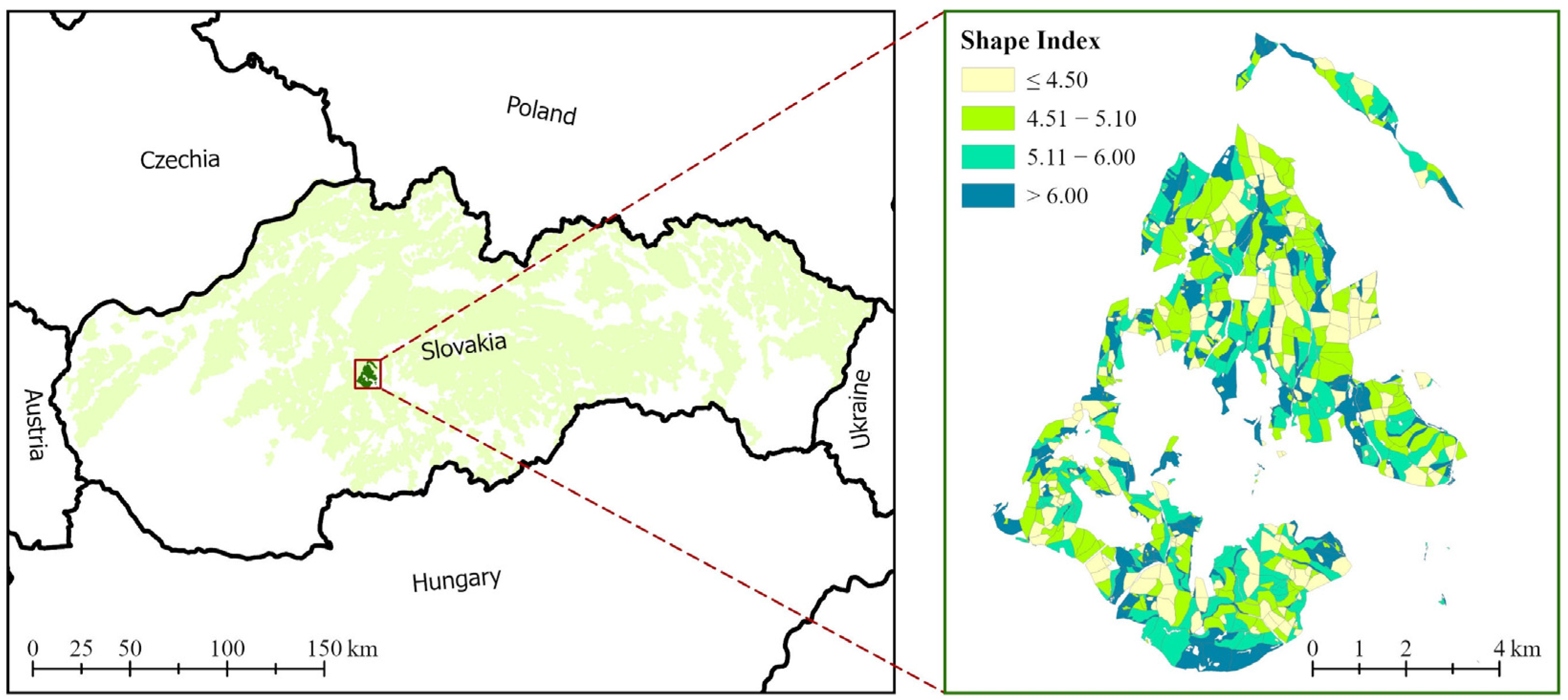
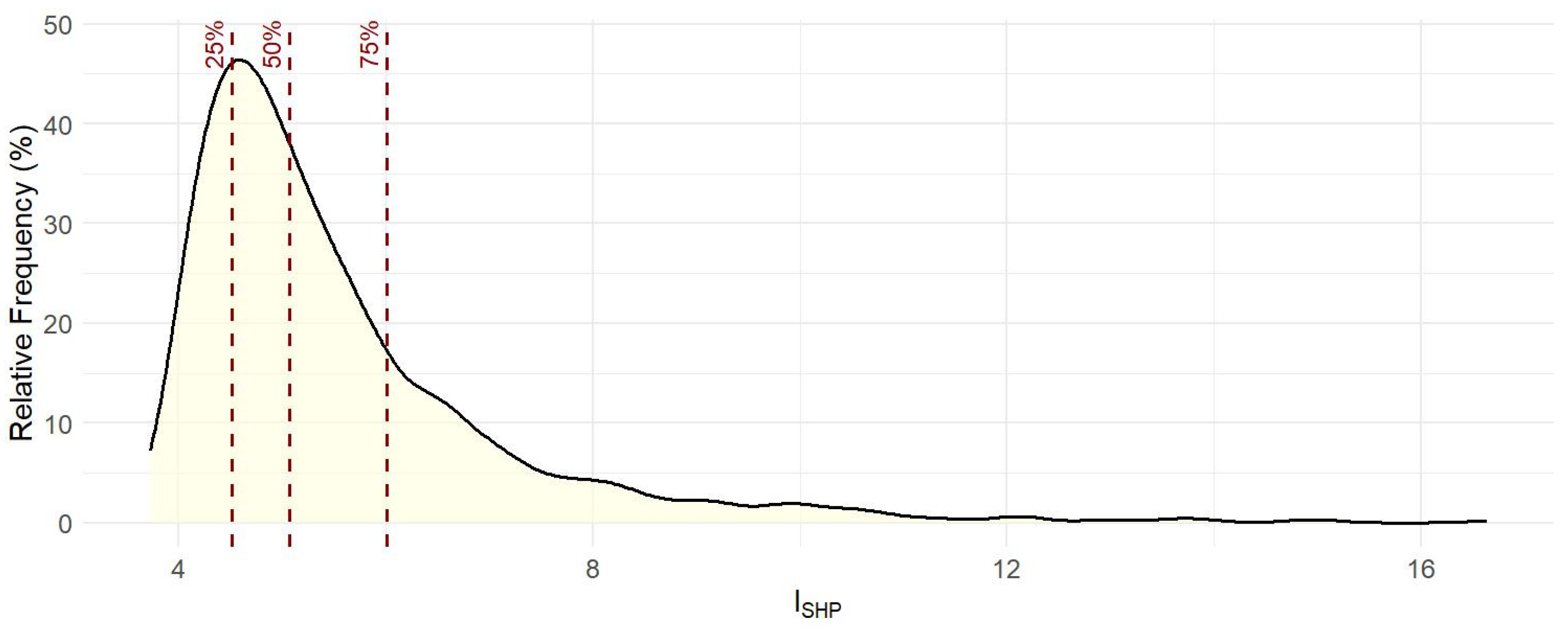
2.6. Study Area and Evaluation Dataset
3. Results
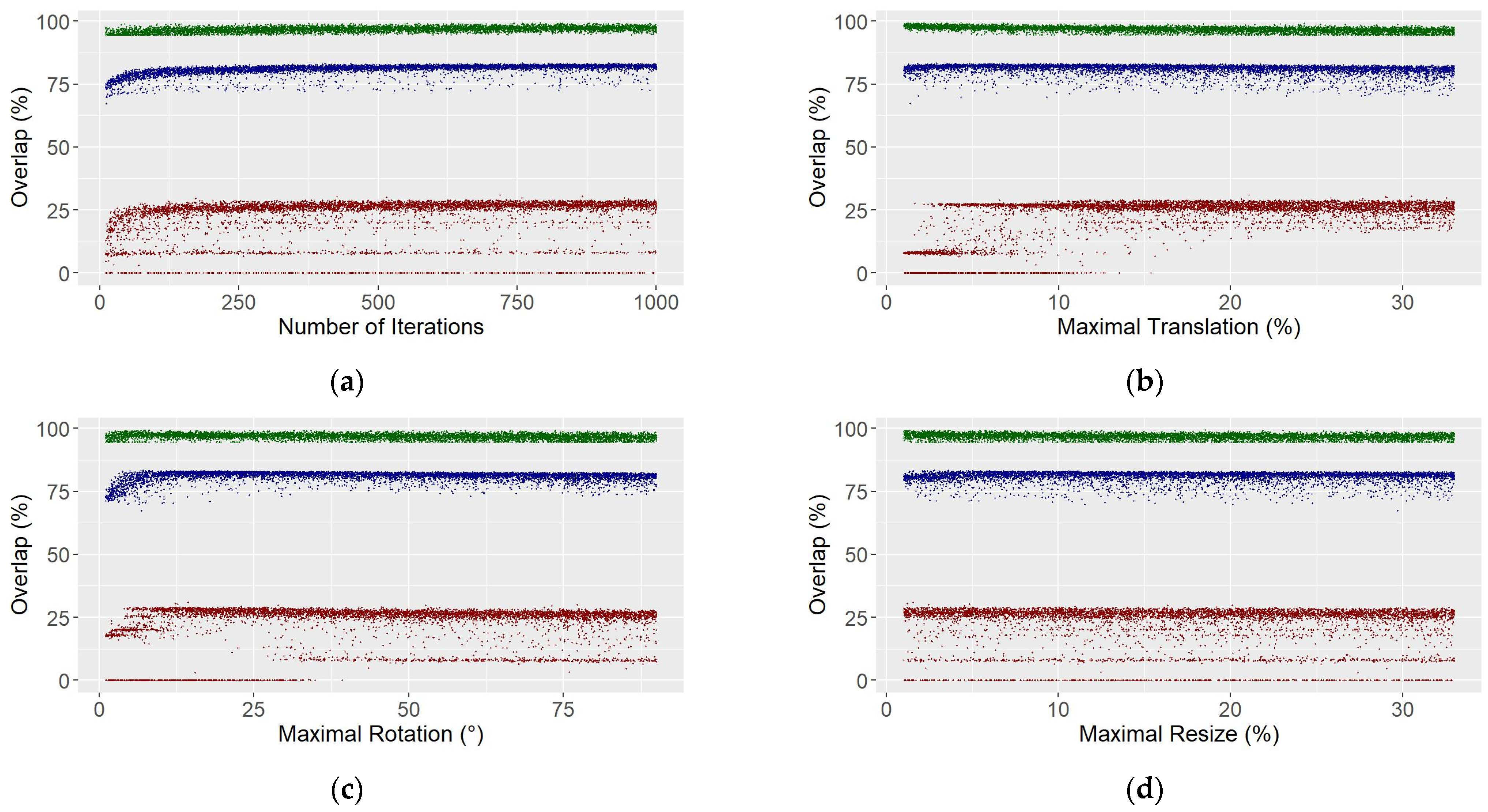
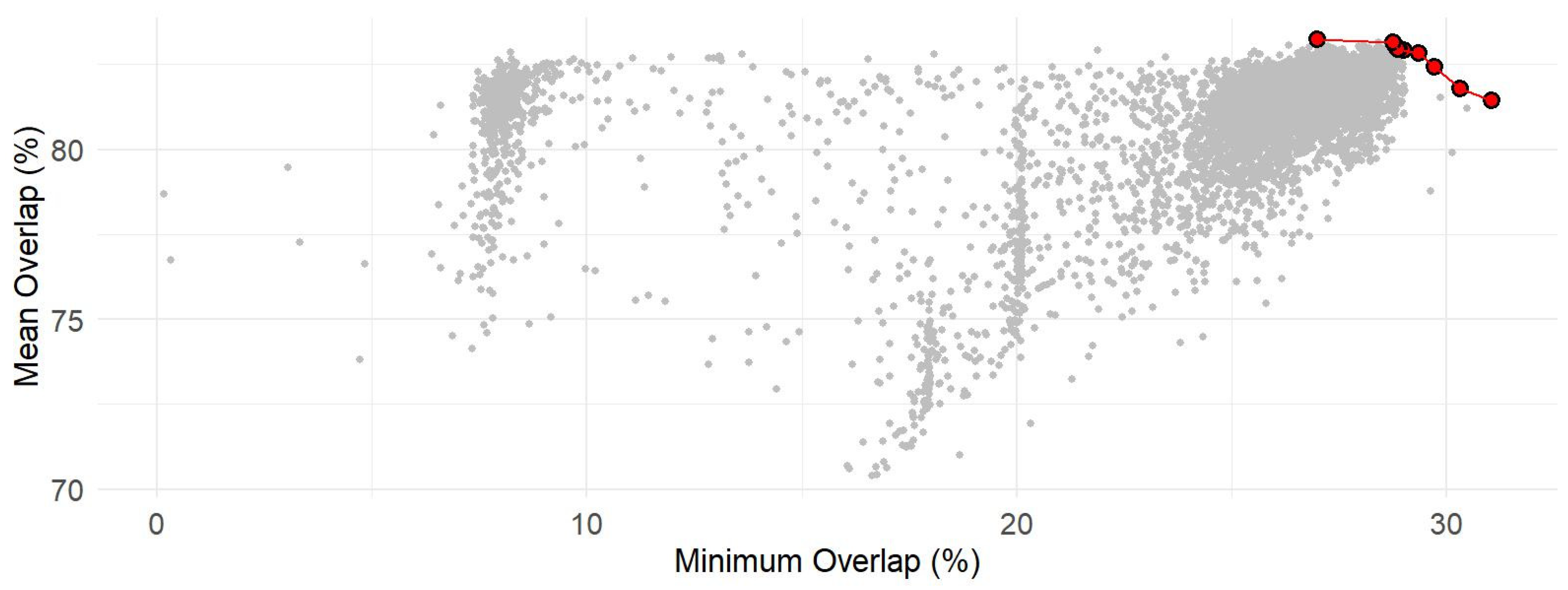
3.1. Hyperparameter Tuning
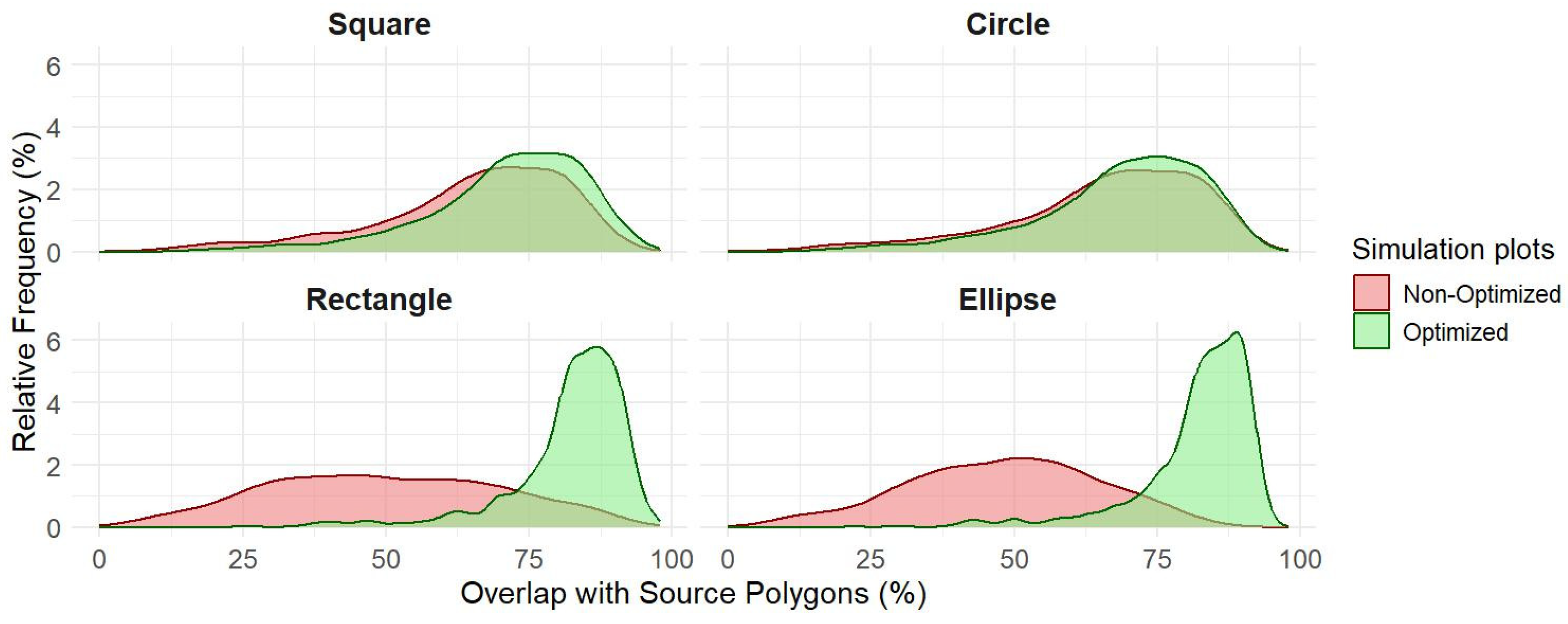
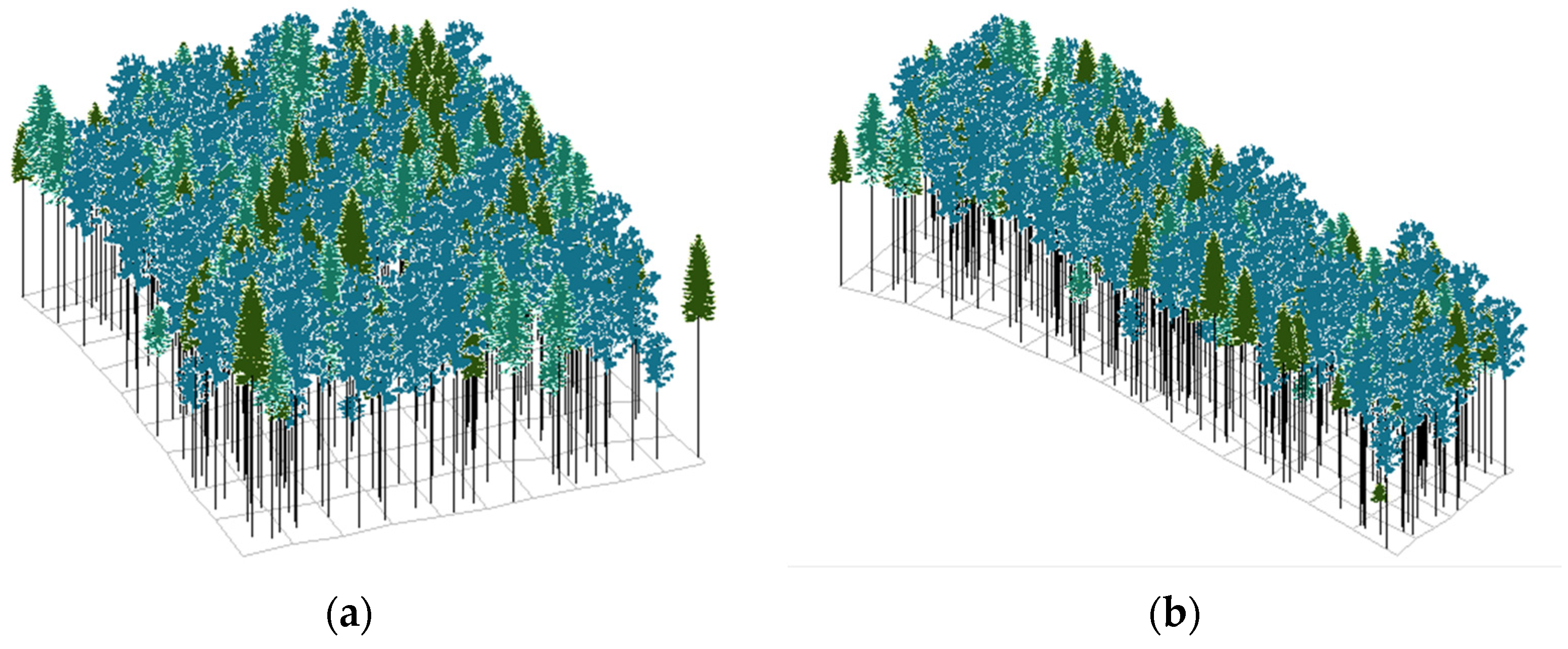
3.2. Performance of Optimized Simulation Plots
4. Discussion
4.1. Methodological and Practical Contributions
4.2. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blanco, J.A.; Lo, Y.-H. Latest Trends in Modelling Forest Ecosystems: New Approaches or Just New Methods? Curr. For. Rep. 2023, 9, 219–229. [Google Scholar] [CrossRef]
- Maréchaux, I.; Langerwisch, F.; Huth, A.; Bugmann, H.; Morin, X.; Reyer, C.P.O.; Seidl, R.; Collalti, A.; Dantas De Paula, M.; Fischer, R.; et al. Tackling Unresolved Questions in Forest Ecology: The Past and Future Role of Simulation Models. Ecol. Evol. 2021, 11, 3746–3770. [Google Scholar] [CrossRef] [PubMed]
- Mahnken, M.; Cailleret, M.; Collalti, A.; Trotta, C.; Biondo, C.; D’Andrea, E.; Dalmonech, D.; Marano, G.; Mäkelä, A.; Minunno, F.; et al. Accuracy, Realism and General Applicability of European Forest Models. Glob. Change Biol. 2022, 28, 6921–6943. [Google Scholar] [CrossRef] [PubMed]
- Boukhris, I.; Marano, G.; Dalmonech, D.; Valentini, R.; Collalti, A. Modeling Forest Growth Under Current and Future Climate. Curr. For. Rep. 2025, 11, 17. [Google Scholar] [CrossRef]
- Grünig, M.; Rammer, W.; Albrich, K.; André, F.; Augustynczik, A.L.D.; Bohn, F.; Bouwman, M.; Bugmann, H.; Collalti, A.; Cristal, I.; et al. A Harmonized Database of European Forest Simulations Under Climate Change. Data Brief 2024, 54, 110384. [Google Scholar] [CrossRef]
- Rammer, W.; Thom, D.; Baumann, M.; Braziunas, K.; Dollinger, C.; Kerber, J.; Mohr, J.; Seidl, R. The Individual-Based Forest Landscape and Disturbance Model iLand: Overview, Progress, and Outlook. Ecol. Model. 2024, 495, 110785. [Google Scholar] [CrossRef]
- Gao, Y.; Li, L.; Du, X.; Meng, J. A Transition-Matrix Growth Model and Equilibrium Curve for Natural Forests in Jiangxi Province. Forests 2023, 14, 2038. [Google Scholar] [CrossRef]
- Lei, K.; Zhang, H.; Qiu, H.; Yang, T.; Liu, Y.; Zhang, J.; Hu, X.; Cui, Z. A Novel Strategy for Constructing Large-Scale Forest Scene: Integrating Forest Hierarchical Models and Tree Growth Models to Improve the Efficiency and Stability of Forest Polymorphism Simulation. Forests 2023, 14, 1595. [Google Scholar] [CrossRef]
- Giebink, C.L.; DeRose, R.J.; Castle, M.; Shaw, J.D.; Evans, M.E.K. Climatic Sensitivities Derived from Tree Rings Improve Predictions of the Forest Vegetation Simulator Growth and Yield Model. For. Ecol. Manag. 2022, 517, 120256. [Google Scholar] [CrossRef]
- Pukkala, T.; Vauhkonen, J.; Korhonen, K.T.; Packalen, T. Self-Learning Growth Simulator for Modelling Forest Stand Dynamics in Changing Conditions. For. Int. J. For. Res. 2021, 94, 333–346. [Google Scholar] [CrossRef]
- Pretzsch, H. The Course of Tree Growth. Theory and Reality. For. Ecol. Manag. 2020, 478, 118508. [Google Scholar] [CrossRef]
- Liu, C.; Calders, K.; Origo, N.; Disney, M.; Meunier, F.; Woodgate, W.; Gastellu-Etchegorry, J.-P.; Nightingale, J.; Honkavaara, E.; Hakala, T.; et al. Reconstructing the Digital Twin of Forests from a 3D Library: Quantifying Trade-Offs for Radiative Transfer Modeling. Remote Sens. Environ. 2023, 298, 113832. [Google Scholar] [CrossRef]
- Toba, A.-L.; Paudel, R.; Davis, C.; Hartley, D.S.; Gandhi Mendadhala, R.V. ITreeForeCast: An Integrated Modeling Software to Simulate Tree Level Growth and Forest Carbon Storage. Comput. Electron. Agric. 2025, 237, 110495. [Google Scholar] [CrossRef]
- Schauberger, B.; Jägermeyr, J.; Gornott, C. A Systematic Review of Local to Regional Yield Forecasting Approaches and Frequently Used Data Resources. Eur. J. Agron. 2020, 120, 126153. [Google Scholar] [CrossRef]
- Paudel, D.; Boogaard, H.; De Wit, A.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine Learning for Large-Scale Crop Yield Forecasting. Agric. Syst. 2021, 187, 103016. [Google Scholar] [CrossRef]
- Dlamini, L.; Crespo, O.; Van Dam, J.; Kooistra, L. A Global Systematic Review of Improving Crop Model Estimations by Assimilating Remote Sensing Data: Implications for Small-Scale Agricultural Systems. Remote Sens. 2023, 15, 4066. [Google Scholar] [CrossRef]
- Xu, X.; Gao, F.; Xiong, D.; Fan, Z.; Xiong, S.; Dong, P.; Qiao, H.; Ma, X. Digital Twin-Based Winter Wheat Growth Simulation and Optimization. Field Crops Res. 2025, 329, 109953. [Google Scholar] [CrossRef]
- Gejdoš, M.; Michajlová, K. Analysis of Current and Future Forest Disturbances Dynamics in Central Europe. Forests 2022, 13, 554. [Google Scholar] [CrossRef]
- Bošeľa, M.; Petráš, R.; Šebeň, V.; Mecko, J.; Marušák, R. Evaluating Competitive Interactions between Trees in Mixed Forests in the Western Carpathians: Comparison Between Long-Term Experiments and SIBYLA Simulations. For. Ecol. Manag. 2013, 310, 577–588. [Google Scholar] [CrossRef]
- Irauschek, F.; Barka, I.; Bugmann, H.; Courbaud, B.; Elkin, C.; Hlásny, T.; Klopcic, M.; Mina, M.; Rammer, W.; Lexer, M.J. Evaluating Five Forest Models Using Multi-Decadal Inventory Data from Mountain Forests. Ecol. Model. 2021, 445, 109493. [Google Scholar] [CrossRef]
- Hlásny, T.; Barcza, Z.; Barka, I.; Merganičová, K.; Sedmák, R.; Kern, A.; Pajtík, J.; Balázs, B.; Fabrika, M.; Churkina, G. Future Carbon Cycle in Mountain Spruce Forests of Central Europe: Modelling Framework and Ecological Inferences. For. Ecol. Manag. 2014, 328, 55–68. [Google Scholar] [CrossRef]
- Hansen, J.W.; Jones, J.W. Scaling-up Crop Models for Climate Variability Applications. Agric. Syst. 2000, 65, 43–72. [Google Scholar] [CrossRef]
- Nabhani, A.; Sjølie, H.K. TreeSim: An Object-Oriented Individual Tree Simulator and 3D Visualization Tool in Python. SoftwareX 2022, 20, 101221. [Google Scholar] [CrossRef]
- Wimmler, M.-C.; Bathmann, J.; Vollhüter, J.; Berger, U. pyMANGA: A Modular, Open and Extendable Software Platform for Modeling of Forest and Vegetation Dynamics. Environ. Model. Softw. 2024, 174, 105973. [Google Scholar] [CrossRef]
- Bravo, F.; Ordóñez, C.; Vázquez-Veloso, A.; Michalakopoulos, S. SIMANFOR Cloud Decision Support System: Structure, Content, and Applications. Ecol. Model. 2025, 499, 110912. [Google Scholar] [CrossRef]
- Thurnher, C.; Klopf, M.; Hasenauer, H. MOSES—A Tree Growth Simulator for Modelling Stand Response in Central Europe. Ecol. Model. 2017, 352, 58–76. [Google Scholar] [CrossRef]
- Fabrika, M.; Ďurský, J. Algorithms and Software Solution of Thinning Models for SIBYLA Growth Simulator. J. For. Sci. 2005, 51, 431–445. [Google Scholar] [CrossRef]
- Machar, I.; Simon, J.; Brus, J.; Pechanec, V.; Kiliánová, H.; Filippovová, J.; Vrublová, K.; Mackovcin, P. A Growth Simulation Model as a Support Tool for Conservation Management Strategy in a Mountain Protected Area. eco.mont 2018, 10, 61–69. [Google Scholar] [CrossRef]
- Fabrika, M.; Valent, P.; Scheer, Ľ. Thinning Trainer Based on Forest-Growth Model, Virtual Reality and Computer-Aided Virtual Environment. Environ. Model. Softw. 2018, 100, 11–23. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, M.; Zhang, B.; Wang, M.; Shen, C.; Yue, S.; Wen, Y.; Lü, G. A Web-Based Integrated Modeling and Simulation Method for Forest Growth Research. Earth Space Sci. 2019, 6, 2142–2159. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, W.; He, J.; Liu, Y.; Ai, T.; Liu, D. A Land-Use Spatial Optimization Model Based on Genetic Optimization and Game Theory. Comput. Environ. Urban Syst. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Baskent, E.Z.; Borges, J.G.; Kašpar, J. An Updated Review of Spatial Forest Planning: Approaches, Techniques, Challenges, and Future Directions. Curr. For. Rep. 2024, 10, 299–321. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z.; Qin, H.; Zhao, Y. Evaluating the Neighborhood, Hybrid and Reversion Search Techniques of a Simulated Annealing Algorithm in Solving Forest Spatial Harvest Scheduling Problems. Silva Fenn. 2016, 50, 1622. [Google Scholar] [CrossRef]
- Mrkvička, T.; Soubeyrand, S.; Myllymäki, M.; Grabarnik, P.; Hahn, U. Monte Carlo Testing in Spatial Statistics, with Applications to Spatial Residuals. Spat. Stat. 2016, 18, 40–53. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Senf, C.; Seidl, R. Airborne Laser Scanning to Optimize the Sampling Efficiency of a Forest Management Inventory in South-Eastern Germany. Ecol. Indic. 2023, 157, 111281. [Google Scholar] [CrossRef]
- Rodríguez-Ruiz, J.; Martínez-Calvo, A.; Pérez-Cruzado, C. Designing Circular Fixed-Area Plots in Large-Scale Forest Inventories: Effect of Horizontal Distance Measurement Uncertainty and Tree Position Pattern. Can. J. For. Res. 2025, 55, 1–14. [Google Scholar] [CrossRef]
- Waeselynck, V.; Saah, D. Importance Sampling for Cost-Optimized Estimation of Burn Probability Maps in Wildfire Monte Carlo Simulations. Fire 2024, 7, 455. [Google Scholar] [CrossRef]
- Gomes, V.d.S.; Monti, C.A.U.; Silva, C.S.J.e.; Gomide, L.R. Operational Harvest Planning Under Forest Road Maintenance Uncertainty. For. Policy Econ. 2021, 131, 102562. [Google Scholar] [CrossRef]
- Zeng, H.; Garcia-Gonzalo, J.; Peltola, H.; Kellomäki, S. The Effects of Forest Structure on the Risk of Wind Damage at a Landscape Level in a Boreal Forest Ecosystem. Ann. For. Sci. 2010, 67, 111. [Google Scholar] [CrossRef]
- Sambakhe, D.; Fortin, M.; Renaud, J.-P.; Deleuze, C.; Dreyfus, P.; Picard, N. Prediction Bias Induced by Plot Size in Forest Growth Models. For. Sci. 2014, 60, 1050–1059. [Google Scholar] [CrossRef]
- Pöpperl, F.; Seidl, R. Effects of Stand Edges on the Structure, Functioning, and Diversity of a Temperate Mountain Forest Landscape. Ecosphere 2021, 12, e03692. [Google Scholar] [CrossRef]
- Torresani, M.; Montagnani, L.; Rocchini, D.; Moudrý, V.; Andreoli, A.; Wellstein, C.; Koyanagi, K.; Ros, L.D.; Bacaro, G.; Perrone, M.; et al. LiDAR Insights on Stand Structure and Topography in Mountain Forest Wind Extreme Events: The Vaia Case Study. Agric. For. Meteorol. 2024, 359, 110267. [Google Scholar] [CrossRef]
- Firmino, P.N.; Tomé, M.; Paulo, J.A. Do Distance-Dependent Competition Indices Contribute to Improve Diameter and Total Height Tree Growth Prediction in Juvenile Cork Oak Plantations? Forests 2023, 14, 1066. [Google Scholar] [CrossRef]
- Rieder, J.S.; Link, R.M.; Köthe, K.; Seidel, D.; Ullmann, T.; Žmegač, A.; Zang, C.; Schuldt, B. TreeCompR: Tree Competition Indices for Inventory Data and 3D Point Clouds. Methods Ecol. Evol. 2024, 15, 2198–2208. [Google Scholar] [CrossRef]
- Fazlollahi Mohammadi, M.; Tobin, B.; Jalali, S.G.; Kooch, Y.; Riemann, R. Fine-Scale Topographic Influence on the Spatial Distribution of Tree Species Diameter in Old-Growth Beech (Fagus orientalis Lipsky.) Forests, Northern Iran. Sci. Rep. 2022, 12, 7633. [Google Scholar] [CrossRef]
- Raigosa-García, I.; Rathbun, L.C.; Cook, R.L.; Baker, J.S.; Corrao, M.V.; Sumnall, M.J. Rethinking Productivity Evaluation in Precision Forestry Through Dominant Height and Site Index Measurements Using Aerial Laser Scanning LiDAR Data. Forests 2024, 15, 1002. [Google Scholar] [CrossRef]
- Nunes, M.H.; Jucker, T.; Riutta, T.; Svátek, M.; Kvasnica, J.; Rejžek, M.; Matula, R.; Majalap, N.; Ewers, R.M.; Swinfield, T.; et al. Recovery of Logged Forest Fragments in a Human-Modified Tropical Landscape During the 2015-16 El Niño. Nat. Commun. 2021, 12, 1526. [Google Scholar] [CrossRef]
- Fiandino, S.; Plevich, J.; Tarico, J.; Utello, M.; Demaestri, M.; Gyenge, J. Modeling Forest Site Productivity Using Climate Data and Topographic Imagery in Pinus elliottii Plantations of Central Argentina. Ann. For. Sci. 2020, 77, 95. [Google Scholar] [CrossRef]
- Li, Q.; Hu, B.; Shang, J.; Remmel, T.K. Two-Stage Deep Learning Framework for Individual Tree Crown Detection and Delineation in Mixed-Wood Forests Using High-Resolution Light Detection and Ranging Data. Remote Sens. 2025, 17, 1578. [Google Scholar] [CrossRef]
- Lisiewicz, M.; Kamińska, A.; Kraszewski, B.; Stereńczak, K. Correcting the Results of CHM-Based Individual Tree Detection Algorithms to Improve Their Accuracy and Reliability. Remote Sens. 2022, 14, 1822. [Google Scholar] [CrossRef]
- Vanderwel, M.C.; Lopez, E.L.; Sprott, A.H.; Khayyatkhoshnevis, P.; Shovon, T.A. Using Aerial Canopy Data from UAVs to Measure the Effects of Neighbourhood Competition on Individual Tree Growth. For. Ecol. Manag. 2020, 461, 117949. [Google Scholar] [CrossRef]
- Holm, S.; Schweier, J. Virtual Forests for Decision Support and Stakeholder Communication. Environ. Model. Softw. 2024, 180, 106159. [Google Scholar] [CrossRef]
- Yu, H.; Wu, M.M.; He, H.S. Developing Platform of 3-D Visualization of Forest Landscape. Environ. Model. Softw. 2022, 157, 105524. [Google Scholar] [CrossRef]
- Merganič, J.; Merganičová, K.; Vlčková, M.; Dudáková, Z.; Ferenčík, M.; Mokroš, M.; Juško, V.; Allman, M.; Tomčík, D. Deadwood Amount at Disturbance Plots After Sanitary Felling. Plants 2022, 11, 987. [Google Scholar] [CrossRef]
- Datasets, National Forest Centre (NLC), Slovakia. Available online: https://web.nlcsk.org/datasety/ (accessed on 5 September 2025).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Kükenbrink, D.; Schneider, F.D.; Schmid, B.; Gastellu-Etchegorry, J.-P.; Schaepman, M.E.; Morsdorf, F. Modelling of Three-Dimensional, Diurnal Light Extinction in Two Contrasting Forests. Agric. For. Meteorol. 2021, 296, 108230. [Google Scholar] [CrossRef]
- Meeussen, C.; Govaert, S.; Vanneste, T.; Calders, K.; Bollmann, K.; Brunet, J.; Cousins, S.A.O.; Diekmann, M.; Graae, B.J.; Hedwall, P.-O.; et al. Structural Variation of Forest Edges Across Europe. For. Ecol. Manag. 2020, 462, 117929. [Google Scholar] [CrossRef]
- Pang, L.; Wang, G.; Sharma, R.P.; Lu, J.; Tang, X.; Fu, L. Simulation of Thinning by Integrating Tree Competition and Species Biodiversity for Target Tree-Based Management of Secondary Forests. Forests 2023, 14, 1896. [Google Scholar] [CrossRef]
- Schmid, U.; Frehner, M.; Glatthorn, J.; Bugmann, H. ProForM: A Simulation Model for the Management of Mountain Protection Forests. Ecol. Model. 2023, 478, 110297. [Google Scholar] [CrossRef]
- Ezquerro, M.; Diaz-Balteiro, L.; Pardos, M. Implications of Forest Management on the Conservation of Protected Areas: A New Proposal in Central Spain. For. Ecol. Manag. 2023, 548, 121428. [Google Scholar] [CrossRef]
- Langhammer, M.; Thober, J.; Lange, M.; Frank, K.; Grimm, V. Agricultural Landscape Generators for Simulation Models: A Review of Existing Solutions and an Outline of Future Directions. Ecol. Model. 2019, 393, 135–151. [Google Scholar] [CrossRef]
- Henniger, H.; Huth, A.; Frank, K.; Bohn, F.J. Creating Virtual Forests around the Globe and Analysing Their State Space. Ecol. Model. 2023, 483, 110404. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Huber, I.; Archontoulis, S.V. Coupling Machine Learning and Crop Modeling Improves Crop Yield Prediction in the US Corn Belt. Sci. Rep. 2021, 11, 1606. [Google Scholar] [CrossRef]
- Hernández-Ochoa, I.M.; Gaiser, T.; Kersebaum, K.-C.; Webber, H.; Seidel, S.J.; Grahmann, K.; Ewert, F. Model-Based Design of Crop Diversification Through New Field Arrangements in Spatially Heterogeneous Landscapes. A Review. Agron. Sustain. Dev. 2022, 42, 74. [Google Scholar] [CrossRef]
- Jahel, C.; Baron, C.; Vall, E.; Karambiri, M.; Castets, M.; Coulibaly, K.; Bégué, A.; Lo Seen, D. Spatial Modelling of Agro-Ecosystem Dynamics across Scales: A Case in the Cotton Region of West-Burkina Faso. Agric. Syst. 2017, 157, 303–315. [Google Scholar] [CrossRef]
- Rahman, M.H.U.; Ahrends, H.E.; Raza, A.; Gaiser, T. Current Approaches for Modeling Ecosystem Services and Biodiversity in Agroforestry Systems: Challenges and Ways Forward. Front. For. Glob. Change 2023, 5, 1032442. [Google Scholar] [CrossRef]
- Kraft, P.; Rezaei, E.E.; Breuer, L.; Ewert, F.; Große-Stoltenberg, A.; Kleinebecker, T.; Seserman, D.-M.; Nendel, C. Modelling Agroforestry’s Contributions to People—A Review of Available Models. Agronomy 2021, 11, 2106. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z. Optimizing Neighborhood-Based Stand Spatial Structure: Four Cases of Boreal Forests. For. Ecol. Manag. 2022, 506, 119965. [Google Scholar] [CrossRef]
- Retzlaff, C.O.; Gollob, C.; Nothdurft, A.; Stampfer, K.; Holzinger, A. Multi-Objective Optimization of Cable-Road Layouts in Smart Forestry. Int. J. For. Eng. 2024, 35, 444–455. [Google Scholar] [CrossRef] [PubMed]
- Castro, I.; Salas-González, R.; Fidalgo, B.; Farinha, J.T.; Mendes, M. Optimising Forest Management Using Multi-Objective Genetic Algorithms. Sustainability 2024, 16, 10655. [Google Scholar] [CrossRef]
- Ding, M.; Yin, X.; Pan, S.; Liu, P. Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China. Forests 2025, 16, 452. [Google Scholar] [CrossRef]
- Fotakis, D.G.; Sidiropoulos, E.; Myronidis, D.; Ioannou, K. Spatial Genetic Algorithm for Multi-Objective Forest Planning. For. Policy Econ. 2012, 21, 12–19. [Google Scholar] [CrossRef]

| Hyperparameter | Lower Boundary | Upper Boundary |
|---|---|---|
| Iterations | 10 | 1000 |
| Maximum Translation [%] | 1 | 33 |
| Maximum Rotation [°] | 1 | 90 |
| Maximum Resize [%] | 1 | 33 |
| Iterations | Maximum Translation [%] | Maximum Rotation [°] | Maximum Resize [%] | Minimum Overlap [%] | Maximum Overlap [%] | Mean Overlap [%] |
|---|---|---|---|---|---|---|
| 426 | 29.0 | 12.7 | 4.8 | 30.3 | 96.3 | 81.8 |
| 719 | 21.1 | 14.4 | 1.6 | 31.0 | 97.4 | 81.4 |
| 785 | 15.9 | 14.7 | 4.2 | 28.9 | 98.0 | 82.9 |
| 827 | 15.5 | 15.2 | 5.0 | 28.8 | 97.8 | 83.1 |
| 880 | 19.4 | 13.9 | 9.2 | 28.9 | 97.3 | 83.0 |
| 916 | 15.6 | 8.6 | 4.3 | 28.8 | 97.8 | 83.1 |
| 925 | 11.2 | 11.4 | 4.8 | 27.0 | 98.6 | 83.2 |
| 941 | 11.3 | 7.1 | 5.9 | 28.9 | 97.8 | 82.9 |
| 942 | 25.8 | 28.9 | 16.4 | 29.7 | 96.5 | 82.4 |
| 950 | 20.6 | 22.9 | 11.0 | 29.6 | 96.3 | 82.8 |
| 982 | 14.7 | 26.7 | 10.0 | 29.0 | 97.6 | 82.9 |
| Hyperparameter | Minimum | Median | Mean | Maximum |
|---|---|---|---|---|
| Iterations | 426 | 916 | 844.8 | 982 |
| Maximum Translation [%] | 11.2 | 15.9 | 18.2 | 29.0 |
| Maximum Rotation [°] | 7.1 | 14.4 | 16.0 | 28.9 |
| Maximum Resize [%] | 1.6 | 4.5 | 7.0 | 16.4 |
| Shape | Non-Optimized Simulation Plots | Optimized Simulation Plots | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std. Dev. | Minimum | Maximum | Mean | Std. Dev. | |
| Square | 6.8 | 93.3 | 65.2 | 16.6 | 17.0 | 97.0 | 71.0 | 13.9 |
| Circle | 4.7 | 93.9 | 66.0 | 16.7 | 15.1 | 94.2 | 68.8 | 14.5 |
| Rectangle | 0.0 | 94.6 | 49.7 | 20.3 | 24.9 | 97.9 | 82.0 | 10.4 |
| Ellipse | 0.0 | 90.4 | 48.0 | 16.8 | 21.9 | 95.7 | 81.9 | 10.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koreň, M.; Márton, P.; Arbain, M.K.A.; Valent, P.; Sitko, R.; Fabrika, M. Monte Carlo-Based Spatial Optimization of Simulation Plots for Forest Growth Modeling. ISPRS Int. J. Geo-Inf. 2025, 14, 408. https://doi.org/10.3390/ijgi14110408
Koreň M, Márton P, Arbain MKA, Valent P, Sitko R, Fabrika M. Monte Carlo-Based Spatial Optimization of Simulation Plots for Forest Growth Modeling. ISPRS International Journal of Geo-Information. 2025; 14(11):408. https://doi.org/10.3390/ijgi14110408
Chicago/Turabian StyleKoreň, Milan, Peter Márton, Mosab Khalil Algidail Arbain, Peter Valent, Roman Sitko, and Marek Fabrika. 2025. "Monte Carlo-Based Spatial Optimization of Simulation Plots for Forest Growth Modeling" ISPRS International Journal of Geo-Information 14, no. 11: 408. https://doi.org/10.3390/ijgi14110408
APA StyleKoreň, M., Márton, P., Arbain, M. K. A., Valent, P., Sitko, R., & Fabrika, M. (2025). Monte Carlo-Based Spatial Optimization of Simulation Plots for Forest Growth Modeling. ISPRS International Journal of Geo-Information, 14(11), 408. https://doi.org/10.3390/ijgi14110408







