Abstract
Street design and land subdivision are significant tasks in the development and redevelopment planning process. Optimizing street and land subdivision layouts within a unified framework to achieve solutions that meet a set of objectives and constraints (e.g., minimizing parcel area deviation from standard values, minimizing land consumption for street construction, etc.) is a critical concern for planners, particularly in complex contexts such as blocks with irregular shapes and parcels of varying sizes and requirements. To address this challenge, a mathematical formulation is presented for the bi-level street network and land subdivision optimization problem. Subsequently, the solution procedure is outlined, which utilizes a genetic-based algorithm for street design and a memetic–genetic-based algorithm for land subdivision. Finally, two cases are presented, solved, and discussed to analyze and verify the proposed mathematical model and solution procedures. The results suggest that the formulated problem is suitable for addressing the coupled street network and land subdivision design problem, and it can be adapted and extended to other case studies. Additionally, the introduced ideas and algorithms satisfactorily solved the stated problem.
1. Introduction
Land subdivision, fragmentation, or partitioning refers to splitting an area into several smaller parcels (also called lots), which has been applied in a wide range of planning practices (e.g., land consolidation [1], agricultural or urban land readjustment [2], urban growth simulation [3], and land subdivision impact analysis before implementation [4]).
In the land subdivision process, planners assign the size and area of a parcel regarding several indicators [5] (e.g., access to the road network, minimum length of sides, etc.). If the area under consideration is small, the geometry is simple (e.g., a perfect rectangle), and the number of contributing factors is limited (e.g., the average size of parcels is equal, and only the elongation of the parcels matters), land subdivision can be performed manually. However, in cases where the size of the problem is not small, the geometry of the area is not simple, and the contributing indices are not limited to one or two items with constant values, planners can no longer adopt manual procedures and require a tool to facilitate addressing the land subdivision problem.
In general, such tools are not replacements for the planners because the land subdivision is an intricate issue and needs the judgment of experts, at least at the final stages, to choose, rectify, or check the qualitative aspects of the layout(s) generated by computational methods. In other words, the end of these tools and techniques is to produce acceptable subdivision layout(s) in line with the planners’ concerns and to support analysts by providing reasonable solution(s) as a base for adding complementary details. Therefore, several pieces of research attempted to develop automated methods to tackle the land subdivision problem.
As a triggering study, Buis and Vingerhoeds [6] used expert systems and geographic information systems (GISs) to create a subdivision module. The introduced module was semi-automated and dependent on the participation of the planner during the model implementation. In addition, the subdivision problem did not follow the optimization structure, which did not necessarily lead to the optimal solution(s). Parish and Müller [7] proposed an approach for modeling street growth and land subdivision through a recursive algorithm dividing the longest pair of parallel edges until the size of the parcels meets a pre-defined threshold. However, this algorithm might generate empty areas inside the blocks that are not justifiable in actual cases. In addition, the algorithm discards the parcels without access to the street network, even if by applying a repairing strategy the resulting solution can be more satisfactory in terms of shape and other indices. Touriño et al. [8] developed a region-growing algorithm and an optimization method for addressing the land partitioning problem in a raster-based GIS. Although this study considers an optimization method, the solution process is limited to the raster environment, which does not represent the geographical areas in the vector-based format that is closer to spatial environments. Moreover, if the raster resolution changes, some lands may be disregarded in the subdivision layout. Halatsch et al. [9] and Marshall [10] used automatic methods for the land subdivision, but their studies were limited to formic controls.
Applying computer graphics, Vanegas et al. [11] and Vanegas et al. [12] developed a tool for coupling geometrical with behavioral modeling. The technique worked based on the recursive binary algorithm and produced streets and parcels close to the real contexts. However, the solution procedure performs well for rectangular- or square-shaped parcels. In addition, the final solution might contain lots without accessibility to the streets. Vanegas et al. [13] established an interactive environment for the procedural generation of land parcels based on skeleton and bounding box algorithms. This interactive environment integrated with the two subdivision algorithms improved the previous studies and resulted in well-ordered land parcels. Furthermore, these methods are fruitful and appropriate options if three conditions are applied: (1) the geometry of the area under consideration provides a relatively uniform depth for the back-to-back subdivision, (2) the area of the required parcels is not highly varied, and (3) the area constraint supports a safe margin that accepts the small- and large-size parcels obtained at the end of the calculation process. It should be noted that such ideas have been implemented in ArcGIS City Engine [14] and improved by Colomb et al. [15].
As well as the research in computer graphics, Wickramasuriya et al. [16] established a tool for land subdivision. This tool partitions regular and irregular parcels so that the subdivision process leads to a layout with the highest land parcels and the lowest streets. Dahal and Chow [17] introduced a toolset for performing the land subdivision task. This toolset attempts to generate streets and land parcels like real-world contexts by applying a few parameters. These two indicated tools are applicable when the areas of lots follow an identical size, and the planner sets the subdivision’s length and width. However, if the size of the parcels considerably varies, and the planner cannot propose a fixed length or width for all parcels in a study area, these methods might produce layouts incompatible with the imposed area constraints.
This way, to include the effect of size variation in the land subdivision process, Demetriou et al. [18] and Demetriou, See, and Stillwell [2] formulated the land subdivision using the structure of the optimization problem statement presented in the literature on operation research (for example, see [19]). The solution procedure generates and improves parcels employing the Voronoi diagram to find a layout with optimum shape, land value, size, and accessibility to the road network surrounding the area considered for land subdivision. Nonetheless, this model does not create the street layout since it is not linked with a street design module. Moreover, in the final solution, lots might be distributed everywhere in the subdivision area because points representing parcels are free to be located everywhere throughout the search space. To this extent, although the final solution might satisfy size constraints, it might not fulfill the planner’s preferences for the subdivision layout arrangement. Also, the procedures proposed for generating new answers might lead to unsatisfactory parcels in the irregular blocks.
In addition to the mentioned studies, Haklı et al. [20] introduced a land partitioning model based on the binary search algorithm and Delaunay triangulation to determine the location of parcels within a block, with shape, size, value, and access as the partitioning objectives. Koc et al. [21] applied a binary search algorithm to automate the parceling task in urban zones given edge, area, or both. These pieces of research aimed to find the arrangement of parcels in a fashion that the parcels cover the given boundary or boundaries without the need for intervention in the boundaries’ structures by creating streets. These models perform parceling on the ribbon-shaped blocks that have a depth value. If the main block has a width longer than the pre-defined depth and supports the creation of two back-to-back subdivisions, the main block is decomposed into two ribbon-shaped blocks. Then, the binary search divides the decomposed blocks into parcels satisfying parcel area constraints. However, if the width of the main block permits the generation of three or more ribbon-shaped areas, the output layout might include inaccessible parcels, unless the main block is turned into parts manually, and the parts are subjected to the subdivision implementation separately. As well as these two studies on land consolidation and urban zoning segmentation, Kucukmehmetoglu and Geymen [22] and Koc et al. [23] presented optimization models for land readjustment and reallocation, where parcels are distributed within blocks so that at least one side of each is facing toward the streets around the blocks.
Despite the satisfactory results of these optimization models and solution methods for land reallocation purposes, these frameworks do not enclose a street design module. This means that if the constraint of access to the block’s peripheral streets is relaxed, these methods might not result in optimal solutions. In other words, if the internal streets can be designed to connect the allocated parcels to the peripheral roads, these algorithms discard layouts that might be optimal during the solution process.
Building upon the indicated literature, there is still room in the body of existing knowledge for developing land subdivision models that can (1) divide blocks with geometries that do not necessarily support a pre-defined subdivision depth value, (2) handle subdivision problems with variations in parcel size, (3) maintain the distribution of parcels in a structure that meets the planner’s requirements, and (4) embed the street design process within the solution procedure to provide internal streets (whether pedestrian or non-pedestrian) for subdivision layouts with inaccessible parcels.
In other words, in irregular blocks and cases with varying parcel areas, procedural operations (e.g., back-to-back or bounding box methods [7,24]) may not satisfy planning requirements such as parcel shape characteristics and parcel distribution within the blocks. Additionally, the indicated methods and processes do not contain a street design module (e.g., the algorithm proposed by Demetriou, See, and Stillwell [2] or the straight skeleton process [13]) or use an operation to provide accessibility in an intuitive or template-based manner (e.g., the bounding box method [7,24] and template-oriented algorithm [17,25]), which may not result in optimal layouts, especially in irregular blocks that should include parcels with varying areas.
Considering all these points, a flexible framework is required—one that is adaptable to blocks with complex geometries, able to handle parcel size variations, and capable of generating solutions that align with planner preferences. This framework should integrate optimization-based land subdivision and street design modules to manage land resources more effectively and rationally.
Thus, this article attempts to fulfill the following objectives: (1) conceptualizing a bi-level system of equations that couples the land subdivision and street design processes and can be modified based on the planner’s and planning requirements, and (2) presenting ideas for solving the elaborated equations. Consequently, this research contributes to the literature on spatial planning and computational geography by (1) developing a flexible bi-level optimization model that embeds a street design unit within the land subdivision problem able to represent alternatives regarding the planning concepts, (2) adapting a memetic–genetic algorithm and operators compatible with the structure of the formulated problem, and (3) evaluating the problem and solution method in some representative.
The rest of this article is structured as follows: Section 2 introduces the bi-level optimization framework, solution algorithm, and case studies. Section 3 presents solution algorithm parameters and outputs. Section 4 discusses problem formulation, the solution method, and results, followed by concluding remarks.
2. Materials and Methods
In this section, the problem formulation and solution algorithm are explained. First, the coupled land subdivision and street design (CLSSD) problem is stated. Second, the solution procedure is given. Finally, cases for model implementation and the data under consideration are presented.
2.1. Coupled Land Subdivision and Street Design Problem Formulation
2.1.1. Modeling Context
Let be a block given to a planner for land partitioning. is surrounded by street , and a set of access points, , is designated on to provide the enter and exit spots for connections from inside to and vice versa if inaccessible parcels exist in the subdivision layout. Each parcel has attributes and (), where the former is the required area for parcel , and the latter is the amount of the area of that can be consumed with the internal streets. Each parcel is modeled by the tuple that shows the coordinate of in the subdivision space. Coordinates of parcels () in are determined by the function , where is a set of reference lines inside , and generates coordinates for each such that falls within , is located on one of the reference lines in , and no pair of has similar coordinates. Reference lines in illustrate the preferences of the planner for the arrangement of the parcels in based on his/her conceptual subdivision plan. The reference lines set the direction and number of rows for the subdivision layout, and their place might change during the optimization process.
Given the parcels’ arrangement , the subdivision layout is obtained by the calculation of the Voronoi diagram of denoted by . The output of represented by is the extent of parcels denoted by and . is specified by a set of vertices, , each element of which is a point with longitude and latitude. In , parcel is called inaccessible if , where if is not toward , and otherwise.
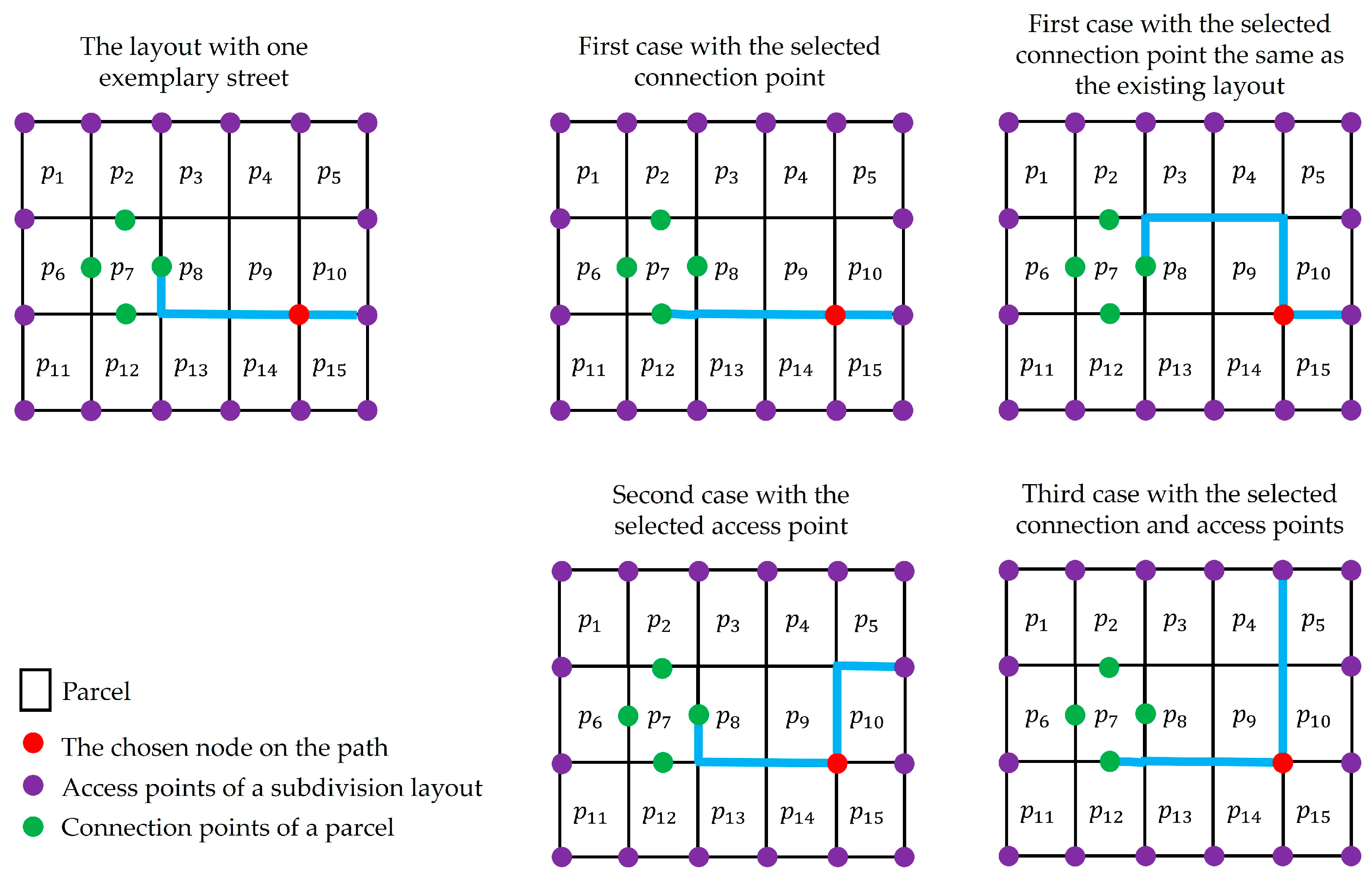
Following the computation of , if there is at least one inaccessible extent in the subdivision layout, connection points are created corresponding to each inaccessible extent. The connection points are created through the application of rules defined by the planner on the inaccessible extents in by using the function . In short, this function outputs set containing the connection point coordinates for each inaccessible extent. For example, assume that is an inaccessible parcel in and has four sides (i.e., ). If only one rule is considered (i.e., ), and , then the inaccessible parcels can be connected to the access points in through the mid-points of their constituting sides; after the implementation of , four connection points are constituted in the middle of each side of , and for , four coordinates are stored in .
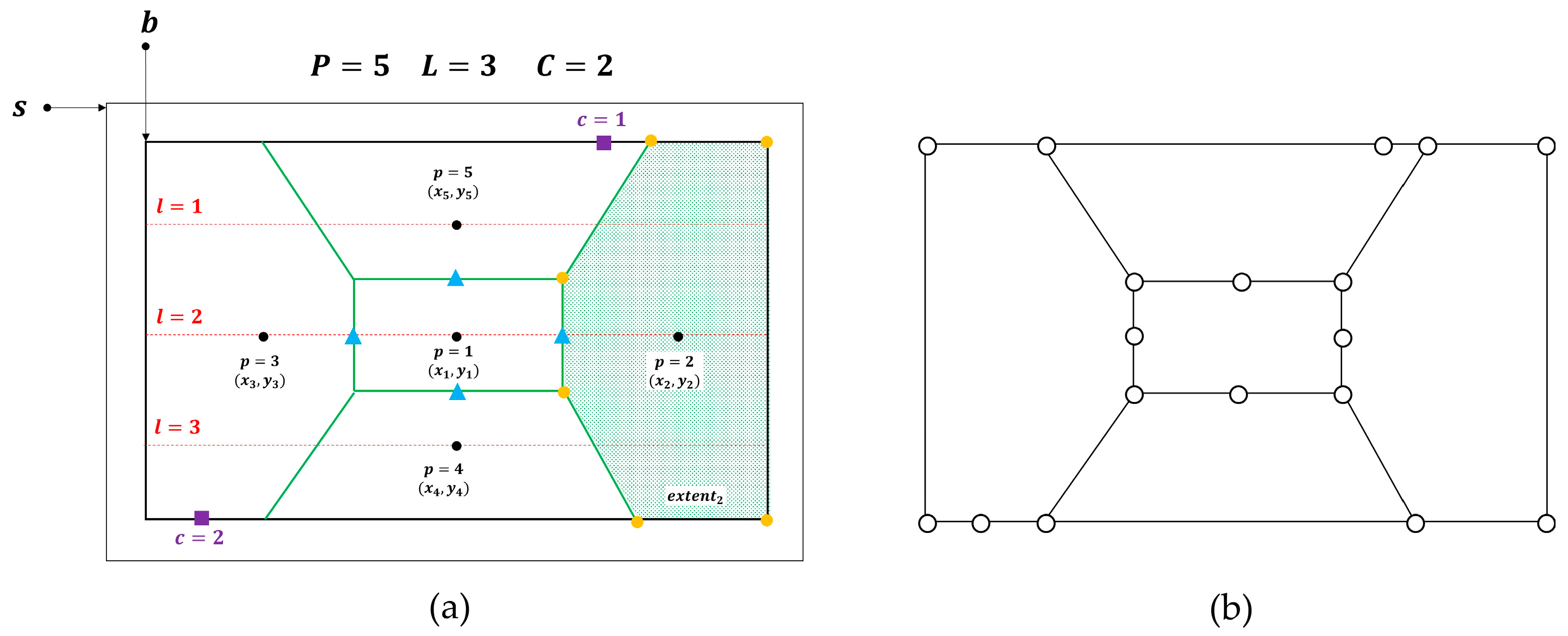
After the calculation of and and having , a network corresponding to the subdivision layout can be built. This network, , is represented by a set of nodes and a set of links denoted by and , respectively. is the union of s in , , and (i.e., ). is the intersection between the nodes in and the union of sides created for the extents in (i.e., ). Figure 1 illustrates a subdivision context and its corresponding network, including the indicated characteristics.
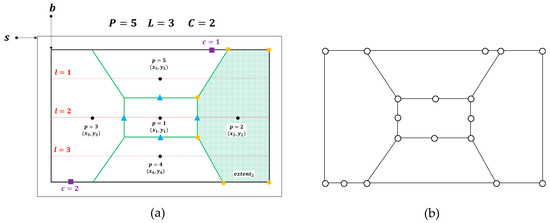
Figure 1.
(a) Subdivision context: The thick black line is the boundary of block . The thin black line is the boundary of street surrounding . Red lines are the subdivision reference lines. Black points with the circle symbol represent parcels, and the parcel with identifier is inaccessible. Green lines are the results of calculating the Voronoi diagram for . Purple points with the square symbol are access points. Blue points with the triangle symbol are the connection points for the inaccessible parcel , after the implementation of the mid-point rule () through the application of function . This way, has four members in , the output of . Orange points with the circle symbol are vertices for exemplary parcel (). And the green shaded area is the extent of (). (b) Corresponding network to the subdivision context. Circles are nodes, and lines are links.
2.1.2. Optimization Problem
Regarding the modeling context mentioned in the previous section, the general CLSSD can be formulated as a bi-level optimization problem. The upper (or leader) level represents the subdivision layout optimization, and the lower (or follower) level models the street design optimization given a subdivision layout. This problem mainly includes two decision variables: (a) the location of parcels (i.e., ), and (2) links in the designed streets, , where , and if link is created, and otherwise.
Without the loss of generality and inspired by [2,18], at the upper level, let the maximization of a set of shape indices and minimization of the area of the created parcels from their required values be the case. The value of these objectives depends on the arrangement of the parcels and the street layout inside simultaneously. At the lower level, finding the configuration of the internal streets that provide access to inaccessible parcels by minimizing factors, such as the street length and the angle between the street’s consecutive links, is formulated. If the shape indices at the upper lever are limited to the number of the sides of the parcels’ extents and the desired length of each side of the parcels, the bi-level CLSSD problem is modeled as follows (Equations (1)–(4)):
The upper-level problem:
Subject to the lower-level problem:
And the lower-level problem is subject to:
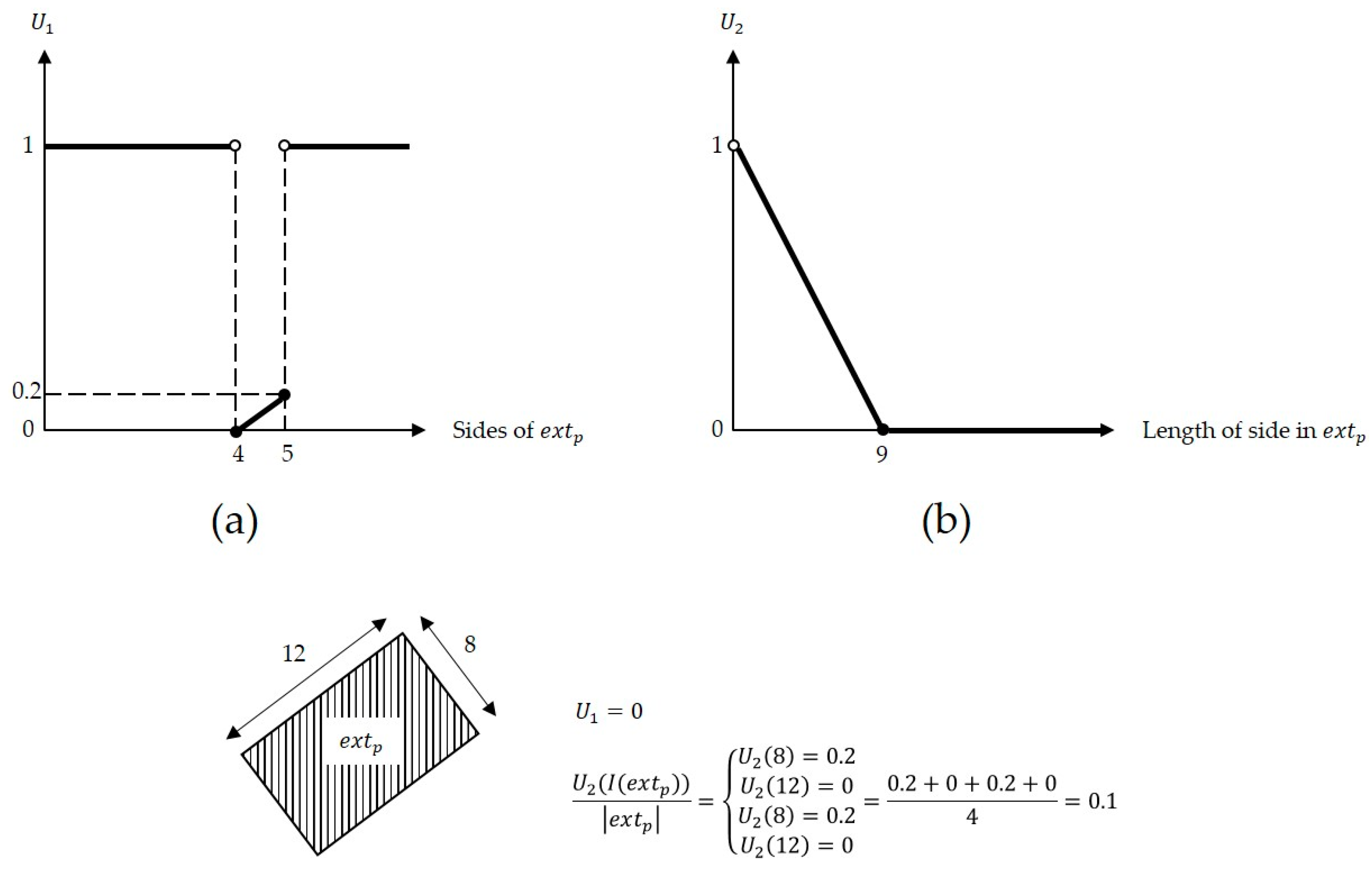
In Equation (1), and are, respectively, the importance values of the shape indices and the area function. and vary between 0 and 1, and . is the number of parcels that should be allocated through the subdivision process. is a set of the shape indices. is the weight of the shape index and is defined by the planner. varies between 0 and 1, and . is a penalty function that maps the value of shape index for to a zero-to-one space. Two types of shape indices can be regarded in the upper level’s objective function: first, the ones directly related to the properties of an extent as a whole (e.g., the number of sides), and second, the indices related to the components of an extent (e.g., the desired length of each side of an extent). Therefore, is a piecewise function that includes sub-function , which decomposes to its constituent parts. If the shape index is of the first type, is not performed on , otherwise, it decomposes , and each component of is penalized by . For instance, if the number of sides () and the length of sides () are the shape indices, and the desired values are 4 with one-side-up tolerance and 10 with 10% tolerance, respectively, and can take the forms illustrated in Figure 2. It should be noted that the penalty functions are not limited to the linear form, and the planner can adopt any type for modeling the penalization behavior. Equation (5) represents in detail.
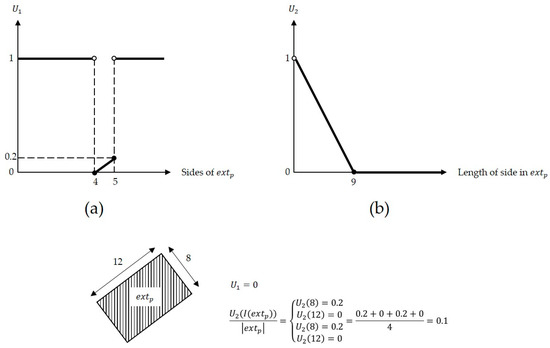
Figure 2.
Examples for the penalty functions and . (a) An extent-related shape index: the parcel’s number of sides (). (b) A shape index related to the components of an extent: length of sides of an extent ().
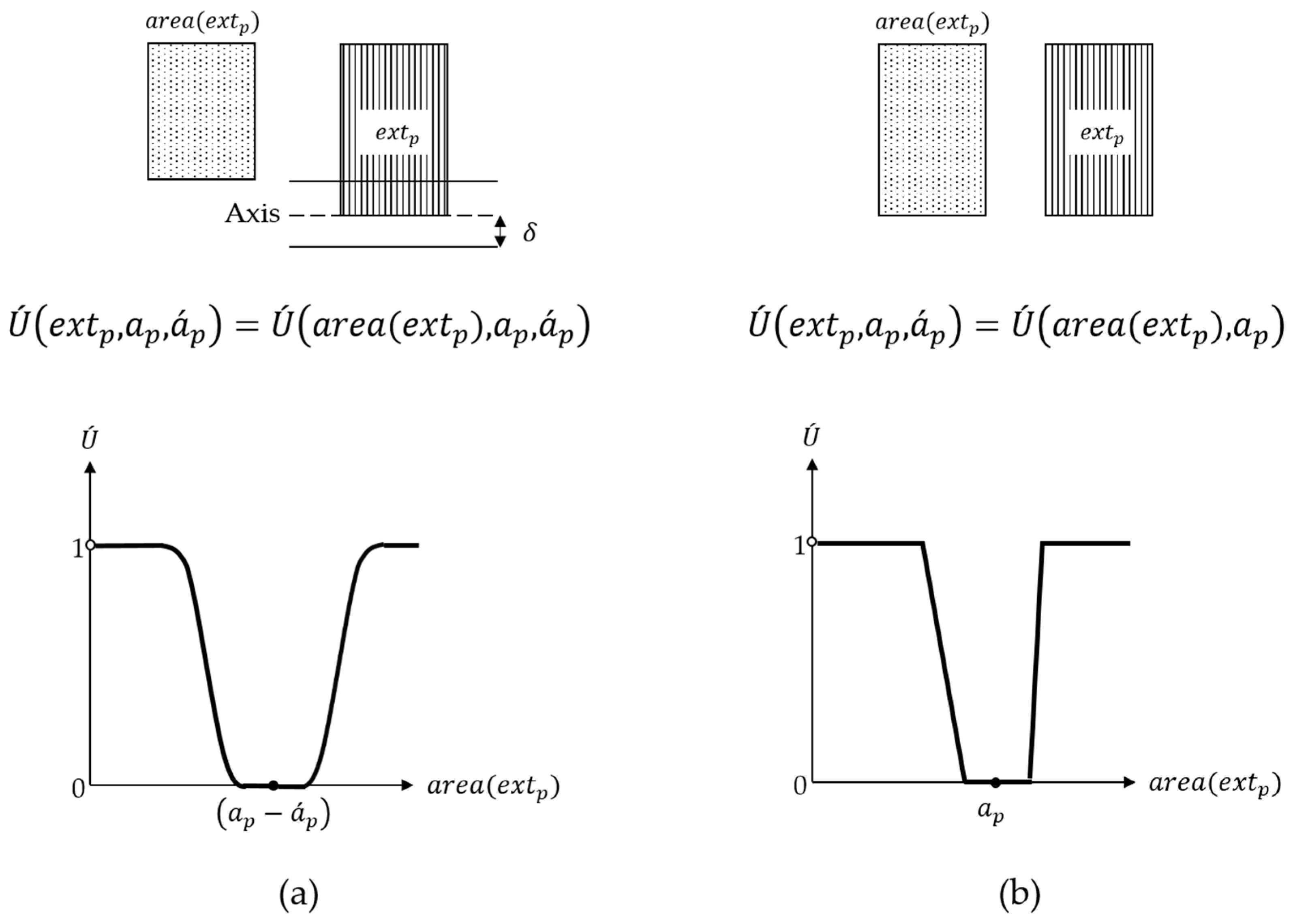
Like , is a function that penalizes based on its deviation from its required area. If after solving the lower-level problem, intersects with the designed streets (i.e., , where is the buffer function with width and the given street axes in ), is penalized according to and , the area of occupied by the streets. Otherwise, it is penalized according to . This function is modeled through Equation (6), and Figure 3 displays a sample for the computation of .
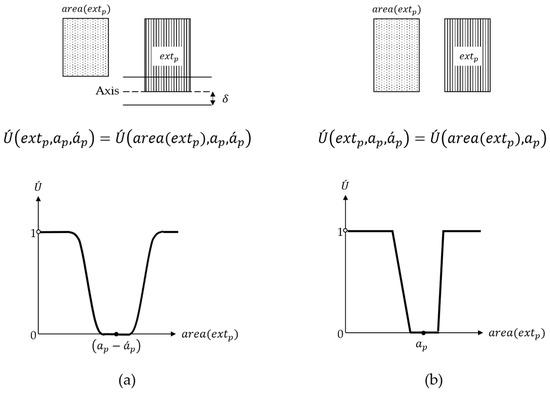
Figure 3.
(a) An example for the calculation of for intersected with a street obtained from solving . (b) An example for the calculation of for , which is not intersected with the streets.
is the upper-level optimization problem, and it also varies between 0 and 1 due to the application of the standardization values (i.e., , , and ).
In Equation (2), the street design problem is formulated at the lower level. It outputs the street configuration of a subdivision layout concerning its corresponding network. In other words, the aim of is to select links in corresponding to the subdivision layout with inaccessible parcels (i.e., ), such that each inaccessible parcel is connected to an access point through one of its connection points in . If a path connecting the connection point to is denoted by , and for each inaccessible parcel , is the set that stores paths from s (the connection points on the inaccessible parcel ) to s (the access points in ), and the objective of the lower-level problem is to find the union of optimal paths generated for each inaccessible parcel , minimizing the length and the angle between consecutive links of s.
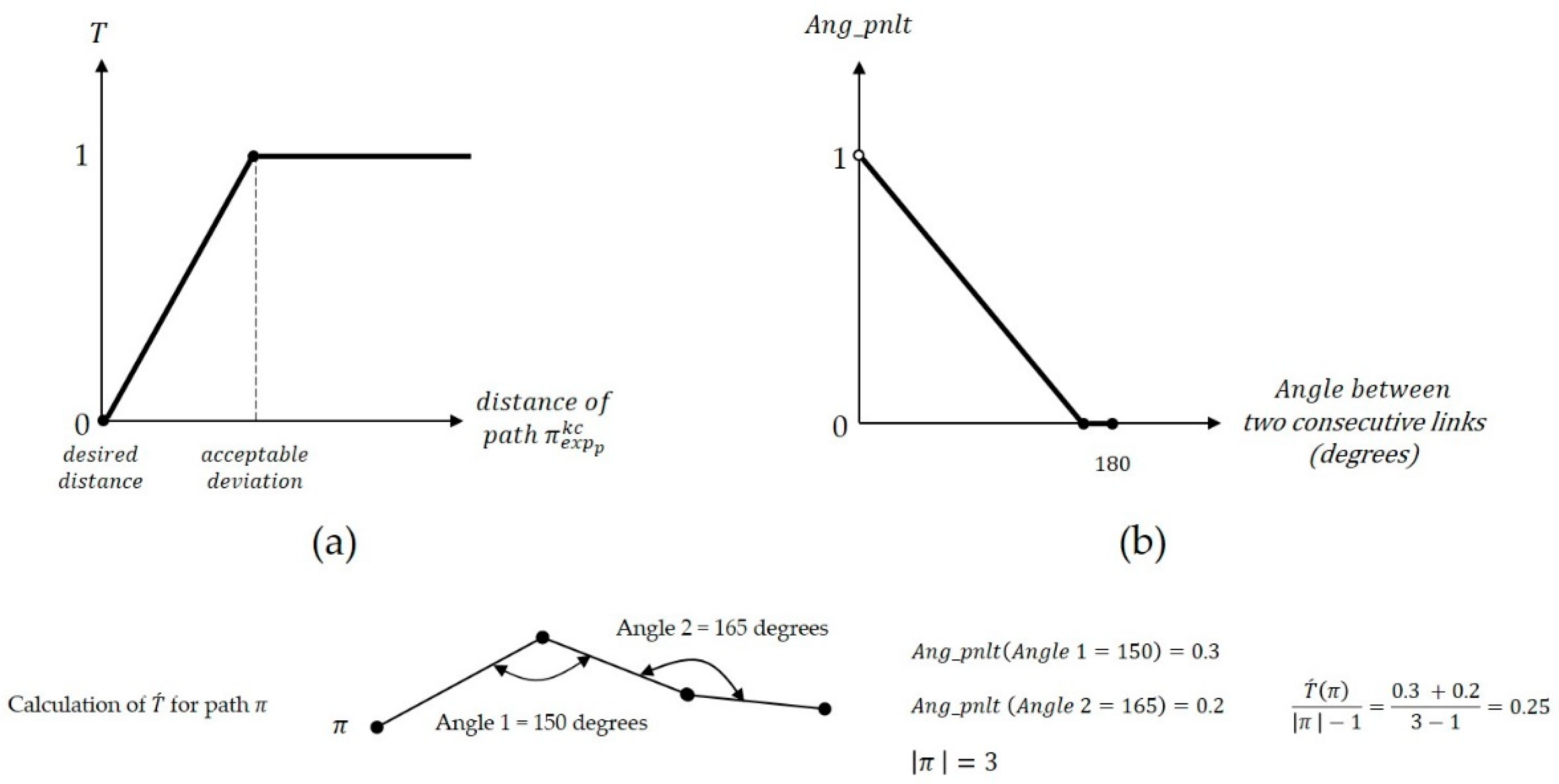
This way, two functions are articulated for the calculation of the length and the angle of a path. Function varies within the range of and penalizes path according to its deviation from a given value. Function decomposes to its constructing links, calculates the angle between the consecutive links, penalizes the obtained angle values, sums the penalties, and divides the sum by , where is the number of links in path . Division to is conducted to set the value between 0 and 1. Figure 4 shows sample functions for and , and the way that can be computed.
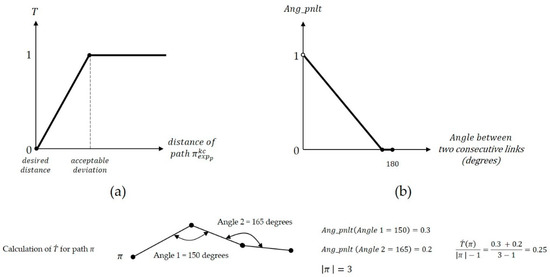
Figure 4.
(a) A sample function for . (b) A sample penalty function for calculating .
and are, respectively, the importance values of the length and angle of the consecutive of links of a path from to . and vary between 0 and 1, and . Consequently, falls between 0 and 1. Equation (3) ensures that the constructed path is acyclic and starts from and ends at . In this equation, and are the set of links exiting from and entering node , respectively. Also, Equation (4) ensures that for every inaccessible parcel with several connection points, only one path is designed to avoid the generation of multi-paths for one parcel.
2.2. Solution Procedure
The CLSSD is an NP-hard problem as (1) the subdivision layout optimization is NP-hard per se [2], and (2) it is proved that bi-level programming belongs to the non-deterministic polynomial-hard class of optimization problems [26]. Concerning this characteristic and non-convexity of bi-level programming problems, refs. [27,28,29] recommend meta-heuristic algorithms for solving such problems.
Several meta-heuristics have been developed and applied in the literature of operation research for addressing NP-hard problems (e.g., particle swarm [30,31], simulated annealing [32,33], ant colony [34,35], and genetic algorithms [36,37]). In this study, a genetic algorithm (GA) is taken as a solution procedure to represent the ideas for finding the optimum answer. It should be noted that the GA is considered because of its characteristics such as the ability to work with multiple solutions extending the area of search in the solution space, compatibility with complex problems with unknown solution spaces [38], and providing room for designing operators compatible with the CLSSD problem. In addition, it should be stated that the aim of this section is to show how the CLSSD problem can be approached. Consequently, the GA is considered a context for examining the applicability of the general solution ideas, which are crystallized in the algorithm’s operators and can be placed into other meta-heuristics.
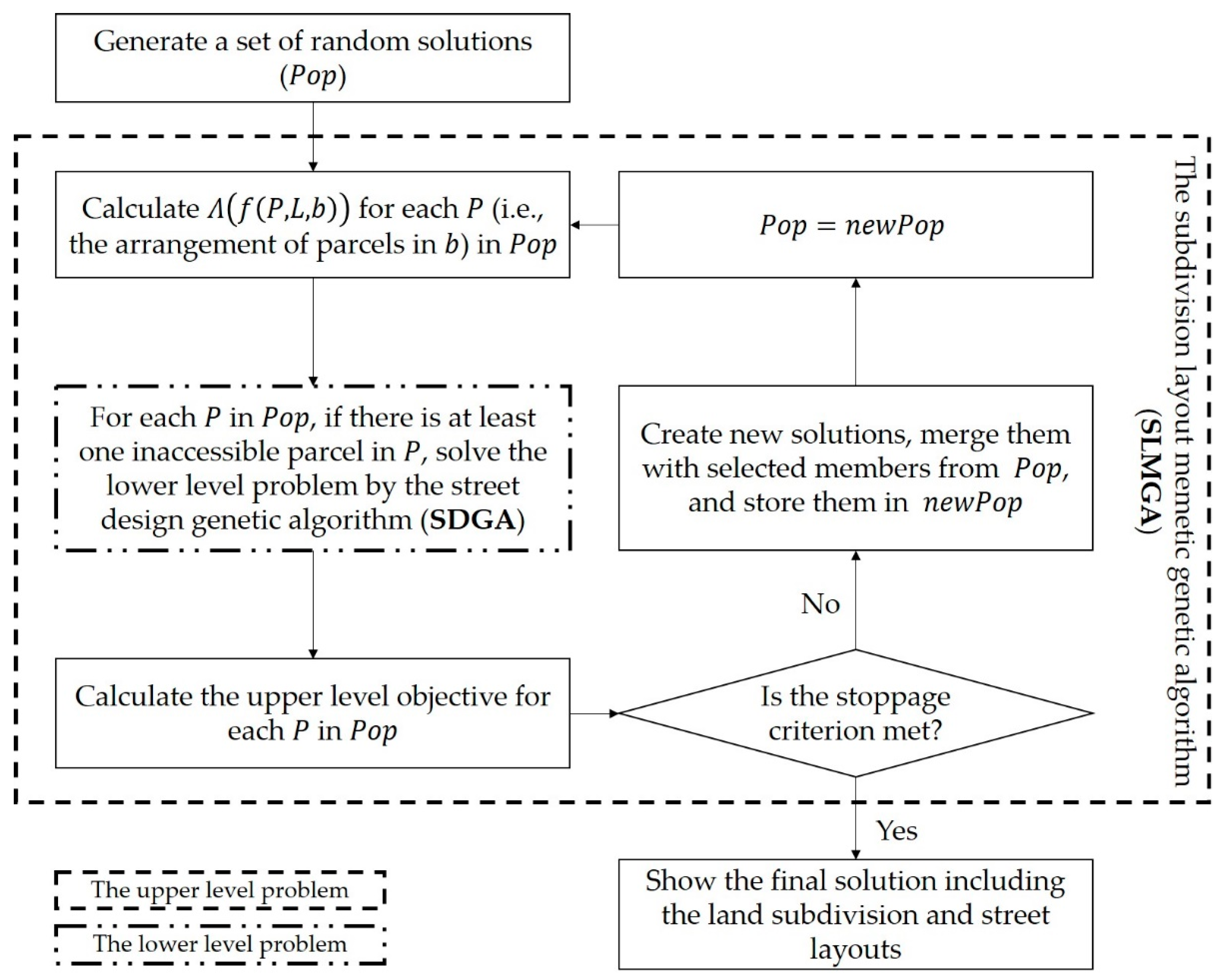
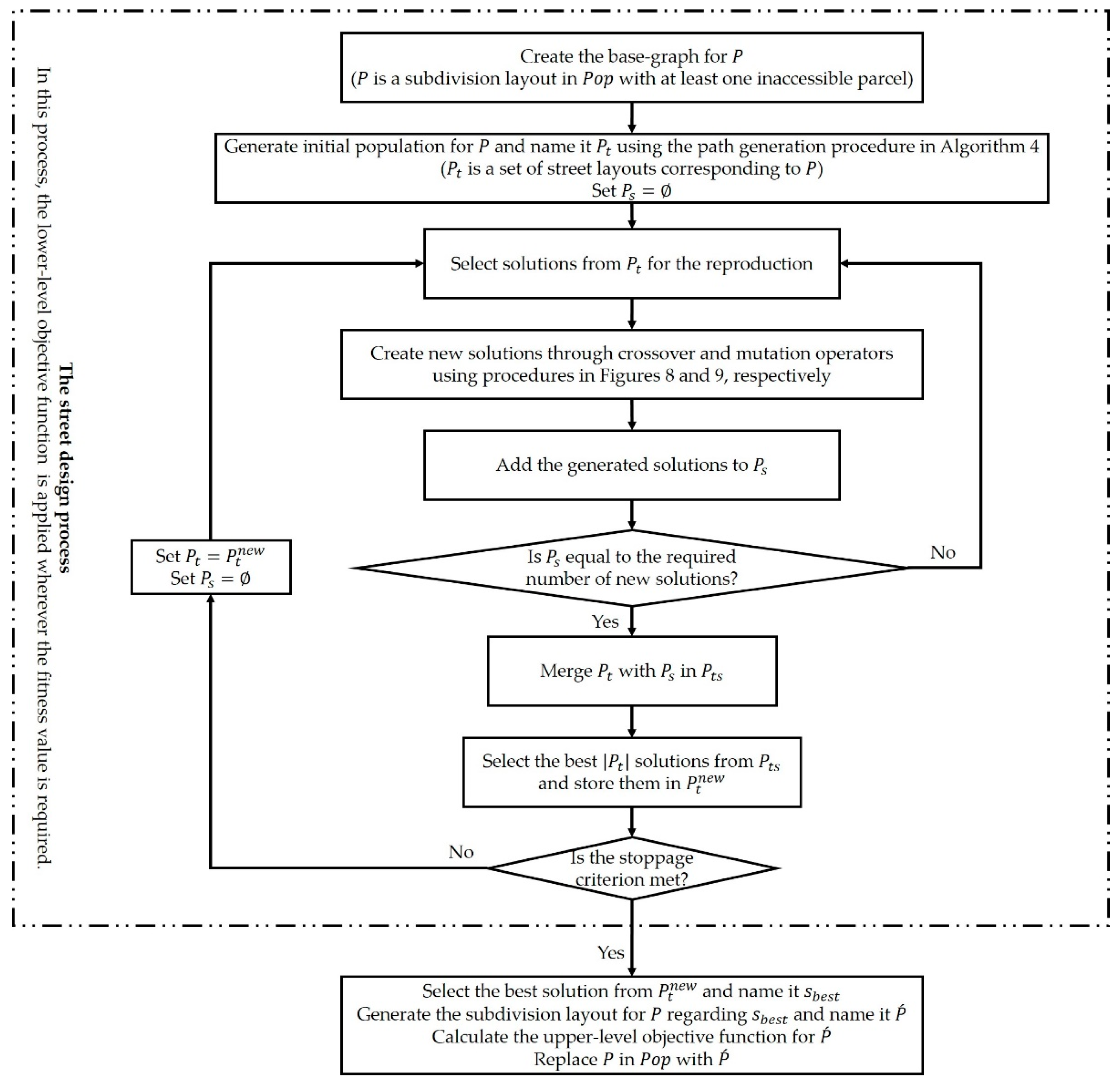
The proposed algorithm consists of three main components: (1) the generation of initial random solutions, (2) the street design genetic algorithm (SDGA), and (3) the subdivision layout memetic–genetic algorithm (SLMGA). First, a population is generated. The population includes several arrangements of parcels in through . Second, the created population enters SLMGA, and the corresponding layout to each member of the population containing the extent of the parcels is computed by . Then, the access condition is checked for each subdivision layout . If has at least one inaccessible parcel, the connection points are created through , and s are calculated. Having access points , the network is made for , and the street layout is designed by the application of SDGA. Third, the upper-level objective is computed for each member of the population. After that, if the stoppage criterion is fulfilled, the best solution is returned; otherwise, new solutions are produced from the answers in the population, and they are stored in a repository along with a certain number of solutions in the population. Note that the size of the repository is fixed during the optimization process, meaning that the number of solutions in the population stays the same after each iteration. Iteration continues until the stoppage criterion is met. Figure 5 depicts the general sequence of calculations for solving the CLSSD. Details of these components are explained in the following sections.
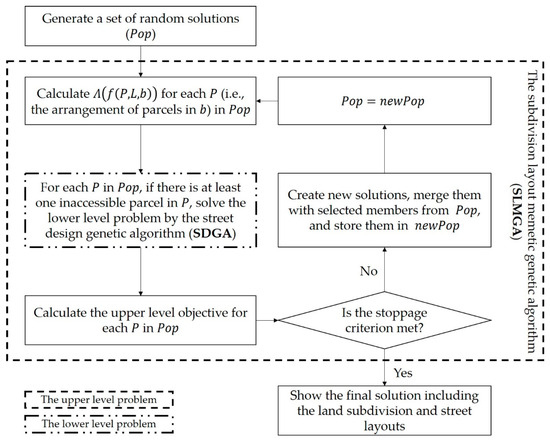
Figure 5.
The general sequence of calculations for solving the CLSSD problem.
2.2.1. Random Solution Generation Procedure
As indicated in Section 2.1.1, the subdivision reference lines in are based on the planner’s preferences and show the subdivision direction and the number of rows. One way to generate a random solution is to distribute parcels on the proposed reference lines. However, as the reference lines represent a subdivision concept, not an exact subdivision grid, sticking to them as the fixed source of population generation decreases the diversity of solutions and reduces the chance of searching the solution space for more satisfactory layouts. For this reason, a procedure is used in this article to keep the direction and number of reference lines the same as the planner’s preferences regarding the diversity quality in the solution procedure. It should be noted that the number of reference lines should not exceed the number of parcels (, where is the number of reference lines, and is the number of parcels).
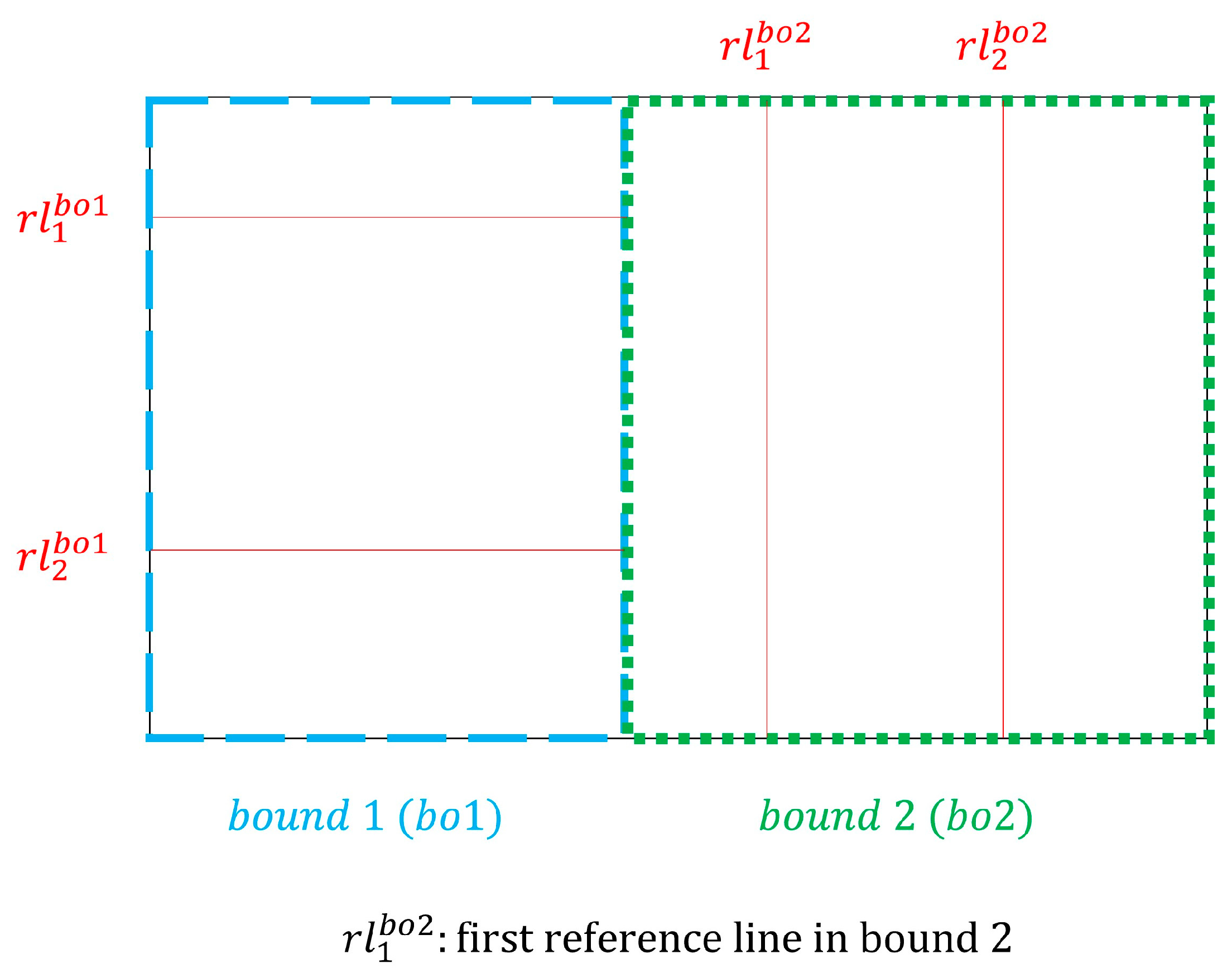
In addition, planners might like to have parcels with different directions within particular areas of . To consider this condition in the solutions, the planner sketches polygons on to set boundaries for special areas including reference lines with different directions. As an example, Figure 6 exhibits a case in which two bounds, each including two reference lines, are sketched.
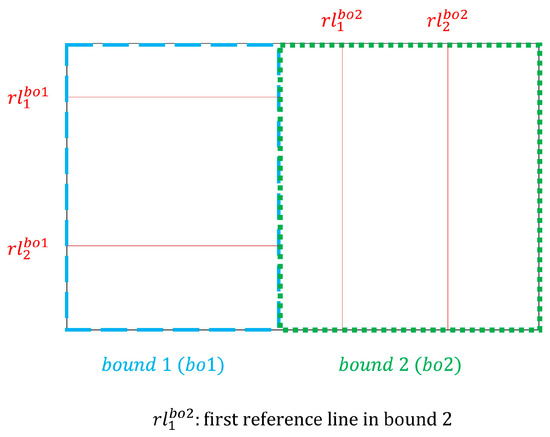
Figure 6.
An example for sketching bounds and reference lines on b.
To do so, first, the random solution generation procedure (RSGP) selects a bound and then the reference line from randomly. Second, the RSGP generates a point inside the chosen bound and creates a line parallel to , which passes through the generated point. If the RSGP has not produced the line before, it stores the line’s intersection with the bound, and . Otherwise, the RSGP generates another point and creates another line until it obtains a unique reference line. This procedure stops when (1) , and (2) the solution contains all the sketched bounds.
After generating the reference lines, first, the empty set is created. Second, the RSGP assigns a random point, , to each reference line and sets . For producing random points, given the starting and ending of a reference line, Equations (7) and (8) are applied, where is a random value between 0 and 1, and are the coordinates of the starting point of a selected reference line, and and are the coordinates of the ending point.
Third, the RSGP generates a random point on a randomly selected reference line. If the point is not in , ; otherwise, the RSGP generates another point. This process iterates until the RSGP obtains a new point not already in . If the size of equals the number of required parcels (), . Otherwise, the RSGP generates another point on a random reference line. This procedure terminates when the number of members in equals (i.e., the number of individuals in the SLMGA). Algorithm A1 shows the RSGP in detail.
2.2.2. SLMGA Procedure
The SLMGA consists of three parts: (1) the initial part, (2) the iterative part, and (3) the memetic part. The initial part receives from the RSGP. Then, for each member of the population, the subdivision layout is generated through the computation of the Voronoi diagram. If the subdivision layout includes at least one inaccessible parcel, the SDGA is performed. Next, the output replaces the previous solution, and the upper-level objective function is calculated for all layouts.
In the iterative part, new land subdivisions are generated by selecting layouts and performing crossover and mutation operators. There are various selection methods for choosing one solution from a population in the literature of GA (e.g., random selection, roulette wheel selection, rank, elitist selection, scale selection, and tournament selection). The SLMGA applies the rank selection because, as indicated by Fattahi [39], it gives the solutions with worse objective values a chance to enter into the new solution creation procedures and has the advantages of the roulette wheel selection (i.e., the increase in the number of better solutions in the population and the improvement of the average objective values of a population compared to its previous one). In the rank selection method, the ranks of solutions are computed based on the objective values, and selection is performed using the roulette wheel method on the rank values.
Selecting solutions by the rank method, the procedure for producing new subdivision layouts is executed. First, the number of subdivision layouts obtained from the crossover and mutation procedures is determined. These numbers depend on the crossover and mutation probabilities denoted by and , respectively. and designate the proportions of the solutions selected from and reproduced by the operators. These parameters affect the computational burden of the solution algorithm such that the larger these values, the slower the algorithm might be [40]. In addition, as the solution algorithms often iterate many times, setting large values for these parameters is unnecessary [39]. This way, several studies recommend the adoption of and between 0.8–0.9 and 0.2–0.3, respectively [2].
Second, the crossover and mutation operators are applied to the selected solutions. The crossover operator takes two layouts and combines them to generate a new subdivision layout. The crossover should hold three conditions: (1) the number of reference lines in each bound of the off-spring equals the number defined by the planner (Equations (9) and (10), where is the number of reference lines on bound , is the set of bounds, and is the total number of reference lines), (2) all reference lines include at least one parcel and do not contain parcels more than (Equation (11), where is the number of points on reference line ), and (3) the number of parcels in the off-spring equals the required number of parcels (Equation (12)).
This way, Algorithm A1 is developed to cross over the parent solutions and repair the off-spring if they violate the constraints in Equations (9)–(12). Assume that and are selected for entering the crossover procedure. Before performing this operator, the location of points and reference lines in and is checked to decide how the solutions are combined. If both solutions have the same reference lines (), a different procedure from the one applying to the layouts with different reference lines () is used. Aside from which of these conditions are accepted, points and reference lines in off-spring are inherited from their parents. However, after performing the crossover operator, the resulting layouts might violate the conditions in Equations (9)–(12). Therefore, according to the concepts of need and capacity (later explained in Algorithm A2), the off-spring are repaired to become feasible and have the characteristics of their parents. Algorithm A2 represents the crossover procedure and its sub-procedures in detail.
The mutation procedure can be defined in several ways. In this article, three mutation types are designed to cover reference line and parcel changes. The first type, called the parcel mutation procedure (PMP), which maintains the arrangement of reference lines like the parent solution, randomly picks a pre-defined number of parcels and redistributes them on the reference lines using Equations (7) and (8). The second type, called the reference line mutation procedure (RLMP), changes the location of some reference lines and projects the parcels on their corresponding lines, keeping the distance between them in the parent solution. The third type, called the parcel and reference line mutation procedure (PRLMP), randomly reallocates a pre-determined number of reference lines together with parcels. Three rates (i.e., , , and ) control the number of solutions generated by PMP, RLMP, or PRLMP. Rates vary between 0 and 100, which is the population percentage candidates for mutation. After determining the number of solutions entering the procedures, the rank selection method is applied for choosing the answers. Algorithm A3 describes the mutation operators in detail.
Once the crossover and mutation operators produce new solutions, they are added to , and the value of the upper-level objective function is computed for them. Next, the answers are entered into the third part, where the memetic stage starts. First, candidate solutions are obtained from by the rank selection method given , the number of candidates. Second, local search is performed to improve and exploit the candidates. In this article, the Hooke and Jeeves algorithm (HJA) (also called direct or pattern search) performs the local search task. The HJA is a numerical optimization model that uses a hill-climbing approach to search the solution space. Due to the independence of this model to a gradient, the HJA can be applied to incontiguous and indifferentiable problems [41]. The HJA begins with an initial solution, that is, the selected solution by the rank selection in the CLLSD problem. As mentioned, the solution is a set of points distributed on reference lines. The HJA moves the points on the reference lines to find a better subdivision layout. Let be the set of parcel coordinates that represents the position of each point by two components; the first is , and the second is . The HJA starts with an exploratory search which changes the location of points by adding and subtracting an interval to each component of the parcels. For the CLLSD problem, this interval, denoted by , is the length each parcel moves along its corresponding reference line. In the exploratory search, each component in is modified one by one through Equation (13), and the objective function is computed for each state, and the parcel’s position is replaced by the best one. A state generated from the movement of parcel along its corresponding reference line is acceptable if the new state does not overlay any other parcel in . This process goes forward to reach the last parcel in (i.e., ). The layout obtained after performing the exploratory search is illustrated by . In the Equation (13), is the reference line that parcel is placed on; is the length of ; and , , , and are the coordinates of start and end points of , respectively.
After the exploratory search, the movement pattern is executed. In this step, the new position of parcels is produced using Equation (14), where is the new position of parcels. The new position is feasible if all parcels fall within the subdivision bounds. Otherwise, is updated by dividing the values into 2, and the process starts over taking the new s into account. These computation steps iterate until all s become smaller than or equal to a pre-defined value that is commonly a very small value (e.g., 0.0001). The compact form of the HJA is presented in Algorithm A4.
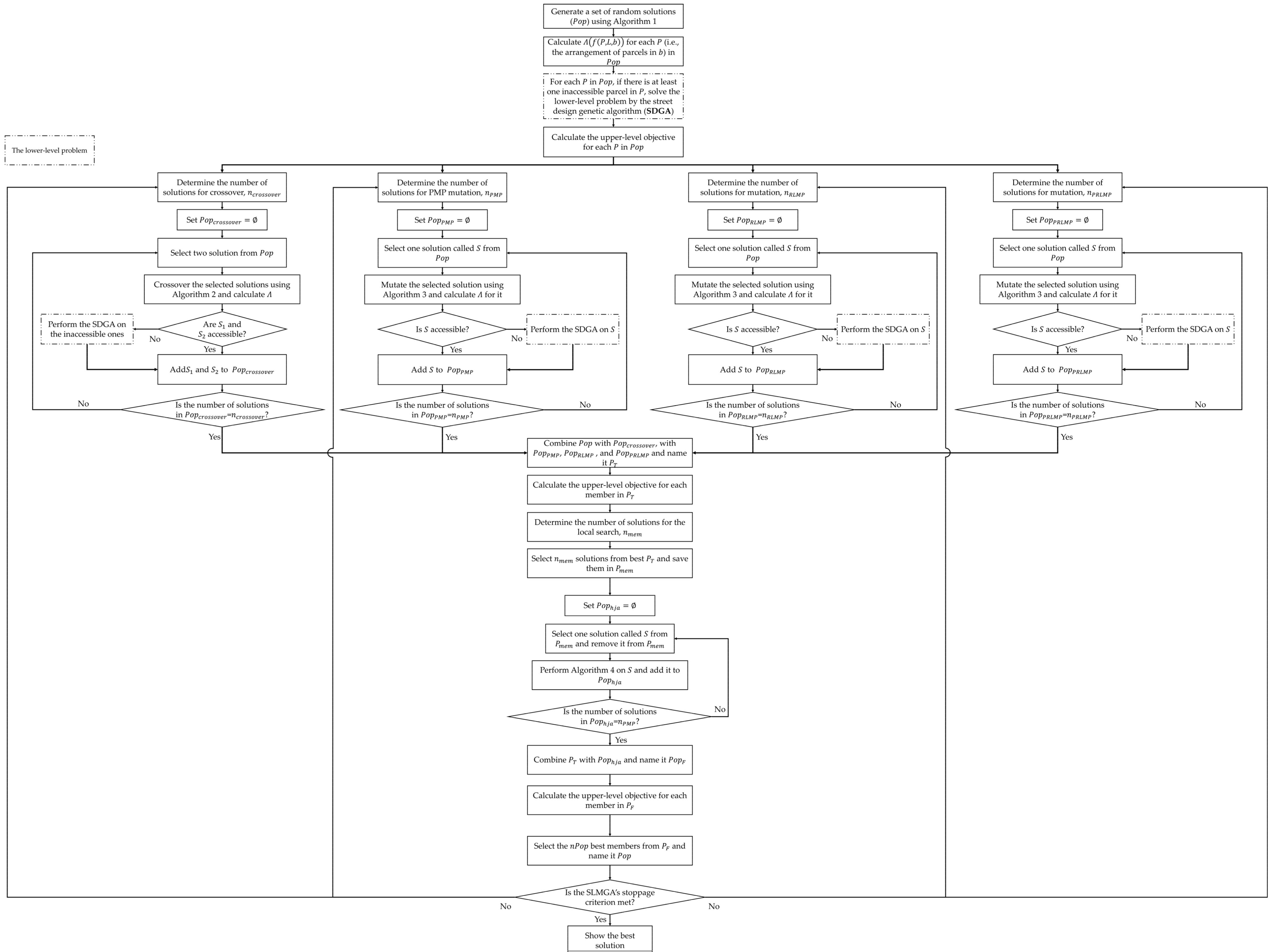
Next, the solutions with the best values are selected and used for regeneration. These steps iterate until the stoppage criterion is met. Figure 7 depicts the SLMGA in detail. It should be noted that the maximum number of iterations, run time limit, and no improvement of the objective value after a certain number of iterations are the common stoppage criteria for the GA algorithm [38,39].
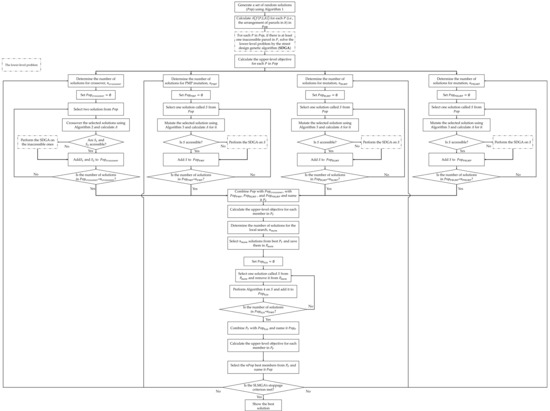
Figure 7.
The procedure of the SLMGA.
2.2.3. SDGA Procedure
As mentioned in Section 2.2.1 and Section 2.2.2, the SDGA is applied to the inaccessible subdivision layouts. First, the corresponding graph for the inaccessible layouts, named base-graph, is created by Algorithm A5, and second, the street design is performed.
Like the SLMGA, the SDGA starts with the creation of the initial population. For each subdivision layout input into the SDGA, an initial population is generated. Each member of the initial population is a street network, which is the union of paths connecting each inaccessible parcel in the subdivision layout from one of its connection points to one of the access points in the base-graph. This way, to generate a solution, the following steps are taken.
For each inaccessible parcel in the subdivision layout, a random connection point and an access point are selected at first. Second, a path from the connection point to the access point is produced through the process inspired by [42] and stored in the solution set. If the created path passes through the connection point of other inaccessible parcels, paths from their connection points to the access point are extracted from the generated path. Then, these parcels are discarded from the set of inaccessible parcels. This process iterates until all inaccessible parcels connect to the outside of the subdivision area. Third, the solution is added to the population. The procedure stops if the number of solutions equals a pre-defined threshold. Otherwise, the indicated steps generate another random street layout. Algorithm A4 shows the population generation procedure for the SDGA in detail.
After applying the path creation procedure in Algorithm A6, the lower-level objective function is calculated for each member of the population. Similar to the SLMGA, the rank selection method is applied to choose candidate solutions for reproduction. New answers are generated using crossover and mutation operators. The number of solutions produced by these operators is controlled by and , which are the crossover and mutation probabilities, respectively.
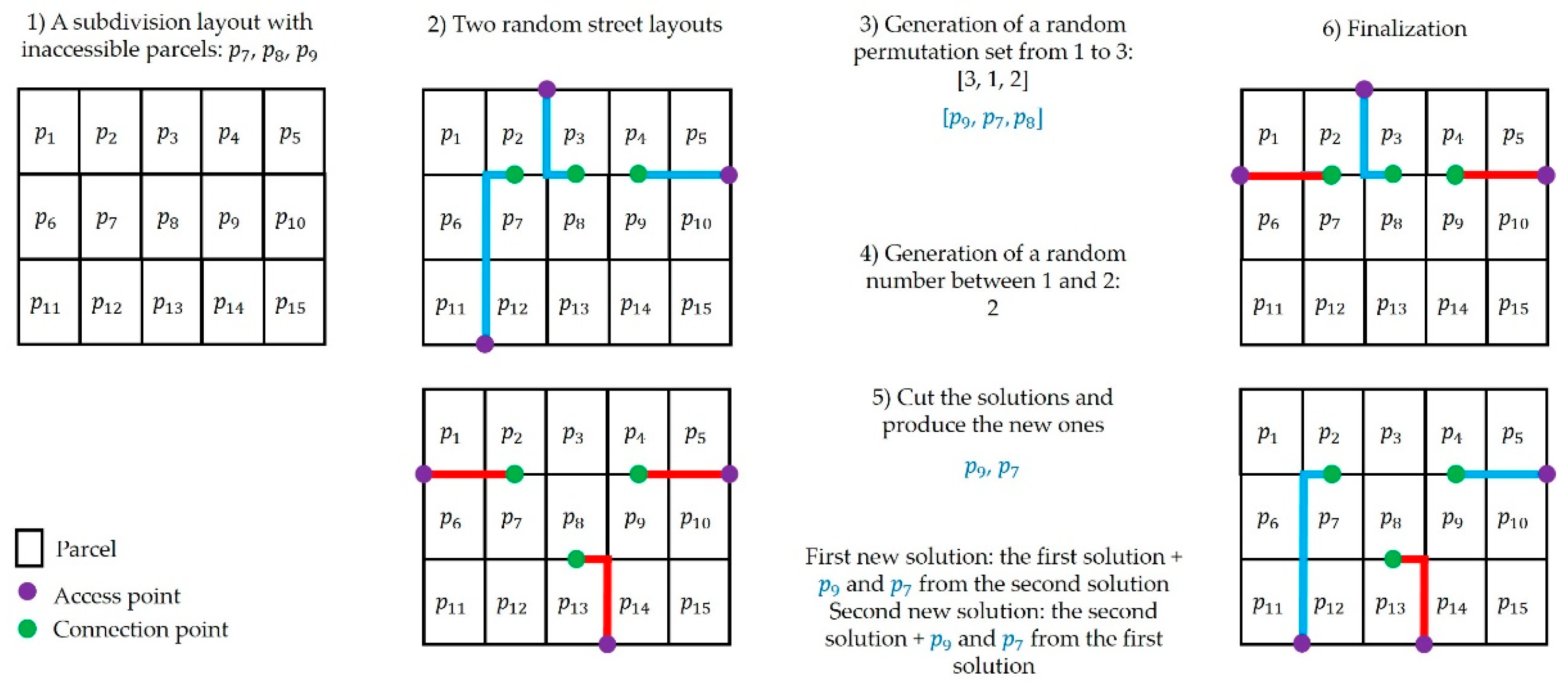
The steps represented in Figure 8 are followed to cross over two selected solutions. Let and be the selected solutions with the inaccessible parcel set of . First, a random permutation is generated equal to the number of inaccessible parcels, . Then, a random integer is generated between 1 and . Second, the random permutation set is cut from , and the streets of the corresponding parcels are combined to form new solutions.
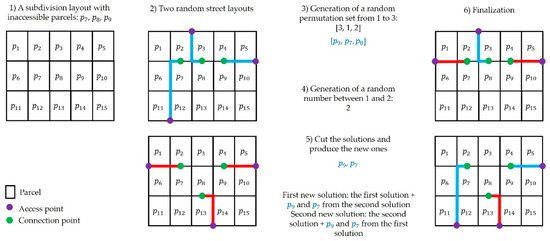
Figure 8.
The crossover operator for the SDGA.
One node other than the origin or destination on the chosen answer is selected for mutation. Then, one of the following states randomly chooses to generate a new solution. (1) The origin is the base of the new solution, (2) the destination is the base of the new solution, or (3) both the origin and destination are the bases of the new solution. For the first two cases, a random connection or access point is selected. Then, a new path is created from the connection point to the chosen node or from the selected node to the access point using the path creation procedure in Algorithm A6. Finally, the obtained path is merged with the remaining part of the solution under consideration. For the third case, at first, a connection and an access point are randomly selected. Second, paths from the connection point to the chosen node and from the selected node to the access point are built applying Algorithm A6. Finally, these paths are combined and replace the existing path. Figure 9 depicts the mutation procedure.
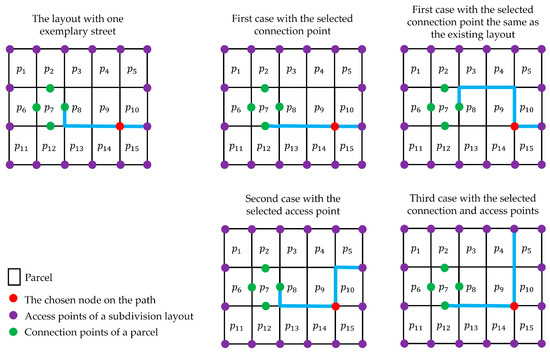
Figure 9.
The mutation operator for the SDGA.
After generating new solutions and adding them to the population, the value of the lower-level objective function is calculated. Next, the best answers are selected to form the new generation. These steps iterate until the stoppage criterion (e.g., reaching a maximum number of iterations or no improvement in the objective value) is met. Figure 10 displays the SDGA in detail.
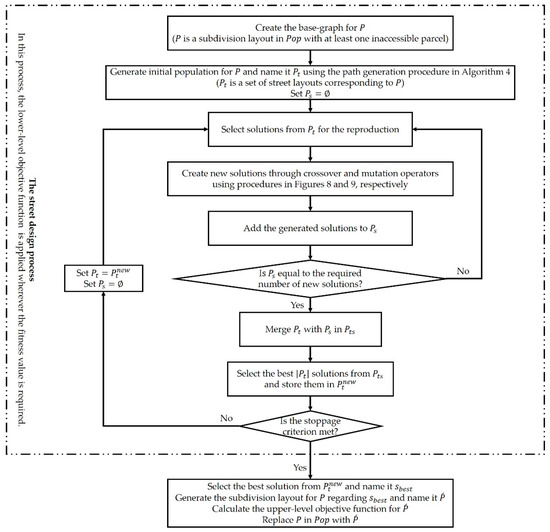
Figure 10.
The procedure of the SDGA.
2.3. Case Studies
Like Demetriou, See, and Stillwell [2] utilized two experimental cases for the model demonstration, two randomly generated cases are presented in this article to analyze the applicability of the instigated ideas for solving the bi-level CLSSD problem. Table 1 illustrates the case studies in detail, and Table 2 portrays the algorithm parameters. These examples are given to an experienced planner and fed into the algorithm concerning the same preferences to provide a verification context by comparing the solutions obtained from the professional designer and the designed algorithm.

Table 1.
Case studies. R1 to R10 are, respectively, the connection point rule (), street width (), number of parcels (), weight of the shape indices () and area deviation (), shape indices and weights (), shape index functions (), area deviation function (), street evaluation functions ( and ), weights of the street evaluation functions ( and ), and area of the required parcels.

Table 2.
The algorithm parameters.
3. Parameters and Outputs
The proposed procedures in Section 2 were programmed in Python using Shapely and Numpy modules for coding spatial operations and carrying out numerical computations, respectively. Table 3 exhibits the outputs of the algorithm given the parameters in Table 2. It also portrays subdivision layouts prepared by a trained and experienced planner.

Table 3.
Algorithm’s outputs compared with the planner’s layouts. (Note that some slight modifications (e.g., smoothness and redrawing) were applied for illustration quality purposes.)
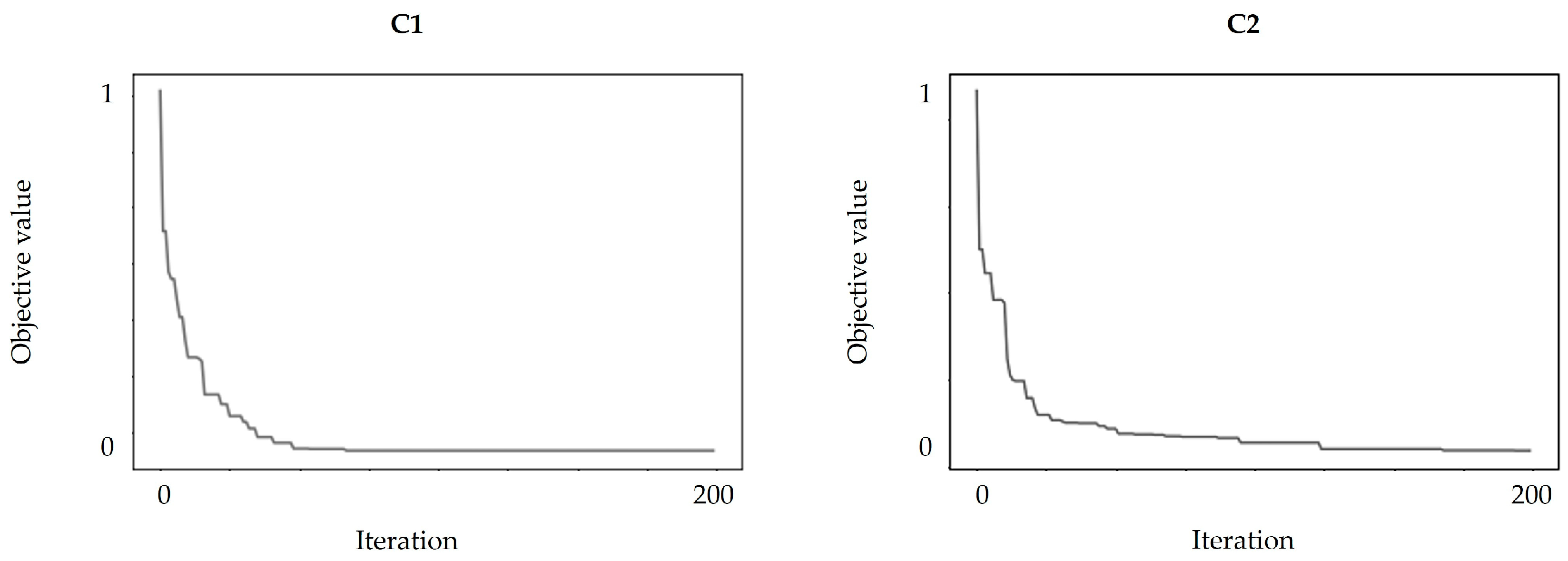
As the C1 row of Table 3 depicts, for the T-shaped block, a case with a straightforward subdivision pattern, the algorithm output was the same as the one prepared by the trained planner. In other words, by giving the planner’s subdivision and street design requirements and conditions to the algorithm, the output was in line with the configuration in the analyst’s mind. In the second case (C2), however, by increasing the variation in parcel areas and the shape irregularity, given the same inputs, layouts obtained from the algorithm and planner were substantially different. The difference between these configurations was not restricted to the arrangement of parcels and streets, but it was rooted in the value of the objective function computed for both layouts as well, which revealed that the output of the proposed algorithm was about 94% more optimal than the one designed by the planner. Figure 11 portrays the convergence process of the algorithm and the value of the objective function for C1 and C2. In addition, the time taken to obtain the final layouts by the algorithm and planner was about 4 min and 3.5 min for C1 and 4.2 min and 55 min for C2, respectively.
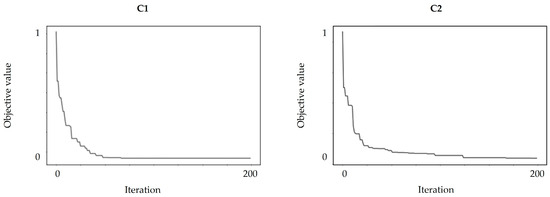
Figure 11.
Algorithm convergence process. The values of the objective function are standardized. The minimum values for C1 and C2 are 0.0042 and 0.0082, respectively.
To assess the variance and consistency of solutions, as well as convergence time based on input parameters, the algorithm underwent 30 runs, during which the objective value and elapsed time were recorded. Subsequently, a t-test was conducted to ascertain if the mean of these metrics significantly deviated from the optimal values. Table 4 presents the outcomes of this analysis for C1 and C2. It suggests that the recorded metrics were statistically significant at a 95% confidence interval, indicating the reliability of the attained objective values and solution times.

Table 4.
t-test results.
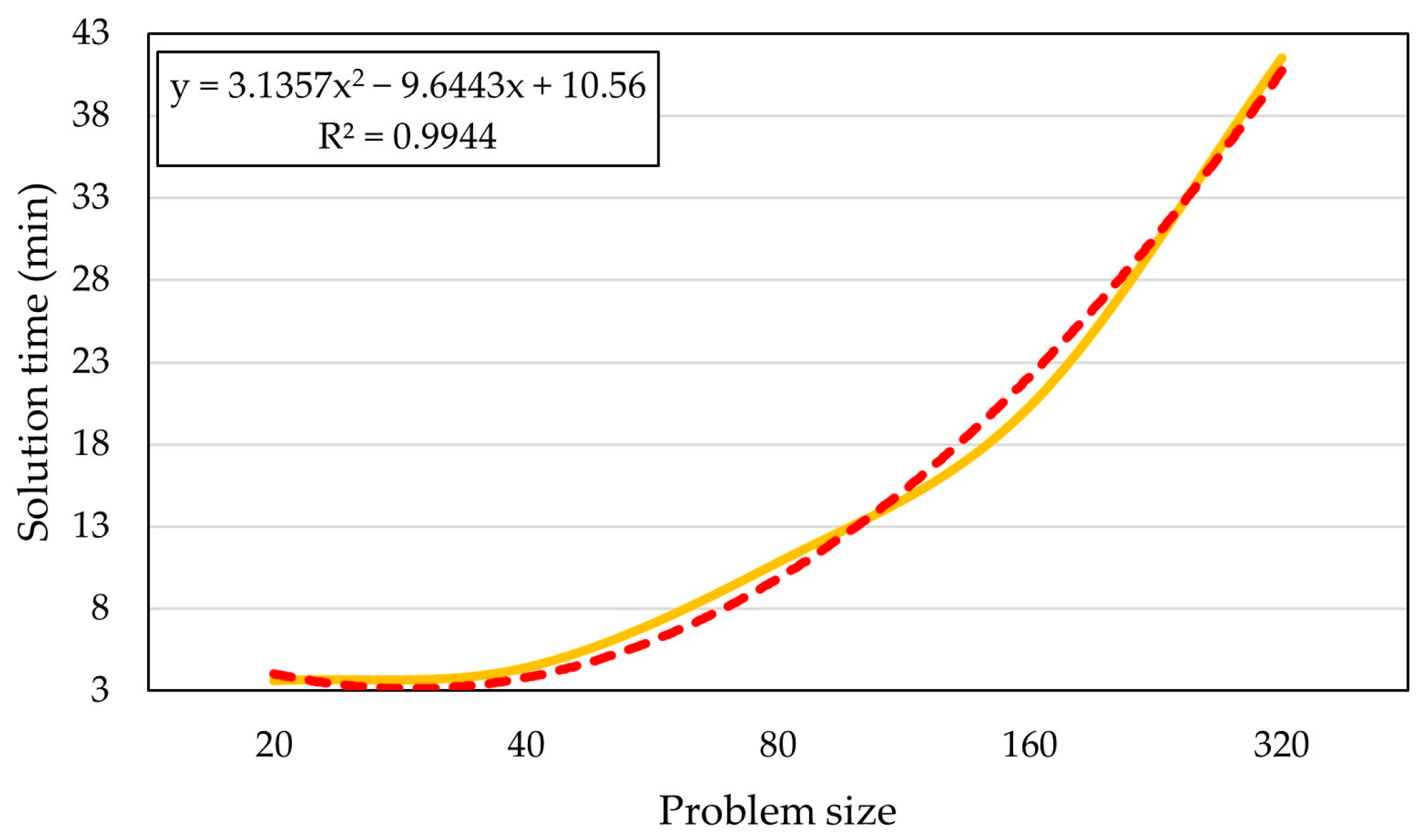
To examine the time complexity of the proposed methods, problems of varying sizes were solved, and the solution times were recorded. The number of iterations was set to 200, and other parameters for calculating the objective functions were consistent with those tuned for C2. Figure 12 illustrates the relationship between problem size and time consumption. Following the experimental procedure in [43,44], a curve was fitted to the data, with the equation and coefficient of determination presented in Figure 12. The results demonstrated that the algorithms performed satisfactorily in polynomial time. Additionally, the complexity of the solution method was , an acceptable order for the algorithms. This is particularly relevant for the presented algorithm, as subdividing a block into more than 100 parcels is exceptionally rare, in practice.
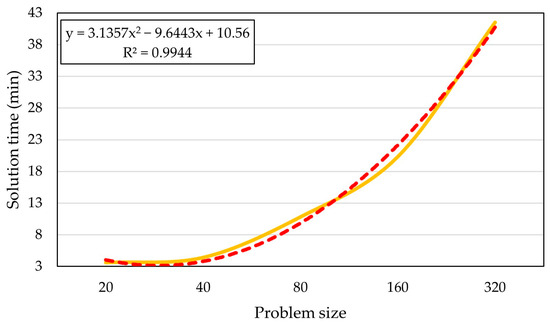
Figure 12.
Complexity analysis of the solution method (the solid line is the actual time consumption, and the dashed line is the regressed curve).
4. Discussion and Conclusions
In this research, a bi-level optimization model was formulated to integrate street design and land subdivision within a unified framework. To solve the presented problems, several ideas were considered and implemented within the genetic algorithm structure. Following the programming of the solution procedure, two cases were presented and solved utilizing the algorithms. Subsequently, the results were verified and assessed by comparing the algorithm outputs with the solutions provided by an experienced and trained planner. This comparison demonstrated the applicability of the algorithms and the acceptability of the street design and land subdivision layouts.
Despite the promising findings, this research has limitations that suggest avenues for future studies. Firstly, the final solution relies on the reference lines proposed by the planner. While this aligns with the purpose of this article, which proposes a supporting system for generating layouts according to the planner’s preferences, generating the optimal arrangement of reference lines could be explored in future research.
Secondly, the optimization model illustrated in this study had a single objective. However, considering the optimization model as a multi-objective problem is another potential direction. Formulating a multiple-objective model based on the concepts explained in this study is therefore recommended.
Thirdly, in addition to the objectives used in this research drawn from the land subdivision literature (e.g., parcel shape indices and area deviation minimization), several other objectives such as maximizing or minimizing land value, minimizing development costs, and maximizing parcel sides benefiting from sunlight could be included, warranting further investigation.
Fourthly, land use allocation, an important factor in subdivision and street design, can be integrated into the proposed model using the concept of a multi-level optimization problem statement. In this approach, land types are assigned to the subdivision and street layouts, and the optimality of the land use locations is evaluated and fed back into the model until the (near-)optimal land subdivision layout, street configuration, and land use arrangement are obtained. Introducing such a multi-level problem and solution approaches are considerable extensions to this research.
Fifthly, conducting sensitivity analysis on the weights and forms of penalty functions, and assessing how these parameters impact optimization results, presents a fascinating research avenue.
Sixthly, exploring more efficient operators and solution algorithms for addressing the stated optimization problem is another significant research direction.
Finally, the solution procedures introduced here could be applied in other cases to establish a solid foundation for the model’s application.
Author Contributions
Conceptualization, Alireza Sahebgharani; methodology, Alireza Sahebgharani; computer programming, Alireza Sahebgharani; fund acquisition, Alireza Sahebgharani; writing—review and editing, Alireza Sahebgharani and Szymon Wiśniewski. All authors have read and agreed to the published version of the manuscript.
Funding
This research is related to the project no.5027 in Isfahan University of Technology, which has been financially supported by Delta Pars Espaneh Consultant Engineers.
Data Availability Statement
Everything about this research from the data to the method has been described within the text.
Acknowledgments
The authors would like to thank the journal’s editor and anonymous reviewers for their insightful, critical, and constructive comments, which considerably helped the authors improve the quality of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Details of the Developed and Applied Algorithms
| Algorithm A1: Random Solution Generation Procedure (RSGP) |
| Inputs: |
| : The set of reference lines |
| : The number of parcels in a layout |
| : The size of the population |
| Procedure: |
| Set |
| : |
| : |
| : |
| : |
| end if |
| end while |
| end for |
| : |
| ) |
| through the application of Equations (7) and (8) |
| end for |
| : |
| ) |
| through the application of Equations (7) and (8) |
| : |
| through the application of Equations (7) and (8) |
| end while |
| end while |
| end while |
| Algorithm A2: Crossover Procedure |
| Inputs: |
| : The first selected solution |
| : The second selected solution |
| Procedure: |
| and are matched: |
| Create two empty solutions including bounds in and and name them and |
| Transfer reference lines to and |
| Perform the point selection and replacement procedure given , , , and |
| and |
| and ): |
| Create two empty solutions including bounds in and and name them and |
| Perform the reference line selection procedure given and |
| Transfer the reference lines and points inherited from and to and given outputs of the reference line selection procedure |
| Perform the need-capacity calculation procedure given |
| Set |
| : |
| Set |
| Take points from the reference lines of matched with the inherited reference lines in and transfer them to |
| Set |
| Take points from the reference lines of matched with the inherited reference lines in and transfer them to |
| Perform solution repair procedure 1 given |
| Set |
| else: |
| Perform solution repair procedure 2 given |
| Set |
| end if |
| Perform the need-capacity calculation procedure given |
| Set |
| : |
| Set |
| Take points from the reference lines of matched with the inherited reference lines in and transfer them to |
| Set |
| else if : |
| else: |
| end if |
| if : |
| return |
| end if |
| end if |
| Point selection and replacement procedure (PSRP) |
| Inputs: |
| : The first selected solution |
| : The second selected solution |
| : The first off-spring |
| : The second off-spring |
| Procedure: |
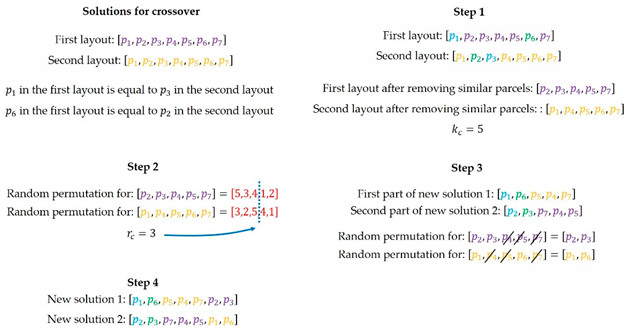
| Assume that and are two lists, including the coordinates of the parcels (e.g., first layout: , and second layout: ). The crossover operator starts with finding and removing parcels with similar coordinates in the two solutions. Then, the PSRP determines the number of remaining parcels denoted by and generates a random permutation for each layout. After that, it produces a cut-off point, , between the number of the remaining parcels in the layouts and . Next, regarding the permutation indices before , the PSRP swaps the remained parcels in the layouts. These parcels and those removed at the beginning of the crossover procedure constitute the first parts of the new solutions. Lastly, the PSRP adds the remaining parcels after to the generated parts, and the off-spring ( and ) are acquired. The figure below displays the PSRP. |
 |
| return populated with parcels |
| Reference line selection procedure (RLSP) |
| Inputs: |
| : The first selected solution |
| : The second selected solution |
| : The first off-spring |
| : The second off-spring |
| Procedure: |
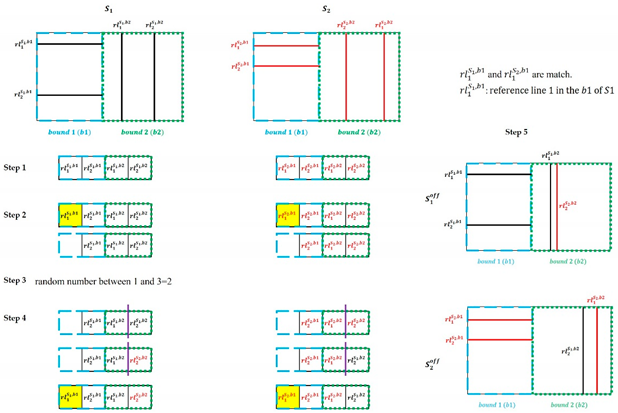
| In the first step, the RLSP arranges reference lines in each bound of sequentially and sorts the bounds in ascending order (). This process is applied to as well (). In the second step, the RLSP identifies and removes the matched reference lines in and . In the third step, it generates a random integer between 1 and the number of remaining reference lines in and . In the fourth step, and are cut and combined. In the last step, the matched reference lines return to and , and the RLSP transfers the reference lines to their corresponding off-spring ( and ). The figure below illustrates the RLSP. |
 |
| return populated with reference lines |
| Need-capacity calculation procedure (NCCP) |
| Inputs: |
| : The first off-spring |
| : The second off-spring |
| Procedure: |
| Given , first, the NCCP counts the number of points on the reference lines inherited from () and calculates the need value () by subtracting from the required number of parcels in the subdivision layout. Second, the NCCP enumerates the number of points on the reference lines inherited from , which is the capacity value () for . Finally, the NCCP returns and . The NCCP is applied to as well. The figure below shows an example of the NCCP application. |
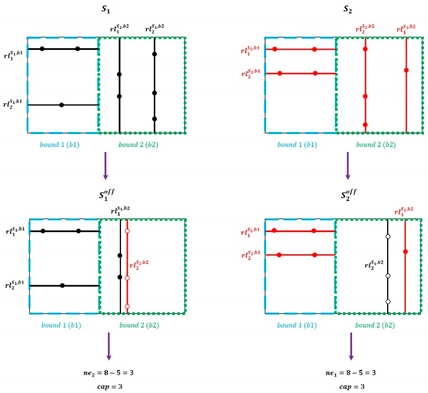 |
| if is the input: |
| return |
| else if is the input: |
| return |
| end if |
| Solution repair procedure 1 (SRP1) |
| Inputs: |
| : Off-spring |
| : Need value |
| : Capacity value |
| Procedure: |
| if: |
| while : |
| while : |
| end while |
| end while |
| return |
| else if : |
| while : |
| while : |
| end while |
| end while |
| return |
| end if |
| Solution repair procedure 2 (SRP2) |
| Inputs: |
| : Off-spring |
| : Need value |
| Procedure: |
| if: |
| , 4], …]). |
| for: |
| end for |
| while : |
| end while |
| return |
| else if : |
| , 8], …]). |
| for: |
| end for |
| while : |
| end while |
| return |
| end if |
| Algorithm A3: Mutation Procedure |
| Parcel mutation procedure (PMP) |
| Inputs: |
| : The selected solution |
| : The number of parcels in |
| : The number of reference lines in |
| Procedure: |
| Set a random integer between 1 and |
| Select parcels from and store them in |
| Set |
| Store reference lines without parcel in in |
| if : |
| for each in : |
| Select a random reference line from and name it |
| Generate a new coordinate on using Equations (7) and (8) and name it |
| while : |
| Select a random reference line from and name it |
| Generate a new coordinate on using Equations (7) and (8) and name it |
| end while |
| Add to |
| end for |
| else: |
| for each : |
| Generate a new coordinate on using Equations (7) and (8) and name it |
| Add to |
| end for |
| Store parcels in in |
| Set |
| if : |
| for each in : |
| Select a random reference line from and name it |
| Generate a new coordinate on using Equations (7) and (8) and name it |
| while : |
| Select a random reference line from and name it |
| Generate a new coordinate on using Equations (7) and (8) and name it |
| end while |
| Add to |
| end for |
| end if |
| end if |
| return |
| Reference line mutation procedure (RLMP) |
| Inputs: |
| : The selected solution |
| : The number of parcels in |
| : The number of reference lines in |
| Procedure: |
| Generate a random number between 1 and and name it |
| Select reference lines from randomly and store them in |
| Set |
| for each in : |
| Create a random point within the bound corresponding to in a way that the point does not intersect with another reference line and name it |
| Create a new reference line passing through and parallel to and name it |
| Project points on onto using the parcel projection procedure (PPP) that keeps the proportion of distances between points on the same as |
| Add to |
| Remove from |
| end for |
| Parcel Projection Procedure (PPP) |
| Inputs: |
| : The main reference line |
| : The new reference line |
| Procedure: |
| Set as the start point of |
| Set as the end point of |
| Set as the beginning point of |
| Set as the last point of |
| Set as the line connecting to |
| Set as the line connecting to |
| if intersects : |
| Set |
| Set |
| else: |
| Set |
| Set |
| end if |
| Set |
| for each on : |
| Set as the distance between and |
| Set |
| Set as the circle with center of and radius of |
| Set as the intersection between and |
| Add to |
| end for |
| Set points in on |
| Parcel and reference line mutation procedure (PRLMP) |
| Inputs: |
| : The selected solution |
| Procedure: |
| Perform RLMP on and name it |
| Perform PMP on and name it |
| return |
| Algorithm A4: Hooke and Jeeves Procedure |
| Inputs: |
| : The selected solution |
| : The vector including distances for the exploratory search |
| : The vector including termination values for each parcel |
| Procedure: |
| : |
| is acceptable: |
| using Equation (14) |
| is acceptable: |
| is acceptable: |
| : |
| is acceptable: |
| is not acceptable: |
| end if |
| else: |
| end while |
| else: |
| else: |
| else: |
| end while |
| Algorithm A5: Graph Generation Procedure for a Subdivision Layout (GGP) |
| Inputs: |
| : The set of parcels |
| : The set of access points |
| : The set of connection rules |
| Procedure: |
| as the access point |
| : |
| and mark each point with the parcels it is on the edge of |
| end for |
| Connect N to M |
| , a connected network in which connection and access points are marked, and each link is separated from the point entities on them |
| Algorithm A6: Population Generation Procedure for the SDGA |
| Inputs: |
| : The set of parcels |
| : The set of inaccessible parcels |
| : The set of access points |
| Procedure: |
| : |
| : |
| : |
| end if |
| end for |
| end while |
| Path creation procedure |
| Inputs: |
| : The connection point or origin |
| : The access point or destination |
| : The base-graph |
| Procedure: |
| Perform Dijkstra’s shortest path algorithm [45] given cc, c, RLC, and G(N‚M) |
| return the path generated by the Dijkstra’s algorithm |
References
- Sonnenberg, J. Fundamentals of land consolidation as an instrument to abolish fragmentation of agricultural holdings. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002. [Google Scholar]
- Demetriou, D.; See, L.; Stillwell, J. A spatial genetic algorithm for automating land partitioning. Int. J. Geogr. Inf. Sci. 2013, 27, 2391–2409. [Google Scholar] [CrossRef]
- Stevens, D.; Dragićević, S. A GIS-based irregular cellular automata model of land-use change. Environ. Plan. B Plan. Des. 2007, 34, 708–724. [Google Scholar] [CrossRef]
- Wakchaure, A.S. An ArcView Tool for Simulating Land Subdivision for Build Out Analysis. Master’s Thesis, Faculty of Virginia Polytechnic Institute and State University, Blacksburg, VN, USA, 2001. [Google Scholar]
- Habib, M. Proposed Algorithm of Land Parcel Subdivision. J. Surv. Eng. 2020, 146, 04020012. [Google Scholar] [CrossRef]
- Buis, A.; Vingerhoeds, R.A. Knowledge-based systems in the design of a new parcelling. Knowl.-Based Syst. 1996, 9, 307–314. [Google Scholar] [CrossRef]
- Parish, Y.I.; Müller, P. Procedural modeling of cities. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 301–308. [Google Scholar]
- Touriño, J.; Parapar, J.; Doallo, R.; Boullón, M.; Rivera, F.F.; Bruguera, J.D.; Gonzalez, X.P.; Crecente, R.; Álvarez, C. A GIS-embedded system to support land consolidation plans in Galicia. Int. J. Geogr. Inf. Sci. 2003, 17, 377–396. [Google Scholar] [CrossRef]
- Halatsch, J.; Kunze, A.; Schmitt, G. Using shape grammars for master planning. In Design Computing and Cognition’08; Springer: Berlin/Heidelberg, Germany, 2008; pp. 655–673. [Google Scholar]
- Marshall, S. Cities, Design and Evolution; Routledge: London, UK, 2009. [Google Scholar]
- Vanegas, C.A.; Aliaga, D.G.; Benes, B.; Waddell, P. Visualization of simulated urban spaces: Inferring parameterized generation of streets, parcels, and aerial imagery. IEEE Trans. Vis. Comput. Graph. 2009, 15, 424–435. [Google Scholar] [CrossRef] [PubMed]
- Vanegas, C.A.; Aliaga, D.G.; Benes, B.; Waddell, P.A. Interactive design of urban spaces using geometrical and behavioral modeling. ACM Trans. Graph. 2009, 28, 1–10. [Google Scholar] [CrossRef]
- Vanegas, C.A.; Kelly, T.; Weber, B.; Halatsch, J.; Aliaga, D.G.; Müller, P. Procedural generation of parcels in urban modeling. Comput. Graph. Forum 2012, 31, 681–690. [Google Scholar] [CrossRef]
- Engine, C. Esri City Engine Documentation—Block Parameters Module. Available online: https://doc.arcgis.com/en/cityengine/latest/help/help-layers-block-parameters.htm (accessed on 20 May 2024).
- Colomb, M.; Tannier, C.; Perret, J.; Chapron, P.; Brasebin, M. Parcel Manager: A parcel reshaping model incorporating design rules of residential development. Trans. GIS 2022, 26, 2558–2597. [Google Scholar] [CrossRef]
- Wickramasuriya, R.; Chisholm, L.A.; Puotinen, M.; Gill, N.; Klepeis, P. An automated land subdivision tool for urban and regional planning: Concepts, implementation and testing. Environ. Model. Softw. 2011, 26, 1675–1684. [Google Scholar] [CrossRef]
- Dahal, K.R.; Chow, T.E. A GIS toolset for automated partitioning of urban lands. Environ. Model. Softw. 2014, 55, 222–234. [Google Scholar] [CrossRef]
- Demetriou, D.; Stillwell, J.; See, L.M. LandParcelS: A Module for Automated Land Partitioning; School of Geography, University of Leeds: Leeds, UK, 2012. [Google Scholar]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research; McGraw-Hill Higher Education: New York, NY, USA, 2010. [Google Scholar]
- Haklı, H.; Uğuz, H.; Çay, T. A new approach for automating land partitioning using binary search and Delaunay triangulation. Comput. Electron. Agric. 2016, 125, 129–136. [Google Scholar] [CrossRef]
- Koc, I.; Cay, T.; Babaoglu, I. Approaches to automated land subdivision using binary search algorithm in zoning applications. Proc. Inst. Civ. Eng. Munic. Eng. 2022, 175, 16–28. [Google Scholar] [CrossRef]
- Kucukmehmetoglu, M.; Geymen, A. Optimization models for urban land readjustment practices in Turkey. Habitat Int. 2016, 53, 517–533. [Google Scholar] [CrossRef]
- Koc, I.; Cay, T.; Babaoglu, I. A novel metaheuristic algorithm by efficient crossover operator for land readjustment. Expert Syst. Appl. 2022, 188, 116082. [Google Scholar] [CrossRef]
- Mustafa, A.; Wei Zhang, X.; Aliaga, D.G.; Bruwier, M.; Nishida, G.; Dewals, B.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Teller, J. Procedural generation of flood-sensitive urban layouts. Environ. Plan. B Urban Anal. City Sci. 2020, 47, 889–911. [Google Scholar] [CrossRef]
- Yang, Y.-L.; Wang, J.; Vouga, E.; Wonka, P. Urban pattern: Layout design by hierarchical domain splitting. ACM Trans. Graph. 2013, 32, 1–12. [Google Scholar] [CrossRef]
- Hejazi, S.R.; Memariani, A.; Jahanshahloo, G.; Sepehri, M.M. Linear bilevel programming solution by genetic algorithm. Comput. Oper. Res. 2002, 29, 1913–1925. [Google Scholar] [CrossRef]
- Miandoabchi, E.; Daneshzand, F.; Szeto, W.Y.; Farahani, R.Z. Multi-objective discrete urban road network design. Comput. Oper. Res. 2013, 40, 2429–2449. [Google Scholar] [CrossRef]
- Wang, Z.; Han, Q.; de Vries, B. Land use oriented bi-level discrete road network design. Transp. Res. Procedia 2019, 37, 35–42. [Google Scholar] [CrossRef]
- Xu, T.; Wei, H.; Hu, G. Study on continuous network design problem using simulated annealing and genetic algorithm. Expert Syst. Appl. 2009, 36, 1322–1328. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Sahebgharani, A. Multi-objective Land Use Optimizarion through Parallel Particle Swarm Algorithm: Cade Study Baboldasht District of Isfahan, Iran. J. Urban Environ. Eng. 2016, 10, 42–49. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Nastaran, M.; Sahebgharani, A. Development, application, and comparison of hybrid meta-heuristics for urban land-use allocation optimization: Tabu search, genetic, GRASP, and simulated annealing algorithms. Comput. Environ. Urban Syst. 2016, 60, 23–36. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Liu, X.; Li, X.; Shi, X.; Huang, K.; Liu, Y. A multi-type ant colony optimization (MACO) method for optimal land use allocation in large areas. Int. J. Geogr. Inf. Sci. 2012, 26, 1325–1343. [Google Scholar] [CrossRef]
- Cao, K.; Liu, M.; Wang, S.; Liu, M.; Zhang, W.; Meng, Q.; Huang, B. Spatial multi-objective land use optimization toward livability based on boundary-based genetic algorithm: A case study in Singapore. ISPRS Int. J. Geo-Inf. 2020, 9, 40. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Alam Tabriz, A.; Zandieh, M.; Mohammad Rahimi, A. Metaheuristic Algorithms in Combinatorial Optimization; Saffar Publications: Harvey, IL, USA, 2013. [Google Scholar]
- Fattahi, P. Metaheuristic Algorithms; Bu-Ali Sina University: Hamedan, Iran, 2011. [Google Scholar]
- Sivanandam, S.; Deepa, S. Genetic algorithms. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–37. [Google Scholar]
- Hamidizadeh, M.R. Nonlinear Programming; Samt Publication: Tehran, Iran, 2022. [Google Scholar]
- Chen, B.Y.; Lam, W.H.; Sumalee, A.; Li, Q.; Shao, H.; Fang, Z. Finding reliable shortest paths in road networks under uncertainty. Netw. Spat. Econ. 2013, 13, 123–148. [Google Scholar] [CrossRef]
- Khalili-Damghani, K.; Aminzadeh-Goharrizi, B.; Rastegar, S.; Aminzadeh-Goharrizi, B. Solving land-use suitability analysis and planning problem by a hybrid meta-heuristic algorithm. Int. J. Geogr. Inf. Sci. 2014, 28, 2390–2416. [Google Scholar] [CrossRef]
- Sahebgharani, A.; Haghshenas, H.; Mohammadi, M. Reliable Space-Time Prisms in the Stochastic Road Networks Under Spatial Correlated Travel Times. Transp. B Transp. Dyn. 2020, 8, 351–375. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).