Non-Uniform Spatial Partitions and Optimized Trajectory Segments for Storage and Indexing of Massive GPS Trajectory Data
Abstract
1. Introduction
2. Related Work
2.1. Spatio-Temporal Index of Trajectory
2.2. Storage and Querying of Trajectory
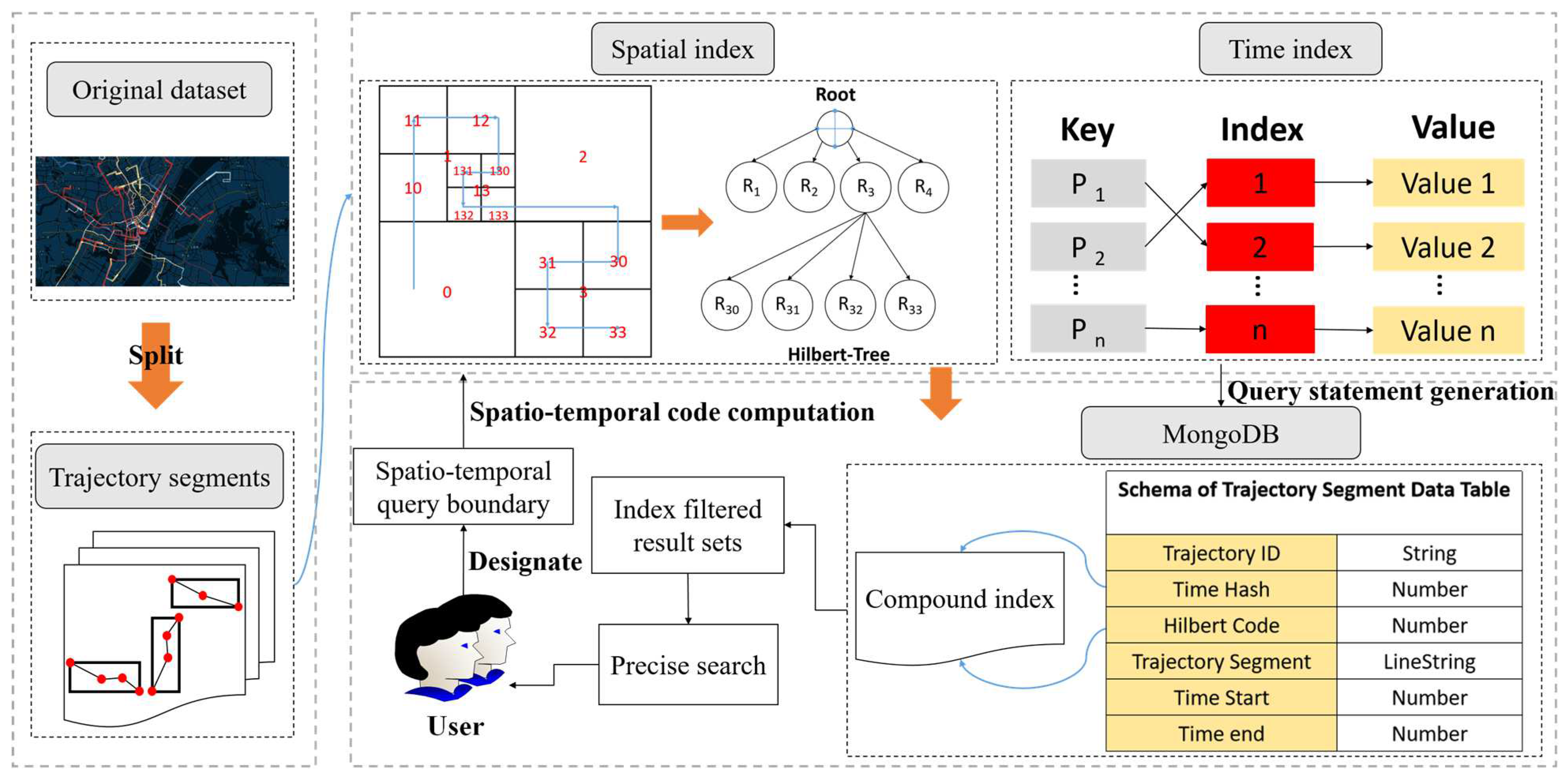
3. Methodology
3.1. Trajectory Segmentation Method
3.1.1. Data Model Definition
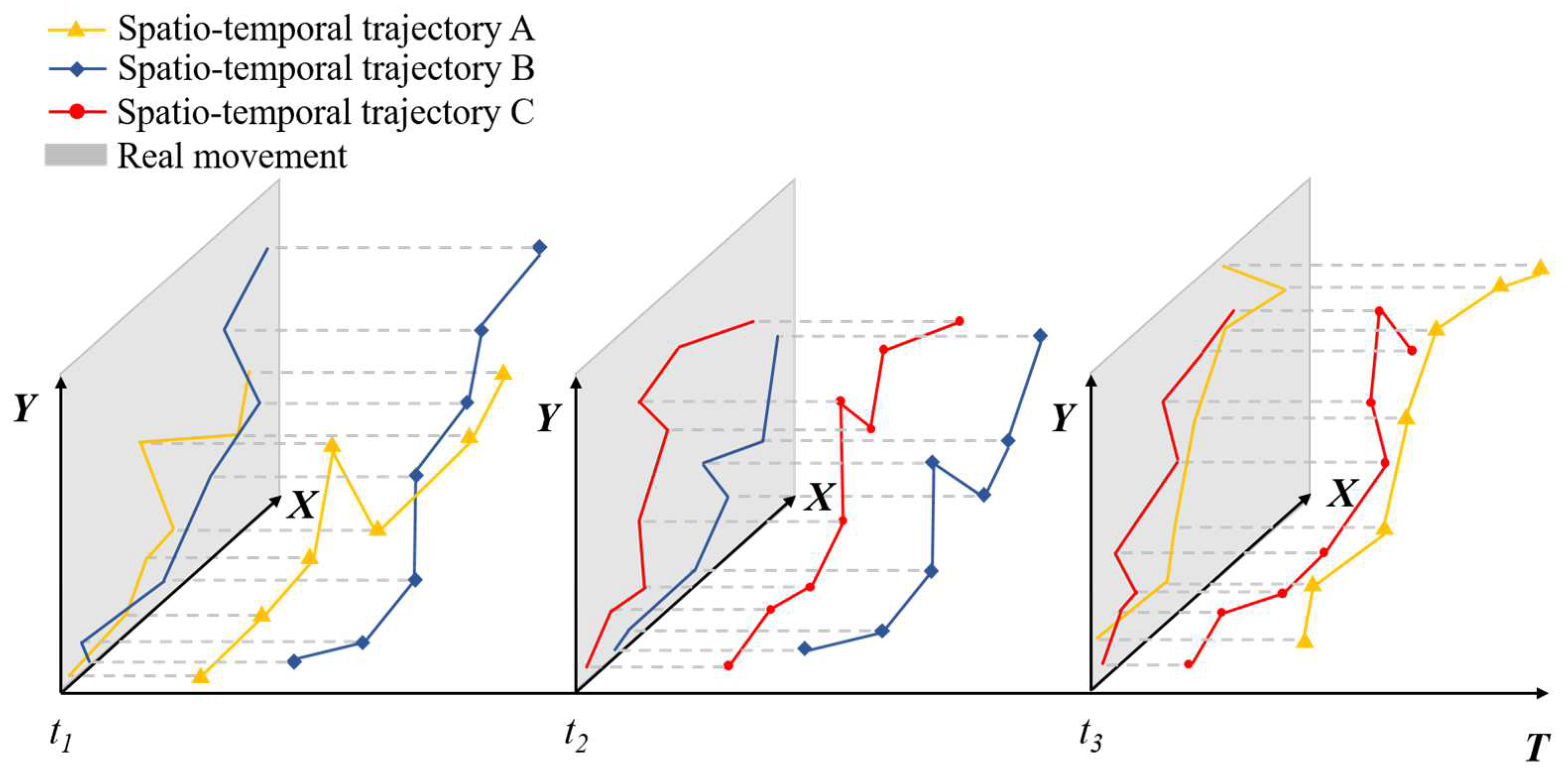
- Point: Since GPS trajectories are described as spatio-temporal points, Point is the basic component of this data model. The spatio-temporal attribute with latitude as x, longitude as y, and timestamp as t is denoted as (x, y, t);
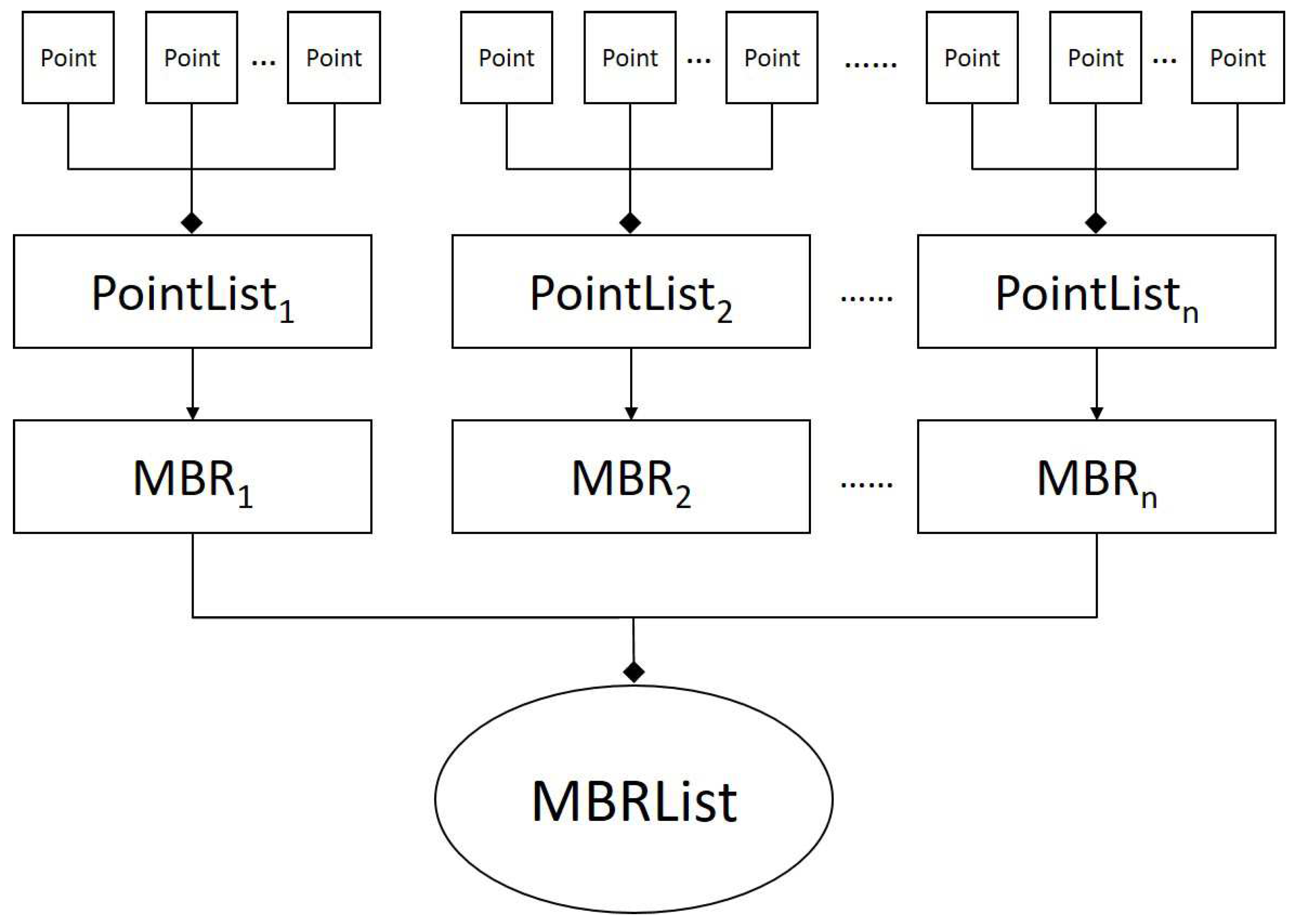
- PointList: a sequence of trajectory points. This study expresses the trajectory segments by means of the PointList class. PointList consists of multiple Point objects, which are internally organized and sorted according to a timestamp-ascending data structure, denoted as follows: {Pointi}N (i = 1,2,…,N);
- MBR: the minimum bounding box of a trajectory segment. The MBR class focuses on operations related to trajectory segments, which are processed as basic spatio-temporal units, such as MBR merging in the trajectory-optimized segmentation algorithm and the construction and maintenance of the HHBITS index, which will be described in detail later on. The MBR consists of the PointList corresponding to the sub-trajectory segment and the diagonal vertices representing that MBR, denoted as (PointList, Pointa, Pointb);
- MBRList: MBR sequence. MBRList is defined as a container data structure for organizing MBRs in a chained table to facilitate batch manipulation and processing of MBRs, denoted as {MBRi} N (i = 1,2,…,N).
3.1.2. Segmentation for Trajectory Optimization Based on Greedy Algorithm
- Select an unvisited trajectory point p as the starting point;
- Calculate the number of data points in the ε-neighborhood of point p. If the number is greater than or equal to minPts, mark p as a core point and create a new cluster;
- Add point p to the current cluster and add all unvisited data points within the ε-neighborhood of p to the current cluster;
- Perform the following operations on each data point q in the current cluster:
- (1)
- If q is a core point, add all unvisited data points within the ε-neighborhood of q to the current cluster;
- (2)
- If q is not a core point but lies within the ε-neighborhood of another cluster, mark q as a boundary point and add it to the current cluster;
- When there are no more data points that can be added to the current cluster, the current cluster is considered a complete cluster;
- Select the next unvisited data point as the starting point and repeat steps 2 to 5 until all data points have been visited;
- Mark the remaining unallocated data points as noise points and clear them.
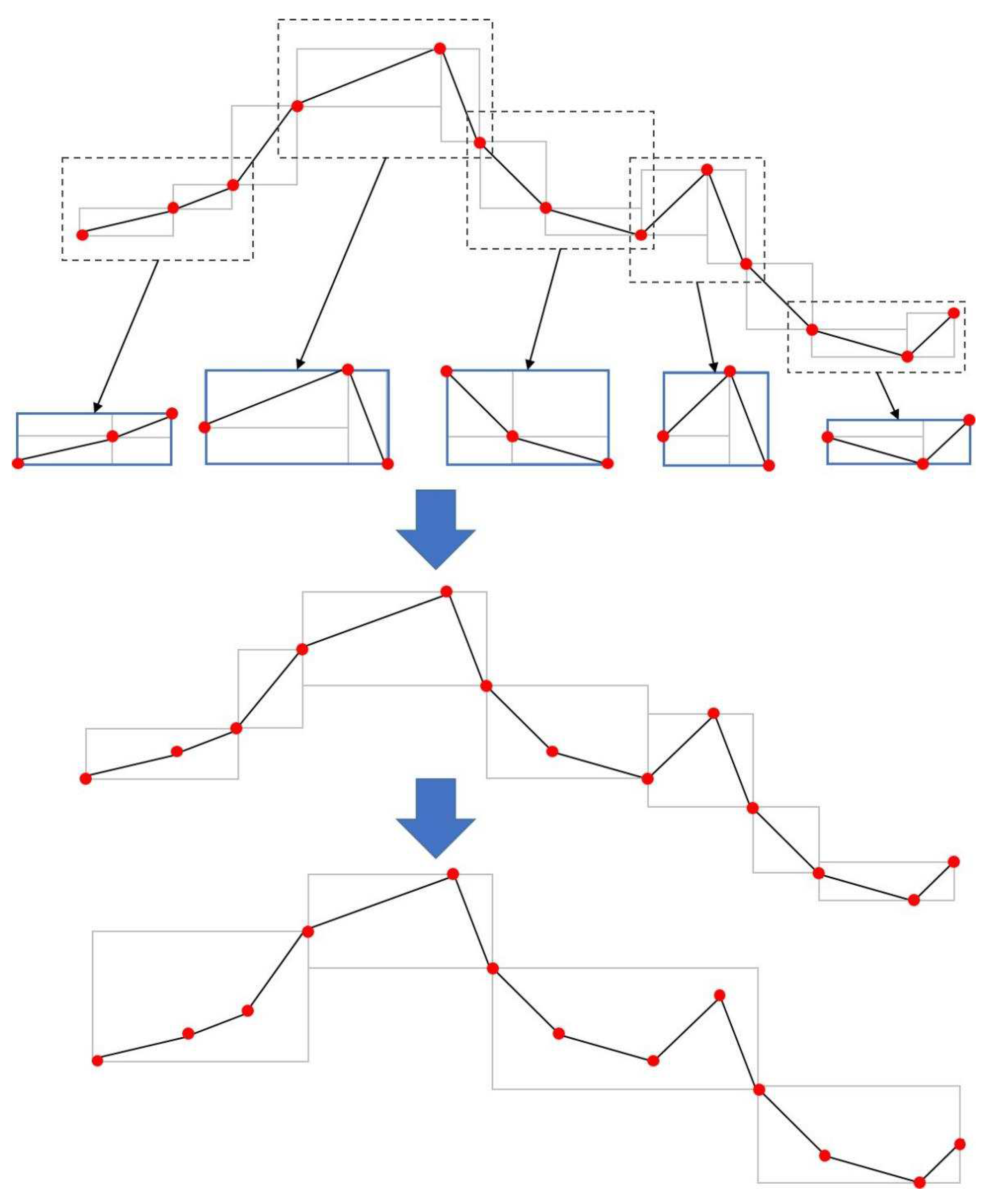
- The greedy segmentation method will be applied independently to each trajectory, executed in three main steps:
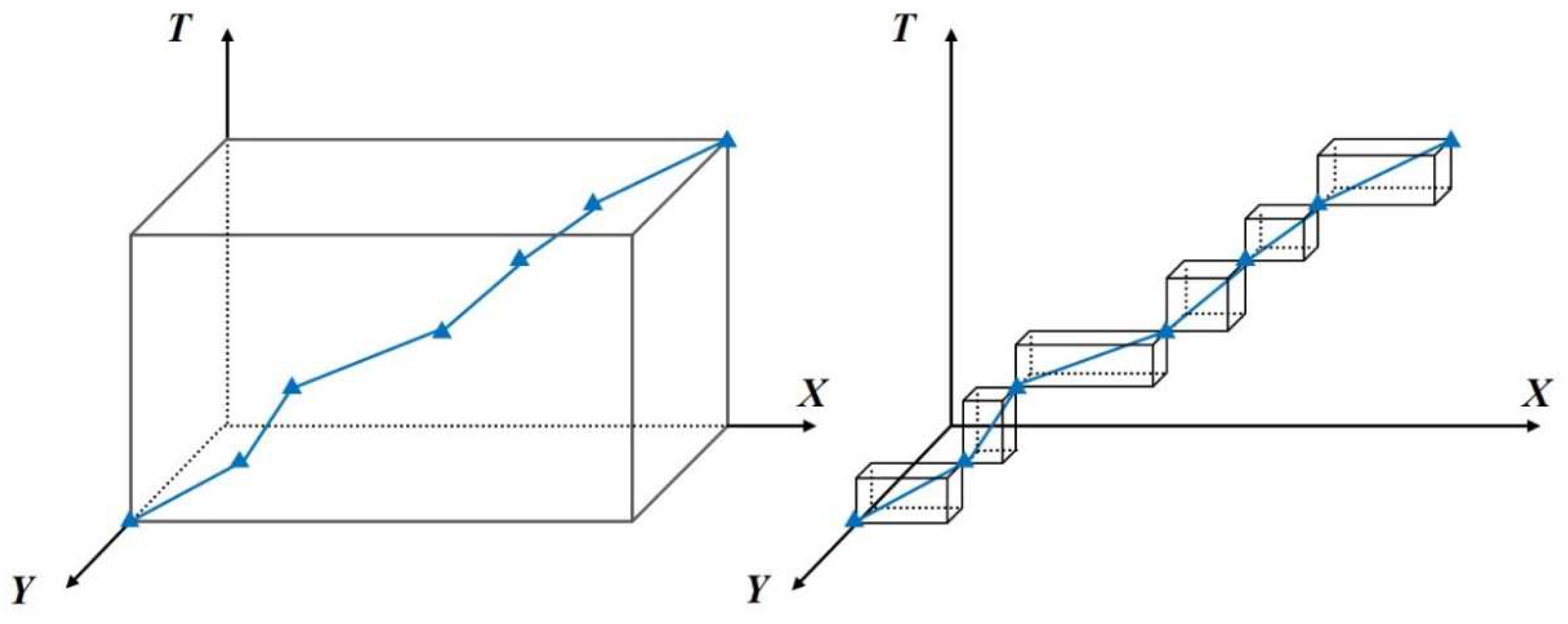
- Select two consecutive points in the trajectory sequence in turn as diagonal vertices to create the MBR sequence;
- 3.
- The merging operation in step 2 is performed cyclically, and the merging process is terminated when the number of trajectory segments reaches the division limit.
| Algorithm 1: Trajectory Segmentation Algorithm. |
| Input: Trajectory = {point1, point2, …}, Trajectory ID TID, segment length N Output: Segments = Map < TID, MBRList = {MBR1, MBR2, …}> 1: MBRList ←∅. 2: for i in range(1, n) do 3: create new Points pt1 =Point(pointi−1 .x, pointi−1 .y), pt2 =Point(pti .x, pti .y); 4: create new MBR MBR =MBR (pt1, pt2); 5: MBRList.add(MBR). 6: end for 7: MBRMergeNorm ←∅. 8: for each MBRi ∈ MBRList and MBRj = MBRi .next() do 9: norm < Norm(MBRi, MBRj), i, j > ← getMergeNorm(MBRi, MBRj). 10: MBRMergeNorm.add(norm); 11: end for 12: Segments ←∅. 13: while MBRList.size() > N do 14: MBRindex[a, b] ← getMin(MBRMergeNorm). 15: create new MBR MBRnew = runMerge (MBRa, MBRb); 16: MBRList.replace(a, MBRnew), MBRList.remove(MBR)b 17: MBRMergeNorm.update(); 18: end while 19: return Segments.Put(TID, MBRList); |
3.2. Trajectory Spatio-Temporal Index Construction
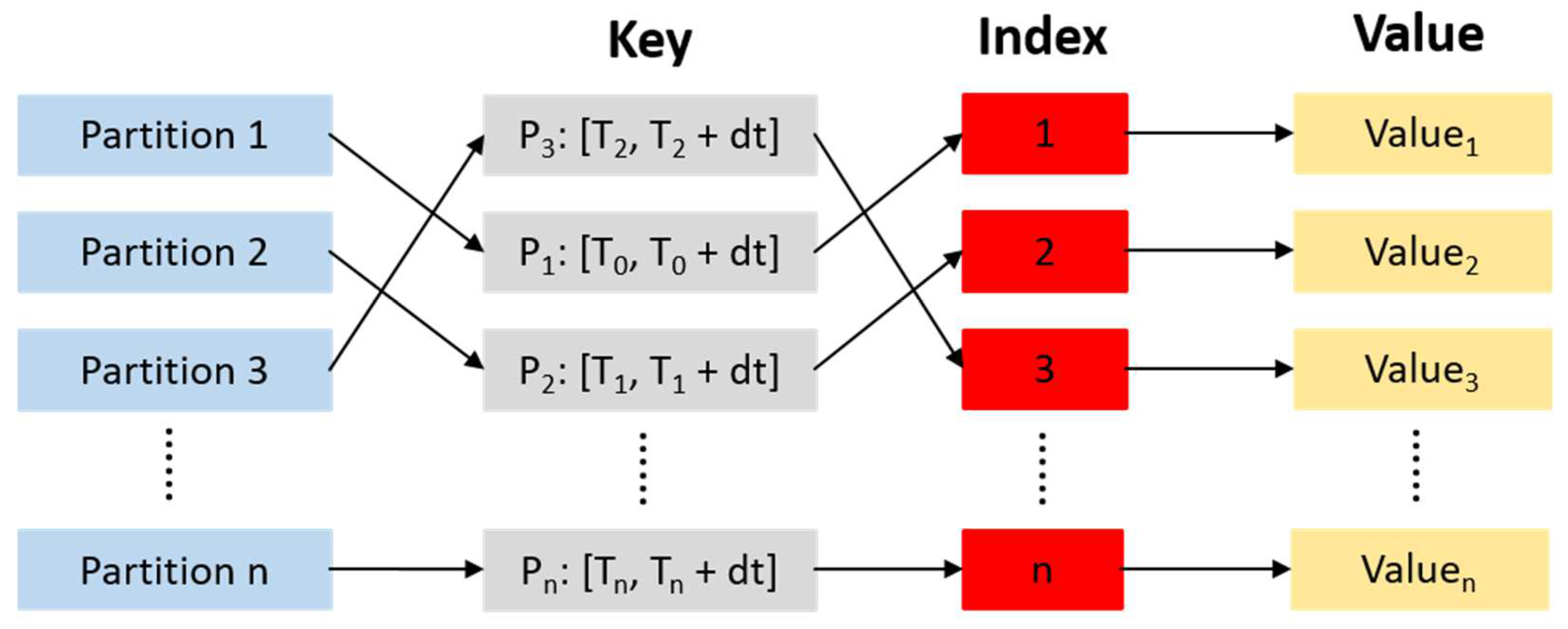
3.2.1. Time Index Based on Hash Table
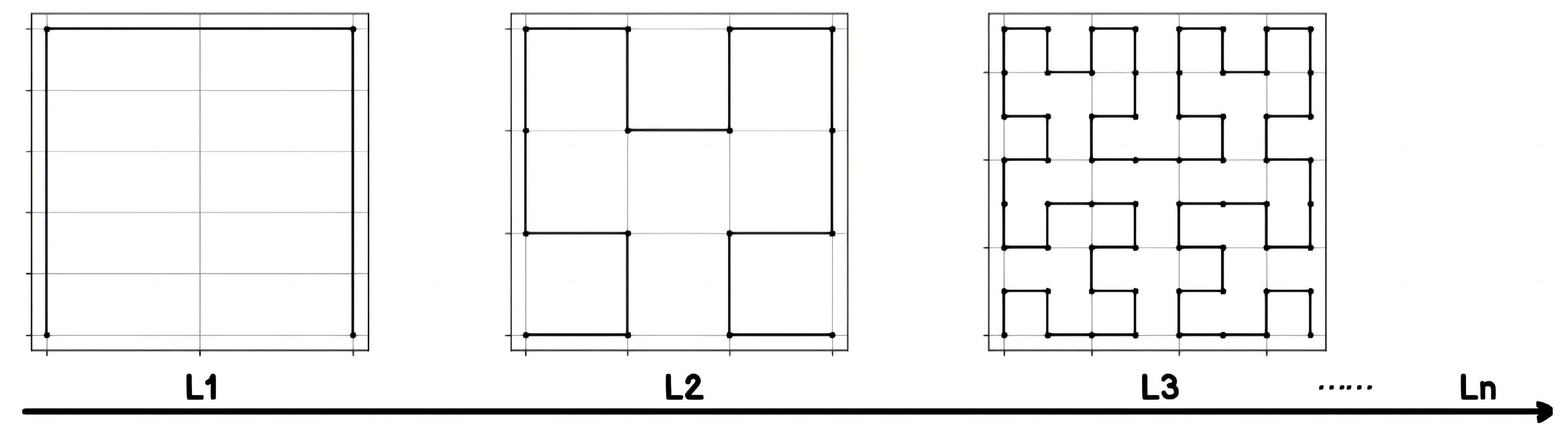
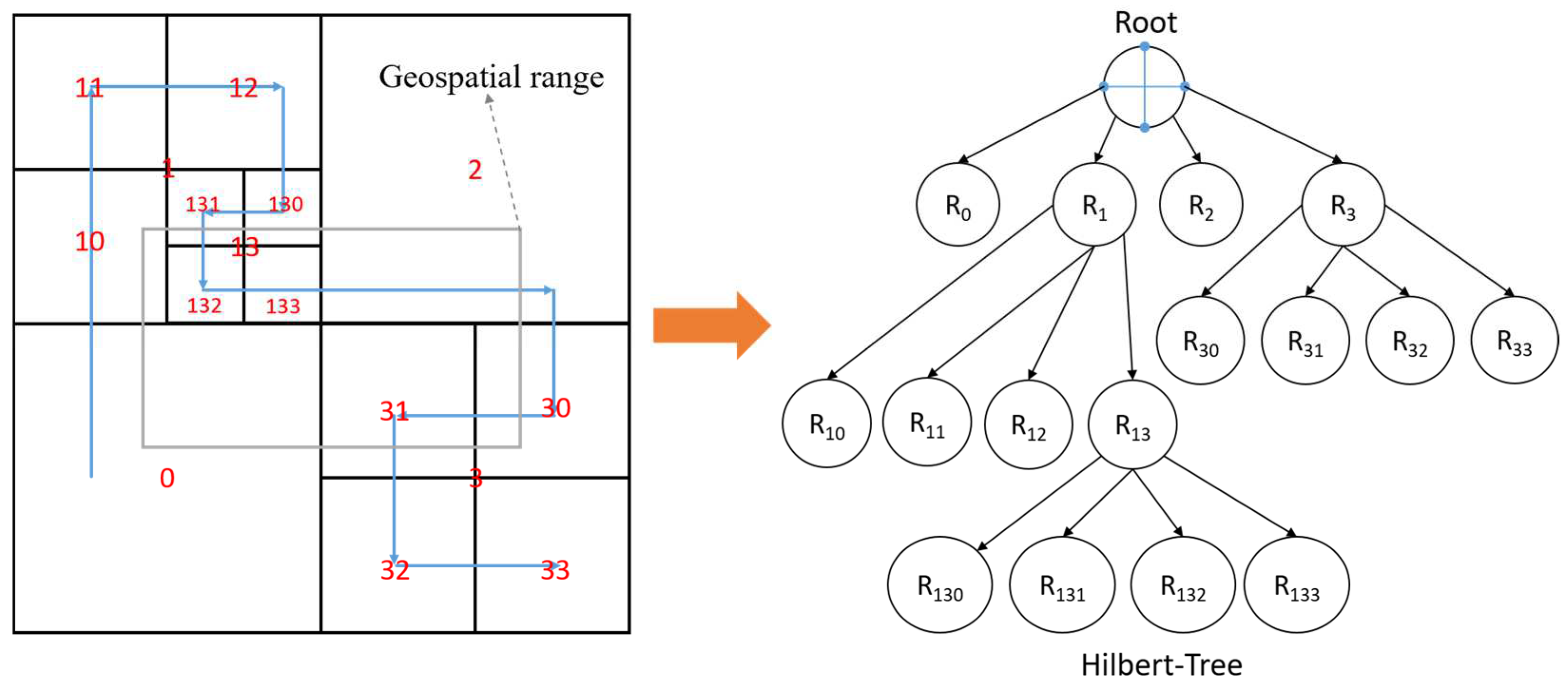
3.2.2. Spatial Index of Trajectories under Adaptive Partition of Space
| Algorithm 2: Adaptive Data Segmentation Algorithm Based on Space-Filling Curve Coding. |
| Input: MBRList = {MBRi} N (i = 1,2,…,N), initially selected level Nini, highest level Nmax, threshold Pmax Output: Physical Partition = GridList 1: GridList ←∅. 2: SubdivideGridList ←∅. 3: GridList ← regularGridSplit(MBRList, Nini); 4: for each gridi ∈ GridList do 5: if (gridi . capacity() > Pmax) then 6: SubdivideGridList.add(gridi); 7: GridList.remove(gridi); 8: end for 9: TempGridList ← ∅. 10: while SubdivideGridList.size() > 0 and Nini < Nmax do 11: TempGridList ← subdivide(SubdivideGridList). 12: Nini ++; 13: SubdivideGridList.clear(); 14: SubdivideGridList ← selectSubdivide(TempGridList, GridList); 15: end while 16: return GridList; |
3.3. Trajectory Storage and Query
3.3.1. Storage of Segmented Trajectory Data with MongoDB
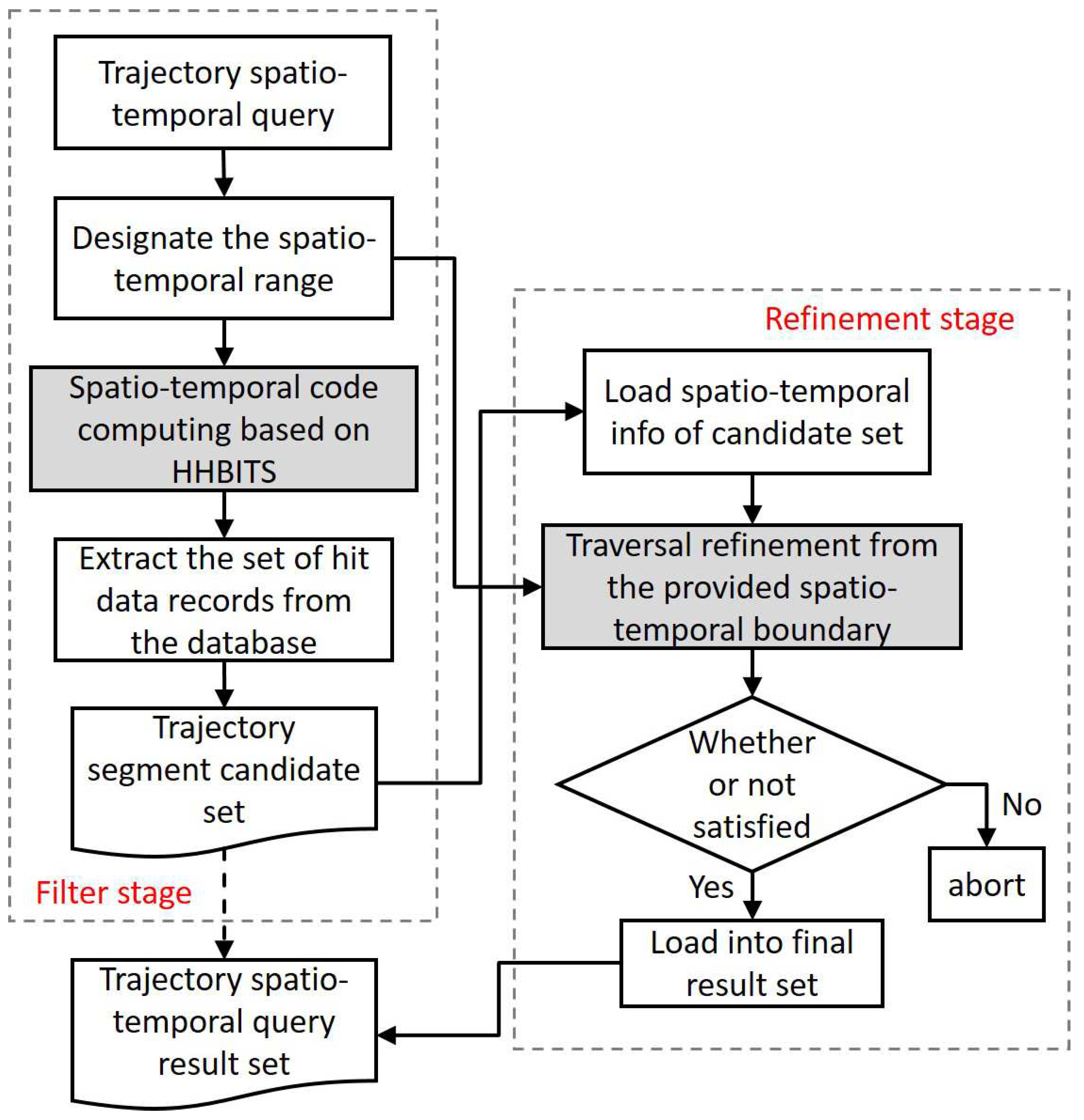
3.3.2. Trajectory Spatio-Temporal Query
- Temporal layer filtering, regardless of the query conditions oriented to a specific point in time or a specific time period, can be indexed and filtered by the temporal Hash table, which maps the temporal range of the query to a specific temporal Hash value or a list of temporal Hash values;
- Spatial layer filtering, which computes a Hilbert grid encoding set from the Hilbert-Tree based on the given spatial query boundaries;
- Generating an indexed filter statement based on the filtering results obtained in steps 1 and 2, with filter conditions constructed by combining the corresponding spatio-temporal encoding sets;
- Delivering the indexed filter statements to the trajectory segment storage table and returning the indexed execution results to await subsequent processing.
4. Experiments and Results
4.1. Data Description and Experimental Platform
4.2. Performance Analysis
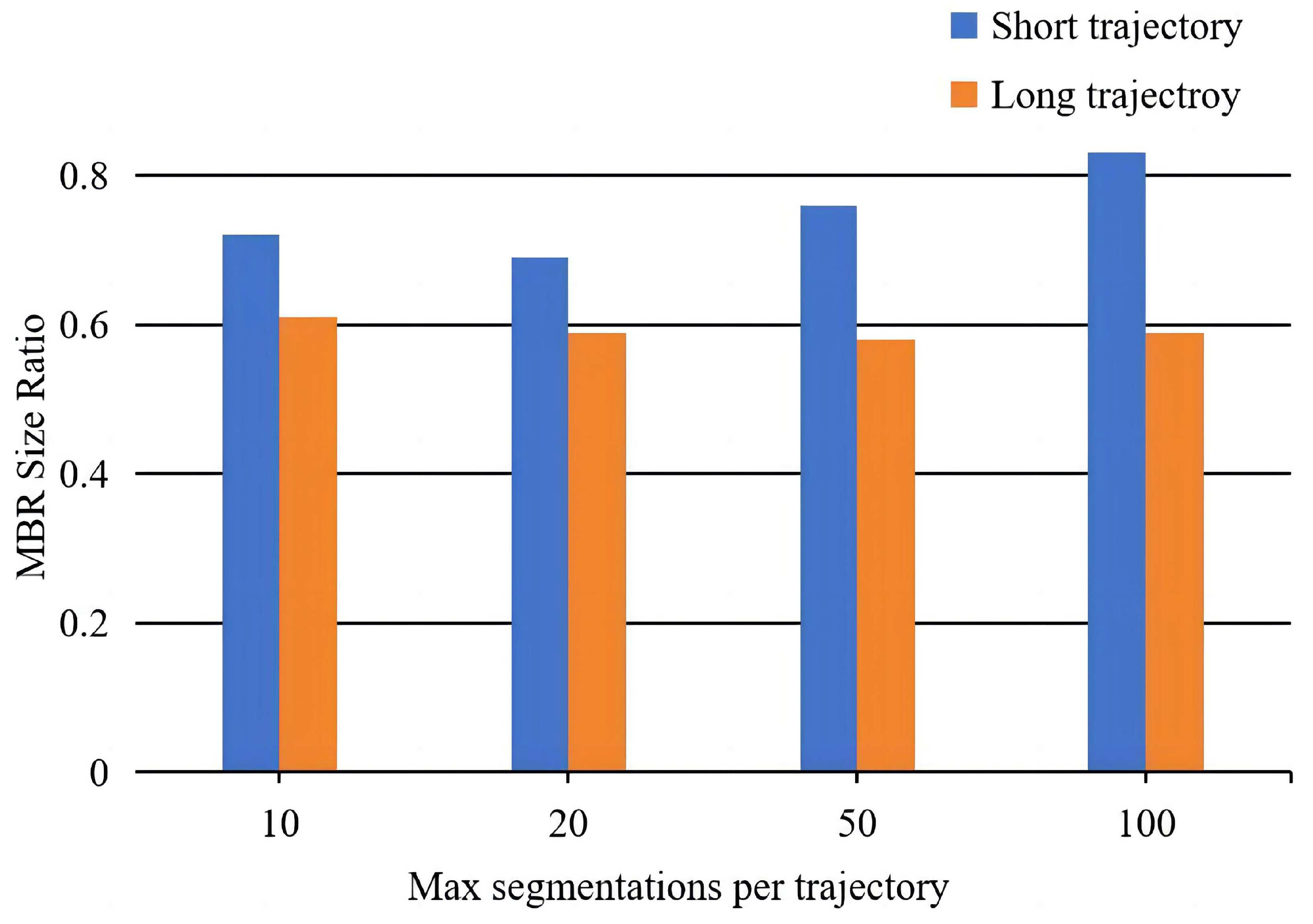
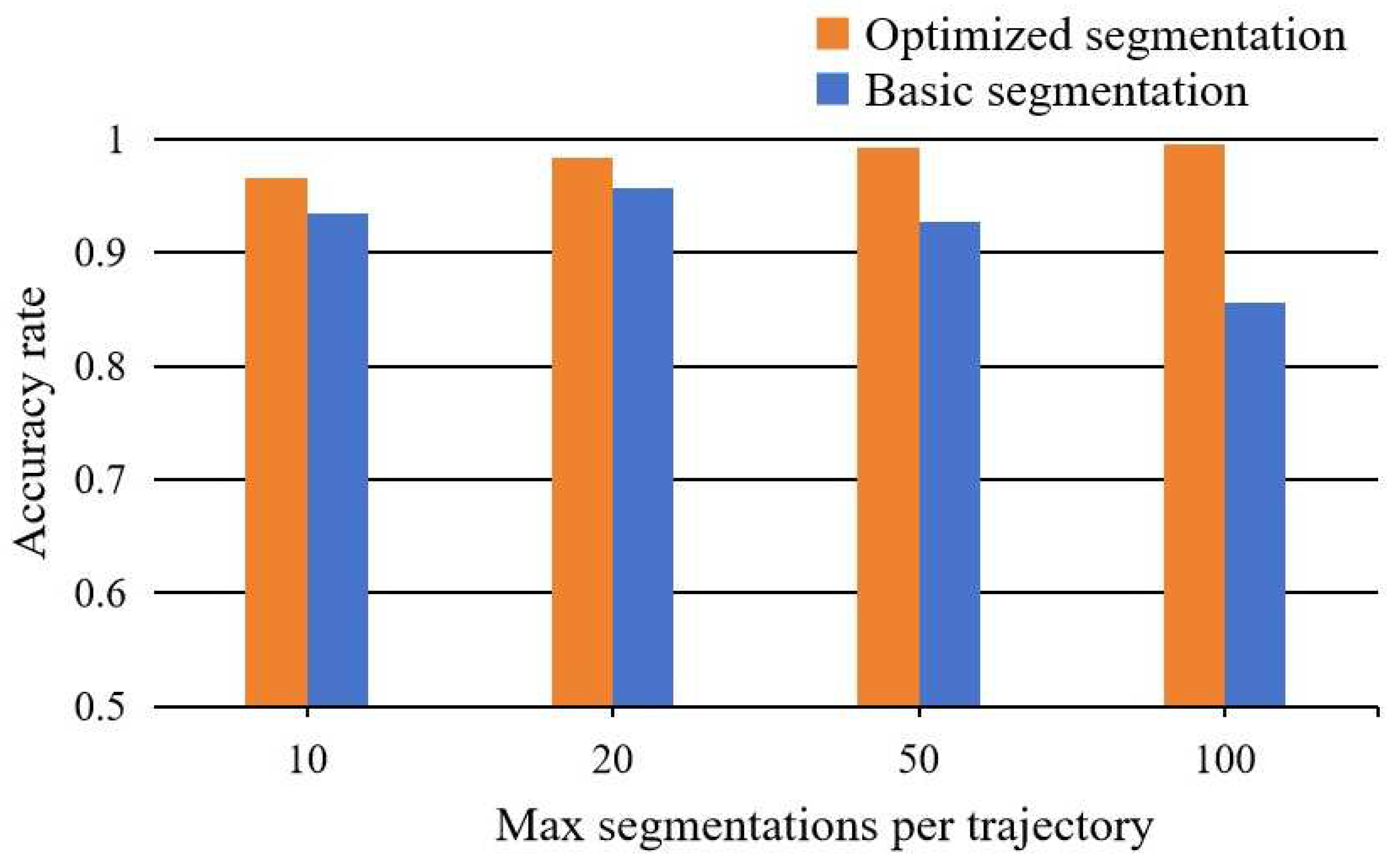
4.2.1. The Effects of Segmentation Optimization
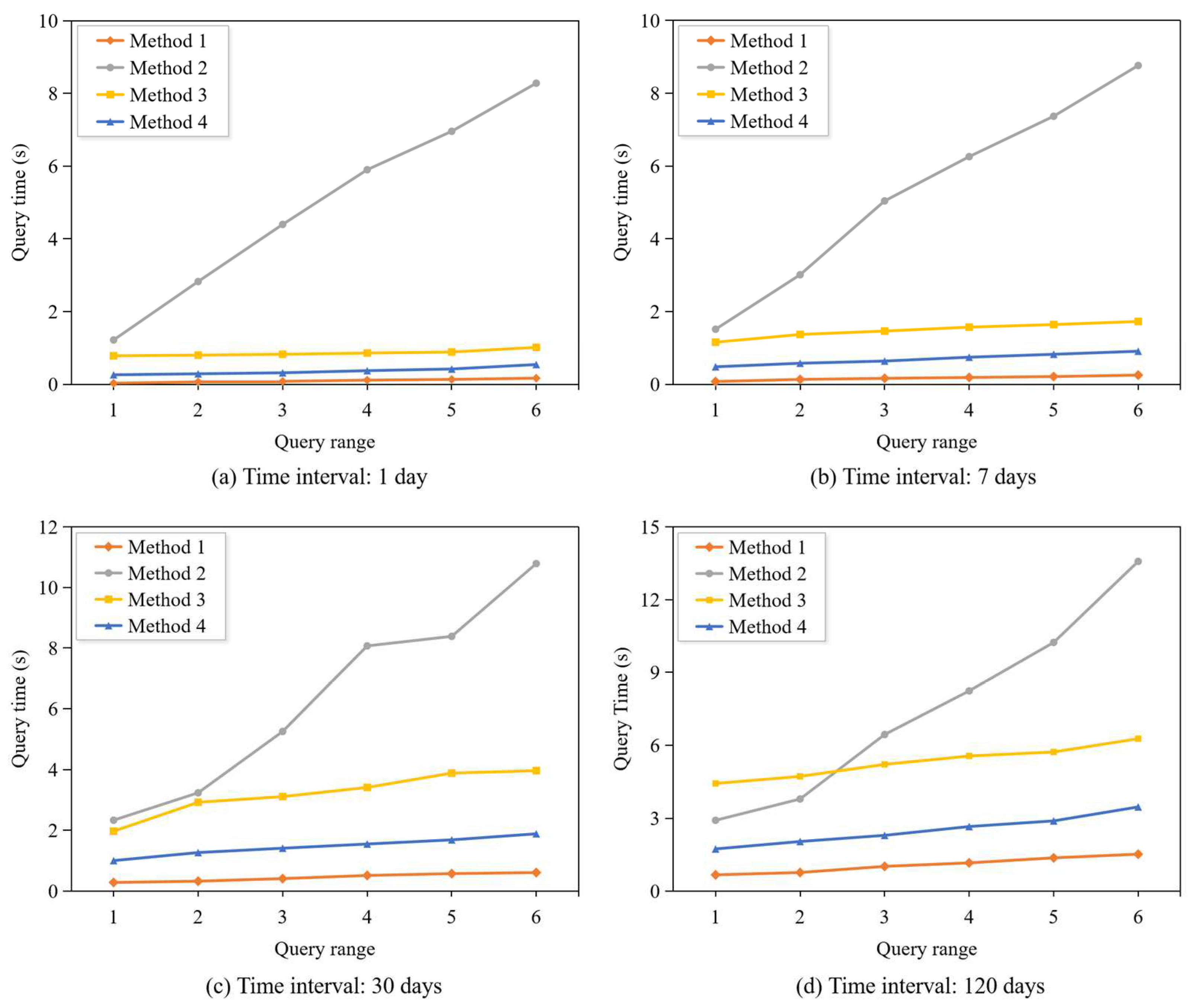
4.2.2. Trajectory Spatio-Temporal Query
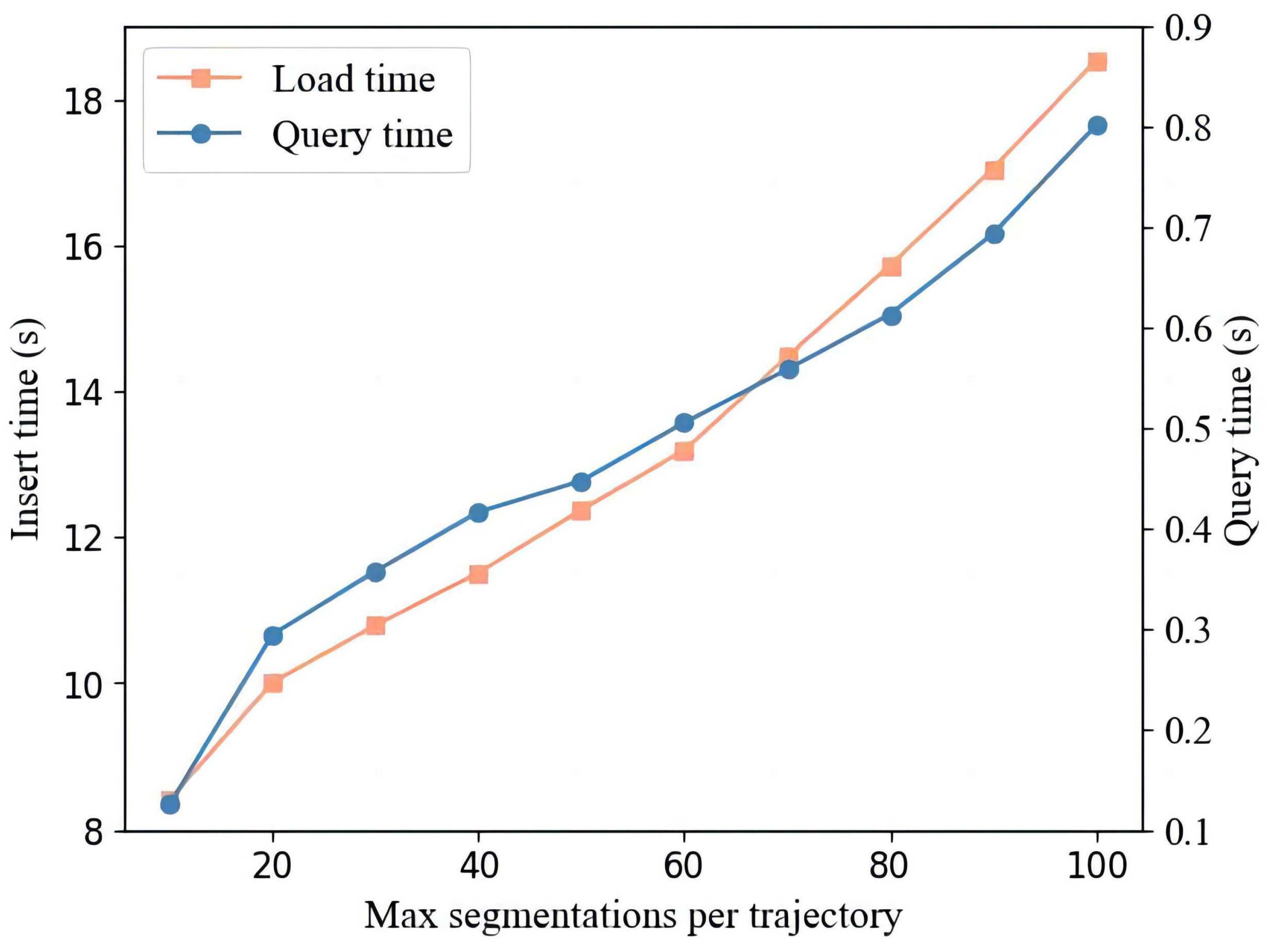
4.2.3. Index Scalability Validation
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Q.; Zhang, F.; Wang, R.; Zhou, F. Trajectory Big Data: A Review of Key Technologies in Data Processing. J. Softw. 2017, 28, 959–992. [Google Scholar]
- Li, J.; Liu, J.; Zhao, X.; Huang, Q.; Sun, W.; Xu, Z.; Wang, H. Trajectory Data Management and Analysis Framework Based on Geographical Grid Model: Method and Application. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 640–649. [Google Scholar]
- Zhao, L.; Mao, J.; Pu, M.; Liu, G.; Jin, C.; Qian, W.; Zhou, A.; Wen, X.; Hu, R.; Chai, H. Automatic Calibration of Road Intersection Topology Using Trajectories. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1633–1644. [Google Scholar]
- Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 29:1–29:41. [Google Scholar] [CrossRef]
- Wang, S.; Bao, Z.; Culpepper, J.S.; Cong, G. A Survey on Trajectory Data Management, Analytics, and Learning. ACM Comput. Surv. 2021, 54, 39:1–39:36. [Google Scholar] [CrossRef]
- Yu, L.; Xiang, L.; Sun, S.; Guan, X.; Wu, H. kNN Query Processing for Trajectory Big Data Based on Distributed Column-Oriented Storage. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 736–745. [Google Scholar]
- Luo, Y.; Chen, B. Adaptive data model and index structure for network- constrained trajectories. J. Geo-Inf. Sci. 2023, 25, 63–76. [Google Scholar]
- Guttman, A. R-Trees: A Dynamic Index Structure for Spatial Searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; Association for Computing Machinery: New York, NY, USA, 1984; pp. 47–57. [Google Scholar]
- Xu, T.; Zhang, X.; Claramunt, C.; Li, X. TripCube: A Trip-Oriented Vehicle Trajectory Data Indexing Structure. Comput. Environ. Urban Syst. 2018, 67, 21–28. [Google Scholar] [CrossRef]
- Aydin, B.; Akkineni, V.; Angryk, R.A. Modeling and Indexing Spatiotemporal Trajectory Data in Non-Relational Databases. In Managing Big Data in Cloud Computing Environments; IGI Global: Hershey, PA, USA, 2016; pp. 133–162. ISBN 978-1-4666-9834-5. [Google Scholar]
- Li, G.; Tang, J. A New R-Tree Spatial Index Based on Space Grid Coordinate Division. In Proceedings of the International Conference on Informatics, Cybernetics, and Computer Engineering (ICCE2011), Melbourne, Australia, 19–20 November 2011; Jiang, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 133–140. [Google Scholar]
- Peng, Z.; Feng, J.; Wang, Q.; Xiong, W. A moving object indexing method that supports frequent location updating. J. Geo-Inf. Sci. 2017, 19, 152–160. [Google Scholar]
- Gong, J.; Ke, S.; Zhu, Q.; Zhang, Y. An Efficient Trajectory Data Index Integrating R-tree, Hash and B*-tree. Acta Geod. Cartogr. Sin. 2015, 44, 570–577. [Google Scholar]
- Qian, C.; Yi, C.; Cheng, C.; Pu, G.; Wei, X.; Zhang, H. GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data. ISPRS Int. J. Geo-Inf. 2019, 8, 284. [Google Scholar] [CrossRef]
- Wang, H.; Belhassena, A. Parallel Trajectory Search Based on Distributed Index. Inf. Sci. 2017, 388–389, 62–83. [Google Scholar] [CrossRef]
- Kang, H.; Liu, Y.; Zhang, W. Cloud-Based Framework for Spatio-Temporal Trajectory Data Segmentation and Query. IEEE Trans. Cloud Comput. 2022, 10, 258–275. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, D.; Gong, Y. Organization and Efficient Range Query of Large Trajectory Data Based on Geohash. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 21–27. [Google Scholar]
- Xiang, L.; Gao, M.; Wang, D.; Gong, Y. Geohash-Trees: An Adaptive Index Which can Organize Large-Scale Trajectories. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 436–442. [Google Scholar]
- Guan, X.; Bo, C.; Li, Z.; Yu, Y. ST-Hash: An Efficient Spatiotemporal Index for Massive Trajectory Data in a NoSQL Database. In Proceedings of the 2017 25th International Conference on Geoinformatics, Redondo Beach, CA, USA, 2–4 August 2017; pp. 1–7. [Google Scholar]
- Liu, H.; Yan, J.; Wang, J.; Chen, B.; Chen, M.; Huang, X. HGST: A Hilbert-GeoSOT Spatio-Temporal Meshing and Coding Method for Efficient Spatio-Temporal Range Query on Massive Trajectory Data. ISPRS Int. J. Geo-Inf. 2023, 12, 113. [Google Scholar] [CrossRef]
- Yang, S.; He, Z.; Chen, Y.-P.P. GCOTraj: A Storage Approach for Historical Trajectory Data Sets Using Grid Cells Ordering. Inf. Sci. 2018, 459, 1–19. [Google Scholar] [CrossRef]
- Pelekis, N.; Frentzos, E.; Giatrakos, N.; Theodoridis, Y. HERMES: A Trajectory DB Engine for Mobility-Centric Applications. IJKBO 2015, 5, 19–41. [Google Scholar] [CrossRef]
- Zimányi, E.; Sakr, M.; Lesuisse, A.; Bakli, M. MobilityDB: A Mainstream Moving Object Database System. In Proceedings of the 16th International Symposium on Spatial and Temporal Databases, Vienna, Austria, 19–21 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 206–209. [Google Scholar]
- Cudre-Mauroux, P.; Wu, E.; Madden, S. TrajStore: An Adaptive Storage System for Very Large Trajectory Data Sets. In Proceedings of the 2010 IEEE 26th International Conference on Data Engineering (ICDE 2010), Long Beach, CA, USA, 1–6 March 2010; pp. 109–120. [Google Scholar]
- Zheng, B.; Wang, H.; Zheng, K.; Su, H.; Liu, K.; Shang, S. SharkDB: An in-Memory Column-Oriented Storage for Trajectory Analysis. World Wide Web 2018, 21, 455–485. [Google Scholar] [CrossRef]
- Mei, S.; Guan, H.; Wang, Q. An Overview on the Convergence of High Performance Computing and Big Data Processing. In Proceedings of the 2018 IEEE 24th International Conference on Parallel and Distributed Systems (ICPADS), Singapore, 11–13 December 2018; pp. 1046–1051. [Google Scholar]
- Xiong, S.; Ouyang, X.; Xiong, W. Distributed or Centralized: An Experimental Study on Spatial Database Systems for Processing Big Trajectory Data. In Proceedings of the 2023 IEEE 8th International Conference on Big Data Analytics (ICBDA), Harbin, China, 3–5 March 2023; pp. 8–13. [Google Scholar]
- Bakli, M.; Sakr, M.; Soliman, T.H.A. HadoopTrajectory: A Hadoop Spatiotemporal Data Processing Extension. J. Geogr. Syst. 2019, 21, 211–235. [Google Scholar] [CrossRef]
- Qin, J.; Ma, L.; Niu, J. THBase: A Coprocessor-Based Scheme for Big Trajectory Data Management. Future Internet 2019, 11, 10. [Google Scholar] [CrossRef]
- Qin, J.; Ma, L.; Liu, Q. DFTHR: A Distributed Framework for Trajectory Similarity Query Based on HBase and Redis. Information 2019, 10, 77. [Google Scholar] [CrossRef]
- Li, R.; He, H.; Wang, R.; Ruan, S.; Sui, Y.; Bao, J.; Zheng, Y. TrajMesa: A Distributed NoSQL Storage Engine for Big Trajectory Data. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 2002–2005. [Google Scholar]
- Zhang, Z.; Jin, C.; Mao, J.; Yang, X.; Zhou, A. TrajSpark: A Scalable and Efficient In-Memory Management System for Big Trajectory Data. In Proceedings of the Web and Big Data, Beijing, China, 7–9 July 2017; Chen, L., Jensen, C.S., Shahabi, C., Yang, X., Lian, X., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 11–26. [Google Scholar]
- Shang, Z.; Li, G.; Bao, Z. DITA: Distributed In-Memory Trajectory Analytics. In Proceedings of the 2018 International Conference on Management of Data, Houston, TX, USA, 10–15 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 725–740. [Google Scholar]
- Ding, X.; Chen, L.; Gao, Y.; Jensen, C.S.; Bao, H. UlTraMan: A Unified Platform for Big Trajectory Data Management and Analytics. Proc. VLDB Endow. 2018, 11, 787–799. [Google Scholar] [CrossRef]
- Jasinski, M. Datamining. Available online: https://github.com/marciogj/datamining (accessed on 8 August 2016).
- Bao, Y.; Huang, Z.; Gong, X.; Zhang, Y.; Yin, G.; Wang, H. Optimizing Segmented Trajectory Data Storage with HBase for Improved Spatio-Temporal Query Efficiency. Int. J. Digit. Earth 2023, 16, 1124–1143. [Google Scholar] [CrossRef]
- Hadjieleftheriou, M.; Kollios, G.; Tsotras, V.J.; Gunopulos, D. Efficient Indexing of Spatiotemporal Objects. In Proceedings of the Advances in Database Technology—EDBT, Prague, Czech Republic, 25–27 March 2002; Jensen, C.S., Šaltenis, S., Jeffery, K.G., Pokorny, J., Bertino, E., Böhn, K., Jarke, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 251–268. [Google Scholar]
- Rasetic, S.; Sander, J.; Elding, J.; Nascimento, M.A. A Trajectory Splitting Model for Efficient Spatio-Temporal Indexing. In Proceedings of the 31st VLDB Conference, Trondheim, Norway, 30 August–2 September 2005. [Google Scholar]
- Cao, B.; Feng, H.; Liang, J.; Li, X. Hilbert Curve and Cassandra Based Indexing and Storing Approach for Large-Scale Spatiotemporal Data. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 620–629. [Google Scholar]
- Gong, X.; Huang, Z.; Wang, Y.; Wu, L.; Liu, Y. High-Performance Spatiotemporal Trajectory Matching across Heterogeneous Data Sources. Future Gener. Comput. Syst. 2020, 105, 148–161. [Google Scholar] [CrossRef]
- Kang, Y.; Gui, Z.; Ding, J.; Wu, J.; Wu, H. Parallel Ripleys’ K function based on Hilbert spatial partitioning and Geohash indexing. J. Geo-Inf. Sci. 2022, 24, 74–86. [Google Scholar]
- Eldawy, A.; Alarabi, L.; Mokbel, M.F. Spatial Partitioning Techniques in SpatialHadoop. Proc. VLDB Endow. 2015, 8, 1602–1605. [Google Scholar] [CrossRef]
- Yao, X.; Yang, J.; Li, L.; Ye, S.; Yun, W.; Zhu, D. Parallel Algorithm for Partitioning Massive Spatial Vector Data in Cloud Environment. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1092–1097. [Google Scholar]
- Zhao, X.; Huang, X.; Qiao, J.; Kang, R.; Li, N.; Wang, J. A Spatio-Temporal Index Based on Skew Spatial Coding and R-Tree. J. Comput. Res. Dev. 2019, 56, 666–676. [Google Scholar]
- Aji, A.; Wang, F.; Vo, H.; Lee, R.; Liu, Q.; Zhang, X.; Saltz, J. Hadoop GIS: A High Performance Spatial Data Warehousing System over Mapreduce. Proc. VLDB Endow. 2013, 6, 1009–1020. [Google Scholar] [CrossRef]
- Wang, J.; Shan, J. Space-Filling Curve Based Point Clouds Index. In Proceedings of the 8th International Conference on GeoComputation, Ann Arbor, MI, USA, 31 July–3 August 2005; pp. 551–562. [Google Scholar]
- Zheng, Y.; Xie, X.; Ma, W.-Y. GeoLife: A Collaborative Social Networking Service among User, Location and Trajectory. IEEE Data Eng. Bull. 2010, 33, 32–39. [Google Scholar]
- Wu, Y.; Cao, X.; An, Z. A Spatiotemporal Trajectory Data Index Based on the Hilbert Curve Code. IOP Conf. Ser. Earth Environ. Sci. 2020, 502, 012005. [Google Scholar] [CrossRef]


| Name | Number of Trajectories | Number of Trajectory Points | Index Construction Time (s) |
|---|---|---|---|
| D1 | 3542 | 5,096,851 | 0.773 |
| D2 | 9092 | 13,321,696 | 2.203 |
| D3 | 18,670 | 24,876,978 | 4.234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zuo, X.; Zhao, K.; Li, Y. Non-Uniform Spatial Partitions and Optimized Trajectory Segments for Storage and Indexing of Massive GPS Trajectory Data. ISPRS Int. J. Geo-Inf. 2024, 13, 197. https://doi.org/10.3390/ijgi13060197
Yang Y, Zuo X, Zhao K, Li Y. Non-Uniform Spatial Partitions and Optimized Trajectory Segments for Storage and Indexing of Massive GPS Trajectory Data. ISPRS International Journal of Geo-Information. 2024; 13(6):197. https://doi.org/10.3390/ijgi13060197
Chicago/Turabian StyleYang, Yuqi, Xiaoqing Zuo, Kang Zhao, and Yongfa Li. 2024. "Non-Uniform Spatial Partitions and Optimized Trajectory Segments for Storage and Indexing of Massive GPS Trajectory Data" ISPRS International Journal of Geo-Information 13, no. 6: 197. https://doi.org/10.3390/ijgi13060197
APA StyleYang, Y., Zuo, X., Zhao, K., & Li, Y. (2024). Non-Uniform Spatial Partitions and Optimized Trajectory Segments for Storage and Indexing of Massive GPS Trajectory Data. ISPRS International Journal of Geo-Information, 13(6), 197. https://doi.org/10.3390/ijgi13060197





