Enhancing Indoor Air Quality Estimation: A Spatially Aware Interpolation Scheme
Abstract
:1. Introduction
2. Related Works
3. Basic Concepts
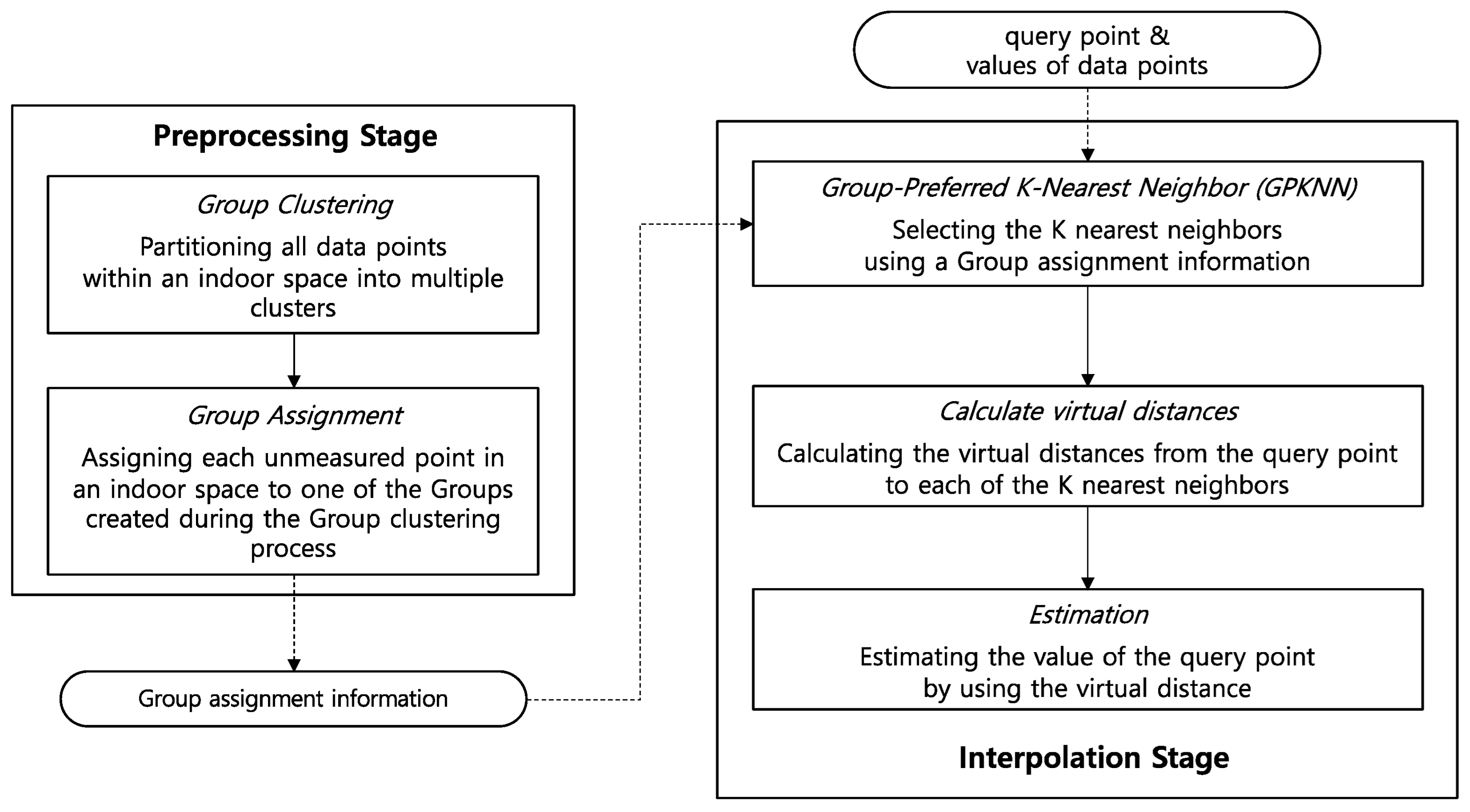
4. Indoor Spatial Interpolation Scheme
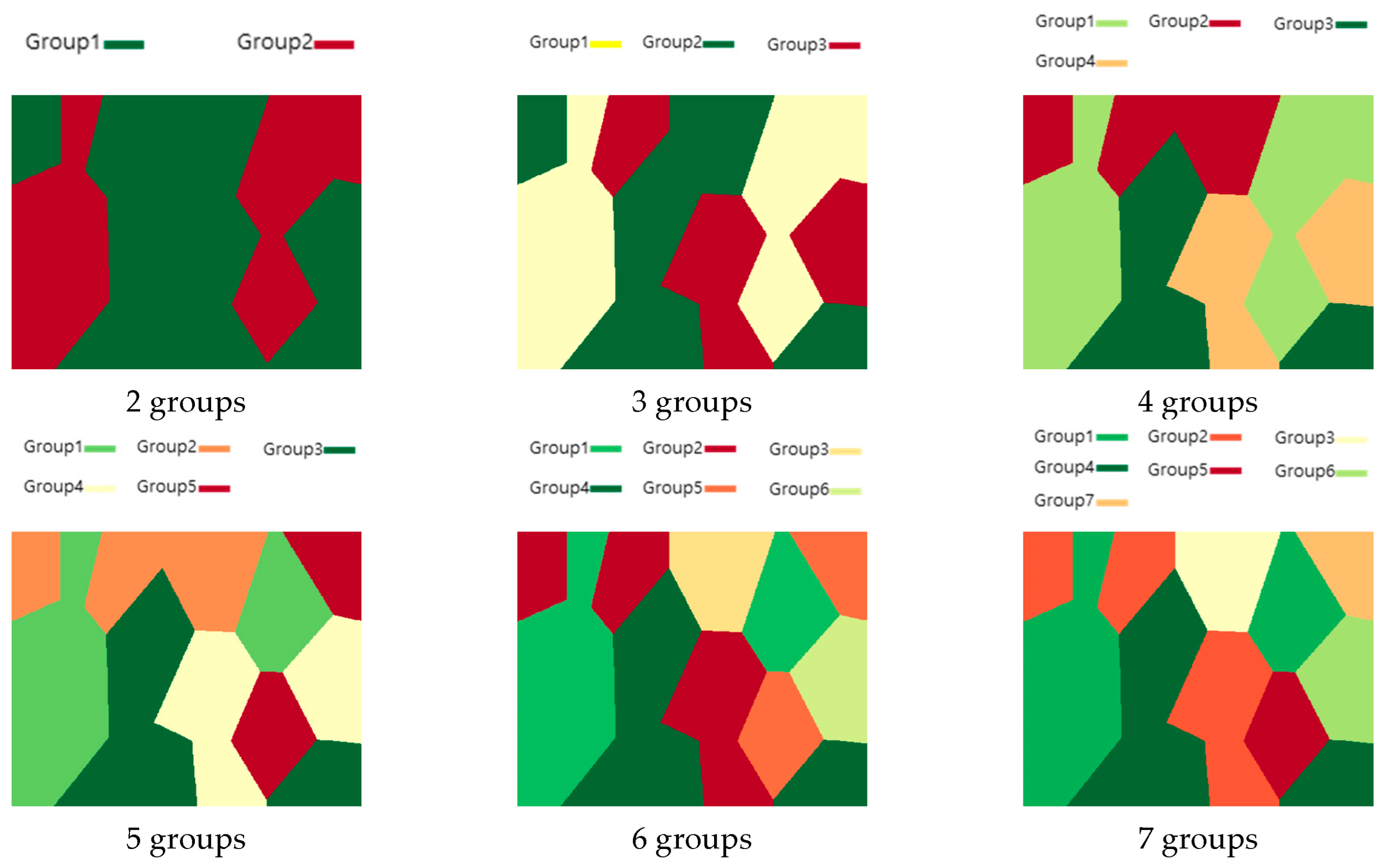
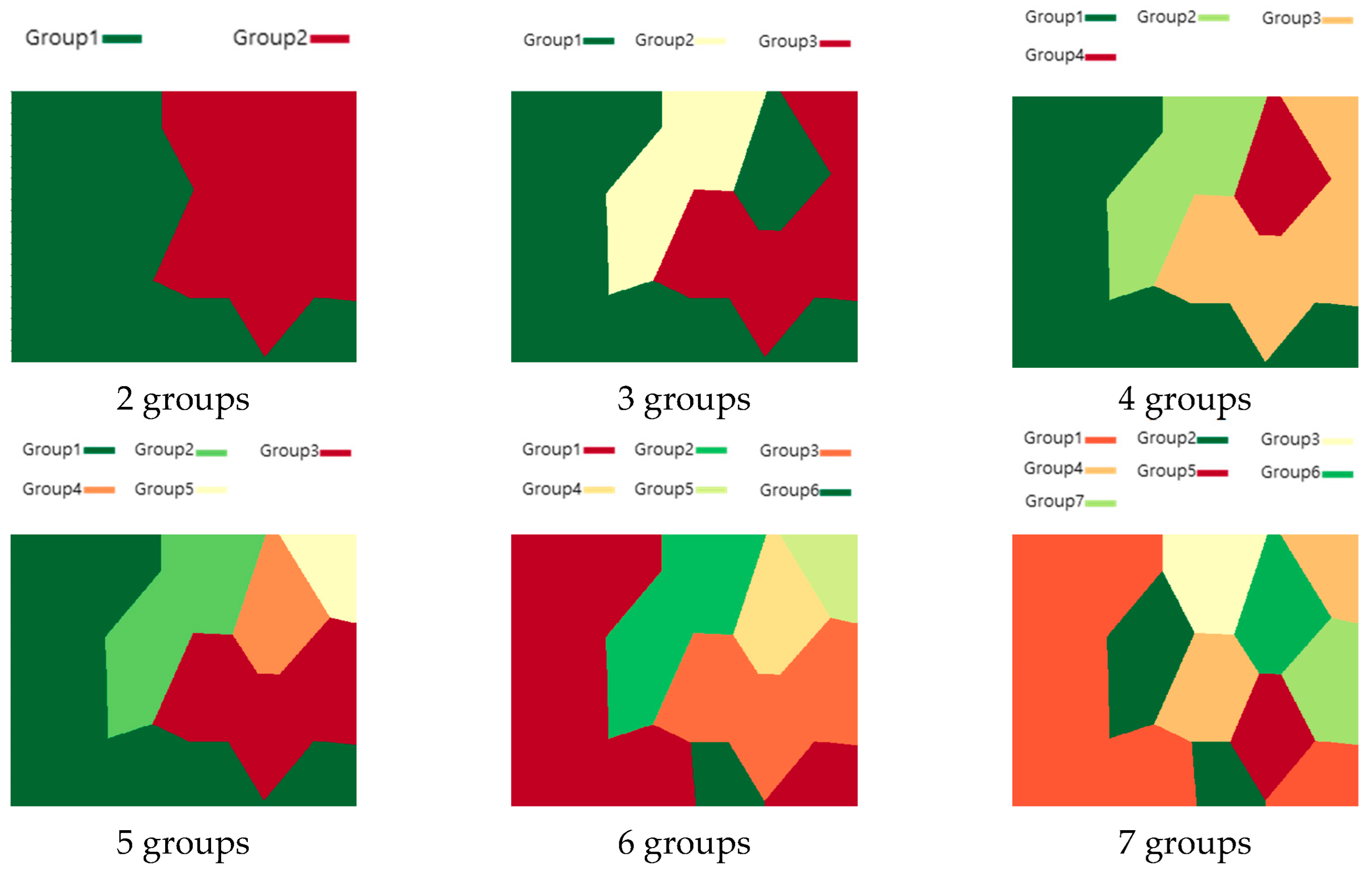
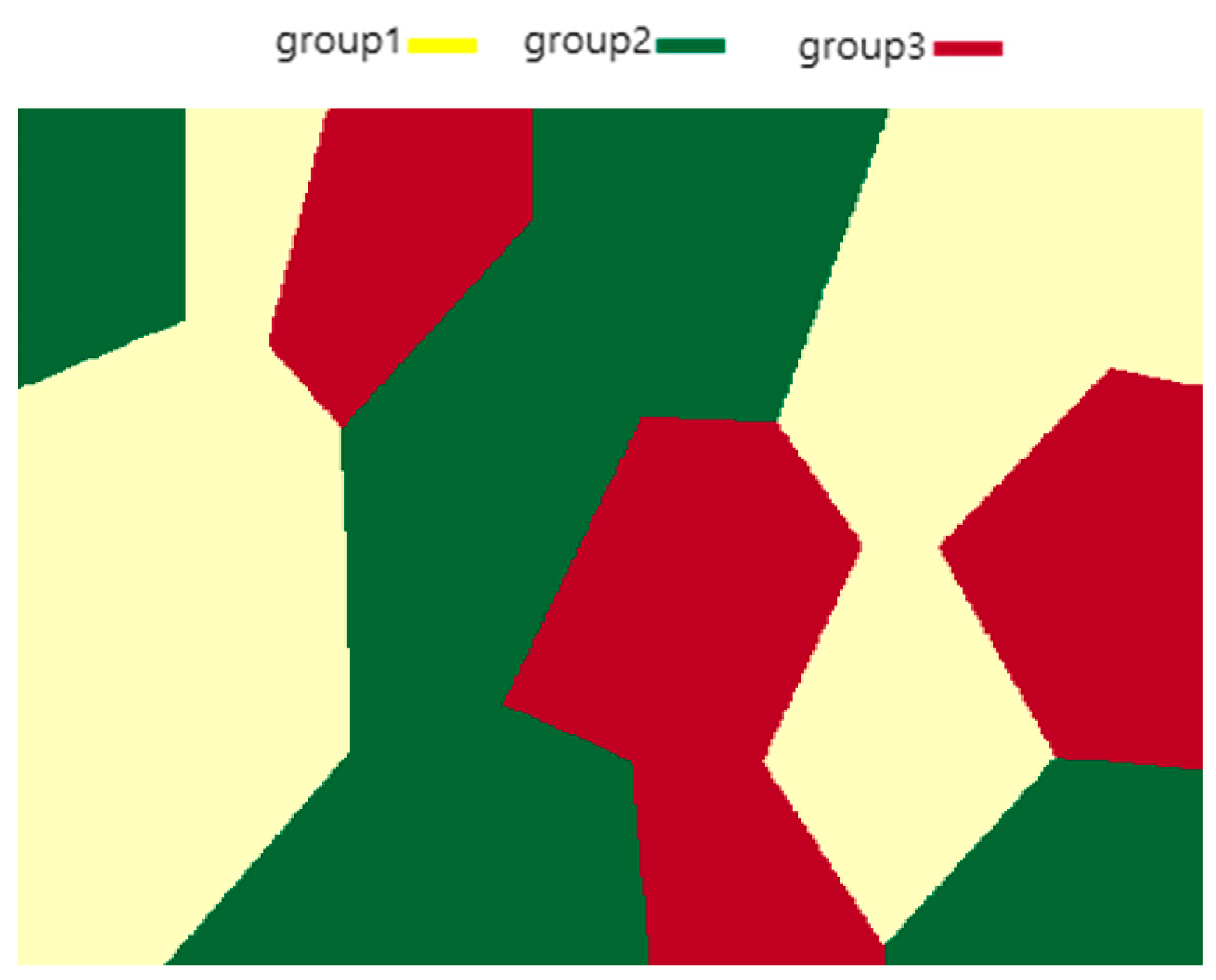
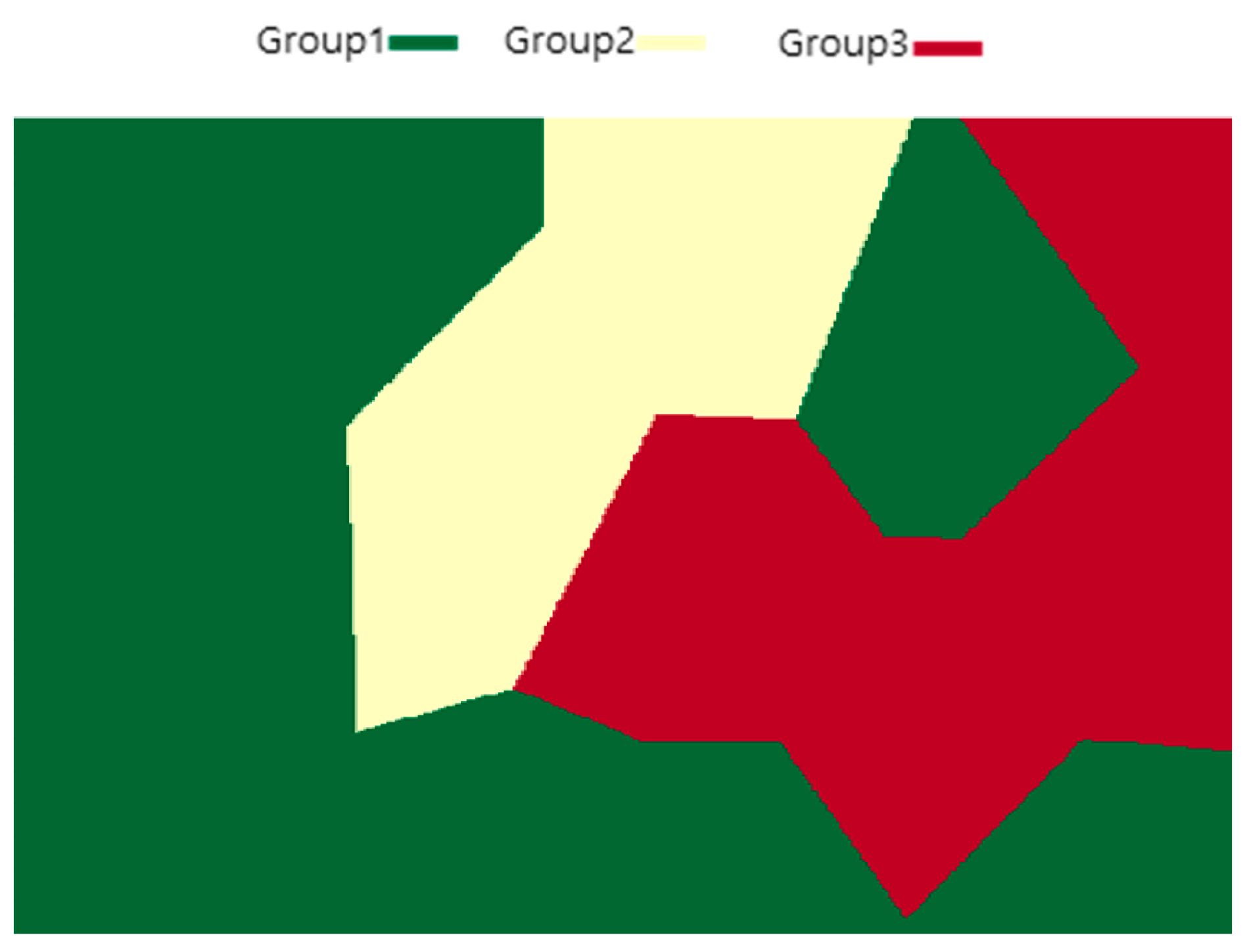
4.1. Group Clustering
4.2. Group Assignment
| Algorithm 1. Assign a group to an unmeasured point |
| procedure Group Assignment (q: unmeasured point) Let p1, …, pn be all the data points in an indoor space G(q) = G(p) end procedure |
4.3. Group-Preferred K-Nearest Neighbor (GPKNN)
| Algorithm 2. Find group-preferred K nearest neighbors |
| procedure GPKNN (q: query point, K: integer) Let DPSet = {p1, …, pn} be a set of all the data points in an indoor space TSet = DPSet KSet = {} while size(KSet) != K and TSet != {} end while return KSet end procedure |
4.4. Spatial Interpolation
4.4.1. Spatial Structure IDW (SSI) Method
| Algorithm 3. Spatial Structure IDW (SSI) Method |
| procedure SSI(q: query point, K: integer) Let DPSet = {p1, …, pn} be a set of all the data points in an indoor space Let y(pi) be the data value of pi for i = 1, …, n. {q1, …, qK} = GPKNN(q, K) where return ŷ(q) end procedure |
4.4.2. Spatial Structure Kriging (SSK) Method
| Algorithm 4. Spatial Structure Kriging (SSK) Method |
| procedure SSK (q: query point, K: integer) Let DPSet = {p1, …, pn} be a set of all the data points in an indoor space Let y(pi) be the data value of pi for i = 1, …, n. {q1, …, qK} = GPKNN(q, K) where return ŷ(q) end procedure |
5. Experimental Results and Discussion
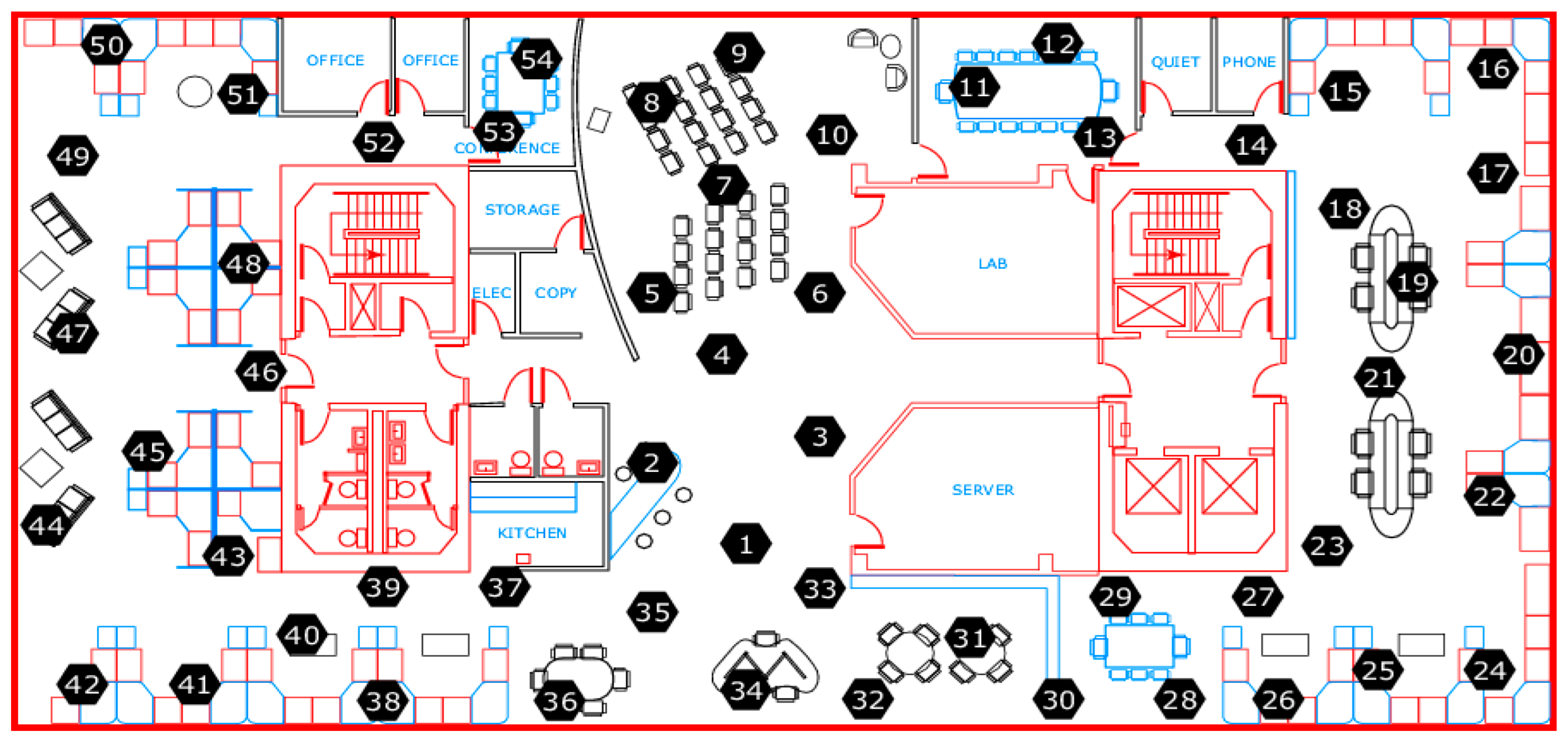
5.1. Experimental Results on an Office Dataset
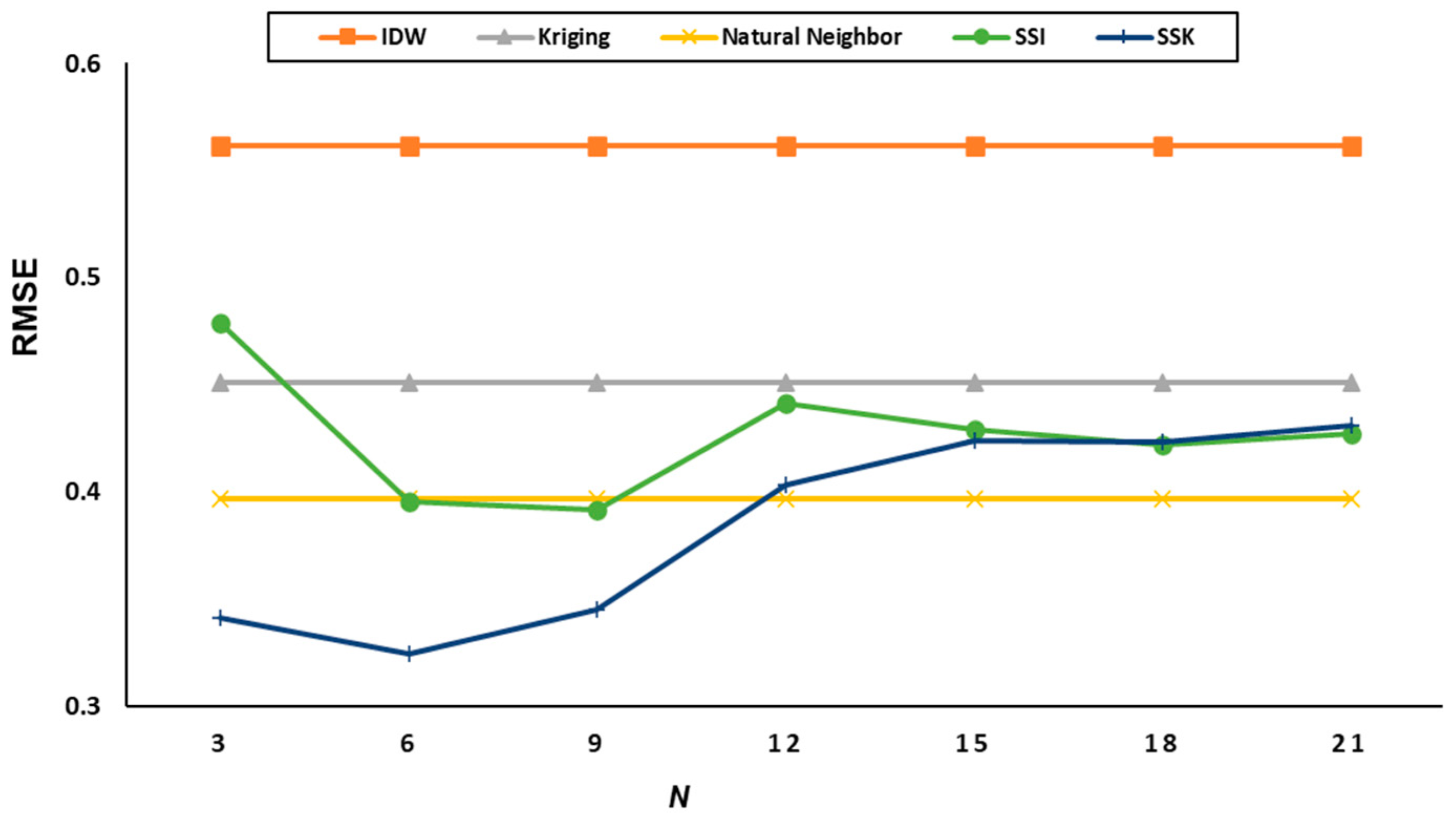
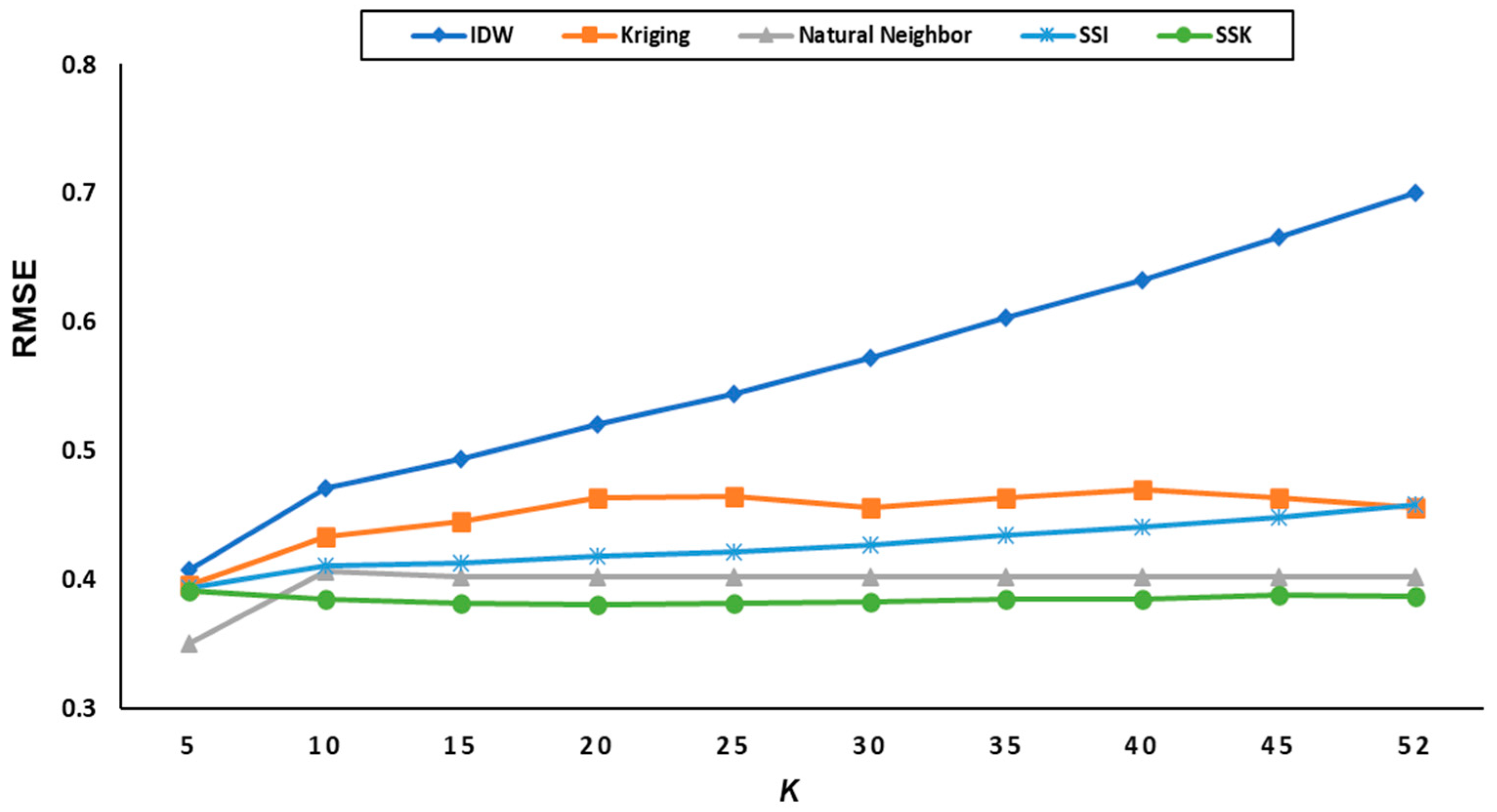
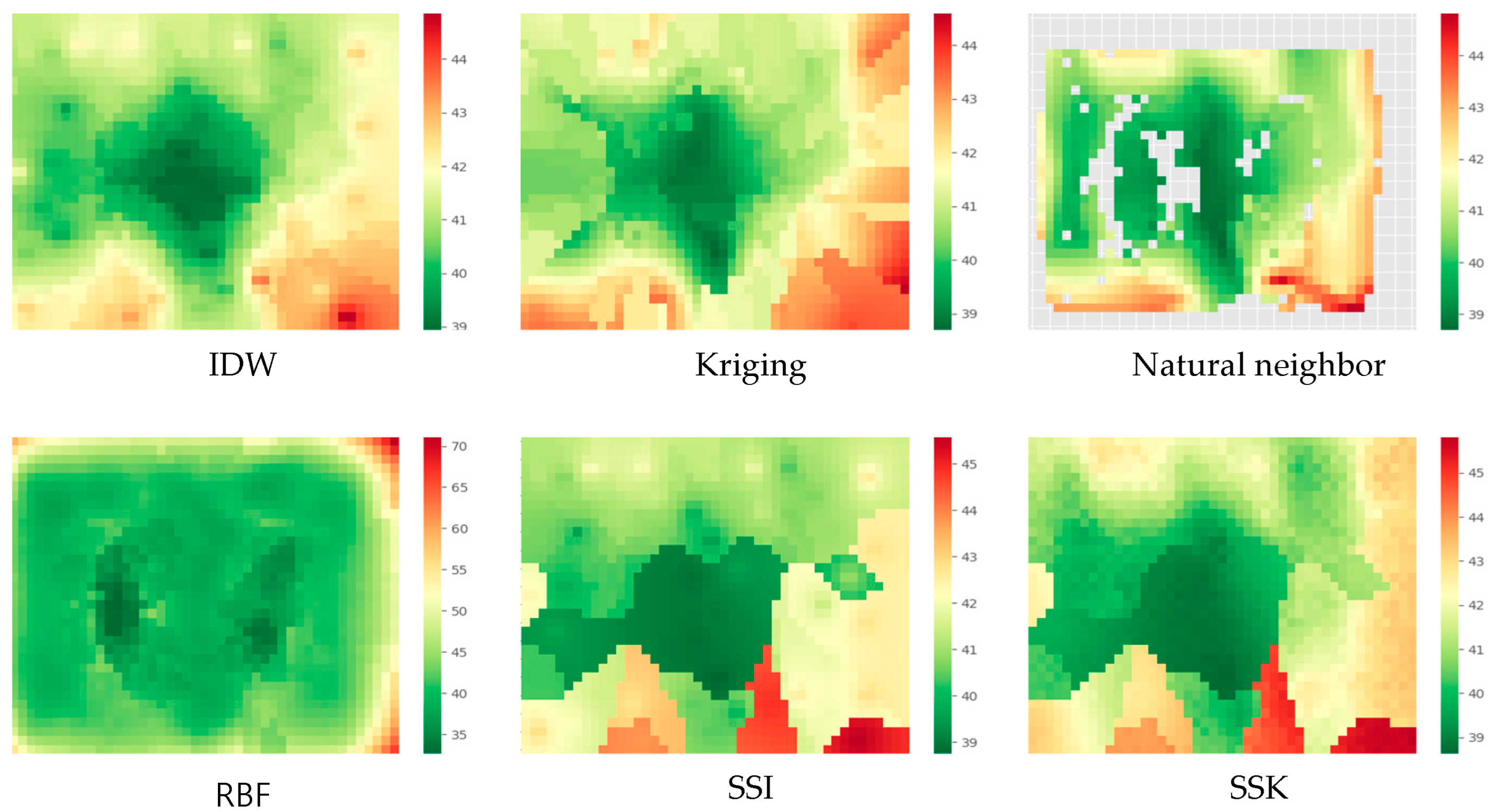
5.1.1. Experimental Results for CO2 Data
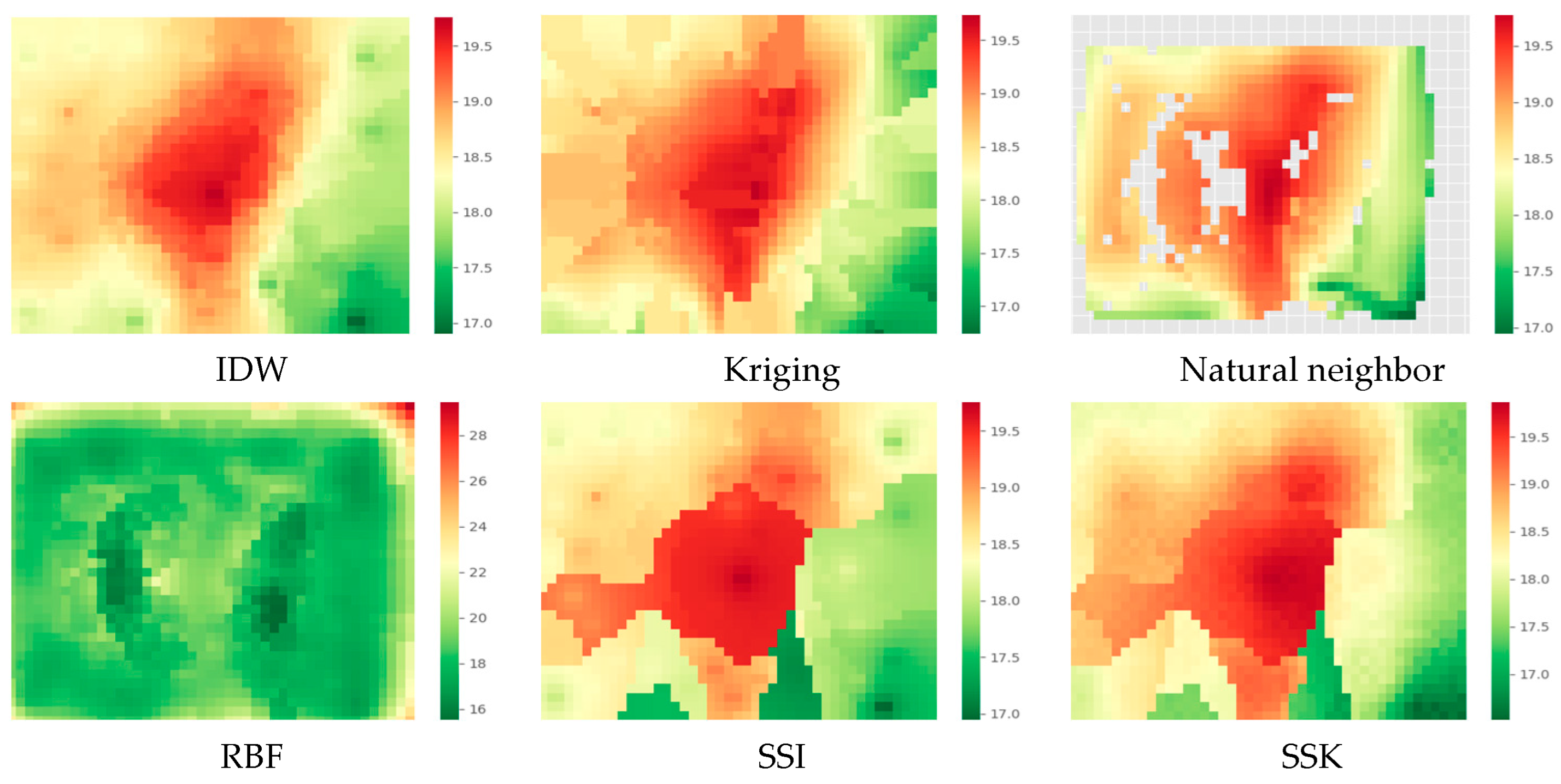
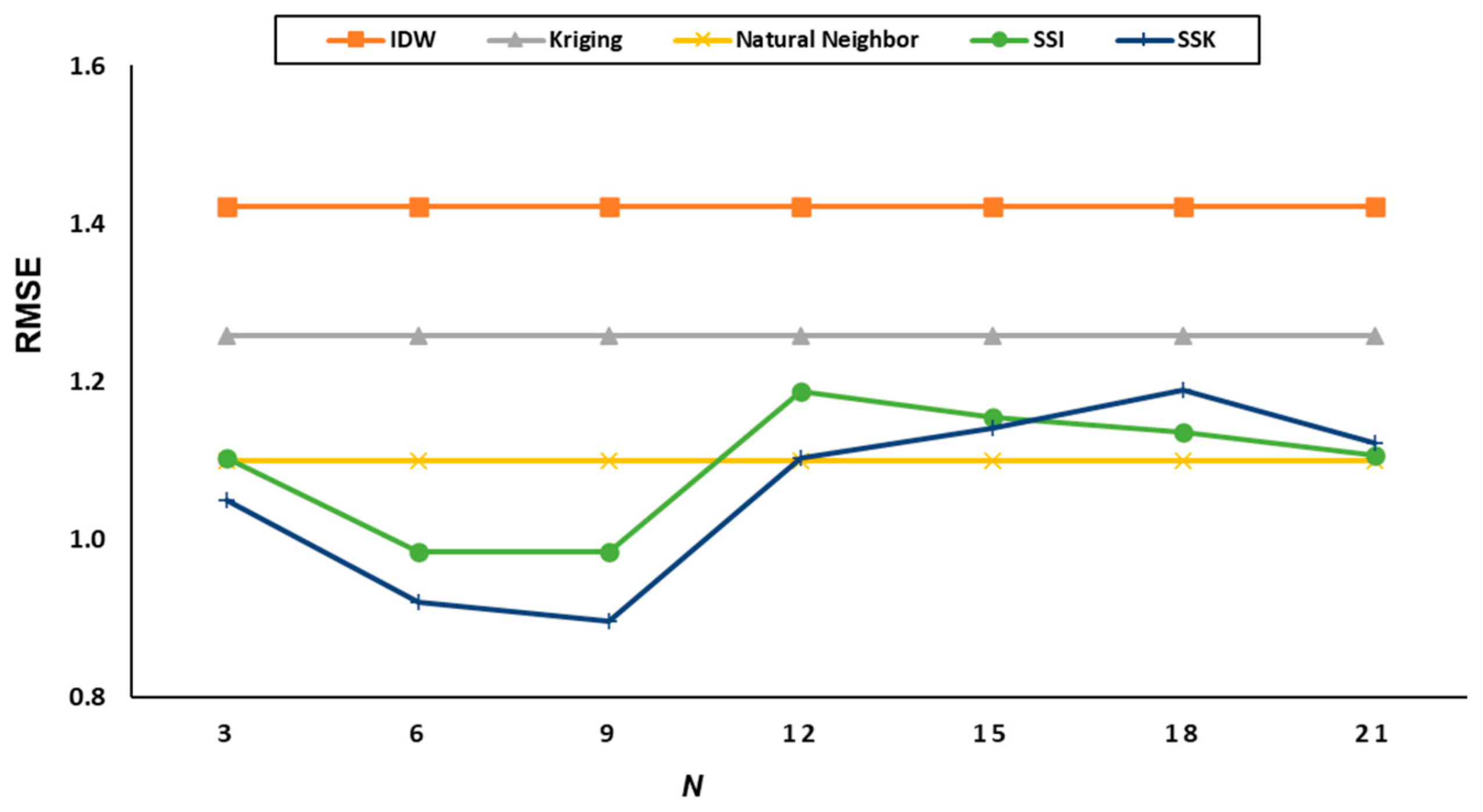
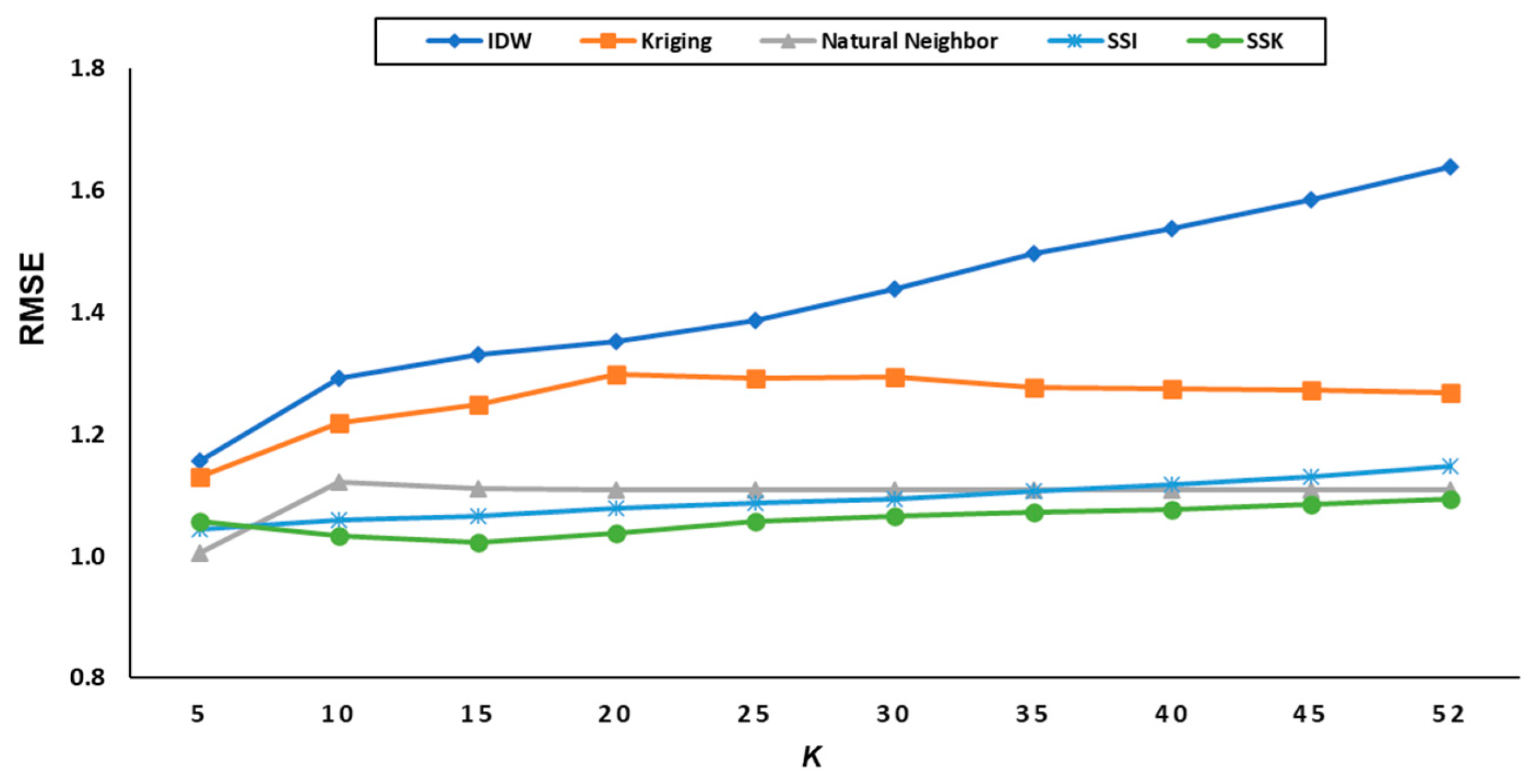
5.1.2. Experimental Results for Temperature Data
5.2. Experimental Results Based on the Intel Lab Dataset
5.2.1. Experimental Results for Temperature Data
5.2.2. Experimental Results for Humidity Data
5.2.3. Experimental Results for Light Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, H.; Hong, T.; Kim, J.; Yeom, S. A psychophysiological effect of indoor thermal condition on college students’ learning performance through EEG measurement. Build. Environ. 2020, 184, 107223. [Google Scholar] [CrossRef]
- Andargie, M.S.; Azar, E. An applied framework to evaluate the impact of indoor office environmental factors on occupants’ comfort and working conditions. Sustain. Cities Soc. 2019, 46, 101447. [Google Scholar] [CrossRef]
- Frontczak, M.; Wargocki, P. Literature survey on how different factors influence human comfort in indoor environments. Build. Environ. 2011, 46, 922–937. [Google Scholar] [CrossRef]
- Calvo, I.; Espin, A.; Gil-García, J.M.; Fernández Bustamante, P.; Barambones, O.; Apiñaniz, E. Scalable IoT Architecture for Monitoring IEQ Conditions in Public and Private Buildings. Energies 2022, 15, 2270. [Google Scholar] [CrossRef]
- Dong, B.; Prakash, V.; Feng, F.; O’Neill, Z. A review of smart building sensing system for better indoor environment control. Energy Build. 2019, 199, 29–46. [Google Scholar] [CrossRef]
- Afonso, J.A.; Monteiro, V.; Afonso, J.L. Internet of things systems and applications for smart buildings. Energies 2023, 16, 2757. [Google Scholar] [CrossRef]
- Ma, C.; Guerra-Santin, O.; Grave, A.; Mohammadi, M. Supporting dementia care by monitoring indoor environmental quality in a nursing home. Indoor Built Environ. 2023. [Google Scholar] [CrossRef]
- Albu, A.V.; Caciora, T.; Berdenov, Z.; Ilies, D.C.; Sturzu, B.; Sopota, D.; Herman, G.V.; Ilies, A.; Kecse, G.; Ghergheles, C.G. Digitalization of garment in the context of circular economy. Ind. Text. 2021, 72, 102–107. [Google Scholar] [CrossRef]
- Bourdeau, M.; Waeytens, J.; Aouani, N.; Basset, P.; Nefzaoui, E. A Wireless Sensor Network for Residential Building Energy and Indoor Environmental Quality Monitoring: Design, Instrumentation, Data Analysis and Feedback. Sensors 2023, 23, 5580. [Google Scholar] [CrossRef]
- Boumpoulis, V.; Michalopoulou, M.; Depountis, N. Comparison between different spatial interpolation methods for the development of sediment distribution maps in coastal areas. Earth Sci. Inform. 2023, 1–19. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, X.; Zhang, F.; Yao, X.; Gao, Y.; Liu, Y. Spatial interpolation using conditional generative adversarial neural networks. Int. J. Geogr. Inf. Sci. 2020, 34, 735–758. [Google Scholar] [CrossRef]
- Comber, A.; Zeng, W. Spatial interpolation using areal features: A review of methods and opportunities using new forms of data with coded illustrations. Geogr. Compass 2019, 13, e12465. [Google Scholar] [CrossRef]
- Martínez-Comesaña, M.; Ogando-Martínez, A.; Troncoso-Pastoriza, F.; López-Gómez, J.; Febrero-Garrido, L.; Granada-Álvarez, E. Use of optimised MLP neural networks for spatiotemporal estimation of indoor environmental conditions of existing buildings. Build. Environ. 2021, 205, 108243. [Google Scholar] [CrossRef]
- Choi, H.; Kim, H.; Yeom, S.; Hong, T.; Jeong, K.; Lee, J. An indoor environmental quality distribution map based on spatial interpolation methods. Build. Environ. 2022, 213, 108880. [Google Scholar] [CrossRef]
- Jin, M.; Liu, S.; Schiavon, S.; Spanos, C. Automated mobile sensing: Towards high-granularity agile indoor environmental quality monitoring. Build. Environ. 2018, 127, 268–276. [Google Scholar] [CrossRef]
- Cheng, J.C.; Kwok, H.H.; Li, A.T.; Tong, J.C.; Lau, A.K. BIM-supported sensor placement optimization based on genetic algorithm for multi-zone thermal comfort and IAQ monitoring. Build. Environ. 2022, 216, 108997. [Google Scholar] [CrossRef]
- Choi, K.; Chong, K. Modified inverse distance weighting interpolation for particulate matter estimation and mapping. Atmosphere 2022, 13, 846. [Google Scholar] [CrossRef]
- Kaligambe, A.; Fujita, G.; Keisuke, T. Estimation of Unmeasured Room Temperature, Relative Humidity, and CO2 Concentrations for a Smart Building Using Machine Learning and Exploratory Data Analysis. Energies 2022, 15, 4213. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, Q.; Han, J.; Wang, J.; Lu, Y.; Shi, J.; Kou, M. Real-time prediction of indoor humidity with limited sensors using cross-sample learning. Build. Environ. 2022, 215, 108964. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.; Jiang, F.; Wan, Z. A temporal-spatial interpolation and extrapolation method based on geographic Long Short-Term Memory neural network for PM2. 5. J. Clean. Prod. 2019, 237, 117729. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, X.; Li, J.; Li, B.; Duan, R.; Lin, C.H.; Chen, Q. A method to optimize sampling locations for measuring indoor air distributions. Atmos. Environ. 2015, 102, 355–365. [Google Scholar] [CrossRef]
- Collins, F.C. A Comparison of Spatial Interpolation Techniques in Temperature Estimation. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, November 1995. [Google Scholar]
- Dhamodaran, S.; Lakshmi, M. Comparative analysis of spatial interpolation with climatic changes using inverse distance method. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 6725–6734. [Google Scholar] [CrossRef]
- Wang, D.W.; Li, L.N.; Hu, C.; Li, Q.; Chen, X.; Huang, P.W. A modified inverse distance weighting method for interpolation in open public places based on Wi-Fi probe data. J. Adv. Transp. 2019. [Google Scholar] [CrossRef]
- Yudison, A.P. Development of Indoor Air Pollution Concentration Prediction by Geospatial Analysis. J. Eng. Technol. Sci. 2015, 47, 306–319. [Google Scholar]
- Li, Z.; Wang, K.; Ma, H.; Wu, Y. An adjusted inverse distance weighted spatial interpolation method. In Proceedings of the 2018 3rd International Conference on Communications, Information Management and Network Security (CIMNS 2018), Wuhan, China, 27 September 2018; Advances in Computer Science Research; Atlantis Press: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Smith, T.E. Spatial Interpolation Models. In Notebook on Spatial Data Analysis; University of Pennsylvania: Philadelphia, PA, USA, 2014; Available online: https://www.seas.upenn.edu/~tesmith/NOTEBOOK/index.html (accessed on 15 March 2021).
- Di Salvo, F.; Ruggieri, M.; Plaia, A. Extending Functional kriging to a multivariate context. Int. J. Stat. Anal. 2020, 18, 1–20. [Google Scholar]
- Ignaccolo, R.; Mateu, J.; Giraldo, R. Kriging with external drift for functional data for air quality monitoring. Stoch. Environ. Res. Risk Assess. 2014, 28, 1171–1186. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Genetic programming-based ordinary kriging for spatial interpolation of rainfall. J. Hydrol. Eng. 2016, 21, 04015062. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Yang, R.; Liu, Q.; Zhao, L.; Dou, B. An extended kriging method to interpolate near-surface soil moisture data measured by wireless sensor networks. Sensors 2017, 17, 1390. [Google Scholar] [CrossRef]
- Jha, D.K.; Sabesan, M.; Das, A.; Vinithkumar, N.V.; Kirubagaran, R. Evaluation of Interpolation Technique for Air Quality Parameters in Port Blair, India. Univers. J. Environ. Res. Technol. 2011, 1, 301–310. [Google Scholar]
- Oktavia, E.; Mustika, I.W. Inverse distance weighting and kriging spatial interpolation for data center thermal monitoring. In Proceedings of the 2016 1st International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 23–24 August 2016; pp. 69–74. [Google Scholar]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Bobach, T.A. Natural Neighbor Interpolation-Critical Assessment and New Contributions. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, April 2008. [Google Scholar]
- Musashi, J.P.; Pramoedyo, H.; Fitriani, R. Comparison of inverse distance weighted and natural neighbor interpolation method at air temperature data in Malang region. CAUCHY J. Mat. Murni Dan Apl. 2018, 5, 48–54. [Google Scholar] [CrossRef]
- Schulte, N.; Li, X.; Ghosh, J.K.; Fine, P.M.; Epstein, S.A. Responsive high-resolution air quality index mapping using model, regulatory monitor, and sensor data in real-time. Environ. Res. Lett. 2020, 15, 1040a7. [Google Scholar] [CrossRef]
- Etherington, T.R. Discrete natural neighbour interpolation with uncertainty using cross-validation error-distance fields. PeerJ Comput. Sci. 2020, 6, e282. [Google Scholar] [CrossRef] [PubMed]
- Bobach, T.; Umlauf, G. Natural Neighbor Interpolation and Order of Continuity. In Proceedings of the First Workshop of the DFG’s International Research Training Group “Visualization of Large and Unstructured Data Sets—Applications in Geospatial Planning, Modeling, and Engineering”, Dagstuhl, Germany, 14–16 June 2006; Hagen, H., Kerren, A., Dannenmann, P., Eds.; Gesellschaft für Informatik (GI): Bonn, Germany, 2006. [Google Scholar]
- Beutel, A.; Mølhave, T.; Agarwal, P.K. Natural neighbor interpolation based grid DEM construction using a GPU. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 172–181. [Google Scholar]
- Zou, B.; Wang, M.; Wan, N.; Wilson, J.G.; Fang, X.; Tang, Y. Spatial modeling of PM 2.5 concentrations with a multifactoral radial basis function neural network. Environ. Sci. Pollut. Res. 2015, 22, 10395–10404. [Google Scholar] [CrossRef] [PubMed]
- Losser, T.; Li, L.; Piltner, R. A spatiotemporal interpolation method using radial basis functions for geospatiotemporal big data. In Proceedings of the 2014 Fifth International Conference on Computing for Geospatial Research and Application, Washington, DC, USA, 4–6 August 2014. [Google Scholar]
- Sajjadi, S.A.; Zolfaghari, G.; Adab, H.; Allahabadi, A.; Delsouz, M. Measurement and modeling of particulate matter concentrations: Applying spatial analysis and regression techniques to assess air quality. MethodsX 2017, 4, 372–390. [Google Scholar] [CrossRef] [PubMed]
- Ha, Q.P.; Wahid, H.; Duc, H.; Azzi, M. Enhanced radial basis function neural networks for ozone level estimation. Neurocomputing 2015, 155, 62–70. [Google Scholar] [CrossRef]
- Chen, C.S.; Noorizadegan, A.; Young, D.L.; Chen, C.S. On the selection of a better radial basis function and its shape parameter in interpolation problems. Appl. Math. Comput. 2023, 442, 127713. [Google Scholar] [CrossRef]
- Huang, Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Selim, S.Z.; Ismail, M.A. K-means-type algorithms: A generalized convergence theorem and characterization of local optimality. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 81–87. [Google Scholar] [CrossRef]
- San, O.M.; Huynh, V.N.; Nakamori, Y. An alternative extension of the k-means algorithm for clustering categorical data. Int. J. Appl. Math. Comput. Sci. 2004, 14, 241–247. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Heo, T.; Kim, H.; Ko, J.; Doh, Y.; Park, J.; Jun, J.; Choi, H. Adaptive dual prediction scheme based on sensing context similarity for wireless sensor networks. Electron. Lett. 2014, 50, 467–469. [Google Scholar] [CrossRef]
- Intel Lab Data. Available online: http://db.csail.mit.edu/labdata/labdata.html (accessed on 3 July 2021).



| Sensor | CO2 | Temperature |
|---|---|---|
| Model | E + E | Sensirion |
| Range | 0~2000 ppm | −4~125 °C |
| Accuracy | <±50 ppm + 2% | ±0.3 °C ± 2% |
| Interface | I2C | I2C |
| Country of manufacture | Austria | Switzerland |
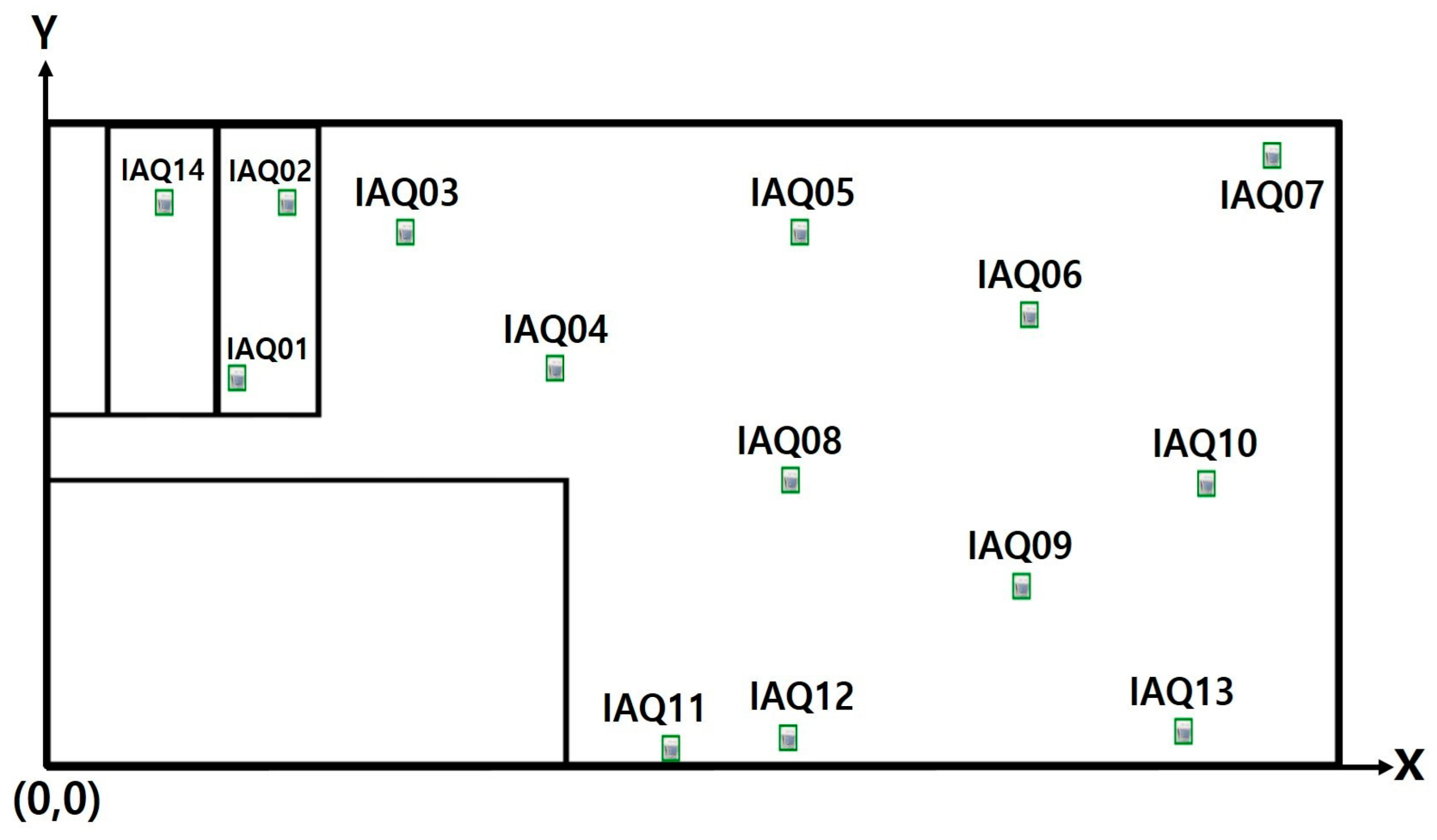
| Data Point | X Location (cm) | Y Location (cm) |
|---|---|---|
| IAQ01 | 100 | 243 |
| IAQ02 | 126 | 354 |
| IAQ03 | 187 | 335 |
| IAQ04 | 265 | 249 |
| IAQ05 | 392 | 335 |
| IAQ06 | 511 | 283 |
| IAQ07 | 637 | 384 |
| IAQ08 | 387 | 178 |
| IAQ09 | 507 | 111 |
| IAQ10 | 603 | 176 |
| IAQ11 | 325 | 8 |
| IAQ12 | 386 | 15 |
| IAQ13 | 591 | 19 |
| IAQ14 | 62 | 354 |
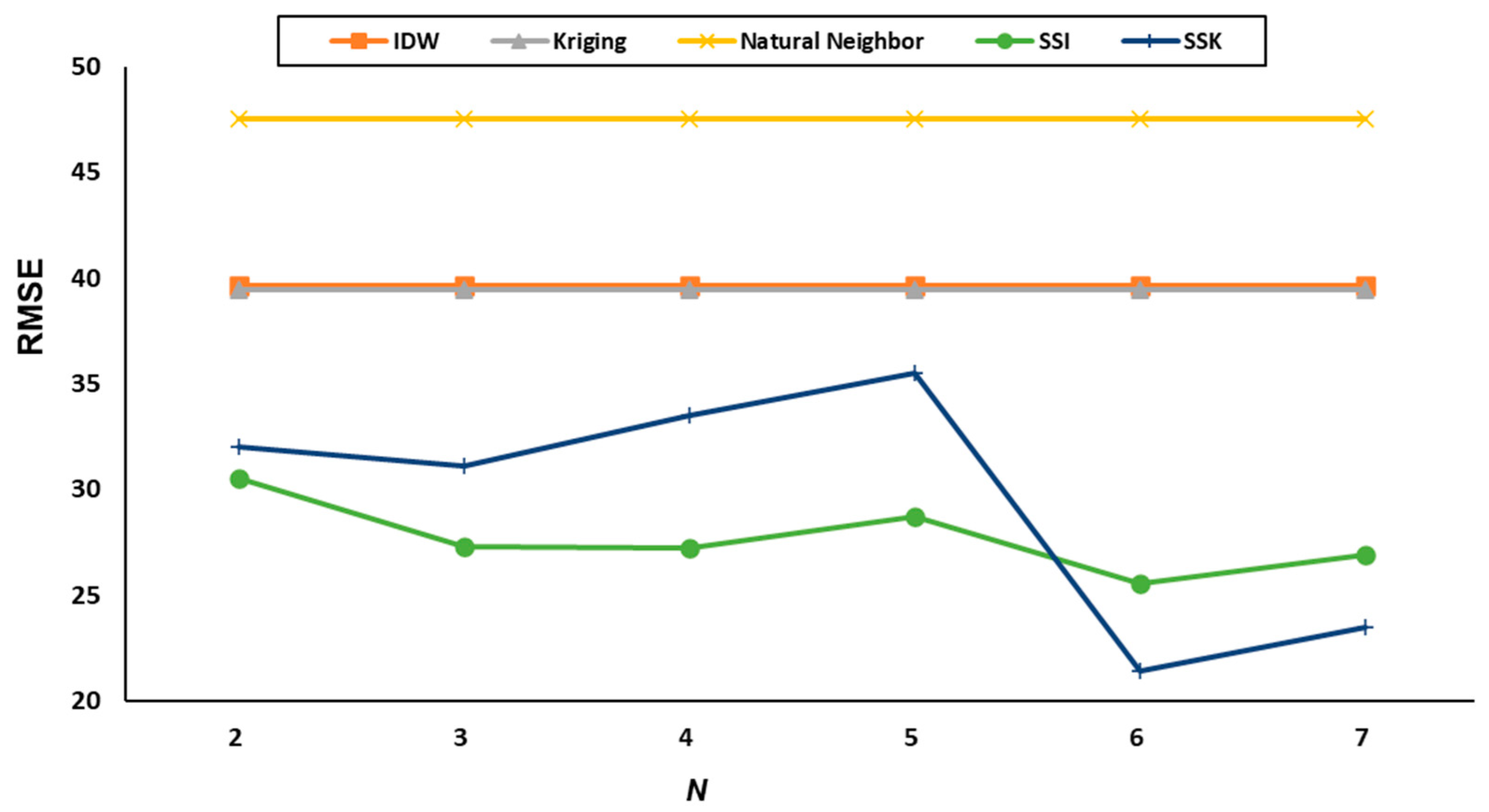
| N | K | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|---|
| 2 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 31.04 | 29.96 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 29.71 | 30.47 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 30.07 | 32.06 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 30.69 | 32.83 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 31.05 | 34.74 | |
| 3 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 25.79 | 26.54 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 26.37 | 27.22 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 26.97 | 29.65 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 28.56 | 33.79 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 28.87 | 38.17 | |
| 4 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 26.03 | 24.00 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 26.54 | 26.12 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 26.80 | 33.52 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 28.30 | 40.42 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 28.60 | 43.37 | |
| 5 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 26.59 | 24.36 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 28.32 | 28.94 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 29.12 | 34.86 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 29.56 | 42.54 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 29.93 | 46.72 | |
| 6 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 22.82 | 22.51 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 23.97 | 20.90 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 25.85 | 21.13 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 27.09 | 21.11 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 27.91 | 21.43 | |
| 7 | 3 | 43.26 | 41.42 | 59.62 | 241.94 | 25.79 | 25.54 |
| 6 | 39.80 | 38.50 | 41.66 | 177.38 | 25.44 | 23.41 | |
| 9 | 38.93 | 39.91 | 41.86 | 159.08 | 26.86 | 22.86 | |
| 12 | 38.11 | 38.36 | 47.18 | 156.94 | 27.71 | 22.52 | |
| 14 | 38.00 | 39.10 | 47.18 | 155.20 | 28.55 | 22.96 |
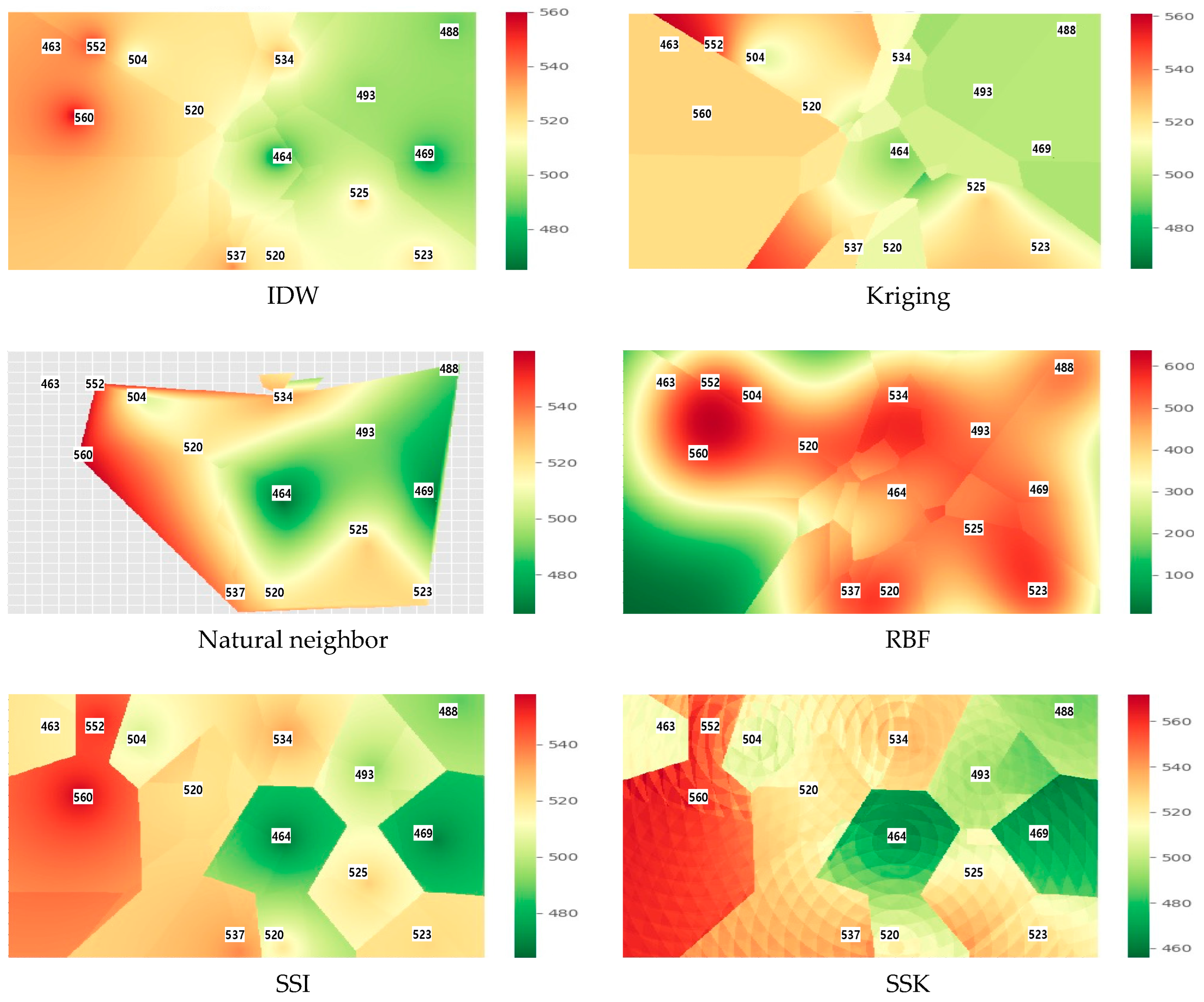
| Method | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|
| RMSE | 45.44 | 46.04 | 43.98 | 175.42 | 28.84 | 26.66 |
| MAE | 38.84 | 37.96 | 38.78 | 166.43 | 23.35 | 21.71 |
| MAPE | 10.21 | 9.94 | 10.97 | 39.12 | 10.13 | 8.00 |
| R2 | 0.40 | 0.42 | 0.34 | 0.07 | 0.51 | 0.57 |
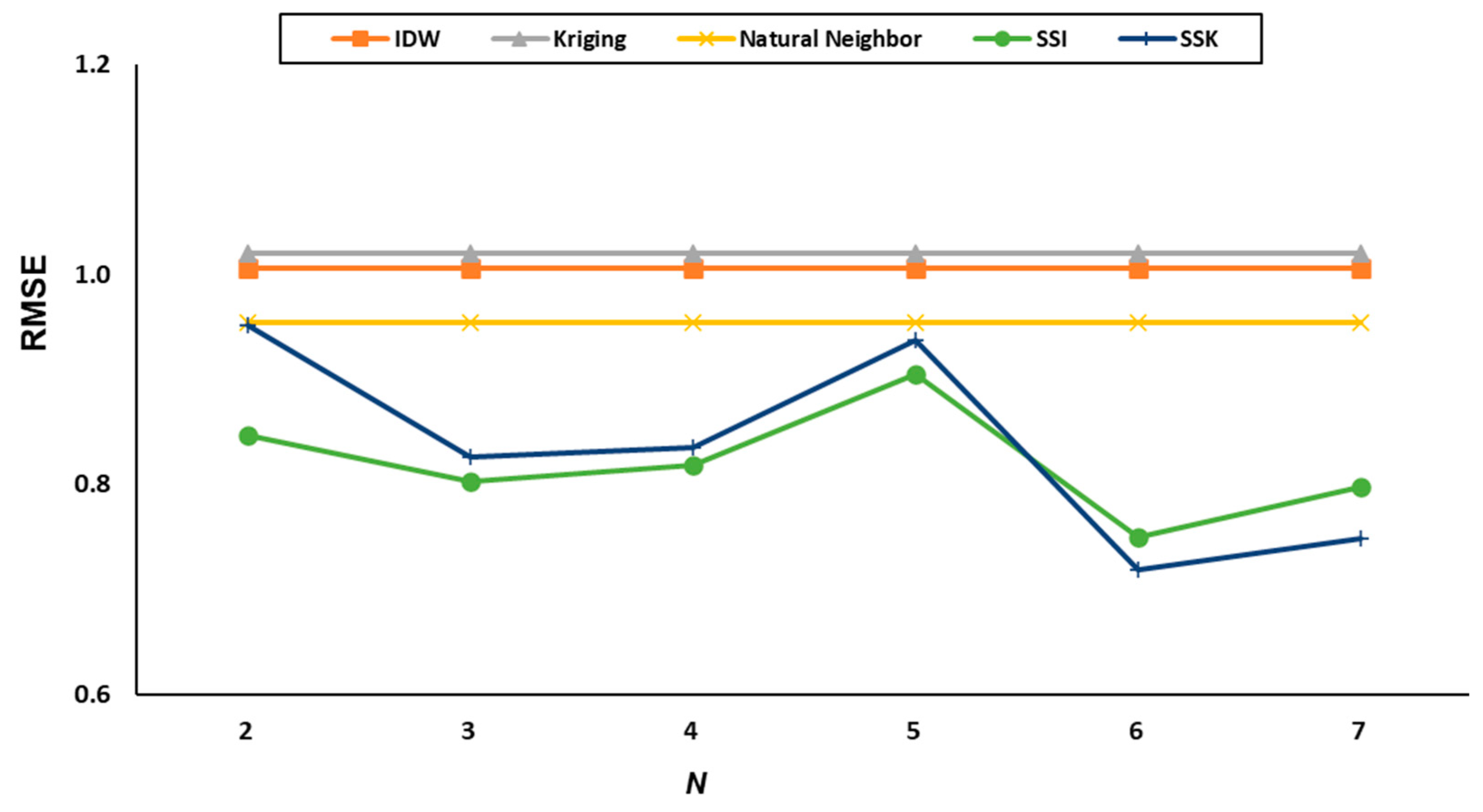
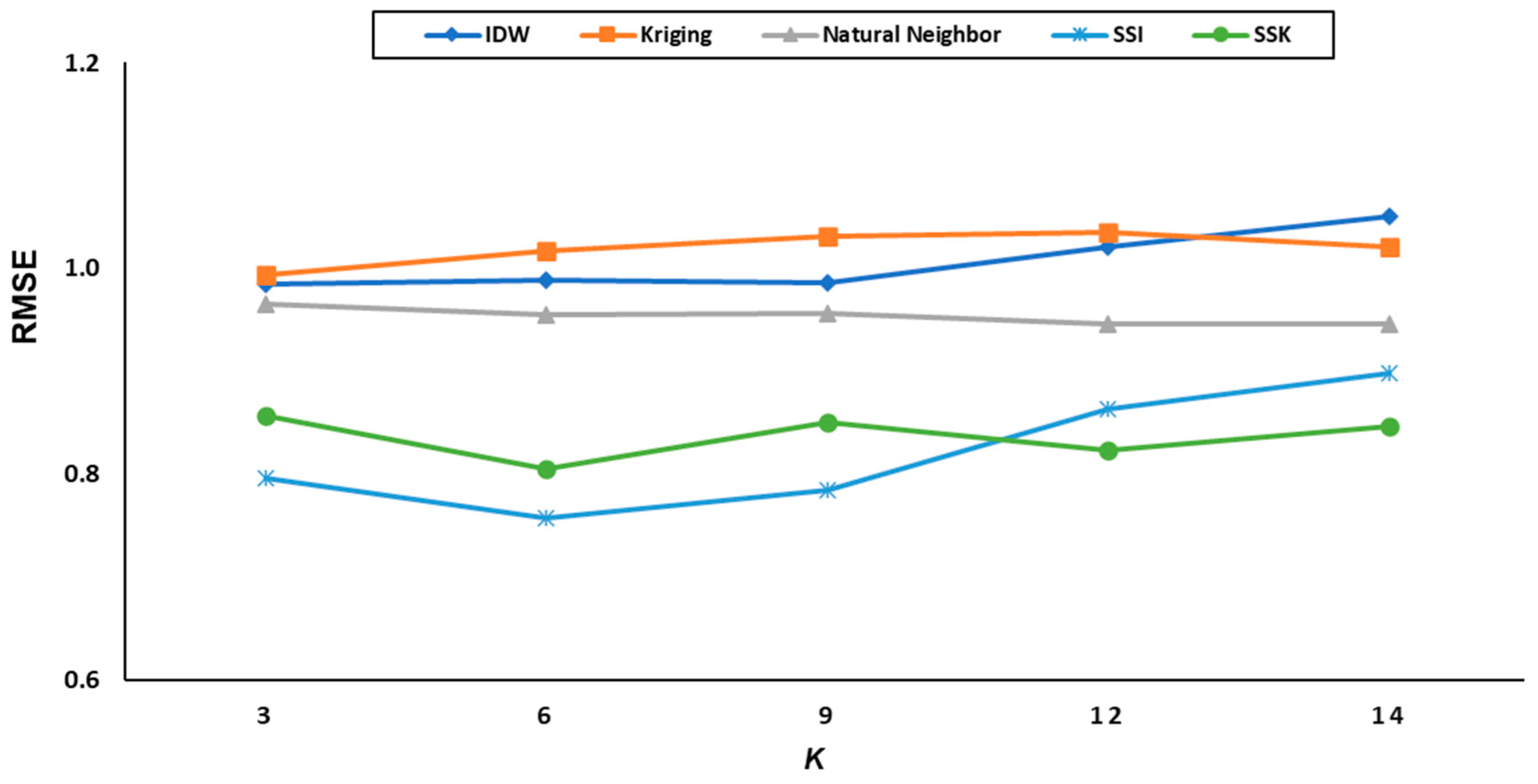
| N | K | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|---|
| 2 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.88 | 0.94 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.83 | 0.88 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.83 | 0.99 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.85 | 0.95 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.85 | 1.00 | |
| 3 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.78 | 0.86 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.75 | 0.81 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.77 | 0.83 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.84 | 0.81 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.87 | 0.83 | |
| 4 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.81 | 0.88 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.77 | 0.81 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.78 | 0.84 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.85 | 0.82 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.89 | 0.83 | |
| 5 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.91 | 0.99 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.83 | 0.90 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.85 | 0.97 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.94 | 0.90 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.98 | 0.92 | |
| 6 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.69 | 0.73 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.66 | 0.72 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.72 | 0.72 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.81 | 0.71 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.86 | 0.72 | |
| 7 | 3 | 0.98 | 0.99 | 0.96 | 12.86 | 0.71 | 0.74 |
| 6 | 0.99 | 1.02 | 0.95 | 10.21 | 0.71 | 0.71 | |
| 9 | 0.99 | 1.03 | 0.96 | 8.15 | 0.76 | 0.76 | |
| 12 | 1.02 | 1.03 | 0.95 | 7.90 | 0.88 | 0.76 | |
| 14 | 1.05 | 1.02 | 0.95 | 8.09 | 0.94 | 0.78 |
| Method | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|
| RMSE | 1.07 | 1.09 | 1.06 | 7.64 | 0.81 | 0.88 |
| MAE | 0.91 | 0.90 | 0.93 | 7.25 | 0.66 | 0.72 |
| MAPE | 4.66 | 4.78 | 4.13 | 35.25 | 4.02 | 4.37 |
| R2 | 0.36 | 0.35 | 0.36 | 0.02 | 0.43 | 0.41 |
| Method | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|
| RMSE | 2.38 | 2.45 | 2.44 | 5.90 | 1.86 | 2.90 |
| MAE | 1.92 | 2.13 | 2.11 | 4.66 | 1.78 | 2.43 |
| MAPE | 10.19 | 12.20 | 10.77 | 35.09 | 9.01 | 14.93 |
| R2 | 0.72 | 0.67 | 0.74 | 0.19 | 0.77 | 0.73 |
| Method | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|
| RMSE | 1.85 | 1.85 | 1.77 | 7.57 | 1.55 | 1.60 |
| MAE | 1.52 | 1.39 | 1.43 | 5.57 | 1.23 | 1.26 |
| MAPE | 6.21 | 6.13 | 4.72 | 12.83 | 4.19 | 4.25 |
| R2 | 0.86 | 0.88 | 0.89 | 0.32 | 0.93 | 0.93 |
| Method | IDW | Kriging | Natural Neighbor | RBF | SSI | SSK |
|---|---|---|---|---|---|---|
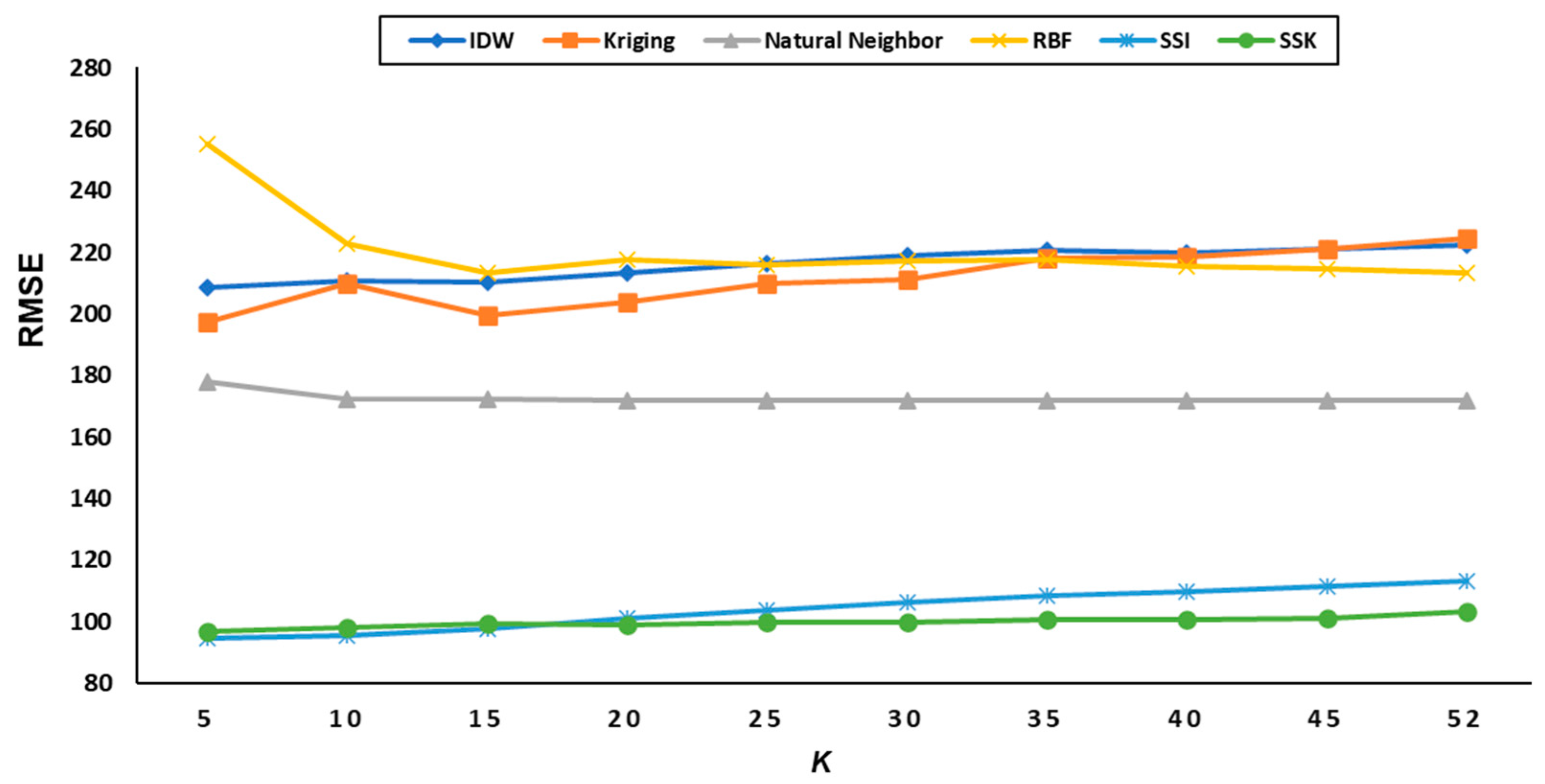
| RMSE | 170.22 | 161.47 | 139.71 | 175.88 | 84.46 | 90.47 |
| MAE | 137.10 | 122.95 | 112.15 | 132.32 | 64.72 | 68.41 |
| MAPE | 17.08 | 15.75 | 14.65 | 18.24 | 8.64 | 9.35 |
| R2 | 0.49 | 0.50 | 0.69 | 0.44 | 0.75 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; Han, S.; Choi, H. Enhancing Indoor Air Quality Estimation: A Spatially Aware Interpolation Scheme. ISPRS Int. J. Geo-Inf. 2023, 12, 347. https://doi.org/10.3390/ijgi12080347
Jung S, Han S, Choi H. Enhancing Indoor Air Quality Estimation: A Spatially Aware Interpolation Scheme. ISPRS International Journal of Geo-Information. 2023; 12(8):347. https://doi.org/10.3390/ijgi12080347
Chicago/Turabian StyleJung, Seungwoog, Seungwan Han, and Hoon Choi. 2023. "Enhancing Indoor Air Quality Estimation: A Spatially Aware Interpolation Scheme" ISPRS International Journal of Geo-Information 12, no. 8: 347. https://doi.org/10.3390/ijgi12080347
APA StyleJung, S., Han, S., & Choi, H. (2023). Enhancing Indoor Air Quality Estimation: A Spatially Aware Interpolation Scheme. ISPRS International Journal of Geo-Information, 12(8), 347. https://doi.org/10.3390/ijgi12080347








