Comparison of Soft Indicator and Poisson Kriging for the Noise-Filtering and Downscaling of Areal Data: Application to Daily COVID-19 Incidence Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. COVID-19 Incidence Data
2.2. Poisson Kriging
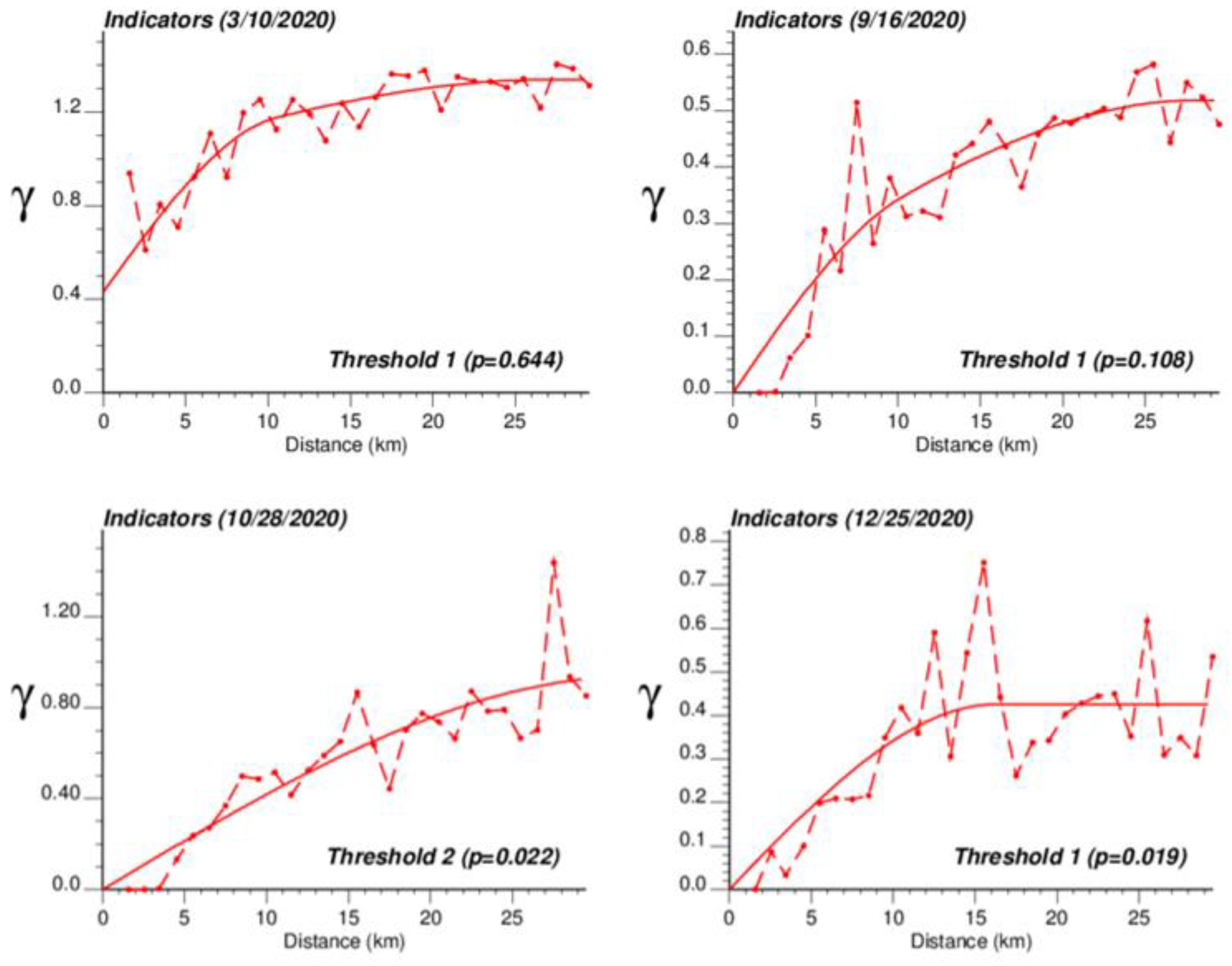
2.3. Soft Indicator Kriging
- Compute K = 50 percentiles of the frequency distribution of M = 581 municipality rates, F(.), as: =F-1() with where is the proportion of rates no greater than the minimum observed rate . This formulation avoids obtaining a series of zero-valued thresholds for days where no cases were recorded in many municipalities.
- For each municipality :
- Create a binomial distribution Bi (,) characterized by the daily incidence rate and the population within that geographical unit. This step allows one to capture the uncertainty attached to the observed rate , which can be substantial for municipalities that are sparsely populated (i.e., small population size
- Discretize the probability distribution using the set of K thresholds calculated at step 1: where is the cumulative binomial distribution for the α-th municipality. The quantity represents the probability that the underlying rate is no greater than the threshold for municipality .
- For each threshold :
- Calculate and model the population-weighted indicator semivariogram as:where N (h) is the number of pairs of municipalities (,) whose population-weighted centroids are separated by the vector h [19].
- Use this model and ATP ordinary kriging to disaggregate the probabilities (i.e., soft indicator data) at the nodes of a 1 km spacing grid discretizing the country (total number of nodes is L = 31,557).
- For each node of the discretization grid:
- Assemble the K estimated probabilities into a probability distribution.
- Correct for order relation deviations [15] as: (1) each probability can be negative or larger than 1 since it was estimated by ATP kriging (same potential issues as PK), and (2) the set of K probabilities were estimated separately, with no guarantee that .
- Create a continuous distribution using linear interpolation between thresholds, as well as between the first (last threshold) and the minimum (maximum) observed rate.
- Calculate the mean and variance of the local probability distribution (ccdf).
- For each municipality :
- Estimate each of the K probabilities as the population-weighted average of the corresponding probabilities for all nodes that fall within that geographical unit, i.e.,with if and 0 otherwise. is the population size within the raster cell centered on node while is the population for the α-th municipality. Each probability can be interpreted as the population-weighted fraction of the α-th municipality area, , where the threshold is not exceeded.
- Assemble the K estimated probabilities into a probability distribution.
- Correct for order relation deviations and create a continuous distribution using linear interpolation between thresholds, as well as between the first (last threshold) and the minimum (maximum) observed rate.
- Calculate the mean and variance of the local probability distribution (ccdf).
2.4. Software
3. Results
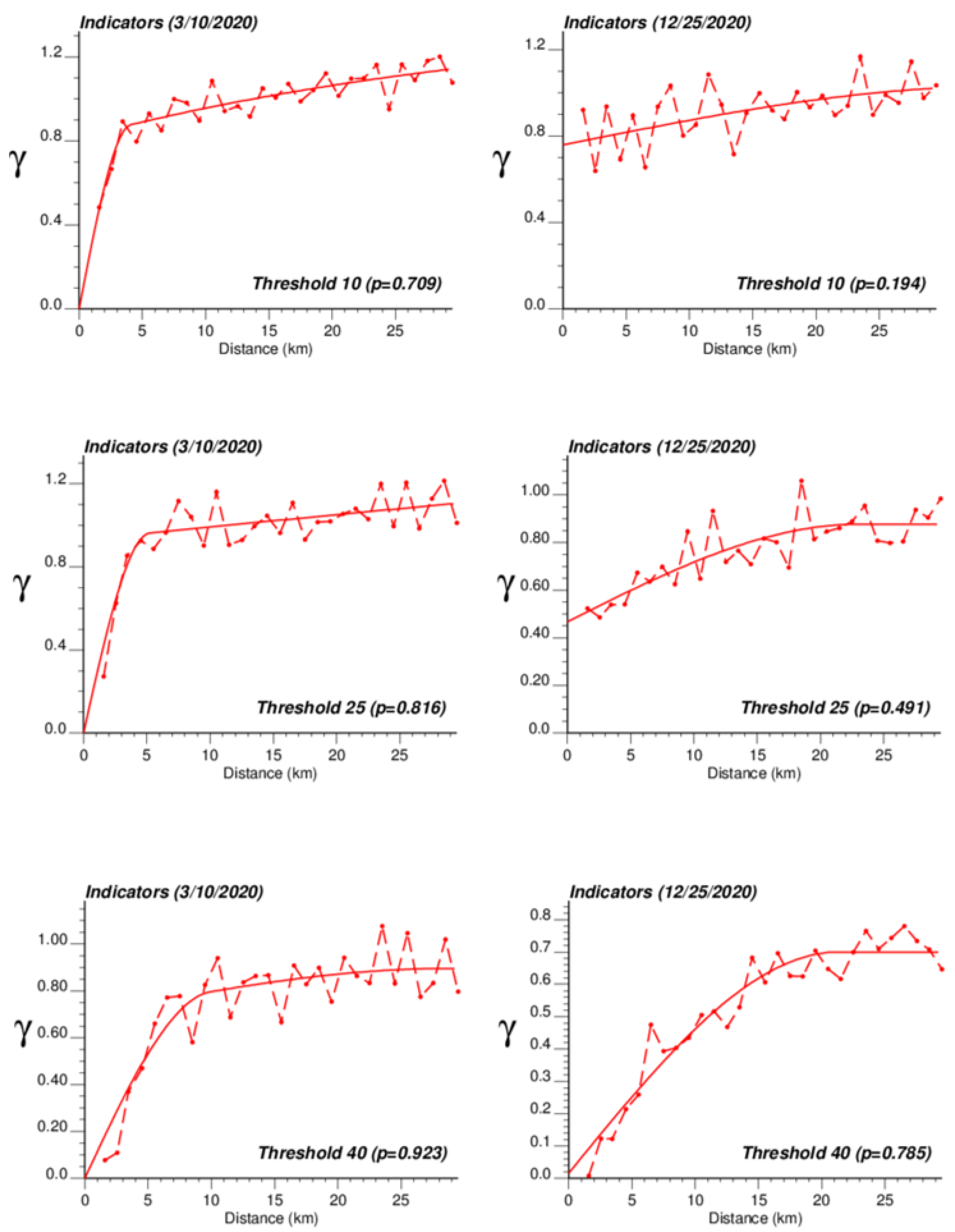
3.1. Temporal Trend and Spatial Patterns
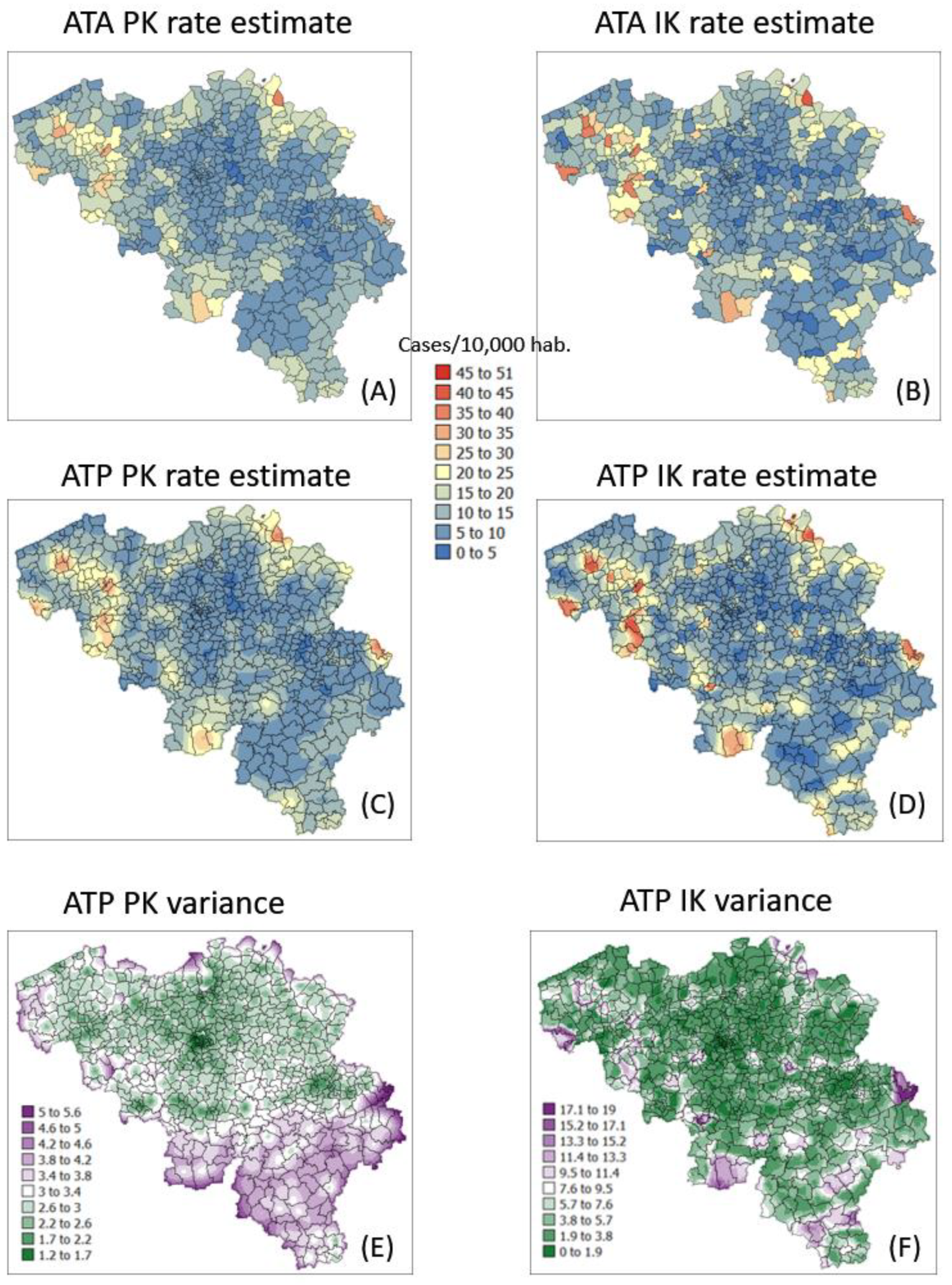
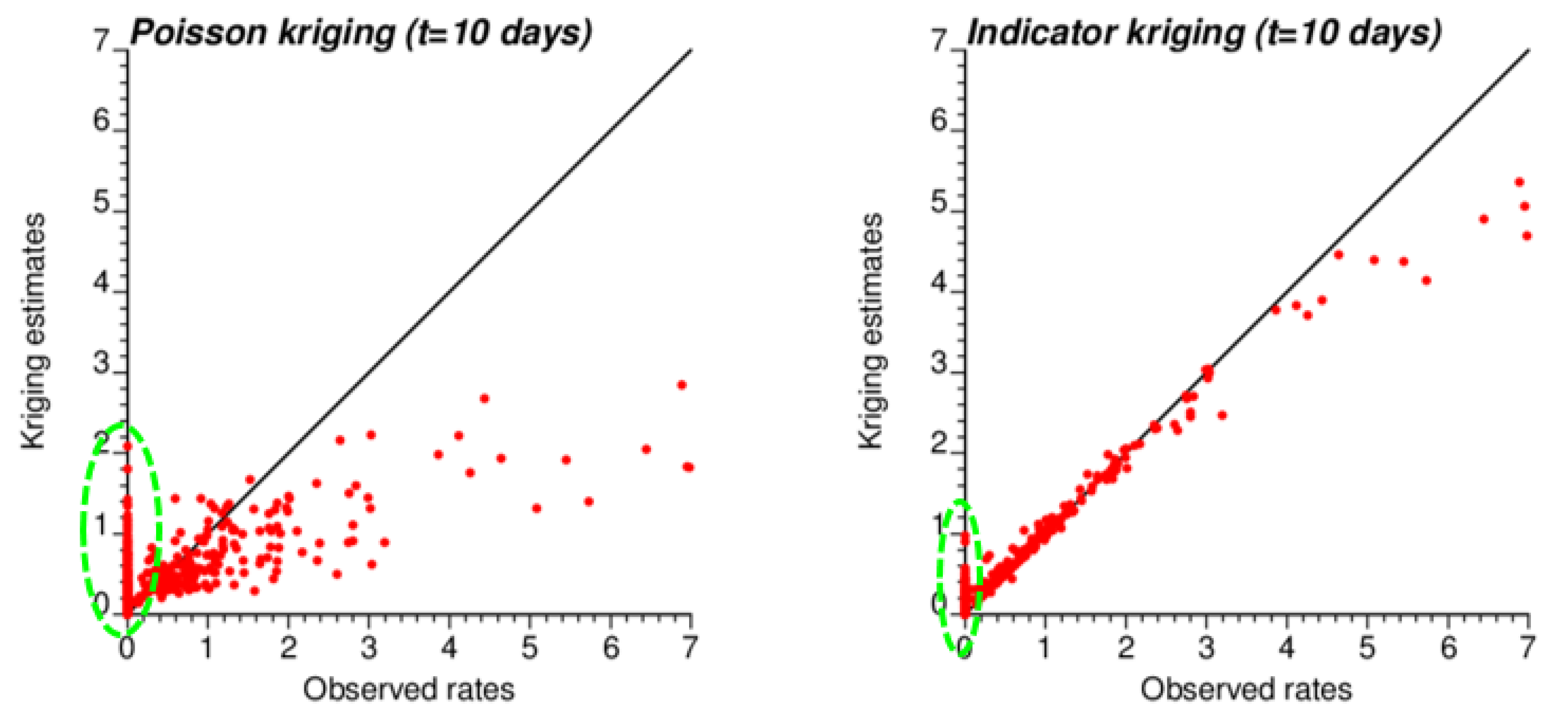
3.2. Kriging Estimates
3.3. Kriging Variances
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goovaerts, P. Medical geography: A promising field of application for geostatistics. Math. Geosci. 2009, 41, 243–264. [Google Scholar] [CrossRef]
- Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Gregorio, D.; DeChello, L.; Samociuk, H.; Kulldorff, M. Lumping or splitting: Seeking the preferred areal unit for health geography studies. Int. J. Health Geogr. 2005, 4, 6. [Google Scholar] [CrossRef]
- Meliker, J.R.; Jacquez, G.M.; Goovaerts, P.; Copeland, G.; Yassine, M. Spatial cluster analysis of early-stage breast cancer: A method for public health practice using cancer registry data? Cancer Causes Control. 2009, 20, 1061–1069. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical analysis of disease data: Accounting for spatial support and population density in the isopleth mapping of cancer mortality risk using area-to-point Poisson kriging. Int. J. Health Geogr. 2006, 5, 52. [Google Scholar] [CrossRef]
- Monestiez, P.; Dubroca, L.; Bonnin, E.; Durbec, J.P.; Guinet, C. Geostatistical modelling of spatial distribution of Balenoptera physalus in the Northwestern Mediterranean Sea from sparse count data and heterogeneous observation efforts. Ecol. Model. 2006, 193, 615–628. [Google Scholar] [CrossRef]
- Ali, M.; Goovaerts, P.; Nazia, N.; Haq, M.Z.; Yunus, M.; Emch, M. Application of Poisson kriging to the mapping of cholera and dysentery incidence in an endemic area of Bangladesh. Int. J. Health Geogr. 2006, 5, 45. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Goovaerts, P.; Gebreab, S. How does Poisson kriging compare to the popular BYM model for mapping disease risks? Int. J. Health Geogr. 2008, 7, 6. [Google Scholar] [CrossRef] [PubMed]
- Kerry, R.; Vowles, M.; Goovaerts, P.; Ingram, B. Spatial analysis of drug poisoning deaths in the American West, particularly Utah. Int. J. Drug Policy 2016, 33, 44–55. [Google Scholar] [CrossRef]
- Gotway, C.A.; Young, L.J. Combining Incompatible Spatial Data. J. Am. Stat. Assoc. 2002, 97, 632–648. [Google Scholar] [CrossRef]
- Kyriakidis, P. A geostatistical framework for area-to-point spatial interpolation. Geogr. Anal. 2004, 36, 259–289. [Google Scholar] [CrossRef]
- Alvo, M.; Mu, J. COVID-19 Data Analysis Using Bayesian Models and Nonparametric Geostatistical Models. Mathematics 2023, 11, 1359. [Google Scholar] [CrossRef]
- Azevedo, L.; Pereira, M.J.; Ribeiro, M.C.; Soares, A. Geostatistical COVID-19 infection risk maps for Portugal. Int. J. Health Geogr. 2020, 19, 25. [Google Scholar] [CrossRef]
- Stach, A. Temporal variation of spatial autocorrelation of COVID-19 cases identified in Poland during the year from the beginning of the pandemic. Geogr. Pol. 2021, 94, 355–380. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Yoo, E.-H.; Kyriakidis, P.C. Area-to-point Kriging with inequality-type data. J. Geogr. Syst. 2006, 8, 357–390. [Google Scholar] [CrossRef]
- Kerry, R.; Goovaerts, P.; Smit, I.; Ingram, B.R. A comparison of multiple indicator kriging and area-to-point Poisson kriging for mapping patterns of herbivore species abundance in Kruger National Park, South Africa. Int. J. Geogr. Inf. Sci. 2013, 27, 47–67. [Google Scholar] [CrossRef]
- Aidoo, E.N.; Mueller, U.; Goovaerts, P.; Hyndes, G. Evaluation of geostatistical estimators and their applicability to characterize the spatial patterns of recreational fishing catch rates. Fish. Res. 2015, 168, 20–32. [Google Scholar] [CrossRef] [PubMed]
- Sciensano. Epistat—COVID-19 Monitoring. 2021. Available online: https://epistat.wiv-isp.be/covid/ (accessed on 10 June 2021).
- Statbel. Structure of the Population. 2023. Available online: https://statbel.fgov.be/en/themes/population/structure-population#documents (accessed on 24 May 2021).
- Goovaerts, P. Kriging and semivariogram deconvolution in presence of irregular geographical units. Math. Geosci. 2008, 40, 101–128. [Google Scholar] [CrossRef]
- Jacquez, G.M.; Goovaerts, P.; Kaufmann, A.; Rommel, R. SpaceStat 4.0 User Manual: Software for the Space-Time Analysis of Dynamic Complex. Systems, 4th ed.; BioMedware: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Goovaerts, P. AUTO-IK: A 2D indicator kriging program for the automated non-parametric modeling of local uncertainty in earth sciences. Comput. Geosci. 2009, 35, 1255–1270. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, C.L.; Mangen, M.J.J.; Plass, D.; Havelaar, A.H.; Brooke, R.J.; Kramarz, P.; Peterson, K.L.; Stuurman, A.L.; Cassini, A.; Fèvre, E.M.; et al. Measuring underreporting and under-ascertainment in infectious disease datasets: A comparison of methods. BMC Public Health 2014, 14, 147. [Google Scholar] [CrossRef] [PubMed]
- Rollier, M.; Miranda, G.H.B.; Vergeynst, J.; Meys, J.; Alleman, T.; Baetens, J.M. Mobility and the spatial spread of sars-cov-2 in Belgium. Math. Biosci. 2023, 360, 108957. [Google Scholar] [CrossRef] [PubMed]
- Aral, N.; Bakir, H. Spatiotemporal analysis of COVID-19 in Turkey. Sustain. Cities Soc. 2022, 76, 103421. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, D.; Dickson, M.M.; Espa, G.; Santi, F. Modelling and predicting the spatio-temporal spread of COVID-19 in Italy. BMC Infect. Dis. 2020, 20, 700. [Google Scholar] [CrossRef]
- Maiti, A.; Zhang, Q.; Sannigrahi, S.; Pramanik, S.; Chakraborti, S.; Cerda, A.; Pilla, F. Exploring spatiotemporal effects of the driving factors on COVID-19 incidences in the contiguous United States. Sustain. Cities Soc. 2021, 68, 102784. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, C.V.; Journel, A.G. GSLIB Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Lin, W.-C.; Lin, Y.-P.; Wang, Y.-C.; Chang, T.-K.; Chiang, L.-C. Assessing and Mapping Spatial Associations among Oral Cancer Mortality Rates, Concentrations of Heavy Metals in Soil, and Land Use Types Based on Multiple Scale Data. Int. J. Environ. Res. Public Health 2014, 11, 2148–2168. [Google Scholar] [CrossRef]
- Liu, X.; Kyriakidis, P.C.; Goodchild, M.F. Population density estimation using regression and area-to-point residual Kriging. Int. J. Geogr. Inf. Sci. 2008, 22, 431–447. [Google Scholar] [CrossRef]
- Kerry, R.; Goovaerts, P.; Rawlins, B.G.; Marchant, B.P. Disaggregation of legacy soil data using area to point kriging for mapping soil organic carbon at the regional scale. Geoderma 2012, 170, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Ge, Y.; Wang, J.; Heuvelink, G.B.; Wang, L. Geographically weighted Area-to-Point regression kriging for spatial downscaling in remote sensing. Remote Sens. 2018, 10, 579. [Google Scholar] [CrossRef]
- Weaver, A.K.; Head, J.R.; Gould, C.F.; Carlton, E.J.; Remais, J.V. Environmental factors influencing COVID-19 incidence and severity. Annu. Rev. Public Health 2022, 43, 271–291. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wu, X.; Li, C.; Han, J.; Yin, J. The impact of geo-environmental factors on global COVID-19 transmission: A review of evidence and methodology. Sci. Total Environ. 2022, 826, 154182. [Google Scholar] [CrossRef]
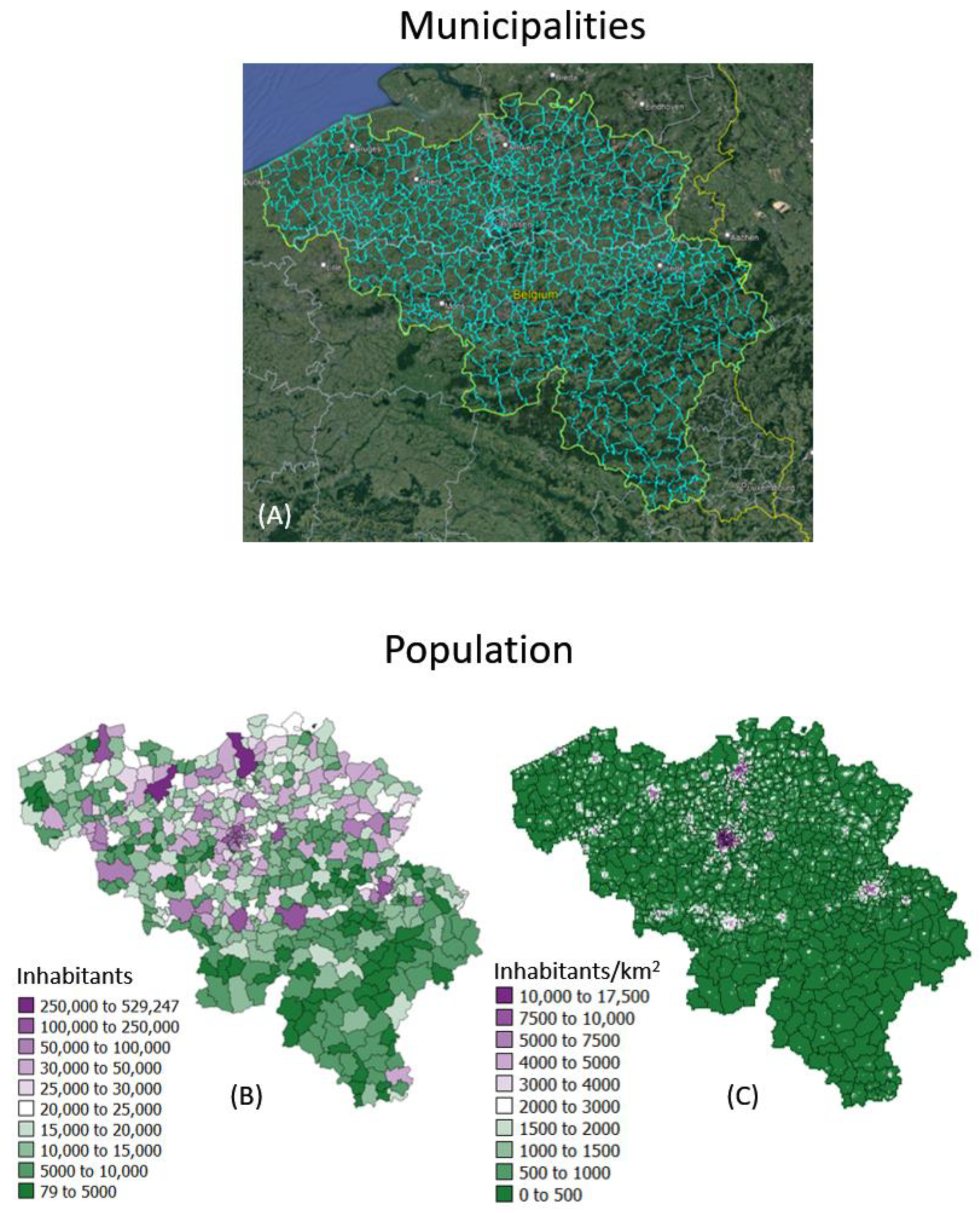
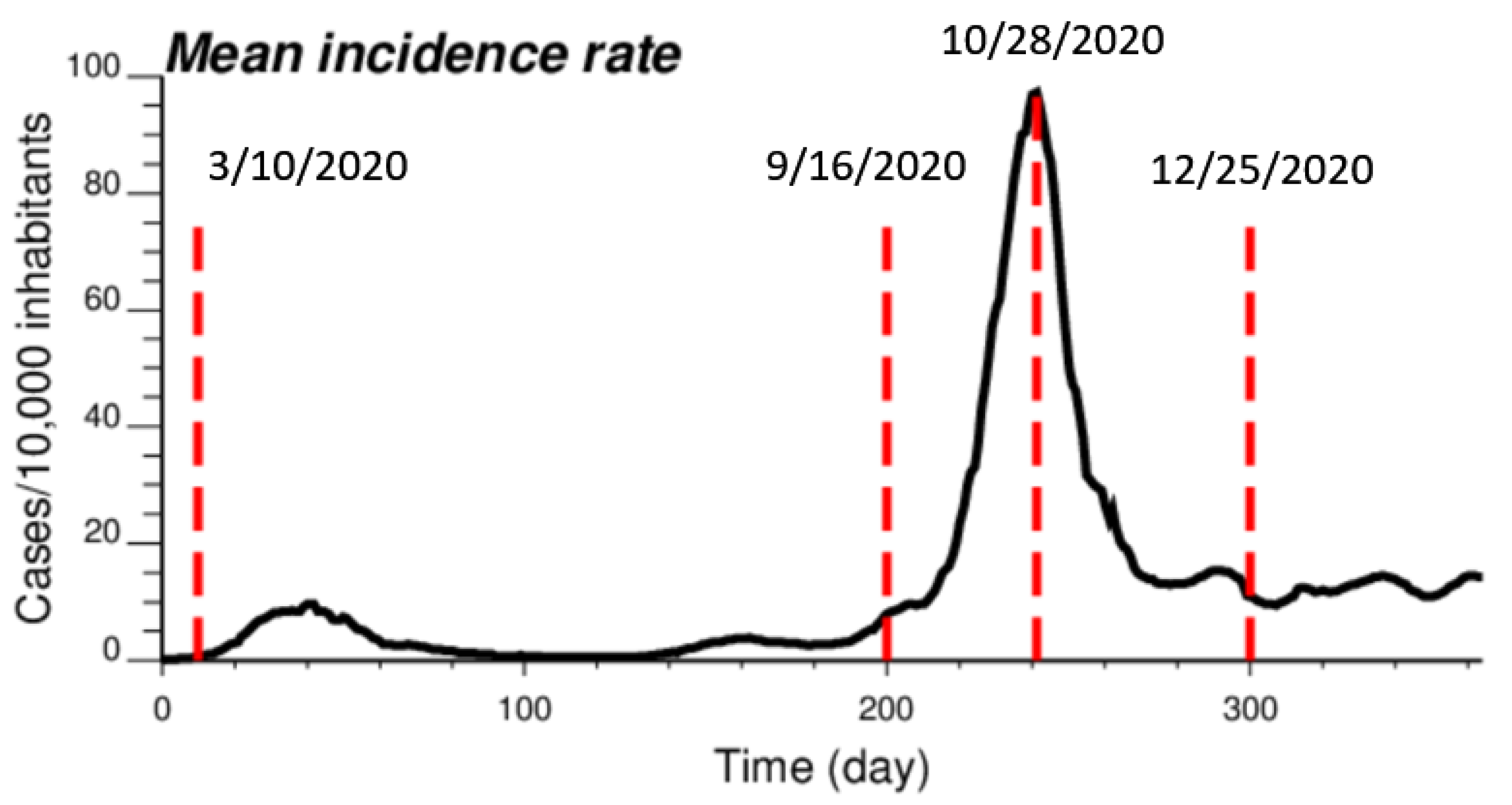
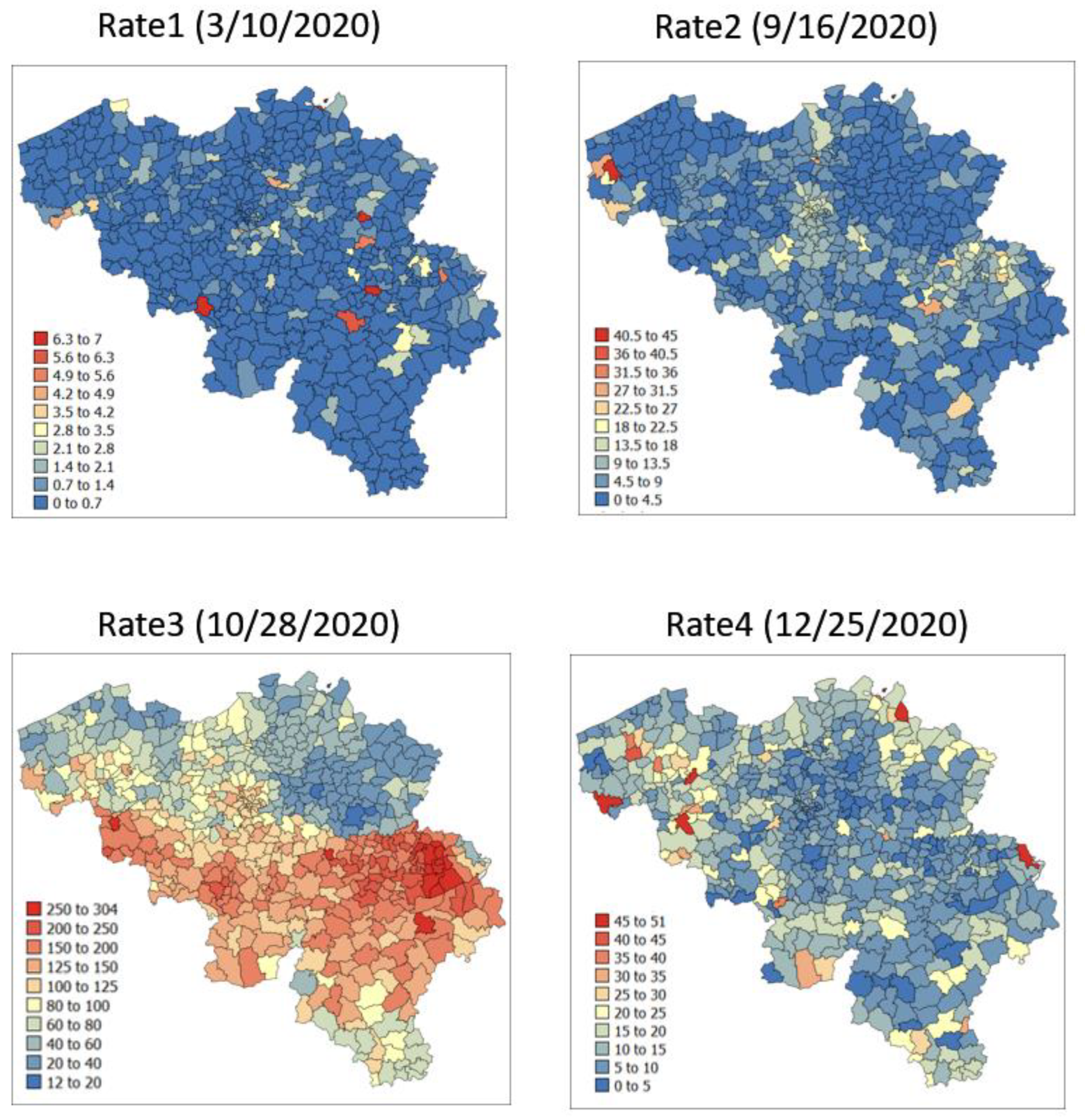
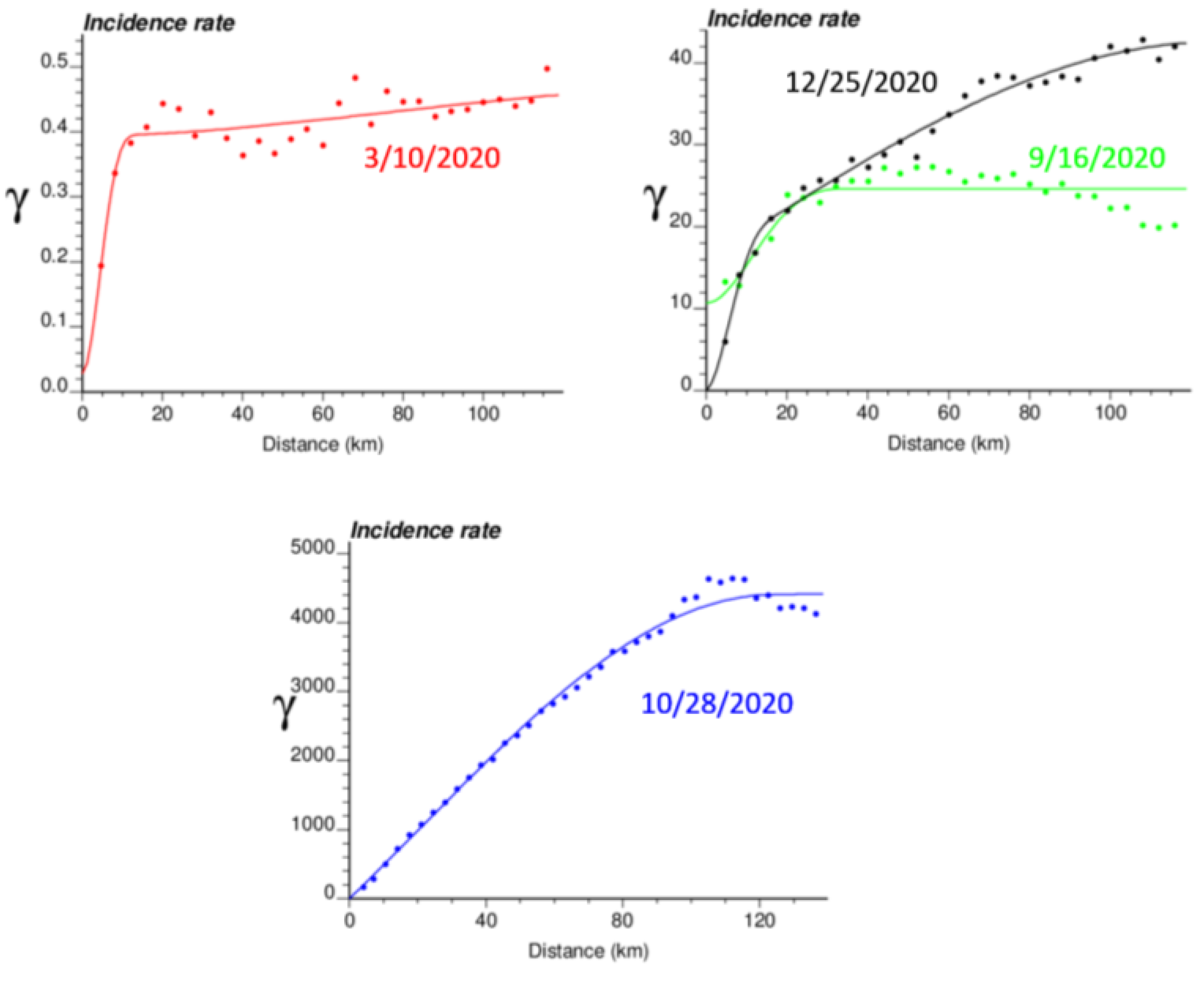

| Dates | ||||
|---|---|---|---|---|
| Statistics | 10 March 2020 (t = 10) | 16 September 2020 (t = 200) | 28 October 2020 (t = 242) | 25 December 2020 (t = 300) |
| Mean | 0.444 | 6.049 | 105.6 | 11.66 |
| Variance | 0.932 | 31.97 | 3573 | 55.65 |
| Minimum | 0.0 | 0.0 | 12.98 | 0.0 |
| Maximum | 6.981 | 45.59 | 303.8 | 50.84 |
| % null values | 64.4 | 10.8 | 0.0 | 1.9 |
| Dates | ||||
|---|---|---|---|---|
| Variance | 10 March 2020 (t = 10) | 16 September 2020 (t = 200) | 28 October 2020 (t = 242) | 25 December 2020 (t = 300) |
| ATA PK | 0.194 | 15.91 | 3219 | 25.10 |
| ATA IK | 0.754 | 25.77 | 3575 | 49.07 |
| ATP PK | 0.190 | 10.49 | 3031 | 26.95 |
| ATP IK | 0.559 | 16.73 | 3225 | 45.81 |
| Dates | ||||
|---|---|---|---|---|
| Correlation | 10 March 2020 (t = 10) | 16 September 2020 (t = 200) | 28 October 2020 (t = 242) | 25 December 2020 (t = 300) |
| ATA PK vs. rate | 0.645 | 0.846 | 0.989 | 0.851 |
| ATA IK vs. rate | 0.883 | 0.976 | 0.998 | 0.997 |
| PK vs. IK (ATA) | 0.645 | 0.889 | 0.989 | 0.862 |
| PK vs. IK (ATP) | 0.849 | 0.875 | 0.980 | 0.907 |
| Dates | ||||
|---|---|---|---|---|
| Order Relations | 10 March 2020 (t = 10) | 16 September 2020 (t = 200) | 28 October 2020 (t = 242) | 25 December 2020 (t = 300) |
| Freq. (ATP) | 0.798 | 0.791 | 0.427 | 0.708 |
| Magn. (ATP) | 0.044 | 0.042 | 0.051 | 0.049 |
| Freq. (ATA) | 0.0 | 0.0 | 0.0 | 0.0 |
| Magn. (ATA) | 0.0 | 0.0 | 0.0 | 0.0 |
| Dates | ||||
|---|---|---|---|---|
| Correlation | 10 March 2020 (t = 10) | 16 September 2020 (t = 200) | 28 October 2020 (t = 242) | 25 December 2020 (t = 300) |
| ATA | ||||
| PKstd vs. IKstd | −0.176 | 0.379 | 0.728 | 0.721 |
| PKstd vs. PKest | −0.197 | −0.053 | 0.259 | 0.115 |
| IKstd vs. IKest | 0.986 | 0.657 | 0.724 | 0.619 |
| PKstd vs. Population | −0.908 | −0.933 | −0.980 | −0.919 |
| IKstd vs. Population | 0.175 | −0.339 | −0.737 | −0.689 |
| ATP | ||||
| PKstd vs. IKstd | −0.106 | 0.414 | 0.499 | 0.508 |
| PKstd vs. PKest | −0.208 | −0.040 | 0.257 | 0.116 |
| IKstd vs. IKest | 0.952 | 0.571 | 0.631 | 0.585 |
| PKstd vs. Population | −0.665 | −0.711 | −0.680 | −0.669 |
| IKstd vs. Population | 0.040 | −0.302 | −0.384 | −0.390 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goovaerts, P.; Hermans, T.; Goossens, P.F.; Van De Vijver, E. Comparison of Soft Indicator and Poisson Kriging for the Noise-Filtering and Downscaling of Areal Data: Application to Daily COVID-19 Incidence Rates. ISPRS Int. J. Geo-Inf. 2023, 12, 328. https://doi.org/10.3390/ijgi12080328
Goovaerts P, Hermans T, Goossens PF, Van De Vijver E. Comparison of Soft Indicator and Poisson Kriging for the Noise-Filtering and Downscaling of Areal Data: Application to Daily COVID-19 Incidence Rates. ISPRS International Journal of Geo-Information. 2023; 12(8):328. https://doi.org/10.3390/ijgi12080328
Chicago/Turabian StyleGoovaerts, Pierre, Thomas Hermans, Peter F. Goossens, and Ellen Van De Vijver. 2023. "Comparison of Soft Indicator and Poisson Kriging for the Noise-Filtering and Downscaling of Areal Data: Application to Daily COVID-19 Incidence Rates" ISPRS International Journal of Geo-Information 12, no. 8: 328. https://doi.org/10.3390/ijgi12080328
APA StyleGoovaerts, P., Hermans, T., Goossens, P. F., & Van De Vijver, E. (2023). Comparison of Soft Indicator and Poisson Kriging for the Noise-Filtering and Downscaling of Areal Data: Application to Daily COVID-19 Incidence Rates. ISPRS International Journal of Geo-Information, 12(8), 328. https://doi.org/10.3390/ijgi12080328








