Abstract
Unlike car navigation, where almost all vehicles can traverse every route, one route might not be optimal or even suitable for all pedestrians. Route geometry information, including tortuosity, twists and turns along roads, junctions, and road slopes, among others, matters a great deal for specific types of pedestrians, particularly those with limited mobility, such as wheelchair users and older adults. Offering practical routing services to these users requires that pedestrian navigation systems provide further information on route geometry. Therefore, this article proposes a novel method for extracting and analyzing the geometry properties of the shortest pedestrian paths, with a focus on open geospatial data across four aspects: (a) similarity, (b) route curviness, (c) road turns and intersections, and (d) road gradients. Deriving from the Hausdorff distance, a metric called the “dissimilarity ratio” was developed, allowing us to determine whether pairs of routes show any tendencies to be similar to each other. Using the “sinuosity index”, a segment-based technique quantified the route curviness based on the number and degree of the road turns along the route. Moreover, relying upon open elevation data, the road gradients were extracted to identify routes offering smoother motion and better accessibility. Lastly, the road turns and intersections were investigated as pedestrian convenience and safety indicators. A local government area of Greater Sydney in Australia was chosen as the case study. The analysis was implemented on OpenStreetMap (OSM) shortest pedestrian paths against Google Maps as a benchmark for real-world commercial applications. The similarity analysis indicated that over 90% of OSM routes were identical or roughly similar to Google Maps. In addition, while Spearman’s rank correlation showed a direct relationship between route curviness and route length, = 0.92, p < 0.001, OSM, on average, witnessed more tortuous routes and, consequently, shorter straight roads between turns. However, OSM routes could be more suitable for pedestrians when the frequency of intersections and road slopes are at the center of attention. Finally, the devised metrics in this study, including the dissimilarity ratio and sinuosity index, showed their practicability in translating raw values into meaningful indicators.
1. Introduction
For a long time, calculating the shortest (or fastest) path between locations A and B has been the center of pedestrian navigation systems’ attention. Nonetheless, “alternative routing” suggests that distance (or travel time) is not the only factor affecting the pedestrian’s route choices [1,2]. Other preferences, such as accessibility, convenience, comfort, etc., could be involved in such decisions [3]. The geometry properties of the shortest paths, including route curviness, the number of turns and intersections along roads, road gradients, sidewalk conditions (surface type, width, texture, etc.), and so on, might influence the route choice decision of particular types of pedestrians [4,5]. This is especially the case for people with limited mobility, like wheelchair users and older adults, experiencing major difficulties getting around urban environments. According to the data from the Centers for Disease Control and Prevention (CDC), about 31 million (11.1%) adults in the United States live with mobility impairments [6]. Previous studies [7,8] have shown that a straighter route (i.e., a route with fewer turns and long straight roads between turns) having equal or even longer travel time might be far preferable to a tortuous route for such users because of the convenience it may provide.
Figure 1 represents the shortest route (a) and alternative routes (b,c) between the “Museum of Sydney” and the “Sydney Opera House” suggested by Google Maps. It can be seen that despite showing small differences in the distance (850 m, 950 m, and 1 km) and travel time (10 min, 11 min, and 12 min), the routes have quite different geometric properties. In such situations, while many pedestrians generally ask “which path takes me to the destination faster?”, others might consider different factors that are directly or indirectly relevant to the geometry of the route as follows:
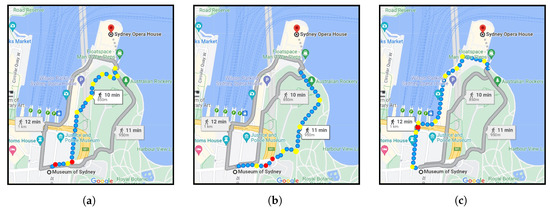
Figure 1.
The shortest path (a) and alternatives (b,c) suggested by Google Maps (yellow and red markers: road turns and intersections).
- Which route shows the least curviness?
- How many twists and turns (or directional changes) and intersections exist on each route?
- Which route shows lower road gradients, making the walking experience more pleasant for pedestrians?
As a result, pedestrians could end up with different route choices depending on their individual preferences. For instance, an ordinary person is more likely to choose “route a”, given that it offers the shortest distance and travel time. Conversely, the possible choice of a wheelchair user might be “route b” as it shows lower average and maximum slopes on roads. On the other hand, an elderly person might choose “route c” as it has the least curviness, allowing the pedestrian to enjoy traversing longer straight streets between turns, thus, avoiding the inconvenience of passing multiple bends and junctions. Of course, the beautiful coastal scenery of “route c” could also be involved in such decisions, but they are out of the scope of this paper.
Pedestrian navigation is considered an area of interest that could significantly benefit from the OpenStreetMap (OSM), a successful crowdsourcing project providing a flexible way to gather and share geospatial data relevant to urban infrastructure and facilities. The OSM project has already received tremendous attention from the research community in urban planning and transportation. Graells-Garrido et al. (2021) [9] used OSM to measure the accessibility to local urban amenities in Barcelona. Liu et al. (2021) [10] proposed a method to quantify pedestrian accessibility at high resolution using open data, including OSM, Global Human Settlements Layer (GHSL), and General Transit Feed Specification (GTFS). Gil (2015) [11] and Prieto-Curiel et al. (2022) [12] applied OSM data for constructing multimodal and interurban network models, respectively. The San Francisco Bay Area’s road networks were extracted using OSM for traffic microsimulation at the metropolitan-scale [13]. Yadav et al. (2021) [14] chose OSM data to visualize traffic estimation results. Klinkhardt et al. (2021) [15] extracted the places of interest (POIs) from OSM for estimating the attractiveness of traffic analysis zones (TAZs). Bartzokas-Tsiompras (2022) [16] conducted a comparison study to analyze pedestrian street lengths in 992 cities worldwide. Moreover, there have recently been some efforts to investigate the fitness of OSM for route planning [17], pedestrian navigation [18,19,20,21,22], and navigation systems designed for disabled pedestrians [23,24,25]. Furthermore, several methods and tools have been developed to assess and enrich OSM’s sidewalk information (width, surface texture, etc.) for pedestrian navigation and similar purposes [25,26,27].
Road datasets owned by commercial mapping platforms (e.g., Google Maps, MapQuest, and ESRI) are not free to access, given that distributing such expensive data to the public might lead to the forfeiting of the company’s competitive advantage in offering web mapping services. Conversely, the OSM project could provide free, open access to a rich database of road data, particularly walkable roads (e.g., roads in residential areas, pedestrian-only streets, narrow roads, and alleyways), for developing navigation systems. Furthermore, while commercial mapping companies generally use a pay-as-you-go pricing model and require payment if you use their APIs for more than a certain amount, the OSM project is quite adaptable to the open-source model, which is important to those individuals and small businesses that cannot afford to buy such services. For instance, OpenRouteService (ORS), Open Source Routing Machine (OSRM), GraphHopper, and OpenTripPlanner (OTP) consume OSM data to offer route-planning services to users. Likewise, various specialized online map services, including bicycle maps, public transport maps, wheelchair user maps, and waymarked trails, rely on data from the OSM project.
To fulfill their tasks most efficiently, pedestrian navigation systems rely heavily on the quality and level of information they provide for users. The collaborative mapping nature of the OSM project could make it easier to gather and share the routing experience of pedestrians about the quality of sidewalks (straightness, surface, width, etc.) and any existent barriers or inconveniences on roads [24]. There exist several crowdsourcing services, including CAP4Access [28], OhsomeHex [29], AXS Map [30], and Project Sidewalk [31], allowing volunteers to contribute their navigation experiences, such as surface conditions and obstacles along roads, to these services. Among these, the European CAP4Access is a successful OSM-centered project that develops methods and tools for pedestrians with limited mobility focusing on (a) quality assessment, (b) accessibility-level tagging of places, (c) route planning and navigation, and (d) raising awareness [25].
Many authors have introduced factors relevant to the built environment affecting the walking behaviors of pedestrians [32,33,34,35]. Addressing the navigation needs of pedestrians, especially those with limited mobility, requires a clear understanding of their route choices and using them in developing navigation systems [8]. Previous studies have demonstrated that besides distance, pedestrian route choice is connected to various other variables, including comfort [36], safety [37], attractiveness [38], and route geometry [4,7,39]. Focusing on route geometry, Kasemsuppakorn et al. (2015) [8] suggested that navigation systems could be more helpful if they provide personalized routes based on individual preferences and physical characteristics of routes (i.e., surface condition and slope); while Jansen-Osmann and Wiedenbauer (2004) [39] indicated that pedestrians perceive curvy routes to be longer than straight routes, a study by D’Acci (2019) [4] flatly contradicted their claims. Using a discrete choice model on over 10,000 GPS trajectory data of pedestrians in two US cities, San Francisco and Boston, Sevtsuk and Basu (2022) [7] found out that the effect of road turns on pedestrian route choice relies on network geometry. Another study listed distance and road turns as the main route choice criteria for pedestrians in Boston [40]. Shatu et al. (2019) [41] showed that distance and road turns contributed to over half of pedestrian route choices, but the latter is more important to pedestrians. Furthermore, pedestrian fatalities and injuries when crossing road intersections have been listed as a significant safety concern worldwide [42]. Lastly, some studies have indicated the major impact of road gradients on walking attractiveness [43,44].
Even though the above studies have highlighted the significance of geometry information related to the route in pedestrian navigation, research has yet to be conducted in practice. Therefore, this study proposes new methodologies for extracting and analyzing the geometry properties of pedestrian shortest paths for navigation applications, focusing on open geospatial data. The analysis is carried out on free, open OSM road networks and elevation data, which are expected to be crucial in providing future data for pedestrian navigation services. A shortest path analysis is conducted on an origin–destination (OD) database within the City of Sydney, a local government area of Greater Sydney in Australia. The “OSRM”, as an OSM-based routing engine, and “Google Maps Directions API” are employed to implement the shortest path analysis. Then, the routes’ geometry characteristics are extracted by the devised measures in this study, and the results are analyzed comprehensively.
The remainder of this article is organized as follows: The methods and materials are introduced in the next section. In Section 3, the results are presented with figures, tables, and relevant interpretations. Section 4 discusses the results in the greatest detail possible. Lastly, Section 5 summarizes the major findings and conclusions.
2. Methodology
This section begins with presenting the designed scenario for the shortest path analysis. Then, the measures used for extracting geometry properties, including (a) dissimilarity ratio, (b) sinuosity index, (c) road turns and intersections, and (d) road gradients, are introduced.
2.1. Shortest Path Analysis
An OD database containing a sample of 20 POIs, including parks, tourist attractions, museums, etc., located in the City of Sydney was created for the shortest path test. Table 1 describes the main characteristics of POIs, including the decimal degrees format of their latitudes and longitudes in the WGS84 coordinate system. Furthermore, Figure 2 shows the designed scenario. The POIs were chosen based on the following criteria:

Table 1.
The characteristics of the origin–destination database used for analysis.
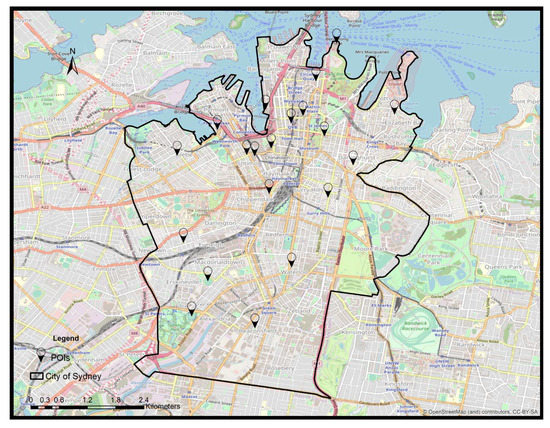
Figure 2.
The distribution map of POIs within the City of Sydney.
- Is the chosen POI listed as a famous place by Google Maps and OSRM?
- Are the distances between POIs no more than the recommended walking distance per day (10,000 steps ≈ 8 km) [45]?
- How well are the POIs distributed uniformly within the study area?
Walking distances and travel times between OD pairs are estimated using (a) OSRM routing engine and (b) Google Maps Directions API. The “OSRM routing engine” is a high-performance open-source C++ service that provides routing services based on data from the OSM project. Investigating the applicability of OSM data for pedestrian navigation requires evaluating its performance compared to a benchmark in the real world. As a commercial web mapping platform, Google Maps is a good choice for performance analysis of OSM data, given that it has been constantly updated by collecting information from satellite imagery, Street View cars, and its user’s daily contributions [46]. As a result, many individuals and businesses worldwide use its APIs for navigation and route planning purposes. Moreover, Google Maps uses almost the same Dijkstra algorithm as the OSRM engine for calculating the shortest paths between two given locations [47]. Google Maps offers two routing services, including (a) Distance Matrix API and (b) Directions API, while the “Distance Matrix API” estimates distance and travel time for a matrix of origins and destinations, it provides no navigation information and route geometry. This aspect has made it unfavorable for our analysis since route geometry information is required for comparative analysis later. Instead, the “Directions API” is utilized as it satisfies those requirements. This web service gives directions for several modes of transport, such as transit, driving, walking, and cycling. Since the average walking speed on Google Maps is about 3 miles (4.8 km) per hour [48], this parameter was adjusted in OSRM to produce analogous outputs.
2.2. Geometry Analysis
Several metrics were devised to extract the geometry properties of the shortest pedestrian paths in various aspects: (a) similarity, (b) route curviness, (c) road turns and intersections, and (d) road gradients, as follows:
2.2.1. Similarity
Distance calculation is fundamental for numerous applications in science and engineering. In spatial sciences, distance is an important parameter to estimate the relative position of spatial objects [49]. The distance can also be used as a metric to examine how similar or dissimilar two point sets (or geometric objects in spatial sciences) are [50]. Generally, three types of distance metrics, including maximum, minimum, and centroid, are defined to measure the degrees of resemblance between two spatial objects:
- (a)
- Minimum distance
- (b)
- Maximum distance
- (c)
- Centroid distancewhere (i = 1, 2, …, m) is the ith vertex of object A, and (j = 1, 2, …, n) is the jth vertex of B.
Hausdorff distance is a powerful metric to quantify the degree of similarity or dissimilarity between two geometries based on MAX–MIN distance between them [51,52,53]. In other words, the Hausdorff distance can be defined as “the maximum distance of a set to the nearest point in the other set” [54]. The main difference between the Euclidean distance and the Hausdorff distance is that the former measures the distance between two individual “point” objects, while the latter is used for the objects containing a set of points such as “line” and “area” [49,52]. The Hausdorff distance has drawn attention from scholars in many branches of science, ranging from mathematics and computer vision to geographic information science (GIS). Given two non-empty point sets, , …, and , the Hausdorff distance can be used for shape matching and error-controlling applications [52]. In GIS, let and be two lines, let and be two points such as and , let be the distance between two points (any norm distance metric such as the Euclidean distance), and let be the Hausdorff distance, estimated as follows [55]:
where
Let and be two lines. Among all points of , the point with the furthest distance from is defined as . Then, among all points, the point having the closest distance to is defined as . Let be the distance between and . Furthermore, can be determined by reversing the roles of and . Consequently, the Hausdorff distance equals to . As illustrated in Figure 3, two compared lines must have almost similar traces and shapes (top-side). Otherwise, the Hausdorff distance is not an ideal indicator of similarity (bottom-side) [56]. If is a small value, and are partially matched, and vice versa. In case is equal to zero, and are exactly matched [49].
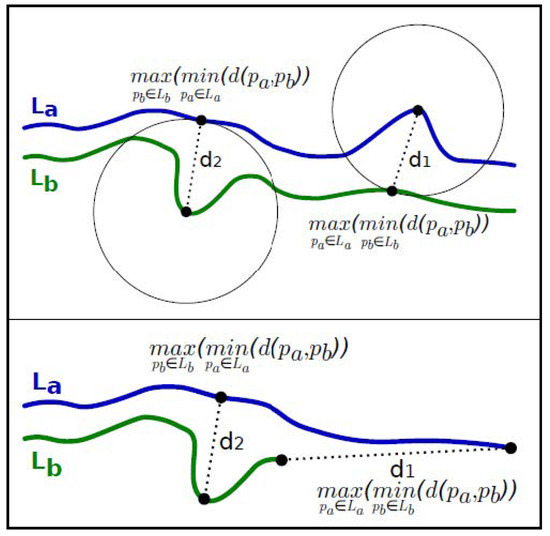
Figure 3.
Hausdorff distance [56].
The lower the Hausdorff distance between the two routes, the more similarity between them. Even though smaller/bigger values of Hausdorff distance indicate the higher/lower resemblance between route pairs, this metric can only provide clear insights into the overall similarity of routes if we can relate these values to route length. Hence, an indicator named “dissimilarity ratio” was devised, allowing us to gain a better understanding of how similar route pairs are in terms of geometric properties, formulated as follows:
where represents the Hausdorff distance between the two routes, and d is the distance between two OD pairs. As a benchmark for real-world commercial applications, Google Maps is a good estimator of the distances between POIs on the ground. Therefore, Google Maps’ calculated distances represent d in the dissimilarity ratio formula. Accordingly, the dissimilarity ratio when the route pairs are exactly matched equals 0, and the lower the estimated value, the more similar the routes. The following shows the calculated dissimilarity ratio for three different route pairs with equal d of 1 km and of 0 (a), 100 m (b), and 500 m (c), where (a) achieved the highest similarity. As mentioned earlier, the Hausdorff distance applies to similarity analysis only if the two routes have almost similar traces and shapes [56]; thus, experiencing high values for compared with d is very unlikely.
The similarity analysis is implemented on the route pairs (OSM, Google Maps) using the “PostGIS” spatial database extender. The PostGIS is an open-source library that allows adding spatial objects to the PostgreSQL object-relational database. Then, the OSM shortest paths are categorized into clusters according to the achieved dissimilarity ratios. In addition, the “t-test” statistical test is used to evaluate whether the estimated Hausdorff distances are significantly different from 0.
2.2.2. Route Curviness
As already mentioned, the quality of how tortuous a route is can be crucial to specific types of pedestrians, such as wheelchair users and older people. Sometimes, they might prefer to traverse a longer path but the most straight one due to its convenience. The curviness of the route pairs (OSM, Google Maps) is estimated using the following Python script:
!Shape.Length! / (math.sqrt(math.pow((float(!Shape.FirstPoint.X!) - float(!Shape.LastPoint.X!)),
2) + math.pow((float(!Shape.FirstPoint.Y!) - float(!Shape.LastPoint.Y!)), 2)))
This script returns a value between [1, ∞), where a straight route gains a weight of 1, and the more tortuous the route, the higher the value [57]. It can be rephrased in routing applications as “the actual route length divided by the shortest path length”. The estimated sinuosity index considerably varies from approximately 1.1 to over 3 for a 30 and a 180 turn, respectively. We realized that calculating the sinuosity index for the shortest paths in one fell swoop leads to misleading results as it fails to consider all turns and twists along the route. Instead, the overall sinuosity index of each shortest path is obtained by averaging the estimated indices of its constituent segments. Therefore, the sinuosity index for a given shortest path depends on (a) the number of turns along the route and (b) the degree amount. As shown in Table 2, route B appears to be more tortuous as the average sinuosity index of its constituent segments is higher than route A.

Table 2.
An example of calculating the route curviness.
In the next step, the sinuosity deviation (%) and distance difference (%) of OSM routes from the corresponding Google Maps routes are estimated. Furthermore, to better perceive to what degree route length is affected by route curviness, the relationship between the sinuosity deviation and distance difference is evaluated using Spearman’s rank correlation. Then, the ANOVA test compares variances across the means of dissimilarity ratios for three correlation groups: (a) positive, (b) negative, and (c) no correlation.
2.2.3. Road Turns and Intersections
The number and degrees of road turns along the route can be critical to wheelchair users and older adults, as they could pose mobility difficulties. Moreover, pedestrians generally avoid intersections because the risk of collision is considerable at such places, especially near bus stops and unsignalized crossings. Ensuring road safety is vital as pedestrians are less protected than other road users (Figure 4a). Therefore, the road turns with different degrees (i.e., 30, 60, 90, 120, 150, and 180) (Figure 4b), and road intersections along each route pair (OSM, Google Maps) are quantified. Accordingly, the average (a) number of turns in 1 km and (b) lengths of straight roads between turns, and (c) the number of intersections are estimated to understand whether the shortest paths based on the OSM project or Google’s road data provide further convenience and safety in taking the same trips between POIs.
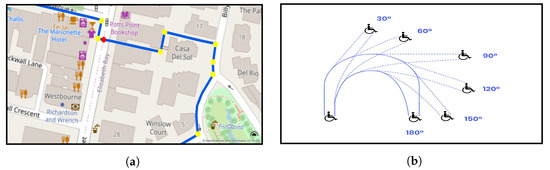
Figure 4.
The number of road turns and intersections (a) and degrees of turns (b) present different mobility problems for a wheelchair user (yellow and red markers: road turns and intersections).
2.2.4. Road Gradients
The degrees of slopes along the shortest pedestrian paths is considered an essential factor in pedestrian route decisions when alternative options are available. Broach and Dill (2015) [43] and Meeder et al. (2017) [44] suggested a 10% reduction in walking attractiveness for a road slope of 1%. Wheelchair users and elderly people with difficulty in movement are the target community that may consider road slopes in their route choices. Over the past decade, new data collection and processing methods have significantly increased the availability of open elevation data. In this study, the Digital Elevation Model (DEM) of NASA Shuttle Radar Topography Mission (SRTM) data with a resolution of global 1 arc-second (≈30 m) is used to generate the slope map of the study area. The original DEM is resampled to smaller cell sizes of 15 m while extracting elevation data corresponding to the road network (Figure 5). As shown in Figure 6, the average slope along each route pair (OSM, Google Maps) is estimated. Although this measure could tell pedestrians how steep the route is on average, it is not informative about the accessibility state of the route. Therefore, the maximum slope parameter was included in the analysis to examine whether OSM or Google Maps show any accessibility issues for pedestrians during walking.
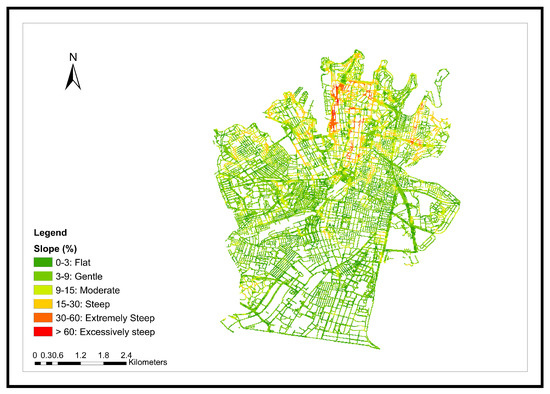
Figure 5.
Road gradient map of the study area.
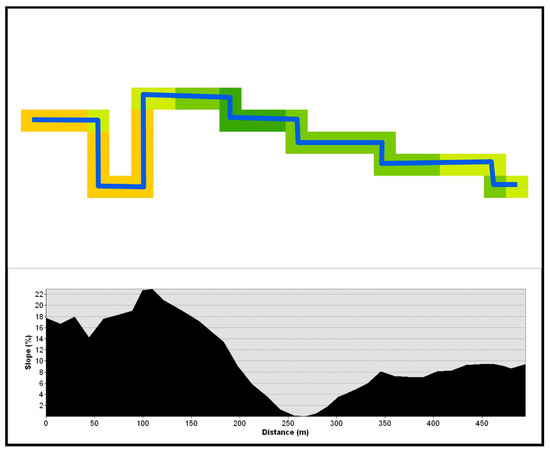
Figure 6.
The average and maximum road gradients with profile graph (blue line: the shortest path).
3. Results
The shortest path analysis between 20 × 20 OD pairs resulted in 380 route pairs (OSM and Google Maps) that were used for the geometry analysis. The results were categorized in distance matrices, and their geometry information was extracted accordingly. Table 3 displays the overall distance and travel time statistics estimated for OSM and Google Maps. It indicates that, on average, OSM resulted in longer routes (1162 km) than Google Maps (1115 km). Likewise, OSM routes achieved longer travel times, an overall of 242 h 12 m against 232 h 28 m for Google Maps routes. Slight variations in distance estimates are normal. Even assuming a similar route pair suggested by two different commercial routing platforms, such as Google Maps and Mapbox, there might still be some differences in distance estimates due to the characteristics of road datasets, utilized algorithms, and other contributing factors.

Table 3.
The overall statistics of shortest path analysis.
Table 4 summarizes the comparative analysis of distance estimates in two separate sections: OSM routes (a) shorter and (b) longer than Google Maps; while about two-thirds of OSM routes were found to be longer than Google Maps, the magnitude of differences was moderate between 0 and 850 m. The average differences for OSM shorter and longer routes than Google Maps consecutively were −116 m and 201 m, indicating that OSM witnessed higher variations in the latter case. In addition, the deviation of OSM from Google Maps was concentrated in a range of −2.9–−12.5% and 2.1–14.5% for OSM shorter and longer routes, respectively. The paired-samples t-test indicate a statistically significant difference between the mean distance estimates of OSM (M = 3.3, SD = 1.6) and Google Maps (M = 3.1, SD = 1.5), = 7.4, p < 0.001. Moreover, the distance average of Google Maps was smaller than OSM.

Table 4.
An overall comparative analysis of distance estimates (d: distance between OD pairs).
Figure 7 presents the calculated shortest paths with road slope profiles between “Elizabeth Bay House” and “Sydney Opera House” locations. According to Table 5, OSM and Google Maps routes were remarkably similar in geometry, with a dissimilarity ratio of about 4%. The remaining statistics shown in Table 6 indicate that the OSM route offers more comfort, convenience, and safety than Google Maps, given that it is less tortuous and pedestrians can expect smoother motion and better accessibility due to its lower average and maximum slopes.
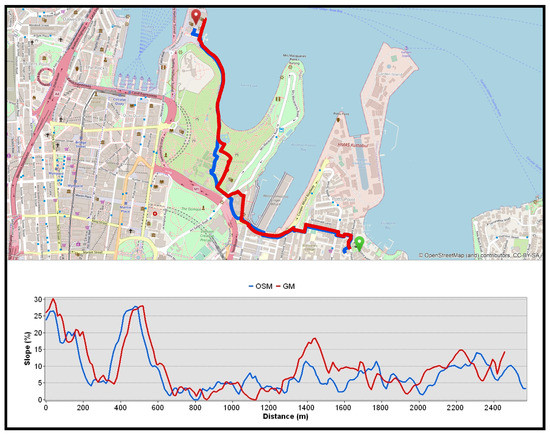
Figure 7.
An example of calculated shortest paths with slope profile (blue line: OSM, red line: Google Maps, and green/red placemark: origin/destination).

Table 5.
Geometry analysis of the route pair (part 1) (: Hausdorff distance, DR: dissimilarity ratio, and SI: sinuosity index).

Table 6.
Geometry analysis of the route pair (part 2) (SL: straight line between turns, and Int.: intersections along the route).
Achieving Hausdorff distances between 19 m and 1116 m from Google Maps, the OSM’s dissimilarity ratios oscillated between 0.87% and 37.56%, with a mean and standard deviation of 12.65% and 7.68%. The one-sample t-test concluded that the Hausdorff distance significantly differs from 0, = 14.05, p < 0.001. Table 7 shows categorized OSM routes under four similarity clusters, including (a) well matched (0–10%), (b) moderately matched (10–20%), (c) slightly matched (20–30%), and (d) not matched (30–40%). It was observed that over half of OSM routes were identified as well matched, indicating high degrees of geometry resemblance to Google Maps. Furthermore, while the moderately matched cluster contained over one-third of the whole routes, less than 15% of routes were labeled as slightly matched and not matched altogether. Even though the average distance between OD pairs followed a descending trend towards the not-matched group, the average Hausdorff distance showed the opposite direction, denoting that on average, the shorter routes witnessed higher dissimilarities from Google Maps.

Table 7.
Similarity classification of the route pairs (DR: dissimilarity ratio, : average Hausdorff distance, and : average distance between OD pairs).
Figure 8 presents four route pairs grouped under different similarity clusters, and Table 8 provides information on their main characteristics. According to Figure 8a, the OSM route for “Elizabeth Bay House” to “Glebe Library” fully overlapped the Google Maps route by achieving a 40 m Hausdorff distance and a dissimilarity ratio of 0.87%. Despite deviations up to 157 m, the OSM route for “Powerhouse Museum” to “WILD LIFE Sydney Zoo” reached a 10.47% dissimilarity ratio as it was almost identical for most of the path (Figure 8b). On the contrary, two OSM routes originating from the “Queen Victoria Building” to destinations “Sydney Opera House” (Figure 8c) and “Surry Hills Library” (Figure 8d) were dissimilar to Google Maps, accounting for 20.87% and 37.56%.
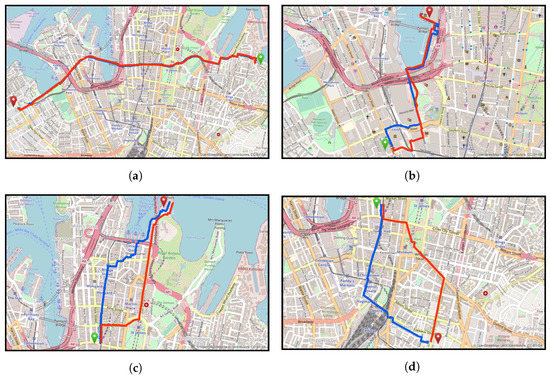
Figure 8.
The selected OSM shortest paths with different dissimilarity ratios (blue line: OSM, red line: Google Maps, green/red placemark: origin/destination).

Table 8.
Description of selected OSM shortest paths categorized under different similarity clusters (: Hausdorff distance and DR: dissimilarity ratio).
Figure 9 illustrates the relationship between the similarity of route pairs and their length deviation. The OSM shortest paths classified as well matched mainly concentrated between 0 and up to nearly 3% divergence from Google Maps (blue oval). A higher frequency of moderately matched occurrences was observed for OSM longer distances than Google Maps, with a maximum of 14.5% (green oval). The OSM routes shorter than Google Maps were mainly classified under the slightly matched cluster (yellow oval). Lastly, the red oval shows that all the non-matched routes occurred in the positive area of the plot.
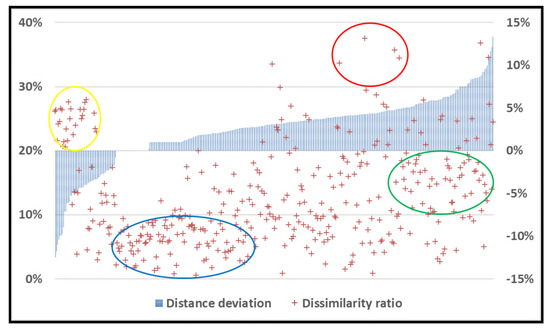
Figure 9.
The relationship between the route pairs’ similarity and distance deviation.
According to Table 9, on average, Google Maps witnessed straighter route geometry than OSM, achieving an average sinuosity index of nearly 1.41% versus 1.58%. The routes with a sinuosity index of over 1.8 could be challenging to walk. The Spearman’s rank correlation indicates a significant association between the sinuosity index and route length, (758) = 0.92, p < 0.001. Therefore, with an increase/decrease in route curviness, there is expected to be an increase/decrease in route length. Similarly, fewer road turns existed on Google Maps routes than OSM ones and, consequently, longer straight lines between each turn. On the other hand, OSM showed fewer intersections and lower average and maximum slopes than Google Maps.

Table 9.
Overall statistics of the geometry analysis (SL: straight line between each turn and Int.: intersections along the route).
Figure 10 shows how the correlated findings between the sinuosity index and route length are distributed within different similarity clusters. According to Table 10, one-way analysis of variance (ANOVA) indicates that the means of the three correlation groups were equal, F(2, 377) = 0.13, p = 0.93.
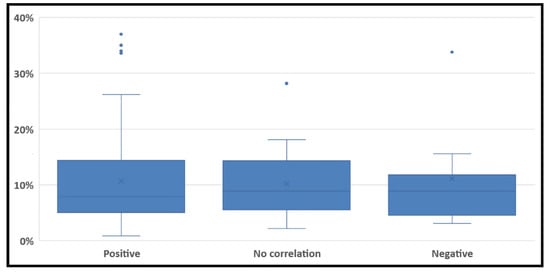
Figure 10.
The distribution of correlations within similarity clusters.

Table 10.
The ANOVA summary table.
According to Figure 11a, while the average road gradients were mainly between 7 and 9%, Google Maps experienced longer roads up to nearly 200 m with very steep slopes, which is more challenging to move than OSM for wheelchair users and older adults (Figure 11b).
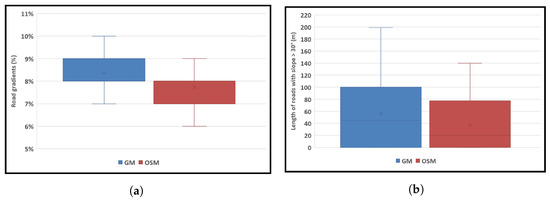
Figure 11.
The overall statistics of the geometry analysis (part 1).
Moreover, Google Maps witnessed lower sinuosity indices compared to OSM, and half of the estimates were distributed between nearly 1.3–1.5% and 1.4–1.7%, respectively (Figure 12a). There were not only more road turns with different degrees (i.e., 30, 60, 90, 120, 150, and 180) that existed on OSM than on Google Maps (Figure 12b), but each route also had, at least, six 90 turns per kilometer (Figure 12c), posing increased inconvenience and difficulty for wheelchair users. Meanwhile, three-fourths of OSM and Google Maps showed straight roads over 50 m up to about 90 m and 95 m between each directional change along the routes (Figure 12d). Figure 12e shows that both mapping services almost followed the same pattern regarding intersection frequency. However, there were some OSM routes with only one intersection.
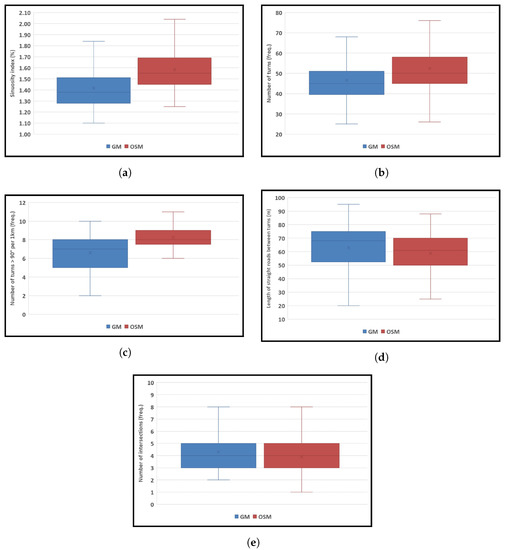
Figure 12.
The overall statistics of the geometry analysis (part 2).
4. Discussion
The shortest path analysis showed a closeness between the distance estimates of OSM and Google Maps, which could partly reflect the good quality of the OSM project’s data within the study area for pedestrian navigation services, especially those dependent on distance estimation. The observed differences can be justified based on the following reasons:
- Road dataset’s characteristicsThe data-related dissimilarities in route length might be derived from (a) differences in road density of networks or/and (b) existent topological inconsistencies in the dataset, such as unidentified connections and intersections. Moreover, (c) the starting/ending edges of calculated routes might have been placed in different positions (i.e., behind or ahead of the POI) for Google’s road dataset and OSM project’s data. As a result, it can be expected that the start or end of the route has yet to reach the exact position of the POI, or it conversely has gone beyond that (Figure 13). Such a circumstance is more likely to occur to the POIs in areas inaccessible by the main street networks.
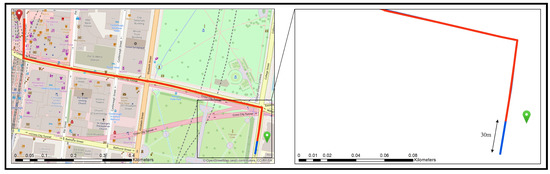 Figure 13. An example of the starting/ending edge problem (blue line: OSM, red line: Google Maps, black line: starting edge of the route, green/red placemark: origin/destination).
Figure 13. An example of the starting/ending edge problem (blue line: OSM, red line: Google Maps, black line: starting edge of the route, green/red placemark: origin/destination). - Utilized routing algorithmAlthough both web mapping services use Dijkstra’s algorithm to calculate the shortest path between points A and B, the OSRM’s algorithm is a modified version of Dijkstra, namely, “MultiLevel Dijkstra (MLD)”, which works on the overlay graph (i.e., an approximation of the original graph with a reduced complexity) produced by a partitioning step. This could result in negligible differences in the lengths of the calculated routes.
Moreover, OSM was inclined to suggest the shortest paths remarkably similar to Google Maps in terms of geometry in such a way that about 90% of the calculated routes were identified as well matched and moderately matched. Nonetheless, the one-sample t-test indicates that the Hausdorff distances significantly differ from 0. It was not noticed any negative influence of the length parameter on the similarity of OSM routes to Google Maps ones. Conversely, almost all long routes with lengths up to 7.6 km appeared to be categorized under the well-matched class. A strong positive correlation was found between route curviness and route length, with an effect size of 0.92 percent. On average, OSM witnessed more tortuous routes and, thus, longer distances than Google Maps. Likewise, Google Maps offered longer straight roads between each turn than OSM, which is more suitable for pedestrians intending to evade frequent directional changes. On the contrary, OSM showed fewer intersections along the streets, thus, lowering the possibility of accidents. By choosing OSM over Google Maps, pedestrians are also expected to traverse the streets with lower road gradients and, thus, higher accessibility to the destination.
The metrics developed in this study, including the dissimilarity ratio and sinuosity index, demonstrated their practicability by quantifying the geometry properties of the shortest paths and offering helpful information for pedestrian navigation. Furthermore, providing further information on the number of road turns and intersections along the route and road gradients (extracted from open elevation data) could enable pedestrians to make wiser route choices according to their preferences, especially for mobility-impaired pedestrians, like wheelchair users and older adults.
5. Conclusions
Pedestrians might choose different routes for the same trip, depending on individual route choice preferences; while calculating the distance between locations A and B might be sufficient for most routing applications, route geometry information could also be important for specific types of pedestrians, especially those with limited mobility, like wheelchair users and older adults. Supplying realistic navigation services to these users requires that pedestrians be offered additional information on route geometry, helping them make more informed route choices. Focusing on open geospatial data, this study suggested an approach to extract and analyze the geometry information of the shortest pedestrian paths across four aspects: (a) similarity, (b) route curviness, (c) road turns and intersections, and (d) road gradients.
Stemming from the Hausdorff distance, the dissimilarity ratio quantified the geometry resemblance between pairs of the shortest pedestrian paths. A striking similarity was found between OSM and Google Maps, such that over half of the route pairs were almost identical. Moreover, a segment-based method measured the route curviness based on the number and degree of the road turns along the route. Spearman’s rank correlation indicated a direct association between route curviness and route length. Furthermore, the extracted road gradients from open elevation data showed the routes with more smoothness and better accessibility, while Google Maps showed less tortuosity and longer straight roads between bends, OSM could offer better choices when the frequency of road intersections and degree of road slopes are essential to pedestrians. The proposed geometry measures, including the dissimilarity ratio and sinuosity index, demonstrated their effectiveness by converting raw values into meaningful indicators. Personalized navigation systems are a target area of interest that can considerably benefit from the devised geometry metrics in this study.
The inadequacy and incompleteness of the OSM project regarding sidewalk information, such as surface type, width, and texture, among others, can be considered a limitation of this study. Such information could dramatically affect pedestrian route choices, given that good or poor sidewalk conditions might make movement easier or more challenging for pedestrians, especially wheelchair users; while little effort has been made to enrich sidewalk information in some countries [25,26,27,28], such data still need to be included in the OSM project for most parts of the world, including our case study, by launching data enrichment campaigns and projects.
Future studies could focus on (1) developing new methods and tools for extracting other information relevant to route geometry, (2) using them in current navigation systems, and (3) investigating how pedestrians benefit from them. Another area of work that could be much improved is (4) constructing a specialized road dataset for pedestrian navigation applications based on a combination of open geospatial sources, including OpenStreetMap, SpaceNet imagery, Google Earth Engine (GEE), and so on. Developing such a dataset could enable navigation systems to estimate more realistic pedestrian routes. Using computer vision models based on available satellite imagery data, like the SpaceNet dataset, could provide updates on road networks and sidewalk attributes far faster than terrestrial methods, especially in natural disasters or other dynamic events. Furthermore, extracting road elevation profiles from the GEE could be beneficial because providing such information allows pedestrians to make more informed route choices.
Author Contributions
Conceptualization, Reza Hosseini, Daoqin Tong, Samsung Lim and Gyözö Gidófalvi; methodology, Reza Hosseini, Daoqin Tong, Samsung Lim and Gyözö Gidófalvi; software and programming, Reza Hosseini; writing—original draft preparation, Reza Hosseini; writing—review and editing, Daoqin Tong, Samsung Lim, Gunho Sohn, Qian Chayn Sun, Gyözö Gidófalvi, Abbas Alimohammadi and Seyedehsan Seyedabrishami; visualization, Reza Hosseini; supervision: Daoqin Tong and Samsung Lim. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We acknowledge that the following libraries and tools were used in this study: Numpy [58], SciPy [59], Open Source Routing Machine (OSRM), Google Maps Directions API [60], and PostGIS [61]. The authors would like to thank the New South Wales State Government in Australia for providing the required data for this study. Finally, we thank the anonymous reviewers for their suggestions to improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | Analysis of Variance |
| DEM | Digital Elevation Model |
| GEE | Google Earth Engine |
| GIS | Geographical Information System |
| NSW | New South Wales |
| POI | Point/Place of Interest |
| ORS | OpenRouteService |
| OSM | OpenStreetMap |
| OSRM | Open Source Routing Machine |
| OTP | OpenTripPlanner |
| SRTM | Shuttle Radar Topography Mission |
| TAZ | Traffic Analysis Zone |
| VGI | Volunteered Geographical Information |
References
- Koritsoglou, K.; Tsoumanis, G.; Patras, V.; Fudos, I. Shortest path algorithms for pedestrian navigation systems. Information 2022, 13, 269. [Google Scholar] [CrossRef]
- Tong, Y.; Bode, N. The principles of pedestrian route choice. J. R. Soc. Interface 2022, 19, 20220061. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Tanaka, T.; Wang, L. Pedestrian cognition of street structure and route choices when strolling: Comparative study based on two experimental methods. J. Urban Plan. Dev. 2022, 148, 05022015. [Google Scholar] [CrossRef]
- D’Acci, L. Aesthetical cognitive perceptions of urban street form. Pedestrian preferences towards straight or curvy route shapes. J. Urban Des. 2019, 24, 896–912. [Google Scholar] [CrossRef]
- Hashemi, M.; Karimi, H.A. Collaborative personalized multi-criteria wayfinding for wheelchair users in outdoors. Trans. GIS 2017, 21, 782–795. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. Disability and Health Data System (DHDS). Available online: https://dhds.cdc.gov (accessed on 22 April 2022).
- Sevtsuk, A.; Basu, R. The role of turns in pedestrian route choice: A clarification. J. Transp. Geogr. 2022, 102, 103392. [Google Scholar] [CrossRef]
- Kasemsuppakorn, P.; Karimi, H.A.; Ding, D.; Ojeda, M.A. Understanding route choices for wheelchair navigation. Disabil. Rehabil. Assist. Technol. 2015, 10, 198–210. [Google Scholar] [CrossRef]
- Graells-Garrido, E.; Serra-Burriel, F.; Rowe, F.; Cucchietti, F.M.; Reyes-Bedoya, P. A city of cities: Measuring how 15-min urban accessibility shapes human mobility in Barcelona. PLoS ONE 2021, 16, e0250080. [Google Scholar] [CrossRef]
- Liu, S.; Higgs, C.; Arundel, J.; Boeing, G.; Cerdera, N.; Moctezuma, D.; Cerin, E.; Adlakha, D.; Lowe, M.; Giles-Corti, B. A generalized framework for measuring pedestrian accessibility around the world using open data. Geogr. Anal. 2022, 54, 559–582. [Google Scholar] [CrossRef]
- Gil, J. Building a multimodal urban network model using OpenStreetMap data for the analysis of sustainable accessibility. In OpenStreetMap in GIScience. Lecture Notes in Geoinformation and Cartography; Jokar Arsanjani, J., Zipf, A., Mooney, P., Helbich, M., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Prieto-Curiel, R.; Heo, I.; Schumann, A.; Heinrigs, P. Constructing a simplified interurban road network based on crowdsourced geodata. MethodsX 2022, 9, 101845. [Google Scholar] [CrossRef]
- Yedavalli, P.; Kumar, K.; Waddell, P. Microsimulation analysis for network traffic assignment (MANTA) at metropolitan-scale for agile transportation planning. Transp. A Transp. Sci. 2021, 18, 1278–1299. [Google Scholar] [CrossRef]
- Yadav, P.; Sarkar, D.; Salwala, D.; Curry, E. Traffic prediction framework for OpenStreetMap using deep learning based complex event processing and open traffic cameras. arXiv 2020, arXiv:2008.00928. [Google Scholar]
- Klinkhardt, C.; Wörle, T.; Briem, L.; Heilig, M.; Kagerbauer, M.; Vortisch, P. Using OpenStreetMap as a data source for attractiveness in travel demand models. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 294–303. [Google Scholar] [CrossRef]
- Bartzokas-Tsiompras, A. Utilizing OpenStreetMap data to measure and compare pedestrian street lengths in 992 cities around the world. Eur. J. Geogr. 2022, 13, 127–141. [Google Scholar]
- Felício, S.; Hora, J.; Ferreira, M.C.; Abrantes, D.; Costa, P.D.; Dangelo, C.; Silva, J.; Galvão, T. Handling OpenStreetMap georeferenced data for route planning. Transp. Res. Procedia 2022, 62, 189–196. [Google Scholar] [CrossRef]
- Novack, T.; Wang, Z.; Zipf, A. A system for generating customized pleasant pedestrian routes based on OpenStreetMap data. Sensors 2018, 18, 3794. [Google Scholar] [CrossRef] [PubMed]
- Omar, K.S.; Moreira, G.; Hodczak, D.; Hosseini, M.; Miranda, F. Crowdsourcing and sidewalk data: A preliminary study on the trustworthiness of OpenStreetMap data in the US. arXiv 2022, arXiv:2210.02350. [Google Scholar]
- Klipp, K.; Kisand, A.; Wortmann, J.; Radusch, I. Multidimensional in- and outdoor pedestrian tracking using OpenStreetMap data. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Rousell, A.; Zipf, A. Towards a landmark-based pedestrian navigation service using OSM data. ISPRS Int. J. Geo-Inf. 2017, 6, 64. [Google Scholar] [CrossRef]
- Graser, A. Integrating open spaces into OpenStreetMap routing graphs for realistic crossing behaviour in pedestrian navigation. GI_Forum 2016, 1, 217–230. [Google Scholar] [CrossRef]
- Cohen, A.; Dalyot, S. Route planning for blind pedestrians using OpenStreetMap. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 1511–1526. [Google Scholar] [CrossRef]
- Mobasheri, A.; Sun, Y.; Loos, L.; Ali, A.L. Are crowdsourced datasets suitable for specialized routing services? Case study of OpenStreetMap for routing of people with limited mobility. Sustainability 2017, 9, 997. [Google Scholar] [CrossRef]
- Zipf, A.; Mobasheri, A.; Rousell, A.; Hahmann, S. Crowdsourcing for individual needs—The case of routing and navigation for mobility-impaired persons. Eur. Handb. Crowdsourced Geogr. Inf. 2016, 325–337. [Google Scholar]
- Mobasheri, A.; Zipf, A.; Francis, L. OpenStreetMap data quality enrichment through awareness raising and collective action tools—Experiences from a European Project. Geo-Spat. Inf. Sci. 2018, 21, 234–246. [Google Scholar] [CrossRef]
- Mobasheri, A.; Huang, H.; Degrossi, L.; Zipf, A. Enrichment of OpenStreetMap data completeness with sidewalk geometries using data mining techniques. Sensors 2018, 18, 509. [Google Scholar] [CrossRef] [PubMed]
- Collective Awareness Platforms for Improving Accessibility (CAP4Access). Available online: https://www.geog.uni-heidelberg.de/gis/cap4access_en.html (accessed on 5 January 2022).
- OhsomeHex. Available online: https://hex.ohsome.org/#/amenity_clinic_healthcare_clinic_ptpl/2022-08-01T00:00:00Z/2/0/0 (accessed on 10 January 2022).
- AXS Map. Available online: https://www.axsmap.com (accessed on 12 January 2022).
- Project Sidewalk. Available online: https://sidewalk-sea.cs.washington.edu (accessed on 12 January 2022).
- López, S.F.; Sánchez, T.R.; Mars, L. A qualitative study on the role of the built environment for short walking trips. Transp. Res. Part F Traffic Psychol. Behav. 2015, 33, 141–160. [Google Scholar]
- Dyck, D.V.; Cerin, E.; Conway, T.L.; Bourdeaudhuij, I.D.; Owen, N.; Kerr, J.; Cardon, G.; Frank, L.D.; Saelens, B.E.; Sallis, J.F. Perceived neighborhood environmental attributes associated with adults’ leisure time physical activity: Findings from Belgium, Australia and the USA. Health Place 2013, 19, 59–68. [Google Scholar] [CrossRef]
- Inoue, S.; Ohya, Y.; Odagiri, Y.; Takamiya, T.; Ishii, K.; Kitabayashi, M.; Suijo, K.; Sallis, J.F.; Shimomitsu, T. Association between perceived neighborhood environment and walking among adults in 4 cities in Japan. J. Epidemiol. 2010, 20, 277–286. [Google Scholar] [CrossRef]
- Ball, K.; Bauman, A.; Leslie, E.; Owen, N. Perceived environmental aesthetics and convenience and company are associated with walking for exercise among Australian adults. Prev. Med. 2001, 33, 434–440. [Google Scholar] [CrossRef] [PubMed]
- Erath, A.; van Eggermond, M.; Medina, S.O.; Axhausen, K. Modelling for Walkability: Understanding pedestrians’ preferences in Singapore. In Proceedings of the 14th International Conference on Travel Behavior Research (IATBR 2015), Beaumont Estate, Windsor, 19–23 July 2015. [Google Scholar] [CrossRef]
- Lue, G.; Miller, E.J. Estimating a Toronto pedestrian route choice model using smartphone GPS data. Travel Behav. Soc. 2019, 14, 34–42. [Google Scholar] [CrossRef]
- Sevtsuk, A.; Basu, R.; Li, X.; Kalvo, R. A big data approach to understanding pedestrian route choice preferences: Evidence from San Francisco. Travel Behav. Soc. 2021, 25, 41–51. [Google Scholar] [CrossRef]
- Jansen-Osmann, P.; Wiedenbauer, G. The representation of landmarks and routes in children and adults: A study in a virtual environment. J. Environ. Psychol. 2004, 24, 347–357. [Google Scholar] [CrossRef]
- Basu, R.; Sevtsuk, A. How do street attributes affect willingness-to-walk? City-wide pedestrian route choice analysis using big data from Boston and San Francisco. Transp. Res. Part A Policy Pract. 2022, 163, 1–19. [Google Scholar] [CrossRef]
- Shatu, F.; Yigitcanlar, T.; Bunker, J. Shortest path distance vs. least directional change: Empirical testing of space syntax and geographic theories concerning pedestrian route choice behaviour. J. Transp. Geogr. 2019, 74, 37–52. [Google Scholar] [CrossRef]
- Mukherjee, D.; Mitra, S. What affects pedestrian crossing difficulty at urban intersections in a developing country? IATSS Res. 2022, 46, 586–601. [Google Scholar] [CrossRef]
- Broach, J.; Dill, J. Pedestrian Route Choice Model Estimated from Revealed Preference GPS Data. 2015. Available online: https://trid.trb.org/view.aspx?id=1338221 (accessed on 10 May 2022).
- Meeder, M.; Aebi, T.; Weidmann, U. The influence of slope on walking activity and the pedestrian modal share. Transp. Res. Procedia 2017, 27, 141–147. [Google Scholar] [CrossRef]
- Crawford, B. Recommended Walking Distances. 2018. Available online: https://www.livestrong.com/article/178069-recommended-walking-distances (accessed on 25 September 2022).
- Google Maps Blog. 9 Things to Know about Google’s Maps Data: Beyond the Map. Available online: https://cloud.google.com/blog/products/maps-platform/9-things-know-about-googles-maps-data-beyond-map (accessed on 24 May 2022).
- CodeChef. The Algorithms behind the Working of Google Maps. Available online: https://blog.codechef.com/2021/08/30/the-algorithms-behind-the-working-of-google-maps-dijkstras-and-a-star-algorithm (accessed on 24 May 2022).
- Google Maps Help. What Is the Google Maps Walking Speed? 2021. Available online: https://support.google.com/maps/thread/92124954/what-is-the-google-map-walking-speed-is-this-a-constant-value-or-does-it-change-depending-on-slope?hl=en (accessed on 14 September 2022).
- Min, D.; Zhilin, L.; Xiaoyong, C. Extended Hausdorff distance for spatial objects in GIS. Int. J. Geogr. Inf. Sci. 2007, 21, 459–475. [Google Scholar] [CrossRef]
- Jungeblut, P.; Kleist, L.; Miltzow, T. The complexity of the Hausdorff distance. In Proceedings of the 38th International Symposium on Computational Geometry (SoCG 2022), Dagstuhl, Germany, 7–10 June 2022. [Google Scholar] [CrossRef]
- Zhang, D.; Zou, L.; Chen, Y.; He, F. Efficient and accurate Hausdorff distance computation based on diffusion search. IEEE Access 2018, 6, 1350–1361. [Google Scholar] [CrossRef]
- Zhang, D.; He, F.; Han, S.; Zou, L.; Wu, Y.; Chen, Y. An efficient approach to directly compute the exact Hausdorff distance for 3D point sets. Integr.-Comput.-Aided Eng. 2017, 24, 261–277. [Google Scholar] [CrossRef]
- Iphar, C. Formalisation of a Data Analysis Environment Based on Anomaly Detection for Risk Assessment: Application to Maritime Domain Awareness. Ph.D. Thesis, Library and Information Sciences, Université Paris Sciences et Lettres, Paris, France, 2017. [Google Scholar]
- Rote, G. Computing the minimum Hausdorff distance between two point sets on a line under translation. Inf. Process. Lett. 1991, 38, 123–127. [Google Scholar] [CrossRef]
- Rucklidge, W.J. Efficient visual recognition using the Hausdorff distance. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Etienne, L. Motifs Spatio-Temporels de Trajectoires d’Objets Mobiles, de l’Extraction a la Detection de Comportements Inhabituels. Application au Trafic Maritime. Ph.D. Thesis, Universite de Bretagne Occidentale, Brittany, France, 2011. [Google Scholar]
- Leopold, L.B.; Wolman, M.G.; Miller, J.P. Fluvial Processes in Geomorphology; W.H. Freeman and Co.: San Francisco, CA, USA, 1964; p. 522. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberl, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Google Maps Directions API. Available online: https://developers.google.com/maps/documentation/directions/overview (accessed on 20 May 2022).
- PostGIS. Available online: https://postgis.net (accessed on 28 April 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).