Abstract
Spatio-temporal association analysis has attracted attention in various fields, such as urban computing and crime analysis. The proliferation of positioning technology and location-based services has facilitated the expansion of association analysis across spatio-temporal scales. However, existing methods inadequately consider the scale differences among spatio-temporal objects during analysis, leading to suboptimal precision in association analysis results. To remedy this issue, we propose a multiscale spatio-temporal object representation method, STO2Vec, for association analysis. This method comprises of two parts: graph construction and embedding. For graph construction, we introduce an adaptive hierarchical discretization method to distinguish the varying scales of local features. Then, we merge the embedding method for spatio-temporal objects with that for discrete units, establishing a heterogeneous graph. For embedding, to enhance embedding quality for homogeneous and heterogeneous data, we use biased sampling and unsupervised models to capture the association strengths between spatio-temporal objects. Empirical results using real-world open-source datasets show that STO2Vec outperforms other models, improving accuracy by 16.25% on average across diverse applications. Further case studies indicate STO2Vec effectively detects association relationships between spatio-temporal objects in a range of scenarios and is applicable to tasks such as moving object behavior pattern mining and trajectory semantic annotation.
1. Introduction
Location-based sharing applications and modern location-aware devices, such as smart wearables and unmanned mobile platforms, have generated and accumulated vast amounts of spatio-temporal data. Spatio-temporal data mining (STDM) research aims to extract valuable information from these data [1]. Spatio-temporal association analysis is a commonly used method to identify groups of entities that exhibit specific spatio-temporal association relationships, such as co-occurrence, in spatio-temporal datasets [2].
Associations are universal [3], making association analysis applicable to various fields with different relationship types. Sharma et al. [2] grouped spatio-temporal associations into three types based on whether a temporal sequence was considered: sequential (e.g., analyzing event-oriented spatio-temporal association in video surveillance [4]), cascading (e.g., studying relationships between events, locations, and criminal activities in criminal geography [5]), and co-occurrences (e.g., similar associations between trajectories [6], co-location patterns between geographic entities [7], semantic annotation of trajectories [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22], and location embedding [23,24,25,26,27,28,29,30,31,32,33], etc.). By comparing their frequency of co-occurrence, spatio-temporal co-occurrence-based association analysis can reveal implicit associations between entities. This facilitates spatio-temporal semantic understanding, such as urban regional functions, moving object location preferences and behavior patterns [34]. It holds important research value by being an association analysis type that this paper focuses on, and has a positive impact on city planning, emergency management, and resource allocation. Therefore, in this paper, “association” refers to the interaction between spatio-temporal objects due to the presence of local or global spatio-temporal co-occurrence relationships.
Relationships between spatio-temporal objects are complex and implicit [1], especially in contexts involving a large number of spatio-temporal objects with different scales. For example, as shown in Figure 1, we need to measure and discover direct or indirect associations between aircraft A and aircraft B, farmland M, lake L, airport P, and airport Q from a large number of spatio-temporal objects. These spatio-temporal objects exist in different scales in space and time. The traditional semantic trajectory achieves the matching of moving objects and geographic entities through the stops detection algorithm while ignoring the semantic information of the moving objects during the move process. As a result, they can only obtain the association information between aircraft A and the airport. Location embedding maps the spatio-temporal objects into a unified vector space. The degree of quantitative association between any spatio-temporal objects can be obtained by measuring distances in the vector space. This allows for the discovery of a richer association of relationships.
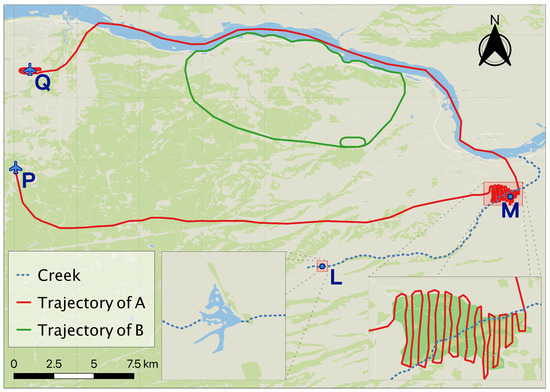
Figure 1.
Illustration of Spatio-Temporal Association. Aircraft A takes off from airport Q to farmland M on a pesticide-spraying mission and then lands at airport P. There is an association between A and B due to similar local trajectories; aircraft A hovers repeatedly over farmland M, so there is a strong association between A and M. There is also an association between A and L as creek C passes through farmland M to deliver pesticides to lake L.
Most studies in location embedding research concentrate on small-scale regions, such as cities [5,10,29,30,35,36], where spatio-temporal objects typically have a uniform scale. As a result, there is a lack of attention paid to the diversity of spatio-temporal object scales. However, the scale attributes of spatio-temporal objects are varied in large geographic regions. Here, “scale” refers to the actual range over which an object exists spatio-temporally, while “multiscale” describes the diversity of scales resulting from differences in the spatio-temporal presence range of the object. As depicted in Figure 1, the scale of the trajectory of aircraft A during its flight to and from farmland M is much larger than the scale over the farmland M. Moreover, there are geographic entities such as creeks, streets, and houses at different scales at M. Existing spatio-temporal object-oriented [23,24,25,26] or discrete unit-oriented [27,28,29,30,31,32,33] embedding algorithms lose many spatial features during the computation resulting in inaccurate association analysis results: the former may obtain stronger associations between aircraft and point of interests(POI) such as houses (rather than farmland M); meanwhile, the latter may ignore the association between A and M due to the large scale of the predefined grid and the small scale of the local trajectory in M.
It can be seen that the diverse scale characteristics of spatio-temporal objects are an important factor affecting the results of association analysis. While location embedding studies utilizing fine-grained grids have been shown to preserve more spatio-temporal features [31], sparse data present a challenge whereby computational resources are not efficiently utilized [5]. Multilevel discretization techniques can overcome this limitation by retaining association information at multiple scales. However, implementing such methods requires prior knowledge to set fixed multiple levels [32,33]. Our research addresses these shortcomings by adaptively selecting different resolution grid units for discretization based on the scale size of spatio-temporal objects. This preserves feature information across diverse scales. To describe associations between spatio-temporal objects with varying structures and grids at different levels, we integrate the approaches for spatio-temporal objects and discretized grids using heterogeneous graphs. Association information for spatio-temporal objects is obtained through node embedding. Specifically, the contributions of this paper are as follows:
- We propose an adaptive discretization method based on hexagons, which can decompose spatio-temporal objects of different scale sizes into a collection of grids with different resolutions, thereby conserving more of the original spatio-temporal features.
- We designed an associated heterogeneous graph model that can describe the geographic scope and frequency of co-occurrence between spatio-temporal objects based on scale differences. This model enables object embedding for association analysis.
- To improve the scalability of representation methods and the quality of representation results, we designed a biased sampling strategy that can provide richer, application-specific associative information for object representation.
- We constructed a multiscale spatio-temporal object representation method called STO2Vec, which is oriented towards association analysis. We performed accuracy tests on association analysis using the representation results of STO2Vec on real datasets.
The remainder of this paper is organized as follows. Section 2 introduces the related work. Section 3 presents the relevant underlying concepts and problem definitions. Section 4 describes the STO2Vec framework specifics. Section 5 presents quantitative experiments and case studies of the proposed framework, while Section 6 presents the discussion and conclusion.
2. Related Work
There are currently numerous studies analyzing the association relationships based on spatio-temporal co-occurrence from different perspectives. These studies can be classified into semantic trajectory-based approaches [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and location embedding-based approaches [23,24,25,26,27,28,29,30,31,32,33] according to the analysis methods.
2.1. Semantic Trajectory
From the perspective of moving objects, the current main research focus is on constructing semantic trajectories by combining trajectory data with geographic information. These trajectories are analyzed to explore spatio-temporal object associations, essentially discovering the relationships between stopping points of moving objects and geographic entities from a spatio-temporal viewpoint. This approach enables a better understanding of spatio-temporal semantics of moving object trajectories.
Alvares et al. proposed the stop-move model, which converts trajectories into sequences with labels through semantic annotation, thereby mining and analyzing the interaction and association of moving objects in geographic space [11]. Based on the stop-move model, some of the research work has focused on how to better geographically associate this semantic annotation of trajectories [9,12,13,14]; meanwhile, many studies have constructed semantic trajectory models and designed corresponding association analysis algorithms for different application domains. For instance, Ying et al. used the frequent pattern of -- in semantic trajectories for location prediction of moving objects [15]. Kontarinis et al. designed an indoor semantic trajectory model to support the mining and analysis of indoor moving-object trajectories, which was used to test existing analysis algorithms and the proposed algorithm in conjunction with trajectory data inside the Louvre [10]. Noureddine et al. put forward a semantic trajectory model that covers both indoor and outdoor spaces, along with an organizational management method. This model enables associative semantic queries to comprehend people’s flow patterns in urban spaces [16]. Based on this model, a graph-based semantic trajectory model was constructed by utilizing open source crowdsourcing data [8] and employing graph analysis algorithms for association analysis among objects. Choi et al. used a semantic trajectory model to mine the movement behavior pattern of pedestrians in the local area [17]. To mine the travel purpose of urban moving objects, Wan et al. developed the SMOPAT algorithm which analyzes frequent patterns in private car trajectories [18]. There are also many studies that focus on association analysis between moving objects such as the similarity metric calculation of trajectories [19,20].
Due to the aggregation of sampled features of trajectories at stopping points that can be explicitly associated with geographic entities, most semantic trajectory studies tend to focus only on the semantic information of the STOP phase. Lehmann observed that current semantic trajectory similarity analysis algorithms neglect the semantic information of moving objects during the MOVE phase [21], particularly during continuous movement scenarios in free space (e.g., drones and fishing boats), where the association semantics between the MOVE phase and geographic entities are abundant. Obviously, the trajectory characteristics of the MOVE phase are more complex and variable compared to the STOP phase, and this difference in semantic distribution makes the analysis of spatio-temporal object associations in free space more difficult. Xiang et al. [22] described the basic spatial associations by deriving topological, orientation, and distance relationships between the move objects and geographic entities. However, this method involves complex modeling, matching, and inference processes. It is better for analyzing topological movement in specific scenarios than it is for discovering association sin general scenarios.
2.2. Location Embedding
In some studies, geographic entities or regions are embedded using representation learning models that integrate road networks, POI, geotags, origin destination(OD) streams, and trajectory data. This approach facilitates discovering associations between spatio-temporal objects and performing tasks such as regional functional analysis and classification of POI. Based on the embedding object structure, it can be categorized into two types: spatio-temporal object-oriented embedding and discrete unit-oriented embedding.
In a spatio-temporal object-oriented approach, the embedding representation of the object itself can be obtained directly. Due to the advantages of POI data such as strong presentational and large data volume, most studies abstract geographic entities into POIs and identify urban functional areas by mining potential associations between POIs and regions [23]. Zhang et al. proposed a global vector-based POI embedding model GPTEM to mine the implicit semantic associations between POIs and urban functional types by integrating the co-occurrence information and spatial contexts of POIs [24]. Zhang et al. proposed Traj2Vec based on Word2Vec to find pedestrian–location associations in trajectory data and obtain mixed land use characteristics of urban areas [25]. Zhu et al. designed a spatial embedding algorithm Location2vec that combines the interrelated effects between urban locations and moving objects [26]. To address the problem that spatial association between regions is ignored, Sun proposed the Block2vec model, which integrates the information of association between regions based on Skip-gram [23]. In reality, geographic entities do not exist in the form of point elements, and thus these approaches lose most of the spatial information.
Discrete unit-oriented embedding offers the advantage of a consistent method for describing diverse spatio-temporal objects through cell aggregation. Different techniques can be used to discretize spatio-temporal objects, such as Zone2Vec by Du et al., which partitions a city into different regions based on its road network and applies the Skip-gram model to obtain region embedding representations from Beijing taxi trajectories. This approach supports applications such as urban region classification and region clustering [27]. In contrast to the discrete approach of Zone2Vec, Crivellari et al. proposed the Mot2Vec, which segments trajectories at equal time intervals. Trajectories are converted to ID sequences by selecting valuable points for nearest neighbor matching with trajectory segments, preserving more semantic information [28]. To obtain richer semantic information from multiple sources, Jenkins et al. divided the study area into rectangular cells according to a predetermined scale and combined multimodal data such as OD stream data, POI, and remote sensing images to construct regional embeddings [29]. This discretization method highlights background semantic information but only for specific topics. It has poor scalability and cannot handle large-scale datasets for discrete tasks. Spatial indexes based on global discrete grids, such as Geohash encoding [37], Google S2 [38], and Uber H3 [39], can be used to solve these problems, where the grid encoding has a hierarchical structure and is capable of uniquely encoding regions. Woźniak et al. used the open source platform OpenStreetMap tagging data combined with Uber H3 grid division to discover the regional functionality of cities [30].
The above studies are all oriented to local areas, which involve spatio-temporal objects at a relatively uniform scale. Some recent studies have started to focus on location embedding at large scales. Tian et al. proposed the GCN-L2V model. It constructs flow graphs based on trajectory and spatial graphs based on spatial relationships. This helps create fine-grained location embedding at large scales for fixed-level Google S2 grids [31]. In response to the difficulty of a fixed-level grid to solve the data sparsity problem caused by fine-grained embedding in a large-scale context, Shimizu et al. proposed a multilevel grid embedding model. This model obtains fine-grained grid embedding representation with proximity information by discretizing a target region with predefined grids of varied resolutions. However, this technique demands predetermined resolution for each level based on prior knowledge, making it incapable of adjusting to multiscale spatio-temporal objects with scale differences [32]. The above studies are still limited to city-wide analysis, and the extension to larger areas will involve challenges related to balancing accuracy and complexity. Yin et al. implemented a global-scale global positioning system (GPS) coding embedding based on Universal Transverse Mercator (UTM). They did not consider associations between locations based on moving objects. Instead, they emphasized the multimodal semantic information of the locations themselves. Relationships between locations according to movements of objects were not explored [33]. Furthermore, these experiments failed to consider the scale differences of spatio-temporal objects during the embedding process. As a result, their representation in vector space is relatively crude.
3. Preliminary
3.1. Spatio-Temporal Object
Entities in geographic space can be abstracted as different spatio-temporal objects [40]. Due to the complexity of the real world, there often exist significant scale differences between such objects. Therefore, we refer to spatio-temporal objects with a notable scale variance as multi-scale spatio-temporal objects.
Moving objects and geographic entities are two types of spatio-temporal objects that are closely related but different in structure. We refer to objects with different structures as heterogeneous spatio-temporal objects and those with the same structure as homogeneous spatio-temporal objects. For example, moving objects and geographic entities are heterogeneous spatio-temporal objects, while moving objects belong to homogeneous spatio-temporal objects among themselves.
Geographic entities are the fundamental units of human cognition of the geographic world. These objects can be either natural or artificial. They have a basic stable spatial position in the world that exists independently. We use a vector data model to describe geographic entities by abstracting them into point, line, and polygon elements:
Definition 1.
Geographic Entity , where T is the time period, and are the coordinates of Eg’s spatial position in that time period. When Eg is a point element, , and when it is a polygon element, , and .
When the geographic entity can be divided into smaller geographic units, called subgeographic entities , that have independent characteristics within —for example, tributaries of a river or cities within a country—we refer to them as the subgeographic entities of . There is a containment relationship between and , where is contained within .
The trajectories generated by moving objects are called spatio-temporal trajectories. Spatio-temporal trajectory data are the raw data collected by the position sensors. In this paper, spatio-temporal trajectories are defined as follows:
Definition 2.
Spatio-Temporal Trajectory , where n is the number of sample points in the trajectory; is a multidimensional sample point in the trajectory, also called a trajectory point; and , , and are the spatial latitude and longitude coordinates of , respectively, while is the sampling time stamp.
Spatio-temporal trajectory segmentation involves dividing a trajectory into segments using various methods. These trajectory segments have similar internal structural features. The trajectory segments are defined as follows:
Definition 3.
Given a spatio-temporal trajectory , we define the segmentation of as , such that
- (i)
- (ii)
- .
The association between spatio-temporal objects often occurs locally rather than globally, and thus dividing spatio-temporal trajectories into segments with complete semantic features can better support the detection of local association relations. There is a containment relationship between and , where is contained within .
3.2. Space Discretization
There are many ways to divide space into units, which can be done manually or according to fixed methods such as administrative divisions. However, these methods cannot flexibly deal with spatio-temporal objects of different scales. Global grid encoding systems such as Google S2, Geohash, and Uber H3 can decompose spatio-temporal objects at different resolutions without being constrained by the background. S2 and Geohash use quadrilaterals for division, while Uber H3 uses hexagons for division. We compared these three grid encoding systems based on projection method, isotropy, and hierarchical coverage. The results are shown in Table 1.

Table 1.
Global grid encoding systems comparison.
In this study, the isotropy of a grid refers to the consistency of its weights with adjacent grids. As shown in Figure 2, quadrilateral grids have two types of neighboring grids, copoint and colinear neighbors, while hexagonal grids have only colinear neighbors. The isotropy of hexagonal grids is superior to that of quadrilateral grids. Since moving objects in the real world is unlikely to involve movement in a way that aligns with the grid, using Google S2 can complicate the analysis because the analyst needs to consider more different types of neighbors than Uber H3 does [39]. In terms of hierarchical coverage, quadrilateral grids can achieve precise coverage between levels, while hexagonal grids cannot. The Uber H3 grid system uses a seven-aperture hierarchical division method, and the approximate coverage between adjacent levels is achieved by rotating the angle.
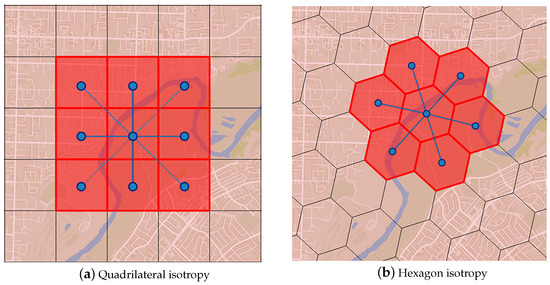
Figure 2.
The difference between quadrilateral and hexagonal grids in terms of isotropy.
We chose to use Uber H3 for the discretization of spatio-temporal objects, mainly for the following three reasons: First, the smaller projection error of Uber H3 grids can more accurately achieve the discretization of spatio-temporal objects [39]. Second, the isotropy of hexagons simplifies the construction of spatial neighbor relationships in association analysis: in the calculation process, grid distance can be used instead of geographic distance. Third, although the hierarchical coverage of hexagonal grids is inferior, the aggregation range of different level neighborhood information matches the resolution of that level. As such, the precise coverage between levels is not required.
Definition 4.
Structural relationships among geographic grids. There are structural relationships between multilevel geographic grids, including adjacency relationships between grids at the same level, and hierarchical relationships between adjacent-level grids.
As shown in Figure 3a, the grids that have adjacency relationships with the red grid on the L-level are the blue grids of the same level. The yellow grids at level and have hierarchical relationships with the red grid. Among them, the yellow grids at level are the parent grids of the red grid and its neighboring grids, while the yellow grids at are the child grids of the red grid.
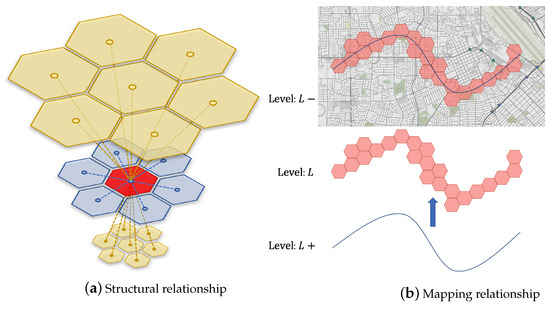
Figure 3.
Structural relationship and mapping relationship.
Definition 5.
Mapping relationship between spatio-temporal objects and grids. There is a mapping relationship between spatio-temporal objects and their discretized grids, i.e., a spatio-temporal object can be mapped to a set of geographic grids.
As shown in Figure 3b, the blue line represents the trajectory, and the red grids represent the discretization result of the trajectory at a certain level. There exists a mapping relationship between the trajectory and the grids in the figure.
3.3. Heterogeneous Graph
Heterogeneous graphs are capable of expressing associations between different types of spatio-temporal objects by utilizing node types. This feature enables researchers to design custom sampling schemes that suit their specific requirements, making it an effective tool for fusing multiple types of nodes with association information. Some important concepts related to heterogeneous graphs and their embedding are as follows:
Definition 6.
Heterogeneous Graph. The heterogeneous graph can be expressed as , where V is the set of all nodes in , E is the set of all edges in , ϕ is the node v-type mapping , ψ is the edge e-type mapping , and are the sets of node type and edge type, respectively, while .
Definition 7.
Heterogeneous Graph Embedding. For a heterogeneous graph with its node attribute matrix , the goal of heterogeneous graph embedding is to obtain the node embedding representation for all by learning so that can reflect the structural and semantic information of the graph G, where , denotes the d-dimensional Euclidean space.
Definition 8.
Association Strength. For spatio-temporal objects and , whose embedding representations are and , respectively, the association strength between and can be expressed as Equation (1).
According to Equation (1), we define the spatio-temporal object association analysis problem as follows:
Definition 9.
Spatio-Temporal Object Association Analysis. Given the set of spatio-temporal objects , , the purpose of spatio-temporal object association analysis is to find the set of spatio-temporal objects , , and , such that , , ; we can thus obtain Equation (2):
where h is the embedding representation, and χ is the association strength threshold, .
4. Method
In this section, we propose a new multiscale spatial-temporal object representation method, named STO2Vec, for association analysis. The overall structure of the method will be introduced in Section 4.1. The process of data preprocessing is described in Section 4.2 while the construction method of the spatio-temporal association heterogeneous graph is presented in Section 4.3. Finally, we introduce the heterogeneous graph node embedding algorithm for spatio-temporal association in Section 4.4.
4.1. Overall Framework
To address the problem of multiscale spatial-temporal object association measurement and discovery, as shown in Figure 4, we propose a multiscale spatial-temporal object representation method named STO2Vec for association analysis. The method is divided into two stages: graph construction and embedding. In the graph construction stage, we decompose spatial-temporal objects into grids at multiple levels using adaptive discretization and describe their associated relationships using a heterogeneous graph that includes discrete spatio-temporal co-occurrence and grid structural relationships. In the embedding stage, biased second-order sampling is performed to obtain node sequences based on the association between homogeneous or heterogeneous spatial-temporal objects. These sequences are combined with an embedding model to generate vector representations of the nodes, facilitating association discovery and measurement between objects.
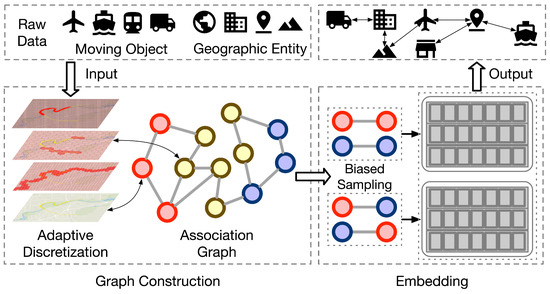
Figure 4.
Overall Framework of STO2Vec.
4.2. Data Preprocessing
We first remove the redundant values from the trajectories in the preprocessing stage. Additionally, we apply the well-established Kalman filtering algorithm to suppress noise. Given that interactions mainly occur locally and the full trajectory can potentially dilute the association information of moving objects at specific points in time, the cleaned trajectory needs to be segmented to describe the association between spatio-temporal objects in as a precise way as possible, which is a common preprocessing operation for most trajectory analysis algorithms [41].
Traditional stopping point segmentation methods are not applicable to the association analysis of moving objects such as aircraft and ships. Due to cost saving or route planning, the movement characteristics such as heading, speed, and altitude of such moving objects tend to be kept stable in the process of transferring and cruising. Nevertheless, their movement characteristics occasionally fluctuate rapidly while interacting with geographic entities. To capture associations more precisely, we extract trajectory segments that exhibit frequent variations in movement features. Joint information entropy is a reliable metric that measures the uncertainty of multiple random events. By considering changes in mobile traits as a sequence of random events, we segment trajectories using a unified joint information entropy metric of mobile features. The algorithmic procedure is as follows.
For each point in the trajectory , the motion features of (heading) and (instantaneous velocity) are first calculated. Other features such as geographic altitude, barometric altitude, and attitude parameters can also be added according to the data situation and background.
Then, the motion features of are clustered by numerical distribution. We use the widely-used DBSCAN algorithm to perform clustering. We obtain the set of heading feature clusters consisting of k clusters and the set of instantaneous velocity clusters consisting of l clusters, where , . The motion feature label of each point is .
To obtain the joint information entropy of motion characteristics for trajectory points within each window, for a sliding window W with window size and sliding step , Equation (3) is sequentially applied in order of trajectory sequence.
where is the joint probability of , and is within the window W. We then extract the set of windows whose entropy values exceed the threshold .
Finally, the consecutive adjacent windows in are merged to obtain the set of trajectory segments which has potential interaction semantics. The remaining trajectory segments in the original trajectory are composed into the set so that the final trajectory segmentation results are obtained.
4.3. Graph Construction
4.3.1. Adaptive Discretization
Previous uniform grid division methods discretize all spatio-temporal objects with the same resolution. When the grid resolution is low, this leads to the loss of a large number of geometric features and association details. This can result in a decrease in embedding quality. Using higher-level grids to process spatio-temporal objects incurs significant computational costs [42]. Discretization methods at the same level are limited in their ability to describe features of spatio-temporal objects at multiple scales, whereas multilevel partitioning methods require prior knowledge to set the level parameters. To this end, we propose an adaptive discretization approach to differentially dissect spatio-temporal objects at different scales based on H3, preserving more detailed features while taking into account computational overhead.
For the spatio-temporal object , let its discretization level be r. We examine the variables that affect the accuracy and computational cost during the discretization process.
- The number of grids : is the total number of grids after discretization of the spatio-temporal object at level r. Obviously, the accuracy of the discretization increases as r increases, which also leads to an increase in and the computational overhead.
- Discretization error : We use to measure the information loss brought by discretization to the spatio-temporal object description, which is calculated as in Equation (4). For polygon elements, inspired by the error analysis method of rasterization of vector elements [43], we choose to use the area relative error to calculate (Equation (5)), where is the area before discretization and is the area after discretization. For line elements, we generate the buffer of line elements with radius and then use the area relative error for calculation (Equation (6)). For point elements, a uniform grid resolution is used for discretization.
Thus, the adaptive discretization problem of multiscale spatio-temporal objects can be transformed into an optimization problem with constraints of the form shown in Equation (7).
where and are the normalized and , respectively. For the spatio-temporal object , we only need to consider the level of the grids that are close in scale to it. Therefore, we first obtain the approximate scale range of the spatio-temporal object by calculating the convex area of the spatio-temporal object . We choose the level with the smallest difference between the average area of the grid [39] and as the upper limit of the search. Search down according to the parameter and let D be the feasible domain of Equation (7); as shown in Equation (8), there exists such a constraint.
As the discretization level for points is the default, we only give the pseudo-code of the discretization algorithm for lines and polygons as Algorithm 1.
| Algorithm 1: Adaptive Discretization Algorithm |
 |
4.3.2. Heterogeneous Graph Model
To describe the associations between multiscale spatio-temporal objects, we map geographic entities and trajectories into a heterogeneous graph. Unlike previous studies, we use heterogeneous rather than homogeneous graphs for the following reasons: Rather than embedding towards the grid, we embed different spatio-temporal objects. We describe the spatio-temporal co-occurrence between spatio-temporal objects through the grid and use the structural relationships of the grid to associate different levels. The nodes in the heterogeneous graph have different categories, which can describe the interaction and association between different spatio-temporal objects. The association semantics between different types of nodes can be explored according to specific requirements. This enhances the generality and scalability of the method and allows for designing sampling algorithms tailored to different applications.
As shown in Figure 5, there are 5 kinds of nodes in the heterogeneous graph , namely , where M is the moving object node, S is the trajectory segment node, H is the grid node, P is the subgeographic entity node, and G is the geographic entity node. M and G are collectively referred to as spatio-temporal object nodes, while S and P are collectively referred to as subobject nodes. Since we are not concerned about the association of moving objects with geographic entities other than spatio-temporal interactions, we describe moving objects by their trajectories. When the trajectory or geographic entity does not exist for a subobject, it is represented by itself instead.
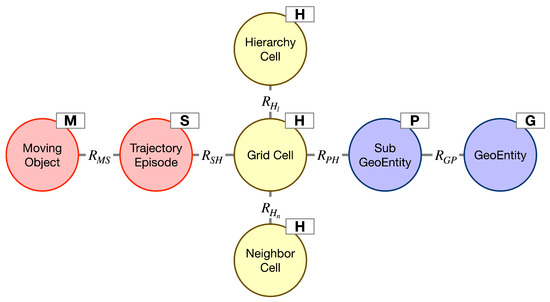
Figure 5.
Illustration of the Association Heterogeneous Graph Model.
Since spatio-temporal objects are discretized into different levels of the grid, we have to consider the structural relations of the grid itself. Additionally, we need to consider the spatio-temporal co-occurrence-based associations between the spatio-temporal objects. The edge in the graph consists of two parts. One part is the containment relationship of spatio-temporal objects and their mapping relationship with the geographic grid, including the edge between moving objects and trajectory segments, the edge between the trajectory segments and geographic grid, the edge between the subgeographic entities and geographic grid, and the edge between geographic entities and subgeographic entities. There is a weight between the edges, where and , indicating the number of times this grid appears in the discretization result of the subobject. This value can reflect the association strength of spatio-temporal objects about a certain grid region. The weights for all edges except , , as shown in Figure 6. The other part is the structural relationship of the geographic grid itself, as shown in the dashed box of Figure 6, including the adjacency relationship between the grid and its surrounding grids (indicated by red lines) as well as the hierarchical relationship between the grid and its neighboring hierarchical grids (indicated by blue lines). For example, for grid , owing to the excellent isotropy of the hexagonal grid, the adjacency relation with and , and the hierarchy relation with the upper grid and the lower grid can be obtained quickly.
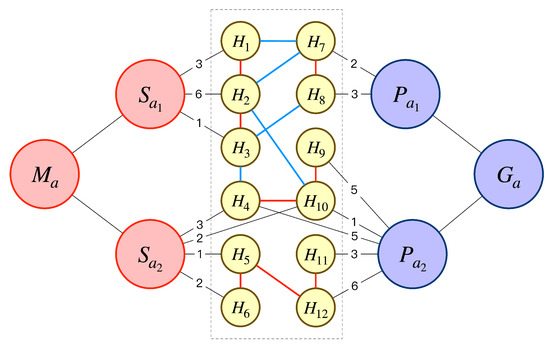
Figure 6.
Example of Association Heterogeneous Graph. The moving object has trajectory segments and , where is discretized with grids , , . The geographic entity has subgeographic entities and , where is discretized with grids are , .
4.4. Embedding
Unlike the previous approach of using feature engineering based on expert knowledge, we obtain the vector representation of each spatio-temporal object by node embedding. This not only captures the interaction information between different spatio-temporal objects in the embedding process but also preserves the spatial proximity information of these objects. We introduce the objective function of embedding learning in Section 4.4.1. A heterogeneous graph sampling algorithm based on biased wandering is proposed in Section 4.4.2. This algorithm is used to implement node embedding for different application contexts.
4.4.1. Objective Function
Our objective is to obtain an embedding representation for objects in a finite spatio-temporal range. The strength of association among these objects is reflected by the cosine similarity of their embedding vectors: the stronger the association is, the higher the cosine similarity. The strength of spatio-temporal association can be reflected by the spatio-temporal co-occurrence frequency [7], which is similar to the learning of word vector representation obtained by word co-occurrence laws in natural language processing. Therefore, we introduce the Skip-gram [44] model in conjunction with the heterogeneous graph constructed in Section 4.3. Given the heterogeneous graph , the objective function of Skip-gram can be expressed as Equation (9):
where denotes the set of neighborhood nodes of node v, and denotes the set of type t neighborhood nodes of node v. For example, the set of type P nodes of in Figure 6 is . denotes the probability of occurrence of node given node v. For , a softmax function is usually used to define [45]: , where is the v-th row of the matrix X, namely the embedding vector of node v. To improve the computational efficiency, we adopt the negative sampling strategy for optimization and set the number of negative samples as K. In this case, Equation (9) can be converted into Equation (10):
where , is a predefined probability distribution, and is the kth negative sample.
4.4.2. Biased Sampling
Since random walks in heterogeneous graphs tend to capture highly visible nodes [46], a meta-path-based algorithm is usually used to constrain sampling in heterogeneous graph embeddings. This can result in sequences of nodes that more accurately reflect information about the structure of the graph. Some scenarios focus more on associations between homogeneous spatio-temporal objects, such as similarity analysis of trajectories and functional analysis of urban areas. In contrast, in environmental management and crime investigation, more attention is paid to associations between heterogeneous spatio-temporal objects. However, realistic data are usually a mixture of several different associations. Similar to the concept of structural equivalence and homogeneous community semantic embedding in node2vec [47], we propose a second-order biased sampling algorithm that uses hyperparameters and multiple meta-paths to generate corresponding sampling strategies for different spatio-temporal associations, enabling diverse association analysis.
The relationship between trajectories and trajectory segments, as well as between geographic entities and subgeographic entities, is a straightforward containment relationship. This allows us to acquire the embedded representations of moving objects and geographic entities by merging their respective subobjects. Therefore, it is only necessary to analyze within the subgraph of , where and . For , given a starting node v and a sampling sequence length , the sampling algorithm will generate a sequence starting with v and containing nodes, where the i-th step transfer probability can be expressed as Equation (11).
where , is the non-normalized transfer probability, and Z is the normalization constant.
Given that the connection among spatio-temporal objects is wide-ranging and nonexclusive, a singular meta-path may skew the embedding reflection of the actual association status. Therefore, we do not adopt predefined meta-paths directly. Instead, we utilize hyperparameters to manage sampling bias and augment the association information captured between homogeneous or heterogeneous objects within a confined range. As shown in Figure 7, assuming that the current node sampled is (i.e., node s in the figure), , whose last visited node is (i.e., node b in the figure), the next visited node is . The transfer probability of visiting from is defined as , where is the weight and is the sampling probability. When , , , where . In contrast, when , as shown in Equation (12), we use the homogeneous parameter m, the heterogeneous parameter n, and the spatial parameter k to control the sampling probability.
where , and the sampling probability is when and are homogeneous spatio-temporal object nodes. The sampling probability is when and are heterogeneous spatio-temporal object nodes; in order to obtain the neighborhood information and hierarchical information of the multilevel grid, we control the sampling of the wandering algorithm among the grid nodes by the spatial parameter k. When is a spatio-temporal object node and is a grid node, the sampling probability is . When is a grid node, we no longer perform the sampling of the neighboring grid so that the association aggregation around the sparse region can be controlled within a reasonable range. In addition, since we are oriented toward spatio-temporal object embedding rather than grid embedding, the grid nodes will be filtered out in the final node sequence so that only spatio-temporal object nodes are retained.
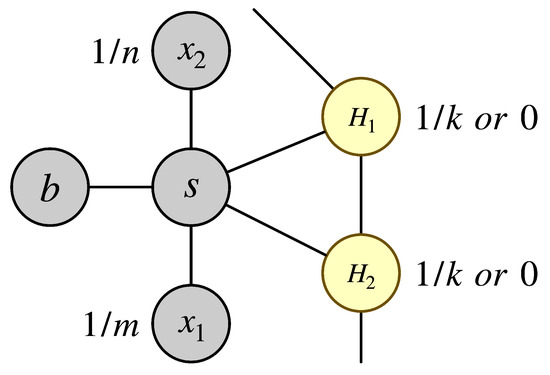
Figure 7.
Illustration of Biased Sampling.
5. Experiment
We tested the effectiveness of our proposed method in discovering and measuring associations between spatio-temporal objects, both homogeneous and heterogeneous, through two quantitative experiments. To visualize the results of the association analysis, we present a case study of it in a visual way.
5.1. Experiment Setup
5.1.1. Data Preparation
We generated a 60 km buffer radius for the US mainland region as a test area for the experiment, with an area size of 9.705 × 10 km, which contains a large number of spatio-temporal objects at different scales. For the geographic entity data, we used the Natural Earth dataset [48] by selecting a part of the data as geographic entity objects, supplemented with OurAirports dataset [49] as airport data. The details are summarized in Table 2.

Table 2.
Statistics of the Geographic Entity Dataset.
For moving object data, we used the open source ADS-B dataset provided by OpenskyNetwork [50], a crowdsourcing-based nonprofit receiving network that has been continuously collecting air traffic monitoring data since 2013. We selected four days of flight trajectory data in June 2022. Since trajectories with lower flight altitudes have a higher probability of being interactively associated with geographic entities, we randomly selected some of the flight trajectories with flight altitudes below 1500 m. After preprocessing according to Section 4.2, we divided the trajectories into datasets A, B, and C. Among these, the International Civil Aviation Organization (ICAO) 24-bit aircraft address in dataset B and C are the same, among which each aircraft has flight records in these 4 days. The preprocessed moving object dataset summary characteristics are shown in Table 3.

Table 3.
Preprocessed moving object dataset summary characteristics.
5.1.2. Parameter Setting
In the association graph construction stage, we set the adaptive discrete hierarchical parameter to 3 so that for each spatio-temporal object, only 3 calculations are needed to obtain a relatively appropriate discretization level. As the point elements are all airports and aprons, whose areas ranges between approximately 0.001 km and 10 km, we set the default level for the point elements to 9, which has a mean grid area of 0.1053 km. We set the buffer radius to 5 m to preserve as much of the line element geometry as possible.
In the embedding phase, we set the vector dimension d of the embedding to 256 in order to retain more association information. Other hyperparameters were set as follows: learning rate , window size , number of sampled sequences of a single node 100, length of sampled sequences , and the number of negative samples .
5.1.3. Evaluation Metrics
We tested the association analysis in terms of both association discovery and association metrics. There was no sequential relationship between the results of association discovery. We used Hitting Ratio in Top K list () [51] to evaluate the results. was defined as shown in Equation (13):
where refers to the spatio-temporal object under the test, is the set of spatio-temporal objects under the test, is the list of spatio-temporal objects in the ground truth that have an association with , and is the list of the top K spatio-temporal objects with the strongest association to output by the model.
The list of results of association metric tests can be sorted according to the strength of association. We used normalized discounted cumulative gain at a particular rank K() [35] to evaluate the association metric results, which was defined as shown in Equation (14):
where IDCG@K is the ideal DCG@K value, which is the DCG@K value of the ground truth list, and DCG@K is defined as shown in Equation (15).
where is the order association of test results at i. For this experiment, takes 0 and 1.
For the ground truth, we will illustrate its generation in the specific experiments.
5.1.4. Baseline
To assess the validity of STO2Vec, the following three models with similar research questions were used as baseline for comparison with STO2Vec.
- Mot2vec [28]: The algorithm is based on the Word2vec model, which uses the trajectories of pedestrians moving between geographic entities to construct a behavioral representation of locations. The algorithm does not use grid partitioning but rather generates IDs of geographic entities based on point clustering and then converts the trajectories into ID sequences for embedding. According to the data characteristics, we use a time window of in the preprocessing stage to label the trajectories with geographic entities, with the minimum spatial resolution being 5 km.
- Hier [32]: This similar algorithm uses a multilevel embedding grid, which aggregates rectangular grid vectors of different levels into fine-grained grids during embedding. Due to the large study area in this paper, we used 100 km and 10 km grid cells in the first and second level, respectively. The fine-grained level uses 1 km grid cells. The embedding dimension is the same as STO2Vec, the first 48 dimensions correspond to 100 km grid, the last 80 dimensions correspond to a 10 km grid, the remaining 128 dimensions correspond to a 1 km grid.
- GCN-L2V [31]: To generate fine-grained grid embeddings, the GCN and Skip-gram models were used to construct spatial graphs and flow graphs to account for both spatial proximity and the movement patterns of moving objects. The algorithm uses a single-level Google S2 grid system. According to the scale of the study area, we mapped trajectories and geographic entities to the 11-level (the average area of each grid area is about 20.2682 km) of Google S2 to generate edges between grids in spatial graphs with a distance threshold of 1 km.
5.2. Homogeneous Association Analysis
To evaluate the effectiveness of association analysis between homogeneous spatio-temporal objects, we examined the effect of the algorithm on the association analysis between moving objects and geographic entities. This evaluation was conducted through two applications: and . We constructed the association heterogeneous graph based on dataset A and geographic entity dataset, in which there are 1,854,380 nodes and 4,986,765 edges. We then performed homogeneous biased sampling in the heterogeneous graph and set the homogeneous parameter to , the heterogeneous parameter to , and the spatial parameter to . Finally, we realized the embedding representation of nodes by embedding the model and calculated the association strength between homogeneous spatio-temporal objects.
5.2.1. Trajectory Similarity Analysis
Ground Truth Generation. For moving objects, the similar association of their trajectories is a typical spatio-temporal association. By comparing the similarity analysis results of trajectories, we could verify the effect of the algorithm in association metrics and discovery between moving objects. There are many existing mature algorithms for trajectory similarity metrics based on geometric features, which accurately calculate the similarity between trajectories by matching point by point.Therefore, we used the dynamic time warping algorithm [52] to generate the similarity matrix between trajectories on the dataset A. We then created the experimental ground truth according to the order of similarity, ensuring that all trajectories had a similarity greater than .
Result for Trajectory Similarity Analysis. We randomly selected 1000 trajectories from the dataset A, using different models to generate a list of similar trajectories for comparison with the ground truth. Since the results of the trajectory similarity metric are order sensitive, we used to evaluate the experimental results. The results are shown in Table 4.

Table 4.
Results of Trajectory Similarity Analysis.
The experimental results show that STO2Vec achieves the best performance. This is because STO2Vec segments trajectories based on the joint information entropy and discretizes trajectory segments according to different spatial resolutions, addressing the problem of uneven spatio-temporal semantic distribution and discovering local similar associations among trajectories better. Mot2Vec converts trajectories into geographic entity sequences at equal time intervals, losing some geometric feature information of the trajectories. Hier also uses a multilevel discretization strategy but needs to set a fixed hierarchical structure based on prior knowledge, without considering the scale of specific spatio-temporal objects. GCN-L2V divides the study area into uniform fine-grained grids but still cannot adaptively discretize the trajectories when facing spatio-temporal objects of multiple scales, resulting in some degree of information loss. In addition, Hier and GCN-L2V do not segment trajectories but convert them into grid sequences using stop detection algorithms. These approaches are more suitable for mining trajectories with obvious stop semantics, such as pedestrian trajectories, while ignoring the association information during the MOVE phase for objects such as aircraft.
5.2.2. Region Association Analysis
Ground Truth Generation. According to the first law of geography [3] and the semantic characteristics of geographic entities, it is known that geographic entities with spatial proximity and semantic similarity are more strongly associated [30]. Region association analysis is often used to discover the functional structure of cities to help in transportation and urban planning. Due to the large-scale of the study area, we consider geospatial entities within the same as clusters that have associations. We generate a ground truth by sorting these clusters according to their distance from each other. The range was generated by the Urban dataset.
Results for Trajectory Similarity Analysis. There are a total of 16,073 other geographic entities with containment relationship with the Urban dataset, from which we randomly selected 2000 for testing. Ideally, the K geographic entities with the greatest association strength with the sample still belong to the region where the sample is located. Moreover, the closer the entities are, the higher the association strength. For this reason, we chose for evaluation. The experimental results are shown in Table 5.

Table 5.
Results of Region Association Analysis.
From the experimental results, GCN-L2V has the best performance for and , while STO2Vec has the best performance for , , and . This is due to the fact that GCN-L2V constructs spatial graphs by performing a large number of distance calculations to accurately describe the distance relationships between the grids. The larger the distance threshold parameter is, the higher the computational cost. The distance threshold parameter used in this experiment was 1 km. Therefore, in and , the geographic entities with greater association strength could be accurately captured by GCN-L2V. However, as the value of K value increases and exceeds the distance threshold, grid association information beyond the threshold becomes difficult to capture, which affects the association accuracy of GCN-L2V. STO2Vec adopts a multilevel discretization strategy, which fully utilizes the structural relationships between grids and obtains more accurate association results over larger ranges. Although Hier also uses a multilevel approach for fine-grained grid embedding, the preset grid resolution cannot match the scale of spatio-temporal objects in the study area accurately, leading to the ignoring of spatial proximity between some geographic entities. Mot2Vec focuses on the association created by human movements between different geographic entities rather than on the spatial association of the entities themselves.
5.3. Heterogeneous Association Analysis
The stronger the association between heterogeneous spatio-temporal objects, the higher the probability of their spatio-temporal co-occurrence. The relationship between moving objects and geographic entities can be used to predict object access patterns. Geographic entities that have a strong association with moving objects are more likely to be accessed by them. Therefore, we use to test heterogeneous spatio-temporal objects. In practical applications, can help people to dispatch and control based on the prediction results, which is important for public security management, airspace control, etc.
Ground Truth Generation. In our experiments, we used different models to output the K geographic entities most associated with moving objects, to test the effectiveness of the algorithm predictions by comparing the actual visit results. The actual access results, namely ground truth, are generated by extracting the geographic entities visited by each moving object from the dataset C.
Result for Trajectory Similarity Analysis. To obtain more information on historical visits, we construct a heterogeneous graph oriented to spatio-temporal association based on the B dataset and the geographic entity dataset, containing nodes and edges, setting the homogeneous parameter , the heterogeneous parameter and the spatial parameter . Since the real visited list is not order sensitive, we used the hit rate as the evaluation metric for this experiment. The experimental results are shown in Table 6.

Table 6.
Results of Heterogeneous Association Analysis.
As shown in Table 6, STO2Vec achieved the best results, while the experimental results of GCN-L2V and Hier were not significantly different, but the results of Mot2Vec were general. STO2Vec can regulate the random walk tendency based on task requirements by adjusting sampling parameters. In this way, it obtains more association information between heterogeneous spatio-temporal objects. This helps to prevent insufficient association information from being present in the embedding results due to differences in structure between those objects. The spatial parameters can aggregate the information around the grid, thus better solving the data sparsity problem. In addition, according to the scale of spatio-temporal objects, the multilevel discretization strategy can describe the geometric features of geographic entities and trajectories more accurately. It provides a more accurate corpus for training models aimed at “spatio-temporal co-occurrence” among heterogeneous objects. Compared with STO2Vec, the discretization method used by GCN-L2V and Hier cannot accurately describe trajectories and geographic entities of different scales. As a result, much local access information is ignored. During clustering, Mot2Vec loses some historical access information of geographic entities, resulting in less information obtained during the embedding process than STO2Vec.
5.4. Case Study
We used a case study to visualize the results of the association analysis in order to better verify the effectiveness of the algorithm. We still used the spatio-temporal association graph constructed in Section 5.2 for embedding learning. To verify the effect of the sampling algorithm on the association results, we modified the sampling hyperparameters by setting the homogeneous parameter to , the heterogeneous parameter to , and the spatial parameter to , thus generating embedding representation results oriented to heterogeneous spatio-temporal object associations. We chose to visualize the results of the association analysis in two areas with significant differences in scale. First, we queried and analyzed the geographic entities associated with the moving objects in the urban area where the geographic entities were dense with a smaller scale. Then, we queried and analyzed the moving objects associated with the geographic entities in the area around the coastline where the moving objects were dense with a larger scale.
5.4.1. Urban Association Analysis
Urban security management often requires the assistance of drones and helicopters, as shown in Figure 8 where the yellow dashed line shows the trajectory of a helicopter conducting security patrols in the urban area of Los Angeles. Los Angeles is the second largest city in the United States, and geographic entities in the urban area mainly include streets, railways, and airports. We selected the 150 geographic entities most strongly associated with the helicopter for visualization. Streets and railways are marked with red lines, and airports are marked with green dots. Moreover, a darker color indicates a stronger association.
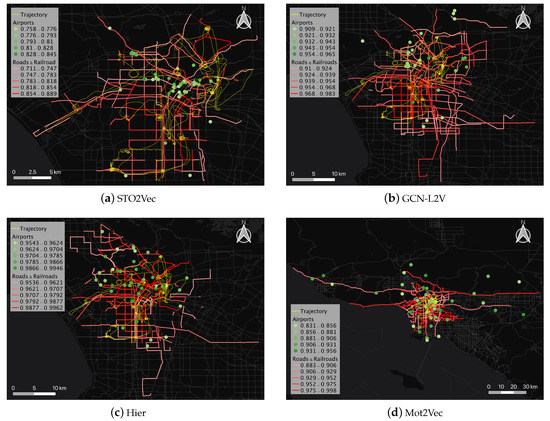
Figure 8.
Results of Urban Association Analysis.
Figure 8a shows the output of STO2Vec; the comparison shows that the associated geographic entities output by STO2Vec are more concentrated in spatial distribution. The strength of association basically matches the spatial characteristics of the trajectory, which can reflect the interaction between this helicopter and various types of geographic entities in urban areas more accurately. Owing to the fact that STO2Vec discretizes the trajectories by segmenting them to different spatial resolutions, it is able to adaptively match the scale size of the trajectories and geographic entities. In data-intensive areas such as urban areas, fine-grained geographic entities are described by a high-level grid that retains most of the spatial characteristics of urban streets, railways, airports, and helicopter trajectories. Furthermore, as can be seen from the color shades of the elements and their corresponding association strength values, STO2Vec has a more dispersed distribution of association strength values than does GCN-L2V and Hier (e.g., 0.758–0.845 for airports and 0.711–0.889 for roads and railroads in Figure 8a); this indicates that the objects are more significantly different in STO2Vec embedding space. Without changing the association structure, the parameters can be set to adjust the sampling trend to the application requirements, which allows the model to learn more information about the interaction between the helicopter and the geographic entities.
As shown in Figure 8b,c, the output of GCN-L2V and Hier can reflect the association between moving objects and geographic entities to some extent. Both models take into account the context of surrounding neighboring areas. However, compared with those of STO2Vec, their associated geographic entities are spatially more dispersed. Since the scale of the upper grid in the Hier model is too large for spatio-temporal objects in the region, the model aggregates information from a large area around the trajectory during training. This can solve the problem of data sparsity but also affects the accuracy of local association analysis. GCN-L2V has difficulty associating smaller-scale objects such as airports. The 11-level grid of Google S2 (with an average grid area of approximately 20.2682 km) is still relatively coarse for a geographic entity in an urban area. The fixed grid resolution makes it difficult to take into account different scales of geographic entities such as railways and airports; therefore, the model learns less variation in features, and the distribution of association strength values is more concentrated. As shown in Figure 8d, the output of Mot2Vec is more dispersed, as most of the spatial proximity information of geographic entities is lost in the process of converting trajectories into ID sequences. For helicopters with strong mobility, the time window size of trajectory segmentation also affects the embedding accuracy.
For the area around the coastline, such as the Martha’s Vineyard coastline area shown by the yellow line in Figure 9a, the island is approximately 32 km long and 3–16 km wide. Summer is the peak tourist season for the area. Therefore, the dataset contains a large number of flight trajectories for tourists traveling to the area and helicopter flight trajectories for sightseeing around the island. The red lines in Figure 9 show the trajectories of the associated moving objects. The top 40 trajectories with the strongest association to the island’s coastline were selected for visualization. As shown in Figure 9a, since STO2Vec segments the trajectory based on joint information entropy, the model can output more accurate results in the form of trajectory segments. Trajectory segments of the moving object during the move phase around the island are most strongly associated with the coastline.This is due to the ability of STO2Vec to use a multilevel grid to portray the geometry of the coastline relatively accurately during the discretization of geographic entities. Moreover, the geographic entities in the area around the coastline are more sparse. The biased sampling algorithm allows the embedding results to be unaffected by the large number of intertrajectory associations.Segments of trajectories that fly around islands and hover near coastlines are able to generate rich co-occurrence contexts with coastline entities. Other trajectory segments that have basic topological associations, such as those adjacent or crossing, exhibited a weaker association strength due to the sparse structure of the association graph.
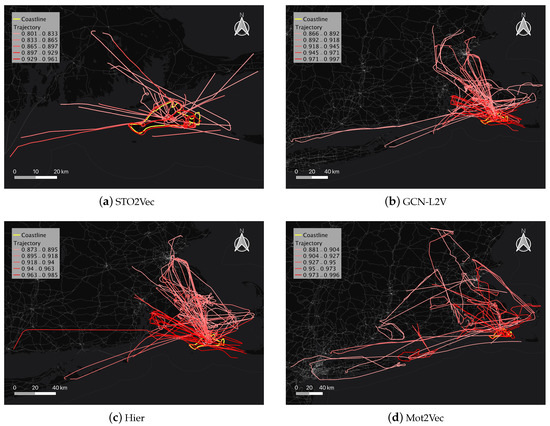
Figure 9.
Results of Coastline Association Analysis.
5.4.2. Coastline Association Analysis
The output of other models can only be visualized as trajectories, as shown in Figure 9b–d. Since geographic entities are sparse and trajectories are richer, a large number of association interactions are covered by similar or topological associations between trajectories. Therefore, the three models tend to discover flying trajectory-based associations between the island, the mainland, and adjacent islands. However, due to the uneven semantic distribution of trajectories, some of the stronger local associations (e.g., local flight around the island, local hovering) are diluted by the full trajectories. As a result, the trajectory segments that are strongly associated with the coastline in STO2Vec do not fully manifest in the output results of the three comparison models. Furthermore, considering spatio-temporal objects of different scales during selection of grid resolution is challenging for Hier and GCN-L2V. Consequently, their analysis may not be accurate or complete. Mot2Vec does not use a discretization approach to consider spatial associations between geographic entities. Accordingly, when data is sparse in specific regions such as the coastline, it relies on the IDs of distributed geographic entities along the continental coast for context rather than grid cells near the coastline.
6. Discussion and Conclusions
In this paper, we proposed a multiscale spatio-temporal object representation method, named STO2Vec, for association analysis. The method aims to address the issue of scale differences among spatio-temporal objects affecting the accuracy of analysis in the association analysis. To this end, we decompose spatio-temporal objects of varying scales into grids of different resolutions and obtain their representations by node embedding of an associated heterogeneous graph. During the embedding process, we enhance its scalability through biased sampling. Quantitative experiments demonstrated that STO2Vec could outperform other methods in various spatio-temporal association analysis applications, such as trajectory similarity analysis, regional association analysis, and visit prediction. This confirms that the resulting representation of STO2Vec retains more spatio-temporal association information by reflecting the scale differences. Additionally, the case analysis results demonstrated the effectiveness of STO2Vec in accurately measuring and discovering associations. These associations occur between spatio-temporal objects that differ in scale, highlighting the ability of STO2Vec to solve problems related to multiscale spatio-temporal object association analysis.
Representing geographic entities as point features can simplify computation but loses their spatial characteristics and most association information. Dividing spatio-temporal objects into fixed grids retains some of the features but struggles to consider scale differences or nonuniform regions. Presetting multilevel grids with prior knowledge partly alleviates scale difference impacts, but discerning suitable levels is difficult. Compared to other methods, STO2Vec provides better representation of various scales of spatio-temporal objects, enabling more accurate measurement and discovery of complex spatio-temporal association relationships. However, STO2Vec has limitations: representing object results in vector form—not grids—sacrifices flexibility, hindering incremental updates or aggregation while placing timeliness demands on data.
In the next step of our research, the focus will be on combining the behavior patterns of moving objects. The aim is to identify specific association semantics that exist between spatio-temporal objects. This will involve constructing a fine-grained association graph enabling deeper association analysis applications.
Author Contributions
Conceptualization, Luo Chen, Anran Yang and Nanyu Chen; methodology, Nanyu Chen; writing—original draft, Nanyu Chen; writing—review and editing, Luo Chen, Anran Yang, Wei Xiong and Nanyu Chen; funding acquisition, Luo Chen and Ning Jing All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 41971362 and 42101432), the Natural Science Foundation of Hunan Province (grant no. 2022JJ40546), and the Innovation Science Fund of NUDT (grant no. 22-ZZCX-058).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are publicly available on the open data portal of The OpenSky Network (https://opensky-network.org, accessed on 15 October 2022), NaturalEarth (https://www.naturalearthdata.com/, accessed on 10 November 2022), and OurAirports (https://ourairports.com/, accessed on 23 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| POI | point of interest |
| OD | origin destination |
| UTM | Universal Transverse Mercator |
| GPS | global positioning system |
| ICAO | International Civil Aviation Organization |
| HR | hitting ratio |
| NDCG | normalized discounted cumulative gain |
References
- Hamdi, A.; Shaban, K.; Erradi, A.; Mohamed, A.; Rumi, S.K.; Salim, F.D. Spatiotemporal Data Mining: A Survey on Challenges and Open Problems. Artif. Intell. Rev. 2022, 55, 1441–1488. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Jiang, Z.; Shekhar, S. Spatiotemporal Data Mining: A Survey. arXiv 2022, arXiv:2206.12753. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, Q.; Zhang, Y.T.; Du, Z.Q.; Zhou, Y.; Xie, X.; He, F. An Adaptive Organization Method of Geovideo Data for Spatio-Temporal Association Analysis. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2015, II-4/W2, 29–34. [Google Scholar] [CrossRef]
- Crivellari, A.; Ristea, A. CrimeVec—Exploring Spatial-Temporal Based Vector Representations of Urban Crime Types and Crime-Related Urban Regions. ISPRS Int. J. Geo-Inf. 2021, 10, 210. [Google Scholar] [CrossRef]
- Riyadh, M.; Mustapha, N.; Riyadh, D. Review of Trajectories Similarity Measures in Mining Algorithms. In Proceedings of the 2018 Al-Mansour International Conference on New Trends in Computing, Communication, and Information Technology (NTCCIT), Baghdad, Iraq, 14–15 November 2018; pp. 36–40. [Google Scholar] [CrossRef]
- Cai, J.; Deng, M.; Guo, Y.; Xie, Y.; Shekhar, S. Discovering Regions of Anomalous Spatial Co-Locations. Int. J. Geogr. Inf. Sci. 2021, 35, 974–998. [Google Scholar] [CrossRef]
- Noureddine, H.; Ray, C.; Claramunt, C. A Hierarchical Indoor and Outdoor Model for Semantic Trajectories. Trans. GIS 2022, 26, 214–235. [Google Scholar] [CrossRef]
- Sakouhi, T.; Akaichi, J. Dynamic and Multi-Source Semantic Annotation of Raw Mobility Data Using Geographic and Social Media Data. Pervasive Mob. Comput. 2021, 71, 101310. [Google Scholar] [CrossRef]
- Kontarinis, A.; Zeitouni, K.; Marinica, C.; Vodislav, D.; Kotzinos, D. Towards a Semantic Indoor Trajectory Model: Application to Museum Visits. Geoinformatica 2021, 25, 311–352. [Google Scholar] [CrossRef]
- Alvares, L.O.; Bogorny, V.; Kuijpers, B.; de Macedo, J.A.F.; Moelans, B.; Vaisman, A. A Model for Enriching Trajectories with Semantic Geographical Information. In Proceedings of the 15th Annual ACM International Symposium on Advances in Geographic Information Systems—GIS’07, Seattle, WA, USA, 7–9 November 2007; p. 1. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, M.; Han, J.; Ji, G.; Liu, X. Efficient Semantic Enrichment Process for Spatiotemporal Trajectories. Wirel. Commun. Mob. Commun. 2021, 2021, 4488781. [Google Scholar] [CrossRef]
- Vidal-Filho, J.N.; Times, V.C.; Lisboa-Filho, J.; Renso, C. Towards the Semantic Enrichment of Trajectories Using Spatial Data Infrastructures. ISPRS Int. J. Geo-Inf. 2021, 10, 825. [Google Scholar] [CrossRef]
- Ibrahim, A.; Zhang, H.; Clinch, S.; Harper, S. From GPS to Semantic Data: How and Why—A Framework for Enriching Smartphone Trajectories. Computing 2021, 103, 2763–2787. [Google Scholar] [CrossRef]
- Ying, J.J.C.; Lee, W.C.; Tseng, V.S. Mining Geographic-Temporal-Semantic Patterns in Trajectories for Location Prediction. ACM Trans. Intell. Syst. Technol. 2013, 5, 1–33. [Google Scholar] [CrossRef]
- Noureddine, H.; Ray, C.; Claramunt, C. Semantic Trajectory Modelling in Indoor and Outdoor Spaces. In Proceedings of the 2020 21st IEEE International Conference on Mobile Data Management (MDM), Versailles, France, 30 June–3 July 2020; pp. 131–136. [Google Scholar] [CrossRef]
- Choi, D.W.; Pei, J.; Heinis, T. Efficient Mining of Regional Movement Patterns in Semantic Trajectories. Proc. VLDB Endow. 2017, 10, 2073–2084. [Google Scholar] [CrossRef]
- Wan, C.; Zhu, Y.; Yu, J.; Shen, Y. SMOPAT: Mining Semantic Mobility Patterns from Trajectories of Private Vehicles. Inf. Sci. 2018, 429, 12–25. [Google Scholar] [CrossRef]
- Fang, Z.; Du, Y.; Zhu, X.; Chen, L.; Gao, Y.; Jensen, C.S. Deep Spatially and Temporally Aware Similarity Computation for Road Network Constrained Trajectories. arXiv 2022, arXiv:2112.09339. [Google Scholar] [CrossRef]
- Karami, F.; Malek, M.R. Trajectory Similarity Measurement: An Enhanced Maximal Travel Match Method. Trans. GIS 2021, 25, 1485–1503. [Google Scholar] [CrossRef]
- Lehmann, A.L.; Alvares, L.O.; Bogorny, V. SMSM: A Similarity Measure for Trajectory Stops and Moves. Int. J. Geogr. Inf. Sci. 2019, 33, 1847–1872. [Google Scholar] [CrossRef]
- Xiang, L.; Wu, T.; Ettema, D. An Intersection-Based Trajectory-Region Movement Study. Trans. GIS 2017, 21, 701–721. [Google Scholar] [CrossRef]
- Sun, Z.; Jiao, H.; Wu, H.; Peng, Z.; Liu, L. Block2vec: An Approach for Identifying Urban Functional Regions by Integrating Sentence Embedding Model and Points of Interest. ISPRS Int. J. Geo-Inf. 2021, 10, 339. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, L.; Yan, Z.; Wu, S. A GloVe-Based POI Type Embedding Model for Extracting and Identifying Urban Functional Regions. ISPRS Int. J. Geo-Inf. 2021, 10, 372. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Yao, Y.; Hong, Y.; He, J.; Jiang, Z.; Sun, J. The Traj2Vec Model to Quantify Residents’ Spatial Trajectories and Estimate the Proportions of Urban Land-Use Types. Int. J. Geogr. Inf. Sci. 2021, 35, 193–211. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, W.; Xia, J.; Ma, Y.; Zhang, Y.; Luo, Y.; Huang, Z.; Liu, L. Location2vec: A Situation-Aware Representation for Visual Exploration of Urban Locations. IEEE Trans. Intell. Transport. Syst. 2019, 20, 3981–3990. [Google Scholar] [CrossRef]
- Du, J.; Chen, Y.; Wang, Y.; Pu, J. Zone2Vec: Distributed Representation Learning of Urban Zones. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 880–885. [Google Scholar] [CrossRef]
- Crivellari, A.; Beinat, E. From Motion Activity to Geo-Embeddings: Generating and Exploring Vector Representations of Locations, Traces and Visitors through Large-Scale Mobility Data. ISPRS Int. J. Geo-Inf. 2019, 8, 134. [Google Scholar] [CrossRef]
- Jenkins, P.; Farag, A.; Wang, S.; Li, Z. Unsupervised Representation Learning of Spatial Data via Multimodal Embedding. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1993–2002. [Google Scholar] [CrossRef]
- Woźniak, S.; Szymański, P. Hex2vec: Context-Aware Embedding H3 Hexagons with OpenStreetMap Tags. In Proceedings of the 4th ACM SIGSPATIAL International Workshop on AI for Geographic Knowledge Discovery, Beijing, China, 2–5 November 2021; pp. 61–71. [Google Scholar] [CrossRef]
- Tian, C.; Zhang, Y.; Weng, Z.; Gu, X.; Chan, W.K. Learning Fine-grained Location Embedding from Human Mobility with Graph Neural Networks. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Shimizu, T.; Yabe, T.; Tsubouchi, K. Enabling Finer Grained Place Embeddings Using Spatial Hierarchy from Human Mobility Trajectories. In Proceedings of the 28th International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2020; pp. 187–190. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Zhang, Y.; Wang, S.; Shah, R.R.; Zimmermann, R. GPS2Vec: Towards Generating Worldwide GPS Embeddings. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 5–8 November 2019; pp. 416–419. [Google Scholar] [CrossRef]
- Souza, A.P.R.; Renso, C.; Perego, R.; Bogorny, V. MAT-Index: An Index for Fast Multiple Aspect Trajectory Similarity Measuring. Trans. GIS 2022, 26, 691–716. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, Z.; Huang, C.; Yin, H.; Yang, Q.; Shao, J. Semantic Trajectory Representation and Retrieval via Hierarchical Embedding. Inf. Sci. 2020, 538, 176–192. [Google Scholar] [CrossRef]
- Chu, C.; Zhang, H.; Lu, F. Inferring Consumption Behavior of Customers in Shopping Malls from Indoor Trajectories. J. Geo-Inf. Sci. 2022, 24, 1034–1046. [Google Scholar]
- Niemeyer, G. Geohash. Available online: http://geohash.org/ (accessed on 16 October 2022).
- GitHub Inc. S2 Geometry. Available online: https://s2geometry.io (accessed on 21 October 2022).
- Uber Technologies Inc. H3: Uber’s Hexagonal Hierarchical Spatial Index. Available online: https://eng.uber.com/h3 (accessed on 17 December 2022).
- Pelekis, N.; Theodoulidis, B.; Kopanakis, I.; Theodoridis, Y. Literature Review of Spatio-Temporal Database Models. Knowl. Eng. Rev. 2004, 19, 235–274. [Google Scholar] [CrossRef]
- Tao, Y.; Both, A.; Silveira, R.I.; Buchin, K.; Sijben, S.; Purves, R.S.; Laube, P.; Peng, D.; Toohey, K.; Duckham, M. A Comparative Analysis of Trajectory Similarity Measures. GIsci. Remote Sens. 2021, 58, 643–669. [Google Scholar] [CrossRef]
- Mai, G.; Janowicz, K.; Hu, Y.; Gao, S.; Yan, B.; Zhu, R.; Cai, L.; Lao, N. A Review of Location Encoding for GeoAI: Methods and Applications. Int. J. Geogr. Inf. Sci. 2022, 36, 639–673. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, C.; Cheng, W. Area Error Analysis of Vector to Raster Conversion of Areal Feature in GIS. Acta Geod. Cartogr. Sin. 2007, 36, 344–350. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed Representations of Words and Phrases and Their Compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Burges, C.J., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Dong, Y.; Chawla, N.V.; Swami, A. Metapath2vec: Scalable Representation Learning for Heterogeneous Networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar] [CrossRef]
- Sun, Y.; Han, J.; Yan, X.; Yu, P.S.; Wu, T. PathSim: Meta Path-Based Top-K Similarity Search in Heterogeneous Information Networks. Proc. VLDB Endow. 2011, 4, 992–1003. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. Node2vec: Scalable Feature Learning for Networks. arXiv 2016, arXiv:1607.00653. [Google Scholar] [CrossRef]
- Kelso, N.V.; Patterson, T. Natural Earth. 2022. Available online: https://www.naturalearthdata.com/ (accessed on 10 November 2022).
- Megginson, D. Ourairports. 2022. Available online: https://ourairports.com (accessed on 23 December 2022).
- Schafer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing up OpenSky: A Large-Scale ADS-B Sensor Network for Research. In Proceedings of the IPSN-14 Proceedings of the 13th International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar] [CrossRef]
- Han, P.; Wang, J.; Yao, D.; Shang, S.; Zhang, X. A Graph-based Approach for Trajectory Similarity Computation in Spatial Networks. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 556–564. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. Scaling up Dynamic Time Warping for Datamining Applications. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 285–289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).