Location Optimization of VTS Radar Stations Considering Environmental Occlusion and Radar Attenuation
Abstract
:1. Introduction
2. Related Works
- A method for judging environmental occlusion induced by obstacles in three-dimensional space is proposed.
- A method for evaluating radar attenuation in three-dimensional space is proposed.
- Taking into account the fact that radar works in a circular pattern, a VTS radar station location optimization model is constructed based on the coverage model.
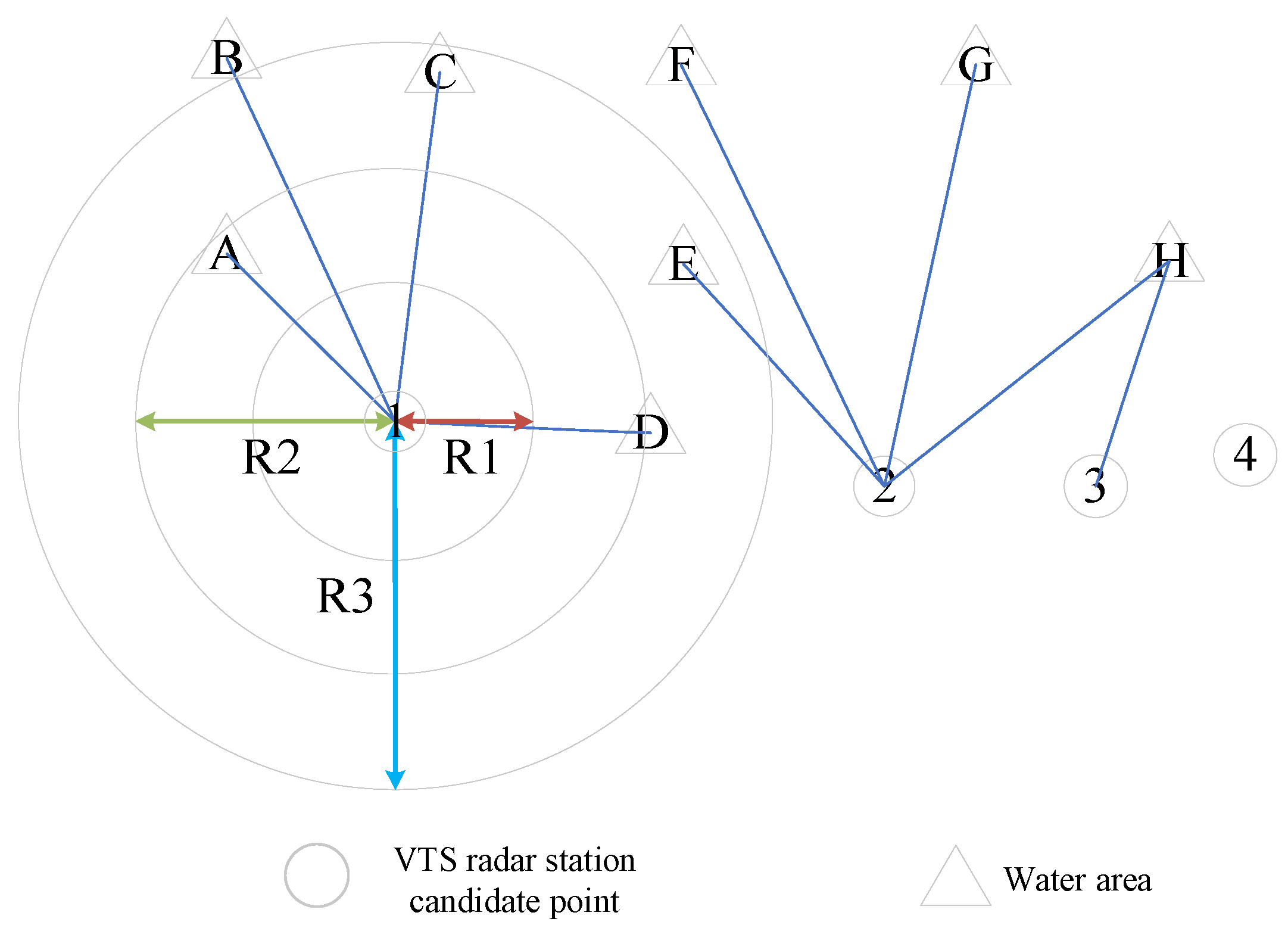
3. Problem Description
3.1. Problem Description
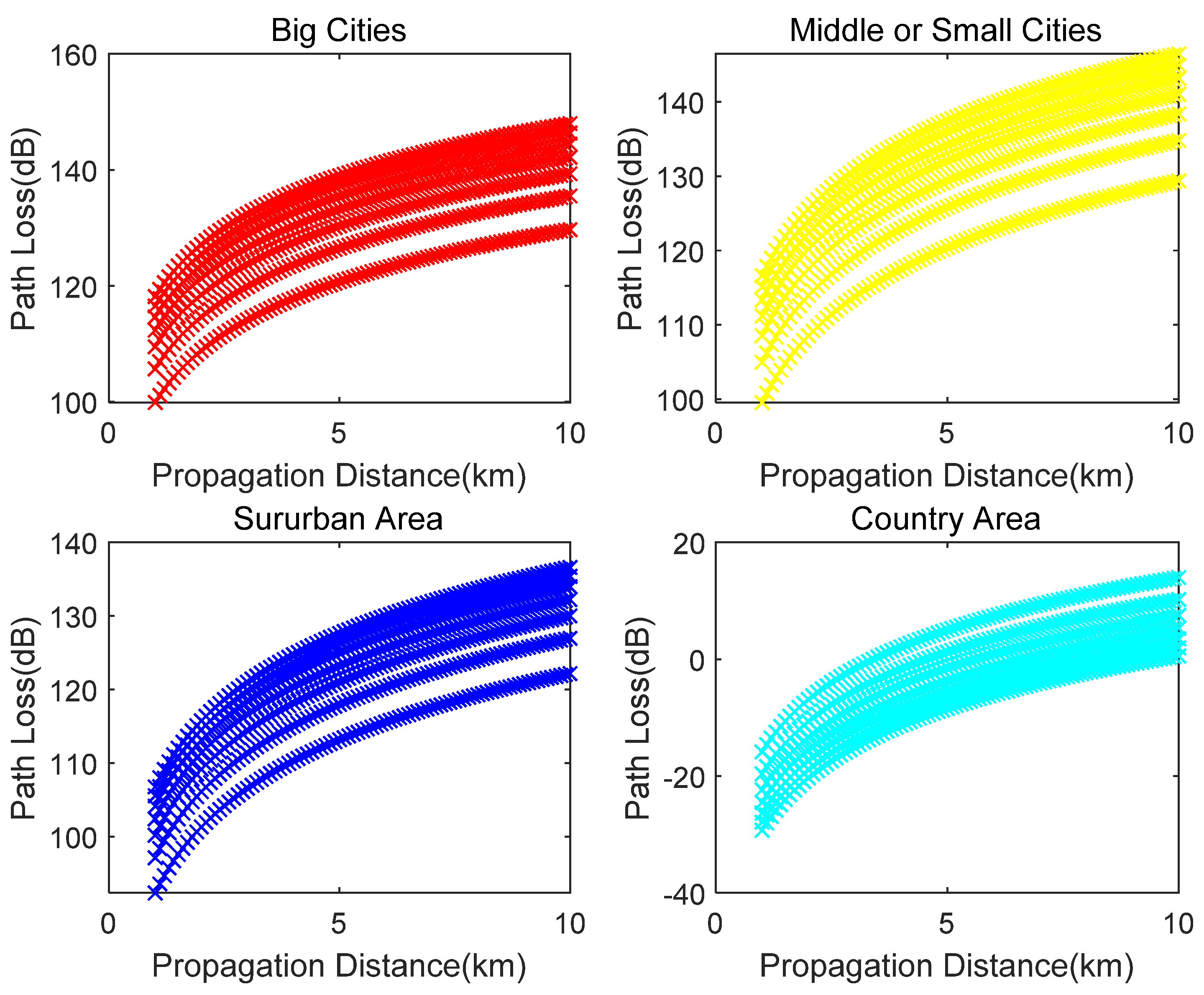
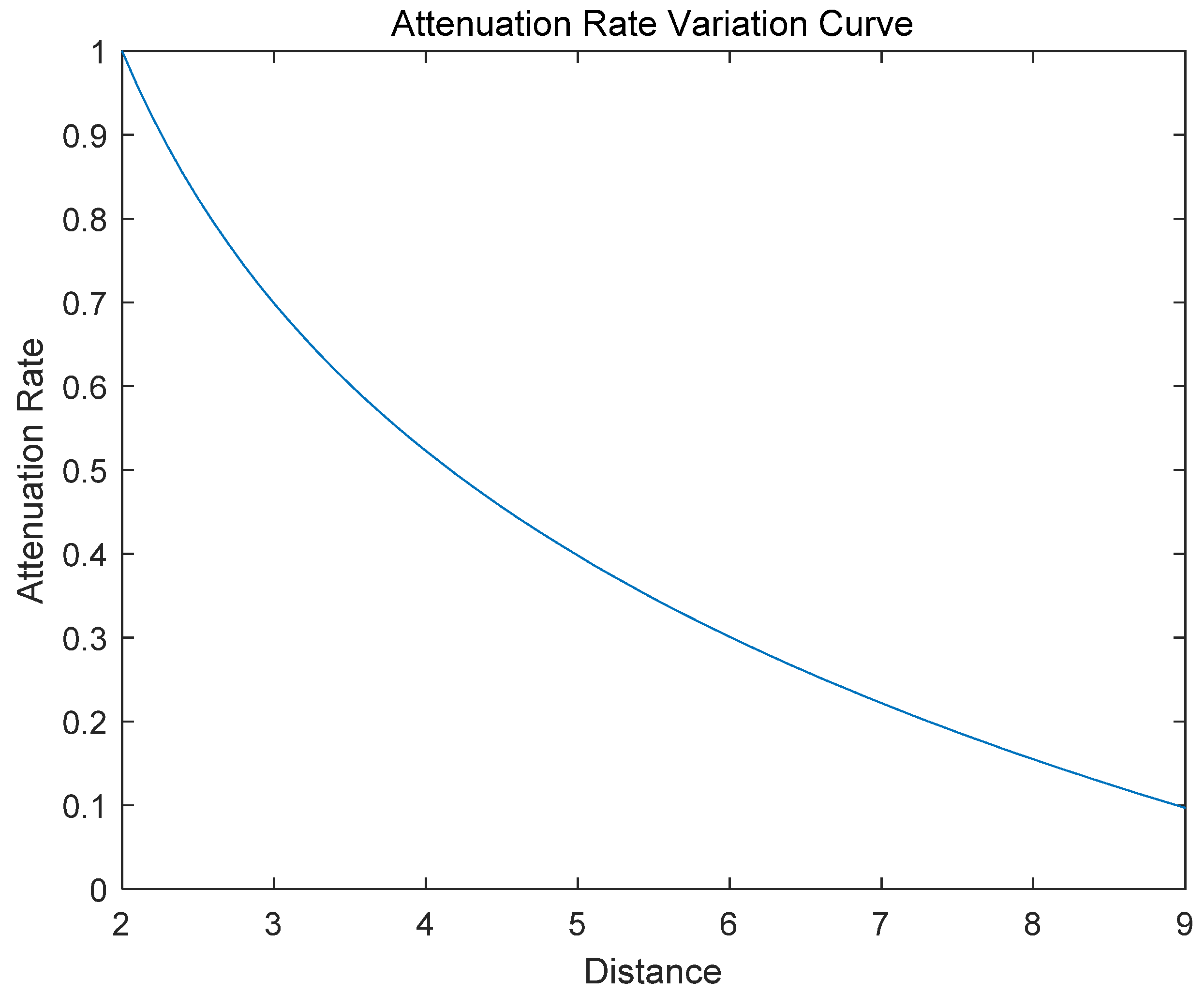
3.2. Radar Attenuation Evaluation
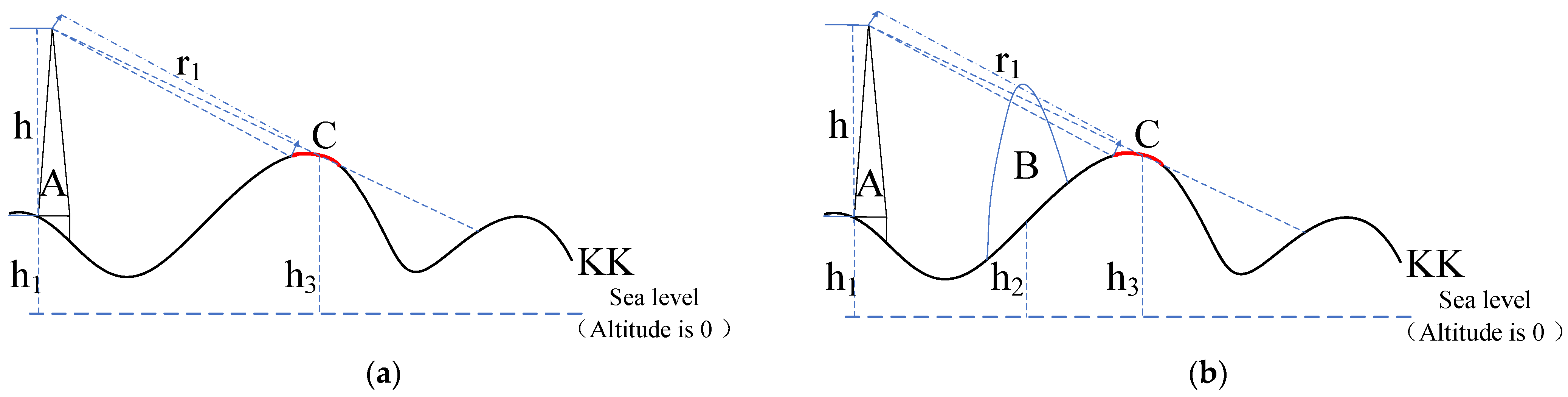
3.3. Environmental Occlusion Judgment and Evaluation Method
3.4. Mathematical Model
3.4.1. Assumption
- (1)
- External surroundings remain unchanged, which means that the number and elevation of obstacles, water area, and potential VTS radar station candidate points will remain unchanged.
- (2)
- The number, geography area, and elevation of covered water areas are known.
- (3)
- The total number and elevation of potential VTS radar station candidate points are known.
- (4)
- The types and their exact parameters of radar are known, as is the height of the radar station.
- (5)
- The number and penetration rate of obstacles, as well as the formula of attenuation function, are specified in advance.
3.4.2. Problem Formulation
- (1)
- Coverage rate computation
- (2)
- Area coverage rate calculation
- (3)
- Model Construction
4. Algorithm Description
5. Experimental Results
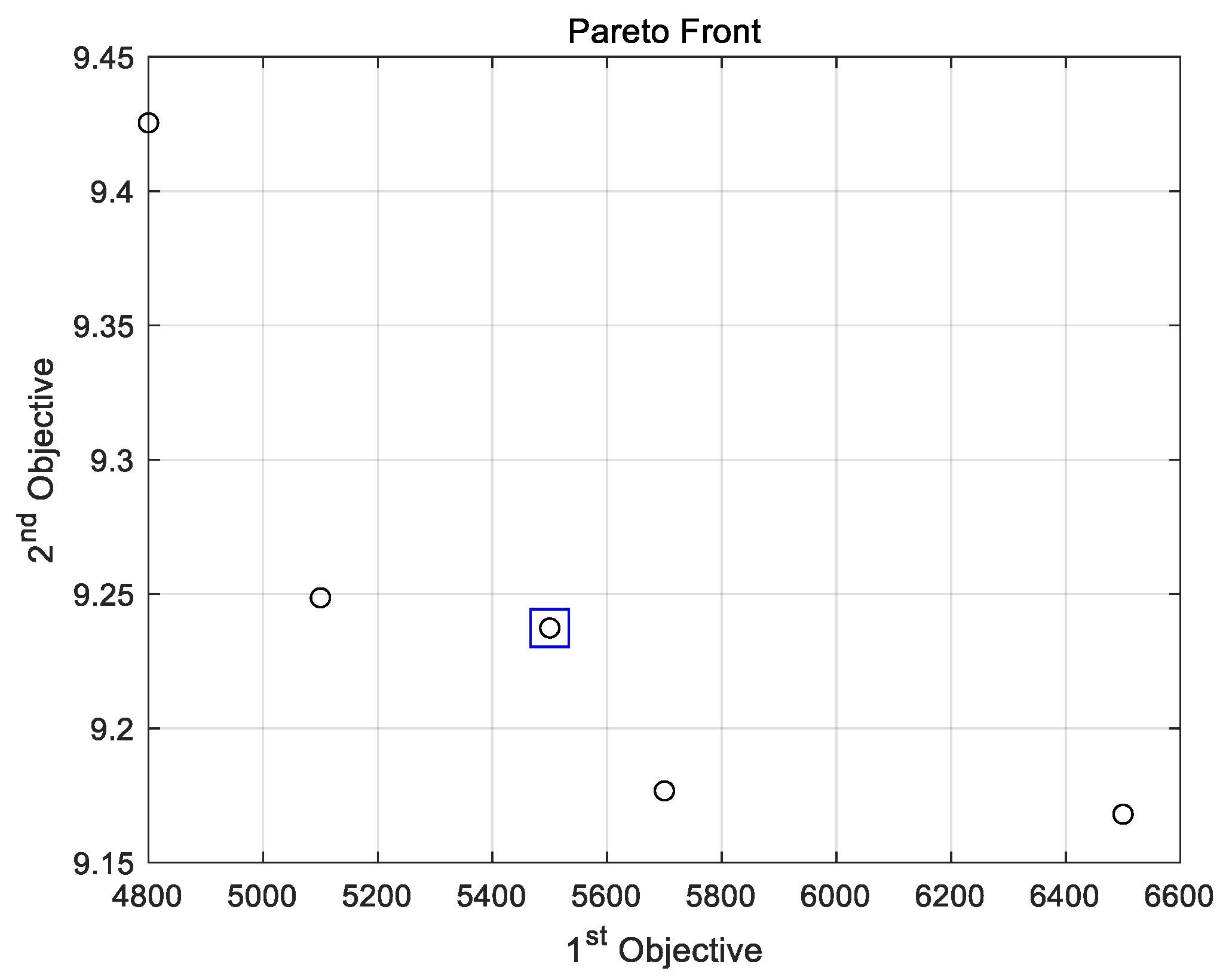
5.1. Numerical Analysis
5.2. Case Study
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| Set and Matrix | |
| Set of water area | |
| Set of VTS radar station candidate points | |
| Set of VTS radar type | |
| Set of obstacles | |
| Euclidean distance matrix between water areas and candidate points in three-dimensional space | |
| Coverage rate matrix between water areas and candidate points | |
| Parameters | |
| Number of times of water area to be covered | |
| Threshold of number of times of water area | |
| The area coverage rate of water area | |
| Geography area of water area | |
| Total geographical area of the water area | |
| Fixed construction cost of radar station candidate | |
| Configuration cost of radar type | |
| Monitoring probability of radar station candidate when radar type is configured | |
| Minimum effective radius of radar | |
| Maximum effective radius of radar | |
| Attenuation function | |
| Euclidean distance between water area and candidate point | |
| Coverage rate between water area and candidate point | |
| Penetration rate of obstacle | |
| Decision variables | |
| Binary variable, equals 1 if a radar station is constructed at a chosen radar station candidate point and equals 0 otherwise. | |
| Binary variable, equals 1 if a radar station is constructed at a chosen radar station candidate point and the radar type is chosen to be configured meanwhile and equals 0 otherwise. | |
References
- National Bureau of Statistics of the People’s Republic of China. China. 2020. Available online: http://www.stats.gov.cn/ (accessed on 3 March 2022).
- Ministry of Transport of the People’s Republic of China. China. 2020. Available online: http://www.mot.gov.cn (accessed on 3 March 2022).
- Rudan, I.; Francic, V.; Valcic, M.; Sumner, M. Early detection of Vessel collision situations in a vessel traffic services area. Transport 2020, 35, 121–132. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.X.; Yu, F.F.; Zheng, Y.Z.; Zhou, C.-H.; Gao, J.-J.; Cheng, X.-D. Research on modeling and simulation in overshadowing influence of coastal building on vessel traffic service radar. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Lee, G.; Kim, S.Y.; Lee, M.K. Economic evaluation of vessel traffic service (VTS): A contingent valuation study. Mar. Policy 2015, 61, 149–154. [Google Scholar] [CrossRef]
- Kao, S.; Lee, K.; Chang, K.; Ko, M.-D. A Fuzzy Logic Method for Collision Avoidance in Vessel Traffic Service. J. Navig. 2007, 60, 17–31. [Google Scholar] [CrossRef]
- Su, C.M.; Chang, K.Y.; Cheng, C.Y. Fuzzy decision on optimal collision avoidance measures for ships in vessel traffic service. J. Mar. Sci. Technol. 2012, 20, 38–48. [Google Scholar] [CrossRef]
- Tsou, M.C. Discovering Knowledge from AIS Database for Application in VTS. J. Navig. 2010, 63, 449–469. [Google Scholar] [CrossRef]
- Tsou, M.C. Online analysis process on Automatic Identification System data warehouse for application in vessel traffic service. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 230, 199–215. [Google Scholar] [CrossRef]
- Relling, T.; Luetzhoeft, M.; Hildre, H.P.; Ostnes, R. How vessel traffic service operators cope with complexity–only human performance absorbs human performance. Theor. Issues Ergon. Sci. 2020, 21, 418–441. [Google Scholar] [CrossRef]
- Chen, H.C.; Lu, H.A.; Lee, H.H. An assessment of job performance of vessel traffic service operations using an analytic hierarchy process and a grey interval measure. J. Mar. Sci. Technol. 2013, 21, 522–531. [Google Scholar]
- Praetorius, G.; Hollnagel, E.; Dahlman, J. Modelling Vessel Traffic Service to understand resilience in everyday operations. Re-Liabil. Eng. Syst. Saf. 2015, 141, 10–21. [Google Scholar] [CrossRef]
- Jia, S.; Wu, L.X.; Meng, Q. Joint Scheduling of Vessel Traffic and Pilots in Seaport Waters. Transp. Sci. 2020, 54, 1495–1515. [Google Scholar] [CrossRef]
- Relling, T.; Lutzhoft, M.L.; Ostnes, R.; Hildre, H.P. The contribution of Vessel Traffic Services to safe coexistence between automated and conventional vessels. Marit. Policy Manag. 2021; early access. [Google Scholar]
- Brodje, A.; Lundh, M.; Jenvald, J.; Dahlman, J. Exploring non-technical miscommunication in vessel traffic service operation. Cogn. Technol. Work 2013, 15, 347–357. [Google Scholar] [CrossRef]
- Mansson, J.; Lutzhoft, M.; Brooks, B. Joint Activity in the Maritime Traffic System: Perceptions of Ship Masters, Maritime Pilots, Tug Masters, and Vessel Traffic Service Operators. J. Navig. 2017, 70, 547–560. [Google Scholar] [CrossRef]
- Costa, N.A.; MacKinnon, S.N. Non-technical communication factors at the Vessel Traffic Services. Cogn. Technol. Work 2018, 20, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Chen, C.; Xu, G.; Chang, D.; Khoo, L.P. Causal Factors and Symptoms of Task-Related Human Fatigue in Vessel Traffic Service: A Task-Driven Approach. J. Navig. 2020, 73, 1340–1357. [Google Scholar] [CrossRef]
- Malagoli, A.; Corradini, M.; Corradini, P.; Shuett, T.; Fonda, S. Towards a method for the objective assessment of cognitive workload: A pilot study in vessel traffic service (VTS) of maritime domain. In Proceedings of the 2017 IEEE 3rd International Forum on Research and Technologies for Society and Industry (RTSI), Modena, Italy, 11–13 September 2017; pp. 1–6. [Google Scholar]
- Xu, G.Y.; Chen, C.H.; Li, F.; Qiu, X. AIS data analytics for adaptive rotating shift in vessel traffic service. Ind. Manag. Data Syst. 2020, 120, 749–767. [Google Scholar] [CrossRef]
- Lei, Z.; Tao, M.; Kun, H.; Wei, Q. Advances in full control of electromagnetic waves with meta-surfaces. Adv. Opt. Mate-Rials 2016, 4, 818–833. [Google Scholar]
- Singh, Y. Comparison of Okumura, Hata and COST-231 Models on the Basis of Path Loss and Signal Strength. Int. J. Comput. Appl. 2012, 59, 37–45. [Google Scholar] [CrossRef]
- Muhammad, F.; Amr, E.K.; Ahmed, S. Empirical Correction of the Okumura-Hata Model for the 900 MHz band in Egypt. In Proceedings of the IEEE 2013 Third International Conference on Communications and Information Technology, Beirut, Lebanon, 19–21 June 2013; pp. 386–395. [Google Scholar]
- Tasmeeh, A.; Fariha, J.; Mannan, P. Inspection of Picocell’s Performance using Different Models in Different Regions. In Proceedings of the IEEE 2020 5th International Conference on Computer and Communication Systems, Shanghai, China, 22–24 February 2020. [Google Scholar]
- Mahmoud, A.; Zia, N.; Hassan, A. Applicability of Okumura-Hata Model for Wireless Communication Systems in Oman. In Proceedings of the IEEE International IOT, Electronics and Mechatronics Conference, Vancouver, BC, Canada, 9–12 September 2020. [Google Scholar]
- Vera, D.; Ruslan, A. Ordinary Least Squares in COST 231 Hata key parameters optimization base on experimental data. In Proceedings of the IEEE 2017 International Multi-Conference on Engineering, Computer and Information Sciences, Hong Kong, 15–17 March 2017. [Google Scholar]
- Keun, Y.; Won, J.; Ho, K. Intelligent Ray Tracing for the Propagation Prediction. In Proceedings of the 2012 IEEE Antennas and Propagation Society International Symposium, Chicago, IL, USA, 8–14 July 2012. [Google Scholar]
- Zheng, Y.; Magdy, I. Ray Tracing for Radio Propagation Modeling: Principles and Applications. IEEE Access 2015, 3, 1089–1100. [Google Scholar]
- Wanderley, P.H.; Terada, M.A. Assessment of the applicability of the Ikegami propagation model in modern wireless communication scenarios. J. Electromagn. Waves Appl. 2012, 26, 1483–1491. [Google Scholar] [CrossRef]
- Har, D.; Watson, A.M.; Chadney, A.G. Comment on diffraction loss of rooftop-to-street in COST 231-Walfisch-Ikegami model. IEEE Trans. Veh. Technol. 1999, 48, 1451–1458. [Google Scholar] [CrossRef]
- Karatas, M. A multi-objective facility location problem in the presence of variable gradual coverage performance and coopertive cover. Eur. J. Oper. Res. 2017, 262, 1040–1051. [Google Scholar] [CrossRef]
- Wang, B.C.; Qian, Q.Y.; Gao, J.J.; Tan, Z.Y.; Zhou, Y. The optimization of warehouse location and resources distribution for emergency rescue under uncertainty. Adv. Eng. Inform. 2021, 48, 101278. [Google Scholar] [CrossRef]
- Du, B.; Zhou, H.; Leus, R. A two-stage robust model for a reliable p-center facility location problem. Appl. Math. Model. 2010, 77, 99–114. [Google Scholar] [CrossRef]
- Tedeschi, D.; Andretta, M. New exact algorithms for planar maximum covering location by ellipses problems. Eur. J. Oper. Res. 2021, 291, 114–127. [Google Scholar] [CrossRef]
- Baray, J.; Cliquet, G. Optimizing locations through a maximum covering/p-median hierarchical model: Maternity hospitals in France. J. Bus. Res. 2013, 66, 127–132. [Google Scholar] [CrossRef]
- Vieira, B.S.; Ferrari, T.; Ribeiro, G.M.; Bahiense, L.; Filho, R.D.O.; Abramides, C.A.; Júnior, N.F.R.C. A progressive hybrid set covering based algorithm for the traffic counting location problem. Expert Syst. Appl. 2020, 160, 113641. [Google Scholar] [CrossRef]
- Sinnl, M. Exact and heuristic algorithms for the maximum weighted submatrix coverage problem. Eur. J. Oper. Res. 2021; early access. [Google Scholar]
- Li, J.L.; Liu, Z.B.; Wang, X.F. Public charging station location determination for electric ride-hailing vehicles based on an im-proved genetic algorithm. Sustain. Cities Soc. 2021, 74, 103181. [Google Scholar] [CrossRef]
- Marinakis, Y. An improved particle swarm optimization algorithm for the capacitated location routing problem and for the location routing problem with stochastic demands. Appl. Soft Comput. 2015, 37, 680–701. [Google Scholar] [CrossRef]
- Rohaninejad, M.; Sahraeian, R.; Tavakkoli-Moghaddam, R. An accelerated Benders decomposition algorithm for reliable facility location problems in multi-echelon networks. Comput. Ind. Eng. 2018, 124, 523–534. [Google Scholar] [CrossRef]
- Vaze, R.; Deshmukh, N.; Kumar, R.; Saxena, A. Development and application of Quantum Entanglement inspired Particle Swarm Optimization. Knowl.-Based Syst. 2021, 219, 106859. [Google Scholar] [CrossRef]
- Squires, M.; Tao, X.; Elangovan, S.; Gururajan, R.; Saxena, A. A novel genetic algorithm based system for the scheduling of medical treatments. Expert Syst. Appl. 2022, 195, 116464. [Google Scholar] [CrossRef]
- Khan, S.; Grudniewski, P.; Muhammad, Y.; Sobey, A. The benefits of co-evolutionary Genetic Algorithms in voyage optimisa-tion. Ocean. Eng. 2022, 245, 110261. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, M.; Hong, Z.; Zhang, H.; Zhu, H. Enhancing differential evolution with a target vector replacement strategy. Comput. Stand. Interfaces 2022, 82, 103631. [Google Scholar] [CrossRef]
- Morais, M.; Ribeiro, M.; Silva, R.; Mariani, V.; Coelho, L. Discrete differential evolution metaheuristics for permutation flow shop scheduling problems. Comput. Ind. Eng. 2022, 166, 107956. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Gholami, D.; Rahmati, O.; Shahabi, H.; Shirzadi, A.; Lee, S.; Bui, D.T.; Pradhan, B. Swarm intelligence optimization of the group method of data handling using the cuckoo search and whale optimization algorithms to model and predict landslides. Appl. Soft Comput. 2022, 116, 108254. [Google Scholar] [CrossRef]
- Peng, J.; Li, Y.; Kang, H.; Shen, Y.; Sun, X.; Chen, Q. Impact of population topology on particle swarm optimization and its variants: An in-formation propagation perspective. Swarm Evol. Comput. 2022, 69, 100990. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. A multi-objective particle swarm optimization algorithm based on two-archive mechanism. Appl. Soft Comput. 2022, 119, 108532. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, J. Mutation-driven grey wolf optimizer with modified search mechanism. Expert Syst. Appl. 2022, 194, 116450. [Google Scholar] [CrossRef]
- Adhikary, J.; Acharyya, S. Randomized Balanced Grey Wolf Optimizer (RBGWO) for solving real life optimization prob-lems. Appl. Soft Comput. 2022, 117, 108429. [Google Scholar] [CrossRef]
- Boumedine, N.; Bouroubi, S. Protein folding in 3D lattice HP model using a combining cuckoo search with the Hill-Climbing algorithms. Appl. Soft Comput. 2022, 119, 108564. [Google Scholar] [CrossRef]
- Bajaj, A.O. Sangwan Discrete cuckoo search algorithms for test case prioritization. Appl. Soft Comput. 2021, 110, 107584. [Google Scholar] [CrossRef]
- Kyriakakis, N.; Marinaki, M.; Matsatsinis, N.; Marinakis, Y. Moving peak drone search problem: An online multi-swarm intelli-gence approach for UAV search operations. Swarm Evol. Comput. 2021, 66, 100956. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, R.; Hao, K.R.; Chen, L.; Wang, T.; Jiang, C. A novel hybrid particle swarm optimization using adaptive strategy. Inf. Sci. 2021, 579, 231–250. [Google Scholar] [CrossRef]
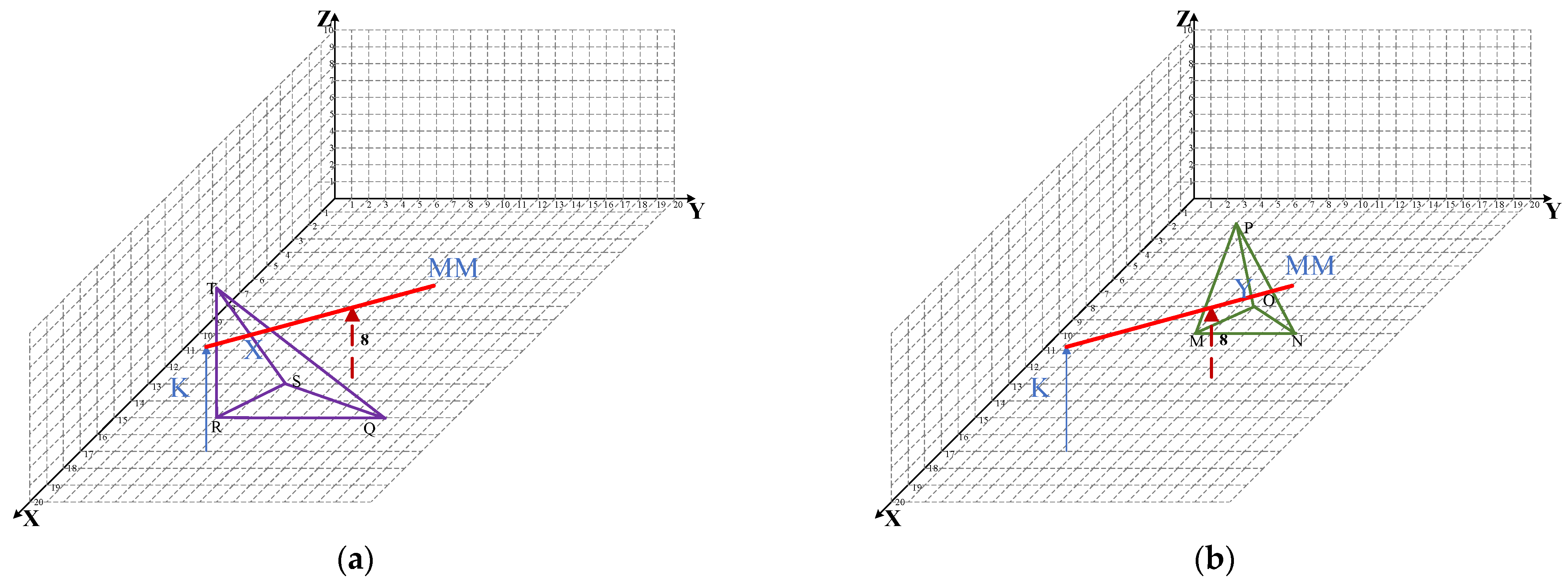

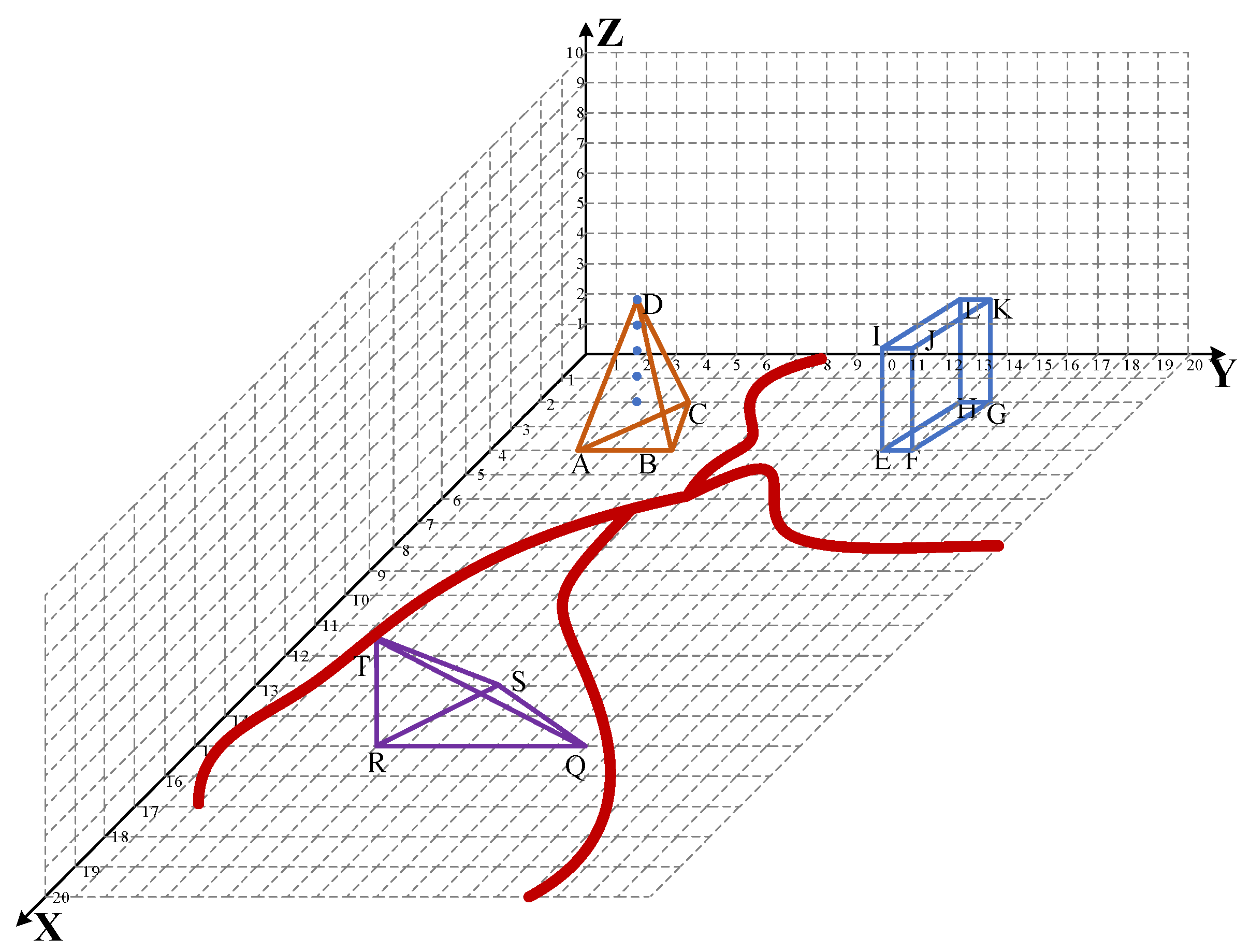


| Obstacle Number | Obstacle Vertex | Vertex Coordinates | Obstacle Penetration Rate |
|---|---|---|---|
| 1 | A | (4, 3, 0) | 0.35 |
| B | (4, 6, 0) | ||
| C | (2, 5, 0) | ||
| D | (3, 4, 3) | ||
| 2 | E | (4, 13, 0) | 0.8 |
| F | (4, 14, 0) | ||
| G | (2, 15, 0) | ||
| H | (2, 14, 0) | ||
| I | (4, 13, 3) | ||
| J | (4, 14, 3) | ||
| K | (2, 15, 3) | ||
| L | (2, 14, 3) | ||
| 3 | Q | (15, 13, 0) | 0.3 |
| R | (15, 6, 0) | ||
| S | (13, 8, 0) | ||
| T | (15, 6, 4) |
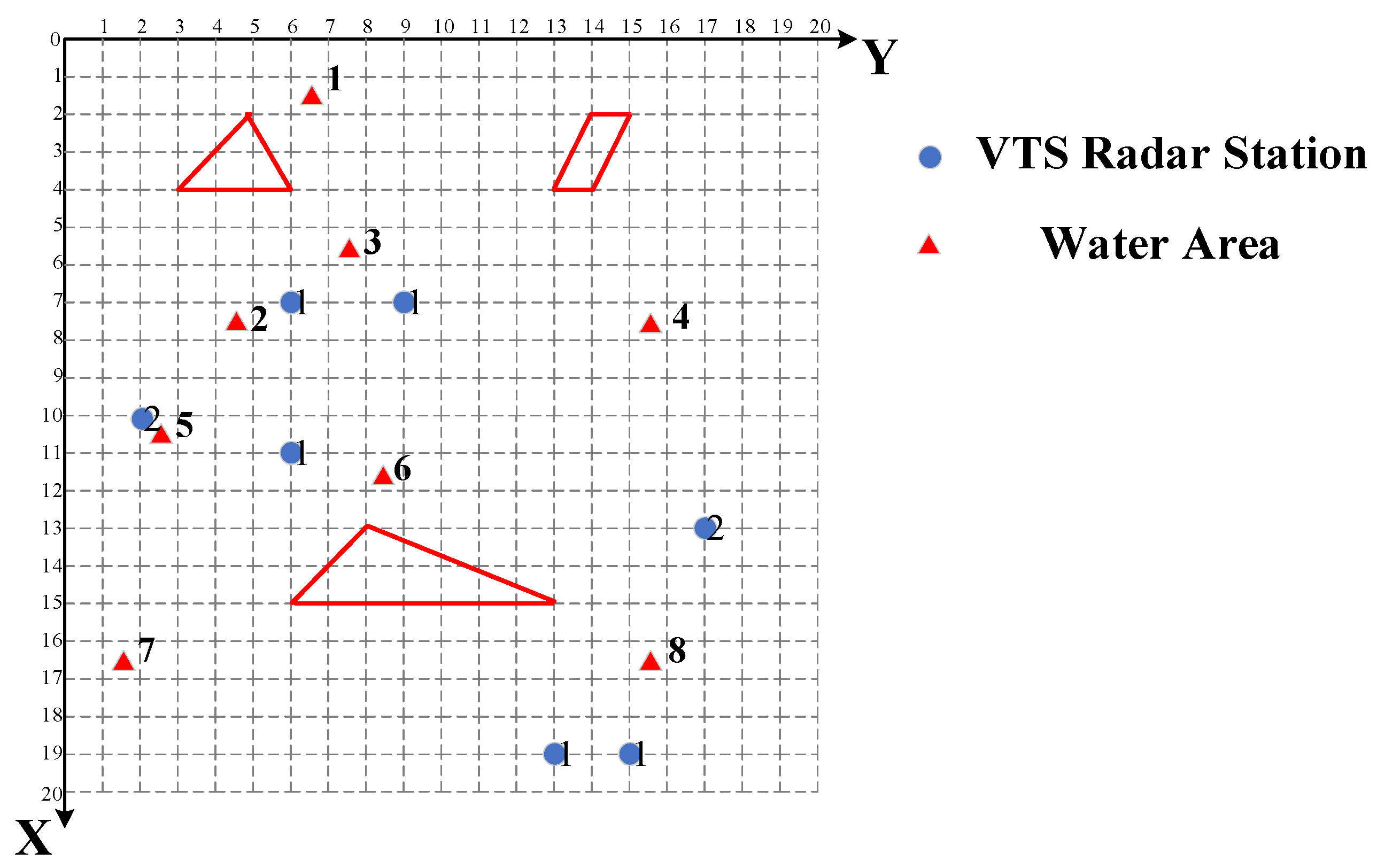
| Water Area Serial Number | Water Area Coordinates | Area | Number of Covering Times |
|---|---|---|---|
| 1 | (1.5, 6.5, 1) | 10 | 1 |
| 2 | (7.5, 4.5, 2) | 8 | 1 |
| 3 | (5.5, 7.5, 2) | 9 | 2 |
| 4 | (7.5, 15.5, 1.5) | 6 | 2 |
| 5 | (10.5, 2.5, 1.5) | 4 | 2 |
| 6 | (11.5, 8.5, 1.5) | 9 | 1 |
| 7 | (16.5, 1.5, 1.5) | 6 | 2 |
| 8 | (16.5, 15.5, 3) | 6 | 2 |
| Radar Type | Minimum Coverage Radius | Maximum Coverage Radius | Radar Monitoring Probability | Cost |
|---|---|---|---|---|
| 1 | 0.5 | 5 | 0.85 | 200 |
| 2 | 0.5 | 7 | 0.9 | 400 |
| 3 | 0.5 | 9 | 0.95 | 600 |
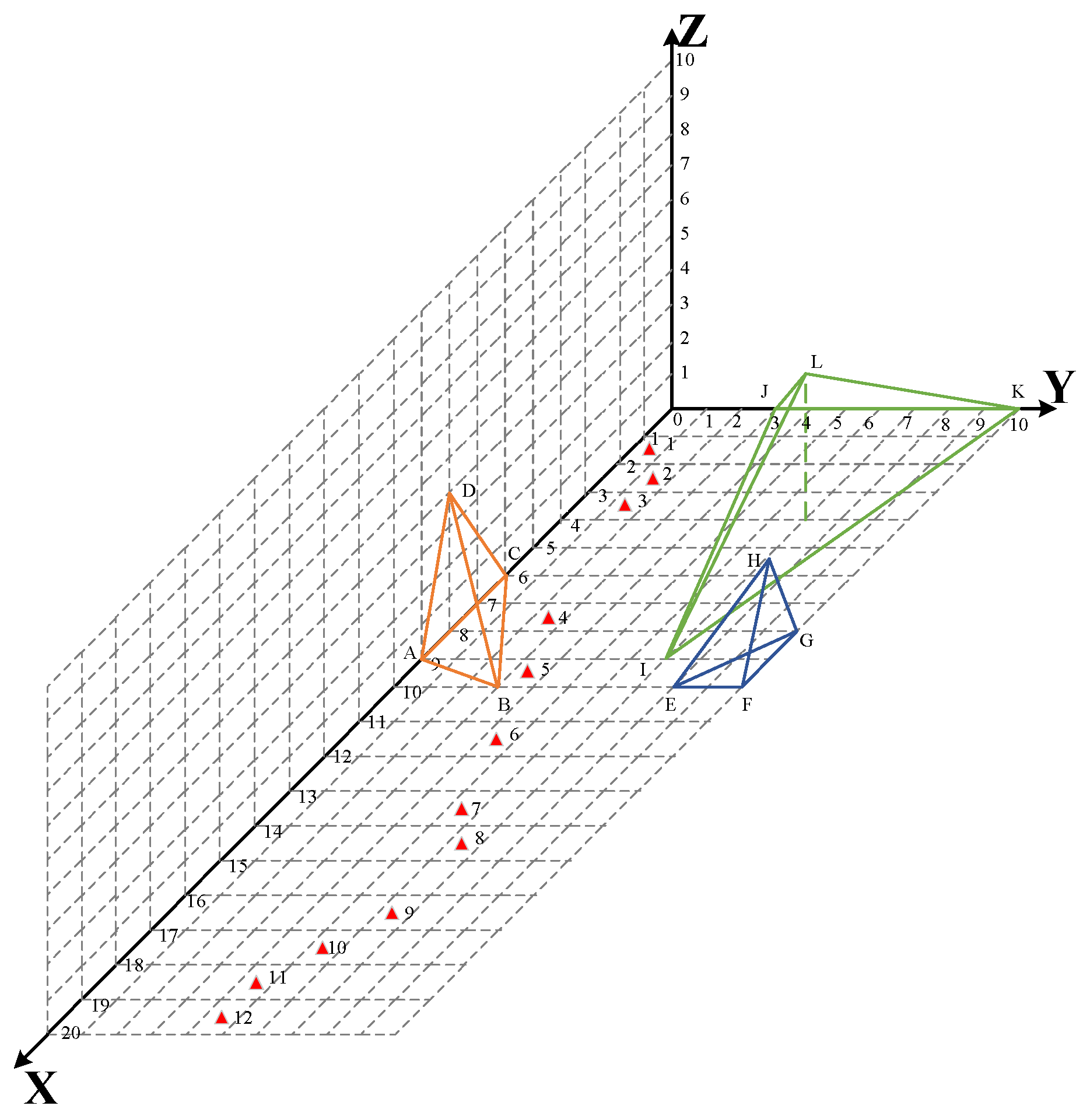
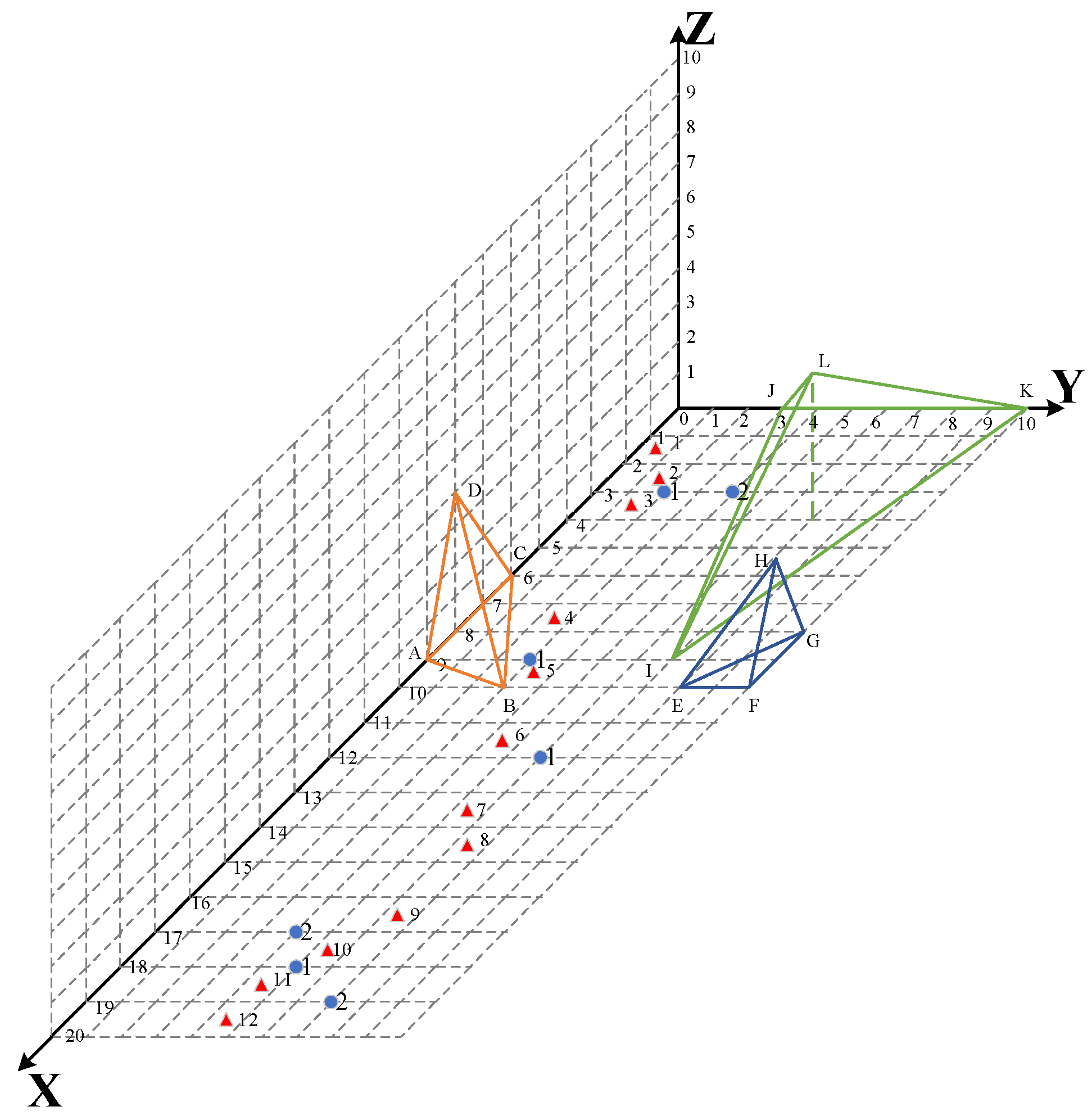
| Obstacle Number | Obstacle Vertex | Vertex Coordinates | Obstacle Penetration Rate |
|---|---|---|---|
| 1 | A | (9, 0, 0) | 0.35 |
| B | (10, 3, 0) | ||
| C | (6, 0, 0) | ||
| D | (8, 0, 4) | ||
| 2 | E | (10, 8, 0) | 0.4 |
| F | (10, 10, 0) | ||
| G | (8, 10, 0) | ||
| H | (9, 10, 3) | ||
| 3 | I | (9, 7, 0) | 0.3 |
| J | (0, 3, 0) | ||
| K | (0, 10, 0) | ||
| L | (4, 7, 5) |
| Water Area Serial Number | Water Area Coordinates | Area | Number of Covering Times |
|---|---|---|---|
| 1 | (1.5, 0.5, 1) | 10 | 1 |
| 2 | (2.5, 1.5, 2) | 8 | 1 |
| 3 | (3.5, 1.5, 2) | 9 | 2 |
| 4 | (7.5, 2.5, 1.5) | 6 | 2 |
| 5 | (9.5, 3.5, 1.5) | 4 | 2 |
| 6 | (11.5, 4.5, 1.5) | 9 | 1 |
| 7 | (13.5, 5.5, 1.5) | 6 | 2 |
| 8 | (14.5, 6.5, 3) | 6 | 2 |
| 9 | (16.5, 6.5, 1.5) | 4 | 2 |
| 10 | (17.5, 5.5, 1.5) | 9 | 1 |
| 11 | (18.5, 4.5, 1.5) | 6 | 2 |
| 12 | (19.5, 4.5, 3) | 6 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Lu, J.; Sun, L.-Q. Location Optimization of VTS Radar Stations Considering Environmental Occlusion and Radar Attenuation. ISPRS Int. J. Geo-Inf. 2022, 11, 183. https://doi.org/10.3390/ijgi11030183
Huang C, Lu J, Sun L-Q. Location Optimization of VTS Radar Stations Considering Environmental Occlusion and Radar Attenuation. ISPRS International Journal of Geo-Information. 2022; 11(3):183. https://doi.org/10.3390/ijgi11030183
Chicago/Turabian StyleHuang, Chuan, Jing Lu, and Li-Qian Sun. 2022. "Location Optimization of VTS Radar Stations Considering Environmental Occlusion and Radar Attenuation" ISPRS International Journal of Geo-Information 11, no. 3: 183. https://doi.org/10.3390/ijgi11030183
APA StyleHuang, C., Lu, J., & Sun, L.-Q. (2022). Location Optimization of VTS Radar Stations Considering Environmental Occlusion and Radar Attenuation. ISPRS International Journal of Geo-Information, 11(3), 183. https://doi.org/10.3390/ijgi11030183





