Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China
Abstract
1. Introduction
2. Materials and Methods
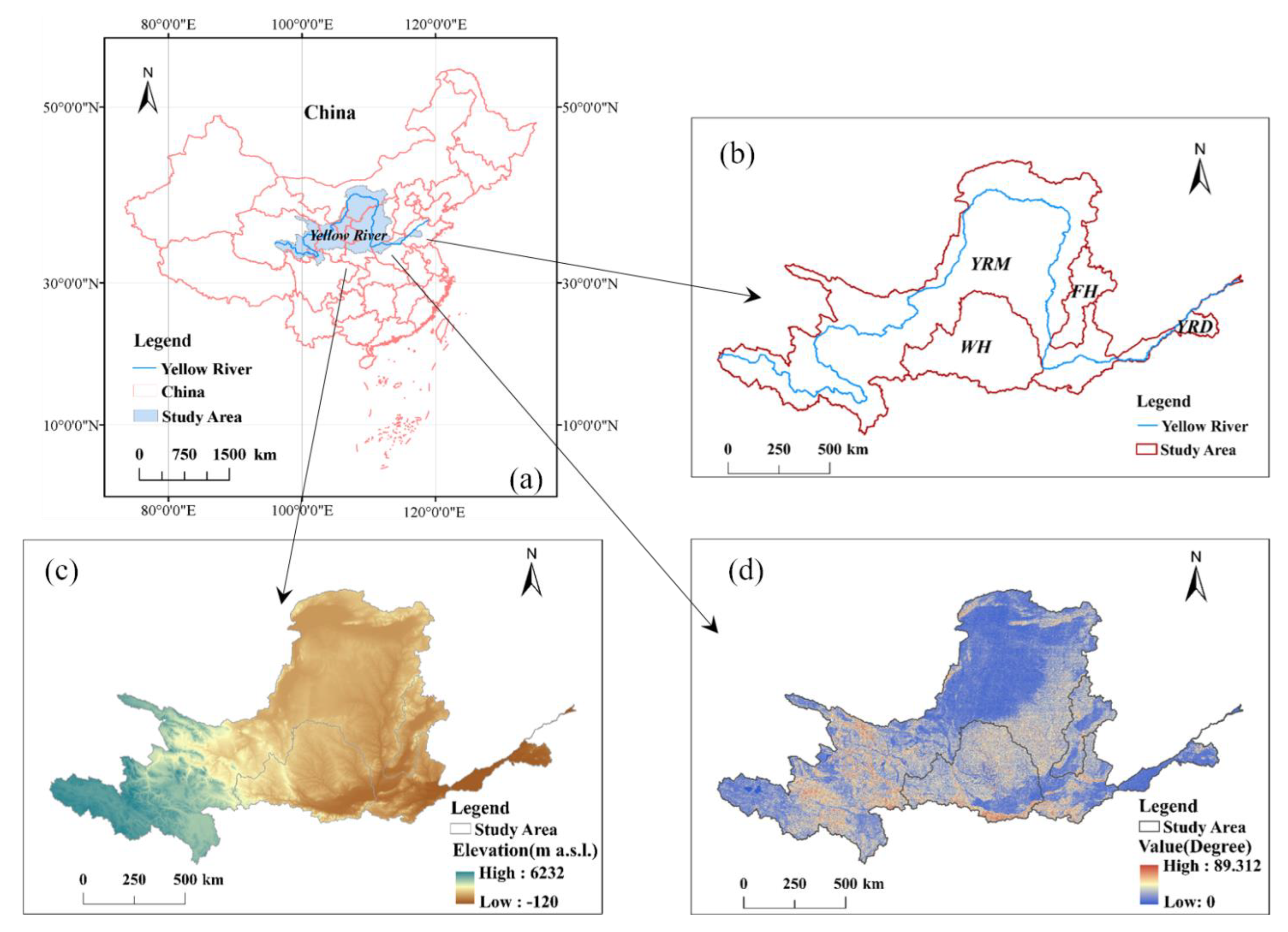
2.1. Study Area
2.2. Data Description
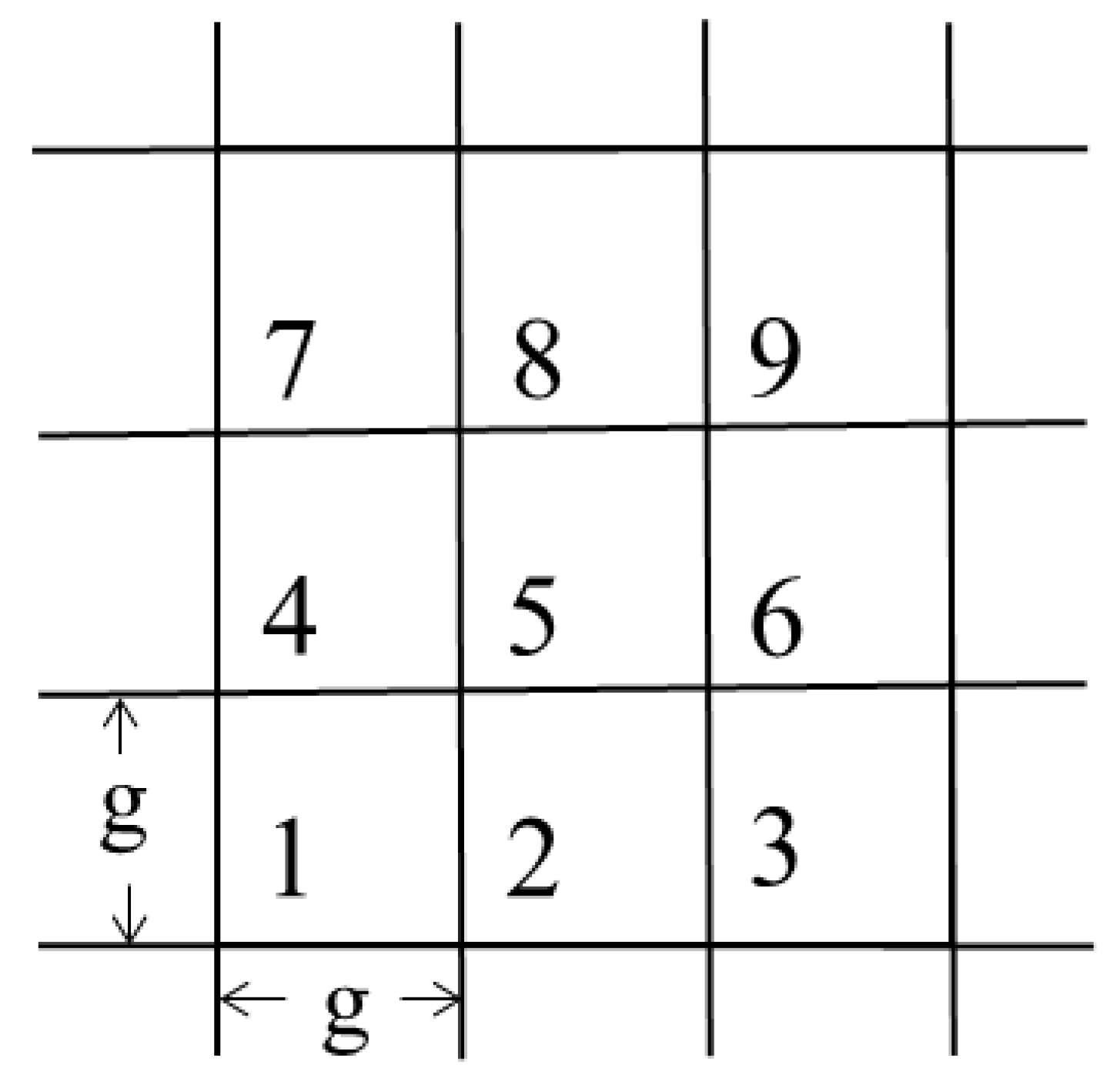
2.3. Multifractal Approach and Geomorphological Parameters
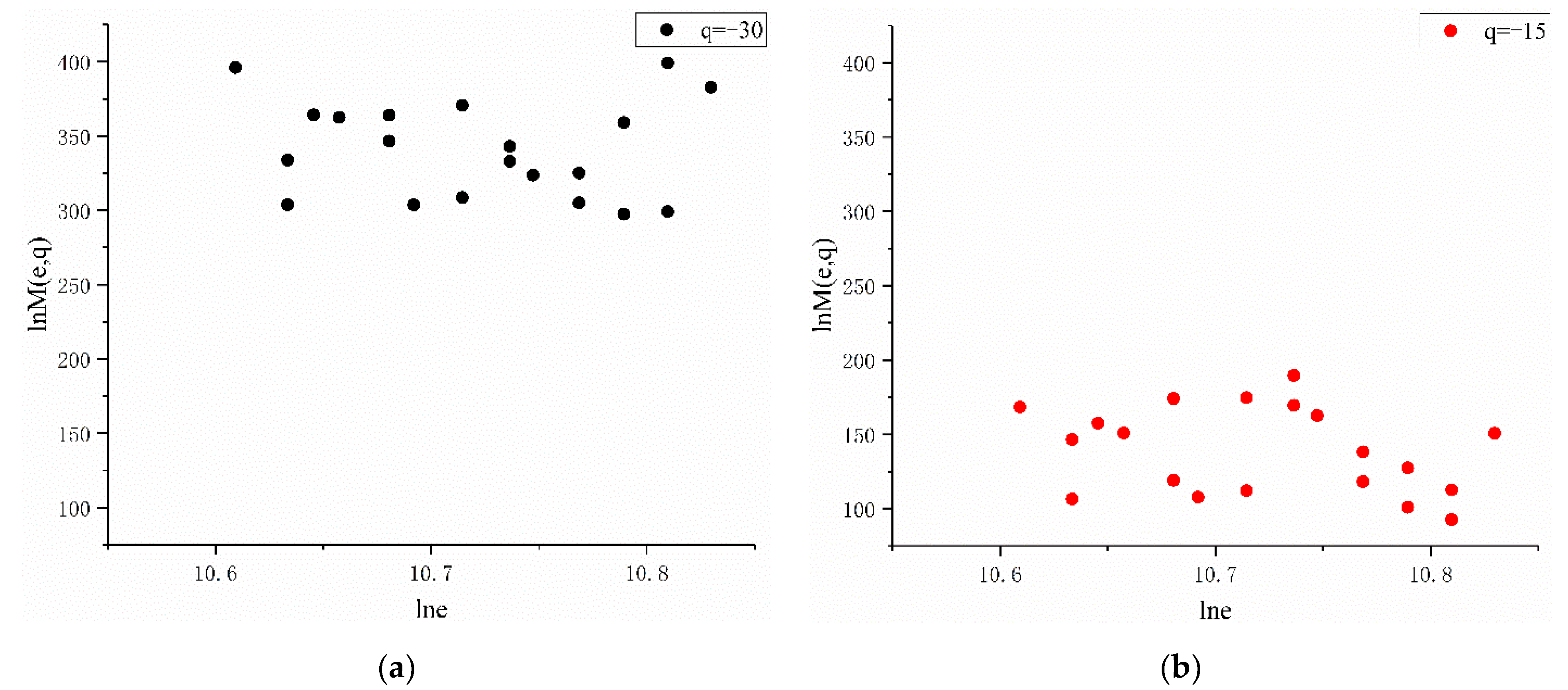
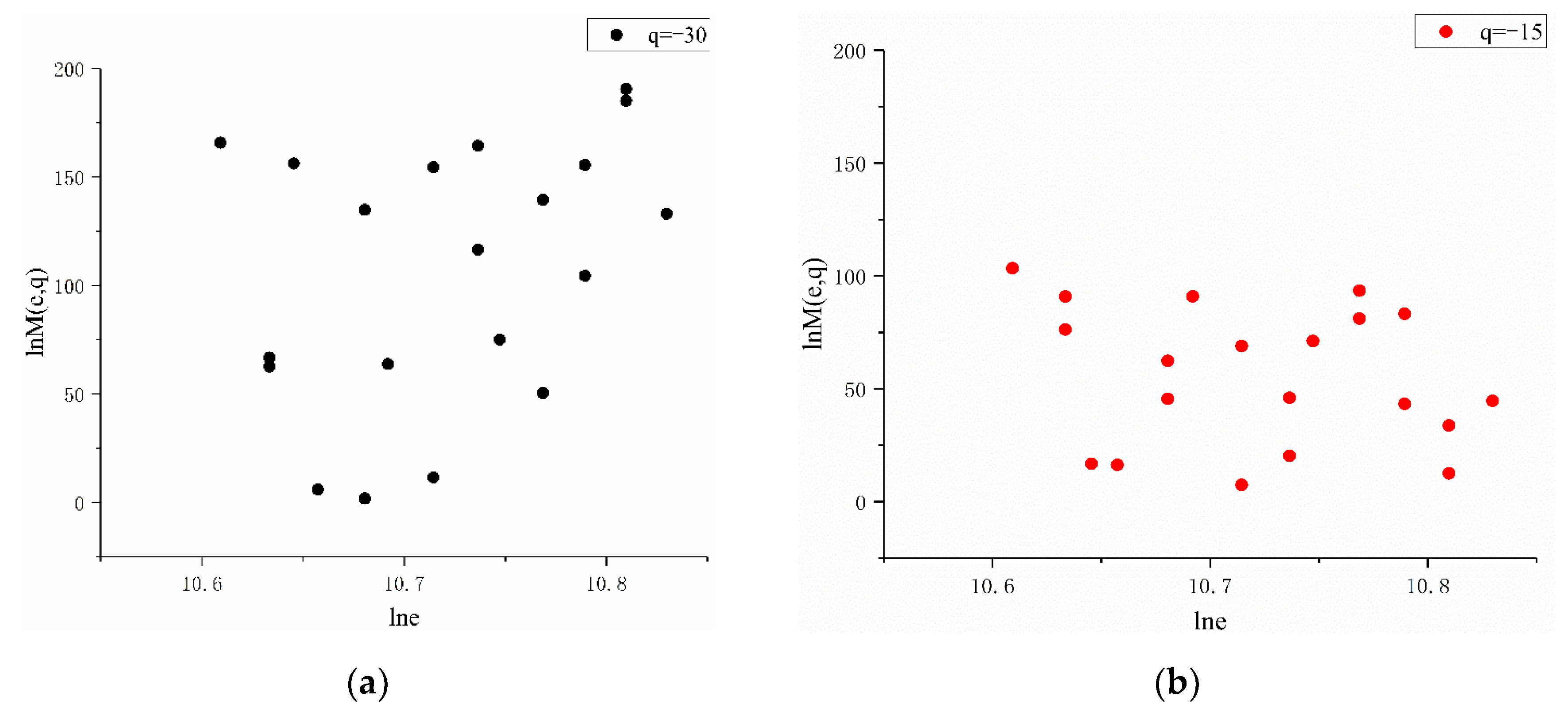
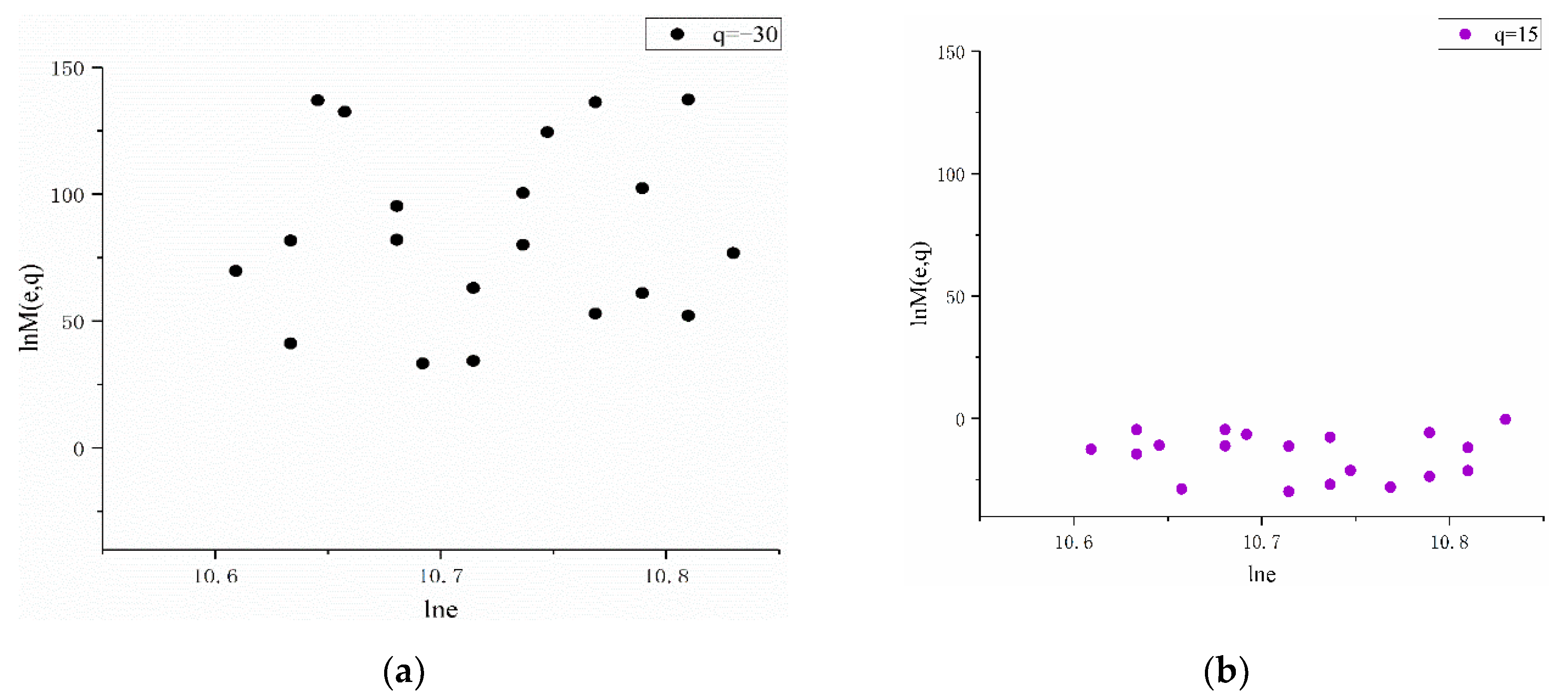
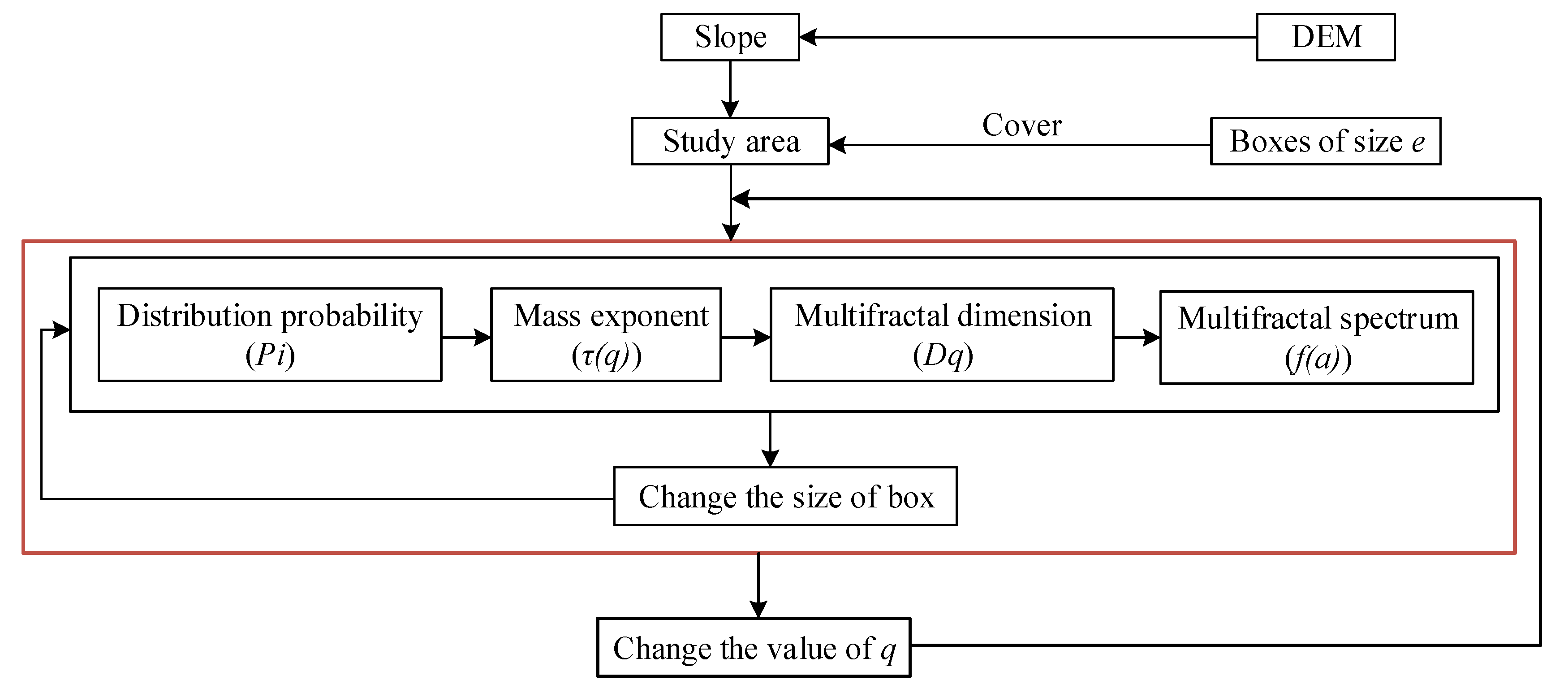
2.4. Multifractal Analysis
3. Results
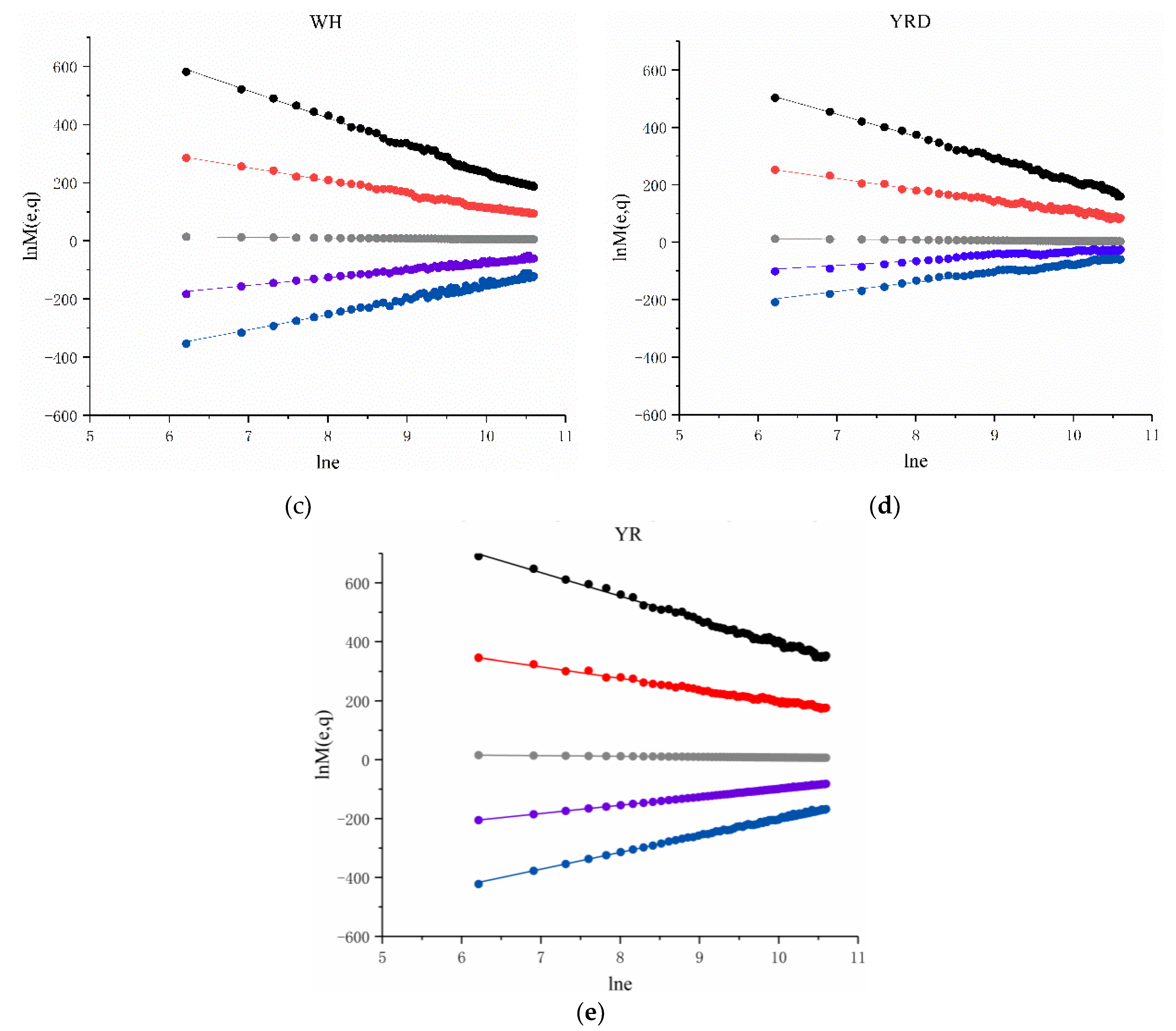
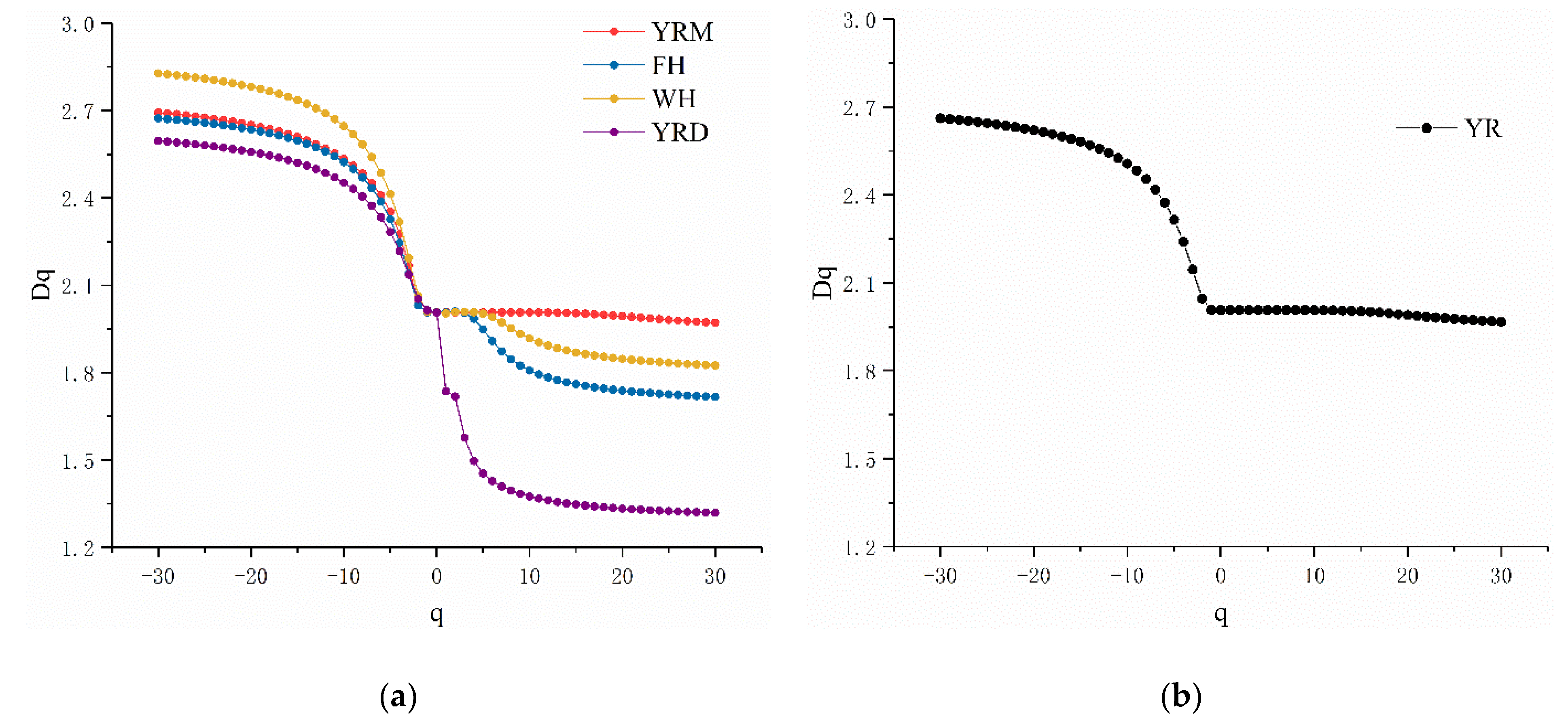
3.1. Determination of Multifractal Characteristics
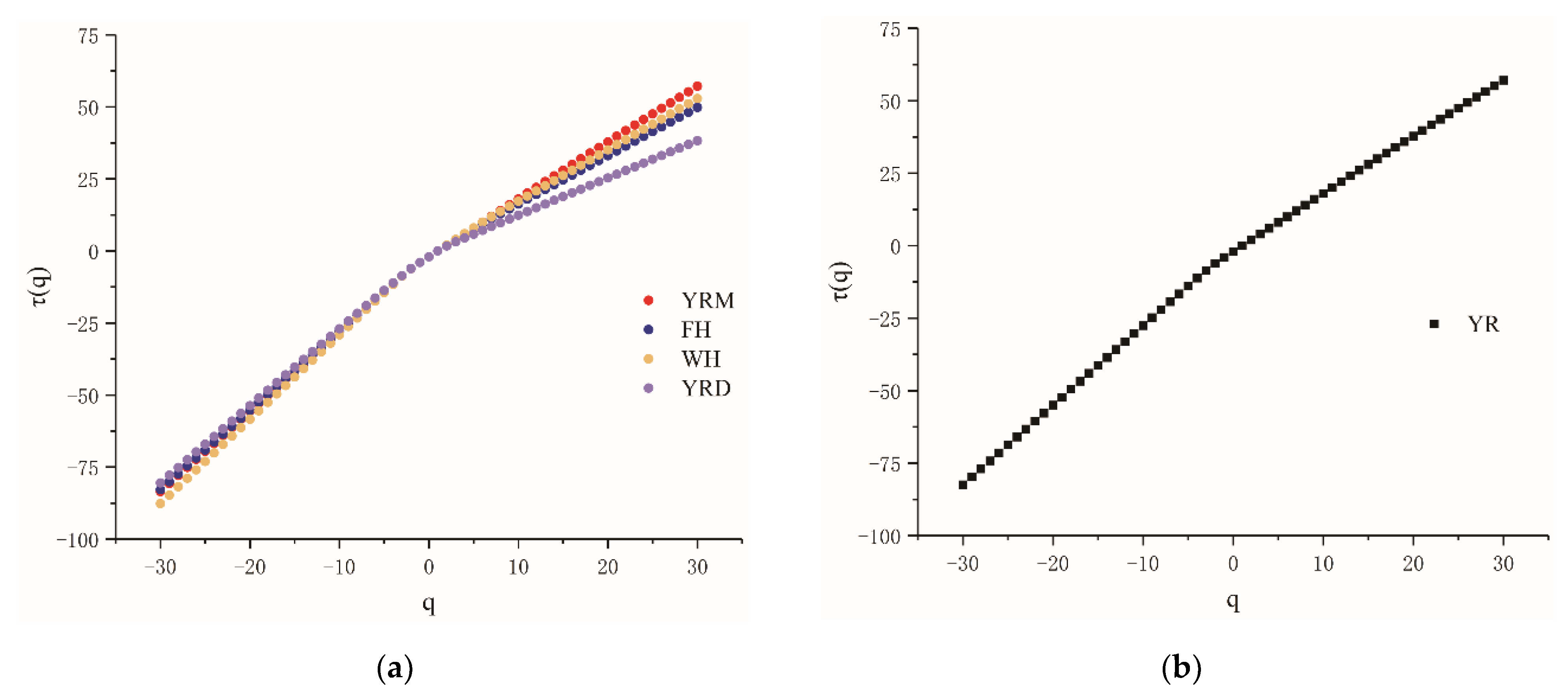
3.2. Multifractal Dimension Analysis
3.3. Multifractal Spectrum Analysis
4. Discussion
4.1. Analysis Scale of Multifractal
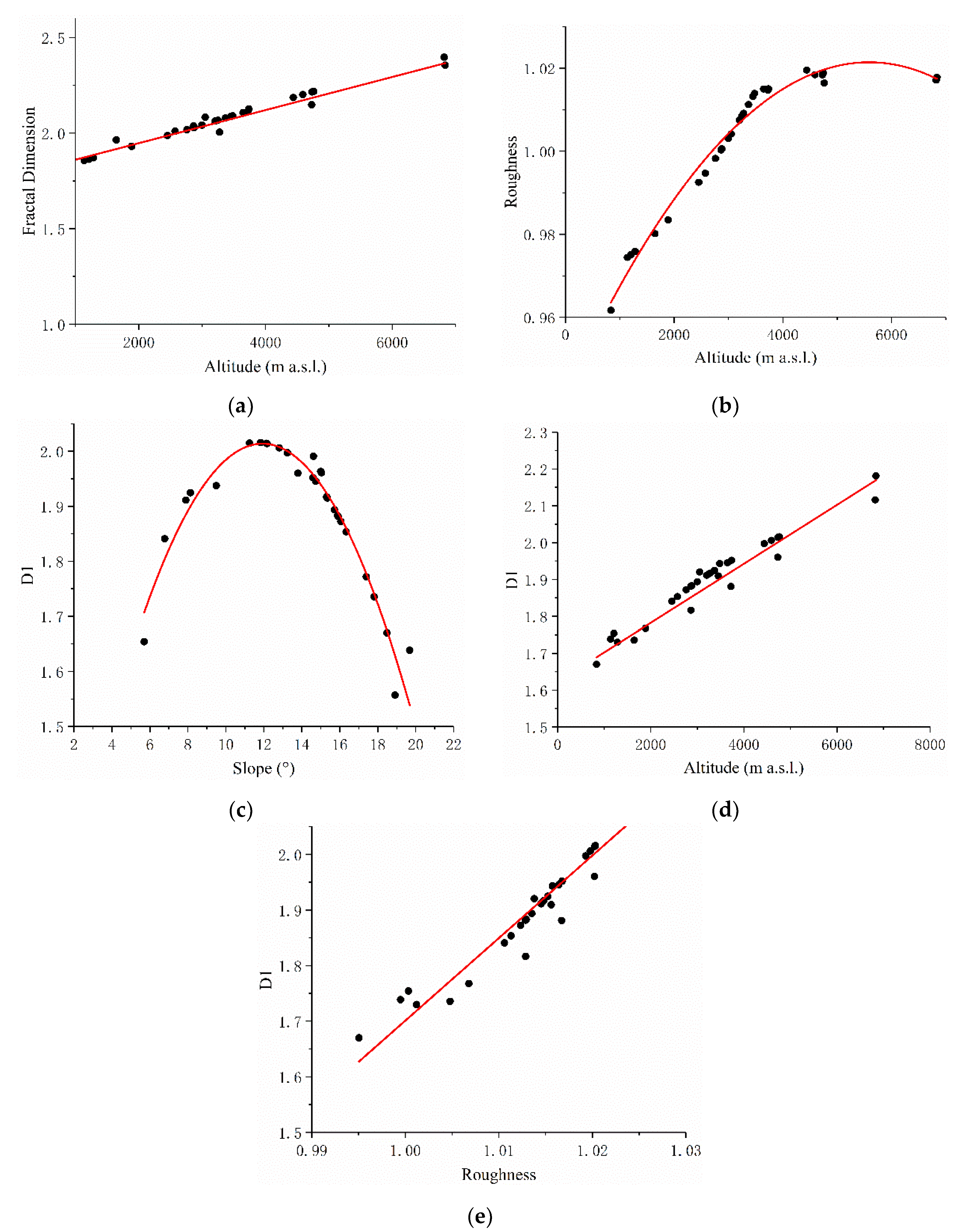
4.2. Common Topographic Parameters and Extra Multifractal Parameters
5. Conclusions
- (1)
- The topography of the Yellow River Basin and its sub-basins exhibited significant multifractal characteristics. The multifractal spectrum showed a hook curve to the left, which indicates that the proportion of the steep slope was large. The relief heterogeneity of the sub-basins was in descending order: the Yellow River Downstream Basin, the Weihe River Basin, the Yellow River Mainstream Basin, and the Fenhe River Basin. This shows that multifractal theory can be applied well to the research of large-scale basin geomorphology landforms or surfaces, and the feasibility of this conclusion has been verified well.
- (2)
- The geomorphometric features of the study areas were obtained using the multifractal theory based on slope distribution probability model, and the results were consistent with the actual terrain. In particular, the Yellow River Downstream Basin had a unique “overhanging river” morphology, leading to strong non-uniformity of the terrain in this region, and this result is consistent with the conclusion obtained by using the multifractal analysis based on slope distribution probability in this study.
- (3)
- The scale-free range of the Yellow River Basin was [500, 40,000] (m) with experiments based on the multifractal theory.
- (4)
- We analyzed the relief, surface, and landforms of the Yellow River Basin and its sub-basins by combining the common topographic parameters with other multifractal parameters. It was found that multifractal analysis can be used to describe the characteristics of the topography, and there is a strong correlation between common topographic parameters and multifractal parameters.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Mandelbrot, B.B. How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Jiang, B.; Brandt, S.A. A Fractal Perspective on Scale in Geography. ISPRS Int. J. Geo-Inf. 2016, 5, 95. [Google Scholar] [CrossRef]
- Karydas, C.; Jiang, B. Scale Optimization in Topographic and Hydrographic Feature Mapping Using Fractal Analysis. ISPRS Int. J. Geo-Inf. 2020, 9, 631. [Google Scholar] [CrossRef]
- Cabrera-Barona, P.F.; Bayón, M.; Durán, G.; Bonilla, A.; Mejía, V. Generating and Mapping Amazonian Urban Regions Using a Geospatial Approach. ISPRS Int. J. Geo-Inf. 2020, 9, 453. [Google Scholar] [CrossRef]
- Iwahashi, J.S.; Watanabeb, S.; Furuya, T. Landform analysis of slope movements using DEM in Higashikubiki area, Japan. Comput. Geosci.-UK 2001, 27, 851–865. [Google Scholar] [CrossRef]
- Feng, M.; Jung, K.; Kim, J.-C. Geomorphologic Analysis of Small River Basin within the Framework of Fractal Tree. Water 2020, 12, 2480. [Google Scholar] [CrossRef]
- Ju, X.N.; Jia, Y.H.; Li, T.C.; Gao, L.; Gan, M. Morphology and multifractal characteristics of soil pores and their functional implication. Catena 2021, 196, 104822. [Google Scholar] [CrossRef]
- Kamila, J.K.-b.; Tang, G.A.; Yang, X.; Na, J.M.; Xiong, L.Y. Spatial Fractal Properties of Loess Plateau in the Northern Shaanxi Province of China. J. Nanjing Norm. Univ. (Nat. Sci. Ed.) 2020, 43, 56–62. [Google Scholar]
- Ciobotaru, A.-M.; Andronache, I.; Ahammer, H.; Radulovic, M.; Peptenatu, D.; Pintilii, R.-D.; Drăghici, C.-C.; Marin, M.; Carboni, D.; Mariotti, G.; et al. Application of Fractal and Gray-Level Co-Occurrence Matrix Indices to Assess the Forest Dynamics in the Curvature Carpathians—Romania. Sustainability 2019, 11, 6927. [Google Scholar] [CrossRef]
- Abdullah, A.-W.; Amro, E.; Ahmed, S.K.; Sameer, B.; Anis, C. Effect of the stream extraction threshold on the morphological characteristics of arid basins, fractal dimensions, and the hydrologic response. J. Afr. Earth Sci. 2019, 172, 103968. [Google Scholar]
- Cao, J.J.; Tang, G.A.; Fang, X.; Liu, Y.J.; Zhu, Y.; Li, J.L.; Wagner, W. Identification of Active Gully Erosion Sites in the Loess Plateau of China Using MF-DFA. Remote Sens. 2020, 12, 589. [Google Scholar] [CrossRef]
- Xiang, J.; Xu, Y.P.; Yuan, J.; Wang, Q.; Wang, J.; Deng, X.J. Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China. Water 2019, 11, 2283. [Google Scholar] [CrossRef]
- Biswas, A. Joint multifractal analysis for three variables: Characterizing the effect of topography and soil texture on soil water storage. Geoderma 2019, 334, 15–23. [Google Scholar] [CrossRef]
- Luo, J.; Zheng, Z.C.; Li, T.X.; He, S.Q. Spatial variation of microtopography and its effect on temporal evolution of soil erosion during different erosive stages. Catena 2020, 190, 104515. [Google Scholar] [CrossRef]
- Liu, Z.; Han, L.; Du, C.; Cao, H.; Guo, J.; Wang, H. Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images. Remote Sens. 2021, 13, 587. [Google Scholar] [CrossRef]
- Benzi, R.P.G.; Parisi, G. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A Gen. Phys. 1999, 17, 3521–3531. [Google Scholar] [CrossRef]
- Siqueira, G.M.; Silva, Ê.F.F.; Vidal-Vázquez, E.; Paz-González, A. Multifractal and joint multifractal analysis of general soil properties and altitude along a transect. Biosyst. Eng. 2018, 168, 105–120. [Google Scholar] [CrossRef]
- Xia, J.B.; Ren, R.R.; Chen, Y.P.; Sun, J.; Zhao, X.M.; Zhang, S.Y. Multifractal characteristics of soil particle distribution under different vegetation types in the Yellow River Delta chenier of China. Geoderma 2020, 368, 14311. [Google Scholar] [CrossRef]
- Li, W.Z.; Wang, J.M.; Zhang, Y.F.; Zhang, M. A novel characterization on the interaction of soil and vegetation in a reclaimed area of opencast coalmine based on joint multi-fractal method. Ecol. Indic. 2020, 107094. [Google Scholar] [CrossRef]
- Dutta, S. Decoding the Morphological Differences between Himalayan Glacial and Fluvial Landscapes Using Multifractal Analysis. Sci. Rep. 2017, 7, 11032. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Li, Z.B.; Li, P.; Lu, K.X. Multifractal arithmethic for watershed topographic feature. Adv. Water Sci. 2009, 20, 385–391. [Google Scholar]
- De Bartolo S G., G.; Gaudio, R. Multifractal behaviour of river networks. Hydrol. Earth Syst. Sci. 2000, 4, 105–112. [Google Scholar] [CrossRef]
- Ijjasz-Vasquez, E.J.; Ignacio, R.-I.; Rafael, L.B. On the multifractal characterization of river basins. Geomorphology 1992, 05, 297–310. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Jiménez-Hornero, F.J.; De Ravé, E.G. Multifractal analysis applied to the study of the accuracy of DEM-based stream derivation. Geomorphology 2013, 197, 85–95. [Google Scholar] [CrossRef]
- Cao, H.Q.; Zhu, G.X.; Li, X.T.; Xia, W.F. Multi-fractal and its application in terrain character analysis. J. Beijing Univ. Aeronaut. Astronaut. 2004, 12, 1182–1185. [Google Scholar]
- Gurugnanam, B.; Kalaivanan, M.; Bairavi, S. ASTER DEM based geological and Geomorphological investigation using GIS. Int. J. Remote Sens. Geosci. 2016, 5, 11–15. [Google Scholar]
- Tang, G.A. Progress of DEM and digital terrain analysis in china. Acta Geogr. Sin. 2014, 69, 1305–1325. [Google Scholar]
- Pike, R.J.; Evans, I.S.; Hengl, T. Geomorphometry: A Brief Guide. In Geomorphometry: Geomorphometry: Concepts, Software, Applications, Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 33, pp. 1–28. [Google Scholar]
- Seo, Y.; Schmidt, A.R.; Kang, B. Multifractal properties of the peak flow distribution on stochastic drainage networks. Stoch. Environ. Res. Risk Assess. 2014, 28, 1157–1165. [Google Scholar]
- Aharony, A. Measuring multifractals. Phys. D Nonlinear Phenom. 1989, 38, 1–4. [Google Scholar] [CrossRef]
- Dombrádi, E.; Timar, G.; Bada, G. Fractal dimension estimations of drainage network in the Carpathian–Pannonian system. Glob. Planet. Chang. 2007, 58, 197–213. [Google Scholar] [CrossRef]
- Ren, J.T.; Chen, Q.L.; Mo, S.J.; Wang, Z.H. Analysis of the scale effect of DEM on topography and watershed characteristics in typical Karst mountainous area. J. Xinyang Norm. Univ. (Nat. Sci. Ed.) 2018, 31, 247–253. [Google Scholar]
- Mach, J.; Mas, F.; Sague´s, F. Two representations in multifractal analysis. J. Phys. A Math. Gen. 1995, 28, 5607–5622. [Google Scholar] [CrossRef]
- Montgomery, D.R. Slope distributions, threshold hillslopes, and steady-state topography. Am. J. Sci. 2001, 301, 432–454. [Google Scholar] [CrossRef]
- Tang, G.A.; Li, F.Y.; Liu, X.J.; Long, Y.; Yang, X. Research on the slope spectrum of the Loess Plateau. Sci. China Ser. E 2008, 51, 175–185. [Google Scholar] [CrossRef]
- Malcai, O.; Lidar, D.A.; Biham, O.; Avnir, D. Scaling Range and Cutoffs in Empirical Fractals. Phys. Rev. Lett. 1998, 56, 2817. [Google Scholar] [CrossRef]
- Lee, J.; Stanley, H.E. Phase transition in the multifractal spectrum of diffusion limited aggregation. Phys. Rev. Lett. 1988, 61, 2945. [Google Scholar] [CrossRef] [PubMed]
- Almqvist, N. Fractal analysis of scanning probe microscopy images. SurfaceSicence 1996, 355, 221. [Google Scholar] [CrossRef]
- Sun, X.; Fu, Z.X.; Wu, Z.Q. Multifractal calculation of thin film growth. Chin. J. Comput. Phys. 2001, 247–252. [Google Scholar]
- Oky Dicky, A.P.; Takeyoshi, Y. Characterization of volcanic geomorphology and geology by slope and topographic openness. Geomorphology 2010, 118, 22–32. [Google Scholar]
- Zhou, Q.M.; Liu, X.J. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Arved, C.S.; David, J.M. Terrestrial structure-from-motion: Spatial error analysis of roughness and morphology. Geomorphology 2020, 350, 106883. [Google Scholar]
- Maan, H. Evaluation of DEM interpolation techniques for characterizing terrain roughness. CATENA 2021, 198, 105072. [Google Scholar]
- He, L.H.; Zhao, H. The fractal dimension of river networks and its interpretation. Sci. Geogr. Sin 1996, 16, 124–128. [Google Scholar]
- Zhu, X.H. Spatial dimension and relationship of mountain system, fault system and water system in Mainland China. Mt. Res. 2003, 21, 311–317. [Google Scholar]
- Kamer, Y.; Ouillon, G.; Sornette, D. Barycentric fixed-mass method for multifractal analysis. Phys. Rev. E 2013, 88, 022922. [Google Scholar] [CrossRef] [PubMed]

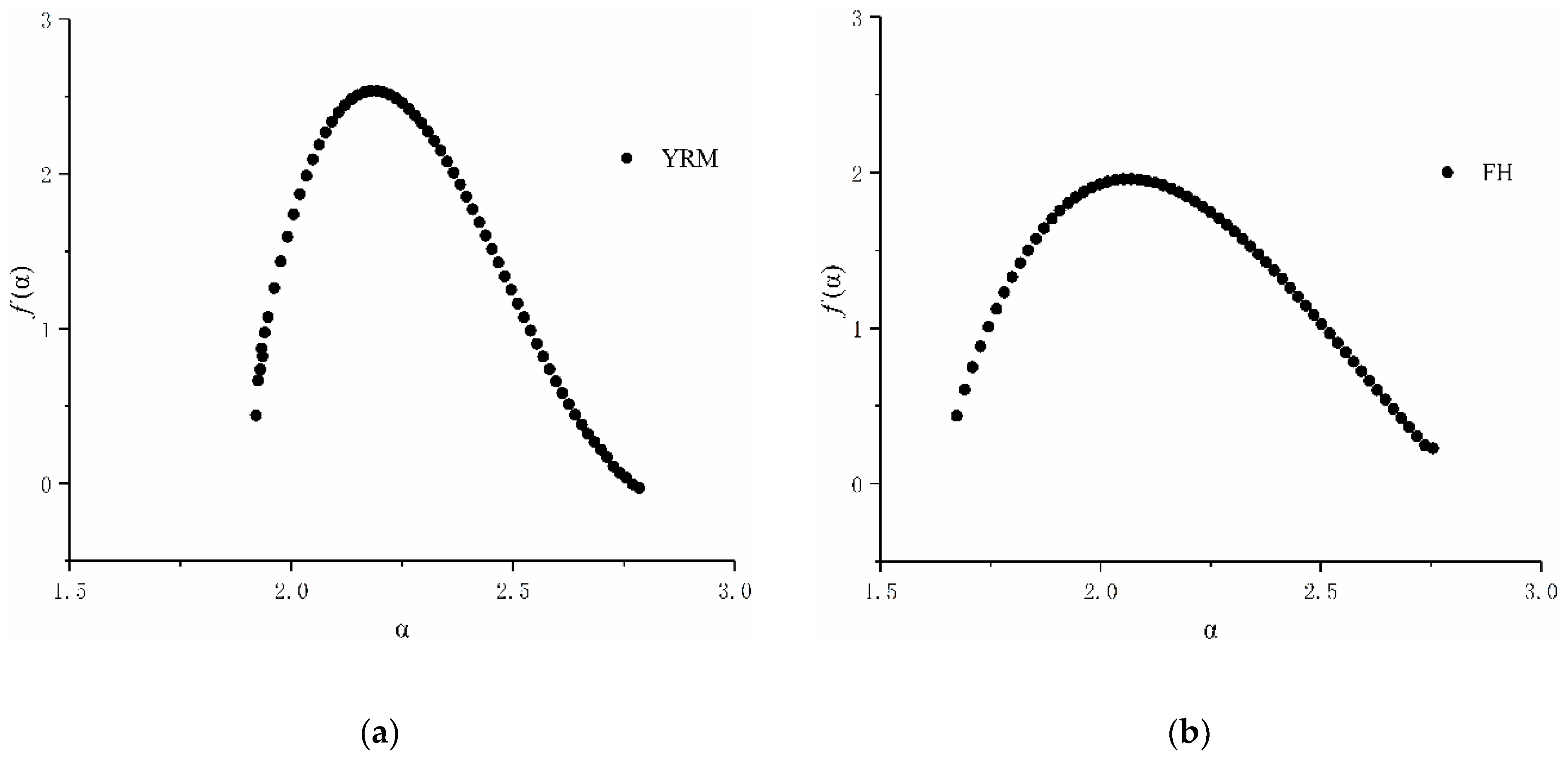


| Study Area | αmin | αmax | f(αmin) | f(αmax) | Δα | Δf |
|---|---|---|---|---|---|---|
| YRM | 1.91998 | 2.78403 | 0.44121 | 0.02846 | 0.86405 | 0.41275 |
| FH | 1.67325 | 2.75445 | 0.43686 | 0.22858 | 1.08120 | 0.20828 |
| WH | 1.78660 | 2.92725 | 0.60605 | 0.06559 | 1.14065 | 0.54046 |
| YRD | 1.28930 | 2.67504 | 0.44354 | 0.23218 | 1.38574 | 0.21136 |
| YR | 1.92088 | 2.74660 | 0.23231 | 0.10422 | 0.82572 | 0.12809 |
| Study Area | Location | Δα | Δf | Symmetry of Multifractal Spectrum | Geomorphological Features |
|---|---|---|---|---|---|
| YRM | The northwest of the Yellow River Basin | medium | , large | asymmetrical | The landform of this region is relatively simple. The proportion of wave peaks is larger than valleys. The terrain is high and undulating, with high mountains as the main terrain. |
| FH | The east of the Yellow River Basin and the Loess Plateau, China | large | , medium | asymmetrical | The terrain is relatively complex but slightly less complex than the WH. FH has fewer large fluctuations, and most of them are low mountains and hilly areas. |
| WH | The south of the Yellow River Basin and the Loess Plateau, China | large | , very large | asymmetrical, and the spectrum has a longer trailing tail | The terrain is also relatively complex, and is higher, the proportion of peaks is greater than that of valleys, and the terrain is mostly dominated by fluctuations with large magnitudes. |
| YRD | The southeast of the Yellow River Basin | Very large | , medium | symmetrical | The distribution of the terrain is not uniform, but the relief is small. It is low-lying and hilly, and the river channel forms the overhanging river. |
| YR | Northwest China | medium | , medium | asymmetrical, and the spectrum has a trailing tail | The terrain is relatively complex. The proportion of peaks is greater than that of the valleys. The topography is mainly dominated by plateaus. |
| Study Areas | Slope (°) (s) | Topographic Altitude (m a.s.l.) (Z) | Topographic Roughness (R) | Fractal Dimension (D) | ||||
|---|---|---|---|---|---|---|---|---|
| YRM | 10.3260 | 6295 | 1.0164 | 2.5354 | 2.0086 | 2.0082 | 0.0004 | 0.9998 |
| FH | 11.2042 | 2807 | 1.0194 | 2.0058 | 2.0065 | 2.0063 | 0.0002 | 0.9999 |
| WH | 13.3426 | 3936 | 1.0277 | 2.0107 | 2.0071 | 2.0030 | 0.0041 | 0.9979 |
| YRD | 5.4959 | 1656 | 1.0046 | 2.0016 | 2.0063 | 1.7359 | 0.2704 | 0.8652 |
| YR | 10.0168 | 6352 | 1.0154 | 2.3294 | 2.0068 | 2.0069 | −0.0001 | 1.0000 |
| Slope | Topographic Altitude | Topographic Roughness | Fractal Dimension | |||
|---|---|---|---|---|---|---|
| Slope | 1.000 | 0.392 | 0.989 ** | 0.142 | 0.314 | 0.893 * |
| Topographic Altitude | 0.392 | 1.000 | 0.979 ** | 0.876 * | 0.698 | 0.812 |
| Topographic Roughness | 0.989 ** | 0.979 ** | 1.000 | −0.072 | 0.237 | 0.919 * |
| Fractal dimension | 0.142 | 0.876 * | −0.072 | 1.000 | 0.862 | 0.327 |
| 0.314 | 0.698 | 0.237 | 0.862 | 1.000 | 0.384 | |
| 0.893 * | 0.812 | 0.919 * | 0.327 | 0.384 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Wang, J.; Lu, Y. Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China. ISPRS Int. J. Geo-Inf. 2021, 10, 337. https://doi.org/10.3390/ijgi10050337
Qin Z, Wang J, Lu Y. Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China. ISPRS International Journal of Geo-Information. 2021; 10(5):337. https://doi.org/10.3390/ijgi10050337
Chicago/Turabian StyleQin, Zilong, Jinxin Wang, and Yan Lu. 2021. "Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China" ISPRS International Journal of Geo-Information 10, no. 5: 337. https://doi.org/10.3390/ijgi10050337
APA StyleQin, Z., Wang, J., & Lu, Y. (2021). Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China. ISPRS International Journal of Geo-Information, 10(5), 337. https://doi.org/10.3390/ijgi10050337





