Detecting Changes in Forest Structure over Time with Bi-Temporal Terrestrial Laser Scanning Data
Abstract
:1. Introduction
2. Material
2.1. Study Area and Field Data Collection
| Plot | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Density (stems/ha) | 637 | 923 | 1,019 | 1,146 | 1,178 | |
| Number (stems) | 20 | 29 | 32 | 36 | 37 | |
| Species (percent) | Pine | 85 | 93 | 3 | 6 | 19 |
| Spruce | 0 | 0 | 88 | 47 | 0 | |
| Deciduous | 0 | 7 | 9 | 31 | 81 | |
| DBH (cm) | Min | 12.1 | 10.7 | 10.0 | 10.9 | 10.2 |
| Max | 29.4 | 27.5 | 51.3 | 26.5 | 30.5 | |
| Mean | 22.8 | 19.4 | 18.8 | 16.7 | 16.1 | |
| std | 5.0 | 4.3 | 7.6 | 4.2 | 5.3 | |
| Height (m) | Min | 14.2 | 11.5 | 10.1 | 10.8 | 10.2 |
| Max | 25.8 | 21.7 | 26.0 | 22.2 | 25.2 | |
| Mean | 21.2 | 17.4 | 17.3 | 15.8 | 18.2 | |
| std | 2.9 | 2.1 | 3.4 | 2.9 | 3.8 |
| Plot | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Number (stems) | 7 | 10 | 13 | 8 | 12 | |
| DBH (cm) | Min | 14.4 | 10.7 | 11.1 | 10.9 | 10.8 |
| Max | 26.0 | 22.2 | 22.2 | 21.0 | 19.5 | |
| Mean | 19.8 | 16.7 | 15.6 | 14.7 | 14.7 | |
| std | 4.4 | 3.6 | 3.4 | 3.2 | 2.6 | |
| Height (m) | Min | 16.1 | 11.5 | 12.8 | 10.8 | 13.0 |
| Max | 23.0 | 19.1 | 19.9 | 17.3 | 21.5 | |
| Mean | 20.2 | 16.1 | 16.6 | 13.9 | 17.8 | |
| std | 2.4 | 2.6 | 2.4 | 2.3 | 2.3 |
2.2. Terrestrial Laser Data Acquisition

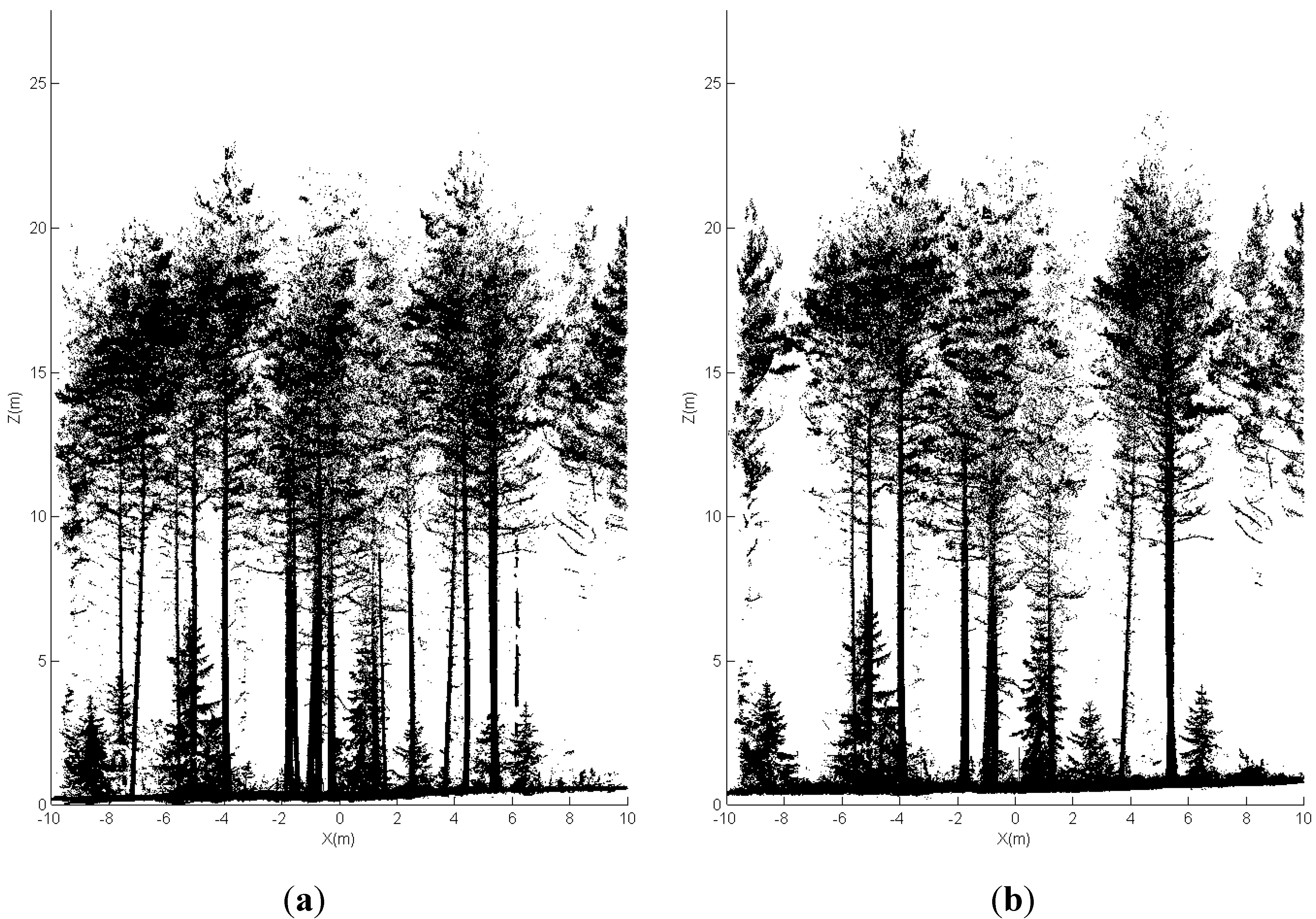
2.3. Pre-Processing
| Distance from Scanner (m) | Diameter of Foot Print (mm) | Distance between Adjacent Foot Prints (mm) |
|---|---|---|
| 1 | 3.22 | 0.63 |
| 2 | 3.44 | 1.26 |
| 3 | 3.66 | 1.88 |
| 4 | 3.88 | 2.51 |
| 5 | 4.10 | 3.14 |
| 6 | 4.32 | 3.77 |
| 7 | 4.54 | 4.40 |
| 8 | 4.76 | 5.03 |
| 9 | 4.98 | 5.65 |
| 10 | 5.20 | 6.28 |
3. Change Detection Methods
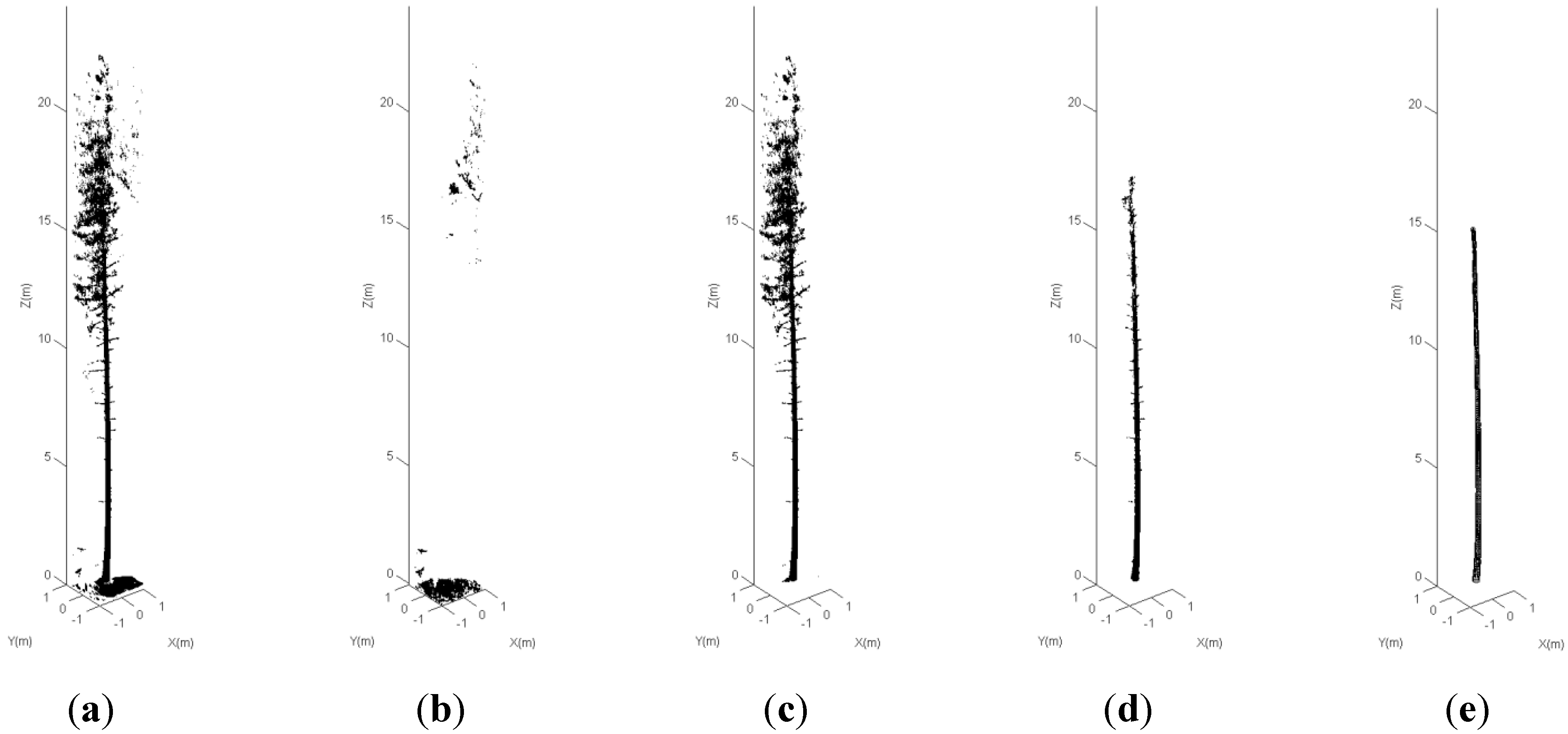
3.1. Data-Orientated Approach


3.2. Object-Orientated Approach


 are the points on the cylinder surface,
are the points on the cylinder surface,  is a point on the axis,
is a point on the axis,  is the direction of the axis of the cylinder with a unit length, and r is the radius. The distance, or the residual, between the laser point and the cylinder surface is
is the direction of the axis of the cylinder with a unit length, and r is the radius. The distance, or the residual, between the laser point and the cylinder surface is  . The laser points were weighted to reduce the effect of cross errors, e.g., the points reflected from the branches. The entire stem model was reconstructed in a growing manner. The initial parameters of the model element were the estimations of the previous cylinder. For more details on the robust modeling procedure, please refer to [27].
. The laser points were weighted to reduce the effect of cross errors, e.g., the points reflected from the branches. The entire stem model was reconstructed in a growing manner. The initial parameters of the model element were the estimations of the previous cylinder. For more details on the robust modeling procedure, please refer to [27]. 3.3. DBH Estimation and Location Map for Changed Stems
4. Results and Discussion
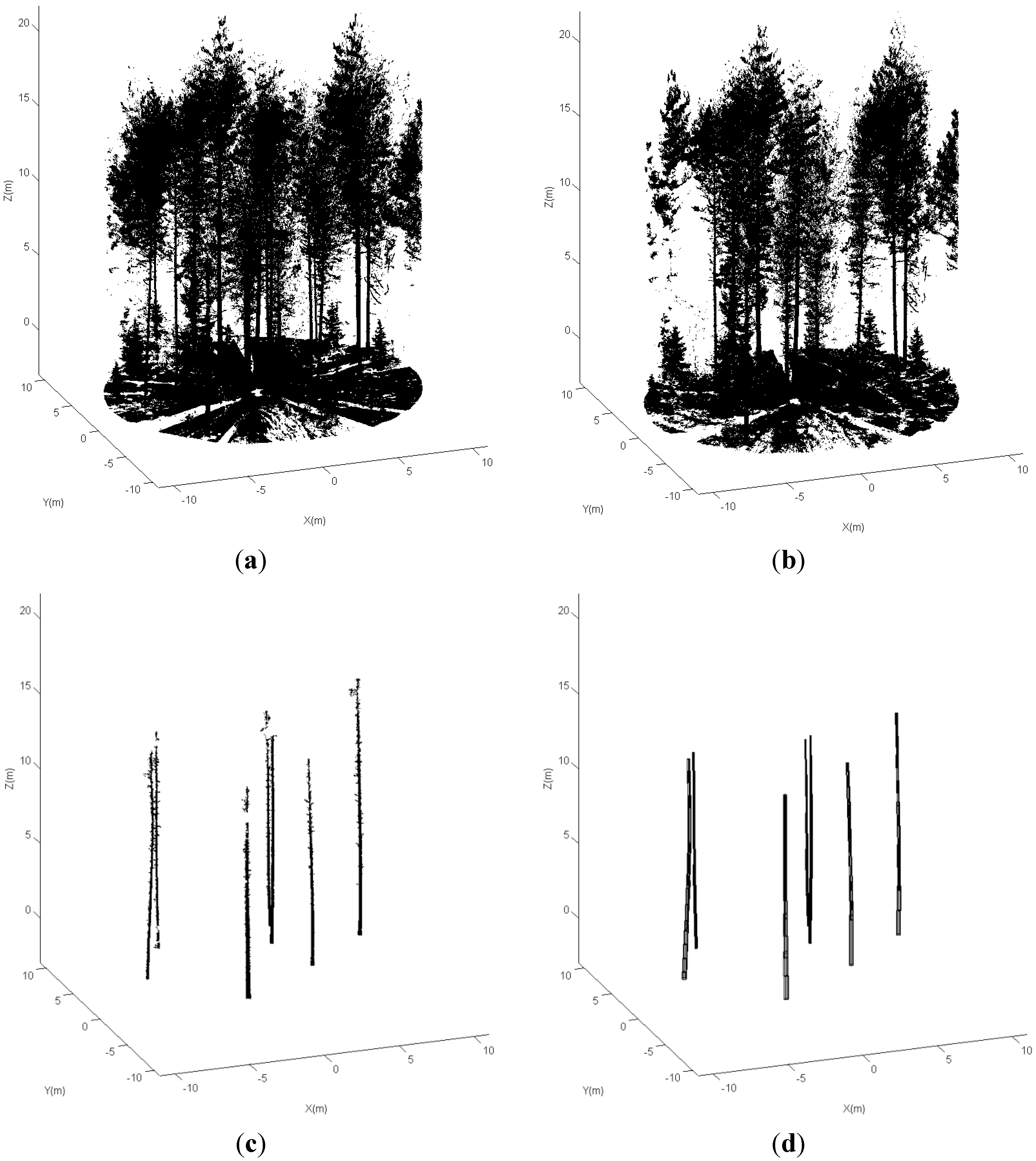
| Plot | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Harvested stems | 7 | 10 | 13 | 8 | 12 |
| Mapped stems | 7 | 8 | 13 | 5 | 12 |
| Omission | 0 | 2 | 0 | 3 | 0 |
| Commission | 0 | 0 | 1 | 1 | 0 |
5. Conclusions
Acknowledgments
References
- Lehtonen, A.; Mäkipää, R.; Heikkinen, J.; Sievänen, R.; Liski, J. Biomass expansion factors (BEFs) for Scots pine, Norway spruce and birch according to stand age for boreal forests. Forest Ecol. Manage. 2004, 188, 211–224. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. Forest Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Kankare, M.; Räty, M.; Vaaja, M.; Liang, X.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Kaasalainen, S.; et al. Biomass Estimation of Individual Trees Using TLS Stem and Crown Diameter Measurements. In Proceedings of ISPRS Workshop Laser Scanning, Calgary, AB, Canada, 29–31 August 2011.
- Vastaranta, M.; Korpela, I.; Uotila, A.; Hovi, A.; Holopainen, M. Mapping of snow-damaged trees in bi-temporal airborne LiDAR data. Eur. J. Forest Res. 2012, 131, 1217–1228. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M. Automatic detection of harvested trees and determination of forest growth using airborne laser scanning. Remote Sens. Environ. 2004, 90, 451–462. [Google Scholar] [CrossRef]
- Pouliot, D.A.; King, D.J.; Bell, F.W.; Pitt, D.G. Automated tree crown detection and delineation in high-resolution digital camera imagery of coniferous forest regeneration. Remote Sens. Environ. 2002, 82, 322–334. [Google Scholar] [CrossRef]
- Holmström, H.; Kallur, H.; Ståhl, G. Cost-plus-loss analyses of forest inventory strategies based on kNN-assigned reference sample plot data. Silva Fennica 2003, 37, 381–398. [Google Scholar]
- Aschoff, T.; Spiecker, H. Algorithms for the automatic detection of trees in laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2004, 36, 71–75. [Google Scholar]
- Thies, M.; Pfeifer, N.; Winterhalder, D.; Gorte, B.G.H. Three-dimensional reconstruction of stems for assessment of taper, sweep and lean based on laser scanning of standing trees. Scand. J. Forest Res. 2004, 6, 571–581. [Google Scholar]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Henning, J.G.; Radtke, P.J. Ground-based laser imaging for assessing three-dimensional forest canopy structure. Photogramm. Eng. Remote Sensing 2006, 72, 1349–1358. [Google Scholar]
- Henning, J.G.; Radtke, P.J. Detailed stem measurements of standing trees from ground-based scanning lidar. Forest Sci. 2006, 52, 67–80. [Google Scholar]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. Forest Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Factors contributing to accuracy in the estimation of the woody canopy leaf-area-density profile using 3D portable lidar imaging. J. Exp. Bot. 2007, 58, 3464–3473. [Google Scholar]
- Maas, H.-G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Lefsky, M.; McHale, M.R. Volume estimates of trees with complex architecture from terrestrial laser scanning. J. Appl. Remote Sens. 2008, 2, 023521. [Google Scholar] [CrossRef]
- Tansey, K.; Selmes, N.; Anstee, A.; Tate, N.J.; Denniss, A. Estimating tree and stand variables in a Corsican Pine woodland from terrestrial laser scanner data. Int. J. Remote Sens. 2009, 30, 5195–5209. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppä, J.; Kaartinen, H.; Kukko, A.; Holopainen, M. Automatic plot-wise tree location mapping using single-scan terrestrial laser scanning. Photogramm. J. Fin. 2011, 22, 37–48. [Google Scholar]
- Seidel, D.; Beyer, F.; Hertel, D.; Fleck, S.; Leuschner, C. 3D-laser scanning: A non-destructive method for studying above-ground biomass and growth of juvenile trees. Agr. Forest Meteorol. 2011, 151, 1305–1311. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kankare, V.; Holopainen, M. Stem Curve Measurement Using Terrestrial Laser Scanning. In Proceedings of 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Hobart, TAS, Australia, 16–20 Ocotober 2011.
- Zogg, H.-M.; Ingensan, H. Terrestrial laser scanning for deformation monitoring—Load tests on the felsenau viaduct (CH). Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2008, 37, 555–562. [Google Scholar]
- Lindenbergh, R.; Pfeifer, N.; Rabbani, T. Accuracy analysis of the Leica HDS3000 and feasibility of tunnel deformation monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2005, 36, 24–29. [Google Scholar]
- Schneider, D. Terrestrial Laser Scanning for Area Based Deformation Analysis of Towers and Water Damns. In Proceedings of 3rd IAG Symposium of Geodesy for Geotechnical and Structural Engineering and 12th FIG Symposium on Deformation Measurements, Baden, Austria, 22–24 May 2006.
- Young, A.P.; Olsen, M.J.; Driscoll, N.; Flick, R.E.; Gutierrez, R.; Guaz, R.T.; Johnstone, E.; Kuester, F. Comparison of airborne and terrestrial Lidar estimates of seacliff erosion in southern California. Photogramm. Eng. Remote Sensing 2010, 76, 421–427. [Google Scholar]
- Resop, J.P.; Hession, W.C. Terrestrial laser scanning for monitoring streambank retreat: Comparison with traditional surveying techniques. J. Hydraul. Eng. 2010, 136, 794–798. [Google Scholar] [CrossRef]
- Litkey, P.; Puttonen, E.; Liang, X. Comparison of Point Cloud Data Reduction Methods in Single-Scan TLS for Finding Tree Stems in Forest. In Proceedings of 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Hobart, TAS, Australia, 16–20 Ocotober 2011.
- Liang, X.; Litkey, P.; Hyyppä, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Gong, P.; Cheng, X.; Clinton, N.; Cao, C.; Ni, W.; Wang, L. Automated methods for measuring DBH and tree heights with a commercial scanning Lidar. Photogramm. Eng. Remote Sensing 2011, 77, 219–227. [Google Scholar]
- Moskal, M.; Zheng, G. Retrieving forest inventory variables with terrestrial laser scanning (TLS) in urban heterogeneous forest. Remote Sens. 2012, 4, 1–20. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liang, X.; Hyyppä, J.; Kaartinen, H.; Holopainen, M.; Melkas, T. Detecting Changes in Forest Structure over Time with Bi-Temporal Terrestrial Laser Scanning Data. ISPRS Int. J. Geo-Inf. 2012, 1, 242-255. https://doi.org/10.3390/ijgi1030242
Liang X, Hyyppä J, Kaartinen H, Holopainen M, Melkas T. Detecting Changes in Forest Structure over Time with Bi-Temporal Terrestrial Laser Scanning Data. ISPRS International Journal of Geo-Information. 2012; 1(3):242-255. https://doi.org/10.3390/ijgi1030242
Chicago/Turabian StyleLiang, Xinlian, Juha Hyyppä, Harri Kaartinen, Markus Holopainen, and Timo Melkas. 2012. "Detecting Changes in Forest Structure over Time with Bi-Temporal Terrestrial Laser Scanning Data" ISPRS International Journal of Geo-Information 1, no. 3: 242-255. https://doi.org/10.3390/ijgi1030242
APA StyleLiang, X., Hyyppä, J., Kaartinen, H., Holopainen, M., & Melkas, T. (2012). Detecting Changes in Forest Structure over Time with Bi-Temporal Terrestrial Laser Scanning Data. ISPRS International Journal of Geo-Information, 1(3), 242-255. https://doi.org/10.3390/ijgi1030242




