1. Introduction
Since human personal and workspaces are built around the human form factor, we expect bipedal robots to be more suitable to integrate in homes, warehouses, and industry as compared to wheeled robots or quadrupedal robots. For bipedal robots to be practical they have to be able to: stabilize themselves when subject to exogenous disturbances (stability), accelerate quickly (agility), and move in complex terrain (versatility).
Controlling bipedal robots is a formidable challenge because of the following reasons. Bipedal robots are unstable due to the inverted pendulum-like dynamics, they have non-linear dynamics, they are under-actuated as there are more joints than there are actuators at the joints, and they are non-smooth due to changing contact dynamics. Although we can achieve control of non-linear, under-actuated systems such as the acrobot and the pendubot using large excursions of the links [
1], the joint kinematic limits prevent such movements on the bipedal robots. In fact, bipedal systems are often instantaneously uncontrollable [
2]. They cannot balance upright like an inverted pendulum because of limited ankle joint torques.
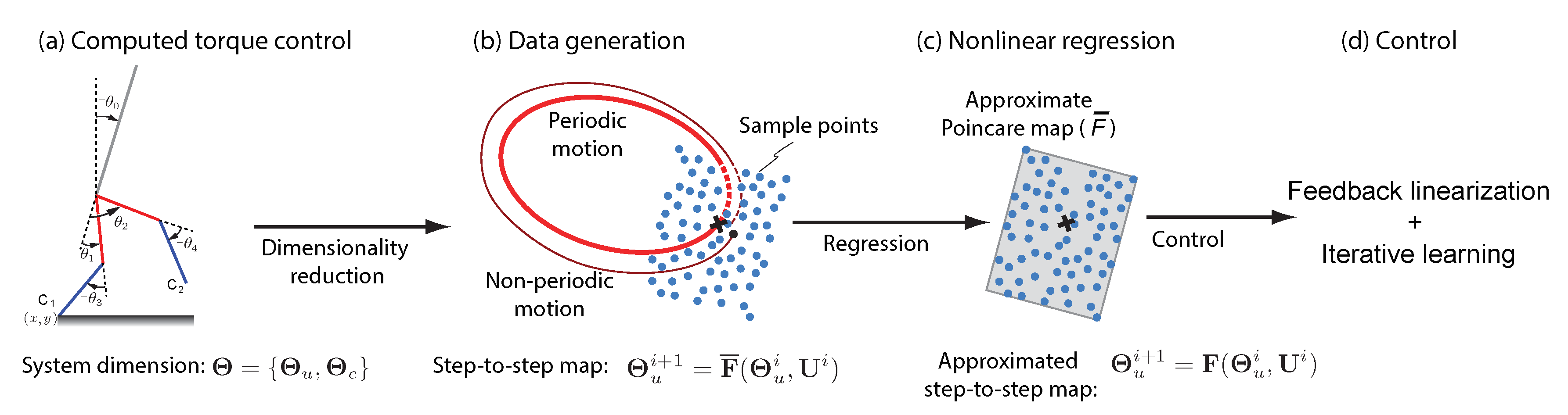
In this paper, we present a control technique that enables high fidelity control without being overly computationally heavy. We use partial feedback linearization to simplify control during the stance phase. This reduces the dynamics of the degrees of freedom planar robot with N actuated degrees of freedom to only 1 dimension. Thereafter, we exploit the fact that the step-to-step dynamics are a smooth function of the state and control, although the instantaneous dynamics are non-smooth, to approximate the step-to-step dynamics using Monte-Carlo simulations and non-linear regression. Finally, we use the one-dimensional step-to-step discrete equation for control without using computationally expensive non-linear optimization.
The most widely used approach is to use a simple model (e.g., linear inverted pendulum model) for control design and then map the simple model to the complex model using inverse kinematics [
3]. Since the inverse kinematics model ignores the dynamics, these mapping technique works well for slow walking but not for fast walking. To realize faster, dynamic walking, one needs to use both the inverse kinematics and inverse dynamics to map from simple to complex models [
4]. Another approach is the virtual model control which combines force control with inverse kinematics. In this method, one applies virtual forces at intuitively chosen locations (e.g., torso, foot) through components such as spring, dampers, dashpots, masses, latches, bearings, nonlinear potential and dissipative fields [
5]. Then, one maps these forces to the joint torques using the appropriate Jacobian. Although the mapping is purely kinematic, it could generate controllers that enabled fast walking on the Spring Flamingo robot.
Nonlinear control may reduce complex dynamics to simpler linear dynamics. One popular approach is the virtual constraints approach [
6,
7]. Here, one slaves the actuated degrees of freedom to the un-actuated degrees of freedom, thus reducing the dimension of the robot to a mechanism with degrees of freedom equal to the un-actuated degrees of freedom. A similar approach is to use partial feedback linearization by inverting the mass matrix, Coriolis, centrifugal, and gravitation torques to decouple the un-actuated degrees of freedom from the actuated degrees of freedom [
8,
9]. Thereafter, one uses computed torque control or sliding mode control for trajectory tracking of the actuated degrees of freedom.
Since bipedal robots are almost impossible to control instantaneously due to under-actuation, they are best controlled over the time scale of step. One prominent idea is the use of capture point, which is the location the biped has to step to come to a complete stop [
10]. A slightly more generalized approach is to use both the ankle push-off at foot-strike and foot placement to control the dynamics over the time scale of a step [
11,
12]. However, these methods use simple models of walking and need inverse kinematics and/or inverse dynamics to map to the full robot dynamics.
The virtual constraint method mentioned earlier affords asymptotic stability over a complete step [
13]. The step-to-step stabilization, also known as orbital stabilization, is a dynamic measure of bipedal stability as compared to instantaneous or local stabilization [
14]. More recent approaches formulate a control Lyapunov function approach within a virtual constraint framework that enables exponential local stabilization [
15]. However, to improve orbital stabilization one can choose control parameters to minimize the biggest eigenvalue of the Jacobian of the step-to-step dynamics, which works well only for small perturbations [
16]. Another method is to use event-based control where the linearization of the step-to-step dynamics is used to find control inputs to cancel the effect of small disturbances, but over the time scale of a step [
17,
18]. However, these linearized control methods can only provide stability for small perturbations.
Lyapunov functions provide a logical method for enabling controllers for large perturbations. Specifically, given a controller, one can compute a Lyapunov function and estimate the region of stability using sum-of-squares optimization provided the system can be approximated as a polynomial. One can then combine these regions of stability to find continuous controllers that stabilize the system from an initial condition to the reference motion using sampling-based methods such as rapidly exploring random trees [
19]. Similarly, one can use the sum-of-squares optimization to compute a Lyapunov function certifying step-to-step or orbital stability [
20,
21]. Both the above methods find the region of stability for a given controller. Alternately, using a control Lyapunov function for orbital stability, one can find a controller and corresponding region of stability for a candidate Lyapunov function [
22].
Deadbeat control refers to complete correction of disturbances/deviations in finite time [
23]. Deadbeat control is unique to discrete-time systems as continuous-time control relying on proportional or proportional-derivative control can only achieve asymptotic convergence but not deadbeat convergence in finite time [
24]. With legged systems, we are interested in one-step deadbeat control as this is important if the system has to meet tight constraints such as velocity tracking or stepping on a foothold. One method of achieving deadbeat control is to do a first order approximation in state and control of the step-to-step dynamics and use a discrete linear quadratic regulator, but this only achieves deadbeat control if the step-to-step dynamics are linear. For example, for the rimless wheel with a torso, the discrete linear quadratic regulator enables setting the torso angle once per step to achieve one-step deadbeat control [
25]. For systems that demonstrate nonlinear step-to-step dynamics, one can use numerical root finding to find a deadbeat controller. For example, the step-to-step dynamics of the 3 dimensional spring-loaded inverted pendulum is non-linear and one can find foot placement angle and spring stiffness that enables two-step deadbeat control [
26]. For more complex systems, simple models help compute control inputs to enable deadbeat control, and then map them to joint torques using inverse kinematics and/or inverse dynamics [
27].
In this paper, we use computed torque control to reduce the dimensionality of the system from 10D to 2D (see
Section 3.1). Thereafter, we use a data-driven approach to approximate the step-to-step dynamics with a simple model. Finally, this model is used for controller design. The use of a closed-form model of the step-to-step dynamics enables fast online control which is the main novelty of this work. Our earlier work demonstrated the approximation of the step-to-step dynamics for a simple model of running [
28,
29]. This paper extends our previous work in several ways as listed below and are the main contributions of this work.
The use of computed torque control to reduce continuous dynamics to low degree of freedom system. Here, we reduce the state space in the single stance (continuous phase) from 10D to 2D.
The use of Monte Carlo sampling followed by a low-order polynomial model and a high order error model to approximate the step-to-step map with relatively high accuracy. We represent the step-to-step map using a low dimensional control affine part comprising of a quadratic polynomial and high dimensional error term using Gaussian process model; the approximated model has about accuracy.
Development of a computationally efficient method to find a one-step deadbeat controller. We use the control affine part to find the control inputs analytically, but then fine tune these control inputs using the Gaussian process error model using iterative learning that converges in less than 10 function evaluations.
A more comprehensive review of biped robots including modeling, design, control, and open problems may be found in these books [
30,
31].
2. Robot Model
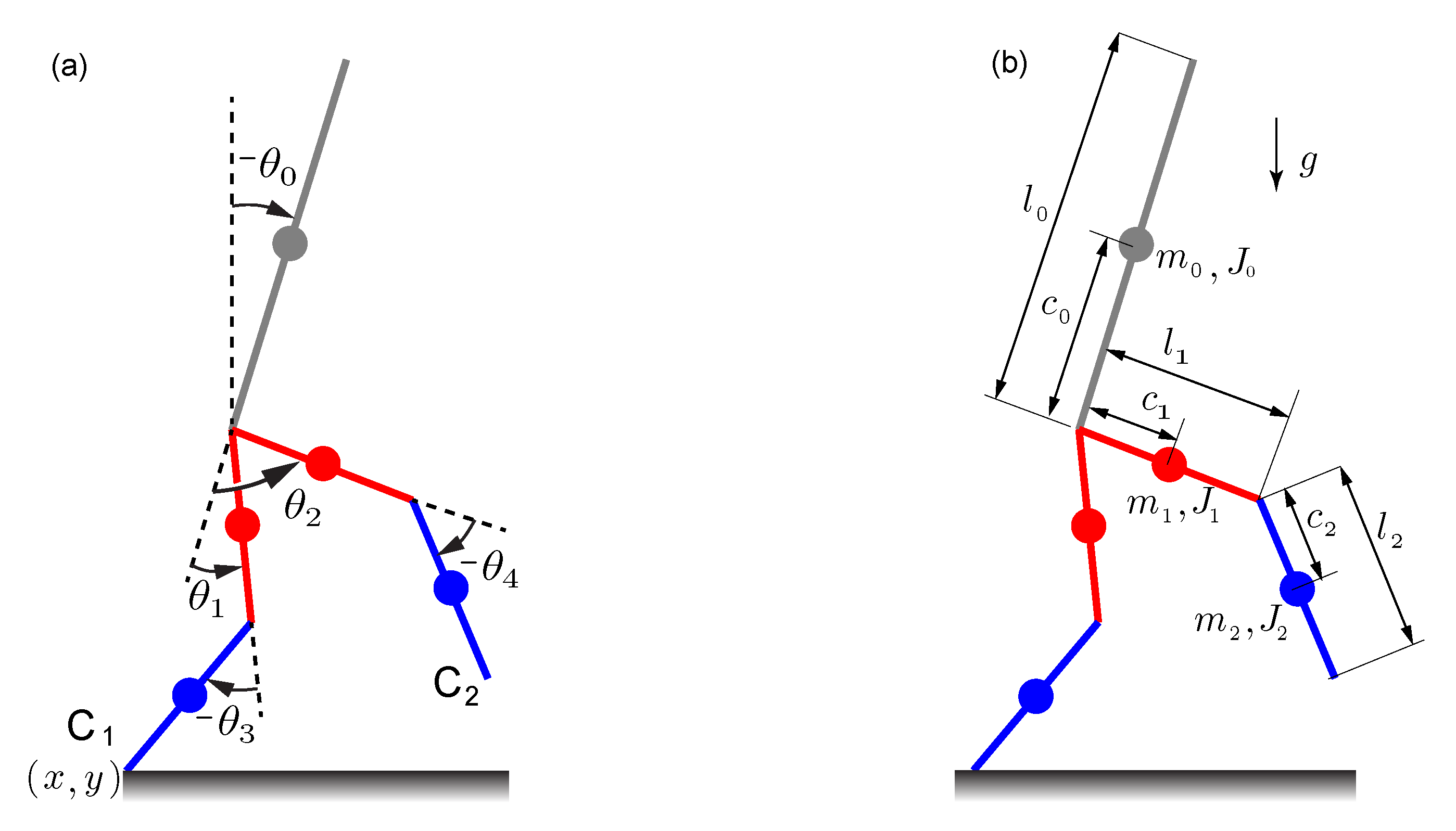
We show the 2D, 5-link model in
Figure 1. We define the stance leg as the one that is in contact with the ground and the swing leg is the other leg. We show the configuration variables in
Figure 1a. The foot in contact with the ground has coordinates
, where the x-axis is horizontal and y-axis is vertical. The torso angle
is the angle between the torso and the vertical direction,
and
are the relative angles made by the thigh links of the stance and swing leg respectively with the torso, and
and
are the angles made by the calf links of the stance and swing leg respectively with their respective thigh links. We chose the mass, inertia, and length parameters to be similar to human morphology. The torso mass is
kg, center of mass is at
m, and inertia about the center of mass is
kg·m
. The thigh links have a mass of
kg, center of mass is at
m, and inertia about the center of mass is
kg·m
. The calf links have a mass of
kg, center of mass at
m, and inertia about the center of mass is
kg·m
. Gravity points downwards and is
m/s
. The torso length
m the thigh link and calf link lengths are equal,
.
There are two sets of equations which are derived using the Euler-Lagrange method [
13]. One for the single stance phase where one foot is on the ground and second for the foot-strike where the legs exchange roles. We derive these next using the Euler-Lagrange method.
2.1. Single Stance Equations
The state variables are
. The Lagrangian
, where
,
,
are the linear velocity, angular velocity, and y-position center of mass of link
i respectively. The summation is taken over all the 5 links. Using the Euler-Lagrange equations using
gives us 7 equations that may be compactly written as
where
,
,
,
are the mass matrix, torques due to Coriolis and centrifugal acceleration, gravitational torque, and torque selection matrices. The control torques are
, where
is the torque for joint with degree of freedom
.
is the Jacobian from the stance leg contact point
and
is the ground reaction force on the stance leg. Note that the top first two lines in Equation (
1) are equivalent to change in linear momentum equals sum of external forces and remaining 5 are equivalent to change angular momentum equals external torques in the Newton-Euler formulation. Without loss of generality, we can assume
. Also, since
is at rest,
. Using these conditions, we use the first two equations in Equation (
1) to find the ground reaction forces
as a function of joint angles, velocities, and acceleration. We may write the remaining 5 equations as follows
where
,
,
,
are appropriately versions of the matrices defined earlier. We use this equation for simulating single stance phase and for controller development later.
2.2. Foot-Strike Equations
When the swing foot
touches the ground, the single stance phase ends and the robot transitions to an instantaneous foot-strike. We also assume that the trailing leg applies an inline impulsive force
. This force comes from the ankle motor at
which is passive during the stance phase, but applies an instantaneous impulse during take off (also see [
32]). In this phase, angular momentum is conserved about new contact point
. We obtain the equations for this phase by integrating Equation (
1) and taking the limit as time goes to 0 to get
where the superscript − and + denote the instance before and after collision respectively.
2.3. Simulating a Single Step
We show the general equation that describes the motion of the system below. In the equation, we identified a single step as the repeating unit consisting of motion from one mid-stance to the next. We now explain the composition of a single step in the above equation. We start the step at mid-stance when stance leg thigh link is vertical given by
. There after we use the single stance Equation (
2) to integrate the system till foot-strike. The foot strike occurs when the swing foot
touches the ground and is given by
. Thereafter we apply the foot strike condition given by Equation (
3). Then we swap the legs using the following
,
,
,
,
. Similarly, for the angular velocities we have
,
,
,
,
. Thereafter we integrate the equations in single stance given by Equation (
2) till the next mid-stance given by
.
4. Results
4.1. Periodic Gait and Optimization Parameters
For the single stance controller, we divided the walking into two phases, mid-stance to foot-strike and foot-strike to mid-stance. In each of these phases we specify the reference position , velocity , and accelerations . We simplify by assuming a fifth order polynomial for each of these phases by specifying the position, velocity, and acceleration at the start and end. Since the reference has 4 references (), we have to specify 8 positions, 8 velocities, and 8 accelerations and 1 time for each phase. Thus, 25 constants per phase and since there are two phases (midstance to foostrike and foostrike to midstance), we have 50 constants per step.
We simplify this assignment as follows. For the mid-stance to footstrike, we set all initial and final velocities and accelerations to zero. We set the position at the start to the current location of the joints, all the end positions to zero except the swing calf angle which we set to to allow for foot clearance during leg swing. We set the time to s assuming that this phase is longer than s. For the footstrike to midstance phase, we again set all initial and final velocities and accelerations to zero. We set the position at the start to the current position of the joints, all the end positions except the swing thigh angle which we set to . We also set the time to s. We set the nominal push-off impulse of , where is the non-dimensional impulse, and . Also, we use .
We use MATLAB to create a simulation of a single step using the description in
Section 2.3 and using Equations (
2) and (
3). Next, to find a periodic gait for the given control parameters
, we solve the following equation for
(see [
34] for more information).
Using numerical integration with
we obtain
. This nominal gait corresponds to a speed of
m/s, step time of
s, and step length of
and is similar to human cadence [
35,
36].
Next, we use central difference to find the Jacobian of Poincaré map
. Then we find the eigenvalues to establish the stability of the system. Only one eigenvalue is non-zero and is equal to
. Having all eigenvalues at zero except one implies that the step-to-step map is only one-dimensional. Since the only nonzero eigenvalue is less than 1, the system is stable for small perturbations [
33]. Thus, the step-to-step map is 1D and the goal of the modeling and control mentioned in the ensuring sections is to nullify the uncontrolled degree of freedom over the time scale of a step.
4.2. Data Generation for the Step-to-Step Map and Curve Fitting
In our MATLAB simulation of a single step, we incorporate falling detection that includes conditions under which we terminate the simulation. These conditions include: (1) leg stubbing during swing phase, (2) swing times is shorter than s, (3) falling backwards by noting the speed at mid-stance, (4) hip inside the ground, and (5) flight phase when the ground reaction forces is zero.
To generate data, our inputs are in the range , and using increments of . Then using the single step simulation to generate the output . The total input had 891 data points (), out of which 649 led to a failed step and 242 gave us valid mid-stance speed . We used or 186 of the valid data points for training and the remaining or 56 for testing the fit.
To fit the data, we first used quadratic polynomials in
for the function
f,
and
in
(see Equation (
11)). For example,
, where
,
, and
are constants found from regression by minimizing the squared error between the model and the data. We then checked if the affine part
is a good fit for the data. We found that
of the test data was within
accuracy and
of the data was within
accuracy. Next, we curve fitted the error using
. We used Gaussian process regression with a constant basis and it resulted in fitting
of the data within
accuracy.
4.3. Stability
Stability is the ability of the system to correct deviation in the state from the nominal state. These deviations could come from exogenous disturbances to the system. The nominal state is
rad/s. We imposed two different perturbations on the system and ran the simulations. In our first perturbation, we slowed the system to
rad/s and second one we speed up the system to
rad/s. We then controlled the system for each of these perturbations. The results are shown in
Figure 4. In
Figure 4a shows the mid-stance speed normalized against nominal speed
and (b) shows the control used subtracted from the nominal control values, both as a function of steps. As discussed earlier, the controller modulates the push-off control to speed up the system (red solid line) and modulates the foot placement to slow down the system (blue dashed line) to the reference speed. In both cases, it takes only one step to get to the nominal speed or onestep deadbeat control.
4.4. Agility
Agility is the ability of the system to rapidly change its speed and/or direction [
37]. Here we consider the ability to change its speed by specifying a sinusoidally varying reference speed that changes at every step for 25 steps as shown in
Figure 5a. The controller can track this reference with negligible error. We show the control in
Figure 5b, where we have shown the net change in control with respect to the nominal control values. In a nutshell, the push-off controller is used to speed up the system and foot-placement control is used to reduce the speed.
4.5. Versatility
Versatility is the robot’s ability to perform a variety of tasks such as walking, standing, turning, climbing stairs [
38]. Here we restrict to the specific task of walking over stepping stones. We can formulate this by specifying footstep locations or fixing the foot placement angle at every step. We generated 25 random foot placement positions from
to
rad. We fixed the foot placement angle to these values and specified the mid-stance speed to be the nominal speed
rad/s. Here, we remove the restriction on the one-sided control and allowed the push-off to vary (decrease/increase) as specified by Equations (
13) and (
15).
Figure 6a shows the foot placement angles (constraints) and
Figure 6b red solid line shows the mid-stance speed subtracted from the nominal value and is zero indicating the tracking is perfect. The black dashed line in
Figure 6b shows the push-off control used to achieve balance stability while achieving foot placement and velocity regulation.
5. Discussion
We demonstrated that by using computed torque control we can reduce the step-to-step dynamics of a 5 degrees of freedom model with a 10 dimensional state space to only 1 dimension. Next, we showed that using Monte-Carlo sampling and forward simulations, we can approximate the 1-dimensional step-to-step dynamics with about accuracy using a control affine model, but with accuracy when we supplement the control affine model with a Gaussian process model. Finally, we demonstrated that the control affine model enabled the analytical solution for the control input which we then fine tuned in 2 to 9 iterations using the Gaussian process model to enable perfect tracking or one-step deadbeat control.
We used computed torque control, a feedback linearization technique, to reduce the dimension of the continuous dynamics from 10 dimensions to 2 dimensions. The resulting feedback linearization is simple, but since it relies on canceling the natural dynamics, the Coriolis, the centrifugal, and gravitational torques, it is not necessarily energy efficient. Another method for feedback linearization is the method of virtual constraints where one controls the actuated degrees of freedom to follow the unactuated degrees of freedom, thus reducing the system dimension to the unactuated degrees of freedom [
6]. The major difference between computed torque control and virtual constraints is that while computed torque control allows actuated degrees of freedom to be controlled independent of each other, the method of virtual constraints does not. Since the actuated degrees of freedom are independent, we may modify them in real time without affecting the step-to-step dynamics. One situation where this is useful is when we need to modify the reference motion to increase the foot clearance during swing. On the other hand, one needs to choose the virtual constraints prior to start of leg swing to avoid scuffing.
One-step deadbeat control is important for bipedal robots to go into environments that pose strict constraints (e.g., foot holds, narrow edges). Since these constraints are imposed over the time scale of a step and the system dynamics are non linear, it is often the case to integrate these equations of motion repeatedly over the time scale of a step to find the control inputs. Here, we simplify finding the deadbeat control strategy by: one, using partial feedback linearization to reduce the dimension of the step-to-step dynamics, and two, approximating the resulting low-dimensional step-to-step dynamics with an analytical control affine model and a Gaussian process model for the error term. The latter enables us to use the control affine model to find an analytical solution for the control input which is then fine-tuned with the Gaussian process error model. The fine tuning takes only about 2 to 9 iterations. The relatively low computational requirements of the method would potentially enable online computation of control inputs.
The under-actuation of walking robots combined with the weak coupling between the swing leg and the torso leads to a significant control problem. Another robot example with these features is the acrobat [
39], a two link pendulum but with a single actuator. In the case of the acrobat, one can stabilize the system by using the unrestricted swinging motion of its actuated link, thus relying on the dynamic coupling. However, the swing leg angles and speeds are severely restricted in walking robots, thus strategies that have worked for acrobat are unusable for walking robots. With walking robots, the step-to-step motion dynamics, particularly managing energy exchanges because of foot collision and push-off, offer a powerful means of control [
40], which we exploit.
The step-to-step controls offer four significant benefits. One is that the step-to-step dynamics are a smooth function of state and control, and thus one may use control techniques that have worked on smooth systems. Two, the step-to-step dynamics are discrete algebraic equations that lead to a regulation problem which is simpler to solve than the continuous-time tracking problem. Three, the time-scale for solving the step-to-step control problem is of the order of half step-time, thus one may use a slow computer processor for online computation. Finally, although the instantaneous dynamics is under-actuated, by a judicious choice of control actions, it is possible to have over-actuation in the step-to-step dynamics, which one may exploit to achieve stabilization of wider range of initial conditions [
41].
Our method of approximating the step-to-step map using data driven methods improves on past approaches. Previous research use small perturbations near the fixed point of the limit cycle to find a linear [
42,
43] or a bilinear approximation [
44] of the step-to-step dynamics to generate a model for control. In our case, we use data over a wide range of states and control through a forward simulation to create a quadratic approximation of the step-to-step map supplemented with a Gaussian process error model. Since our step-to-step model is valid over a wider range of states and controls, we can stabilize over a wider range of perturbations and stipulate rapid change in states.
Our work has several limitations that we describe next. First, we rely on a good parameterization of the controls to enable a succinct representation of the step-to-step map. Unfortunately, this is a designer’s choice and might entail trial-and-error to find the best combination. Second, the once-per-step control using the step-to-step map is oblivious of the timing of the disturbances/perturbations. Thus, disturbances/perturbations just after state measurements (e.g., just after mid-stance) might be catastrophic. We may circumvent this issue by having multiple step-to-step maps along the trajectory. Third, although there are formal certificates for control affine systems, we need more nonlinear terms to create the model, thus limiting the possibility of providing formal guarantees. One way to circumvent this issue might be to use multiple control affine models, with a restricted region of application, over the state space rather than a single one. The computed torque control relies on inverting the model which also requires estimates of state of the system including the acceleration. Since computed torque control is model and sensor dependent, one needs to consider robust control for practical implementation. Since, we use a data-driven method to compute the step-to-step model for step-to-step control, it is not possible to provide control guarantees.