Abstract
In this paper, we present an approach for the minimum-energy trajectory planning in industrial robotic systems. The method is based on the dynamic and electro-mechanical modeling of one-degree-of-freedom systems and the derivation of the energy formulation for standard point-to-point trajectories, as, for instance, trapezoidal and cycloidal speed profiles. The proposed approach is experimentally validated on two robotic systems, namely a linear axis of a Cartesian manipulator built in the 1990’s, and a test bench composed of two servomotors directly connected or coupled by means of a planetary gear. During the tests, the electrical power expended by the systems is measured and integrated over time to compute the energy consumption for each trajectory. Despite the limitations of the energy measurement systems, the results reveal a trend in agreement with the theoretical calculations, showing the possibility of applying the method for enhancing the performance of industrial robotic systems in terms of energy consumption in point-to-point motions.
1. Introduction
Nowadays, the reduction of energy consumption is recognized to be one of the main goals in industrial and manufacturing sectors for both economical and environmental reasons [1]. In this context, several energy-saving methods have been developed over the years, showing their potential application to robotic and mechatronic systems [2]. The reduction of actuator effort can be achieved in different ways, ranging from the reducing the weight and inertia of the mechanical system [3], to the introduction of regenerative drives [4,5], and the optimal robot positioning with respect to the required task [6]. Another approach for energy reduction relies on the adoption of elastic elements that work in parallel to the main actuators and allows the system to perform a continuous conversion between potential and kinetic energy, following the concept of natural motion [7,8,9]. A further strategy for energy minimization in industrial robots is the optimal planning of trajectories in order to reduce the energy or torque expenditure of the motors [10,11].
The motion planning approach for energy efficiency has the advantage that no physical components have to be substituted or introduced in the mechanical system for the implementation of the method. In this framework, the optimal trajectory planning can be considered to be one of the main software-based approaches for energy efficiency [2]. Examples of motion planning for energy reduction include [12], which presents the minimum-energy B-splines trajectory optimization for multi-axis manipulators using electrical energy sharing. In [13], a energy-saving method for industrial machines is presented using simple motion trajectories, such as trapezoidal and S-curve velocity profiles. The method only considers the acceleration time to improve energy efficiency of a gantry crane system. Furthermore, in [14], a point-to-point trajectory based on a S-curve is designed in order to reduce energy consumption of a robotic linear axis, yet, only numerical results have been presented. In [15], an analytical model for minimum-energy planning in rest-to-rest motion is presented. The method is suitable for constant inertia systems and allows one to select the optimal motion law and duration.
Another recent example of motion planning for energy reduction is given by [16], where optimal point-to-point motions using trapezoidal speed profiles are analytically studied in order to enhance energetic performance. In [17], the problem of energy efficiency is addressed in closed form using piece-wise polynomial multi-point trajectories, whereas, in [18], the problem of energy optimization in functional redundant robots is addressed. These methods have not been experimentally validated yet.
In this paper, an analytical model and experimental results on minimum-energy trajectory planning in industrial robotic systems are presented. The method is based on the dynamic and electro-mechanical modeling of one-degree-of-freedom systems and the derivation of the energy formulation for standard point-to-point trajectories, as for instance trapezoidal and cycloidal speed profiles. The proposed approach is experimentally validated on two robotic systems, namely a linear axis of a Cartesian manipulator built in the 1990’s, and a test bench composed of two servomotors directly connected or coupled by means of a planetary gear. During the tests, the electrical power expended by the systems is measured and integrated over time to compute the energy consumption for each trajectory. Despite the limitations of the energy measurement systems, the results reveal a trend that is in agreement with the theoretical calculations, showing the possibility of applying the method for enhancing the performance of industrial robotic systems in terms of energy consumption in point-to-point motions.
This paper is an extended version of a preliminary work presented at the 29th International Conference on Robotics in Alpe-Adria-Danube Region (RAAD 2020) [19]. With respect to [19], additional experimental results are presented here, i.e., by applying the proposed method to a test bench composed of two servomotors available at Free University of Bozen-Bolzano, Italy. The rest of the paper is organized, as follows: Section 2 describes the dynamic and electro-mechanical modeling of the one-degree-of-freedom robotic systems, Section 3 reports the minimum-energy trajectory planning, whereas the experimental results are presented in Section 4. In particular, the tests performed on a linear axis of a Cartesian manipulator are shown in Section 4.1, whereas the results on a 1-DOF system with two coupled servomotors are given in Section 4.2. Finally, Section 5 concludes the paper.
2. Dynamic and Electro-Mechanical Modeling
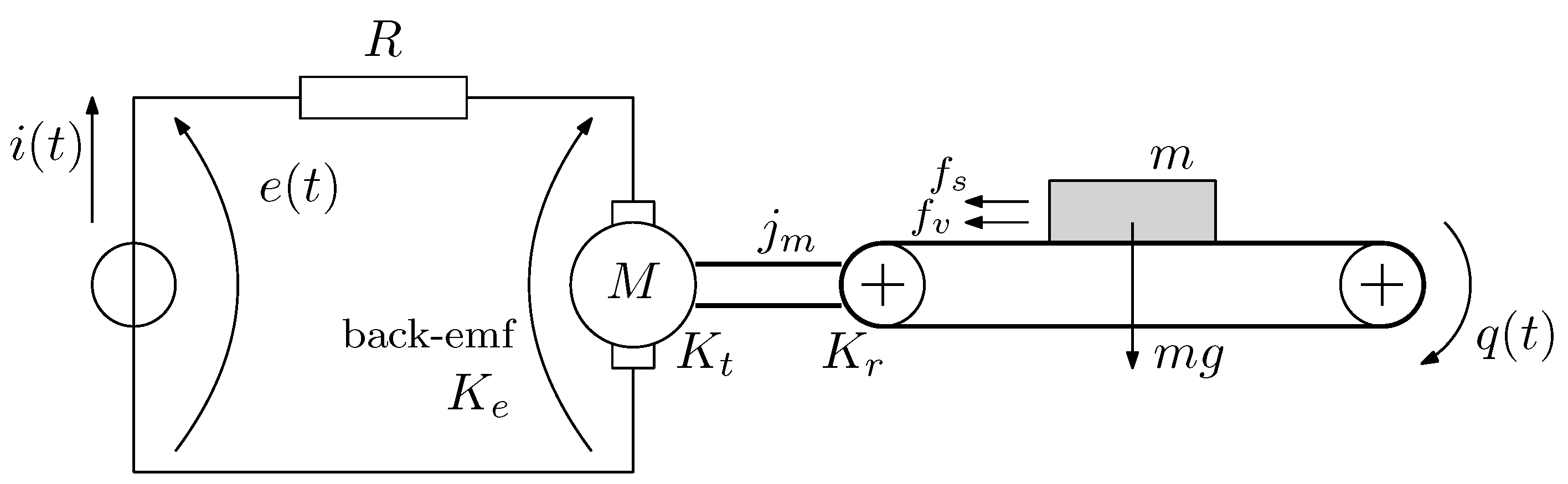
In this section, the dynamic and electro-mechanical model of a generic 1-DOF mechatronic system with a constant inertia is described. Figure 1 shows the model. In particular, a brushless AC servo-motor is coupled with the load by using a toothed belt and a geared transmission with reduction ratio equal to . The equivalent DC motor model is used to describe the AC servo-motor. The dynamic model of the system takes into account the motor inertia , the mass of the load m, and the Coulomb and viscous friction coefficients, and (Table 1). The torque required for the motion of the linear axis, described by the joint variable , is given by:
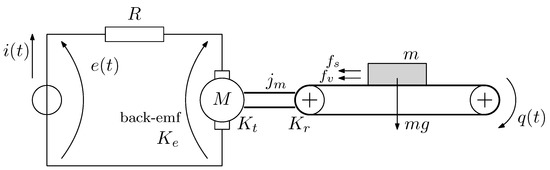
Figure 1.
Model of a generic 1-DOF system with constant inertia (i.e., linear axis of a Cartesian robot).

Table 1.
Dynamic parameters of the linear axis of the Cartesian robot.
The instantaneous current and voltage in the motor phase are:
where and are the motor torque and back-emf constants, and the are:
The motor input energy E that is required to perform a motion in the time period T is obtained by computing the integral of the electric power over time:
3. Minimum-Energy Trajectory Planning
Following the approaches that are presented in [13,14,16], it is possible to derive a formulation for the energy consumption related to the parameters that describe the given trajectory. In this work, we consider the trapezoidal and cycloidal profiles [20], which are characterized by four parameters: acceleration time , constant velocity time , deceleration time , and total length of the path L.
The trapezoidal trajectory can be defined by the following formulations for position q, velocity , and acceleration . In the following, and represent the time at the end of the acceleration phase and at the beginning of the deceleration, respectively. and are the acceleration and deceleration values, being defined by imposing the total length of the path L and maximum velocity [16].
The cycloidal trajectory is characterized by two S-speed profiles separated by a middle constant-speed phase, and it ensures continuous accelerations and smooth jerk profile [14]. Its formulation is given by:
where , , and . The constant is derived by imposing the total length of the path, resulting in .
By considering the trapezoidal profile and substituting the equations of motion in Equations (2) and (5) into Equation (4), the generic energy formulation for the mechanical system under study in the generic case with , is obtained [16]:
The same approach can be applied to the cycloidal speed profile by including the terms of the motion law of Equation (6) in the expression of energy of Equation (4). The following formulation for the energy consumption is obtained, as in [14]:
In Equations (7) and (8), the assume the following values: , , , and . When considering a fixed path length, the energy formulations of and only depend on three parameters: the acceleration and deceleration times and , and the total time T. These parameters are chosen as optimization variables to minimize the energy consumption of the system. In this work, equal acceleration and deceleration times are considered, i.e., , since this is demonstrated to be the optimal solution for both the trapezoidal [16] and the cycloidal trajectory [14].
Two cases are taken into account in the optimization problem: energy minimization with total time T free, and fixed (named Test T), and energy minimization with free, and total time T fixed (named Test ). The minimum of energy consumption is found in closed-form by deriving Equations (7) and (8) with respect to the free parameters (i.e., and T) and then equaling zero:
4. Experimental Results
To validate the proposed method, experimental tests are conducted on two 1-DOF mechatronic systems with constant inertia: a linear axis of a Cartesian robot and a system composed of two servomotors directly connected or coupled by means of a planetary gear. During the tests, the systems perform different point-to-point trajectories, and the electrical power is measured and integrated over time to compute the energy consumption for each trajectory. The results are then compared with the predictions of the theoretical model.
4.1. Linear Axis of a Cartesian Manipulator
The Cartesian manipulator used in the experimental tests is a 3-DOF robot built in the 1990’s and it is available in the Robotics and Mechatronics Lab at University of Udine, Italy [21,22]. The robot, as shown in Figure 2a, is actuated by three brush-less AC servo-motors Siemens 1FK6, and is equipped with a Siemens Simodrive 611 industrial drive unit. This PLC board performs torque and speed control, whereas the position loop is closed on an external NI PXI-8110 embedded controller (Figure 2b). This real-time module is equipped with a NI PCI-6221 and a NI PCI-6259: the first multi-functional board is used to acquire signals from the resolvers, whereas the second one is adopted to generate the analog signals (i.e., voltage command) needed to drive the motors. The NI PCI-6259 is also employed for the acquisition of the signals of current and voltage adsorbed by the servo-motor. These signals are sent by the driver as a parameterized analog signals and filtered by means of a physical RC low-pass filter at . The measure of current and voltage is challenging without a proper power measurement system, since the parameterized signals from the driver are noisy and limited in resolution.

Figure 2.
(a) The Cartesian robot available at the Robotics and Mechatronics Lab, University of Udine, Italy; and, (b) schematics of the control and data acquisition system for one axis of the robot.
The position control loop and the data acquisition are based on a custom NI LabVIEW real-time software, which runs on the NI-PXI at a frequency of . The robot is operated by feeding a text file that contains a sequence of position values, planned in Matlab™. The control architecture is based on three nested loops: the outer position loop is based on a PID control scheme, whereas the internal velocity and current loops are based on two different PI, as provided by the Siemens Simodrive control unit. The tuning of the controller, especially for the position loop, is fundamental in obtaining a good compromise between induced vibration and trajectory tracking, also considering the friction and stick-slip phenomena of the axis. Anyhow, this latter is not a requirement for the effectiveness of the presented method, which is based on the optimization of trajectories that are tested on the same system with the same gains.
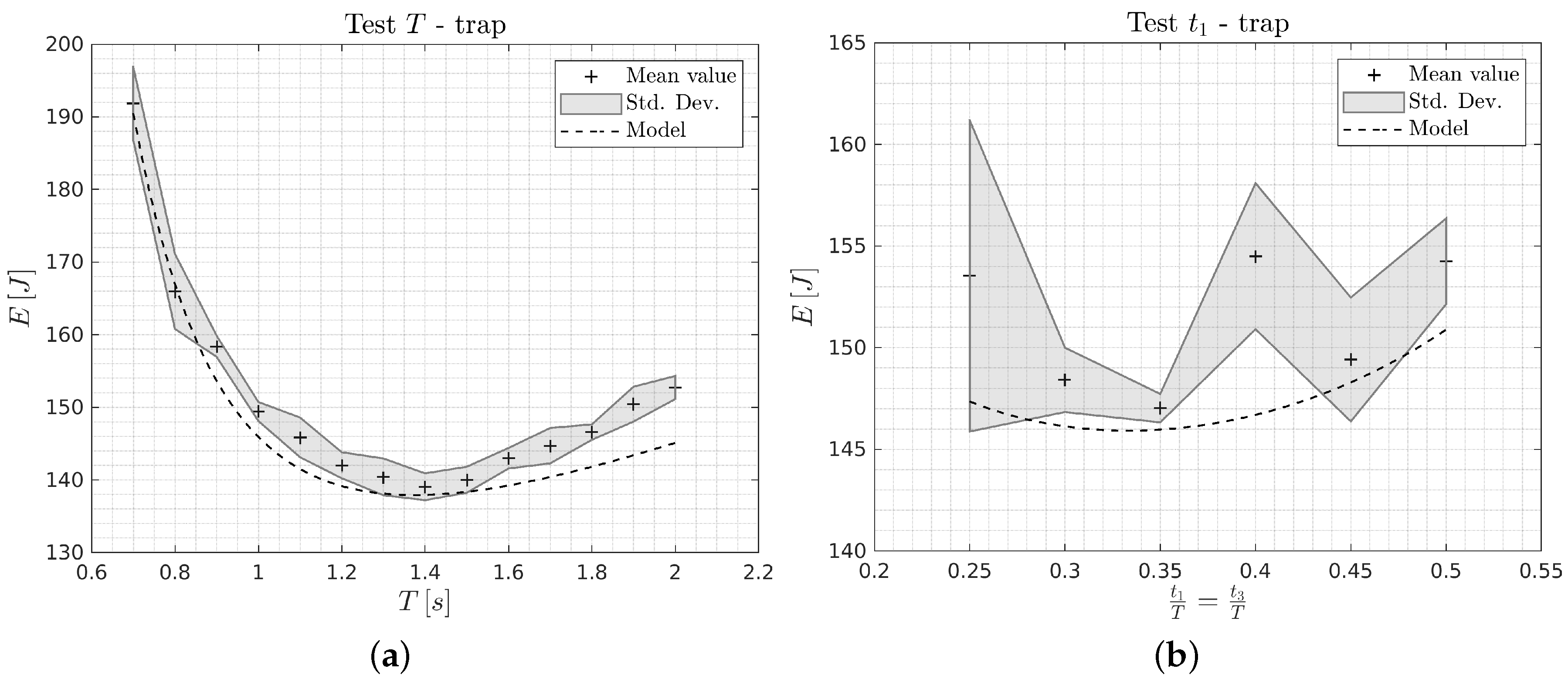
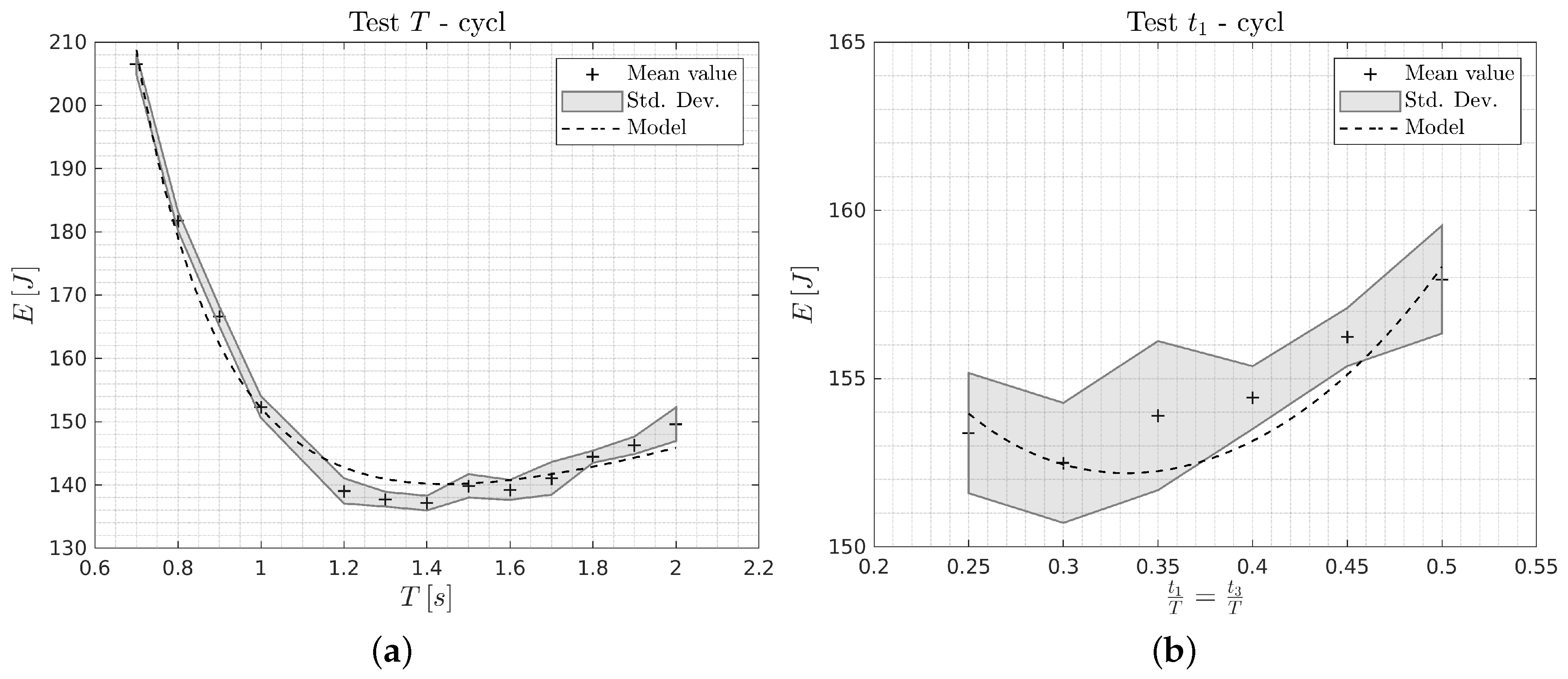
Figure 3 and Figure 4 report the theoretical and experimental results obtained with the trapezoidal and cycloidal trajectories, respectively. For each test, 10 round trips are performed by the manipulator. Dashed lines represent the theoretical curves, whereas shaded areas illustrate mean and standard deviation of the experimental data. Each cross represents the mean value of the 10 complete round trips of the main linear axis of the Cartesian robot through a path of length . Figure 3a and Figure 4a are related to the case of energy minimization with total time T free, which ranges from 0.7 to 2.0 s, and fixed, whereas Figure 3b and Figure 4b consider the case of energy minimization with free, ranging from 0.25 to 0.50 s, and total time T = 1.00 s fixed. The theoretical and experimental minimum-energy solutions for the two different trajectories are reported in Table 2. In the table, the values of consumed energy are calculated as the mean over the 10 tests.
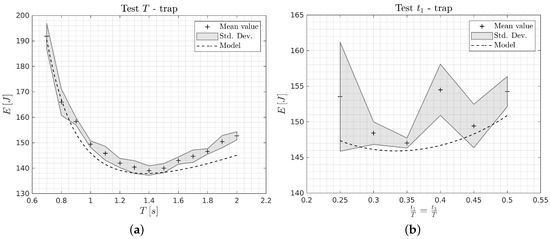
Figure 3.
Results on the Cartesian robot using the trapezoidal trajectory: (a) Test T, (b) Test .

Figure 4.
Results on the Cartesian robot using the cycloidal trajectory: (a) Test T, (b) Test .

Table 2.
Theoretical and experimental minimum-energy solutions.
By considering the trapezoidal trajectory, the minimum-energy solution for Test T is located at ( exp.) and corresponds to a energy consumption of ( exp.), whereas, for Test , the minimum is at ( exp.) and corresponds to ( exp.). For the cycloidal trajectory the minimum for Test T is found for ( exp.) and ( exp.), whereas for Test the minimum solution is found for ( exp.) and ( exp.). A good agreement between theoretical and experimental results is found, as it can be seen from the graphs and from the minimum values. As an example, in Test T, if the optimal trajectory is considered, the percentage of energy consumption reduction results equal to and for the trapezoidal and cycloidal trajectories, respectively, with respect to the worst case in which . A lower decrement is achieved in Test . For instance, moving from to the optimal value , a reduction of and is obtained in the case of trapezoidal and cycloidal motion primitive, respectively.
The experimental data in Test T show the typical convex trend of energy versus the motion time period T: for small values of T, high acceleration and speed lead to high torque requirements. Therefore, the energy dissipation in motor winding resistance and in viscous friction is increased. On the other hand, for higher values of T, the actuator has to counteract the constant friction terms for longer time, resulting in an increase of the Joule effect dissipation. In case Test , the acceleration and deceleration times and influence the energy consumption due to the higher acceleration in the left part of the plots (i.e., Joule effect dissipation), and higher speeds in the right part (i.e., viscous friction dissipation).
4.2. 1-DOF System with Two Coupled Servomotors
Further experimental tests are conducted on a 1-DOF system composed of two coupled servomotors Bonfiglioli BMD 170 34, available at the Mechanical Lab of the Free University of Bozen-Bolzano, Italy. One motor is the active motor, whereas the second motor acts as a load, applying a constant resistant torque to the shaft. Two different cases for the coupling of the motors are considered:
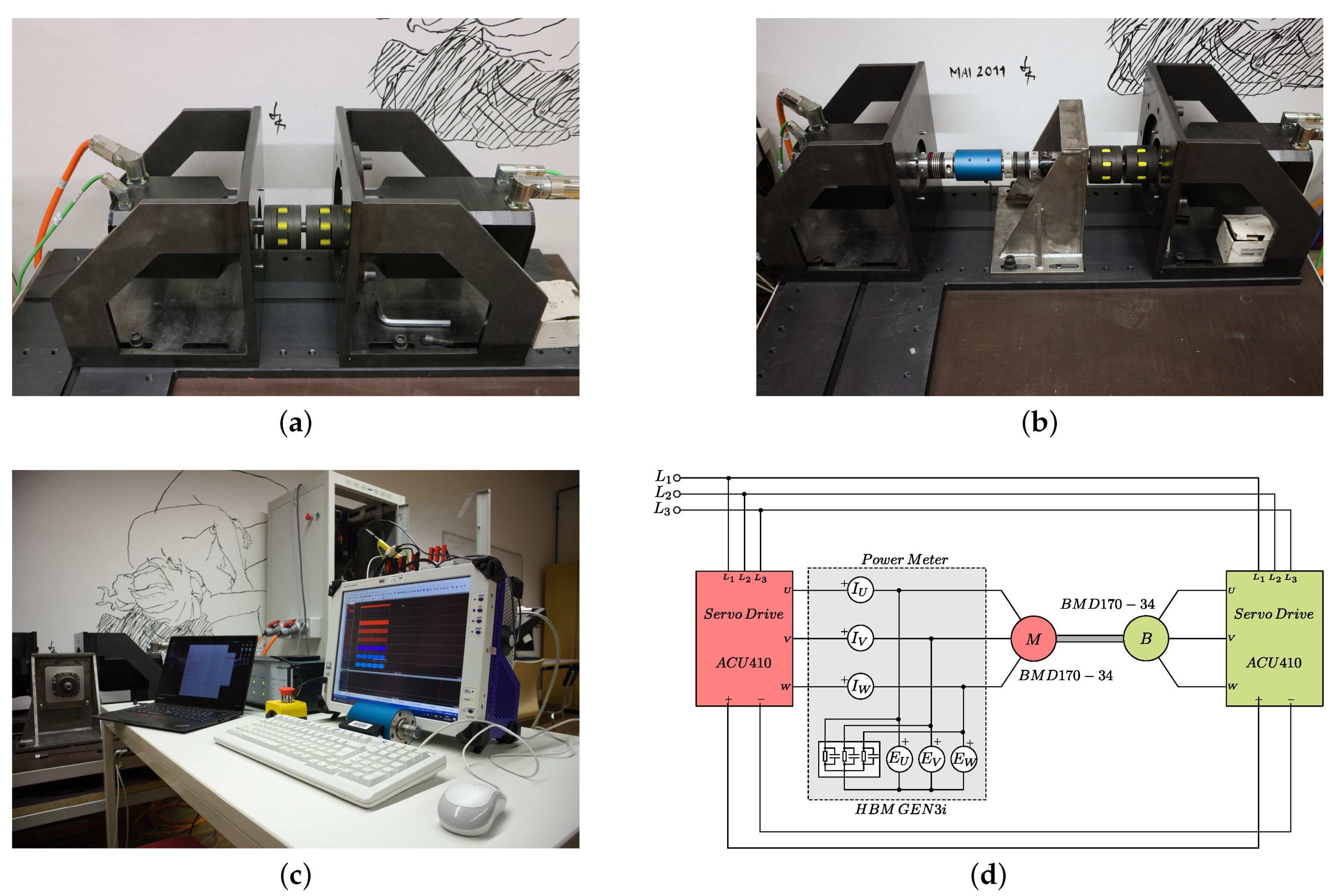
- Case (1): direct coupling (Figure 5a);
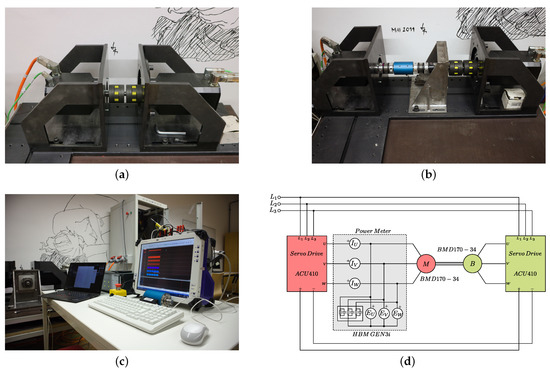 Figure 5. Test-bench of the 1-DOF system available at the Mechanical Lab, Free University of Bozen-Bolzano, Italy: (a) direct coupling of Case (1); (b) coupling of Case (2) with interposition of a planetary gear; (c) HBM GEN3i power meter system; and, (d) schematics of the control and data acquisition system.
Figure 5. Test-bench of the 1-DOF system available at the Mechanical Lab, Free University of Bozen-Bolzano, Italy: (a) direct coupling of Case (1); (b) coupling of Case (2) with interposition of a planetary gear; (c) HBM GEN3i power meter system; and, (d) schematics of the control and data acquisition system. - Case (2): coupling with the interposition of a Bonfiglioli TQ 070 planetary gear (Figure 5b).
It can be demonstrated that the model derived in Section 2 is still valid. The total length L of the path has only to be substituted with the angular displacement U in the energy equation and in the optimal solution that ensures a minimum-energy consumption.
When considering the electrical aspects of the system, the two permanent magnet synchronous motors are driven by the respective Bonfiglioli ACU410 servo drives, as shown in Figure 5d. Both of them are powered by the three-phase network, but they also share their DC bus. In this way, the power generated by the brake is recovered and directly used by the motor. Thus, ideally, only the energy to counteract the friction is supplied by the network.
In Table 3, the values of the model parameters are reported for the 1-DOF system in both of the coupling cases. In this regard, all of the parameters are determined from the data-sheets with the exception of the friction terms and . Indeed, for the friction coefficients, no data are available and they are identified through preliminary experiments. The systems are operated with the brake deactivated, using several trajectories with different values of speed and acceleration in order to excite the system in different working points. The friction terms are then optimized in order to obtain a matching between the consumed electrical energy obtained in the experimental and numerical results.

Table 3.
Dynamic parameters of the 1-DOF system with two coupled servomotors.
For what concerns the trajectory generation, the two Bonfiglioli servo drives can only adopt trapezoidal speed profiles. Because the drive has only a built-in velocity controller, the implementation of the desired profile, which covers the angular displacement U in period T with acceleration and deceleration times equal to and , respectively, requires some expedients. In particular, the acceleration , the deceleration values , and the maximum travel speed are set. Moreover, a drive built-in timer starts the braking phase after a time from the beginning. In the brake motor drive, instead, the reference speed of the velocity control is set to zero, while a torque limit is imposed. Thus, the motor shaft starts turning only if an external torque overcome the limit set point. All of these parameters are set through a serial communication channel and a Python script, in order to automatize the process.
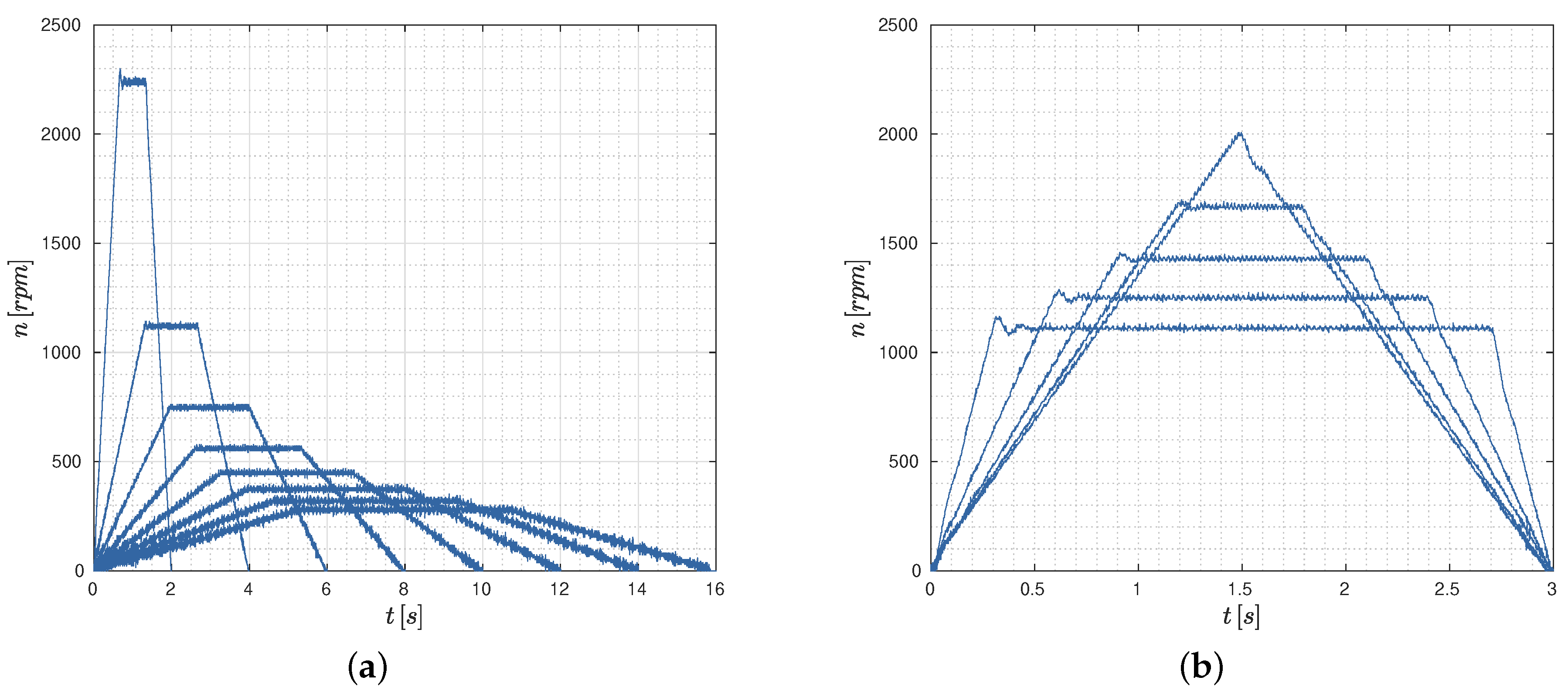
Two different tests are considered, named Test T and Test . In Test T, the same values for acceleration and deceleration times are considered and set equal to , while different values for the time period T are tested (Figure 6a). In particular, T ranges from 0 to with an interval of with and in the other cases. In Test , a fixed period time is considered, while the value of is varied from to with an interval of (Figure 6b).
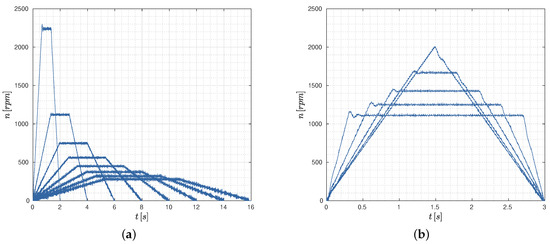
Figure 6.
Examples of trajectory profiles considered in (a) Test T, and (b) Test . The speed profiles are directly measured by the servo-motors.
A power meter is connected between the servo output and the motor in order to measure the energy consumed and generated (i.e., during the braking phase) by the motor. It consists of a HBM GEN3i data acquisition system (Figure 5c) that is used to measure the motor phase voltages , and and the phase currents , and , as shown in Figure 5d, with a sampling rate of .
The energy consumption is calculated by integrating the power over the time, where:
and the electrical power is calculated as the sum of each phase voltage multiplied by the correspondent phase current.
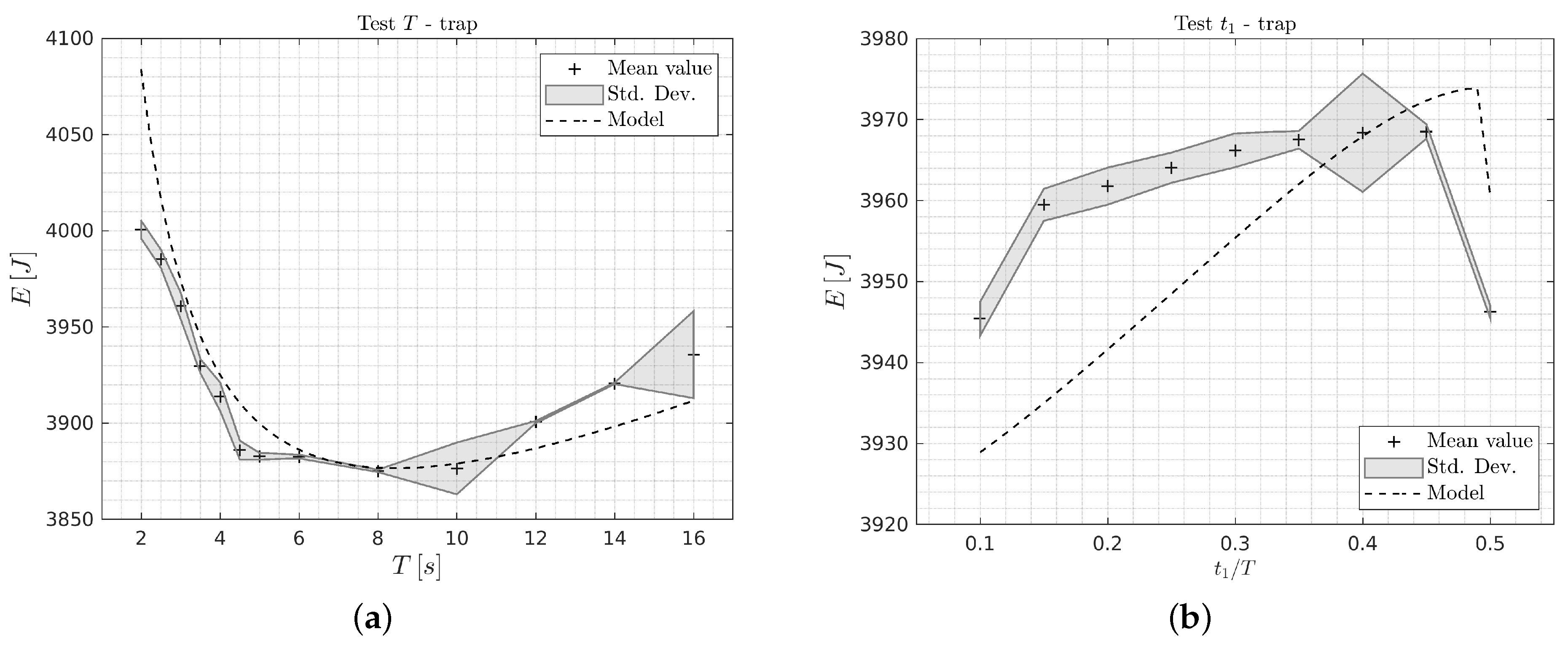
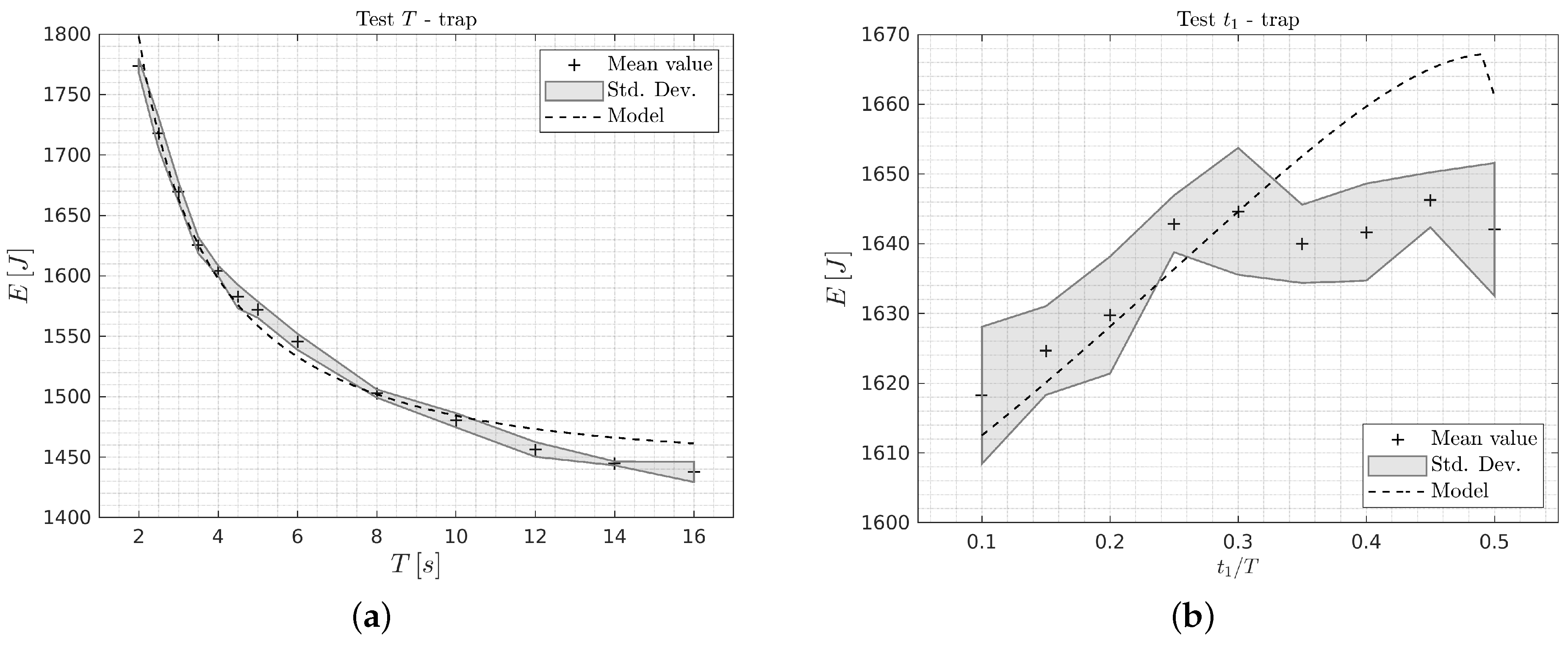
In Table 4, the results for Test T (i.e., optimization of T, with equal and fixed acceleration and deceleration times), and for Test (i.e., optimization of , with fixed cycle time T) are reported. In Figure 7 and Figure 8, the results of the experimental tests are compared with the numerical ones for both the system configurations. As in the previous graphs, dashed lines represent the theoretical curves, whereas shaded areas illustrate mean and standard deviation of the experimental data. For each test, five round trips are run on the 1-DOF system. When considering Test T for Case (1) (Figure 7a), it can be seen that the energy function has a convex trend and presents a minimum of energy consumption for . On the contrary, this behavior is only partially visible in Case (2) (Figure 8a), since the range of T for the experimental tests has been limited to lower values due to the computation efforts that are required in the post-processing. In this case, the minimum of energy consumption is expected to be found for values of T that are greater than (i.e., , as reported in Table 4). The maximum energy consumption reduction that can be obtained in Case (1) results in being equal to , if the worst scenario (i.e., ) is compared with the optimal one (i.e., ). In Case (2) this percentage assumes the value of , if the worst scenario (i.e., ) is compared with the optimal value, assumed as . It can be noted that in Case (1) the percentage value is lower, since the constant torque is higher and more relevant with respect to the inertial terms.

Table 4.
Theoretical minimum-energy solutions.
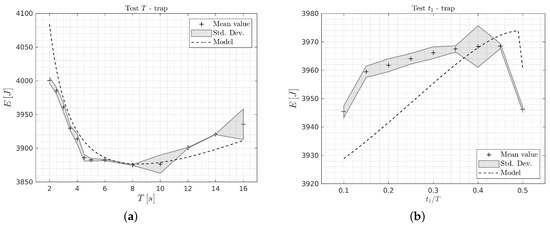
Figure 7.
Experimental results on the 1-DOF system with coupling of Case (1): (a) Test T, (b) Test .
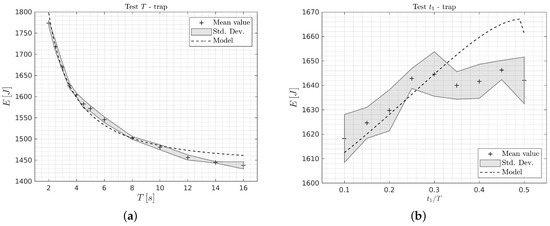
Figure 8.
Experimental results on the 1-DOF system with the coupling of Case (2): (a) Test T, (b) Test .
In Figure 7b and Figure 8b, the results of Test are reported. Experimental and numerical data do not overlap perfectly as in the previous case. This can be explained by considering that the energy variation with is limited and in the order of 1% within the considered range of . Thus, its measure is more challenging considering the adopted measurement devices. Anyway, the optimization of has a lower effect on the energy consumption in the considered experimental case. Indeed, it has practically no effect if the inertial terms of the system are negligible with respect to the constant terms (i.e., gravity and friction terms), as in the considered system. On the other hand, the optimization of is more effective in systems where the inertia value plays an important role.
5. Conclusions
In this paper, an analytical model and experimental results on minimum-energy trajectory planning in industrial robotic systems has been presented. The method is based on the dynamic and electro-mechanical modeling of one-degree-of-freedom systems and the derivation of the energy formulation for standard point-to-point trajectories, as, for instance, trapezoidal and cycloidal speed profiles. The proposed approach has been experimentally validated on two robotic systems, namely a linear axis of a Cartesian manipulator built in the 1990’s, and a test bench that was composed of two servomotors directly connected or coupled together by means of a planetary gear. During the tests, the electrical power expended by the systems is measured and integrated over time to compute the energy consumption for each trajectory. Despite the limitations of the energy measurement systems, the results revealed a trend in good agreement with the theoretical calculations, showing the possibility of applying the method for enhancing the performance of industrial robotic systems in terms of energy consumption in point-to-point motions. The proposed approach is based on a closed-form analytical formulation, which requires low implementation effort and computational resources. Moreover, this method can also be easily implemented in existing systems without the need of introducing additional hardware elements, as in [4,8]. Therefore, the method only acts on the trajectory planning aspects.
Future developments of this work will include the extension and validation of the proposed approach on more complex robotic systems. Furthermore, we plan to test further trajectories and motion profiles, such as polynomial and trigonometrical [20], in order to evaluate their performance in point-to-point motions.
Author Contributions
Conceptualization, methodology and investigation, software, validation, data curation, writing–original draft preparation, writing–review and editing, L.S. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Free University of Bozen-Bolzano funds within the project TN2803: Mech4SME3: Mechatronics for Smart Maintenance and Energy Efficiency Enhancement.
Acknowledgments
The authors would like to thank Alessandro Gasparetto and Renato Vidoni for their administrative and technical support during several stages of the current work, and Luca Favaretto for his help in collecting the experimental data from the Cartesian robot at University of Udine.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kucukvar, M.; Cansev, B.; Egilmez, G.; Onat, N.C.; Samadi, H. Energy-climate-manufacturing nexus: New insights from the regional and global supply chains of manufacturing industries. Appl. Energy 2016, 184, 889–904. [Google Scholar] [CrossRef]
- Carabin, G.; Wehrle, E.; Vidoni, R. A review on energy-saving optimization methods for robotic and automatic systems. Robotics 2017, 6, 39. [Google Scholar] [CrossRef]
- Yin, H.; Liu, J.; Yang, F. Hybrid Structure Design of Lightweight Robotic Arms Based on Carbon Fiber Reinforced Plastic and Aluminum Alloy. IEEE Access 2019, 7, 64932–64945. [Google Scholar] [CrossRef]
- Carabin, G.; Palomba, I.; Wehrle, E.; Vidoni, R. Energy Expenditure Minimization for a Delta-2 Robot Through a Mixed Approach. In Multibody Dynamics 2019; Springer: Cham, Switzerland, 2019; pp. 383–390. [Google Scholar]
- Khalaf, P.; Richter, H. Trajectory optimization of robots with regenerative drive systems: Numerical and experimental results. IEEE Trans. Robot. 2019, 36, 501–516. [Google Scholar] [CrossRef]
- Scalera, L.; Boscariol, P.; Carabin, G.; Vidoni, R.; Gasparetto, A. Enhancing Energy Efficiency of a 4-DOF Parallel Robot Through Task-Related Analysis. Machines 2020, 8, 10. [Google Scholar] [CrossRef]
- Barreto, J.P.; Schöler, F.; Corves, B. The concept of natural motion for pick and place operations. In New Advances in Mechanisms, Mechanical Transmissions and Robotics; Springer: Cham, Switzerland, 2017; pp. 89–98. [Google Scholar]
- Scalera, L.; Carabin, G.; Vidoni, R.; Wongratanaphisan, T. Energy efficiency in a 4-DOF parallel robot featuring compliant elements. Int. J. Mech. Control. 2019, 20, 1–9. [Google Scholar]
- Scalera, L.; Palomba, I.; Wehrle, E.; Gasparetto, A.; Vidoni, R. Natural Motion for Energy Saving in Robotic and Mechatronic Systems. Appl. Sci. 2019, 9, 3516. [Google Scholar] [CrossRef]
- Paes, K.; Dewulf, W.; Vander Elst, K.; Kellens, K.; Slaets, P. Energy efficient trajectories for an industrial ABB robot. Procedia Cirp 2014, 15, 105–110. [Google Scholar] [CrossRef]
- Trigatti, G.; Boscariol, P.; Scalera, L.; Pillan, D.; Gasparetto, A. A look-ahead trajectory planning algorithm for spray painting robots with non-spherical wrists. In Mechanism Design for Robotics; Springer: Cham, Switzerland, 2018; pp. 235–242. [Google Scholar]
- Hansen, C.; Kotlarski, J.; Ortmaier, T. Experimental validation of advanced minimum energy robot trajectory optimization. In Proceedings of the 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013; pp. 1–8. [Google Scholar]
- Ho, P.M.; Uchiyama, N.; Sano, S.; Honda, Y.; Kato, A.; Yonezawa, T. Simple motion trajectory generation for energy saving of industrial machines. Sice J. Control. Meas. Syst. Integr. 2014, 7, 29–34. [Google Scholar] [CrossRef]
- Boscariol, P.; Carabin, G.; Gasparetto, A.; Lever, N.; Vidoni, R. Energy-efficient point-to-point trajectory generation for industrial robotic machines. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Barcelona, Spain, 29 June–2 July 2015; pp. 1425–1433. [Google Scholar]
- Richiedei, D.; Trevisani, A. Analytical computation of the energy-efficient optimal planning in rest-to-rest motion of constant inertia systems. Mechatronics 2016, 39, 147–159. [Google Scholar] [CrossRef]
- Carabin, G.; Vidoni, R.; Wehrle, E. Energy saving in mechatronic systems through optimal point-to-point trajectory generation via standard primitives. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2018; pp. 20–28. [Google Scholar]
- Boscariol, P.; Richiedei, D. Energy-efficient design of multipoint trajectories for Cartesian robots. Int. J. Adv. Manuf. Technol. 2019, 102, 1853–1870. [Google Scholar] [CrossRef]
- Boscariol, P.; Caracciolo, R.; Richiedei, D.; Trevisani, A. Energy Optimization of Functionally Redundant Robots through Motion Design. Appl. Sci. 2020, 10, 3022. [Google Scholar] [CrossRef]
- Scalera, L.; Carabin, G.; Vidoni, R.; Gasparetto, A. Minimum-Energy Trajectory Planning for Industrial Robotic Applications: Analytical Model and Experimental Results. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2020; pp. 334–342. [Google Scholar]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Boscariol, P.; Gasparetto, A.; Vidoni, R. Planning continuous-jerk trajectories for industrial manipulators. In Proceedings of the ASME 2012 11th Biennial Conf. on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; pp. 127–136. [Google Scholar]
- Gasparetto, A.; Lanzutti, A.; Vidoni, R.; Zanotto, V. Validation of minimum time-jerk algorithms for trajectory planning of industrial robots. J. Mech. Robot. 2011, 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).