Multi-Agent Collaborative Path Planning Based on Staying Alive Policy †
Abstract
1. Introduction
2. Notation and Preliminaries
3. Cooperative Exploration and Coverage Scheme
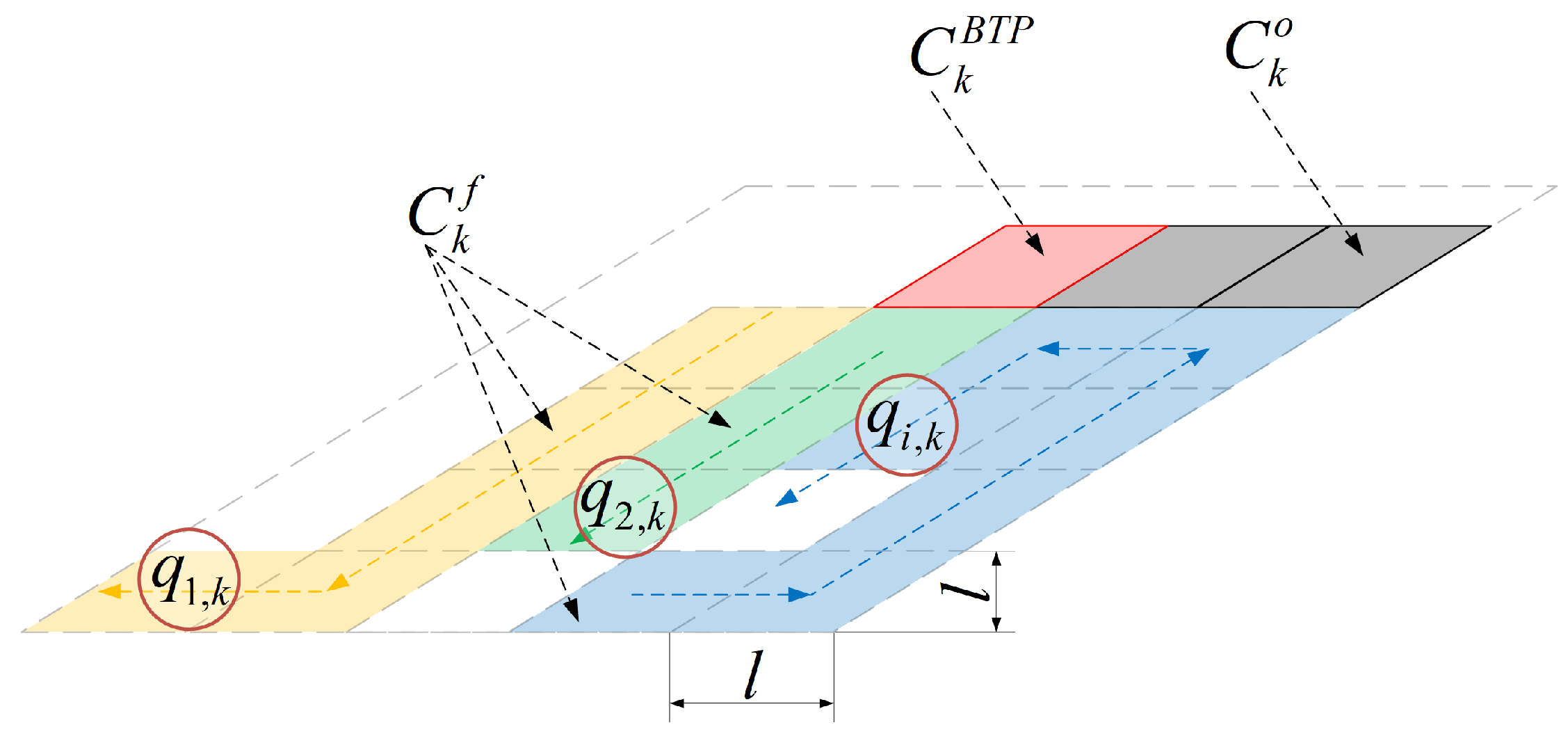
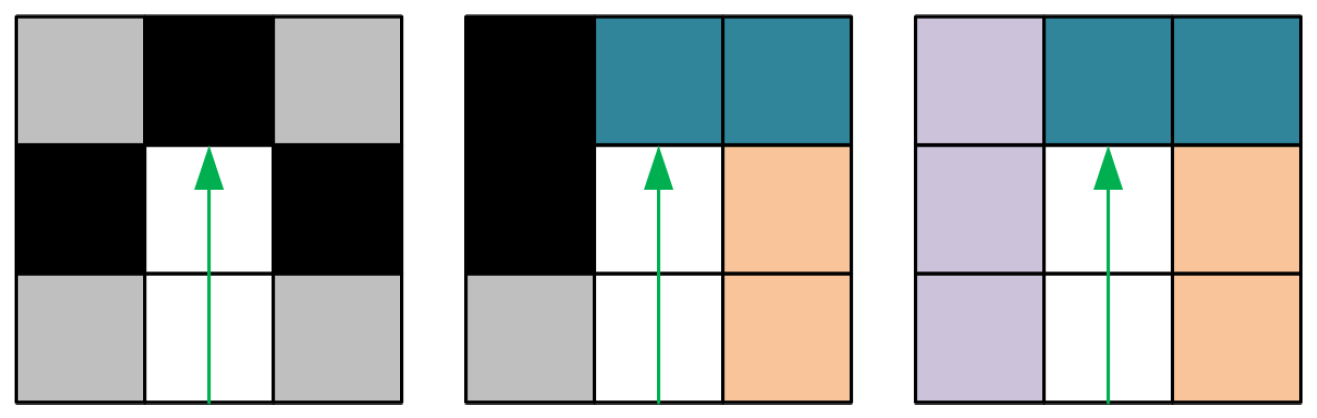
3.1. Exploration Method
| Algorithm 1 Boustrophedon motion (BM) algorithm |
| Require:, M |
|
3.2. Staying Alive Policy
| Algorithm 2 Staying alive policy algorithm |
| Require:, |
|
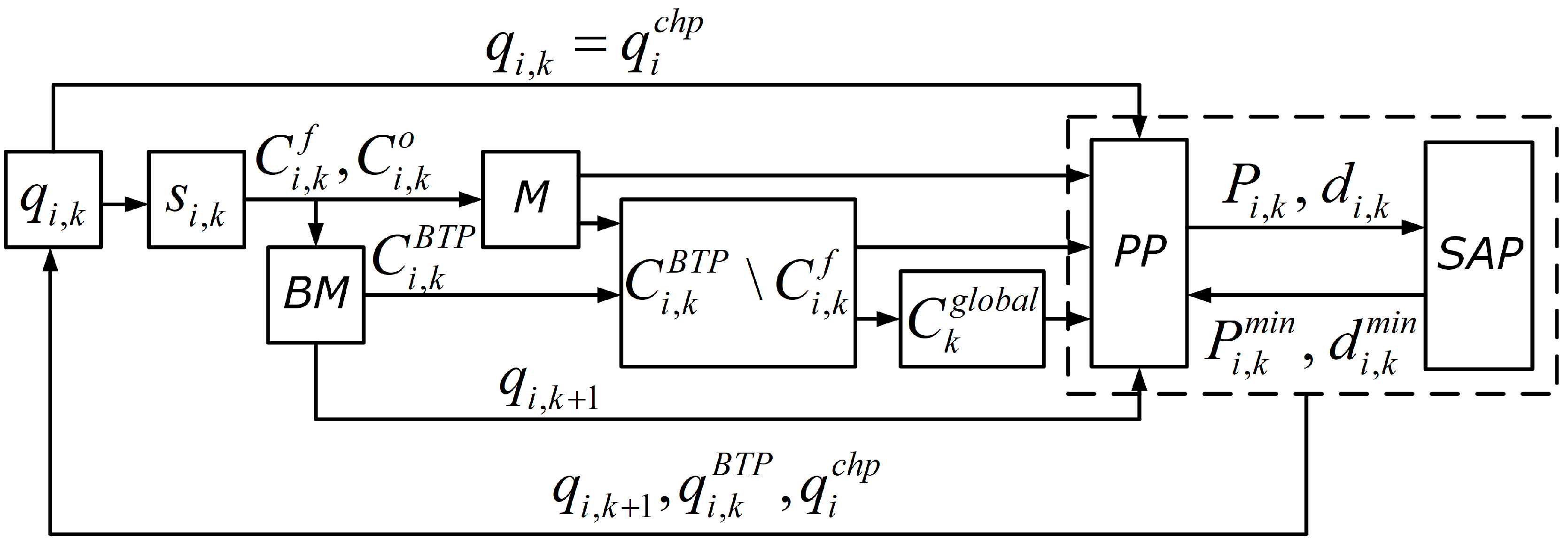
3.3. Path Planner
| Algorithm 3 Path planner |
| Require:, , |
|
| Algorithm 4 Cooperative exploration and coverage algorithm with multiple agents |
| Require:, , M, n |
|
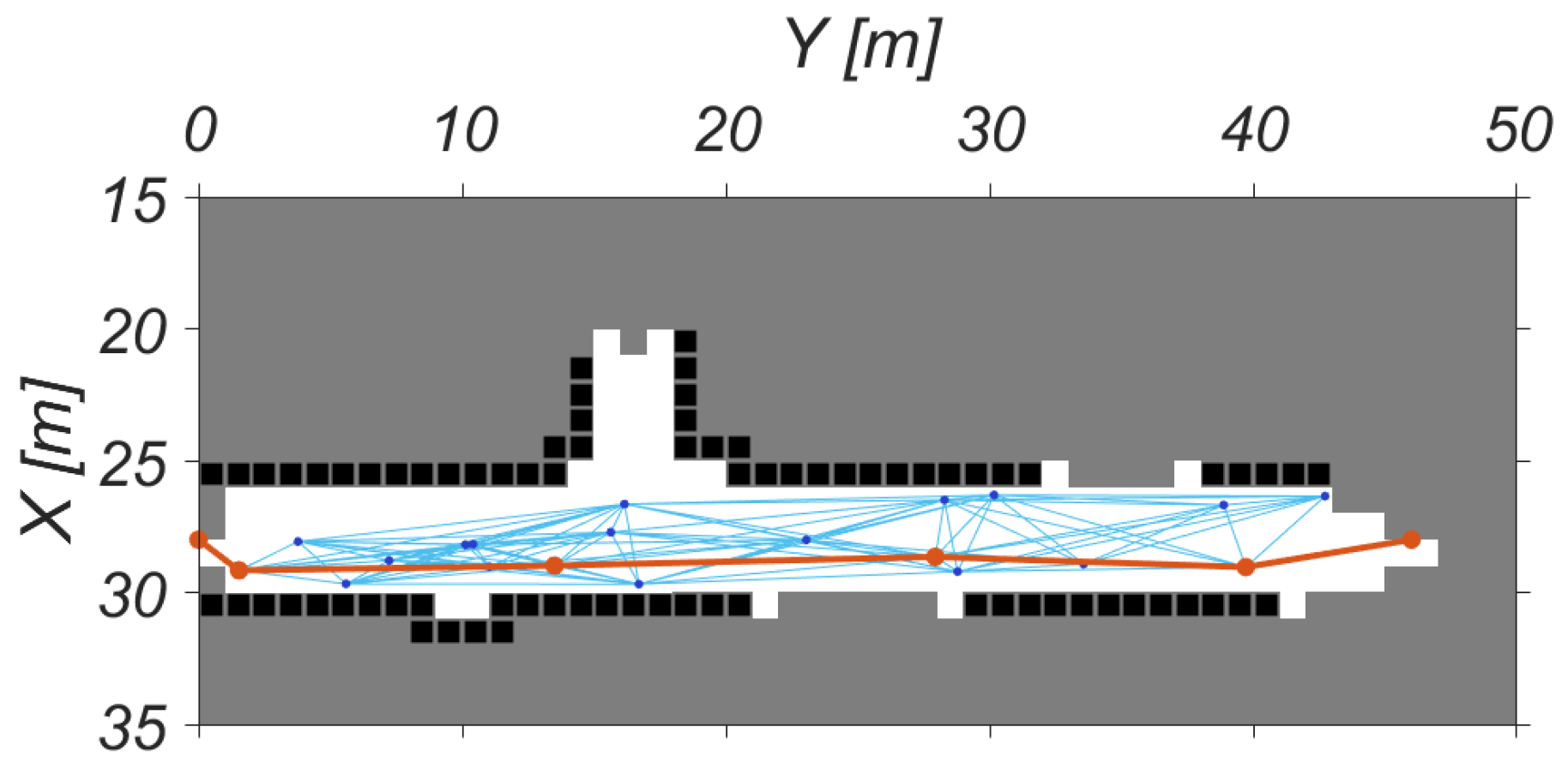
4. Simulation Results
4.1. Discussions of the Design Choices
4.2. Design of Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wasik, A.; Pereira, J.N.; Ventura, R.; Lima, P.U.; Martinoli, A. Graph-Based Distributed Control for Adaptive Multi-Robot Patrolling through Local Formation Transformation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Yashoda, H.; Piumal, A.; Polgahapitiya, P.; Mubeen, M.; Muthugala, M.; Jayasekara, A. Design and Development of a Smart Wheelchair with Multiple Control Interfaces. In Proceedings of the 2018 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 30 May–1 June 2018; pp. 324–329. [Google Scholar]
- Dautenhahn, K. Roles and functions of robots in human society: Implications from research in autism therapy. Robotica 2003, 21, 443–452. [Google Scholar] [CrossRef]
- Thrun, S.; Bennewitz, M.; Burgard, W.; Cremers, A.B.; Dellaert, F.; Fox, D.; Hahnel, D.; Rosenberg, C.; Roy, N.; Schulte, J.; et al. MINERVA: A second-generation museum tour-guide robot. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; Volume 3. [Google Scholar]
- Cubber, G.D.; Doroftei, D.; Rudin, K.; Berns, K.; Serrano, D.; Sanchez, J.; Govindaraj, S.; Bedkowski, J.; Roda, R. Search and Rescue Robotics-From Theory to Practice; IntechOpen Limited: London, UK, 2017. [Google Scholar]
- Montambault, S.; Pouliot, N. Design and validation of a mobile robot for power line inspection and maintenance. In Proceedings of the 6th International Conference on Field and Service Robotics-FSR, Chamonix, France, 9–12 July 2007; Springer: Berlin/Heidelberg, Germany, 2007; Volume 42. [Google Scholar]
- Das, J.; Cross, G.; Qu, C.; Makineni, A.; Tokekar, P.; Mulgaonkar, Y.; Kumar, V. Devices, systems, and methods for automated monitoring enabling precision agriculture. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 462–469. [Google Scholar]
- Biswas, J.; Veloso, M. Depth camera based indoor mobile robot localization and navigation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 1697–1702. [Google Scholar]
- Suarez, J.; Murphy, R.R. Using the Kinect for search and rescue robotics. In Proceedings of the 2012 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), College Station, TX, USA, 5–8 November 2012; pp. 1–2. [Google Scholar]
- Okura, F.; Ueda, Y.; Sato, T.; Yokoya, N. Teleoperation of mobile robots by generating augmented free-viewpoint images. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 665–671. [Google Scholar]
- Pandey, A.; Pandey, S.; Parhi, D. Mobile robot navigation and obstacle avoidance techniques: A review. Int. Robot. Autom. J. 2017, 2, 00022. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Kanellakis, C.; Kominiak, D.; Nikolakopoulos, G. Deploying MAVs for autonomous navigation in dark underground mine environments. Robot. Auton. Syst. 2020, 126, 103472. [Google Scholar] [CrossRef]
- Koval, A.; Kanellakis, C.; Vidmark, E.; Haluska, J.; Nikolakopoulos, G. A Subterranean Virtual Cave World for Gazebo based on the DARPA SubT Challenge. arXiv 2020, arXiv:2004.08452. [Google Scholar]
- Rodrigues de Campos, G.; Dimarogonas, D.V.; Seuret, A.; Johansson, K.H. Distributed control of compact formations for multi-robot swarms. IMA J. Math. Control Inf. 2017, 35, 805–835. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Kanellakis, C.; Fresk, E.; Lindqvist, B.; Kominiak, D.; Koval, A.; Sopasakis, P.; Nikolakopoulos, G. Subterranean MAV Navigation based on Nonlinear MPC with Collision Avoidance Constraints. arXiv 2020, arXiv:2006.04227. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Khan, A.; Noreen, I.; Habib, Z. On Complete Coverage Path Planning Algorithms for Non-holonomic Mobile Robots: Survey and Challenges. J. Inf. Sci. Eng. 2017, 33, 101–121. [Google Scholar]
- Rekleitis, I.; New, A.P.; Rankin, E.S.; Choset, H. Efficient boustrophedon multi-robot coverage: An algorithmic approach. Ann. Math. Artif. Intell. 2008, 52, 109–142. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, Z.; Li, Z.; Li, Y. Complete coverage path planning of mobile robot based on dynamic programming algorithm. In Proceedings of the 2nd International Conference on Electronic and Mechanical Engineering and Information Technology, Shenyang, China, 7 September 2012; pp. 1837–1841. [Google Scholar]
- Batsaikhan, D.; Janchiv, A.; Lee, S.G. Sensor-based incremental boustrophedon decomposition for coverage path planning of a mobile robot. In Intelligent Autonomous Systems 12; Springer: Berlin/Heidelberg, Germany, 2013; pp. 621–628. [Google Scholar]
- Bretl, T.; Hutchinson, S. Robust coverage by a mobile robot of a planar workspace. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4582–4587. [Google Scholar]
- Wang, Z.; Zhu, B. Coverage path planning for mobile robot based on genetic algorithm. In Proceedings of the 2014 IEEE Workshop on Electronics, Computer and Applications, Ottawa, ON, Canada, 8–9 May 2014; pp. 732–735. [Google Scholar]
- Yu, X.; Hung, J.Y. Coverage path planning based on a multiple sweep line decomposition. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 004052–004058. [Google Scholar]
- Broderick, J.; Tilbury, D.; Atkins, E. Energy usage for UGVs executing coverage tasks. In Unmanned Systems Technology XIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8387, p. 83871A. [Google Scholar]
- Broderick, J.; Tilbury, D.; Atkins, E. Maximizing coverage for mobile robots while conserving energy. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 791–798. [Google Scholar]
- Strimel, G.P.; Veloso, M.M. Coverage planning with finite resources. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2950–2956. [Google Scholar]
- Viet, H.H.; Choi, S.; Chung, T. An online complete coverage approach for a team of robots in unknown environments. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS), Gwangju, Korea, 20–23 October 2013; pp. 929–934. [Google Scholar]
- Viet, H.H.; Dang, V.H.; Laskar, M.N.U.; Chung, T. BA*: An online complete coverage algorithm for cleaning robots. Appl. Intell. 2013, 39, 217–235. [Google Scholar] [CrossRef]
- Viet, H.H.; Dang, V.H.; Choi, S.; Chung, T.C. BoB: An online coverage approach for multi-robot systems. Appl. Intell. 2015, 42, 157–173. [Google Scholar] [CrossRef]
- Choi, S.; Lee, S.; Viet, H.H.; Chung, T. B-Theta*: An Efficient Online Coverage Algorithm for Autonomous Cleaning Robots. J. Intell. Robot. Syst. 2017, 87, 265–290. [Google Scholar] [CrossRef]
- Masehian, E.; Jannati, M.; Hekmatfar, T. Cooperative mapping of unknown environments by multiple heterogeneous mobile robots with limited sensing. Robot. Auton. Syst. 2017, 87, 188–218. [Google Scholar] [CrossRef]
- Rekleitis, I.; New, A.P.; Choset, H. Distributed coverage of unknown/unstructured environments by mobile sensor networks. In Multi-Robot Systems. From Swarms to Intelligent Automata Volume III; Springer: Berlin/Heidelberg, Germany, 2005; pp. 145–155. [Google Scholar]
- Kong, C.S.; Peng, N.A.; Rekleitis, I. Distributed coverage with multi-robot system. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 2423–2429. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Balampanis, F.; Maza, I.; Ollero, A. Area partition for coastal regions with multiple UAS. J. Intell. Robot. Syst. 2017, 88, 751–766. [Google Scholar] [CrossRef]
- Khan, A.; Noreen, I.; Ryu, H.; Doh, N.L.; Habib, Z. Online complete coverage path planning using two-way proximity search. Intell. Serv. Robot. 2017, 10, 229–240. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Karvelis, P.; Georgoulas, G.; Nikolakopoulos, G. Remaining useful battery life prediction for UAVs based on machine learning. IFAC-PapersOnLine 2017, 50, 4727–4732. [Google Scholar] [CrossRef]
- Wei, H.; Wang, B.; Wang, Y.; Shao, Z.; Chan, K.C. Staying-alive path planning with energy optimization for mobile robots. Expert Syst. Appl. 2012, 39, 3559–3571. [Google Scholar] [CrossRef]
- Svestka, P.; Latombe, J.; Overmars Kavraki, L. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3, p. 5. [Google Scholar]





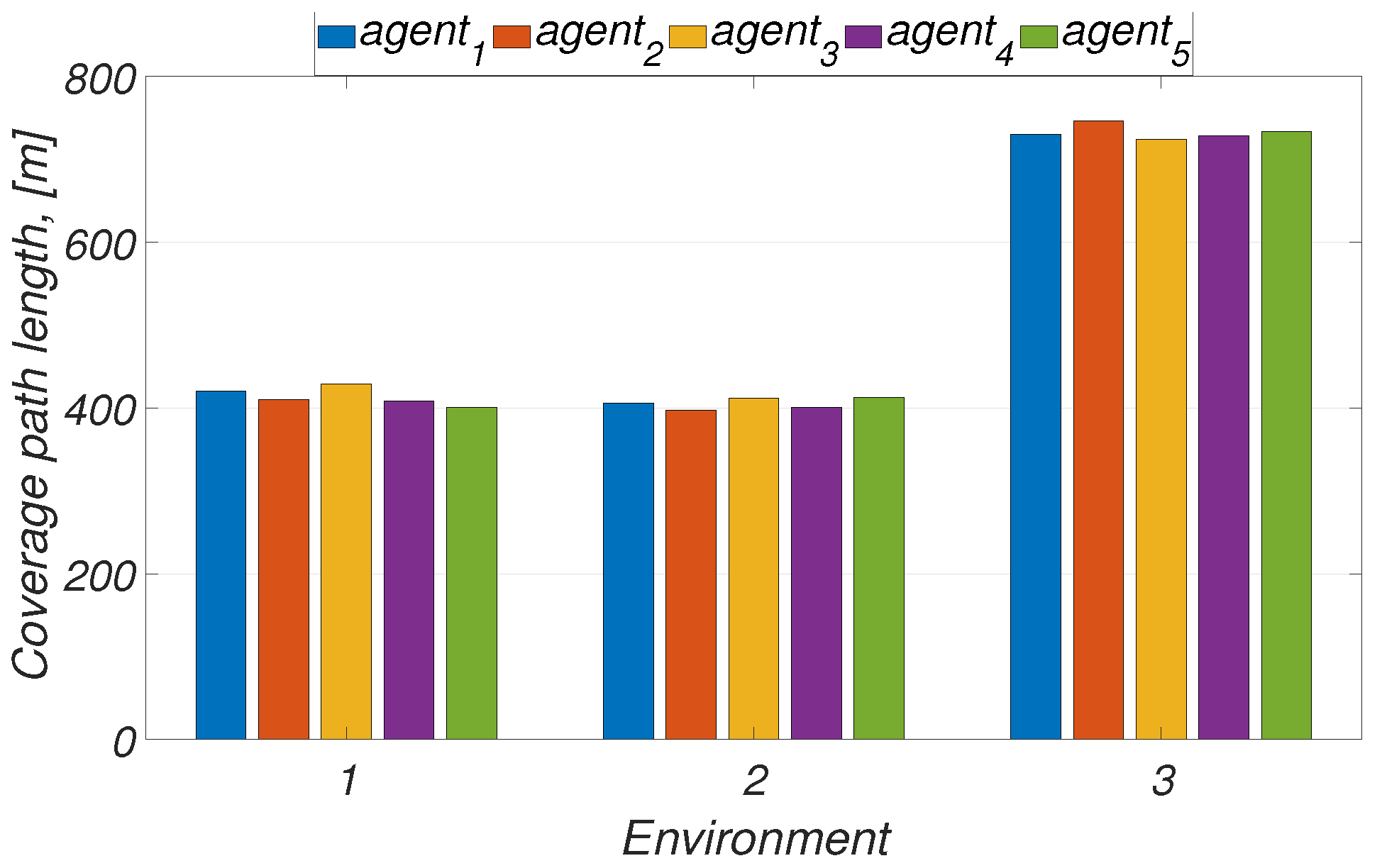
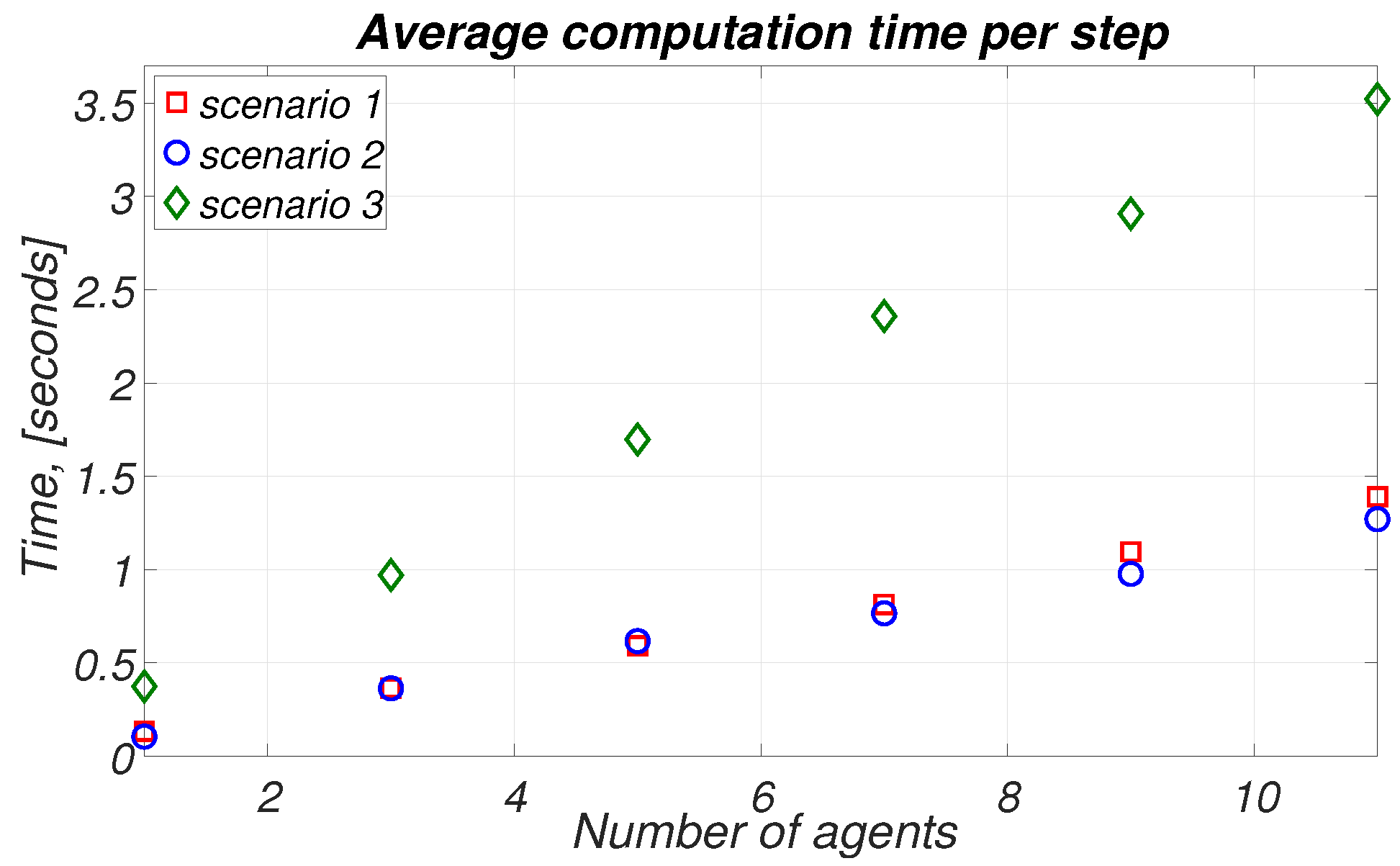
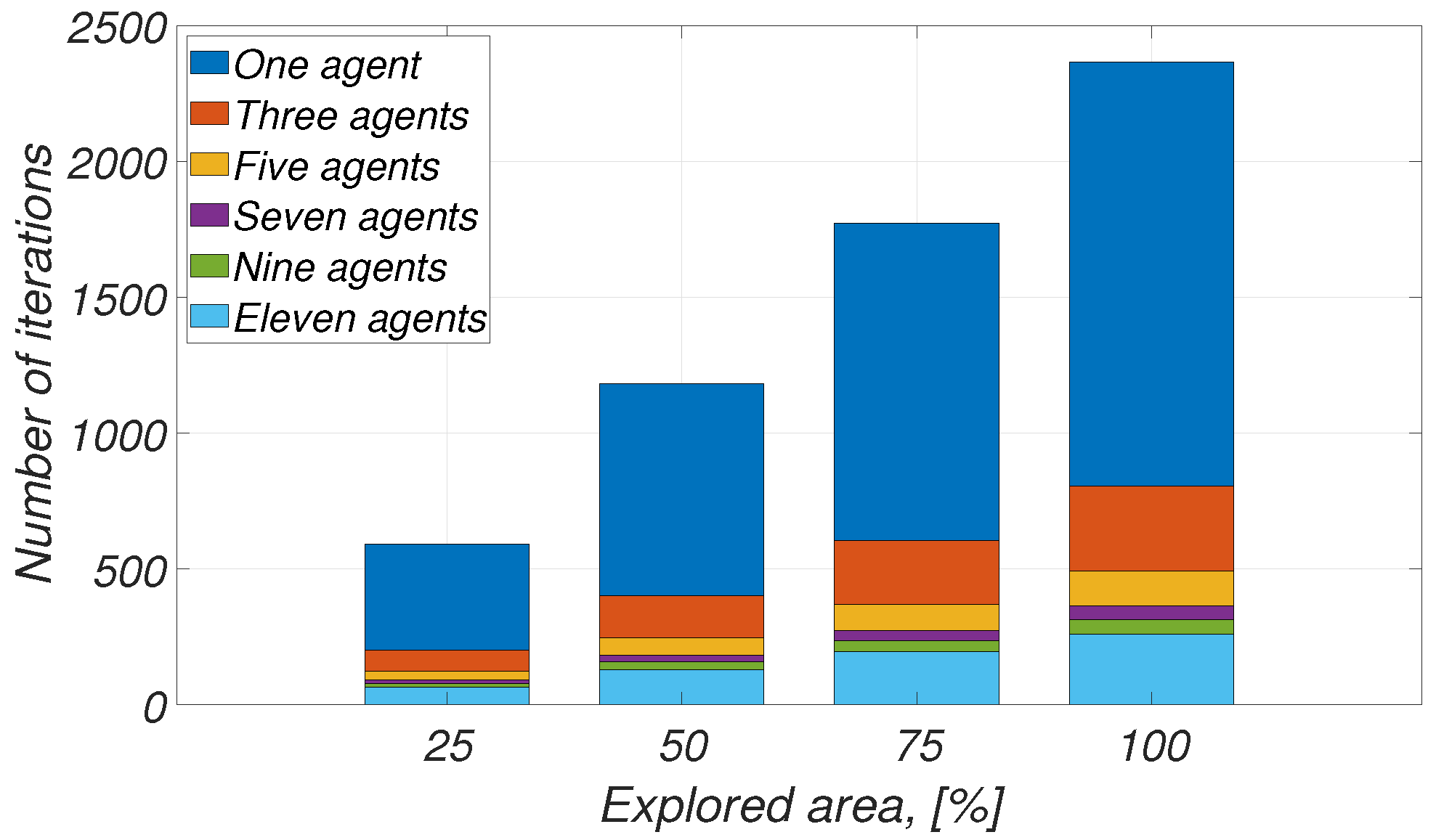
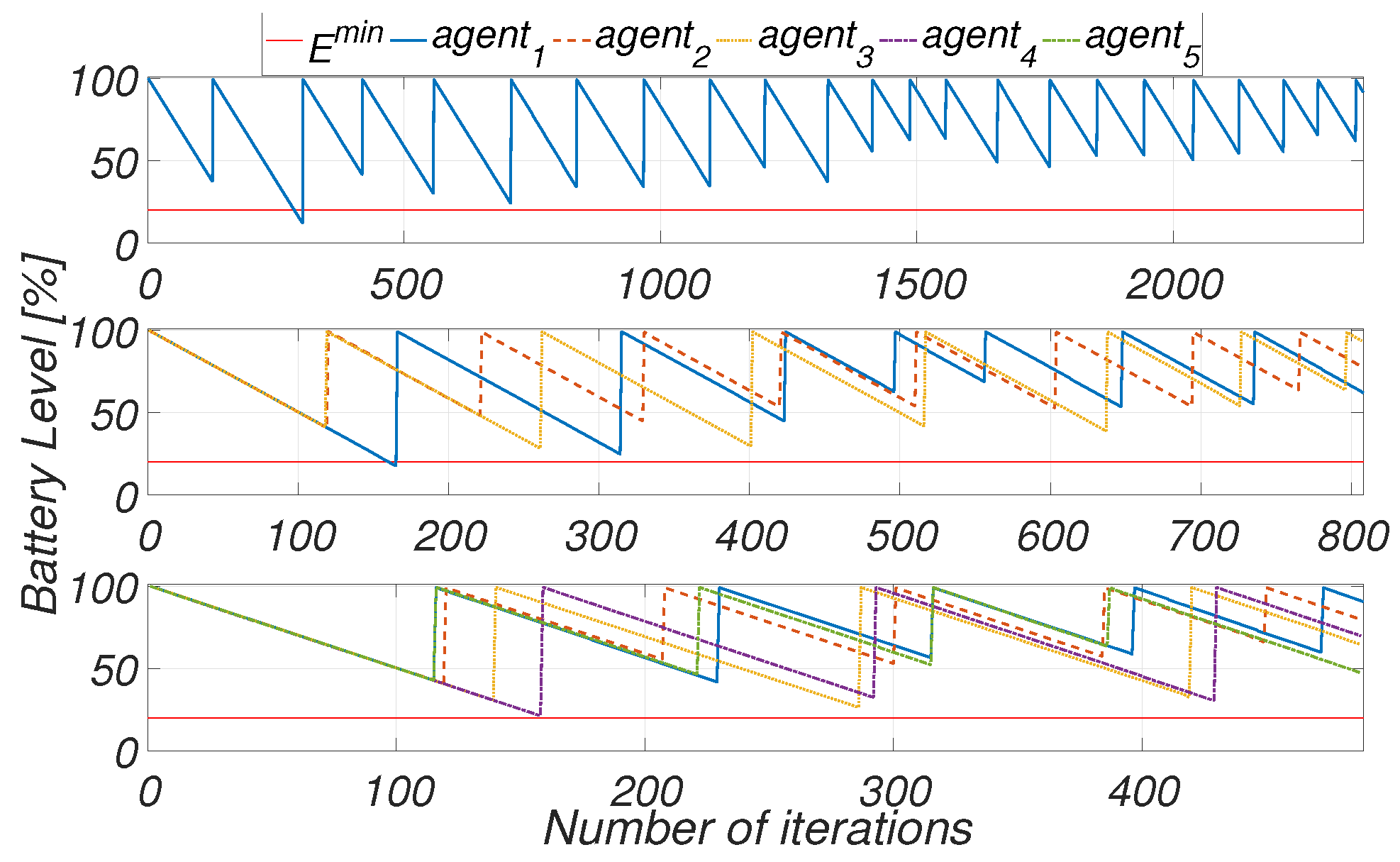


| Environment | Size of Environment, | Number of Agents | Total Number of Charges for One Agent | Average Computation Time for 1 Step, s | Number of Iterations |
|---|---|---|---|---|---|
| 1 | 22 | 0.13 | 2365 | ||
| 3 | 7 | 0.36 | 804 | ||
| Scenario 1 | 2068 | 5 | 5 | 0.59 | 491 |
| 7 | 3 | 0.81 | 363 | ||
| 9 | 3 | 1.09 | 314 | ||
| 11 | 2 | 1.39 | 259 |
| Algorithm | Coverage Path Length by Agent, [m] | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| NB-MSTC | 172 | 400 | 24 | 21 |
| BoB | 199 | 215 | 224 | 233 |
| Proposed approach | 171 | 187 | 178 | 180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koval, A.; Sharif Mansouri, S.; Nikolakopoulos, G. Multi-Agent Collaborative Path Planning Based on Staying Alive Policy. Robotics 2020, 9, 101. https://doi.org/10.3390/robotics9040101
Koval A, Sharif Mansouri S, Nikolakopoulos G. Multi-Agent Collaborative Path Planning Based on Staying Alive Policy. Robotics. 2020; 9(4):101. https://doi.org/10.3390/robotics9040101
Chicago/Turabian StyleKoval, Anton, Sina Sharif Mansouri, and George Nikolakopoulos. 2020. "Multi-Agent Collaborative Path Planning Based on Staying Alive Policy" Robotics 9, no. 4: 101. https://doi.org/10.3390/robotics9040101
APA StyleKoval, A., Sharif Mansouri, S., & Nikolakopoulos, G. (2020). Multi-Agent Collaborative Path Planning Based on Staying Alive Policy. Robotics, 9(4), 101. https://doi.org/10.3390/robotics9040101






