Abstract
In the last decade, the objectives outlined by the needs of personal robotics have led to the rise of new biologically-inspired techniques for arm motion planning. This paper presents a literature review of the most recent research on the generation of human-like arm movements in humanoid and manipulation robotic systems. Search methods and inclusion criteria are described. The studies are analyzed taking into consideration the sources of publication, the experimental settings, the type of movements, the technical approach, and the human motor principles that have been used to inspire and assess human-likeness. Results show that there is a strong focus on the generation of single-arm reaching movements and biomimetic-based methods. However, there has been poor attention to manipulation, obstacle-avoidance mechanisms, and dual-arm motion generation. For these reasons, human-like arm motion generation may not fully respect human behavioral and neurological key features and may result restricted to specific tasks of human-robot interaction. Limitations and challenges are discussed to provide meaningful directions for future investigations.
1. Introduction
New questions inevitably arise during the design of novel Human-Robot Interaction (HRI) or Collaboration (HRC) paradigms and often concern the authority and the autonomy level of new intelligent devices [1]. Ethical and anthropological issues have been recently considered by the government of Japan with the initiative called Society 5.0 [2]. As described by Gladden [2], the evolution of human society has been featured by a Society 1.0 of hunters-gatherers, a Society 2.0 of farmers, a Society 3.0 that results from the Industrial Revolution and by the current Society 4.0, which adds value to the industry by digitally connecting informative networks (an “information society”). The Society 5.0 is expected to be a technologically post-humanized society where humans and robots coexist in the same environment and work to improve the quality of life by offering customized services to cope with various needs. The new social paradigm differs from the current Society 4.0 by the fact that robots will not only be passive tools as they are today. On the contrary, they are expected to be active agents capable of proactive data collecting, making decisions and friendly behaving to maintain human beings at the core of the society, but not alone within it. Due to the process of post-humanization that is taking place, this new anticipated society is significantly dependent on the emerging transformative technologies that will impact the interactions among individuals as it has never happened so far. For example, a humanoid robot can be considered a personal helper designed to respond to the needs of human beings. Such an artificial man [3] could carry and manipulate objects for people with disabilities, could replace some cognitive functions, or take part in the education of children. A robot with these features is human-centered because it is meant to interact, collaborate, and work in unstructured environments with human beings [4]. For this reason, research in robotics and artificial intelligence needs to be necessarily enriched by different scientific disciplines, such as ethics, psychology, anthropology, and neuroscience, to simulate or mimic life-like activities and appearance [2,4,5,6]. These new abilities in robots significantly influence how they are perceived by interacting human partners.
Studies have revealed a very positive attitude towards robots and the idea of being surrounded by them in different personal and societal contexts [7,8]. People commonly expect from robots a very pragmatic daily help in domestic, entertaining, and educational applications. Moreover, having intelligent devices that perform repetitive or dangerous tasks is desirable because safety and monotonousness seem to be the most important issues in industrial settings. Particularly, robotics, in the upcoming Society 5.0, is expected to augment the capabilities of human workers instead of replacing them. The current industry has been featured by robots designed for complete automation of workflows, while, in the next future, industry will include robots intended to satisfy the necessities of human co-workers with the consequent increase of the productivity of an entire company [8]. Therefore, in this new human-centered robotics, augmentation will gradually replace automation with the introduction of novel artificially intelligent devices that enhance collaboration in shared workspaces. For instance, the fundamental principles of motor interpretation behind successful human-human joint actions can be used when adopting motion planning strategies [9,10,11,12]. Koppenborg et al. [13] showed that the predictability and the velocity of the motion in robotic manipulators significantly influence the performance of the collaboration with human partners. Specifically, high-speed movements increase anxiety and risk perception of human co-workers, whom, consequently, act unpleasantly and inefficiently. Therefore, time parametrization also plays an essential role in any motion planning process that is intended for human-robot interaction. Body motion in robotics has also been recently considered a language to communicate emotional states of social robots [14]. This study revealed that social robots for educational support had more significant impressions on learners with body language than without it. However, movements of robots without a social role are also interpreted as social cues by human observers [15]. Therefore, there is an automatic and implicit cognitive process for the attribution of mental states in robots to anticipate their behaviors, which is independent of their assigned purposes. For these reasons, designers of human-centered robots and roboticists of different areas of research cannot skip accurate strategies of motion planning to obtain socially acceptable interactions with humans.
In the past decade, the action research area (of the so-called “New Robotics” introduced by Schaal [4]) has been densely characterized with the proposal of a wide range of techniques for human-like arm motion generation. This review provides an overview of the primary studies on novel human-like arm motion planners that are meant to enhance human-robot interactions and collaborations. Through the analysis and the assessment of the most recent studies, major limitations can be identified, and future investigations can be directed.
The remainder of the paper is organized as follows: in Section 2, the design of this review and the search methods are defined; in Section 3, the collection of the search outcomes is provided, and the results are discussed accordingly to the features of the proposed solutions; the paper ends in Section 4 with a discussion of the obtained results, and, in Section 5, with a description of the open issues in the current literature.
2. Literature Review
The aim of this paper was to provide a comprehensive background of human-like arm motion generation for robots by reviewing the corresponding most recent literature. An extensive description of different approaches and techniques is essential for the identification of the current issues and the definition of new activities of investigation. Special attention was put on the criteria used for the evaluation of human-likeness of the generated movements, on the tools and the robotic devices used for experimentations, on the physical nature of the applied methodologies and on obstacles-avoidance. The reliability, the performance, advantages and disadvantages were analyzed and generally discussed to summarize the modern state of the art in the generation of human-like arm motion.
Being the sources of the vast majority of peer-reviewed publications on human-robot interaction and, more generically, robotics, the Association for Computing Machinery (ACM) Digital Library, the IEEEXplore, the Scopus, and the Web of Science were searched. The search terms that were used in the advanced boolean method are: (TITLE-ABS-KEY (arm) OR TITLE-ABS-KEY (upper-limb))AND (TITLE-ABS-KEY (human-like) OR TITLE-ABS-KEY (legible) OR TITLE-ABS-KEY (predictable)) AND (TITLE-ABS-KEY (motion) OR TITLE-ABS-KEY (movement) OR TITLE-ABS-KEY (trajectory)) AND (humanoid OR robot) AND (planning OR generation) AND PUBYEAR > 2005 AND (LIMIT-TO (LANGUAGE, “English”)) AND (LIMIT-TO (SRCTYPE, “p”) OR LIMIT-TO (SRCTYPE, “j”)).
The sources published in peer-reviewed conferences or journals were included, while unpublished or non-peer-reviewed manuscripts, book chapters, posters, and abstracts were excluded. Moreover, anything published before 2006 was also excluded because the state of the art might not reflect the capabilities that robots have today. For the sake of completeness, papers proposing methodologies tested only on simulated frameworks were included as well as on real robotic platforms. The focus is on those methods and techniques capable of generating human-like arm movements on humanoid and generic robotic devices. The minimum inclusion requirement of the proposed planning techniques is the capability of producing arm and hand trajectories showing typical human-like characteristics, which have been widely analyzed and described in psychology and neurophysiology.
3. Results
In this section, the results are guided by specific research questions and analyzed according to the schema illustrated in Figure 1. The reviewed papers are firstly examined according to the sources of publication and the equipment used for experimentation (Section 3.1). Then, in Section 3.2, general concepts and assumptions behind the generation of human-like arm motion are investigated by taking into consideration the space of incoming information, the physical nature of the involved variables and the spaces of formation of a trajectory. A deeper analysis is reported in Section 3.3, which describes how different techniques for transferring human regularities into the robotics domain work. Specifically, the applied principles of human motor control (HMC) are discussed (Section 3.3.1) to better understand the underlying inspirational concepts. The included studies are also classified according to the type of movement that is generated (Section 3.3.2) and how obstacles-avoidance is addressed (Section 3.3.3).
Figure 1.
Organization and analysis of the included studies.
Finally, efficiency is studied by the analysis of applied techniques of optimization, capabilities of generalization of the proposed learning methods are investigated and adaptation to unpredictable external perturbations is examined by the description of the reviewed closed-loop controllers (Section 3.3.4). The main characteristics of the included studies are summarized and can be compared in Table A1.
3.1. Overview of the Results
The original search returned 156 results. There were 54 publications left after removing the duplicates across the databases and applying the inclusion and exclusion criteria described in Section 2. The included papers were published starting from 2006 and, therefore, concern the most recent research in the topic. Figure 2 illustrates how the publications are shared among the databases of search. Scopus with 61.11% of papers is clearly the primary source of knowledge. It is followed by IEEEXplore follows with 22.22%, Web of Science with 11.11%, and ACM Digital Library with 5.56%.
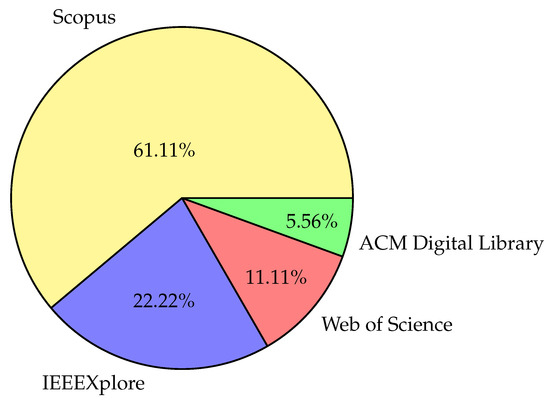
Figure 2.
Pie chart showing the percentage of papers related to the databases.
Before describing more in detail the selected studies, an overview concerning the experimental equipment is presented. The types of results were classified according to the robotic systems that were used to validate the proposed methods of human-like arm motion generation. This preliminary distinction is important to deduce implications regarding their level of applicability. For this purpose, the pie chart in Figure 3 illustrates the percentage of papers describing methods that were tested on robotic manipulators (37.03%), on humanoid robots (35.19%), and on simulations only (27.78%).
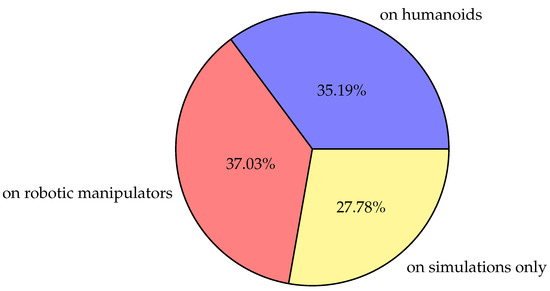
Figure 3.
Pie chart showing the types of experimental results.
Robotic manipulators and, in second place, humanoids are arguably the most preferred tool for testing and showing the level of human-likeness provided by different generation techniques. A humanoid robot can provide a high level of anthropomorphism that can be used to encourage interactions with human partners [16,17]. Figure 4 shows the anthropomorphic robotic systems that were utilized in the included studies. They are briefly presented to indicate the number of degrees of freedom (DOFs) and provide an overview of their technical capabilities that allowed to implement and test the proposed methods of human-like arm motion generation.

Figure 4.
Humanoid robots that have been used to test human-like arm motion generation, namely: ARoS [18] (a), iCub [19] (b), ROMEO [20] (c), NAO [21] (d), ABB FRIDA [22] (e), HRP-2 [23] (f), Rollin’ Justin [24] (g), HERB 2.0 [25] (h), MAHRU [26] (i), and Simon [27] (j).
ARoS [18] (Figure 4a) is an anthropomorphic robotic system composed by a static torso, two 7-DOFs lightweight Amtec arms, each one equipped with a three-fingered Barrett hand, a 2-DOFs neck, and a stereo vision system. iCub [19] (Figure 4b), with 30 DOFs in its upper torso, was designed to have a high degree of manipulation: each hand has 9 DOFs, and the two arms have 7 DOFs each. Additionally, it has cameras, microphones and position/force sensors that permit it to obtain audiovisual information and to safely interact with the environment. ROMEO [20] (Figure 4c) has a total of 37 DOFs, which include 7 DOFs per arm, 6 DOFs per leg, 2 DOFs for each eye, 1 DOF for each foot, 2 DOFs for the neck, 2 DOFs for the head and 1 DOF for the spine. NAO [21] (Figure 4d) is a humanoid robot designed to adopt specific behaviors according to the needs of the user. It has a total of 25 DOFs of which 14 DOFs are in the upper body, with two 5-DOFs arms, each one equipped with a 1-DOF hand. Designed for assembly applications, ABB FRIDA [22] (Figure 4e) is an upper-torso humanoid robot with two 7-DOFs arms, each one equipped with a servo gripper for small-part handling. The HRP-2 robot [23] (Figure 4f) is a humanoid robot equipped with two legs and two 6-DOFs arms, each one equipped with grippers. It has been designed for cooperative works with humans and has three Charge-Coupled Device (CCD) cameras mounted in the head. Rollin’ Justin [24] (Figure 4g) is a humanoid robot with 43 DOFs in the upper-body and an omnidirectional torso driven by 4 wheels. HERB 2.0 [25] (Figure 4h) is a humanoid robot specifically designed to operate with human partners in domestic environments. It is equipped with wheels, which allow the robot to navigate indoors, and with two 7-DOFs arms, each one equipped with a three-fingered Barrett hand. It also has an array of four laser scanners that provides clouds of 3D points in the surrounding environment. MAHRU [26] (Figure 4i) is a network-based humanoid robot with 35 DOF, including 6-DOFs for each arm and 4-DOFs for each hand. It also has two 6-DOFs legs, a stereo camera is mounted on the head and a microphone and four force sensors allow the robots to physically interact with the environment. Simon [27] (Figure 4j) is an upper-torso humanoid robot with two DOFs on the torso, two 7-DOFs arms, each one equipped with a four-fingered hand, a microphone and cameras for a stereo vision.
3.2. General Insights on Approaching Human-Likeness of Arm Motion
The procedures of human-like arm motion generation can be classified according to primary features that offer general but important insights on concepts, ideas and choices that are behind the genesis of a motion. A first classification addresses how the knowledge regarding the workspace of a robot is used to plan a feasible path. A method can be called global when the information of the entire workspace is processed off-line before the execution of a movement. On the contrary, local methods plan a motion on-line by taking into account portions of the workspace that are of immediate interest. This division is not always distinct, but, typically, these two approaches concern the implementation of strategies for the avoidance of collisions, when it is addressed. A second classification focuses on the physical nature of the variables that are involved in the motion generation process. Some methods are based on kinematic variables only (position, velocity and acceleration), while others also consider dynamical quantities (forces and torques). A proper selection of these physical variables defines the state space of a robot and might be driven by the expected interaction with the environment or with a human partner. However, the choice of considering dynamics, instead of kinematics only, is often influenced by biological motor principles when human-like motion generation is supported by discoveries in neuroscience. Regularities of human upper-limb motion can also be replicated on different levels concerning the space where a robot acts. Some applications may constraint the dimensionality of this space that consequently affects the complexity of a planning algorithm. For these reasons, a third classification concerns the space in which the generation of a motion takes place: it could be the operational space or the joints space of manipulation [28].
For example, Chen et al. [29] introduced a technique to reduce the dimensionality of the joints space for human-like dual-arm motion planning. This approach wants to replicate the demonstrations of human operators acting on common daily tasks. In particular, the replica of a bi-manual task of pouring water from a cup to another one was performed. The position and the orientation of human hands were mapped into the joints space of two 6-DOFs manipulators by inverse kinematics. Then, the configuration space (i.e., the joints space) is reduced to minimize the computational burden of the search of a collision-free path, which is provided by the bi-directional Rapidly-exploring Random Trees (RRT-Connect) algorithm [30]. Therefore, this approach works in the joints space of a manipulator; it runs off-line and globally deals with the workspace of the robot. Dynamical variables of the motion were not considered because Chen et al. [29] focused on the study of the non-linear relationship of the joints positions in the attempt of extracting this particular aspect of the human upper-limb motion.
An example of local planning in the operational space is described by Rano and Iossifidis [31], who presented an attractor dynamics approach for human-like hand motion generation. The authors considered the spherical coordinates (the heading directions and the velocity vector) of an end-effector to model human arm motion of reaching movements with a robotic manipulator. The proposed dynamical systems are based on attractive vector fields in the vicinity of a goal for the end-effector and repulsive vector fields for the obstacles in the workspace. Importantly, the attractor dynamics were properly designed to replicate the planarity characteristic of a human hand motion, which is also observed in scenarios cluttered with obstacles [32]. In other words, a straight-line solution for the trajectory of the end-effector was analytically determined in obstacles-free scenarios where expectations on planarity were respected. However, to prevent unwanted collisions with obstacles, the trajectory could not maintain small values of torsion (i.e., good planarity) because the repulsion effects are significant only in the proximity of the obstacles and poor on other regions of the workspace [31].
A hybrid joints/operational-space approach based on dynamic movement primitives [33] was proposed by Lauretti et al. [34] to enhance functional anthropomorphism in redundant manipulators. Specifically, Cartesian and joints-related characteristics are extracted from recorded human upper-limb movements during the execution of reaching tasks. The parameters of Cartesian and of joint Dynamical Movement Primitives (DMPs) are learnt from the recorded demonstrations and used to compute compatible desired trajectories in the operational and in the joints spaces. These references are coupled into an inverse dynamics controller that prioritizes operational-space constraints, while exploits the redundant variables of manipulation to replicate human recorded motion. Experiments with a 7-DOFs robotic arm and comparisons with classical Cartesian DMPs approaches demonstrated that the proposed hybrid method could provide acceptable accuracy in positioning and orientating the end-effector, higher levels of anthropomorphism within given physical joint limits and a successful obstacles-avoidance.
Dynamic models that simulate the capabilities of the human arm have also been used to generate biologically-inspired arm motion [35,36]. For example, Fu et al. [35] investigated how the motor synergies hypothesis behind the motion of human arms can improve planning reaching movements for a planar manipulator. Specifically, motor synergies are responsible for the activation of a group of muscles in a coordinated manner. Therefore, approaching control can be simplified by managing fewer variables corresponding to the synergies of a motion. The general planning strategy is formulated with a framework for optimal control that minimizes the contribution of the control activation inputs acting on the joints of the manipulator. Fu et al. [35] proposed the extraction of motor synergies from control inputs to solve the optimization problem in a lower dimensionality and, consequently, decrease the computational burden of the algorithm. Experiments on a 3-DOFs planar human-like arm moving on a bi-dimensional workspace demonstrated how the reduction of dimensionality generally improved the performance of planning by providing a higher success rate and a lower cost of the objective function spending less computation time. Further investigations on the properties of motor synergies showed their capability to adapt for the optimization of specific criteria, such as energy efficiency, jerk, and smoothness of the resulting trajectory, while achieving the intended goal of a movement.
Figure 5 illustrates a classification of the included studies concerning how the available workspace is approached, the physical nature of the variables that are involved in the planning process, and the space of configurations.
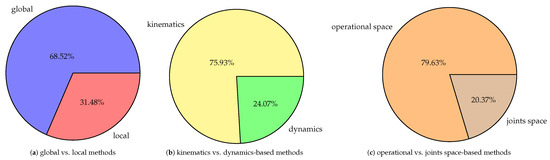
Figure 5.
A preliminary distinction of the included studies.
There is a clear predominance of global methods acting in the operational space and physically operating with the kinematic variables of a robotic device. Figure 5a shows that 68.52% of the included studies proposed global planning strategies, while only 31.48% of them treated the workspace locally. Modeling the workspace of a robot as a unique static environment generally simplifies the planning algorithms, permits taking advantage of the same assumptions in different portions of the scenario and can generally replicate more loyal human-like regularities of the arm-hand motion. On the contrary, local methods are generally more complex and can normally operate in dynamic scenarios accounting for on-line obstacles-avoidance. However, the risk of generating motion in local portions of the workspace is to lose the efficacy in replicating the kinematic features of human arm-hand motion.
As it can been seen in Figure 5b, 75.93% of the reviewed studies introduced techniques that operate with kinematic variables, while 24.07% of them also considered the dynamics of manipulation. These findings are mainly due to the requirements of simplicity of the proposed solutions, as well as to the fact that most of the studies on human arm motion have been conducted on a kinematic level of the analysis. However, dynamic variables are necessarily introduced in biologically-inspired solutions that aim at replicating the muscles activities in humans. Moreover, the dynamics of a robotic agent is also needed in applications when specific physical interactions with the environment are required.
The vast majority of the included studies presented solutions that operate in the operational space (79.63%) and only 20.37% of them in the joints space of manipulation (Figure 5c). Generating motion in the operational space generally means searching for a trajectory in a space with lower dimensionality than in the joints space. Additionally, patterns on human movements have been principally analyzed by considering the hand motion, which reflects properties on the end-effector trajectory in robotics. However, techniques that exclusively perform in the operational space may discard shreds of evidence of human arm movements that arise on different degrees of freedom, such as joint synchrony and a bell-shaped angular velocity profile [37,38,39]. A largely observed disadvantage of working in the joints space is related to a higher dimensionality of the search space that significantly influences the computational expense of the proposed solutions. For this reason, many authors introduced techniques of dimensionality reduction to achieve better performance without degrading the intended level of human-likeness.
3.3. From Humans to Robots
3.3.1. Applied Principles of Human Motor Control
In many and different ways, the included studies have considered human motor control in the construction of the proposed methods. For this reason, it is important to have specific insights into the principles and techniques that transfer human motion into robotics and assess the human-likeness of the generated movements. In Figure 6, the most relevant principles and metrics of human-like motion in robotics are illustrated. In this section, robotic applications are analyzed according to the popularity and originality of the human motor consistencies that support a proposed solution to the human-like motion generation problem.
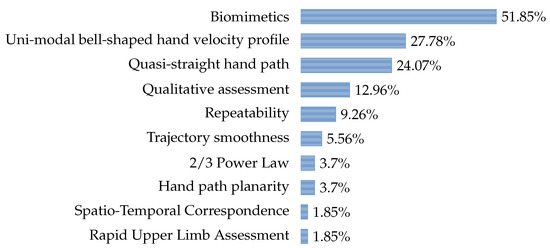
Figure 6.
Bar chart showing in which percentage principles of human-likeness have been used for development and assessment in the included studies.
Biomimetics
In the majority of the reviewed articles, human-like arm motion generation has been approached with techniques of biomimetics (51.85%). This particular set of solutions is based on the extraction of bio-markers and of physical regularities from recorded movements with the ultimate purpose of mimicking arm trajectories. For instance, Kim et al. [40] proposed a technique for deriving values of the elbow elevation angle from series of recorded human reaching movements in a three-dimensional environment. The elbow elevation angle (also called swivel angle or simply elbow angle) is the angle between the sagittal body plane and the plane formed by the triangle shoulder-elbow-wrist [40,41]. This angle features a human arm posture uniquely when the wrist is fully constrained in position and orientation. For this reason, it is the key human-like factor for transferring motion from human records to the humanoid robot MAHRU (Figure 4i). A trajectory is computed in the joints space by analytical inverse kinematics that considers six holonomic constraints concerning the position of the wrist, the hand palm direction and the elbow elevation angle, which encodes the human-likeness of a movement. Experimental results showed the similarity with the recorded human motion and the possibility of addressing real-time applications with the proposed solution. The latter was also upgraded with further functionalities that improve the communication with a human partner that might be moving in front of the robot [42]. Specifically, Kim et al. [42] defined the concepts of motion plane, which is the closest plane where the wrist trajectory belongs to, and of motion center, which is the centroid of the wrist trajectory on the motion plane. Changing the direction of the movement is possible by aligning the normal vector to the motion plane applied in the motion center with the desired direction that keeps attention on a human observer. Additionally, the elbow elevation angle and the magnitude of the wrist position are properly scaled to maintain human-like characteristics on the modified movement.
Mimicking reaching and grasping movements was also addressed by Zhao et al. [43] through the minimization of the total potential energy of a human arm. The considered potential energy is the sum of a gravitational component, which is derived from the physical parameters of the arm, and of an elastic component that is obtained from acquisitions of human motion data on different subjects. Considering the planning of reaching movements, the minimization is permitted by the application of the Gradient Projection Method (GPM) that accounts for exploiting the null space of the Jacobian matrix [28]. The position of the end-effector is assumed to reflect a minimum jerk trajectory with null boundary conditions, which has been observed in human reaching motion [44]. Moreover, Zhao et al. [43] extended this solution to grasping movements by the introduction of a novel human-like arm motion planner that combines the advantages of the Gradient Projection Method in redundant manipulators and the RRT algorithm [45] (a GPM-RRT planner). A sampling-based planner, like RRT, allows to define a trajectory for the end-effector orientation, which is unknown a priori, and, most importantly, permits biasing the construction of a tree with optimal configurations provided by the GPM. Notably, in the case of grasping, further human data are needed to be acquired to quantify how determined hand orientations affect wrist discomfort, which is defined as the distance from a comfortable wrist posture. Therefore, when the robotic arm acts on grasping not only minimizes its potential energy but also its wrist discomfort to mimic human demonstrations (Figure 7). Qualitative observations on the human and on the robotic swivel angle trajectories showed the validity of the proposed planner in comparison with non-human-like alternatives.
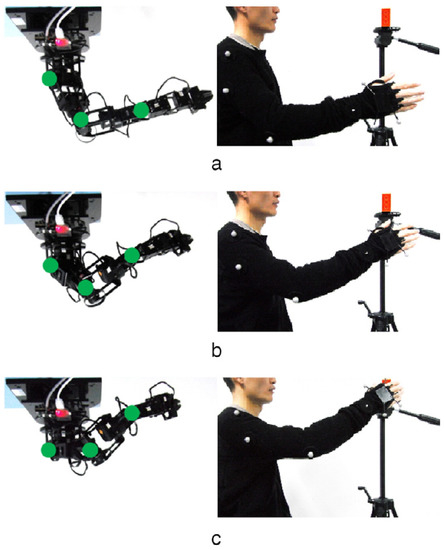
Figure 7.
Comparisons of the human grasping movement and the human-like grasping movement of a 7-DOFs robotic arm [43]: (a) the start arm configuration, (b) an intermediate arm configuration, (c) the final arm configuration.
Liarokapis et al. [46] introduced an optimization-based technique of human-robot arm mapping that takes inspiration from the principles of functional anthropomorphism [16]. The priority is the successful accomplishment of a task in the operational space, while human-like prerequisites of the motion are secondarily satisfied. A magnetic motion capture system provides the positions of shoulder, elbow and wrist from random reaching movements of different participants. Then, anthropomorphism can be transferred to complex robotic arm-hand platforms by the minimization of dissimilarity metrics, which represent different geometrical distance with human recorded motion. In particular, a sum of distances between the positions of recorded human arm points and the robotic joints revealed to be the most efficient metric. The proposed solution is formulated with a non-linear constrained optimization problem that guarantees a low computational cost and applicability on chains of arbitrary kinematics. The objective function of the optimization problem concerns the distance with the goal pose for a selected fingertip of the robotic hand, which replicates the human hand thumb during mimicking. Only the forward kinematics of the arm and of the fingers are used to determine end-effector and phalanxes poses, respectively. Constraints on anthropomorphism are softly added to the objective function through parameters that weight the influence of human postures in the accomplishment of a task. Comparisons with the classical inverse kinematics and simple joint-to-joint mapping showed that the proposed method was the only one capable of achieving strong similarity with recorded human postures while successfully reaching goals in the operational space. Although the significant non-linearities in the formulation of the optimization problem, the proposed method of human-robot mapping revealed to be suitable for tele-operation and general applications with real-time requirements.
One of the advantages of human-like arm motion planning based on biomimetic principles is the possibility of customizing movements on the characteristics of human operators. Expressing anthropomorphism by mimicking humans is arguably the most intuitive and direct way that roboticists have at their disposal, and, probably for this reason, biomimetic approaches are mainly preferred. Additionally, an efficient motion mapping from humans permits remote tele-manipulation in real-time when there is the need, for instance, to operate in dangerous or inaccessible environments. On the other hand, biomimetics methods require accurate and expensive motion capture systems that cannot always be available, as well as complex post-processing frequently due to noisy signals and adaptation on different embodiments. Moreover, these methods are often tailored for the recorded human movements or specific manipulation tasks, even though some effort on generalization has been carried on by applying techniques of machine learning. A learned model often results very dependent on a task or a set of movements that compose a training dataset and, therefore, represent patterns that cannot be generalized on any human-like upper-limb behavior. It is also worth noting that, while biomimetics focuses on joints-space patterns of human motion to encapsulate human-likeness, kinematic analysis of the human hand is often neglected in the generation of end-effector trajectories. However, many studies on human reaching and manipulation have shown specific regularities in the operational space of the human arm [47,48,49].
Kinematic Assessment of the End-Effector Trajectory
It is state of the art that the human hand is typically featured by a quasi-straight path and a uni-modal bell-shaped velocity profile during reaching and prehension [47,48,50]. For this reason, many of the proposed solutions have taken inspiration from these psychological pieces of evidence to generate human-like arm motion. Specifically, the 27.78% and the 24.07% of the included studies, respectively, considered the hand velocity profile and the shape of the hand path to synthesize and assess human-likeness. For example, Arimoto and Sekimoto [51] introduced a virtual spring-damper hypothesis for three-dimensional reaching movements of a 5-DOFs robotic manipulator that is driven by the Euclidean distance between the initial and the goal end-effector positions. This method extends a virtual spring hypothesis for bi-dimensional reaching movements and avoids the application of any inverse kinematics or dynamics to resolve the redundancy of the problem. Taking inspiration from the physiology of the human arm motion, Arimoto and Sekimoto [51] proposed to directly generate torque controls by the parametrization of stiffness and damping factors belonging to a virtual spring-damper system that connects the initial and the goal positions of the end-effector. Additionally, control signals are featured by passive damping on the joints of the manipulator and are influenced by the effect of the gravity force. Interestingly, the latter is estimated according to studies in handwriting control. The kinematic analysis of the generated reaching movements showed quasi-straight paths and single-peaked profiles of the velocity in the operational space. Acting on stiffness, different end-effector velocity peaks can be produced, while the shape of the end-effector path remains invariant.
Atawnih et al. [52] introduced a control scheme that does not depend on the dynamic model of a manipulator and, therefore, does not suffer of the corresponding uncertainties. The proposed solution takes advantage of a prescribed performance control that allows to impose bounds on the evolution of the operational-space error over a given period of time. These bounds are set to reflect the minimum jerk principle of human arm motion in order to replicate the kinematic characteristics of a hand during reaching: a quasi-straight path and a single-peaked bell-shaped velocity profile (Figure 8). The control design provides torques on the joints by setting their angular velocity deviations from reference joints-space velocities, which are dependent on the evolution of the operational-space error through the pseudo-inverse of the Jacobian matrix. Moreover, the addition of active compliance to external forces on the end-effector increases safety and offers a major degree of human-likeness for physical interaction. A desired impedance between an external force and the resulting displacement of the end-effector is modeled and integrated into the proposed control scheme. Simulations with a 5-DOFs arm and real experiments with a 7-DOFs robotic manipulator demonstrated the capability of the system to reach a given operational-space target in a required period of time. The produced end-effector trajectories are replicable in the same conditions and are featured with human-like quasi-straight paths and bell-shaped velocity profiles. Additionally, the manifestation of external forces is successfully absorbed by the motion in stationary and moving conditions.
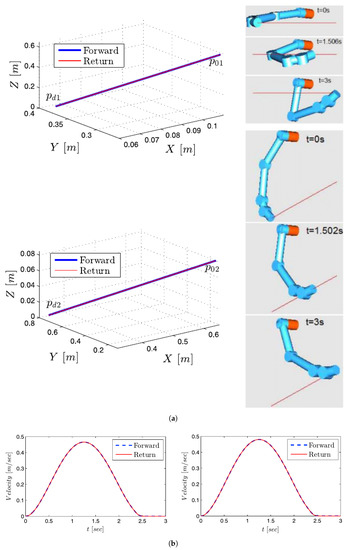
Figure 8.
Straight path and a single-peaked bell-shaped velocity profile of the end-effector motion [52]. (a) End-effector paths and joint configurations during unconstrained movement to and . (b) Cartesian velocity profile to (left) and (right).
A technique for time adjustment of the end-effector velocity was presented by Kashima and Hori [53]. Taking inspiration from observations of delays in human arm motion between the elbow and the shoulder, the authors proposed a modified minimum angular jerk principle for the optimal selection of this delay. This inter-joints time adjustment is designed to obtain exact symmetric end-effector velocities over a given duration of a reaching movement. This trajectory generation method was tested on a 4-DOFs simulated arm acting on a three-dimensional operational space, and it was compared with recorded human reaching movements and classical minimum jerk models. Investigation on short and lengthy distances from a goal position showed that the proposed trajectory formulation is featured by a symmetric uni-modal bell-shaped hand velocity profile and can replicate different curvatures of the human hand better than traditional methods that minimize either the angular or the hand jerk.
An accurate replica of human hand positions and velocities during arm movements is strongly motivated by clear shreds of evidence in neuroscience and psychology. For this reason, many of the proposed human-like arm motion generation methods can synthesize these kinematic features by taking inspiration from different principles of the human upper-limb movements. Additionally, these techniques often take advantage of controlling schemas, which find applications when real-time requirements are needed. However, planning movements with kinematic constraints in the operational space is often intended for specific tasks and for reaching movements only, which transport the end-effector by point-to-point trajectories that ignore manipulation in the workspace. This is arguably due to the inevitable constraints that manipulation introduces and that may negatively affect the kinematic analysis of human-likeness.
Qualitative Assessment
A qualitative assessment for the synthesis and the evaluation of human-likeness of robotic manipulation was also taken into consideration by the 12.96% of the included studies. For instance, Dragan and Srinivasa [54] proposed an arm motion planning method that integrates the inferences of human observers to mathematically formalize principles of the action interpretation theory. Specifically, Dragan and Srinivasa [54] introduced the notions of legibility and predictability as opposite properties of the motion that stem from inferences of an observer. In a scenario with multiple potential goals for a movement, a motion is predictable when, given a goal, it matches human expectations. On the contrary, a motion is legible when permits an observer to quickly and confidently infer the correct goal. These concepts are translated into trajectory functionals for a constrained optimization that can plan predictable or legible arm movements in robots. Although the goal of the authors is not to explicitly generate human-like arm movements, the latter may be the outcome if this matches the expectations of a human observer. Legible movements, in particular, are intended to show the underlying intention of an action in ambiguous environments (with multiple potential goals) that might be shared with human partners. Thus, the integration of human inferences into robotic manipulation may significantly improve human-robot collaboration. Experiments with the robot HERB (Figure 4h) demonstrated the feasibility of the proposed planners and the exposition of the robot motion to human volunteers fairly supported the formulations of predictability and legibility in the domain of robotics.
The support from subjective ratings of robotic movements has also been used in combination with quantitative metrics of evaluation. For example, the trajectory planner described by De Momi et al. [55] finds support in different validating options. Specifically, De Momi et al. [55] introduced a neural network-based approach for robot-human handover tasks, which involves four independent neural networks (NNs) trained to learn the features of real human reaching movements towards evenly distributed goal positions in a three-dimensional space. After the training, the proposed solution is capable of predicting a human-like end-effector trajectory and its corresponding time of execution. Then, inverse kinematics is applied to transfer the motion to a 7-DOFs robotic manipulator. A qualitative assessment of the proposed solution was performed by recruiting volunteers for classifying an observed robotic movement as “biologically-inspired” or as “non biologically-inspired”. In order to focus the attention on the end-effector and not on the motion of joints, the robot was covered and participants wore soundproof headset that mitigated the motor noise. Experimental results of this subjective ratings and of quantitative evaluations of human-likeness were in support of the proposed approach.
Collecting and analyzing qualitative opinions of naïve subjects concerning the intention and the biological origin of a motion is certainly an easy and immediate manner of receiving descriptive feedback. However, the intrinsic subjectivity of such an analysis is the major drawback that induces the researchers to not only rely on it. Additionally, a qualitative assessment may also be misled by embodiment factors of the moving agent, which might distort the opinion of a human observer and contaminate the results. For these reasons, the number and the type of participants, as well as the experimental protocol design, are essentially important in user studies for the assessment of human-like arm movements in robotics.
Repeatability
The consistency and repeatability of robotic arm motion have been considered important human-like properties by the 9.26% of the included studies (Figure 6). For instance, Koskinopoulou and Trahanias [56] presented an observation-based imitation framework capable of replicating human arm movements, as well as producing novel (unseen) actions. The proposed solution overcomes common correspondence issues that might affect standard learning from demonstration techniques by the employment of intermediate latent space representations. Specifically, human actions are visually recorded, while robotic actions are kinesthetically taught. Then, these high dimensional spaces of action are reduced to bi-dimensional latent spaces by non-linear techniques of principal components extraction. During the training phase, these latent spaces are associated by the minimization of the errors between human and robotic trajectories pairings. After training, the reproduction of human movements is performed by inversely projecting the robotic latent space back onto its high dimensional action space in the respect of physical joints limits. Experimental results with a 6-DOFs robotic manipulator showed the feasibility of the described imitation framework on writing and pick-and-place tasks. The ability to consistently generate similar arm motions on the basis of human repetitions was quantitatively assessed on the reduced latent space, as well as on the action space, of the robot. The detection of irrelevant operational-space errors also exhibited the capability of repeating arm trajectories when comparable human trials are observed.
Methods that enhance repeatability during imitation can certainly generate human-like arm movements. However, there is a relevant risk of ignoring other characteristics that are typical of human upper-limb motion. While providing repeatable features can simplify observation-based learning and intensify predictability, it can also seriously undermine human-like generalization capabilities. Similarly to biomimetic approaches, expensive equipments and complex post-processing might also be required to record human demonstrations and show consistency on different kinematic levels (e.g., velocity, acceleration, etc.).
Trajectory Smoothness
While in classical motion planning techniques the smoothness of a movement is measured by the sum of squared velocities or accelerations along a trajectory [57,58], smooth human arm motion needs to be recognized by the mean of jerk-based metrics [59]. Only the 5.56% of the included studies considered such a validation to assess human-likeness with the generation of limited jerky movements. For instance, the movements generated by the solution from De Momi et al. [55] were also evaluated through a measure of jerk on the principal plane of motion. Specifically, the sum of the squared norms of the jerk vectors in the path is normalized along the total time of execution and the length of the trajectory. This metric offers an independent index of smoothness for the detection of biological behaviors during the analysis of generic reaching movements [59].
The measure of the jerk of the motion provides a compact and intuitive manner to validate the smoothness of human-like arm trajectories. However, in many of the included studies, this metric was totally ignored. It is also important to note the fact that a measure of the jerk cannot be the only tool of assessment, but it must be included in a multiple validation system. Otherwise, a null jerk motion, which produces a triangle-shaped velocity profile, might be wrongly associated with the smoothest human-like trajectory that can be ever generated.
2/3 Power Law
The two-thirds power law (2/3-PL) formulates the non-linear relationship that exists between the wrist velocity and curvature of human planar reaching movements [60,61]. This kinematic characteristic was considered by only the 3.7% of the included studies as a valid reference of human-likeness in robotics. For instance, the 2/3-PL was part of the set of metrics that De Momi et al. [55] used to support and consolidate the biological origin of the generated arm movements.
The two-thirds power law was also used for determining its impact on the perception of robotic motion in comparison with other levels of anthropomorphism [62]. Specifically, Hugues et al. [62] designed a virtual car assembly scenario with different robotic platforms for the establishment of a small user study with naïve participants. Geometric inverse kinematics procedures on a given set of robots were modified to provide three parameters of anthropomorphism: namely, a base inertia, an end-effector inertia and the two-thirds power law. While inertia on the base and on the end-effector was simulated by spring-damper systems, the 2/3-PL was respected by forcing the end-effector velocity in accordance to the curvature of its path. A simple protocol was set up by questioning on singular perceived sensations and feelings, while a simulated robotic manipulator was watched moving its end-effector on a circling planar path. Results showed that the most influencing criterion was the end-effector inertia, which positively impacts on the perceived flexibility, naturalness and human-likeness of the generated motion. Consequently, these movements encouraged safety, less stress, and willingness to work with a robotic partner. On the contrary, the impact of the 2/3-PL on the perceived motion was mostly neutral.
In general, the application of the two-thirds power law in the generation of biologically-inspired arm movements is relatively simple and can be eventually used to replicate common human tasks, like hand writing. On the other hand, the assessment of human-likeness in robotic motion may require the planning and recording of a significant number of arm movements with the corresponding kinematic features. The 2/3-PL is only exhibited by bi-dimensional human trajectories, but it was shown that introduces systematic errors in correlation with the overall shape of the path [49].
Hand Path Planarity
The planarity of the hand path is a characteristic of human upper-limb movements that also occurs in the presence of obstacles [32]. For this reason, the 3.7% of the included studies took operational-space planarity into consideration of human-like arm motion generation (Figure 6). It can be used to assess human-likeness, simplify arm motion planning and mimic human arm postures. For instance, Xu and Ding [63] presented a method for bi-manual transporting tasks that constrains the motion of the end-effectors to lay on separated planes and utilizes synergies to reduce the dimensionality of the search for a feasible movement. Specifically, the definition of planes of motion in the operational space allows the control of the wrists by two virtual 2-DOFs manipulators that are attached on a torso-like structure. From an anthropomorphic arm, a virtual manipulator is obtained by restraining a wrist to move along different possible shoulder-wrist lines, which can draw planar curves in the operational space. Positional constraints between the left and the right arms permit to find an analytical solution to the translation planning problem. While translations are planned, orientations are consequently stabilized to maintain a constant rotation matrix between the left and the right wrists and to keep contact with the transported object. Simulations demonstrated the feasibility of the proposed motion planner for bi-manual transportation tasks. Moreover, comparisons with conventional inverse kinematics methods showed more natural end-effector trajectories and the avoidance of awkward arm postures.
On the one hand, planar human hand paths in reaching and transporting tasks can be used to significantly simplify the arm motion generation problem to show human-like features. On the other hand, this simplification might only result valid on specific scenarios and movements. Moreover, a serious reduction of the search-space dimensionality might negatively affect other important aspects that are typically observed on human arm movements. For this reason, planar operational-space trajectories should be analyzed in connection with other human-like metrics and should preferably emerge from independently applied human motor control principles.
Spatio-Temporal Correspondence (STC)
Taking inspiration from the theory of chaos, Gielniak et al. [27] introduced the Spatio-Temporal Correspondence (STC) as a tool to synthesize and evaluate human-like motion. Similarly to biomimetics, the proposed algorithm starts from recorded human trajectories and brings together three procedures into a pipeline to generate human-like robotic movements. The first step produces human-like motion through the maximization of the correspondence in space and time with a reference trajectory extracted from human goal-directed activities. This correspondence emulates the local couplings of connected degrees of freedom that, in biological structures, like humans, are exerted by groups of muscles. The attempt of coordinating a reference trajectory through spatial and temporal shifts is realized by the minimization of a measure of dissimilarity, which has been generally used for chaotic signals: the Spatio-Temporal Correspondence. After this step, the resulting human-like trajectory is subjected to optimal control [64] to produce a certain degree of variance for the motion. This second step is motivated by the fact that humans rarely replicate the same movement twice, even when the same task is performed. Adding variance around the reference trajectory (from the previous step) preserves the original human-like characteristics and, most importantly, respects the constraints of the motion in the joints space. Then, the optimal control provides a variant of the reference trajectory within the physical limits of the joints and respects any eventual synchrony. The third step projects the torque control commands onto the null space of the Jacobian that maps forces on the end-effector to the torque on the joints. This projection guarantees that the variant joints space trajectory does not compromise the operational space constraints of the reference trajectory, like holding a cup or pointing an object. Several tests with the humanoid robot Simon (Figure 4j) demonstrated that mapped motion from humans is perceived more natural, and its intention is easier to identify when it is coordinated with the STC method. Further experiments showed the capability of the proposed method of recovering human-likeness even in the presence of imperfect embodiments (e.g., any agent kinematically or dynamically different than the original one) or of lost information during mapping (e.g., down-sampling of the trajectory signal). Adding variance to the generated human-like trajectories did not degrade the ability to recognize motion’s intentions by human observers, and the variants exhibited the capacity of respecting both operational- and joints-space constraints. However, as expected, the performance and the ability to generate human-like variants of the proposed solution decrease as the number of constraints increases.
The Spatio-Temporal Correspondence is a versatile tool that can be used either to generate human-like arm movements or to quantitatively and objectively evaluate human-likeness. Another advantage is that the proposed solution is not heavily data-dependent because only one input trajectory is necessary for the generation of many possible variants around it. However, like for biomimetics approaches, there is the need for recording task-oriented human movements that often require the application of expensive equipments. This also means that, for each constraint in the operational space (end-effector position and orientation), an input reference movement is needed and one of its generated variants has to be appropriately selected. Notably, the proposed method also risks undermining fluent real-time interactions with human partners because two optimization processes in the pipeline (first and second steps) may significantly slow down the generation of the final human-like motion.
Rapid Upper Limb Assessment (RULA)
Advances in ergonomics research have been an inspiration for novel human-like manipulation techniques that can also improve the performance of traditional motion planners in robotics. Zacharias et al. [65] proposed a solution that takes advantage of the RULA (Rapid Upper Limb Assessment) criterion to generate human-like configurations and towards a determined end-effector pose in the operational space of a robot. In ergonomics, the RULA criterion scores conditions of stress and strain of human arm postures on a range from 1 to 7 with lower scores identifying more natural and comfortable configurations. The proposed path planner is equipped with knowledge concerning the reachability of the workspace in a human-like manner. This knowledge is generated off-line and depends on the robotic agent that is applied for manipulation. In this particular study, Zacharias et al. [65] conducted simulations and tests with the robot Rollin’ Justin that is illustrated in Figure 4g. The dexterous workspace is modeled by a capability map that is composed of discrete subregions where the end-effector can reach determined positions with different orientations. Each subregion includes spheres with a certain index of reachability, which measures the success rate in finding inverse kinematics solutions that place the end-effector onto uniformly distributed points on these spheres. Then, the restriction of the capability map to those robotic postures that possess acceptable RULA scores (usually no more than 4) provides a portion of that workspace that intuitively manifests the preferences of human manipulation. Given this restricted capability map, a RULA-driven inverse kinematics process (RulaIK) is proposed for reachable goal positions and orientations. While standard IK solvers depend on randomly selected initial arm configurations, the RulaIK iteratively try to solve the inversion of the kinematics starting from human-like postures with limited RULA scores that interest the region in the vicinity of a goal. Compared with standard methods, the application of the RulaIK demonstrated to generate awkward postures with a significantly lower frequency. Moreover, the computed restricted capability map is also used to bias the sampling of a bi-directional RRT planner [30] by selecting arm postures in a preferred range of RULA scores and that are feasible configurations in the region between the start and the goal postures. Tests on pick-and-place tasks in comparisons with standard methods exhibited a faster convergence and smaller mean RULA scores over the resulting trajectories when the RulaIK was used in combination with RULA-biased sampling for path planning. Interestingly, a similar but slightly worse performance was achieved when the RulaIK was used in combination with uniform random sampling for path planning. This result shows the significant influence of a human-like goal configuration on the planning time and on the overall ergonomics of a trajectory.
RULA-driven arm motion planning provides human-like arm trajectories that can also be perceived natural because they are acting on a region of the workspace that is usually preferred by human operators. However, typical human time parametrization is ignored, and, for this reason, the proposed planner might negatively affect human observations of a resulting trajectory. Although a faster convergence is achieved by the mean of RULA-biased IK and sampling, the total planning time is not compatible with the requirements of a fluent human-robot interaction. Additionally, the construction of a capability map with restriction on RULA configurations is robot-dependent and also adds a level of complexity that has to be negotiated with the level of accuracy in the discretization of the workspace.
3.3.2. Classification of the Generated Human-Like Arm Movements
In this section, more insights regarding the type of movements that can be generated by the reviewed solutions are provided. Specifically, a proper classification is necessary to understand better the degree of applicability of the proposed techniques and how they should be upgraded for a wider generalization in different tasks. As Figure 9 illustrates, 87.04% of the included studies addressed human-like single-arm motion generation, while only 18.52% of them proposed techniques for dual-arm motion planning. This outcome certainly depends on the robotic devices that are available for experimentation and on the tasks being addressed. Featured by a limited degree of complexity, reaching (sometimes also called point-to-point) movements have been the focus of the 74.07% of the included studies. This category of movements generally transports an end-effector from one point to another point of the Euclidean space SE (3) without the engagement of any particular manipulation of objects. On the contrary, picking and placing actions of the presented planners concern manipulation of rigid objects in the workspace of a robot. In particular, 37.04% of the reviewed papers addressed the generation of human-like pick movements, while 20.37% of them considered placing (Figure 9). Interestingly, most of the placing actions were part of the planning and execution of more general pick-and-place tasks. A more specialized branch of robotics research in human-like arm motion generation has investigated planar movements for writing/drawing applications and the reproduction of rhythmic trajectories, which regards the 14.81% and the 9.26% of the included studies, respectively (Figure 9). The latter areas of research attract particular attention for their originality and vast unexplored fields of application.
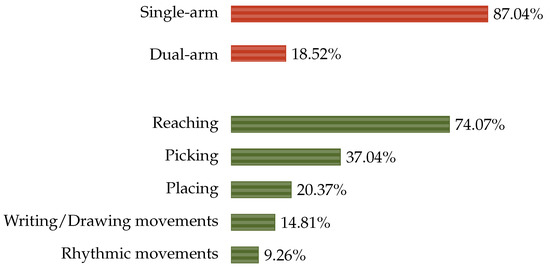
Figure 9.
Classification of the human-like arm movements that are generated by the reviewed motion planners.
For instance, Li et al. [66] introduced a trajectory planning method that can test different hypotheses concerning the role of the human Central Nervous System (CNS) in handwriting and drawing. Human actions seem to be represented in the CNS in more abstractive terms than with specific commands to the muscles [67]. For this reason, handwriting and drawing are encoded in terms of strokes in positions and directions without any specific motor command [66]. Specifically, three methods for imitating human handwriting and drawing are described: basic strokes, Bezier curves and non-gradient numerical optimization methods. The basic stroke method addresses the writing of alphanumeric characters with two basic elements (or strokes): circular arcs and line segments. Both of them are described analytically, and the inverse kinematics of a 2-DOFs manipulator is computed. The time parametrization of the resulting path is adaptable to different velocities profiles that can also simulate neurophysiological injuries and diseases. Concerning the Bezier curve method, Li et al. [66] took inspiration from computer graphics for the definition of a particular parametric curve, i.e., the cubic Bezier. This curve depends on four control points that are recorded after the visual acquisition of the image that has to be drawn. Then, a decoding process loads the saved parameters into a piecewise Bezier function that reproduces the handwriting. Finally, a trapezoidal speed profile is defined, and the end-effector motion is translated into specific joints-space commands. A variation of the Bezier curve method provides the non-gradient numerical optimization method that takes inspiration from vehicle guidance. Simulations with a three-links manipulator demonstrated the feasibility of the proposed trajectory planners in drawing complex figures mixed with alphanumeric characters.
Yang et al. [68] introduced a biologically-inspired method for the generation of cyclic (or rhythmic) arm movements that resemble the stability properties of animal and human motion. Specifically, the neural oscillatory circuits on the spinal cord, which are known as Central Pattern Generators (CPG), are formulated into artificial neural oscillatory networks and combined with a virtual force inducer (VFI) acting in the operational space of a manipulator. The VFI interacts with a series of oscillators that operate on each joint influencing the corresponding torque. Particularly, each neural oscillator tracks the joint sensory signal feedback to exhibit an adaptive behavior during interactions with the environment (the phenomenon of “entrainment”). The control scheme accounts for the joints space dynamical model of a multi-DOFs manipulator, which is featured by a Proportional Derivative (PD) controller in the operational space that follows a desired trajectory and by the scaled contribution of the rhythmic commands from the neural oscillators. Interestingly, the proposed scheme can achieve cyclic pattern generation without calculating the inverse dynamics and confronting the ill-posed problem of redundant systems. Simulations and experiments with planar and multi-DOFs manipulators demonstrated the capability of the proposed solution of generating smooth reaching movements, of producing cyclic repeatability of the joint positions, and of adapting to unexpected environmental changes.
Being a relatively recent and trending topic of research, techniques of human-like dual-arm motion and manipulation are of particular interest. Some authors presented algorithms designed for single- and dual-arm applications [22,27,69], while others only addressed bi-manual planning problems [70,71,72]. Lamperti et al. [22] proposed a solution for resolving the redundancy of an anthropomorphic dual-arm robotic system through the minimization of muscular effort. With two 7-DOFs arms, the redundant variables raise from 1 in uni-manual motion to 8 in bi-manual motion when there are constant rules of inter-limbs cooperation with one object. The right hand posing problem is solved by minimizing the muscular activation that supports a manipulator against gravity with respect to given operational-space constraints. The right arm configuration is uniquely identified by the hand pose and by an optimal swivel angle that minimizes muscular effort. A swivel angle, indeed, is the angle between the sagittal body plane of motion and the plane projected by the triangle wrist-elbow-shoulder, which is a key factor in featuring the human-likeness of a posture [41]. Then, the left hand posing problem is solved by considering the relative translational and rotational constraints with a given right hand pose. Similarly, the definition of the left arm posture is completed by the left swivel angle that minimizes the muscular effort of the left robotic arm. Addressing many samples of different dual-arm tasks, Lamperti et al. [22] fitted the data that relate arm configurations (14 variables) to the eight redundant variables that define the right hand pose, the right and the left swivel angles. Under the limits of the selected tasks, the fitting algorithm improves the performance of the proposed dual-arm redundancy solver because approximates the redundant variables by linear combinations of polynomial basis functions. Experiments with the humanoid robot ABB FRIDA (Figure 4e) showed the necessity of scaling the fitted functions according to the dimensions of the robotic manipulators. Results demonstrated the ability of the proposed method to generate human-like dual-arm movements when compared with those ones of a simulated bi-manual human kinematic model, which has spherical joints on the shoulders and the wrists.
Through the study of synergies in dual-arm manipulation tasks, Suarez et al. [72] designed a dual-arm human-robot mapping system that is based on the extraction of principal movement directions (PMDs) to simplify sampling-based motion planning in the joints space. Specifically, the positions and the orientations of the hands of a human operator are firstly recorded and sampled during the execution of an assigned assembly task. Then, these data are transformed into the operational space of a humanoid robot with two 6-DOFs manipulators equipped with a 16-DOFs hand each. Subsequently, the samples are translated into the joints space of the robot and the values of the joints are properly filtered to minimize their variance. The synergies of a particular task are then extracted as principal components of the dual-arm configurations that are the result of the mapping process. These principal components were called principal movement directions (PMDs) and represent the recorded dispersion of the samples. After the selection of feasible and collision-free dual-arm goal configurations, more instances of the RRT-Connect algorithm [30] are launched in a PMDs-subspace that reduces the dimensionality of the original search space (i.e., the dual-arm joints space). Experiments with assembly and free-movement tasks showed a significant increase of the planning computational performance when a minimal number of PMDs, which are sufficiently representative of the task-related human variance, is adopted.
In the same direction of research, Garcia et al. [73] proposed a synergies-based partition of the operational space for dual-arm reaching and grasping with a humanoid robot mounted on a mobile platform. The synergies represent a human-like coordination between the translational movements and the dual-arm motion of the robot that is approaching a region of the workspace for grasping two cylindrical objects on a table. Human motion is captured and used as reference for transferring human-likeness, which is maximized by an optimization-based human-robot mapping that ensures the correct placement of the end-effectors for a successful grasping. Then, principal components analysis is run on the space of configurations for the torso and the joints to extract a minimum number of synergies that significantly comprise the variance of the samples. This analysis permits to partition the torso translational space of the robot according to similarities of the captured dual-arm movements and, consequently, reduce the dimensionality of the planning search space for new joints-space states. For this reason, the proposed motion planner modifies the original version of the RRT-Connect algorithm [30] to take advantage of the acquired knowledge and considerably decreases the required planning time and iterations.
The vast majority of the included studies presented methods for the human-like generation of single-arm reaching movements, while poor attention has been put on drawing and rhythmic motion. More recently, more complex robotic applications of pick-and-place and dual-arm manipulation has started to attract the interest of an interdisciplinary research that takes inspiration from biological and behavioral findings. Although more generic tools of arm motion generation that can offer human-like solutions for different classes of robotic movements are often auspicious, it emerged that research seems to be focused on narrow sets of applications. For instance, while more advanced solutions might potentially integrate simpler utilizations with few modifications, the techniques for planning human-like writing/drawing and rhythmic movements seem to be an isolated branch of investigation that can hardly be merged with more classical methods for reaching, picking and placing. Additionally, the great part of the included human-like dual-arm motion planners depends on biomimetic measures and on databases of human captured motion data that strongly limit task generalization.
3.3.3. Obstacles-Avoidance in Human-Like Arm Motion Generation
Endowing robots with the capability of avoiding and preventing collisions with obstacles in the workspace is a necessary skill in scenarios that are shared with humans for interacting purposes [1,3,4]. However, only the 27.78% of the reviewed papers addressed this particular issue. The proposed obstacles-avoidance mechanisms are summarized in Table A2. For example, Rosell et al. [74] proposed a human-like sampling of the configurations of a robotic arm-hand system that also improve the efficiency of a PRM-based graph building [75] in hand pre-shaping movements during grasping. Specifically, the hand motion of a human operator is captured during the execution of unconstrained movements and then mapped onto a robotic anthropomorphic hand to extract the inter-fingers coordination by a principal component analysis. Rosell et al. [74] took into consideration human-like requirements that may regulate the palm orientation constantly facing an object to be grasped during prehension. These considerations, and the principal components of the fingers’ motion, permit to solve a planning query between two feasible arm-hand configurations with reduced dimensionality. The feasibility of the proposed virtually constrained planner was successfully tested with a 6-DOFs arm equipped with a four-fingered hand. The arm-hand system moves from an unconstrained to a constrained configuration in order to grasp a can on a table in a environment cluttered with obstacles. Additionally, comparisons with standard PRM planning showed that the proposed method can provide sequences of human-like postures with a higher success rate in a minor computational time.
Assuming a pre-determined mental image of a final arm posture in human goal-directed movements, Xie et al. [76] introduced the hypothesis of the “Target Arm Pose” (TAP) in human-like arm motion planning for robotic manipulators. The TAP hypothesis determines final arm configurations that maximize dexterity by seeking for a high Jacobian condition number in the inversion of the kinematics. A detailed analysis of the obstacles in the workspace and the proper selection of intermediate TAP configurations facilitate the generation of collision-free human-like arm movements. While the human motion of the fingers is mimicked by the minimum jerk model, the inversion of the kinematics at joint jerk level (IK-JJL) generates reaching movements by tracking an end-effector trajectory, which respects the boundary conditions with given TAPs and avoids the physical limits of the joints. In presence of obstacles, the TAP hypothesis for intermediate via postures is combined with the RRT-Connect algorithm [30] to generate collision-free paths. Simulation and tests showed the feasibility of the IK-JJL in planning reaching movements in obstacles-free scenarios. Moreover, the combination of the TAP hypothesis with the RRT-Connect algorithm improved the performance of the latter in planning reaching and grasping movements through narrow passages.
Liu et al. [77] proposed an analytical inverse kinematics algorithm for anthropomorphic manipulators to map human-like configurations from recorded human arm motion data. In particular, the shoulder, elbow, wrist and palm points are operational-space key positions for a task-constrained human-robot mapping. While the position of the shoulder is fixed at the base of a robotic arm and the position of the palm/end-effector is dictated by the task, there is some flexibility in mapping the position of the elbow and the wrist because only a grasping direction constrains the end-effector orientation. The proposed human-robot configuration correspondence solves the inverse kinematics problem with respect to the link lengths and the joints limits of the manipulator. Specifically, the wrist key position is constrained to be on the line connecting the elbow and the palm positions (wrist-elbow-in-line) so that all the key positions lie on the same reference plane. Then, the obtained posture is iteratively adjusted if any of the joints limits is surpassed. This adjustment procedure starts by circularly moving the wrist position to obtain a feasible elbow joint angle. Next, the elbow key position is initially chosen to be the closest to the captured human elbow that lies on the reference plane. If any joints-space infeasibility is detected, then the position of the elbow is iteratively moved on an arc that defines different swivel angle values. The simulations with a 7-DOFs redundant arm demonstrated that the proposed IK method provides a high end-effector accuracy that slightly decrease in motion tracking but can show sufficiently rigorous human-likeness, which is manifested by the detected similarities with the human swivel angle. Interestingly, the human-like performance does not degrade when simple avoidance of a spherical obstacle is considered. The elbow key position is maintained, while the flexibility of the wrist is exploited to adjust the robot configuration and avoid collisions.
Although preventing self-collisions and avoiding obstacles in the workspace of a robot is a priority of human-centered robotics, the reviewed techniques of human-like arm motion generation rarely address it. Most of the proposed solutions for obstacles avoidance work under assumptions that significantly simplify a planning problem and take advantages of sampling-based motion planners that can surely provide collisions-free paths, but, on the other hand, require smoothing procedures and neglect typical human-like time parametrizations. Additionally, experiments on collisions prevention often ignore assessing kinematic human-like features that characterize human arm movements [32].
3.3.4. Efficient, Generalized, and Adaptive Human-Like Arm Motion Generation
Human voluntary movements are the physical linkage that the brain uses to communicate with the external world [78]. The movement generation system embodies the intentionality of a subject as the desire to change a portion of the surrounding environment, and the prediction of an action, which is based on learned internal models. The sensations and changes resulting from the execution of a movement feedback to the nervous system that might adjust the motion generation mechanisms (adaptation). There is a complete specification of upper-limb trajectories before the beginning of the action, but there is also a continuous motion redefinition as an arm moves [78]. This implies that planning and controlling arm trajectories can be considered independent and interconnected stages of human-like arm motion generation [79]. The planning stage of volitional movements, in particular, is featured by optimality requirements (efficiency) when accurate prediction is necessary to satisfy the specifications of goal-directed actions [44,80]. As part of a more general feed-forward control policy, human motor planning also evokes “internal models” (generalization) that are constructed by learning from prior knowledge and offer more precise expressions of an intended action [78]. Being part of a combined human motor framework, it is important to analyze optimization, learning, and control techniques that have been proposed as solutions for human-like arm motion generation.
In the last decades, optimality principles and models have been studied and empirically developed under biological and psychological perspectives as a manifestation that features the evolution of the human motor system [81,82,83]. The 37.04% of the reviewed papers presented different optimization-based solutions that consider the minimization of typical costs in human upper-limb movements. For instance, Albrecht et al. [84] applied bilevel optimization to imitate human reaching movements that were tracked and clustered during the execution of daily kitchen routines. Specifically, a human-like arm trajectory is obtained by optimizing on two levels to address the replication of a wide range of movements. The resolution of a low-level problem comprehends the minimization of a weighted combination of three cost functions that have been experimentally observed in humans: a hand jerk cost [44], an angular jerk cost [38], and a torque change cost [80]. The resolution of a high-level problem finds the correct combination of the weights to minimize the distance between the optimal solution and the recorded human data in a single cluster. The availability of weighting factors permits adapting the cost according to the diverse tasks that identify the clusters. Simulations and experiments with the robot iCub (Figure 4b) demonstrated that the proposed method can correctly imitate human reaching movements better than the single optimal criteria alone, even though similarities can be limited by the embodiment of a robotic device.
In our previous studies, a human-like arm motion planning that minimizes the angular jerk of collisions-free trajectories was described [70,85,86]. Taking inspiration from psychological findings in human prehension [48], the proposed method is based on the resolution of two non-linearly constrained optimization problems: one for the selection of a goal posture, which ensures a correct collisions-free posing of an end-effector; and another for the selection of a bounce posture, which guarantees naturalistic obstacles-avoidance on the entire generated path. Then, the selected goal and bounce postures are integrated to compose a minimum angular jerk trajectory that endows a humanoid robot with the capability of manipulating objects in scenarios cluttered with obstacles. The goal and bounce postures selection problems are formulated in AMPL [87] (A Mathematical Programming Language) and are solved by IPOPT [88], which is an Interior Point OPTimizer [89] for large-scale non-linear optimization. Simulations and experiments on assembly tasks with the robot ARoS (Figure 4a) demonstrated the feasibility of the proposed solutions in generating human-like single-arm movements [85], as well as bi-manual asynchronous [86] and synchronous [70] movements.
Training and learning models and processes in human arm-hand motion can describe how adult motor behavior emerge [90] and how the information of actions can be memorized and stored in internal models for generating prehension and manipulation [38,48]. The 22.22% of the included studies introduced techniques for learning and generalizing from the observation of human patterns of motion during the execution of particular tasks. For instance, Park and Kim [91] described an optimal database construction of human re-targeted motion to learn arm motion primitives for a real-time human-like trajectory planning. Particularly, an Evolutionary Algorithm (EA) is applied as a global optimizer to iteratively select minimal joint torques trajectories among a collection of captured human motion data. The latter are clustered according to task-related conditions, which need to be respected for the correct accomplishment of an intended action. Within these conditions, the principal components of motion are extracted for a dimensionality reduction and for reconstructing new evolved movements that locally minimize the joint torque along the movement duration. Experiments with the humanoid MAHRU (Figure 4i) demonstrated that the proposed method is capable of learning minimal torque arm trajectories and generate human-like motion in real-time by reconstructing a movement through its principal components under given boundary conditions. The general performance decreases as the size of the clusters in the database increases because the selected principal components may not fully describe the variance of the captured motion.
Taking inspiration from human adaptation to perturbations in reach-to-grasp movements, Shukla and Billard [92] introduced a coupled dynamical system to control the arm-hand interdependency during task execution. Specifically, a Programming by Demonstration approach [93] is followed to learn the explicit coupling between the hand and the fingers motion during unperturbed and perturbed grasping actions. Human movements from different subjects were recorded, transferred to a robotic embodiment, and modeled as Gaussian Mixture Models [94] for estimating operational-space position and velocities, which maximize the likelihood of the generated demonstrations. In particular, three joint distributions are learned to form the proposed coupled dynamical system (CDS): one encodes the dynamics of the hand transportation, one encodes the fingers motion, and one encodes the state of the fingers inferred from the hand position. The norm of the distance between the hand position and its target represents the coupling function to deduce the state of the fingers, which activates a controller to update the values of the finger joints. When perturbations occur, tuning the controlling parameters can regulate the speed and the amplitude of hand reopening, which can either adhere to human-like requirements or surpass human physical limitations to cope with fast adaptation demands. Simulations and tests with the robot iCub (Figure 4b) showed the necessity of having an explicit arm-hand coupling for a successful grasping when, for example, a target suddenly changes after the onset of the motion and when a grip type needs to be substituted.
A deep neural network approach was proposed by Su et al. [95] to optimize the redundancy of anthropomorphic manipulators and reproduce the human-like features of human recorded motion. In particular, target poses and swivel angle motion are mapped from the given demonstrations with a network of five hidden modules, which apply convolution, a drop-out module to prevent over-fitting, and a regression layer. After training, the regression model can predict human-like swivel angle kinematics from novel target end-effector poses. Then, the predicted swivel angle motion is fed to an inverse kinematics controller to reproduce human-like elbow positions through the redundant variables of an anthropomorphic manipulator. Simulations with a 7-DOFs robotic arm showed the capability of replicating human-like postures in tracking tasks. Additionally, compared with other artificial neural network-based models, the proposed learning approach exhibited a higher reconstruction accuracy, a lesser predicting time and a greater noise robustness.
Studies in humans have shown that there is a complete trajectory specification before the onset of, for example, reaching and drawing movements. However, this specification continues throughout the motion and shows adaptations to unpredicted task-related variations [78]. Although visual information and, more generally, sensory feedback, necessarily close a controlling loop, some evidence on humans concerning fast motion adaptation suggests the existence of feedback-free internal controlling models that emerge from experience [78,96]. However, accuracy requirements seem to be achieved by visually detecting a hand moving, which suggests motion modifications based on physical and environmental sensations [78]. The 29.63% of the included studies introduced closed-loop controllers to cope with fast unpredicted changes that may occur in the workspace of a robot and to allow a compliant physical interaction with the environment. For instance, starting from the Virtual Spring-Damper controller introduced by Arimoto and Sekimoto [51], Bae et al. [97] took inspiration from the human muscle tension effect under gravity to increase energy efficiency and conform to a more repeatable human-like motion. Specifically, a torsional spring effect in the joints-space is added to the previous proportional derivative closed-loop controller, which ensures a correct trajectory tracking in the operational space. Feeding back a joints-space signal permits to privilege arm configurations, which are usually adopted by humans to minimize the tension of the muscles under gravity. Experiments with a 7-DOFs redundant manipulator revealed that the introduction of the muscle tension effect can reduce the average power consumption and trigger joints-space repeatability, which would otherwise be lost after a few repetitions. Moreover, it was shown that the proposed human-like controller is featured by compliant behaviors because it can promptly absorb external disturbances and maintain good operational-space tracking capabilities and joints-space repeatability.
Stefanovic and Galiana [98] introduced a spinal-like regulator for replicating behavioral patterns that are typical in volitional reaching movements. In particular, this approach finds its foundations on the imitation of the centers of pattern generation that exist in the spinal cord and couple brain activity with the spinal motor areas. For this reason, the proposed controller is based on spinal-like circuits, which can exhibit intelligent functions that resemble internal models and reflexive reactions to external perturbations. The applicability of the proposed biological-like controller to multi-joint artificial limbs is tested using a two-links simulated robotic arm, which executes planar reaching tasks on different ranges of the available workspace. The results showed the capability of the proposed method of scaling the operational-space trajectories on spatial and temporal levels to fit with human-like arm motion requirements. Specifically, the inherent spinal gains of the controller can be tuned to change the end-effector path curvatures and speeds to generate quasi-straight trajectories with bell-shaped velocity profiles. The regulator can also successfully absorb sustained perturbations and adaptively track moving targets to restore and maintain a human-like trajectory profile.
With the purpose of mimicking the human joint coordination at a behavioral level, Togo et al. [99] took inspiration from the uncontrolled manifold (UCM) concept [100] to introduce a feedback controller capable of reproducing the trial-to-trial joints-space variance of reaching movements. This variance of redundant motor elements (i.e., joint angles) is quantified by a UCM component, which is orthogonal to another component (ORT) that directly affects the performance variables (i.e., coordinates in the operational space of a manipulator). The proposed “UCM reference feedback controller” (Figure 10) regulates the task-relevant elements (the ORT component) with respect to the minimum intervention principle introduced by Todorov and Jordan [101].
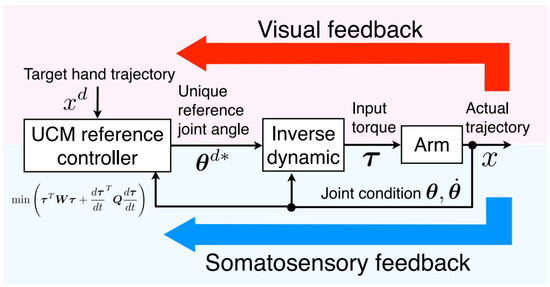
Figure 10.
Concept of the uncontrolled manifold (UCM) reference feedback controller [99].
A one-dimensional target tracking task with a simulated 3-DOFs arm is addressed for tests and comparisons with captured human reaching motion. The minimum jerk criterion with null boundary conditions [44] is used to generate human-like operational-space trajectories, which are then tracked by the proposed human-like regulating method. In conformity with the minimum torque change principle of human reaching movements [80], a task-constrained optimal problem is analytically solved to provide a reference configuration and, through inverse dynamics, a torque signal for the arm. Visual information of the actual trajectory is fed back to the controller with added normal distributed noise that simulates human imperfections in the visual perception of moving targets. Additionally, the proposed controller is supplied with a somato-sensory feedback for internally monitoring the joint position and velocities during motion. Normal distributed noise signals are also added to the joints torque signals and to the optimal configuration references to simulate signal-dependent noise of motor commands and the influence of visual perception uncertainties on the variability of the joints angles, respectively. The efficacy and the capability of reproducing human-like joints coordination of the proposed uncontrolled manifold regulator were statistically assessed by simulations and comparisons with captured human reaching movements.
From the analysis of the included studies emerges a wide variety of optimization, learning, and controlling methods that have been fairly applied for human-like arm motion generation. However, a common motor framework capable of an efficient modular integration seems to be still missing, even though roboticists have often referred to the genesis of movements as a linked functional decomposition of these technical features [79,102]. The proposed human-like arm motion planning and learning methods are generally based on task-related human captured data. They involve optimization techniques on a global level in the attempt of clustering motion patterns, as well as on a local level with respect to human motion minimization principles. Learning approaches take advantage of dimensionality reduction mechanisms to simplify the generation process and extract synergies for a motion reconstruction in unseen environmental situations. Additionally, decision-making systems have also been presented as the result of learning from captured human data to select the most appropriate movement planning method. Although collections of human motor features guarantee an authentic source of knowledge and an unequivocal tool of comparison, these optimization and learning techniques may suffer from a lack of generalization because of internal models that store and feed experience in a categorical and human-dependant manner. Controlling human-like trajectories have also been studied to optimize the input motor commands of robotic manipulators. The reviewed controllers are of biological and behavioral inspiration and have been tested with devices of few degrees of freedom. Therefore, their application on complex human-like redundant circumstances remains unaccounted. The regulated trajectories are often generated on-line without any given reference from prior planning stages, even though the human Central Nervous System seems to generate optimized motion outputs close to a final motor solution before the onset of a movement [78,99]. Learning of control parameters and internal models are also absent in the analyzed human-like arm motion regulators, despite the fact that training and practice find neuroscientific and psychological bases in planning and controlling voluntary movements [103,104].
4. Discussion
A literature review on the most recent techniques of human-like arm motion generation has been presented. The analysis included 54 papers that were firstly classified according to the sources of knowledge. The vast majority of the papers was found in Scopus, immediately followed by the IEEEXplore, Web of Science, and, with minor contribution, ACM Digital Library. The equipment of the included studies was roughly equally composed by simulators, robotic manipulators and anthropomorphic platforms. The latter devices are of particular impact on motion planning solutions because provide a significant level of anthropomorphism that can positively influence interactions with humans [16,17]. The large majority of the reviewed papers proposed global methods that operate with kinematic variables and address the generation of trajectories in the operational space of robotic manipulators. This result might be due to the fact that a globally-considered static environment can provide solutions in a low dimensional space and a more accurate match with kinematic human-like features [48,50,105]. However, such methods might be reductive and risk to ignore human-like characteristics of the joints space, such as synchrony and bell-shaped angular velocity profiles [37]. Dynamics variables are often the focus of biologically-inspired solutions, which have been poorly addressed due to the difficulties that arise in transferring the activities of the muscles into robotic manipulators. Local human-like arm motion generation methods have also been scarcely proposed, but they can introduce the capability of simulating human reflexes and react to changing scenarios during the execution of a movement. However, these techniques only partially consider the workspace and, therefore, may fail to achieve human-likeness in complex tasks.
Roboticists have considered a variety of human motor control principles as inspirational and evaluational tools for proposing techniques of human-like arm motion generation. The included studies showed that researchers have mainly focused on biomimetic and human-robot mapping approaches, which can ensure a strong resemblance with human motion that is acknowledged as an objective reference of an action. In particular, human-robot transferring techniques can guarantee real-time execution of the movements, which is essential during tele-operation. However, most of these methods need expensive and complicated equipment for capturing human movements, databases to collect them and post-processing for features extraction. Additionally, these techniques generally lack of generalization because usually work for a limited range of goal-directed tasks. Similar issues are also experienced by learning-based methods to teach specific tasks to a robot by imitation or training. Although learning from observations ensures a stable repeatability and a degree of adaptation to external perturbations, generalization is seldom achieved.
The kinematics of the obtained end-effector trajectories have often been compared to the hand path and hand velocity profile of human reaching to show similarities and divergences between robotic and human movements. Most of these particular solutions were developed for single-arm motion and based on human-like optimization principles that minimize energy under tasks-related constraints. Manipulation in the workspace of a robot is often neglected when kinematics is assessed because of the inevitable complications that pick-and-place tasks would import into the analysis of human-likeness. The majority of the proposed methods were not tested with qualitatively assessments to understand the perception of human observers. However, there are many scientific shreds of evidence demonstrating that, for pleasant human-robot interactions and collaborations, the movements of the robot have to be perceived as natural, predictable, and showing the intention of the underlying action without any verbal communication [12,106,107,108].
The smoothness of a trajectory has often been measured in relation with the third derivative of position, i.e., the jerk, which is a compact and intuitive index of human-likeness. However, smoothness is not exclusively connected with jerk, but it must be assessed more comprehensively with other validation systems, such as, for example, the number of movement units [109]. The application of the two-third power law (2/3-PL) is relatively simple for the generation of biologically-inspired planar movements, like writing or drawing. However, the 2/3-PL has shown to introduce systematic errors on the complete shape of a trajectory and needs to be extended to explain regularities of three-dimensional reaching movements [49]. Although path planarity in the operational space may significantly simplify a planning problem, this human motor principle should emerge from other independent human-like motor principles instead of being a constraint of the generation process. Otherwise, there is a risk of complicating a planning problem and decrease the overall performance. The repeatability of motion on imitating observed human movements can certainly increase predictability and simplify learning, but it can seriously undermine generalization on different tasks. With two optimization processes in sequence, the Spatio-Temporal Correspondence [27] can negatively affect real-time interactions with humans, but it is a versatile tool that can be used to either assess or generate human-like body trajectories from one single sample. Human-like arm motion has also been achieved by the RULA-driven technique [65], which introduced an upper limb assessment of the inverse kinematics and the sampling of the search space to enhance ergonomics, but ignored human-like time parametrizations.
Most of the included studies addressed single-arm reaching movements, while human-like dual-arm applications are emerging and pick-and-place tasks still deserve more attention. The simple nature of motion without manipulation and the vast literature concerning the psychology of human reaching have probably encouraged roboticists towards this direction of investigation. Replicating human writing, drawing, and rhythmic movements revealed to be a small research branch, which seems to be isolated because not of easy integration with more classical methods of picking, placing, and reaching motion generation.
The prevention of self-collisions and the avoidance of obstacles in the workspace of a robot were rarely considered in the reviewed papers, even though these are necessary features for interacting devices in human-centered environments. Additionally, many of the proposed solutions ignored a human-like kinematic analysis during the avoidance of obstacles and addressed collisions prevention under simplifying assumptions, which reduce their range of applicabilities.
Roboticists have usually defined the genesis of human-like motion as a connected system of different functional modules [79] where optimization, learning, and control are integrated. However, the included studies do not refer to a common framework of motor generation for optimizing human motor models, learning internal models and control on external disturbances. On a local level, human motor minimization principles are applied, while learning techniques are used for clustering motion on a global level, for extracting regularities of captured human movements and for implementing decision-making settings. Studies have shown that the synthesis of motor solutions happens in the Central Nervous System before execution [78]. However, the reviewed controllers act in the absence of prior optimized trajectories that may guide the process of on-line regulation. Moreover, these controllers are applied to a few degrees of freedom and remain to be tested on more complex redundant manipulators and interacting tasks.
A categorization of the included studies in accordance with their most peculiar methodological features permits to analyze their possible fields of application. With a significant presence in the current literature of human-like arm motion generation, biomimetic techniques for the generation of single-arm reaching movements certainly endow human operators with novel capabilities. For instance, for an efficient tele-operation of a robotic manipulator, accurate human-robot mapping methods for a real-time execution are necessary. Additionally, biomimetic methods privilege the mimicking of simple reaching motion because it is often sufficient for tele-operated tasks and the activation of different types of end-effector might not resemble typical human prehension. Due to the complexity of joint manipulation, dual-arm human-like mimicking is at its early stage of investigation and is expected to advance in the near future. While such techniques aim at directly augmenting human capabilities, the rest of the proposed methods aims at a more indirect augmentation, which passes through human-robot interactions that resemble human-human interactions. In these situations, arm movements are planned to achieve human-like kinematic characteristics and high levels of smoothness to meet the expectations of human observers and co-workers. A full autonomy of such human-like devices is achieved by, for instance, their capability of successfully accomplishing pick-and-place tasks in office-like and industrial-like scenarios, which are often cluttered with generic obstacles. The analysis of the included studies also showed that an advanced level of motor independence is also reached when internal human-like functionals are minimized, repetitive human-like behaviors are learned, and human-like reactions to external perturbations are controlled. It is also worth noticing that, in a broader sense, robots are more human-centered through the generation of human-like arm motion. Their ultimate services augment the human capabilities of action because their goal is not to replace human operators but, instead, to interact and collaborate with them.
5. Conclusions
The limitations of the discussed literature on robotic human-like arm motion generation show the necessities of investigating comprehensive solutions, which can benefit from generalization capabilities for a wide range of tasks, types of movements, and scenarios. The intentionality of motion needs to be encoded because it plays an essential role during interaction and collaboration between robots and human partners. More focus is needed on manipulative features and on obstacles-avoidance mechanisms that do not degrade the level of human-likeness with the increase of the complexity of a given task. For instance, behavioral studies show that collisions between the upper-limbs and objects in the environment seem to be anticipated and prevented through specific via postures during grasping [48,110]. For this reason, the generation of collisions-free arm trajectories in robotics should take inspiration from similar techniques of human obstacles-avoidance instead of relying on non-human-like solutions, such as sampling-based path planning algorithms.
What emerges is the necessity of having quantitative and qualitative means of assessment to obtain objective and complementary information concerning the human-likeness of robotic trajectories. Many of the reviewed techniques mainly referred to either task-related metrics or biomimetics, which might mismatch with the perception of human interacting partners during the applications on different situations. Moreover, clinical protocols and numerical indices for the detection of upper-limb motion pathologies [111,112,113,114] have been totally ignored by the included studies but can certainly inspire future work. For instance, a kinematic movement analysis of the upper extremity functions was proposed by van Andel et al. [111] to assess motion disorders in daily living activities. Similarly, Gates et al. [112] identified the kinematical requirements of upper-limb ranges of motion that are necessary on several human self-caring and ordinary actions. The construction of an open ongoing database of human upper-limb ranges of motion was proposed by Major et al. [113] to share feasible inputs for the design of tunable robotic rehabilitation solutions. An upper-limb motion deviation index (ULMDI) was also introduced [114] as a synthetic and comprehensive measure of arm motion pathologies that cause kinematic deviations from healthy upper-limb gestures. Such diagnostic tools should inspire the design of anthropomorphic manipulators and the development of novel solutions of human-like arm motion generation that improve interactions with healthy and impaired human peers.
Further investigations on dual-arm human-like motion generation should be also addressed and, for example, undertaken as an extensive branch of the single-arm counterparts. Many of the reviewed solutions to the bi-manual planning problem refer to mapping configurations of fixed-structures, instead, which show a lack of flexibility and of merging capabilities with single-arm tasks. Human principles of optimization, learning, and control should also find place in a modular framework where a continuous and smooth interaction is enhanced to mimic the functioning of the Central Nervous System and respond with the challenges of the human-centered robotics [78,79,102].
Author Contributions
Conceptualization, G.G., E.B., and W.E.; methodology, G.G.; formal analysis, G.G.; investigation, G.G. and E.B.; resources, G.G. and E.B.; data curation, G.G.; writing—original draft preparation, G.G.; writing—review and editing, G.G., E.B., and W.E.; visualization, G.G.; supervision, E.B. and W.E.; project administration, E.B. and W.E.; funding acquisition, E.B. and W.E. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the EU Project FP7 Marie Curie NETT-Neural Engineering and Transformative Technologies (ID 289146), the FCT PhD grant (ref. SFRH/BD/114923/2016), the FCT Project UID/MAT/00013/2013, and the FCT–Fundação para a Ciência e Tecnologia within the R&D Units Project Scope: UIDB/00319/2020.
Conflicts of Interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Appendix A

Table A1.
Literature review analysis.
Table A1.
Literature review analysis.
| Authors | Year | Type of Robot | Approach | Human-Like Metrics | Types of the Generated Movements | Key Features of the Proposed Method |
|---|---|---|---|---|---|---|
| Kim et al. [40] | 2006 | humanoid | global; kinematic; operational space | biomimetics | single-arm; dual-arm; reaching | A Response Surface Methodology (RSM) allows the estimation of human swivel angles during reaching in order to solve the inverse kinematics of a 6-DOFs robotic arm in a closed-form. |
| Caggiano et al. [115] | 2006 | simulated | global; kinematic; operational space | biomimetics | single-arm; writing | A closed-loop inverse kinematic algorithm is tuned to mimic recorded human hand writing by a simulated 7-DOFs arm with human-like dimensions. |
| Arimoto and Sekimoto [51] | 2006 | manipulator | local; dynamic; operational space | kinematic assessment | single-arm; reaching | A control law based on the Virtual Spring-Damper hypothesis is proposed to solve the Bernstein’s Degree-of-Freedom problem and tested on bi-dimensional and three-dimensional reaching motion. |
| Kim et al. [42] | 2007 | humanoid | global; kinematic; operational space | biomimetics | single-arm; reaching | The regeneration of human-like arm motion enhances HRI through the engagement of the human attention by suitably changing motion direction and scaling its magnitude. |
| Yang et al. [116] | 2009 | manipulator | local; dynamic; operational space | repeatability | single-arm; reaching; rhythmic | A biologically-inspired dynamic controller combines a Virtual Spring-Damper hypothesis and neural oscillators in the joints space to achieve human-like reaching and rhythmic arm motion. |
| Artemiadis et al. [117] | 2010 | manipulator | local; kinematic; operational space | biomimetics | single-arm; reaching | The inter-joints dependency of human arm reaching is probabilistically modeled and maximized by a closed-loop inverse kinematic algorithm. |
| Park and Kim [91] | 2010 | simulated | global; dynamic; joints space | biomimetics | single-arm; pick | A clustered database structure is built off-line by applying an evolutionary process on captured human arm motion to collect torque efficient movement primitives. |
| Pattacini et al. [118] | 2010 | humanoid | local; kinematic; operational space | kinematic assessment; trajectory smoothness | single-arm; reaching; rhythmic | A multi-referential Cartesian controller follows the minimum-jerk principle in both operational and joints spaces to ensures typical human-like hand kinematic behavior and robustness against singularities. |
| Yang et al. [68] | 2010 | manipulator | local; dynamic; operational space | repeatability | single-arm; rhythmic | The coupling between a virtual spring-damper and human-like Central Pattern Generators (CPGs) at the joints is proposed to achieve cyclic motion and adapt to external perturbations. |
| Albrecht et al. [84] | 2011 | humanoid | global; dynamic; joints space | biomimetics | single-arm; reaching | A bilevel optimization is applied to imitate clustered human arm reaching movements: the best imitation performance results from the combination of typical human-like minimization principles. |
| Bae et al. [97] | 2011 | manipulator | local; dynamic; operational space | repeatability | single-arm; rhythmic | The Virtual Spring-Damper controller [51] is augmented with the capability of generating human-like energy efficient arm reaching motion by introducing, at the level of the joints, a human muscle tension effect under the gravity. |
| Silva et al. [85] | 2011 | humanoid | global; kinematic; joints space | kinematic assessment | single-arm; pick; reaching | Single-arm human-like manipulation is achieved by the selection of optimal goal and bounce arm configurations, which are composed to obtain minimum-jerk collisions-free trajectories. |
| Xie et al. [76] | 2011 | manipulator | global; kinematic; joints space | kinematic assessment | single-arm; pick; reaching | Based on the introduction of Target Arm Poses (TAPs), a human-like arm-hand motion planner that solves the inverse kinematic problem at a jerk level is proposed and tested in scenarios cluttered with obstacles. |
| Bhattacharjee et al. [119] | 2011 | simulated | local; dynamic; operational space | kinematic assessment | single-arm; reaching; writing | A control scheme, which takes inspiration from the human muscle damping and stiffness properties, proposes the formulation of a bijective function that uniquely maps the joint actuators to time-varying weights that simulate brain-muscles communication delays. |
| Rosell et al. [74] | 2011 | manipulator | global; kinematic; operational space | biomimetics | single-arm; reaching | A human-like sampling is proposed for grasping in presence of obstacles. From recorded human hand motion, inter-fingers coordination is extracted to reduce the dimensionality of finger motion sampling, while the motion of the end-effector is planned under palm orientating constraints. |
| Zacharias et al. [65] | 2011 | humanoid | global; kinematic; operational space | qualitative assessment; RULA | single-arm; pick; place; reaching | The ergonomic RULA criterion is used to identify regions of the workspace with human-like RULA scores, which guide the inversion of the kinematics, as well as any sampling-based planning, towards the selection of ergonomic configurations. |
| Fu et al. [35] | 2012 | simulated | global; dynamic; operational space | kinematic assessment | single-arm; reaching | Motor synergies of a 3-DOFs human-like arm are studied to reduce the dimensionality of an optimal control problem for the generation of reaching planar movements. A human-like time parametrization of the motion is also considered. |
| Shukla and Billard [92] | 2012 | humanoid | local; kinematic; operational space | biomimetics | single-arm; pick | A Coupled Dynamical System (CDS) is proposed and learned by demonstrations of human grasping movements. The coupling of hand motion and aperture of the fingers is mimicked and stable to fast perturbations of the target in the operational space. |
| Strauss and Heinke [120] | 2012 | manipulator | local; kinematic; operational space | kinematic assessment | single-arm; reaching | Dynamical Neural Fields are proposed to generate planar reaching motion for a 2-DOFs arm, which exhibited a human-like kinematic behavior of the end-effector. |
| Taïx et al. [36] | 2013 | humanoid | global; dynamic; operational space | kinematic assessment | single-arm; reaching | The biological model of antagonist muscles is applied for the generation of human-like reaching motion. The control variables are optimally selected in order to minimize the energy of the moto-neuronal signals over the duration of a movement. |
| Gielniak et al. [27] | 2013 | humanoid | global; dynamic; joints space | biomimetics; STC | single-arm; dual-arm; reaching | Human-like arm motion is generated by the maximization of a Spatio-Temporal Correspondence (STC) with a set of task-related exemplar trajectories that are tracked from human agents. |
| Wang and Artemiadis [121] | 2013 | simulated | global; kinematic; operational space | biomimetics | single-arm; reaching | Every-day human reaching movements are captured to estimate human swivel angle values and propose a closed-form of the inverse kinematic algorithm for anthropomorphic robotic arms. |
| Li et al. [66] | 2013 | simulated | global; kinematic; operational space | biomimetics | single-arm; writing | Three methods are implemented and compared to replicate human hand writing and drawing capabilities and suggest how handwriting actions might be encoded in the Central Nervous System. |
| Rano and Iossifidis [31] | 2013 | simulated | local;kinematic; operational space | hand path planarity | single-arm; reaching; pick | A dynamical systems approach, which represents targets as attractors and obstacles as repellors, is proposed to generate human-like arm reaching. |
| Rosado et al. [69] | 2013 | simulated | global; kinematic; operational space | biomimetics | single-arm; dual-arm; reaching | A Kinetic-based motion capture method is proposed to transfer human arm motion onto a simulated upper-body humanoid system equipped with a 4-DOFs right arm and a 7-DOFs left arm. |
| Dragan and Srinivasa [54] | 2014 | humanoid | global; kinematic; joints space | qualitative assessment | single-arm; pick | Legible arm motion is generated to enhance the intentionality of robotic actions and improve non-verbal communication with human partners in shared workspaces with multiple possible targets. |
| Atawnih et al. [52] | 2014 | manipulator | local; dynamic; operational space | kinematic assessment | single-arm; reaching | A redundant arm torque controller capable of imitating a human-like kinematic behavior during reaching is proposed. Its compliant properties allow a safe physical human-robot interaction. |
| Stefanovic and Galiana [98] | 2014 | manipulator | local; kinematic; operational space | kinematic assessment | single-arm; reaching | Planar reaching motion with human-like kinematic behavior of the end-effector is generated by a spinal-like controller, which finds biological inspiration in the spinal motor circuits of primates. |
| Xia et al. [122] | 2014 | simulated | global; kinematic; operational space | biomimetics | single-arm; reaching | A novel method to compute swivel angle values under the physical limits of the joints is proposed starting from biomimetic studies of the human arm. The resulting feasible regions constrain the optimal selection of arm configurations for human-like motion generation. |
| Zhao et al. [43] | 2014 | manipulator | global; kinematic; operational space | biomimetics | single-arm; pick; reaching | A novel planner named Gradient Projection Method Rapidly-exploring Random Trees (GPM-RRT) is proposed to generate human-like arm trajectories that minimize gravitational energy, muscular elastic energy and wrist discomfort in case of grasping. |
| Gulletta et al. [70] | 2015 | humanoid | global; kinematic; joints space | kinematic assessment | dual-arm; pick; place; reaching | Based on psychological evidence in human motor control, a human-like bi-manual synchronous motion planner is proposed as an extended framework of the single-arm solution presented by Silva et al. [85]. |
| Hugues et al. [62] | 2015 | simulated | global; kinematic; operational space | qualitative assessment; 2/3 power law | single-arm; rhythmic | User studies on the subjective perception of human-like motion are performed to compare different strategies for transferring motion onto virtual robots, which operate in an industrial-like scenario. |
| Lamperti et al. [22] | 2015 | humanoid | global; kinematic; operational space | qualitative assessment | single-arm; dual-arm; reaching | A redundancy resolution method for dual-arm motion generation that minimizes the muscular effort of the manipulation chain is presented. A fitting algorithm also permitted to extract the relationships between the task and the redundancy variables (swivel angles). |
| Liu et al. [123] | 2015 | simulated | global; kinematic; operational space | biomimetics | single-arm; reaching | A reinforcement learning algorithm with an adaptive noise exploration strategy is proposed to learn the shape and the goal parameters of dynamical movement primitives, which compose energy-efficient and collisions-free arm trajectories. |
| Shin and Kim [71] | 2015 | humanoid | global; dynamic; operational space | biomimetics | dual-arm; pick; place; reaching | An imitation learning technique from captured human dual-arm motion is proposed and applied for the generation of novel robotic arm trajectories. A controller based on a virtual dynamics model refers to the planned trajectories for the bi-manipulation of one object. |
| Silva et al. [86] | 2015 | humanoid | global; kinematic; joints space | kinematic assessment | single-arm; pick; place; reaching | A method for generating human-like asynchronous bi-manual movements is proposed and based on the sequential selection of optimal configurations for both arms of a humanoid robot. |
| Suarez et al. [72] | 2015 | simulated | global; kinematic; operational space | biomimetics | dual-arm; pick; place; reaching | A principal component analysis is applied to extract the synergies of captured dual-arm human motion and identify the major dispersion of human activity. The most significant components define Principal Movement Directions (PMDs), which guide sampling-based planners to generate human-like arm trajectories. |
| Xie and Zhao [124] | 2015 | manipulator | global; kinematic; operational space | qualitative assessment | single-arm; place | Optimal handing over positions for HRI are investigated and minimum hand jerk movements are generated by minimizing the gravitational energy and muscular effort. Via postures in the free joints space are suggested to guide sampling-based planners in obstacles-avoidance. |
| De Momi et al. [55] | 2016 | manipulator | global; kinematic; joints space | kinematic assessment; trajectory smoothness; 2/3 power law; qualitative assessment | single-arm; reaching | In order to generate human-like handover motion, four neural networks are trained on captured human reaching movements in a structured workspace. Starting from the Cartesian coordinates of a target, time duration and ten via points of a new trajectory are predicted. |
| Chen et al. [125] | 2016 | manipulator | local; kinematic; operational space | biomimetics; kinematic assessment | single-arm; reaching | Human-like hand reaching motion is formed by the composition of a high level of control, which applies the dynamics of two potential fields, and of a low level of control, which considers joints synergies of captured human self-reaching movements to solve the inverse kinematics of the manipulator in a closed form. |
| Kashima and Hori [53] | 2016 | simulated | global; kinematic; operational space | biomimetics; kinematic assessment | single-arm; reaching | A time adjustment of the elbow and shoulder relative motions modifies the formulation of the minimum angular jerk principle for the generation of human-like arm reaching movements. |
| Koskinopoulou and Trahanias [56] | 2016 | manipulator | global; kinematic; operational space | biomimetics; repeatability | single-arm; pick; place; reaching; writing | A novel Learning from Demonstrations (LfD) called IMFO (IMitation Framework by Observation) is proposed. Human observed actions are mapped onto a manipulator on a latent space of representation, which reduces the dimensionality of the motion and extracts small variations for a better generalization. |
| Togo et al. [99] | 2016 | simulated | local; dynamic; operational space | biomimetics; kinematic assessment | single-arm; reaching | An UnControlled Manifold (UCM) reference that incrementally minimizes joints torque and torque change is provided to an inverse dynamics controller for the generation of human-like arm reaching motion. |
| Liarokapis et al. [46] | 2017 | manipulator | global; kinematic; joints space | biomimetics | single-arm; pick; reaching | Three geometrical metrics of functional anthropomorphism are studied to reduce the dissimilarity in mapping captured human arm-hand motion onto redundant and hyper-redundant arms and multi-fingered robotic hands. |
| Zhao and Wei [126] | 2017 | manipulator | global; kinematic; operational space | biomimetics | single-arm; reaching | From captured human reaching and grasping motion, a hierarchical planning strategy (HPS) is proposed and a Bayesian network is learned to select one of three optimal human-like arm motion planning algorithms. |
| Alibeigi et al. [127] | 2017 | humanoid | global; kinematic; operational space | biomimetics | single-arm; reaching | A real-time human arm motion mimicking system is proposed. The null space of the Jacobian matrix is used to maintain a high joints-space similarity with the human movements and to respect the angular physical limits of the robot. |
| Liu et al. [77] | 2017 | simulated | global; kinematic; operational space | biomimetics | single-arm; pick; reaching | A wrist-elbow-in-line method is proposed to constrain and analytically solve the inverse kinematics of a manipulator starting from tracked human arm motion demonstrations. Extensions to obstacles-avoidance have been addressed. |
| Xu and Ding [63] | 2017 | simulated | global; kinematic; joints space | hand path planarity | dual-arm; place | Defined two planes of motion on which the wrists are moving, a synergic method for the human-like bi-manual transportation of one object is proposed and based on the planning of translations and the stabilization of orientations. |
| Chen et al. [29] | 2018 | humanoid | global; kinematic; joints space | biomimetics | dual-arm; pick; place; reaching | The application of a neural network auto-encoder with one hidden layer is proposed to reduce the dimensionality of the search space for sampling-based algorithms and mimic human dual-arm goal-directed actions. |
| Su et al. [128] | 2018 | manipulator | local; kinematic; operational space | biomimetics; qualitative assessment | single-arm; reaching | Human-like motion planning for anthropomorphic manipulators in tele-operated tasks is proposed. From captured human reaching movements, a regression function is trained to obtain feasible human-like swivel angles and solve the inverse kinematic problem in real-time. |
| Tomić et al. [20] | 2018 | humanoid | global; kinematic; operational space | biomimetics | dual-arm; pick; place; reaching | Human dual-arm manipulation actions are mimicked by optimally transferring the trajectories of real and virtual markers’ frames onto a humanoid robot. |
| Garcia et al. [73] | 2018 | humanoid | global; kinematic; operational space | biomimetics | dual-arm; pick | Synergies of dual-arm grasping are extracted from captured human motion in correlation with approaching actions towards the targets and used to partition the operational space for a better imitation in humanoid mobile platforms. |
| Su et al. [95] | 2019 | simulated | local; kinematic; operational space | biomimetics | single-arm; reaching | Improving the learning technique proposed by Su et al. [128], a deep convolutional neural network (DCNN) is applied to train a regression function that maps human swivel angles to hand target poses with smaller mean errors and higher robustness to noise. |
| Lauretti et al. [34] | 2019 | manipulator | local; kinematic; operational space | biomimetics; qualitative assessment | single-arm; reaching | A hybrid joint/Cartesian LfD approach based on Dynamical Motion Primitives that is capable of avoiding self collisions and obstacles is proposed. The two spaces are coupled by the Gradient Projection Method, which favors the Cartesian-space constraints of a given task. |

Table A2.
Avoidance of obstacles in the reviewed techniques.
Table A2.
Avoidance of obstacles in the reviewed techniques.
| Authors | Year | Algorithm | Test Scenario | Key Features of the Obstacles-Avoidance Mechanism |
|---|---|---|---|---|
| Silva et al. [85] | 2011 | Optimal bounce posture selection | Assembly-like | A back-and-forth movement is superimposed onto a minimum angular jerk trajectory. |
| Rosell et al. [74] | 2011 | PRM [75] | Grasping an object on a table cluttered with obstacles | The construction of a probabilistic roadmap is biased with a constrained orientation of the palm of the robotic hand. |
| Xie et al. [76] | 2011 | RRT-Connect [30] | Reaching movements through narrow passages | Target Arm Poses (TAPs) are defined in the crucial points of the expected path, which is divided in segments where the RRT-Connect algorithm is applied. |
| Zacharias et al. [65] | 2011 | RRT-Connect [30] | Pick-and-place tasks of cubes on a table in front of a humanoid robot | Configurations with human-like RULA scores are provided to initialize the IK solver and to bias the sampling routine of path planners, such as the RRT-Connect algorithm. |
| Rano and Iossifidis [31] | 2013 | Repellors dynamics | Picking on a table while avoiding objects along the path | An angle and a distance factors in relation with an obstacle and a relative positional factor between a target and an obstacle contribute in the formation of a repulsive vector field. |
| Dragan and Srinivasa [54] | 2014 | CHOMP [58] | Picking an object on a table with multiple possible target | A defined legibility functional replaces a classical cost function in the CHOMP algorithm, which ensures the generation of a collisions-free arm path. |
| Gulletta et al. [70] | 2015 | Optimal bi-manual bounce posture selection | Assembly-like | A bi-manual back-and-forth movement is superimposed onto a bi-manual minimum angular jerk trajectory. |
| Liu et al. [123] | 2015 | DMPs-based LfD algorithm | Reaching while avoiding a static spherical object | Shape and goal parameters of DMPs are learned from demonstrations of human reaching while avoiding one obstacle along the path. |
| Silva et al. [86] | 2015 | Optimal bounce posture selection | Assembly-like | A back-and-forth movement is superimposed onto a minimum angular jerk trajectory. |
| Suarez et al. [72] | 2015 | RRT-Connect [30] | Assembly-like | The identification of synergies in dual-arm manipulation tasks allows to run sampling-based planners on a human-like low dimensional space. |
| Xie and Zhao [124] | 2015 | FR-RRT [129] | Handing over a cube in presence of one obstacle | After the selection of an appropriate via posture that facilitates the avoidance of the obstacle, the end-effector trajectory follows an extended minimum jerk principle and is tracked by the FR-RRT algorithm. |
| Liu et al. [77] | 2017 | Analytical IK with human-like constraints | Avoidance of a moving spherical-like object | The flexibility of the wrist position is used to maintain the captured human swivel angle values. |
| Chen et al. [29] | 2018 | RRT-Connect [30] | Dual-arm manipulation with objects on a table | RRT-Connect is applied in the hidden layer of the proposed Auto-Encoder and the selected samples in this space are mapped onto the original space for the detection of collisions in the decoding process. |
| Garcia et al. [73] | 2018 | RRT-Connect [30] | Dual-arm grasping two objects on a table. | A modified RRT-Connect is proposed to generate collisions-free configurations that relates the torso postures with the robot position with respect of the human-like synergies of the captured motion. |
| Lauretti et al. [34] | 2019 | Joint/Cartesian DMPs | Reaching in presence of a static spherical obstacle | Distance-based terms are added to Joint and Cartesian DMPs to place the end-effector and each joint of the manipulator away from the obstacles in the workspace. |
References
- Sheridan, T.B. Human-Robot Interaction: Status and Challenges. Hum. Factors J. Hum. Factors Ergon. Soc. 2016, 58, 525–532. [Google Scholar] [CrossRef]
- Gladden, M.E. Who Will Be the Members of Society 5.0? Towards an Anthropology of Technologically Posthumanized Future Societies. Soc. Sci. 2019, 8, 148. [Google Scholar] [CrossRef]
- Fukuda, T.; Michelini, R.; Potkonjak, V.; Tzafestas, S.; Valavanis, K.; Vukobratovic, M. How far away is “artificial man”. IEEE Robot. Autom. Mag. 2001, 8, 66–73. [Google Scholar] [CrossRef]
- Schaal, S. The new robotics: Towards human-centered machines. HFSP J. 2007, 1, 115–126. [Google Scholar] [CrossRef]
- Fong, T.; Nourbakhsh, I.; Dautenhahn, K. A survey of socially interactive robots. Robot. Auton. Syst. 2003, 42, 143–166. [Google Scholar] [CrossRef]
- Wiese, E.; Metta, G.; Wykowska, A. Robots as intentional agents: Using neuroscientific methods to make robots appear more social. Front. Psychol. 2017, 8, 1–19. [Google Scholar] [CrossRef]
- Ray, C.; Mondada, F.; Siegwart, R. What do people expect from robots? In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3816–3821. [Google Scholar]
- Welfare, K.S.; Hallowell, M.R.; Shah, J.A.; Riek, L.D. Consider the Human Work Experience When Integrating Robotics in the Workplace. In Proceedings of the 2019 14th ACM/IEEE International Conference on Human-Robot Interaction (HRI), Daegu, Korea, 11–14 March 2019; pp. 75–84. [Google Scholar]
- Sebanz, N.; Bekkering, H.; Knoblich, G. Joint action: Bodies and minds moving together. Trends Cogn. Sci. 2006, 10, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Bicho, E.; Louro, L.; Hipolito, N.; Erlhagen, W. A dynamic field approach to goal inference and error monitoring for human-robot interaction. In Proceedings of the International Symposium on New Frontiers in Human-Robot Interaction, Edinburgh, UK, 6–9 April 2009; pp. 31–37. [Google Scholar]
- Glasauer, S.; Huber, M.; Basili, P.; Knoll, A.; Brandt, T. Interacting in time and space: Investigating human-human and human-robot joint action. In Proceedings of the 19th International Symposium in Robot and Human Interactive Communication, Viareggio, Italy, 13–15 September 2010; pp. 252–257. [Google Scholar]
- Bicho, E.; Erlhagen, W.; Louro, L.; Costa e Silva, E. Neuro-cognitive mechanisms of decision making in joint action: A human-robot interaction study. Hum. Mov. Sci. 2011, 30, 846–868. [Google Scholar] [CrossRef] [PubMed]
- Koppenborg, M.; Nickel, P.; Naber, B.; Lungfiel, A.; Huelke, M. Effects of movement speed and predictability in human-robot collaboration. Hum. Factors Ergon. Manuf. Serv. Ind. 2017, 27, 197–209. [Google Scholar] [CrossRef]
- Tanizaki, Y.; Jimenez, F.; Yoshikawa, T.; Furuhashi, T. Impression Investigation of Educational Support Robots using Sympathy Expression Method by Body Movement and Facial Expression. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 1254–1258. [Google Scholar]
- Erel, H.; Shem Tov, T.; Kessler, Y.; Zuckerman, O. Robots are Always Social. In Extended Abstracts of the 2019 CHI Conference on Human Factors in Computing Systems—CHI EA ’19; ACM Press: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Duffy, B.R. Anthropomorphism and the social robot. Robot. Auton. Syst. 2003, 42, 177–190. [Google Scholar] [CrossRef]
- Strait, M.K.; Floerke, V.A.; Ju, W.; Maddox, K.; Remedios, J.D.; Jung, M.F.; Urry, H.L. Understanding the Uncanny: Both Atypical Features and Category Ambiguity Provoke Aversion toward Humanlike Robots. Front. Psychol. 2017, 8, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; Bicho, E.; Erlhagen, W. AROS: An anthropomorphic robot for human-robot interaction and coordination studies. In Proceedings of the CONTROLO 2008 Conference—8th Portuguese Conference on Automatic Control, UTAD, Vila Real, Portugal, 21–23 July 2008; pp. 819–826. [Google Scholar]
- Sandini, G.; Metta, G.; Vernon, D. The iCub Cognitive Humanoid Robot: An Open-System Research Platform for Enactive Cognition. In 50 Years of Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 358–369. [Google Scholar]
- Tomić, M.; Chevallereau, C.; Jovanović, K.; Potkonjak, V.; Rodić, A. Human to humanoid motion conversion for dual-arm manipulation tasks. Robotica 2018, 36, 1167–1187. [Google Scholar] [CrossRef]
- Gouaillier, D.; Hugel, V.; Blazevic, P.; Kilner, C.; Monceaux, J.; Lafourcade, P.; Marnier, B.; Serre, J.; Maisonnier, B. The NAO humanoid: A combination of performance and affordability. arXiv 2008, arXiv:0807.3223v1. [Google Scholar]
- Lamperti, C.; Zanchettin, A.M.; Rocco, P. A redundancy resolution method for an anthropomorphic dual-arm manipulator based on a musculoskeletal criterion. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 1846–1851. [Google Scholar]
- Kaneko, K.; Kanehiro, F.; Kajita, S.; Hirukawa, H.; Kawasaki, T.; Hirata, M.; Akachi, K.; Isozumi, T. Humanoid robot HRP-2. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004; pp. 1083–1090. [Google Scholar]
- Fuchs, M.; Borst, C.; Giordano, P.R.; Baumann, A.; Kraemer, E.; Langwald, J.; Gruber, R.; Seitz, N.; Plank, G.; Kunze, K.; et al. Rollin’ Justin—Design considerations and realization of a mobile platform for a humanoid upper body. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4131–4137. [Google Scholar]
- Srinivasa, S.S.; Berenson, D.; Cakmak, M.; Collet, A.; Dogar, M.R.; Dragan, A.D.; Knepper, R.A.; Niemueller, T.; Strabala, K.; Vande Weghe, M.; et al. Herb 2.0: Lessons Learned From Developing a Mobile Manipulator for the Home. Proc. IEEE 2012, 100, 2410–2428. [Google Scholar] [CrossRef]
- You, B.J.; Kim, D.; Kim, C.; Oh, Y.H.; Jeong, M.H.; Oh, S.R. Network-based Humanoid ‘MAHRU’ as Ubiquitous Robotic Companion. IFAC Proc. Vol. 2008, 41, 724–729. [Google Scholar] [CrossRef]
- Gielniak, M.; Liu, K.; Thomaz, A. Generating human-like motion for robots. Int. J. Robot. Res. 2013, 32, 1275–1301. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics, 1st ed.; Springer: London, UK, 2009. [Google Scholar]
- Chen, P.; Zhao, H.; Zhao, X.; Ge, D.; Ding, H. Dimensionality Reduction for Motion Planning of Dual-arm Robots. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 718–723. [Google Scholar]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Rano, I.; Iossifidis, I. Modelling human arm motion through the attractor dynamics approach. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 2088–2093. [Google Scholar]
- Grimme, B.; Lipinski, J.; Schöner, G. Naturalistic arm movements during obstacle avoidance in 3D and the identification of movement primitives. Exp. Brain Res. 2012, 222, 185–200. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Lauretti, C.; Cordella, F.; Zollo, L. A Hybrid Joint/Cartesian DMP-Based Approach for Obstacle Avoidance of Anthropomorphic Assistive Robots. Int. J. Soc. Robot. 2019, 11, 783–796. [Google Scholar] [CrossRef]
- Fu, K.C.D.; Nakamura, Y.; Yamamoto, T.; Ishiguro, H. Studies of motor synergies in generating optimal goal-directed movements in human-like robotic arm. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 808–813. [Google Scholar]
- Taïx, M.; Tran, M.T.; Souères, P.; Guigon, E. Generating human-like reaching movements with a humanoid robot: A computational approach. J. Comput. Sci. 2013, 4, 269–284. [Google Scholar] [CrossRef]
- Breteler, M.D.K.; Meulenbroek, R.G.J. Modeling 3D object manipulation: Synchronous single-axis joint rotations? Exp. Brain Res. 2006, 168, 395–409. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, D.A.; Loukopoulos, L.D.; Meulenbroek, R.G.J.; Vaughan, J.; Engelbrecht, S.E. Planning reaches by evaluating stored postures. Psychol. Rev. 1995, 102, 28–63. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; Kawato, M. A via-point time optimization algorithm for complex sequential trajectory formation. Neural Netw. 2004, 17, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, C.; Park, J. Human-like Arm Motion Generation for Humanoid Robots Using Motion Capture Database. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3486–3491. [Google Scholar]
- Zanchettin, A.M.; Rocco, P.; Bascetta, L.; Symeonidis, I.; Peldschus, S. Kinematic analysis and synthesis of the human arm motion during a manipulation task. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2692–2697. [Google Scholar]
- Kim, C.; Kim, S.; Ra, S.; You, B.J. Regenerating human-like arm motions of humanoid robots for a movable object. In Proceedings of the SICE Annual Conference, Takamatsu, Japan, 17–20 September 2007; pp. 1081–1086. [Google Scholar]
- Zhao, J.; Xie, B.; Song, C. Generating human-like movements for robotic arms. Mech. Mach. Theory 2014, 81, 107–128. [Google Scholar] [CrossRef]
- Flash, T.; Hogan, N. The Coordination of Arm Movements: An Experimentally Confirmed Mathematical Model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef] [PubMed]
- LaValle, S.M. Rapidly Exploring Random Trees: A New Tool For Path Planning; Technical Report; The Pennsylvania State University: State College, PA, USA, 1998. [Google Scholar]
- Liarokapis, M.; Bechlioulis, C.P.; Artemiadis, P.K.; Kyriakopoulos, K.J. Deriving Humanlike Arm Hand System Poses. J. Mech. Robot. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Jeannerod, M. The Timing of Natural Prehension Movements. J. Mot. Behav. 1984, 16, 235–254. [Google Scholar] [CrossRef]
- Rosenbaum, D.A.; Meulenbroek, R.J.; Vaughan, J.; Jansen, C. Posture-based motion planning: Applications to grasping. Psychol. Rev. 2001, 108, 709–734. [Google Scholar] [CrossRef]
- Pollick, F.E.; Maoz, U.; Handzel, A.A.; Giblin, P.J.; Sapiro, G.; Flash, T. Three-dimensional arm movements at constant equi-affine speed. Cortex 2009, 45, 325–339. [Google Scholar] [CrossRef] [PubMed]
- Morasso, P. Spatial control of arm movements. Exp. Brain Res. 1981, 42, 223–227. [Google Scholar] [CrossRef] [PubMed]
- Arimoto, S.; Sekimoto, M. Human-like movements of robotic arms with redundant DOFs: Virtual spring-damper hypothesis to tackle the Bernstein problem. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1860–1866. [Google Scholar]
- Atawnih, A.; Papageorgiou, D.; Doulgeri, Z. Reaching for redundant arms with human-like motion and compliance properties. Robot. Auton. Syst. 2014, 62, 1731–1741. [Google Scholar] [CrossRef]
- Kashima, T.; Hori, K. Control of biomimetic robots based on analysis of human arm trajectories in 3D movements. Artif. Life Robot. 2016, 21, 24–30. [Google Scholar] [CrossRef]
- Dragan, A.; Srinivasa, S. Integrating human observer inferences into robot motion planning. Auton. Robot. 2014, 37, 351–368. [Google Scholar] [CrossRef]
- De Momi, E.; Kranendonk, L.; Valenti, M.; Enayati, N.; Ferrigno, G. A Neural Network-Based Approach for Trajectory Planning in Robot-Human Handover Tasks. Front. Robot. AI 2016, 3, 1–10. [Google Scholar] [CrossRef]
- Koskinopoulou, M.; Trahanias, P. A methodological framework for robotic reproduction of observed human actions: Formulation using latent space representation. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 565–572. [Google Scholar]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4569–4574. [Google Scholar]
- Zucker, M.; Ratliff, N.; Dragan, A.D.; Pivtoraiko, M.; Klingensmith, M.; Dellin, C.M.; Bagnell, J.A.; Srinivasa, S.S. CHOMP: Covariant Hamiltonian optimization for motion planning. Int. J. Robot. Res. 2013, 32, 1164–1193. [Google Scholar] [CrossRef]
- Chang, J.J.; Wu, T.I.; Wu, W.L.; Su, F.C. Kinematical measure for spastic reaching in children with cerebral palsy. Clin. Biomech. 2005, 20, 381–388. [Google Scholar] [CrossRef]
- Lacquaniti, F.; Terzuolo, C.; Viviani, P. The law relating the kinematic and figural aspects of drawing movements. Acta Psychol. 1983, 54, 115–130. [Google Scholar] [CrossRef]
- Wann, J.; Nimmo-Smith, I.; Wing, A.M. Relation between velocity and curvature in movement: Equivalence and divergence between a power law and a minimum-jerk model. J. Exp. Psychol. Hum. Percept. Perform. 1988, 14, 622–637. [Google Scholar] [CrossRef]
- Hugues, O.; Weistroffer, V.; Paljic, A.; Fuchs, P.; Karim, A.A.; Gaudin, T.; Buendia, A. Determining the Important Subjective Criteria in the Perception of Human-Like Robot Movements Using Virtual Reality. Int. J. Hum. Robot. 2016, 13, 1550033. [Google Scholar] [CrossRef]
- Xu, H.; Ding, X. A synergic method for anthropomorphic dual-arm robots to plan bimanual transport tasks. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1020–1025. [Google Scholar]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zacharias, F.; Schlette, C.; Schmidt, F.; Borst, C.; Rossmann, J.; Hirzinger, G. Making planned paths look more human-like in humanoid robot manipulation planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1192–1198. [Google Scholar]
- Li, B.; Zheng, Y.F.; Hemami, H.; Che, D. Human-like robotic handwriting and drawing. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4942–4947. [Google Scholar]
- Morsella, E.; Bargh, J.A.; Gollwitzer, P.M. Oxford Handbook of Human Action; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Yang, W.; Bae, J.H.; Oh, Y.; Chong, N.Y.; You, B.J. CPG based self-adapting multi-DOF robotic arm control. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4236–4243. [Google Scholar]
- Rosado, J.; Silva, F.; Santos, V.; Lu, Z. Reproduction of human arm movements using Kinect-based motion capture data. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 885–890. [Google Scholar]
- Gulletta, G.; Araújo, S.M.; Costa e Silva, E.; Costa, M.F.; Erlhagen, W.; Bicho, E. Nonlinear optimization for human-like synchronous movements of a dual arm-hand robotic system. In Proceedings of the International Conference of Numerical Analysis and Applied Mathermatics, Rhodes, Greece, 22–28 September 2015; p. 140007. [Google Scholar]
- Shin, S.Y.; Kim, C. Human-Like Motion Generation and Control for Humanoid’s Dual Arm Object Manipulation. IEEE Trans. Ind. Electron. 2015, 62, 2265–2276. [Google Scholar] [CrossRef]
- Suarez, R.; Rosell, J.; Garcia, N. Using synergies in dual-arm manipulation tasks. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5655–5661. [Google Scholar]
- Garcia, N.; Roseli, J.; Suarez, R. Modeling human-likeness in approaching motions of dual-arm autonomous robots. In Proceedings of the 2018 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), Brisbane, Australia, 16–19 May 2018; pp. 43–48. [Google Scholar]
- Rosell, J.; Suarez, R.; Perez, A.; Rosales, C. Including virtual constraints in motion planning for anthropomorphic hands. In Proceedings of the 2011 IEEE International Symposium on Assembly and Manufacturing (ISAM), Tampere, Finland, 25–27 May 2011; pp. 1–6. [Google Scholar]
- Kavraki, L.E.; Švestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Xie, B.; Zhao, J.; Liu, Y. Human-like motion planning for robotic arm system. In Proceedings of the 2011 15th International Conference on Advanced Robotics (ICAR), Tallinn, Estonia, 20–23 June 2011; pp. 88–93. [Google Scholar]
- Liu, W.; Chen, D.; Steil, J. Analytical Inverse Kinematics Solver for Anthropomorphic 7-DOF Redundant Manipulators with Human-Like Configuration Constraints. J. Intell. Robot. Syst. 2017, 86, 63–79. [Google Scholar] [CrossRef]
- Schwartz, A.B. Movement: How the Brain Communicates with the World. Cell 2016, 164, 1122–1135. [Google Scholar] [CrossRef] [PubMed]
- Burdet, E.; Franklin, D.W.; Milner, T.E. Human Robotics; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Uno, Y.; Kawato, M.; Suzuki, R. Formation and Control of Optimal Trajectory in Human Multijoint Arm Movement-Minimum Torque-Change Model. Cybern. Biol. 1989, 61, 89–101. [Google Scholar] [CrossRef]
- Engelbrecht, S.E. Minimum Principles in Motor Control. J. Math. Psychol. 2001, 45, 497–542. [Google Scholar] [CrossRef]
- Todorov, E. Optimality principles in sensorimotor control. Nat. Neurosci. 2004, 7, 907–915. [Google Scholar] [CrossRef]
- Ivaldi, S.; Sigaud, O.; Berret, B.; Nori, F. From Humans to Humanoids: The Optimal Control Framework. Paladyn J. Behav. Robot. 2012, 3, 75–91. [Google Scholar] [CrossRef]
- Albrecht, S.; Ramirez-Amaro, K.; Ruiz-Ugalde, F.; Weikersdorfer, D.; Leibold, M.; Ulbrich, M.; Beetz, M. Imitating human reaching motions using physically inspired optimization principles. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; IEEE: Bled, Slovenia, 2011; pp. 602–607. [Google Scholar]
- Silva, E.C.; Costa, M.F.; Bicho, E.; Erlhagen, W. Human-Like Movement of an Anthropomorphic Robot: Problem Revisited. AIP Conf. Proc. 2011, 1389, 779–782. [Google Scholar]
- Silva, E.C.; Costa, M.F.; Araújo, J.P.; Machado, D.; Louro, L.; Erlhagen, W.; Bicho, E. Towards human-like bimanual movements in anthropomorphic robots: A nonlinear optimization. Appl. Math. Inf. Sci. 2015, 9, 619–629. [Google Scholar]
- Fourer, R.; Gay, D.M.; Kernighan, B.W. AMPL: A Mathematical Programming Language; Technical Report; AT & T Bell Laboratories: Murray Hill, NJ, USA, 1989. [Google Scholar]
- Wachter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2005, 106, 25–57. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Burdet, E.; Milner, T.E. Quantization of human motions and learning of accurate movements. Biol. Cybern. 1998, 78, 307–318. [Google Scholar] [CrossRef] [PubMed]
- Park, G.R.; Kim, C. Constructing of optimal database structure by imitation learning based on evolutionary algorithm. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2698–2703. [Google Scholar]
- Shukla, A.; Billard, A. Coupled dynamical system based arm-hand grasping model for learning fast adaptation strategies. Robot. Auton. Syst. 2012, 60, 424–440. [Google Scholar] [CrossRef]
- Billard, A.; Calinon, S.; Dillmann, R.; Schaal, S. Robot Programming by Demonstration. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 48, pp. 1371–1394. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Su, H.; Qi, W.; Yang, C.; Aliverti, A.; Ferrigno, G.; De Momi, E. Deep Neural Network Approach in Human-Like Redundancy Optimization for Anthropomorphic Manipulators. IEEE Access 2019, 7, 124207–124216. [Google Scholar] [CrossRef]
- Floreano, D.; Ijspeert, A.J.; Schaal, S. Robotics and Neuroscience. Curr. Biol. 2014, 24, R910–R920. [Google Scholar] [CrossRef]
- Bae, J.H.; Yang, W.; Kim, D.; Oh, Y.; You, B.J.; Oh, S.R. Robotic arm control inspired by human muscle tension effect under the gravity. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1404–1411. [Google Scholar]
- Stefanovic, F.; Galiana, H.L. An adaptive spinal-like controller: Tunable biomimetic behavior for a robotic limb. BioMed. Eng. Online 2014, 13, 151. [Google Scholar] [CrossRef]
- Togo, S.; Kagawa, T.; Uno, Y. Uncontrolled Manifold Reference Feedback Control of Multi-Joint Robot Arms. Front. Comput. Neurosci. 2016, 10, 1–18. [Google Scholar] [CrossRef]
- Scholz, J.P.; Schöner, G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp. Brain Res. 1999, 126, 289–306. [Google Scholar] [CrossRef]
- Todorov, E.; Jordan, M.I. Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 2002, 5, 1226–1235. [Google Scholar] [CrossRef]
- Schaal, S. Learning Robot Control. In The handbook of Brain Theory and Neural Networks, 2nd ed.; MIT Press: Cambridge, UK, 2002; pp. 983–987. [Google Scholar]
- Kawato, M.; Furukawa, K.; Suzuki, R. A hierarchical neural-network model for control and learning of voluntary movement. Biol. Cybern. 1987, 57, 169–185. [Google Scholar] [CrossRef]
- Kawato, M. Internal models for motor control and trajectory planning. Curr. Opin. Neurobiol. 1999, 9, 718–727. [Google Scholar] [CrossRef]
- Milner, T.E. A model for the generation of movements requiring endpoint precision. Neuroscience 1992, 49, 487–496. [Google Scholar] [CrossRef]
- Kupferberg, A.; Huber, M.; Helfer, B.; Lenz, C.; Knoll, A.; Glasauer, S. Moving Just Like You: Motor Interference Depends on Similar Motility of Agent and Observer. PLoS ONE 2012, 7, e39637. [Google Scholar] [CrossRef] [PubMed]
- Dragan, A.D.; Lee, K.C.T.; Srinivasa, S.S. Legibility and predictability of robot motion. In Proceedings of the 2013 8th ACM/IEEE International Conference on Human-Robot Interaction (HRI), Tokyo, Japan, 3–6 March 2013; pp. 301–308. [Google Scholar]
- Bisio, A.; Sciutti, A.; Nori, F.; Metta, G.; Fadiga, L.; Sandini, G.; Pozzo, T. Motor Contagion during Human-Human and Human-Robot Interaction. PLoS ONE 2014, 9, e106172. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.J.; Yang, Y.S.; Guo, L.Y.; Wu, W.L.; Su, F.C. Differences in reaching performance between normal adults and patients post stroke a kinematic analysis. J. Med. Biol. Eng. 2008, 28, 53–58. [Google Scholar]
- Vaughan, J.; Rosenbaum, D.A.; Meulenbroek, R.G.J. Modeling Reaching and Manipulating in 2- and 3-D Workspaces: The Posture-Based Model. In Proceedings of the International Conference on Development and Learning (ICDL), Bloomington, IN, USA, 3 June 2006; Volume 1, pp. 3–8. [Google Scholar]
- Van Andel, C.J.; Wolterbeek, N.; Doorenbosch, C.A.M.; Veeger, D.H.E.J.; Harlaar, J. Complete 3D kinematics of upper extremity functional tasks. Gait Posture 2008, 27, 120–127. [Google Scholar] [CrossRef]
- Gates, D.H.; Walters, L.S.; Cowley, J.; Wilken, J.M.; Resnik, L. Range of Motion Requirements for Upper-Limb Activities of Daily Living. Am. J. Occup. Ther. 2016, 70, 7001350010. [Google Scholar] [CrossRef]
- Major, K.A.; Major, Z.Z.; Carbone, G.; Pîslă, A.; Vaida, C.; Gherman, B.; Pîslă, D.L. Ranges of motion as basis for robot-assisted poststroke rehabilitation. Hum. Vet. Med. 2016, 8, 200–204. [Google Scholar]
- Jurkojć, J.; Wodarski, P.; Michnik, R.; Nowakowska, K.; Bieniek, A.; Gzik, M. The upper limb motion deviation index: A new comprehensive index of upper limb motion pathology. Acta Bioeng. Biomech. 2017, 19, 175–185. [Google Scholar]
- Caggiano, V.; De Santis, A.; Siciliano, B.; Chianese, A. A biomimetic approach to mobility distribution for a human-like redundant arm. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20–22 February 2006; Volume 2006, pp. 393–398. [Google Scholar]
- Yang, W.; Bae, J.H.; Oh, Y.; Chong, N.Y.; You, B.J. Biologically inspired control for robotic arm using neural oscillator network. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St Louis, MO, USA, 10–15 October 2009; pp. 135–141. [Google Scholar]
- Artemiadis, P.K.; Katsiaris, P.T.; Kyriakopoulos, K.J. A biomimetic approach to inverse kinematics for a redundant robot arm. Auton. Robot. 2010, 29, 293–308. [Google Scholar] [CrossRef]
- Pattacini, U.; Nori, F.; Natale, L.; Metta, G.; Sandini, G. An experimental evaluation of a novel minimum-jerk cartesian controller for humanoid robots. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1668–1674. [Google Scholar]
- Bhattacharjee, T.; Oh, Y.; Bae, J.H.; Oh, S.R. Control design for human-like reaching movements using redundancy in robot arm-trunk systems. Int. J. Control Autom. Syst. 2011, 9, 1173–1186. [Google Scholar] [CrossRef]
- Strauss, S.; Heinke, D. A Robotics-Based Approach to Modeling of Choice Reaching Experiments on Visual Attention. Front. Psychol. 2012, 3, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Artemiadis, P. Closed-Form Inverse Kinematic Solution for Anthropomorphic Motion in Redundant Robot Arms. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2013. [Google Scholar]
- Xia, J.; Jiang, Z.; Liu, H.; Cai, H. Analytical inverse kinematic computation for anthropomorphic manipulator based on human-like motion optimization and maximum reachable region optimization. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 2292–2297. [Google Scholar]
- Liu, Z.; Hu, F.; Luo, D.; Wu, X. Learning arm movements of target reaching for humanoid robot. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 707–713. [Google Scholar]
- Xie, B.; Zhao, J. Handing Over Objects to Human in a Friendly and Comfortable Manner. Int. J. Hum. Robot. 2015, 12, 1550012-20. [Google Scholar] [CrossRef]
- Chen, W.; Xiong, C.; Yue, S. On Configuration Trajectory Formation in Spatiotemporal Profile for Reproducing Human Hand Reaching Movement. IEEE Trans. Cybern. 2016, 46, 804–816. [Google Scholar] [CrossRef]
- Zhao, J.; Wei, Y. A Novel Algorithm of Human-Like Motion Planning for Robotic Arms. Int. J. Humanoid Robot. 2017, 14, 1650023. [Google Scholar] [CrossRef]
- Alibeigi, M.; Rabiee, S.; Ahmadabadi, M.N. Inverse Kinematics Based Human Mimicking System using Skeletal Tracking Technology. J. Intell. Robot. Syst. 2017, 85, 27–45. [Google Scholar] [CrossRef]
- Su, H.; Enayati, N.; Vantadori, L.; Spinoglio, A.; Ferrigno, G.; De Momi, E. Online human-like redundancy optimization for tele-operated anthropomorphic manipulators. Int. J. Adv. Robot. Syst. 2018, 15, 172988141881469. [Google Scholar] [CrossRef]
- Stilman, M. Global Manipulation Planing in Robot Joint Space with Task Constraints. IEEE Trans. Robot. 2010, 26, 576–584. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).