Proximity Operations and Three Degree-of-Freedom Maneuvers Using the Smartphone Video Guidance Sensor

Abstract

This paper presents the first demonstration of NASA’s Smartphone Video Guidance Sensor (SVGS) as real-time position and attitude estimator for proximity and formation maneuvers. An optimal linear quadratic Gaussian controller was used, combining a linear quadratic regulator and a Kalman filter. The system was demonstrated controlling the 3-degree of freedom planar motion of the RINGS ground units (Resonant Inductive Near-field Generation Systems). A state-space model of the system’s 3-DOF motion dynamics was derived, and model parameters extracted using a system identification technique. The system’s motion control performance is experimentally demonstrated in both tracking and formation maneuvers. The results highlight the capabilities and performance of the Smartphone Video Guidance Sensor (SVGS) as a vision-based real-time position and attitude sensor for motion control, formation flight and proximity operations. A leader-follower formation maneuver approach is demonstrated, as well as position hold and path following.

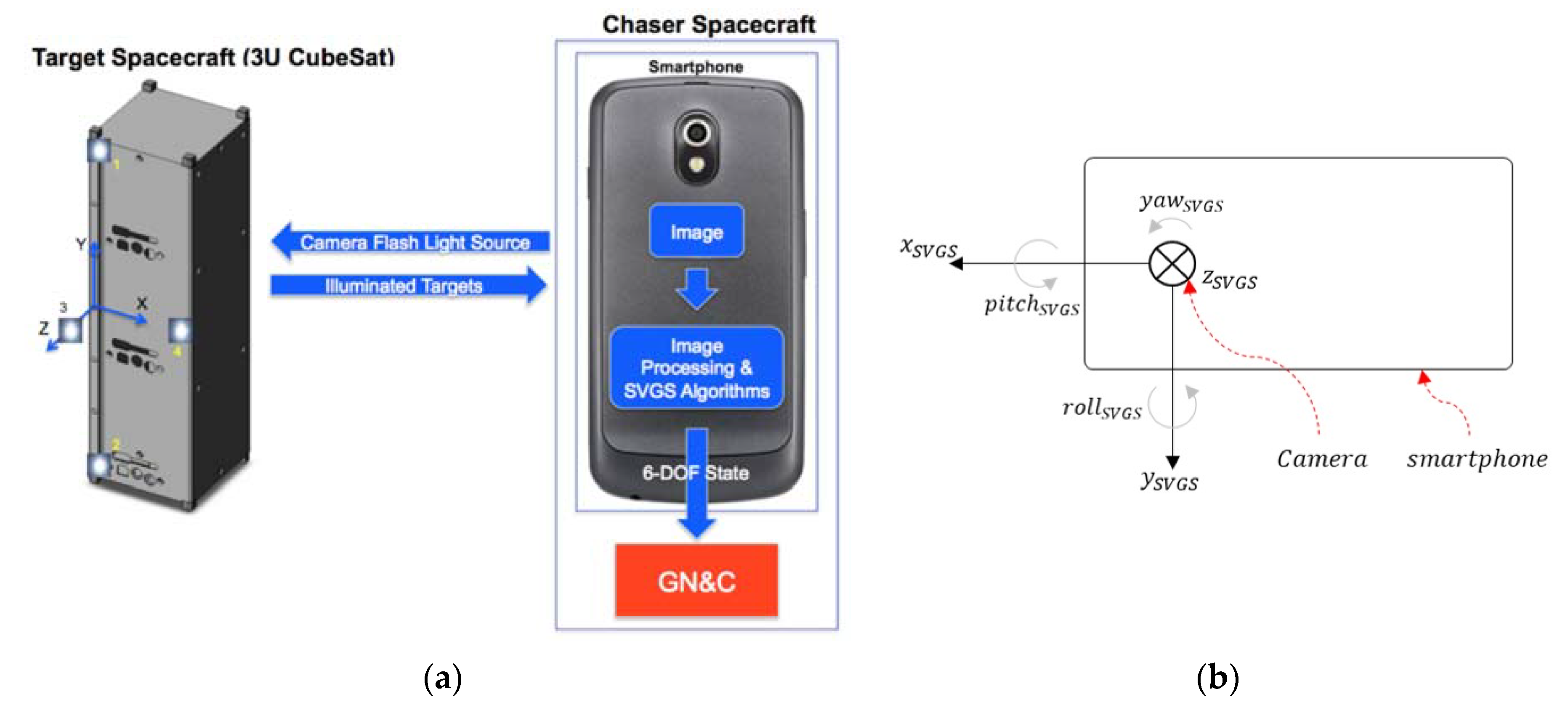
1. Introduction

The interest in formation maneuvers and distributed space missions has grown significantly in recent years [1,2,3,4,5,6], including follower formations and station keeping [7,8]. Proximity maneuvers rely on accurate and reliable position and attitude tracking between individual spacecraft involved [9]. The Smartphone Video Guidance Sensor (SVGS) [10,11,12] is a miniature, self-contained autonomous rendezvous and docking sensor developed at the NASA Marshall Space Flight Center using an Android-based smartphone to enable proximity operations and formation flight in small satellite platforms. SVGS determines the relative position and orientation of a moving target relative to a coordinate system attached to the phone by capturing an image of a set of illuminated targets mounted in a known pattern on the target spacecraft. The image is processed using a modification of algorithms originally developed for the Advanced Video Guidance Sensor (AVGS) [13,14,15,16,17], which successfully flew on the Demonstration for Autonomous Rendezvous Technology (DART) and Orbital Express missions [13,18]. SVGS is part of the development at NASA Marshall Space Flight Center of a low-cost, low mass, embedded sensor that will enable formation flight and navigation within proximity distance between small satellites in autonomous rendezvous and capture maneuvers. SVGS is capable of estimating the full six-degree-of-freedom relative position and attitude vector of a target in the near range (up to tens of meters) without incurring a computational burden on the motion platform controller, since the image processing and motion estimation algorithm are performed on the SVGS device itself. This paper demonstrates for the first time the capability and performance of SVGS as a real-time position and attitude sensor for proximity and formation maneuvers using the ground units of RINGS as a demonstration platform.

Vision-based navigation for spacecraft proximity operations is of significant current interest [19]. Figure 1a shows the operational concept of SVGS [10]. Estimating the target’s position and attitude relative to the camera’s coordinate system starts with image capture of a set of illuminated points in the target. The target’s 6-DOF position and attitude vector was estimated using geometric photogrammetry techniques [10,12,20]. Image processing and state estimation, outlined on Figure 2, take place onboard the SVGS device, avoiding additional computational burden on the motion control computer. SVGS output data are sent in each control cycle to the motion control computer through a serial communication link such as UART.

RINGS (Resonant Inductive Near-field Generation Systems) [21,22,23] are prototype systems developed to investigate electromagnetic formation flight and wireless power transfer between spacecraft. RINGS were designed to operate with the ISS free-flying robot SPHERES (Synchronized Position Hold, Engaged, Reorient, Experimental Satellites) [24], using the SPHERES metrology system to estimate RINGS position and attitude. SPHERES also act as motion control systems to regulate the degrees of freedom in RINGS not controlled by electromagnetic forces during formation flight maneuvers. Two RINGS-SPHERES assemblies are shown in Figure 3.

2. Materials and Methods

A 3-DOF planar motion platform (Figure 4a: design, Figure 4b: implementation) was developed for ground testing of RINGS using SVGS feedback. This section presents the system identification and controller design for motion control of SVGS–RINGS on a flat glass surface using ducted fans. The motion platform provides alternative actuation to the one provided on ISS by the free-flying robot attached to RINGS, enabling assessment of the functionality of RINGS using the ground units.

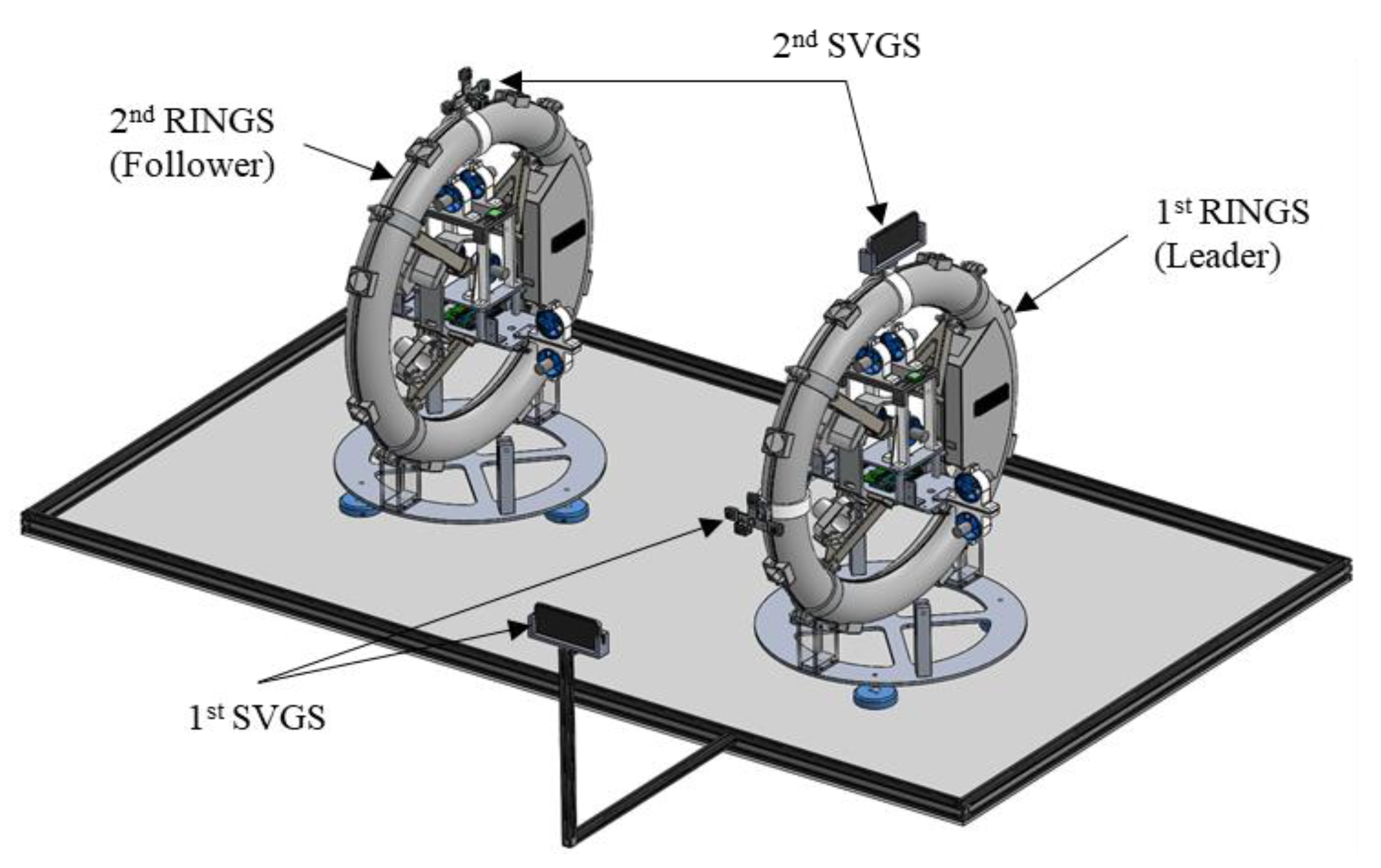
2.1. State-Space Model of the 3-DOF Ground Motion Platform

The translation and rotation dynamics of the RINGS assemblies are derived from the Newton–Euler equations [25,26]:

$$\mathit{F}=\dot{\mathit{P}}$$

(1)

$$\mathit{M}=\dot{\mathit{H}}$$

(2)

where $\mathit{F}$ is the resultant external force applied to the system, $\dot{\mathit{P}}$ the rate of change of linear momentum, $\mathit{M}$ the sum of external torques, and $\dot{\mathit{H}}$ the corresponding rate of change in angular momentum. For a rigid-body rotating about the center of mass, linear and angular momentums can be expressed as $\mathit{P}=m\mathit{v}$ and ${\mathit{H}}_c={\mathit{I}}_c\mathit{\omega }$, where $\mathit{v}$ is the linear velocity and $\mathit{\omega }$ the angular velocity vectors of the system. The Newton–Euler equations can therefore be written as:

$$\left[\begin{array}{cc}\mathit{m}& 0\\ 0& {\mathit{I}}_c\end{array}\right]\left\{\begin{array}{c}\dot{\mathit{v}}\\ \dot{\mathit{\omega }}\end{array}\right\}=\left(\begin{array}{c}\mathit{F}\\ \mathit{M}\end{array}\right)+\left(\begin{array}{c}0\\ -\mathit{\omega }\times {\mathit{I}}_c\mathit{\omega }\end{array}\right)$$

(3)

where $\mathit{m}$ is the mass matrix, ${\mathit{I}}_c$ the mass moment of inertia, $\dot{\mathit{v}}$ the linear acceleration vector of the center of mass, and $\dot{\mathit{\omega }}$ the angular acceleration vector. Since the motion is planar, the angular momentum can be simplified into ${\mathit{H}}_c={\mathit{I}}_c\dot{\theta }$, and the Newton–Euler equations can then be:

$$\left(\begin{array}{c}{I}_z\ddot{\theta }\\ m\ddot{x}\\ m\ddot{y}\end{array}\right)=\left(\begin{array}{c}{M}_z\\ F_x\\ F_y\end{array}\right)$$

(4)

where x, y, θ are two translational and one attitude coordinates that describe the planar motion of the 3-DOF platform relative to the inertial frame. This corresponds to the linear time-invariant state-space model {A,B,C,D} with state vector: $\mathit{x}\left(t\right)={\left\{\begin{array}{cccccc}\theta & \dot{\theta }& x& \dot{x}& y& \dot{y}\end{array}\right\}}^T$, as described in Section 2.2:

$$\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+\mathit{B}\mathit{u}\left(t\right)$$

(5)

$$\mathit{y}\left(t\right)=\mathit{C}\mathit{x}\left(t\right)+\mathit{D}\mathit{u}\left(t\right)$$

(6)

2.2. System Identification of the 3-DOF Motion Dynamics

A system identification procedure was used to experimentally identify the unknown parameters in the state-space model (Equations (5) and (6)). Chirp excitation signals were used as speed commands to the ducted fans that control forces and torques applied to the system. The sinusoidal chirp function has frequency $f\left(t\right)$ (Equation (7)), where $f_0$ and $f_1$ are the initial and final frequencies of the chirp signal, and the rate of frequency change is $k=\frac{f_1-f_0}{T}$, where $T$ is the total duration of the signal:

$$f\left(t\right)=f_0+kt$$

(7)

The chirp signal covers the desired frequency range of the system (0.1 to 2 Hz) and has a total duration of 10 s. Experimental measurements for displacement and velocity are shown in Figure 5.

A prediction error method was used to estimate the unknown system parameters of the state-space model (Equations (5) and (6)) based on experimental input-output sequences. SVGS provides an update of the six-state position and attitude vector on each control cycle (every 35 msec in this case). The position and attitude vector is sent as a serial data packet to the local motion control computer, where it is decoded to the corresponding floating point values. The system identification procedure uses the forces and torques directly available from linear regression curves of the fan thrusters as input, and uses the six-state position and attitude vector available from SVGS as output. Position and attitude measurements (x, y, θ) and linear velocity estimates (based on finite differences) were obtained from the SVGS sensor, while a MEMS gyroscope was used to collect angular velocity data. While SVGS provides good estimates of attitude (roll angle in this case), the estimation of angular velocity from SVGS measurements by finite differences is noisy compared to MEMS gyro measurements. Each motion control platform uses a MEMS gyro to estimate angular velocity in real time.

Figure 5a shows linear displacement predictions compared to measured response, and Figure 5b linear velocity estimation of the same axis, compared to finite-difference velocity estimation using SVGS measurements. The procedure was performed for all three degrees-of-freedom of the planar motion dynamics, achieving model fits of 97.2% and 79.8% in linear position and velocity estimation, and 96.4% and 88.64% for angular position and velocity estimations (θ axis). The estimated state-space model of the 3-DOF motion dynamics of the RINGS motion platform is:

$$\begin{array}{cc}\left\{\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\\ {\dot{x}}_5\\ {\dot{x}}_6\end{array}\right\}& =\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 0& -0.009521& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& -0.03117& 0& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& -0.03238\end{array}\right]\left\{\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\end{array}\right\}\\ & \hspace{1em}\hspace{1em} +\left[\begin{array}{ccc}0& 0& 0\\ 0.02374& 0& 0\\ 0& 0& 0\\ 0& 0.00663& 0\\ 0& 0& 0\\ 0& 0& 0.005813\end{array}\right]\left\{\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right\}\end{array}$$

(8)

$$\left\{\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\\ y_5\\ y_6\end{array}\right\}=\left[\begin{array}{cccccc}0.5693& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 2.14& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 2.145& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]\left\{\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\end{array}\right\}$$

(9)

The state-space matrices are computed by a prediction error method (PEM), a gradient-based optimization that calculates model parameters from a set of input–output sequences; the PEM method and system identification procedure is described in detail in [27]. The C matrix in Equation (9) is initialized as a unity matrix, but is later updated by the gradient descent algorithm to provide minimum mean square error to the predicted output for the given input–output data sets.

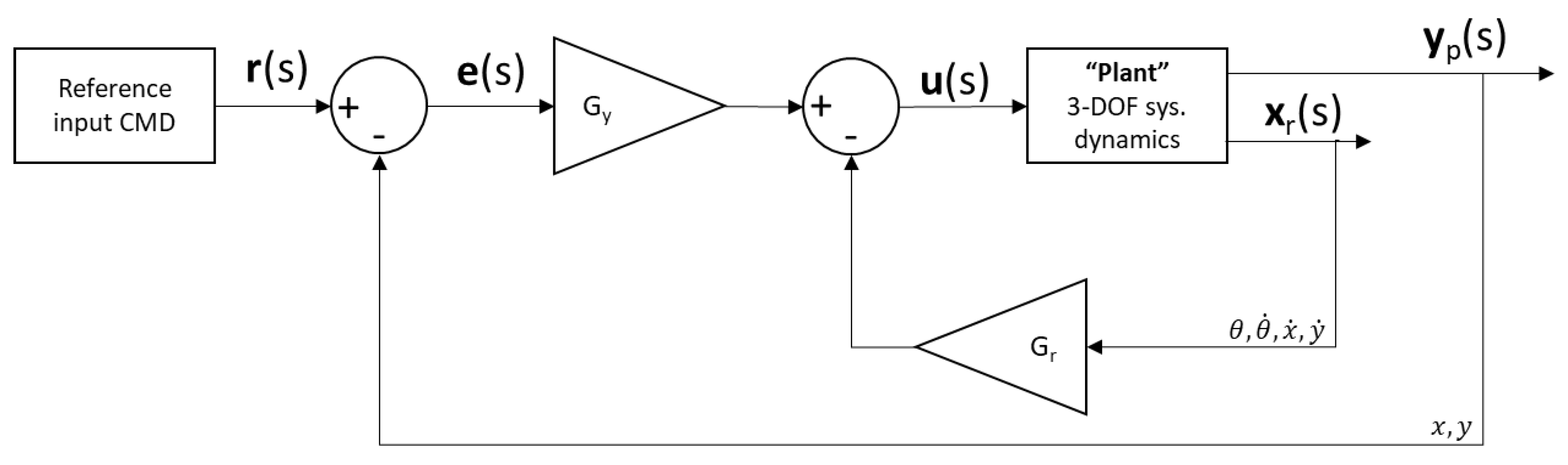
2.3. 3-Degree of Freedom Motion Control via LQG-Servo

A linear quadratic Gaussian (LQG) full-state feedback controller [28,29,30] was designed based on the experimental model of the 3-DOF dynamics (Equations (8) and (9)). The LQG-servo combines a linear quadratic regulator with an optimal state estimator (Kalman filter). The formulation of a linear quadratic (LQ) servo controller starts with the typical LQR cost function:

$$J=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\left[{\mathit{x}}^T\left(t\right)\mathit{Q}\mathit{x}\left(t\right)+{\mathit{u}}^T\left(t\right)\mathit{R}\mathit{u}\left(t\right)\right]dt$$

(10)

An LQR controller with diagonal Q and R matrices considers the minimization of (Equation (10)) for the state equations (Equations (5) and (6)):

$$J=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\left[q_{\theta }{\theta }^2+q_x{x}^2+q_y{y}^2+q_{\dot{\theta }}{\dot{\theta }}^2+q_{\dot{x}}{\dot{x}}^2+q_{\dot{y}}{\dot{y}}^2+{\rho }_{\theta }{u}_{\theta }^2+{\rho }_x{u}_x^2+{\rho }_y{u}_y^2\right]dt$$

(11)

where the semi-positive definite state weighting matrix $\mathit{Q}$ is:

$$\mathit{Q}={\mathit{N}}^T\mathit{N}=\left[\begin{array}{cccccc}{q}_{\theta }& 0& 0& 0& 0& 0\\ 0& q_{\dot{\theta }}& 0& 0& 0& 0\\ 0& 0& q_x& 0& 0& 0\\ 0& 0& 0& q_{\dot{x}}& 0& 0\\ 0& 0& 0& 0& q_y& 0\\ 0& 0& 0& 0& 0& q_{\dot{y}}\end{array}\right]$$

(12)

where $\mathit{N}$ is a diagonal matrix with entries equal to the square root of the diagonal entries of $\mathit{Q}$, $q_i$ are the weight penalties to each state, and the control weighting matrix, $\mathit{R}$ is:

$$\mathit{R}=\left[\begin{array}{ccc}{\rho }_{\theta }& 0& 0\\ 0& {\rho }_x& 0\\ 0& 0& {\rho }_y\end{array}\right]$$

(13)

If the system ($\mathit{A}$, $\mathit{B}$) is stabilizable and ($\mathit{A}$, $\mathit{N}$) is detectable, a unique solution $\mathit{K}$ to the optimal control problem can be found by solving the Algebraic Riccati equation:

$$\mathit{K}\mathit{A}+{\mathit{A}}^T\mathit{K}+\mathit{Q}-\mathit{K}\mathit{B}{\mathit{R}}^{-1}{\mathit{B}}^T\mathit{K}=\mathbf{0}$$

(14)

The optimal control gain matrix $\mathit{G}$ is:

$$\mathit{G}={\mathit{R}}^{-1}{\mathit{B}}^T\mathit{K}$$

(15)

A critically damped response (damping ratio ~1) was desired, to provide fast rising and settling times with minimal overshoot and zero steady state error. The effects of varying the state weighting matrix Q and control weighting matrix R are shown in Figure 6, for one degree of freedom (x-axis).

Similar analyses were done to tune the other two axes of motion (y- and $\theta$-axis). The full state weighting matrix $\mathit{Q}$ and control weighting matrix $\mathit{R}$ were finally chosen as:

$$\mathit{Q}={10}^3\ast \left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0& 0\\ 0& 0& 8& 0& 0& 0\\ 0& 0& 0& 100& 0& 0\\ 0& 0& 0& 0& 8& 0\\ 0& 0& 0& 0& 0& 100\end{array}\right];$$

(16)

$$\mathit{R}=\left[\begin{array}{ccc}0.3& 0& 0\\ 0& 0.6& 0\\ 0& 0& 0.6\end{array}\right]$$

(17)

Larger penalties correspond to the velocity states of the system ($q_{\dot{\theta }}$, $q_{\dot{x}}$, and $q_{\dot{y}}$) to restriction velocity in all three axes to prevent overshooting. The optimal control gain matrix $\mathit{G}$ was then:

$$\mathit{G}=\left[\begin{array}{cccccc}57.7& 134.5& 0& 0& 0& 0\\ 0& 0& 115.5& 444.2& 0& 0\\ 0& 0& 0& 0& 115.5& 448.8\end{array}\right]$$

(18)

To implement a tracking LQ-servo from the LQR control law, the control gain matrix is decomposed to separate the gains for the tracking states, ${\mathit{G}}_y$, from the gains of the regulated states, ${\mathit{G}}_r$, such that $\mathit{G}=\left[\begin{array}{cc}{\mathit{G}}_y& {\mathit{G}}_r\end{array}\right]$:

$${\mathit{G}}_y=\left[\begin{array}{cc}0& 0\\ 115.5& 0\\ 0& 115.5\end{array}\right];$$

(19)

$${\mathit{G}}_r=\left[\begin{array}{cccc}57.7& 134.5& 0& 0\\ 0& 0& 444.2& 0\\ 0& 0& 0& 448.8\end{array}\right]$$

(20)

The states $\mathit{x}\left(t\right)$ are divided into output vector ${\mathit{y}}_p\left(t\right)={\left\{\begin{array}{cc}x& y\end{array}\right\}}^T$ and the remaining state vector ${\mathit{x}}_r\left(t\right)={\left\{\begin{array}{cccc}\theta & \dot{\theta }& \dot{x}& \dot{y}\end{array}\right\}}^T$. The optimal feedback control vector $\mathit{u}\left(t\right)={\left\{\begin{array}{ccc}{u}_{\theta }& u_x& u_y\end{array}\right\}}^T$ for the LQ-servo formulation is:

$$\mathit{u}\left(t\right)={\mathit{G}}_y\mathit{e}\left(t\right)-{\mathit{G}}_r{\mathit{x}}_r\left(t\right)$$

(21)

where the tracking error is $\mathit{e}\left(t\right)=\mathit{r}\left(t\right)-{\mathit{y}}_p\left(t\right)$, and the reference command $\mathit{r}\left(t\right)={\left\{\begin{array}{cc}{x}_d& y_d\end{array}\right\}}^T$. Figure 7 shows a block diagram of the proposed 3-degree of freedom LQ-servo system.

SVGS provides only relative position and attitude information. Implementation of a full-state feedback law requires a real-time velocity estimation. Finite differences provide noisy velocity estimates, and low-pass filtering the corresponding estimates introduces delays that can significantly affect stability and performance. A Kalman state estimator [31,32,33] was implemented to provide robust estimation of the non-measurable states, and integrated with the LQ-servo control law as a model-based compensator. A state-space model of the 3-DOF planar motion system subject to both process and measurement noise is:

$$\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+\mathit{B}\mathit{u}\left(t\right)+\mathit{P}\mathit{\xi }\left(t\right);$$

(22)

$$\mathit{y}\left(t\right)=\mathit{C}\mathit{x}\left(t\right)+\mathit{\theta }\left(t\right)$$

(23)

where $\mathit{\xi }\left(t\right)$ and $\mathit{\theta }\left(t\right)$ are process and sensor noise, respectively. It is assumed that the statistical properties of the process and measuring device do not change with time, therefore a steady-state Kalman filter can be used. A design parameter, $\mu$, was added to the Kalman formulation to shape the response of the filter. The state estimation error is $\mathit{\epsilon }\left(t\right)=\mathit{x}\left(t\right)-\widehat{\mathit{x}}\left(t\right)$, and the cost function $J$ to be minimized is defined as the sum of error variances, i.e., the trace of the error covariance matrix:

$$J=tr\left(E\left\{\mathit{\epsilon }\left(t\right){\mathit{\epsilon }}^T\left(t\right)\right\}\right)={\displaystyle \sum }_{i=1}^{n}E\left\{{\left(x_i\left(t\right)-{\widehat{x}}_i\left(t\right)\right)}^2\right\}$$

(24)

If ($\mathit{A}$, $\mathit{P}$) is stabilizable and ($\mathit{A}$, $\mathit{C}$) detectable, a unique solution to the optimal error covariance matrix $\Sigma \ge \mathbf{0}$ can be found by solving the filter algebraic Riccati equation:

$$\mathit{A}\Sigma +\Sigma A^{\mathrm{T}}+P{P}^{\mathrm{T}}-\frac{1}{\mu }\Sigma C^{\mathrm{T}}\mathit{C}\Sigma =\mathbf{0}$$

(25)

The noise and error statistics of SVGS were estimated using accuracy assessment experiments, in which SVGS measurements were compared to known motion profiles in each axes of motion. The “true position” was estimated from encoder readings from a computer controlled motion stage used to apply known motion profiles to a SVGS target while collecting SVGS readings. By these means, the statistics of sensor noise (mean, standard deviation, variance and covariance) were estimated. The sensor noise covariance matrix $\mathit{\Theta }$ is:

$$\mathit{\Theta }=E\left\{\mathit{\theta }\left(t\right){\mathit{\theta }}^T\left(t\right)\right\}=\mu \mathit{I}\delta \left(t-\tau \right)$$

(26)

where the diagonal entries represent the variance ${\sigma }_{x_i}^2$, and the off-diagonal entries the covariance ${\sigma }_{x_i}{\sigma }_{{\dot{x}}_i}$ between state variables. Both were estimated from SVGS accuracy assessment tests, yielding:

$$\mathit{\Theta }=\mu \left[\begin{array}{cccccc}{\sigma }_{\theta }^2& {\sigma }_{\dot{\theta }}{\sigma }_{\theta }& {\sigma }_x{\sigma }_{\theta }& {\sigma }_{\dot{x}}{\sigma }_{\theta }& {\sigma }_y{\sigma }_{\theta }& {\sigma }_{\dot{y}}{\sigma }_{\theta }\\ {\sigma }_{\theta }{\sigma }_{\dot{\theta }}& {\sigma }_{\dot{\theta }}^2& {\sigma }_x{\sigma }_{\dot{\theta }}& {\sigma }_{\dot{x}}{\sigma }_{\dot{\theta }}& {\sigma }_y{\sigma }_{\dot{\theta }}& {\sigma }_{\dot{y}}{\sigma }_{\dot{\theta }}\\ {\sigma }_x{\sigma }_{\theta }& {\sigma }_x{\sigma }_{\dot{\theta }}& {\sigma }_x^2& {\sigma }_x{\sigma }_{\dot{x}}& {\sigma }_x{\sigma }_y& {\sigma }_x{\sigma }_{\dot{y}}\\ {\sigma }_{\dot{x}}{\sigma }_{\theta }& {\sigma }_{\dot{x}}{\sigma }_{\dot{\theta }}& {\sigma }_{\dot{x}}{\sigma }_x& {\sigma }_{\dot{x}}^2& {\sigma }_{\dot{x}}{\sigma }_y& {\sigma }_{\dot{x}}{\sigma }_{\dot{y}}\\ {\sigma }_{\theta }{\sigma }_y& {\sigma }_{\dot{\theta }}{\sigma }_y& {\sigma }_x{\sigma }_y& {\sigma }_{\dot{x}}{\sigma }_y& {\sigma }_y^2& {\sigma }_{\dot{y}}{\sigma }_y\\ {\sigma }_{\dot{y}}{\sigma }_{\theta }& {\sigma }_{\dot{y}}{\sigma }_{\dot{\theta }}& {\sigma }_x{\sigma }_{\dot{y}}& {\sigma }_{\dot{x}}{\sigma }_{\dot{y}}& {\sigma }_{\dot{y}}{\sigma }_y& {\sigma }_{\dot{y}}^2\end{array}\right]$$

(27)

$$\mathit{\Theta }=\mu \left[\begin{array}{cccccc}0.000027& -0.000003& 0& 0& 0& 0\\ -0.000003& 0.000016& 0& 0& 0& 0\\ 0& 0& 0.006& -0.0069& 0& 0\\ 0& 0& -0.0069& 0.0552& 0& 0\\ 0& 0& 0& 0& 0.0051& 0.0003\\ 0& 0& 0& 0& 0.0003& 0.0405\end{array}\right]$$

(28)

Angular position is measured in radians, while linear position state variables ($x$ and $y)$ are in meters. The process noise covariance matrix $\Xi$ is defined as:

$$\Xi =\Psi {\mathit{I}}_6=\Psi \left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]$$

(29)

where $\mu$ and $\Psi$ are design parameters used to shape the performance of the model-based state estimator: small values of $\mu$ in Equation (28) represent “accurate” sensor measurements, leading to larger values of filter gain. ψ is a tuning parameter: the chosen value was selected by optimizing performance of the nominal Kalman filter so that it gives less weight to noisy measurements. After tuning, these parameters were selected as μ = 1.6 and $\Psi$. = 0.01, respectively. After solving Equation (25) for the optimal error covariance matrix, the gain matrix of the Kalman filter $L$ is:

$$\mathit{L}=\frac{1}{\mu }\Sigma C^{\mathrm{T}}=\left[\begin{array}{cccccc}0.0381& 0.05& 0& 0& 0& 0\\ 0.1088& 0.998& 0& 0& 0& 0\\ 0& 0& 0.1194& 0.0346& 0& 0\\ 0& 0& 0.494& 0.2782& 0& 0\\ 0& 0& 0& 0& 0.1188& 0.0316\\ 0& 0& 0& 0& 0.281& 0.2957\end{array}\right].$$

(30)

The state estimate ${\widehat{\mathit{x}}}_n$ based on the Kalman filter is a discrete-time process based on the model matrices, the previous state estimate ${\widehat{\mathit{x}}}_{n-1}$ and the control effort ${\mathit{u}}_n$:

$${\widehat{\mathit{x}}}_n={\mathit{A}}_d{\widehat{\mathit{x}}}_{n-1}+{\mathit{B}}_d{\mathit{u}}_n+\mathit{L}\left({\mathit{y}}_n-{\mathit{C}}_d{\widehat{\mathit{x}}}_{n-1}-{\mathit{D}}_d{\mathit{u}}_n\right)$$

(31)

where ${\mathit{A}}_d$, ${\mathit{B}}_d$, ${\mathit{C}}_d$, and ${\mathit{D}}_d$ are the matrices of the discretized state-space model at a nominal sampling rate of 50 msec. The estimated output ${\widehat{\mathit{y}}}_n$ based on the state estimator is:

$${\widehat{\mathit{y}}}_n={\mathit{C}}_d{\widehat{\mathit{x}}}_n$$

(32)

Figure 8 shows the proposed LQG-servo controller, where the estimated plant output is ${\widehat{\mathit{y}}}_p\left(t\right)={\left\{\begin{array}{cc}\widehat{x}& \widehat{y}\end{array}\right\}}^T$, and the estimated remaining state vector is ${\widehat{\mathit{x}}}_r\left(t\right)={\left\{\begin{array}{cccc}\widehat{\theta }& \widehat{\dot{\theta }}& \widehat{\dot{x}}& \widehat{\dot{y}}\end{array}\right\}}^T$.

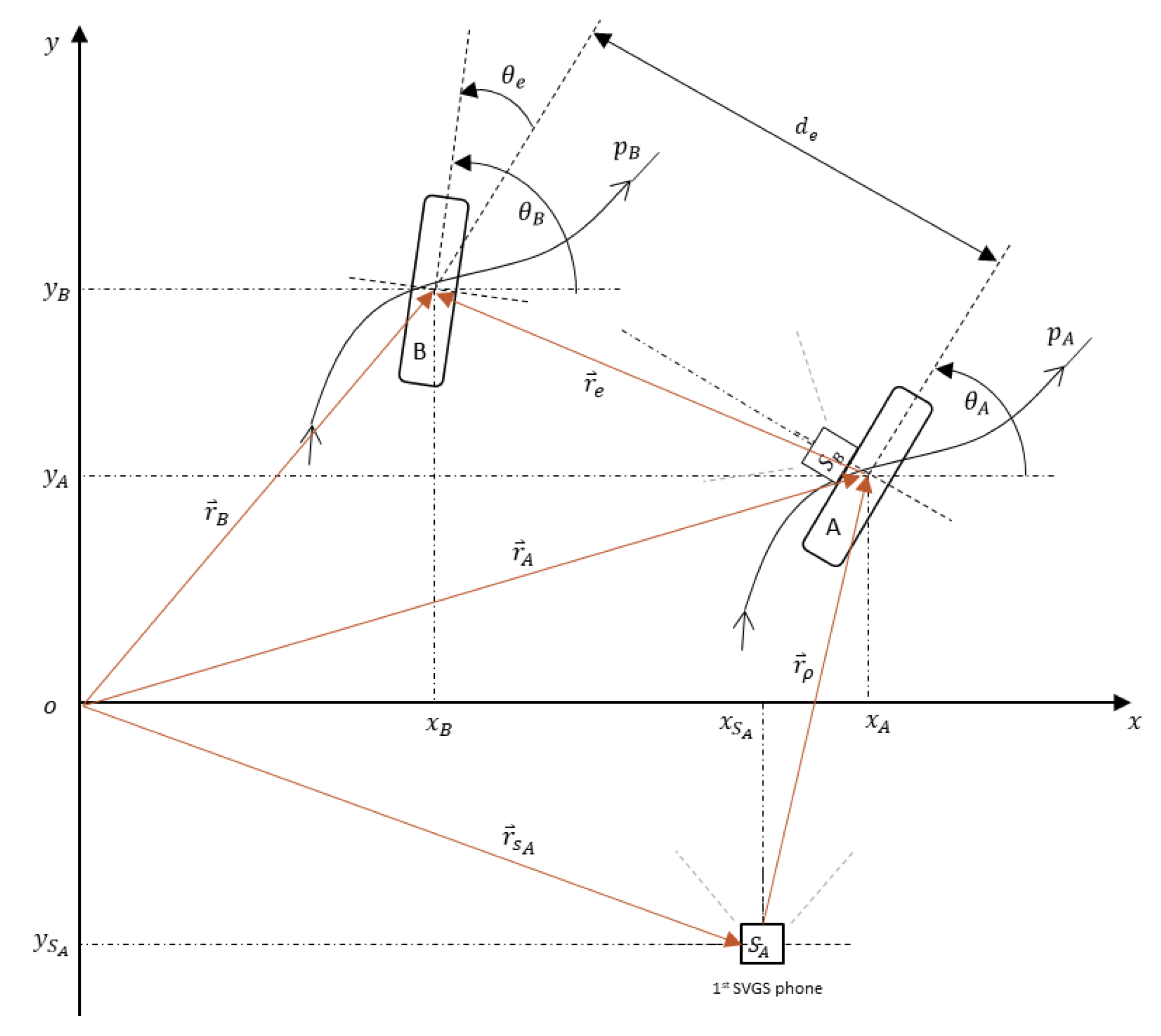
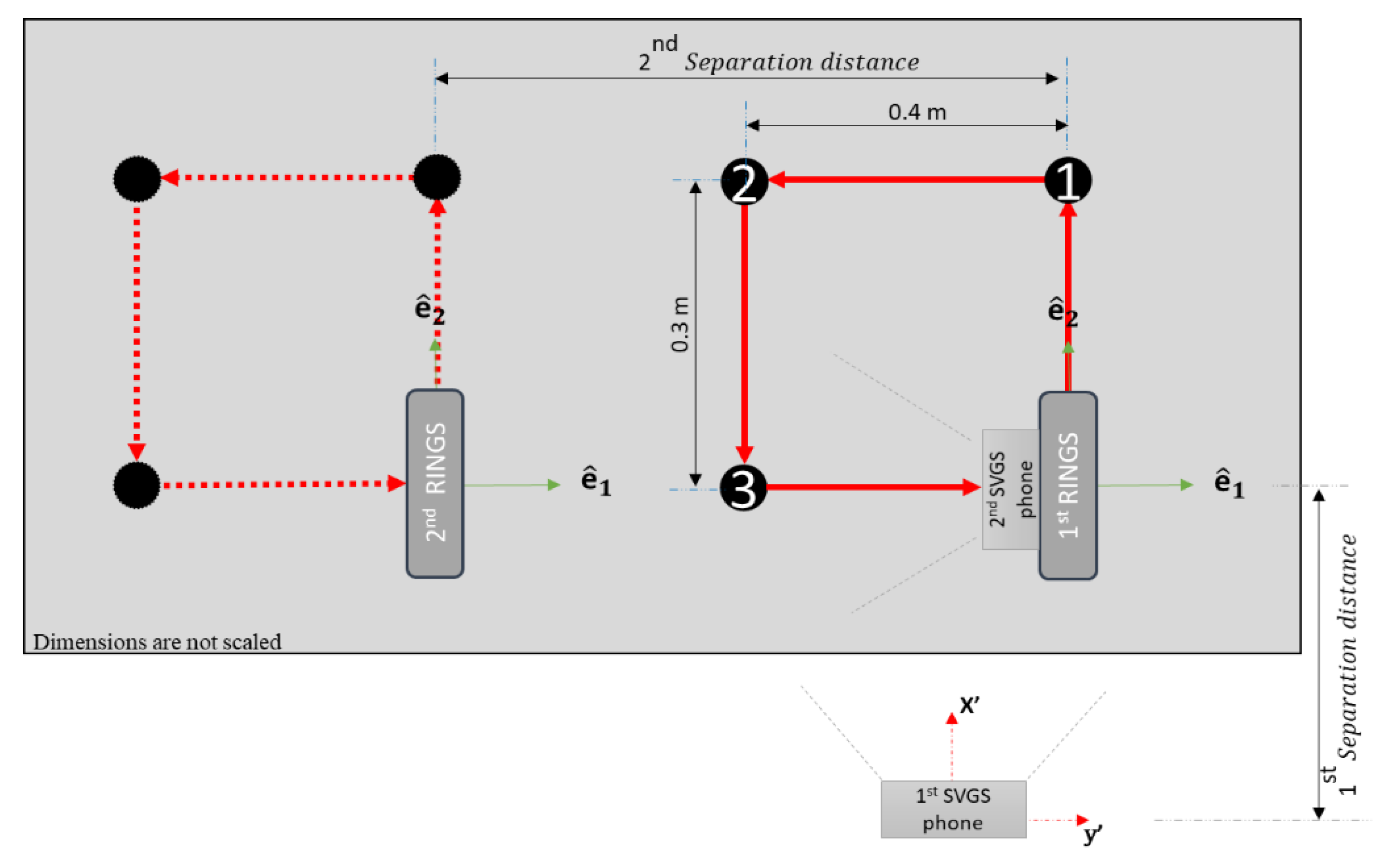
2.4. Path Following and Formation Maneuvers

Figure 9 shows the experimental setup to demonstrate the use of SVGS in path following and formation maneuvers. The setup consists of two RINGS units integrated to their 3-DOF motion control platforms using SVGS. In this implementation, the first SVGS device provides position and attitude information to the RINGS leader relative to the inertial frame, while the second SVGS unit provides motion information to the RINGS follower relative to the leader. The workspace has a dimension of 2.1 × 1.2 m. In both units, SVGS data are transmitted to the corresponding 3-DOF motion control computer using Bluetooth serial links.

The path following problem for a leader-follower formation maneuver is illustrated in Figure 10, where the leader tracks a predefined path, while the follower keeps a fixed coaxial distance to the leader (d_e) while holding a constant relative attitude (θ_e).

The position of both spacecraft relative to the coordinate system attached to the workspace is defined as follows. The first SVGS device is fixed relative to the ground, and its position (${\stackrel{\rightharpoonup }{\mathit{r}}}_{{\mathit{s}}_{\mathit{A}}}$) is

$${\stackrel{\rightharpoonup }{\mathit{r}}}_{{\mathit{s}}_{\mathit{A}}}={\mathit{x}}_{{\mathit{s}}_{\mathit{A}}}\widehat{\mathit{i}}+{\mathit{y}}_{{\mathit{s}}_{\mathit{A}}}\widehat{\mathit{j}}$$

(33)

where ${\mathit{x}}_{{\mathit{s}}_{\mathit{A}}}$ and ${\mathit{y}}_{{\mathit{s}}_{\mathit{A}}}$ are constants given by the fixed location of SVGS relative to the origin. The position of the leader spacecraft ${\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{A}}$ is defined as:

$${\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{A}}={\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{s}}{}_{\mathit{A}}+{\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{\rho }}=\left({\mathit{x}}_{{\mathit{s}}_{\mathit{A}}}+{\mathit{r}}_{{\mathit{\rho }}_{\mathit{x}}}\right)\widehat{\mathit{i}}+\left({\mathit{y}}_{{\mathit{s}}_{\mathit{A}}}+{\mathit{r}}_{{\mathit{\rho }}_{\mathit{y}}}\right)\widehat{\mathit{j}}$$

(34)

where ${\mathit{r}}_{{\mathit{\rho }}_{\mathit{x}}}$ and ${\mathit{r}}_{{\mathit{\rho }}_{\mathit{y}}}$ are position data for the x and z states from the first SVGS device, respectively. The position of the follower spacecraft (${\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{B}}$) can be now defined as:

$${\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{B}}={\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{A}}+{\stackrel{\rightharpoonup }{\mathit{r}}}_{\mathit{e}}=\left({\mathit{x}}_{{\mathit{s}}_{\mathit{A}}}+{\mathit{r}}_{{\mathit{\rho }}_{\mathit{x}}}-{\mathit{r}}_{{\mathit{e}}_{\mathit{x}}}\right)\widehat{\mathit{i}}+\left({\mathit{y}}_{{\mathit{s}}_{\mathit{A}}}+{\mathit{r}}_{{\mathit{\rho }}_{\mathit{y}}}+{\mathit{r}}_{{\mathit{e}}_{\mathit{y}}}\right)\widehat{\mathit{j}}$$

(35)

where ${\mathit{r}}_{{\mathit{e}}_{\mathit{y}}}$ and ${\mathit{r}}_{{\mathit{e}}_{\mathit{x}}}$ are position data for the x and z states from the second SVGS device, respectively. During all maneuvers, the motion of both leader and follower spacecraft are controlled using the SVGS devices relative to this coordinate frame.

3. Results

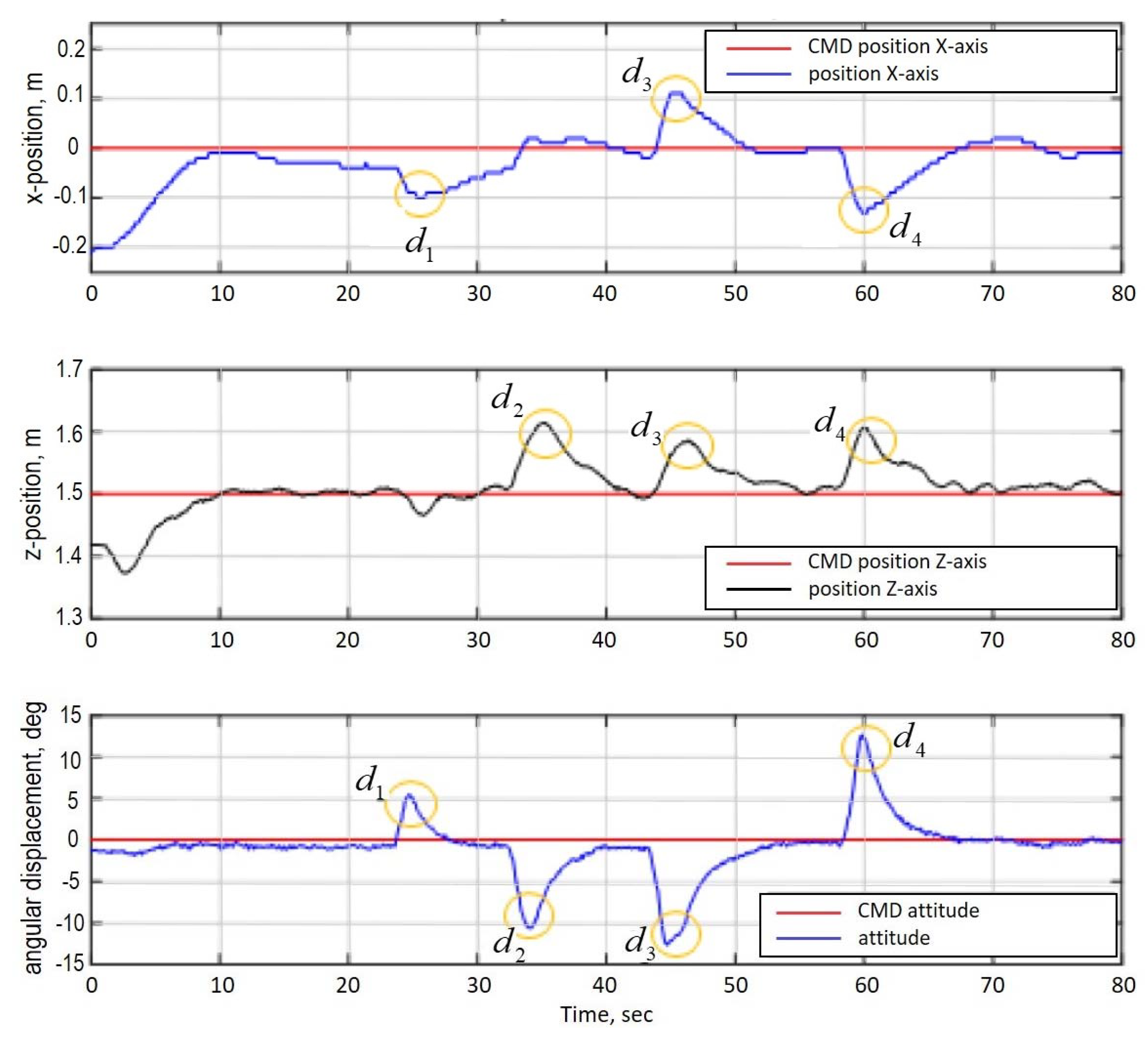
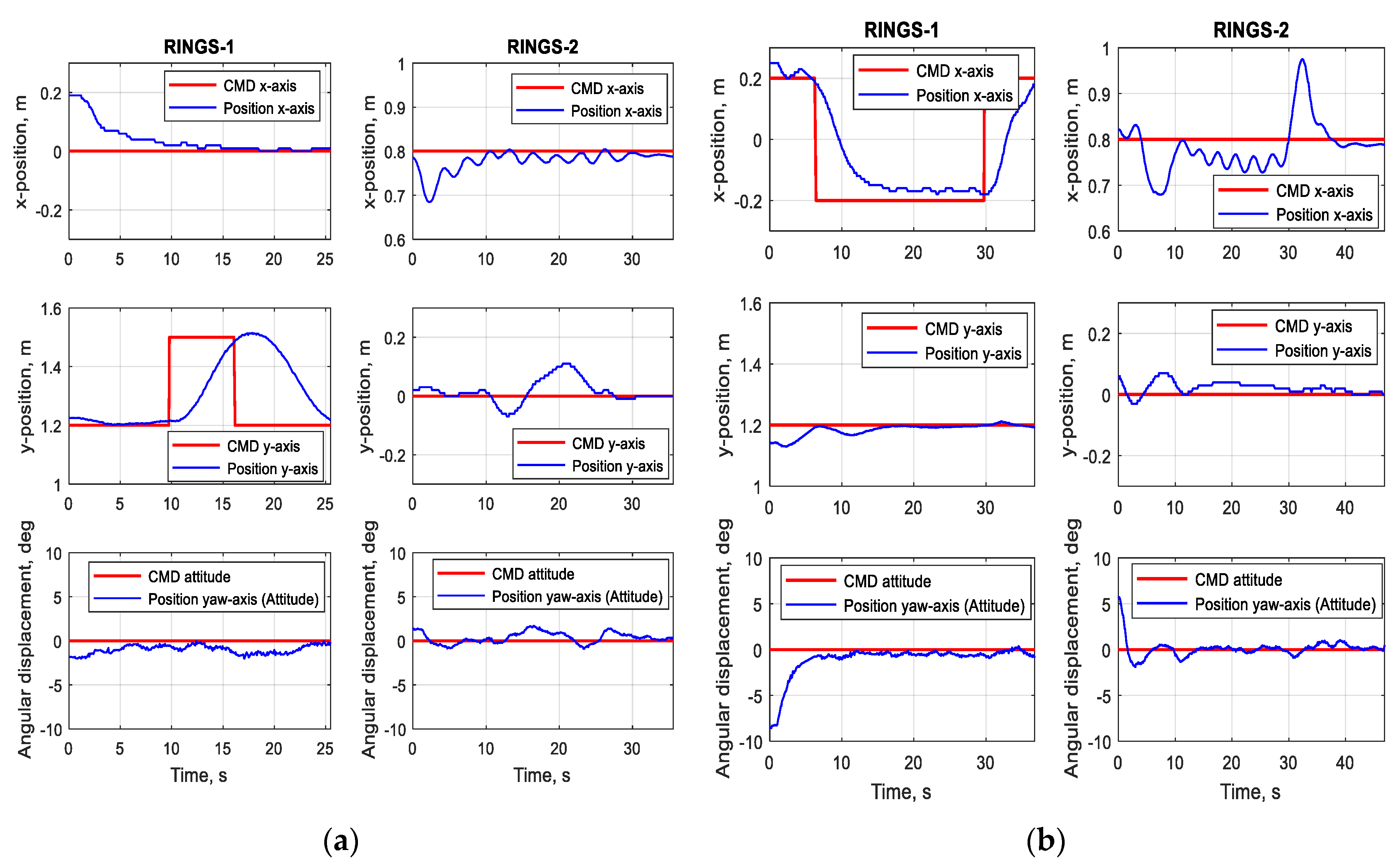
3.1. Response to Single Axis and Dual Axes Commands, and Response to External Disturbances

SVGS is only functional in proximity operations: it requires line of sight and a clear picture of all four illuminated points in the target to provide an estimate of the 6-DOF position and attitude state. The preconditions to use SVGS need to be met by an additional navigation system until proximity is reached.

Figure 11a shows the time response of the 3-DOF closed-loop system using SVGS feedback during a single axis maneuver: a 0.5 m pulse command in x-axis while the remaining 2-DOFs (z and θ) were kept constant at 1.5 m and 0°, respectively. The command signals are internally generated by the motion controller, whereas position and attitude output is measured by SVGS. Figure 11b shows the 3-DOF closed-loop response by SVGS feedback in a dual-axis maneuver: a 0.5 m pulse command (starting at −0.25 m in the x-axis) and 0.3 m pulse commands (starting at 1.35 m in the z-axis) in x- and z-axis, respectively, while the remaining DOF (θ) is regulated at 0°.

Figure 12 compares the SVGS velocity estimation using filtered finite differences vs. Kalman velocity estimates for all 3-DOFs. The Kalman filter leads to a significant improvement in velocity estimates compared to finite difference followed by a first order filter. This is important since the LQG-servo controller gives high penalties to the velocity states to achieve higher control gain values, thereby requiring lower error/noise in the velocity estimates. The 3-DOF motion controller uses x- and z-axes velocity estimates from the Kalman filter and MEMS gyro measurements for angular rate.

Figure 13 shows the response of each degree-of-freedom (x, y, θ) to a position hold command (red trace) in the presence of externally applied disturbances. Four external disturbances d₁, d₂, d₃, and d₄, were applied as external forces and torques at approximately 25, 34, 45, and 60 sec., respectively, illustrating the ability of the LQG-servo controller to regulate disturbances that do not exceed the limits of the available thruster forces.

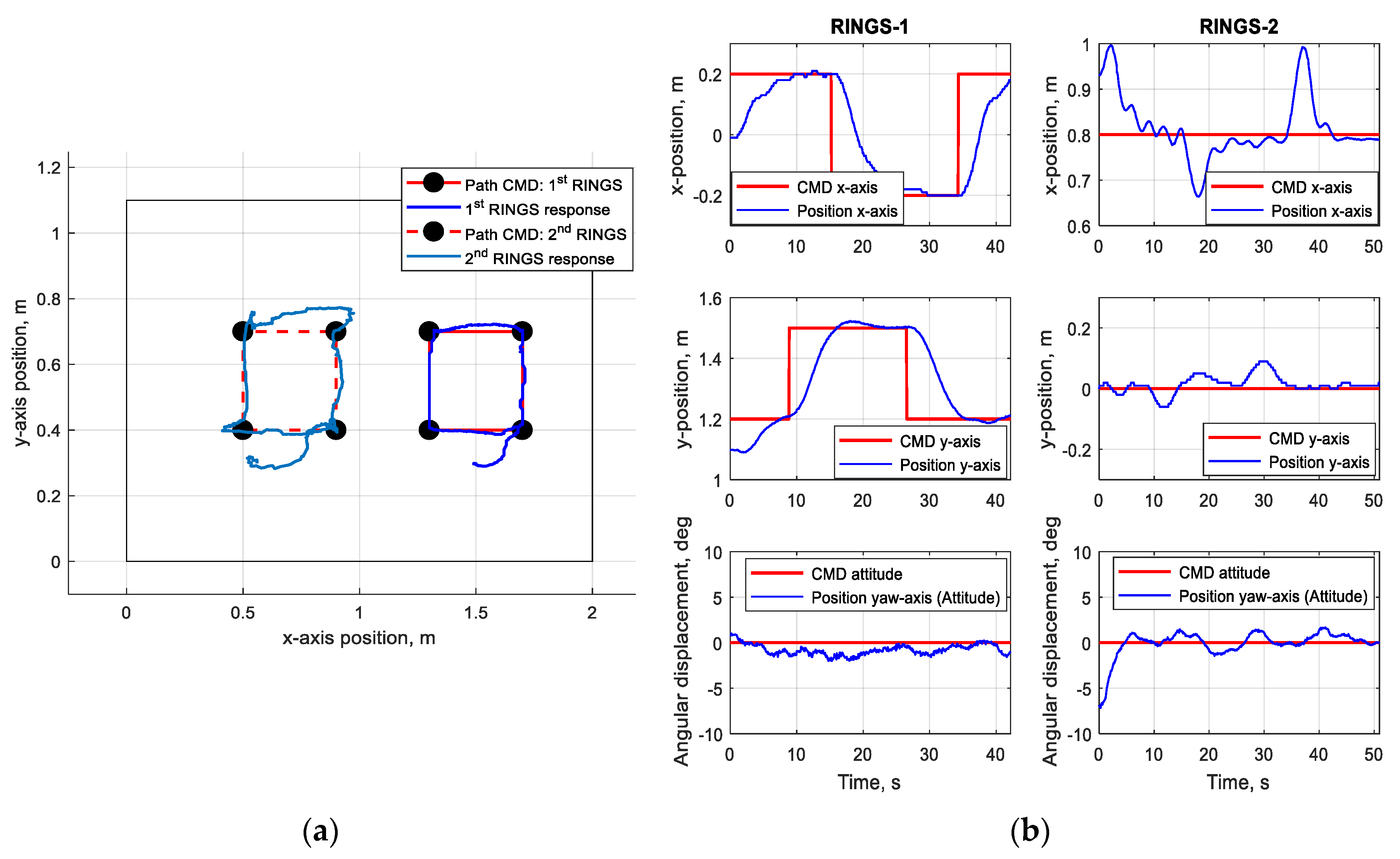
3.2. Performance in Proximity Operations and Path Following Maneuvers

To assess the capabilities of SVGS in formation maneuvers, three different experiments were implemented: coaxial, colinear, and combined maneuvers, where the leader spacecraft follows a predefined path, while the follower tracks the leader’s path while keeping a constant coaxial distance and constant attitude relative to the leader. The maneuvers were chosen to demonstrate RINGS functionality in support of their proposed science missions on the ISS using the RINGS ground units, which implied motion control while keeping a zero relative attitude angle. This also enables to assume that the dynamics of the slave RINGS are pure translation, since the motion control system is actively regulating the attitude angle at zero, and the master unit is keeping zero attitude relative to the inertial frame.

First path following maneuver. The leader RINGS moves from the home position to waypoint “1” and then returns home. The follower RINGS is kept colinear and coaxial relative to the master, at a constant separation distance of 0.8 m, as shown in Figure 14.

Second path following maneuver. The leader RINGS moves 0.4 m from the home position to waypoint “1” and then returns home along the same line. The follower RINGS is kept coaxial relative to the master at a constant separation distance of 0.8 m, as shown in Figure 15.

Figure 16a shows the time domain performance of the first path following maneuver: a 0.3 m pulse command of 6 s of duration is applied on the Y-axis while the X and θ axes are regulated at zero. Figure 16b shows the time domain performance of the second path following maneuver: a 0.4 m pulse command of 12 s duration is applied on the X-axis while the Y axes is regulated at 1.2 m and the θ axes is regulated at zero degrees.

Third path following maneuver. The leader spacecraft follows a predetermined path (Figure 17) from the home position to waypoints “1”, “2”, “3” and back home, while the follower keeps a constant separation distance and zero-degree attitude relative to the leader. The experimental performance is shown in Figure 18a,b.

4. Discussion

The single and dual axis tracking capabilities of a real-time trajectory control system based on SVGS are demonstrated in Figure 11. Figure 13 shows the ability of the SVGS-based LQG-Servo system to reject external disturbances, while Figure 12 illustrates the performance of the SVGS Kalman filter to provide robust velocity estimates in all three axes of motion (X, Y, θ).

The performance of the SVGS-based system in proximity operations and path following maneuvers is shown in Section 3.2 using three basic maneuvers (Figure 1, Figure 14b, Figure 15b and Figure 18a). The X, Y, θ trajectories of both leader and follower spacecraft for all three maneuvers are shown in Figure 16 and Figure 18b. In all three maneuvers, the leader (RINGS-1) shows good tracking of the desired path. The follower (RINGS-2) was also capable of maintaining good overall performance in keeping the desired motion relative to the leader; however, the response of the follower relative to the workspace coordinate frame shows less accurate tracking and overshoot at the edges of the commanded paths compared to the leader, reflecting the fact that the absolute position of the follower is calculated from the position states of the leader: any positioning errors in the leader therefore accumulate and reflect in the absolute position errors of the follower. The overall performance shown in Section 3 underscores the ability of the SVGS-based system to successfully control multi-axis position and attitude in proximity operations. SVGS is particularly well suited for cooperative maneuvers since it provides a direct measurement of the relative position and attitude between two agents within the line of sight of each other, as required in operations such as docking, landing and formation maneuvers. SVGS does not burden the motion control computer with the computation of the position-attitude state estimate since the SVGS algorithm runs on a separate auxiliary system, enabling implementation in real-time at closed loop rates up to 20 updates/s with the hardware used in this study.

5. Conclusions

This paper presents the first demonstration of real-time motion control, proximity operations and formation maneuvers using SVGS as position and attitude sensor. SVGS is a compact, self-contained sensor for relative position and attitude that can be used for a variety of robotic proximity operations (docking, landing, line of sight approach) and not just in space guidance and control, as the Advanced Video Guidance Sensor (AVGS, [13,14,15,16]) has been. The demonstration was implemented on the 3-DOF planar motion platform of two RINGS ground units. Test results on glass table experiments demonstrate the capabilities of the proposed approach to perform 3-axial motion control of a single unit and formation maneuvers of two units using SVGS and the proposed LQG-servo controller. A Kalman filter based on the noise statistics of SVGS was used to provide improved x- and z-velocity estimates, compared to filtered finite difference velocity estimates. The process noise model used in the Kalman filter design provides successful results within the accuracy required in this application. Three different path following maneuvers were implemented to demonstrate performance of SVGS and the proposed LQG-servo controller in providing accurate tracking and regulation in three degrees of freedom.

SVGS has the potential to be used in a variety of robotic applications where proximity operations such as landing, coordination of agents or docking is needed, and can therefore be of potential use to a larger community outside aerospace applications. The error statistics of SVGS enable its incorporation (by synthesis of a Kalman estimator) in advanced motion control systems for navigation and guidance. Future work will investigate the performance of the integrated SVGS with LQG-servo control in the demonstration of electromagnet formation flight (EMFF) of RINGS using SVGS, where reduction in power consumption by the use of electromagnetic motion-assist will be investigated.