A Novel 3-URU Architecture with Actuators on the Base: Kinematics and Singularity Analysis

1. Introduction

Parallel manipulators (PMs) feature two rigid bodies, one fixed (base) and the other mobile (platform), connected to one another through a number of kinematic chains (limbs). Translational PMs (TPMs) are 3-degrees-of-freedom (DOF) PMs whose platform can perform only spatial translations. TPMs are a particular family of lower-mobility PMs. DELTA-like architectures [1,2] are the most known and affirmed [3] TPM architectures, even though many (see [4,5,6,7,8] for instances and for further Refs.) other TPM architectures have been proposed and studied in the literature.

Lower-mobility PMs must be preferred to 6-degrees-of-freedom (6-DOF) PMs in all the industrial manipulation tasks that do not require a general spatial motion since they have simpler and faster architectures. Unfortunately, among the usual PM singularities [9,10] that fall inside the operational space, lower-mobility PMs may have particular singularities, named “constraint singularities” [11], where they can change their operating mode. Thus, the identification of architectures with wide regions of the operational space that are free from singularities, which is central for PMs, becomes somehow more complex and critical in the design of lover-mobility PMs.

TPMs with 3-URU1 architectures [8] have been studied by many researchers. Such architectures feature three limbs of Universal-Revolute-Universal (URU) type that simultaneously connect the platform to the base. The ones proposed in the literature [12,13,14] have the R-pairs, adjacent to the base, as actuated joints or, when presented as a spatial mechanism without actuated joints [11], have the axes of the three R-pairs adjacent to the base (to the platform) that are coplanar and with a common intersection. Changing the actuated joints and/or modifying the base (the platform) geometry affect the behavior of the machine in a substantial manner as regard both to the load redistribution among the links and to the functional aspects (e.g., useful workspace sizes and location).

The novelty of the translational 3-URU proposed in this paper, hereafter named LaMaViP 3-URU, stands in the fact that:

(i)

the actuators are on the base even though the actuated joints are not on the base,

(ii)

in each URU limb, the actuated R-pair is the one not adjacent to the base in the U-joint adjacent to the base, and

(iii)

it has a particular base (platform) geometry where the axes of the three R-pairs adjacent to the base (to the platform) share a common intersection point but are not coplanar.

Putting the actuators on the base allows a significant reduction of the mobile masses, thus promising good dynamic performances, and makes the remaining part of the limb a simple chain constituted by only passive R-pairs.

This paper addresses the kinematics and the singularity analysis of the LaMaViP 3-URU and proves the effectiveness of the new design choices by demonstrating that the adopted design choices provide wide free-from-singularity regions of the operational space. The results presented here form the technical basis for a patent application of the author.

The organization of the paper is as follows. Section 2 presents the LaMaViP 3-URU together with some background concepts and the adopted notations. Section 3 analyzes the instantaneous kinematics and identifies the singularity loci. Then, Section 4 discusses the results and draws the conclusions.

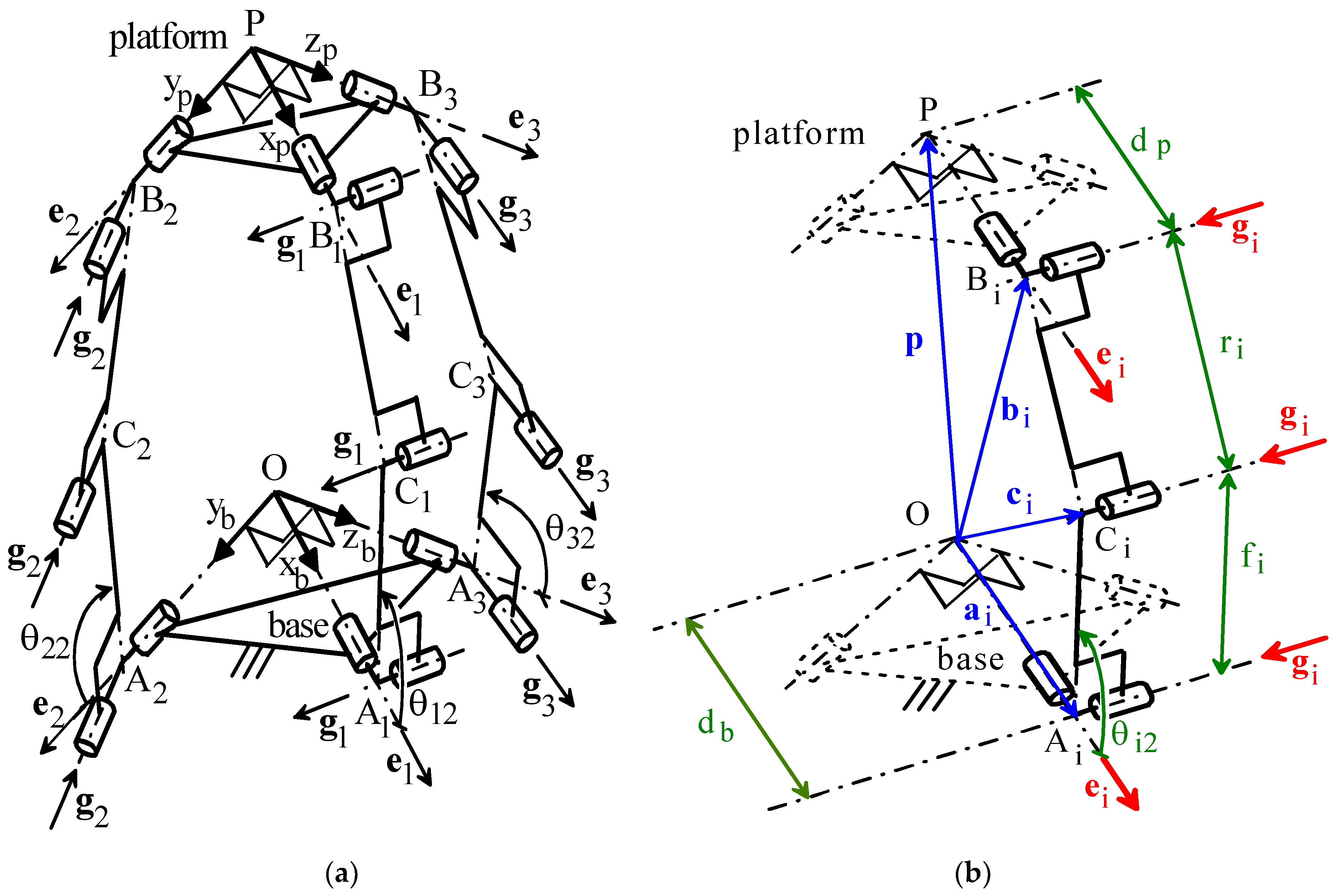
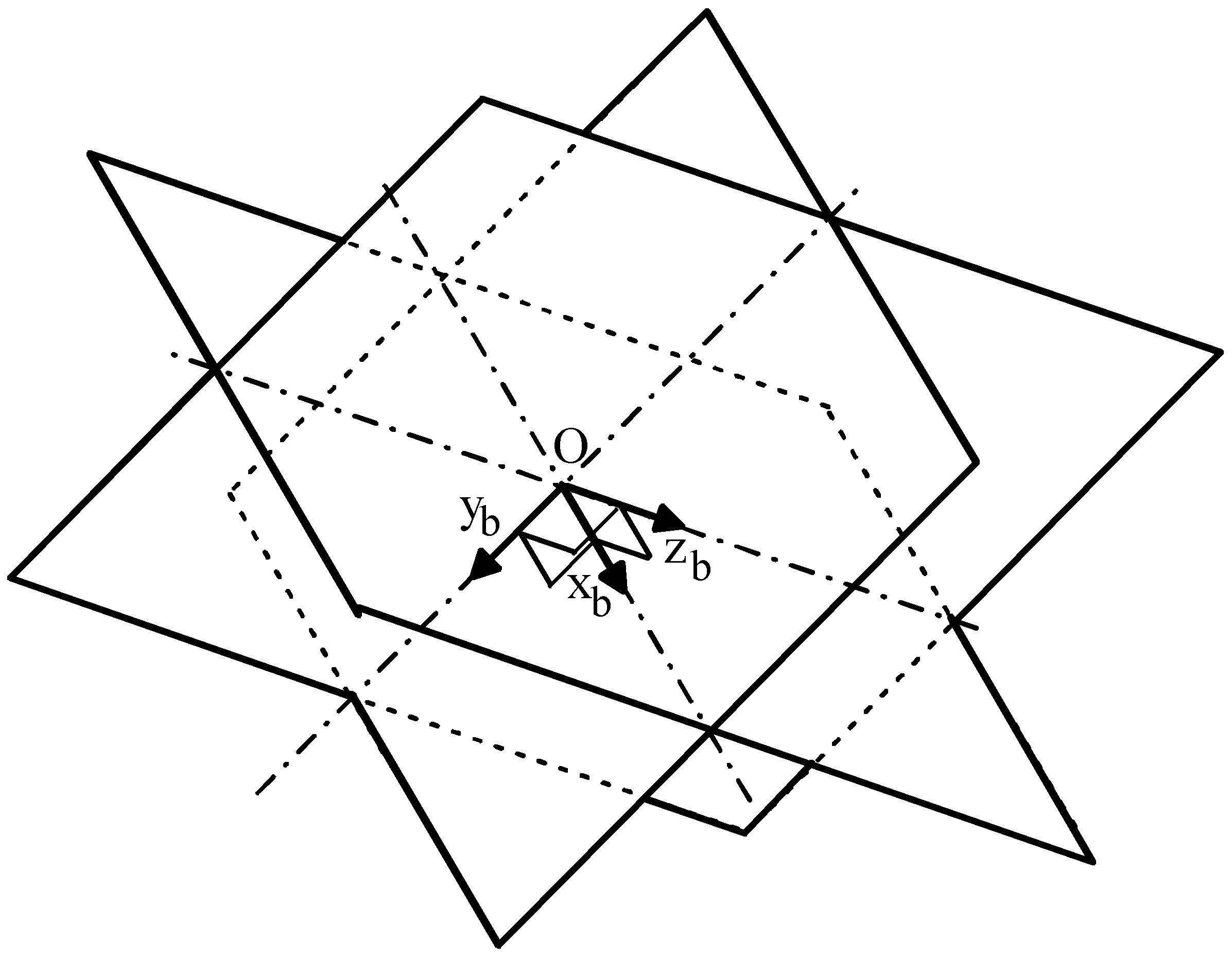
2. The Novel Translational 3-URU

Out of constraint singularities [8,11], a 3-URU architecture is a TPM if it is manufactured and assembled so that in each URU limb the axes of the two ending R-pairs are parallel to one another and the axes of the three intermediate R-pairs are all parallel [8].

Figure 1 shows the reference geometry for a LaMaViP 3-URU. The geometry of Figure 1 has the axes of the three R-pairs adjacent to the base (to the platform) that are mutually orthogonal and share a common intersection point.

With reference to Figure 1,

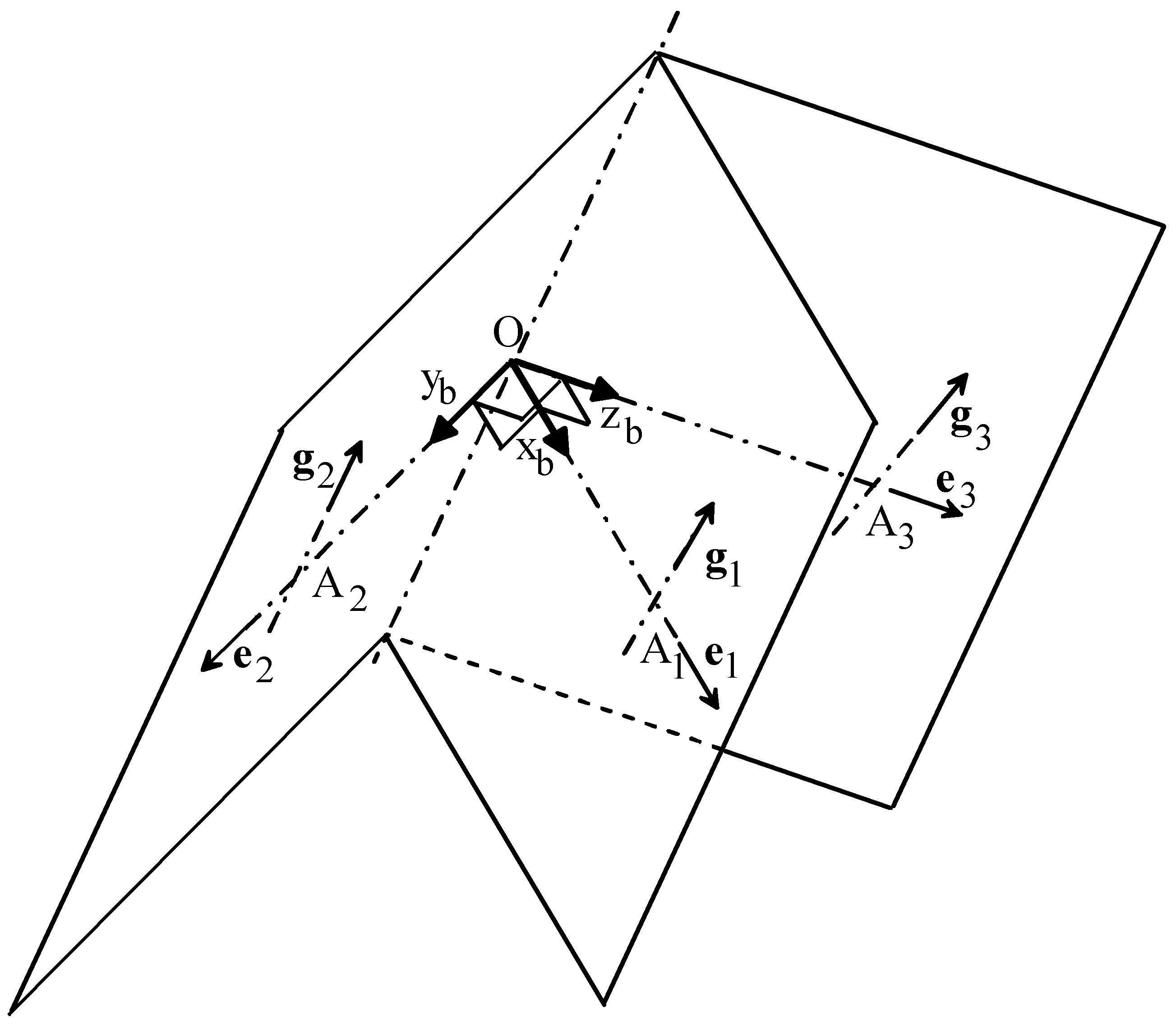
• Ox_by_bz_b and Px_py_pz_p are two Cartesian references fixed to the base and to the platform, respectively; without losing generality, these two references have been chosen with the homologous coordinate axes that are parallel to one another2;
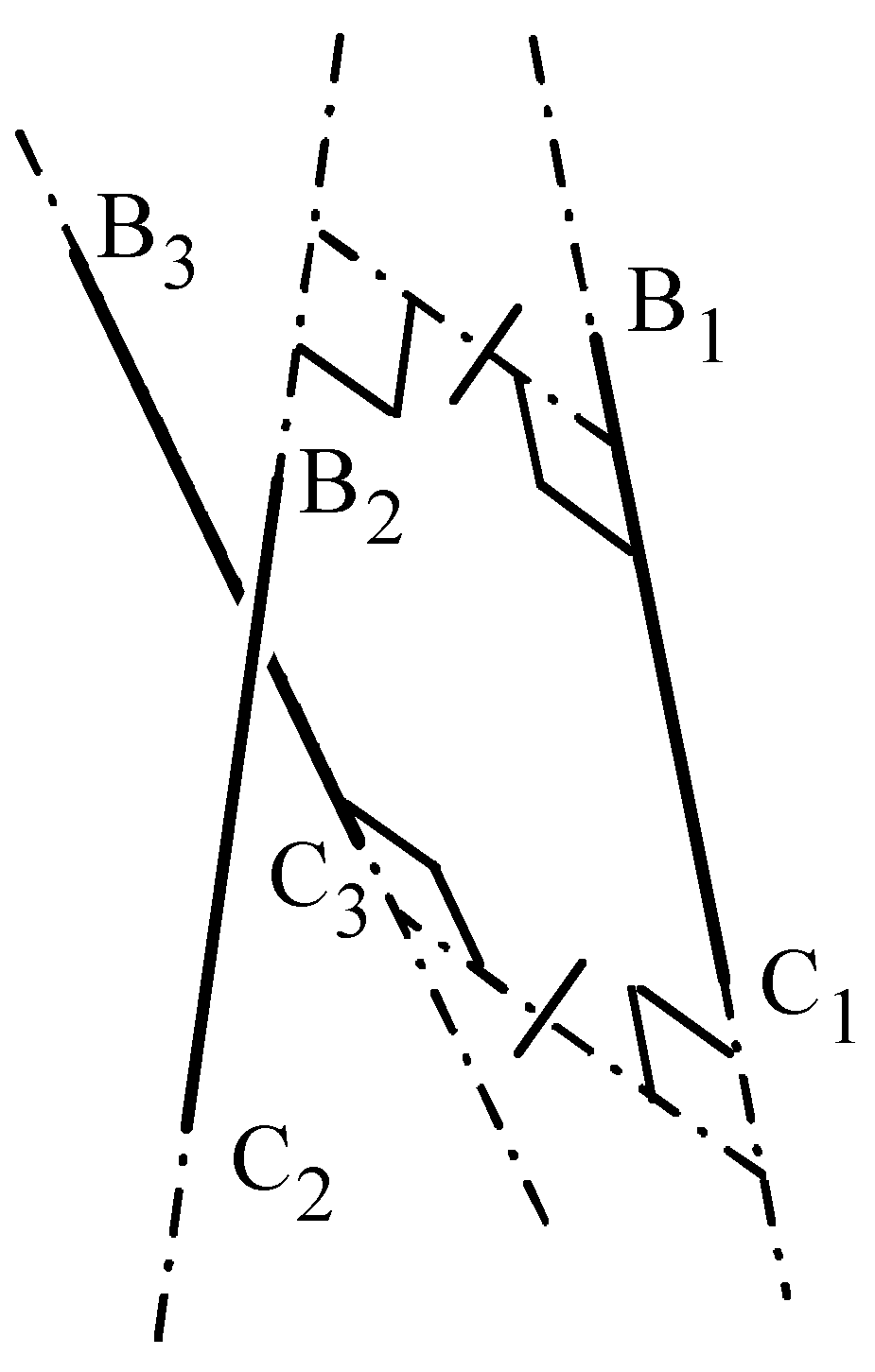
• A_i (B_i) for i = 1,2,3 are the centers of the U joints adjacent to the base (to the platform);
• without losing generality [15], in the i-th limb, i=1,2,3, the points A_i and B_i are assumed to lie on the same plane perpendicular to the axes of the three intermediate R-pairs; such plane intersects at C_i the axis of the R-pair between the two U-joints;
• e₁, e₂, and e₃ are unit vectors of the coordinate axes x_b, y_b, and z_b (x_p, y_p, and z_p), respectively, and, at the same time, unit vectors of the three R-pair axes fixed to the base (to the platform);
• g_i, i = 1, 2, 3, is the unit vector parallel to the axes of the three intermediate R-pairs of the i-th limb.

Moreover, the following definition/choices are introduced:

• d_p = B₁P = B₂P = B₃P;
• d_b = A₁O = A₂O = A₃O;
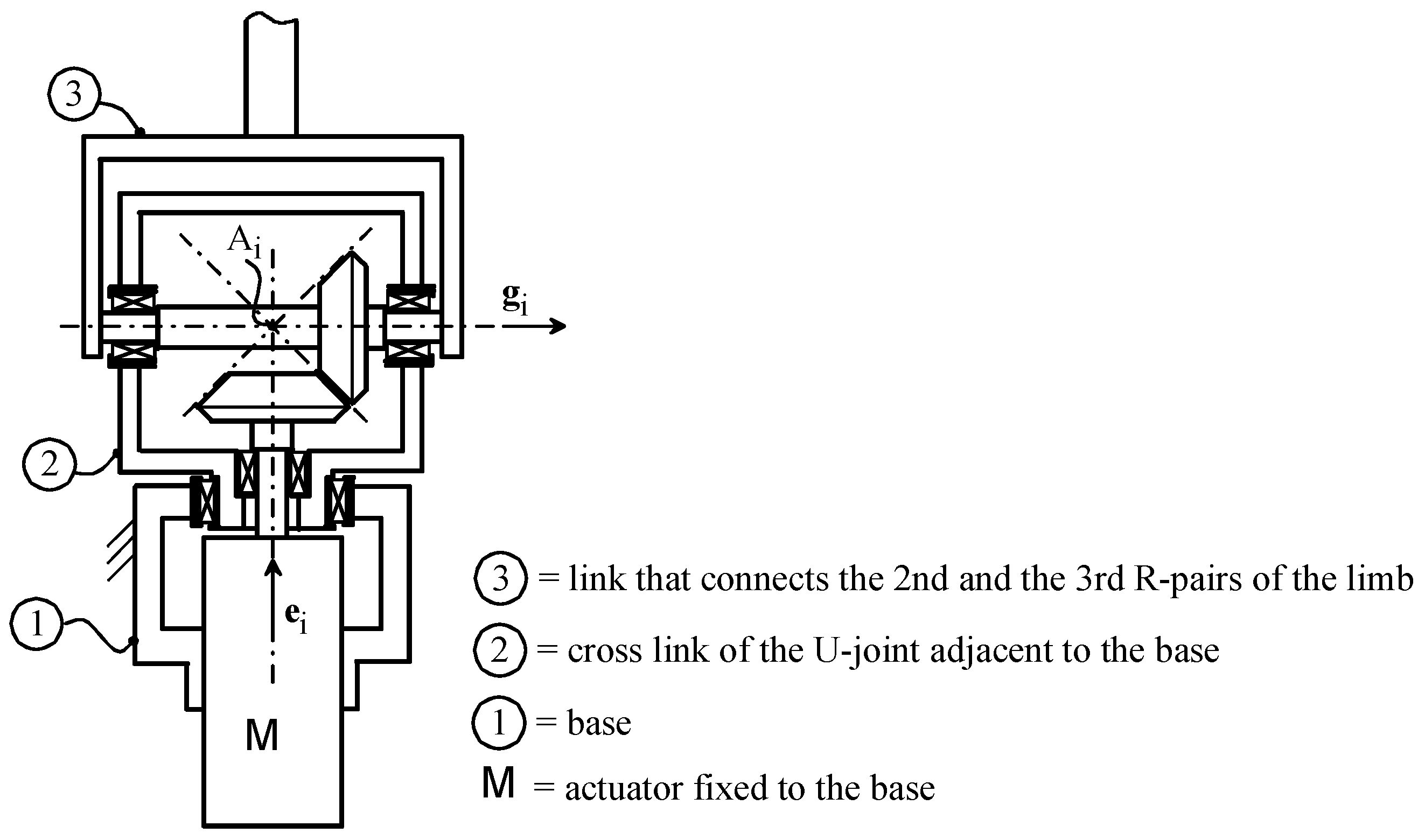
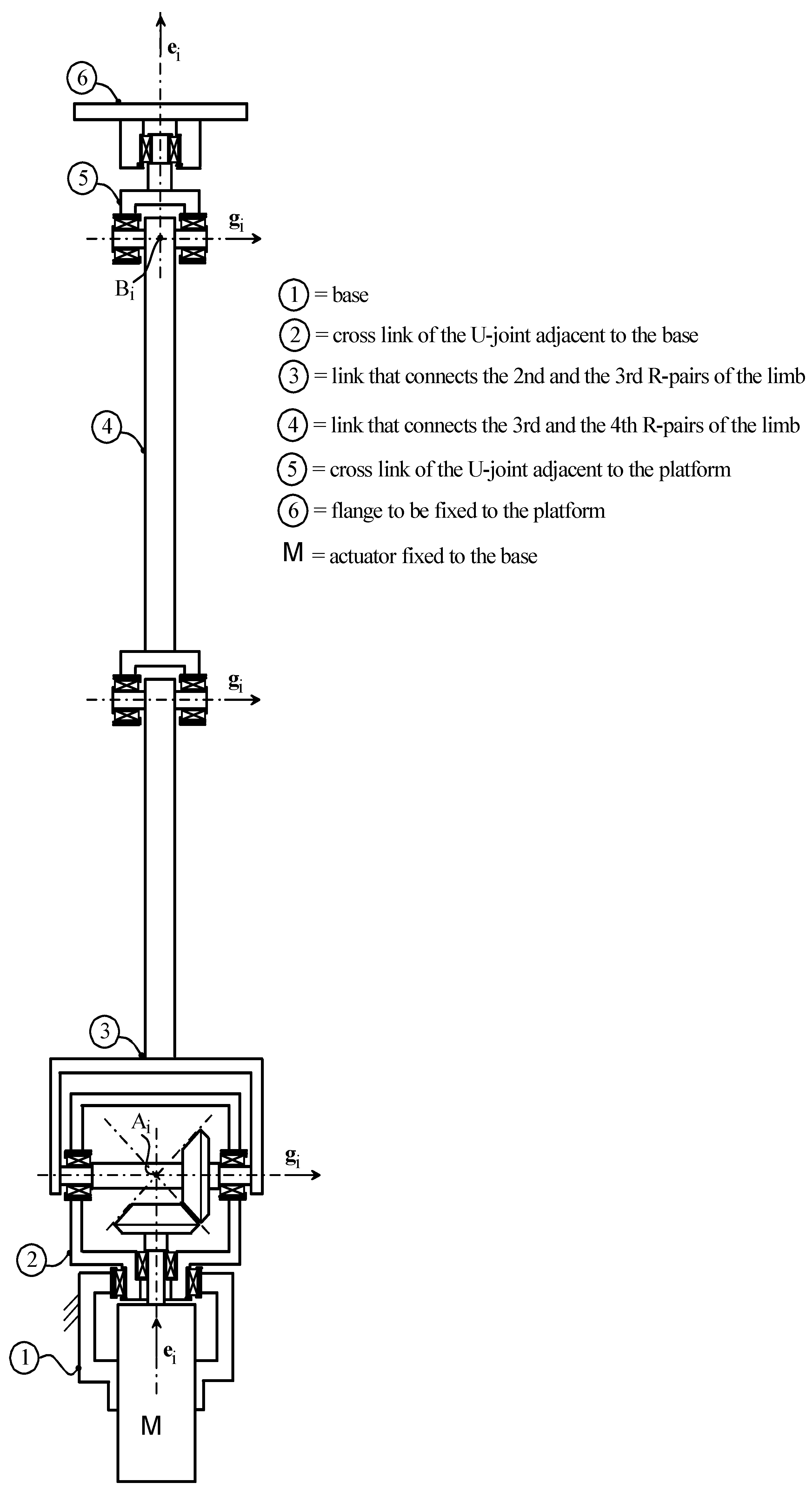
• in each URU limb, the five R-pairs are numbered with an index, j, that increases by moving from the base toward the platform; the actuated joint is the second R-pair;
• the angle θ_ij, for i = 1, 2, 3, and j = 1,…, 5, is the joint variable of the j-th R-pair of the i-th limb; the actuated-joint variables are the angles θ_i2, i = 1, 2, 3 (see Figure 1); also, the phase reference of the angles θ_i1, i = 1, 2, 3, are given by the relationships (see Figure 1):
• g₁ = cosθ₁₁ e₂ + sinθ₁₁ e₃, g₂ = −cosθ₂₁ e₁ + sinθ₂₁ e₃, g₃ = cosθ₃₁ e₁ + sinθ₃₁ e₂;
• θ_iM, for i = 1, 2, 3, is the rotation angle of the motor shaft (see Figure 2) of the actuator of the i-th limb;
• f_i = A_iC_i, for i = 1, 2, 3; r_i = B_iC_i, for i = 1, 2, 3;
• h_i = g_i × e_i, for i = 1, 2, 3;
• u_i = (C_i − A_i)/f_i = cosθ_i2 e_i + sinθ_i2 h_i, for i =1, 2, 3;
• v_i = (B_i − C_i)/r_i = cosθ_i3 u_i + sinθ_i3 (cosθ_i2 h_i − sinθ_i2 e_i) for i = 1, 2, 3, which also defines the phase reference of the angle θ_i3;
• p = (P − O) = xe₁ + ye₂ + ze₃, where (x, y, z)^T collects the coordinates of point P in Ox_by_bz_b; such coordinates also identify the platform pose during motion since the studied 3-URU is translational;
• a_i = (A_i − O) = d_be_i, for i = 1, 2, 3;
• b_i = (B_i − O) = p + d_pe_i, for i = 1, 2, 3;
• c_i = (C_i − O) = a_i + f_iu_i, for i = 1, 2, 3.

Figure 2 shows a possible mechanical transmission, based on a bevel gearbox that actuates the second R-pair of the i-th limb by keeping the actuator on the base. Figure 3 shows a constructive scheme of the i-th URU limb. Figure 2 and Figure 3 highlight that the actual construction of the proposed type of URU limb is quite simple.

3. Mobility Analysis

In this section, the instantaneous input–output relationship of the LaMaViP 3-URU is deduced, and then, it is used for determining its singularity loci. The instantaneous input–output relationship is a linear mapping that relates the actuated-joint rates (instantaneous inputs), which, in the studied 3-URU, are ${\stackrel{.}{\mathsf{\theta }}}_{\mathrm{i}2}$, i = 1, 2, 3, and the platform twist (instantaneous outputs), that is, $\widehat{\mathbf{\$}}={\left({\dot{\mathbf{p}}}^T,{\mathsf{\omega }}^T\right)}^T$ where ω is the angular velocity of the platform.

In the case under study, the three URU limbs allow the platform angular velocity to be expressed in the following three different ways

$$\mathsf{\omega }=({\stackrel{.}{\mathsf{\theta }}}_{\mathrm{i}1}+{\stackrel{.}{\mathsf{\theta }}}_{\mathrm{i}5}){\mathbf{e}}_{\mathrm{i}}+({\stackrel{.}{\mathsf{\theta }}}_{\mathrm{i}2}+{\stackrel{.}{\mathsf{\theta }}}_{\mathrm{i}3}+{\stackrel{.}{\mathsf{\theta }}}_{i4}){\mathbf{g}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(1)

whose dot product by h_i (= g_i × e_i) yields

h_i ⋅ ω = 0                    i = 1,2,3

(2)

Moreover, $\dot{\mathbf{p}}$ enters into the following kinematic relationships3

$$\dot{\mathbf{p}}-\mathsf{\omega }\times (\mathbf{p}-{\mathbf{b}}_{\mathrm{i}})={\dot{\mathbf{b}}}_{\mathrm{i}}=({\dot{\mathsf{\theta }}}_{\mathrm{i}1}\hspace{0.17em}{\mathbf{e}}_{\mathrm{i}}+{\dot{\mathsf{\theta }}}_{\mathrm{i}2}\hspace{0.17em}{\mathbf{g}}_{\mathrm{i}})\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})+{\dot{\mathsf{\theta }}}_{\mathrm{i}3}\hspace{0.17em}{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{c}}_{\mathrm{i}})\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(3)

whose dot product by (b_i − c_i) = r_i v_i yields

$${\mathbf{v}}_{\mathrm{i}}\cdot \dot{\mathbf{p}}+[{\mathbf{v}}_{\mathrm{i}}\times (\mathbf{p}-{\mathbf{b}}_{\mathrm{i}})]\cdot \mathsf{\omega }={\dot{\mathsf{\theta }}}_{\mathrm{i}2}\hspace{0.17em}[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot {\mathbf{v}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(4)

Equations (2) and (4) provide the following instantaneous input–output relationship for the LaMaViP 3-URU

$$\left[\begin{array}{cc}\mathbf{V}& \mathbf{T}\\ {\mathbf{0}}_{3\times 3}& \mathbf{H}\end{array}\right]\left(\begin{array}{c}\dot{\mathbf{p}}\\ \mathsf{\omega }\end{array}\right)=\left[\begin{array}{c}\mathbf{G}\\ 0_{3\times 3}\end{array}\right]\left(\begin{array}{c}{\dot{\mathsf{\theta }}}_{12}\\ {\dot{\mathsf{\theta }}}_{22}\\ {\dot{\mathsf{\theta }}}_{32}\end{array}\right)$$

(5)

where 0_{3 × 3} is the 3 × 3 null matrix,

$$\mathbf{V}=\left[\begin{array}{c}{\mathbf{v}}_1^T\\ {\mathbf{v}}_2^T\\ {\mathbf{v}}_3^T\end{array}\right],\mathbf{T}=\left[\begin{array}{c}{[{\mathbf{v}}_1\times (\mathbf{p}-{\mathbf{b}}_1)]}^T\\ {[{\mathbf{v}}_2\times (\mathbf{p}-{\mathbf{b}}_2)]}^T\\ {[{\mathbf{v}}_3\times (\mathbf{p}-{\mathbf{b}}_3)]}^T\end{array}\right],\mathbf{H}=\left[\begin{array}{c}{\mathbf{h}}_1^T\\ {\mathbf{h}}_2^T\\ {\mathbf{h}}_3^T\end{array}\right]$$

(6a)

and

$$\mathbf{G}=\left[\begin{array}{ccc}[{\mathbf{g}}_1\times ({\mathbf{b}}_1-{\mathbf{a}}_1)]\cdot {\mathbf{v}}_1& 0& 0\\ 0& [{\mathbf{g}}_2\times ({\mathbf{b}}_2-{\mathbf{a}}_2)]\cdot {\mathbf{v}}_2& 0\\ 0& 0& [{\mathbf{g}}_3\times ({\mathbf{b}}_3-{\mathbf{a}}_3)]\cdot {\mathbf{v}}_3\end{array}\right]$$

(6b)

Since the actuators are not directly mounted on the actuated joints, Equation (5) has to be accompanied by additional equations coming from the kinematic analysis of the actuation device (Figure 2) in order to implement control algorithms. Such equations can be deduced as follows. With reference to Figure 2 and Figure 3, the following formulas can be stated

$${}^{\mathrm{i}}\mathsf{\omega }_{21}={\dot{\mathsf{\theta }}}_{\mathrm{i}1}{\mathbf{e}}_{\mathrm{i}},{}^{\mathrm{i}}\mathsf{\omega }_{32}={\dot{\mathsf{\theta }}}_{\mathrm{i}2}{\mathbf{g}}_{\mathrm{i}},{}^{\mathrm{i}}\mathsf{\omega }_{\mathrm{M}1}={\dot{\mathsf{\theta }}}_{\mathrm{iM}}{\mathbf{e}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(7)

where ⁱ ω_pq denotes the angular velocity of link p with respect to link q in the i-th limb, and the index M denotes the motor shaft. In addition, the relative motion theorems [16] states that

$${}^{\mathrm{i}}\mathsf{\omega }_{\mathrm{M}2}={}^{\mathrm{i}}\mathsf{\omega }_{\mathrm{M}1}-{}^{\mathrm{i}}\mathsf{\omega }_{21}=({\dot{\mathsf{\theta }}}_{\mathrm{iM}}-{\dot{\mathsf{\theta }}}_{\mathrm{i}1}){\mathbf{e}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(8)

Eventually, let k_i be the speed ratio of the bevel gearbox of the i-th limb, the following relationship must hold:

$${\mathrm{k}}_{\mathrm{i}}=\frac{{}^{\mathrm{i}}\mathsf{\omega }_{32}\cdot {\mathbf{g}}_{\mathrm{i}}}{{}^{\mathrm{i}}\mathsf{\omega }_{\mathrm{M}2}\cdot {\mathbf{e}}_{\mathrm{i}}}=\frac{{\dot{\mathsf{\theta }}}_{\mathrm{i}2}}{{\dot{\mathsf{\theta }}}_{\mathrm{iM}}-{\dot{\mathsf{\theta }}}_{\mathrm{i}1}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(9)

which yields

$${\dot{\mathsf{\theta }}}_{\mathrm{i}2}={\mathrm{k}}_{\mathrm{i}}({\dot{\mathsf{\theta }}}_{\mathrm{iM}}-{\dot{\mathsf{\theta }}}_{\mathrm{i}1})\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(10)

whose integration gives

$${\mathsf{\theta }}_{\mathrm{i}2}={\mathrm{k}}_{\mathrm{i}}[({\mathsf{\theta }}_{\mathrm{iM}}-{\mathsf{\theta }}_{\mathrm{i}1})-({\mathsf{\theta }}_{\mathrm{iM}|0}-{\mathsf{\theta }}_{\mathrm{i}1|0})]\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(11)

where θ_iM|0 and θ_i1|0 are the values of θ_iM and θ_i1, respectively, when θ_i2 is equal to zero.

Equation (10) relates the actuated-joint rates to the angular velocities of the motor shafts and involves the non-actuated joint rates ${\dot{\mathsf{\theta }}}_{\mathrm{i}1}$, for i = 1, 2, 3. The dot product of Equation (3) by g_i, after some algebraic manipulations, relates the joint rates ${\dot{\mathsf{\theta }}}_{\mathrm{i}1}$, for i = 1, 2, 3, to the platform twist as follows:

$${\dot{\mathsf{\theta }}}_{\mathrm{i}1}=\frac{{\mathbf{g}}_{\mathrm{i}}\cdot \dot{\mathbf{p}}+[{\mathbf{g}}_{\mathrm{i}}\times (\mathbf{p}-{\mathbf{b}}_{\mathrm{i}})]\cdot \mathsf{\omega }}{{\mathbf{h}}_{\mathrm{i}}\cdot ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(12)

The introduction of ${\dot{\mathsf{\theta }}}_{\mathrm{i}1}$’s expressions given by Equation (12) into Equation (10) and, then, of the resulting expressions of ${\dot{\mathsf{\theta }}}_{\mathrm{i}2}$ into Equation (4) yields

$$\begin{array}{c}\left({\mathbf{v}}_{\mathrm{i}}+{\mathrm{k}}_{\mathrm{i}}\frac{[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot {\mathbf{v}}_{\mathrm{i}}}{{\mathbf{h}}_{\mathrm{i}}\cdot ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})}{\mathbf{g}}_{\mathrm{i}}\right)\hspace{0.17em}\cdot \dot{\mathbf{p}}+\left({\mathbf{v}}_{\mathrm{i}}\times (\mathbf{p}-{\mathbf{b}}_{\mathrm{i}})+{\mathrm{k}}_{\mathrm{i}}\frac{[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot {\mathbf{v}}_{\mathrm{i}}}{{\mathbf{h}}_{\mathrm{i}}\cdot ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})}{\mathbf{g}}_{\mathrm{i}}\times (\mathbf{p}-{\mathbf{b}}_{\mathrm{i}})\right)\cdot \mathsf{\omega }={\dot{\mathsf{\theta }}}_{\mathrm{iM}}\hspace{0.17em}{\mathrm{k}}_{\mathrm{i}}[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot v_{\mathrm{i}}\\ \hfill \mathrm{i}=1,2,3\end{array}$$

(13)

System (13) is the direct relationship between the angular velocities of the motor shafts, ${\dot{\mathsf{\theta }}}_{\mathrm{iM}}$, for i = 1, 2, 3, and the platform twist, that is, it is the instantaneous-kinematics model necessary to the control system of the machine which replaces the first three equations of system (5).

3.1. Singularity Analysis

The availability of the instantaneous input–output relationship allows the solution of two instantaneous-kinematics’ problems [10]: the forward instantaneous-kinematics (FIK) problem and the inverse instantaneous-kinematics (IIK) problem. The FIK problem is the determination of the platform twist for assigned values of the actuated-joint rates; vice versa, the IIK problem is the determination of the actuated joint rates for an assigned value of the platform twist.

Singular configurations (singularities) are the PM configurations where one or the other or both of the two above-mentioned problems are indeterminate [9,10]. In particular [9], type-I singularities refer to the indetermination of the IIK problem, type-II singularities refer to the indetermination of the FIK problem, and type-III singularities refer to the indetermination of both the two problems. From a kinematic point of view, type-I singularities correspond to limitations of the instantaneous mobility of the platform and are located at the workspace boundary; they are present in all the manipulators and are sometimes called “serial singularities”. Differently, type-II singularities are mainly inside the workspace and correspond either (a) to a local increase of platform’s instantaneous DOFs4 or (b), without any local variation of platform’s instantaneous DOFs, to some platform DOFs that locally become non-controllable through the actuated joints (i.e., the physical constraints locally become no longer independent). They are present only in closed kinematic chains (i.e., in PMs) and are sometimes called “parallel singularities”.

Type-II(b) singularities may occur in any PM; whereas, type-II(a) singularities may occur only in lower-mobility PMs, whose limb connectivity5 is higher than the PM DOFs. Type-II(a) singularities are named “constraint singularities” [11] since the additional platform DOFs acquired at such singularities may make the platform change its type of motion (operating mode). In particular, in a TPM, such additional DOFs can only be instantaneous rotations which may make the platform exit from the pure-translation operating mode; that is why TPMs’ constraint singularities are also named “rotation singularities” and TPMs’ type-II(b) singularities are also named “translation singularities” [8].

3.1.1. Rotation (Constraint) Singularities of LaMaViP 3-URU

The platform translation is guaranteed if and only if the constraints applied to the platform by the three URU limbs make the platform angular velocity, ω, equal to zero. The last three equations of system (5) are able to impose ω = 0, if the determinant of the coefficient matrix, H, is different from zero. Therefore, the constraint singularities are the configurations that satisfy the geometric condition6

det(H) = h₁⋅(h₂ × h₃) = 0

(14)

Equation (14) is satisfied when the unit vectors h_i, for i = 1, 2, 3, are coplanar. Since the i-th unit vector h_i is perpendicular to the plane passing through the coordinate axis of Ox_by_bz_b with the direction of e_i where the unit vector g_i lies on (that is, to the plane where the cross link of the i-th U-joint lies on (see Figure 1)) and the three so-identified planes always share point O as common intersection, such a geometric condition occurs when these three planes simultaneously intersect themselves in a common line passing through point O (see Figure 4).

From an analytic point of view, the notations introduced in Section 2 make it possible to write

$${\mathbf{g}}_{\mathrm{i}}=\frac{{\mathbf{e}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})}{\left|{\mathbf{e}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})\right|}=\frac{{\mathbf{e}}_{\mathrm{i}}\times [\mathbf{p}+({\mathrm{d}}_{\mathrm{p}}-{\mathrm{d}}_{\mathrm{b}}){\mathbf{e}}_{\mathrm{i}}]}{\left|{\mathbf{e}}_{\mathrm{i}}\times [\mathbf{p}+({\mathrm{d}}_{\mathrm{p}}-{\mathrm{d}}_{\mathrm{b}}){\mathbf{e}}_{\mathrm{i}}]\right|}=\frac{{\mathbf{e}}_{\mathrm{i}}\times \mathbf{p}}{\left|{\mathbf{e}}_{\mathrm{i}}\times \mathbf{p}\hspace{0.17em}\right|}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(15a)

and

$${\mathbf{h}}_{\mathrm{i}}={\mathbf{g}}_{\mathrm{i}}\times {\mathbf{e}}_{\mathrm{i}}=\frac{({\mathbf{e}}_{\mathrm{i}}\times \mathbf{p})\times {\mathbf{e}}_{\mathrm{i}}}{\left|{\mathbf{e}}_{\mathrm{i}}\times \mathbf{p}\hspace{0.17em}\right|}=\frac{\mathbf{p}-({\mathbf{e}}_{\mathrm{i}}\cdot \mathbf{p}){\mathbf{e}}_{\mathrm{i}}}{\left|{\mathbf{e}}_{\mathrm{i}}\times \mathbf{p}\hspace{0.17em}\right|}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(15b)

Then, the introduction of the analytic expression of p (i.e., p = xe₁ + ye₂ + ze₃) into Equation (15b) yields

$${\mathbf{h}}_1=\frac{\mathrm{y}{\mathbf{e}}_2+\mathrm{z}{\mathbf{e}}_3}{\sqrt{{\mathrm{y}}^2+{\mathrm{z}}^2}};{\mathbf{h}}_2=\frac{\mathrm{x}{\mathbf{e}}_1+\mathrm{z}{\mathbf{e}}_3}{\sqrt{{\mathrm{x}}^2+{\mathrm{z}}^2}};{\mathbf{h}}_3=\frac{\mathrm{x}{\mathbf{e}}_1+\mathrm{y}{\mathbf{e}}_2}{\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}}$$

(16)

Eventually, the introduction of the explicit expressions given by Equation (16) into the singularity condition (14) provides the following analytic equation of the geometric locus of the rotation (constraint) singularities

$${\mathbf{h}}_1\cdot ({\mathbf{h}}_2\times {\mathbf{h}}_3)=\frac{2\mathrm{xyz}}{\sqrt{\left({\mathrm{x}}^2+{\mathrm{z}}^2\right)\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)\left({\mathrm{y}}^2+{\mathrm{z}}^2\right)}}=0$$

(17)

The analysis of Equation (17) reveals that the rotation singularity locus is constituted by the 3 coordinate planes x = 0, y = 0, and z = 0 (Figure 5). Additionally, the analysis of Figure 1, of Formula (16) and Equation (2) reveals that

• when point P lies on the y_bz_b coordinate plane (i.e., x = 0), the three unit vectors h_i, for i = 1, 2, 3, (see Formulas (16)) are all parallel to the y_bz_b coordinate plane; therefore, the component of ω along e₁ is not locked (see Equations (2)) and the platform can perform rotations around axes parallel to the x_b axis;
• when point P lies on the x_bz_b coordinate plane (i.e., y = 0), the three unit vectors h_i, for i = 1, 2, 3, (see Formulas (16)) are all parallel to the x_bz_b coordinate plane; therefore, the component of ω along e₂ is not locked (see Equations (2)) and the platform can perform rotations around axes parallel to the y_b axis;
• when point P lies on the x_by_b coordinate plane (i.e., z = 0), the three unit vectors h_i, for i = 1, 2, 3, (see Formulas (16)) are all parallel to the x_by_b coordinate plane; therefore, the component of ω along e₃ is not locked (see Equations (2)) and the platform can perform rotations around axes parallel to the z_b axis.

As a consequence, when P lies on a coordinate axis the platform locally acquires 2 rotational DOFs; whereas, when P coincides with O (i.e., x = y = z = 0) the platform locally acquires 3 rotational DOFs, even though the expression at the left-hand side of Equation (17) becomes indeterminate in all these cases.

In short, the rotation-singularity locus is constituted by three mutually orthogonal planes (i.e., the three coordinate planes of Ox_by_bz_b). Such a locus leaves eight wide simply-connected convex regions (i.e., the eight octants of Ox_by_bz_b) of the operational space, where the platform is constrained to translate. Inside any of these regions, the useful workspace of the studied 3-URU can be safely located. Moreover, since ω = 0 in them, the instantaneous input–output relationship (i.e., system (5)) simplifies itself as follows

$$\mathbf{V}\hspace{0.17em}\dot{\mathbf{p}}=\mathbf{G}\hspace{0.17em}{\dot{\mathsf{\theta }}}_2$$

(18)

where ${\dot{\mathsf{\theta }}}_2={({\dot{\mathsf{\theta }}}_{12},{\dot{\mathsf{\theta }}}_{22},{\dot{\mathsf{\theta }}}_{32})}^T$; whereas, the instantaneous-kinematics model necessary to the machine control (i.e., system (14)) simplifies itself as follows

$$\left({\mathbf{v}}_{\mathrm{i}}+{\mathrm{k}}_{\mathrm{i}}\frac{[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot {\mathbf{v}}_{\mathrm{i}}}{{\mathbf{h}}_{\mathrm{i}}\cdot ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})}{\mathbf{g}}_{\mathrm{i}}\right)\hspace{0.17em}\cdot \dot{\mathbf{p}}={\dot{\mathsf{\theta }}}_{\mathrm{iM}}\hspace{0.17em}{\mathrm{k}}_{\mathrm{i}}[{\mathbf{g}}_{\mathrm{i}}\times ({\mathbf{b}}_{\mathrm{i}}-{\mathbf{a}}_{\mathrm{i}})]\cdot {\mathbf{v}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(19)

3.1.2. Translation (Type-II(b)) Singularities of LaMaViP 3-URU

Out of constraint singularities, system (18) is the instantaneous input–output relationship to consider. With reference to system (18), the FIK is the determination of $\dot{\mathbf{p}}$ for an assigned ${\dot{\mathsf{\theta }}}_2$. This problem has a unique solution if and only if the determinant of the coefficient matrix, V, is different from zero. Therefore, the translation singularities are the configurations that satisfy the geometric condition

det(V) = v₁⋅(v₂ × v₃) = 0

(20)

Equation (20) is satisfied when the unit vectors v_i, for i = 1, 2, 3, are coplanar. This geometric condition occurs when the three segments B_iC_i, i = 1, 2, 3, (see Figure 1) are all parallel to a unique plane (see Figure 6). From an analytic point of view, the adopted notations (see Section 2 and Figure 1) bring to light the following relationships

(b_i − c_i) = r_i v_i = p + (d_p − d_b) e_i − f_i (cosθ_i2 e_i + sinθ_i2 h_i)            i = 1,2,3

(21)

which, after the introduction of the analytic expressions of p (i.e., p = xe₁ + ye₂ + ze₃) and of h_i (i.e., Equations (16)), become

b₁−c₁ = [x + (d_p − d_b) − f₁ cosθ₁₂]e₁ + [1 − f₁ m₁ sinθ₁₂] ye₂ + [1 − f₁ m₁ sinθ₁₂] ze₃

(22a)

b₂−c₂ = [1 − f₂ m₂ sinθ₂₂] xe₁ + [y + (d_p − d_b) − f₂ cosθ₂₂]e₂ + [1 − f₂ m₂ sinθ₂₂] ze₃

(22b)

b₃−c₃ = [1 − f₃ m₃ sinθ₃₂] xe₁ + [1 − f₃ m₃ sinθ₃₂] ye₂ + [z + (d_p − d_b) − f₃ cosθ₃₂]e₃

(22c)

with

$${\mathrm{m}}_1=\frac{1}{\sqrt{{\mathrm{y}}^2+{\mathrm{z}}^2}},{\mathrm{m}}_2=\frac{1}{\sqrt{{\mathrm{x}}^2+{\mathrm{z}}^2}},{\mathrm{m}}_3=\frac{1}{\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2}},$$

(23)

Eventually, the product of Equation (20) by the non-null constant r₁ r₂ r₃ yields the equivalent equation

(b₁ − c₁) ⋅ [(b₂ − c₂) × (b₃ − c₃)] = 0

(24)

which, after the introduction of Formulas (22a), (22b) and (22c), becomes the following analytic expression of the translation-singularity locus

xyz [1 − n₂n₃ − n₁n₂ − n₁n₃ + 2 n₁n₂n₃]+ xy q₃(1− n₁n₂) + xz q₂(1 − n₁n₃) + yz q₁(1 − n₂n₃) +
 x q₂q₃+ y q₁q₃ + z q₁q₂ + q₁q₂q₃ = 0                        

(25)

where

n₁ = [1 − f₁ m₁ sinθ₁₂]; n₂ = [1 − f₂ m₂ sinθ₂₂]; n₃ = [1 − f₃ m₃ sinθ₃₂]

(26a)

q₁ = (d_p − d_b) − f₁ cosθ₁₂; q₂ = (d_p − d_b) − f₂ cosθ₂₂; q₃ = (d_p − d_b) − f₃ cosθ₃₂

(26b)

The actuated-joint variables, θ₁₂, θ₂₂, and θ₃₂, can be eliminated from Equation (25) by using the solution formulas of the inverse position analysis [18] reported in Appendix A. In doing so, Equation (25) becomes an equation that contains only the geometric constants of the machine and the platform pose coordinates, x, y, and z. Such equation, which is the analytic expression of a surface (the translation-singularity surface) in Ox_by_bz_b, can be exploited, during design, to determine the optimal values of the geometric constants of the machine that move the translation singularities into regions of the operational space which are far from the useful workspace.

3.1.3. Serial (Type-I) Singularities of LaMaViP 3-URU

The solution of the IIK problem involves only the first three equations of system (5). The analysis of these three equations reveals that they can be separately solved with respect to θ_i2, i = 1, 2, 3, since matrix G is diagonal, and that the solution is indeterminate when at least one of the following geometric condition is satisfied (see Figure 1):

g_i ⋅ [(b_i − a_i) × (b_i − c_i)] = g_i ⋅ [(c_i − a_i) × (b_i − c_i)] = f_i r_i sinθ_i3 = 0            i = 1,2,3

(27)

The i-th Equation (27) is satisfied when the i-th limb is fully extended (θ_i3 = 0) or folded (θ_i3 = π). These two geometric conditions identify two concentric spherical surfaces with point A_i as center, which point B_i must lie on. From an analytic point of view, since b_i = p + d_pe_i and a_i = d_be_i, the equations of these two spherical surfaces in Ox_by_bz_b can be written as follows (here, the square of a vector denotes the dot product of the vector by itself)

         (b_i − a_i)² = [p + (d_p − d_b)e_i]² = p² + (d_p − d_b)² + 2 (d_p − d_b) p ⋅ e_i = (f_i + r_i)²         i = 1,2,3

(28a)

         (b_i − a_i)² = [p + (d_p − d_b)e_i]² = p² + (d_p − d_b)² + 2 (d_p − d_b) p ⋅ e_i = (f_i − r_i)²         i = 1,2,3

(28b)

Equation (28) are also the equations of the reachable-workspace boundaries. Therefore, the reachable workspace of the LaMaViP 3-URU can be analytically defined by the following system of inequalities

(f₁ − r₁)² ≤ x² + y² + z² + (d_p − d_b)² + 2 (d_p − d_b) x ≤ (f₁ + r₁)²

(29a)

(f₂ − r₂)² ≤ x² + y² + z² + (d_p − d_b)² + 2 (d_p − d_b) y ≤ (f₂ + r₂)²

(29b)

(f₃ − r₃)² ≤ x² + y² + z² + (d_p − d_b)² + 2 (d_p − d_b) z ≤ (f₃ + r₃)²

(29c)

In the case d_b = d_p and f_i = r_i = R for i = 1, 2, 3, inequalities (29) give a sphere with center O and radius 2R as reachable workspace (see Figure 7).

3.2. Singularity Analysis of the Actuation Device

Since the actuators are not directly mounted on the actuated joint in the LaMaViP 3-URU, the motion transmission must be analyzed to check whether there are configurations (hereafter called “actuation singularities”) in which the relationship (i.e., Equations (10)) between the actuated-joint rates, ${\dot{\mathsf{\theta }}}_{\mathrm{i}2}$, i = 1, 2, 3, and the angular velocities of the motor shafts, ${\dot{\mathsf{\theta }}}_{\mathrm{iM}}$, i = 1, 2, 3, is indeterminate. In this subsection, such relationship is deduced and analyzed.

The introduction of ω = 0 and of $\dot{\mathbf{p}}={\mathbf{V}}^{-1}\mathbf{G}\hspace{0.17em}{\dot{\mathsf{\theta }}}_2$ (see Equation (18)) into Equation (12) yields

$${\dot{\mathsf{\theta }}}_1=\mathbf{N}\hspace{0.17em}\mathbf{M}{\mathbf{V}}^{-1}\mathbf{G}{\dot{\mathsf{\theta }}}_2$$

(30)

with

$$\mathbf{M}=\left[\begin{array}{c}{\mathbf{g}}_1^T\\ {\mathbf{g}}_2^T\\ {\mathbf{g}}_3^T\end{array}\right],\mathbf{N}=\left[\begin{array}{ccc}{[{\mathbf{h}}_1\cdot ({\mathbf{b}}_1-{\mathbf{a}}_1)]}^{-1}& 0& 0\\ 0& {[{\mathbf{h}}_2\cdot ({\mathbf{b}}_2-{\mathbf{a}}_2)]}^{-1}& 0\\ 0& 0& {[{\mathbf{h}}_3\cdot ({\mathbf{b}}_3-{\mathbf{a}}_3)]}^{-1}\end{array}\right]$$

(31)

Then, the introduction of Equation (30) into Equation (10), after some rearrangements, gives the sought-after relationship between the actuated-joint rates, and the angular velocities of the motor shafts, that is,

$$\mathbf{S}\hspace{0.17em}{\dot{\mathsf{\theta }}}_2=\mathbf{K}\hspace{0.17em}{\dot{\mathsf{\theta }}}_{\mathrm{M}}$$

(32)

with ${\dot{\mathsf{\theta }}}_{\mathrm{M}}=({{\dot{\mathsf{\theta }}}_{1\mathrm{M}},{\dot{\mathsf{\theta }}}_{2\mathrm{M}},{\dot{\mathsf{\theta }}}_{3\mathrm{M}})}^T$, S = I_{3 × 3} + KNMV⁻¹G where, I_{3 × 3} is the 3 × 3 identity matrix, and

$$\mathbf{K}=\left[\begin{array}{ccc}{\mathrm{k}}_1& 0& 0\\ 0& {\mathrm{k}}_2& 0\\ 0& 0& {\mathrm{k}}_3\end{array}\right];{\mathbf{V}}^{-1}=\frac{1}{{\mathbf{v}}_1\cdot ({\mathbf{v}}_2\times {\mathbf{v}}_3)}[{\mathbf{v}}_2\times {\mathbf{v}}_3,{\mathbf{v}}_3\times {\mathbf{v}}_1,{\mathbf{v}}_1\times {\mathbf{v}}_2]$$

(33)

The expansion of the above expression of matrix S = [s_ij] gives the following explicit expression of its ij-th entry, s_ij for i,j = 1, 2, 3,

$${\mathrm{s}}_{\mathrm{ij}}={\mathsf{\delta }}_{\mathrm{ij}}+\frac{{\mathrm{k}}_{\mathrm{i}}[g_{\mathrm{i}}\cdot (v_{(\mathrm{i}+1)\mathrm{mod}3}\times v_{(\mathrm{i}+2)\mathrm{mod}3})][g_{\mathrm{j}}\times (b_{\mathrm{j}}-a_{\mathrm{j}})]\cdot v_{\mathrm{j}}}{v_1\cdot (v_2\times v_3)[h_{\mathrm{i}}\cdot (b_{\mathrm{i}}-a_{\mathrm{i}})]}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i},\mathrm{j}=1,2,3$$

(34)

where δ_ij denotes the Kronecker delta and the subscript “(n+m) mod 3” denotes the sum with modulus 3 of the two integers n and m as defined in modular arithmetic [19].

The analysis of matrix S immediately reveals that, when matrix V is not invertible (i.e., when Equation (20) is satisfied), relationship (32) is indeterminate. Such a condition does not provide further reductions of the regions where the useful workspace can be located since it coincides with the translation-singularity locus (i.e., with Equation (20)) analyzed in Section 3.1.2. Over this condition, Equation (32) fails to give unique values of the actuated-joint rates, ${\dot{\mathsf{\theta }}}_{\mathrm{i}2}$, i = 1, 2, 3, for assigned values of the angular velocities of the motor shafts, ${\dot{\mathsf{\theta }}}_{\mathrm{iM}}$, i = 1, 2, 3, when the determinant of matrix S is equal to zero, that is, when the following geometric condition is satisfied

det(S) = s₁·(s₂ × s₃) = 0

(35)

where s_i, for i = 1, 2, 3, are the column vectors of matrix S. Therefore, an actuation singularity occurs when the three vectors s_i, for i = 1, 2, 3, are coplanar. From an analytic point of view, Equation (35) is the equation of a surface in Ox_by_bz_b, which corresponds to the actuation-singularity locus. Such equation can be put in the form f(x, y, z) = 0 by exploiting the above-reported expressions of the terms appearing in Equation (34) and can be used to size the geometric constants and the speed ratios k_i, i = 1, 2, 3, so that the actuation singularity locus is far from the useful workspace.

From the point of view of the platform control, the presence of the actuation singularities justifies the difference between System (18) and System (19). In particular, unlike System (18), System (19) yields the following geometric expression of the translation-singularity locus

$$\left({\mathbf{v}}_1+{\mathrm{k}}_1\frac{[{\mathbf{g}}_1\times ({\mathbf{b}}_1-{\mathbf{a}}_1)]\cdot {\mathbf{v}}_1}{{\mathbf{h}}_1\cdot ({\mathbf{b}}_1-{\mathbf{a}}_1)}{\mathbf{g}}_1\right)\hspace{0.17em}\cdot \left[\left({\mathbf{v}}_2+{\mathrm{k}}_2\frac{[{\mathbf{g}}_2\times ({\mathbf{b}}_2-{\mathbf{a}}_2)]\cdot {\mathbf{v}}_2}{{\mathbf{h}}_2\cdot ({\mathbf{b}}_2-{\mathbf{a}}_2)}{\mathbf{g}}_2\right)\times \left({\mathbf{v}}_3+{\mathrm{k}}_3\frac{[{\mathbf{g}}_3\times ({\mathbf{b}}_3-{\mathbf{a}}_3)]\cdot {\mathbf{v}}_3}{{\mathbf{h}}_3\cdot ({\mathbf{b}}_3-{\mathbf{a}}_3)}{\mathbf{g}}_3\right)\right]=0$$

(36)

which imposes the zeroing of the mixed product of the three vectors that dot multiply $\dot{\mathbf{p}}$ in the three equations of System (19). The i-th vector, for i = 1, 2, 3, of this vector triplet is associated to the i-th limb and lies on a plane spanned by the two unit vectors v_i and g_i. Differently from Equation (20), which is satisfied by the coplanarity of the three unit vectors v_i, i = 1, 2, 3, Equation (36) is satisfied by the coplanarity of these other three vectors that are not aligned with the unit vectors v_i, i = 1, 2, 3, any longer. Equation (36) can be put in the form f(x, y, z) = 0 by exploiting the above-reported expressions of the terms appearing in it and can be used as an alternative to Equations (20) and (35) to size the geometric constants and the speed ratios k_i, i = 1, 2, 3, so that both the translation and the actuation singularity loci are far from the useful workspace.

4. Conclusions

The kinematics and the singularity analysis of a novel translational architecture of 3-URU type, named LaMaViP 3-URU, have been addressed. With respect to other translational 3-URU, the novelty of the LaMaViP 3-URU stands on the fact that i) it has the actuators on the base even though the actuated joints are not on the base, ii) in each URU limb, the actuated R-pair is the one not adjacent to the base in the U-joint adjacent to the base, and (iii) it has a particular base (platform) geometry where the axes of the three R-pairs adjacent to the base (to the platform) share a common intersection point, but are not coplanar. These features are the premises to have a translational 3-URU with overall sizes and performances similar to the ones of the DELTA robot.

Here, the instantaneous input–output relationship of the LaMaViP 3-URU has been deduced together with the instantaneous relationship that directly relates the platform twist to the angular velocities of the 3 motor shafts. Then, the singularity analysis has been addressed. Both the geometric and the analytic conditions that identify all the singularities of the LaMaViP 3-URU have been determined.

The results of this study prove that there are eight wide simply-connected convex regions of the operational space where the platform is constrained to translate and the useful workspace can be safely located, which makes the proposed architecture a viable alternative to other translational PMs. Additionally, the reachable-workspace boundaries equations, the translation, and the actuation singularity loci equations as a function of the geometric constants and of the transmission constants have been provided. Such equations are all the necessary tools for the dimensional synthesis of the LaMaViP 3-URU. These results form the technical basis of a patent application of the author.

Future works on the LaMaViP 3-URU will address the dimensional synthesis of the LaMaViP 3-URU together with the kinematic and dynamic performance analyses.

5. Patents

The results of this work form the basis for the following Italy patent application:

Di Gregorio, R. Meccanismo Parallelo Traslazionale. Patent No. 102020000006100, 23 March 2020.