Next Article in Journal
Synthesis and Analysis of a Novel Linkage Mechanism with the Helical Motion of the End-Effector
Next Article in Special Issue
Is Artificial Man Still Far Away: Anthropomimetic Robots Versus Robomimetic Humans
Previous Article in Journal
Least Squares Optimization: From Theory to Practice
Previous Article in Special Issue
Learning Sequential Force Interaction Skills
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Robotics
Volume 9
Issue 3
10.3390/robotics9030052
robotics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors

by
Charbel Tawk
1,2 and
Gursel Alici
1,2,*
1
School of Mechanical, Materials, Mechatronic and Biomedical Engineering, and Applied Mechatronics and Biomedical Engineering Research (AMBER) Group, University of Wollongong, Northfields Ave, Wollongong, NSW 2522, Australia
2
ARC Centre of Excellence for Electromaterials Science, University of Wollongong Innovation Campus, North Wollongong, NSW 2500, Australia
*
Author to whom correspondence should be addressed.
Robotics 2020, 9(3), 52; https://doi.org/10.3390/robotics9030052
Submission received: 27 May 2020 / Revised: 30 June 2020 / Accepted: 6 July 2020 / Published: 7 July 2020
(This article belongs to the Special Issue Feature Papers 2020)
Browse Figures
Versions Notes

Abstract

:
The modeling of soft structures, actuators, and sensors is challenging, primarily due to the high nonlinearities involved in such soft robotic systems. Finite element modeling (FEM) is an effective technique to represent soft and deformable robotic systems containing geometric nonlinearities due to large mechanical deformations, material nonlinearities due to the inherent nonlinear behavior of the materials (i.e., stress-strain behavior) involved in such systems, and contact nonlinearities due to the surfaces that come into contact upon deformation. Prior to the fabrication of such soft robotic systems, FEM can be used to predict their behavior efficiently and accurately under various inputs and optimize their performance and topology to meet certain design and performance requirements. In this article, we present the implementation of FEM in the design process of directly three-dimensional (3D) printed pneumatic soft actuators and sensors to accurately predict their behavior and optimize their performance and topology. We present numerical and experimental results to show that this approach is very effective to rapidly and efficiently design the soft actuators and sensors to meet certain design requirements and to save time, modeling, design, and fabrication resources.

1. Introduction

Soft robots are ideal to interact safely with humans and operate in highly dynamic environments since they are made of excessively deformable and stretchable materials [1,2]. The development of these soft systems is inspired by soft biological structures present in nature, such as an elephant trunk, octopus arm, squid tentacles, and worms that are made mostly of compliant materials and liquids [3]. The structures, actuators, sensors, electronics, and power sources of a soft robotic system should primarily be made of soft materials [4]. However, the realization of completely soft robots remains a great challenge for scientists and engineers.
The soft actuators and sensors involved in every soft robotic system are the major and critical components that make such systems functional and useful. Soft robots demand dexterous soft actuators that can generate relatively low and high forces (i.e., controllable forces) to facilitate soft and adaptive interaction with their environments [5]. In addition, soft robots require robust flexible, stretchable, or compressive soft sensors that can sustain large deformations repeatedly over sustained periods, while providing consistent output signals [6]. Such reliable and stable sensors are essential for soft robots to develop reliable feedback control systems [7,8].
The soft robotics field has grown hugely in recent years during which many untethered soft robots have been developed [9]. In addition to being safe to interact directly with humans and delicate objects, soft robots have multiple advantages compared to conventional robotic systems. First, soft robots are made of low-cost soft materials that make them accessible and affordable [1]. Second, soft robots are made of soft monolithic bodies. Therefore, these systems require minimal or no assembly processes in some cases. Third, soft robots can be directly fabricated using various three-dimensional (3D) printing technologies in addition to conventional manufacturing techniques [10,11,12,13,14]. Fourth, soft robotic systems can be used and implemented in diverse robotic applications, such as locomotion robots, adaptive grippers, artificial muscles, parallel manipulators, prostheses, robotic hands, human-machine interfaces, and many others [5]. Finally, the compliance of soft robots makes them ideal for handling extreme external mechanical deformations [15] without any damage and for manipulating delicate and fragile objects without damaging them [16].
In general, the development of soft robots relies heavily on experimental results and prototyping [17,18]. Although the soft robotics field has several advantages to offer various solutions to applications requiring human-robot interaction, this field still faces limitations in terms of modeling, design optimizing, and fabricating soft bodies, especially when it comes to designing automation tools [19]. Modeling is critical for the design and development of novel soft robots [10]. Since it is very challenging to derive analytical models [20] for soft robots, due to nonlinearities, numerical methods are used instead [10]. Finite element modeling (FEM) is one approach to model and simulate soft robotic components. For instance, the mechanical and/or electrical behavior of soft sensors [21,22] can be predicted and/or optimized using FEM. However, the implementation of FEM can be challenging. The main reason is that the FEM of soft robotic actuators and sensors involves multiple nonlinearities, including geometric nonlinearities, material nonlinearities, and contact nonlinearities, resulting from different surfaces coming into contact upon deforming a soft body. Additionally, soft robots are usually made of complex geometries (i.e., complicated topologies).
The FEM of soft systems is used for several important reasons [23]. First, the behavior of soft robotic systems can be accurately predicted under a specific input (i.e., pressure, displacement, etc.). Second, the performance of soft robotic systems can be quickly predicted and optimized accurately before their fabrication [24,25]. Therefore, the simulations save huge amounts of time and potential fabrication resources. Third, the geometry or topology of soft robotic devices can be optimized and modified to meet certain design or performance requirements [23]. Fourth, the simulations can be used to iterate rapidly and efficiently between several designs to optimize their behavior and performance. Finally, FEM can be efficiently used to accurately control soft robotic systems [8,26] in real-time [27,28].
There are several FEM software that use hyper-elastic material models to perform highly nonlinear simulations to predict and optimize the performance of soft robots, such as SOFA [29], Abaqus (Dassault Systèmes Simulia Corp., Waltham, MA, USA) [30], COMSOL Multiphysics® [31] and ANSYS (ANSYS Inc., Canonsburg, PA, USA) [32]. In addition, there are several other methods to model soft robotic systems, including lumped parameter modeling [33], point-lattices connected by linear beam elements [34], and Cosserat elements [35].
In this work, FEM is used in the design process of directly 3D printed soft pneumatic actuators and sensors to efficiently and accurately predict their behavior under various inputs and to optimize their performance and geometry to meet certain design and performance requirements before their fabrication. This work focuses specifically on how a commercial FEM tool can be used to design and optimize soft and 3D printable pneumatic actuators and sensors. A hyper-elastic materials model is developed for use in FE simulations, based on the experimental stress-strain data of the soft 3D printable material used to 3D print the actuators and sensors. The FEM results, in all cases, are validated using experimental data and only the final optimized designs are presented. This work presents a roadmap on how to implement FEM in the design process of soft pneumatic actuators and sensors using a commercially available FE analysis software. In addition, it presents the challenges encountered in simulating soft bodies and provides some useful recommendations for successfully simulating such bodies.

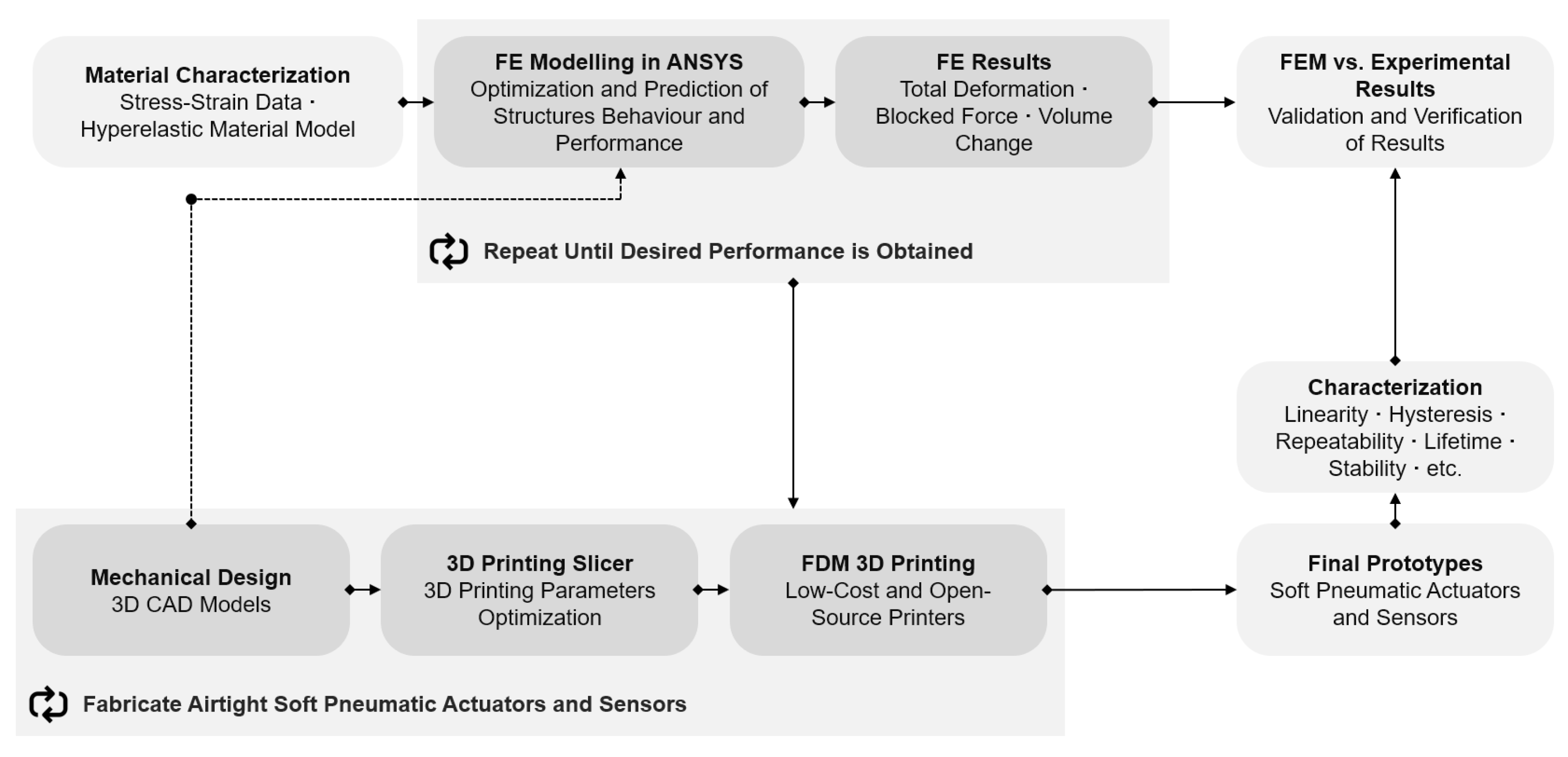
2. Design Process

The design process starts with modeling the 3D computer-aided design (CAD) models of the soft actuators and sensors, as shown in Figure 1. The structures are designed so that they can be 3D printed using affordable and accessible fused deposition modeling (FDM) 3D printers without using support materials and postprocessing. Additionally, the soft material used to 3D print the soft actuators and sensors is characterized to extract its stress-strain data that can be used to develop a hyper-elastic material model for use in FE simulations. Afterwards, the designed CAD models are imported to the FEM software along with the material model developed to simulate the soft actuators and sensors to predict their behavior and optimize their performance. Based on the FEM results, the CAD models are modified, and their simulation is repeated accordingly until the desired performance is achieved before their fabrication. Once the desired or optimized performance is obtained, the 3D CAD models are sliced in 3D printing commercial slicing software where the printing parameters are optimized to fabricate airtight and functional soft actuators and sensors. Finally, the fabricated prototypes are characterized to assess their experimental performance and to compare it with its FEM counterpart to verify and validate the simulation results.

3. Materials and Methods

3.1. Materials, Models, and 3D Printing Technology

A thermoplastic poly(urethane) (TPU), known commercially as NinjaFlex (NinjaTek, Manheim, Pennsylvania, PA, U.S.A.), was used to 3D print the soft pneumatic actuators and sensors using low-cost and open-source FDM 3D printers (FlashForge Creator Pro; FlashForge Inventor, FlashForge Corporation, Hangzhou, ZheJiang Province, China). The actuators and sensors were modeled using CAD software (Dassault Systèmes, SOLIDWORKS Corp., Waltham, Massachusetts, MA, U.S.A.; Fusion 360, Autodesk Inc., San Rafael, CA, U.S.A.). The 3D CAD models were sliced using a commercially available slicer (Simplify3D, Simplify3D Inc., Cincinnati, OH, U.S.A.). The 3D printing parameters were optimized in the slicer to 3D print completely airtight, reliable, and functional soft pneumatic actuators and sensors [32,36,37,38].

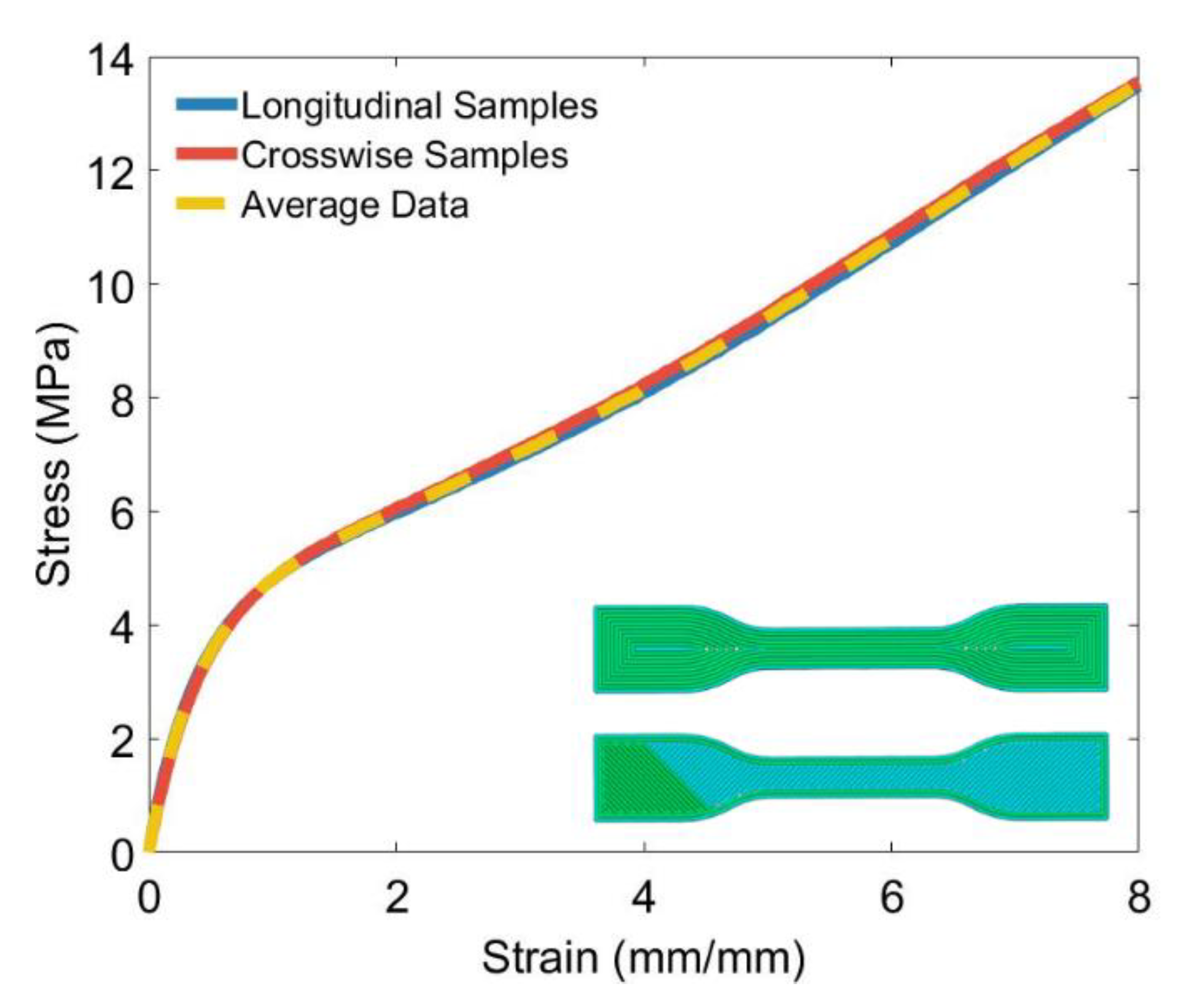
3.2. TPU Stress-Strain Data

The stress-strain relationship of the TPU used was extracted to assess its behavior using an experimental uniaxial tensile test. Eight TPU samples were printed using a longitudinal infill pattern and another eight samples were printed using a crosswise infill pattern to assess the effect of different infill patterns on the behavior of the TPU. The two infill patterns had an insignificant effect on the average stress-strain data of the TPU, as shown in Figure 2.
The tests were conducted on the TPU samples, according to the ISO 37 standard, where all the samples were stretched by 800% at a rate of 100mm/s using an electromechanical Instron Universal Testing machine (Instron8801, Instron, Norwood, MA, U.S.A.).

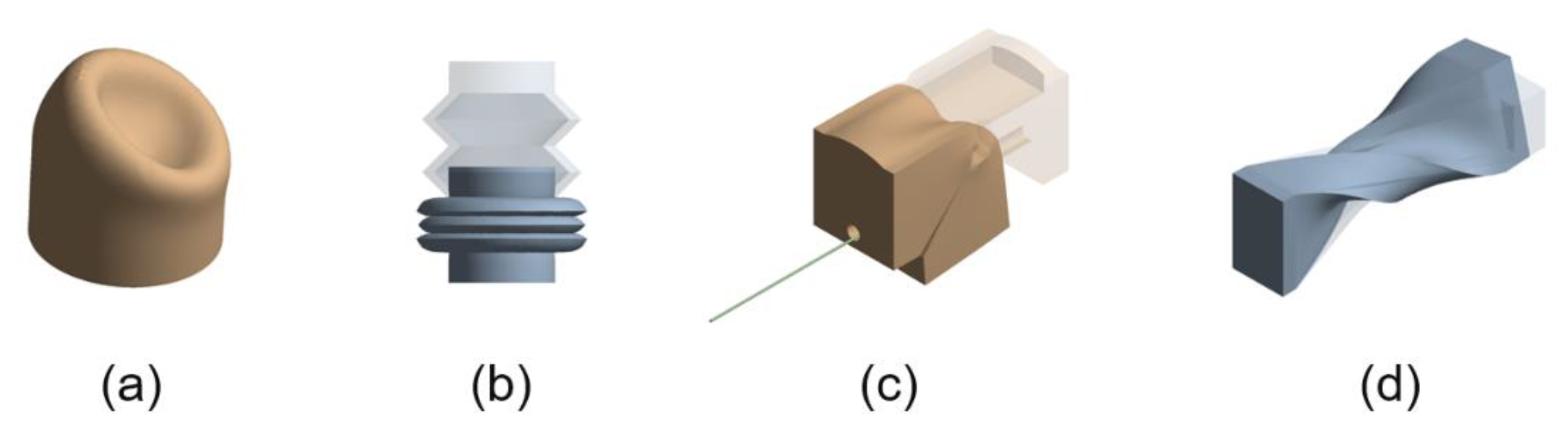
4. 3D Printable Soft Actuators and Sensors

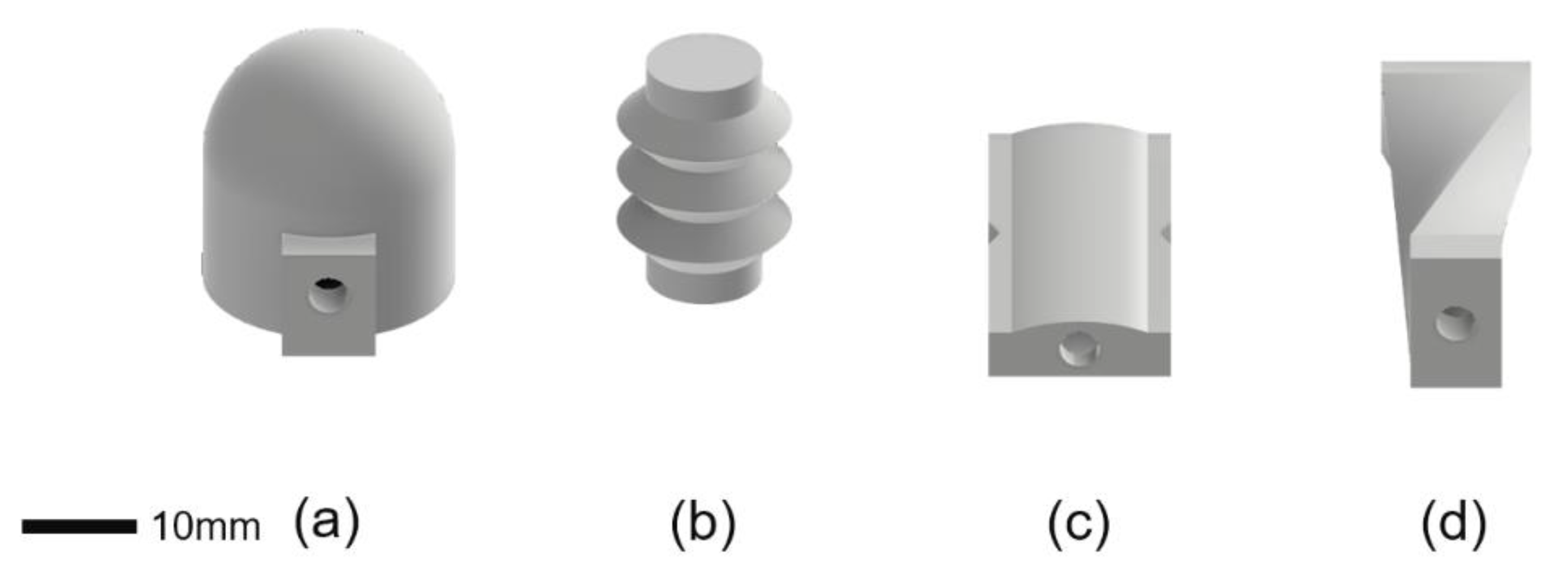
4.1. Bending Soft Vacuum Actuators (SOVA)

Bioinspired bending soft vacuum actuators are developed for use in diverse soft robotic applications, including locomotion robots, adaptive grippers, artificial muscles, and modular soft robotic pneumatic hinges [32]. A single SOVA is shown in Figure 3. The SOVA actuators are activated using negative pressure (i.e., 90% vacuum). When negative pressure is applied to the actuator, consisting of five pneumatic bending hinges, it generates a bending motion, as shown in Figure 3. The objective of the FE simulations was to design a single chamber that could achieve a bending angle higher than 80° when 90% vacuum was applied. The geometry of a single chamber was modified and optimized to achieve this bending angle when 90% vacuum was applied.

4.2. Linear Soft Vacuum Actuators (LSOVA)

Similarly, linear soft vacuum actuators are developed for use in diverse soft robotic applications, including locomotion robots, adaptive grippers, artificial muscles, parallel manipulators, and soft prosthetic fingers [36,37]. A single LSOVA actuator, consisting of five pneumatic chambers, is shown in Figure 4. The objective of the FE simulations was to design a single chamber that could generate a maximum linear displacement under an applied negative pressure (i.e., 95.7% vacuum). The thickness of the thin walls and the topology of a single chamber were optimized to achieve the desired performance. The wall thickness played an important role in the design process since it is directly related to the airtightness of the 3D printed LSOVA actuators.

4.3. Soft Pneumatic Sensing Chambers (SPSC)

Soft pneumatic sensing chambers (SPSCs), that are sensitive to the four main mechanical input modalities of compression, bending, torsion, and rectilinear displacement, are developed for use in diverse robotic applications, such as soft touch human-machine interfaces, soft wearable gloves, soft controllers and throttles, and soft bending sensors. The distinct SPSCs are shown in Figure 5. The main objective of the FE simulations was to modify and optimize the topology of the various SPSCs to obtain a linear relationship between the applied input mechanical loads and the output change in their internal volume [38]. This linearity means that the sensors can be directly 3D printed and used. The relationship between the input displacement and output pressure can be obtained by using two experimental data points and, consequently, can be used consistently since the SPSCs are stable over time, reliable, and repeatable. Therefore, there is no need for an empirical formula that requires an experimental evaluation using a specific experimental setup to obtain and describe the relationship between the input displacement and the output pressure for each 3D printed SPSC. Linearity is one of the desired performance metrics for actuators and sensors.

5. Finite Element Modeling

The FE diagram that shows and describes all the steps involved in a single simulation of a soft pneumatic actuator or sensor is shown in Figure 6.

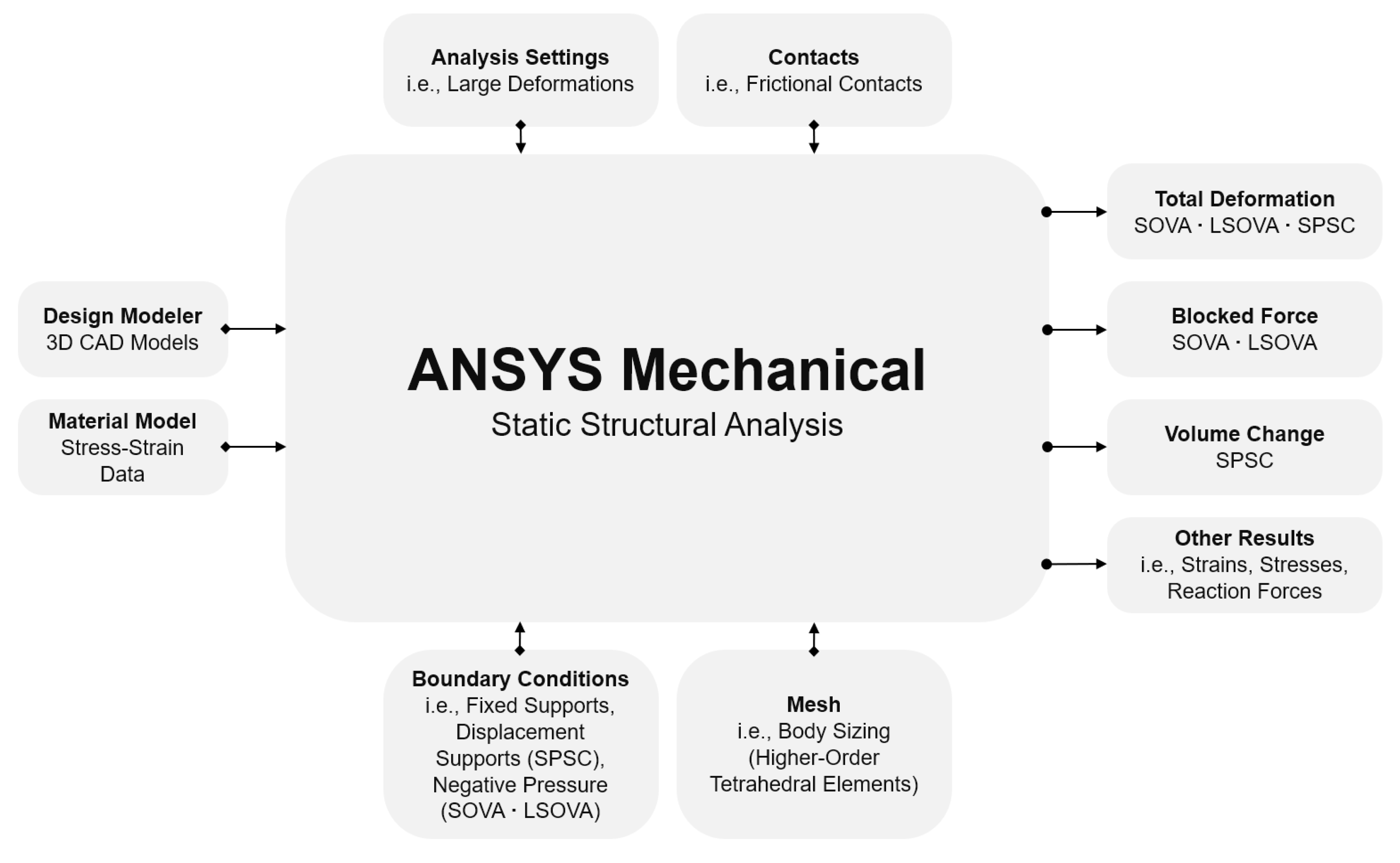
5.1. FEM Software

The FE simulations were performed in ANSYS Workbench (ANSYS Inc.) using a “Static Structural Analysis”. The 3D CAD models of the soft actuators and sensors (i.e., geometries) were directly imported to ANSYS “Design Modeler”. Here, ANSYS was used to perform the FE simulations of the soft actuators and sensors presented, since it offers various hyper-elastic materials models and it is ideal for performing static structural simulations using hyper-elastic materials.

5.2. Material Model

The average experimental stress-strain data of the TPU were imported and used in a manually defined material (i.e., NinjaFlex) in the “Engineering Data”. The data were imported as “Uniaxial Test Data” for the “Hyperelastic Experimental Data”. The TPU was modeled using a five-parameter Mooney-Rivlin hyper-elastic material model that fitted its average stress-strain data. The five-parameter Mooney-Rivlin model was chosen since it best fitted the TPU experimental data compared to other available models, such as Neo-Hookean, Yeoh, and Ogden. The parameters of the material model are listed in Table 1. The model was fitted to the experimental stress-strain data using the available curve fitting tools in ANSYS.

5.3. Meshing

The CAD models of the soft actuators and sensors are meshed using an adaptive mesh with higher-order tetrahedral elements. A sizing function is applied when necessary to obtain a mesh with a specific element size. The mesh used in all cases is suitable for hyper-elastic materials. Since such materials can undergo large deformations, a very fine mesh is not recommended. A relatively coarse mesh is desired for convergence. The mesh size is carefully studied and selected to ensure that the solution is not dependent on it.

5.4. Analysis Settings

The “Large Deformation” option is activated in all the performed simulations to account for the large deflections exhibited by the soft structures upon activation. Additionally, a specific number of “Substeps” of 20 is imposed in each simulation to apply the loads gradually. This is an important parameter to consider since it prevents the load from being applied in one step which, in most cases, results in convergence issues, especially when dealing with soft materials that have a relatively low Young’s modulus.

5.5. Contacts

Frictional contact pairs are defined between all the surfaces that come into contact upon deformation. The behavior of the contacts is set to “Symmetric” to minimize penetration, which results in more accurate results and realistic behavior. The “Augmented Lagrange” formulation is used since it is suitable for frictional and self-contacts.

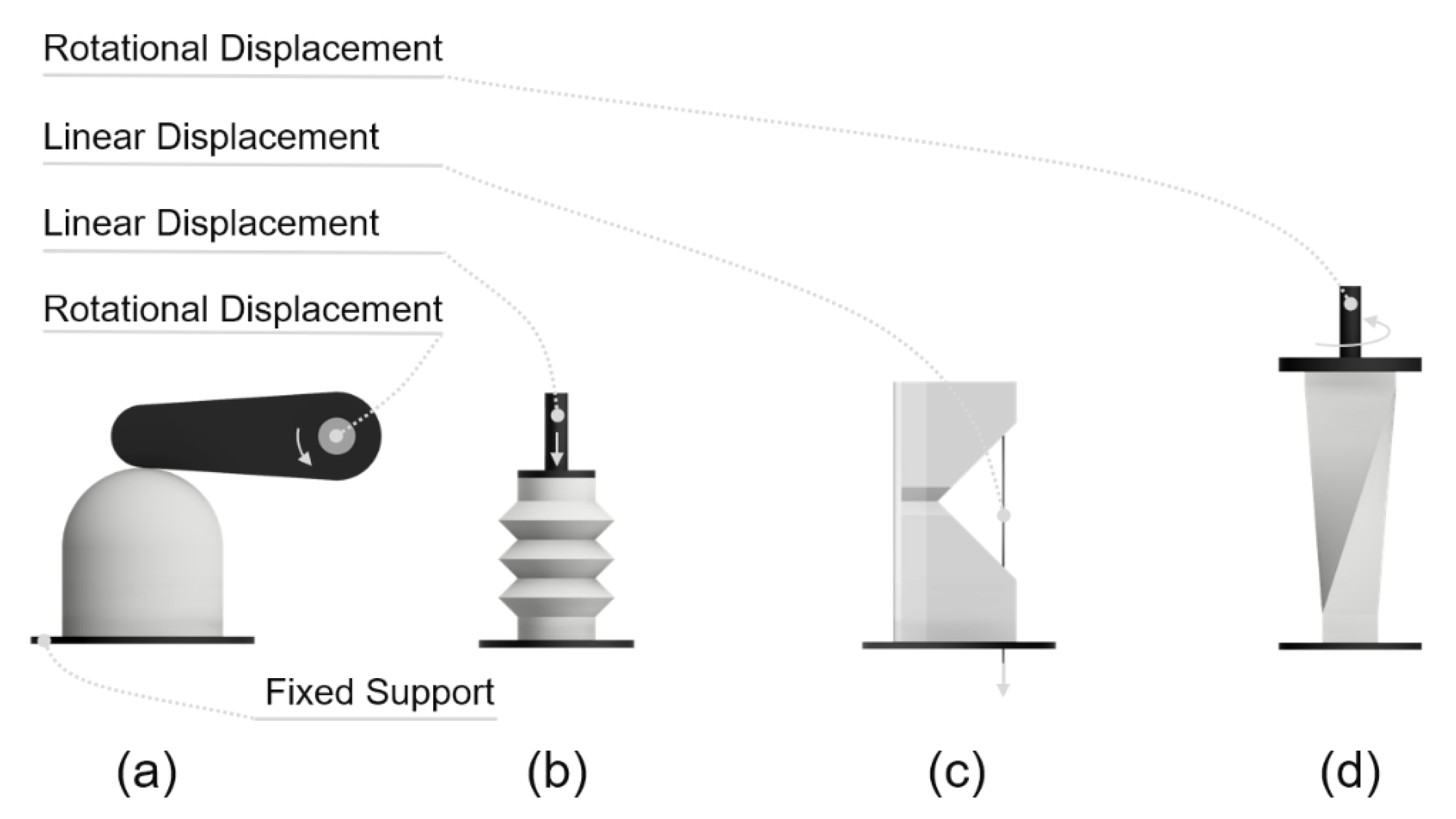
5.6. Boundary Conditions

In addition to the contact pairs defined in all the structures, for SOVA, a “Fixed Support” boundary condition is applied to their base to fix them and a negative pressure (up to 90% vacuum) is applied to the internal surfaces of their hollow chambers. Similarly, for LSOVA, a “Fixed Support” is applied to their base and a negative pressure (up to 95.7% vacuum) is applied to the internal surfaces of their hollow chambers. The FEM and experimental boundary conditions applied to the various SPSCs are shown in Figure 7.
A “Fixed Support” is defined on one side of each structure and an appropriate “Displacement Support” (i.e., a linear or rotational displacement) is imposed on their opposite ends to simulate the mechanical deformations applied for each mode of deformation, as shown in Figure 7.

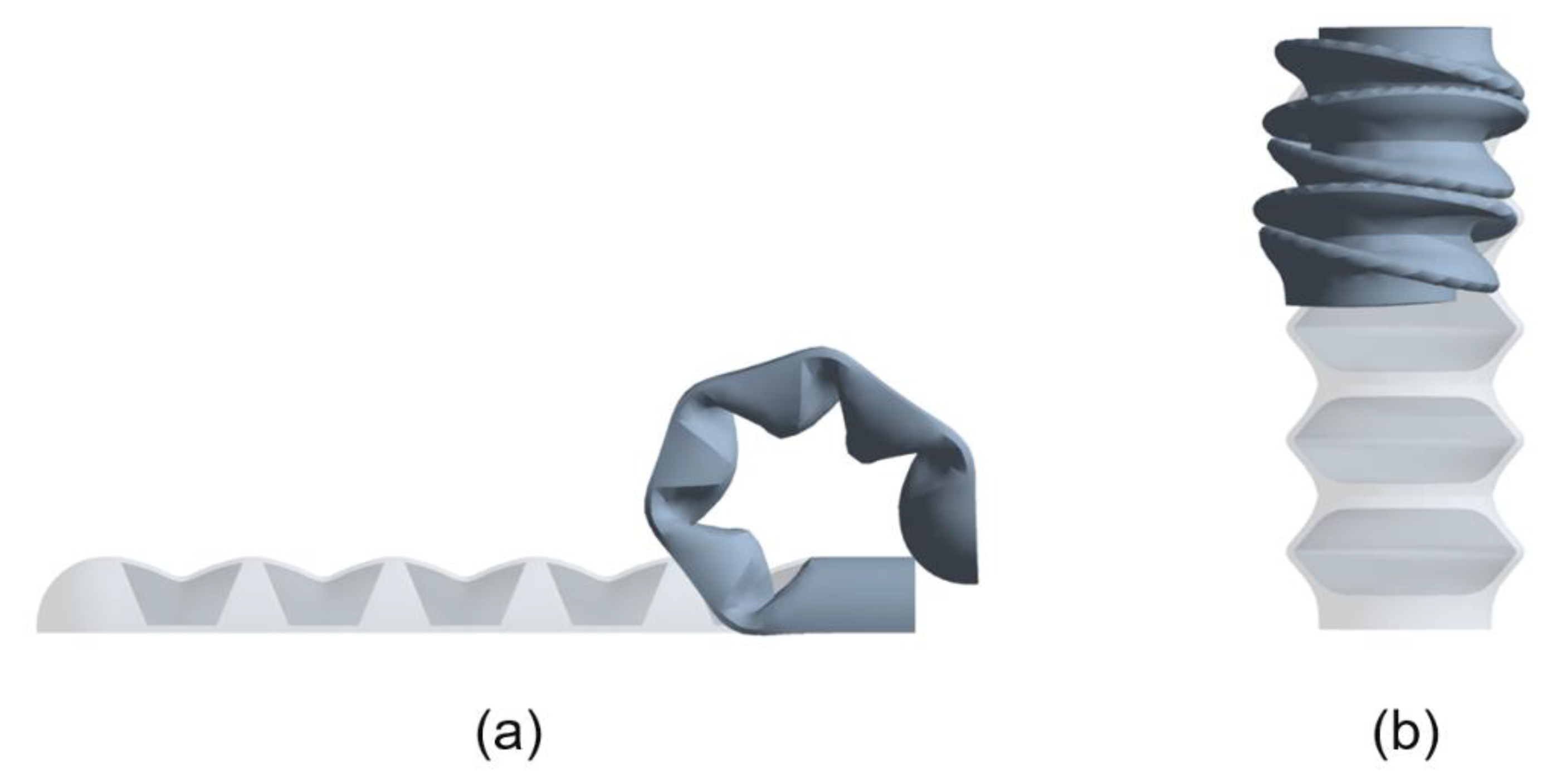
5.7. FEM Results

Various important results can be effectively used to assess and interpret the simulation of a soft body, as shown in Figure 6. The total deformation is the result of the load applied to a soft body and it shows how the body is deformed at different stages of the load applied, as shown in Figure 8. This deformation can be directly compared with its experimental counterpart to verify it. The volume change of the various SPSC was assessed at different stages of the applied load to obtain a relationship between this change and the applied mechanical load, as shown in Figure 9. As stated earlier, the aim was to obtain a linear relationship between the applied mechanical loads and the change in their internal volume. Ideally, a relationship exists between the change in the internal volume (V1/V2) of the soft chambers and the experimental pressure change (P1V1 = P2V2), obtained due to the mechanical deformation applied.
Additionally, the blocked force, which is the reaction force obtained when the actuators are activated but restricted from moving at both sides, can be computed and compared to its experimental counterpart to verify it, as shown in Figure 10. This reaction force is a measure of the output force that a soft actuator can generate.
Finally, the stresses and strain resulting from the load applied can be assessed as presented in Table 2. These two parameters are very important since they should be minimized as much as possible to enhance the lifetime of the soft actuators and sensors developed.

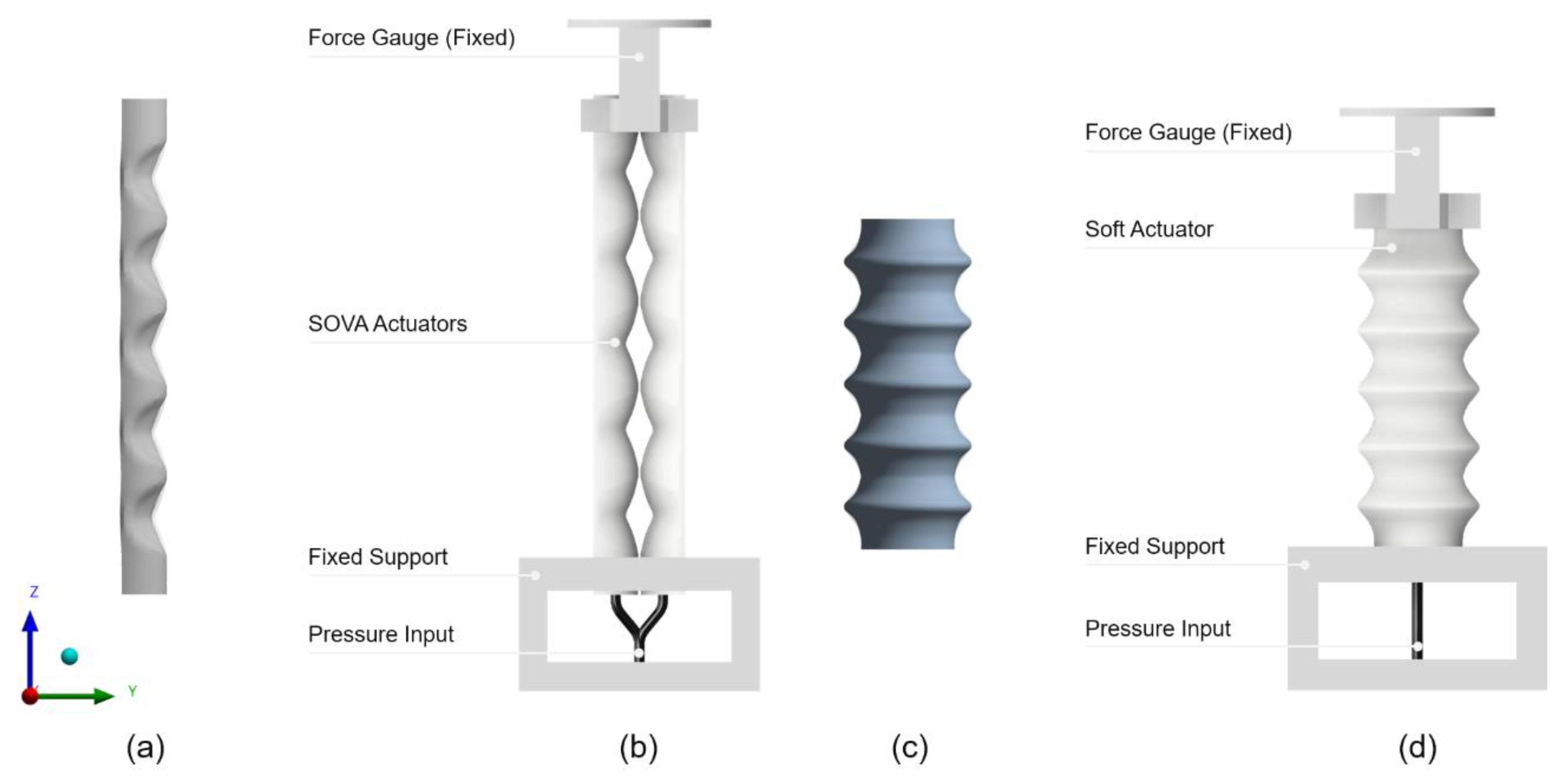
6. Verification of FEM Results

The FE results, in terms of total deformation and output blocked force for SOVA and LSOVA, were compared to their experimental counterparts to assess their validity. In addition, the relationship between the input mechanical loads and the change in the air pressure was obtained experimentally to verify that this relationship is linear, as the FE simulations of the SPSCs predicted.

6.1. Total Deformation

The experimental total deformation of SOVA and LSOVA actuators were obtained and compared with their FEM counterparts. The difference between the experimental bending angle of SOVA of 265.50° and its FEM bending angle of 269.63° is 1.56%. Similarly, the difference between the experimental linear displacement of LSOVA of 35.03 mm and its FEM linear displacement of 39.47 mm is 12.67% (this difference is higher due to the printing artifacts in LSOVA that interfered with its linear displacement [36]). These differences verify that the FEM results can accurately predict the deformation of the soft pneumatic bending and linear actuators.

6.2. Blocked Force

Likewise, the experimental blocked force of SOVA and LSOVA actuators were obtained and compared with their FEM counterparts. The difference between the experimental blocked force of SOVA of 10.72N and the FEM blocked force of 12.33N is 15.02%. This difference is higher since, at higher pressures, the force sensor moved slightly, which reduced the experimental blocked force of SOVA and the two actuators did not perfectly align, as shown in Figure 10b in the experimental setup, compared to the simulation [32]. Although ultimate attention was provided to fabricate two identical SOVA actuators, there were differences in their mechanical output under the same pressure. Similarly, the difference between the experimental blocked force of LSOVA of 27.66N and its FEM blocked force of 28.66N is 3.62%. These differences verify, again, that the FEM results can accurately predict the blocked force of the soft pneumatic bending and linear actuators.

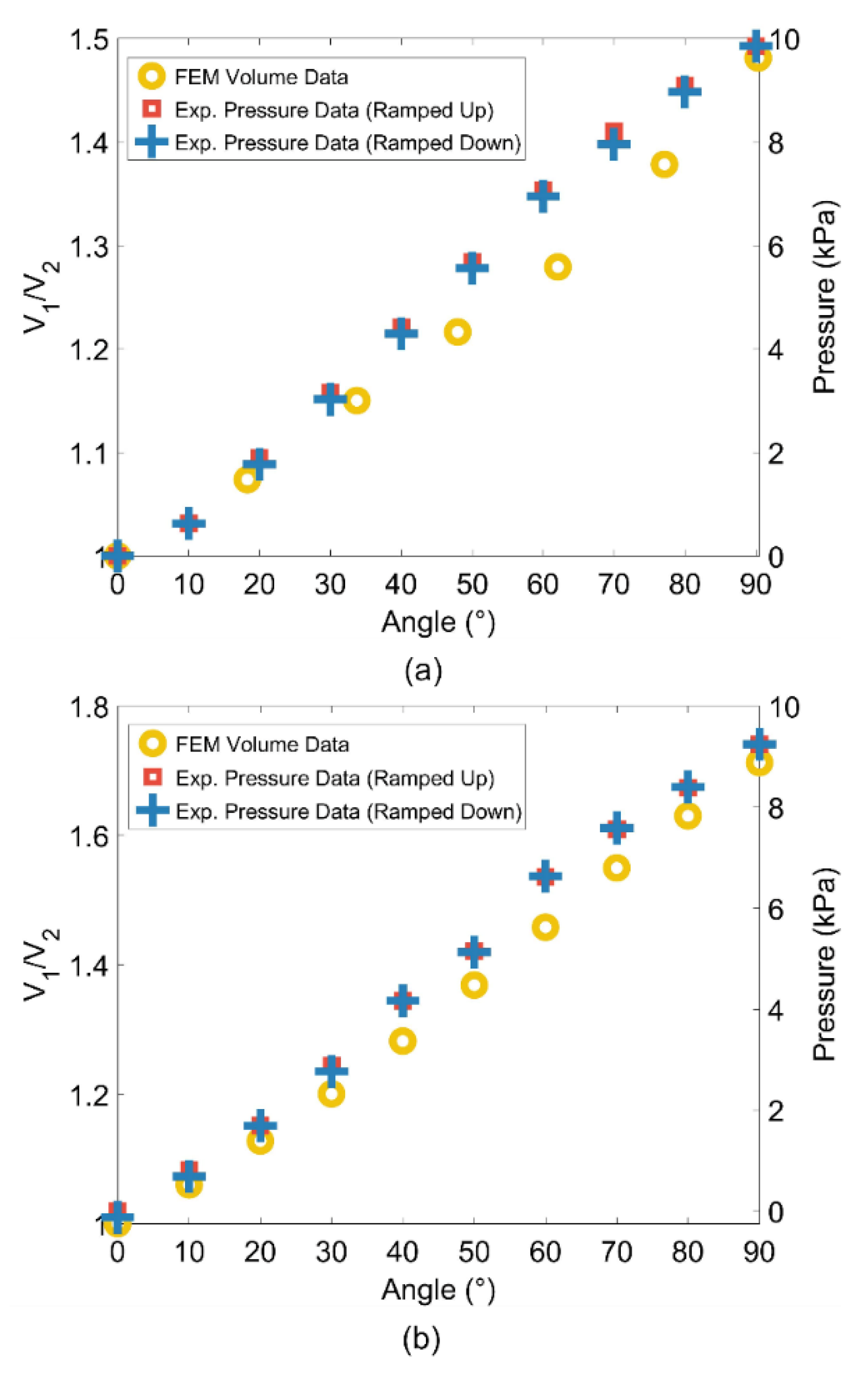
6.3. Volume Change Linearity

The change in the internal volume of the various SPSCs changed linearly with the applied load [38]. The experimental load was ramped up and down by a step of 10°, as shown in Figure 11, where at each step enough time (i.e., 5 s) was given for the various SPSCs to ensure that the pressure value recorded was the final steady-state value. This change was verified experimentally by obtaining a linear relationship between the internal pressure change in the various SPSCs and the corresponding applied load, as shown in Figure 7, since a relationship exists between the change in the internal volume (V1/V2) and the experimental pressure change (P1V1 = P2V2). V1 is the initial volume of single SPSC and V2 is the internal volume at a corresponding input displacement. V1 is computed from the initial CAD models of the SPSCs and V2 is computed from the deformed CAD models, resulting from the FE simulations. Figure 11a shows the experimental linear relationship between the input displacement and the output pressure for the bending sensor and its corresponding FEM linear relationship between the same input displacement and the output volume change. The linear fit of both relationships resulted in a coefficient of determination of R2 = 0.995 for the experimental data and R2 = 0.988 for the FEM data. Similarly, Figure 11b shows the experimental linear relationship between the input displacement and the output pressure for the torsional sensor and its corresponding FEM linear relationship between the same input displacement and the output volume change. The linear fit of both relationships resulted in a coefficient of determination of R2 = 0.996 for the experimental data and R2 = 0.997 for the FEM data. These results show that the FEM predicted the behavior of the physical bending and torsional sensors accurately.

6.4. Stress-Strain Results

The stress and strain results were obtained to assess the regions of each structure that experience high stresses and large strains, as presented in Table 2. High stress and strain values led to a significantly shorter lifetime due to the failure of the material (i.e., separation of the printed layers). However, it is important to note that, although in some regions the stress values might be high, they might not have a significant effect on the lifetime or performance of the structure, since they do not lead to the failure of the actuator or sensor. For instance, for the push button, the high stress leads to a shorter lifetime compared with the lifetime of the remaining SPSCs [38]. The push button sustained 60,000 activation cycles, while the bending sensor, which exhibits higher stresses and strains, sustained more than 150,000 activation cycles, since these high stresses and strains occurred on the top of the sensor in the groove area, which is far from the thin walls. However, for the LSOVA, since the stress concentration occurs on the corners of the thin walls, their lifetime was significantly shorter (~20,000 activation cycles) compared to the SOVA, which sustained more than 120,000 cycles. The stress and strain data were taken into consideration in the design process to minimize them and to ensure that they minimally affected the lifetime of the soft actuators and sensors.

7. Discussion

7.1. Challenges and Recommendations

One challenge encountered is the distortion of some elements in the FE model due to the large mechanical deformations. However, this issue was alleviated by incorporating a coarser mesh, when needed, that was suitable for hyper-elastic materials. The mesh used in each case was selected to verify that the results were accurate and mesh independent.
Another possible challenge was the difficulty to achieve convergence (i.e., solution) due to the multiple contacts involved in each structure. The reason is that the “Symmetric” frictional contacts imposed imply that no penetration is allowed between the surfaces that come into contact. Although in the contact settings, the “Penetration Tolerance” is set to “Program Controlled”, in some cases it is recommended to put a reasonable manual value to relax this constraint to achieve convergence. This tolerance should be chosen such that the simulations must be realistic where no excess penetration is allowed.
Another recommendation for simulating pneumatic soft bodies successfully is that there is no need to include all the details involved in the real geometry in the simulation. However, the simulated geometry must be simplified as much as possible as long as it can be still considered as the real body and captures the most significant features. This simplification will eliminate several problems that might be encountered during meshing and solving to save considerable amounts of computing power and time. For instance, for SOVA and LSOVA, the holes connecting the different chambers were ignored in the simulated body, since they have an insignificant effect on the final solution. Similarly, the input holes in the different SPSCs are ignored in the simulated bodies, as shown in Figure 5 and Figure 9.

7.2. An Effective Solution to a Soft Robotic Challenge

Developing soft pneumatic actuators and sensors for soft robotic systems using various manufacturing techniques and technologies is both time and material consuming. As stated earlier, although the modeling of soft actuators and sensors is an indispensable part of the soft robotics field, it is a very challenging problem, due to nonlinearities. However, in this study, we showed that FEM can be effectively used to handle the nonlinearities involved in modeling soft robotic actuators and sensors to optimize and predict their behavior accurately. Therefore, this study has effectively presented a roadmap for efficiently designing and modeling soft pneumatic actuators and sensors.

7.3. Future Work

In future work, various materials can be considered to fabricate various soft actuators and sensors using different manufacturing technologies with different geometries where their appropriate material models can be developed for use in simulations. Additionally, coupled simulations that account for fluid-structure interaction can be used for both actuators, and sensors and dynamic simulations can be performed to assess their behavior under dynamic conditions where inertial forces are significant. Finally, FEM is not limited to soft actuators and sensors that are made of TPU or silicone materials that are not responsive (i.e., cannot be controlled) to external stimuli. Smart materials (e.g., shape memory alloys, dielectric, ionic polymer-metal composites, coiled polymer fibers, hydrogels, humidity-responsive materials, magnetic responsive structures, etc.) that can be excited by external stimuli can be used as actuators and sensors in some cases and, therefore, can be also simulated.

8. Conclusions

The modeling of soft and highly deformable robotic structures and systems is challenging, due to nonlinearities, such as geometric, material, and contact nonlinearities. Although the modeling of such soft robotic systems is challenging, it should be integrated into the design process of these systems before their fabrication to efficiently and accurately predict their behavior and to optimize their performance and topology to meet certain design and performance requirements. Soft pneumatic actuators and sensors that can be directly 3D printed using open source and low-cost FDM 3D printers can be optimized in terms of performance and topology using FEM that predicts their behavior and performance accurately. This means that tremendous amounts of time and resources can be saved, and that FEM can be efficiently used to handle the nonlinearities involved in modeling soft robotic actuators and sensors, which are essential elements of soft robotic systems.

Author Contributions

Conceptualization, G.A. and C.T.; methodology, G.A. and C.T.; software, C.T.; validation, G.A. and C.T.; writing—original draft preparation, C.T.; writing—review and editing, G.A.; visualization, C.T.; supervision, G.A.; project administration, G.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research has been supported by ARC Centre of Excellence for Electromaterials Science (Grant No. CE140100012) and the University of Wollongong, Australia.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Majidi, C. Soft-Matter Engineering for Soft Robotics. Adv. Mater. Technol. 2019, 4, 1800477. [Google Scholar] [CrossRef] [Green Version]
  2. Alici, G. Softer is Harder: What Differentiates Soft Robotics from Hard Robotics? MRS Adv. 2018, 3, 1557–1568. [Google Scholar] [CrossRef] [Green Version]
  3. Kim, S.; Laschi, C.; Trimmer, B. Soft robotics: A bioinspired evolution in robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef] [PubMed]
  4. Trimmer, B. Soft robots. Curr. Biol. 2013, 23, R639–R641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [Green Version]
  6. Sencadas, V.; Tawk, C.; Alici, G. Highly Sensitive Soft Foam Sensors to Empower Robotic Systems. Adv. Mater. Technol. 2019, 4, 1900423. [Google Scholar] [CrossRef]
  7. Wang, H.; Totaro, M.; Beccai, L. Toward Perceptive Soft Robots: Progress and Challenges. Adv. Sci. 2018, 5, 1800541. [Google Scholar] [CrossRef]
  8. Zolfagharian, A.; Kaynak, A.; Kouzani, A. Closed-loop 4D-printed soft robots. Mater. Des. 2020, 188, 108411. [Google Scholar] [CrossRef]
  9. Rich, S.I.; Wood, R.J.; Majidi, C. Untethered soft robotics. Nat. Electron. 2018, 1, 102–112. [Google Scholar] [CrossRef]
  10. Schmitt, F.; Piccin, O.; Barbé, L.; Bayle, B. Soft Robots Manufacturing: A Review. Front. Robot. AI 2018, 5, 84. [Google Scholar] [CrossRef] [Green Version]
  11. Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.-H.; Lee, J.-W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [Green Version]
  12. Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
  13. Zolfagharian, A.; Kouzani, A.Z.; Khoo, S.Y.; Moghadam, A.A.A.; Gibson, I.; Kaynak, A. Evolution of 3D printed soft actuators. Sens. Actuators A Phys. 2016, 250, 258–272. [Google Scholar] [CrossRef]
  14. Walker, S.; Yirmibeşoğlu, O.D.; Daalkhaijav, U.; Mengüç, Y. 14—Additive manufacturing of soft robots. In Robotic Systems and Autonomous Platforms; Walsh, S.M., Strano, M.S., Eds.; Woodhead Publishing: Cambridge, UK, 2019; pp. 335–359. [Google Scholar] [CrossRef]
  15. Tolley, M.T.; Shepherd, R.F.; Mosadegh, B.; Galloway, K.C.; Wehner, M.; Karpelson, M.; Wood, R.J.; Whitesides, G.M. A Resilient, Untethered Soft Robot. Soft Robot. 2014, 1, 213–223. [Google Scholar] [CrossRef]
  16. Jun, S.; Vito, C.; Dario, F.; Herbert, S. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar]
  17. Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467. [Google Scholar] [CrossRef] [Green Version]
  18. Marchese, A.D.; Katzschmann, R.K.; Rus, D. A Recipe for Soft Fluidic Elastomer Robots. Soft Robot. 2015, 2, 7–25. [Google Scholar] [CrossRef] [Green Version]
  19. Lipson, H. Challenges and Opportunities for Design, Simulation, and Fabrication of Soft Robots. Soft Robot. 2013, 1, 21–27. [Google Scholar] [CrossRef]
  20. Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 2016. [Google Scholar] [CrossRef] [Green Version]
  21. Overvelde, J.T.B.; Mengüç, Y.; Polygerinos, P.; Wang, Y.; Wang, Z.; Walsh, C.J.; Wood, R.J.; Bertoldi, K. Mechanical and electrical numerical analysis of soft liquid-embedded deformation sensors analysis. Extreme Mech. Lett. 2014, 1, 42–46. [Google Scholar] [CrossRef]
  22. Sencadas, V.; Tawk, C.; Alici, G. Environmentally Friendly and Biodegradable Ultrasensitive Piezoresistive Sensors for Wearable Electronics Applications. ACS Appl. Mater. Interfaces 2020, 12, 8761–8772. [Google Scholar] [CrossRef] [PubMed]
  23. Moseley, P.; Florez, J.M.; Sonar, H.A.; Agarwal, G.; Curtin, W.; Paik, J. Modeling, Design, and Development of Soft Pneumatic Actuators with Finite Element Method. Adv. Eng. Mater. 2016, 18, 978–988. [Google Scholar]
  24. Cao, J.; Qin, L.; Liu, J.; Ren, Q.; Foo, C.C.; Wang, H.; Lee, H.P.; Zhu, J. Untethered soft robot capable of stable locomotion using soft electrostatic actuators. Extreme Mech. Lett. 2018, 21, 9–16. [Google Scholar] [CrossRef]
  25. Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef] [Green Version]
  26. Bieze, T.M.; Largilliere, F.; Kruszewski, A.; Zhang, Z.; Merzouki, R.; Duriez, C. Finite Element Method-Based Kinematics and Closed-Loop Control of Soft, Continuum Manipulators. Soft Robot. 2018, 5, 348–364. [Google Scholar] [CrossRef] [Green Version]
  27. Duriez, C. Control of elastic soft robots based on real-time finite element method. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3982–3987. [Google Scholar]
  28. Zhang, Z.; Bieze, T.M.; Dequidt, J.; Kruszewski, A.; Duriez, C. Visual servoing control of soft robots based on finite element model. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2895–2901. [Google Scholar]
  29. Faure, F.; Duriez, C.; Delingette, H.; Allard, J.; Gilles, B.; Marchesseau, S.; Talbot, H.; Courtecuisse, H.; Bousquet, G.; Peterlik, I.; et al. SOFA: A Multi-Model Framework for Interactive Physical Simulation. In Soft Tissue Biomechanical Modeling for Computer Assisted Surgery; Payan, Y., Ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2012; pp. 283–321. [Google Scholar] [CrossRef] [Green Version]
  30. Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
  31. Galley, A.; Knopf, G.; Kashkoush, M. Pneumatic Hyperelastic Actuators for Grasping Curved Organic Objects. Actuators 2019, 8, 76. [Google Scholar] [CrossRef] [Green Version]
  32. Tawk, C.; In Het Panhuis, M.; Spinks, G.M.; Alici, G. Bioinspired 3D Printable Soft Vacuum Actuators for Locomotion Robots, Grippers and Artificial Muscles. Soft Robot. 2018, 5, 685–694. [Google Scholar] [CrossRef]
  33. Rieffel, J.; Saunders, F.; Nadimpalli, S.; Zhou, H.; Hassoun, S.; Rife, J.; Trimmer, B. Evolving soft robotic locomotion in PhysX. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, Montreal, QC, Canada, 8–12 July 2009; pp. 2499–2504. [Google Scholar]
  34. Hiller, J.; Lipson, H. Dynamic Simulation of Soft Multimaterial 3D-Printed Objects. Soft Robot. 2014, 1, 88–101. [Google Scholar] [CrossRef]
  35. Renda, F.; Boyer, F.; Dias, J.; Seneviratne, L. Discrete Cosserat Approach for Multisection Soft Manipulator Dynamics. IEEE Trans. Robot. 2018, 34, 1518–1533. [Google Scholar] [CrossRef] [Green Version]
  36. Tawk, C.; Spinks, G.M.; In Het Panhuis, M.; Alici, G. 3D Printable Linear Soft Vacuum Actuators: Their Modeling, Performance Quantification and Application in Soft Robotic Systems. IEEE ASME Trans. Mechatron. 2019, 24, 2118–2129. [Google Scholar] [CrossRef]
  37. Tawk, C.; Spinks, G.M.; In Het Panhuis, M.; Alici, G. 3D Printable Vacuum-Powered Soft Linear Actuators. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 50–55. [Google Scholar]
  38. Tawk, C.; In Het Panhuis, M.; Spinks, G.M.; Alici, G. Soft Pneumatic Sensing Chambers for Generic and Interactive human-machine Interfaces. Adv. Intell. Syst. 2019, 1, 1900002. [Google Scholar] [CrossRef] [Green Version]
Robotics 09 00052 g001 550
Figure 1. The design process for simulating and fabricating airtight and optimized soft 3D printable pneumatic actuators and sensors.
Figure 1. The design process for simulating and fabricating airtight and optimized soft 3D printable pneumatic actuators and sensors.
Robotics 09 00052 g001
Robotics 09 00052 g002 550
Figure 2. Experimental stress-strain data of the TPU used to 3D print the soft pneumatic actuators and sensors. Inset: Longitudinal sample (top) and crosswise sample (bottom).
Figure 2. Experimental stress-strain data of the TPU used to 3D print the soft pneumatic actuators and sensors. Inset: Longitudinal sample (top) and crosswise sample (bottom).
Robotics 09 00052 g002
Robotics 09 00052 g003 550
Figure 3. Bending soft vacuum actuators (SOVA). The initial position of a single SOVA actuator when (a) no vacuum is applied and (b) its corresponding final position when 90% vacuum is applied.
Figure 3. Bending soft vacuum actuators (SOVA). The initial position of a single SOVA actuator when (a) no vacuum is applied and (b) its corresponding final position when 90% vacuum is applied.
Robotics 09 00052 g003
Robotics 09 00052 g004 550
Figure 4. Linear soft vacuum actuators (LSOVA). The initial position of a single LSOVA actuator when (a) no vacuum is applied and (b) its corresponding final position when 95.7% vacuum is applied.
Figure 4. Linear soft vacuum actuators (LSOVA). The initial position of a single LSOVA actuator when (a) no vacuum is applied and (b) its corresponding final position when 95.7% vacuum is applied.
Robotics 09 00052 g004
Robotics 09 00052 g005 550
Figure 5. Soft pneumatic sensing chambers (SPSCs). 3D printed (a) Push Button (i.e., touch sensor), (b) Linear Sensor, (c) Bending Sensor, and (d) Torsional Sensor.
Figure 5. Soft pneumatic sensing chambers (SPSCs). 3D printed (a) Push Button (i.e., touch sensor), (b) Linear Sensor, (c) Bending Sensor, and (d) Torsional Sensor.
Robotics 09 00052 g005
Robotics 09 00052 g006 550
Figure 6. Finite element simulations diagram for pneumatic soft actuators and sensors.
Figure 6. Finite element simulations diagram for pneumatic soft actuators and sensors.
Robotics 09 00052 g006
Robotics 09 00052 g007 550
Figure 7. The applied boundary conditions on each SPSC. (a) The push button is activated through a solid rotating crank that pushes through its soft deformable wall. (b) The linear sensor is attached to a motor that generates a rectilinear stroke. (c) The bending sensor is attached to a soft flexure joint that generates a bending angle between 0° and 90° when a tendon is pulled using a linear motor. (d) The torsional sensor is attached to a servo motor that generates an angular displacement between 0° and 90°.
Figure 7. The applied boundary conditions on each SPSC. (a) The push button is activated through a solid rotating crank that pushes through its soft deformable wall. (b) The linear sensor is attached to a motor that generates a rectilinear stroke. (c) The bending sensor is attached to a soft flexure joint that generates a bending angle between 0° and 90° when a tendon is pulled using a linear motor. (d) The torsional sensor is attached to a servo motor that generates an angular displacement between 0° and 90°.
Robotics 09 00052 g007
Robotics 09 00052 g008 550
Figure 8. FEM deformed shape for (a) SOVA when 90% vacuum is applied and (b) LSOVA when 95.7% vacuum is applied.
Figure 8. FEM deformed shape for (a) SOVA when 90% vacuum is applied and (b) LSOVA when 95.7% vacuum is applied.
Robotics 09 00052 g008
Robotics 09 00052 g009 550
Figure 9. FEM deformed shape for (a) the push button when 24.5° remote rotating displacement is applied on the crank which not shown for visual purposes, (b) linear sensor when a 10 mm displacement is applied, (c) bending sensor when a 90° bending angle is applied by pulling the tendon, and (d) torsional sensor when a 90° remote rotating displacement is applied on its end.
Figure 9. FEM deformed shape for (a) the push button when 24.5° remote rotating displacement is applied on the crank which not shown for visual purposes, (b) linear sensor when a 10 mm displacement is applied, (c) bending sensor when a 90° bending angle is applied by pulling the tendon, and (d) torsional sensor when a 90° remote rotating displacement is applied on its end.
Robotics 09 00052 g009
Robotics 09 00052 g010 550
Figure 10. SOVA and LSOVA blocked force. (a) SOVA FEM deformed shape results (i.e., SOVA behavior when both horizontal upper and lower faces at both ends are fixed and restricted from moving using a fixed support). (b) SOVA experimental blocked force setup, where two actuators are placed and fixed facing each other. (c) LSOVA deformed shape results (i.e., LSOVA behavior when both horizontal upper and lower faces at both ends are fixed and restricted from moving using a fixed support). (d) LSOVA experimental blocked force setup.
Figure 10. SOVA and LSOVA blocked force. (a) SOVA FEM deformed shape results (i.e., SOVA behavior when both horizontal upper and lower faces at both ends are fixed and restricted from moving using a fixed support). (b) SOVA experimental blocked force setup, where two actuators are placed and fixed facing each other. (c) LSOVA deformed shape results (i.e., LSOVA behavior when both horizontal upper and lower faces at both ends are fixed and restricted from moving using a fixed support). (d) LSOVA experimental blocked force setup.
Robotics 09 00052 g010
Robotics 09 00052 g011 550
Figure 11. FEM versus experimental results for (a) a soft bending sensor and (b) a soft torsional sensor.
Figure 11. FEM versus experimental results for (a) a soft bending sensor and (b) a soft torsional sensor.
Robotics 09 00052 g011
Table
Table 1. TPU hyper-elastic material model constants.
Table 1. TPU hyper-elastic material model constants.
Hyper-Elastic Material ModelMaterial ConstantValue (Unit)
Five-parameter
Mooney-Rivlin 		C10−0.233 (MPa)
C012.562 (MPa)
C200.116 (MPa)
C11−0.561 (MPa)
C020.900 (MPa)
Incompressibility Parameter D10.000 MPa−1
Table
Table 2. stress-strain FEM results when the maximum input load is applied to each structure.
Table 2. stress-strain FEM results when the maximum input load is applied to each structure.
Structure Equivalent Elastic Stress (von-Mises) (MPa)Equivalent Elastic Strain (von-Mises) (mm/mm)
SOVA2.7240.185
LSOVA6.1930.300
Push Button25.2760.10378
Linear Sensor3.09330.222
Bending Sensor8.4560.656
Torsional Sensor1.1740.099

Share and Cite

MDPI and ACS Style

Tawk, C.; Alici, G. Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors. Robotics 2020, 9, 52. https://doi.org/10.3390/robotics9030052

AMA Style

Tawk C, Alici G. Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors. Robotics. 2020; 9(3):52. https://doi.org/10.3390/robotics9030052

Chicago/Turabian Style

Tawk, Charbel, and Gursel Alici. 2020. "Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors" Robotics 9, no. 3: 52. https://doi.org/10.3390/robotics9030052

APA Style

Tawk, C., & Alici, G. (2020). Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors. Robotics, 9(3), 52. https://doi.org/10.3390/robotics9030052

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop