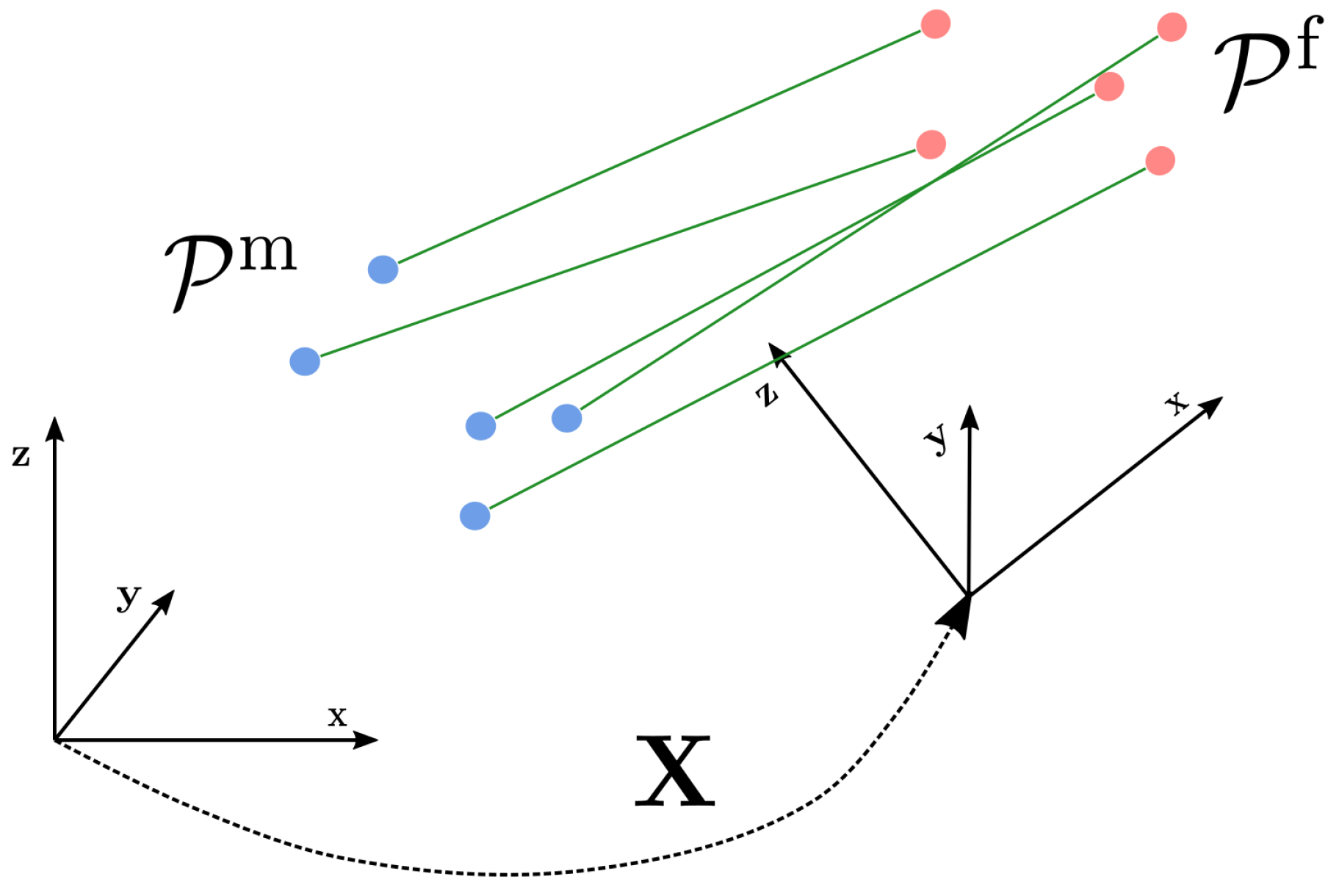
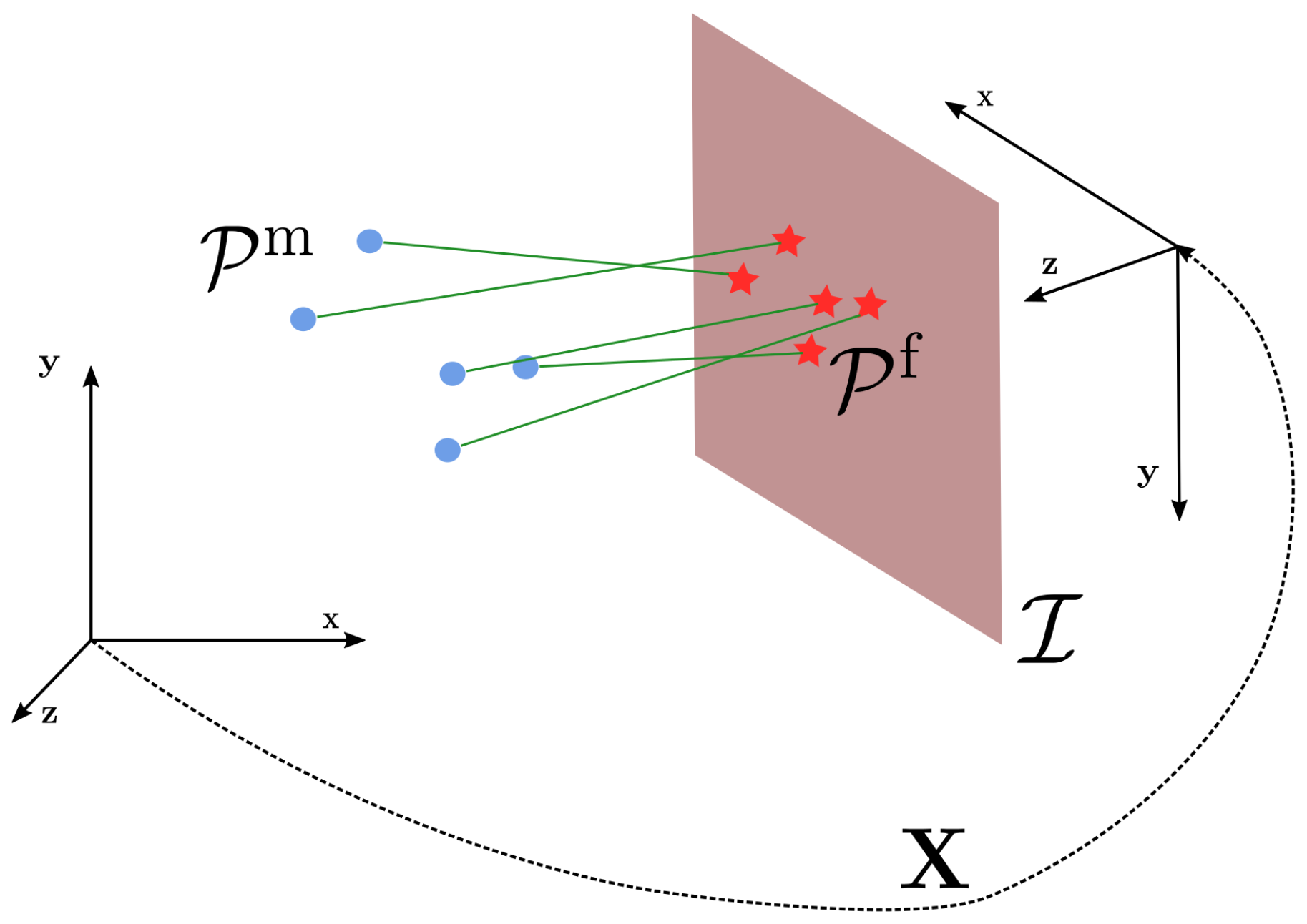
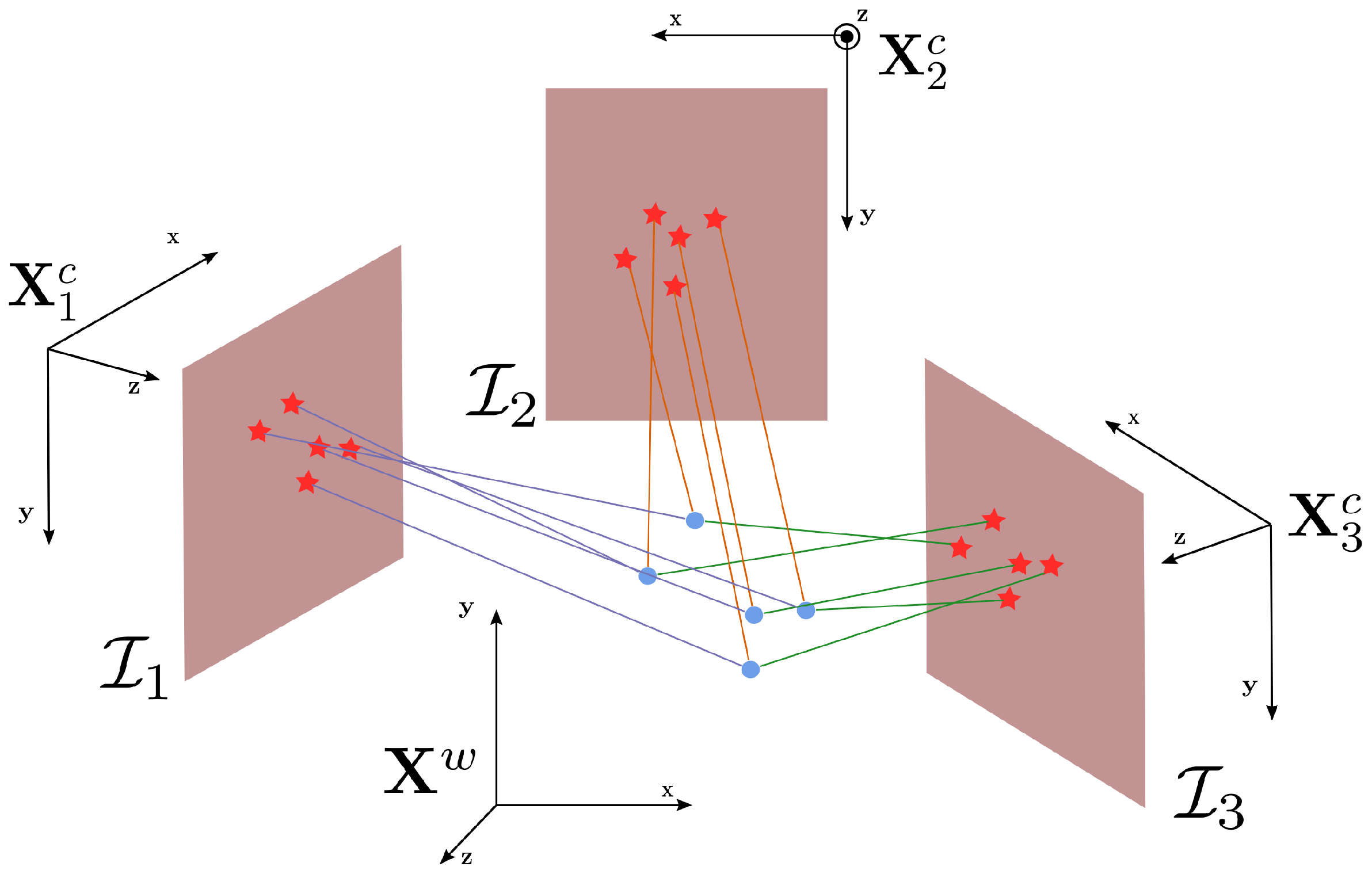
1. Introduction
Iterative Least-Squares (ILS) solvers are core building blocks of many robotic applications, systems, and subsystems [
1]. This technique has been traditionally used for calibration [
2,
3,
4], registration [
5,
6,
7], and global optimization [
8,
9,
10,
11]. In particular, modern Simultaneous Localization and Mapping (SLAM) systems typically employ multiple ILS solvers at different levels: in computing the incremental ego-motion of the sensor, in refining the localization of a robot upon loop closure and—most notably—to obtain a globally consistent map. Similarly, in several computer vision systems, ILS is used to compute/refine camera parameters, estimating the structure of a scene, the position of the camera or both. Many inference problems in robotics are effectively described by a factor graph [
12], which is a graphical model expressing the joint likelihood of the
known measurements with respect to a set of unknown conditional variables. Solving a factor graph requires finding the values of the variables that maximize the joint likelihood of the measurements. If the noise affecting the sensor data are Gaussian, the solution of a factor graph can be computed by an ILS solver implementing variants of the well known Gauss–Newton (GN) algorithm.
The relevance of the topic has been addressed by several works such as GTSAM [
9],
[
8], SLAM++ [
13], or the Ceres solver [
10] by Google. These systems have grown over time to include comprehensive libraries of factors and variables that can tackle a large variety of problems, and, in most cases, these systems can be used as black boxes. Since they typically consist of an extended codebase, entailing them to a particular application/architecture to achieve maximum performance is a non-trivial task. In contrast, extending these systems to approach new problems is typically easier than customizing: in this case, the developer has to implement some additional functionalities/classes according to the API of the system. In addition, in this case, however, an optimal implementation might require a reasonable knowledge of the solver internals.
We believe that, at the current time, a researcher working in robotics should possess the knowledge on how to design factor graph solvers for specific problems. Having this skill enables us to both effectively extend existing systems and realize custom software that leverages maximally on the available hardware. Accordingly, the primary goal of this paper is to provide the reader with a methodology on how to mathematically define such a solver for a problem. To this extent in
Section 4, we start by revising the nonlinear least squares by highlighting the connections between inference on conditional Gaussian distributions and ILS. In the same section, we introduce the ⊞ (i.e., boxplus) method introduced by Hertzberg et al. [
14] to deal with non-Euclidean domains. Furthermore, we discuss how to cope with outliers in the measurements through robust cost functions and we outline the effects of sparsity in factor graphs. We conclude the section by presenting a general methodology on how to design factors and variables that describe a problem. In
Section 5, we validate this methodology by providing examples that approach four prominent problems in Robotics: Iterative Closest Point (ICP), projective registration, Bundle Adjustment (BA), and Pose-Graph Optimization (PGO). When it comes to the implementation of a solver, several choices have to be made in the light of the problem structure, the compute architecture and the operating conditions (online or batch). In this work, we characterize ILS problems, distinguishing between dense and sparse, batch and incremental, stationary, and non-stationary based on their structure and application domain. In
Section 2, we provide a more detailed description of these characteristics, while, in
Section 3, we discuss how ILS has been used in the literature to approach various problems in Robotics and by highlighting how addressing a problem according to its traits leads to effective solutions.
The second orthogonal goal of this work is to propose a unifying system that deals with dense/sparse, stationary/non-stationary, and batch problems, with no apparent performance loss compared to ad-hoc solutions. We build on the ideas that are at the base of the
optimizer [
8], in order to address some requirements arising from users and developers, namely: fast convergence, small runtime per iteration, rapid prototyping, trade-off between implementation effort and performances, and, finally, code compactness. In
Section 6, we highlight from the general algorithm outlined
Section 4 a set of functionalities that result in a modular, decoupled, and minimal design. This analysis ultimately leads to a modern compact and efficient C++ library released under BSD3 license for ILS of Factor Graphs that relies on a component model, presented in
Section 7, that effectively runs on both on
x86-64 and
ARM platforms (Source code:
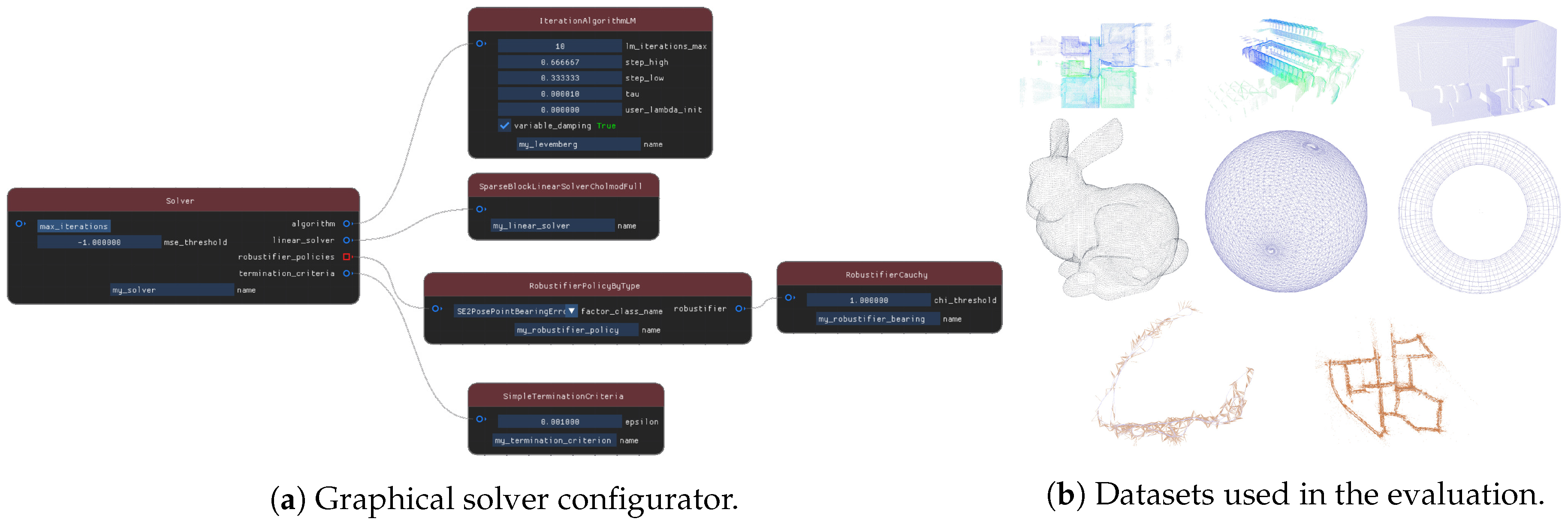
http://srrg.gitlab.io/srrg2-solver.html). To ease prototyping, we offer an interactive environment to graphically configure the solver (
Figure 1a). The core library of our solver consists of no more than 6000 lines of C++ code, whereas the companion libraries implementing a large set of factors and variables for approaching problems -for example, 2D/3D ICP, projective registration, BA, 2D/3D PGO and Pose-Landmark Graph Optimization (PLGO), and many others—is at the time of this writing below 4000 lines. Our system relies on our visual component framework, image processing, and visualization libraries that contain no optimization code and consists of approximately 20,000 lines. To validate our claims, we conducted extensive comparative experiments on publicly available datasets (
Figure 1b)—in dense and sparse scenarios. We compared our solver with sparse approaches such as GTSAM,
and Ceres, and with dense ones, such as the well-known PCL library [
15]. The experiments presented in
Section 8 confirm that our system has performances that are on par with other state-of-the-art frameworks.
Summarizing, the contribution of this work is twofold:
- —
We present a methodology on how to design a solver for a generic class of problems, and we exemplify such a methodology by showing how it can be used to approach a relevant subset of problems in Robotics.
- —
We propose an open-source, component-based ILS system that aims to coherently address problems having a different structure, while providing state-of-the-art performances.
2. Taxonomy of ILS Problems
Whereas the theory on ILS is well-known, the effectiveness of an implementation greatly depends on the structure of the problem being addressed and on the operating conditions. We qualitatively distinguish between dense and sparse problems, by discriminating on the connectivity of the factor graph. A dense problem is characterized by many measurements affected by relatively few variables. This occurs in typical registration problems, where the likelihoods of the measurements (for example, the intensities of image pixels) depend on a single variable expressing the sensor position. In contrast, sparse problems are characterized by measurements that depend only on a small subset of variables. Examples of sparse problems include PGO or BA.
A further orthogonal classification of the problems divides them into
stationary and
non-stationary. A problem is stationary when the associations do not change during the iterations of the optimization. This occurs when the data-association is known a priori with sufficient certainty. Conversely, non-stationary problems admit associations that might change during the optimization, as a result of a modification of the variables being estimated. A typical case of a non-stationary problem is point registration [
16], when the associations between the points in the model and the references are computed at each iteration based on a heuristic that depends on the current estimate of their displacement.
Finally, the problem might be extended over time by adding new variables and measurements. Several Graph-Based SLAM systems exploit this intrinsic characteristic in online applications, reusing the computation done while solving the original problem to determine the solution for the augmented one. We refer to a solver with this capability as an incremental solver, in contrast to batch solvers that carry on all the computation from scratch once the factor graph is augmented.
In this taxonomy, we left out other crucial aspects that affect the convergence basin of the solver such as the linearity of the measurement function, or the domain of variables and measurements. Exploiting the structure of these domains has shown to provide even more efficient solutions [
17], with the obvious shortcoming that they are restricted to the specific problem they are designed to address.
Using a sparse stationary solver on a dense non-stationary problem results in carrying on useless computation that hinders the usability of the system. Using a dense dynamic solver to approach a sparse stationary problem presents similar issues. State-of-the-art open-source solvers like the ones mentioned in
Section 1 focus on sparse stationary or incremental problems. Dense solvers are usually within the application/library using it and tightly coupled to it. On the one hand, this allows reducing the time per iteration, while, on the other hand, it results in avoidable code replication when multiple systems are integrated. This might result in potential inconsistencies among program parts and consequent bugs.
4. Least Squares Minimization
This section describes the foundations of ILS minimization. We first present a formulation of the problem that highlights its probabilistic aspects (
Section 4.1). In
Section 4.2, we review some basic rules for manipulating the Normal distribution and we apply these rules to the definition presented in
Section 4.1, leading to the initial definition of linear Least-Squares (LS). In
Section 4.3, we discuss the effects of a nonlinear observation model, assuming that both the state space and the measurements space are Euclidean. Subsequently, we relax this assumption on the structure of state and measurement spaces, proposing a solution that uses smooth manifold encapsulation. In
Section 4.4, we introduce effects of outliers in the optimization and we show commonly used methodologies to reject them. Finally, in
Section 4.5, we address the case of a large, sparse problem characterized by measurement functions depending only on small subsets of the state. Classical problems such as SLAM or BA fall in this category and are characterized by a rather sparse structure.
4.1. Problem Formulation
Let
be a stationary system whose non-observable state variable is represented by
and let
be a measurement, i.e., a perception of the environment. The state is distributed according to a prior distribution
, while the conditional distribution of the measurement given the state
is known.
is commonly referred to as the
observation model. Our goal is to find the most likely distribution of states, given the measurements—i.e.,
. A straightforward application of the Bayes rule results in the following:
The proportionality is a consequence of the normalization factor , which is constant.
In the remainder of this work, we will consider two key assumptions:
- –
the prior about the states is uniform, i.e.,
- –
the observation model is Gaussian, i.e.,
Equation (
2) expresses the uniform prior about the states using the canonical parameterization of the Gaussian. Alternatively, the moment parameterization characterizes the Gaussian by the information matrix—i.e., the inverse of the covariance matrix
—and the information vector
. The canonical parameterization is better suited to represent a non-informative prior, since
does not lead to numerical instabilities while implementing the algorithm. In contrast, the moment parameterization can express in a stable manner situations of absolute certainty by setting
. In the remainder, we will use both representations upon convenience, their relation being clear.
In Equation (
3), the mean
of the predicted measurement distribution is controlled by a generic nonlinear function of the state
, commonly referred to as
measurement function. In the next section, we will derive the solution for Equation (
1), imposing that the measurement function is an
affine transformation of the state—i.e.,
—illustrated in
Figure 2. In
Section 4.3, we address the more general nonlinear case.
4.2. Linear Measurement Function
In the case of linear measurement function, expressed as
, the prediction model has the following form:
with
constant and
being the mean of the prior. For convenience, we express the stochastic variable
as
Switching between
and
is achieved by summing or subtracting the mean. To retrieve a solution for Equation (
1), we first compute the joint probability of
using the chain rule and, subsequently, we condition this joint distribution with respect to the known measurement
. For further details on the Gaussian manipulation, we refer the reader to [
59].
4.2.1. Chain Rule
Under the Gaussian assumptions made in the previous section, the parameters of the joint distribution over states and measurements
have the following block structure:
The value of the terms in Equation (
7) are obtained by applying the chain rule to multivariate Gaussians to Equations (
4) and (
5), according to [
59], and they result in the following:
Since we assumed the prior to be non-informative, we can set
. As a result, the information vector
of the joint distribution is computed as:
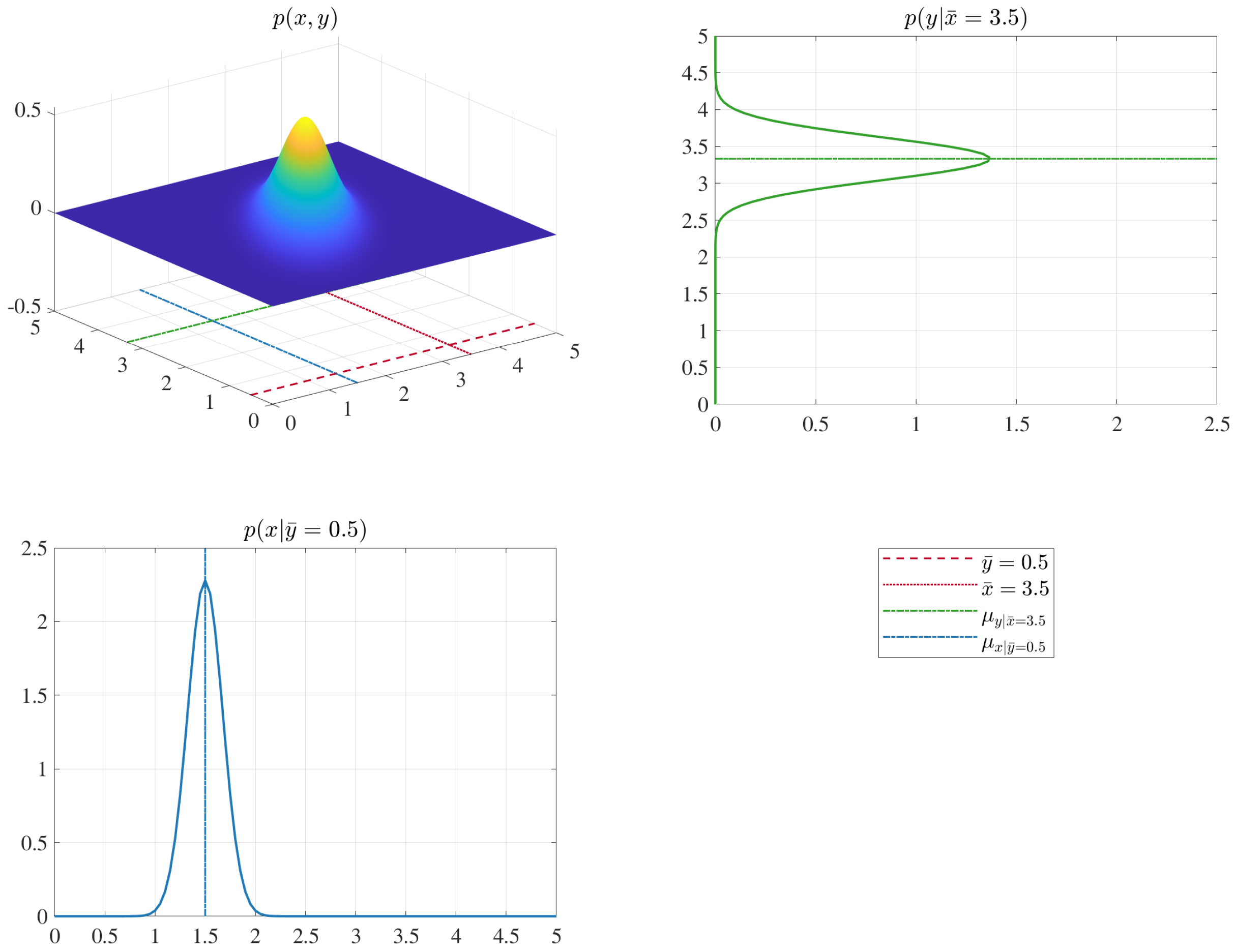
Figure 3 shows visually the outcome distribution.
4.2.2. Conditioning
Integrating the known measurement
in the joint distribution
of Equation (
6) results in a new distribution
. This can be done by conditioning in the Gaussian domain. Once again, we refer the reader to [
59] for the proofs, while we report here the results that the conditioning has on the Gaussian parameters:
where
The conditioned mean
is retrieved from the information matrix and the information vector as:
Remembering that
, the Gaussian distribution over the conditioned states has the same information matrix, while the mean is obtained by summing the increment’s mean
as
An important result in this derivation is that the matrix
is the information matrix of the estimate; therefore, we can estimate not only the optimal solution
, but also its uncertainty
.
Figure 4 illustrates visually the conditioning of a bi-variate Gaussian distribution.
4.2.3. Integrating Multiple Measurements
Integrating multiple independent measurements
requires stacking them in a single vector. As a result, the observation model becomes
Hence, matrix
and vector
are composed by the sum of each measurement’s contribution; setting
, we compute them as follows:
4.3. Nonlinear Measurement Function
Equations (
12), (
13) and (
15) allow us to find the exact mean of the conditional distribution, under the assumptions that (i) the measurement noise is Gaussian, (ii) the measurement function is an affine transform of the state, and (iii) both measurement and state spaces are Euclidean. In this section, we first relax the assumption on the affinity of the measurement function, leading to the common derivation of the GN algorithm. Subsequently, we address the case of non-Euclidean state and measurement spaces.
If the measurement model mean
is controlled by a nonlinear but
smooth function
, and that the prior mean
is reasonably close to the optimum, we can approximate the behavior of
through the first-order Taylor expansion of
around the mean, namely:
The Taylor expansion reduces conditional mean to an affine transform in
. Whereas the conditional distribution will not be in general Gaussian, the parameters of a Gaussian approximation can still be obtained around the optimum through Equations (
11) and (
13). Thus, we can use the same algorithm described in
Section 4.2, but we have to compute the linearization at each step. Summarizing, at each iteration, the GN algorithm:
- –
processes each measurement
by evaluating error
and Jacobian
at the current solution
:
- –
builds a coefficient matrix and coefficient vector for the linear system in Equation (
12), and computes the optimal perturbation
by solving a linear system:
- –
applies the computed perturbation to the current state as in Equation (
13) to get an improved estimate
A smooth prediction function has lower-magnitude higher order terms in its Taylor expansion. The smaller these terms are, the better its linear approximation will be. This leads to the situations close to the ideal affine case. In general, the smoother the measurement function is and the closer the initial guess is to the optimum, the better the convergence properties of the problem.
Non-Euclidean Spaces
The previous formulation of GN algorithm uses vector addition and subtraction to compute the error
in Equation (
17) and to apply the increments in Equation (
20). However, these two operations are only defined in Euclidean spaces. When this assumption is violated—as it usually happens in Robotics and Computer Vision applications—the straightforward implementation does not generally provide satisfactory results. Rotation matrices or angles cannot be directly added or subtracted without performing subsequent non-trivial normalization. Still, typical continuous states involving rotational or similarity transformations are known to lie on a smooth manifold [
60].
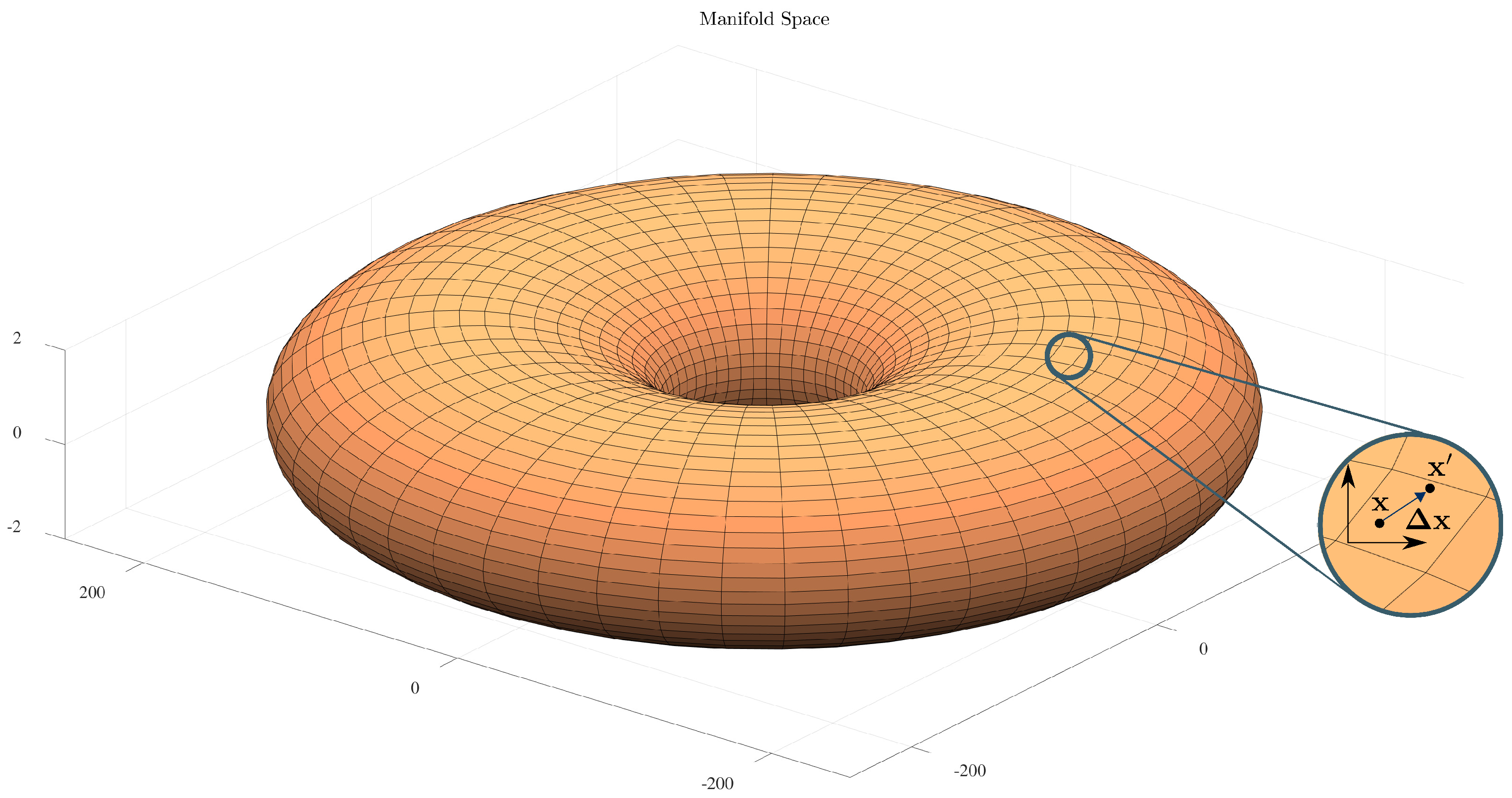
A smooth manifold
is a space that, albeit not homeomorphic to
, admits a locally Euclidean parameterization around each element
of the domain, commonly referred to as
chart—as illustrated in
Figure 5. A chart computed in a manifold point
is a function from
to a new point
on the manifold:
Intuitively, is obtained by “walking” along the perturbation on the chart, starting from the origin. A null motion () on the chart leaves us at the point where the chart is constructed—i.e., .
Similarly, given two points
and
on the manifold, we can determine the motion
on the chart constructed on
that would bring us to
. Let this operation be the inverse chart, denoted as
. The direct and inverse charts allow us to define operators on the manifold that are analogous to the sum and subtraction. Those operators, referred to as ⊞ and ⊟, are, thence, defined as:
This notation—firstly introduced by Smith et al. [
61] and then generalized by Hertzberg et al. [
14,
62]—allows us to straightforwardly adapt the Euclidean version of ILS to operate on manifold spaces. The dimension of the chart is chosen to be the minimal needed to represent a generic perturbation on the manifold. On the contrary, the manifold representation can be chosen arbitrarily.
A typical example of smooth manifold is the
domain of 3D rotations. We represent an element
on the manifold as a rotation matrix
. In contrast, the for perturbation, we pick a minimal representation consisting on the three Euler angles
. Accordingly, the operators become:
The function
computes a rotation matrix as the composition of the rotation matrices relative to each Euler angle. In formulae:
The function does the opposite by computing the value of each Euler angle starting from the matrix . It operates by equating each of its element to the corresponding one in the matrix product , and by solving the resulting set of trigonometric equations. As a result, this operation is quite articulated. Around the origin the chart constructed in this manner is immune to singularities.
Once proper ⊞ and ⊟ operators are defined, we can reformulate our minimization problem in the manifold domain. To this extent, we can simply replace the + with a ⊞ in the computation of the Taylor expansion of Equation (
16). Since we will compute an increment on the chart, we need to compute the expansion on the chart
at the local optimum that is at the origin of the chart itself
, in formulae:
The same holds when applying the increments in Equation (
20), leading to:
Here, we denoted with capital letters the manifold representation of the state , and with the Euclidean perturbation. Since the optimization within one iteration is conducted on the chart, the origin of the chart on the manifold stays constant during this iteration.
If the measurements lie on a manifold too, a local ⊟ operator is required to compute the error, namely:
To apply the previously defined optimization algorithm, we should linearize the error around the current estimate through its first-order Taylor expansion. Posing
, we have the following relation:
The reader might notice that, in Equation (
30), the error space may differ from the increments one, due to the ⊟ operator. As reported in [
63], having a different parametrization might enhance the convergence properties of the optimization in specific scenarios. Still, to avoid any inconsistencies, the information matrix
should be expressed on a chart around the current measurement
.
4.4. Handling Outliers: Robust Cost Functions
In
Section 4.3, we described a methodology to compute the parameters of the Gaussian distribution over the state
, which minimizes the Omega-norm of the error between prediction and observation. More concisely, we compute the optimal state
such that:
The mean of our estimate is the local optimum of the GN algorithm, and the information matrix is the coefficient matrix of the system at convergence. The procedure reported in the previous section assumes all measurements correct, albeit affected by noise. Still, in many real cases, this is not the case. This is mainly due to aspects that are hard to model—i.e., multi-path phenomena or incorrect data associations. These wrong measurements are commonly referred to as outliers. On the contrary, inliers represent the good measurements.
A common assumption made by several techniques to reject outliers is that the inliers tend to agree towards a common solution, while outliers do not. This fact is at the root of consensus schemes such as RANSAC [
29]. In the context of ILS, the quadratic nature of the error terms leads to over-accounting for measurement whose error is large, albeit those measurements are typically outliers. However, there are circumstances where all errors are quite large even if no outliers are present. A typical case occurs when we start the optimization from an initial guess which is far from the optimum.
A possible solution to this issue consists of carrying on the optimization under a cost function that grows sub-quadratically with the error. Indicating with
the L1 Omega-norm of the error term in Equation (
17), its derivatives with respect to the state variable
can be computed as follows:
We can generalize Equation (
31) by introducing a scalar function
that computes a new error term as a function of the L1-norm. Equation (
31) is a special case for
. Thence, our new problem will consist of minimizing the following function:
Going more into detail and analyzing the gradients of Equation (
34), we have the following relation:
where
The
robustifier function
acts on the gradient, modulating the magnitude of the error term through a scalar function
. Still, we can also compute the gradient of the Equation (
31) as follows:
We notice that Equations (
35) and (
37) differ by a scalar term
that depends on
. By absorbing this scalar term at each iteration in a new information matrix
, we can rely on the iterative algorithm illustrated in the previous sections to implement a robust estimator. In this sense, at each iteration, we compute
based on the result of the previous iteration. Note that upon convergence the Equations (
35) and (
37) will be the same, therefore, they lead to the same optimum. This formalization of the problem is called Iterative Reweighed Least-Squares (IRLS).
The use of robust cost functions biases the information matrix of the system
. Accordingly, if we want to recover an estimate of the solution uncertainty when using robust cost functions, we need to “undo” the effect of function
. This can be easily achieved recomputing
after convergence considering only inliers and disabling the robustifier—i.e., setting
.
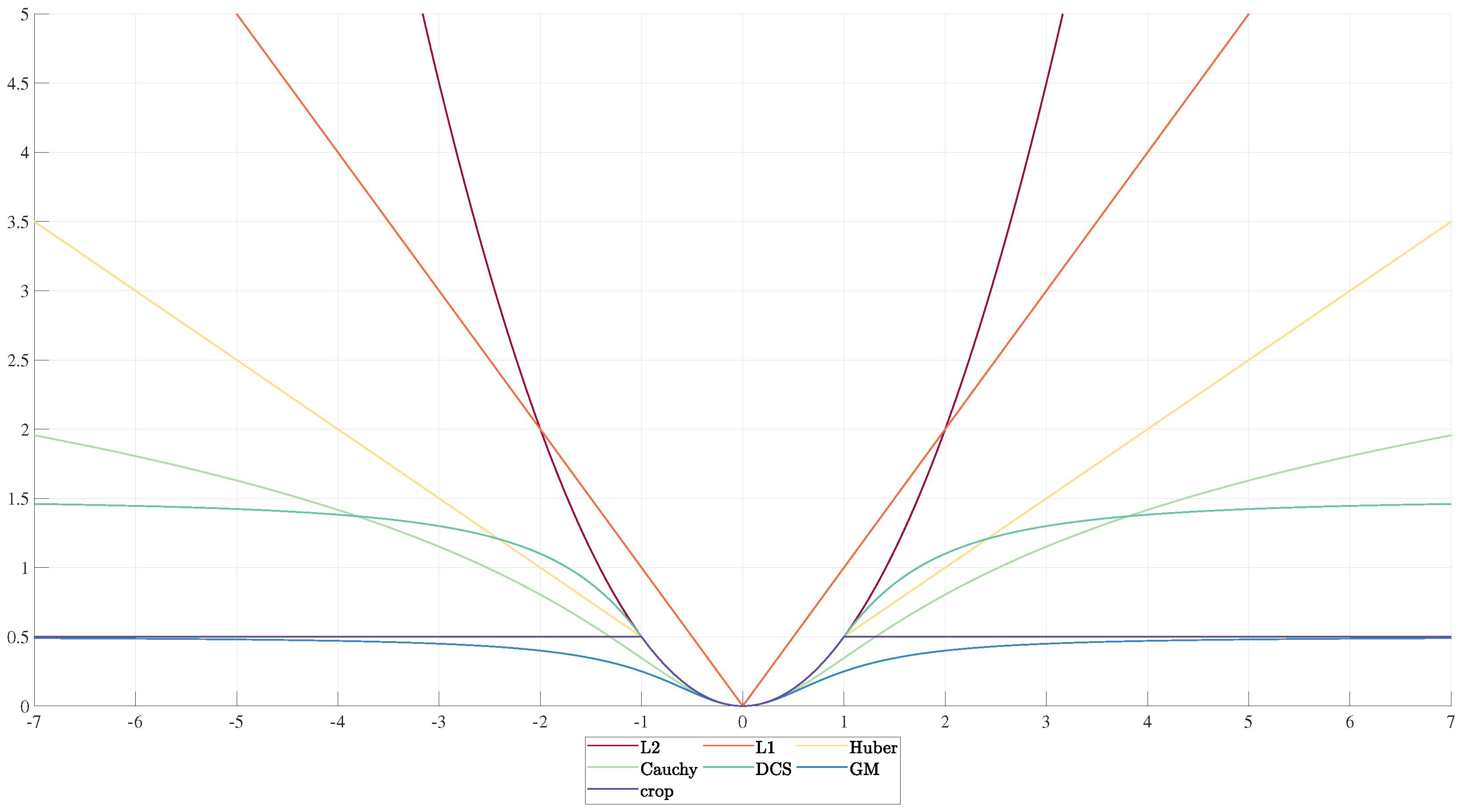
Figure 6 illustrates some of the most common cost function used in Robotics and Computer Vision.
Further information on modern robust cost function can be found in the work of MacTavish et al. [
64].
4.5. Sparsity
Minimization algorithms like GN or Levenberg-Marquardt (LM) lead to the repeated construction and solution of the linear system
. In many cases, each measurement
only involves a small subset of state variables, namely:
Therefore, the Jacobian for the error term
k has the following structure:
According to this, the contribution
of the
measurement to the system matrix
exhibits the following pattern:
Each measurement introduces a finite number of non-diagonal components that depends quadratically on the number of variables that influence the measurement. Therefore, in the many cases when the number of measurements is proportional to the number of variables such as SLAM or BA, the system matrix
is sparse, symmetric and positive semi-definite
by construction. Exploiting these intrinsic properties, we can efficiently solve the linear system in Equation (
12). In fact, the literature provides many solutions to this kind of problem, which can be arranged in two main groups: (i) iterative methods and (ii) direct methods. The former computes an iterative solution to the linear system by following the gradient of the quadratic form. These techniques often use a
pre-conditioner for example, Preconditioned Conjugate Gradient (PCG), which scales the matrix to achieve quicker convergence to take steps along the steepest directions. Further information about these approaches can be found in [
65]. Iterative methods might require a quadratic time in computing the exact solution of a linear system, but they might be the only option when the dimension of the problem is very large due to their limited memory requirements. Direct methods, instead, compute return the exact solution of the linear system, usually leveraging on some matrix decomposition followed by backsubstitution. Typical methods include: the
Cholesky factorization
or the
QR-decomposition. A crucial parameter controlling the performances of a sparse direct linear solver is the fill-in that is the number of new non-zero elements introduced by the specific factorization. A key aspect in reducing the fill in is the ordering of the variables. Since computing the optimal reordering is NP-hard, approximated techniques [
66,
67,
68] are generally employed.
Figure 7 shows the effect of different variable ordering on the
same system matrix. A larger fill-in results in more demanding computations. We refer to [
69,
70] for a more detailed analysis about this topic.
4.6. A Unifying Formalism: Factor Graphs
In this section, we introduce a formalism to represent a super-class of the minimization problems discussed so far:
factor graphs. We recall that (i) our state
is composed by
N variables, (ii) the conditional probabilities
might depend only on a subset of the state variables
and (iii) we have no prior about the state
. Given this, we can expand Equation (
1) as follows:
Equation (
40) expresses the likelihood of the measurements as a product of factors. This concept is elegantly captured in the
factor graph formalism, which provides a graphical representation for these kinds of problems. A factor graph is a bipartite graph where each node represents either a variable
, or a
factor .
Figure 8 illustrates an example of factor graph. Edges connect a factor
with each of its variables
. In the remainder of this document, we will stick to the factor graph notation and we will refer to the measurement likelihoods
as factors. Note that the main difference between Equation (
40) and Equation (
14) is that the former highlights the subset of state variables
from which the observation depends, while the latter considers
all state variables and also those that have a null contribution.
The aim of this section is to use the factor graph formulation to formalize the ILS minimization exposed so far. In this sense, Algorithm 1 reports a step-by-step expansion of the vanilla GN algorithm exploiting the factor graph formalism—supposing that both states and measurement belong to a smooth manifold. In the remainder of this document, we indicate with bold uppercase symbols elements lying on a manifold space—for example,
; lowercase bold symbols specify their corresponding vector perturbations—for example,
. Going into more detail, at each iteration, the algorithm re-initializes its workspace to store the current linear system (lines 6–7). Subsequently, it processes each measurement
(line 8), computing (i) the prediction (line 9), (ii) the error vector (line 10), and (iii) the coefficients to apply the robustifier (lines 13–15). While processing a measurement, it also computes the blocks
of the Jacobians with respect to the variables
involved in the factor. We denote with
the block
of the
matrix corresponding to the variables
and
; similarly, we indicate with
the block of the coefficient vector for the variable
. This operation is carried on in the lines 18–20. The contribution of each measurement to the linear system is added in a block fashion. Further efficiency can be achieved exploiting the symmetry of the system matrix
, computing only its lower triangular part. Finally, once the linear system
has been built, it is solved using a general sparse linear solver (line 21) and the perturbation
is applied to the current state in a block-wise fashion (line 23). The algorithm proceeds until convergence is reached, namely when the delta of the cost-function
F between two consecutive iterations is lower than a threshold
—line 3.
| Algorithm 1 Gauss–Newton minimization algorithm for manifold measurements and state spaces |
Require: Initial guess ; Measurements
Ensure: Optimal solution - 1:
- 2:
- 3:
whiledo - 4:
- 5:
- 6:
- 7:
- 8:
for all do - 9:
- 10:
- 11:
- 12:
- 13:
- 14:
- 15:
- 16:
for all do - 17:
- 18:
for all do - 19:
- 20:
- 21:
- 22:
for all do - 23:
- 24:
return
|
Summarizing, instantiating Algorithm 1 on a specific problem requires to:
- –
Define for each type of variable (i) an extended parametrization , (ii) a vector perturbation and (iii) a ⊞ operator that computes a new point on the manifold . If the variable is Euclidean, the extended and the increment parametrization match and thus ⊞ degenerates to vector addition.
- –
For each type of factor , specify (i) an extended parametrization , (ii) a Euclidean representation for the error vector and (ii) a ⊟ operator such that, given two points on the manifold and , represents the motion on the chart that moves onto . If the measurement is Euclidean, the extended and perturbation parametrizations match and, thus, ⊟ becomes a simple vector difference. Finally, it is necessary to define the measurement function that, given a subset of state variables , computes the expected measurement .
- –
Choose a robustifier function for each type of factor. The non-robust case is captured by choosing .
Note that depending on the choices and on the application, not all of these steps indicated here are required. Furthermore, the value of some variables might be known beforehand—for example, the initial position of the robot in SLAM is typically set at the origin. Hence, these variables do not need to be estimated in the optimization process, since they are constants in this context. In Algorithm 1, fixed variables can be handled in the solution step—i.e., line 21—suppressing all block rows and columns in the linear system that arise from these special nodes. In the next section, we present how to formalize several common SLAM problems through the factor graph formalization introduced so far.
6. A Generic Sparse/Dense Modular Least Squares Solver
The methodology presented in
Section 4.6 outlines a straight path to the design of an ILS optimization algorithm. Robotic applications often require running the system online, and, thus, they need efficient implementations. When extreme performances are needed, the ultimate strategy is to
overfit the solution to the specific problem. This can be done both at an algorithmic level and at an implementation level. To improve the algorithm, one can leverage on the a priori known structure of the problem, by removing parts of the algorithm that are not needed or by exploiting domain-specific knowledge. A typical example is when the structure of the linear system is known in advance—for example, in BA—where it is common to use specialized methods to solve the linear system [
71].
Focusing on the implementation, we reported two main bottlenecks: the computation of the linear system and its solution. Dense problems such as ICP, Sensor Calibration, or Projective Registration are typically characterized by a small state space and many factors of the same type. In ICP, for instance, the state contains just a single object—i.e., the robot pose. Still, this variable might be connected to hundreds of thousands of factors, one for each point correspondence. Between iterations, the ICP mechanism results in these factors to change, depending on the current status of the data association. As a consequence, these systems spend most of their time in constructing the linear system, while the time required to solve it is negligible. Notably, applications such as Position Tracking or VO require the system to run at the sensor frame-rate, and each new frame might take several ILS iterations to perform the registration. On the contrary, sparse problems like PGO or large scale BA are characterized by thousands of variables, and a number of factors which is typical in the same order of magnitude. In this context, a factor is connected to very few variables. As an example, in case of PGO, a single measurement depends only two variables that express mutually observable robot poses, whereas the complete problem might contain a number of variables proportional to the length of the trajectory. This results in a large-scale linear system, albeit most of its coefficients are null. In these scenarios, the time spent to solve the linear system dominates over the time required to build it.
A typical aspect that hinders the implementation of a ILS algorithm by a person approaching this task for the first time is the calculation of the Jacobians. The labor-intensive solution is to compute them analytically, potentially with the aid of some symbolic-manipulation package. An alternative solution is to evaluate them numerically, by calculating the Jacobians column-by-column with repeated evaluation of the error function around the linearization point. Whereas this practice might work in many situations, numerical issues can arise when the derivation interval is not properly chosen. A third solution is to delegate the task of evaluating the analytic solution directly to the program, starting from the error function. This approach is called AD and Ceres Solver [
10] is the most representative system to embed this feature—later also adopted by other optimization frameworks.
In the remainder of this section, we first revisit and generalize Algorithm 1 to support multiple solution strategies. Subsequently, we outline some design requirements that will finally lead to the presentation of the overall design of our approach proposed in
Section 7.
6.1. Revisiting the Algorithm
In the previous section, we presented the implementation of a vanilla GN algorithm for generic factor graphs. This simplistic scheme suffers under high nonlinearities, or when the cost function is under-determined. Over time, alternatives to GN have been proposed, to address these issues, such as LM or Trusted-Region Method (TRM) [
72]. All of these algorithms present some common aspects or patterns that can be exploited when designing an optimization system. Therefore, in this section, we reformulate Algorithm 1 to isolate different independent sub-modules. Finally, we present both the GN and the LM algorithms rewritten by using these sub-modules.
In Algorithm 2, we isolate the operations needed to compute the scaling factor
for the information matrix
, knowing the current
. Algorithm 3 performs the calculation of the error
and the Jacobian
for a factor
at the current linearization point. Algorithm 4 applies the robustifier to a factor, and updates the linear system. Algorithm 5 applies the perturbation
to the current solution
to obtain an updated estimate. Finally, in Algorithm 6, we present a revised version of Algorithm 1 that relies on the modules described so far. In Algorithm 7, we provide an implementation of the LM algorithm that makes use of the same core sub-algorithms used in Algorithm 6. The LM algorithm solves a damped version of the system, namely
. The magnitude of the damping factor
is adjusted depending on the current variation of the
. If the
increases upon an iteration,
increases too. In contrast, if the solution improves,
is decreased. Variants of these two algorithms—for example, damped GN that solves
—can be straightforwardly implemented by slight modification to the algorithm presented here.
| Algorithm 2—computes the robustification coefficient |
Require: Current .
Ensure: computed from the actual error,
- 1:
- 2:
- 3:
return
|
6.2. Design Requirements
While designing our system, we devised a set of requirements stemming from our experience both as developers and as users. Subsequently, we turned these requirements into some design choices that lead to our proposed optimization framework. Although most of these requirements indicate good practices to be followed in potentially any new development, we highlight here their role in the context of a solver design.
6.2.1. Easy to Use and Symmetric API
As users, we want to configure, instantiate, and run a solver in the same manner, regardless of the specific problem to which it is applied. Ideally, we do not want the user to care if the problem is dense or sparse. Furthermore, in several practical scenarios, one wants to change aspects of the solver while it runs—for example, the minimization algorithm chosen, the robust kernel, or the termination criterion. Finally we want to save/retrieve the configuration of a solver and all of its sub-modules to/from disk. Thence, the expected usage pattern should be: (i) load the specific solver configuration from disk and eventually tune it, (ii) assign a problem to the solver or load it from file, (iii) compute a solution and eventually (iv) provide statistics about the evolution of optimization.
| Algorithm 3—computes the error and the Jacobians at the current linearization point |
Require: Initial guess ; Current measurement ;
Ensure: Error: ; Jacobians ;
- 1:
- 2:
- 3:
- 4:
for alldo - 5:
- 6:
- 7:
return
|
| Algorithm 4 updates a linear system with a factor current linearization point , and returns the of the factor |
Require: Initial guess ; Coefficients of the linear system and ; Measurement
Ensure: Coefficients of the linear system after the update and ; Value of the cost function for this factor - 1:
- 2:
- 3:
- 4:
- 5:
for alldo - 6:
for all do - 7:
- 8:
- 9:
return
|
| Algorithm 5 applies a perturbation to the current system solution |
Require: Current solution ; Perturbation
Ensure: New solution , moved according to - 1:
for alldo - 2:
- 3:
return
|
| Algorithm 6—Gauss–Newton minimization algorithm for manifold measurements and state spaces |
Require: Initial guess ; Measurements
Ensure: Optimal solution - 1:
, - 2:
whiledo - 3:
- 4:
for all do - 5:
- 6:
- 7:
- 8:
- 9:
return
|
| Algorithm 7—Levenberg–Marquardt minimization algorithm for manifold measurements and state spaces |
Require: Initial guess ; Measurements ; Maximum number of internal iteration
Ensure: Optimal solution - 1:
, , - 2:
- 3:
- 4:
whiledo - 5:
, , , - 6:
for all do - 7:
- 8:
- 9:
- 10:
while do - 11:
- 12:
- 13:
- 14:
- 15:
if then - 16:
- 17:
- 18:
- 19:
else - 20:
- 21:
- 22:
- 23:
return
|
Note that many current state-of-the-art ILS solver allow for easily performing the last three steps of this process; however, they do not provide the ability of permanently write/read their configuration on/from disk—as our system does.
6.2.2. Isolating Parameters, Working Variables and Problem Description/Solution
When a user is presented to a new potentially large code-base, having a clear distinction between what the variables represent and how they are used, which substantially reduces the learning curve. In particular, we distinguish between parameters, working variables, and the input/output. Parameters are those objects controlling the behavior of the algorithm, such as number of iterations or the thresholds in a robustifier. Parameters might also include processing sub-modules, such as the algorithm to use or the algebraic solver of the linear system. In summary, parameters characterize the behavior of the optimizer, independently from the input, and represent the configuration that can be stored/retrieved from disk.
In contrast to parameters, working variables are altered during the computation, and are not directly accessible to the end user. Finally, we have the description of the problem—i.e., the factor graph, where the factors and the variables expose an interface agnostic to the approach that will be used to solve the problem.
6.2.3. Trade-off Development Effort/Performance
Quickly developing a proof of concept is a valuable feature to have while designing a novel system. At the same time, once a way to approach the problem has been found, it becomes perfectly reasonable to invest more effort to enhance its efficiency.
Upon instantiation, the system should provide an off-the shelf generic and fair configuration. Obviously, this might be tweaked later for enhancing the performances on the specific class of problems. A possible way to enhance performances is by exploiting the special structure of a specific class of problems, overriding the general APIs to perform ad-hoc computations. This results in layered APIs, where the functionalities of a level rely only on those of the level below. As an example, in our architecture, the user can either specify the error function and let the system to compute the Jacobians using AD or provide the analytical expression of the Jacobians if more performances are needed. Finally, the user might intervene at a lower level, providing directly the contribution to the linear system
given by the factor. In a certain class of problems also computing this product represents a performance penalty. An additional benefit provided by this design is the direct support for
Newton’s method, which can be straightforwardly achieved by substituting the approximated Hessian
with the analytic one
. This feature captures second order approaches such as NDT [
26] in the language of our API.
6.2.4. Minimize Codebase
The likelihood of bugs in the implementation grows with the size of the code-base. For small teams characterized by a high turnover—like the ones found in academic environments—maintaining the code becomes an issue. In this context, we choose to favor the code reuse in spite of a small performance gain. The same class used to implement an algorithm, a variable type or a robustifier should be used in all circumstances, namely sparse and dense problems—where it is needed.
7. Implementation
As support material for this tutorial, we offer an own implementation of a modular ILS optimization framework that has been designed around the methodology illustrated in
Section 4.6. Our system is written in modern C++17 and provides static type checking, AD and a straightforward interface. The core of our framework fits in less than 6000 lines of code, while the companion libraries to support the most common problems—for example, 2D and 3D SLAM, ICP, Projective and Dense Registration, Sensor Calibration—are contained in 6500 lines of code. For comparison,
is around 45,000 lines, GTSAM 303,000 and ceres 80,000. Albeit originally designed as a tool for rapid prototyping, our system achieves a high degree of customization and competes with other state-of-the-art systems in terms of performances.
Based on the requirements outlined in
Section 6.2, we designed a component model, where the processing objects (named
Configurable) can possess parameters, support dynamic loading, and can be transparently serialized. Our framework relies on a custom-built serialization infrastructure that supports format independent serialization of arbitrary data structures, named
Basic Object Serialization System (BOSS). Furthermore, thanks to this foundation, we can provide both a graphical configurator—that allows for assembling and easily tuning the modules of a solver—and a command-line utility to edit and run configurations on the go.
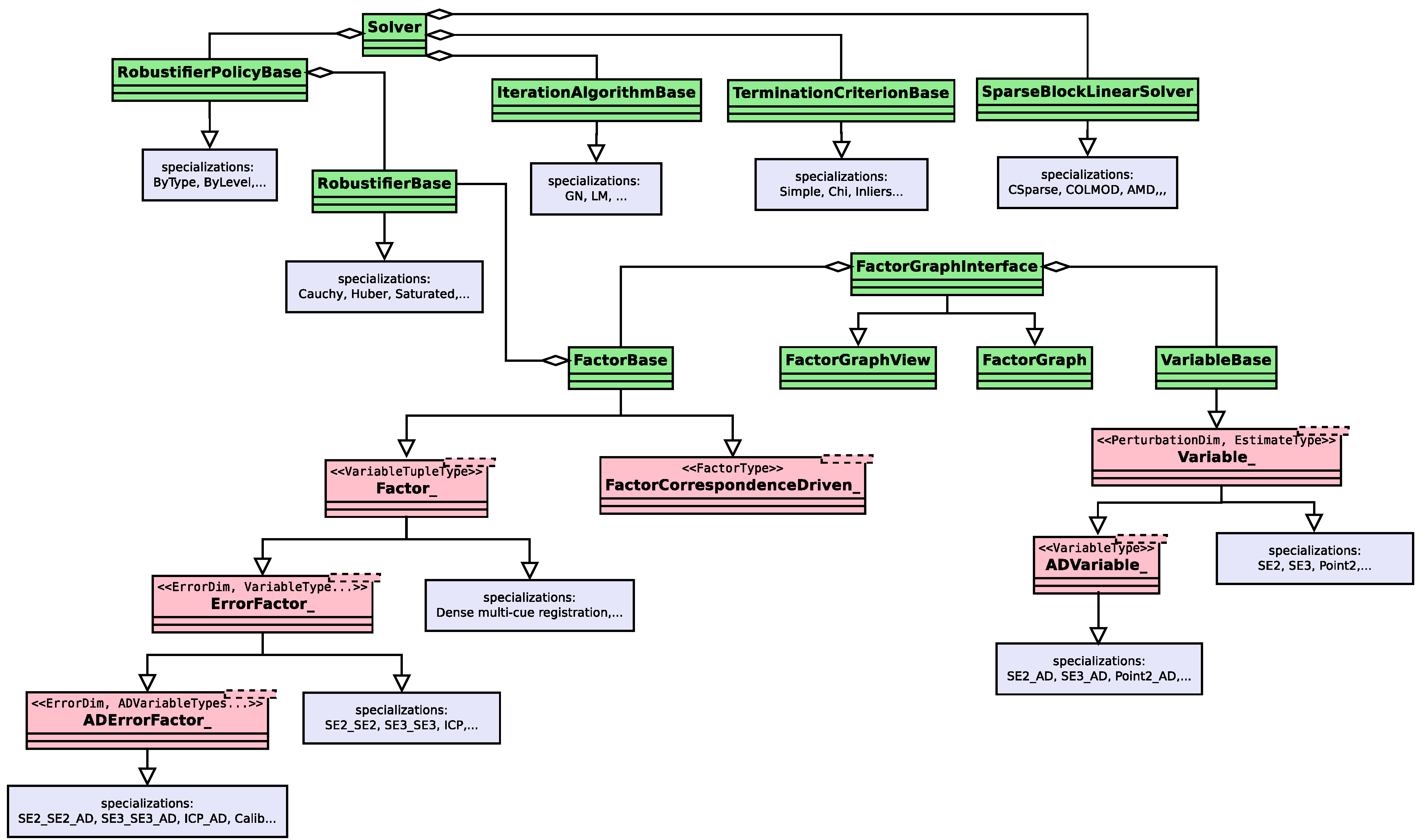
The goal of this section is to provide the reader with a quick overview of the proposed system, focusing on how the user interacts with it. Given the class-diagram illustrated in
Figure 12, in the remainder, we will first analyze the core modules of the solver and then provide two practical examples on how to use it.
7.1. Solver Core Classes
Our framework has been designed to satisfy the requirements stated in
Section 6, embedding unified APIs to cover both dense and sparse problems symmetrically. Furthermore, thanks to the
BOSS serialization library, the user can generate permanent configuration of the solver, to be later read and reused on the go. The configuration of a solver generally embeds the following parameters:
- –
Optimization Algorithm: the algorithm that performs the minimization; currently, only GN and LM are supported, still, we plan to also add TRM approaches
- –
Linear Solver: the algebraic solver that computes the solution of the linear system
; we embed a naive AMD-based [
66] linear solver together with other approaches based on well-known highly-optimized linear algebra libraries—for example, SuiteSparse (
http://faculty.cse.tamu.edu/davis/suitesparse.html)
- –
Robustifier: the robust kernel function applied to a specific factor; we provide several commonly used instances of robustifier, together with a modular mechanism to assign specific robustifier to different types of factor—called robustifier policy
- –
Termination Criterion: a simple modules that, based on optimization statistics, checks whether convergence has been reached.
Note that, in our architecture, there is a clear separation between solver and problem. In the next section, we will describe how we formalized the latter. In the remainder of this section, instead, we will focus on the solver classes, which are in charge of computing the problem solution.
The class Solver implements a unified interface for our optimization framework. It presents itself to the user with a unified data-structure to configure, control, run, and monitor the optimization. This class allows for selecting the type of algorithm used within one iteration, which the algorithm uses to solve the linear system, or which termination criterion to use. This mechanism is achieved by delegating the execution of these functions to specific interfaces. In more detail, the linear system is stored in a sparse-block-matrix structure that effectively separates the solution of the linear system from the rest of the optimization machinery. Furthermore, our solver supports incremental updates, and can provide an estimate of partial covariance blocks. Finally, our system supports hierarchical approaches. In this sense, the problem can be represented at different resolutions (levels), by using different factors. When the solution at a coarse level is computed, the optimization starts from the next denser level, enabling a new set of factors. In the new step, the initial guess is computed from the solution of the coarser level.
The IterationAlgorithmBase class defines an interface for the outer optimization algorithm—i.e., GN or LM. To carry on its operations, it relies on the interface exposed by the Solver class. The latter is in charge to invoke the IterationAlgorithmBase, which will run a single iteration of its algorithm.
Class
RobustifierBase defines an interface for using arbitrary
functions—as illustrated in
Section 4.4. Robust kernels can be directly assigned to factors or, alternatively, the user might define a
policy that is based on the status of the actual factor decides on which robustifier to use. The definition of a policy is done by implementing the
RobustifierPolicyBase interface.
Finally, TerminationCriterionBase defines an interface for a predicate that, exploiting the optimization statistics, detects whether the system has converged to a solution or a fatal error has occurred.
7.2. Factor Graph Classes
In this section, we provide an overview of the top-level classes constituting a factor graph—i.e., the optimization problem—in our framework. In specifying new variables or factors, the user can interact with the system through a layered interface. More specifically, factors can be defined using AD and, thus, contained in few lines of code for rapid prototyping or the user can directly provide how to compute analytic Jacobians if more speed is required. Furthermore, to achieve extreme efficiency, the user can choose to compute its own routines to update the quadratic form directly, consistently in line with our design requirement of more-work/more-performance. Note that we observed in our experiments that in large sparse problems the time required to linearize the system is marginal compared to the time required to solve it. Therefore, in most of these cases, AD can be used without significant performance losses.
7.2.1. Variables
The VariableBase implements a base abstract interface the variables in a factor graph, whereas
Variable_<PerturbationDim, EstimateType> specializes the base interface on a specific type. The definition of a new variable extending the
Variable_ template requires the user to specify (i) the type
EstimateType used to store the value of the variable
, (ii) the dimension
PerturbationDim of the perturbation
and (iii) the ⊞ operator. This is coherent with the methodology provided in
Section 4.6. In addition to these fields, the variable has an integer key, to be uniquely identified within a factor graph. Furthermore, a variable can be in either one of these three states:
- –
Active: the variable will be estimated
- –
Fixed: the variable stays constant through the optimization
- –
Disabled: the variable is ignored and all factors that depend on it are ignored as well.
To provide roll-back operations—such as those required by LM—a variable also stores a stack of values.
To support AD, we introduce the ADVariable_ template, that is instantiated on a variable without AD. Instantiating a variable with AD requires to define the ⊞ operator by using the AD scalar type instead of the usual float or double. This mechanism allows us to mix in a problem factors that require AD with factors that do not.
7.2.2. Factors
The base level of the hierarchy is the FactorBase. It defines a common interface for this type of graph objects. It is responsible for (i) computing the error and, thus, the —(ii) updating the quadratic form and the right-hand side vector and (iii) invoking the robustifier function (if required). When an update is requested, a factor is provided with a structure on which to write the outcome of the operation. A factor can be enabled or disabled. In the latter case, it will be ignored during the computation. In addition, upon updating a factor might become invalid, if the result of the computation is meaningless. This occurs for instance in BA, when a a point is projected outside the image plane.
The
Factor_<VariableTupleType> class implements a typed interface for the factor class. The user willing to extend the class at this level is responsible for implementing the entire
FactorBase interface, relying on functions for typed access to the blocks of the system matrix
and of the coefficient vector
. In this case, the block size is determined from the dimension of the perturbation vector of the variables in the template argument list. We extended the factors at this level to implement approaches such as dense multi-cue registration [
31]. Special structures in the Jacobians can be exploited to speed up the calculation of
whose computation has a non negligible cost.
The ErrorFactor_<ErrorDim, VariableTypes...> class specializes a typed interface for the factor class, where the user has to implement both the error function and the Jacobian blocks . The calculation of the and the blocks is done through loops unrolled at compile time since the types and the dimensions of the variables/errors are part of the type.
The ADErrorFactor_<Dim, VariableTypes...> class further specializes the ErrorFactor_. Extending the class at this level only required specifying only the error function. The Jacobians are computed through AD, and the updates of and the are done according to the base class.
Finally, the FactorCorrespondenceDriven_<FactorType> implements a mechanism that allows the solver to iterate over multiple factors of the same type and connecting the same set of variables, without the need of explicitly storing them in the graph. A FactorCorrespondenceDriven_ is instantiated on a base type of factor, and it is specialized by defining which actions should be carried on as a consequence of the selection of the “next” factor in the pool by the solver. The solver sees this type of factor as multiple ones, albeit a FactorCorrespondenceDriven_ is stored just once in memory. Each time a FactorCorrespondenceDriven_ is accessed by the solver a callback changing the internal parameters is called. In its basic implementation, this class takes a container of corresponding indices, and two data containers: Fixed and Moving. Each time a new factor within the FactorCorrespondenceDriven_ is requested, the factor is configured by: selecting the next pair of corresponding indices from the set, and by picking the elements in Fixed and Moving at those indices. As an instance, to use our solver within an ICP algorithm, the user has to configure the factor by setting the Fixed and Moving point clouds. The correspondence vector can be changed anytime to reflect a new data association. This results in different correspondences being considered at each iteration.
7.2.3. FactorGraph
To carry on an iteration, the solver has to iterate over the factors and, hence, it requires randomly accessing the variables. Restricting the solver to access a graph through an interface of random access iterators enables us to decouple the way the graph is accessed from the way it is stored. This would allow us to support transparent off-core storage that can be useful on very large problems.
A FactorGraphInterface defines the way to access a graph. In our case, we use integer values as key for variables and factors. The solver accesses a graph only through the FactorGraphInterface and, thence, it can read/write the value of state variables, read the factors, but it is not allowed to modify the graph structure.
A heap-based concrete implementation of a factor graph is provided by the
FactorGraph class that specializes the interface. The
FactorGraph supports transparent serialization/deserialization. Our framework makes use of the open-source math library Eigen [
73], which provides fast and easy matrix operation. The serialization/deserialization of variable and factors that are constructed on eigentypes is automatically handled by our
BOSS library.
In sparse optimization, it is common to operate on a local portion of the entire problem. Instrumenting the solver with methods to specify the local portions would bloat the implementation. Alternatively, we rely on the concept of FactorGraphView that exposes an interface on a local portion of a FactorGraph—or of any other object implementing the FactorGraphInterface.
8. Experiments
In this section, we propose several comparisons between our framework and other state-of-the-art optimization systems. The aim of these experiments is to support the claims on the performance of our framework and, thus, we focused on the accuracy of the computed solution and the time required to achieve it. Experiments have been performed both on dense scenarios—such as ICP—and sparse ones—for example, PGO and PLGO.
8.1. Dense Problems
Many well-known SLAM problems related to the front-end can be solved exploiting the ILS formulation introduced before. In such scenarios—for example, point-clouds registration—the number of variables is small compared to the observations’ one. Furthermore, at each registration step, the data-association is usually recomputed to take advantage of the new estimate. In this sense, one has to build the factor graph associated with the problem from scratch at each step. In such contexts, the most time-consuming part of the process is represented by the construction of linear system in Equation (
19) and not its solution.
To perform dense experiments, we choose a well-known instance of these kinds of problems: ICP. We conducted multiple tests, comparing our framework to the current state-of-the-art PCL library [
15] on the standard registration datasets summarized in
Table 1.
In all of the cases, we setup a controlled benchmarking environment, in order to have a precise ground-truth. In the ETH-Hauptgebaude, ETH-Apartment, and Stanford-Bunny, the raw data consist of a series of range scans. Therefore, in such cases, we constructed the ICP problem as follows:
- –
reading of the first raw scan and generate a point cloud
- –
transformation of the point cloud according to a known isometry
- –
generation of perfect association between the two clouds
- –
registration starting from .
Since our focus is on the ILS optimization, we used the same set of data-associations and the same initial guess for all approaches. This methodology renders the comparison fair and unbiased. As for the ICL-NUIM dataset, we obtained the raw point cloud unprojecting the range image of the first reading of the lr-0 scene. After this initial preprocessing, the benchmark flow is the same as described before.
In this context, we compared (i) the accuracy of the solution obtained computing the translational and rotational error of the estimate and (ii) the time required to achieve that solution.
We compared the recommended PCL registration suite that uses the Horn formulas against our framework with and without AD. Furthermore, we also provide results obtained using PCL implementation of the LM optimization algorithm.
As reported in
Table 2, the final registration error is almost negligible in all cases. Instead, in
Figure 13, we document the speed of each solver. When using the full potential of our framework—i.e., using analytic Jacobians—it is able to achieve results in general equal or better than the off-the-shelf PCL registration algorithm. Using AD has a great impact on the iteration time, however, our system is able to be faster than the PCL implementation of LM also in this case.
8.2. Sparse Problems
Sparse problems are mostly represented by generic global optimization scenarios, in which the graph has a large number of variables while each factor connects a very small subset of those (typically two). In these kinds of problems, the graph remains unchanged during the iterations; therefore, the most time-consuming part of the optimization is the solution of the linear system, not its construction. PGO and PLGO are two instances of this problem that are very common in the SLAM context and, therefore, we selected these two to perform comparative benchmarks.
8.2.1. Pose-Graph Optimization
PGO represents the backbone of SLAM systems and it has been well investigated by the research community. For these experiments, we employed standard 3D PGO benchmark datasets—all publicly available [
63]. We added to the factors Additive White Gaussian Noise (AWGN) and we initialized the graph using the breadth-first initialization.
We report in
Table 3 the complete specifications of the datasets employed together with the noise statistics used. Given the probabilistic nature of the noise imposed on the factors, we performed experiments over 10 noise realizations and we report here the statistics of the results obtained—i.e., mean and standard deviation. To avoid any bias in the comparison, we used the native LM implementation of each framework, since it was the only algorithm common to all candidates. Furthermore, we imposed a maximum number of 100 LM iterations. Still, each framework has its own termination criterion active, so that each one can detect when to stop the optimization. Finally, no robust kernel has been employed in these experiments.
In
Table 4, we illustrate the Absolute Trajectory Error (ATE) (RMSE) computed on the optimized graph with respect to the ground truth. The values reported refer to mean and standard deviation over all noise trials. As expected, the result obtained are in line with all other methods.
Figure 14, instead, reports a detailed timing analysis. The time to perform a complete LM iteration is always among the smallest, with a very narrow standard deviation. Furthermore, since the specific implementation of LM is slightly different in each framework, we also reported the total time to perform the full optimization, while the number of LM iterations elapsed are shown in
Table 5. In addition, in this case, our system is able to achieve state-of-the-art performances that are better than or equal to the other approaches.
8.2.2. Pose-Landmark Graph Optimization
PLGO is another common global optimization task in SLAM. In this case, the variables contain both robot (or camera) poses and landmarks’ position in the world. Factors, instead, embody spatial constraints between either two poses or between a pose and a landmark. As a result, these kinds of factor graphs are the perfect representative of the SLAM problem, since they contain the robot trajectory and the map of the environment.
To perform the benchmarks, we used two datasets: Victoria Park [
77] and KITTI-00 [
78]. We obtained the last one running ProSLAM [
79] on the stereo data and saving the full output graph. We super-imposed to the factors specific AWGN and we generated the initial guess through the breadth-first initialization technique.
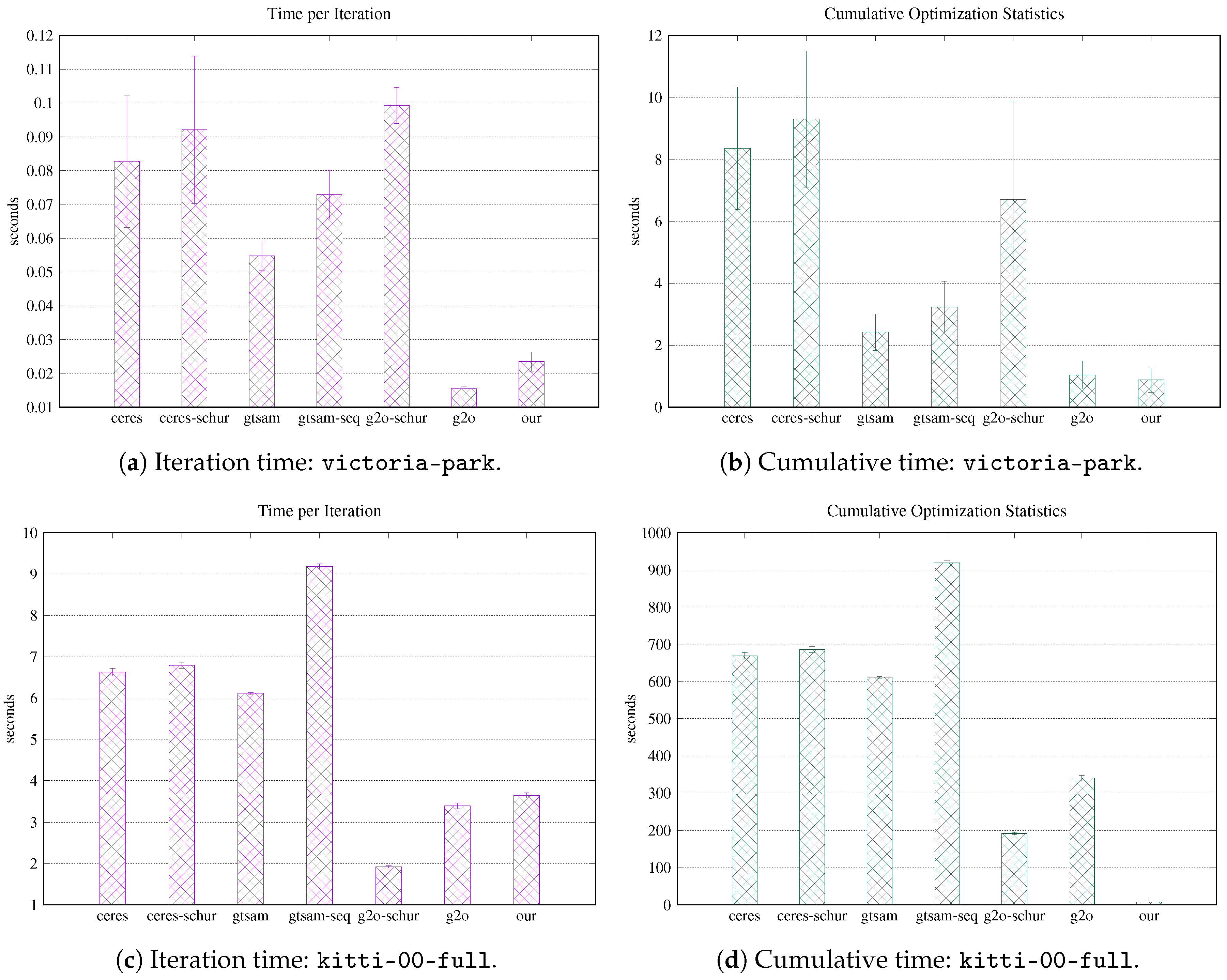
Table 6 summarizes the specification of the datasets used in these experiments. In addition, in this case, we sampled multiple noise trials (5 samples) and reported mean and standard deviation of the results obtained. The configuration of the framework is the same as the one used in PGO experiments—i.e., 100 LM iterations at most, with termination criterion active.
As reported in
Table 7, the ATE (RMSE) that we obtain is compatible with the one of the other frameworks. The higher error in the
kitti-00-full dataset is mainly due to the slow convergence of LM that triggers the termination criterion too early, as shown in
Table 8. In such case, the use of GN leads to better results; however, in order to not bias the evaluation, we choose to not report results obtained with different ILS algorithms.
As for the wall times to perform the optimization, the results are illustrated in
Figure 15. In PLGO scenarios, given the fact that there are two types of factors, the linear system in Equation (
19) can be rearranged as follows:
A linear system with this structure can be solved more efficiently through the Schur complement of the Hessian matrix [
80], namely:
Ceres-Solver and can make use of the Schur complement to solve this kind of special problem; therefore, we also reported the wall times of the optimization when this technique is used. Obviously, using the Schur complement leads to a major improvement in the efficiency of the linear solver, leading to very low iteration times. For completeness, we reported the results of GTSAM with two different linear solvers: cholesky_multifrontal and cholesky_sequential. Our framework does not provide at the moment any implementation of a Schur-complement-based linear solver; still, the performance achieved is in line with all the non-Schur methods, confirming our conjectures.
9. Conclusions
In this work, we propose a generic overview on ILS optimization for factor graphs in the fields of robotics and computer vision. Our primary contribution is providing a unified and complete methodology to design efficient solutions to generic problems. This paper analyzes in a probabilistic flavor the mathematical fundamentals of ILS, addressing also many important collateral aspects of the problem such as dealing with non-Euclidean spaces and with outliers, exploiting the sparsity or the density. Then, we propose a set of common use-cases that exploit the theoretic reasoning previously done.
In the second half of the work, we investigate how to design an efficient system that can work in all the possible scenarios depicted before. This analysis led us to the development of a novel ILS solver, focused on efficiency, flexibility, and compactness. The system is developed in modern C++ and almost entirely self-contained in less than 6000 lines of code. Our system can seamlessly deal with sparse/dense, static/dynamic problems with a unified consistent interface. Furthermore, thanks to specific implementation designs, it allows easy prototyping of new factors and variables or to intervene at a low level when performances are critical. Finally, we provide an extensive evaluation of the system’s performances, both in dense—for example, ICP—and sparse—for example, batch global optimization—scenarios. The evaluation shows that the performances achieved are in line with contemporary state-of-the-art frameworks, both in terms of accuracy and speed.