Adjustable and Adaptive Control for an Unstable Mobile Robot Using Imitation Learning with Trajectory Optimization
Abstract
1. Introduction
2. Related Work
2.1. Training Robust Parametric Controllers
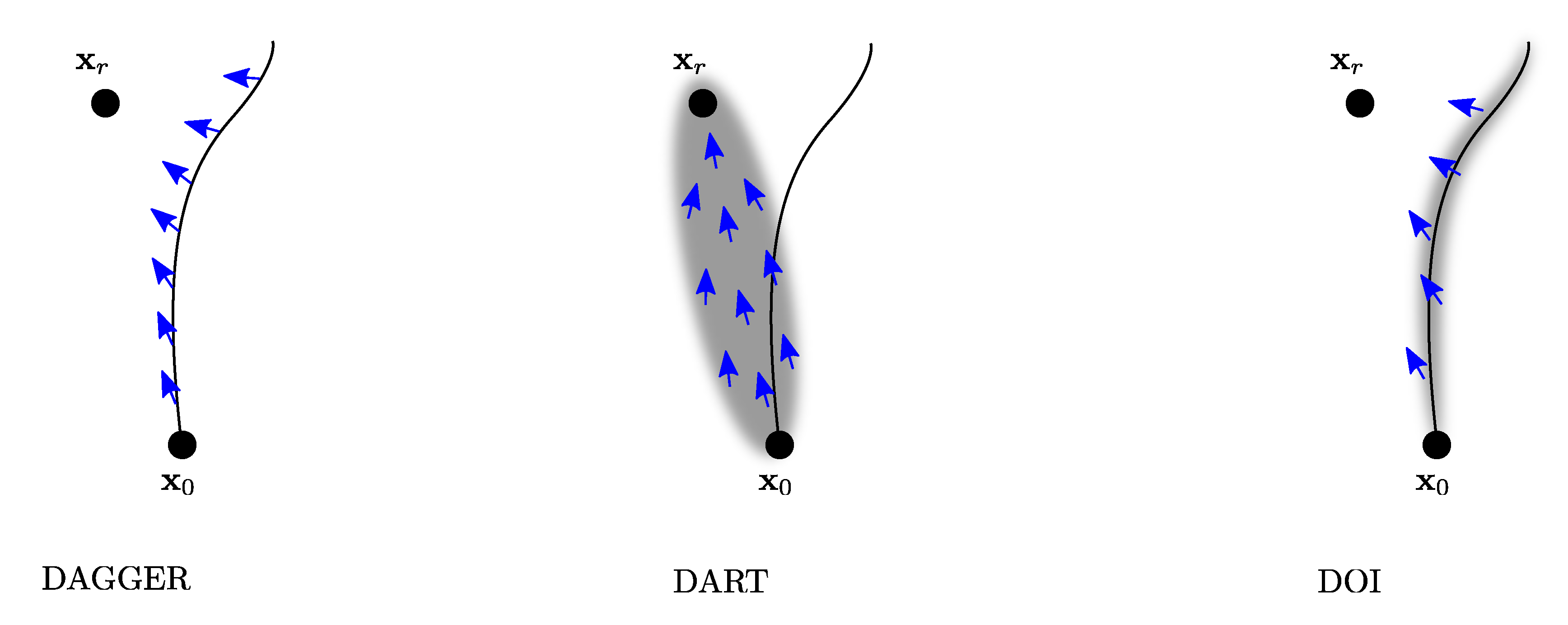
2.2. Imitation Learning with Trajectory Optimization
3. Design of an Adaptive and Adjustable Controller Using Imitation Learning
- Trajectory optimization with randomized model parameters.
- Training an intermediate oracle network.
- Training of a controller with internal states.
3.1. Trajectory Optimization
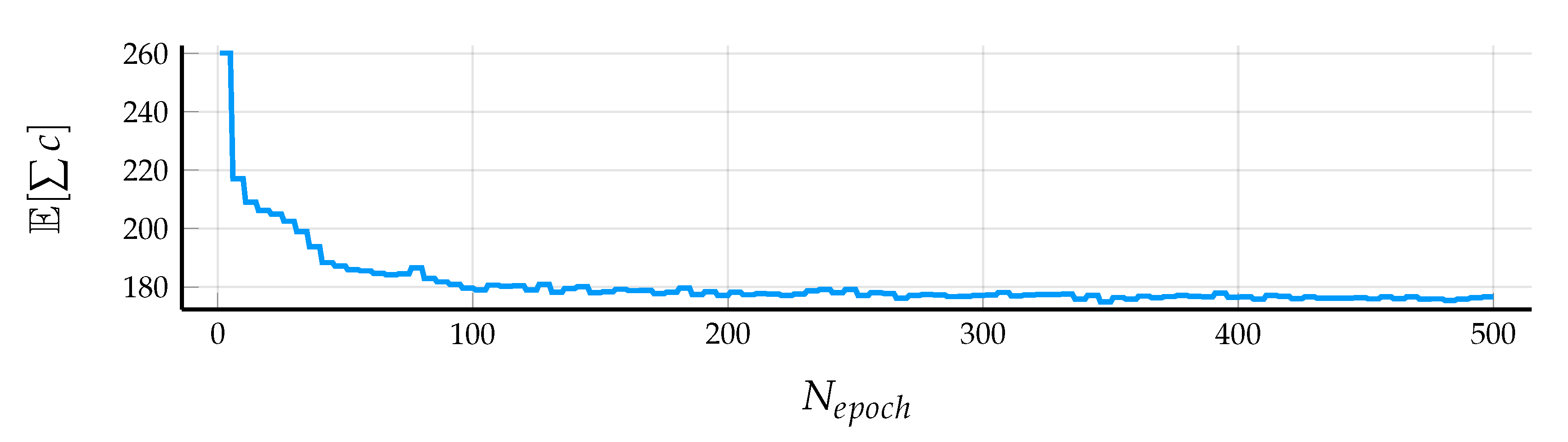
3.2. Oracle Training
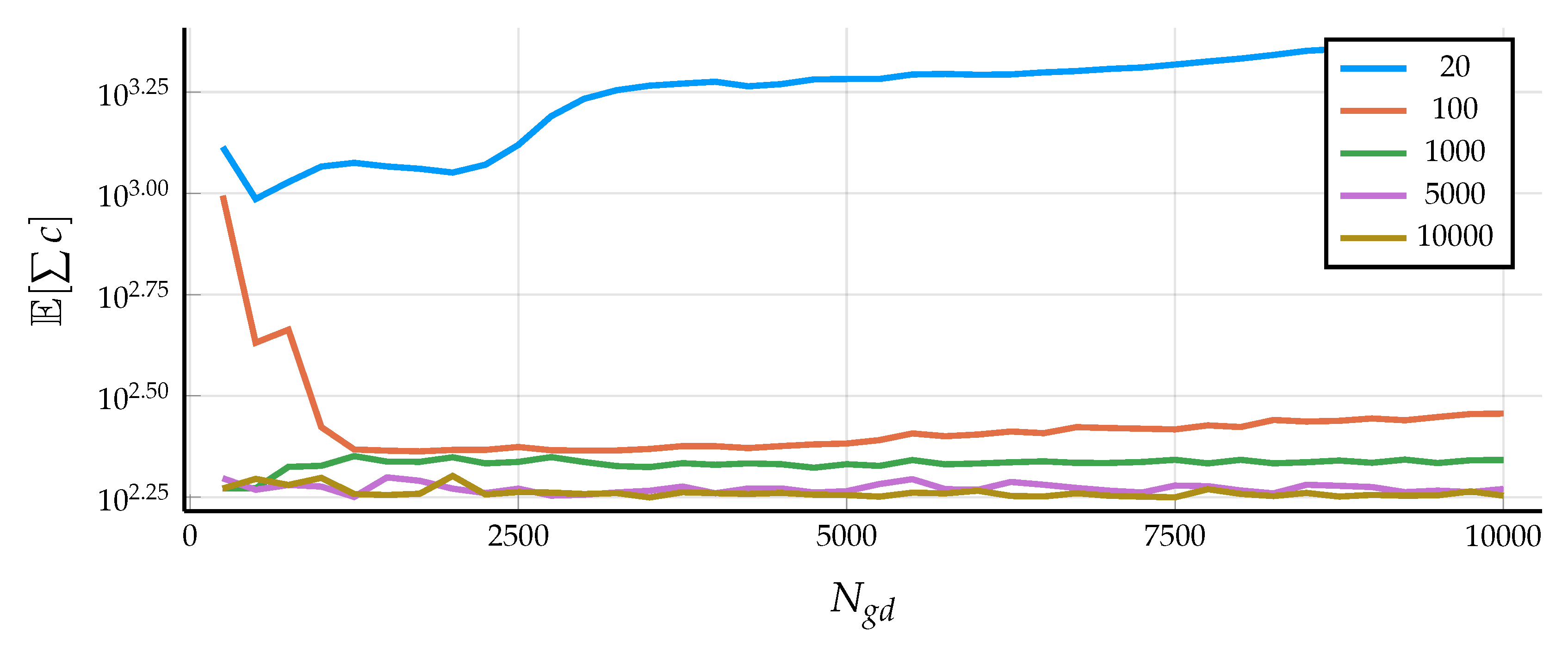
3.3. Training a Robust Recurrent Network
| Algorithm 1 Generating training data for the recurrent neural network | |
|
Inputs: for do end for return | ▹ Evaluate oracle ▹ Evaluate controller ▹ Disturbed dynamics |
| Algorithm 2 Disturbed Oracle Imitation (DOI) |
| fordo for do sample sequence end for for do Update using TBPTT. end for end for |
3.4. Adding Adjustable Behavior
4. Task and Model Description
4.1. System and Task
4.2. Mathematical Model
5. Application and Results
5.1. Control Design Details
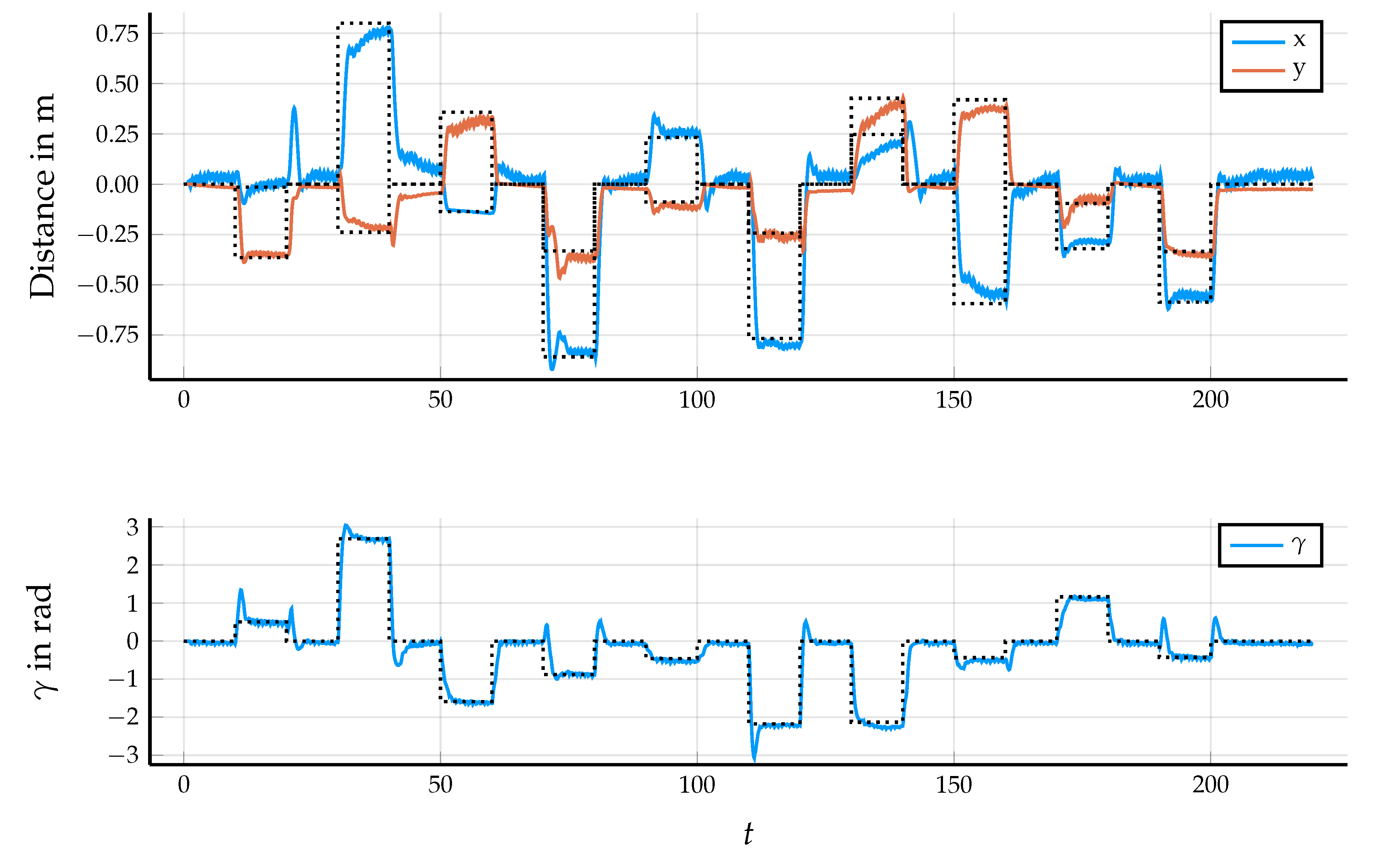
5.2. Results in Simulation
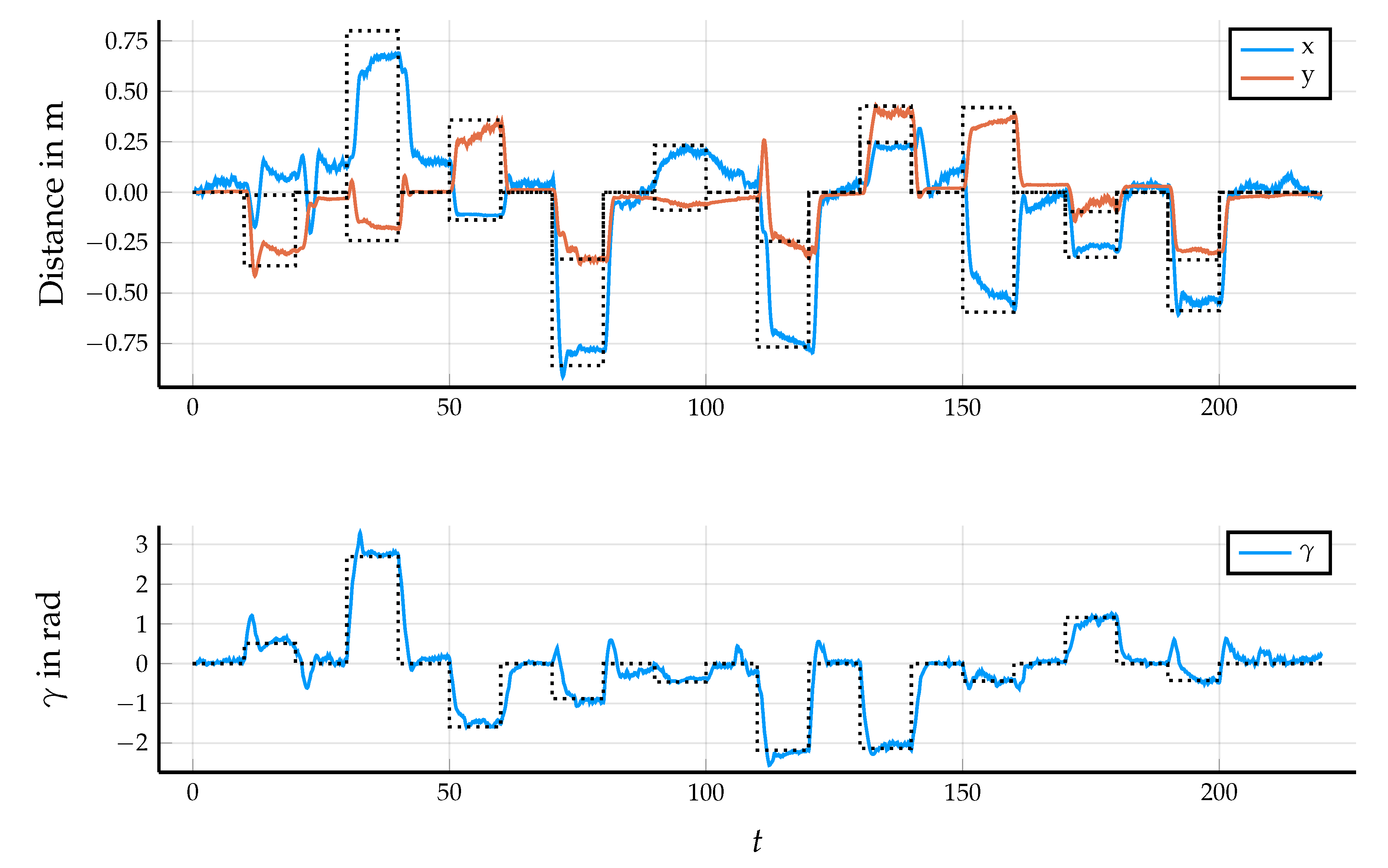
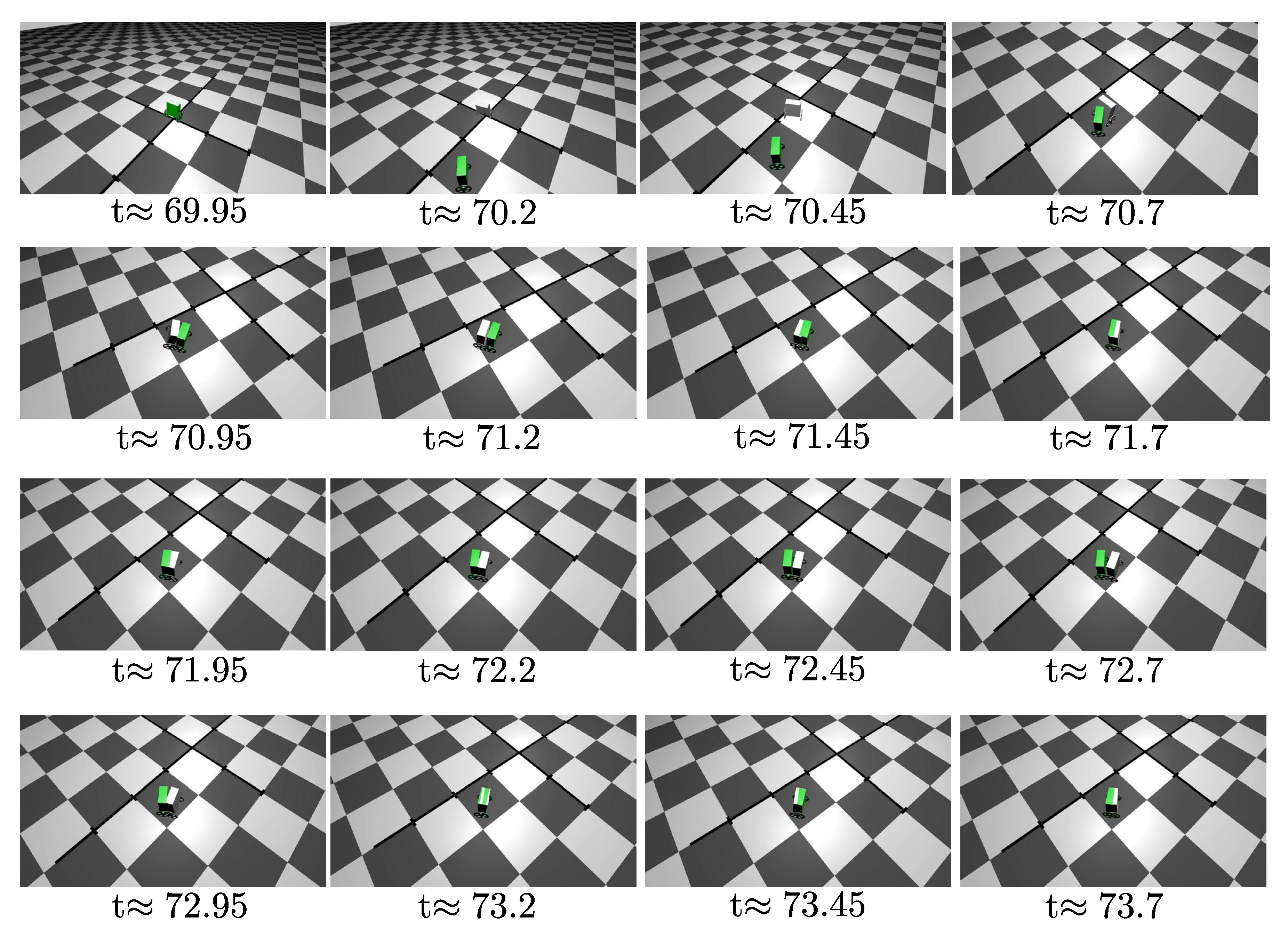
5.3. Control Performance in the Application
5.4. Outlook of Application Specific Variations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DAGGER | Dataset aggregation |
| DART | Disturbances for augmenting robot trajectories |
| DOI | Disturbed oracle imitation |
| MIP | Mobile inverted pendulum |
| MPC | Model Predictive Control |
| TBPTT | Truncated backpropagation through time |
Appendix A. Rigid Body Dynamics Model
References
- Yang, C.; Li, Z.; Li, J. Trajectory planning and optimized adaptive control for a class of wheeled inverted pendulum vehicle models. IEEE Trans. Cybern. 2012, 43, 24–36. [Google Scholar] [CrossRef] [PubMed]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Faulwasser, T.; Weber, T.; Zometa, P.; Findeisen, R. Implementation of nonlinear model predictive path-following control for an industrial robot. IEEE Trans. Control Syst. Technol. 2016, 25, 1505–1511. [Google Scholar] [CrossRef]
- Deisenroth, M.; Rasmussen, C.E. PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 465–472. [Google Scholar]
- Golemo, F.; Taiga, A.A.; Courville, A.; Oudeyer, P.Y. Sim-to-Real Transfer with Neural-Augmented Robot Simulation. In Proceedings of the Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; pp. 817–828. [Google Scholar]
- Pattanaik, A.; Tang, Z.; Liu, S.; Bommannan, G.; Chowdhary, G. Robust deep reinforcement learning with adversarial attacks. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 2040–2042. [Google Scholar]
- Pinto, L.; Davidson, J.; Sukthankar, R.; Gupta, A. Robust adversarial reinforcement learning. arXiv 2017, arXiv:1703.02702. [Google Scholar]
- Rajeswaran, A.; Ghotra, S.; Ravindran, B.; Levine, S. Epopt: Learning robust neural network policies using model ensembles. arXiv 2016, arXiv:1610.01283. [Google Scholar]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-real transfer of robotic control with dynamics randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Muratore, F.; Treede, F.; Gienger, M.; Peters, J. Domain randomization for simulation-based policy optimization with transferability assessment. In Proceedings of the Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; pp. 700–713. [Google Scholar]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. (CSUR) 2017, 50, 21. [Google Scholar] [CrossRef]
- Dessort, R.; Chucholowski, C. Explicit model predictive control of semi-active suspension systems using Artificial Neural Networks (ANN). In 8th International Munich Chassis Symposium 2017; Pfeffer, P.E., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017; pp. 207–228. [Google Scholar]
- Mordatch, I.; Todorov, E. Combining the benefits of function approximation and trajectory optimization. Robot. Sci. Syst. 2014, 4, 5–32. [Google Scholar]
- Abbeel, P.; Quigley, M.; Ng, A.Y. Using inaccurate models in reinforcement learning. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 1–8. [Google Scholar]
- Mordatch, I.; Lowrey, K.; Todorov, E. Ensemble-CIO: Full-body dynamic motion planning that transfers to physical humanoids. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5307–5314. [Google Scholar]
- Liu, C.; Li, H.; Gao, J.; Xu, D. Robust self-triggered min–max model predictive control for discrete-time nonlinear systems. Automatica 2018, 89, 333–339. [Google Scholar] [CrossRef]
- Yu, W.; Liu, C.K.; Turk, G. Preparing for the Unknown: Learning a Universal Policy with Online System Identification. arXiv 2017, arXiv:1702.02453. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Muratore, F.; Gienger, M.; Peters, J. Assessing Transferability from Simulation to Reality for Reinforcement Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Bousmalis, K.; Irpan, A.; Wohlhart, P.; Bai, Y.; Kelcey, M.; Kalakrishnan, M.; Downs, L.; Ibarz, J.; Pastor, P.; Konolige, K.; et al. Using simulation and domain adaptation to improve efficiency of deep robotic grasping. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4243–4250. [Google Scholar]
- Chebotar, Y.; Handa, A.; Makoviychuk, V.; Macklin, M.; Issac, J.; Ratliff, N.; Fox, D. Closing the sim-to-real loop: Adapting simulation randomization with real world experience. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8973–8979. [Google Scholar]
- Salimans, T.; Ho, J.; Chen, X.; Sutskever, I. Evolution strategies as a scalable alternative to reinforcement learning. arXiv 2017, arXiv:1703.03864. [Google Scholar]
- Chrabaszcz, P.; Loshchilov, I.; Hutter, F. Back to Basics: Benchmarking Canonical Evolution Strategies for Playing Atari. arXiv 2018, arXiv:1802.08842. [Google Scholar]
- Rückstieß, T.; Sehnke, F.; Schaul, T.; Wierstra, D.; Sun, Y.; Schmidhuber, J. Exploring parameter space in reinforcement learning. Paladyn 2010, 1, 14–24. [Google Scholar] [CrossRef]
- Ortega, J.G.; Camacho, E. Mobile robot navigation in a partially structured static environment, using neural predictive control. Control Eng. Pract. 1996, 4, 1669–1679. [Google Scholar] [CrossRef]
- Åkesson, B.M.; Toivonen, H.T.; Waller, J.B.; Nyström, R.H. Neural network approximation of a nonlinear model predictive controller applied to a pH neutralization process. Comput. Chem. Eng. 2005, 29, 323–335. [Google Scholar] [CrossRef]
- Ross, S.; Gordon, G.; Bagnell, D. A reduction of imitation learning and structured prediction to no-regret online learning. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 627–635. [Google Scholar]
- He, H.; Eisner, J.; Daume, H. Imitation learning by coaching. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 3149–3157. [Google Scholar]
- Laskey, M.; Lee, J.; Fox, R.; Dragan, A.; Goldberg, K. Dart: Noise injection for robust imitation learning. arXiv 2017, arXiv:1703.09327. [Google Scholar]
- Mordatch, I.; Lowrey, K.; Andrew, G.; Popovic, Z.; Todorov, E.V. Interactive control of diverse complex characters with neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 3132–3140. [Google Scholar]
- Levine, S.; Koltun, V. Guided policy search. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; pp. 1–9. [Google Scholar]
- Levine, S.; Koltun, V. Learning complex neural network policies with trajectory optimization. In Proceedings of the International Conference on Machine Learning, Bejing, China, 22–24 June 2014; pp. 829–837. [Google Scholar]
- Zhang, T.; Kahn, G.; Levine, S.; Abbeel, P. Learning deep control policies for autonomous aerial vehicles with mpc-guided policy search. In Proceedings of the 2016 IEEE international conference on robotics and automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 528–535. [Google Scholar]
- Kahn, G.; Zhang, T.; Levine, S.; Abbeel, P. PLATO: Policy Learning using Adaptive Trajectory Optimization. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Levine, S.; Finn, C.; Darrell, T.; Abbeel, P. End-to-end training of deep visuomotor policies. J. Mach. Learn. Res. 2016, 17, 1334–1373. [Google Scholar]
- Paul, S.; Kurin, V.; Whiteson, S. Fast Efficient Hyperparameter Tuning for Policy Gradient Methods. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 4618–4628. [Google Scholar]
- Von Stryk, O.; Bulirsch, R. Direct and indirect methods for trajectory optimization. Ann. Oper. Res. 1992, 37, 357–373. [Google Scholar] [CrossRef]
- Bock, H.G.; Plitt, K.J. A multiple shooting algorithm for direct solution of optimal control problems. IFAC Proc. Vol. 1984, 17, 1603–1608. [Google Scholar] [CrossRef]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; SIAM: Philadelphia, PA, USA, 2010; Volume 10. [Google Scholar]
- Wächter, A. An Interior Point Algorithm for Large-Scale Nonlinear Optimization with Applications in Process Engineering. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2002. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Tallec, C.; Ollivier, Y. Unbiasing Truncated Backpropagation Through Time. arXiv 2017, arXiv:1705.08209. [Google Scholar]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Muralidharan, V.; Mahindrakar, A.D. Position Stabilization and Waypoint Tracking Control of Mobile Inverted Pendulum Robot. IEEE Trans. Control Syst. Technol. 2014, 22, 2360–2367. [Google Scholar] [CrossRef]
- Dini, N.; Majd, V.J. Model predictive control of a wheeled inverted pendulum robot. In Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 152–157. [Google Scholar] [CrossRef]
- Ha, J.; Lee, J. Position control of mobile two wheeled inverted pendulum robot by sliding mode control. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, JeJu Island, Korea, 17–21 October 2012; pp. 715–719. [Google Scholar]
- Pathak, K.; Franch, J.; Agrawal, S.K. Velocity and position control of a wheeled inverted pendulum by partial feedback linearization. IEEE Trans. Robot. 2005, 21, 505–513. [Google Scholar] [CrossRef]
- Kara, T.; Eker, I. Nonlinear modeling and identification of a DC motor for bidirectional operation with real time experiments. Energy Convers. Manag. 2004, 45, 1087–1106. [Google Scholar] [CrossRef]
- Achiam, J.; Held, D.; Tamar, A.; Abbeel, P. Constrained Policy Optimization. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]



| Variable | Value | Unit | Description |
|---|---|---|---|
| 1.76 | Mass of the body | ||
| 0.147 | Mass of a wheel | ||
| R | 0.07 | Radius of the wheels | |
| Height of the center of mass above wheel axis | |||
| b | 0.09925 | Half length between wheels | |
| 0.0191 | Moment of inertia, x-axis | ||
| Moment of inertia, y-axis | |||
| 0.0048 | Moment of inertia, z-axis | ||
| Moment of inertia. Wheel, y-axis | |||
| Moment of inertia. Wheel, z-axis | |||
| 0.018 | Motor constant | ||
| 0.61 | Motor constant | ||
| Friction model constant | |||
| 2.0 | / | Friction model constant | |
| 0.4 | / | Friction model constant | |
| Friction model constant |
| opt. | ||||||
|---|---|---|---|---|---|---|
| 181.47 | 178.33 | 176.58 | 185.81 | 185.75 | 155.163 | |
| 712.03 | 520.95 | 121.38 | 494.27 | 182.67 | 0 | |
| 0.133 | 0.102 | 0.090 | 0.070 | 0.051 | 0 | |
| 1.10 | 2.13 | 1.34 | 1.092 | 0.524 | 0 |
| 5221.86 | 3957.26 | 4062.04 | 4131.76 | |
| 1674.85 | 1566.88 | 1265.35 | 1431.55 | |
| 6896.71 | 5524.14 | 5327.39 | 5563.31 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dengler, C.; Lohmann, B. Adjustable and Adaptive Control for an Unstable Mobile Robot Using Imitation Learning with Trajectory Optimization. Robotics 2020, 9, 29. https://doi.org/10.3390/robotics9020029
Dengler C, Lohmann B. Adjustable and Adaptive Control for an Unstable Mobile Robot Using Imitation Learning with Trajectory Optimization. Robotics. 2020; 9(2):29. https://doi.org/10.3390/robotics9020029
Chicago/Turabian StyleDengler, Christian, and Boris Lohmann. 2020. "Adjustable and Adaptive Control for an Unstable Mobile Robot Using Imitation Learning with Trajectory Optimization" Robotics 9, no. 2: 29. https://doi.org/10.3390/robotics9020029
APA StyleDengler, C., & Lohmann, B. (2020). Adjustable and Adaptive Control for an Unstable Mobile Robot Using Imitation Learning with Trajectory Optimization. Robotics, 9(2), 29. https://doi.org/10.3390/robotics9020029





