Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller
Abstract
1. Introduction
- First evaluation of SMC parameter optimization for quadrotor flight system with hunting-based algorithms ALO and GWO
- Parameters obtained by ALO and GWO provided more confidence and repeatability during optimization process
- Parameters obtained by ALO and GWO provided lower tracking error
- Novel extension of such optimization approaches to SMC controller tuning, usually applied to PID control
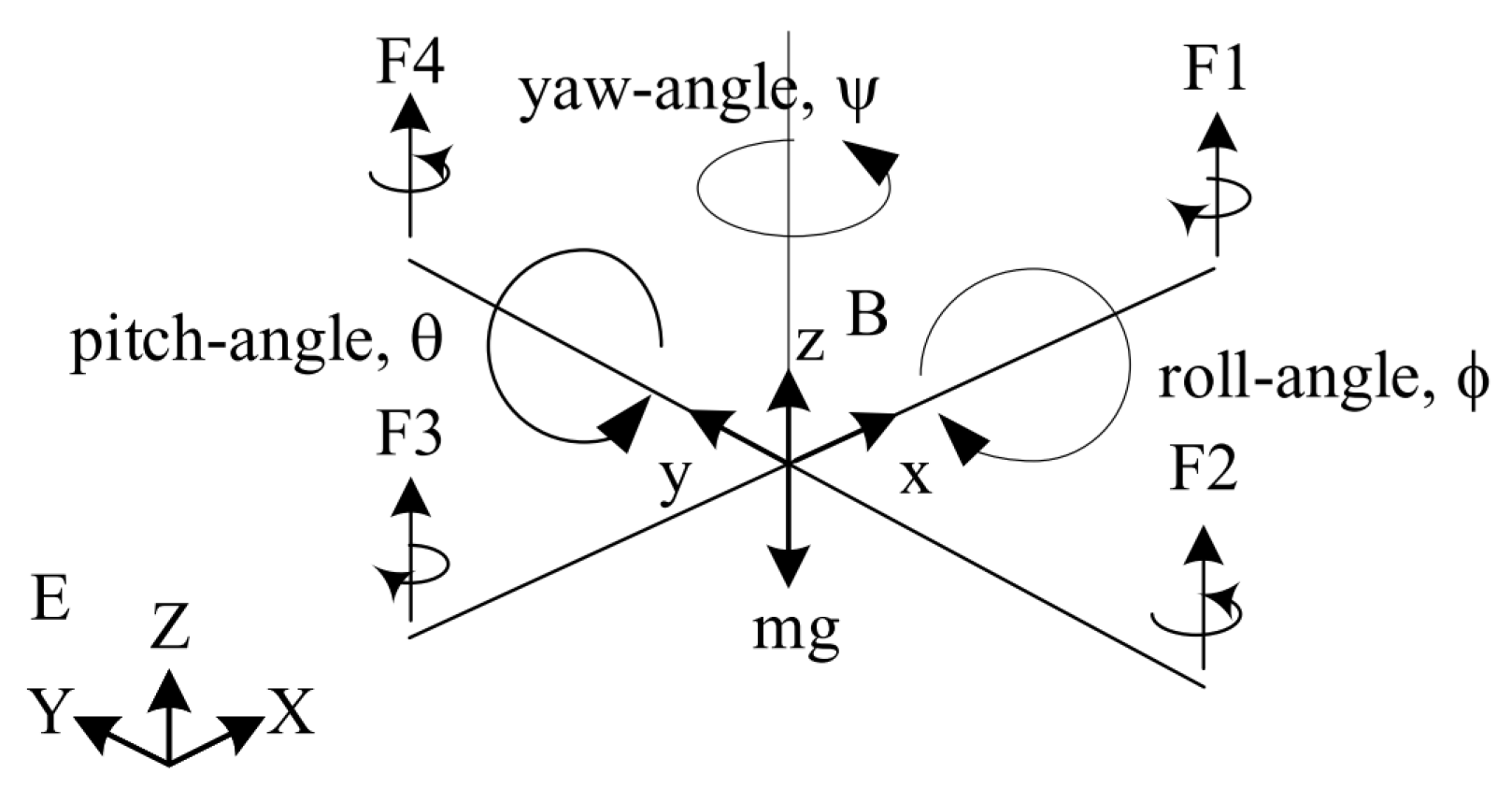
2. Quadrotor Dynamics
3. Altitude and Attitude Control—Sliding Mode Flight System
4. Hunting-Based Optimizers
4.1. Ant Lion Optimizer
4.1.1. Random Walk of Ants
4.1.2. Ant Lions Building Traps
4.1.3. The Entrapment of Ants in Traps
4.1.4. Ant Lions Catching Ants and Re-Building Traps
| Algorithm 1: ALO algorithm pseudocode. |
 |
4.2. Grey Wolf Optimizer
- Alpha () are dominant wolves and thus followed by the rest of the pack.
- Beta () are second in command helping alphas in the decision process and establish a bridge between alphas and the lower levels.
- Delta () are third in the pack hierarchy; while submitted to alphas and betas, they submit the lowest rank, which is called omega. Deltas represent wolves such as scouts, sentinels, elders, hunters, and caretakers.
- Omega () represent the rest of population solutions.
| Algorithm 2: Pseudocode for the GWO algorithm. |
 |
5. Simulations and Discussion
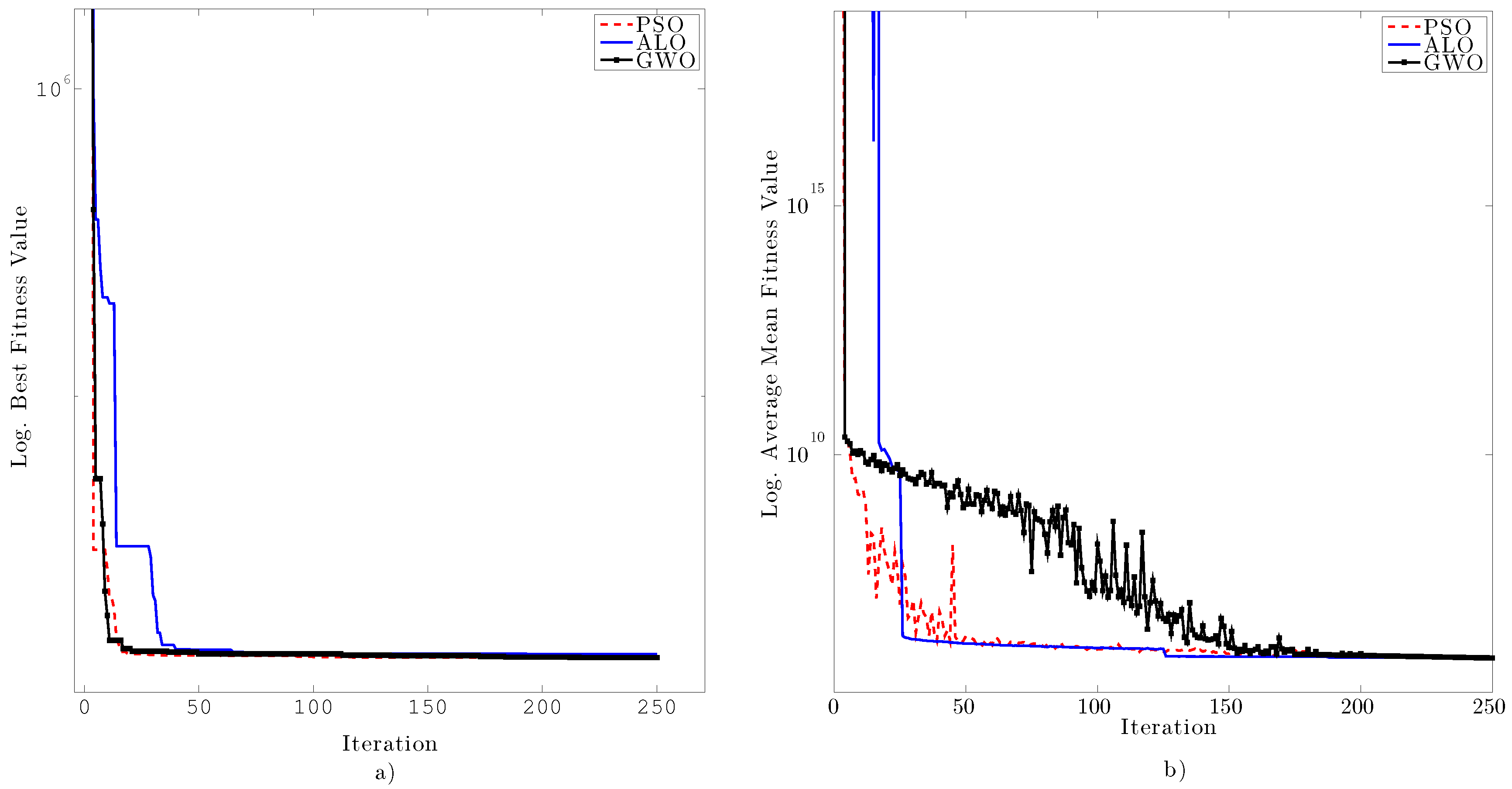
5.1. Fitness Function and Optimization Methodology
- statistical Best is the minimum fitness function value () (or best value) obtained in .
- statistical Worst is the maximum fitness function value () (or worst value) obtained in .
- statistical Median is the middle fitness function value () in a sorted list (or median value) obtained in . If there are two middle numbers ( is even), the median is their average.
- statistical Mean is the average performance of a stochastic algorithm applied times, where is the optimal solution at the ith run.
- statistical Standard deviation (Std) indicates the optimizer stability and robustness, preferably as small as possible.
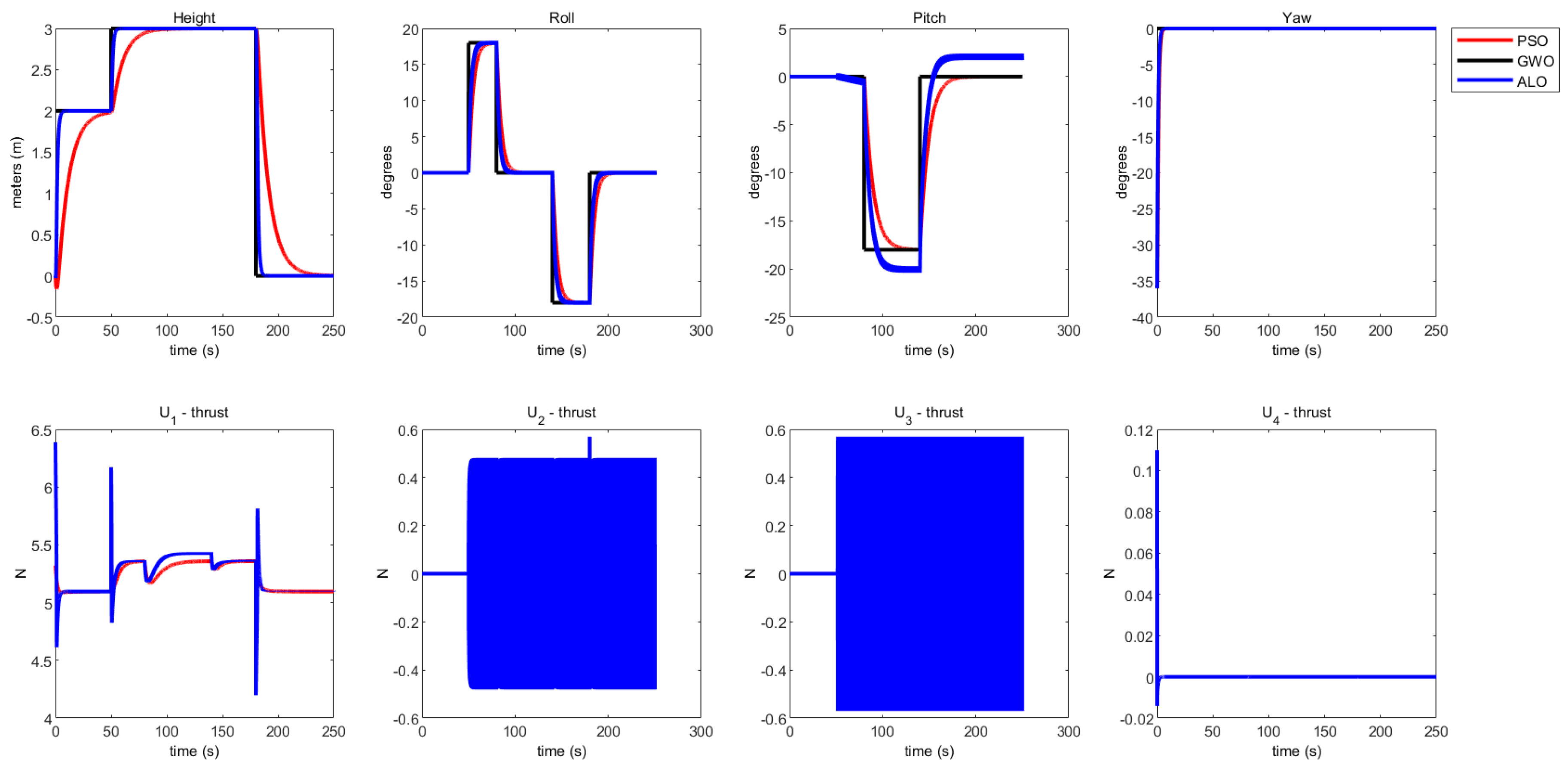
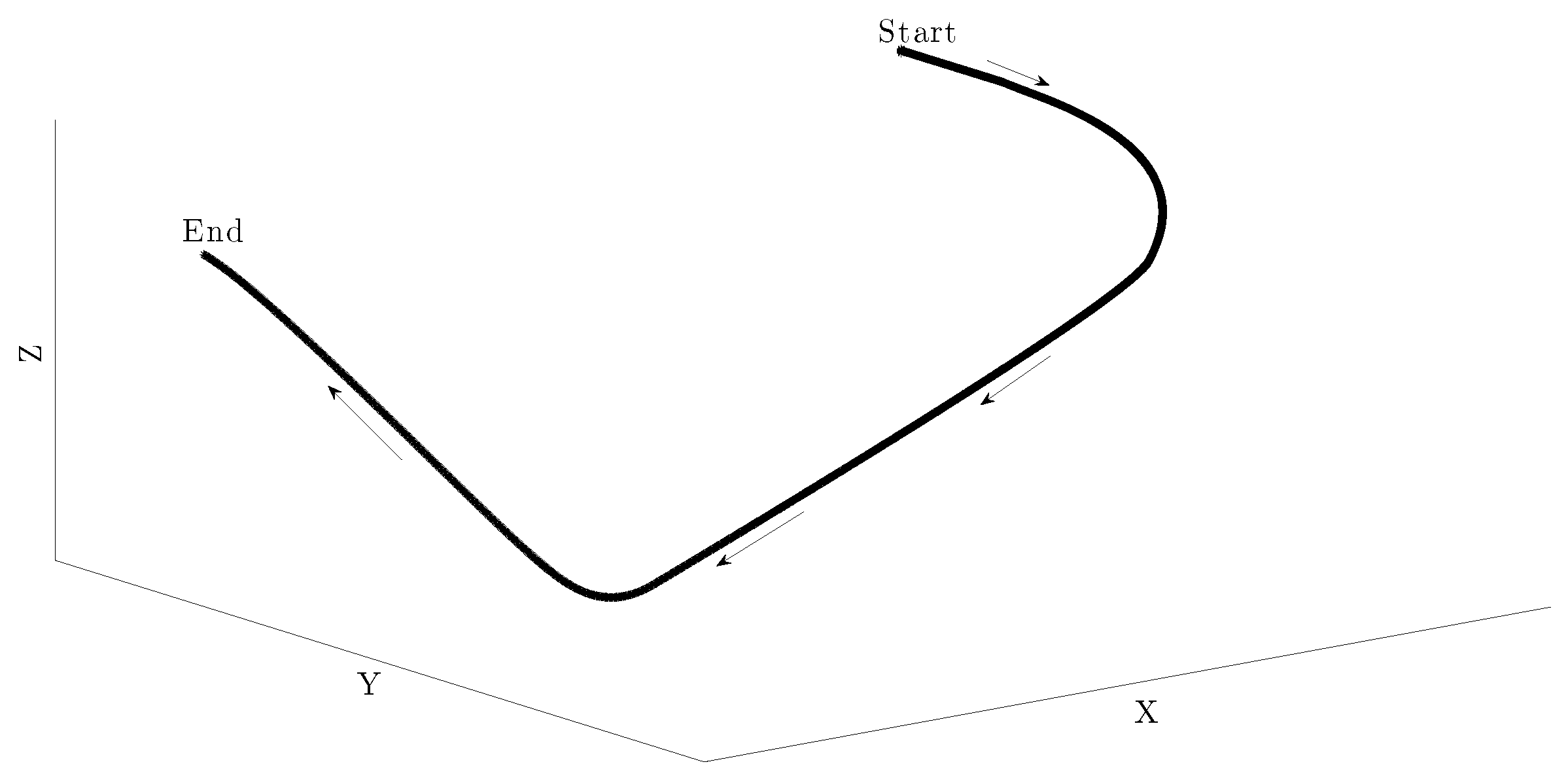
5.2. Flight Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simelli, I.; Tsagraris, A. The Use of Unmanned Aerial Systems (UAS) in Agriculture. In Proceedings of the 7th International Conference on Information and Communication Technologies in Agriculture, Food and Environment (HAICTA 2015), Kavala, Greece, 17–20 September 2015; pp. 730–736. [Google Scholar]
- Dief, T.; Yoshida, S. Review: Modeling and Classical Control of Quad-rotor. Int. J. Comput. Sci. Inf. Technol. Secur. 2015, 5, 314–319. [Google Scholar] [CrossRef]
- Bolandi, H.; Rezaei, M.; Mohsenipour, R.; Nemati, H.; Smailzadeh, S. Attitude Control of a Quadrotor with Optimized PID Controller. Intell. Control. Autom. 2013, 4, 335–342. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Modes in Control and Optimization; Springer: Berlim/Heidelberg, Germany, 1992. [Google Scholar]
- Swarup, A.; Sudhir. Comparison of Quadrotor Performance using Backstepping and Sliding Mode Control. In Proceedings of the International Conference on Circuits, Systems and Control, Interlaken, Switzerland, 22–24 February 2014; pp. 79–82. [Google Scholar]
- Runcharoon, K.; Srichatrapimuk, V. Sliding Mode Control of Quadrotor. In Proceedings of the 45th International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 552–557. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zhang, G. Discrete-time Sliding Mode Control for a Quadrotor UAV. Int. J. for Light Electron Opt. 2016, 127, 3718–3722. [Google Scholar] [CrossRef]
- González, J.; Salazar, S.; Lozano, R. Chattering-Free Sliding Mode Altitude Control for a Quad-Rotor Aircraft: Real-time Application. J. Intell. Robot. Syst. 2014, 73, 137–155. [Google Scholar] [CrossRef]
- Zhang, E.H.; Xiong, J.J.; Luo, J.L. Second Order SMC for a quadrotor UAV. Isa Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef]
- Berkenkamp, F.; Schoellig, A. Safe and Robust Learning Control with Gaussian Processes. In Proceedings of the 14th European Control Conference, Linz, Austria, 15–17 July 2015; pp. 2501–2506. [Google Scholar]
- Yacef, F.; Bouhali, O.; Hamerlain, M.; Rezoug, A. PSO Optimization of Integral Backstepping Controller for Quadrotor Attitude Stabilization. In Proceedings of the 3th IEEE International Conference on Systems and Control, Algiers, Algeria, 29–31 October 2013; pp. 462–466. [Google Scholar] [CrossRef]
- Basri, M.; Danapalasingam, K.; Husain, A. Design and Optimization of Backstepping Controller for an Underactuated Autonomous Quadrotor Unmanned Aerial Vehicle. Trans. Famena 2014, 38, 27–44. [Google Scholar]
- Herrera, M.; Chamorro, W.; Gómez, A.; Camacho, O. Sliding Mode Control: an Approach to Control a Quadrotor. In Proceedings of the Asia-Pacific Conference on Computer Aided System Engineering, Quito, Ecuador, 14–16 July 2015; pp. 314–319. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The Particle Swarm—Explosion, Stability and Convergence in a Multidimensional Complex Space. IEEE Trans. Evol. Computation 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Oliveira, J.; Oliveira, P.; Boaventura-Cunha, J.; Pinho, T. Chaos-based grey wolf optimizer for higher order sliding mode position control of a robotic manipulator. Nonlinear Dyn. 2017, 1–10. [Google Scholar] [CrossRef]
- Panda, M.; Das, B. Grey Wolf Optimizer and Its Applications: A Survey. In Proceedings of the Third International Conference on Microelectronics, Computing and Communication Systems, Ranchi, India, 12–13 May 2019; pp. 179–194. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Heidari, A.; Faris, H.; Mirjalili, S.; Aljarah, I.; Mafarja, M. Nature-Inspired Optimizers; Chapter Ant Lion Optimizer: Theory, Literature Review, and Application in Multi-layer Perceptron Neural Networks; Springer: Berlin, Germany, 2020; Volume 811, pp. 23–46. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Gao, Z.M.; Zhao, J. An Improved Grey Wolf Optimization Algorithm with Variable Weights. Comput. Intell. Neurosci. 2019, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Wang, H. Dynamic Adaptive Ant Lion Optimizer Applied to Route Planning for Unmanned Aerial Vehicle. Soft Comput. 2016, 1–14. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, Y.; Li, Z.; Pei, W. Grey Wolf Optimizer for Unmanned Combat Aerial Vehicle Path Planning. J. Adv. Eng. Softw. 2016, 99, 121–136. [Google Scholar] [CrossRef]
- Radmanesh, M.; Kumar, M. Grey Wolf Optimization based Sense and Avoid Algorithm for UAV Path Planning in Uncertain Environment using a Bayesian Framework. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 68–76. [Google Scholar]
- Raju, M.; Saikia, L.; Sinha, N. Automatic Generation Control of a Multi-area System using Ant Lion Optimizer Algorithm based PID plus Second Order Derivative Controller. Int. J. Electr. Power Energy Syst. 2016, 80, 52–63. [Google Scholar] [CrossRef]
- Nischal, M.; Mehta, S. Optimal Load Dispatch using Ant Lion Optimization. J. Eng. Res. Appl. 2015, 5, 10–19. [Google Scholar]
- Gupta, E.; Saxena, A. Grey wolf optimizer based regulator design for automatic generation control of interconnected power system. Cogent Eng. 2016, 3, 1–20. [Google Scholar] [CrossRef]
- Mehta, S.; Nischal, M. Ant Lion Optimization for Optimum Power Generation with Value Point Effects. Int. J. Res. Appl. Sci. Eng. Technol. 2015, 3, 1–6. [Google Scholar]
- Milica, P.; Jelena, P.; Mitić, M.; Vuković, N.; Miljković, Z.; Babić, B. The Ant Lion Algorithm for Integrated Process Planning and Sheduling. Appl. Mech. Mater. 2016, 384, 187–192. [Google Scholar]
- Yogarajan, G.; Revathi, T. A Discrete Ant Lion Optimization (DALO) for Solving Data Gathering Tour Problem in Wireless Sensor Networks. Middle-East J. Sci. Res. 2016, 24, 3113–3120. [Google Scholar]
- Dubey, H.; Pandit, M.; Panigrahi, B. Hydro-thermal-wind Scheduling Employing Novel Ant Lion Optimization Technique with Composite Ranking Index. Renew. Energy 2016, 99, 18–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.; Coelho, L. Multi-objective Grey Wolf Optimizer: A Novel Algorithm for Multi-Criterion Optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Oliveira, P.; Vrančić, D. Grey Wolf, Gravitational Search and Particle Swarm Optimizers: A Comparison for PID Controller Design. In Proceedings of the 12th Portuguese Conference on Automatic Control (CONTROLO 2016), Guimarães, Portugal, 14–16 September 2016; pp. 239–249. [Google Scholar]
- Oliveira, P.; Freire, H.; Pires, E. Grey wolf optimization for PID controller design with prescribed robustness margins. Soft Comput. 2016, 20, 4243–4255. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Towards Autonomous Indoor Micro VTOL. Auton. Robot. 2005, 18, 171–183. [Google Scholar] [CrossRef]
- Lee, H.; Utkin, V. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control. 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Samir, Z. Sliding Mode Control of a 6 DOF Quadrotor Helicopter. J. Electr. Eng. 2010, 10, 126–132. [Google Scholar]
- Batmaz, A.; Elbir, O.; Kasnakoglu, C. Design of a Quadrotor Roll Controller Using System Identification to Improve Empirical Results. Int. J. Mater. Mech. Manuf. 2013, 1, 347–349. [Google Scholar] [CrossRef]
- Wahab, M.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Zawbaa, H.; Emary, E.; Grosan, C. Feature Selection via Chaotic Antlion Optimization. PLoS ONE 2016, 11. [Google Scholar] [CrossRef]


| Subsystems | |
|---|---|
| Translational | Rotational |
| Parameter | Description | Value |
|---|---|---|
| m | total quadrotor mass | kg |
| g | gravity acceleration | ms |
| L | quadrature arm length | m |
| d | propeller resistance coefficient (drag factor) | |
| b | propeller lift coefficient (thrust factor) | |
| moment of propeller inertia around Z axis | ||
| moment of inertia around X axis | kgm | |
| moment of inertia around Y axis | kgm | |
| moment of inertia around Z axis | kgm |
| Roll |
| Pitch |
| Yaw |
| Control Component | Controller Parameters | |||
|---|---|---|---|---|
| Altitude z | Roll | Pitch | Yaw | |
| Time Interval | ||||
|---|---|---|---|---|
| 5 | 0 | 0 | 0 | |
| 3 | 0 | 0 | ||
| 1 | 0 | 0 | ||
| 4 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
| Measure Fitness Value | Method | ||
|---|---|---|---|
| PSO | ALO | GWO | |
| Best | |||
| Worst | |||
| Median | |||
| Mean | |||
| Std | |||
| Controller Parameters | Mean Values (30 runs) | Best Values (30 runs) | |||||
|---|---|---|---|---|---|---|---|
| PSO | ALO | GWO | PSO | ALO | GWO | ||
| Height z | |||||||
| Roll | |||||||
| Pitch | |||||||
| Yaw | |||||||
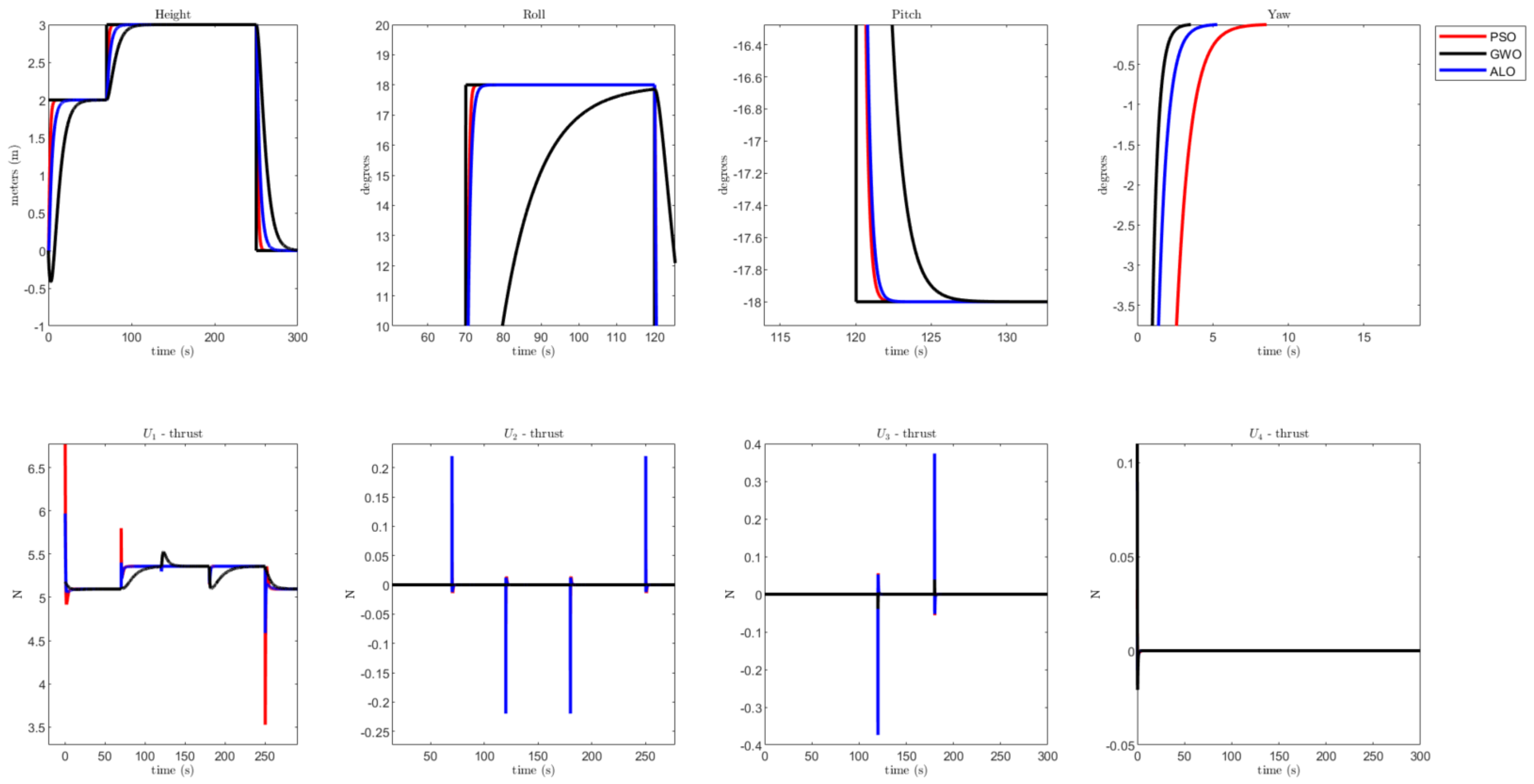
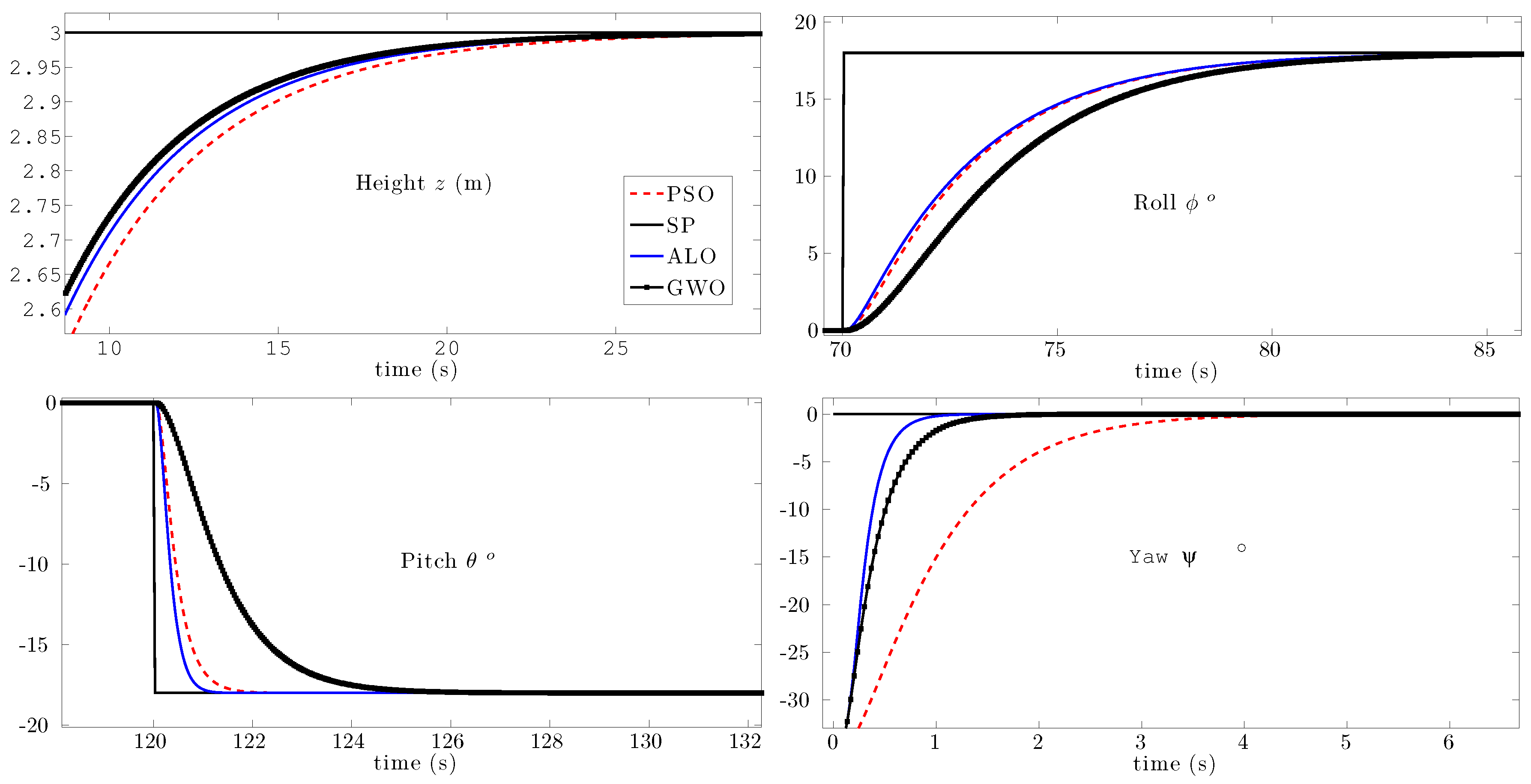
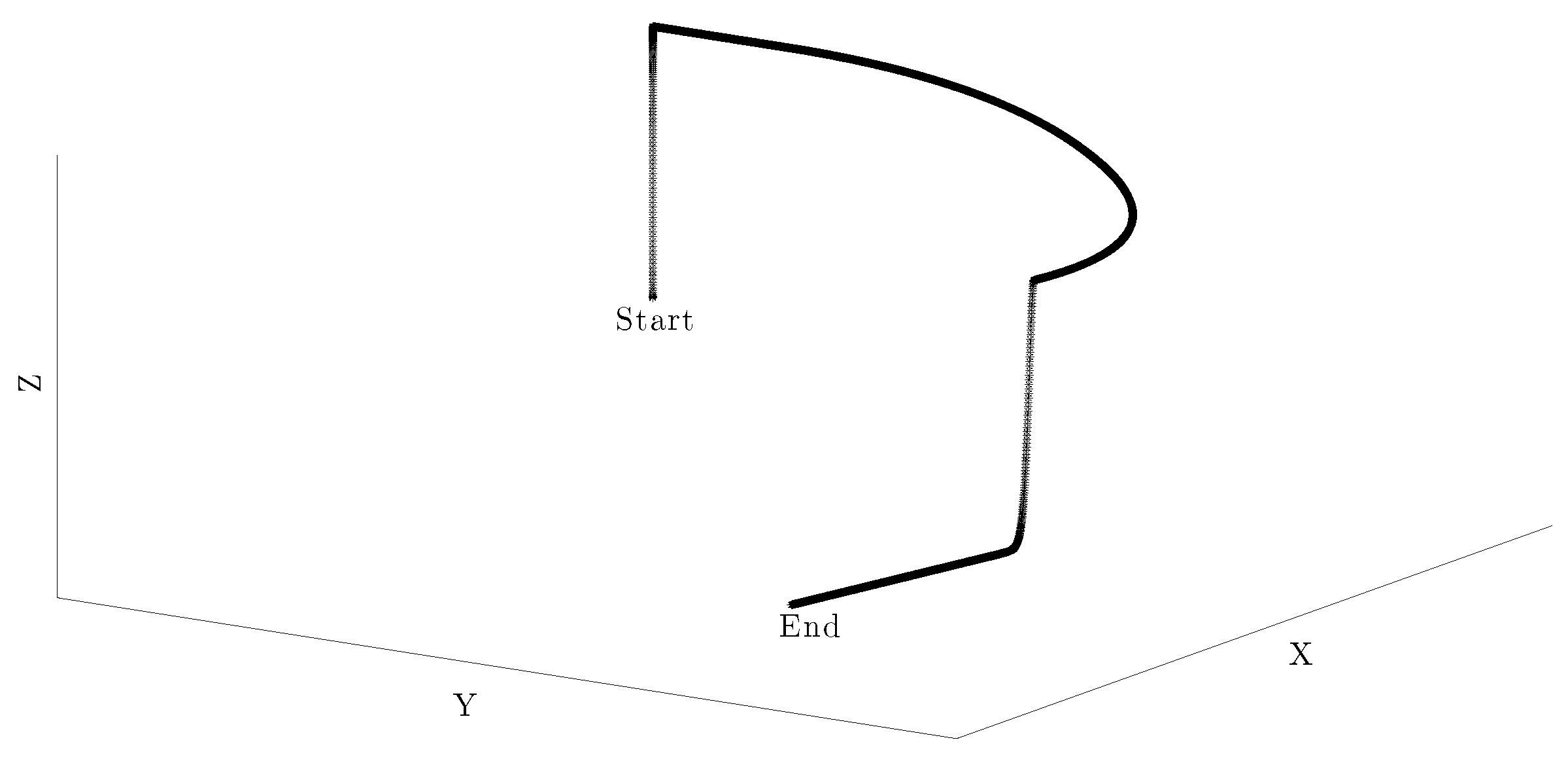
| Flight Plan 1 |
| , |
| , |
| , |
| , |
| , |
| Flight Plan 2—Parameter variation |
| , |
| , Parameter variation of in |
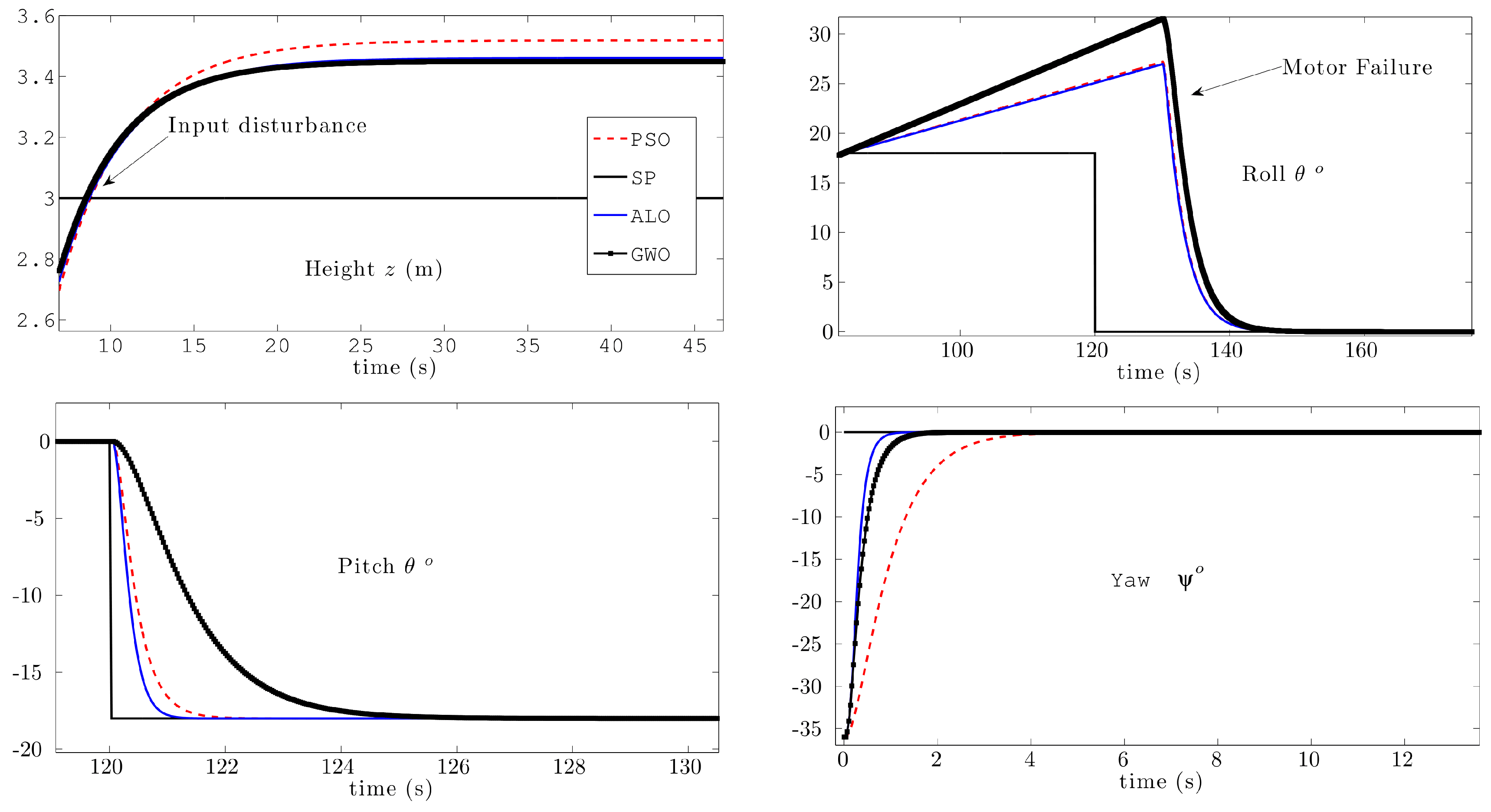
| Flight Plan 3—Input disturbance and temporary motor failure |
| the same FP 1 with constant input disturbance of in |
| , |
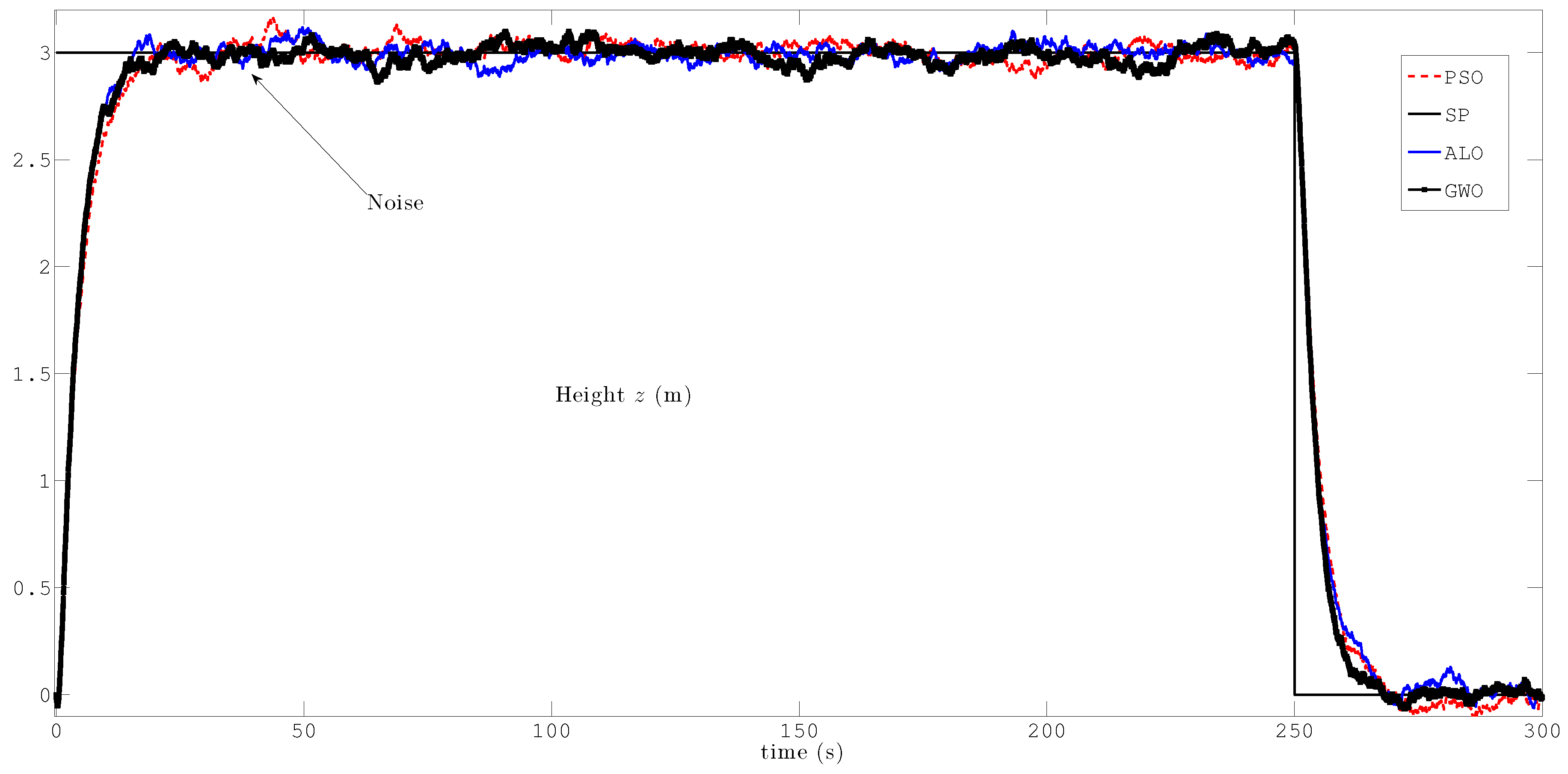
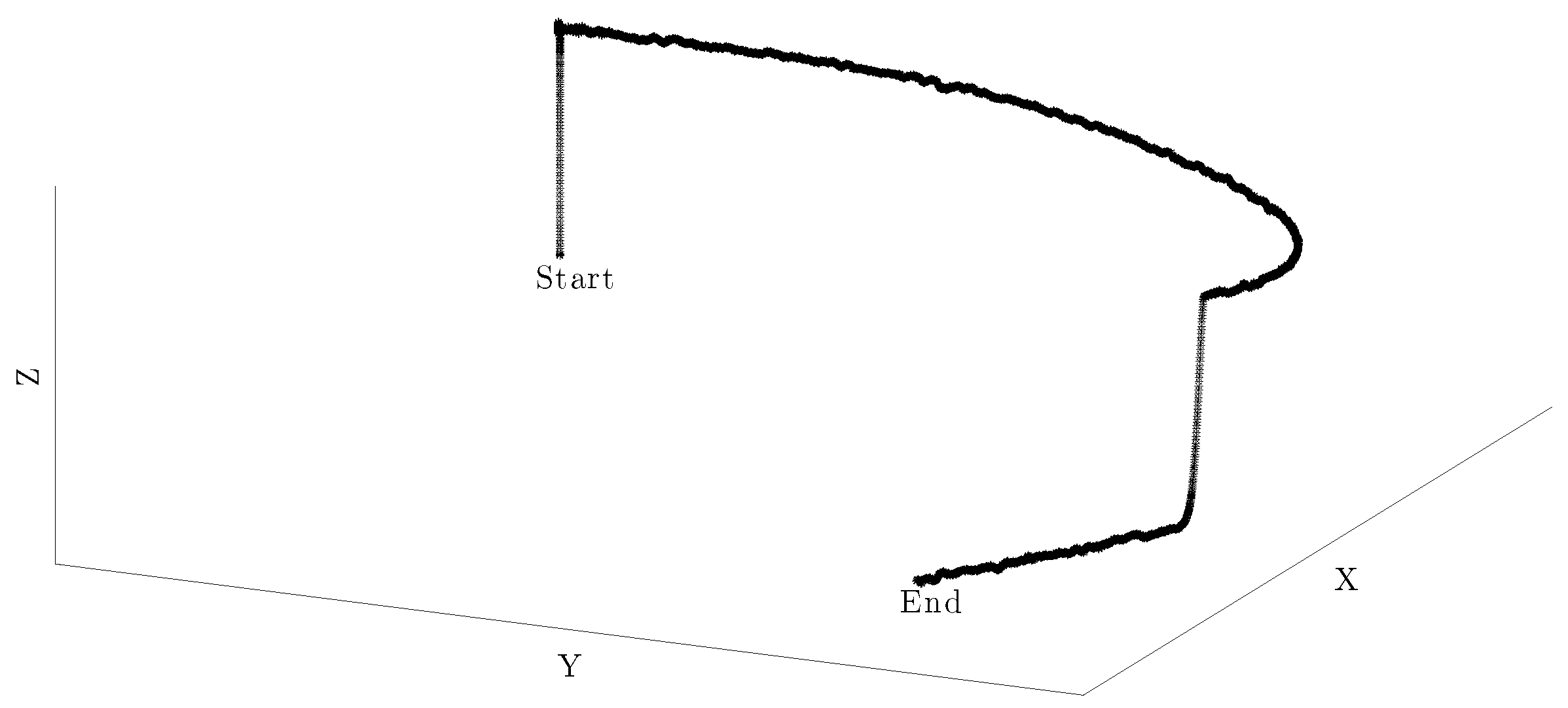
| Flight Plan 4—Measurement noise |
| the same FP 1 with added noise in |
| Flight Plan | Method | ||||
|---|---|---|---|---|---|
| PSO | |||||
| ALO | |||||
| FP1 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP2 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP3 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP4 | GWO |
| Flight Plan | Method | ||||
|---|---|---|---|---|---|
| PSO | |||||
| ALO | |||||
| FP1 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP2 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP3 | GWO | ||||
| PSO | |||||
| ALO | |||||
| FP4 | GWO |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, J.; Oliveira, P.M.; Boaventura-Cunha, J.; Pinho, T. Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller. Robotics 2020, 9, 22. https://doi.org/10.3390/robotics9020022
Oliveira J, Oliveira PM, Boaventura-Cunha J, Pinho T. Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller. Robotics. 2020; 9(2):22. https://doi.org/10.3390/robotics9020022
Chicago/Turabian StyleOliveira, Josenalde, Paulo Moura Oliveira, José Boaventura-Cunha, and Tatiana Pinho. 2020. "Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller" Robotics 9, no. 2: 22. https://doi.org/10.3390/robotics9020022
APA StyleOliveira, J., Oliveira, P. M., Boaventura-Cunha, J., & Pinho, T. (2020). Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller. Robotics, 9(2), 22. https://doi.org/10.3390/robotics9020022







