Classification of All Non-Isomorphic Regular and Cuspidal Arm Anatomies in an Orthogonal Metamorphic Manipulator
Abstract
1. Introduction
2. Cuspidality Investigation in Orthogonal—Metamorphic Modular Arm
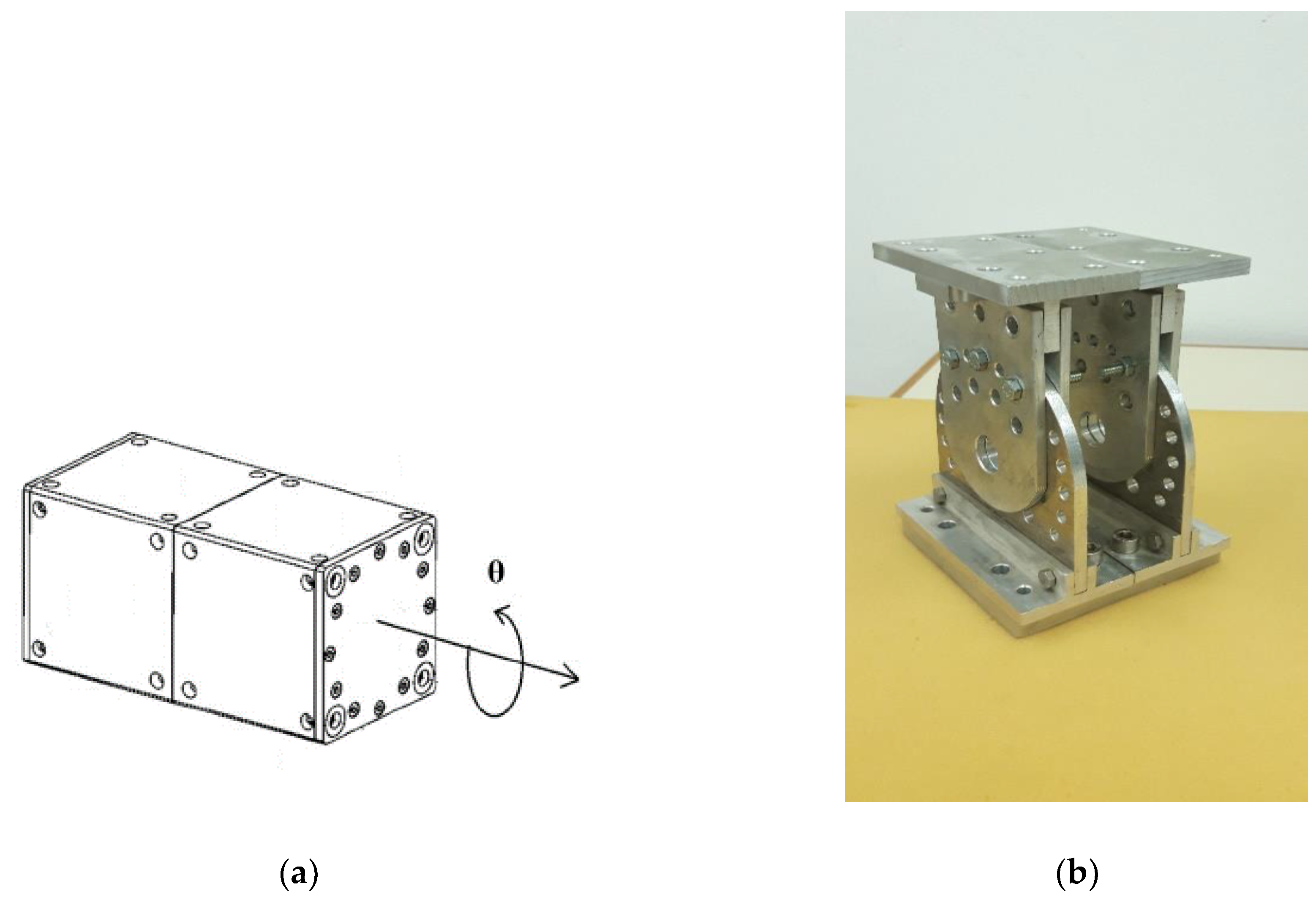
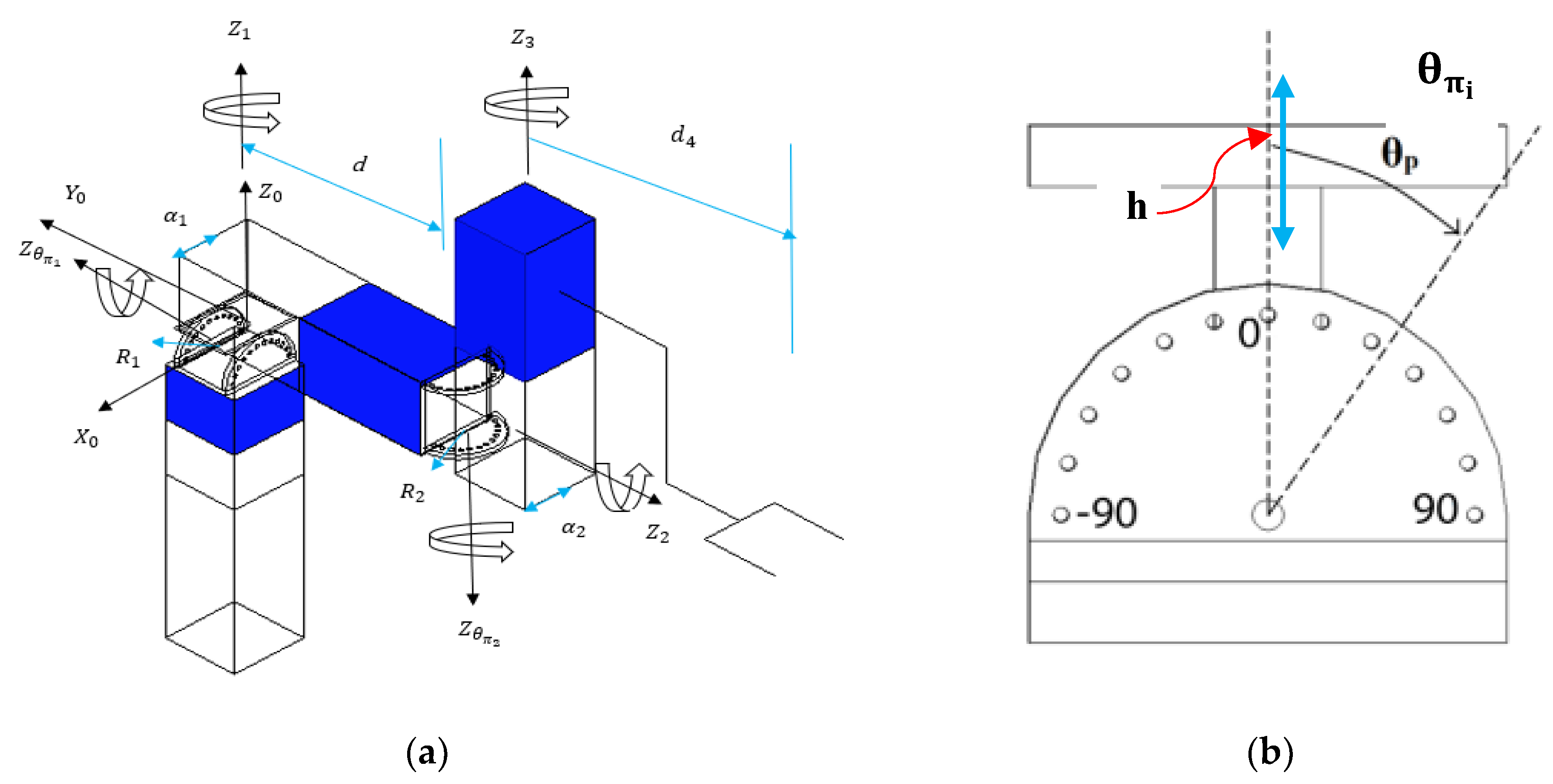
2.1. Presentation of Metamorphic Manipulator
2.2. The Proposed Method
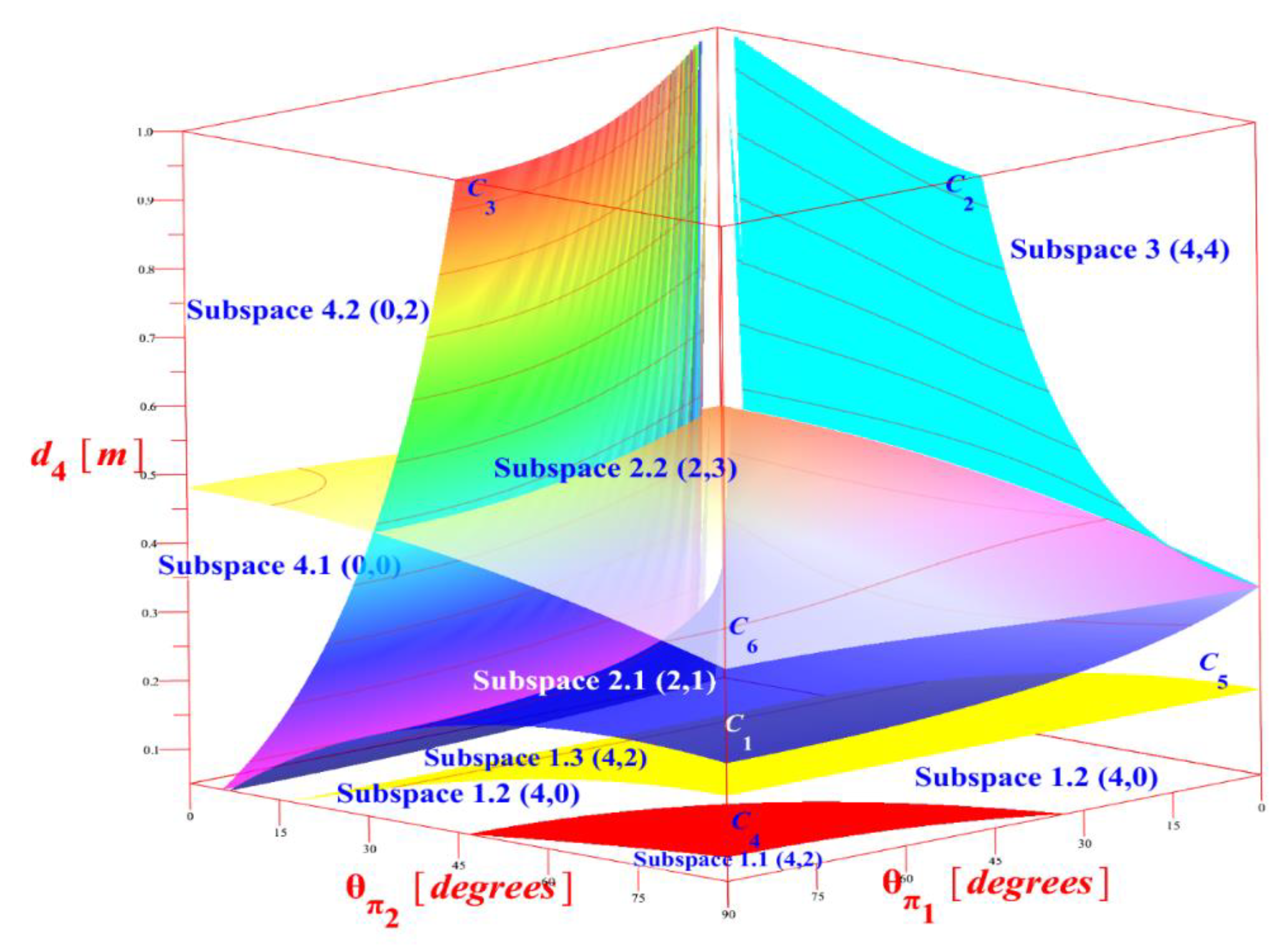
3. Classification of Orthogonal Kinematic Non-Isomorphic Configurations of 3R Metamorphic Manipulator according to the Topology of Metamorphic Workspace
3.1. Necessary and Sufficient Conditions to Investigate Cuspidality
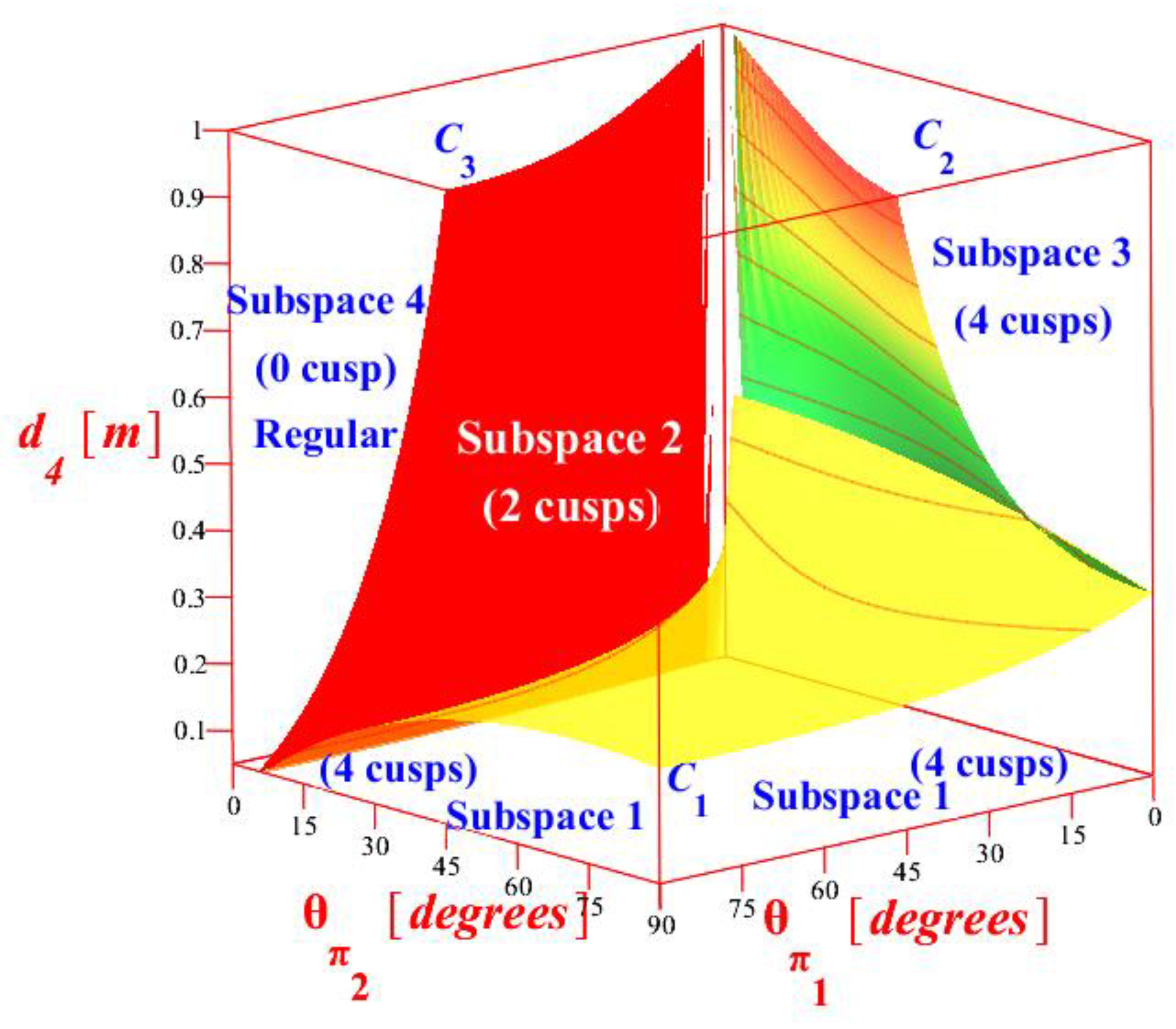
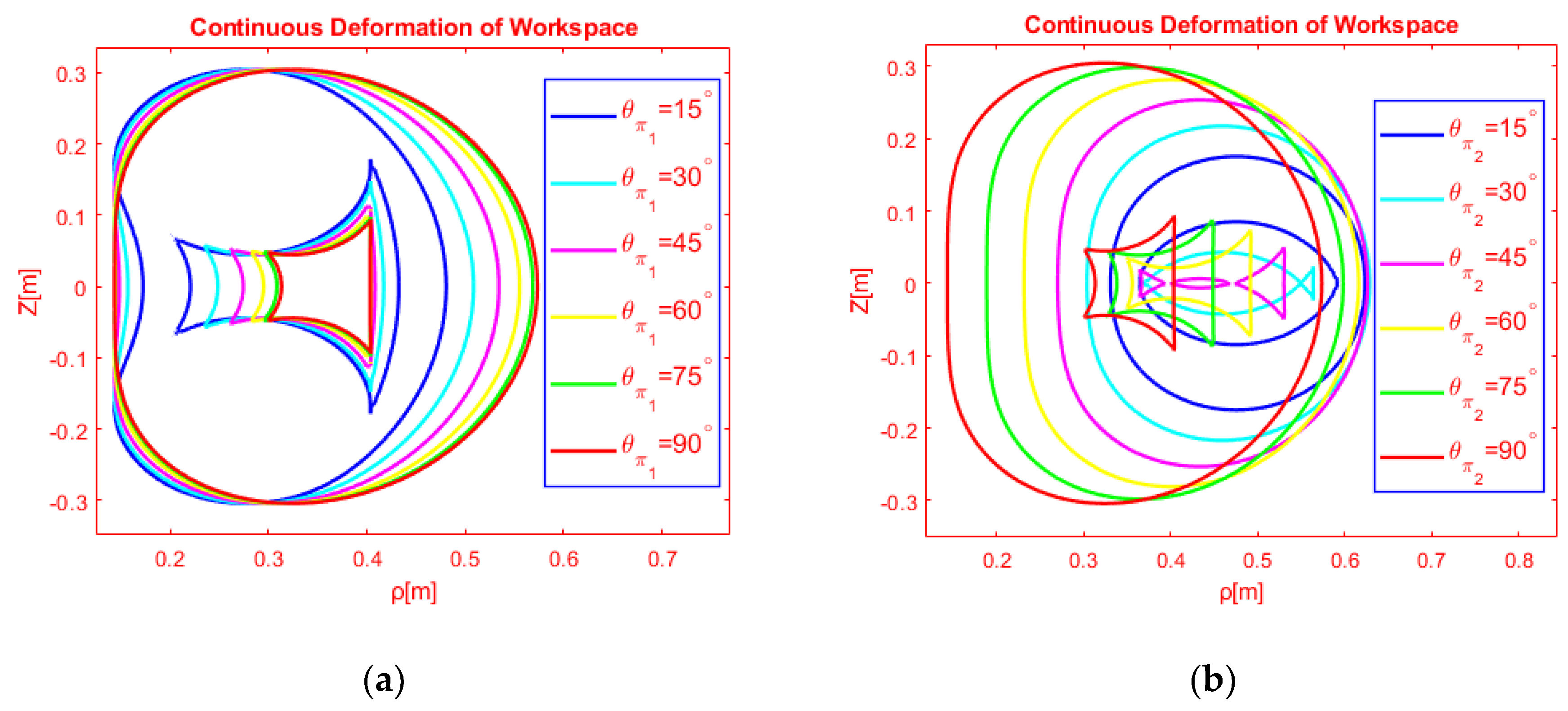
3.2. Separating Algebraic Equations through Investigation of det
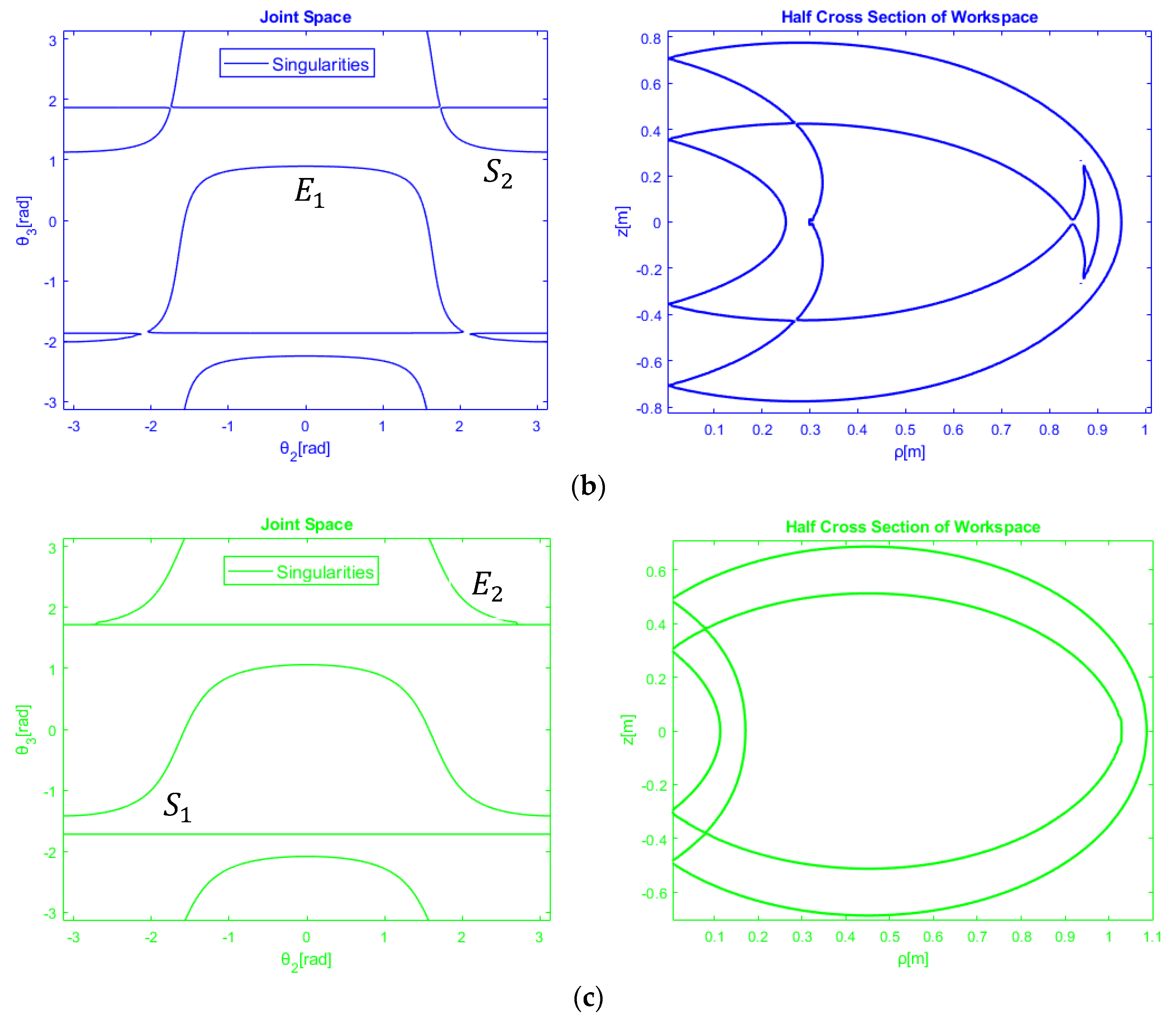
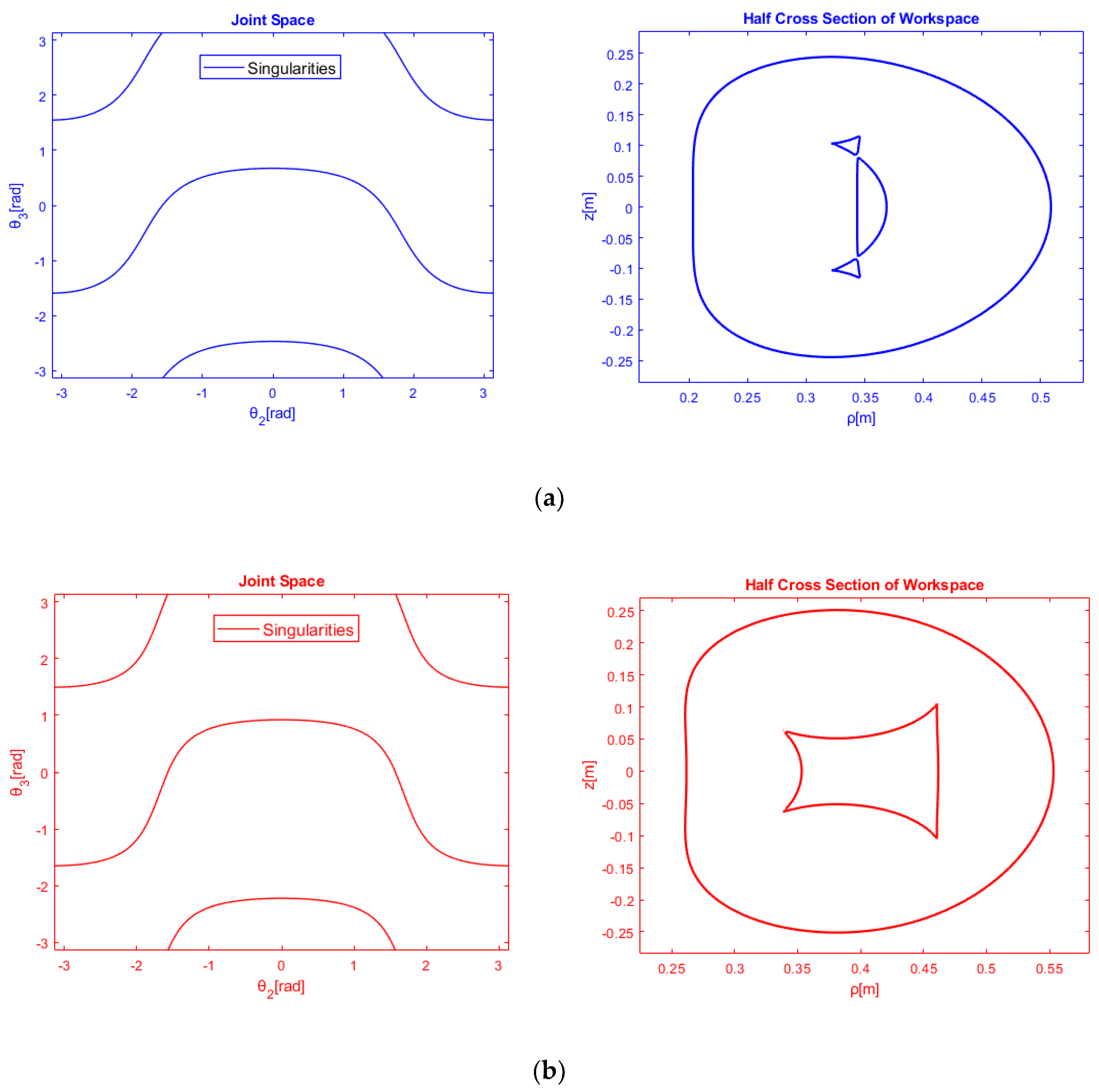
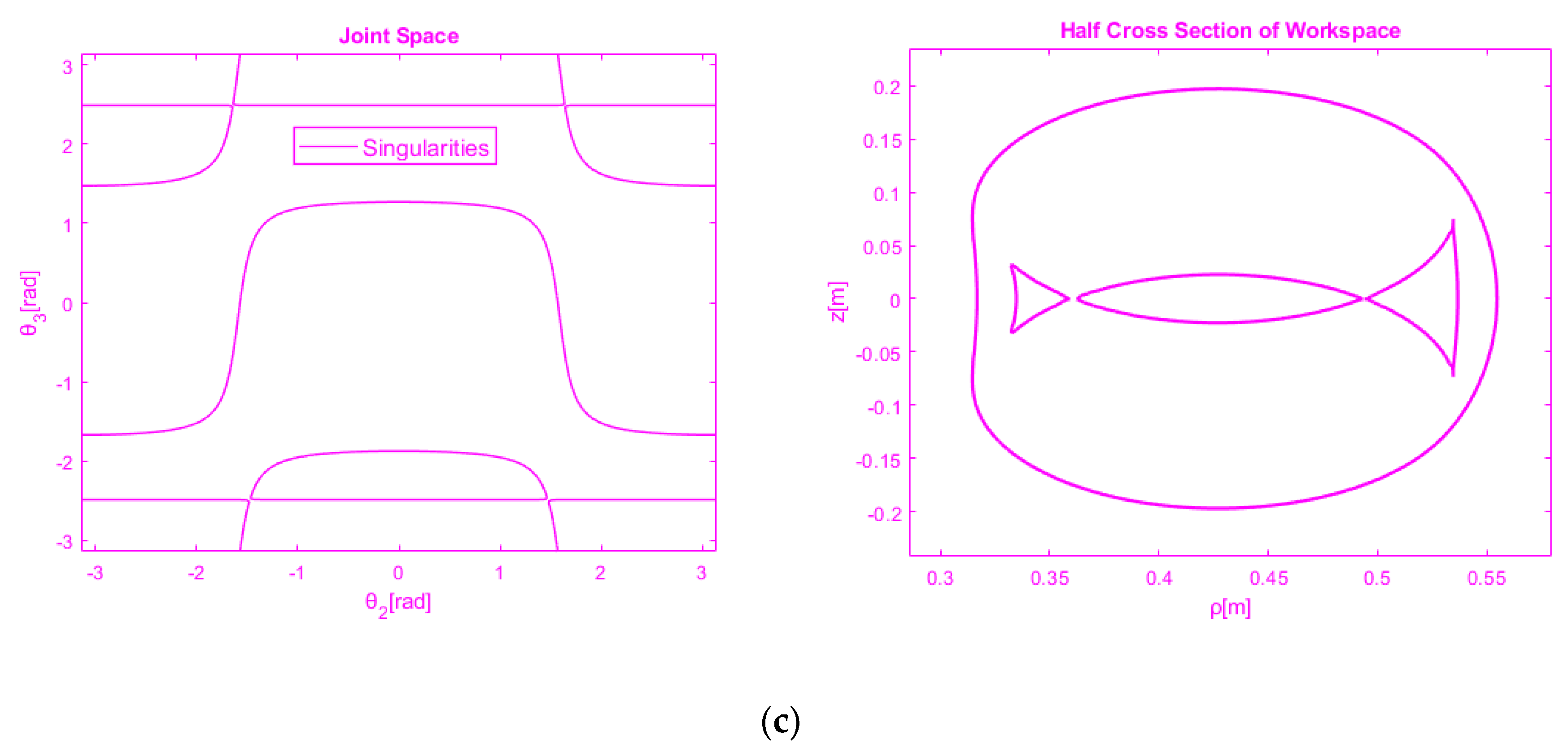
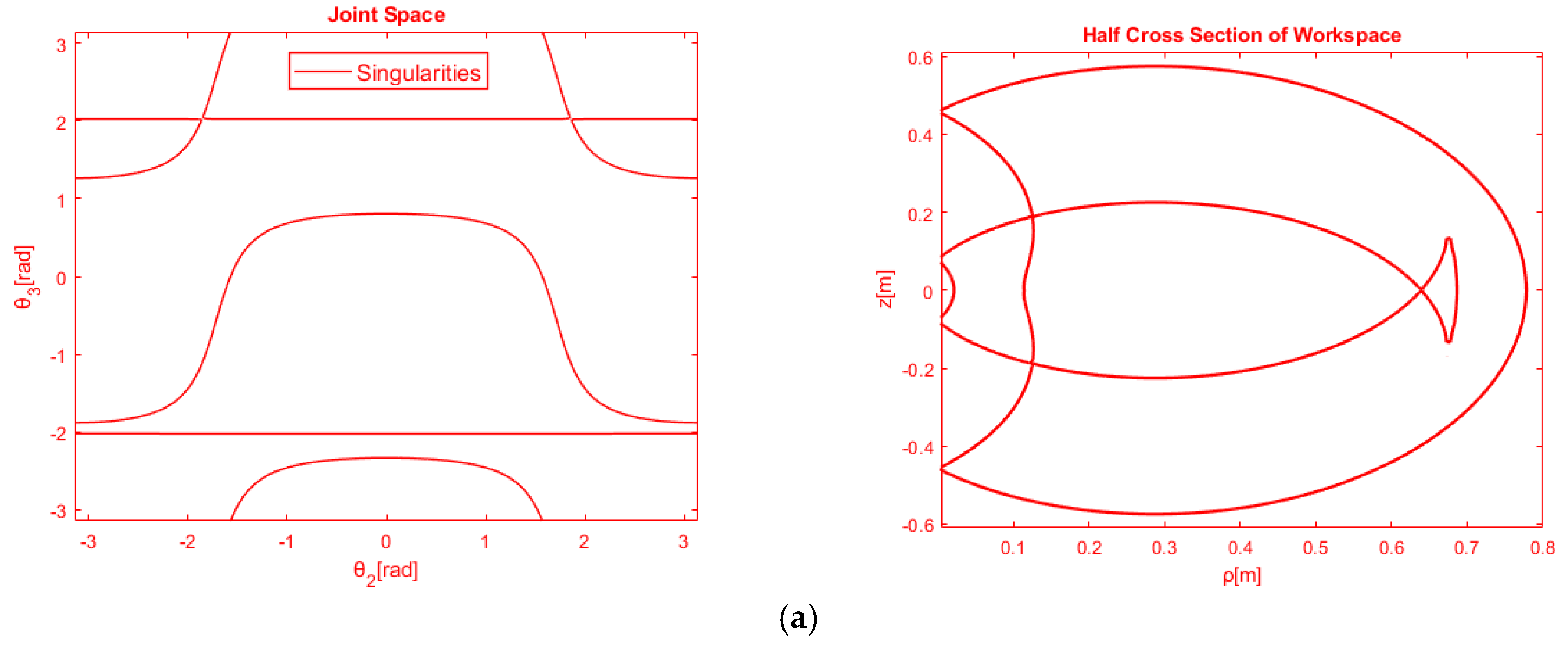
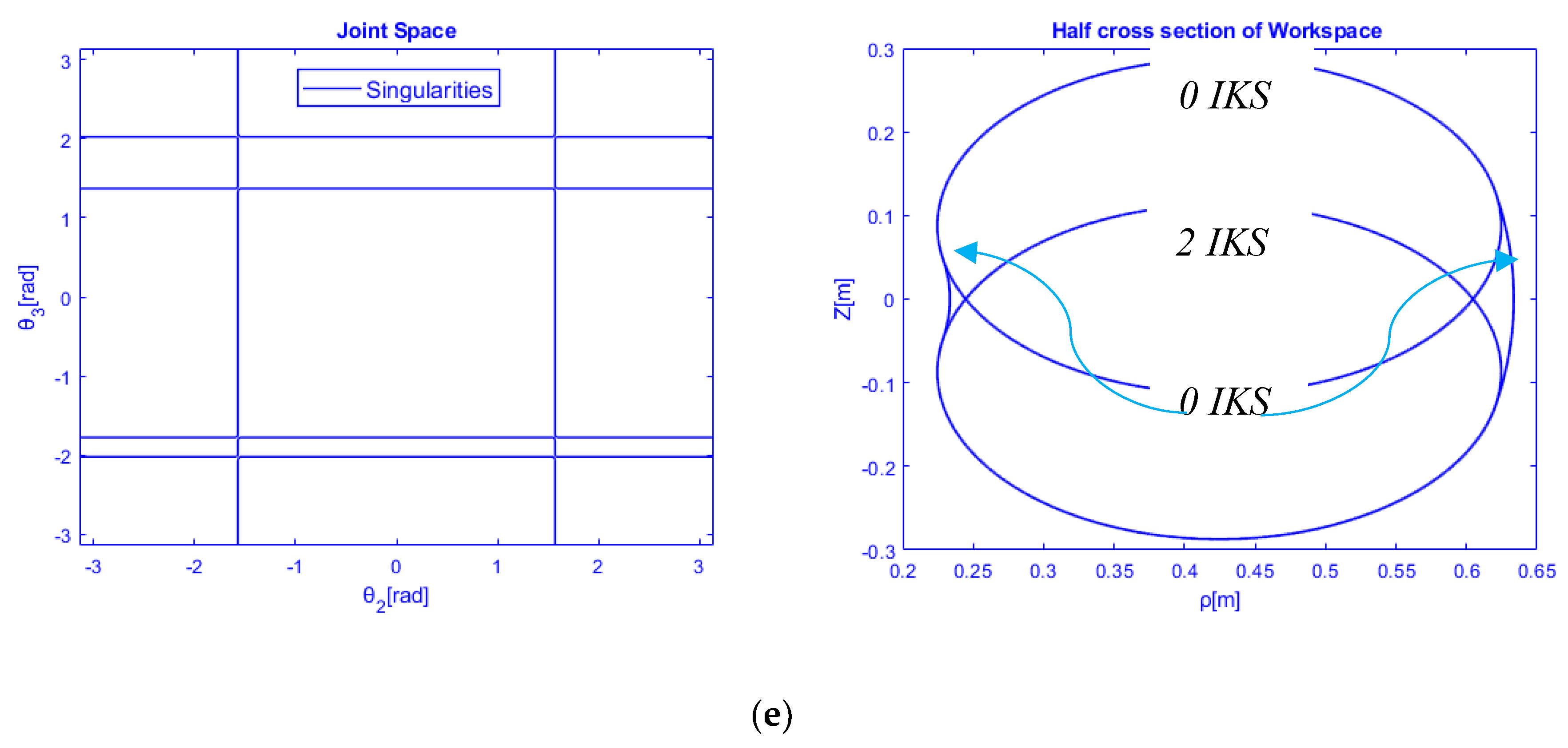
3.3. Classification According to the Number of Nodes
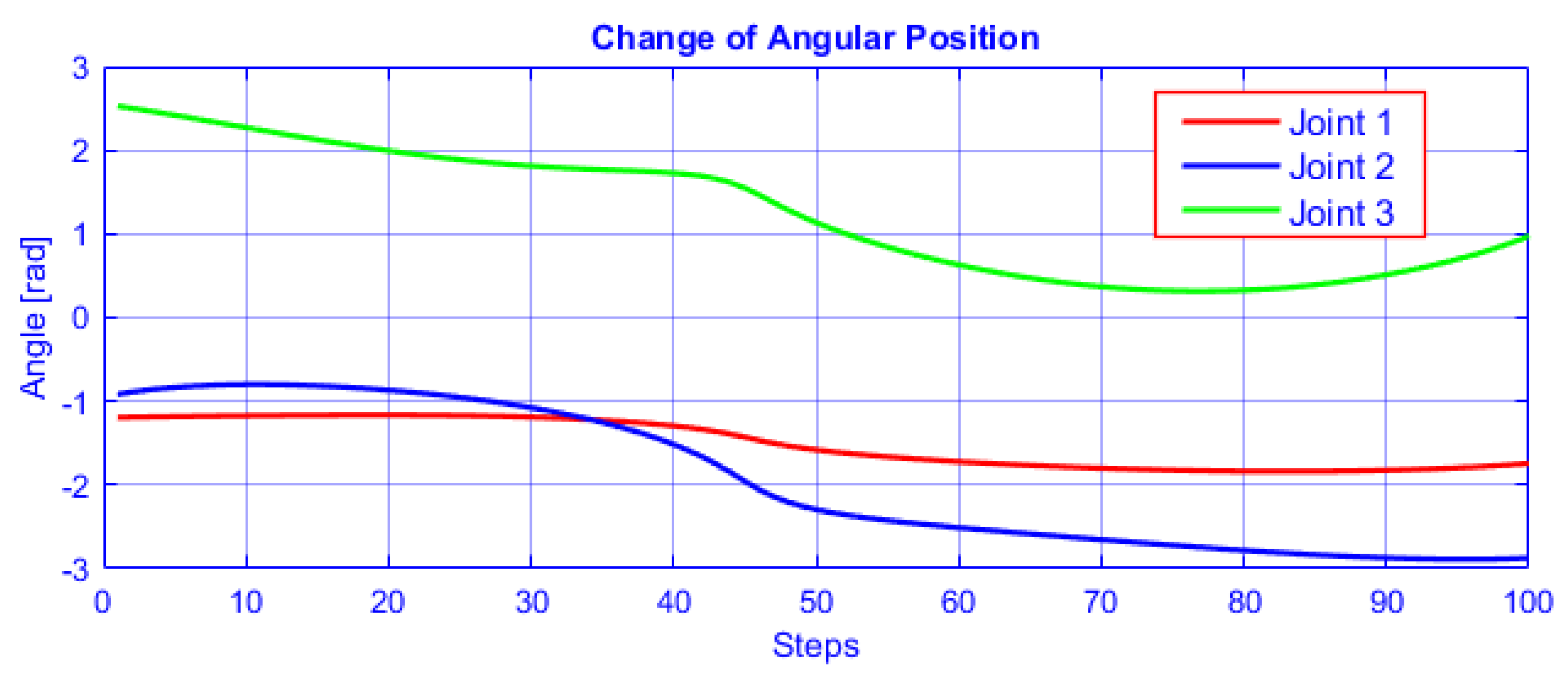
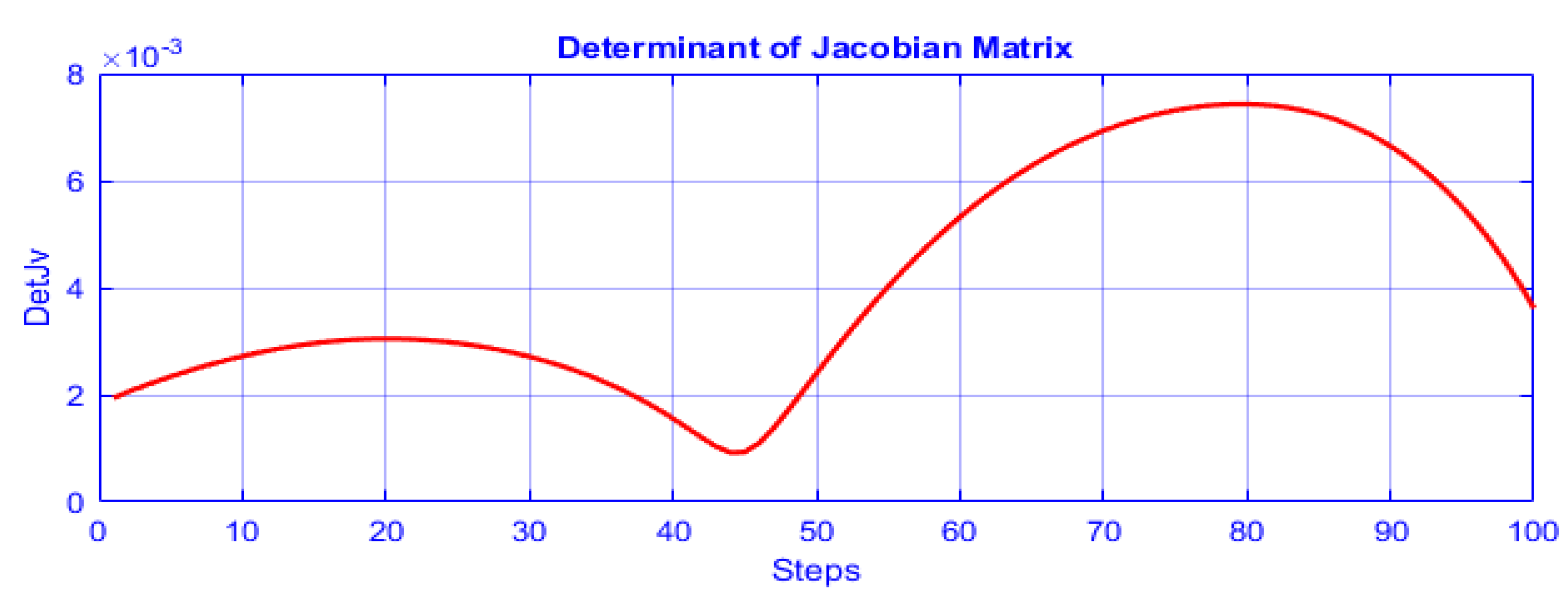
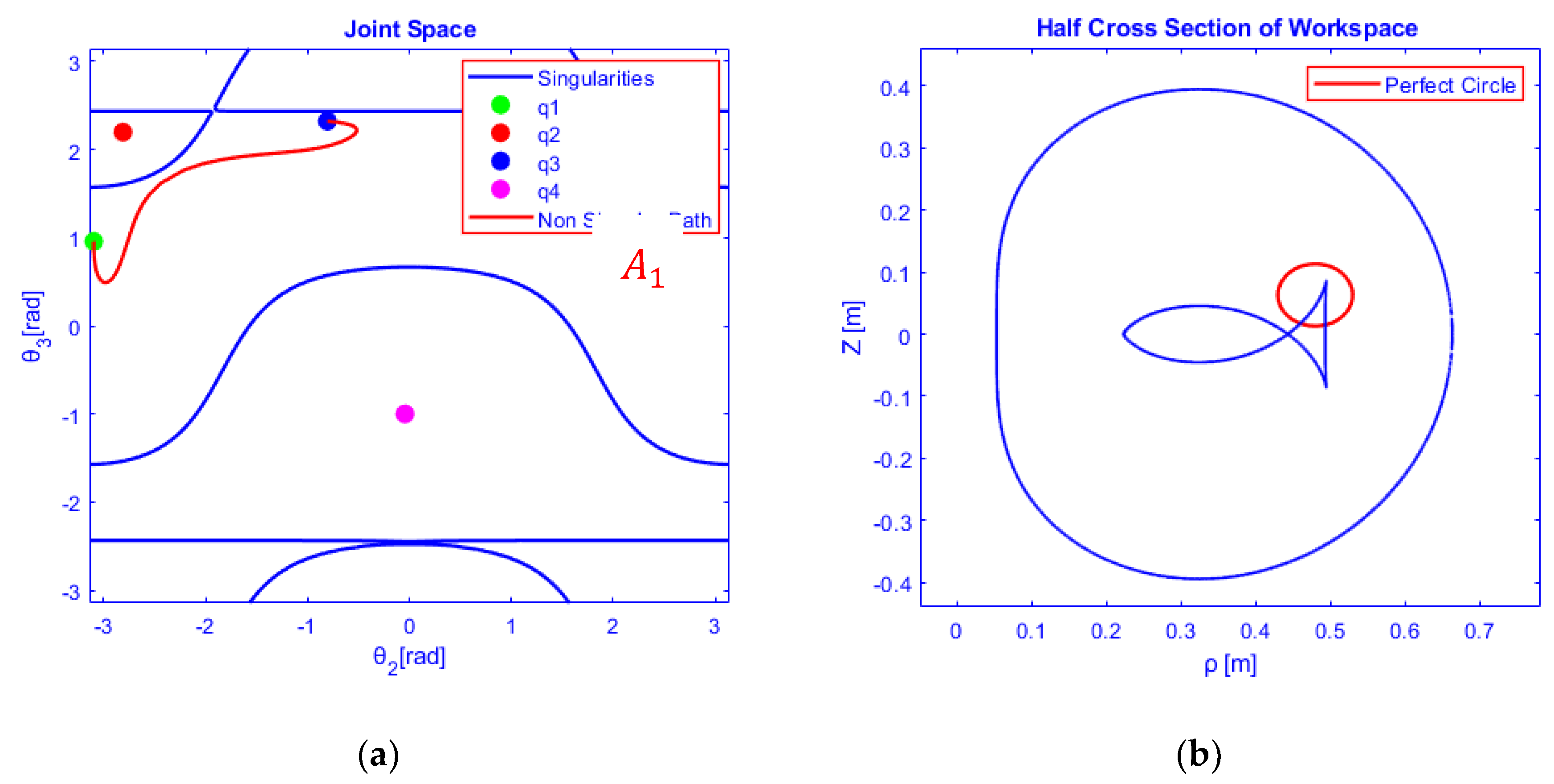
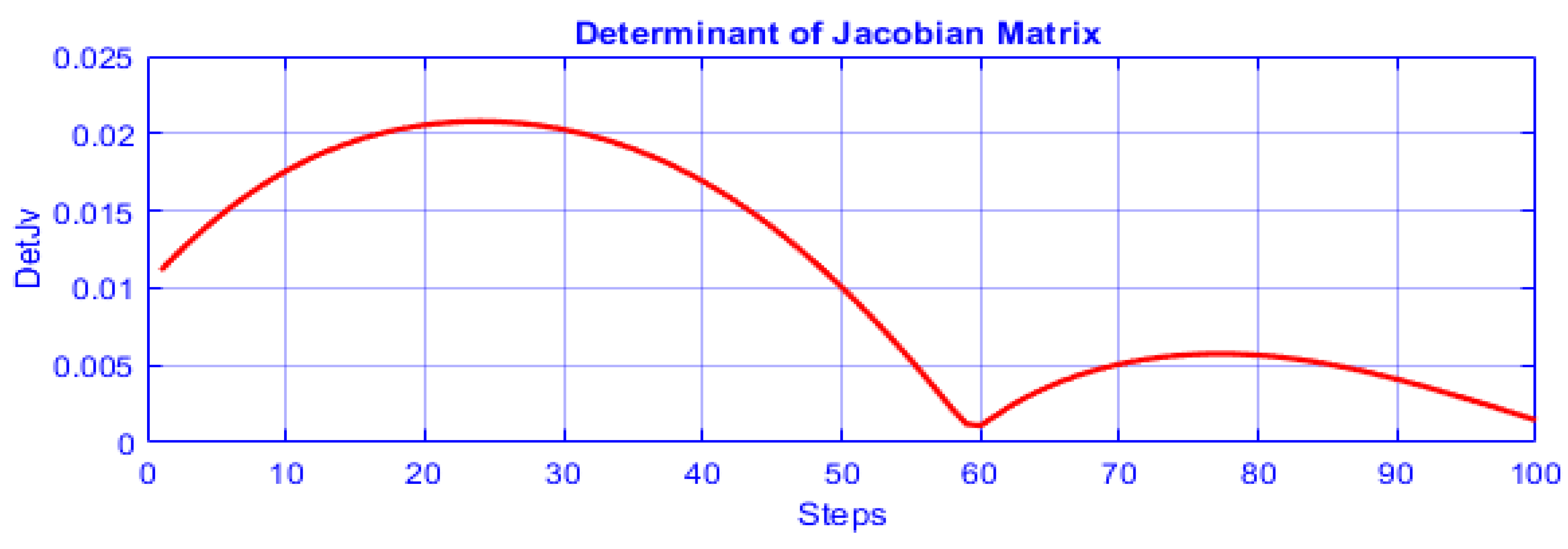
4. Planning Non-Singular Posture Changing Trajectories
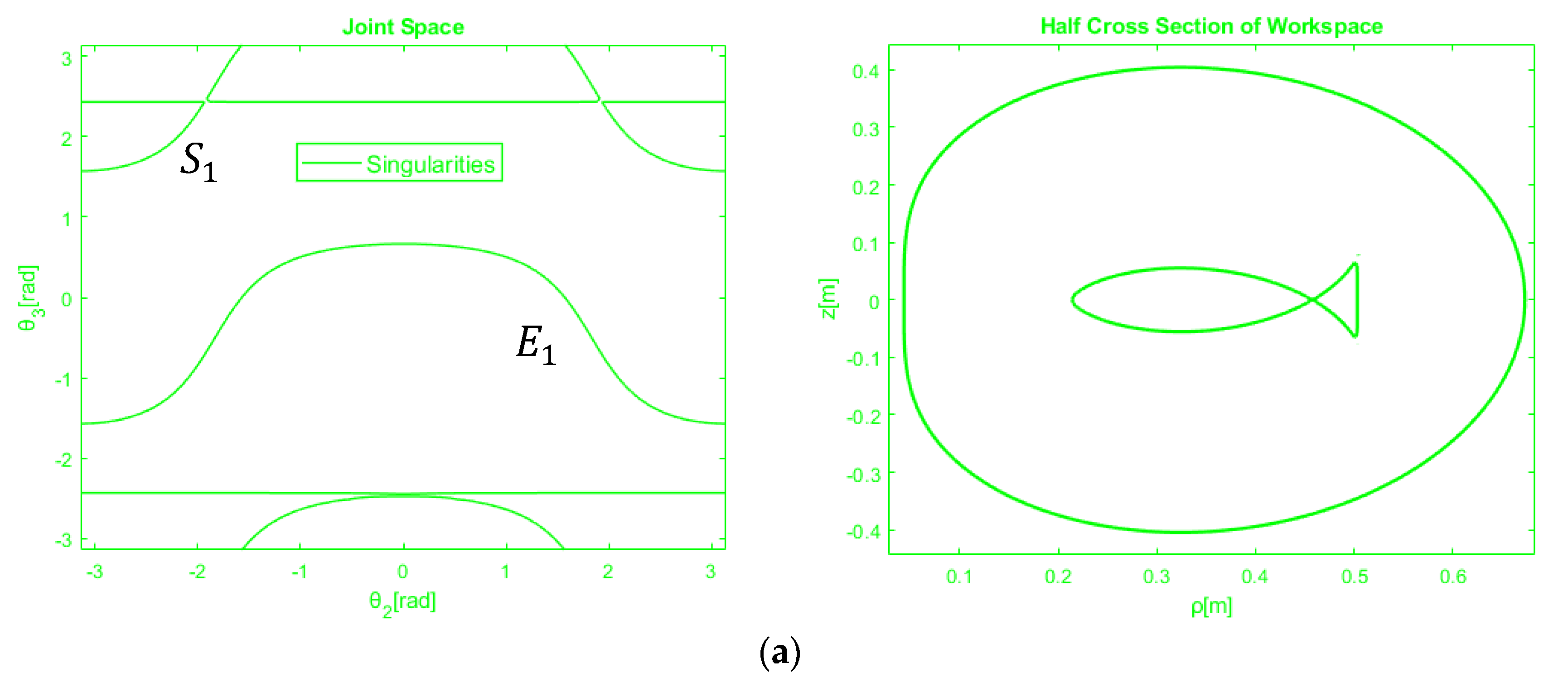
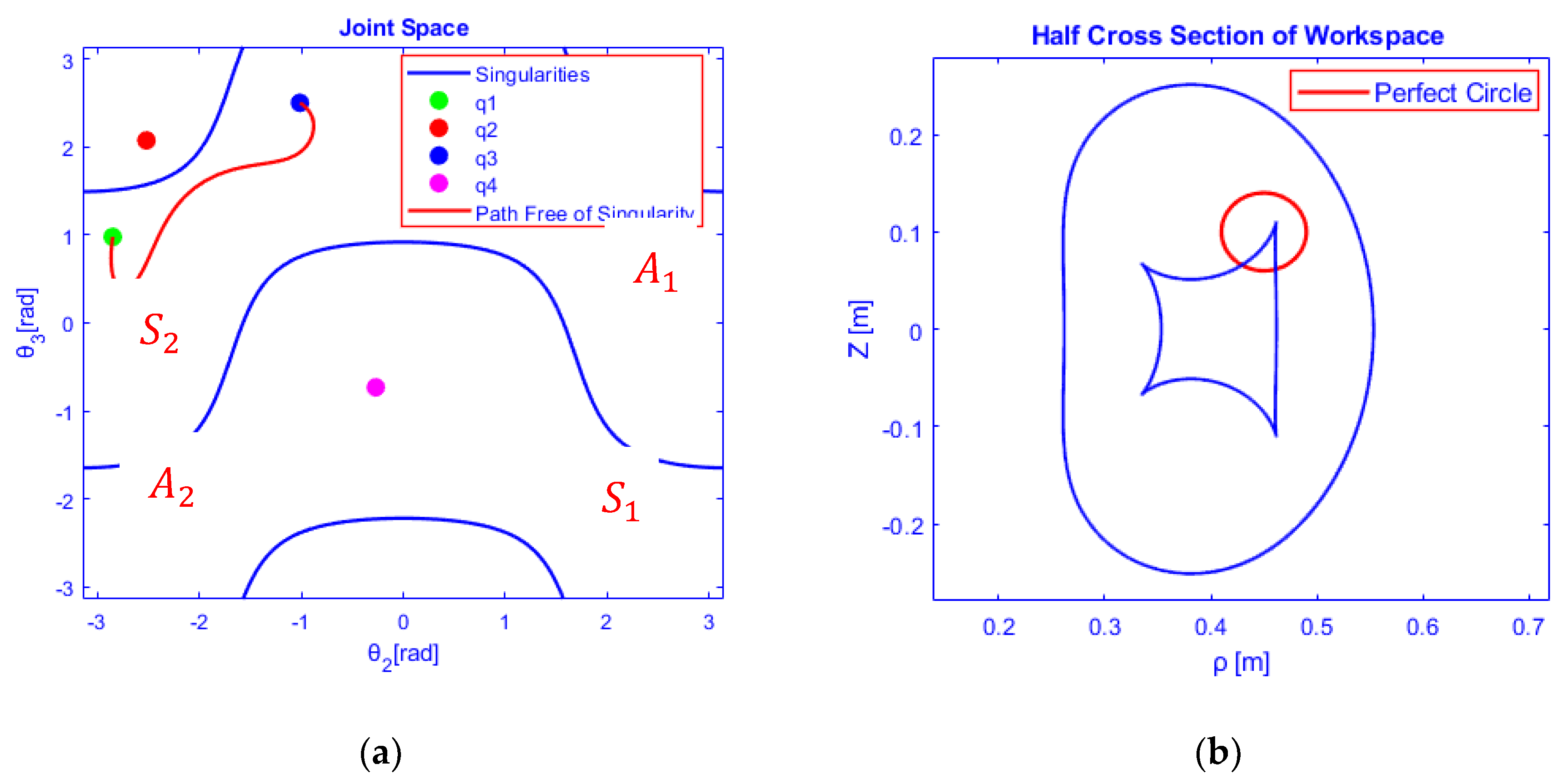
4.1. Generic Mechanism
4.2. Non-Generic Anatomy
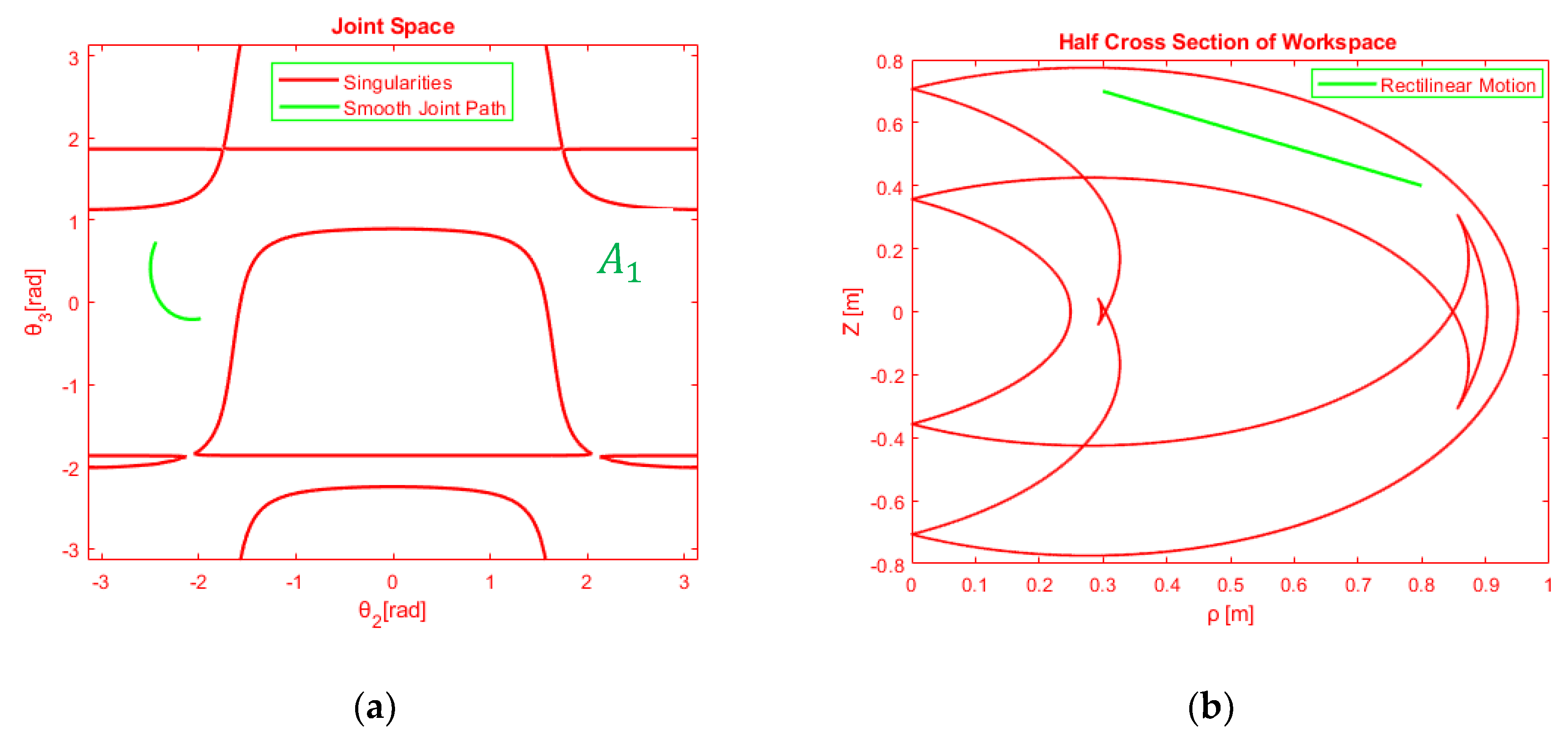
4.2.1. Planning Closed Smooth and Continuous Path
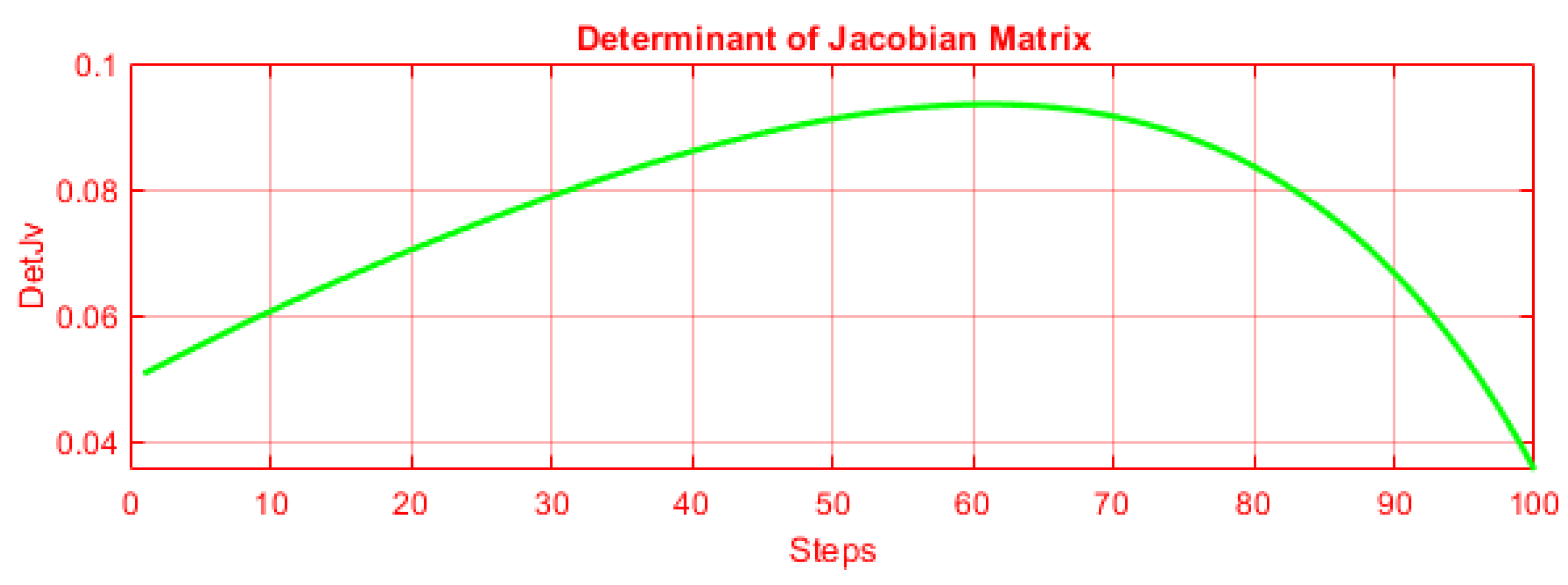
4.2.2. Rectilinear Trajectory
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aspragathos, N. Reconfigurable robots towards the manufacturing of the future. In Intelligent Production Machines and Systems-First I* PROMS Virtual Conference: Proceedings and CD-ROM Set; Elsevier: Amsterdam, the Netherlands, 2005; p. 447. [Google Scholar]
- Valsamos, H.; Aspragathos, N. Design of a Versatile Passive Connector for Reconfigurable Robotic Manipulators with Articulated Anatomies and their Kinematic Analysis. In Proceedings of the I* PROMS 2007 Virtual Conference, 2–13 July 2007; Available online: https://app.knovel.com/web/toc.v/cid:kpIPMSTIP1/viewerType:toc/ (accessed on 27 March 2020).
- Valsamos, C.; Moulianitis, V.; Aspragathos, N. Kinematic synthesis of structures for metamorphic serial manipulators. J. Mech. Robot. 2014, 6. [Google Scholar] [CrossRef]
- Valsamos, H.; Aspragathos, N. Determination of anatomy and configuration of a reconfigurable manipulator for the optimal manipulability. In Proceedings of the 2009 ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 505–511. [Google Scholar]
- Valsamos, C.; Moulianitis, V.; Aspragathos, N. Index based optimal anatomy of a metamorphic manipulator for a given task. Robot. Comput. Integr. Manuf. 2012, 28, 517–529. [Google Scholar] [CrossRef]
- Matsumaru, T.; Matsuhira, N. Design and Control of the Modular Manipulator System: TOMMS. J. Robot. Soc. Jpn. 1996, 14, 428–435. [Google Scholar] [CrossRef]
- Paredis, C.J.; Brown, H.B.; Khosla, P.K. A rapidly deployable manipulator system. Robot. Auton. Syst. 1997, 21, 289–304. [Google Scholar] [CrossRef]
- Chen, I.M.; Chen, P.; Yang, G.; Chen, W.; Kang, I.G.; Yeo, S.H.; Chen, G. Architecture for rapidly reconfigurable robot workcell. In Proceedings of the 5th International Conference of Control, Automation, Robotics and Vision, Singapore, 9–11 December 1998; pp. 100–104. [Google Scholar]
- Chen, I.M. Rapid response manufacturing through a rapidly reconfigurable robotic workcell. Robot. Comput. Integr. Manuf. 2001, 17, 199–213. [Google Scholar] [CrossRef]
- Yang, G.; Chen, I.M. Task-based optimization of modular robot configurations: Minimized degree-of-freedom approach. Mech. Mach. Theory 2000, 35, 517–540. [Google Scholar] [CrossRef]
- Chen, I.M.; Gao, Y. Closed-form inverse kinematics solver for reconfigurable robots. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; Volume 3, pp. 2395–2400. [Google Scholar]
- Tzivaridis, M.; Moulianitis, V.C.; Aspragathos, N.A. Approximation of Inverse Kinematic Solution of a Metamorphic 3R Manipulator with Multilayer Perceptron. In International Conference on Robotics in Alpe-Adria Danube Region; Springer: Berlin, Germany, 2019; pp. 43–50. [Google Scholar]
- Chen, I.M. On optimal configuration of modular reconfigurable robots. In Proceedings of the 4th International Conference on Control, Automation, Robotics, and Vision, Raffles City, Singapore, 4–6 December 1996. [Google Scholar]
- Moulianitis, V.C.; Synodinos, A.I.; Valsamos, C.D.; Aspragathos, N.A. Task-based optimal design of metamorphic service manipulators. J. Mech. Robot. 2016, 8. [Google Scholar] [CrossRef]
- Valsamos, C.; Moulianitis, V.; Synodinos, A.; Aspragathos, N. Introduction of the high performance area measure for the evaluation of metamorphic manipulator anatomies. Mech. Mach. Theory 2015, 86, 88–107. [Google Scholar] [CrossRef]
- Moulianitis, V.; Xidias, E.; Azariadis, P. Optimal Task Placement in a Metamorphic Manipulator Workspace in the Presence of Obstacles. International Conference on Robotics in Alpe-Adria Danube Region; Springer: Berlin, Germany, 2018; pp. 359–367. [Google Scholar]
- Bi, Z.; Gruver, W.A.; Zhang, W.J. Adaptability of reconfigurable robotic systems. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwai, 14–19 September 2003; Volume 2, pp. 2317–2322. [Google Scholar]
- Li, Z. Development and Control of a Modular and Reconfigurable Robot with Harmonic Drive Transmission System. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2007. [Google Scholar]
- Katrantzis, E.F.; Aspragathos, N.A.; Valsamos, C.D.; Moulianitis, V.C. Anatomy optimization and experimental verification of a metamorphic manipulator. In Proceedings of the 2018 IEE International Conference on Reconfigurable Mechanisms and Robots (ReMAR), Delft, The Netherlands, 20–22 June 2018; pp. 1–7. [Google Scholar]
- Wenger, P. Uniqueness domains and regions of feasible paths for cuspidal manipulators. IEEE Trans. Robot. 2004, 20, 745–750. [Google Scholar] [CrossRef]
- Wenger, P. Cuspidal robots. In Singular Configurations of Mechanisms and Manipulators; Springer: Berlin, Germany, 2019; pp. 67–99. [Google Scholar]
- Corvez, S.; Rouillier, F. Using computer algebra tools to classify serial manipulators. In International Workshop on Automated Deduction in Geometry; Springer: Berlin, Germany, 2002; pp. 31–43. [Google Scholar]
- Baili, M. Analyse et Classification de Manipulateurs 3R à Axes Orthogonaux. Ph.D. Thesis, Ecole Centrale de Nantes (ECN), Université de Nantes, Nantes, France, 2004. [Google Scholar]
- Smith, D.R. Design of Solvable 6R Manipulators. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1990. [Google Scholar]
- Tsai, K.Y. Admissible Motions in Manipulator’s Workspace. Ph.D. Thesis, University of Wisconsin-Milwaukee, Milwaukee, WI, USA, 1990. [Google Scholar]
- Kohli, D.; Hsu, M.S. The Jacobian analysis of workspaces of mechanical manipulators. Mech. Mach. Theory 1987, 22, 265–275. [Google Scholar] [CrossRef]
- Ottaviano, E.; Husty, M.; Ceccarelli, M. A Cartesian representation for the boundary workspace of 3R manipulators. In On Advances in Robot Kinematics; Springer: Berlin, Germany, 2004; pp. 247–254. [Google Scholar]
- El Omri, J.; Wenger, P. How to recognize simply a non-singular posture changing 3-DOF manipulator. In Proceedings of the 7th International Conference on Advanced Robotics, Tokyo, Japan, 20–22 September 1995; pp. 215–222. [Google Scholar]
- Lazard, D.; Rouillier, F. Solving parametric polynomial systems. J. Symb. Comput. 2007, 42, 636–667. [Google Scholar] [CrossRef]
- Gerhard, J.; Jeffrey, D.; Moroz, G. A package for solving parametric polynomial systems. ACM Commun. Comput. Algebra 2010, 43, 61–72. [Google Scholar] [CrossRef]
- Baili, M.; Wenger, P.; Chablat, D. A classification of 3R orthogonal manipulators by the topology of their workspace. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2, pp. 1933–1938. [Google Scholar]
- Wenger, P.; Chablat, D.; Baili, M. A dh-parameter based condition for 3r orthogonal manipulators to have four distinct inverse kinematic solutions. J. Mech. Des. 2005, 127, 150–155. [Google Scholar] [CrossRef]



| i | di | |||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
| # | |||
|---|---|---|---|
| 1 | −1.7417 | −2.8731 | 0.9736 |
| 2 | −1.4908 | −2.5800 | 2.0697 |
| 3 | −1.1937 | −0.9150 | 2.5274 |
| 4 | −0.7096 | −0.2471 | −0.7420 |
| # | |||
|---|---|---|---|
| 1 | −1.8502 | −3.0993 | 0.9560 |
| 2 | −1.2824 | −2.8118 | 2.1946 |
| 3 | −1.1706 | −0.8051 | 2.3190 |
| 4 | −0.1677 | −0.0435 | −0.9986 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koukos-Papagiannis, C.; Moulianitis, V.; Aspragathos, N. Classification of All Non-Isomorphic Regular and Cuspidal Arm Anatomies in an Orthogonal Metamorphic Manipulator. Robotics 2020, 9, 20. https://doi.org/10.3390/robotics9020020
Koukos-Papagiannis C, Moulianitis V, Aspragathos N. Classification of All Non-Isomorphic Regular and Cuspidal Arm Anatomies in an Orthogonal Metamorphic Manipulator. Robotics. 2020; 9(2):20. https://doi.org/10.3390/robotics9020020
Chicago/Turabian StyleKoukos-Papagiannis, Christos, Vassilis Moulianitis, and Nikos Aspragathos. 2020. "Classification of All Non-Isomorphic Regular and Cuspidal Arm Anatomies in an Orthogonal Metamorphic Manipulator" Robotics 9, no. 2: 20. https://doi.org/10.3390/robotics9020020
APA StyleKoukos-Papagiannis, C., Moulianitis, V., & Aspragathos, N. (2020). Classification of All Non-Isomorphic Regular and Cuspidal Arm Anatomies in an Orthogonal Metamorphic Manipulator. Robotics, 9(2), 20. https://doi.org/10.3390/robotics9020020






