1. Introduction
Robotic rehabilitation started with passive exoskeletons [
1], or devices that impose (on the interested limbs) a forced motion. An early example for lower limbs is Lokomat [
2]. It evolved into systems that create force tunnels to address the motion generated by the patient [
3]. These were further extended with the introduction of a feedback from the patient, to offer cooperative controls (also called hybrid control) not only to guide but also to contribute to the efforts of the patient [
4]. An extensive state-of-the-art of cooperative exoskeletons for rehabilitation is contained in [
5]. Following this line of approach, we proposed a haptic exoskeleton where the joints are actuated using admittance control based on the patient’s Electromiographical (EMG) signals [
6].
One classical exercise for postural rehabilitation performed in a fixed position is the “sit-to-stand”. Then, a haptic exoskeleton able to guide the patient to perform this exercise is highly desirable. The study of the motion of the body during this apparently simple, but in reality not so simple, exercise has attracted interest for a long time [
7], not only to understand the human physiological behavior, but also to mimic the control for autonomous biped robots or for actively cooperating exoskeletons.
The majority of available studies are related to the analysis of the human physiological behavior [
8,
9], but also examples of synthesis of the control based on optimization are available [
10,
11]. A recent comprehensive review can be found in [
12]. However, none discussed the key determinants at the root of the exercise. Here, we follow a different approach. Recognizing that the human motion in performing the exercise is the direct consequence of the respect of physical laws of dynamics, these laws are analyzed and a feedback control based on them is synthesized. This also offers an explanation of well know physiological results such as the “Alexander STS technique” [
11].
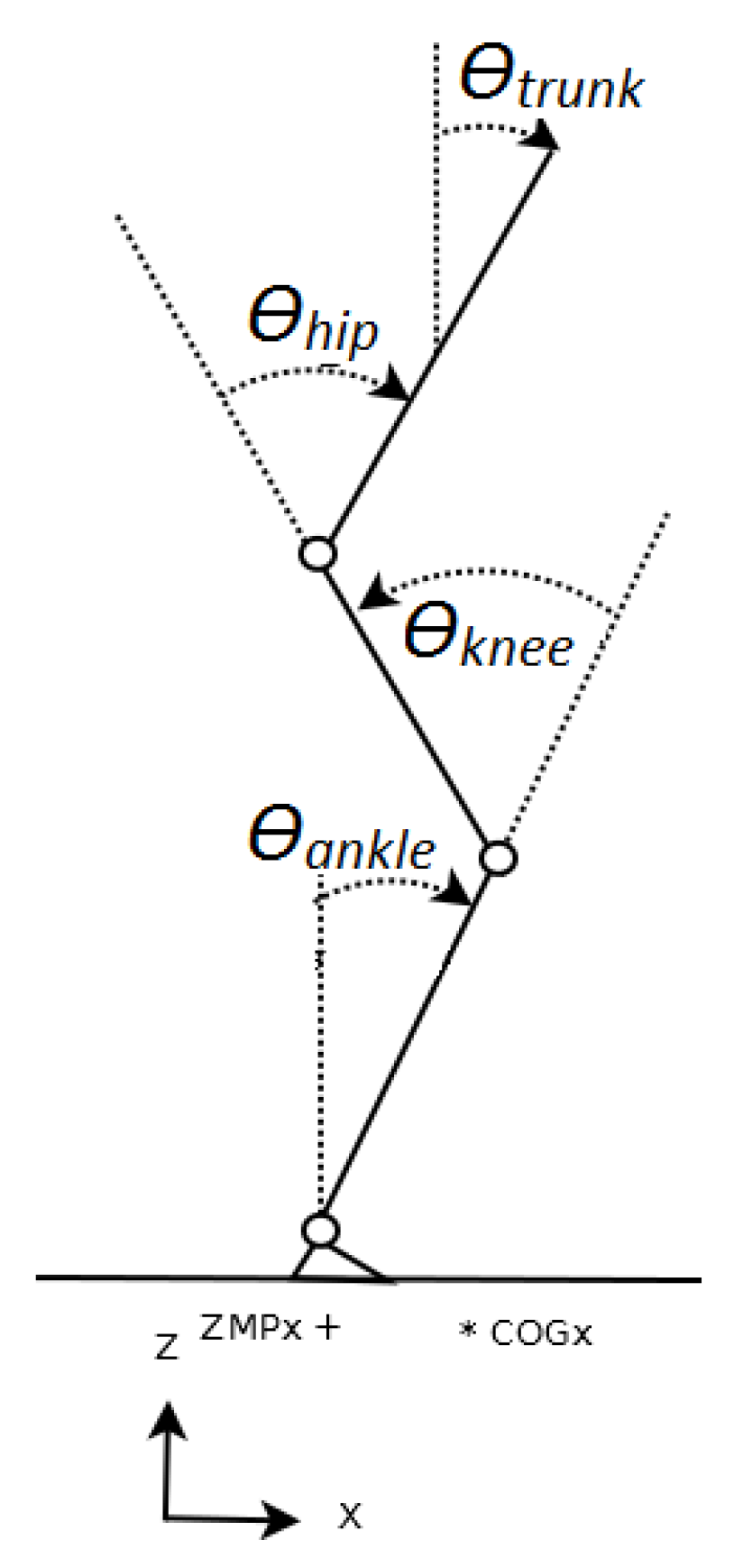
The exercise is composed of two dynamical phases: phase 1, when still sitting on the chair, the trunk, through the hips, is moved forward to gain balance on the feet, and phase 2, when the balance is maintained moving from the chair to an erect posture. In both phases, postural balance plays a key role, however, in phase 1, the coordination between the motion of the trunk and the torques on ankles and knees to release the load from the chair are also important. From the understanding of these dynamics, an automatic control can be synthesized. However, in the case of a lower limb exoskeleton for rehabilitation, such as in [
6], where an automatic postural feedback operates in the
Cartesian space and the patient controls the joints in the
joint space, the interaction between the two players has to be considered. This paper proposes to program the exoskeleton to perform the exercise autonomously, then, with an innovative approach, to blend the two actions, moving seamlessy during the evolution of the rehabilitation, under the direction of the physiotherapist, from purely automatic to completely under the control of the patient. Moreover, according to the needs of the rehabilitation, some of the components of the coordinates of the
Cartesian space, indicated here as elemental postural tasks, can be actuated by the automatic control and the remaining components, through selected joints by the patient, keeping the two groups separat from postural tasks without interfering between each other.
Section 2 contains a background on the dynamics of the exercise.
Section 3 presents the problem, describes the general adopted model and the autonomous control. Details of control during both phases are in
Section 3.3.
Section 4 applies the approach to a haptic exoskeleton. The results of a simulation are discussed in
Section 5. The conclusions, mentioning future ongoing researches, in
Section 6 complete the paper. Details of the control algorithms are contained in
Appendix A,
Appendix B and
Appendix C.
4. A Haptic Exoskeleton
The control described in the previous sections refers to an autonomous behavior, and it can be used to program the exercise into a biped robot, or applied in an exoskeleton in the first phase of the reabilitation when a patient is completely unable to operate.
In the case of a haptic exoskeleton partially or totally controlled by the patient, two different aspects have to be considered: the joints controlled in torque and the jonts controlled in velocity. For both aspects, EMG signals that are measured on the appropriate muscles offer approximate information of the torques applied by the patient to his joints. For the torque control, the contribution to the patient’s effort is achieved with a classical technique as described in [
22].
For the motion, admittance control is adopted as described in [
6]. The EMG signals, processed by an admittance filter, are translated into motion information that is used as reference velocity of the corresponding joint speed drivers of the exoskeleton.
Torque control applies to phase 1 of the exercise, the contribution of the exoskeleton is to help the patient to coordinate the two actions; motion with the rotation of the trunk and contemporaneously torque for the release of the load from the chair. This can be achieved by plotting on a display in front of the patient the position of the center of pressure in relation to the feet, with total or partial automatic support of the exoskeleton. Two options are available: automatic motion tracking a preview (different previews can be tested), and torques supported by the patient, or vice versa.
After transition to phase 2, only motion is involved, with three postural tasks, described in (
4), to execute, and three joints to control. Let indicate the motion references driven by the patient’s efforts, as output of the admittance filters, for ankle, knee and hip as
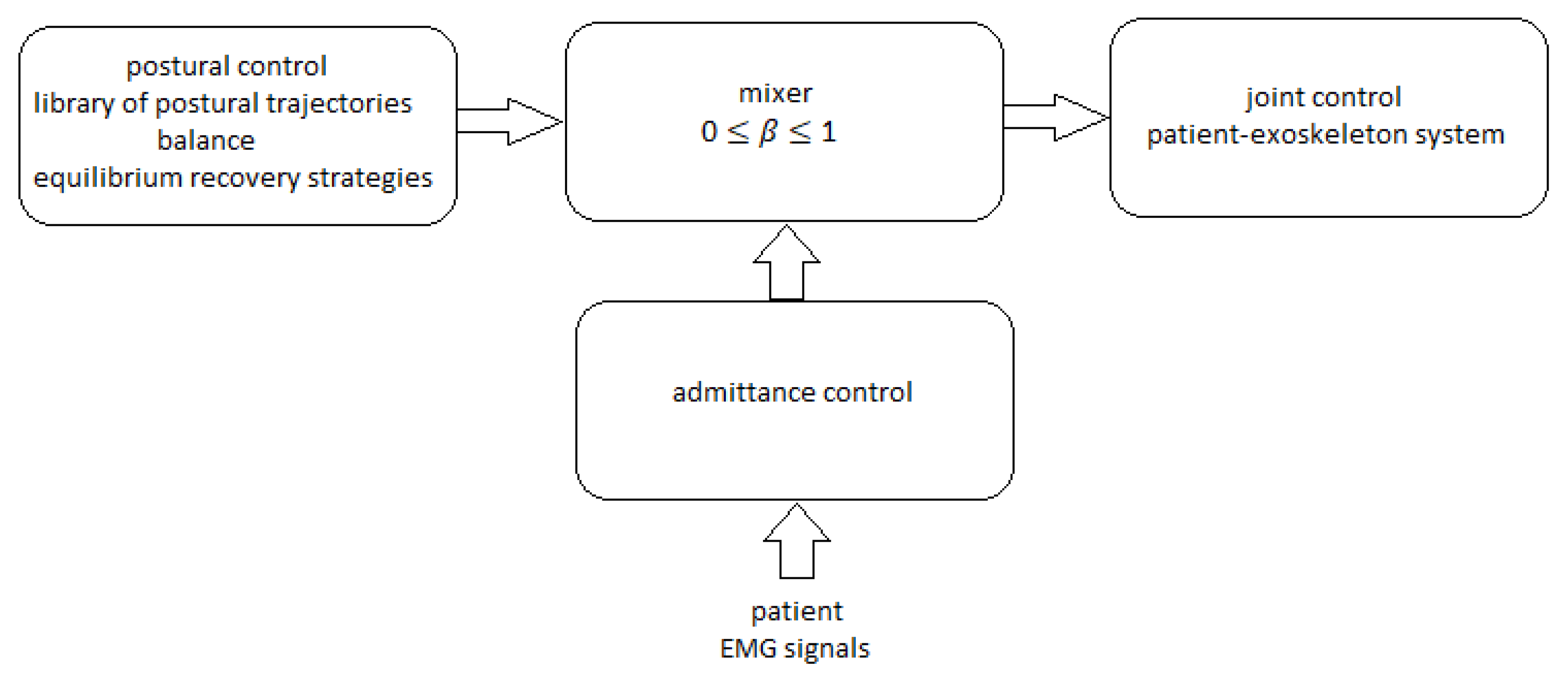
In a training program, it is desirable that the patient progressively takes control, in number and strength, of the joints of the exoskeleton, and in so doing assumes responsibility of one or more of the postural tasks, without affecting the remaining tasks performed autonomously by the feedback. For this, the concept of
tutoring-cooperation-coordination is introduced, where some of the elemental postural tasks, under the control of the patient, and the complementary tasks, under the automatic postural loop, can be completely decupled. This is a variant of whole body coordination (WBC) discussed in [
16] and introduced in [
23].
Tutoring means that all tasks are performed fully automatically, without intervention of the patient that is completely tutored, it is equivalent to the WBC.
Coordination is when the patient takes complete control, through some joints, of one or more elemental postural tasks of the exercise, without interfering with the complementary tasks controlled by the automatic postural loop and, hence, he must perform coordinate motions. In between of the two extreme situations with
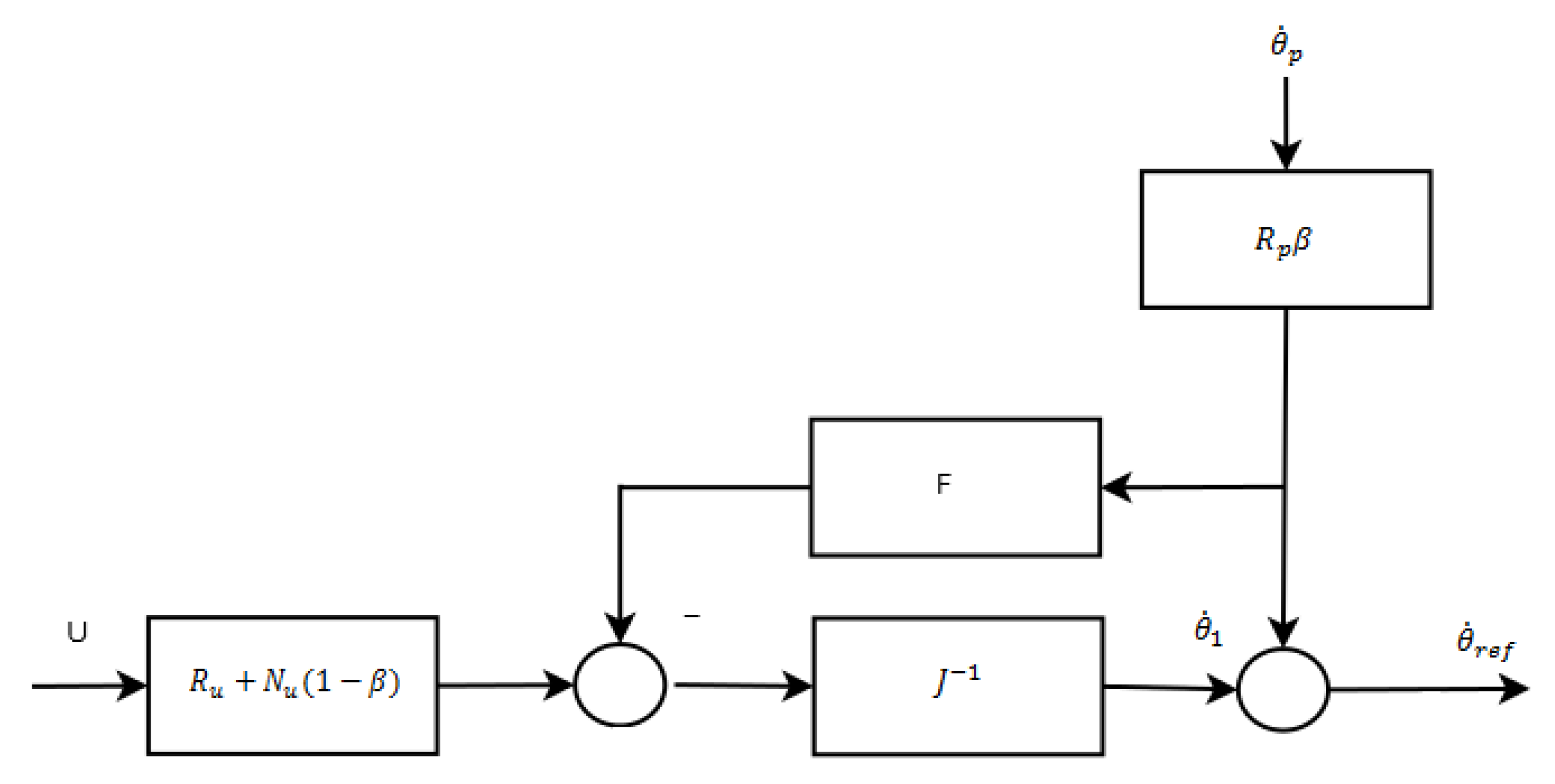
cooperation, the two players can operate jointly on some tasks and their actions are overlapped. Through a modulation parameter
the patient takes partial control and must cooperate with the automatic tasks, as depicted in
Figure 6. The approach is based on two aspects: the separation of the elemental postural tasks operated by the two players, and for the tasks operated jointly, on the modulation of the two actions.
Let
represents the 3 × 3 selection matrix, with ones and zeros on the diagonal covering the range of the elemental tasks performed exclusively by the autonomous feedback and
its nullspace with tasks controlled partially or totally by the patient through the joints in the range of
. As an example, when autonomous processes control
and trunk attitude and the patient controls the height of the pelvis through the knee, the matrices
and
are:
or, the patient, through knees and hips, controls height and attitude of the trunk, with the balance, through
, guarateed automatically, the matrices
and
are:
The postural tasks in the range of are completely controlled by the postural feedback, while the complementary tasks in its null-space are jointly controlled by the feedback and by the patient, through the joints in the range of , according to the value of a coefficient . indicates the level of the patient’s involvement in the control: tutoring is when , coordination is when , cooperation is when . As the coefficient modifies the admittance filter gain, it has, also, influence on the compliance felt by the patient on the joints in the range of (in fact, the joints in its null-space, not being controlled by the patient, don’t offer any compliance): completely stiff joints, fully compliant.
The general expression for the references of the speed control of the actuators, merging automatic postural control and patient action through EMG signals, according to
tutoring-cooperation-coordination is:
where
, and with the condition
During phase 1, while the torque control operates on ankle and knee, the
tracking (
9) is modified as follows
Moving from 0 to 1, the physiotherapist increases the admittance of the joints, so that the patient gains more and more control of them. Changing to the zero matrix, and to the identity, with , the patient assumes complete control of the exoskeleton. In this condition, the autonomous control can continue to monitor the postural balance, and eventually, it inhibits incorrect patient postures, by automatically returning to 0.
5. A Simulation Example and Comparisons
In this section the simulation of the automatic control is offered. The test of the complete exercise on the exoskeleton of
Figure 7 has not been performed yet. However, in [
6] several examples (phase 2 only) of the transition with the cooperation of the patient using this control have been reported.
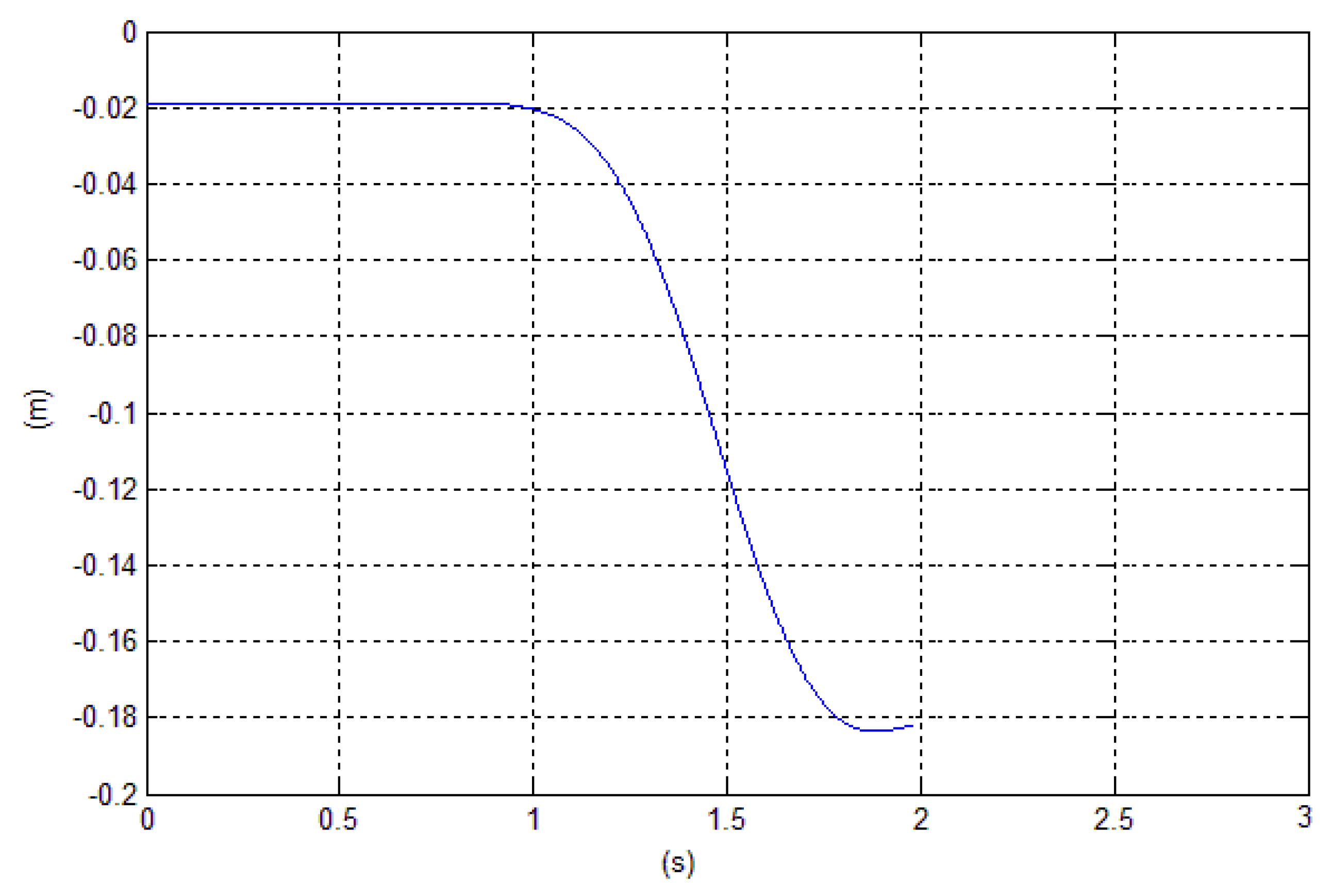
The simulation uses the same data of a patient of 75 kg, 1.8 m tall wearing an exoskeleton of 35 kg presented in [
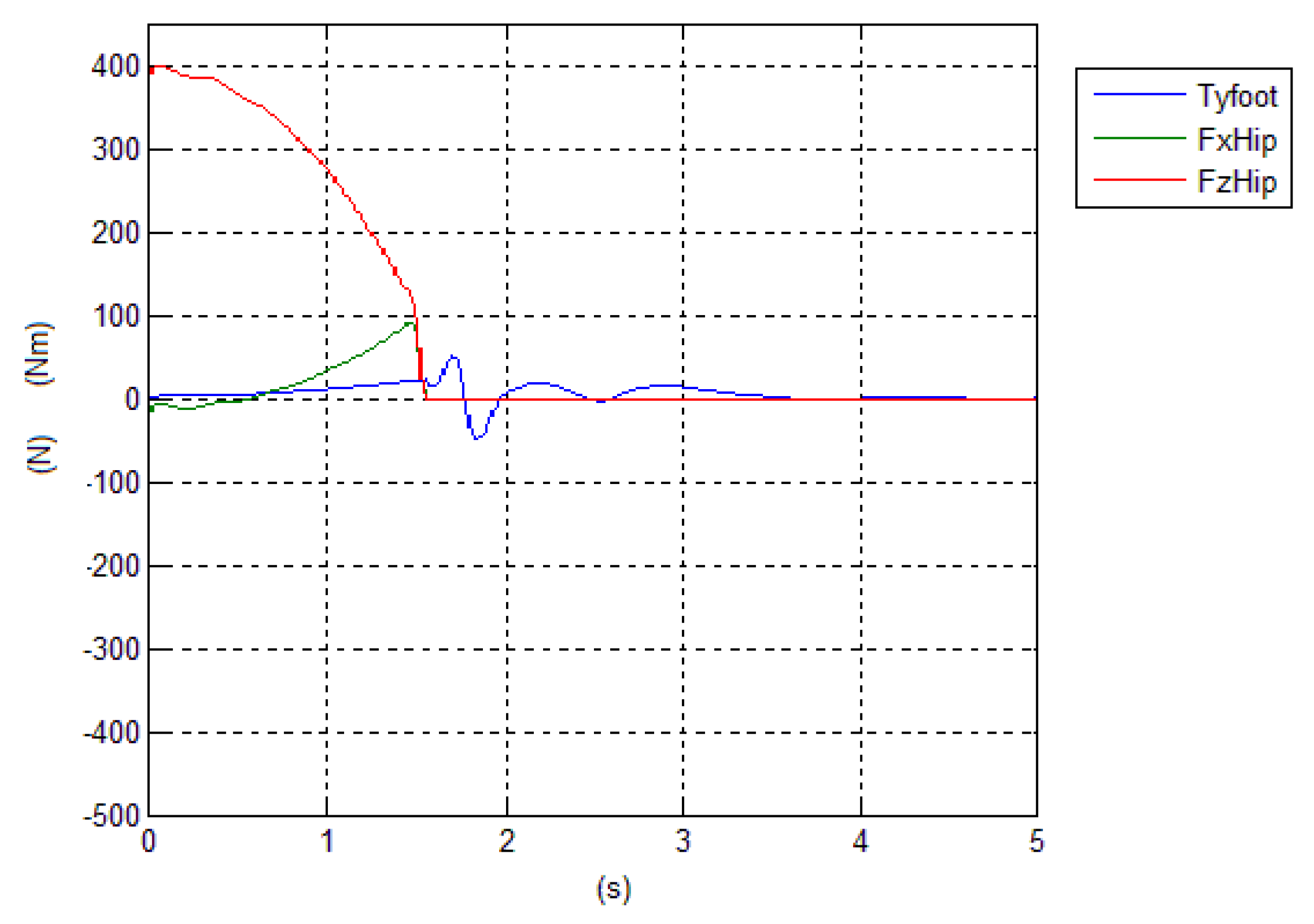
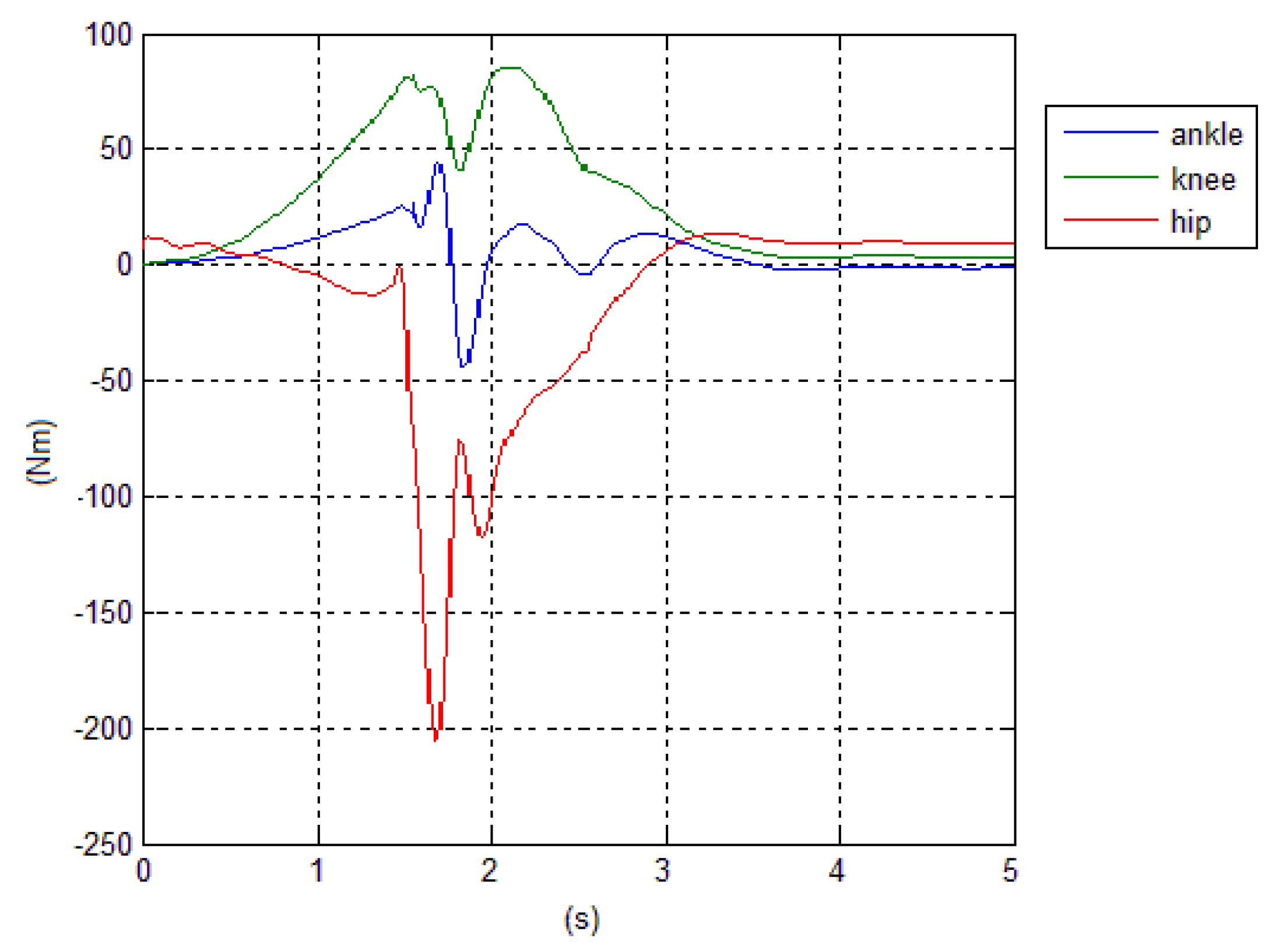
6]. The model considers only one leg and the weight of the trunk (hat) is divided by 2. So that the magnitudes of forces (N) and torques (Nm) are referred to each leg. The exercise lasts 3 s. Approximately at 1.5 s the transition from phase 1 to phase 2 occurs, with the lift off. The
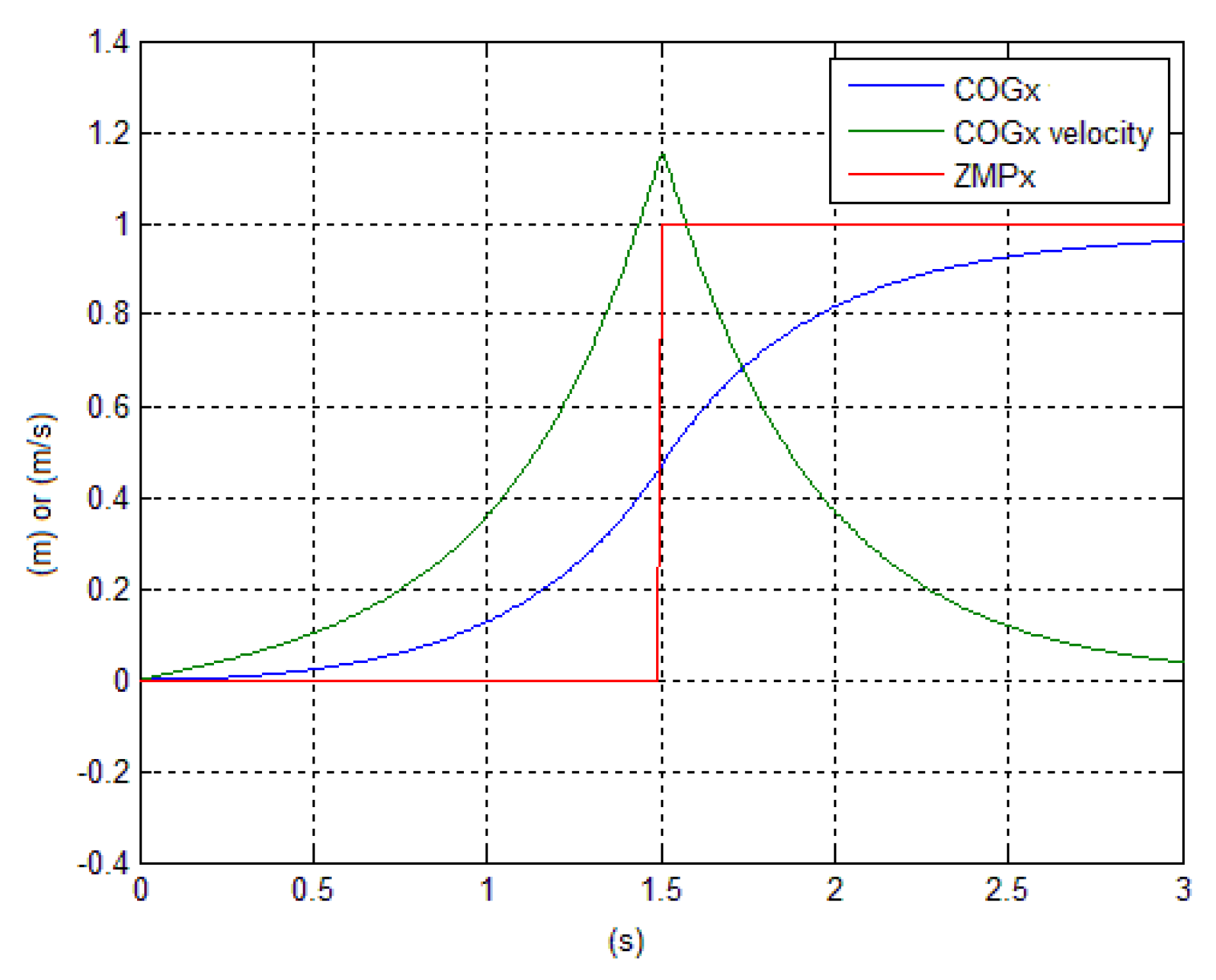
preview for a step transiton of the
of
Figure 2 has been chosen, testing different values of the parameter
. Different experiments, with different degrees of difficulty, obtained with the feet in different positions with respect to the initial value of
, i.e., to the chair, have been performed. Each position is characterized by the angle of the ankles from
to
when sitting, (i.e., feet far away from the chair and exercise more difficult, in the first case, or feet under the chair and easier exercise, in the second case). The lift-off time and transition from phase 1 to phase 2 is triggered when the module of the reaction forces on the pelvis enter into a neighbour of few Newtons of the zero. During phase 2, simple transition functions drive knees and trunk attitude angle positions and velocities from their initial values, left from phase 1, to zero in 1.5 s. The next figures represent the most difficult experiment (experiment 1) that can be performed using this control with ankle angle of
. With a lower angle, e.g.,
, the
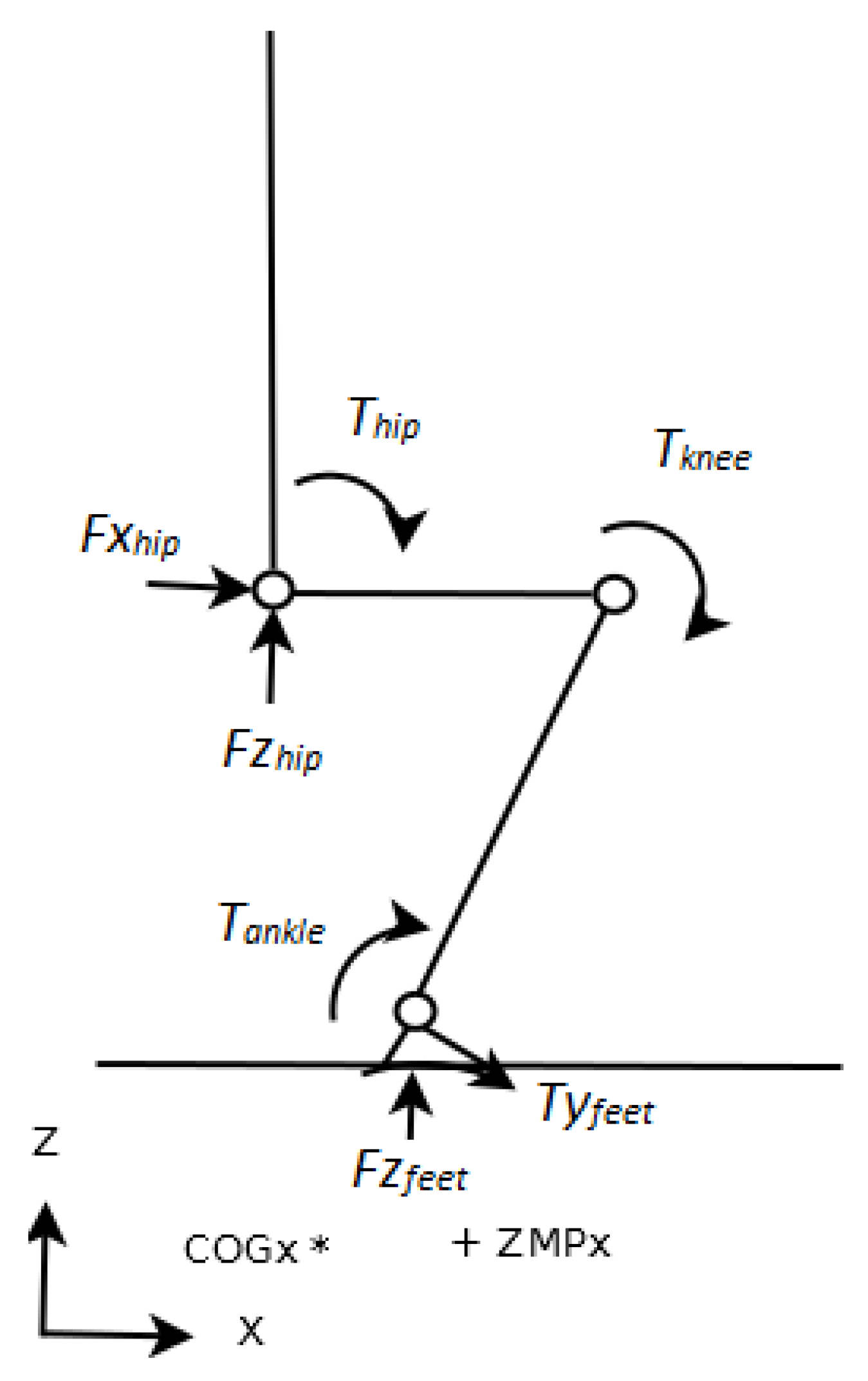
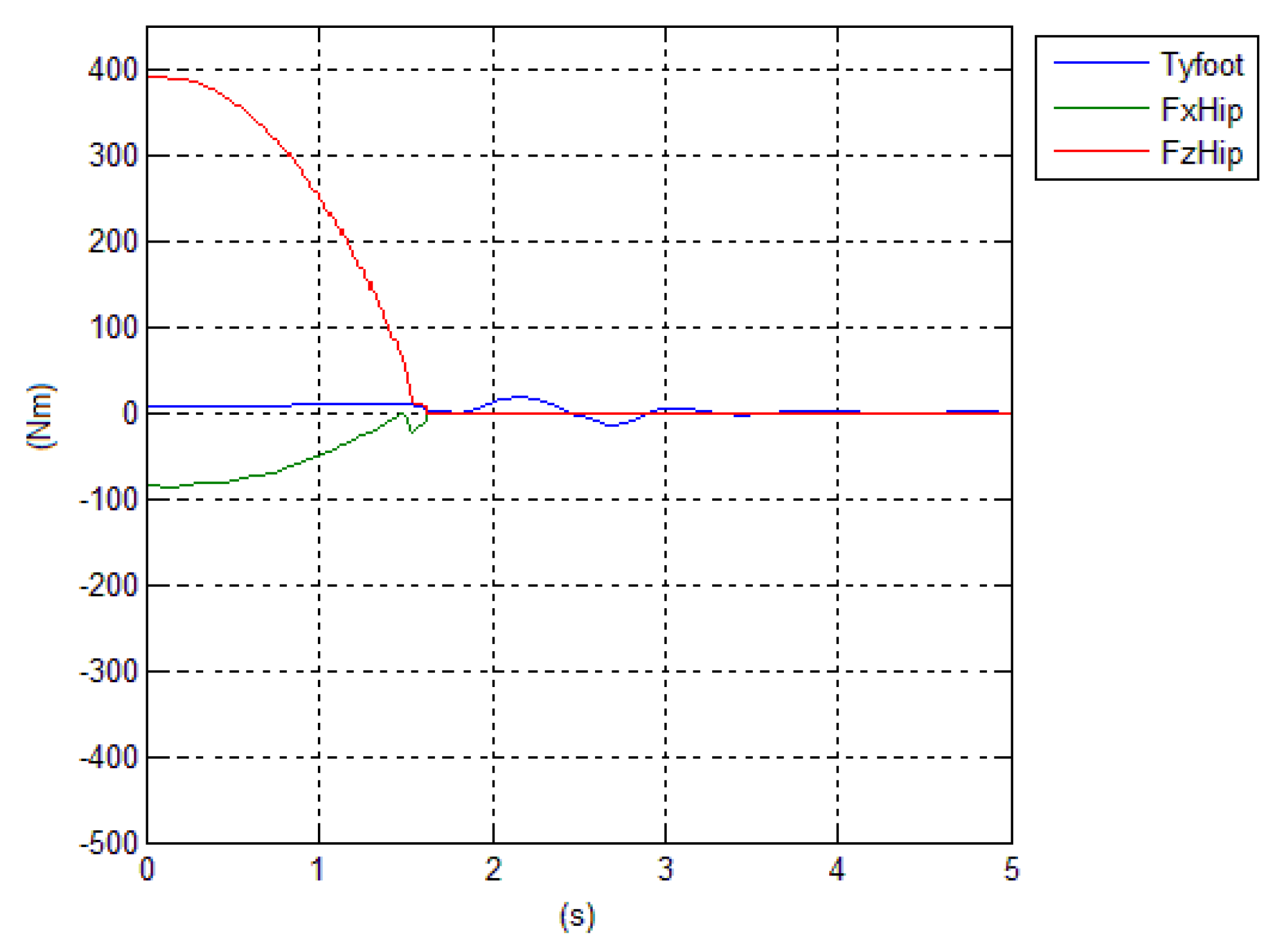
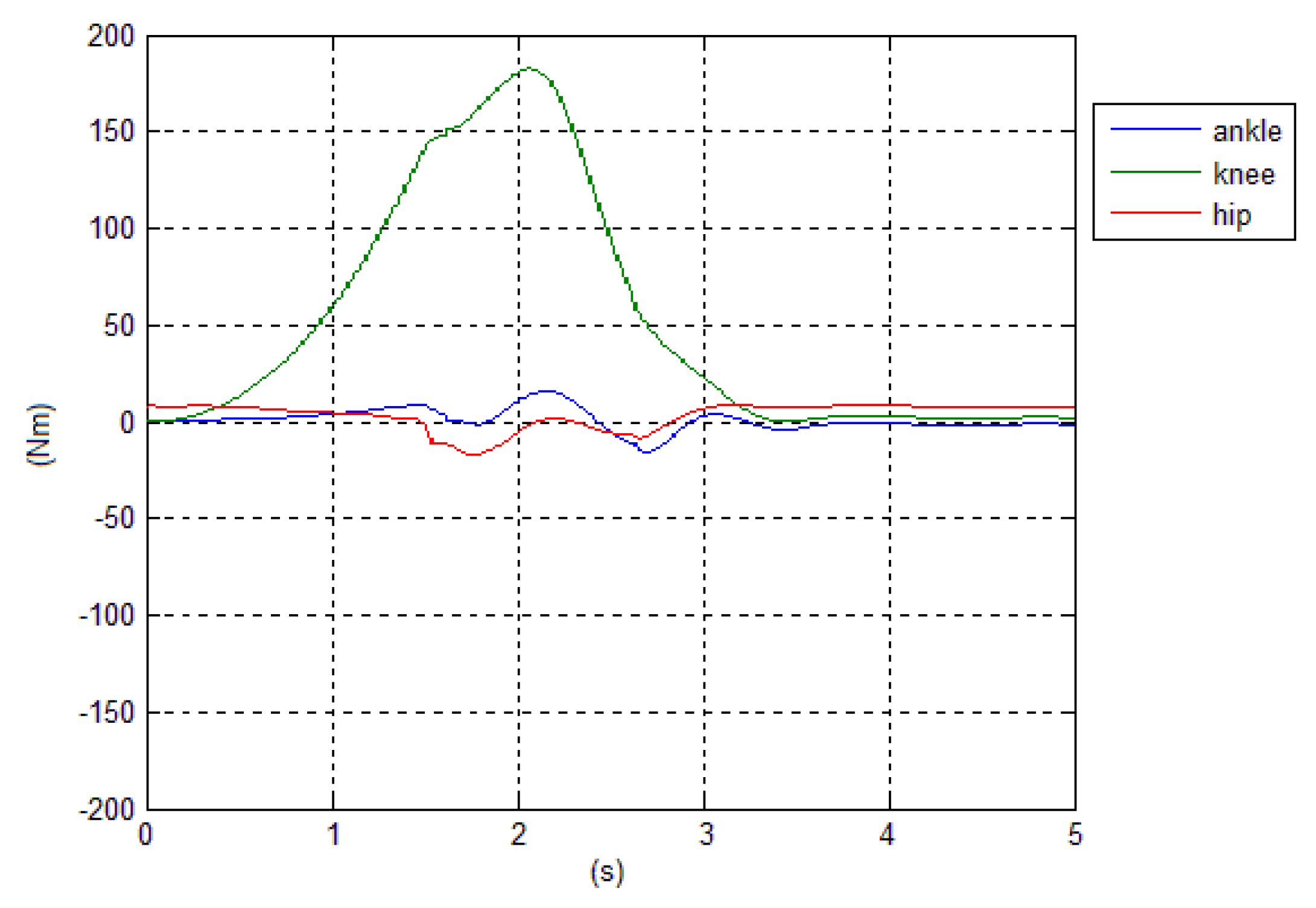
cannot be guaranteed to remain inside the foot print. The behavior of reaction forces and torques are shown in
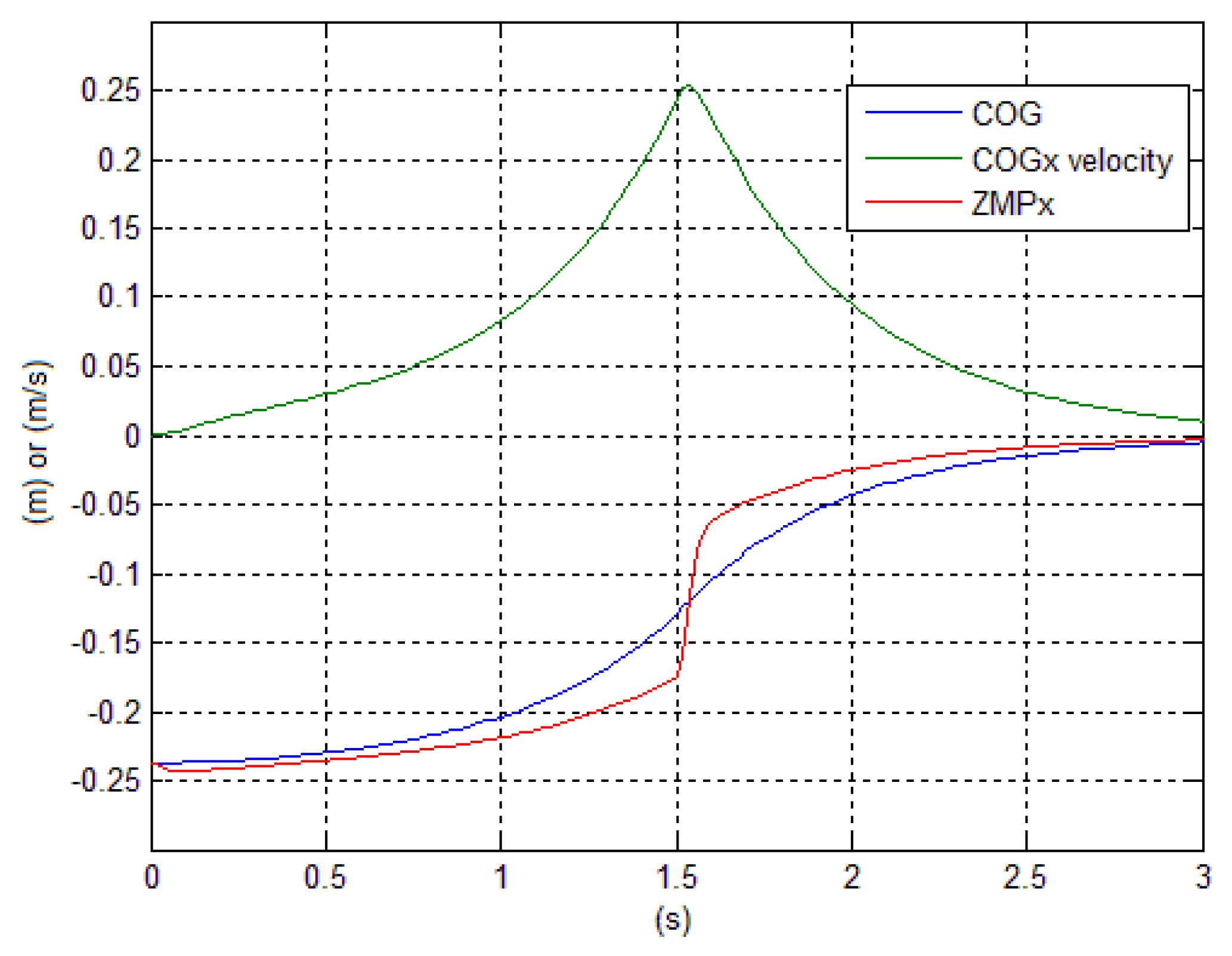
Figure 8.
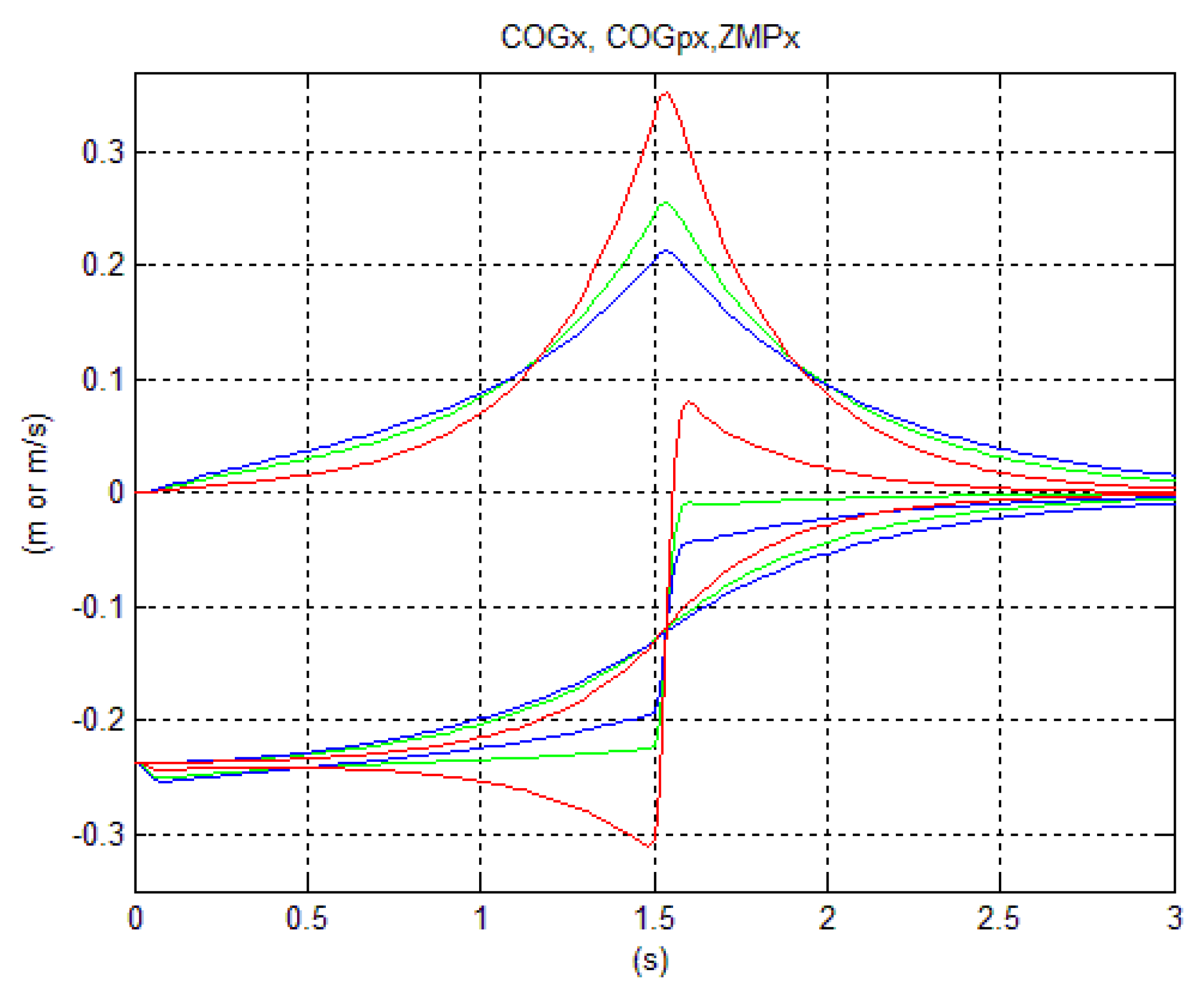
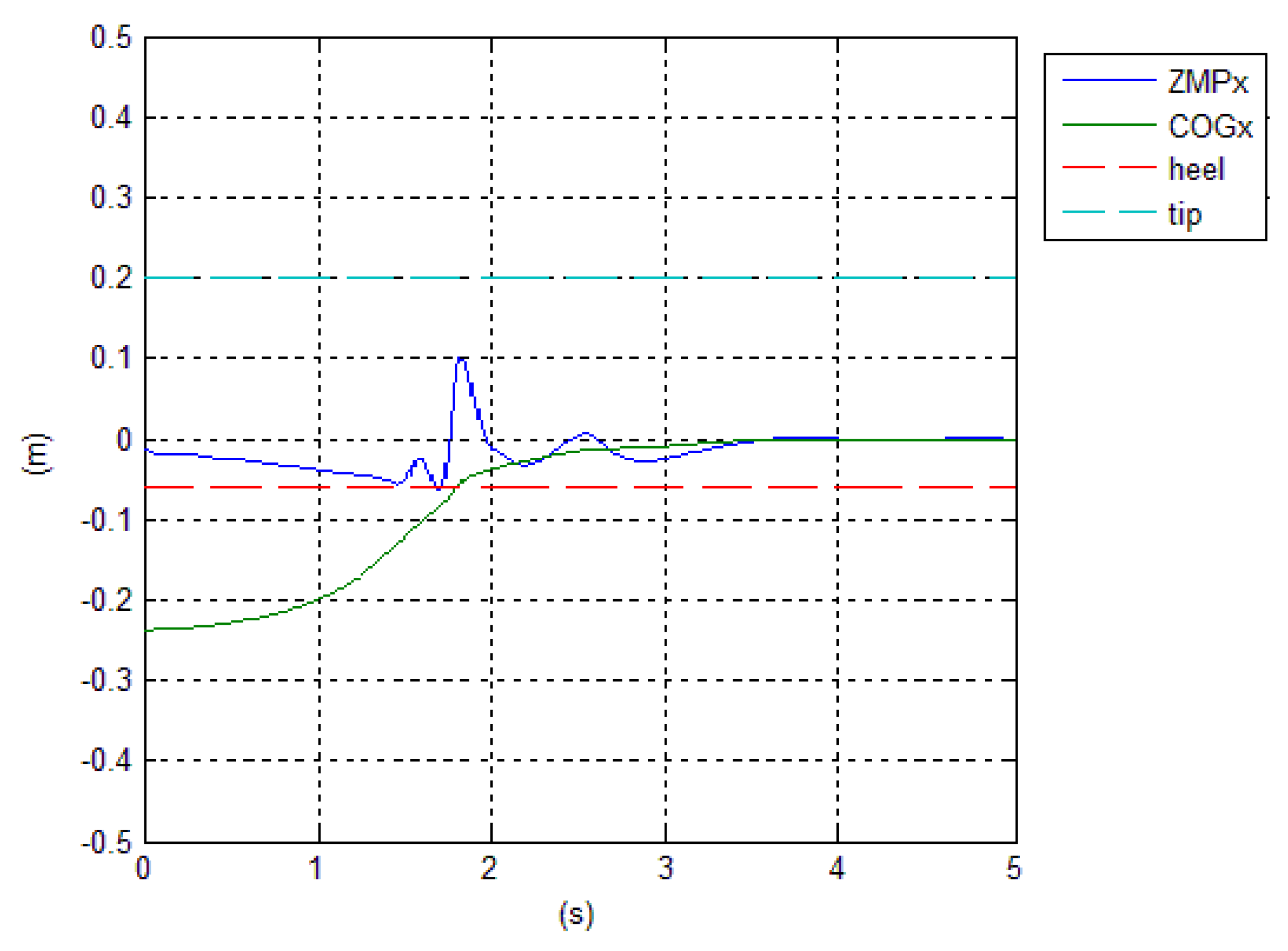
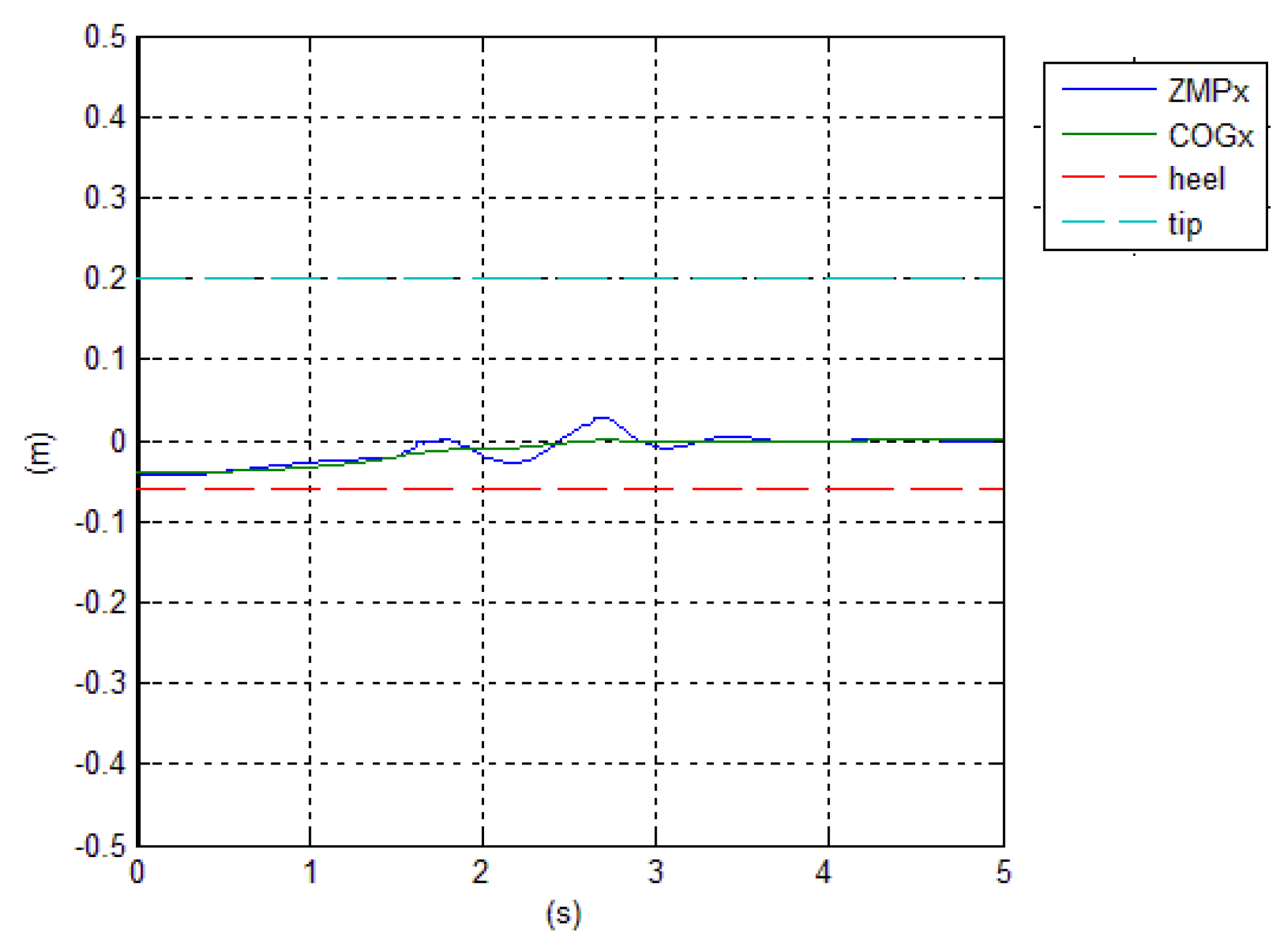
The behavior of
and
during the transition is given in
Figure 9. The position of
is 0.
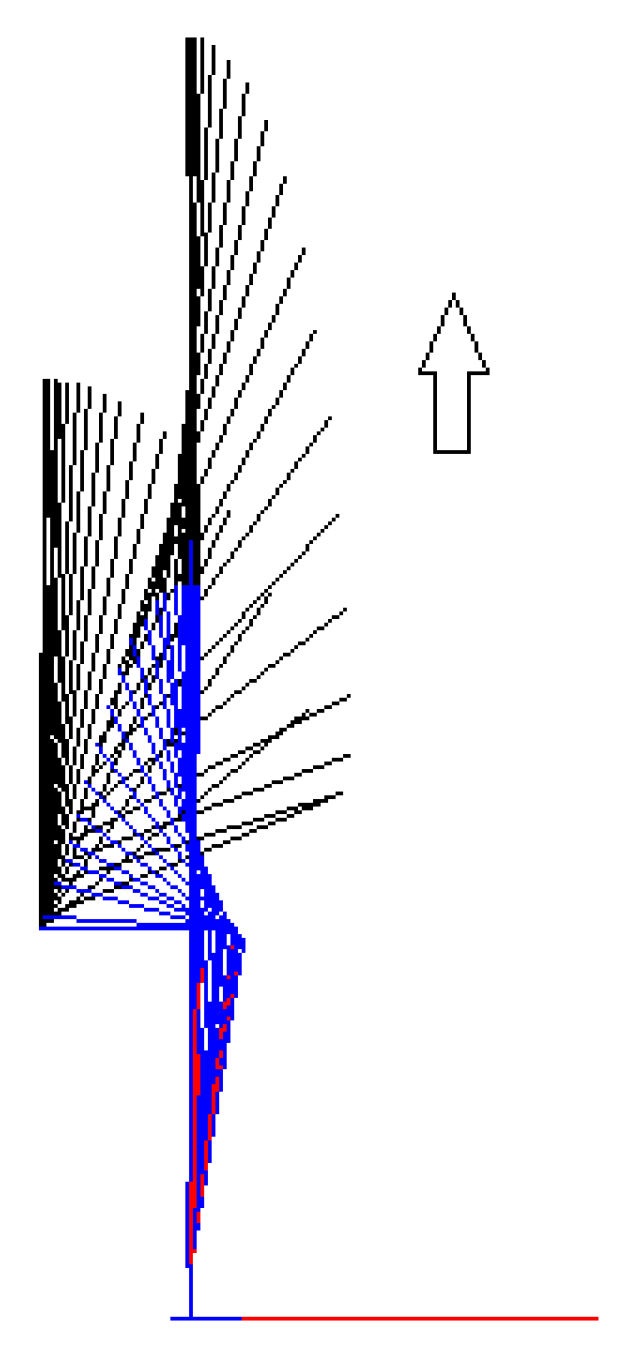
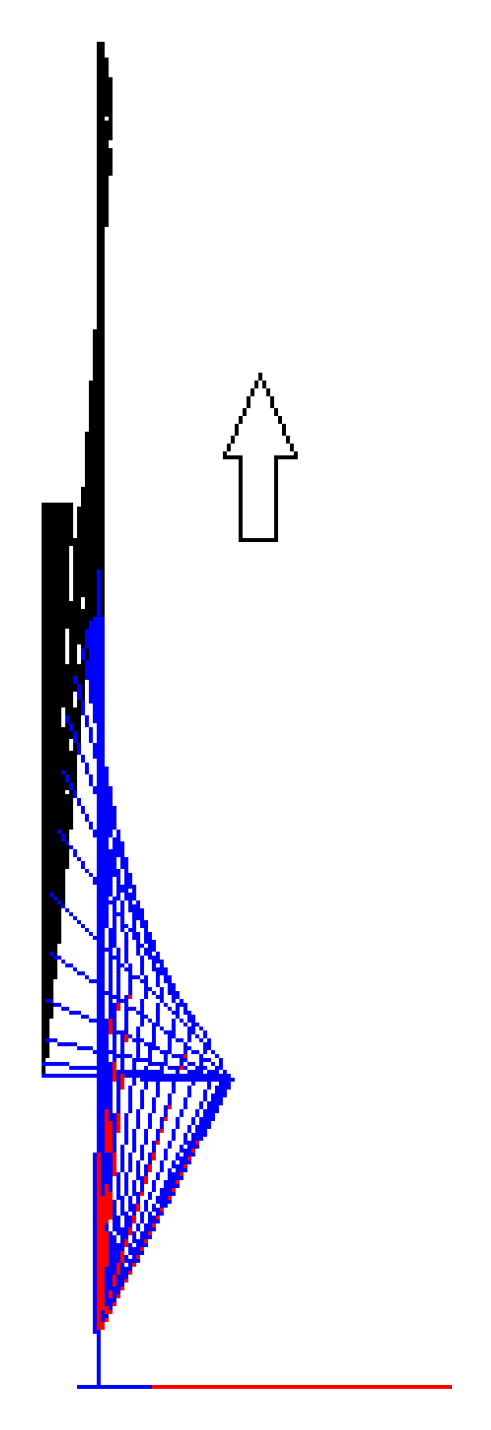
Figure 11 shows the animation of the exercise.
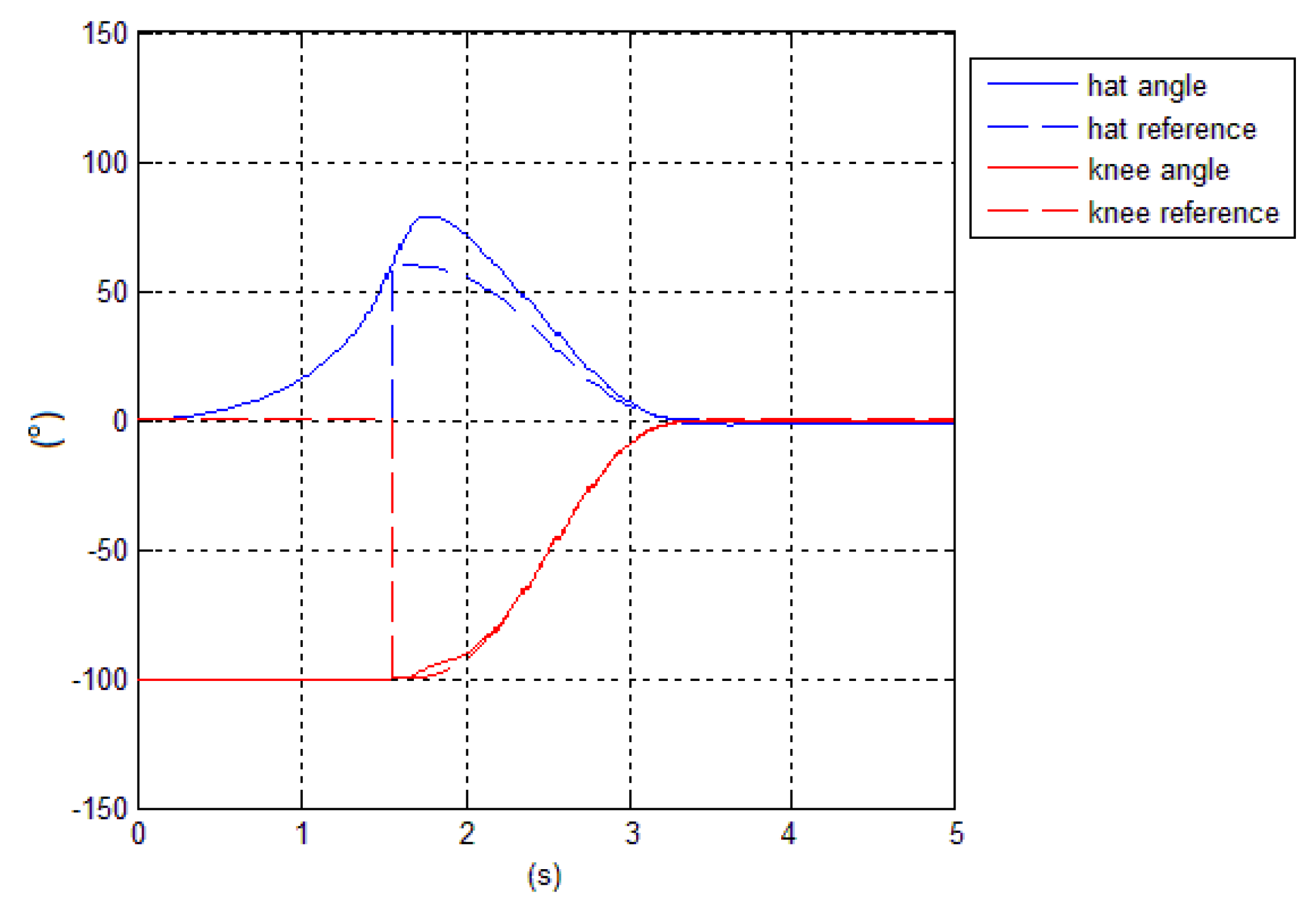
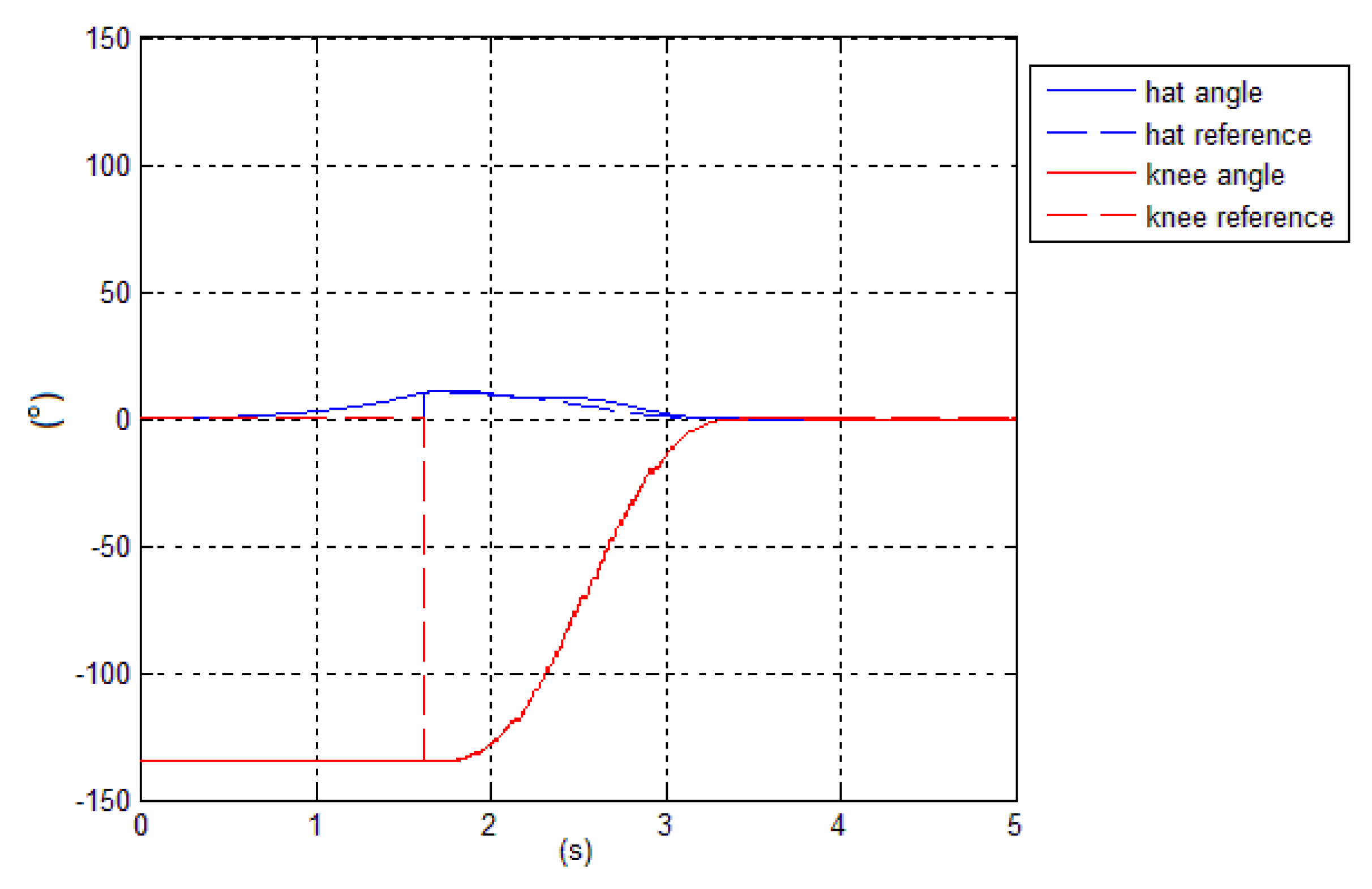
Figure 12 shows how the hat and knee angles track the references.
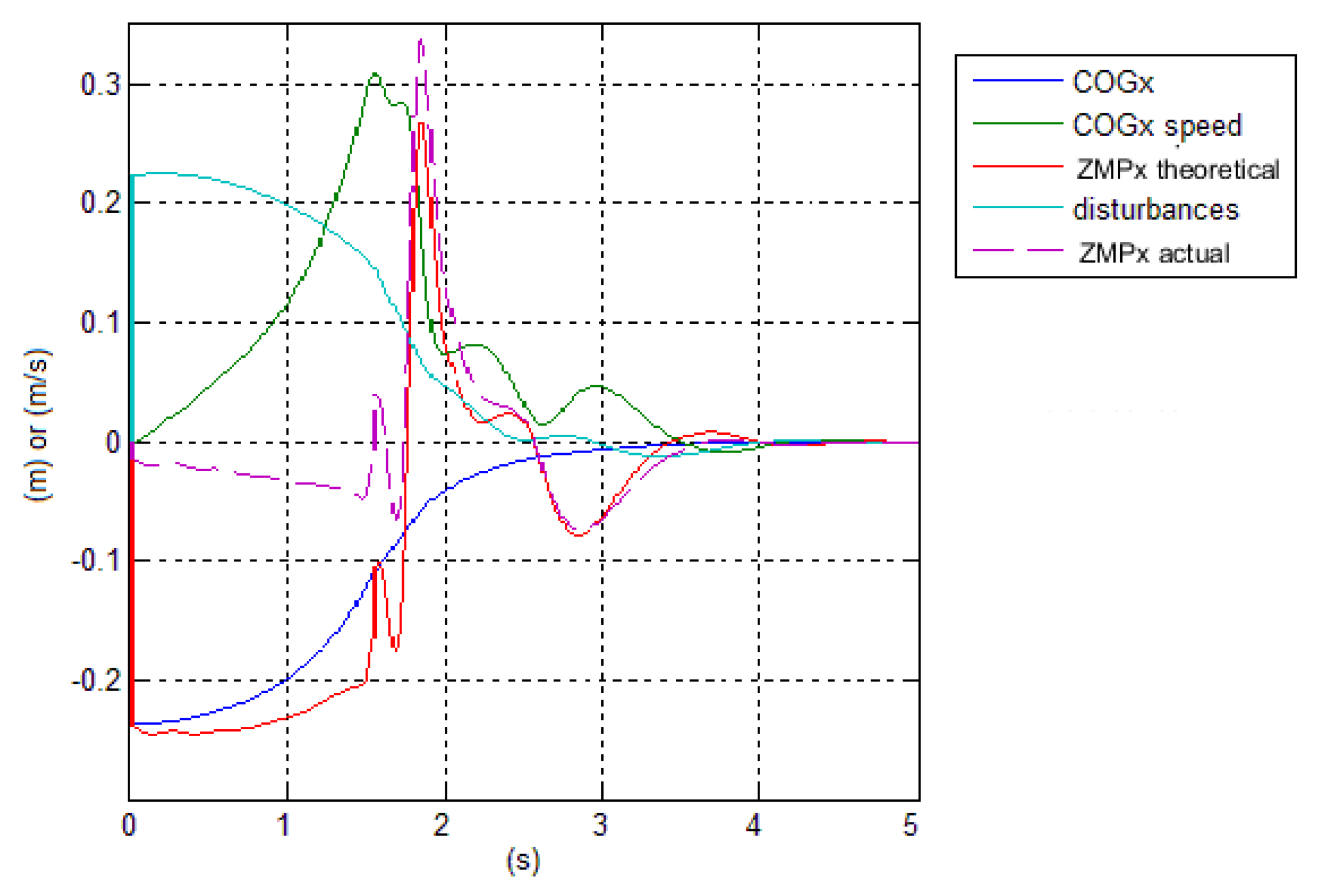
It is interesting to see the estimates
,
theoretical assuming no disturbances and
actual (i.e., the
), along with the estimate of the disturbances, i.e., the reaction forces on the chair, obtained by the extended estimator [
17]. These are given in
Figure 13.
The performance of the exercise, expressed as the ratio between the change in potential energy and the total work consumed to complete the motion, as defined in [
11] is 60%, and the maximum angle reached by the trunk is
. As oppose, the remaining figures, from
Figure 14,
Figure 15,
Figure 16,
Figure 17 and
Figure 18, show a relatively easy exercise (experiment 2) with an ankle angle of
. The performance here is 95% with a maximum trunk angle value of
. To show the robustness of the control this exercise was performed with the identical control parameters of the previous experiment.
The behavior of
and
during the transition is given in
Figure 15.
Figure 17 shows the animation of the exercise, while
Figure 18 shows how the hat and knee angles track the references.
6. Conclusions
The paper approaches the sit-to-stand exercise under two aspects: analysis of the dynamics of the exercise/design of the feedback control of an autonomous biped device, and its application to an haptic exoskeleton with the cooperation of a patient.
In regard to the autonomous execution of the exercise, several authors have argued that two components are involved in solving the control problem in the humanoid STS motion: (1) phase and trajectory planning, and (2) feedback control.
With respect to the former, the most significant are the COM preview to follow in the transition, and the time coordination between motion of the hips and torques on ankles and knees in phase 1. From the experiments, the chair reaction forces, the knee angle and trunk attitude to reach an erect posture are not critical. The COM preview can be synthesized by exploiting the linearized inverted pendulum model, with basis the step transition of the , and selecting the appropiate parameter . The value of this parameter is not necessarily identical to the real height of the COG of the biped, but it is chosen according to the difficulty of the exercise. This difficulty here is represented by the distance of , i.e., the chair, from the feet when sitting. The design parameter can explain the Alexander STS technique. If its value is lower or equal than the height of the , the transition is steep, the lift off is early, the biped will be in dynamical balance, with the still far from the feet, and with a relatively high trunk angular velocity to be conveyed in the successive lift motion, on the contrary if the transistion is slower, the balance will be almost statical with the already under the feet, and the trunk attitude almost stationary. Based on these elements, the final trajectories can easily be planned to reduce maximum torque on the joints and energy expenditure. In the simulated experiments, two examples are considered: one is difficult with a performance, expressed as the ratio between the change in potential energy and the total work consumed to complete the motion of 60%, with the trunk reaching a maximum angle of ; the other is relatively easy with a performance of 95% and a maximum trunk angle of .
With respect to the latter, exploiting the inverse or pseudo-inverse of Jacobian matrices and a linearized inverted pendulum model of a simple linear feedback, based on feet and chair pressure sensors, and position/velocity measures of the joint angles, can be obtained either for joint velocity or torque controls. This feedback requires a limited number of model parameters and design gains without the need to perform cumbersome inverse kinematics or dynamics. Symbolic environments such as Autolev can offer efficient expressions for the necessary Jacobians that can be computed in real time.
When the postural control is applied to an exoskeleton interacting with a patient, the paper proposes an innovative approach to blend the patient’s actions with the automatic execution of the exercise. Several options are offered by the approach for proposing protocols of physiotherapy tracking the evolution of the process of rehabilitation, in terms of strenght of the support offered by the exoskeleton, and specific joints and postural tasks to be controlled by the patient. The process of rehabilitation can start with a complete tutoring of the patient, evolving to a cooperation between automatic control and patient on the same postural tasks and jonts, e.g., reaching an erect posture moving the knees, or a coordination between the two players operating on different tasks, e.g., the patient raises the pelvis and rotates the trunk through knees and hips while an automatic balance is guaranteed with a feedback on the ankles.
An exoskeleton for this specific exercise has been built, and some preliminary tests of phase 2 have been documented in a previous paper. However, more work is needed in future research: testing a complete exercise using the exoskeleton, not only during phase 2; decoupling the interaction not only from joints to elemental postural tasks, but also vice versa; generalizing the admittance filters from single joints and related muscles to multivariable filters processing the vector of the available EMG signals to collectively control all joints. This will be obtained exploiting muscle synergies, and training artificial neural networks that directly link EMG patterns to motion.