Design of Multiple Wearable Robotic Extra Fingers for Human Hand Augmentation
Abstract
1. Introduction
1.1. Robotic Hands
1.2. Wearable Robotic Extra Fingers
1.3. Underactuation in Robotic Extra Fingers
1.4. Differential Mechanisms
1.5. Paper Contribution
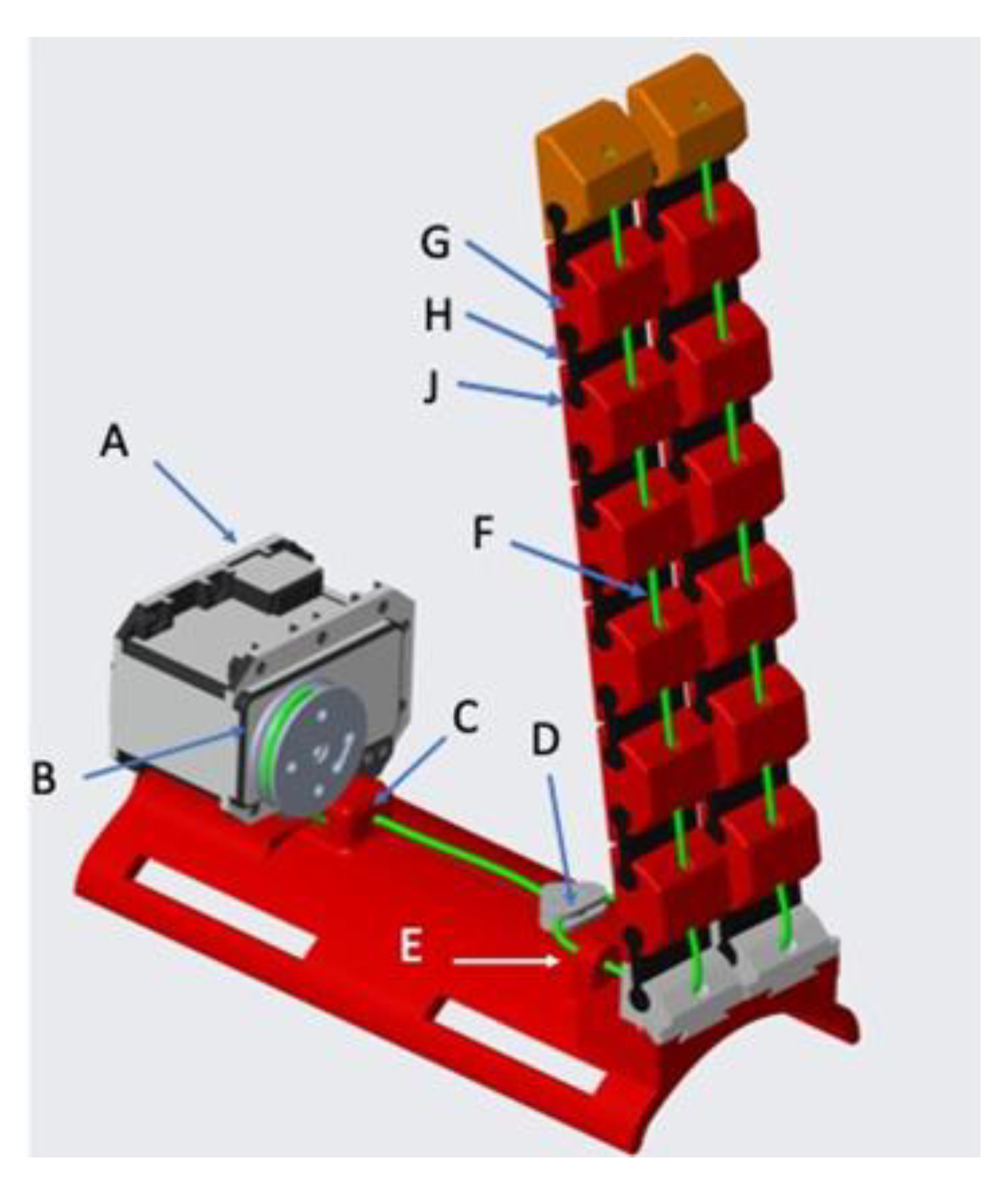
2. Device Overview
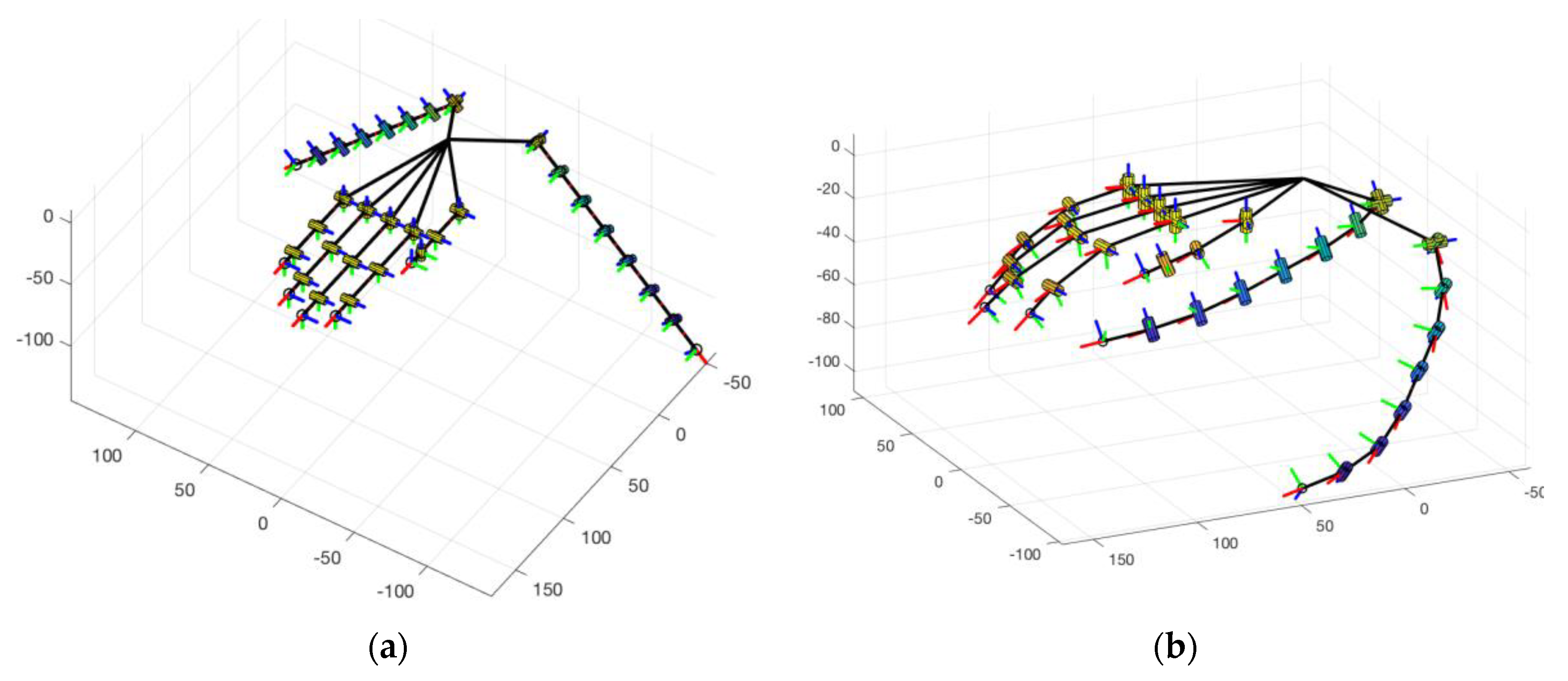
3. Analysis
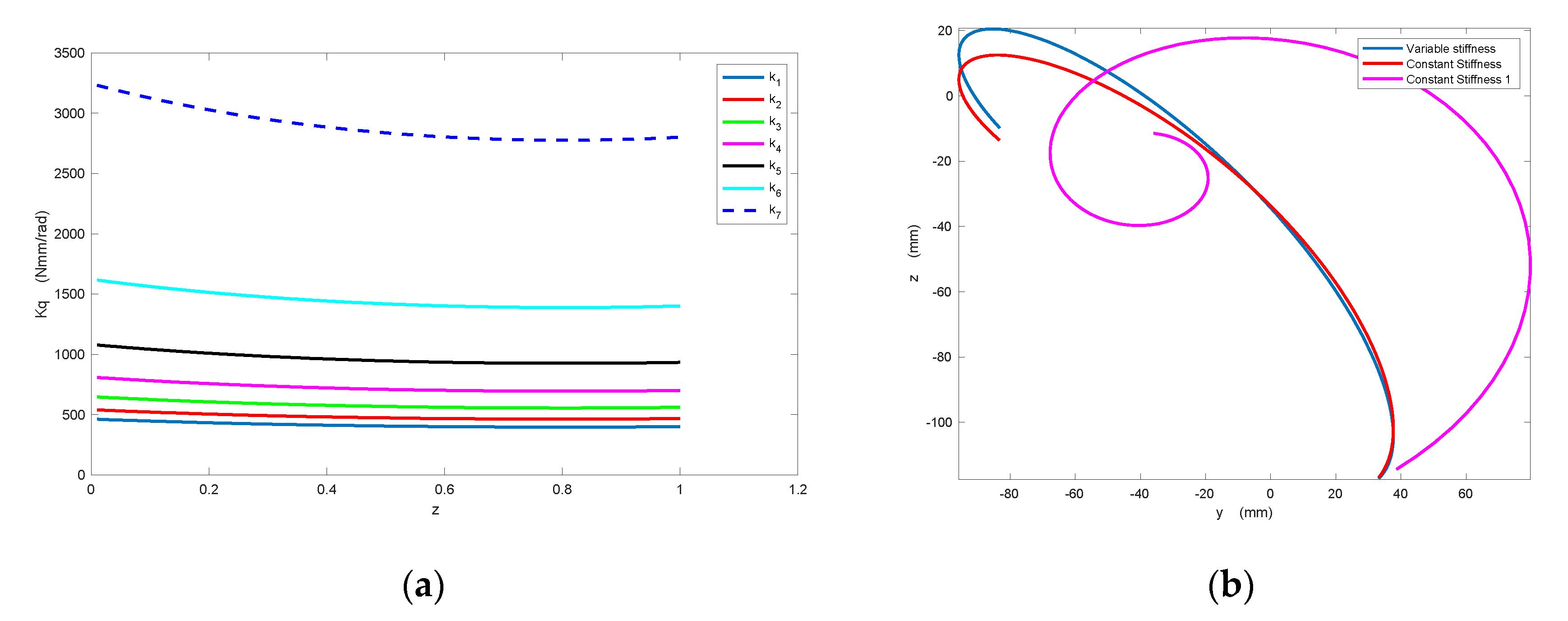
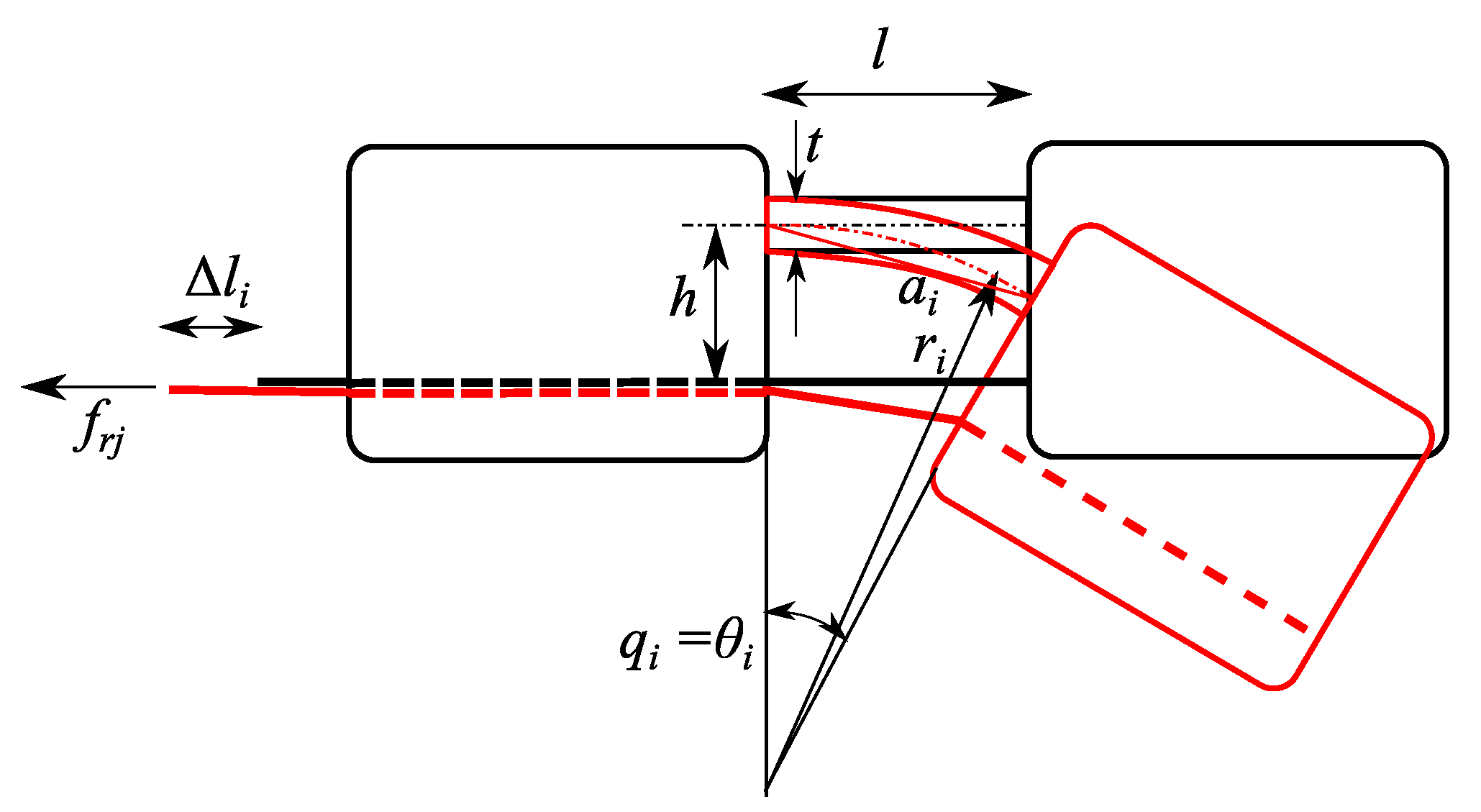
3.1. Design of Finger Passive Elements
- values vary as a function of hand configuration, however, for the motion that we selected, such a variation is not very high.
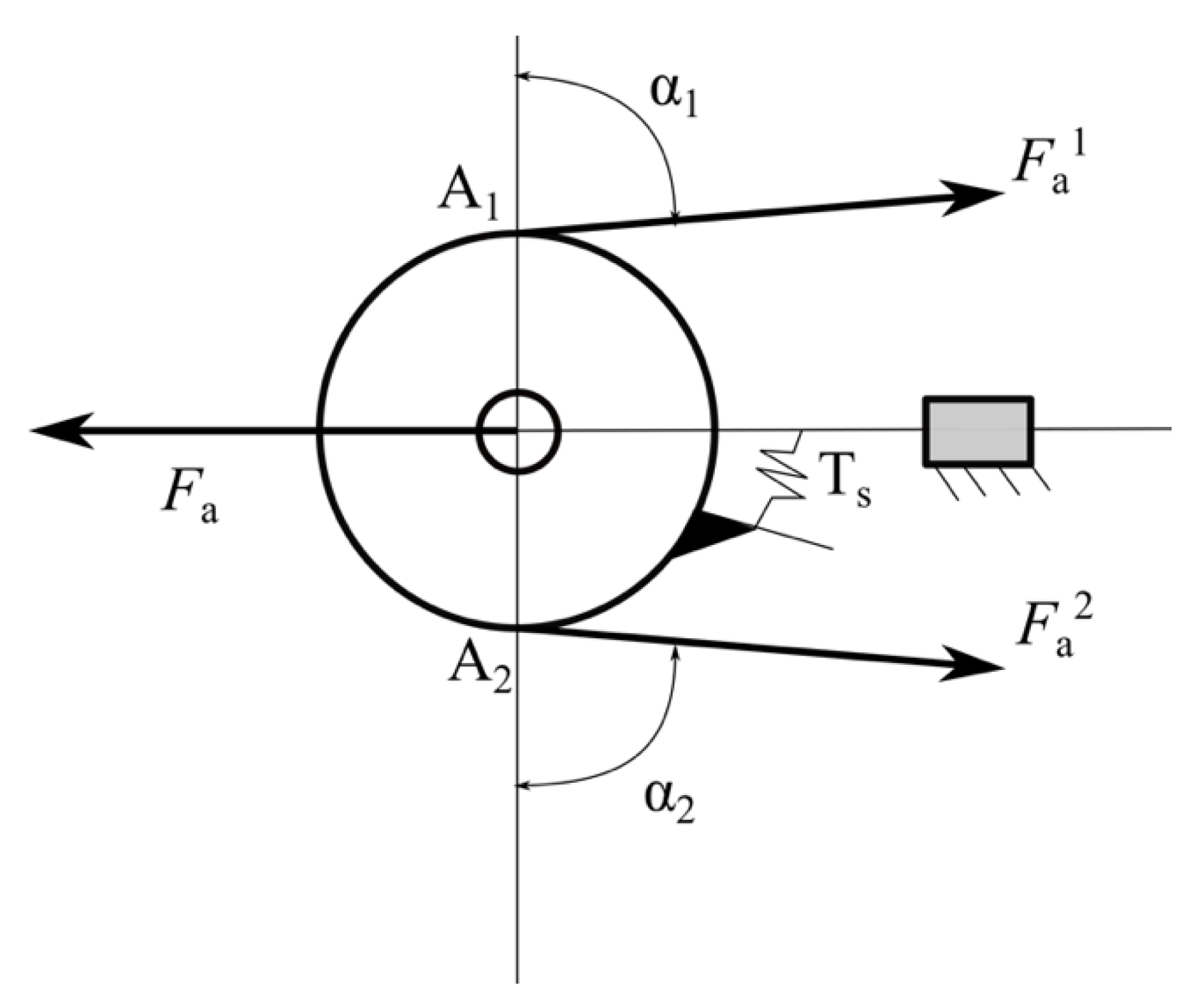
3.2. Mechanical Transmission and Differential Mechanism Analysis
3.3. Structural Analysis of Rigid Elements
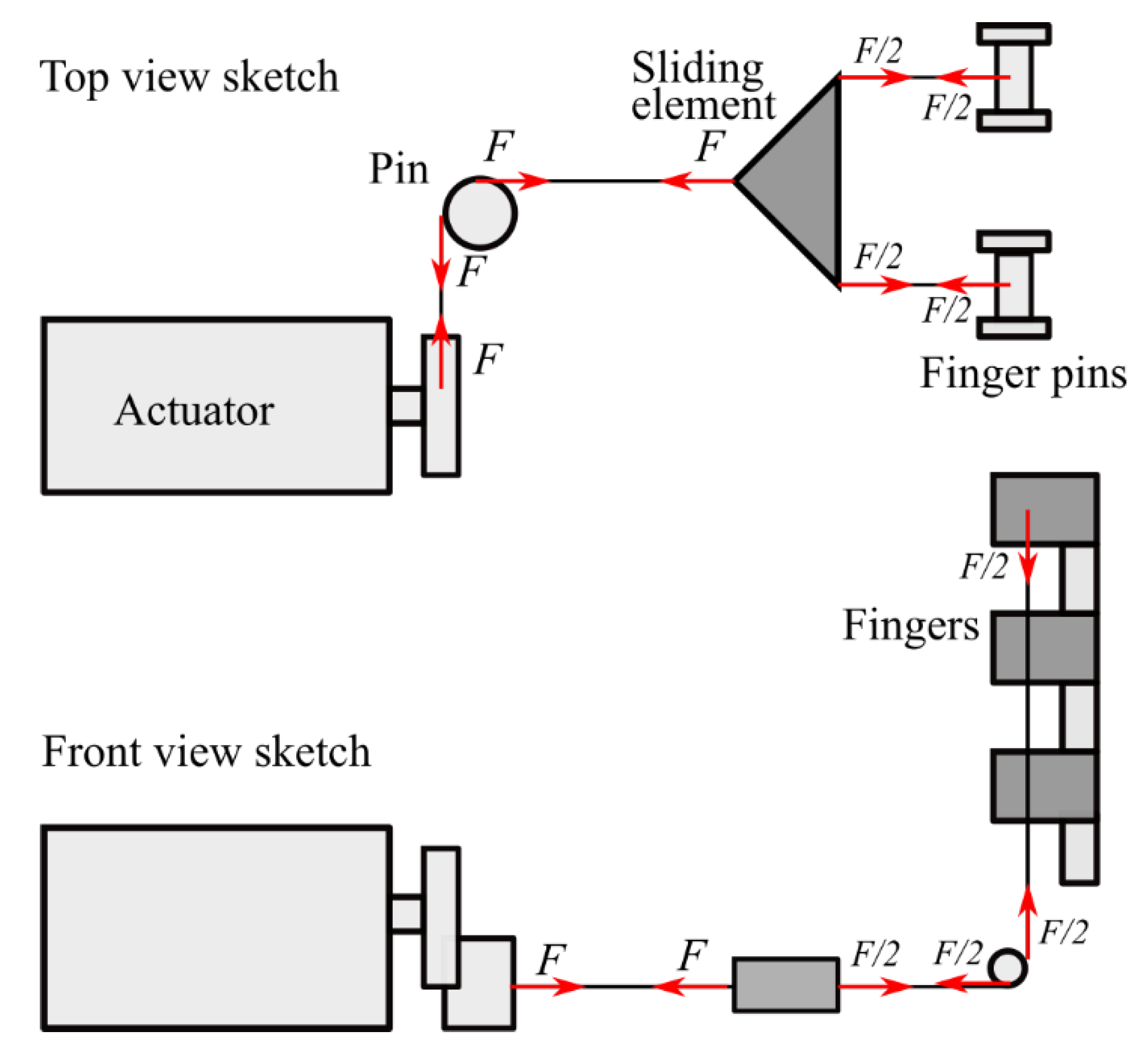
3.3.1. Force Analysis
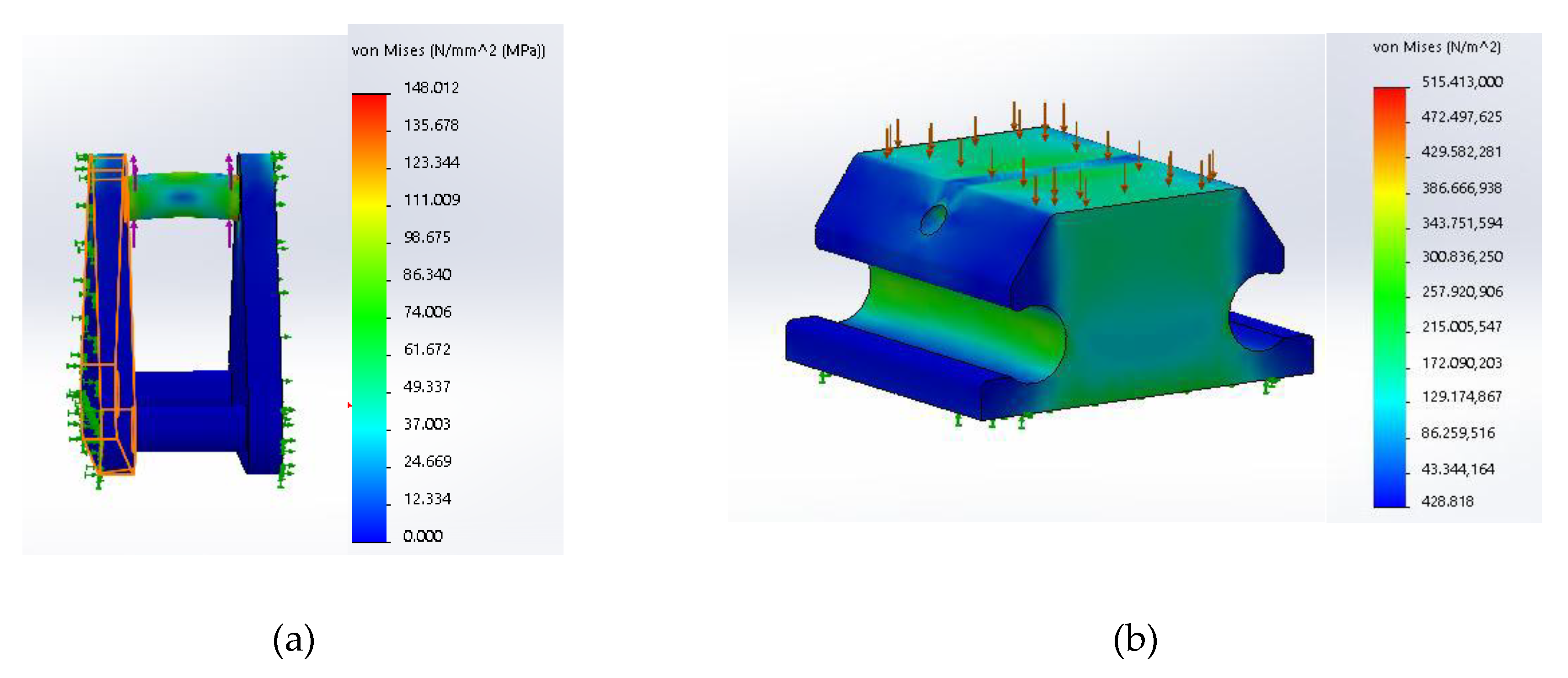
3.3.2. Stress Analysis Results
4. Prototype Presentation
5. Discussion on Potential Applications, Links
- Actuation: while other devices available in the literature have a rigid and fully actuated structures, in the device presented in this work only one motor is necessary to actuate both the single and the double finger configurations. This feature limits the weight, complexity of the device, and improve its wearability and user comfort.
- Modularity: as discussed in Section 2, the structure of the fingers is modular at the phalanx level, the same modules can be used both for the single and double finger configurations. The device can be easily adapted to user’s specific needs and features. For instance, a smaller hand would need a device with smaller dimensions that can be easily obtained realizing fingers with less modules.
- Robustness, safety for the user: in this type of devices the fingers are the elements more sensitive to unexpected contacts with the environment and shocks. Passive elements present in the interphalangeal joints of the fingers are realized by TPU, a material that presents high resistance to impacts and elongation at break. As a result, the fingers are quite robust and can resist to uncertainties and unpredictable impacts that may occur during activities of daily living (ADL). At the same time, their compliance limits the risks for the user and for other people.
- Adaptability: the compliant structure provided by deformable elements in interphalangeal joints and the differential mechanism allow the device to automatically adapt to different objects with different shapes and dimensions, without the need of specific sensors on the fingers and complex control strategies.
- Costs: the simple but versatile mechanical structure, the choice of widely diffused and affordable manufacturing technologies and materials, and the modularity, lead to a cost of the device that is quite limited.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mason, M.T.; Salisbury, J.K. Robots Hands and the Mechanics of Manipulation; MIT Press: Cambridge, MA, USA, 1985; ISBN 9780262132053. [Google Scholar]
- Carbone, G. Grasping in Robotics; Springer: Dordertch, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Fukaya, N.; Toyama, S.; Asfour, T.; Dillmann, R. Design of the TUAT/Karlsruhe humanoid hand. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; pp. 1754–1759. [Google Scholar] [CrossRef]
- Butterfass, J.; Grebenstein, M.; Liu, H.; Hirzinger, G. DLR-hand II: Next generation of a dexterous robot hand. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 109–114. [Google Scholar] [CrossRef]
- Martin, E.; Desbiens, A.L.; Laliberté, O.T.; Gosselin, C. SARAH hand used for space operation on STVF robot. In Proceedings of the Intelligent Manipulation and Grasping, Genoa, Italy, 1–2 July 2004; pp. 279–284. [Google Scholar]
- Roccella, S.; Carrozza, M.C.; Cappiello, G.; Dario, P.; Cabibihan, J.J.; Zecca, M.; Hiwa, H.; Itoh, K.; Matsumoto, M.; Takanishi, A. Design, fabrication and preliminary results of a novel anthropomorphic hand for humanoid robotics: RCH-1. In Proceedings of the IEEE/RSJInternational Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 266–271, ISBN 0780384636. [Google Scholar]
- Dechev, N.; Cleghorn, W.L.; Nauman, S. Multiple finger, passive adaptive grasp prosthetic hand. Mech. Mach. Theory 1999, 36, 1157–1173. [Google Scholar] [CrossRef]
- Raparelli, T.; Mattiazzo, G.; Mauro, S.; Velardocchia, M. Design and development of a Pneumatic anthropomorphic hand. J. Robot. Syst. 2000, 17, 1–15. [Google Scholar] [CrossRef]
- Maffiodo, D.; Raparelli, T. Three-Fingered Gripper with Flexure Hinges Actuated by Shape Memory Alloy Wires. Int. J. Autom. Technol. 2017, 11, 355–360. [Google Scholar] [CrossRef]
- Niola, V.; Penta, F.; Rossi, C.; Savino, S. An underactuated mechanical hand: Theoretical studies and prototyping. Int. J. Mech. Control 2015, 16, 11–19. [Google Scholar]
- Cosenza, C.; Niola, V.; Savino, S. Analytical study for the capability implementation of an underactuated three-finger hand. Mech. Mach. Sci. 2019, 65, 161–168. [Google Scholar] [CrossRef]
- Niola, V.; Rossi, C.; Savino, S.; Timpone, F. Study of an underactuated mechanical finger driven by tendons. Int. J. Autom. Technol. 2017, 11, 344–354. [Google Scholar] [CrossRef]
- Maffiodo, D.; Raparelli, T. Comparison among different modular SMA actuated flexible fingers. Mech. Mach. Sci. 2019, 68, 324–331. [Google Scholar] [CrossRef]
- Carbone, G.; Rossi, C.; Savino, S. Performance comparison between FEDERICA hand and LARM hand. Int. J. Adv. Robot. Syst. 2015, 12, 90. [Google Scholar] [CrossRef]
- Kobayashi, H.; Hyodo, K.; Ogane, D. On tendon-driven robotic mechanisms with redundant tendons. Int. J. Robot. Res. 1998, 17, 561–571. [Google Scholar] [CrossRef]
- Parietti, F.; Asada, H. Supernumerary robotic limbs for human body support. IEEE Trans. Robot. 2016, 32, 301–311. [Google Scholar] [CrossRef]
- Wu, F.Y.; Asada, H.H. “Hold-and-manipulate” with a single hand being assisted by wearable extra fingers. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Prattichizzo, D.; Malvezzi, M.; Hussain, I.; Salvietti, G. The sixth-finger: A modular extra-finger to enhance human hand capabilities. In Proceedings of the 23rd IEEE International Symposium on Robot and Human Interactive Communication, Edinburgh, UK, 25–29 August 2014; pp. 993–998. [Google Scholar] [CrossRef]
- Hussain, I.; Salvietti, G.; Spagnoletti, G.; Prattichizzo, D. The soft-sixthfinger: A wearable emg controlled robotic extra-finger for grasp compensation in chronic stroke patients. IEEE Robot. Autom. Lett. 2016, 1, 1000–1006. [Google Scholar] [CrossRef]
- Hu, Y.; Leigh, S.W.; Maes, P. Hand Development Kit: Soft Robotic Fingers as Prosthetic Augmentation of the Hand. In Proceedings of the Adjunct Publication of the 30th Annual ACM Symposium on User Interface Software and Technology, Québec City, QC, Canada, 22–25 October 2017. [Google Scholar]
- Hussain, I.; Salvietti, G.; Spagnoletti, G.; Malvezzi, M.; Cioncoloni, D.; Rossi, S.; Prattichizzo, D. A soft supernumerary robotic finger and mobile arm support for grasping compensation and hemiparetic upper limb rehabilitation. Robot. Auton. Syst. 2017, 93, 1–12. [Google Scholar] [CrossRef]
- Laliberté, T.; Gosselin, C.M. Underactuation in space robotic hands. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space, Montréal, QC, Canada, 18–22 June 2001. [Google Scholar]
- Birglen, L.; Gosselin, C.M. Force Analysis of Connected Differential Mechanisms: Application to Grasping. Int. J. Robot. Res. 2006, 25, 1033–1046. [Google Scholar] [CrossRef]
- Zappatore, G.A.; Reina, G.; Messina, A. Analysis of a highly underactuated robotic hand. Int. J. Mech. Control 2017, 18, 17–24. [Google Scholar]
- Birglen, L.; Gosselin, C.M. On the force capability of underactuated fingers. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 1139–1145. [Google Scholar] [CrossRef]
- Massa, B.; Roccella, S.; Carrozza, M.C.; Dario, P. Design and development of an underactuated prosthetic hand. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 3374–3379. [Google Scholar] [CrossRef]
- Baril, M.; Laliberté, T.; Gosselin, C.; Routhier, F. On the design of a mechanically programmable underactuated anthropomorphic prosthetic gripper. J. Mech. Des. 2013, 135, 121008. [Google Scholar] [CrossRef]
- Kontoudis, G.P.; Liarokapis, M.V.; Zisimatos, A.G.; Mavrogiannis, C.I.; Kyriakopoulos, K.J. Open-source, anthropomorphic, underactuated robot hands with a selectively lockable differential mechanism: Towards affordable prostheses. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5857–5862. [Google Scholar]
- Hussain, I.; Spagnoletti, G.; Salvietti, G.; Prattichizzo, D. Toward wearable supernumerary robotic fingers to compensate missing grasping abilities in hemiparetic upper limb. Int. J. Robot. Res. 2017, 36, 1414–1436. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Valigi, M.C.; Logozzo, S.; Canella, G. A new automated 2 DOFs 3D desktop optical scanner. In Mechanisms and Machine Science; Springer: Berlin, Germany, 2017; Volume 47, pp. 231–238. [Google Scholar] [CrossRef]
- Valigi, M.C.; Logozzo, S.; Canella, G. A robotic 3D vision system for automatic cranial prostheses inspection. Mech. Mach. Sci. 2018, 49, 328–335. [Google Scholar] [CrossRef]
- Salvietti, G.; Hussain, I.; Malvezzi, M.; Prattichizzo, D. Design of the passive joints of underactuated modular soft hands for fingertip trajectory tracking. IEEE Robot. Autom. Lett. 2017, 2, 2008–2015. [Google Scholar] [CrossRef]
- Wu, F.Y.; Asada, H. Bio-Artificial Synergies for Grasp Posture Control of Supernumerary Robotic Fingers; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Santello, M.; Flanders, M.; Soechting, J.F. Postural Hand Synergies for Tool Use. J. Neurosci. 1998, 18, 10105–10115. [Google Scholar] [CrossRef]
- Malvezzi, M.; Valigi, M.C.; Salvietti, G.; Iqbal, Z.; Hussain, I.; Prattichizzo, D. Design criteria for wearable robotic extra–fingers with underactuated modular structure. Mech. Mach. Sci. 2019, 68, 509–517. [Google Scholar] [CrossRef]
- Malvezzi, M.; Gioioso, G.; Salvietti, G.; Prattichizzo, D. SynGrasp: A Matlab Toolbox for Underactuated and Compliant Hands. IEEE Robot. Autom. Mag. 2015, 22, 52–68. [Google Scholar] [CrossRef]
- Cobos, S.; Ferre, M.; Uran, M.S.; Ortego, J.; Pena, C. Efficient human hand kinematics for manipulation tasks. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2246–2251. [Google Scholar]
- Bianchi, M.; Liarokapis, M.V. HandCorpus, a new open-access repository for sharing experimental data and results on human and artificial hands. In Proceedings of the IEEE World Haptics Conference (WHC), Daejeon, Korea, 14–17 April 2013. [Google Scholar]
- Dollar, A.M.; Howe, R.D. The highly adaptive sdm hand: Design and performance evaluation. Int. J. Robot. Res. 2010, 29, 585–597. [Google Scholar] [CrossRef]
- Ahmed, M.; Islam, M.; Vanhoose, J.; Rahman, M. Comparisons of Elasticity Moduli of Different Specimens Made Through Three Dimensional Printing. 3D Print. Addit. Manuf. 2017, 4, 105–109. [Google Scholar] [CrossRef]
- Robotis. Dynamixel Mx-28t Robot Actuator. 2012. Available online: http://www.trossenrobotics.com/dynamixel-mx-28-robotactuator.aspx (accessed on 10 December 2019).
- ArbotiX. Arbotix-m Robocontroller, Open Source. 2012. Available online: http://www.trossenrobotics.com/p/arbotix-robotcontroller.aspx (accessed on 10 December 2019).
- Spagnoletti, G.; Hussain, I.; Pacchierotti, C.; Salvietti, G.; Prattichizzo, D. The hRing: A haptic interface for an extra robotic finger. In Proceedings of the IEEE Haptic symposium, Philadelphia, PA, USA, 8–11 April 2016. [Google Scholar]
- Salvietti, G.; Hussain, I.; Cioncoloni, D.; Taddei, S.; Rossi, S.; Prattichizzo, D. Compensating Hand Function in Chronic Stroke Patients Through the Robotic Sixth Finger. Trans. Neural Syst. Rehabil. Eng. 2016. [Google Scholar] [CrossRef]
- Cyberglove. Cyberglove Systems. 2019. Available online: http://www.cyberglovesystems.com/ (accessed on 10 December 2019).
- Mozaffarian, D.; Benjamin, E.J.; Go, A.S.; Arnett, D.K.; Blaha, M.J.; Cushman, M.; Howard, V.J. Heart disease and stroke statistics—2016 update: A report from the American Heart Association. Circulation 2015. [Google Scholar] [CrossRef]


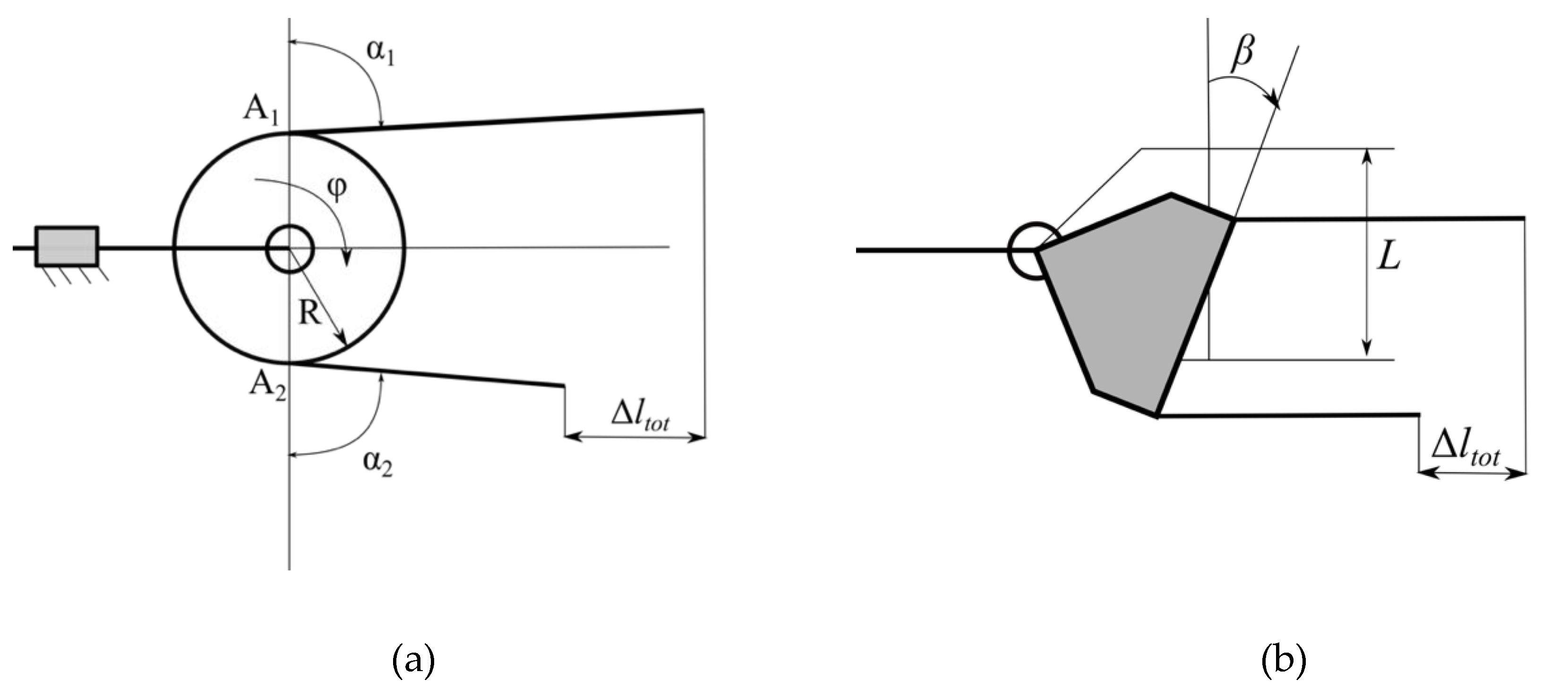

| Configuration | k1/k1 | k2/k1 | k3/k1 | k4/k1 | k5/k1 | k6/k1 | k7/k1 |
|---|---|---|---|---|---|---|---|
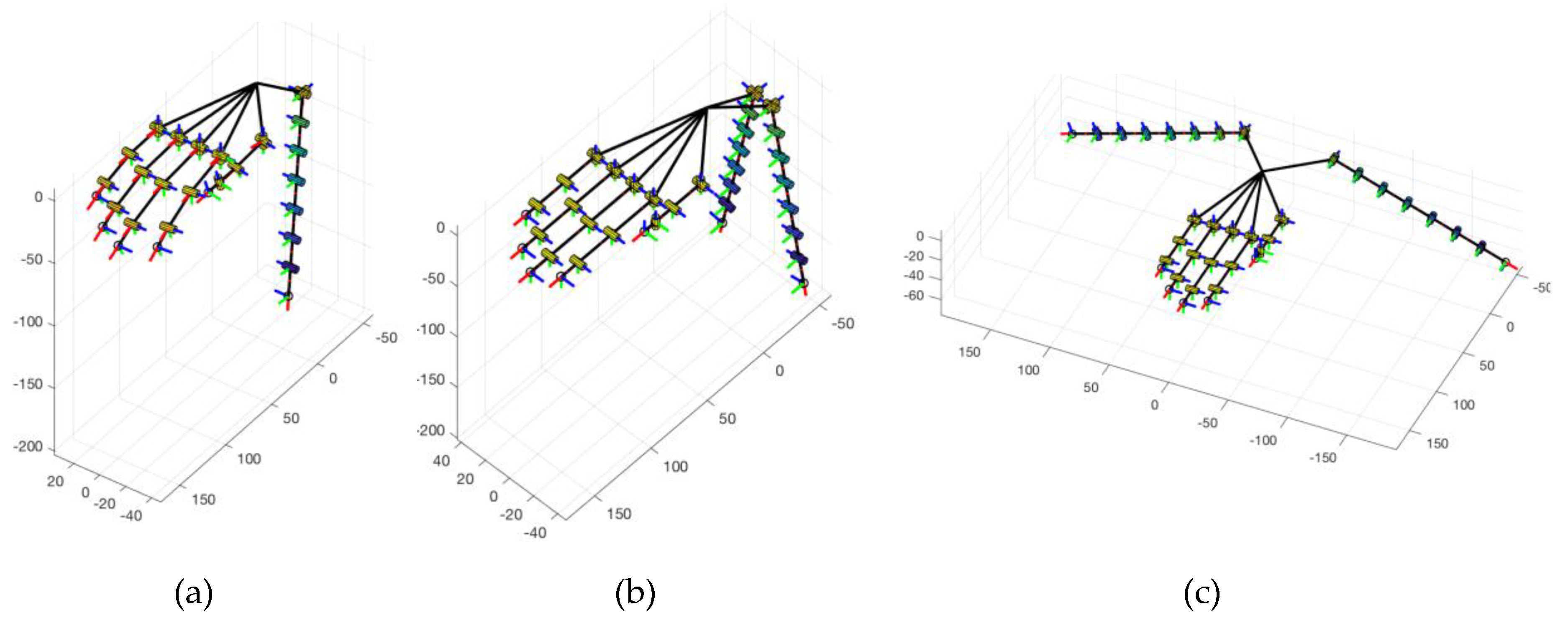
| Single (Figure 5a) | 1.00 | 1.17 | 1.39 | 1.74 | 2.32 | 3.50 | 6.98 |
| Double, opposite to the palm (Figure 5b) | 1.00 | 1.10 | 1.33 | 1.65 | 2.20 | 3.31 | 6.61 |
| Double, aligned with the palm (Figure 5c) | 1.00 | 1.43 | 1.71 | 2.14 | 2.85 | 4.28 | 8.57 |
| Infill Density % | E (MPa) |
|---|---|
| 10 | 1.07 |
| 30 | 1.38 |
| 50 | 2.07 |
| 70 | 6.53 |
| 90 | 9.45 |
| 100 | 10.5 |
| Property | Value | Unit |
|---|---|---|
| Density | 1.03 | kg/m3 |
| Elastic modulus | 2000 | MPa |
| Poisson’s coefficient | 0.394 | |
| Yield stress | 45–60 MPa | MPa |
| Specific heat | 1386 J/(kg K) | J/(kg K) |
| Thermal conductivity | 0.2256 W/(m k) | W/(m k) |
| Description | Value | Unit |
|---|---|---|
| Rigid module, dimension | 20 × 31 × 12 | mm |
| Flexible module, dimension | 20 × 18 × 2 | mm |
| Support base, dimension (approx.) | 170 × 50 × 40 | mm |
| Actuator, dimension | 71 × 71 × 45 | mm |
| Actuator, weight | 146 | g |
| Max torque (@ 12V) | 3.1 | Nm |
| Pulley radius | 11 | mm |
| Max current (@ 12 V) | 1.4 | A |
| Operating angles | 300 | ° |
| Max unloaded velocity | 684 | °/s |
| Total weight | 210 | g |
| Description | Value | Unit |
|---|---|---|
| Max payload | 2 | kg |
| Max force at the fingertip (closed) | 12 | N |
| Max force at the fingertip (open) | 6 | N |
| Diameter of the smallest graspable object | 17 | mm |
| Diameter of the largest graspable object | 180 | mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malvezzi, M.; Iqbal, Z.; Valigi, M.C.; Pozzi, M.; Prattichizzo, D.; Salvietti, G. Design of Multiple Wearable Robotic Extra Fingers for Human Hand Augmentation. Robotics 2019, 8, 102. https://doi.org/10.3390/robotics8040102
Malvezzi M, Iqbal Z, Valigi MC, Pozzi M, Prattichizzo D, Salvietti G. Design of Multiple Wearable Robotic Extra Fingers for Human Hand Augmentation. Robotics. 2019; 8(4):102. https://doi.org/10.3390/robotics8040102
Chicago/Turabian StyleMalvezzi, Monica, Zubair Iqbal, Maria Cristina Valigi, Maria Pozzi, Domenico Prattichizzo, and Gionata Salvietti. 2019. "Design of Multiple Wearable Robotic Extra Fingers for Human Hand Augmentation" Robotics 8, no. 4: 102. https://doi.org/10.3390/robotics8040102
APA StyleMalvezzi, M., Iqbal, Z., Valigi, M. C., Pozzi, M., Prattichizzo, D., & Salvietti, G. (2019). Design of Multiple Wearable Robotic Extra Fingers for Human Hand Augmentation. Robotics, 8(4), 102. https://doi.org/10.3390/robotics8040102







