Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles
Abstract
1. Introduction
1.1. Inverse Kinematics and Resolution of Task Redundancy for Serial-Link Robots
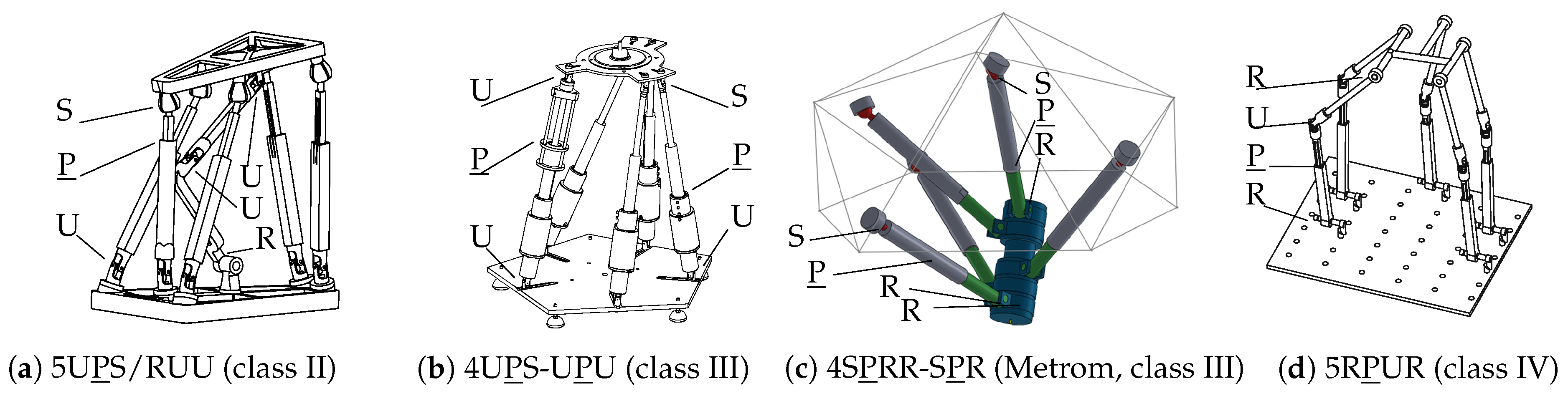
1.2. Overview of Parallel Robots Structures for 3T2R Tasks
- I
- mechanisms with full platform mobility (3T3R) that are redundantly controlled to five DoF,
- II
- mechanisms with 3T2R platform mobility enforced with a passive five-DoF constraining leg and five other legs with six DoF each,
- III
- mechanisms with 3T2R platform mobility resulting from the mobility of five actuated legs with five or six DoF each,
- IV
- mechanisms with 3T2R platform mobility and five legs with only five DoF each.
1.3. Inverse Kinematics of Parallel Robots for 3T2R Tasks
1.4. Motivation and Summary of the State of the Art
- a general kinematics model for parallel robots using the concept of reciprocal Euler angles [5],
- a complete elimination of the redundant operational space coordinate in this formulation for 3T2R tasks allowing a nullspace optimization in the gradient-based inverse kinematics,
- proofs, examples and simulations to show the performance for single serial kinematic leg chains and complete parallel robots.
2. Inverse Kinematics Problem for Parallel Robots
- The velocity-based theory of linear transformations used by [11] allows determining the mobility of arbitrary parallel robots. The linear transformation is generalized in [12] to accuracy and stiffness modeling by means of screw theory resulting in the “generalized Jacobian”. Both concepts are similar to (10) and do not provide a direct appliance to solve the IKP, since this requires a formulation of the orientation at position level, not velocity level.
- Exploiting the reduction of end-effector coordinates for 3T2R tasks is not possible, since all end-effector coordinates are included in (7).
3. Reciprocal Sets of Euler Angles for the Kinematics of a Serial Leg Chain
4. Full Kinematic Constraints for Parallel Robots Using Reciprocal Sets of Euler Angles
5. Differential Kinematics for Parallel Robots
5.1. Constraint Gradients for the Leading Leg of the 3T2R and All Legs of the 3T3R Case
5.2. Constraint Gradients for the Following Leg in the 3T2R Case
5.3. Gradient-Based Solution of the Inverse Kinematics Problem with Redundancy Resolution
5.4. Differential Kinematics for the Parallel Robot and Its Applications
6. Results
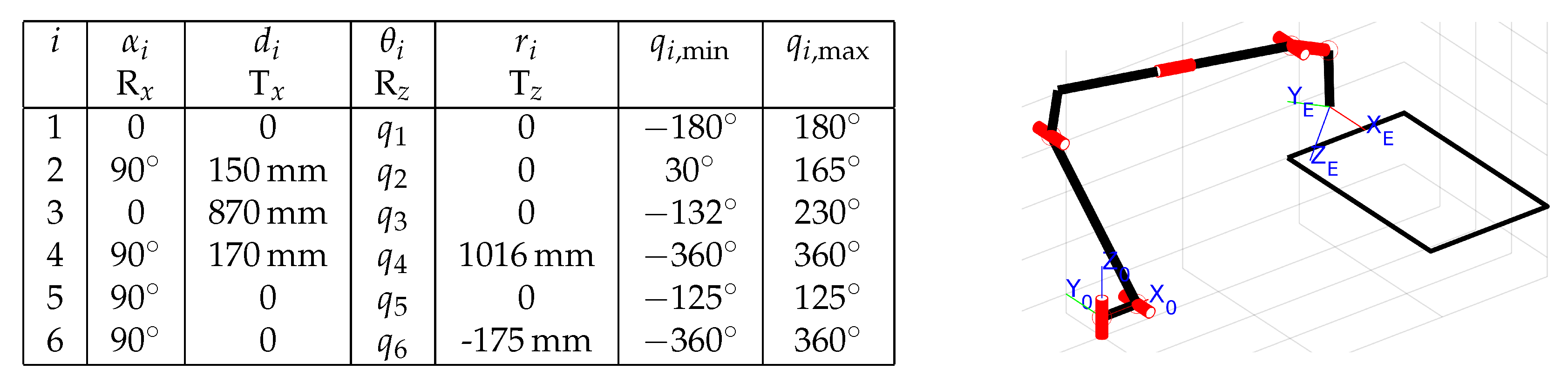
6.1. Resolution of Functional Redundancy of a Serial-Link Six-DoF Robot in 3T2R tasks
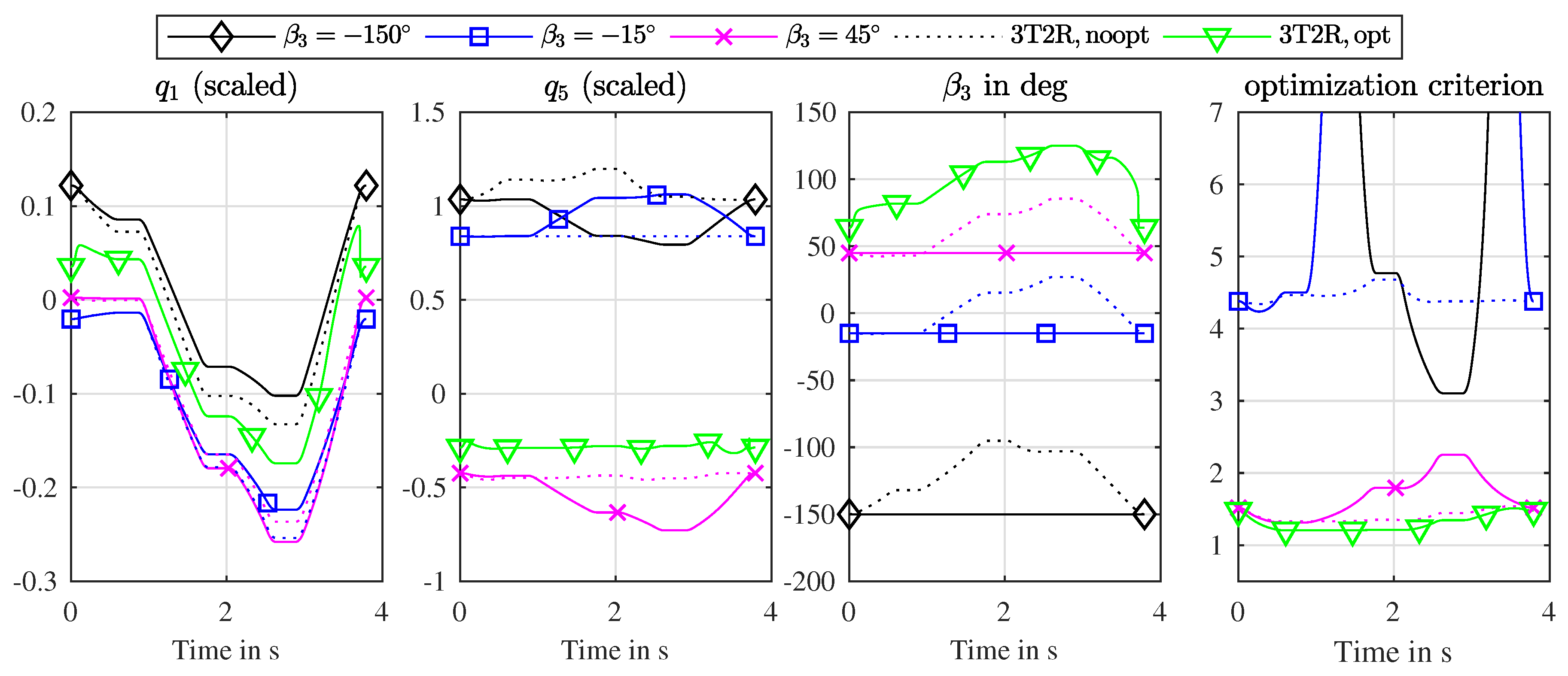
6.2. Resolution of Functional Redundancy of a Parallel Robot in 3T2R Tasks
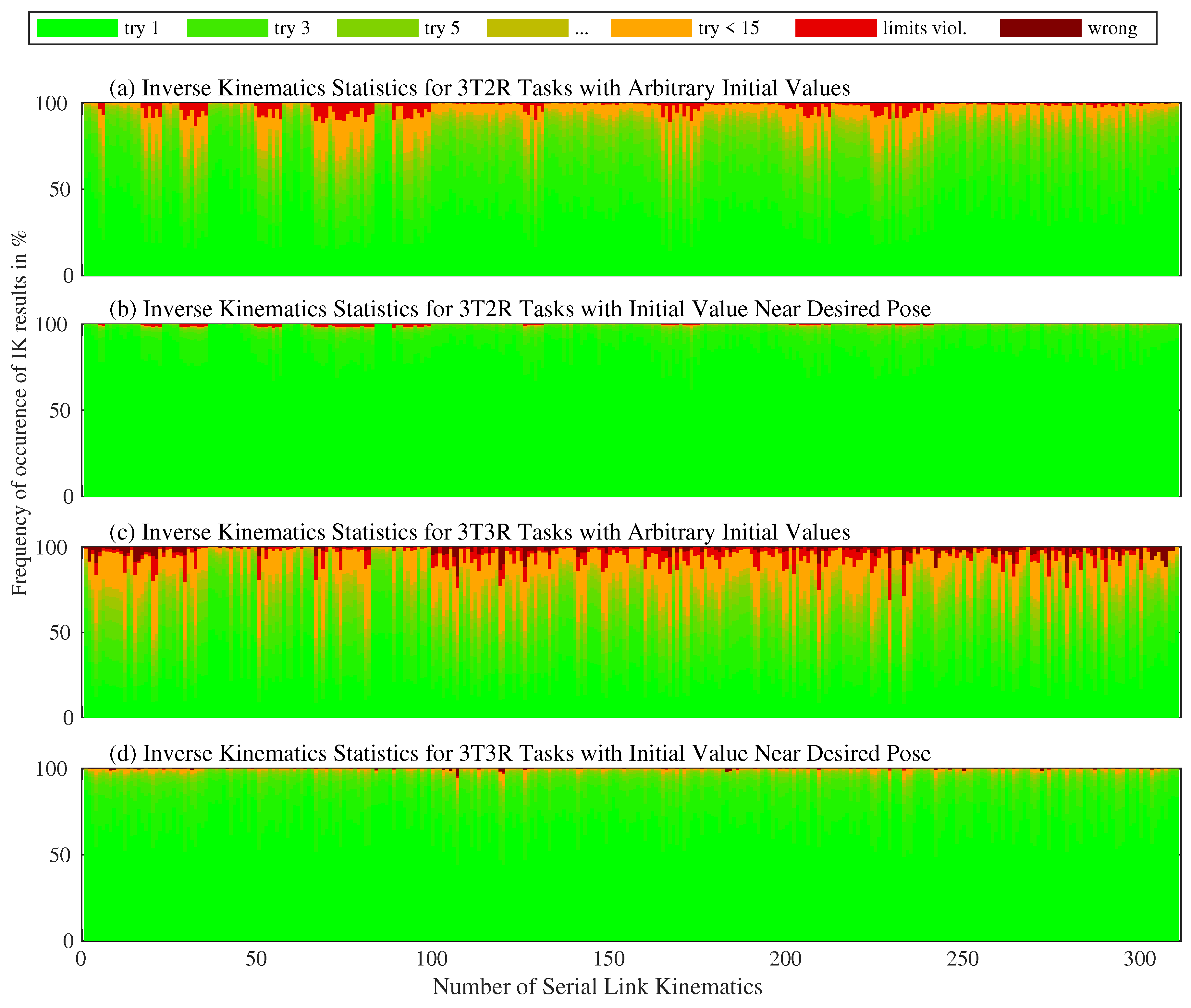
6.3. Statistic Results for the Inverse Kinematics of Serial Link Chains
7. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PKM | parallel kinematic machine (parallel robot) |
| IKP | inverse kinematics problem |
| DoF | degrees of freedom |
| xTyR | x translational and y rotational degrees of freedom |
Appendix A. Mathematical Symbols for Reciprocal Euler Angles in Inverse Kinematics
Appendix A.1. Proof for the Properties of Reciprocal Euler Angles
Appendix A.2. Relation of the Geometric Jacobian and the Partial Derivative of the Rotation Matrix
Appendix A.3. Relation of the Inverse- and Direct-Kinematics Matrices to the Analytic Jacobian
Appendix A.4. Matrix Operations for Partial Derivatives
Appendix A.5. Contents of the Partial Derivatives
References
- Baron, L. A joint-limits avoidance strategy for arc-welding robots. Presented at the International Conference on Integrated Design and Manufacturing in Mechanical Engineering, Montreal, QC, Canada, 16–19 May 2000; note: the paper is not part of the conference proceedings published by Springer. Available online: https://www.researchgate.net/profile/Luc_Baron (accessed on 2 August 2019).
- Huo, L.; Baron, L. Kinematic inversion of functionally-redundant serial manipulators: Application to arc-welding. Trans. Can. Soc. Mech. Eng. 2005, 29, 679–690. [Google Scholar] [CrossRef]
- Žlajpah, L. On orientation control of functional redundant robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2475–2482. [Google Scholar] [CrossRef]
- Léger, J.; Angeles, J. Off-line programming of six-axis robots for optimum five-dimensional tasks. Mech. Mach. Theory 2016, 100, 155–169. [Google Scholar] [CrossRef]
- Schappler, M.; Tappe, S.; Ortmaier, T. Resolution of Functional Redundancy for 3T2R Robot Tasks using Two Sets of Reciprocal Euler Angles. In Advances in Mechanism and Machine Science, Proceedings of the 15th IFToMM World Congress on Mechanism and Machine Science, Kraków, Poland, 30 June–4 July 2019; Springer: Berlin, Germany, 2019; Volume 73, pp. 1701–1710. [Google Scholar] [CrossRef]
- Yoshikawa, T. Analysis and control of robot manipulators with redundancy. In Robotics Research: The 1st International Symposium; MIT Press: Cambridge, MA, USA, 1984; pp. 735–747. ISBN 0262022079. [Google Scholar]
- Goldenberg, A.; Benhabib, B.; Fenton, R. A complete generalized solution to the inverse kinematics of robots. IEEE J. Robot. Autom. 1985, 1, 14–20. [Google Scholar] [CrossRef]
- Zhu, W.; Qu, W.; Cao, L.; Yang, D.; Ke, Y. An off-line programming system for robotic drilling in aerospace manufacturing. Int. J. Adv. Manuf. Technol. 2013, 68, 2535–2545. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, H.; Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robot. Comput. Integr. Manuf. 2015, 27, 367–376. [Google Scholar] [CrossRef]
- Tale-Masouleh, M.; Gosselin, C. Singularity analysis of 5-RPUR parallel mechanisms (3T2R). Int. J. Adv. Manuf. Technol. 2011, 57, 1107–1121. [Google Scholar] [CrossRef]
- Gogu, G. Solid Mechanics and Its Applications. In Structural Synthesis of Parallel Robots, Part 1: Methodology; Springer: Berlin, Germany, 2008; Volume 866. [Google Scholar]
- Huang, T.; Liu, H.; Chetwynd, D. Generalized Jacobian analysis of lower mobility manipulators. Mech. Mach. Theory 2011, 46, 831–844. [Google Scholar] [CrossRef]
- Merlet, J.P.; Perng, M.W.; Daney, D. Optimal trajectory planning of a 5-axis machine-tool based on a 6-axis parallel manipulator. In Advances in Robot Kinematics; Springer: Berlin, Germany, 2000; pp. 315–322. [Google Scholar] [CrossRef]
- Hong, K.S.; Kim, J.G. Manipulability analysis of a parallel machine tool: application to optimal link length design. J. Robot. Syst. 2000, 17, 403–415. [Google Scholar] [CrossRef]
- Merlet, J.P. Solid mechanics and its applications. In Parallel Robots, 2nd ed.; Springer: Berlin, Germany, 2006; Volume 128. [Google Scholar]
- Zhang, D. Parallel Robotic Machine Tools; Springer: Berlin, Germany, 2009. [Google Scholar]
- Wang, J.; Gosselin, C.M. Kinematic analysis and singularity representation of spatial five-degree-of-freedom parallel mechanisms. J. Robot. Syst. 1997, 14, 851–869. [Google Scholar] [CrossRef]
- Zhang, D.; Gosselin, C.M. Kinetostatic modeling of N-DOF parallel mechanisms with a passive constraining leg and prismatic actuators. J. Mech. Des. 2001, 123, 375–381. [Google Scholar] [CrossRef]
- Zheng, K.J.; Gao, J.S.; Zhao, Y.S. Path control algorithms of a novel 5-DOF parallel machine tool. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; Volume 3, pp. 1381–1385. [Google Scholar] [CrossRef]
- Gao, J.S.; Sun, H.; Zhao, Y.S. The primary calibration research of a measuring limb in 5-UPS/PRPU parallel machine tool. In Proceedings of the IEEE International Conference on Intelligent Mechatronics and Automation, Chengdu, China, 26–31 August 2004; pp. 304–308. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Yao, J.; Xu, J.; Wen, S.; Zhao, Y. Control-faced dynamics with deformation compatibility for a 5-DOF active over-constrained spatial parallel manipulator 6PUS–UPU. Mechatronics 2015, 30, 107–115. [Google Scholar] [CrossRef]
- Wen, S.; Qin, G.; Zhang, B.; Lam, H.K.; Zhao, Y.; Wang, H. The study of model predictive control algorithm based on the force/position control scheme of the 5-DOF redundant actuation parallel robot. Robot. Auton. Syst. 2016, 79, 12–25. [Google Scholar] [CrossRef]
- Mbarek, T.; Nefzi, M.; Corves, B. Prototypische Entwicklung und Konstruktion eines neuartigen Parallelmanipulators mit dem Freiheitsgrad fünf. VDI-Berichte 1892 2005. Available online: https://www.igmr.rwth-aachen.de/index.php/en/rob-en/rob-pentapod-en (accessed on 20 June 2019). (In German).
- Schreiber, H.; Gosselin, C. Analyse et conception d’un manipulateur parallèle spatial à cinq degrés de liberté. In French. Mech. Mach. Theory 2003, 38, 535–548. [Google Scholar] [CrossRef]
- Gao, F.; Peng, B.; Zhao, H.; Li, W. A novel 5-DOF fully parallel kinematic machine tool. Int. J. Adv. Manuf. Technol. 2006, 31, 201. [Google Scholar] [CrossRef]
- Bär, G.F.; Weiß, G. Kinematic Analysis of a Pentapod Robot. J. Geometry Graph. 2006, 10, 173–182. [Google Scholar]
- Lin, W.; Li, B.; Yang, X.; Zhang, D. Modelling and control of inverse dynamics for a 5-DOF parallel kinematic polishing machine. Int. J. Adv. Robot. Syst. 2013, 10, 314. [Google Scholar] [CrossRef]
- Alagheband, A.; Mahmoodi, M.; Mills, J.K.; Benhabib, B. Comparative analysis of a redundant pentapod parallel kinematic machine. J. Mech. Robot. 2015, 7, 034502. [Google Scholar] [CrossRef]
- Gogu, G. Fully-isotropic parallel manipulators with five degrees of freedom. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1141–1146. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Q.C. General Methodology for Type Synthesis of Symmetrical Lower-Mobility Parallel Manipulators and Several Novel Manipulators. Int. J. Robot. Res. 2002, 21, 131–145. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type synthesis of 5-DOF parallel manipulators based on screw theory. J. Robot. Syst. 2005, 22, 535–547. [Google Scholar] [CrossRef]
- Tale-Masouleh, M.; Saadatzi, M.H.; Gosselin, C.; Taghirad, H.D. A geometric constructive approach for the workspace analysis of symmetrical 5-PRUR parallel mechanisms (3T2R). In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; pp. 1335–1344. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, H.; Zhao, Y. Analysis and experimental investigation of parallel machine tool with redundant actuation. In Intelligent Robotics and Applications, Proceedings of the International Conference on Intelligent Robotics and Applications, Wuhan, China, 15–17 October 2008; Springer: Berin, Germany, 2008; pp. 179–188. [Google Scholar] [CrossRef]
- Ramirez, D.; Kotlarski, J.; Ortmaier, T. Automatic generation of a minimal set of serial mechanisms for a combined structural—Geometrical synthesis. In Proceedings of the 14th IFToMM World Congress, Taipeh, Taiwan, 25–30 October 2015. [Google Scholar] [CrossRef]
- Briot, S.; Khalil, W. Dynamics of Parallel Robots; Springer: Berlin, Germany, 2015. [Google Scholar]
- Huo, L.; Baron, L. The joint-limits and singularity avoidance in robotic welding. Ind. Robot. 2008, 35, 456–464. [Google Scholar] [CrossRef]





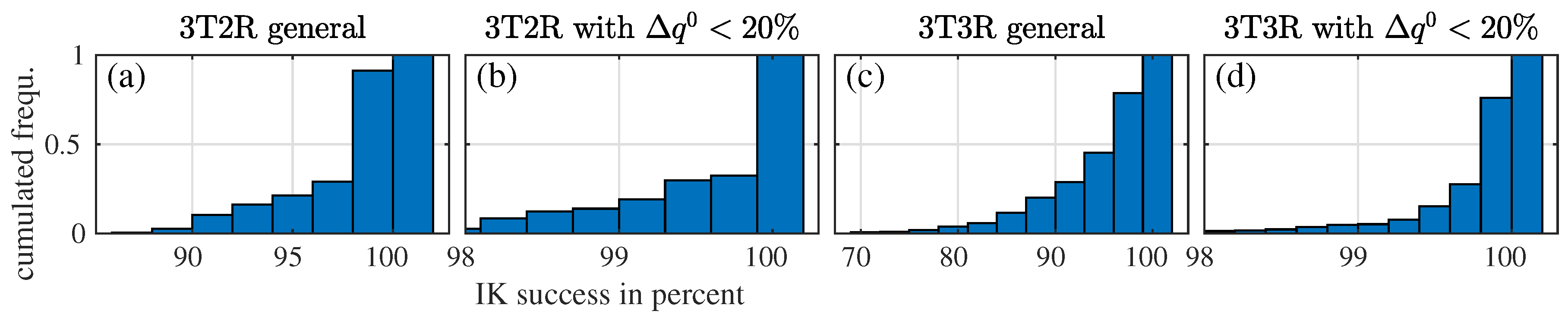
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schappler, M.; Tappe, S.; Ortmaier, T. Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles. Robotics 2019, 8, 68. https://doi.org/10.3390/robotics8030068
Schappler M, Tappe S, Ortmaier T. Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles. Robotics. 2019; 8(3):68. https://doi.org/10.3390/robotics8030068
Chicago/Turabian StyleSchappler, Moritz, Svenja Tappe, and Tobias Ortmaier. 2019. "Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles" Robotics 8, no. 3: 68. https://doi.org/10.3390/robotics8030068
APA StyleSchappler, M., Tappe, S., & Ortmaier, T. (2019). Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles. Robotics, 8(3), 68. https://doi.org/10.3390/robotics8030068




