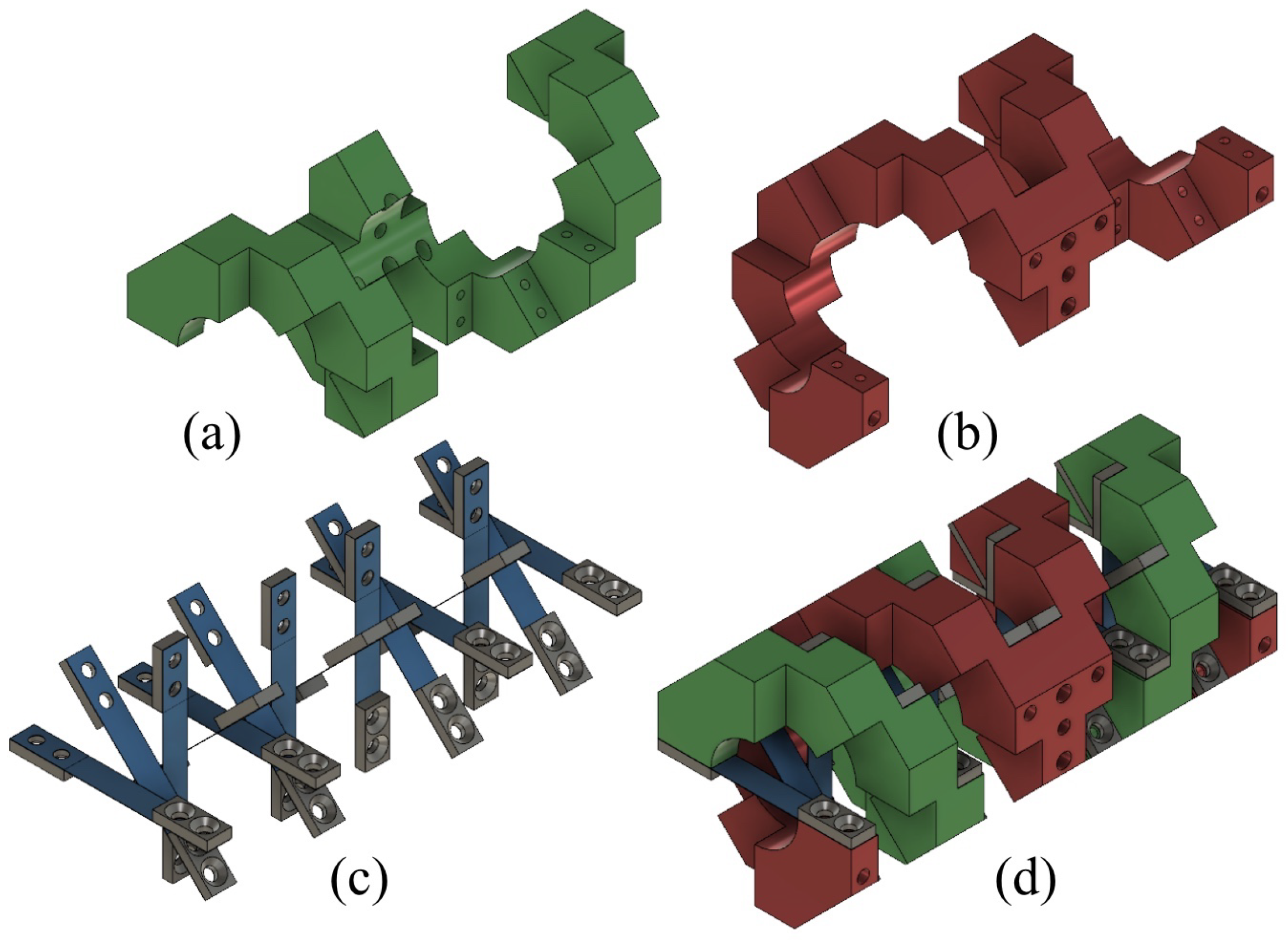
This section describes the design of the SMA component and the DHCJ in combination as a special compliant SMA actuator. The idea is to keep the size compact, by replacing some leaf springs of the DHCJ with SMA, and without increasing the external mass of the system. When no power is applied to the system, the actuator behaves as a passive compliant joint. When the proper energy in applied to it, the actuator transforms from a passive to an active component. The modeling and the idea of this conceptual design are shown.
3.1. Modeling of the SMA Leaf
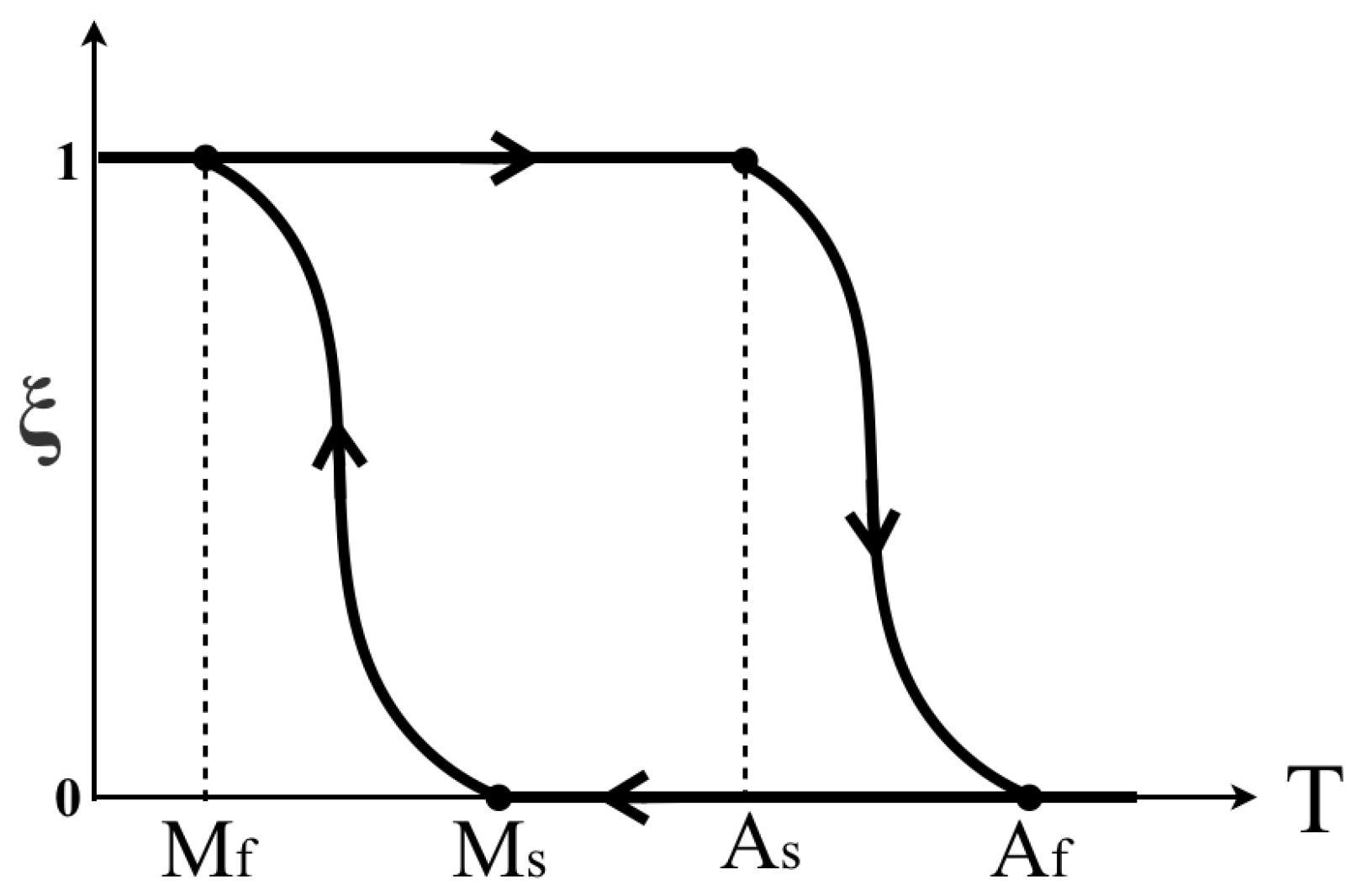
SMA is a special material whose phase changes when the proper heat is applied to it. At the low-temperature or martensite phase (
M), the crystalline structure of an SMA is quite flexible and can be easily deformed into new shapes when force is applied. Upon heating, the crystalline structure returns to a memorized configuration in austenite phase (
A). The transformation of
A to
M and
M to
A are characterized by four temperatures:
and
are the start and finish temperatures, respectively, for the A phase;
and
are the start and finish temperature, respectively, for the
M phase. The phase transformation curve can be expressed in terms of a martensite fraction,
. The martensite fraction is bounded between 0 (fully austenite) and 1 (fully martensite) as shown in
Figure 6. As seen in the phase transformation, SMAs show significant hysteresis during the two transformations. Many studies show that the behavior of SMA depends not only on temperature, but also on the stress acting on it. At any value of stress or temperature, the material can be in one of three states: fully martensite, fully austenite, or a mixture of austenite and martensite. The phase transformation of the SMA can be expressed as
where
and
, are material constants.
T is the applied temperature,
is the pre-stress, and
and
are the slope of the stress and transformation temperature from experimental data.
For simplicity, for the first prototype, the one-dimensional constitutive model from Liang and Roger [
12] was used to describe the SMA behavior as shown in Equation (
2).
where
and
represent the stress and the pre-stress of the SMA actuator;
E is the Young’s modulus and
and
are the current and initial strain;
and
are the current and initial value of martensite fraction and
is the transformation coefficient of the material constant. The coefficient can be obtained from the residual strain and modulus of elasticity as
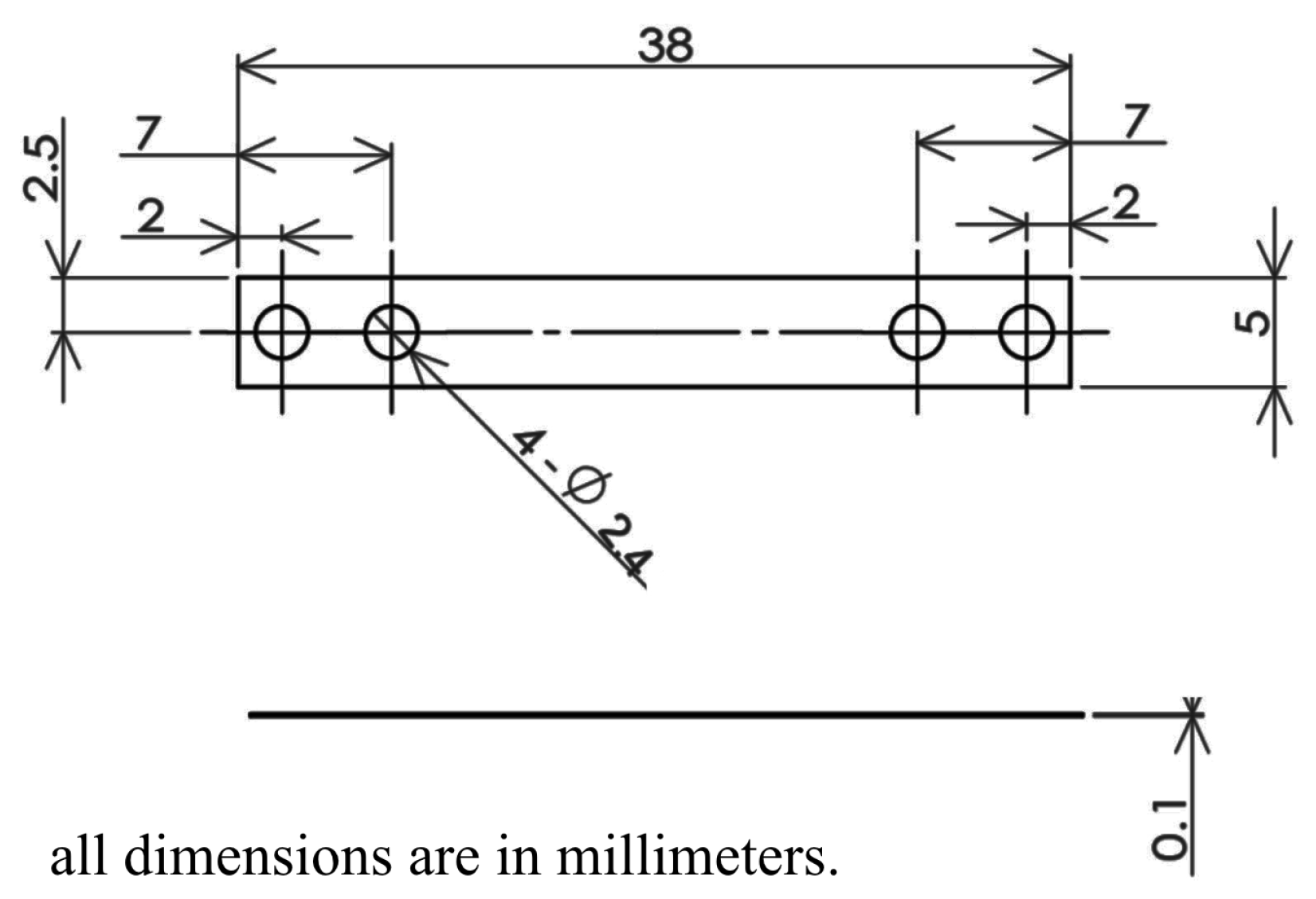
. From this equation, when SMA changes its phase from martensite to austenite, the strain changes because of the SMA motion. The change from the right-hand side of the equation causes the SMA to generate stress which turn induces force and torque to the system. In this research, the SMA strip type was designed in a similar shape as the leaf spring in DHCJ as shown in
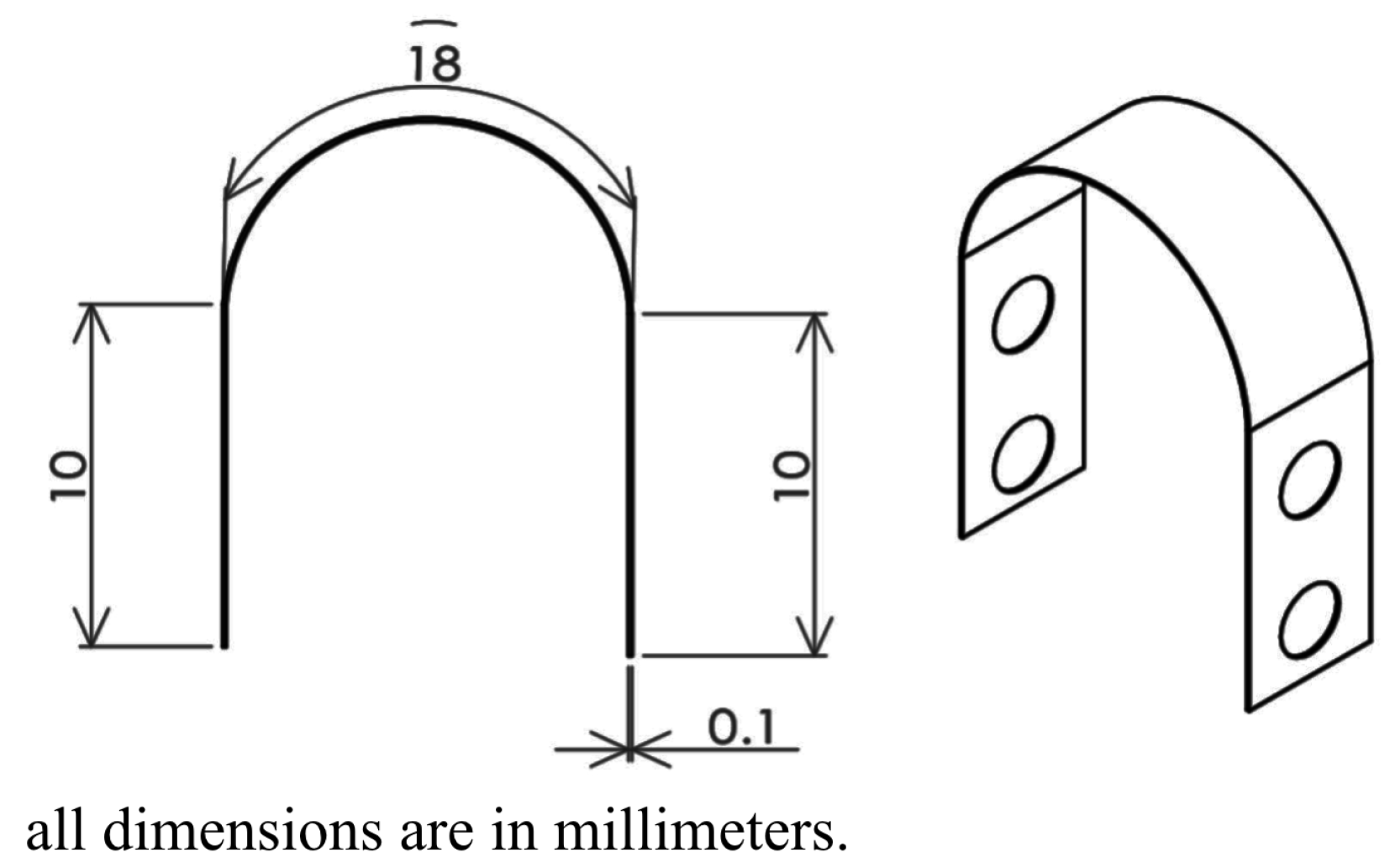
Figure 7. The memorized shape (austenite phase shape) was set as a U-shape as shown in
Figure 8. The material composition of the SMA using in this research is NiTi-Cu with
of Ni,
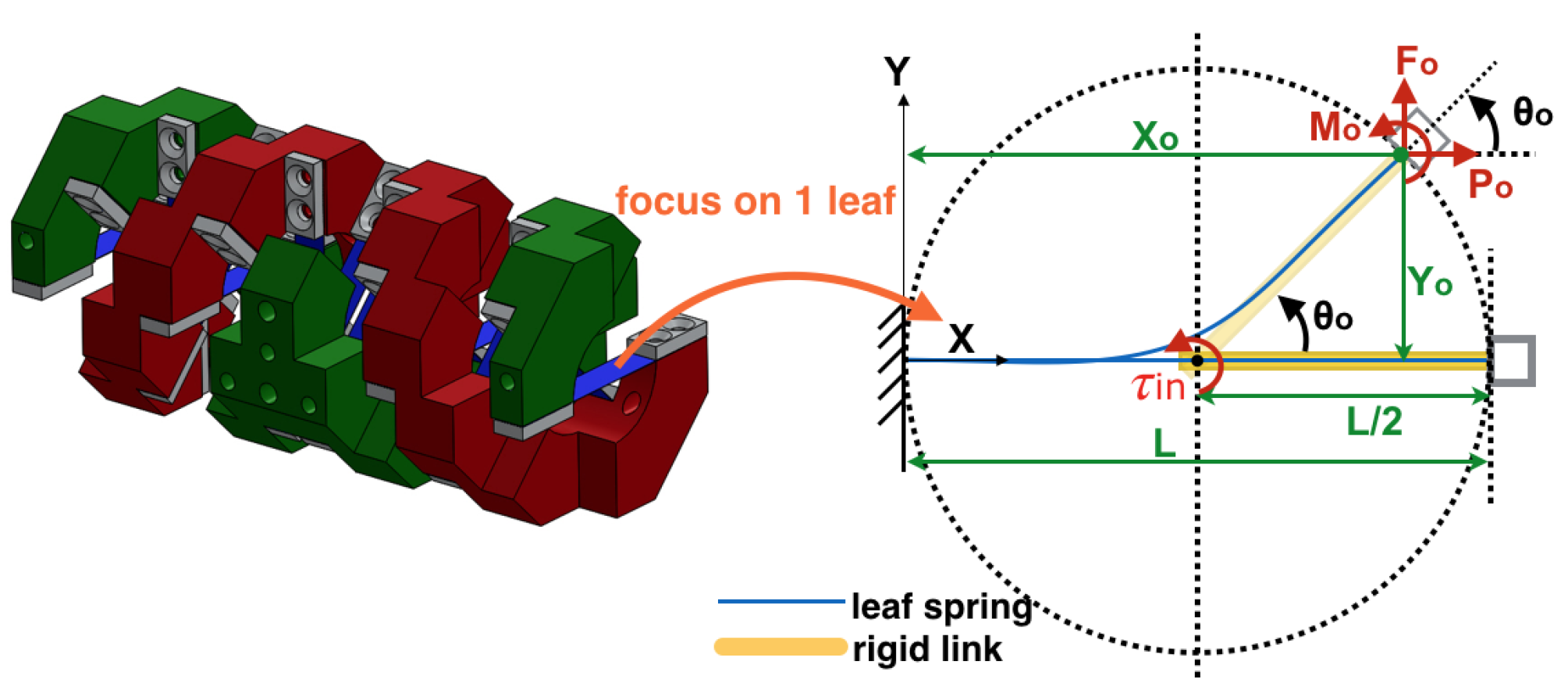
of Cu and the remaining of Ti. Considering a single leaf, with one end was fixed and the other end was bent in a circular path, the forward kinematics transforms the deflection angle
to strain
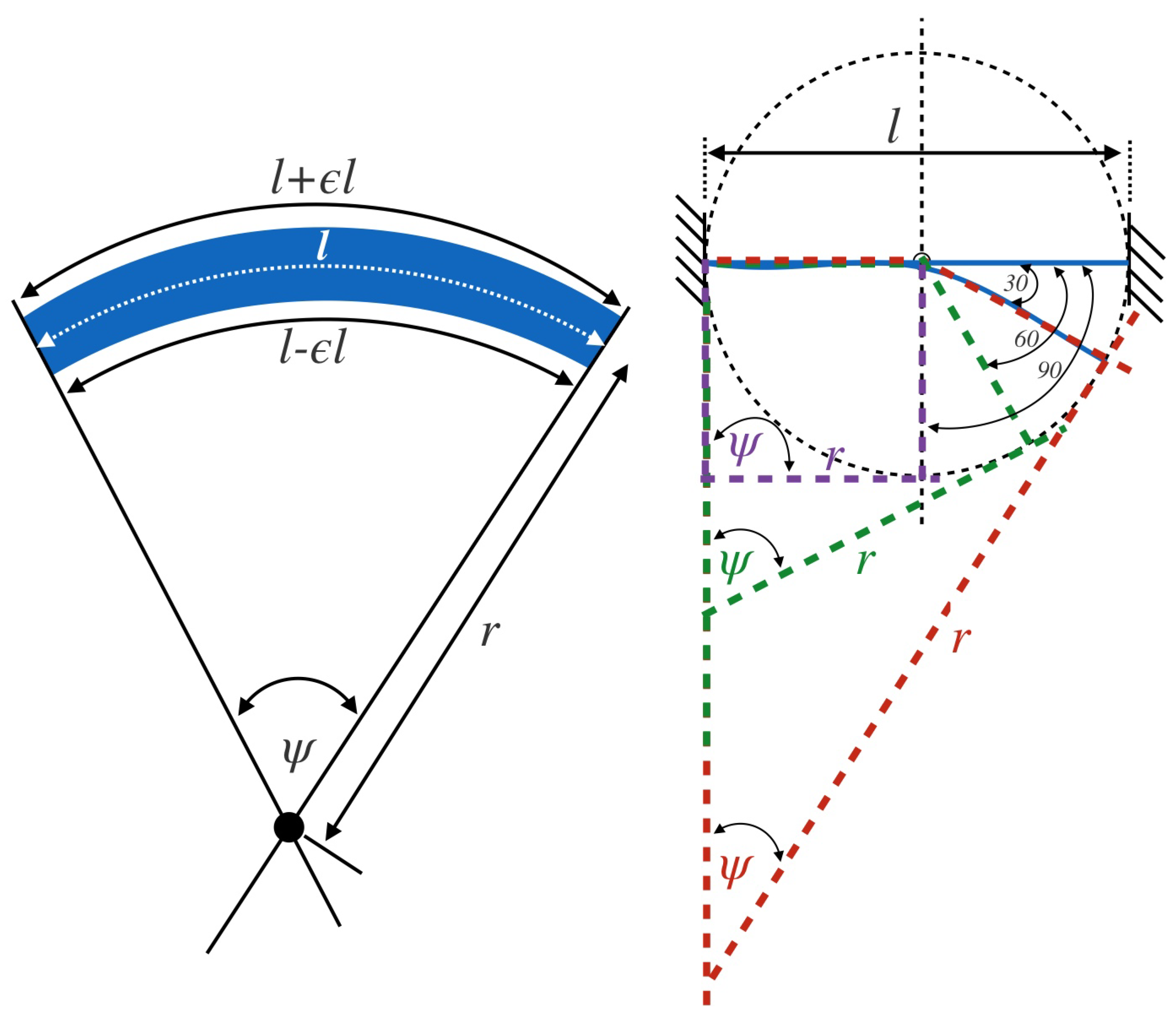
by considering the arc shape as shown in
Figure 9. When the SMA leaf bends into each angle, the deflection angle
is equal to arc angle
, so the strain can be expressed in term of deflection angle as
where
t is the leaf’s thickness,
l is the leaf’s length,
is the arc angle (where
) and
r is the radius of curvature, where
.
In the robotics field, the proper way to energize the SMA is to use electrical power, Ramio and Edwin [
2] proposed a classical differential equation that expresses the heat store in SMA as
where
is the density of the SMA,
C is the specific heat,
V is the volume of the SMA,
i is the electrical current,
R is the elements electrical resistance,
h is the heat-exchange coefficient between the SMA and the surrounding air,
A is the surface area of the SMA,
is the environmental temperature and
T is the SMA temperature at time
t.
When electrical current is applied to the SMA leaf, it can generate a bending moment, which can be considered as generated torque
from the SMA. The equation of rotational motion can be expressed as
where
J is the moment of inertia,
D is the damping coefficient,
k is the rotational stiffness and
is the deflection angle.
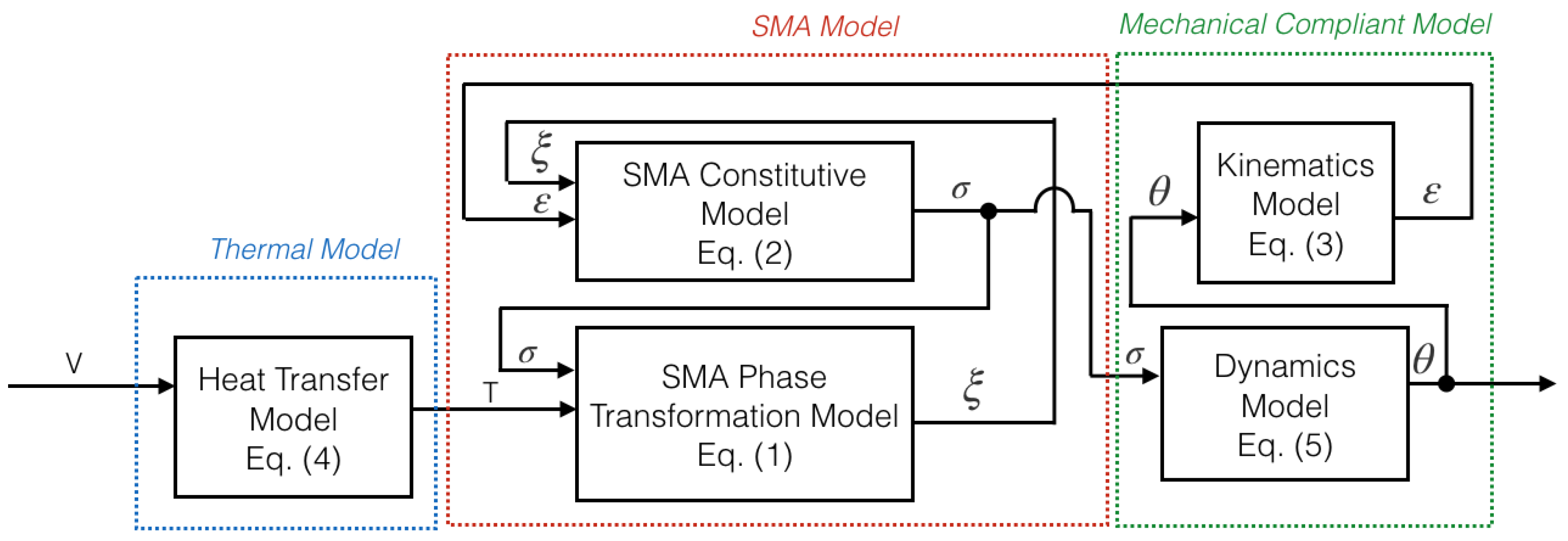
By combining each elements as proposed previously, the overall block diagram of the SMA driven compliant actuator is as shown in
Figure 10. First, the proper voltage was applied to the SMA strip; then from the heat transfer model of Equation (
4), the heat changes the crystalline structure of the SMA from martensite (initial shape) to austenite state (memorized shape) as expressed in Equation (
1). Those changes induced the SMA to generate stress or torque on the system as expressed in Equation (
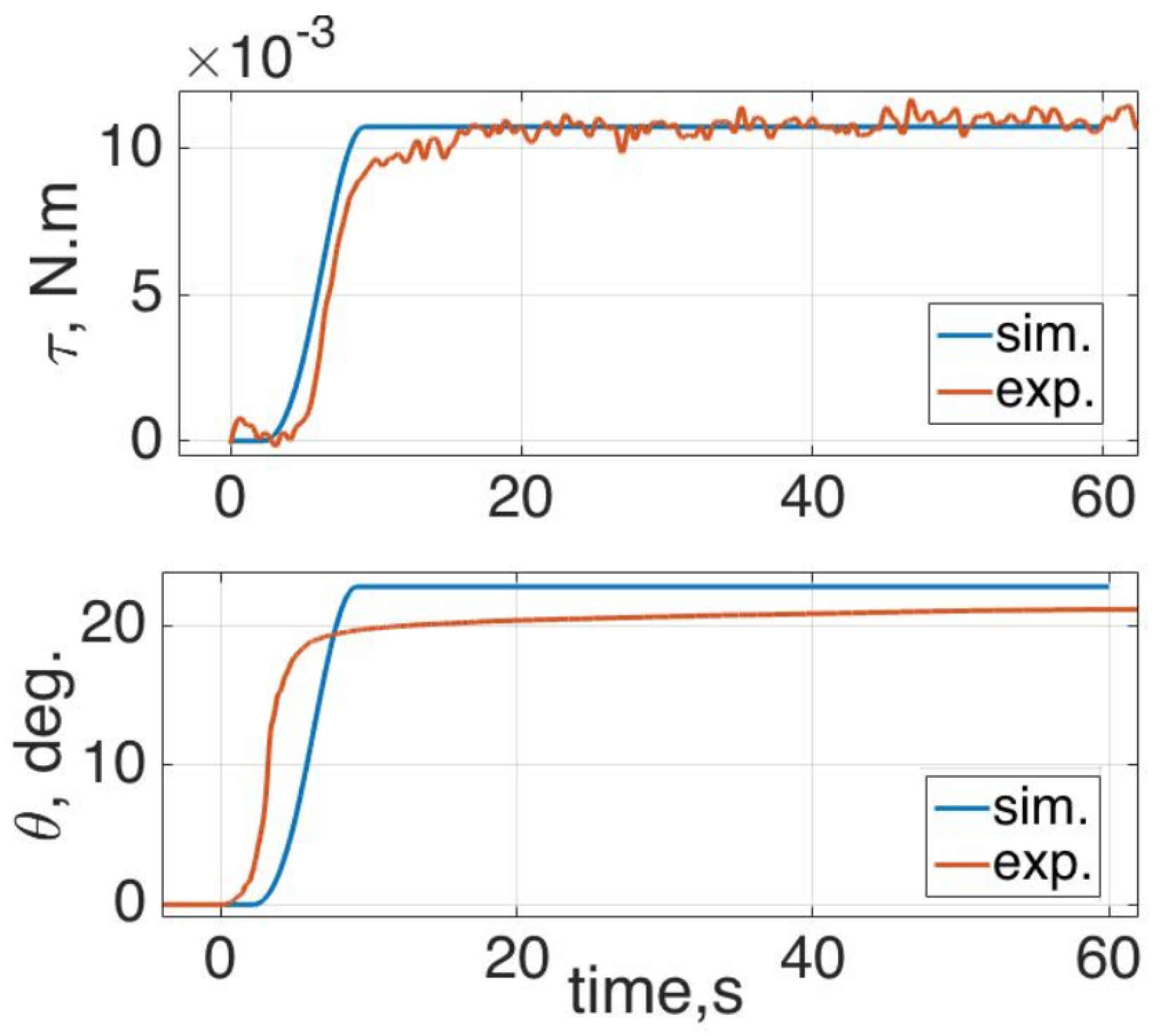
2). Because of the input torque, the mechanical system generated motion according to the dynamic parameters and yielded angular motion as the output. From this concept block diagram, the feed-forward controller is considered to evaluate the precision of the model from theory to practice.
3.2. Characteristics of a Single SMA Leaf
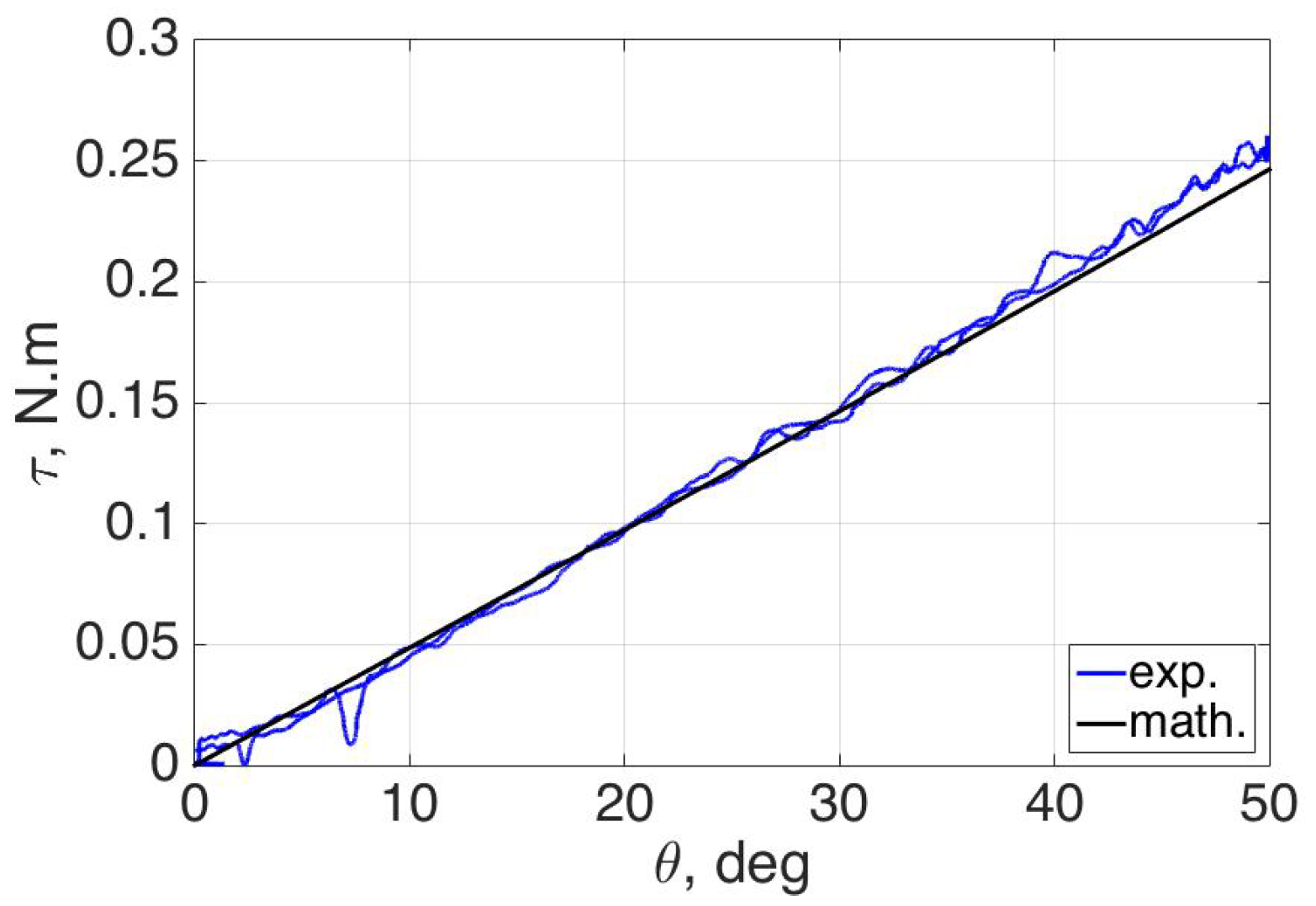
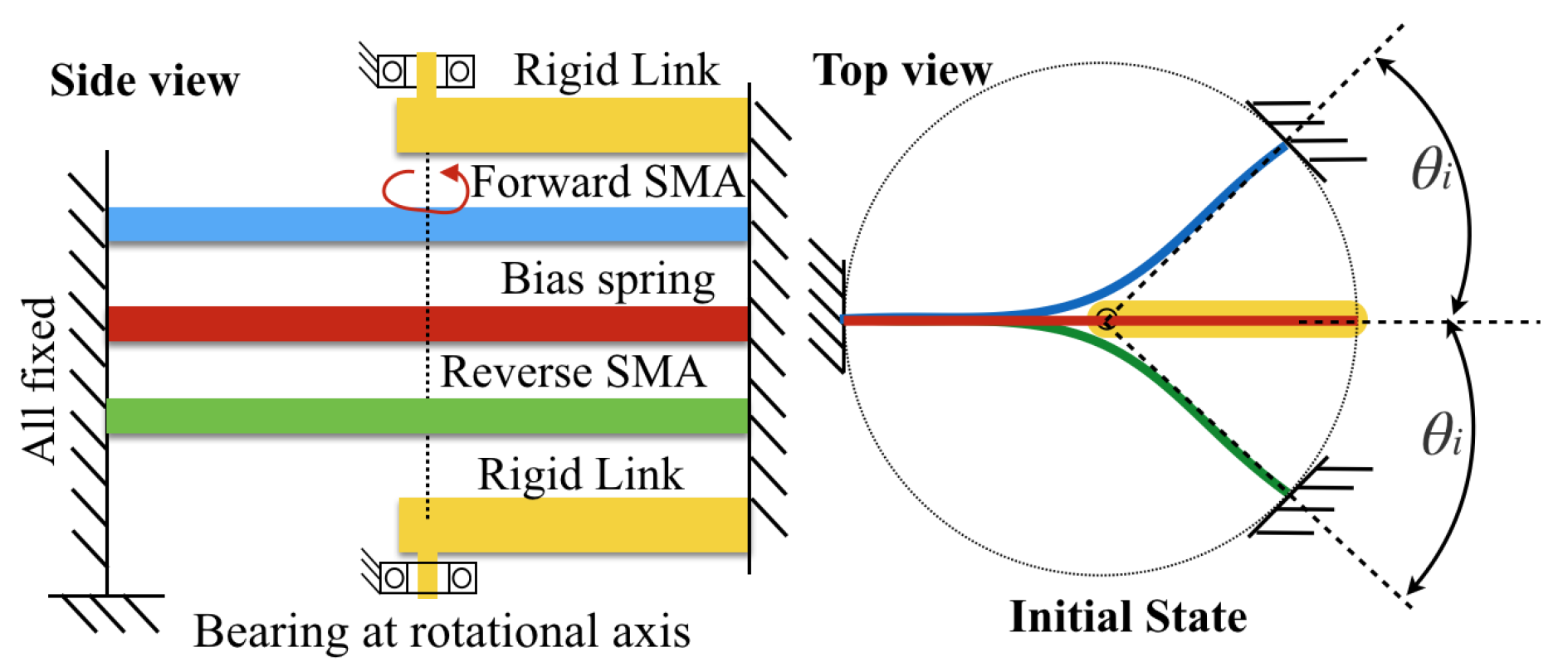
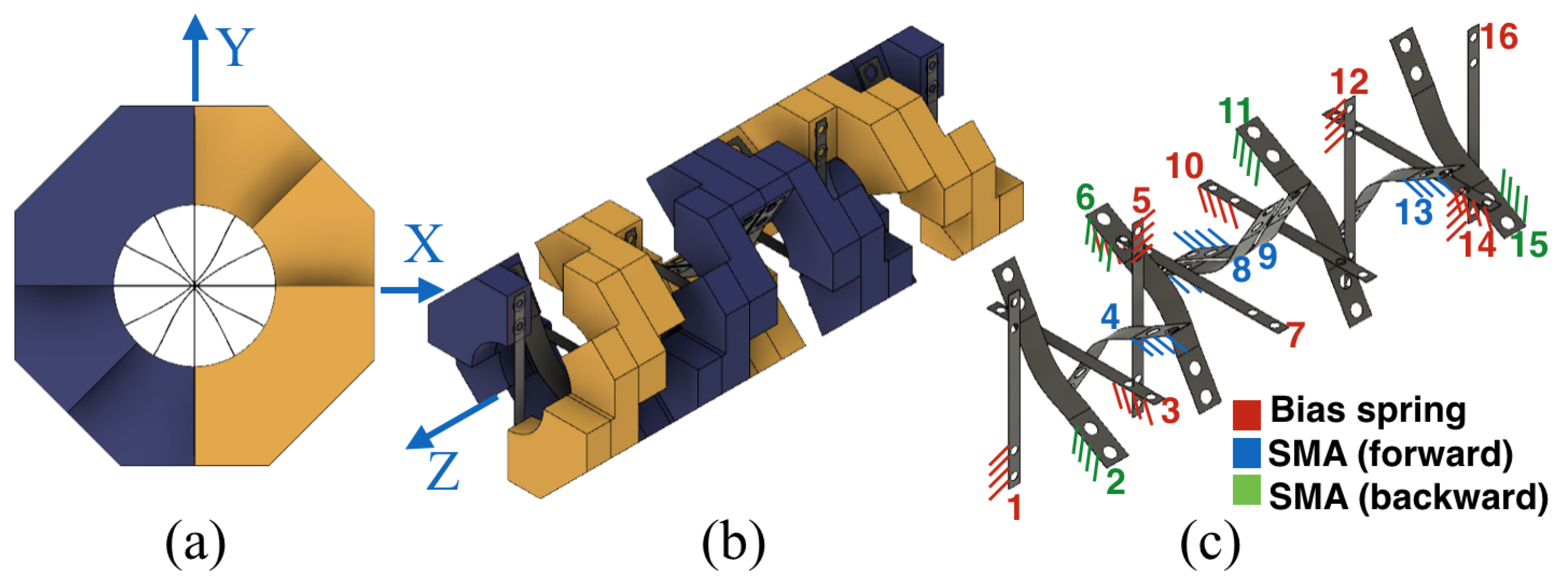
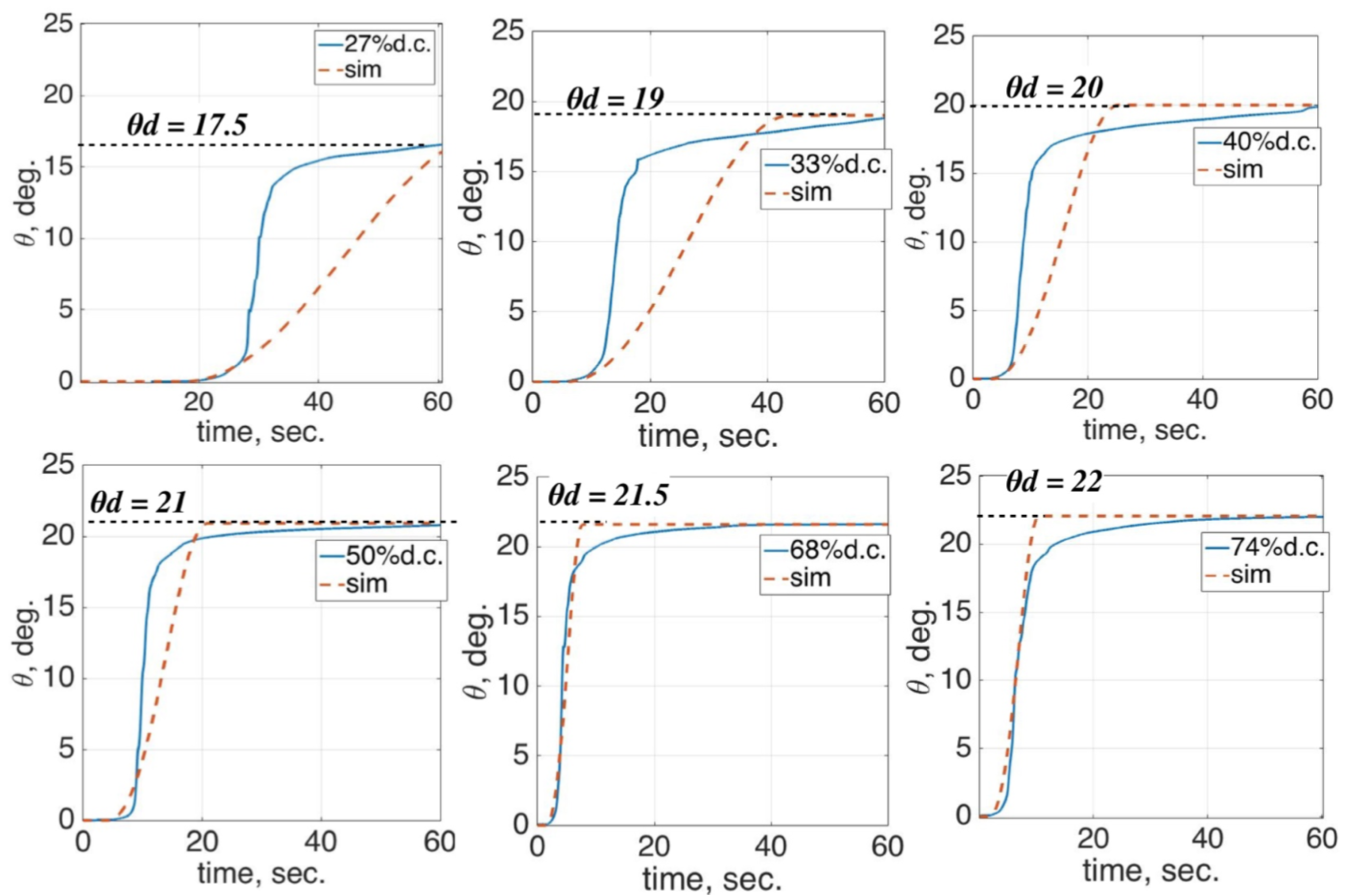
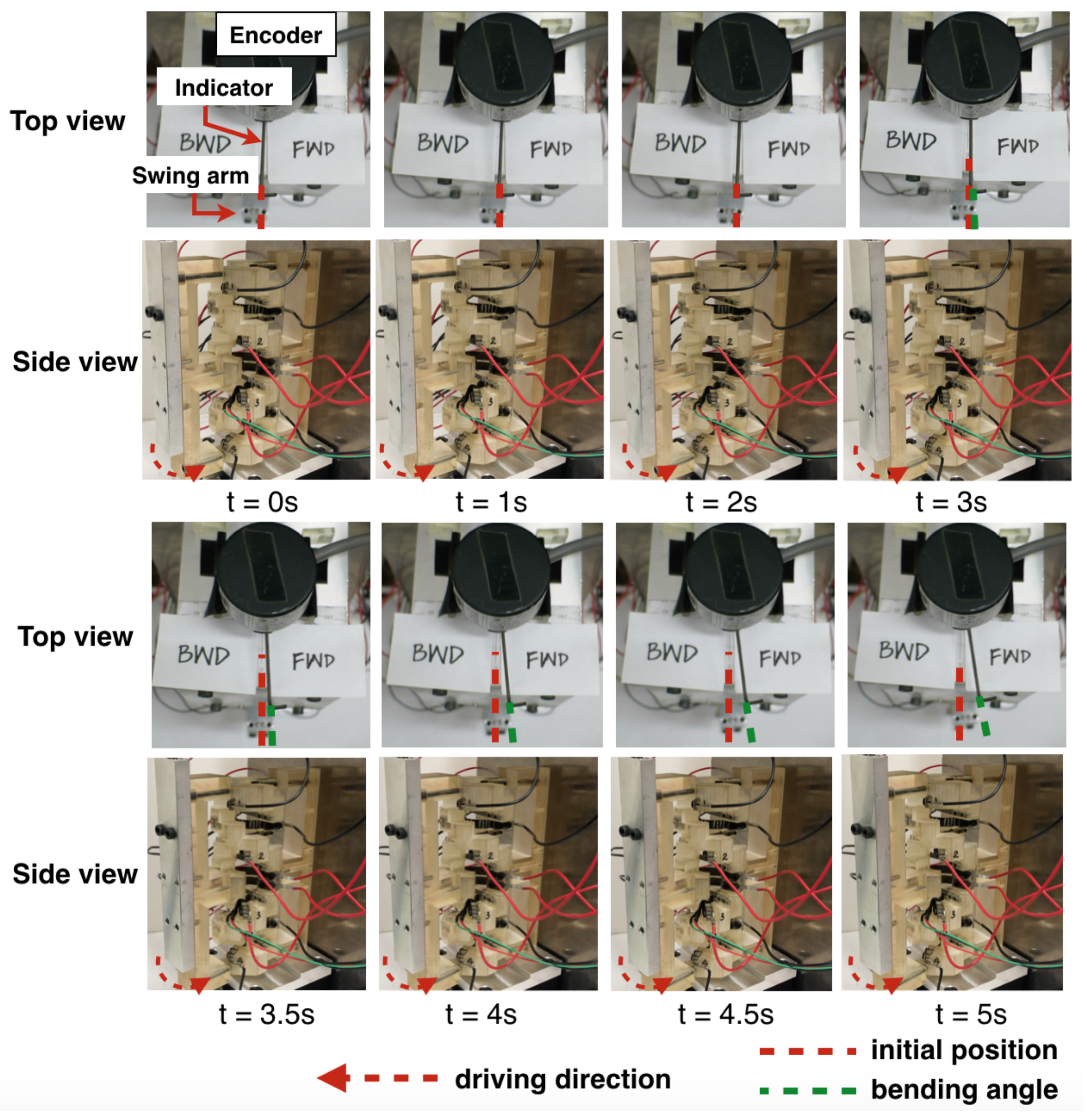
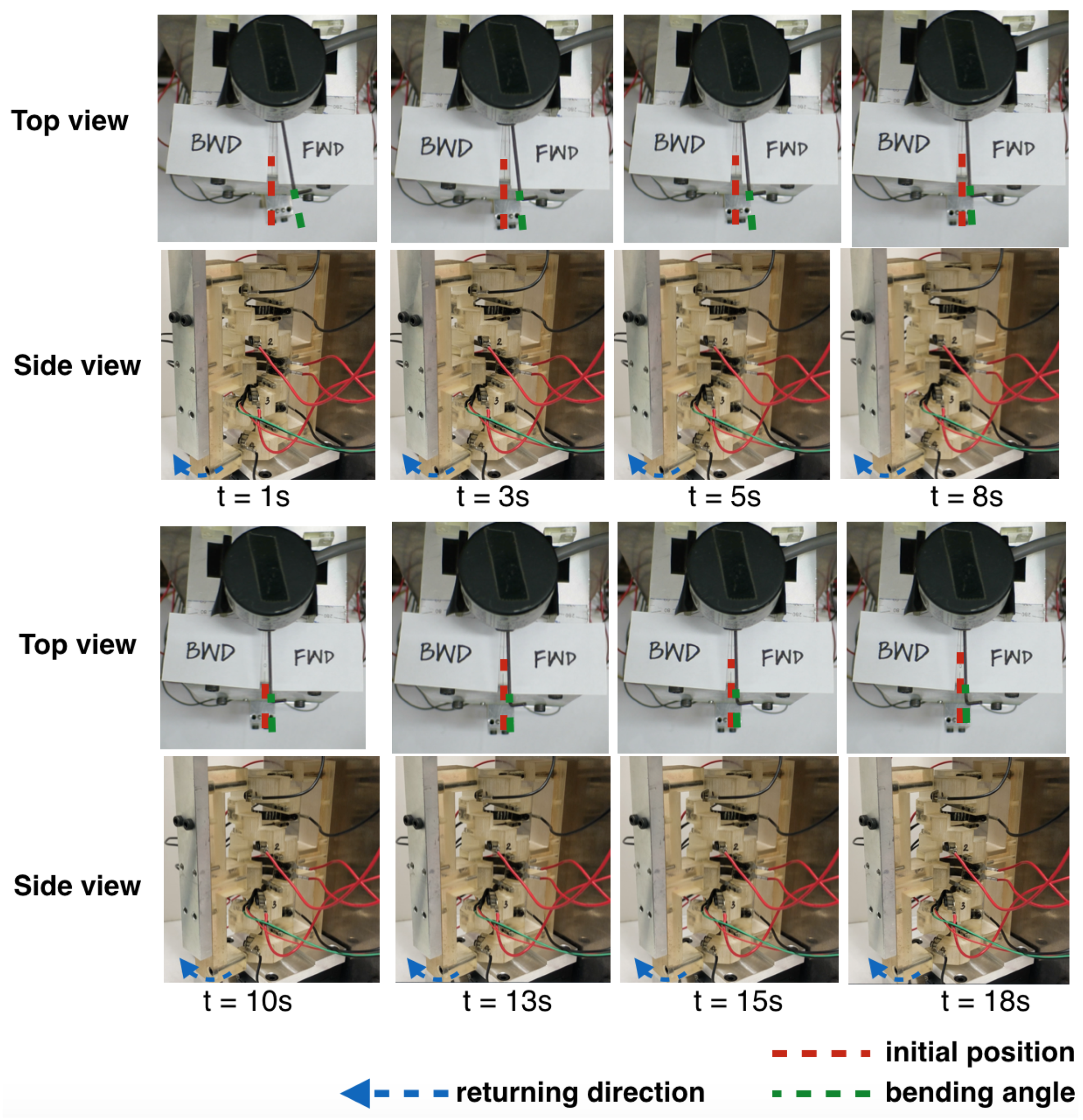
In order to understand the physical behavior of the SMA before combining it with the DHCJ frame, a single SMA leaf was tested to validate the model. A driver circuit and proper mechanical structure were also tested to validate the concept. The approximated kinematics of DHCJ with the SMA leaf and leaf spring are shown in
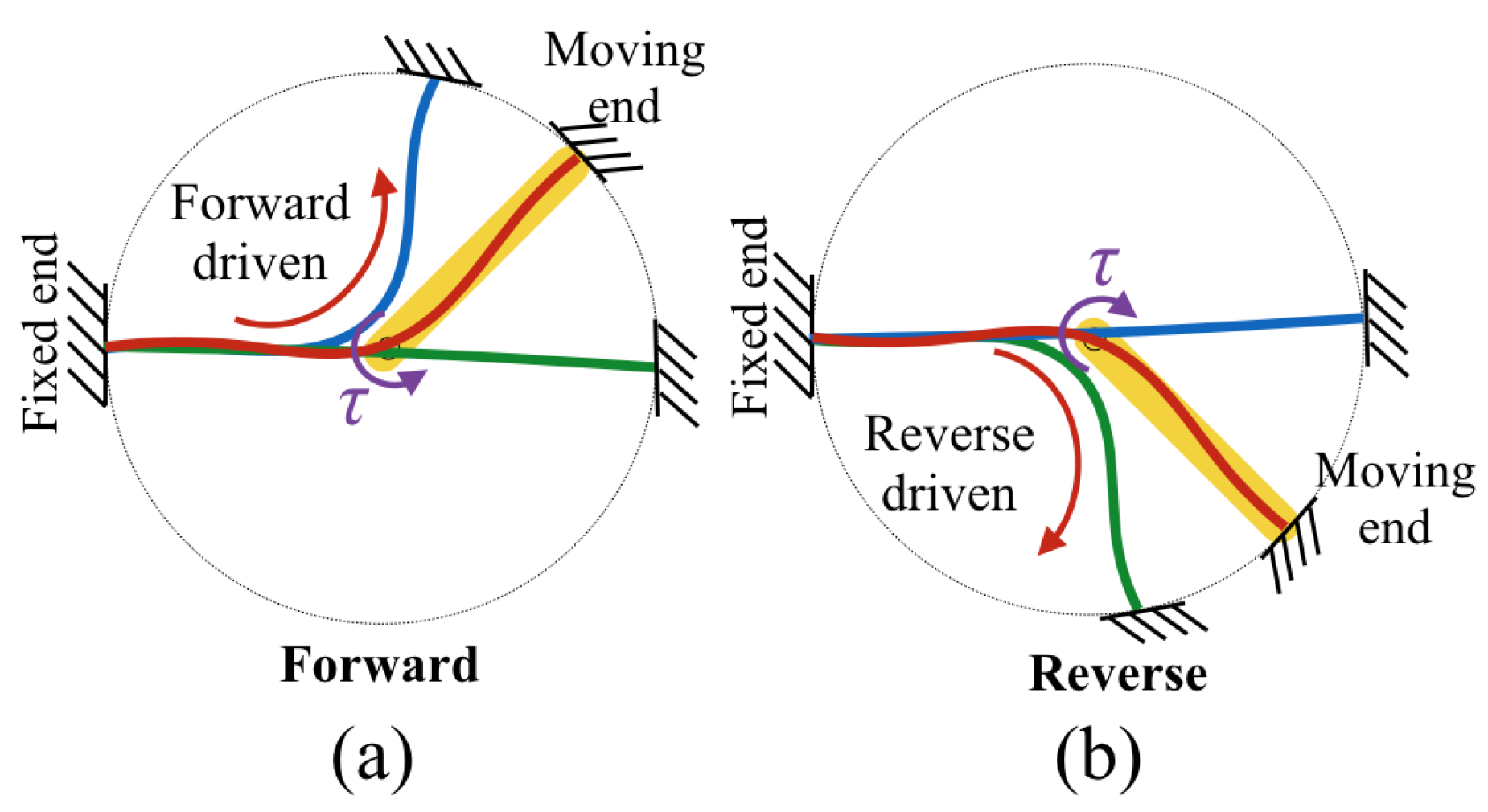
Figure 11. According to the DHCJ motion that can rotate in a circular path, the rigid link that acts as the radius arm is attached at the upper and lower parts. Two bearings are used to constrain the motion only around the principal axis. There are two SMA leaves for forward and reverse driving. A pre-bent angle was added to both leaves to avoid the beam buckling shape problem. When the SMA is energized at the forward side, the reverse SMA is bent to a straight shaped. Similarly, when the reverse SMA is energized, the forward SMA will become straight either as shown in
Figure 12.
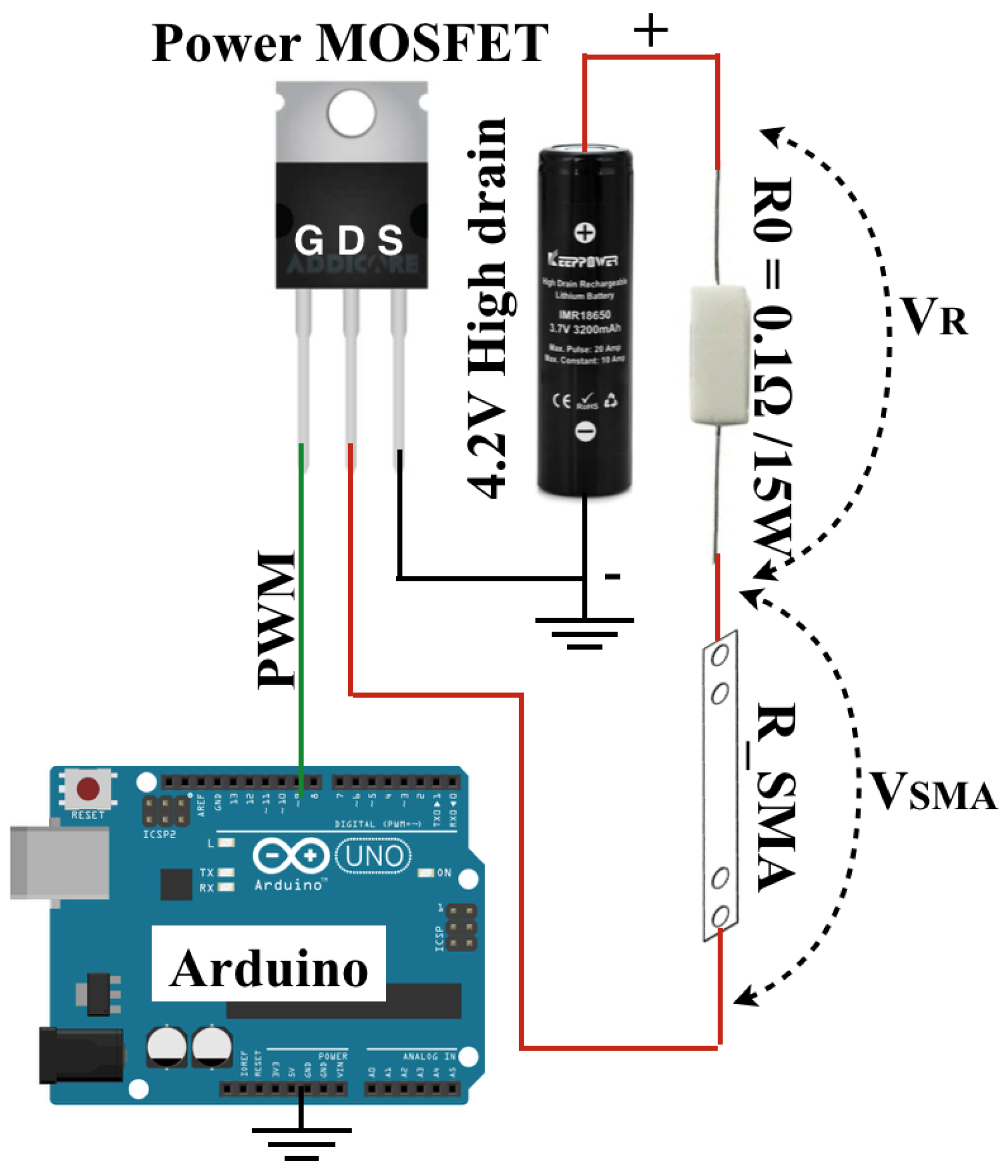
A pulse-width modulation (PWM) drive was used because it is an efficient way to control the SMA and it exhibits a linear proportional relationship between the power and duty cycle. To provide the proper amount of electrical energy, a high drain lithium ion battery (IMR 18650) was used. To generate heat in a short time, the SMA strip was shorted-circuited. For this experiment, the circuit shown in
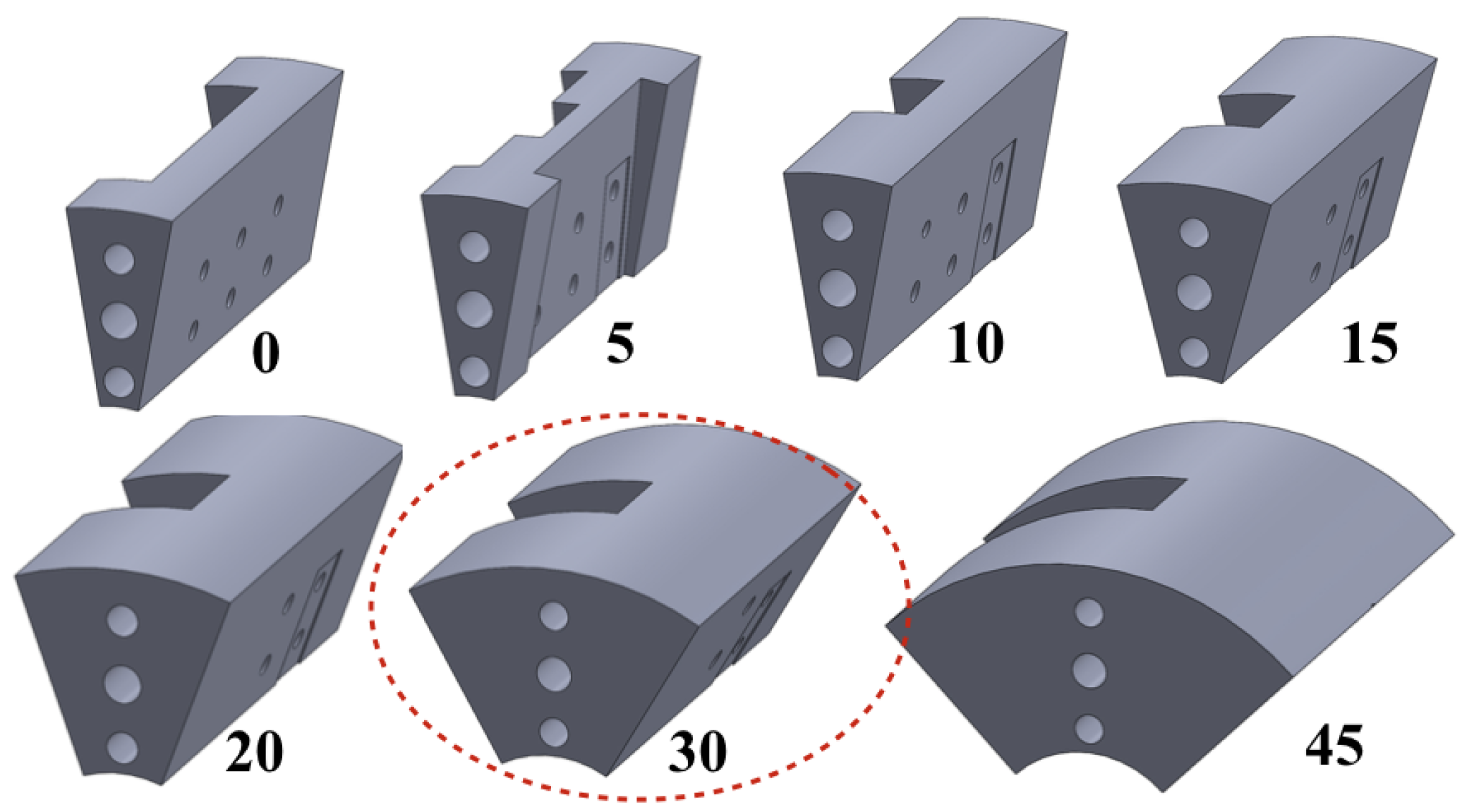
Figure 13 was used as the SMA driver. The various pre-bent angles of SMA as shown in
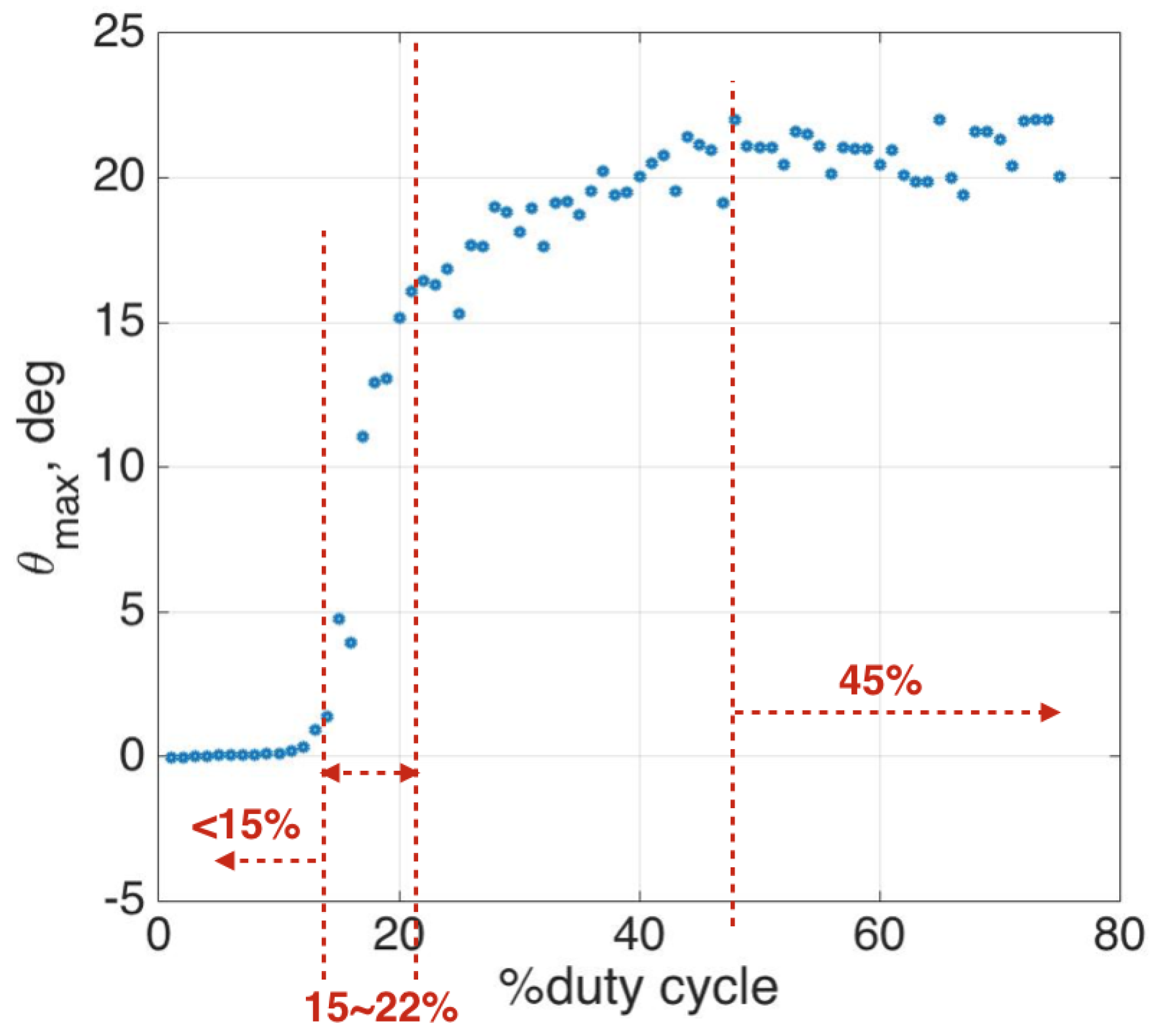
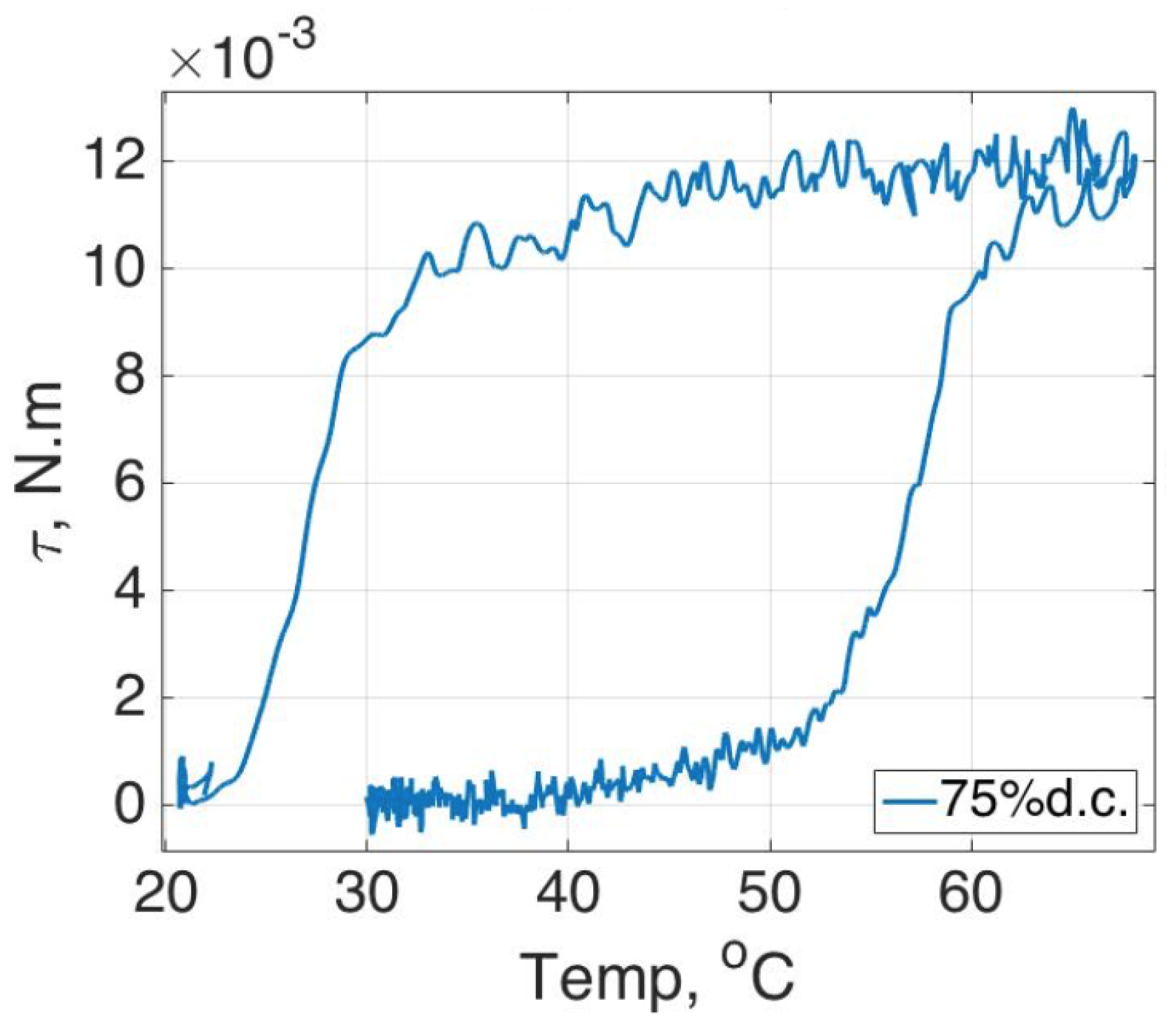
Figure 14 were tested with the same configuration, and the result shows that from no pre-bent angle to a small pre-bent angle, the SMA seemed to give much power to drive, but in fact the opposite SMA resisted the motion, resulting in only a small angle movement. A large pre-bent angle, such as 45 degrees, yielded the expected result in which the overall motion turned by only a small angle because the initial point was already half of the memorized shape, so the power was not enough to induce a large deflection angle. The pre-bent angle of 30 degrees was chosen because it can have the largest deflection angle at 30 degrees for each side.
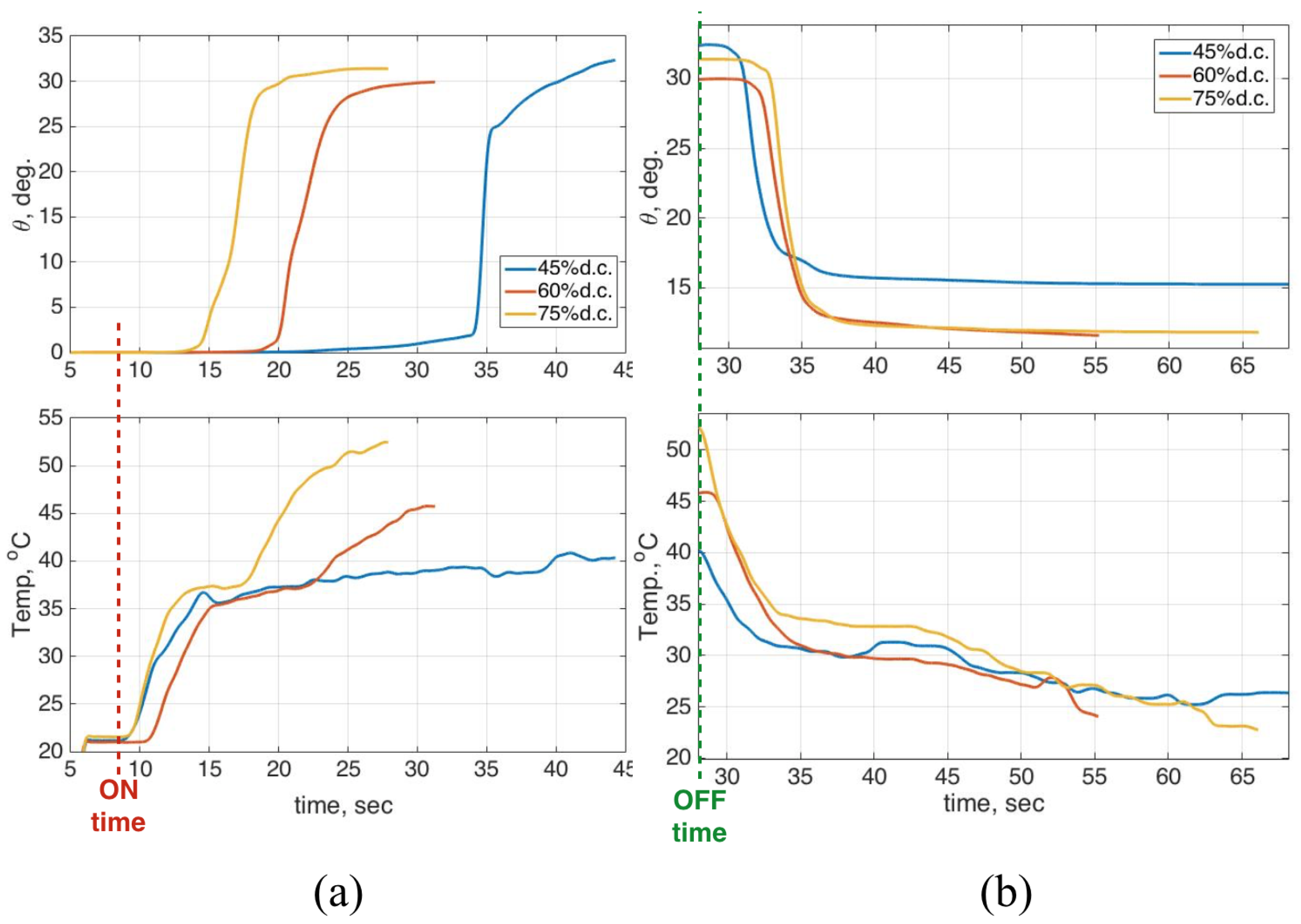
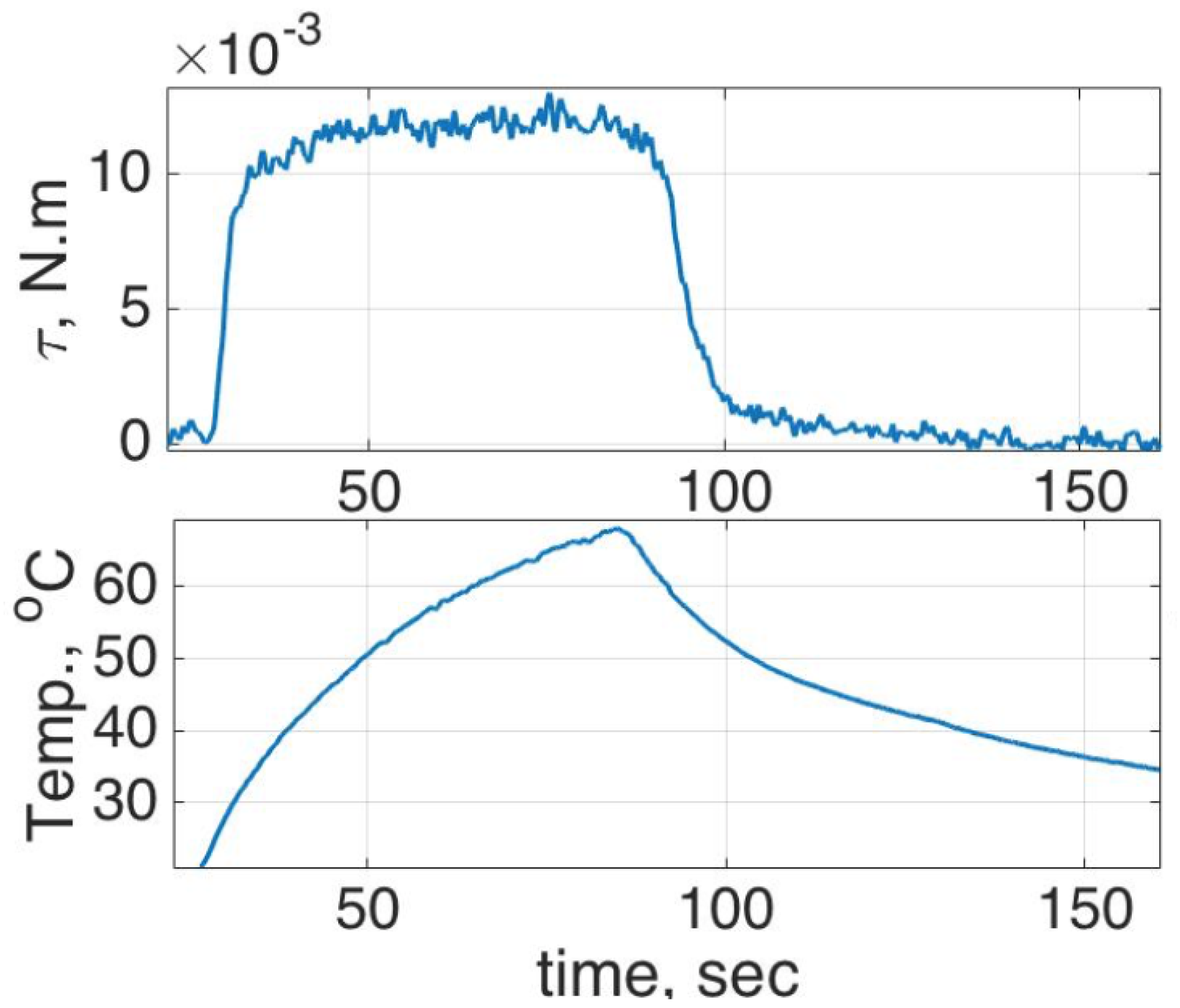
The ambient temperature during testing was 20–22
C. The SMA started to rotate when it reached the temperature of 38–40
C, and reached the maximum angle of 30 degrees at a temperature of approximately 50–55
C. When the power was released, the temperature decreased to approximately 33
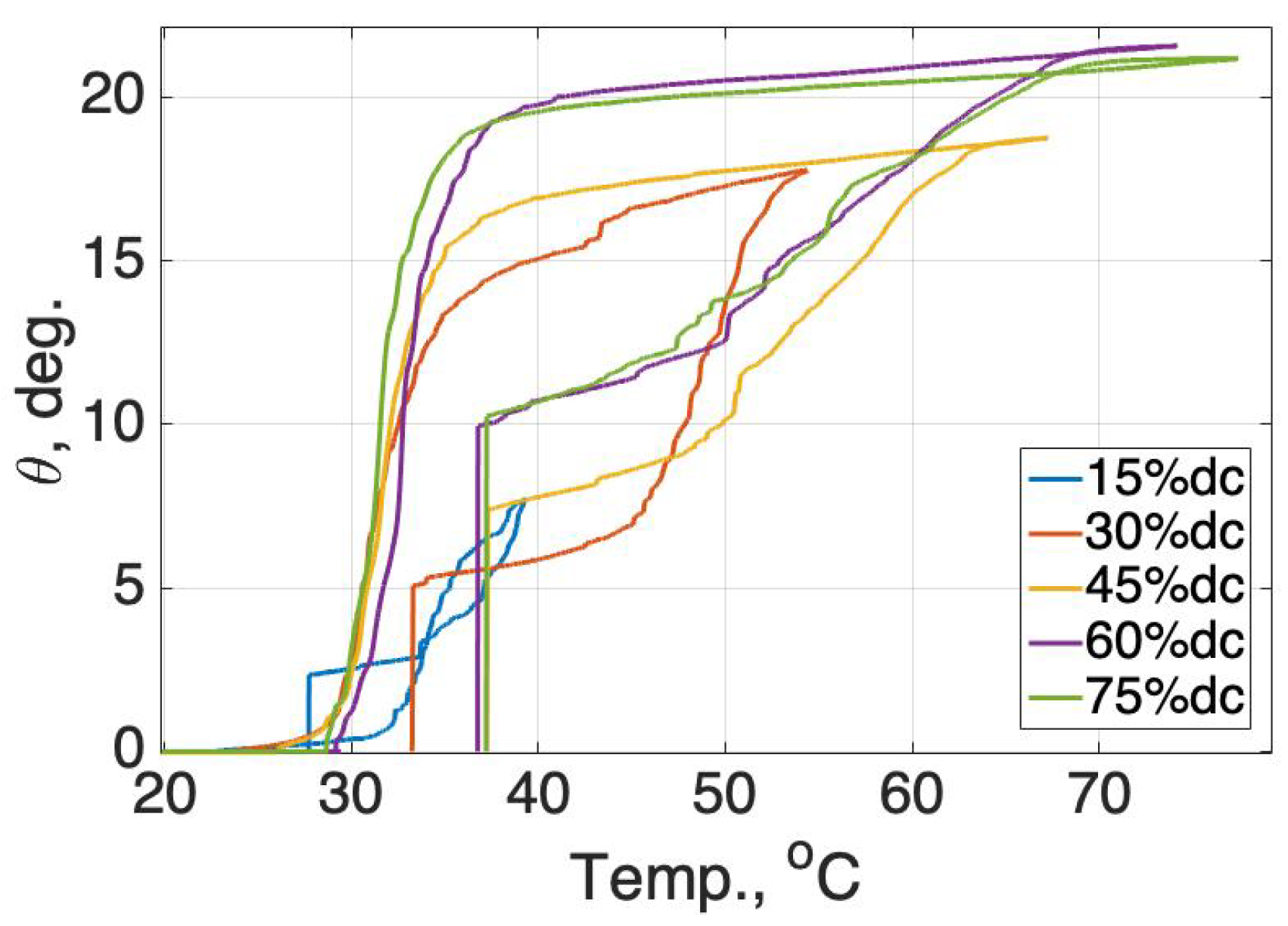
C while maintaining the position at the same angle; then the bias spring tried to rotate the SMA back to its initial position. The deflection angle and temperature of the SMA are represented with respect to time by changing the duty cycle to
,
and
as shown in
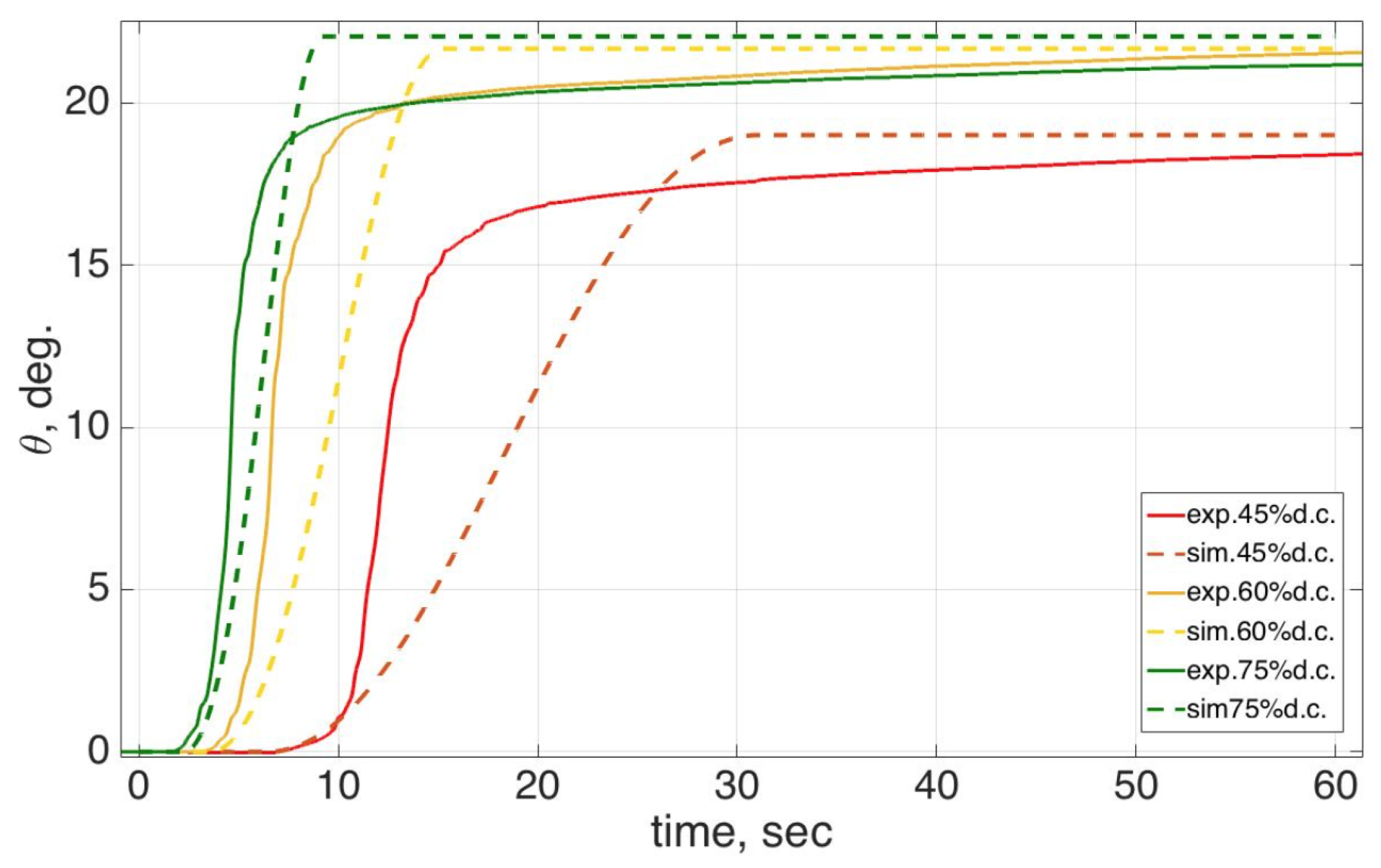
Figure 15. A 45% duty cycle yielded a lower temperature, but it required more time to reach the maximum angle.
Figure 15a shows that the higher voltage can decrease the SMA response time, but it also caused higher temperature. When the energy was released during the “off” time, all of the SMA’s temperature dropped down similarly from the maximum temperature to approximately 30
C, then linearly decreased to room temperature as shown
Figure 15b. The testing results show that the SMA strip works from 45% to 75% duty cycle with 4 V amplitude and 10 A drawing currents; for lower duty cycles, the SMA only slightly changed and never reached the maximum angle of 30
C.