Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey
Abstract
1. Introduction
2. Preliminaries
2.1. Topologies
2.2. Algebraic Graph Theory
2.3. Consensus in Multi-Robot Systems
- Alignment (Pointing in the same direction),
- Synchronization (Agreeing on the same time),
- Distributed Estimation (Agreeing on the estimation/measurement of the distributed quantity),
- Rendezvous (Meeting at a common point).
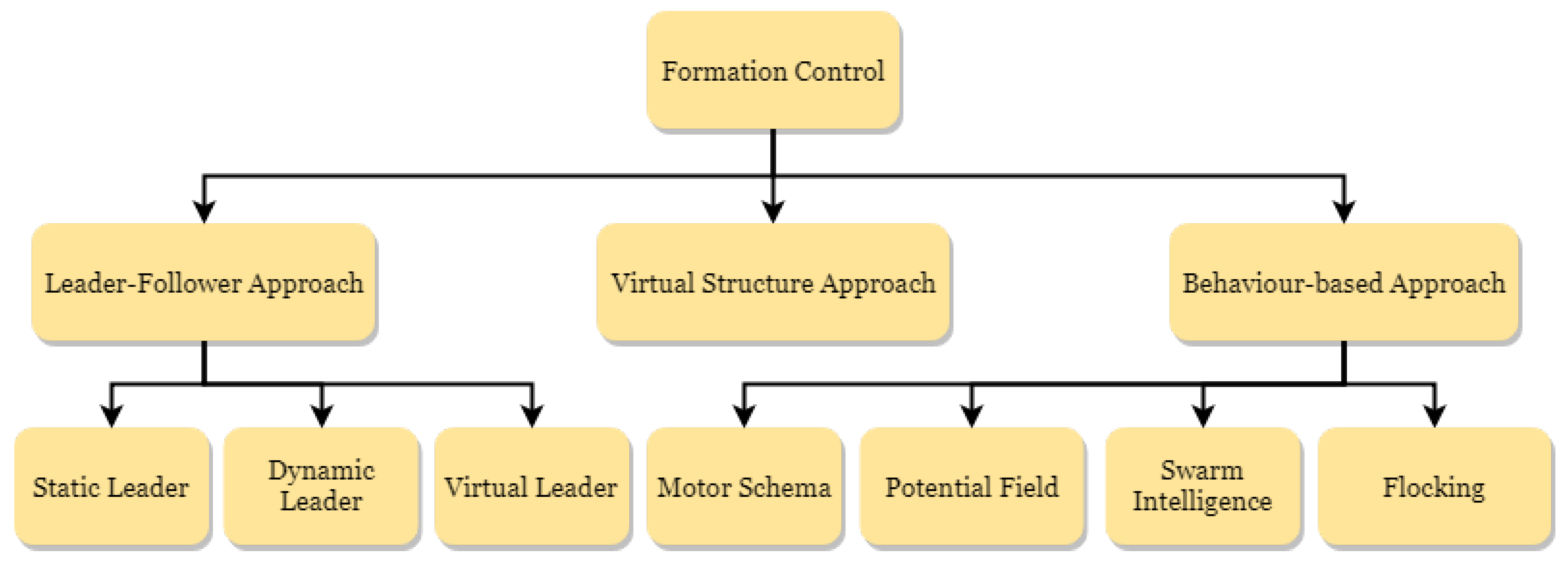
3. Leader–Follower Approach
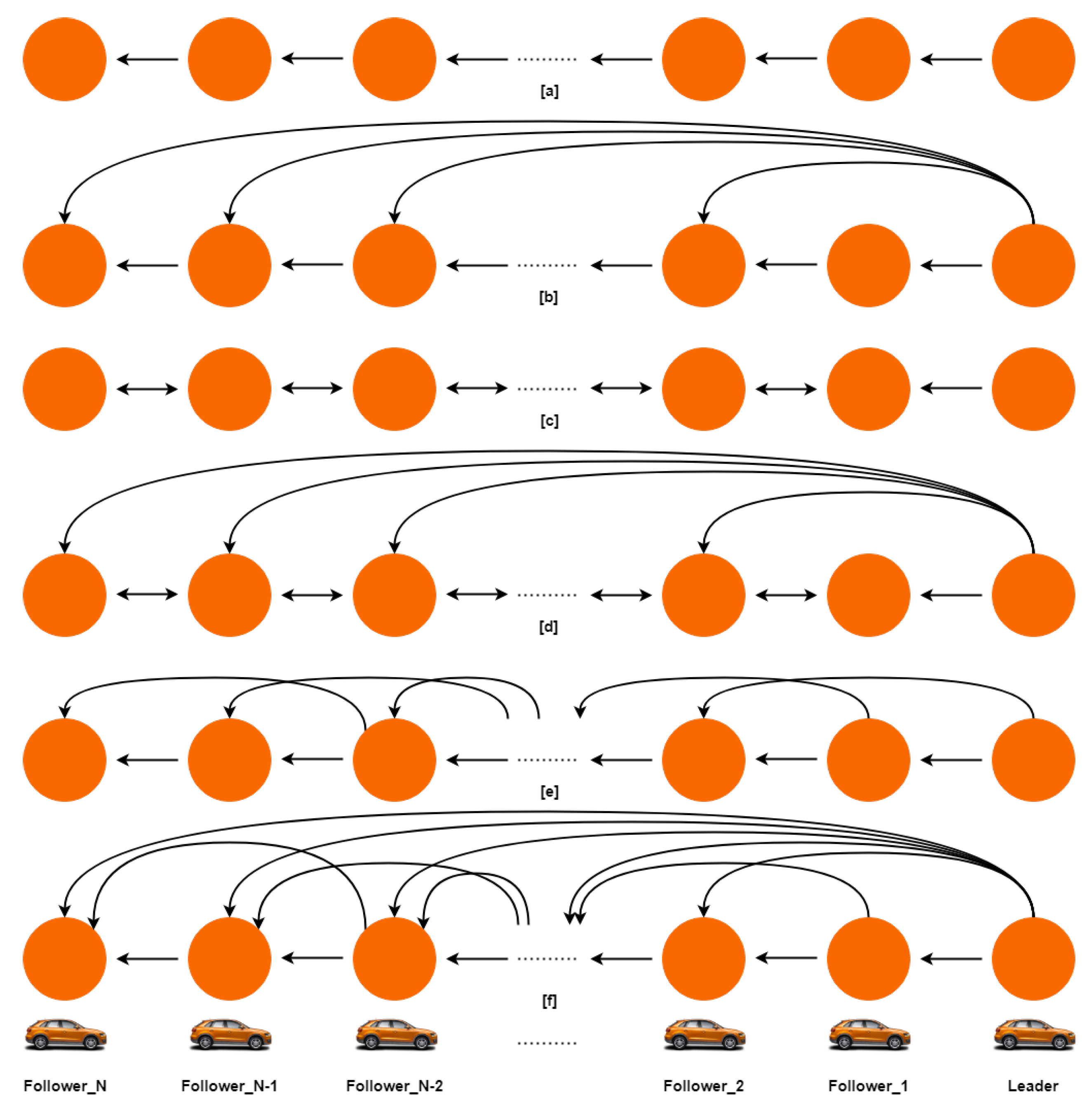
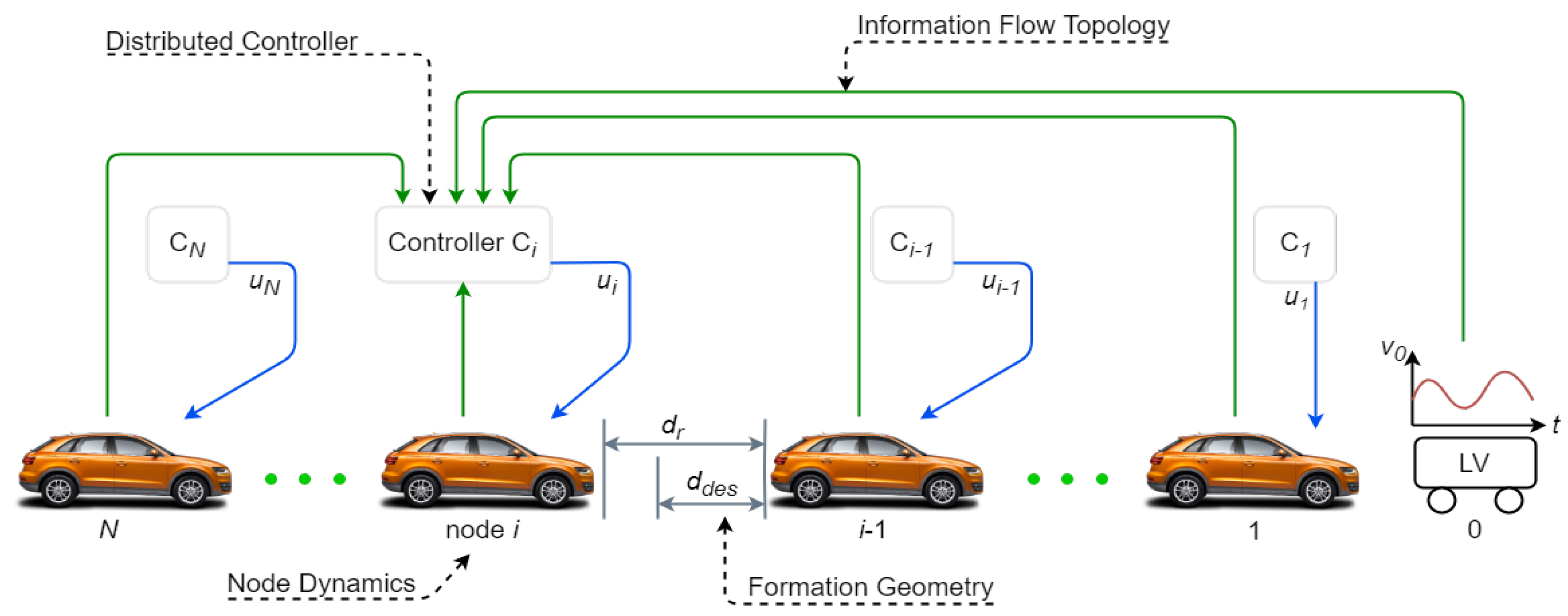
3.1. Leader–Follower Formation Controllers
3.2. Second-Order Dynamics
3.3. Third-Order Dynamics
3.4. Platoon Management
4. Behaviour-Based Approach
4.1. Basic Principles
- Behaviours are implemented as control laws, either in software or hardware, as a processing element or as a procedure.
- Each behaviour can take inputs from the robot’s sensors and/or from other modules in the system, and send outputs to the robot’s effectors and/or to other modules.
- Many different behaviours may independently receive input from the same sensors and output action commands to the same actuators.
- Behaviours are encoded to be relatively simple, and are added to the system incrementally.
- Behaviours are executed concurrently, not sequentially, in order to exploit parallelism and speed of computation, as well as the interaction dynamics among behaviours and between behaviours and the environment.
4.2. Motor Schema-Based Control
4.3. Artificial Potential Field
4.4. Flocking
4.5. Swarm Intelligence
4.5.1. Exploration and Exploitation
4.5.2. Swarm Intelligence and Formation Control
5. Virtual Structure Approach
5.1. Basic Principles
- Capability of achieving high-precision control.
- Inherently fault tolerant during the failure of robots by maintaining formation.
- No need to elect leader robot.
- Reconfigurable for different kinds of virtual structures with no modification.
- Can be implemented in a distributed fashion with no increase in communications from a centralized implementation.
- No explicit functional decomposition.
- A decentralized framework for a large number of agents/robots and for a strict limitation on inter-vehicle communication.
- Integration of formation feedback in the framework to improve group robustness.
- Ability to prescribe a group manoeuvre directly in the framework.
- A framework to guarantee high precision for maintaining formation during manoeuvre.
5.2. Virtual Structure Controllers
6. Remaining Challenges
6.1. Technical Challenges
6.1.1. Communication
6.1.2. Error Accumulation
6.1.3. Deadlock and Livelock
6.1.4. Limit on Maximum Scalability
- Communication loss or delay due to a time taken for a signal or message to transmit in a large vehicular network.
- Errors accumulation as explained above.
- Higher time to derive decision (consensus control) at every situation and moment.
6.1.5. Cybersecurity
6.2. Implementation Challenges
6.2.1. Platoon Formation
- If any vehicle leaves the formation or joins another platoon, other vehicles should rearrange their position to maintain the formation by feeling the gap in the formation.
- If a leader leaves the platoon, then it should not affect the formation but a subsequent vehicle inside the platoon should take the role of the leader.
- This platoon based formation can also have a fixed number of vehicles that can be allowed and, if the number increases, then another platoon should be created for autonomous vehicles.
- The above discussed problems can be extended to the multi-lane platoon and two-way traffic platoon formation.
- Moreover, different platoons and vehicles inside the platoon should share information with each other. This is helpful for other vehicles to join another platoon.
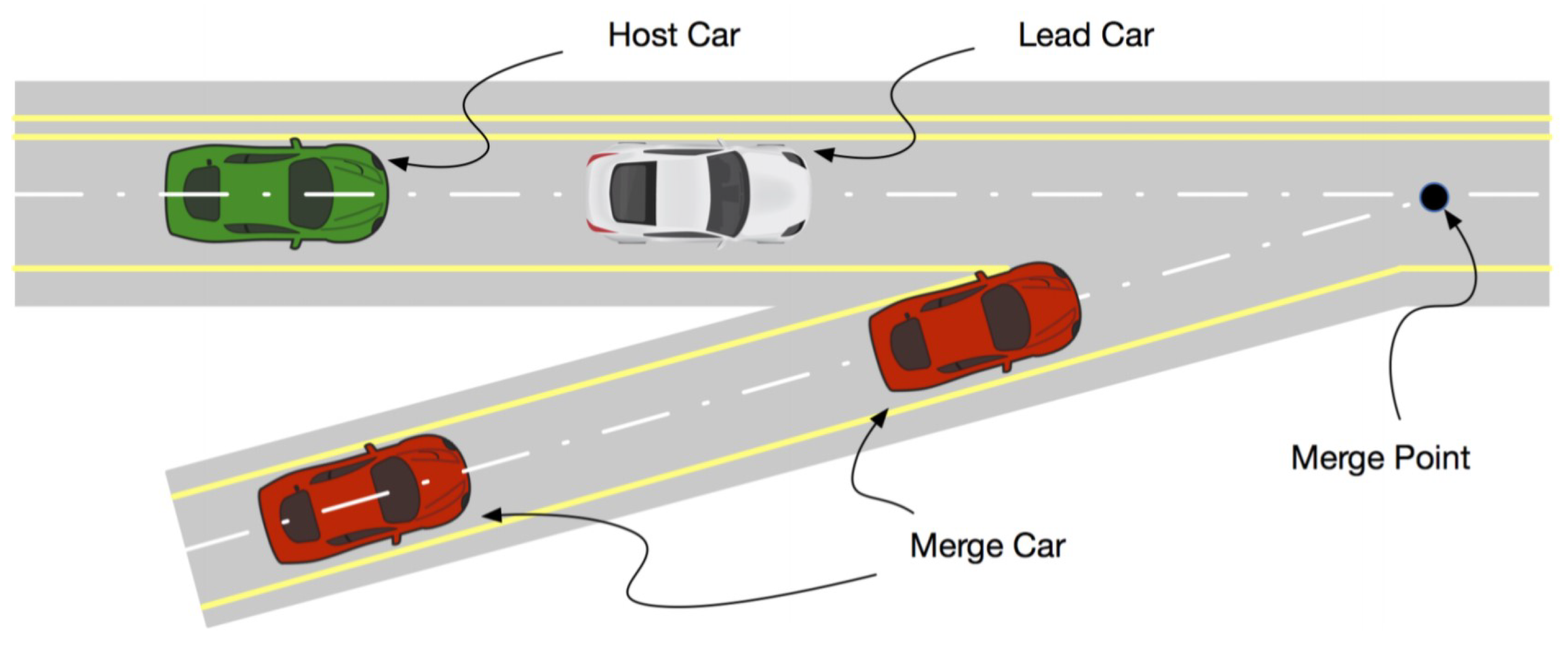
6.2.2. Lane Merge and Change
6.2.3. Emergency Vehicle Response
6.2.4. Intersection Management
7. Conclusions
- Few controllers and algorithms in a leader–follower approach targets third-order consensus control and real robot experiments. Furthermore, a dynamic role changing leader should be targeted in a leader–follower approach.
- Considering the swarm intelligence based algorithms, it can be observed that they can handle a population of robots, but they do not offer formation control ability; therefore, new parameters or another algorithm should be implemented along with these algorithms.
- A machine learning approach is not applied to the formation control problem compared to other techniques and deep learning remains unexplored for multi-robot formation control problems.
Author Contributions
Funding
Conflicts of Interest
References
- The SAE On-Road Automated Vehicle Standards Committee. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Hyde, S.; Dalton, P.; Stevens, A. Attitudes to Autonomous Vehicles; TRL Limited: Wokingham, UK, 2017; ISBN 978-1-910377-91-8. [Google Scholar]
- UK Government. Centre for Connected and Autonomous Vehicles. Available online: https://www.gov.uk/government/organisations/centre-for-connected-and-autonomous-vehicles (accessed on 28 June 2018).
- Kavathekar, P.; Chen, Y.Q. Vehicle Platooning: A Brief Survey and Categorization. In Proceedings of the 2011 ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Washington, DC, USA, 28–31 August 2011. [Google Scholar] [CrossRef]
- Chunyu, J.; Qu, Z.; Pollak, E.; Falash, M. A New Multi-objective Control Design for Autonomous Vehicles. In Optimization and Cooperative Control Strategies; Hirsch, M.J., Commander, C.W., Pardalos, P.M., Murphey, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 81–102. ISBN 978-3-540-88063-9. [Google Scholar]
- Lawton, J.R.T.; Beard, W.A.; Young, B.J. A Decentralized Approach to Formation Maneuvers. IEEE Trans. Robot. Autom. 2003, 19, 933–941. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Decentralized Scheme for Spacecraft Formation Flying via the Virtual Structure Approach. J. Guid. Control Dyn. 2004, 27, 73–82. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.E.; Wang, J.; Cao, D.; Li, K. Stability and Scalability of Homogeneous Vehicular Platoon: Study on the Influence of Information Flow Topologies. IEEE Trans. Intell. Transp. Syst. 2016, 17, 14–26. [Google Scholar] [CrossRef]
- Olfati-Saber, O.; Murray, R.M. Consensus Problems in Networks of Agents With Switching Topology and Time-Delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Gong, S.; Zhou, A.; Wang, J.; Li, T.; Peeta, S. Cooperative Adaptive Cruise Control for a Platoon of Connected and Autonomous Vehicles Considering Dynamic Information Flow Topology. arXiv, 2018; arXiv:1807.02224. [Google Scholar]
- Diestel, R. Graph Theory, 2nd ed.; Springer: New York, NY, USA, 2000; ISBN 0-387-98976-5. [Google Scholar]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001; ISBN 978-0-387-95220-8. [Google Scholar]
- Bliman, P.A.; Ferrari-Trecate, G. Average consensus problems in networks of agents with delayed communications. Automatica 2008, 44, 1985–1995. [Google Scholar] [CrossRef]
- Tian, Y.P.; Liu, C.L. Consensus in Networks with Diverse Input and Communication Delays. IFAC Proc. Vol. 2008, 41, 10764–10769. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems. Automatica 2010, 46, 1089–1095. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus in multi-agent systems with communication constraints. Int. J. Robust Nonlinear Control 2011, 22, 170–182. [Google Scholar] [CrossRef]
- Cao, Y.F.; Sun, Y.G. Necessary and Sufficient Conditions for Consensus of Third-Order Multi-Agent Systems. In Proceedings of the 14th International Conference on Control, Automation and Systems (ICCAS 2014), Gyeonggi, Korea, 22–25 October 2014. [Google Scholar] [CrossRef]
- Cao, Y.; Sun, Y. Consensus of discrete-time third-order multi-agent systems in directed networks. Neurocomputing 2016, 177, 394–400. [Google Scholar] [CrossRef]
- Zhao, H.; Fei, S. The Consensus for Discrete-Time Heterogeneous Networked Systems Consisting of Second-Order Agents and Third-Order Agents. IEEE Access 2018, 6, 14204–14211. [Google Scholar] [CrossRef]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Loria, A.; Dasdemir, J.; Alvarez-Jarquin, N. Leader-follower formation and tracking control of mobile robots along straight paths. IEEE Trans. Control Syst. Technol. 2016, 24, 2–727. [Google Scholar] [CrossRef]
- Wan, S.; Lu, J.; Fan, P. Semi-centralized Control for Multi Robot Formation. In Proceedings of the 2nd International Conference on Robotics and Automation Engineering (ICRAE), Shanghai, China, 29–31 December 2017. [Google Scholar] [CrossRef]
- Li, R.; Zhang, L.; Han, L.; Wang, J. Multiple Vehicle Formation Control Based on Robust Adaptive Control Algorithm. IEEE Intell. Transp. Syst. Mag. 2017, 9, 41–51. [Google Scholar] [CrossRef]
- Peng, Z.; Yang, S.; Wen, G.; Rahmani, A.; Yu, Y. Adaptive distributed formation control for multiple nonholonomic wheeled mobile robots. Neurocomputing 2016, 173, 1485–1494. [Google Scholar] [CrossRef]
- Maghenem, M.; Loria, A.; Panteley, E. A robust delta-persistently exciting controller for leader–follower tracking-agreement of multiple vehicles. Eur. J. Control 2017, 40, 1–12. [Google Scholar] [CrossRef]
- Chen, X.; Jia, Y. Adaptive leader–follower formation control of non-holonomic mobile robots using active vision. IET Control Theory Appl. 2014, 9, 1302–1311. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, W.; Chen, Y.; Ke, F.; Chu, X.; Chen, C.L. Neural-Dynamic Optimization-Based Model Predictive Control for Tracking and Formation of Nonholonomic Multirobot Systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mariottini, G.L.; Morbidi, F.; Prattichizzo, D.; Valk, N.V.; Michael, N.; Pappas, G.; Daniilidis, K. Vision-Based Localization for Leader-Follower Formation Control. IEEE Trans. Robot. 2009, 25, 1431–1438. [Google Scholar] [CrossRef]
- Maei, H.R.; Sutton, R.S. GQ(λ): A general gradient algorithm for temporal-difference prediction learning with eligibility traces. In Proceedings of the Third Conference on Artificial General Intelligence (AGI 2010), Lugano, Switzerland, 5–8 March 2010. [Google Scholar] [CrossRef]
- Knopp, M.; Aykın, C.; Feldmaier, J.; Shen, H. Formation Control using GQ(λ) Reinforcement Learning. In Proceedings of the IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Lisbon, Portugal, 28 August–1 September 2017. [Google Scholar] [CrossRef]
- Zhu, Q.; Huang, Z.; Sun, Z.; Liu, D.; Dai, B. Reinforcement Learning based Throttle and Brake Control for Autonomous Vehicle Following. In Proceedings of the Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar] [CrossRef]
- Li, S.E.; Zheng, Y.; Li, K.; Wang, J. An Overview of Vehicular Platoon Control under the Four-Component Framework. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015. [Google Scholar] [CrossRef]
- Chen, G.; Lewis, F.L. Leader-following control for multiple inertial agents. Int. J. Robust Nonlinear Control 2010, 21, 925–942. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Zheng, T.; Hu, X.; Feng, H.; Li, Y. Evaluating the performance of vehicular platoon control under different network topologies of initial states. Physica A 2016, 450, 359–368. [Google Scholar] [CrossRef]
- Oncu, S.; Ploeg, J.; Wouw, N.; Nijmeijer, H. Cooperative Adaptive Cruise Control: Network-Aware Analysis of String Stability. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1527–1537. [Google Scholar] [CrossRef]
- Xiao, L.; Gao, F. Practical String Stability of Platoon of Adaptive Cruise Control Vehicles. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1184–1194. [Google Scholar] [CrossRef]
- Bernardo, M.; Salvi, A.; Santini, S. Distributed Consensus Strategy for Platooning of Vehicles in the Presence of Time-Varying Heterogeneous Communication Delays. IEEE Trans. Intell. Transp. Syst. 2015, 16, 102–112. [Google Scholar] [CrossRef]
- Bernardo, M.; Falcone, P.; Salvi, A.; Santini, S. Design, Analysis, and Experimental Validation of a Distributed Protocol for Platooning in the Presence of Time-Varying Heterogeneous Delays. IEEE Trans. Control Syst. Technol. 2016, 24, 413–427. [Google Scholar] [CrossRef]
- Oncu, S.; Wouw, N.; Heemels, W.P.; Nijmeijer, H. String stability of interconnected vehicles under communication constraints. In Proceedings of the IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012. [Google Scholar] [CrossRef]
- Santini, S.; Salvi, A.; Valente, A.S.; Pescapé, A.; Segata, M.; Cigno, R. A Consensus-Based Approach for Platooning with Intervehicular Communications and Its Validation in Realistic Scenarios. IEEE Trans. Veh. Technol. 2016, 66, 1985–1999. [Google Scholar] [CrossRef]
- Chehardoli, H.; Homaeinezhad, M.R. Stable control of a heterogeneous platoon of vehicles with switched interaction topology, time-varying communication delay and lag of actuator. Proc. Inst. Mech. Part C J. Mech. Eng. Sci. 2017, 231, 4197–4208. [Google Scholar] [CrossRef]
- Jia, D.; Ngoduy, D. Enhanced cooperative car-following traffic model with the combination of V2V and V2I communication. Transp. Res. Part B 2016, 90, 172–191. [Google Scholar] [CrossRef]
- Jia, D.; Ngoduy, D. Platoon based cooperative driving model with consideration of realistic inter-vehicle communication. Transp. Res. Part C 2016, 68, 245–264. [Google Scholar] [CrossRef]
- Bernardo, M.; Salvi, A.; Santini, S.; Valente, A.S. Third-order consensus in vehicles platoon with heterogeneous time-varying delays. IFAC-PapersOnLine 2015, 48, 358–363. [Google Scholar] [CrossRef]
- Chehardoli, H.; Homaeinezhad, M.R. Third-order safe consensus of heterogeneous vehicular platoons with MPF network topology: constant time headway strategy. Proc. Inst. Mech. Part D J. Autom. Eng. 2017, 1–12. [Google Scholar] [CrossRef]
- Salvia, A.; Santinia, S.; Valente, A.S. Design, analysis and performance evaluation of a third order distributed protocol for platooning in the presence of time-varying delays and switching topologies. Transp. Res. Part C Emerg. Technol. 2017, 80, 360–383. [Google Scholar] [CrossRef]
- Chehardoli, H.; Homaeinezhad, M.R. Third-order leader-following consensus protocol of traffic flow formed by cooperative vehicular platoons by considering time delay: constant spacing strategy. Proc. Inst. Mech. Part I J. Syst. Control Eng. 2018, 232, 285–298. [Google Scholar] [CrossRef]
- Fernandes, P.; Nunes, U. Multiplatooning Leaders Positioning and Cooperative Behavior Algorithms of Communicant Automated Vehicles for High Traffic Capacity. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1172–1187. [Google Scholar] [CrossRef]
- Amoozadeh, M.; Deng, H.; Chuah, C.; Zhang, H.M.; Ghosal, D. Platoon management with cooperative adaptive cruise control enabled by VANET. Veh. Commun. 2015, 2, 110–123. [Google Scholar] [CrossRef]
- Fernandes, P.; Nunes, U. Platooning of Autonomous Vehicles with Intervehicle Communications in SUMO Traffic Simulator. In Proceedings of the 13th Annual Conference on Intelligent Transportation, Funchal, Portugal, 19–22 September 2010. [Google Scholar] [CrossRef]
- Navarro, I.; Zimmermann, F.; Vasic, M.; Martinoli, A. Distributed Graph-Based Control of Convoys of Heterogeneous Vehicles using Curvilinear Road Coordinates. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016. [Google Scholar] [CrossRef]
- Jia, D.; Ngoduy, D.; Vu, H.L. A multiclass microscopic model for heterogeneous platoon with vehicle-to-vehicle communication. Transp. B Transp. Dyn. 2018, 1–25. [Google Scholar] [CrossRef]
- HasanzadeZonuzy, A.; Arefizadeh, S.; Talebpour, A.; Shakkottai, S.; Darbha, S. Collaborative Platooning of Automated Vehicles Using Variable Time Gaps. arXiv, 2017; arXiv:1710.02186. [Google Scholar]
- United States Department of Transportation. How an Automated Car Platoon Works. Available online: https://www.volpe.dot.gov/news/how-automated-car-platoon-works (accessed on 19 July 2018).
- Arkin, R.C. Behavior-Based Robotics, 3rd ed.; MIT Press: Cambridge, MA, USA, 1998; ISBN 0262011654. [Google Scholar]
- Birk, A. Behavior-based robotics, its scope and its prospects. In Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society (IECON ’98), Aachen, Germany, 31 August–4 September 1998. [Google Scholar] [CrossRef]
- Mataric, M.J.; Michaud, F. Behavior-Based Systems. In Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 891–909. ISBN 978-3-540-30301-5. [Google Scholar]
- Dong, J.; Chen, H.; Liu, S. A Behavior-based Policy for Multirobot Formation Control. Appl. Mech. Mater. 2012, 220, 1181–1185. [Google Scholar] [CrossRef]
- Handayani, A.S.; Husni, N.L.; Nurmaini, S.; Yani, I. Formation Control Design for Real Swarm Robot Using Fuzzy Logic. In Proceedings of the International Conference on Electrical Engineering and Computer Science (ICECOS), Palembang, Indonesia, 22–23 August 2017. [Google Scholar] [CrossRef]
- Parker, L.E. Motor Schemas in Robot Learning. In Encyclopedia of the Sciences of Learning; Seel, N.M., Ed.; Springer: Boston, MA, USA, 2012. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-Based Formation Control for Multirobot Teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Kuppan Chetty, R.M.; Singaperumal, M.; Nagarajan, T. Behaviour Based Multi Robot Formations with Active Obstacle Avoidance based on Switching Control Strategy. Adv. Mater. Res. 2012, 433, 6630–6635. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Zhu, Z.; Chen, C.; Yang, P. Behavior-Based Formation Control of Swarm Robots. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized behaviour-based formation control of multiple robots considering obstacle avoidance. Intell. Serv. Robot. 2017, 11, 127–138. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, G.; Qiao, G.; Zhang, J.; Peng, J. Consensus and Obstacle Avoidance for Multi-robot Systems with Fixed and Switching Topologies. In Proceedings of the 2014 International Conference on Robotics and Biomimetics, Bali, Indonesia, 5–10 December 2014. [Google Scholar] [CrossRef]
- Semsar-Kazerooni, E.; Elferink, K.; Ploeg, J.; Nijmeijer, H. Multi-objective platoon maneuvering using artificial potential fields. IFAC-PapersOnLine 2017, 50, 15006–15011. [Google Scholar] [CrossRef]
- Dang, A.; La, H.M.; Nguyen, T.; Horn, J. Distributed Formation Control for Autonomous Robots in Dynamic Environments. arXiv, 2017; arXiv:1705.02017. [Google Scholar]
- Elkilany, B.; Abouelsoud, A.; Fathelbab, A. Adaptive formation control of robot swarms using optimized potential field method. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017. [Google Scholar] [CrossRef]
- Huang, Z.; Chu, D.; Wu, C.; He, Y. Path Planning and Cooperative Control for Automated Vehicle Platoon Using Hybrid Automata. IEEE Trans. Intell. Transp. Syst. 2018, 1–16. [Google Scholar] [CrossRef]
- Do, K.D. Formation Tracking Control of Unicycle-Type Mobile Robots With Limited Sensing Ranges. IEEE Trans. Control Syst. Technol. 2008, 16, 527–538. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Parker, L. Multiple Mobile Robot Systems. In Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 921–941. ISBN 978-3-540-30301-5. [Google Scholar]
- Dimarogonas, D.V.; Kyriakopoulos, K.J. A connection between formation control and flocking behavior in nonholonomic multiagent systems. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar] [CrossRef]
- Hayashi, Y.; Namerikawa, T. Flocking algorithm for multiple nonholonomic cars. In Proceedings of the 55th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Tsukuba, Japan, 20–23 September 2016. [Google Scholar] [CrossRef]
- Lei, B.; Li, W. Formation Control for Multi-robots Based on Flocking Algorithm. In Intelligent Robotics and Applications; Xiong, C., Liu, H., Huang, Y., Xiong, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1238–1247. ISBN 3-540-88512-9. [Google Scholar]
- Reyes, L.A.V.; Tanner, H.G. Flocking, Formation Control, and Path Following for a Group of Mobile Robots. IEEE Trans. Control Syst. Technol. 2015, 23, 1268–1282. [Google Scholar] [CrossRef]
- Savkina, A.V.; Wang, C.; Baranzadeh, A.; Xi, Z.; Nguyen, H. Distributed formation building algorithms for groups of wheeled mobile robots. Robot. Auton. Syst. 2016, 75, 463–474. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A survey of historical and recent developments with hybridization perspectives. arXiv, 2018; arXiv:1804.05319. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle Swarm Optimization: An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Dorigo, M.; Caro, G.D.; Gambardella, L. Ant Algorithms for Discrete Optimization. Artif. Life 1999, 5, 137–172. [Google Scholar] [CrossRef] [PubMed]
- Mohan, B.C.; Baskaran, R. A survey: Ant Colony Optimization based recent research and implementation on several engineering domain. Expert Syst. Appl. 2012, 39, 4618–4627. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Li, X.L.; Shao, Z.J.; Qian, J.X. An Optimizing Method Based on Autonomous Animats: Fish-swarm Algorithm. Syst. Eng. Theory Pract. 2002, 22, 32–38. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.M.; Wu, H.S. Improved artificial fish swarm algorithm. In Proceedings of the IEEE 9th Conference on Industrial Electronics and Applications (ICIEA), Tianjin, China, 14–16 August 2009. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Passino, K. Biomimicry of bacterial foraging for distributed optimisation and control. IEEE Control Syst. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Rani, B.S.; Kumar, A. A Comprehensive Review on Bacteria Foraging Optimization Technique. In Multi-Objective Swarm Intelligence; Dehuri, S., Jagadev, A., Panda, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–25. ISBN 978-3-662-46308-6. [Google Scholar]
- Krishnanand, K.; Ghose, D. Detection of Multiple Source Locations using a Glowworm Metaphor with Applications to Collective Robotics. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005. [Google Scholar] [CrossRef]
- Karegowda, A.G.; Prasad, M. A Survey of Applications of Glowworm Swarm Optimization Algorithm. In Proceedings of the 2013 IJCA International Conference on Computing and Information Technology, Bangkok, Thailand, 9–10 May 2013; pp. 39–42. [Google Scholar]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In Stochastic Algorithms: Foundations and Applications; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. ISBN 978-3-642-04943-9. [Google Scholar]
- Tilahun, S.; Ngnotchouye, J. Firefly algorithm for discrete optimization problems: A survey. KSCE J. Civ. Eng. 2017, 21, 535–545. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. arXiv, 2010; arXiv:1004.4170. [Google Scholar]
- Chawla, M.; Duhan, M. Bat Algorithm: A Survey of the State-of-the-Art. Appl. Artif. Intell. 2015, 29, 617–634. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Yang, X.S. Swarm Intelligence Based Algorithms: A Critical Analysis. Evol. Intell. 2014, 7, 17–28. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef] [PubMed]
- Pessin, G.; Osorio, F.; Wolf, D. Particle Swarm Optimization Applied to Intelligent Vehicles Squad Coordination. IFAC Proc. Vol. 2010, 43, 401–406. [Google Scholar] [CrossRef]
- Lee, S.M.; Myung, H. Particle Swarm Optimization-based Receding Horizon Control for Multi-Robot Formation. In Proceedings of the 9th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Daejeon, Korea, 26–28 November 2012. [Google Scholar] [CrossRef]
- Lee, S.M.; Myung, H. Cooperative Particle Swarm Optimization-Based Predictive Controller for Multi-robot Formation. In Intelligent Autonomous Systems 12; Lee, S., Cho, H., Yoon, K.J., Lee, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 533–541. ISBN 978-3-642-33932-5. [Google Scholar]
- Kamel, M.A.; Yu, X.; Zhang, Y. Real-time optimal formation reconfiguration of multiple wheeled mobile robots based on particle swarm optimization. In Proceedings of the 2016 Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016. [Google Scholar] [CrossRef]
- Han, G.; Fu, W.; Wang, W. The Study of Intelligent Vehicle Navigation Path Based on Behavior Coordination of Particle Swarm. Comput. Intell. Neurosci. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Kamel, A.E. V2X-Based Decentralized Cooperative Adaptive Cruise Control in the Vicinity of Intersections. IEEE Trans. Intell. Transp. Syst. 2016, 17, 644–658. [Google Scholar] [CrossRef]
- Marjovi, A.; Vasic, M.; Lemaitre, J.; Martinoli, A. Distributed Graph-based Convoy Control for Networked Intelligent Vehicles. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015. [Google Scholar] [CrossRef]
- Grandi, R.; Falconi, R.; Melchiorri, C. Coordination and Control of Autonomous Mobile Robot Groups using a Hybrid Technique based on Particle Swarm Optimization and Consensus. In Proceedings of the 2013 International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013. [Google Scholar] [CrossRef]
- Yang, L.; Gongyou, T.; Peidong, W. Formation Distance Problem in Multi-Agents Control. In Proceedings of the 2012 Fifth International Conference on Intelligent Computation Technology and Automation, Zhangjiajie, China, 12–14 January 2012. [Google Scholar] [CrossRef]
- Oikawa, R.; Takimoto, M.; Kambayashi, Y. Composing Swarm Robot Formations Based on Their Distributions Using Mobile Agents. In Multi-Agent Systems and Agreement Technologies; Rovatsos, M., Vouros, G., Julian, V., Eds.; Springer: Cham, Switzerland, 2015; pp. 108–120. ISBN 978-3-319-33509-4. [Google Scholar]
- Oikawa, R.; Takimoto, M.; Kambayashi, Y. Distributed Formation Control for Swarm Robots Using Mobile Agents. In Proceedings of the IEEE 10th Jubilee International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 21–23 May 2015. [Google Scholar] [CrossRef]
- Yajima, H.; Oikawa, R.; Takimoto, M.; Kambayashi, Y. Practical formation control of swarm robots using mobile agents. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017. [Google Scholar] [CrossRef]
- Roy, D.; Maitra, M.; Bhattacharya, S. Study of Formation Control and Obstacle Avoidance of Swarm Robots using Evolutionary Algorithms. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016. [Google Scholar] [CrossRef]
- Li, G.; Xu, H.; Lin, Y. Application of Bat Algorithm Based Time Optimal Control in Multi-robots Formation Reconfiguration. J. Bion. Eng. 2018, 15, 126–138. [Google Scholar] [CrossRef]
- Bang, S.; Ahn, S. Platooning Strategy for Connected and Autonomous Vehicles Transition from Light Traffic. Transp. Res. Rec. J. Transp. Res. Board 2017, 2623, 73–81. [Google Scholar] [CrossRef]
- Tan, K.H.; Lewis, M.A. Virtual Structures for High-Precision Cooperative Mobile Robotic Control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Osaka, Japan, 8 November 1996. [Google Scholar] [CrossRef]
- Qian, X.; Fortelle, A.; Moutarde, F. A Hierarchical Model Predictive Control Framework for On-road Formation Control of Autonomous Vehicles. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016. [Google Scholar] [CrossRef]
- Low, C.B. Adaptable Virtual Structure Formation Tracking Control Design for Nonholonomic Tracked Mobile Robots, with Experiments. In Proceedings of the IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015. [Google Scholar] [CrossRef]
- Essghaier, A.; Beji, L.; El Kamel, M.A.; Abichou, A.; Lerbet, J. Co-leaders and a flexible virtual structure based formation motion control. Int. J. Veh. Auton. Syst. 2011, 9, 108–125. [Google Scholar] [CrossRef]
- Chen, L.; Baoli, M. A Nonlinear Formation Control of Wheeled Mobile Robots with Virtual Structure Approach. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015. [Google Scholar] [CrossRef]
- Dong, L.; Chen, Y.; Qu, X. Formation Control Strategy for Nonholonomic Intelligent Vehicles Based on Virtual Structure and Consensus Approach. Procedia Eng. 2016, 137, 415–424. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, H.; Liu, Y.; Ding, Z. Collision and Deadlock Avoidance in Multirobot Systems: A Distributed Approach. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1712–1726. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; DeCastro, J.A.; Raman, V.; Rus, D.; Kress-Gazit, H. Reactive mission and motion planning with deadlock resolution avoiding dynamic obstacles. Auton. Robots 2017, 42, 801–824. [Google Scholar] [CrossRef]
- Dong, C.; Dolan, J.M.; Litkouhi, B. Interactive Ramp Merging Planning in Autonomous Driving: Multi-Merging Leading PGM (MML-PGM). In Proceedings of the 2017 International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar] [CrossRef]
- Scottish Government. Designing Streets: A Policy Statement for Scotland. Available online: https://beta.gov.scot/publications/designing-streets-policy-statement-scotland/pages/6/ (accessed on 25 June 2018).

| Algorithms | Algorithm Details | Survey Papers |
|---|---|---|
| Particle Swarm Optimization (PSO) | [78,79] | [80,81] |
| Ant Colony Optimization (ACO) | [82] | [83] |
| Artificial Bees Colony Optimization (ABCO) | [84,85] | [86] |
| Artificial Fish Swarm Algorithm (AFSA) | [87,88] | [89] |
| Bacteria Foraging Optimization (BFO) | [90] | [91] |
| Glowworm Swarm Optimization (GSO) | [92] | [93] |
| Firefly Algorithm (FA) | [94] | [95] |
| Bat Algorithm (BA) | [96] | [97] |
| Grey Wolf Optimizer (GWO) | [98] | [99] |
| Algorithms | Algorithm Parameters |
|---|---|
| PSO | Inertia Weight, w |
| ACO | Pheromone evaporation rate (Good at exploring) |
| ABCO | Distance between food source (Good at exploring) |
| AFSA | Visual and step |
| BFO | Run length |
| GSO | Euclidean Distance |
| FA | Attractiveness (Good at exploring) |
| BA | Frequency, loudness and pulse emission rates |
| GWO | a and A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soni, A.; Hu, H. Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey. Robotics 2018, 7, 67. https://doi.org/10.3390/robotics7040067
Soni A, Hu H. Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey. Robotics. 2018; 7(4):67. https://doi.org/10.3390/robotics7040067
Chicago/Turabian StyleSoni, Aakash, and Huosheng Hu. 2018. "Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey" Robotics 7, no. 4: 67. https://doi.org/10.3390/robotics7040067
APA StyleSoni, A., & Hu, H. (2018). Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey. Robotics, 7(4), 67. https://doi.org/10.3390/robotics7040067






