Reconfiguration Analysis of an RRRRS Single-Loop Mechanism
Abstract
1. Introduction
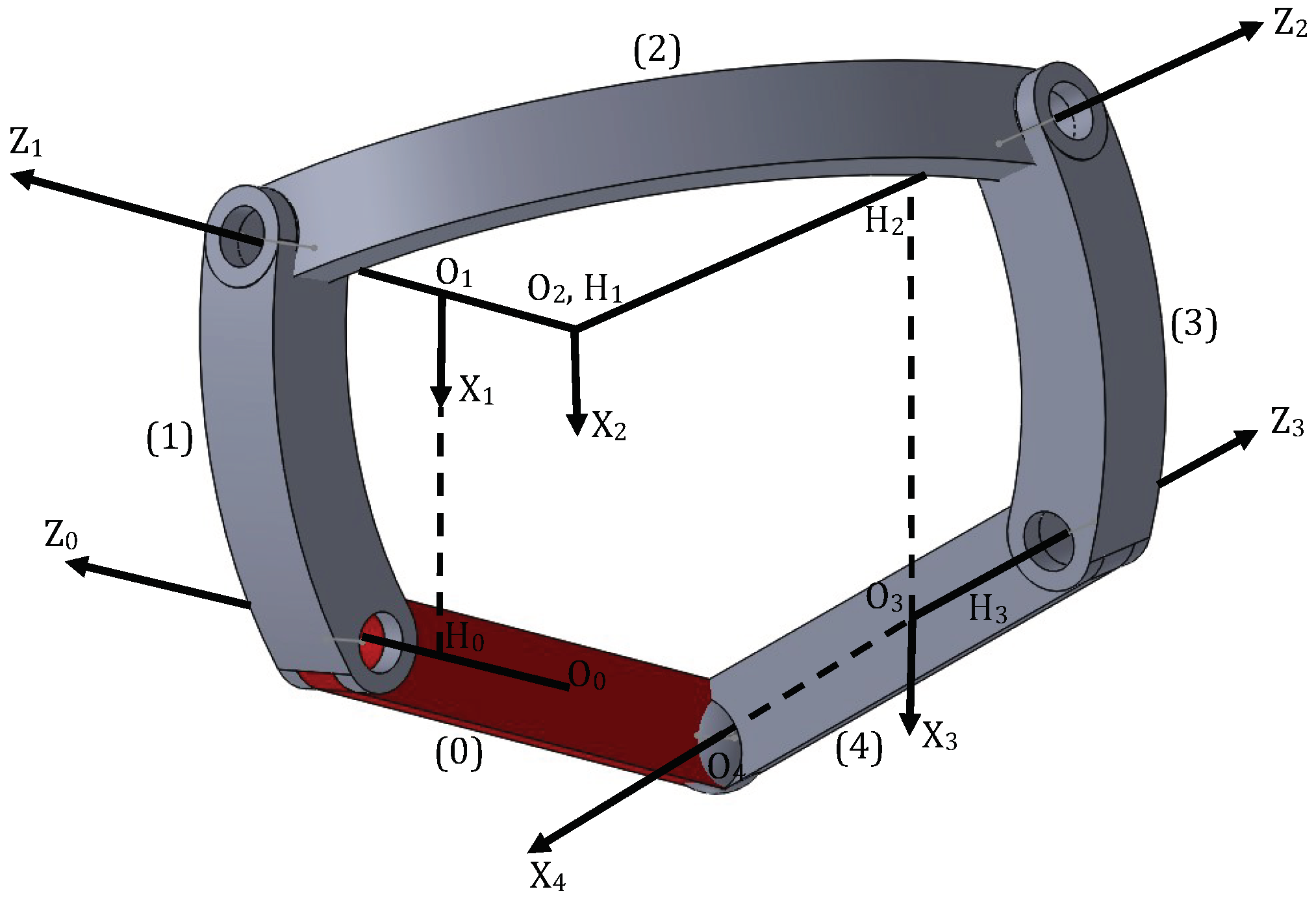
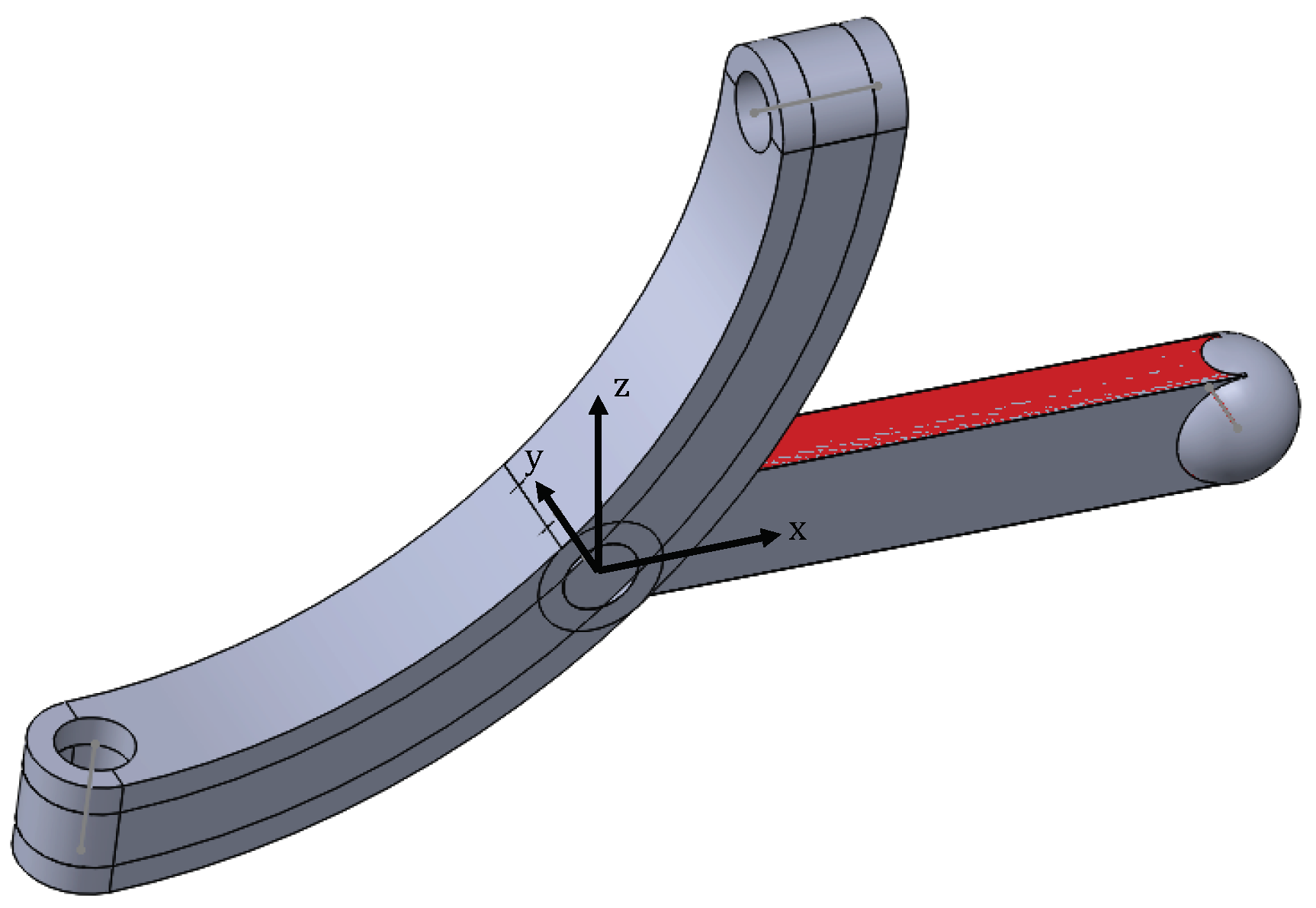
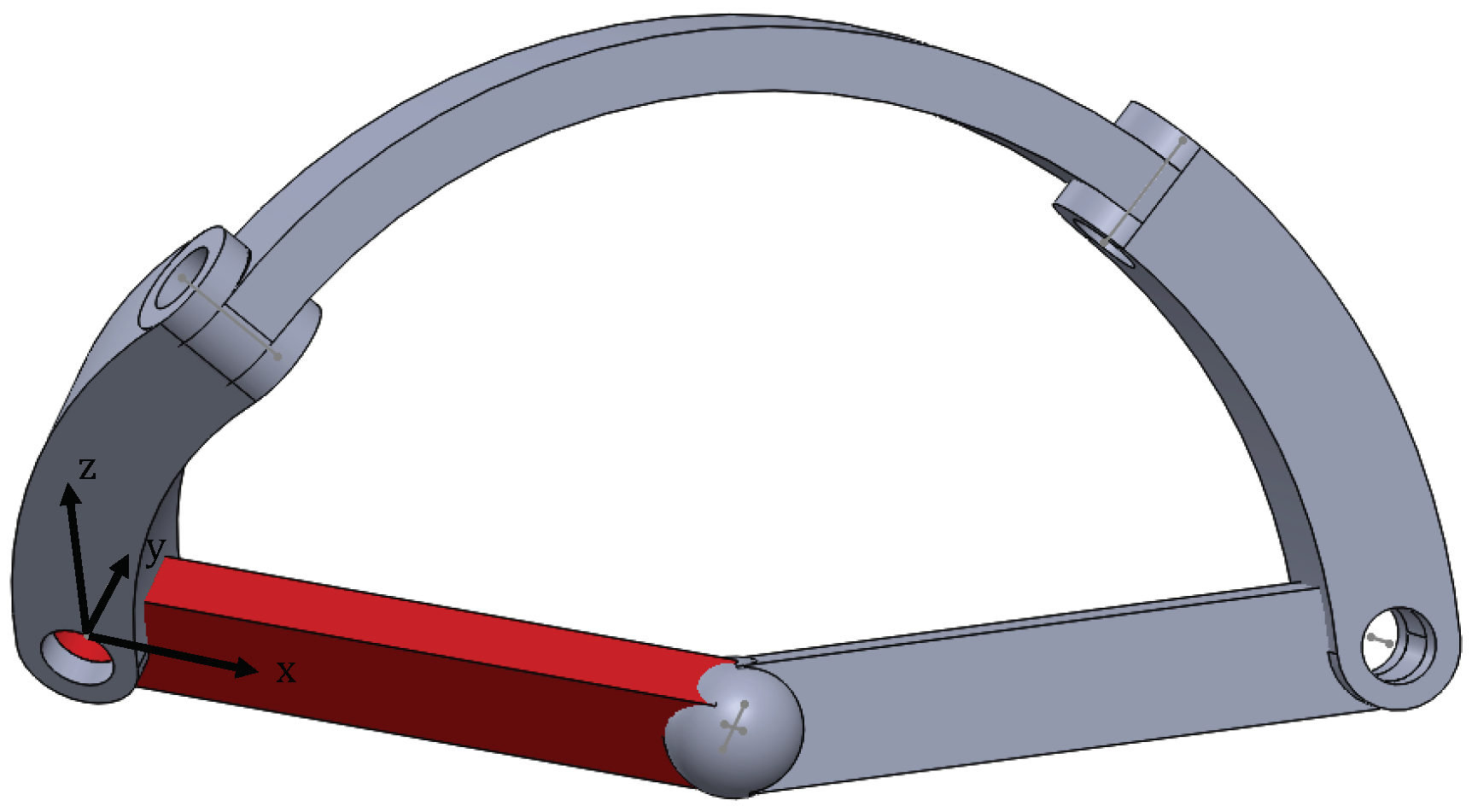
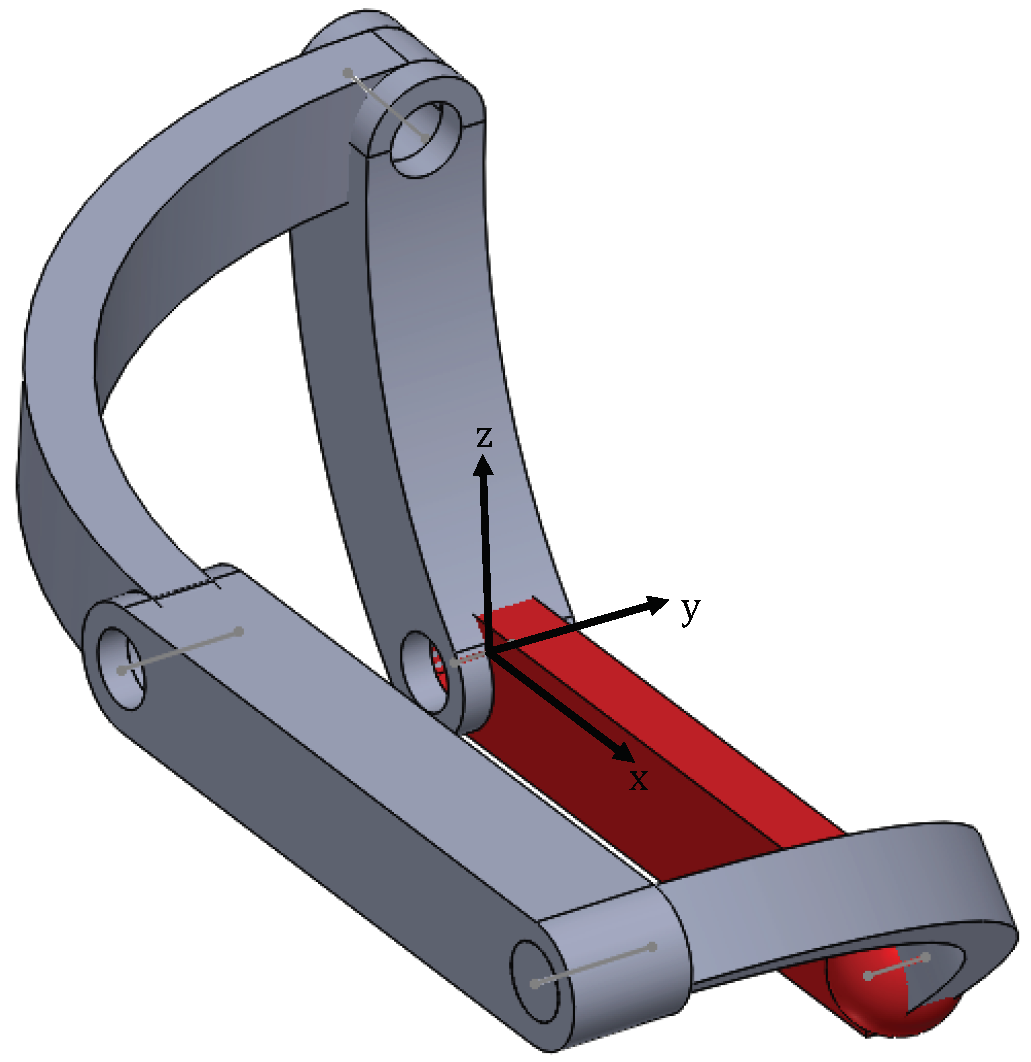
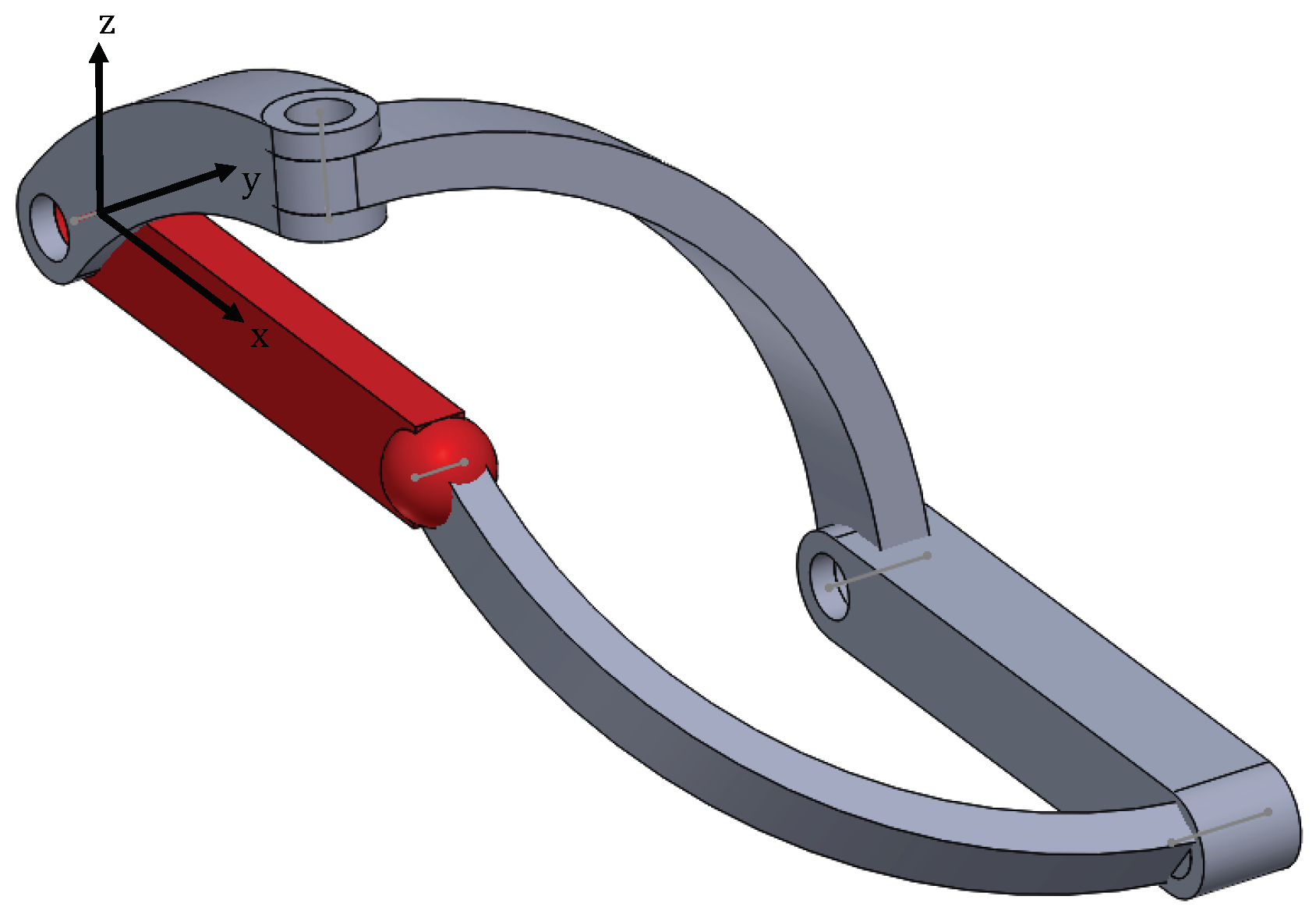
2. Description of the RRRRS Variable-DOF Mechanism
3. Kinematic Analysis
4. Operation Modes
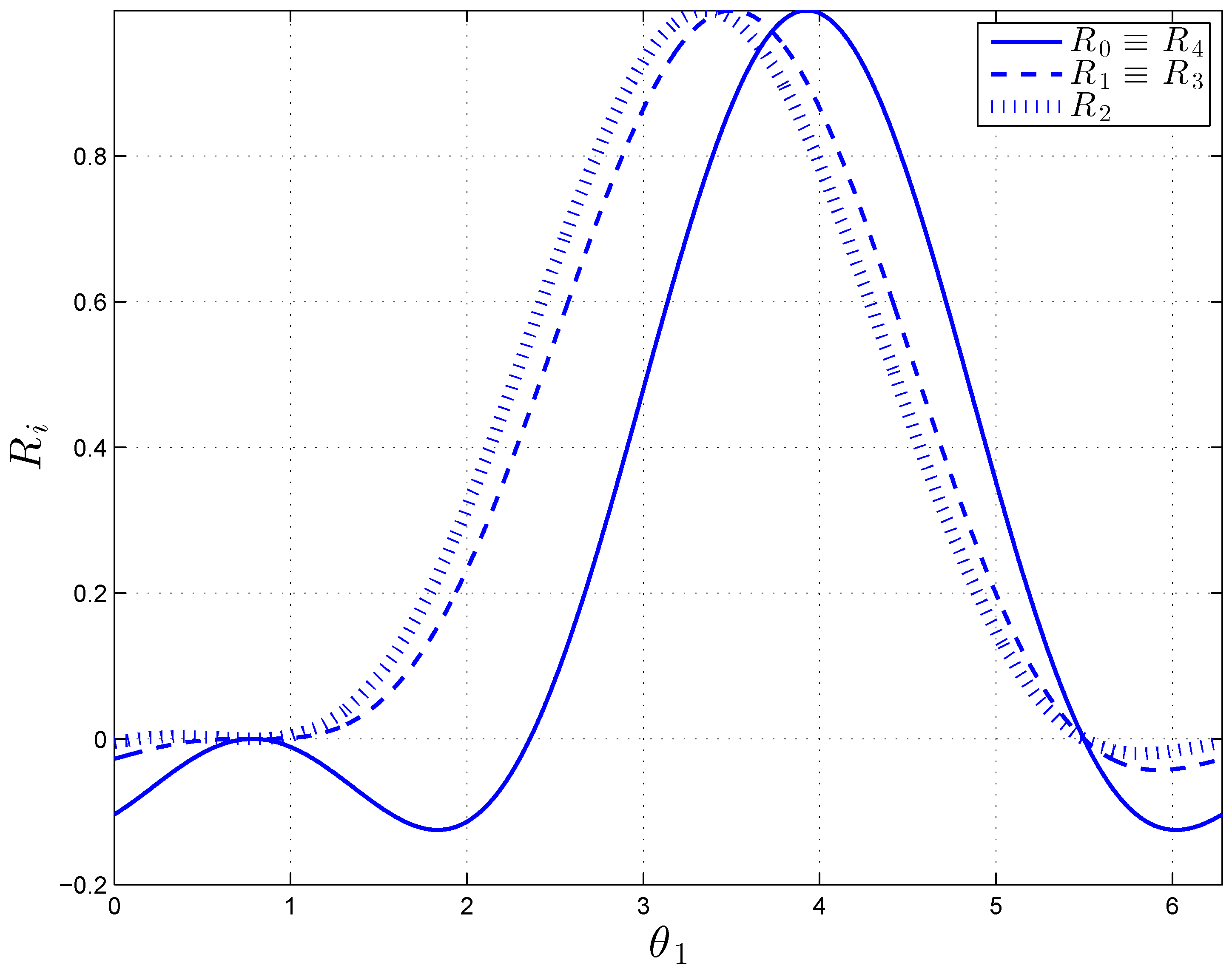
4.1. Perpendicular Architecture
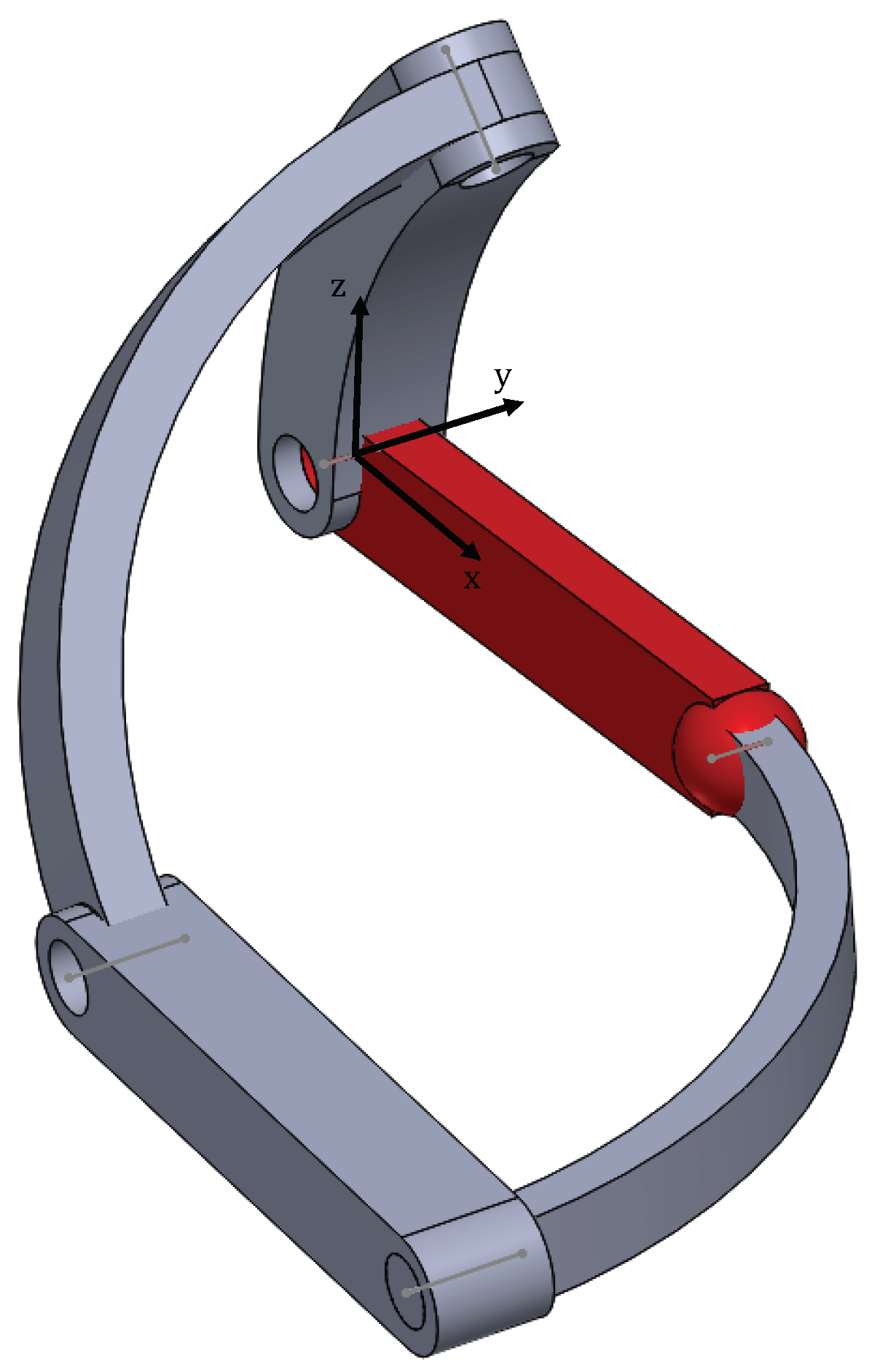
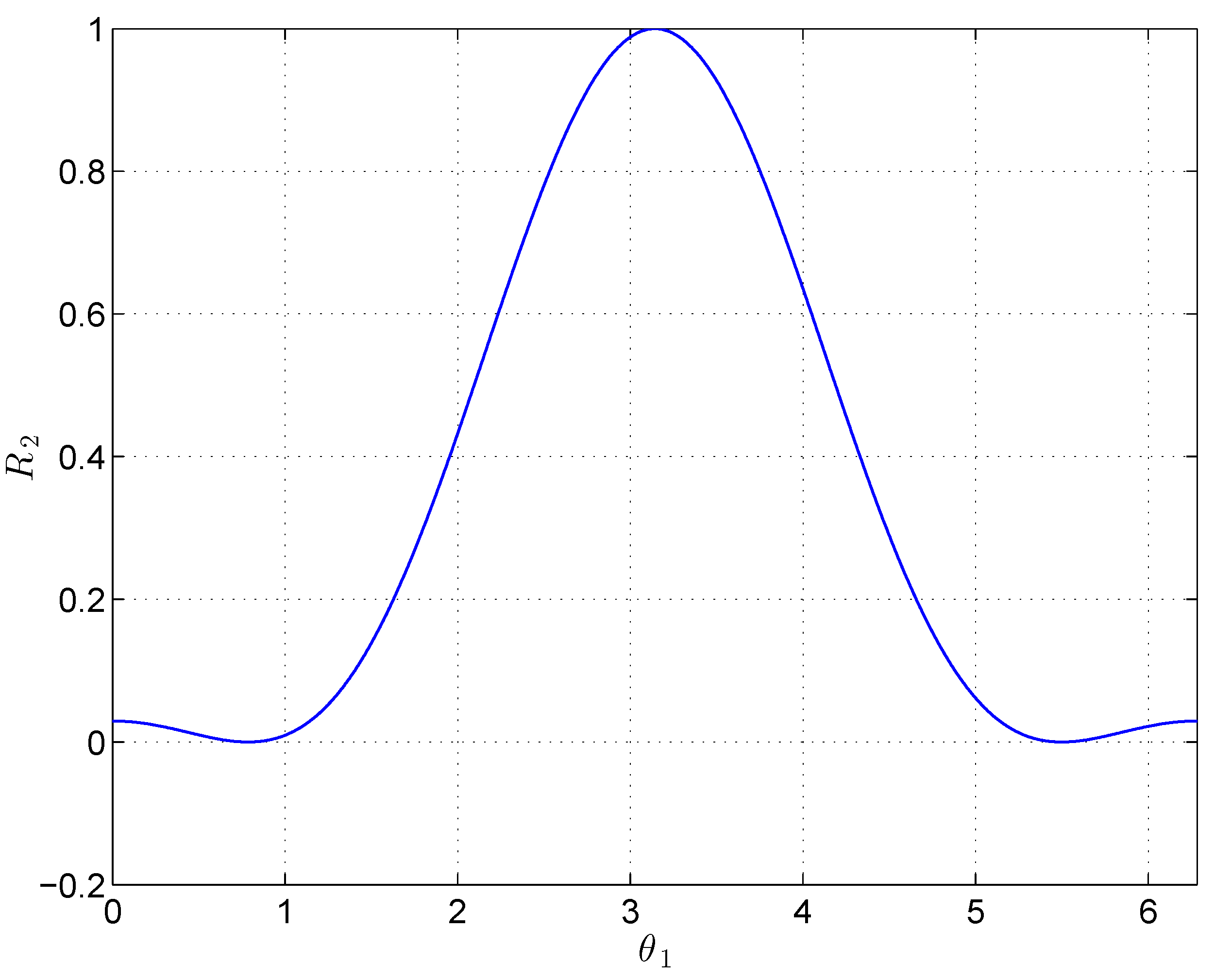
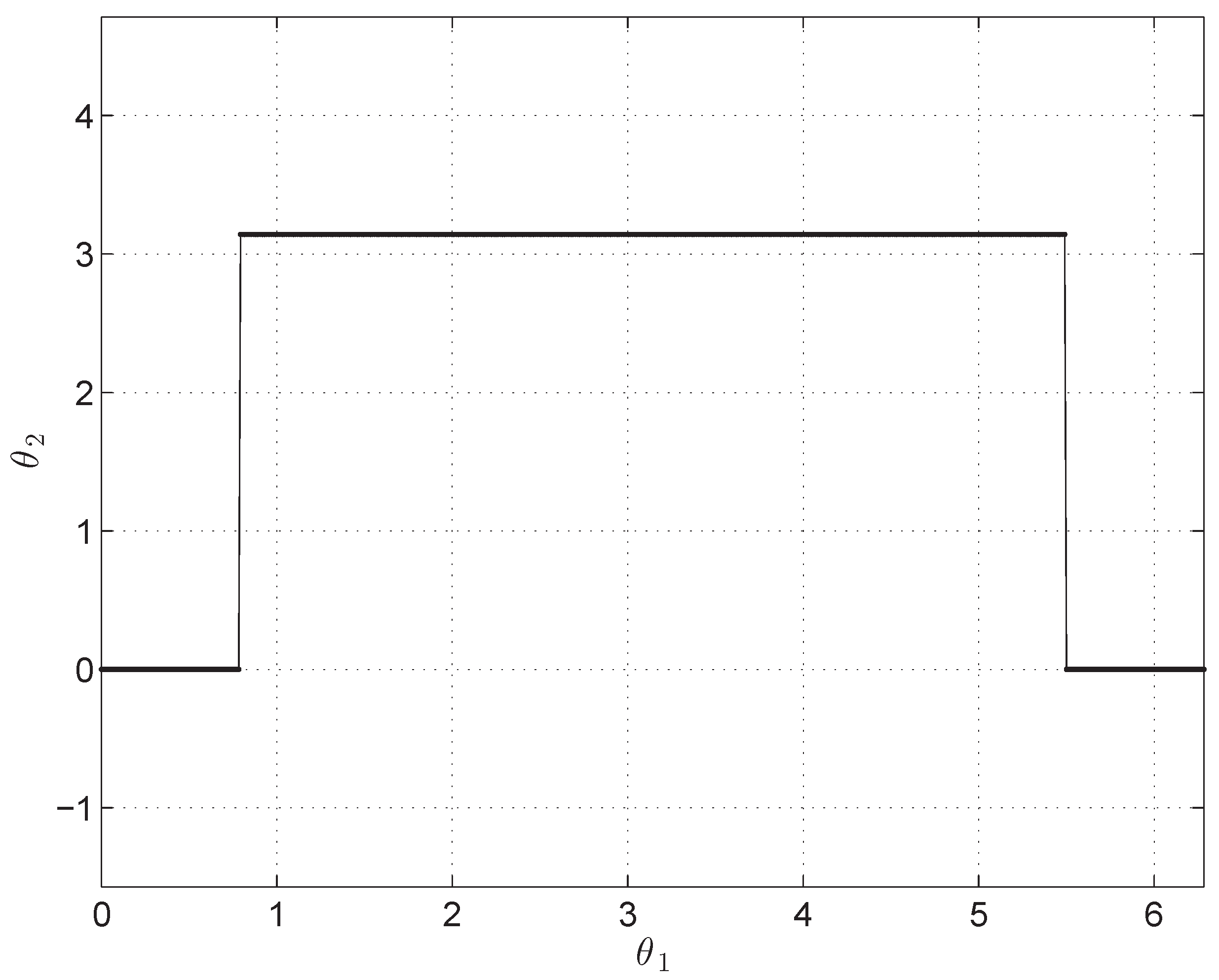
- .In this interval . Indeed, the mechanism is in the folded configuration shown in Figure 5 where the - and -axes coincide and they are perpendicular to the plane formed by the - and -axes. The mechanism has 1 DOF being the rotation about the -axis.As mentioned, there are two exceptions due to the fact that the QME coefficients ’s may all vanish as soon as . In these configurations the mechanism has 2 DOF, can take any value whilst as proved by the first equation of Equation (4). Furthermore, when point coincides with the sperichal joint S: (Figure 6).
- .
4.2. Parallel Architecture
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wohlhart, K. Kinematotropic Linkages. In Recent Advances in Robot Kinematics; Lenarcic, J., Parenti-Castelli, V., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1996; pp. 359–368. [Google Scholar]
- Galletti, C.; Fanghella, P. Single-loop kinematotropic mechanisms. Mech. Mach. Theory 2001, 36, 743–761. [Google Scholar] [CrossRef]
- Fanghella, P.; Galletti, C.; Gianotti, E. Parallel robots that change their group of motion. In Advances in Robot Kinematics; Lenarcic, J., Roth, B., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 49–56. [Google Scholar]
- Lee, C.C.; Hervé, J.M. Discontinuously Movable Seven-Link Mechanisms via Group-Algebraic Approach. Proc. Inst. Mech. Eng. Part C 2005, 219, 577–587. [Google Scholar] [CrossRef]
- Kong, X.; Huang, C. Type Synthesis of Single-DOF Single-Loop Mechanisms with Two Operation Modes, Reconfigurable Mechanisms and Robots; KC Edizioni: Genova, Italy, 2009; pp. 141–146. [Google Scholar]
- Wohlhart, K. Multifunctional 7R Linkages. In Proceedings of the International Symposium on Mechanisms and Machine Theory, AzCIFToMM, Izmir, Turkey, 5 October 2010; Volume 8, pp. 85–91. [Google Scholar]
- Lopez-Custodio, P.C.; Rico, J.M.; Cervantes-Sanchez, J.J.; Perez-Soto, G.I. Reconfigurable Mechanisms from the Intersection of Surfaces. ASME J. Mech. Robot. 2016, 8, 021029. [Google Scholar] [CrossRef]
- Zhang, K.; Muller, A.; Dai, J.S. A Novel Reconfigurable 7R Linkage With Multifurcation. In Advances in Reconfigurable Mechanisms and Robots II; Ding, X., Kong, X., Dai, J.S., Eds.; Springer: Cham, Switzerland, 2015; pp. 15–25. [Google Scholar]
- Huang, C.; Kong, X.; Ou, T. Position Analysis of a Bennett-Based Multiple-Mode 7R Linkage. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009. ASME Paper No. DETC2009-87241. [Google Scholar]
- He, X.; Kong, X.; Chablat, D.; Caro, S.; Hao, G. Kinematic Analysis of a Single-Loop Reconfigurable 7R Mechanism With Multiple Operation Modes. Robotica 2014, 32, 1171–1188. [Google Scholar] [CrossRef]
- Kong, X.; Pfurner, M. Type Synthesis and Reconfiguration Analysis of a Class of Variable-DOF Single-Loop Mechanisms. Mech. Mach. Theory 2015, 85, 116–128. [Google Scholar] [CrossRef]
- Huang, C.; Tseng, R.; Kong, X. Design and Kinematic Analysis of a Multiple-Mode 5R2P Closed-Loop Linkage. In New Trends in Mechanism Science: Analysis and Design, Mechansims and Machine Science 5; Pisla, D., Ed.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Zhang, K.; Dai, J.S. Screw-System-Variation Enabled Reconfiguration of the Bennett Plano-Spherical Hybrid Linkage and its evolved Parallel Mechanism. J. Mech. Des. 2015, 137, 062303. [Google Scholar] [CrossRef]
- He, X.; Kong, X.; Hao, G.; Ritchie, J.M. Design and Analysis of a New 7R Single-Loop Mechanism With 4R, 6R and 7R Operation Modes. In Advances Reconfigurable Mechanisms and Robots II; Ding, X., Kong, X., Dai, J.S., Eds.; Springer: Cham, Switzerland, 2015; pp. 27–37. [Google Scholar]
- Walter, D.R.; Husty, M.L.; Pfurner, M. A complete kinematic analysis of the SNU 3-UPU parallel manipulator, Contemporary Mathematics. Am. Math. Soc. 2009, 496, 331–346. [Google Scholar]
- Kong, X. Reconfiguration analysis of a 3-DOF parallel mechanism using Euler parameter quaternions and algebraic geometry method. Mech. Mach. Theory 2014, 74, 188–201. [Google Scholar] [CrossRef]
- Kong, X.; Yu, J.; Li, D. Reconfiguration Analysis of a Two Degrees-of-Freedom 3-4R Parallel Manipulator with Planar Base and Platform. ASME J. Mech. Robot. 2015, 8, 011019. [Google Scholar] [CrossRef]
- Carbonari, L.; Callegari, M.; Palmieri, G.; Palpacelli, M.C. A new class of reconfigurable parallel kinematic machines. Mech. Mach. Theory 2014, 79, 173–183. [Google Scholar] [CrossRef]
- Nurahmi, L.; Schadlbauer, J.; Caro, S.; Husty, M.; Wenger, P. Kinematic Analysis of the 3-RPS Cube Parallel Manipulator. ASME J. Mech. Rob. 2015, 7, 011008. [Google Scholar] [CrossRef]
- Kong, X. Reconfiguration analysis of a 4-DOF 3-RER parallel manipulator with equilateral triangular base and moving platform. Mech. Mach. Theory 2016, 98, 180–189. [Google Scholar] [CrossRef]
- Kong, X. Reconfiguration Analysis of a Variable Degrees-of-Freedom Parallel Manipulator With Both 3-DOF Planar and 4-DOF 3T1R Operation Modes. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. ASME Paper No. DETC2016-59203. [Google Scholar]
- Coste, M.; Demdah, K.M. Extra Modes of Operation and Self Motions in Manipulators Designed for Schoenflies Motion. ASME J. Mech. Robot. 2015, 7, 041020. [Google Scholar] [CrossRef]
- Nurahmi, L.; Caro, S.; Wenger, P.; Schadlbauer, J.; Husty, M. Reconfiguration Analysis of a 4-RUU Parallel Manipulator. Mech. Mach. Theory 2016, 96 (Pt 2), 269–289. [Google Scholar] [CrossRef]
- Arponen, T.; Piipponen, S.; Tuomela, J. Kinematical Analysis of Wunderlich Mechanism. Mech. Mach. Theory 2013, 70, 16–31. [Google Scholar] [CrossRef]
- Pfurner, M.; Kong, X. Algebraic analysis of a new variable-DOF 7R mechanism. In New Trends in Mechanism and Machine Science, Theory and Industrial Applications; Wenger, P., Flores, P., Eds.; Springer: Berlin, Germany, 2016; pp. 71–79. [Google Scholar]
- Kong, X. Reconfiguration analysis of multimode single-loop spatial mechanisms using dual quaternions. J. Mech. Robot. ASME 2017, 9, 051002. [Google Scholar] [CrossRef]
- Kong, X. A variable-DOF single-loop 7R spatial mechanism with five motion modes. Mech. Mach. Theory 2018, 120, 239–249. [Google Scholar] [CrossRef]
- Angeles, J. Fundamental of Robotic Mechanical Systems, 3rd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]

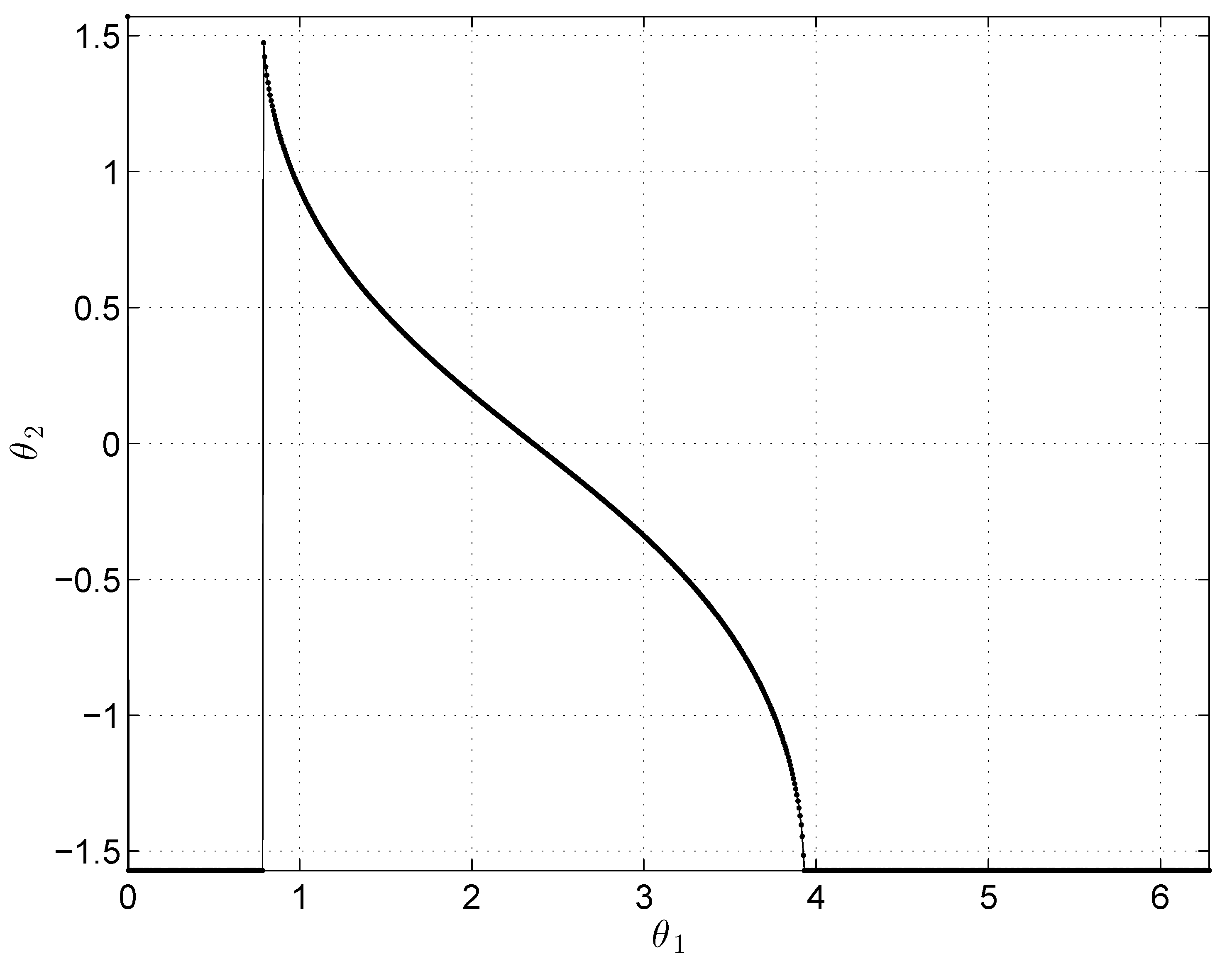
| 0 | ||
| 0 | ||
| 0 |
| 0 | ||
| 0 | ||
| 0 | r | r |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruggiu, M.; Kong, X. Reconfiguration Analysis of an RRRRS Single-Loop Mechanism. Robotics 2018, 7, 51. https://doi.org/10.3390/robotics7030051
Ruggiu M, Kong X. Reconfiguration Analysis of an RRRRS Single-Loop Mechanism. Robotics. 2018; 7(3):51. https://doi.org/10.3390/robotics7030051
Chicago/Turabian StyleRuggiu, Maurizio, and Xianwen Kong. 2018. "Reconfiguration Analysis of an RRRRS Single-Loop Mechanism" Robotics 7, no. 3: 51. https://doi.org/10.3390/robotics7030051
APA StyleRuggiu, M., & Kong, X. (2018). Reconfiguration Analysis of an RRRRS Single-Loop Mechanism. Robotics, 7(3), 51. https://doi.org/10.3390/robotics7030051





