Abstract
This paper describes the design of a robust composite high-order super-twisting sliding mode controller (HOSTSMC) for robot manipulators. Robot manipulators are extensively used in industrial manufacturing for many complex and specialized applications. These applications require robots with nonlinear mechanical architectures, resulting in multiple control challenges in various applications. To address this issue, this paper focuses on designing a robust composite high-order super-twisting sliding mode controller by combining a higher-order super-twisting sliding mode controller as the main controller with a super-twisting higher-order sliding mode observer as unknown state measurement and uncertainty estimator in the presence of uncertainty. The proposed method adaptively improves the traditional sliding mode controller (TSMC) and the estimated state sliding mode controller (ESMC) to attenuate the chattering. The effectiveness of a HOSTSMC is tested over six degrees of freedom (DOF) using a Programmable Universal Manipulation Arm (PUMA) robot manipulator. The proposed method outperforms the TSMC and ESMC, yielding 4.9% and 2% average performance improvements in the output position root-mean-square (RMS) error and average error, respectively.
1. Introduction
Robot manipulators are extensively used in industry for specialized tasks. These systems are nonlinear, time-varying, and dynamically coupled. Thus, the design of a robust and stable controller for these systems is very complicated. In recent years, research in the field of control techniques for industrial robots has increased. The performance of industrial robot manipulators has increased in terms of stability and safety due to developments in robust controller design, fault diagnosis algorithms and fault tolerant techniques. Nevertheless, designing a stable and reliable control method for a robot manipulator is important for real-world applications [1,2].
Several types of controllers have been developed for robot manipulators. These controllers can be divided into two main categories: linear control algorithms and nonlinear control theories. For linear controllers, there are two challenges to overcome related to the coupling effect, i.e., limitations on the velocity and acceleration of systems, and an increase in the gear ratio for linearization [3]. Because of these restrictions on linear controllers, nonlinear controllers are recommended in this research. Nonlinear control algorithms are divided into three main categories: model-based control algorithms, soft computing (artificial intelligence)-based control theory and hybrid control procedures. The main advantage of a nonlinear model-free controller is system knowledge, which has been improved by researchers over the years [2,4,5,6,7]. Although it has several advantages, this method has challenges associated with system reliability and robustness. Model reference control algorithms are recommended to improve the stability, robustness, and reliability. The feedback linearization technique (FLC), back-stepping control algorithm (BSC), passivity-based control (PBC), Lyapunov-based algorithm (PBC) and sliding mode control (SMC) are popular methods for designing model-based controllers. However, selecting a suitable control technique is a major challenge for many researchers [4,5,6,7,8,9].
A feedback linearization algorithm is a powerful nonlinear technique for the control of a robot manipulator [4,5]. Although it has several advantages, this method has three significant challenges associated with extreme dynamic dependency on the system, robustness, and the need for an acceleration sensor. To overcome these challenges, a TSMC is a good candidate [6,7,8,9]. This controller is an excellent candidate for systems, which operate in uncertain and noisy conditions. Apart from several advantages such as stability and reliability, a SMC must overcome the problems of chattering and robustness [8,9,10,11,12,13].
Several techniques have been proposed for attenuating the chattering in sliding mode controllers, such as saturation continuous control technique [8,9], fuzzy-based boundary layer function [10], fuzzy sliding mode controller [11], adaptive fuzzy sliding mode controller [12,13], output feedback techniques [14,15,16], observation technique [17,18,19,20], gain scheduling method [21,22,23], state estimation techniques [24,25], and higher-order sliding mode control [26,27,28]. Although saturation continuous control technique reduces chattering in a conventional sliding mode controller, it increases the performance error and decreases the dynamic response of the system. To improve the performance of saturation continuous control technique [8,9], Palm [10] defined a PD-fuzzy-based nonlinear boundary layer function and applied it to a TSMC. Although this procedure solves the chattering and improves performance error, tuning the gain updating factors in the fuzzy section remains a challenge for this algorithm. To solve the challenge of designing a nonlinear intelligent saturation continuous control algorithm [10], Wu et al. [11] have proposed a PI fuzzy SMC (FSMC). The main drawback of their method is sensitivity to the uncertainty caused by chattering. To reduce the sensitivity to uncertainty, improve robustness and reduce chattering, an adaptive FSMC was proposed [12,13]. Apart from the different advantages of adaptive techniques, a TSMC has an important drawback in its real-time implementation. Rubio et al. [14] have presented an observer-less stable regulator sliding mode controller to attenuate the chattering in the presence of uncertainty. To improve the chattering attenuation in the immeasurable states, sliding mode observers have been presented in [17,18,19,20]. Piltan et al. [23] have presented the adaptive fuzzy gain scheduling technique to reduce the chattering in internal combustion engine. Liu et al. [25] have proposed an extended-state observer for three-phase power converters in the presence of uncertainties and disturbances. They propose a composite control law consisting of sliding mode control technique and an extended state observe to improve the performance of disturbance rejection, uncertainty estimation, and the reduction of chattering.
Among these methods, HOSMC is suitable for reducing chattering and obtaining a smooth signal. HOSMC works with a discontinuous control algorithm on the higher-order time derivative. Thus, chattering is attenuated by moving the switching to higher derivatives in HOSMC. Apart from their various advantages, the sub-optimal HOSMC [29], the quasi-continuous HOSMC [30], and the twisting HOSMC [31], have a critical limitation of using the first-time derivative of the sliding variable. To overcome the above limitation, a higher-order super-twisting sliding mode control technique has been recommended in [32]. To measure the unknown inputs, i.e., external disturbances, and improve the estimation of uncertainties, an observation technique is recommended [33]. For immeasurable state observers, and high accuracy velocity estimation without filtration, the super-twisting higher order sliding mode observer (STHOSMO) was proposed [33,34,35,36]. In this paper, we propose a robust high-order super-twisting sliding mode observer-controller to control a 6-DOF robot manipulator. First, a traditional sliding mode controller for robot manipulator is designed and the disadvantages of this method are discussed. Then, to estimate velocity and reduce chattering, an estimated-state sliding mode controller based on the observation technique is designed. Furthermore, to improve the uncertainty estimation, accuracy, and attenuate the chattering, a higher-order super-twisting sliding mode controller is combined with super-twisting higher-order sliding mode observer (STHOSMO). The stability and convergence are presented based on the Lyapunov technique. The main objective is to design a chattering-free and robust HOSTSMC for industrial robots. The rest of this paper is organized as follows: Section 2 gives the problem statement and control objectives. Section 3 provides the design for a TSMC, ESMC, STHOSMO and HOSTSMC to control a 6-DOF robot manipulator. Results and discussion are presented in Section 4. Section 5 gives the conclusions.
2. Problem Statement and Control Objectives
The main challenge in this study is to control multiple degrees of freedom in a robot manipulator based on a higher-order super-twisting sliding mode controller, in the presence of uncertainty and disturbance. The corresponding Lagrange formulation consists of disturbance, uncertainty, and generalized torque as described below:
If , the Lagrange dynamic formulation of robot manipulator can be written as follows:
where and are an torque vector, disturbance of load vector, time variant inertial matrix, time variant nonlinearity term matrix, time variant gravity vector, friction matrix, time variant Coriolis force matrix, time variant centrifugal matrix, unknown modeling parameters, position vector, velocity vector, and acceleration vector, respectively. To simplify the modeling and analysis, (1) is re-written in the following formulation.
where are nonlinearity parameters robot modeling uncertainties vector, , and represent the modeling uncertainty of the robot manipulators. It is assumed that the uncertainty is bounded as follows:
where is a constant. Based on (3), the main objective of this work is to control the robot arm in the presence of uncertainty. Therefore, HOSTSMC is recommended for improving robot performance in certain and uncertain operation models. The general block diagram for controlling robot manipulators is depicted in Figure 1. The control objectives for a robot manipulator in the presence of uncertainty are defined in (5) and (6):
where are the actual and desired positions, respectively. Reduce or attenuation the chattering as follows:
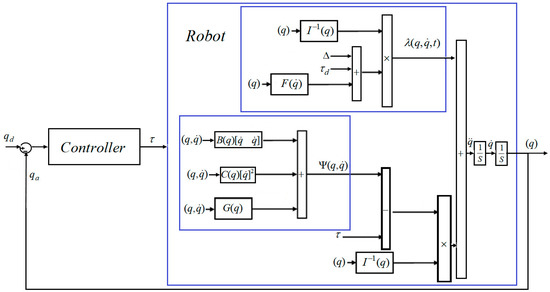
Figure 1.
Robot manipulator dynamic and control.
3. Proposed Method
There are different kinds of disturbances, such as parameter uncertainties and load variations, which can affect the control of a robot manipulator. Designing a controller that is robust against such disturbances requires improving the performance of the robot manipulator. A HOSTSMC is used to govern the robot manipulator. For position tracking, a HOSTSMC is designed to achieve faster convergence of the actual positions to the desired positions in the presence of uncertainty. First, a TSMC will be briefly discussed. Second to reduce chattering, ESMC will be analyzed. Third, to attenuate the chattering and improve the accuracy, the design of a HOSTSMC will be presented.
3.1. Traditional Sliding Mode Control Algorithm
As the robot manipulator is a highly nonlinear system with multiple degrees of freedom and coupling effects, hence, if and , the Lagrange formulation of the robot manipulator can be written in state space form as follows [1]:
where and . In the TSMC, the main challenge is reaching the desired control in a finite amount of time. Thus, first a sliding surface is designed that converges to zero, and then a control technique is designed that improves the system response time to reach the sliding surface in a minimum time. The controller has two main parts, the first part , is used to control the nominal system, the next part , is used for compensation.
Based on [37] the TSMC for a robot manipulator is obtained by the following formulation:
where and are sliding mode control output, sliding mode part to compensate for the effects of uncertainty (switching mode part of control law), model-reference part of control law, the error, desired state, sliding surface, positive constant sliding surface slope, derivative of sliding surface, estimate of , and sliding mode constant chosen based on [38], respectively. Based on [39], the Lyapunov function for TSMC is defined by
Similarly, the derivative of Lyapunov function is defined by the following formulation [39]:
where is a constant. For .
Based on (11) it can be shown that
Based on (12), , and it can converge to zero in finite time. Figure 2 illustrates the block diagram of TSMC for a robot arm. Though, TSMC is a stable controller but chattering and velocity estimation are the main drawbacks of this controller. To solve these challenges the ESMC is introduced in the next part.
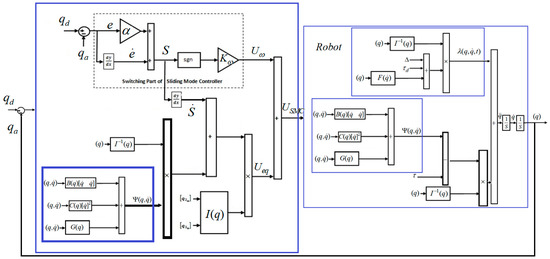
Figure 2.
Block diagram of TSMC for robot arm.
3.2. Estimated State Sliding Mode Control
As described above, the performance of TSMC is measured by severity of chattering. To reduce the chattering, estimated-state sliding mode controller is introduced. This method reduces the chattering based on estimated uncertainties. This controller has three main parts, the first part is used to control the nominal system , the next part is proposed to compensate the uncertainty and unknown input , and the third part is for compensating the error observation based on state estimation. The mathematical formulation of ESMC is given as follows:
where and are designed to compensate for the uncertainty based on output error injection, to compensate for the error, and are the sliding mode coefficient, and uncertainty estimate, respectively. Different techniques have been used to estimate , such as observation techniques [31,37]. To solve the problem of estimating , a 3rd order super-twisting sliding mode observer (STSMO) is recommended. In ESMC, the estimated uncertainty is bounded by . According to [38], the sliding surface converges to zero if . It is clear that , so in (14) is smaller than in (8), so the chattering generated by EMC is significantly reduced compared to TSMC.
Figure 3 illustrates the block diagram of ESMC for a robot manipulator. According to [32,40], the 3rd order STSMO is obtained by the following formulations:
where and are the state estimates, sliding mode gains and observer injection, respectively. The observer injection is designed to reduce the error of system estimation. Based on (7) and (14), the state estimation error is obtained by the following formulation:
where and Based on (4), if we defined a constant, () and , then according to [32,40,41] the convergence and stability can be guaranteed by defining the sliding gains as follows:
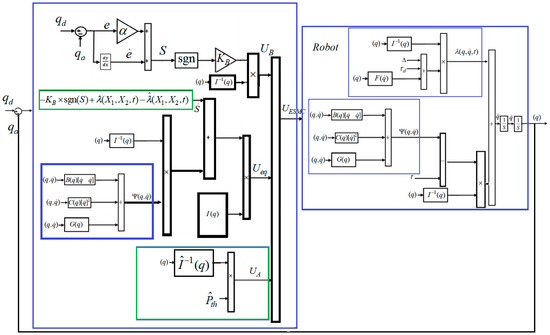
Figure 3.
Block diagram of ESMC for robot arm.
Based on convergence theory and (16), the state estimations converge to the nominal states and based on (15), we can extract the following equation:
Therefore, the uncertainties can be estimated based on the following formulation:
Based on (14) and (18), the uncertainties are estimated by observation technique. Based on (13), the main positive point of ESMC is to compensate the uncertainties based on observer injection in order to reduce chattering. Based on (15)–(17) the super-twisting higher order sliding mode observer has a finite time convergence. Thus, the TSMC and super-twisting higher-order sliding mode observer can be designed separately, and their stability can be verified separately.
3.3. Proposed Method
According to (13), the ESMC reduces chattering by reducing the sliding mode gain compared to TSMC, however, it cannot attenuate it. To attenuate the chattering and improve the performance of the ESMC and the TSMC, the HOSTSMC is proposed. The block diagram of the proposed method is shown in Figure 4. A discontinuous function is used in this method, but based on the integral term the overall chattering is attenuated by improving the estimation of uncertainties. The main contribution of the proposed observer-controller is to control the robot manipulator in the presence of uncertainty without velocity measurement by combining higher-order super-twisting sliding mode controller with super twisting higher order sliding mode observer.
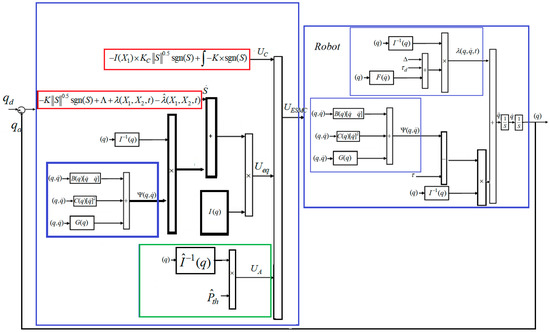
Figure 4.
Block diagram of HOSTSMC for robot manipulator.
The new control function is defined by the following formulation [42]
where and are the control function and sliding mode coefficient, respectively. Under the condition, i.e., , the compensation for the dynamic sliding variable is calculated by:
Based on the integration of (20), we have [42]:
and based on (21), the reaching time is
where is the reaching time. Thus, sliding variable converges to zero in finite time. In the next step, under uncertain condition (), the compensation for the dynamic sliding variable is defined by:
If the uncertainties are estimated and cancelled, the dynamic sliding variable converges to the zero in finite time.
where and are the control input, sliding mode coefficient, and super-twisting variable, respectively. The compensation for the dynamic sliding variable is defined as follows:
Based on (24), the new control technique solves the challenge of uncertainty estimation in finite time and based on (24), and (20), the sliding surface converges to zero in finite time. The equation (25) is called the super-twisting control algorithm. This technique drives and to convergence to zero in finite time. Thus, the HOSTSMC is defined by the following formulations:
According to (26), the control input is based on the higher order super twisting sliding mode control algorithm and to compensate the uncertainties, a super-twisting higher-order sliding mode observer is designed. Based on [43,44] the sliding mode coefficients are calculated as follows to guarantee the stability and the convergence of the sliding surface to zero:
Based on [31,32,41] the super-twisting higher order sliding mode observer has a finite time convergence. Thus, the stability of higher-order super-twisting sliding mode controller and super-twisting higher-order sliding mode observer has been guaranteed separately. The stability of higher-order super-twisting sliding mode controller for any match uncertainties has been proved by Kamal and Bandyopadhyay in [45]. The authors in [32,40,41] have demonstrated the robustness of super-twisting higher-order sliding mode observer to uncertainties. Therefore, the proposed method can be used for the control of an uncertain robot manipulator without stability problems. Based on [44], the Lyapunov function for the proposed controller is defined by
The derivative of Lyapunov function is defined by the following formulation [44]:
If the band of uncertainty is defined by the following equation
where is a positive constant. Then, based on (29) it can be shown that
Based on [44] if then, . It is clear that based on (27), and according to (27), it can converge to zero in finite time.
4. Results and Analysis
The effectiveness of the proposed method, ESMC, and TSMC are evaluated using 6-DOF, PUMA robot arm, which is shown in Figure 5. To examine the power of the control algorithm based on the HOSTSMC, we investigate two cases defined as follows.
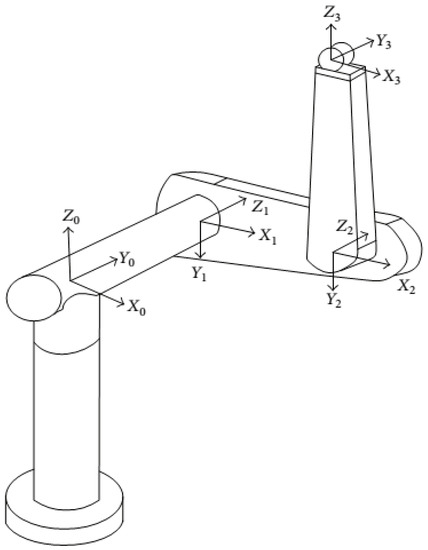
Figure 5.
PUMA robot manipulator.
A. Certain Conditions
Figure 6, Figure 7 and Figure 8, demonstrate the robot’s joint signals, torque signals, and output position’s RMS error signal in the TSMC, ESMC and HOSTSMC under certain conditions.
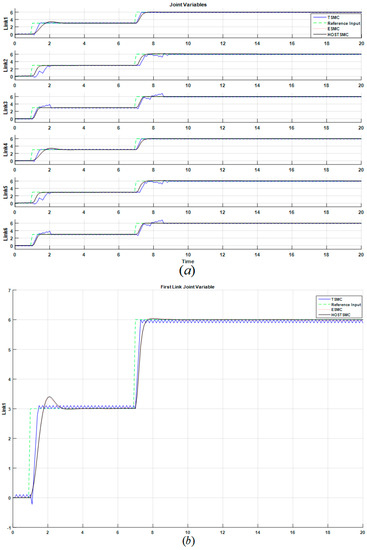
Figure 6.
Joint variables signals in the TSMC, ESMC, and HOSTSMC: (a) all joints, (b) First link (certain condition).
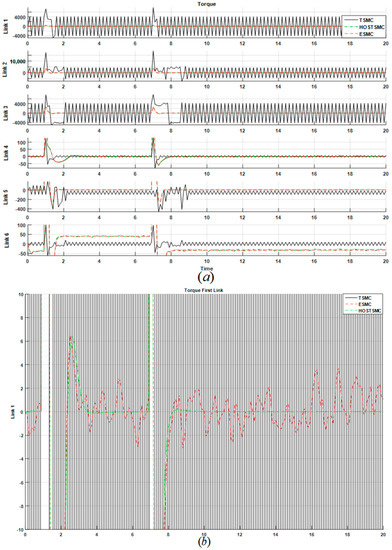
Figure 7.
Torque signals in the TSMC, ESMC, and HOSTSMC: (a) all joints, (b) First link (certain condition).
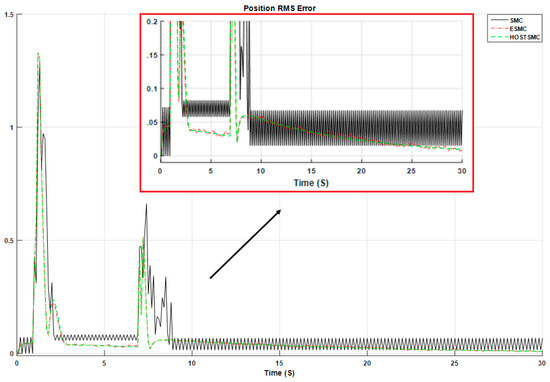
Figure 8.
RMS error signals in the TSMC, ESMC, and HOSTSMC (certain condition).
Based on Figure 6, the ESMC and the HOSTSMC both reduce chattering under certain conditions. The ESMC reduces chattering, but it has fluctuations compared to HOSTSMC (Figure 7). Figure 7 shows the torque signals in robot manipulator for TSMC, ESMC and HOSTSMC. Though, the ESMC improves the chattering of TSMC, it has fluctuations compared to the HOSTSMC. The output position based on the forward kinematics formulations in PUMA robot manipulator is calculated by the following formulations [46]:
where and are output position, desired and actual joint variables, and number of joint variables, respectively. According to Equations (32)–(34), the RMS error for output position is defined as follows:
where and are RMS errors of output position, desired position, and actual position, respectively. Figure 8 illustrates the position RMS error signals in the TSMC, ESMC and HOSTSMC. According to this figure, the error signals in the ESMC and HOSTSMC converge to zero.
B. Uncertain Conditions
Figure 9, Figure 10 and Figure 11, illustrate the robot’s joint signals, torque signals, and output position’s RMS error signal in the TSMC, ESMC and HOSTSMC, respectively, in the presence of uncertainty. In the presence of uncertainty, based on Figure 9 and Figure 10, the TSMC has chattering and the ESMC has fluctuations. The HOSTSMC is more robust than the TSMC and the ESMC. Figure 6, Figure 7, Figure 9, and Figure 10 show that, though, TSMC has chattering in the presence of uncertainty, nevertheless, it is more robust than most of the traditional nonlinear model reference controllers e.g., feedback linearization method. Figure 11 demonstrates the comparison between output position RMS error signals in the TSMC, ESMC, and HOSTSMC in the presence of uncertainty.
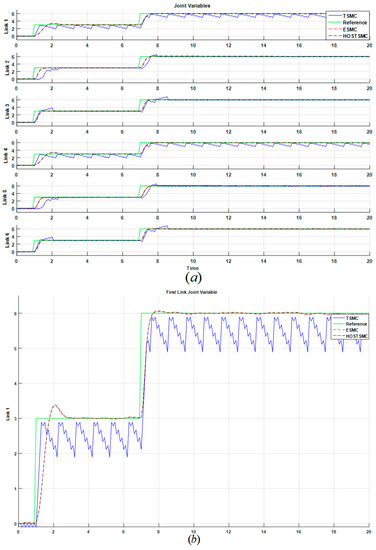
Figure 9.
Joint variables signals in the TSMC, ESMC, and HOSTSMC: (a) all joints, (b) First link (Uncertain condition).
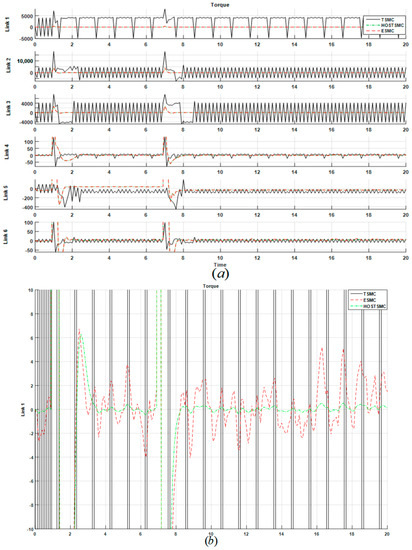
Figure 10.
Torque signals in the TSMC, ESMC, and HOSTSMC: (a) all joints, (b) First link (Uncertain condition).
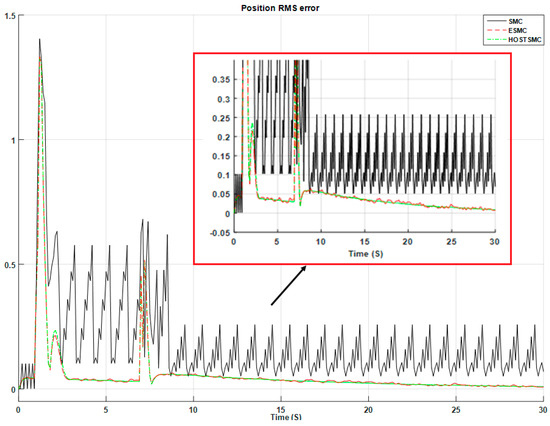
Figure 11.
RMS error signals in the TSMC, ESMC, and HOSTSMC (uncertain condition).
Based on this figure, the error signals in the ESMC and HOSTSMC converge to zero. According to the results in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, we can see that our proposed method is highly effective in controlling the robot arm in both certain and uncertain conditions. To further validate our technique, we calculate the control accuracy for these three techniques with the RMS and average position error analysis.
Table 1 and Table 2 show the control accuracy of a TSMC, ESMC and HOSTSMC in terms of each type of error. As shown in Table 1 and Table 2, the HOSTSMC outperforms the state-of-the-art, and yields 4.9%, and 2%, average performance improvement compared to TSMC and ESMC, respectively. This performance improvement can be further validated by the fact that the HOSTSMC is highly effective in controlling the robot manipulator, as shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.

Table 1.
RMS Error Result in SMC, ESMC, and STSMC in Certain and Uncertain Conditions.

Table 2.
Average Error Result in SMC, ESMC, and STSMC in Certain and Uncertain Conditions.
5. Conclusions
This paper presented a nonlinear model-based method by combining higher-order super-twisting sliding mode controller with a super-twisting higher-order sliding mode observer as an undefined and uncertain input estimator for robot manipulators. Robot manipulators are composed of uncertain dynamic parameters and include coupling effects, thus the design of a robust controller for these systems is highly desirable. A HOSTSMC is a robust controller-observer for nonlinear systems in the presence of uncertainty. The effectiveness of HOSTSMC is tested using a PUMA robot manipulator model, which outperforms the TSMC and ESMC, yielding 4.9%, and 2% average performance improvements in terms of RMS and average output position error, respectively. Based on the results and analysis, the proposed method attenuates chattering in the presence of uncertainty and disturbance. In the future, other types of controller-observer will be designed for perturbation attenuation, fault diagnosis and fault tolerance. The extended state observer will be combined with higher-order super-twisting sliding mode observer-controller to improve fault diagnosis and tolerance in a faulty system.
Acknowledgments
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy (MOTIE) of the Republic of Korea (No. 20162220100050, No. 20161120100350, and No. 20172510102130). It was also funded in part by The Leading Human Resource Training Program of the Regional Neo industry through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and future Planning (NRF-2016H1D5A1910564) and in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2016R1D1A3B03931927).
Author Contributions
S. T.-H., F. P. and J.-M. K. contributed equally to the conception of the idea, the design of experiments, the analysis and interpretation of results, and the writing and improvement of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Siciliano, B.; Khatib, O. (Eds.) Springer Handbook of Robotics; Springer: Berlin, Germany, 2016; pp. 67–90. [Google Scholar]
- Ngoc Son, N.; Anh, H.P.H.; Thanh Nam, N. Robot manipulator identification based on adaptive multiple-input and multiple-output neural model optimized by advanced differential evolution algorithm. Int. J. Adv. Robot. Syst. 2016, 14. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Seth Hutchinson, and Mathukumalli Vidyasagar. In Robot Modeling and Control; Wiley: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Alonge, F.; Cirrincione, M.; Pucci, M.; Sferlazza, A. Input–output feedback linearization control with on-line MRAS-based inductor resistance estimation of linear induction motors including the dynamic end effects. IEEE Trans. Ind. Appl. 2016, 52, 254–266. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, M.S.; Blaabjerg, F. Direct torque control with feedback linearization for induction motor drives. IEEE Trans. Power Electron. 2017, 32, 2072–2080. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009; Volume 34. [Google Scholar]
- Li, H.; Wang, J.; Shi, P. Output-feedback based sliding mode control for fuzzy systems with actuator saturation. IEEE Trans. Fuzzy Syst. 2016, 24, 1282–1293. [Google Scholar] [CrossRef]
- Slotine, J.J.; Sastry, S. Tracking control of non-linear systems using sliding surfaces, with application to robot manipulators. Int. J. Control 1983, 38, 465–492. [Google Scholar] [CrossRef]
- Slotine, J.J.E. Sliding controller design for non-linear systems. Int. J. Control 1984, 40, 421–434. [Google Scholar] [CrossRef]
- Palm, R. Sliding mode fuzzy control. In Proceedings of the IEEE International conference on Fuzzy Systems, San Diego, CA, USA, 8–12 March 1992; pp. 519–526. [Google Scholar]
- Wu, B.; Dong, Y.; Wu, S.; Xu, D.; Zhao, K. An integral variable structure controller with fuzzy tuning design for electro-hydraulic driving Stewart platform. In Proceedings of the 1st International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, 19–21 January 2006; pp. 940–945. [Google Scholar]
- Barrero, F.; Gonzalez, A.; Torralba, A.; Galvan, E.; Franquelo, L.G. Speed control of induction motors using a novel fuzzy sliding-mode structure. IEEE Trans. Fuzzy Syst. 2002, 10, 375–383. [Google Scholar] [CrossRef]
- Shahnazi, R.; Shanechi, H.M.; Pariz, N. Position control of induction and DC servomotors: A novel adaptive fuzzy PI sliding mode control. IEEE Trans. Energy Convers. 2008, 23, 138–147. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Soriano, E.; Juarez, C.F.; Pacheco, J. Sliding mode regulator for the perturbations attenuation in two tank plants. IEEE Access 2017, 5, 20504–20511. [Google Scholar] [CrossRef]
- Aguilar-Ibañez, C. Stabilization of the PVTOL aircraft based on a sliding mode and a saturation function. Int. J. Robust Nonlinear Control 2017, 27, 843–859. [Google Scholar] [CrossRef]
- De Jesús Rubio, J. Sliding mode control of robotic arms with dead-zone. IET Control Theory Appl. 2016, 11, 1214–1221. [Google Scholar] [CrossRef]
- Aguilar-Ibañez, C.; Sira-Ramirez, H.; Acosta, J.Á. Stability of active disturbance rejection control for uncertain systems: A Lyapunov perspective. Int. J. Robust Nonlinear Control 2017, 27, 4541–4553. [Google Scholar] [CrossRef]
- De Jesús Rubio, J. Hybrid controller with observer for the estimation and rejection of disturbances. ISA Trans. 2016, 65, 445–455. [Google Scholar] [CrossRef] [PubMed]
- De Wit, C.C.; Slotine, J.J. Sliding observers for robot manipulators. Automatica 1991, 27, 859–864. [Google Scholar] [CrossRef]
- Spurgeon, S.K. Sliding mode observers: A survey. Int. J. Syst. Sci. 2008, 39, 751–764. [Google Scholar] [CrossRef]
- Palm, R.; Driankov, D. Stability of fuzzy gain-schedulers: Sliding-mode based analysis. In Proceedings of the Sixth IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 5 July 1997; Volume 1. [Google Scholar]
- Xu, J.X.; Pan, Y.J.; Lee, T.H. A gain scheduled sliding mode control scheme using filtering techniques with applications to multilink robotic manipulators. J. Dyn. Syst. Meas. Control 2000, 122, 641–649. [Google Scholar] [CrossRef]
- Piltan, F.; Sulaiman, N.A.S.I.R.I.; AsadiTalooki, I. AsadiTalooki. Evolutionary Design on-line Sliding Fuzzy Gain Scheduling Sliding Mode Algorithm: Applied to Internal Combustion Engine. Int. J. Eng. Sci. Technol. 2011, 3, 7301–7308. [Google Scholar]
- Li, F.; Wu, L.; Shi, P.; Lim, C.C. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties. Automatica 2015, 51, 385–393. [Google Scholar] [CrossRef]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended state observer-based sliding-mode control for three-phase power converters. IEEE Trans. Ind. Electron. 2017, 64, 22–31. [Google Scholar] [CrossRef]
- Oliveira, J.; Oliveira, P.M.; Boaventura-Cunha, J.; Pinho, T. Chaos-based grey wolf optimizer for higher order sliding mode position control of a robotic manipulator. Nonlinear Dyn. 2017, 90, 1353–1362. [Google Scholar] [CrossRef]
- Han, Y.; Liu, X. Continuous higher-order sliding mode control with time-varying gain for a class of uncertain nonlinear systems. ISA Trans. 2016, 62, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Ferrara, A.; Rubagotti, M. A sub-optimal second order sliding mode controller for systems with saturating actuators. IEEE Trans. Autom. Control 2009, 54, 1082–1087. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Shin, K.S. Backstepping quasi-continuous high-order sliding mode control for a Takagi–Sugeno fuzzy system with an application for a two-link robot control. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1488–1500. [Google Scholar] [CrossRef]
- Bartolini, G.; Pisano, A.; Punta, E.; Usai, E. A survey of applications of second-order sliding mode control to mechanical systems. Int. J. Control 2003, 76, 875–892. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Suh, Y.S.; Shin, K.S. Output feedback tracking control of uncertain robot manipulators via higherorder sliding-mode observer and fuzzy compensator. J. Mech. Sci. Technol. 2013, 27, 2487–2496. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L. Uniform second-order sliding mode observer for mechanical systems. In Proceedings of the 2010 11th International Workshop on Variable Structure Systems (VSS), Mexico City, Mexico, 26–28 June 2010. [Google Scholar]
- Van, M.; Kang, H.J.; Suh, Y.S. A novel neural second-order sliding mode observer for robust fault diagnosis in robot manipulators. Int. J. Precis. Eng. Manuf. 2013, 14, 397–406. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Suh, Y.S. A novel fuzzy second-order sliding mode observer-controller for a TS fuzzy system with an application for robot control. Int. J. Precis. Eng. Manuf. 2013, 14, 1703–1711. [Google Scholar] [CrossRef]
- Capisani, L.M.; Ferrara, A.; de Loza, A.F.; Fridman, L.M. Manipulator fault diagnosis via higher order sliding-mode observers. IEEE Trans. Ind. Electron. 2012, 59, 3979–3986. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer: Berlin, Germany, 1992. [Google Scholar]
- Van, M.; Kang, H.J. Robust fault-tolerant control for uncertain robot manipulators based on adaptive quasi-continuous high-order sliding mode and neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1425–1446. [Google Scholar] [CrossRef]
- Lu, X. An Investigation of Adaptive Fuzzy Sliding Mode Control for Robotic Manipulators; Carleton University: Ottawa, ON, Canada, 2007. [Google Scholar]
- Fraguela, L.; Fridman, L.; Alexandrov, V.V. Position stabilization of a Stewart platform: High-order sliding mode Observers-based approach. J. Frankl. Inst. 2012, 349, 441–455. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhauser: New York, NY, USA, 2014; Volume 10. [Google Scholar]
- Van, M.; Kang, H.J.; Suh, Y.S. Second order sliding mode based output feedback tracking control for uncertain robot manipulators. Int. J. Adv. Robot. Syst. 2013, 10, 16. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Kamal, S.; Bandyopadhyay, B. Higher Order Sliding Mode Control: A Control Lyapunov Function Based Approach. WSEAS Trans. Syst. Control 2014, 9, 38–46. [Google Scholar]
- Piltan, F.; Emamzadeh, S.; Hivand, Z.; Shahriyari, F.; Mirazaei, M. PUMA-560 robot manipulator position sliding mode control methods using MATLAB/SIMULINK and their integration into graduate/undergraduate nonlinear control, robotics and MATLAB courses. Int. J. Robot. Autom. 2012, 3, 106–150. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).