Abstract
Hexapod walking robots have been widely addressed in the literature with a very large number of design and engineering solutions. However, specific design approaches and solutions are needed to cope with specific novel applications. This paper aims to address the design of a hexapod walking robot having exploration, architectonic survey, and maintenance of cultural heritage goods as its main application tasks. This specific case of study is addressed by carrying out a detailed design, which led to the construction of a novel hexapod walking robot, named Cassino Hexapod III. The proposed robot is composed of hybrid legs of a modular anthropomorphic architecture with omni-wheels as feet at its extremity. The proposed design and engineering solutions can overcome the limits of other existing prototypes and to fulfil the specific application requirements and constraints with a cost-effective and user-friendly solution. The proposed novel solutions have also originated an Italian patent No. 102014902238772.
1. Introduction
Hexapod walking robots (HWRs) are very complex mechatronic systems where six legs are connected to a main body that performs the function of support frame. The legs are controlled with a degree of autonomy so that the robot can move within its environment, to perform intended tasks [1]. HWRs possess clear advantages over wheeled or crawler robots noted widely in the literature such as those reported in [2,3,4], since multi-legged locomotion allows obstacle climbing capability, omnidirectional motion, variable geometry, stability, access to uneven terrain, and fault tolerant locomotion. Despite the above mentioned aspects, many challenges remain before HWRs can see widespread use. Some of their current disadvantages include relatively low energy efficiency and low speed [5]. Other key factors that have restricted a pervasive application of hexapod robots are high complexity and costs. In fact, HWRs are usually expensive machines, consisting of many actuators, sensors, transmissions, and supporting hardware [6,7]. The complexity of legged locomotion requires careful attention also to the control strategy by considering both path and gait planning. A discussion of these key aspects for walking hexapod robots can be found, for example, in [8,9,10].
This work deals with the design of a leg-wheel walking robot named Cassino Hexapod III, which is the third version of Cassino Hexapod series. Cassino Hexapod II had a significant drawback in terms of a very complex turning strategy, since—to achieve a lightweight design—it did not have any rotational degree of freedom along vertical axis. Accordingly, the rotation of such a robot is achieved by coordinating the legs to have an oscillation of the center of mass about the middle legs, which is quite slow and inefficient. Further details on the design and control features of Cassino Hexapod II are reported in [11,12,13]. Cassino Hexapod III has been fully redesigned to overcome the above issues by designing a hybrid leg, whose distal part is equipped with an omni-wheel. Additionally, Cassino Hexapod III has been completely redesigned from mechanical viewpoint to achieve a larger step size and a significantly higher payload capability as compared with Cassino Hexapod III. The proposed design solution avoids increasing the number of actuators, keeps the leg weight low, while increasing maneuverability over flat surfaces is greatly with omnidirectional motion features. It is important to point out that Cassino Hexapod III can achieve the advantages of both wheeled locomotion and legged locomotion thanks to its multi-legged hybrid design. Namely, it can be energy efficient while moving over flat surfaces by using only wheels and it can overcome obstacles as well as avoid, or at least minimize, the eventual damage to the walking surface by using its multiple legs in combination with a careful strategy in footholds positioning. This also allows useful stability features as well as fault tolerance, since the robot can still achieve its motion while one actuator or even one leg is not operational.
The paper is organized as follows: Section 2 describes the attached problem also by referring to the milestones in HWR evolution. The proposed design procedure is described in Section 3. A design concept of a hybrid leg-wheel HWR is presented in order to show the effectiveness and feasibility of the proposed procedure. Finally, path planning is described for the legs of Cassino Hexapod III together with its preliminary validation.
2. The Attached Problem
A great deal of literature can be found on HWRs. The evolution of HWR design was outlined for example in [14]; an overview of the state of art of hexapod robot was also given in [15,16]. Some early design solutions have been for example, OSU Hexapod [17], Odex I [18], Aquarobot [19], ASV [20], Ambler [21]. Remarkable hexapod robots in recent design solutions have included Hamlet [22], Rhex [23], Athlete [24], and Lauron [25].
In the available literature on HWRs, one can identify a very large number of solutions having many different designs and applications. Despite the high number of proposed solutions, no authors have explicitly suggested the use of HWR for applications in the domain of cultural heritage. Most of the proposed works, in fact, have focused their approach on wheeled solutions, which have well-known drawbacks in terms of mobility. This paper deals with a novel challenge in the analysis and safeguard of cultural heritage goods through the use of HWR for performing complex survey and maintenance tasks. In particular, Figure 1a shows a specific application in Cassino: the Roman amphitheater of Cassino which dates back to the first century BC. It is one of the most typical achievements of Roman architecture that was born for typical shows of ancient Rome: the gladiatorial games. In particular, the area of interest is the paved surface that was discovered in the 1950s, (Figure 1b). The roadway is large (about 2.50 m) and has a flagstone paving stones in white limestone perfectly preserved. By referring to this operating scenario, the first robot characteristic is its capacity to move within the area under examination, carrying image capturing equipment to perform survey analyses. For this specific application, the main attention needs to be focused on walking gaits and basic operations such as step climbing, and crest and ditch overcoming. At the same time, since the surface is delicate and extremely irregular, in addition to motion the robot must also ensure that the image capturing equipment remains always horizontal so that the image post processing and reconstruction can always refer to the same horizontal plane. Since the variety of irregular terrain is very large, it is difficult to cover all the different cases of operation. In order to study this problem systematically, the real features have been simplified into standard geometric features. Figure 2 shows the geometric features and related parameters that have been considered in term of crests, ditches, and vertical steps. Typical values have been identified as reported in Table 1, by referring to previous experiences at the LARM Laboratory.

Figure 1.
The prosed scenario at Casinum amphitheater: (a) an overall view; (b) a zoom view of the paved road.
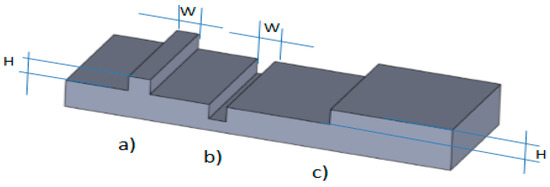
Figure 2.
Basic obstacles with main parameters: (a) vertical step; (b) ditch; (c) crest.

Table 1.
Main size (mm) of basic obstacles.
3. The Proposed Design Procedure
The proposed design procedure has been divided in two main stages as proposed in [26]. The first stage consists of a preliminary architecture design. The second stage is focused on the necessary design refinements. A preliminary design is usually a trade-off solution between design requirements and key features. A systematic preliminary design procedure for HWR has been developed as referring to specific functional requirements and relationships between the design configuration and the robot capabilities or key features for specific tasks such as reported in [26,27,28,29,30,31,32,33,34].
This section aims to design a HWR for tasks such as the inspection and operation in archeological sites, as reported for example in [27]. Based on this selected application, key feature requirements can be summarized as follows:
- -
- low-cost both in design and operation (<1000 Euros);
- -
- user-friendly operation, also for non-expert users;
- -
- wireless operation;
- -
- capability to negotiate obstacles:
- -
- a crest, with maximum width W = 100, height H = 60 mm;
- -
- a ditch, with maximum width W = 100 mm;
- -
- a step, with maximum height H = 60 mm;
- -
- capability to carry surveying devices;
- -
- operating speed on regular terrain >0.1 m/s;
- -
- operating speed on uneven terrain >0.05 m/s;
- -
- payload >1 kg;
- -
- continuous operation in walking mode >1 h;
- -
- continuous operation in omni-wheels mode >3 h.
Several sensors can be considered for identification of environment and obstacles such as Lidar, 3D scanning, sonar, radar.
Design refinements have been carried out by considering the outcome of the preliminary design step. Then, several models and analyses have been carried out for achieving a suitable refined design. For example, it has been considered the kinematic and dynamic model of one leg, and the dynamic model of one leg and of the whole body in order to identify proper components (motors, sensors, control hardware) and proper robot sizes.
3.1. Kinematic Model of One Leg
Figure 3 shows a kinematic model of the proposed leg architecture. Leg kinematics consist of two links that are connected through a knee joint. Each of the legs has three DOFs: two of them have a movement that has a range between −90 and 90 deg. that allow the robot to overpass obstacles and to walk without moving the wheels. The third motor allows to move the wheels in a full rotation range. Forwards kinematics is described by Equation (1).
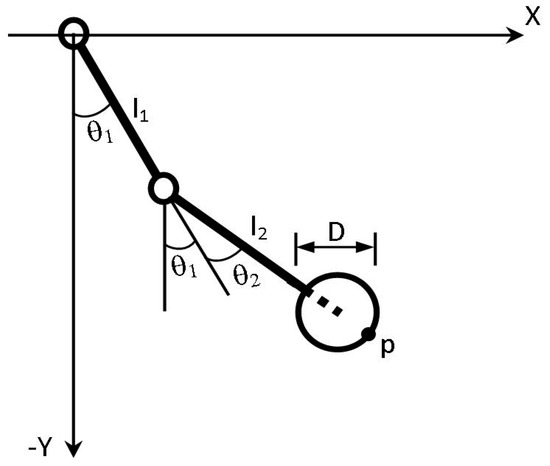
Figure 3.
One leg kinematic model.
Inverse kinematics can be solved calculating
where
similarly
where
θ1 = Atan2(sinθ1, cosθ1)
Figure 4 reports as example, a MATLAB plot of reachable area by single leg. The work area has been defined by referring the end-point p, by considering 0° < θ1 < 30°, −30° < θ2 < 0°, l1 = l2 = 70 mm D = 66 mm.
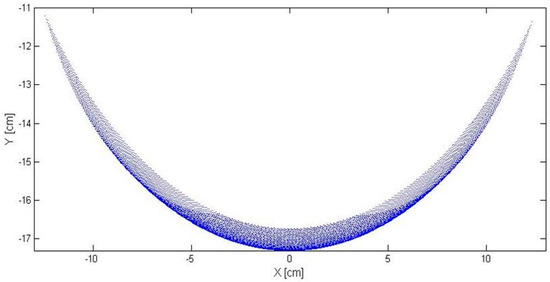
Figure 4.
Reachable area for one leg.
The proposed kinematic architecture can be seen as a tradeoff solution to limit the number of required actuators while achieving a sufficient mobility of the leg.
3.2. Dynamic Model of One Leg—Transfer Phase
The selection of proper actuators has required an estimation of needed motor torque. For this purpose, a preliminary dynamic model of robot leg has been carried out by means of a Lagrange formulation. This model can perform a preliminary actuator choice and leg size synthesis.
Figure 5 shows a scheme of the proposed preliminary dynamic model. It is composed of two revolute joints and two links. The masses are considered to be lumped at the edge of each link, inertia is considered negligible at this stage by referring to slow static walking.
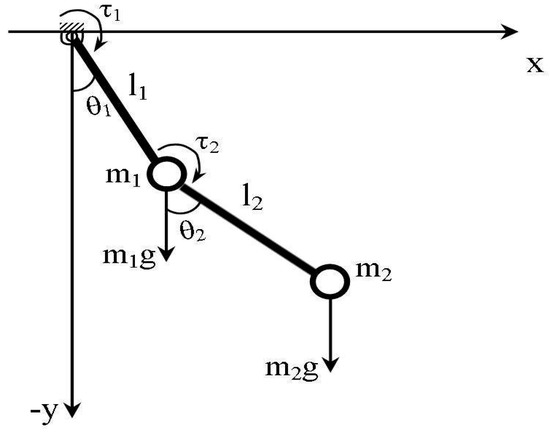
Figure 5.
One leg dynamic model for transfer phase.
The dynamic model of a two-joint robot leg can be written in the Lagrangian form as
where θ is the joint variable vector and τ is the vector of generalized forces acting on the robot manipulator. M(θ) is the inertia matrix, are the Coriolis/centripetal forces, and G(θ) is the gravity vector. In Equation (8) we are not taking into account the friction torques since we consider them as negligible. The dynamic model of the two-link planar arm can be written by substituting the following data in Equation (8)
where
The dynamic model for transfer phase was also implemented in SimMechanics environment, as aid for the leg sizes synthesis process and also in order to estimate the needed actuator torques. Figure 6 shows the SimMechanics model that can find the torques τ1 and τ2 required to obtain a prescribed movement of robotics leg as referring to the model and formalism in the scheme of Figure 6, further details on simulation symbolism and operation can be found, for example, in [32].
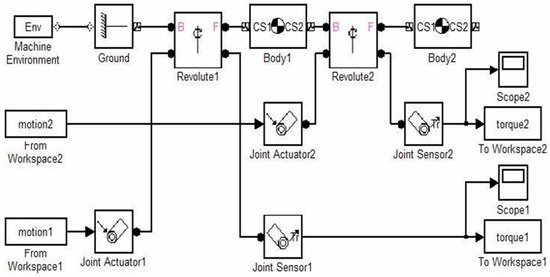
Figure 6.
One leg dynamic model in SimMechanics.
Figure 7 shows an example of trajectory that has been tested. The end-point p is moved from the initial to the goal position, along a trajectory with a predefined path. Figure 8 and Figure 9 show, for example, the workspace variables in terms of angular displacements, velocities, and accelerations that have been considered as joint inputs for the simulation. A fifth degree polynomial has been chosen for the angular rotations interpolation. At the beginning as well as at the end point of the movement, the velocity and acceleration of point p has been set equal to zero. Figure 10 and Figure 11 show time diagrams of torques τ1 and τ2 that have been obtained by solving the proposed model in Equations (8)–(16) for the specific trajectory that is shown in Figure 9.
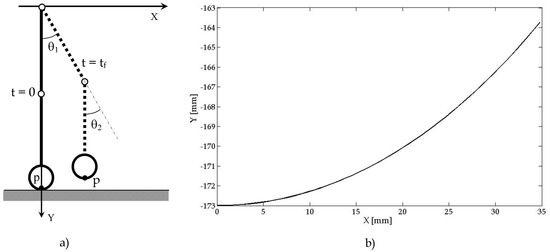
Figure 7.
Planned trajectory of the endpoint p of the robotic leg: (a) scheme of the initial and final configuration at t = 0 and t = tf; (b) plot of the position of point p.
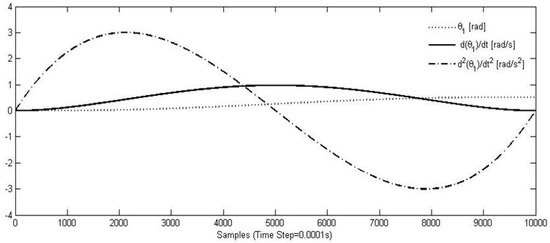
Figure 8.
Path planned for θ1(t).
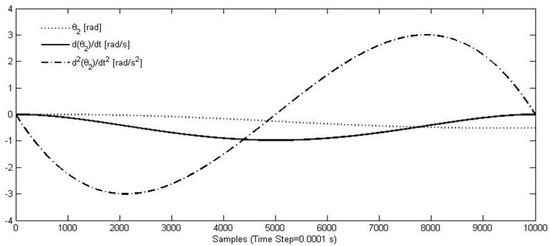
Figure 9.
Path planned for θ2(t).
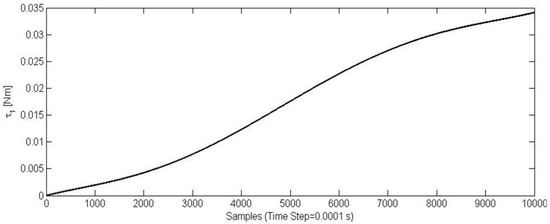
Figure 10.
Time diagram of torque τ1.
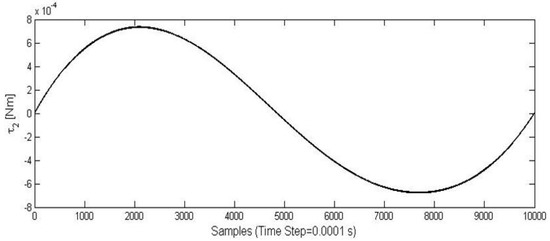
Figure 11.
Time diagram of torque τ2.
3.3. Actuator Type
The adopted actuator can be a digital servo model DS RDS3115MG [35] since they are small, light, and low-cost. Max torque is 1.47 Nm at 6 V. Weight is 0.06 kg. Continuous rotation servo for wheels operation can be the RC servo model DS AS3103PG [35]. Max torque is 0.39 Nm at 6 V. Weight is 0.04 kg. The feasibility of the proposed solution will be validated by means of a dynamic simulation of the whole robotic system.
3.4. Dynamic Model of the Hexapod
The low-cost design of the leg architecture has been obtained by using a mechanical solution with few components made with aluminum and by selecting as much as possible commercial components. The proposed leg measures 160 mm in length, 45 mm in width, and 20 mm in depth. The total weight is about 2.5 N. It has been chosen to use Mecanum-wheels with a 60 mm diameter. Mecanum-wheels are wheels with small discs around the circumference which are inclined 45 degrees to the rolling direction. The effect is that the wheel can roll, but can also slide laterally. The proposed solution has been adopted in order to allow the changing of direction strategy in wheeled operation. SolidWorks environment has been used for carrying out simulations of the proposed design solution due to its convenient features in structure analysis and in the operation study of multi-body systems. Simulations have been carried out investigating basic robot performances in a virtual environment in order to check the design feasibility before prototyping. The overall robot configuration is presented in Figure 12. The hexapod can fit into a cube of 0.4 × 0.3 × 0.2 m. Total weight of the robot is about 30 N.
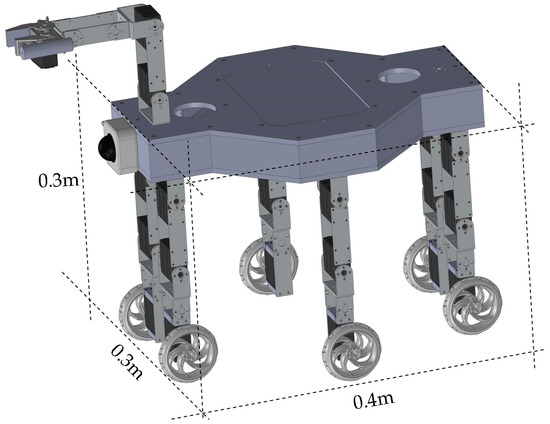
Figure 12.
Solidworks 3D CAD model of Cassino Hexapod III.
The Lagrange formulation can also be used to define a dynamic model of the overall robotic system, as proposed in [36,37]. The total kinetic energy is given by the sum of the kinetic energy of the main body TB, legs Tli and wheels Twi
where
by referring to Figure 13 the kinetic energy of a single leg is
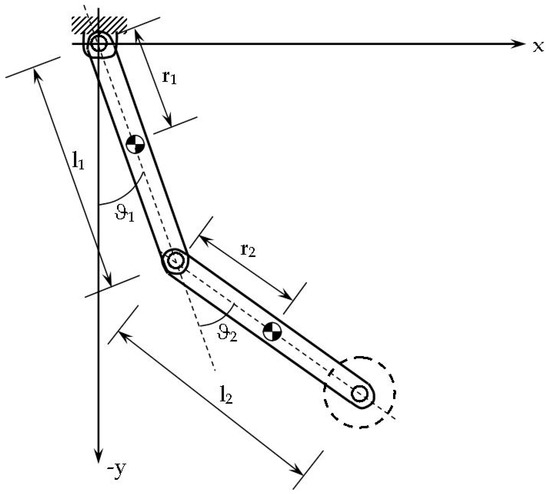
Figure 13.
Dynamic model of one leg with centers of mass.
The total potential energy of the robot is represented by the sum of the potential energy of the body and of the six legs
where
The potential energy of a single leg is
The Lagrange formulation can be written as
The dynamic behavior of a hexapod robot has been also modelled according to Figure 14. Dynamic simulation of the whole hexapod has also been carried out in MSC.ADAMS environments such as outlined in [30]. In particular, the model can take in to account several aspects—such as external forces, gravity, contacts constraints, friction, and inertia properties. The model has been elaborated by introducing each component with its specific characteristics in terms of material, mass, density, shape, and mechanical design as referring to the proposed solution. Servomotors have been modelled by using the results that have been obtained in the simulation of one leg transfer phase. Simulation shows that actuators and leg architecture can be suitable for operating the hexapod.
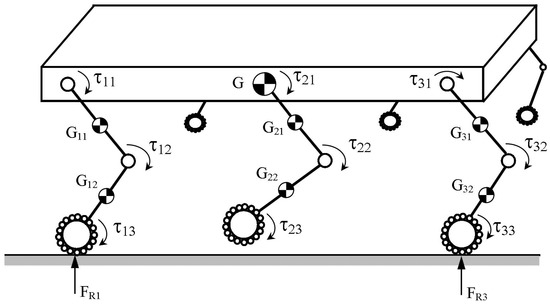
Figure 14.
A scheme of Cassino Hexapod III dynamic model.
3.5. Control Architecture
A low-cost control architecture has been developed by using a commercial control card Arduino Mega 2560, by referring to previous experience at LARM in Cassino [33,34,35]. The remote interface has been achieved by means of an Arduino Wi-Fi shield such as outlined in [35]. The high level remote control was developed in a Java environment. The proposed solution allows task planning between a Wi-Fi network using a PC or smartphone interface. A Li-Po battery 7.4 V-2600 mAh, has been selected as suitable power supply. The overall weight of the battery is 0.35 kg. Figure 15 shown a prototype of Cassino Hexapod III that has been developed at LARM. Component manufacturing has been carried out by using a CNC milling machine. The degree of autonomy of the path planning layer includes active human robot interaction. The high level remote control can be made by using a PC or a smart device that will send a task planning to the robot by using the Wi-Fi network. At this stage, obstacles or ditches are detected by means of the camera visual feedback.

Figure 15.
A built prototype of Cassino Hexapod III developed at LARM in Cassino.
4. Leg Path Planning
It is worth noting that the study of the gait and kinematic analysis is specifically needed only when obstacles exceed the radius of the wheel so that the wheel alone is unable to overcome them. In principle, a longer leg will be able to overcome higher obstacles provided that the leg has the same kinematic architecture and the same modular design (each module having identical size). Otherwise, search algorithms and optimal design procedures can be used to optimize the leg size in comparison with an obstacle size. The legs path planning has been defined by referring to a tripod gait strategy. Tripod gait consists in front and back legs on one side lifting simultaneously with the contralateral middle leg, forming alternating tripods as shown in Figure 16a. Figure 16b shows the legs phase relations: each of contralateral leg pairs has a phase shift of half period. Figure 17 shows a simplified model of the tripod gait in which each set of three legs is modelled as an equivalent leg that can follow a gait planning similar to the one shown in [37]. The gait is composed of a single support and a double support phase. Gait planning is needed while swinging a leg from a single support to a double support phase. Figure 17 shows also a model of the swing phase that is basically characterized by two parameters:
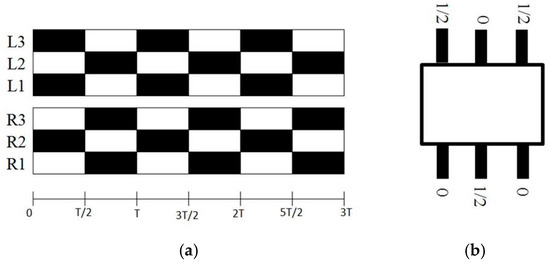
Figure 16.
Walking strategy (a) footfall formula for tripod gait (black color indicates the contact of a leg with the ground; L1, L2, L3 stands for left legs 1, 2, and 3, respectively; R1, R2, R3 stands for right legs 1, 2, and 3, respectively) (b) legs phase relations.
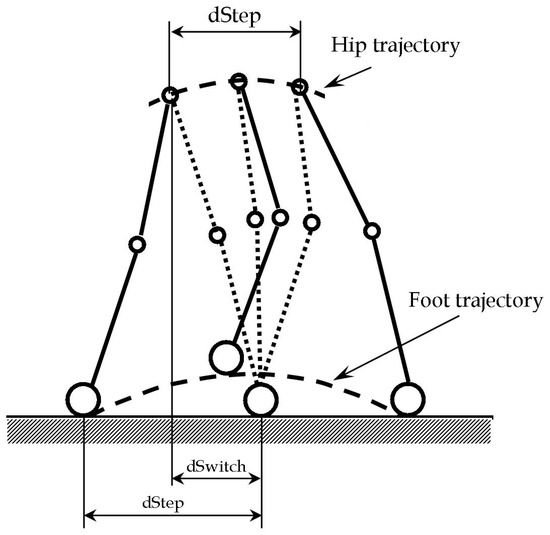
Figure 17.
The scheme for Cassino Hexapod path planning.
- -
- dStep, is a distance measured on the X-axis between the support foots. It represents the length of the step.
- -
- dSwitch, is the distance, measured along the X-axis, between the projection of hip and the front foot support.
In the double support, both feet are fixed on the ground; accordingly, one can assign the position of the hip. Several strategies are possible, for example, one can choose to maximize the walking step (dStep) and speed or can choose to minimize energy consumption by keeping the hip at a constant height. As a trade-off solution, one can limit the hip vertical motion to a given percentage of dStep such as 20% of dStep. Accordingly, one can define the hip coordinates as
In Equation (25), one can set the initial and final conditions as
combining Equations (25) and (26) one can write
xh(0) = 0
xh(tf) = dStep
xh(0) = 0; xh(tf) = 0
xh(tf) = dStep
xh(0) = 0; xh(tf) = 0
Solving the system for example for tf = 1 s and dStep = 25 mm, one can compute the values of coefficients ax and bx and xh coordinate for the hip can be written as
xh = −50t3 + 75t2
Similarly, for the polynomial function yh(t) one can write: yh(0) = 0; yh(tf) = 0; (0) = 0; (tf) = 0 and
Accordingly, one can obtain
yh = 80t4 − 160t3 + 80t2
The movement is now fully known, as the reference values for the joints of the legs can be obtained through the inverse kinematics equations by substituting Equations (25) and (30) into Equations (2)–(6).
In the single support phase, one of the legs stands on the ground, while the other one is brought forward to complete the step. The point of the hip must travel the distance dStep. Only a part of this distance will be covered during the single support and the remaining part will be covered in the double support phase. One can define the parameter Csingle < 1 as expressing the fraction of dStep that is travelled with in the single support. The values of Csingle that give the most favorable results have been experimentally found to be in the range of 0.3–0.4, while for humans it is around 0.8 [37]. The single support begins with the hip in the position xh0, and ends in the position xh0 + Csingle·dStep, in which the swing foot must be placed on the ground. To determine the intermediate positions, one can define the parameter s where xh(t) is the position of the hip along x axis at a given time t. The parameter s can be used for scaling and synchronizing the trajectory of the hip with the trajectory of the swing foot.
The trajectory (xsf(s); ysf(s)) of the swing foot can be defined by polynomials third and fourth order as
where s is obtained by Equation (31). A polynomial of third order for X-axis can specify the boundary conditions (initial and final) in terms of position and speed of the trajectory. A polynomial of fourth order for Y-axis specifies the same boundary conditions, but also can assign the height h0 of the foot at a given time. This can be useful for avoiding undesired impacts with the ground or for avoiding obstacles. The trajectory is normalized to the parameter s such as proposed in [38]. This technique of scaling the trajectory is applied since the actual final time tf at which the foot will rest on the ground is not known a priori. It depends on the dynamic evolution of the system. Assuming sf = 1, the transition in the point of maximum height h0 will occur at s = sf/2. Accordingly, one can write the boundary conditions as
The origin of the x axis is placed in the support foot, then the swing foot will leave from xsf(0) = −dStep then get a xsf(tf) = +dStep. Reasonable value of h0 for the Cassino Hexapod ranges from 2 to 6 cm. During the single support, one assigns the trajectory expressed in Equation (25), by assigning the parameter t. For example, if one assigns dStep = 25 mm, CSingle = 0.4, h0 = 40 mm Equations (25)–(33) lead to
xsf(s) = −3.2s3 + 12s2 − 25
ysf(s) = 16.28s4 − 81.41s3 + 101.77s2
ysf(s) = 16.28s4 − 81.41s3 + 101.77s2
5. Preliminary Validation
Preliminary tests of the built prototype are currently in progress. For example, Figure 18 shows several frames that refer to a step climbing strategy. In this experiment, the step height is 50 mm. The robot approaches the step as shown in Figure 18a. Then, the robot lifts the right forward leg and places it on the step as shown in Figure 18b. In Figure 18c the left forward leg is lifted and placed on the step after a forward rolling of wheels. Next step is the lifting of both middle legs together with a forward rolling of wheels, which brings the middle legs in contact with the step as shown in Figure 18d. This phase is followed by a forward rolling of wheels, which lets the rear legs approach the step as shown in Figure 18e. The last phases consist in the backward lifting of the rear legs followed by a forward rolling of wheels, which allows the robot to fully overcome the step as shown in Figure 18f. Further experiments have been carried out to verify the turning ability of Cassino Hexapod III by using omni-wheels operation. Namely, a large radius and small radius turning of 90 degrees have been carried out as shown in Figure 19 and Figure 20, respectively. The experiment in Figure 19 is achieved by rotating the left legs’ wheels at a different speed than the right legs’ wheels. The experiment in Figure 20 is achieved by counter rotations of omni-wheels, which allow first a horizontal motion of the robot, Figure 20a followed by a diagonal motion as shown in Figure 20b, finally a vertical motion is achieved as in Figure 20c.

Figure 18.
Main frames of step climbing strategy: (a) approach to a vertical step; (b) forward legs negotiating the step; (c) middle legs approaching the step; (d) middle legs climbing the step; (e) rear legs approaching the step; (f) hexapod completes the step.

Figure 19.
Main frames of a 90 degrees rotation with large radius: (a) initial configuration; (b) intermediate; (c) final configuration.

Figure 20.
Main frames of a 90 degrees rotation with small radius achieved with counter rotations of the omni-wheels: (a) initial configuration; (b) intermediate; (c) final configuration.
Preliminary results show the effectiveness and feasibility of the proposed design solution as well as its gait strategy. In particular, Cassino Hexapod III has successfully achieved preliminary tests in terms of steps overcoming and turning strategies with proper matching with the design specifications as well as with proper operation as based on the developed models and simulations. Future works will be focused on implementation and tests of complex operation tasks according to the proposed specific application. Although on-site operation will require significant time to get the required permissions by the national and local authorities.
6. Conclusions
This paper describes the main steps towards the design and construction of a novel hexapod walking robot, which can fulfill tasks of exploration, architectural survey, and maintenance of cultural heritage goods. A systematic design procedure has been carried out by referring to this specific case study. A specific design solution has been identified as evolution of previous experiences at LARM in Cassino. Then, kinematic and dynamic models have been developed and used for improving the proposed design solution. A novel prototype has been built as Cassino Hexapod III robot at LARM laboratory in Cassino. Furthermore, a gait and path planning analysis has been carried out for validating the feasibility and effectiveness of the proposed design solution. Experimental tests have been carried out for preliminary validation of the operation of Cassino Hexapod III in terms of obstacle overcoming as well as turning by using omni-wheels. Future work will include testing further operation strategies and paths, which can benefit from omni-wheels as well as tests at cultural heritage sites.
Acknowledgments
This work has been supported by own funding of LARM laboratory.
Author Contributions
F.T. and G.C. have jointly conceived the design of Cassino Hexapod III as well as the simulations and experiments. F.T. did the numerical simulations and first experiments under the supervision of G.C. Paper writing has been equally distributed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tedeschi, F.; Carbone, G. Design issues for hexapod walking robots. Robotics 2014, 3, 181–206. [Google Scholar] [CrossRef]
- Zdesar, G.K.A.; Blazic, S.; Skrjanc, I. Wheeled Mobile Robotics: From Fundamentals towards Autonomous Systems; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Belter, D.; Skrzypczynski, P.; Walas, K.; Wlodkowic, D. Affordable multi-legged robots for research and STEM education: A case study of design and technological aspects. In Progress in Automation, Robotics and Measuring Techniques; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Germany, 2015; Volume 351, pp. 23–34. [Google Scholar]
- Elfes, A.; Steindl, R.; Talbot, F.; Kendoul, F.; Sikka, P.; Lowe, T.; Kottege, N.; Bjelonic, M.; Dungavell, R.; Bandyopadhyay, T.; et al. The Multilegged Autonomous eXplorer (MAX). In Proceedings of the International Conference on Robotics and Automation (ICRA 2017), Singapore, 29 May–3 June 2017; pp. 1050–1057. [Google Scholar]
- Gregorio, P.; Ahmadi, M.; Buehler, M. Design, control, and energetics of an electrically actuated legged robot. IEEE Trans. Syst. Man Cybern. Part B 1997, 27, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Nonami, K.; Barai, R.K.; Irawan, A.; Daud, M.R. Hydraulically Actuated Hexapod Robots; Springer: Tokyo, Japan, 2014; pp. 78–104. [Google Scholar]
- Genta, G. Introduction to the Mechanics of Space Robots; Springer: Berlin/Heidelberg, Germany, 2012; pp. 381–423. [Google Scholar]
- Arena, P.; Fortuna, L.; Frasca, M. Attitude control in walking hexapod robots: An analogic spatio-temporal approach. Int. J. Circuit Theory Appl. 2002, 30, 349–362. [Google Scholar] [CrossRef]
- Ding, X.; Rovetta, A.; Zhu, J.M.; Wang, Z. Locomotion analysis of Hexapod robot. In Climbing and Walking Robots; Miripour, B., Ed.; Intech: Rijeka, Croatia, 2010; Available online: http://www.intechopen.com/books/climbing-and-walking-robots/locomotion-analysis-of-hexapod-robot (accessed on 8 December 2017).
- Manoiu-Olaru, S.; Nitulescu, M.; Stoian, V. Hexapod robot. mathematical support for modeling and control. In Proceedings of the 2011 15th International Conference on System Theory, Control, and Computing (ICSTCC), Sinaia, Romania, 14–16 October 2011; pp. 1–6. [Google Scholar]
- Cafolla, D.; Tedeschi, F.; Carbone, G. Design and simulation on Cassino Hexapod II. In Proceedings of the 3rd International Symposium on Robotics and Mechatronics (IFToMM), Singapore, 2–4 October 2013; pp. 3–12. [Google Scholar]
- Carbone, G.; Tedeschi, F. A low cost control architecture for Cassino Hexapod II. Int. J. Mech. Control 2013, 14, 19–24. [Google Scholar]
- Tedeschi, F.; Cafolla, D.; Carbone, G. Design and operation of Cassino Hexapod II. Int. J. Mech. Control 2014, 15, 19–25. [Google Scholar]
- Silva, M.F.; Machado, J.A.T. A historical perspective of legged robots. J. Vib. Control 2007, 13, 1447–1486. [Google Scholar] [CrossRef]
- Schneider, A.; Schmucker, U. Force sensing for multi-legged walking robots: Theory and experiments part 1: Overview and force sensing. In Mobile Robots, Moving Intelligence; Buchli, J., Ed.; Intec: Rijeka, Croatia, 2006; Available online: http://cdn.intechweb.org/pdfs/98.pdf (accessed on 8 December2017).
- Carbone, G.; Ceccarelli, M. Legged robotic systems. In Cutting Edge Robotics; Kordic, V., Lazinica, A., Merdan, M., Eds.; InTech: Rijeka, Croatia, 2005; pp. 553–576. Available online: https://www.intechopen.com/books/cutting_edge_robotics/legged_robotic_systems (accessed on 8 December 2017).
- McGhee, R. Control of legged locomotion systems. In Proceedings of the 18th Automatic Control Conference, San Francisco, CA, USA, 3–8 December 1997; pp. 205–215. [Google Scholar]
- Byrd, J.; de Vries, K. A six-legged telerobot for nuclear applications development. Int. J. Robot. Res. 1990, 9, 43–52. [Google Scholar] [CrossRef]
- Akizono, J.; Iwasaki, M.; Asakura, O. Development on a walking robot for underwater inspection. In Proceedings of the International Conference on Arabidopsis Research, Columbus, OH, USA, 13–15 June 1989. [Google Scholar]
- Song, S.M.; Waldron, K. Machines That Walk: The Adaptive Suspension Vehicle; MIT Press: London, UK, 1989; pp. 283–299. [Google Scholar]
- Bares, J.; Hebert, M.; Kande, T.; Krotkov, E.; Mitchell, T.; Simmons, R.; Whittaker, W. Ambler: An autonomous rover for planetary exploration. IEEE Comput. 1989, 22, 18–26. [Google Scholar] [CrossRef]
- Fielding, M.R.; Dunlop, R.; Damaren, C.J. Hamlet: Force/Position controlled hexapod walker, design and systems. In Proceedings of the IEEE Conference on Control Applications, Mexico City, Mexico, 7 September 2001; pp. 984–989. [Google Scholar]
- Saranli, U.; Buehler, M.; Koditschek, D.E. RHex a simple and highly mobile hexapod robot. Int. J. Robot. Res. 2001, 20, 616–631. [Google Scholar] [CrossRef]
- Showalter, M. Hexapod Work Space and Walking Algorithm; VDM Verlag: Saarbrcken, Germany, 2009; pp. 20–34. [Google Scholar]
- Roennau, A.; Heppner, G.; Pfozter, L.; Dillman, R. Lauron V: Optimized leg configuration for the design of a bio-inspired walking robot. In Proceedings of the 16th International CLAWAR Conference, Sydney, Australia, 14–17 July 2013; pp. 563–571. [Google Scholar]
- Tedeschi, F.; Carbone, G. Towards the design of Hexapod walking robots. In Proceedings of the 10th IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications, Senigallia, Italy, 10–12 September 2014. [Google Scholar]
- Rashid, M.Z.A.; Aras, M.S.M.; Radzak, A.A.; Kassim, A.M.; Jamali, A. Development of hexapod robot with manoeuvrable wheel. Int. J. Adv. Sci. Technol. 2012, 49, 119–136. [Google Scholar]
- Zielinska, T. Autonomous walking machines-discussion of the prototyping problems. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 443–451. [Google Scholar] [CrossRef]
- Tedeschi, F.; Carbone, G. Design of hexapod walking robots: Background and challenges. In Handbook of Research on Advancements in Robotics and Mechatronics; IGI Global: Hershey, PA, USA, 2015; pp. 527–566. [Google Scholar]
- Madden, J.D. Mobile Robots: Motor Challenges and Materials Solutions. Science 2007, 318, 1094–1097. [Google Scholar] [CrossRef] [PubMed]
- Fujiya, T.; Mikami, S.; Nakamura, T.; Hama, K. Locomotion method of a rescue robot with multi-legs and omni-directional wheel. In Proceedings of the 13th International Conference on Control, Automation, Robotics & Vision (ICARCV 2014), Marina Bay Sands, Singapore, 10–12 December 2014; pp. 1627–1630. [Google Scholar]
- Carbone, G.; Tedeschi, F.; Cigola, M. The challenge of service robotic for survey analysis and conservation of historical sites. In Proceedings of the International Advanced Robotics Program Workshop Conference on Bio-Inspired Robotics, Frascati, Roma, Italy, 14–15 May 2014; pp. 132–138. [Google Scholar]
- Frankovsky, P.; Hroncova, D.; Delyova, I.; Hudak, P. Inverse and forward dynamic analysis of two link manipulator. Proceedia Eng. 2012, 48, 158–163. [Google Scholar] [CrossRef]
- Carbone, G.; Tedeschi, F. Sistema Robotico a Gambe per Telerilevamento (Legged Robotic System for Teleoperation Tasks). Italy Patent No. 102014902238772, 23 January 2017. [Google Scholar]
- Dsservo Home Page. Available online: www.dsservo.com (accessed on 8 November 2017).
- Ding, X.; Li, K.; Xu, R. Dynamics and wheel’s slip ratio of a wheel-legged robot in wheeledmotion considering the change of height. Chin. J. Mech. Eng. 2012, 25, 1–8. [Google Scholar] [CrossRef]
- Mahapatra, A.; Shekhar, R.S.; Pratihar, D.K. Modeling and simulation of wave gait of a hexapod walking robot: A CAD/CAE approach. Int. J. Robot. Autom. 2013, 2, 104–111. [Google Scholar] [CrossRef]
- Zonfrilli, F.; Oriolo, G.; Nardi, D. A biped locomotion strategy for the quadruped robot Sony ERS-210. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 2768–2774. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).