Workspace Limiting Strategy for 6 DOF Force Controlled PKMs Manipulating High Inertia Objects
Abstract
:1. Introduction
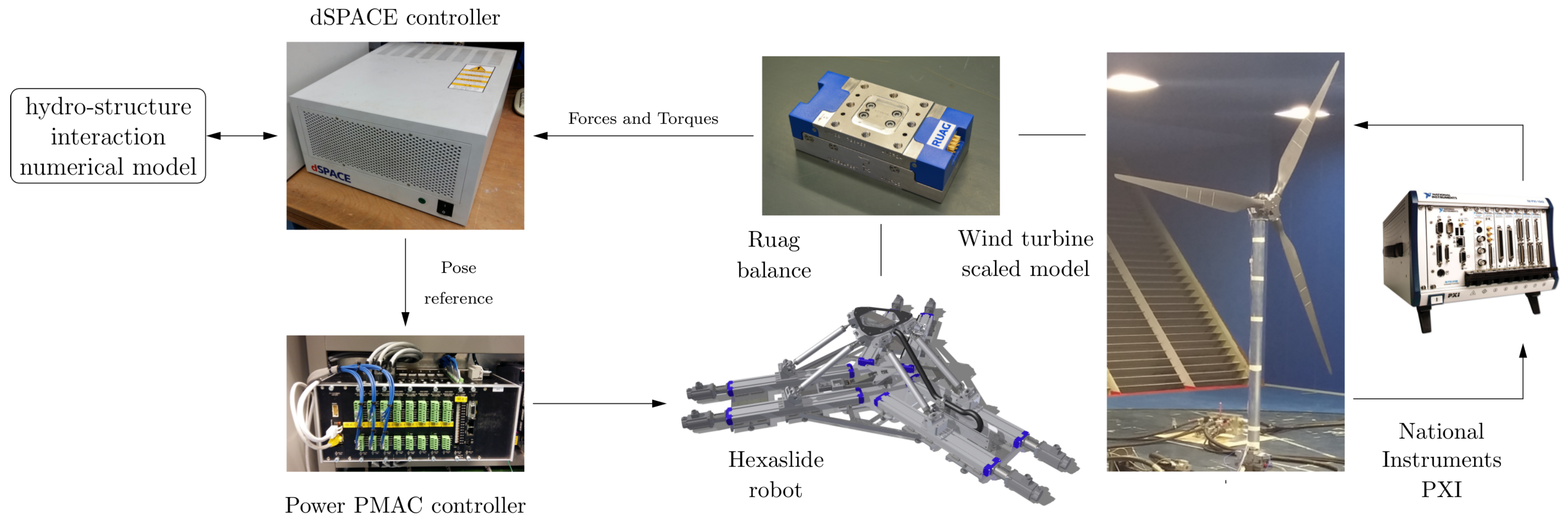
2. Hexafloat Robot Description
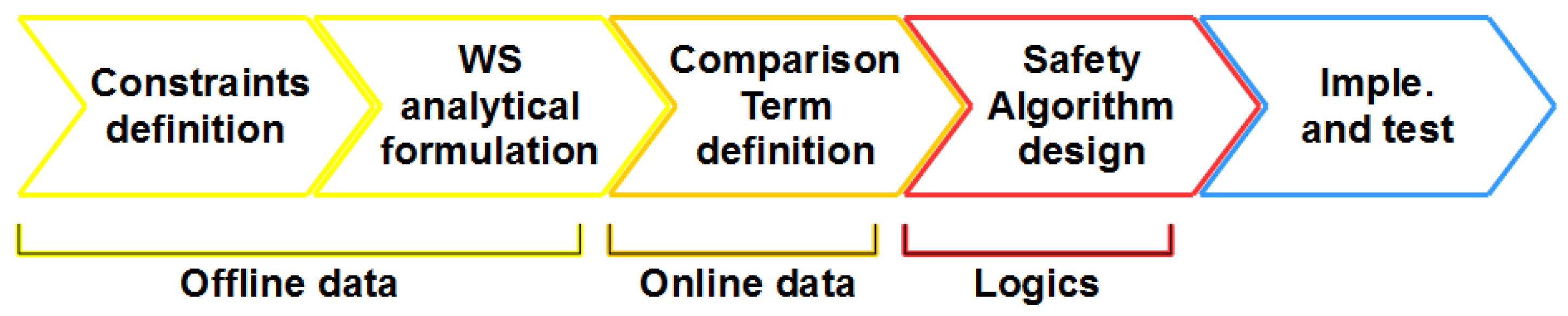
3. Workspace Safe Limiting
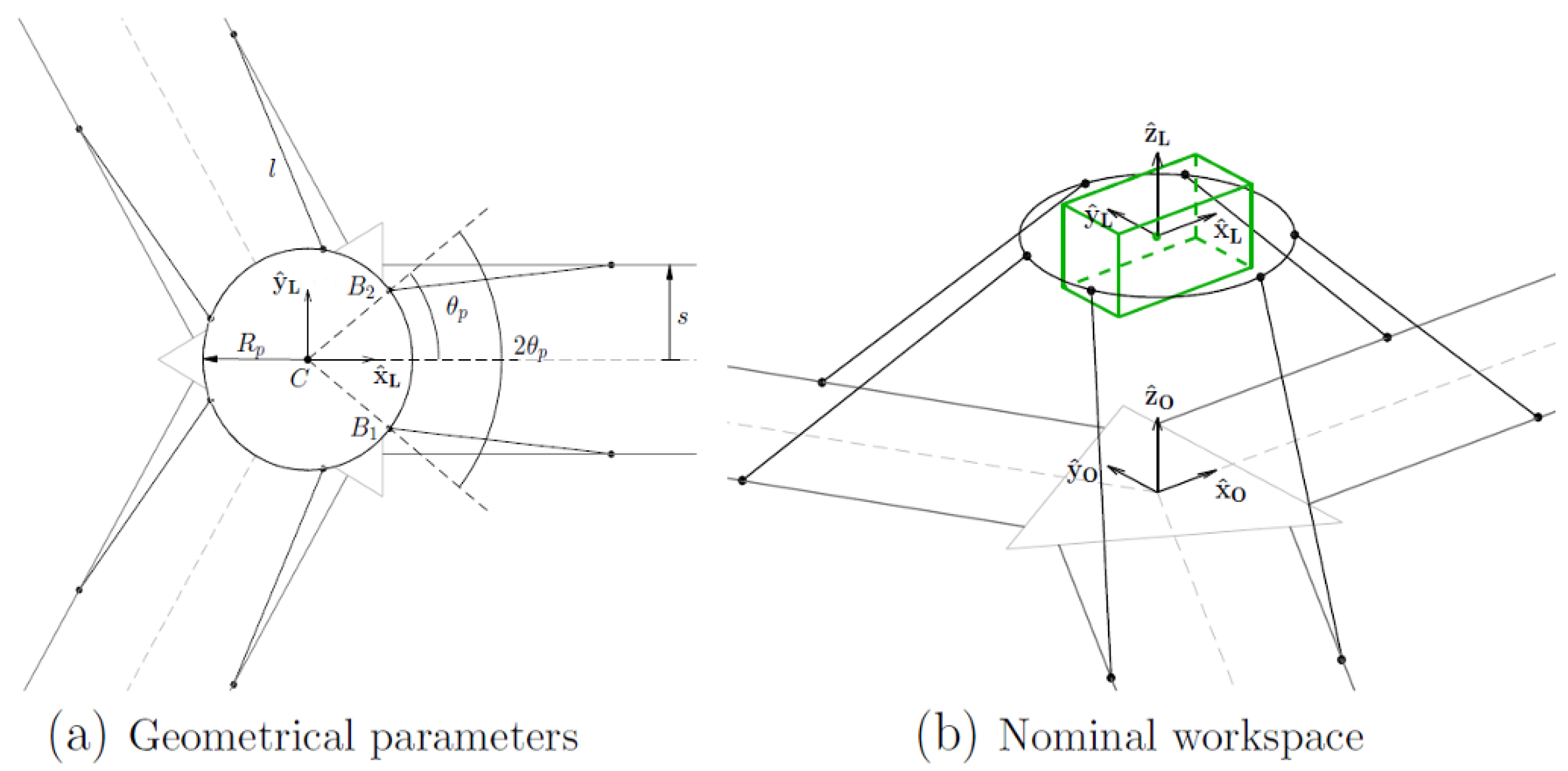
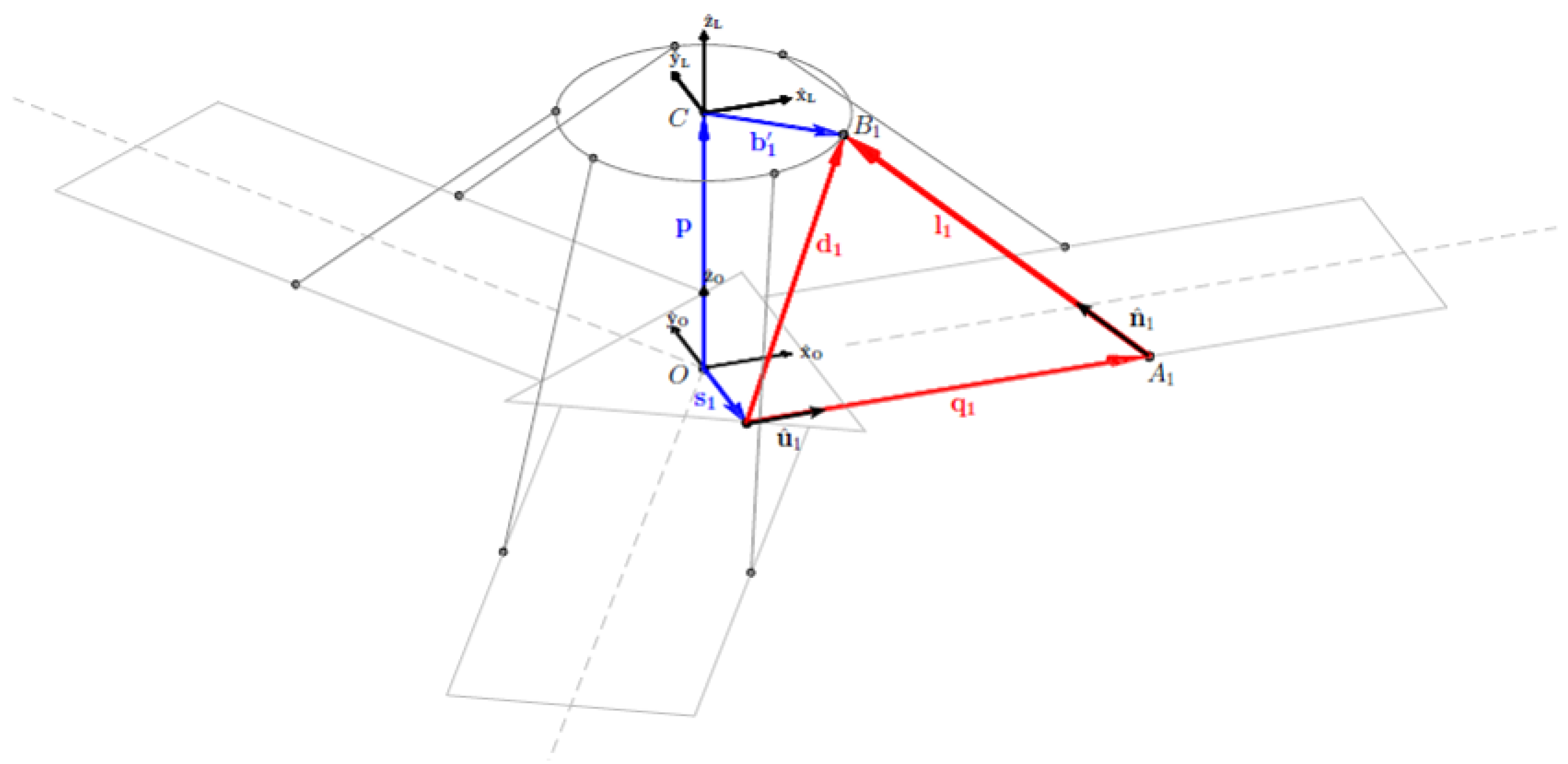
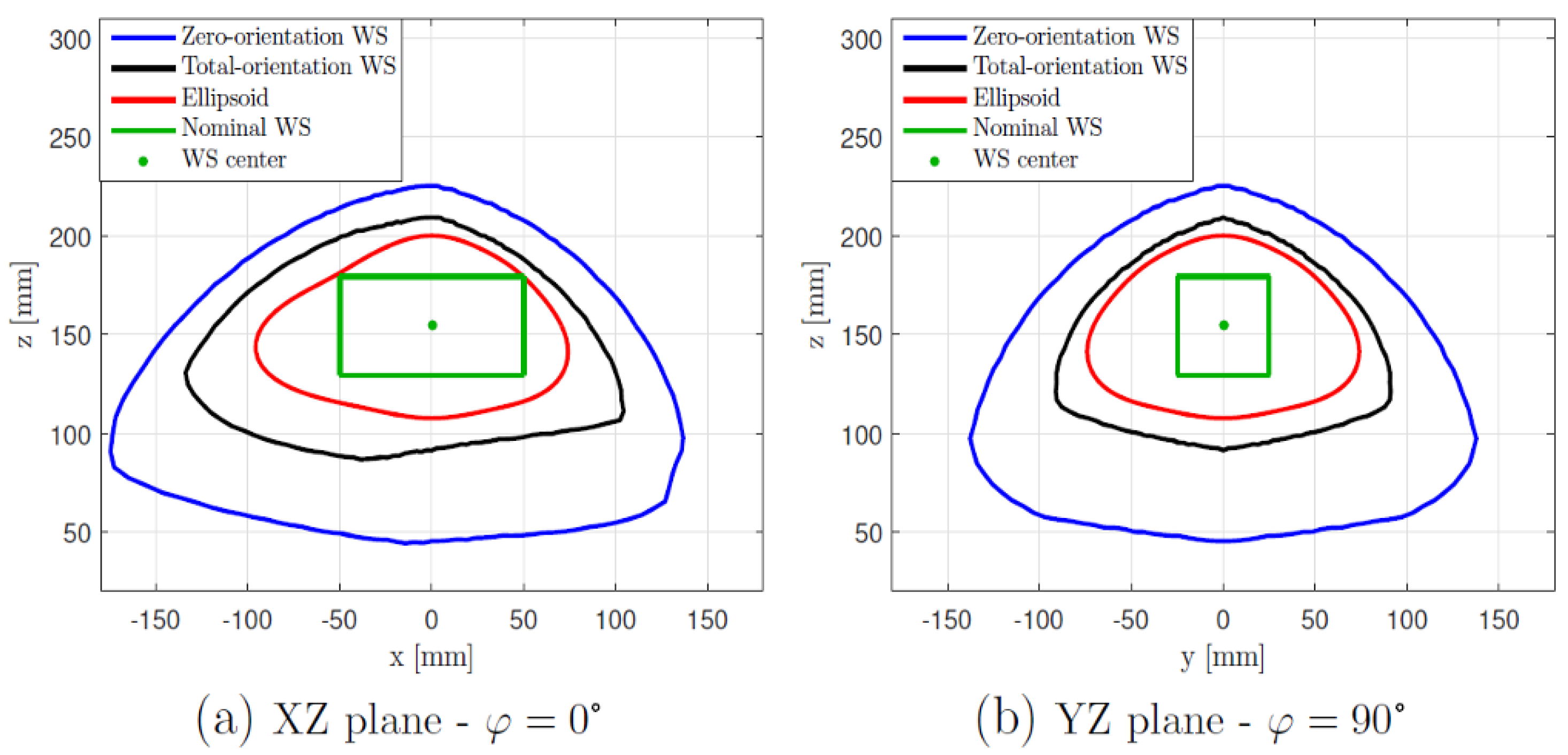
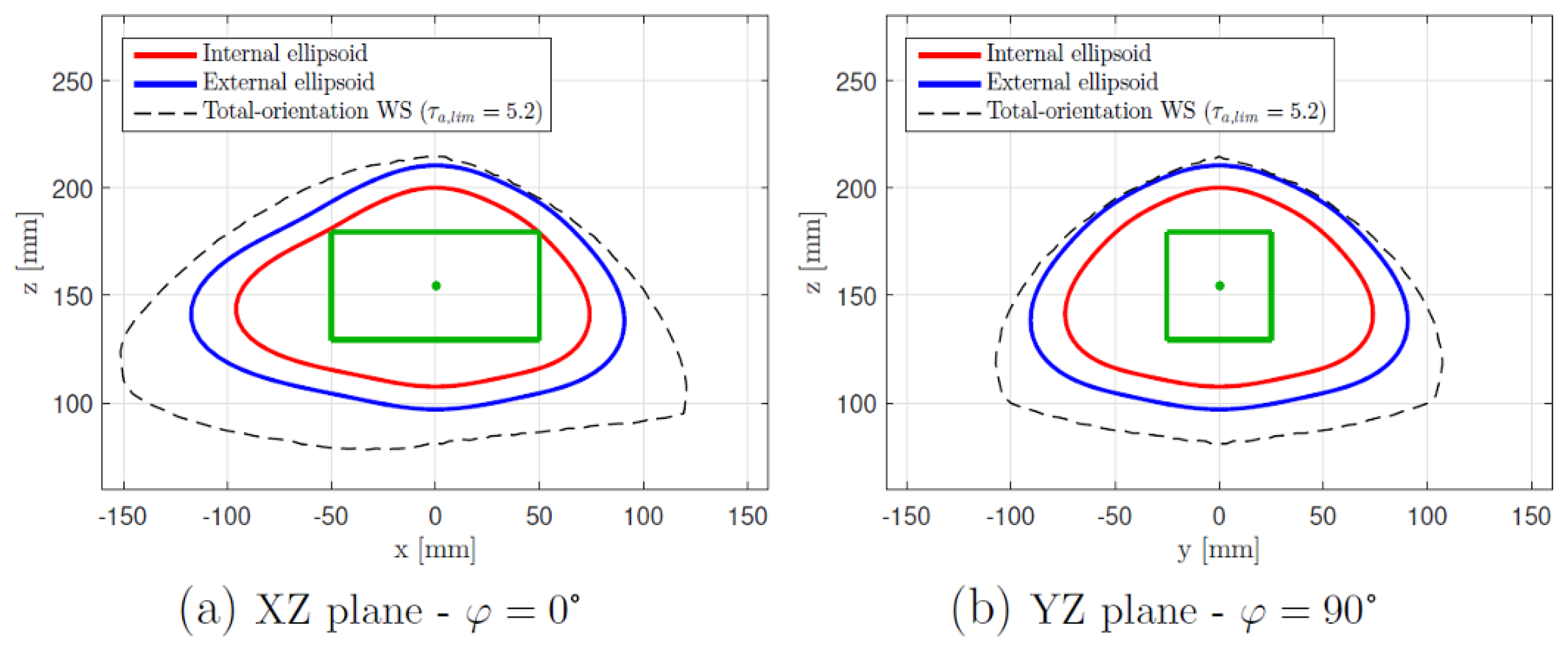
3.1. Workspace Analytical Formulation
- Kinematic constraints:
- -
- : with reference to Equation (2), . This condition is relative to top-base joints distance consistency with respect to links length.
- -
- Actuated joints range of motion.
- -
- Passive universal joints range of motion.
- Kinetostatic constraints:
- -
- Maximum multiplication of external loads. This criterion is based on limiting starting from that bounds the external loads to the actuation torques through the Jacobian matrix , obtained by differential kinematics analysis.
- both the ranges of and are properly discretized through the chosen resolution and ;
- a proper value of is chosen as the radius of a spherical surface that contains the whole total-orientation workspace;
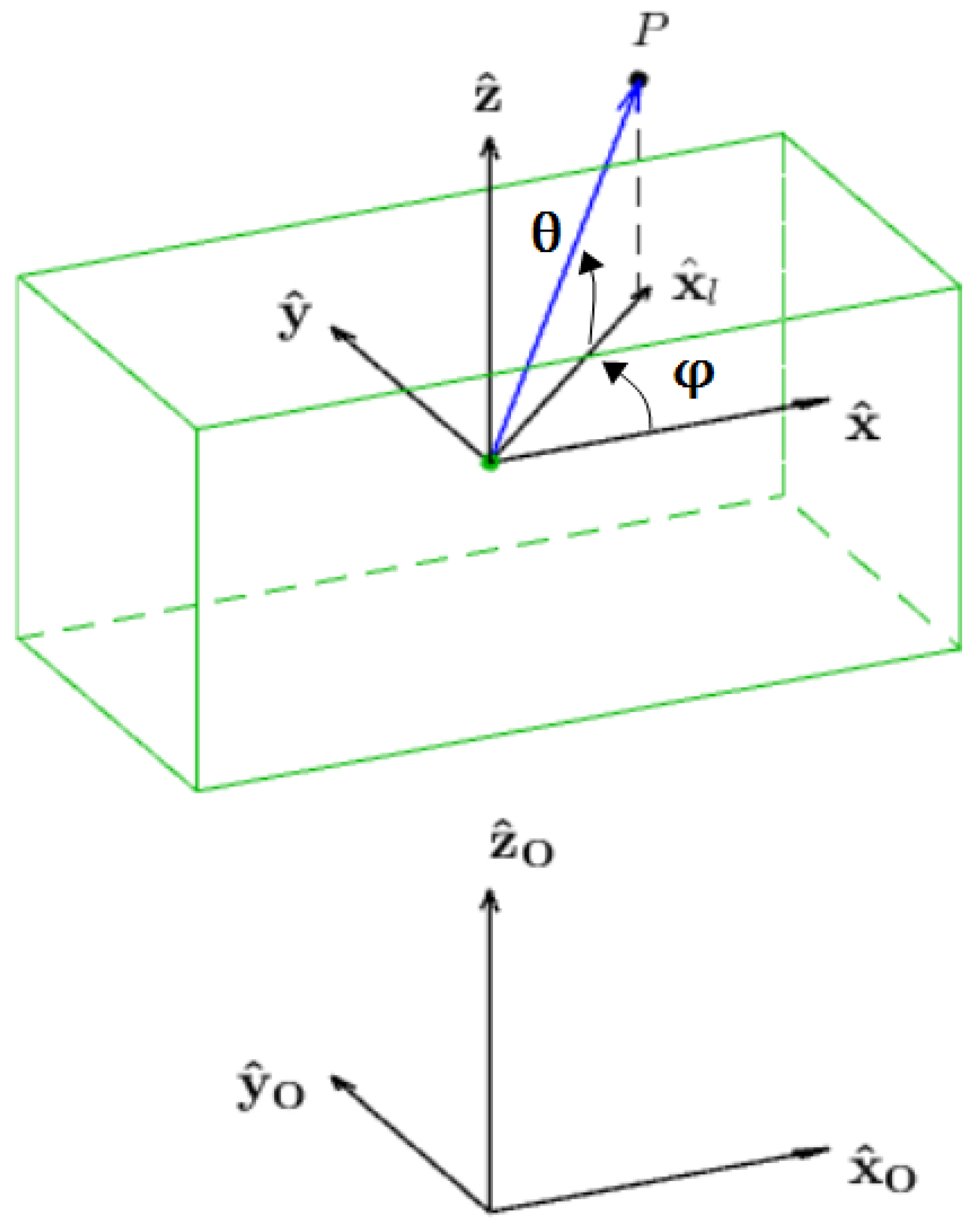
- for each plane identified by , all the values are analysed. For each combination, the point P determined by the parameters is considered, as shown in Figure 6.
- for each point, all the possible combinations of orientation inside the given range must be evaluated, which means that the orientation angles also have to be discretized with a proper resolution;
- if all the constraints are satisfied for each possible orientation, the point is contained in the total-orientation workspace: the value of r is saved in a proper matrix and the algorithm proceeds with the next value of or with the next value of if all the values have been analysed for the current plane;
- if at least one constraint is violated, the algorithm stops the calculations for the current set of parameters , and the point P is rejected and the value of the radius r is decreased of a proper step ; and
- the algorithm stops when all the values have been evaluated.
3.2. Robot Pose Monitoring
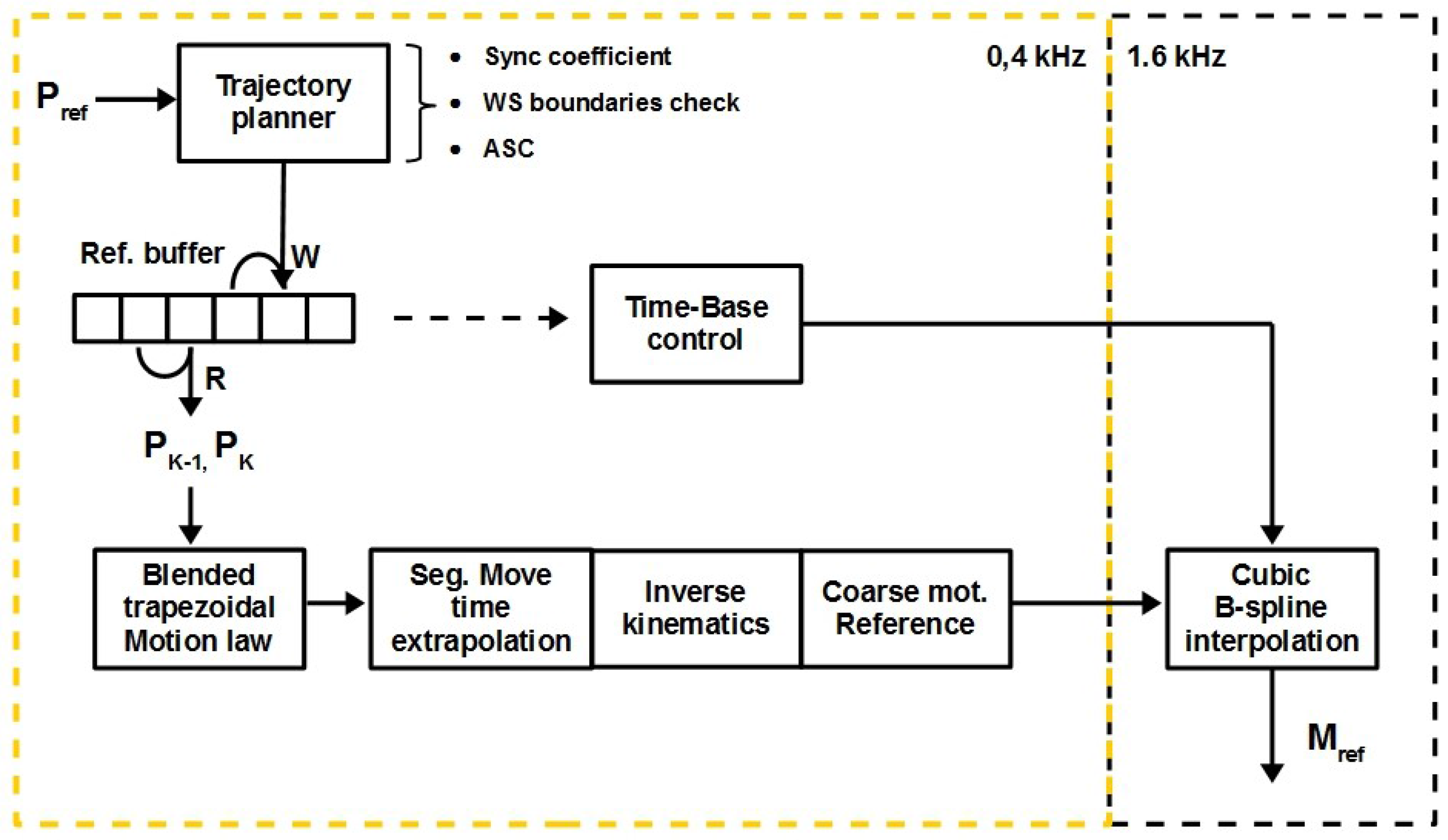
3.3. Motion Planner
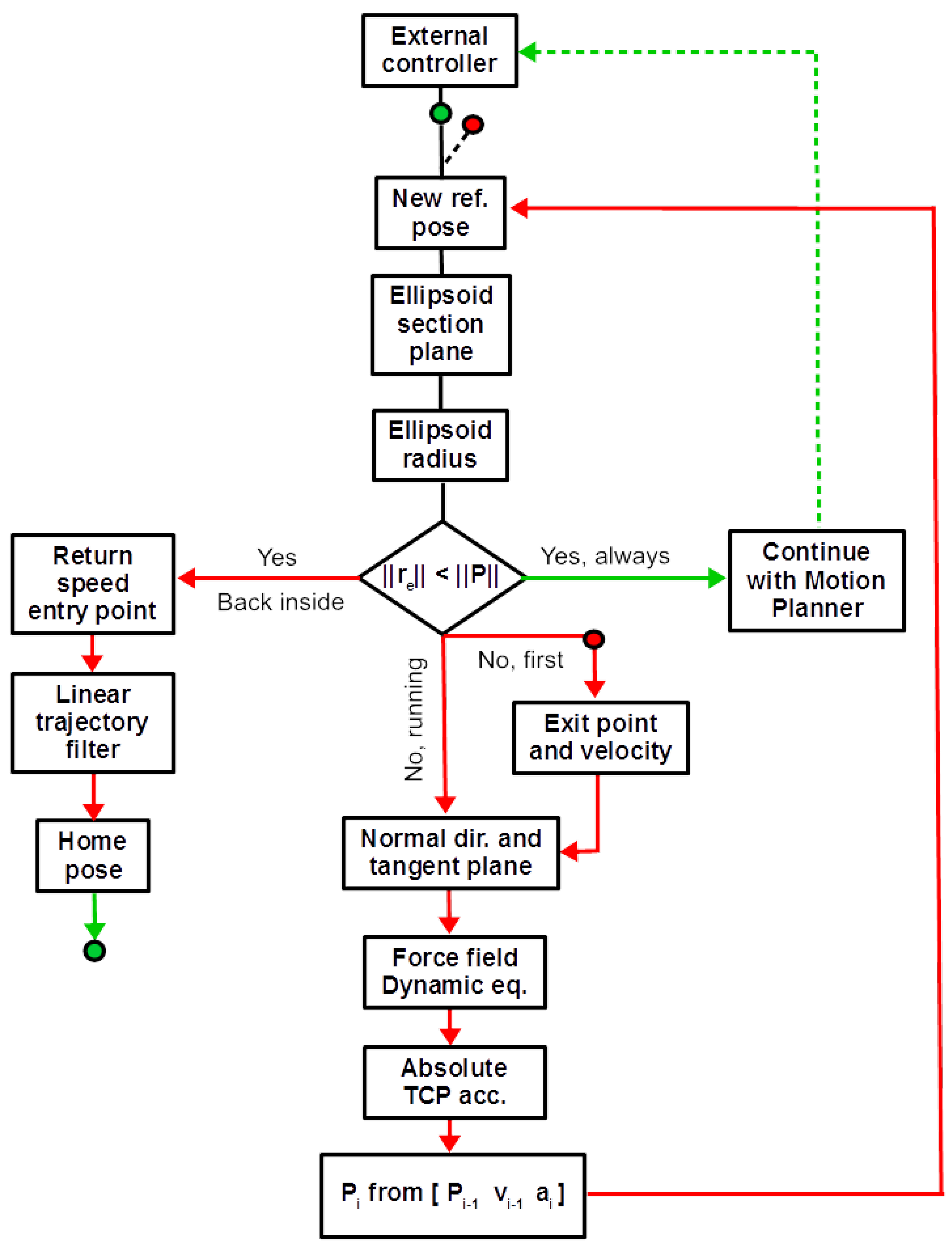
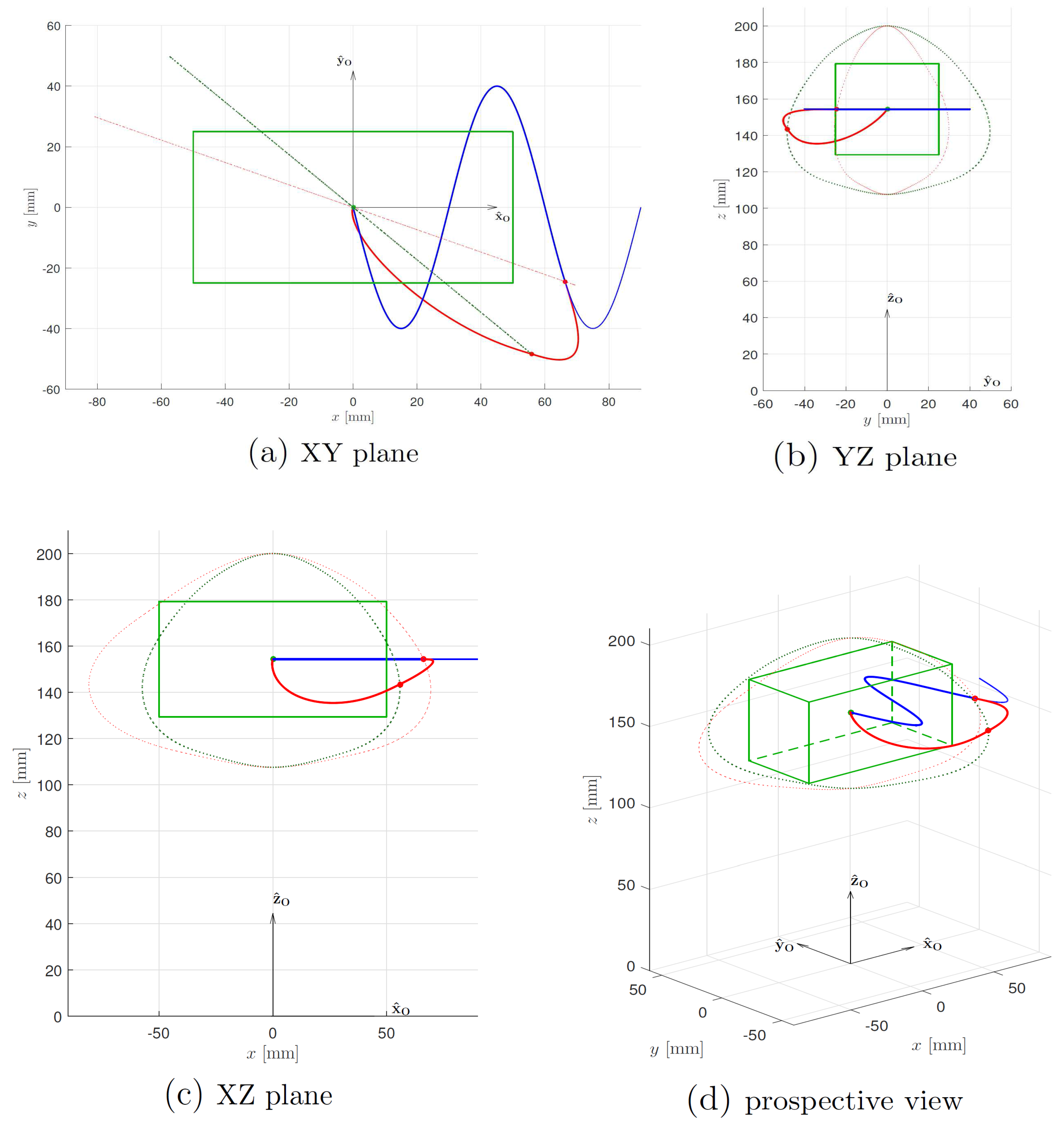
3.4. Workspace Safety Algorithm
- Exit velocity magnitude and direction.
- Ellipsoid shape near the exit point; velocity components on normal and tangent direction evolve influenced even by ellipsoid shape found during trajectory progression.
- Dynamic parameters of the compliant limit.
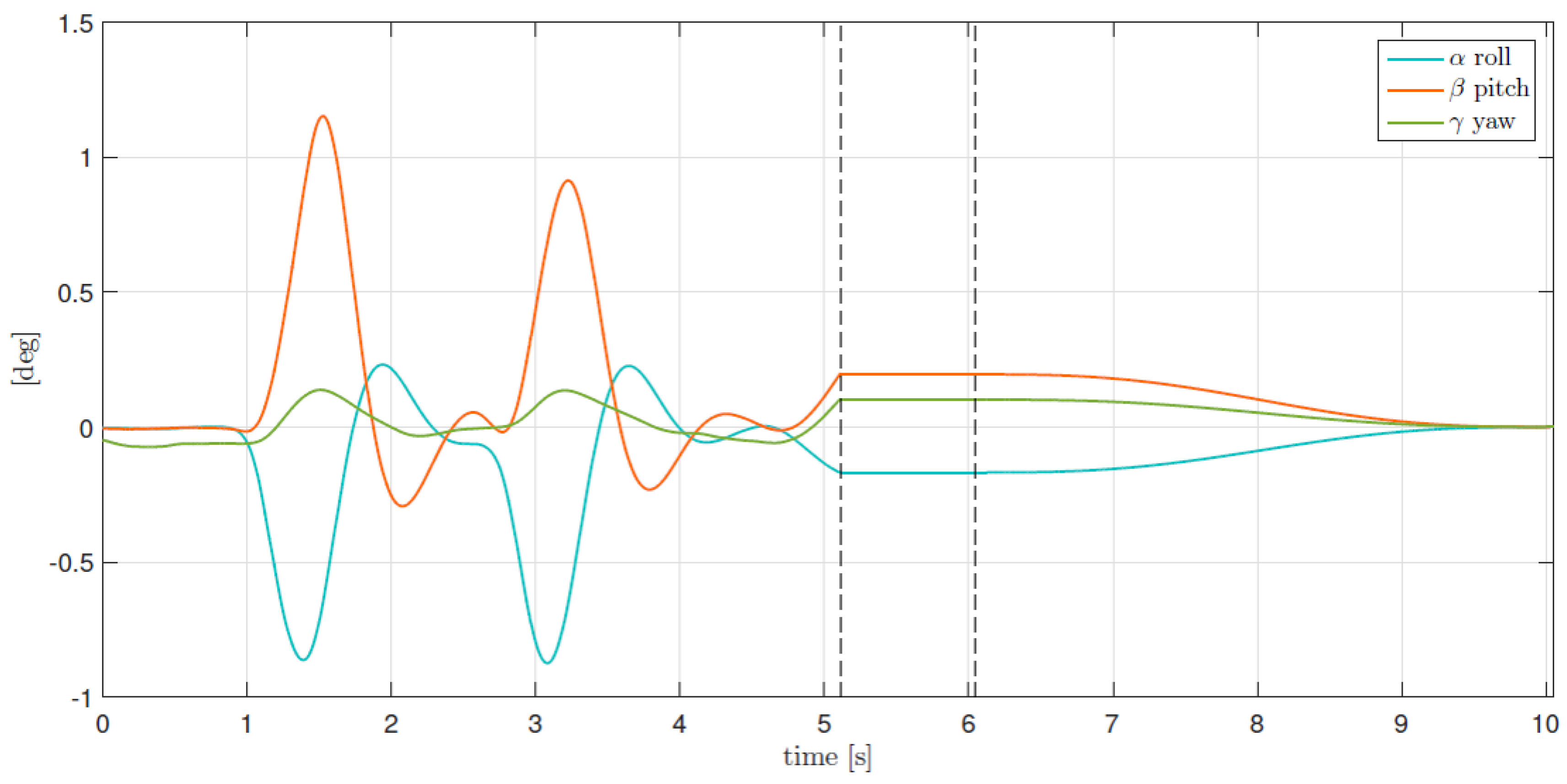
4. Simulation
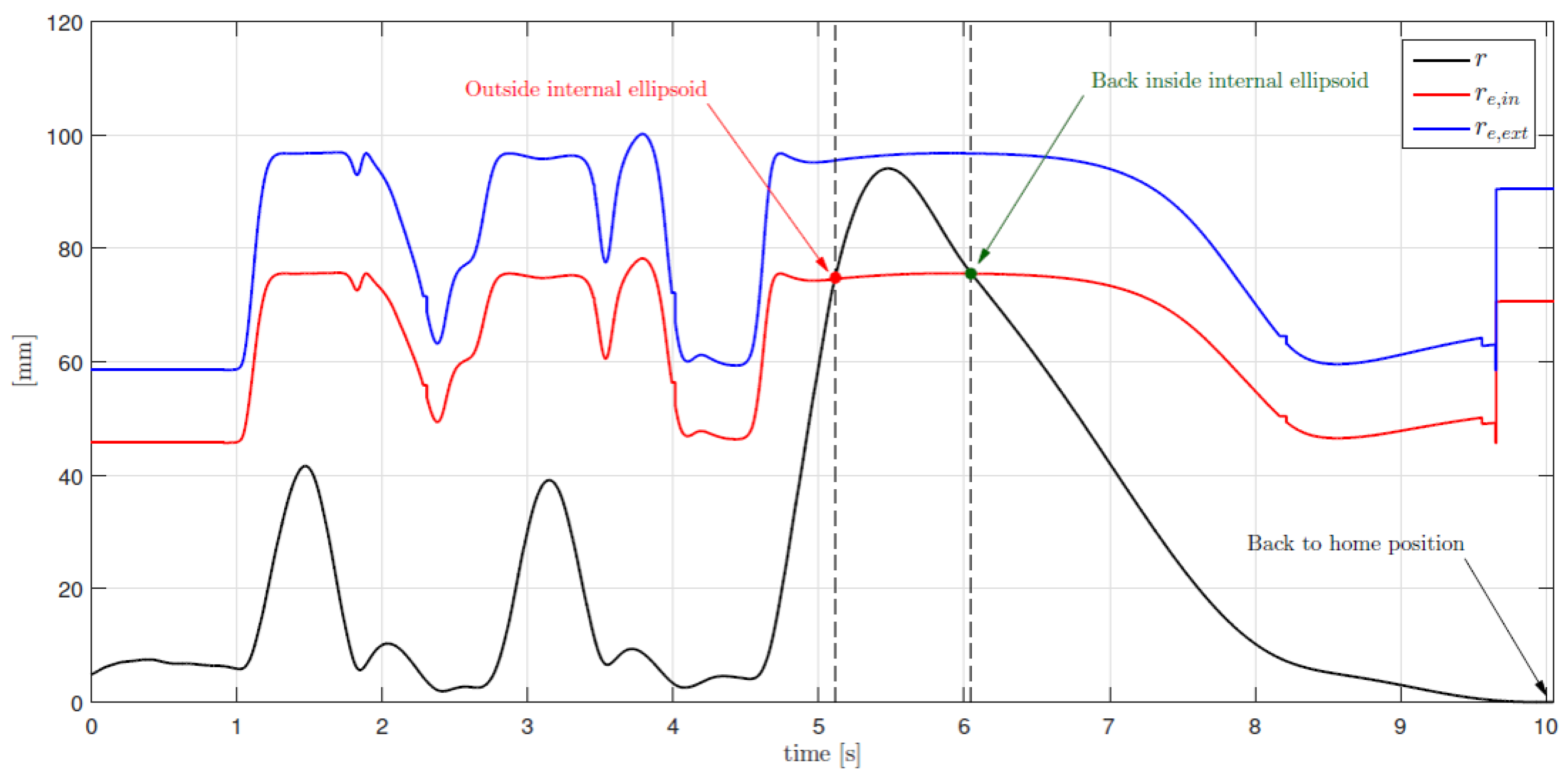
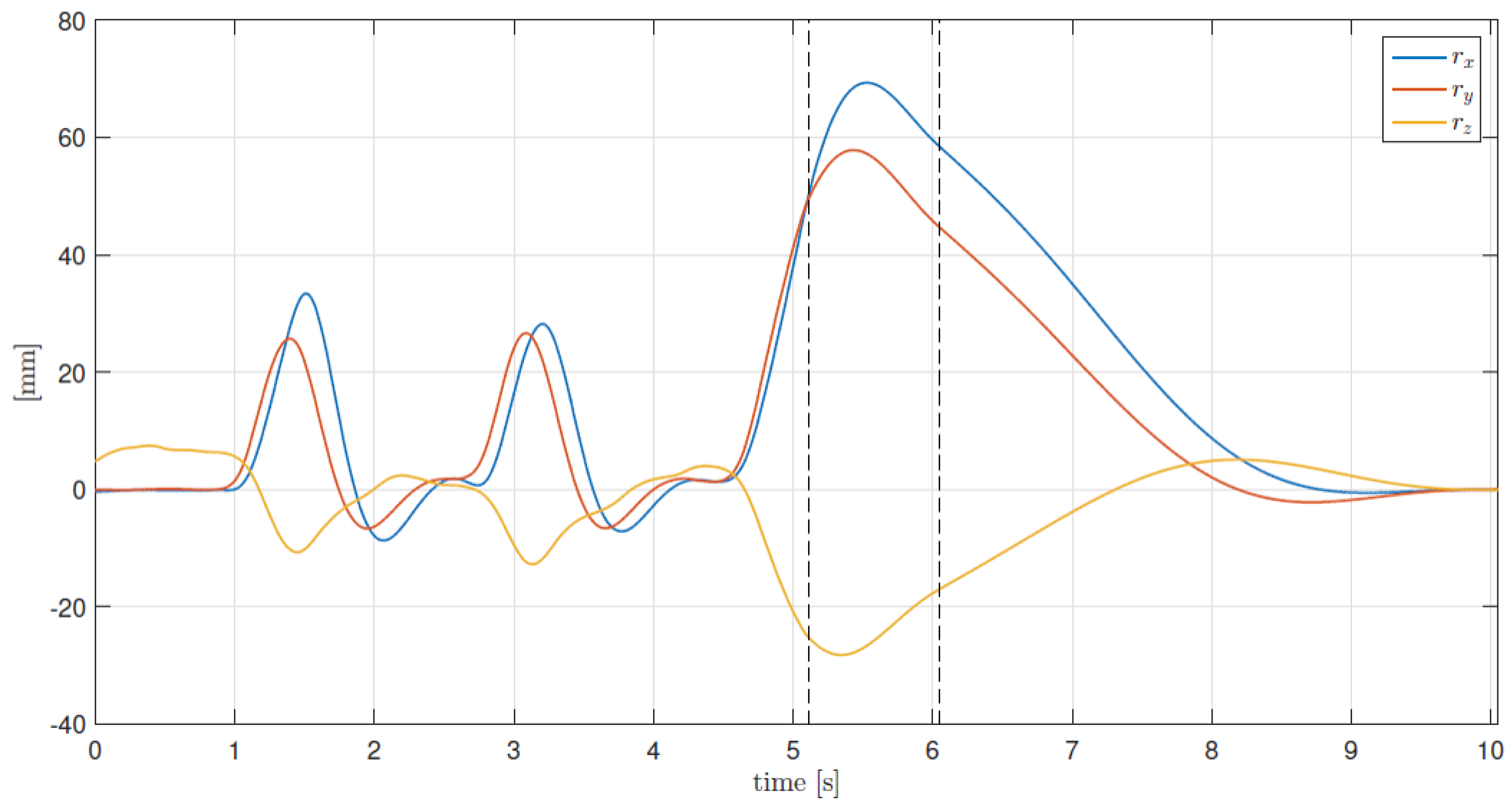
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bayati, I.; Belloli, M.; Bernini, L.; Fiore, E.; Giberti, H.; Zasso, A. On the functional design of the DTU10 MW wind turbine scale model of LIFES50+ project. J. Phys. 2016, 753, 052018. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW reference wind turbine. In Danish Wind Power Research 2013; Technical University of Denmark: Kongens Lyngby, Denmark, 2013. [Google Scholar]
- Fathy, H.K.; Filipi, Z.S.; Hagena, J.; Stein, J.L. Review of hardware-in-the-loop simulation and its prospects in the automotive area. Ann. Arbor. 2006, 6228, 62280E-1. [Google Scholar]
- Carignan, C.; Scott, N.; Roderick, S. Hardware-in-the-loop simulation of satellite capture on a ground-based robotic testbed. In Proceedings of the 12th International Symposium on Artificial Intelligence, Robotics and Automation in Space (iSAIRAS), Montreal, QC, Canada, 17–19 June 2014. [Google Scholar]
- Isermann, R.; Schaffnit, J.; Sinsel, S. Hardware-in-the-loop simulation for the design and testing of engine-control systems. Control Eng. Pract. 1999, 7, 643–653. [Google Scholar] [CrossRef]
- Brünger-Koch, M. Motion parameter tuning and evaluation for the DLR automotive simulator. In Proceedings of the 2005 Driving Simulator Conference (DSC NA CD-ROM), Orlando, FL, USA, 30 November–2 December 2005. [Google Scholar]
- Giberti, H.; Ferrari, D. A novel hardware-in-the-loop device for floating offshore wind turbines and sailing boats. Mech. Mach. Theory 2015, 85, 82–105. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Facchinetti, A.; Giappino, S. Wind tunnel tests on floating offshore wind turbines: A proposal for hardware-in-the-loop approach to validate numerical codes. Wind Eng. 2013, 37, 557–568. [Google Scholar] [CrossRef]
- D’Antona, G.; Davoudi, M.; Ferrero, R.; Giberti, H. A model predictive protection system for actuators placed in hostile environments. In Proceedings of the 2010 IEEE International Instrumentation and Measurement Technology Conference (I2MTC 2010), Austin, TX, USA, 3–6 May 2010; pp. 1602–1606. [Google Scholar]
- Bayati, I.; Belloli, M.; Ferrari, D.; Fossati, F.; Giberti, H. Design of a 6-DoF robotic platform for wind tunnel tests of floating wind turbines. Energy Procedia 2014, 53, 313–323. [Google Scholar] [CrossRef]
- Fiore, E.; Giberti, H. Optimization and comparison between two 6-DoF parallel kinematic machines for HIL simulations in wind tunnel. In Proceedings of the MATEC Web of Conferences, Singapore, Singapore, 13–14 January 2016; Volume 45. [Google Scholar]
- Ferrari, D.; Giberti, H. A genetic algorithm approach to the kinematic synthesis of a 6-DoF parallel manipulator. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA 2014), Juan Les Antibes, France, 8–10 October 2014; pp. 222–227. [Google Scholar]
- Giberti, H.; Ferrari, D. Drive system sizing of a 6-DOF parallel robotic platform. In Proceedings of the ASME 12th Biennial Conference on Engineering Systems Design and Analysis (ESDA 2014), Copenhagen, Denmark, 25–27 July 2014; Volume 3. [Google Scholar]
- Fiore, E.; Giberti, H.; Ferrari, D. Dynamics modeling and accuracy evaluation of a 6-DoF hHexafloat robot. In Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1, pp. 473–479. [Google Scholar]
- Fiore, E.; Giberti, H.; Bonomi, G. An innovative method for sizing actuating systems of manipulators with generic tasks. Mech. Mach. Sci. 2017, 47, 297–305. [Google Scholar]
- Bonev, I.A.; Ryu, J. A geometrical method for computing the constant-orientation workspace of 6-RRS parallel manipulators. Mech. Mach. Theory 2001, 36, 1–13. [Google Scholar] [CrossRef]
- Merlet, J.P. Determination of 6D workspaces of Gough-type parallel manipulator and comparison between different geometries. Int. J. Robot. Res. 1999, 18, 902–916. [Google Scholar] [CrossRef]
- Gosselin, C. Determination of the workspace of 6-dof parallel manipulators. ASME J. Mech. Des. 1990, 112, 331–336. [Google Scholar] [CrossRef]
- Kim, D.; Chung, W.K.; Youm, Y. Geometrical approach for the workspace of 6-dof parallel manipulators. In Proceedings of the 1997 IEEE International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 4, pp. 2986–2991. [Google Scholar]
- Cao, Y.; Huang, Z.; Zhou, H.; Ji, W. Orientation workspace analysis of a special class of the Stewart–Gough parallel manipulators. Robotica 2010, 28, 989–1000. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J. A new approach to orientation workspace analysis of 6-DOF parallel manipulators. Mech. Mach. Theory 2001, 36, 15–28. [Google Scholar] [CrossRef]
- Shen, G.; Tang, Y.; Zhao, J.; Lu, H.; Li, X.; Li, G. Jacobian free monotonic descent algorithm for forward kinematics of spatial parallel manipulator. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- La Mura, F.; Todeschini, G.; Giberti, H. High Performance Motion-Planner Architecture for Hardware-In-the-Loop System Based on Position-Based-Admittance-Control. Robotics 2018, 7, 8. [Google Scholar] [CrossRef]
- Adams, R.J.; Hannaford, B. Stable haptic interaction with virtual environments. IEEE Trans. Robot. Autom. 1999, 15, 465–474. [Google Scholar] [CrossRef]


| 1 | 1 | ||||
| 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 |
| Parameter | Value | |
|---|---|---|
| Actual | Scaled | |
| Home position height | 463 mm | 154.3 mm |
| Half-distance between base joints centers s | 203 mm | 67.7 mm |
| Links length l | 686.6 mm | 228.9 mm |
| Platform joints radius | 238.71 mm | 79.6 mm |
| Platform joints angle | 38.474° | 38.5° |
| Workspace | Specifications |
|---|---|
| Surge x | mm |
| Sway y | mm |
| Heave z | mm |
| Roll | |
| Pitch | |
| Yaw |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Mura, F.; Romanó, P.; Fiore, E.; Giberti, H. Workspace Limiting Strategy for 6 DOF Force Controlled PKMs Manipulating High Inertia Objects. Robotics 2018, 7, 10. https://doi.org/10.3390/robotics7010010
La Mura F, Romanó P, Fiore E, Giberti H. Workspace Limiting Strategy for 6 DOF Force Controlled PKMs Manipulating High Inertia Objects. Robotics. 2018; 7(1):10. https://doi.org/10.3390/robotics7010010
Chicago/Turabian StyleLa Mura, Francesco, Piergiorgio Romanó, Enrico Fiore, and Hermes Giberti. 2018. "Workspace Limiting Strategy for 6 DOF Force Controlled PKMs Manipulating High Inertia Objects" Robotics 7, no. 1: 10. https://doi.org/10.3390/robotics7010010
APA StyleLa Mura, F., Romanó, P., Fiore, E., & Giberti, H. (2018). Workspace Limiting Strategy for 6 DOF Force Controlled PKMs Manipulating High Inertia Objects. Robotics, 7(1), 10. https://doi.org/10.3390/robotics7010010






