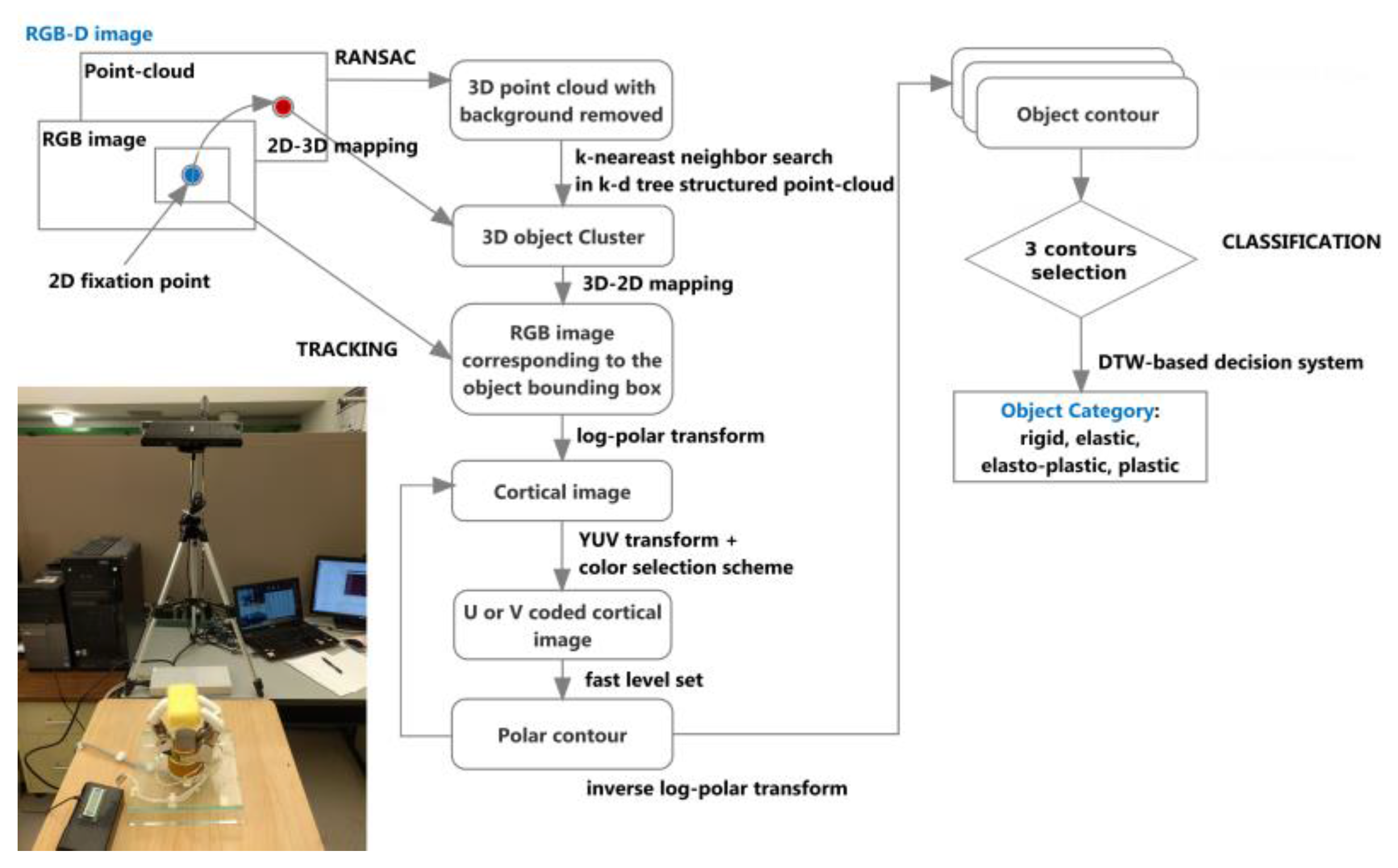
In a separate step, after all frames have been processed, three representative frames and their corresponding contour maps are extracted from the sequence and the object material is classified based on the behavior of the contour during the manipulation with the robot hand. Four categories can be identified: rigid, elastic, plastic, or elasto-plastic objects. A dynamic time warping (DTW) approach is applied to perform this classification task.
3.1. Initialization Stage
Upon analyzing a sequence of RGB-D data, a user-selected point is fed in the system to initially guide the algorithm towards the location of the object of interest. This selection is only required in the first frame of the data stream and allows the system to rapidly locate the deformable object independently from its color, shape, location or orientation in the workspace, and also independently from the complexity of the background or from the relative configuration of the robot hand and Kinect sensor. Such user guidance is common in the current feature tracking literature, but in many cases is more extreme than what is required in the proposed solution. For example, a prior selection of the object of interest is assumed to be available in [
5], or the user is asked to crop the object in the initial frame in [
23]. In our case, a single fixation point is needed and it can be selected randomly over the object of interest. Its coordinates are used by the system to indicate the general location of the object. Experiments demonstrated that while the algorithm works regardless of the position of this point over the surface of the object of interest, a 2D fixation point,
, chosen roughly at the centre of the object leads in general to more accurate contour estimation. The idea of using a central fixation point is inspired by the work of Mishra and Aloimonos [
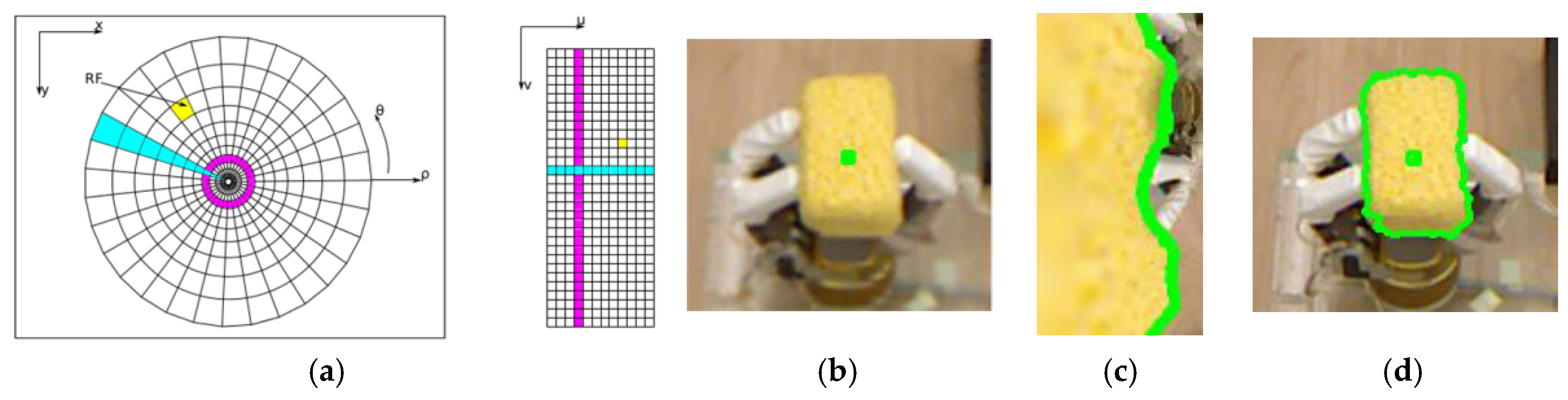
27]. The authors suggest that human retina fixates an interesting object with a high resolution captured by the fovea and the rest of the visual information at lower resolution. In the current work, this process is replicated by the use of a log-polar mapping to perform contour detection and tracking. In the log-polar map, the 2D fixation point represents the centre of the transformation, where the precision of the log-polar image is maximal.
A 2D-3D mapping that takes into consideration the intrinsic calibration parameters of the Kinect sensor [
28] is applied to estimate the 3D fixation point,
, in the point cloud corresponding to the 2D fixation point,
, in the color image. The initial goal is to separate the points representing the object of interest from the background in the RGB-D data stream. During experimentation the object is placed in a robot hand situated over a table (
Figure 1) and pointing upward while manipulating the deformable object, and a Kinect sensor is positioned above the scene. Under the current assumptions, an efficient way to remove most of the background is to locate the planar surface representing the table and to extract that surface from the RGB-D data. This surface is the one closest to the object and its identification improves the definition of the area in which the object lies. In a more general context where the robot hand would reach to manipulate an object in any location in space, an equivalent background removal procedure could consist of applying a threshold on the distance map to remove all surfaces located behind the object of interest. However, this would also impose strategically positioning the RGB-D sensor according to the object location, which remains beyond the scope of the current research.
Under the consideration of a planar surface behind the manipulated object, the planar surface identification is viewed as a plane-fitting problem which can be resolved with the RANSAC algorithm [
17]. The approach, implemented as per the “plane model segmentation” and “extracting indices from a point cloud” algorithms of the Point Cloud Library (PCL) [
29,
30], is applied over the 3D point cloud in the RGB-D data stream. Given that at least three non-collinear points are required to estimate the plane model, the minimum size of the sample set,
s, is set to 3. The distance threshold is chosen empirically and set to
t = 1 cm to ensure a good balance between the background table removal and processing time. An example of the reduced point cloud,
, after removal of the table and background visible in
Figure 2a, is shown in
Figure 2b.
The next step consists of narrowing down the search area to the object of interest in the reduced point cloud,
. The purpose of this step is to extract a single cluster containing the nearest elements to the fixation point identified by the user in a Euclidean sense and that represents the object of interest. The solution capitalizes on a k-d tree structure and the use of the fixed-radius near neighbors search algorithm. Because an estimation is used to approximate the location of the 3D fixation point from the 2D-3D mapping described previously, and also due to the errors on depth that characterize the Kinect sensor, the estimated 3D coordinates,
, may not exactly correspond to an existing point in the point cloud. Moreover, because the point cloud recuperated is unstructured, in order to find the neighbor of each point, the k-d tree data structure supports a faster nearest neighbor search. Therefore, a k-nearest neighbors search [
18] is applied to identify the k-nearest points,
, in the reduced point cloud,
, to the estimated 3D fixation point,
. An empirically chosen value of
k = 100 is used to accelerate the computation of the clustering approach while also guaranteeing that the cluster of the object of interest contains at least 100 points. Beginning with these 100 points, the neighborhood of each is further researched for extra points located within a maximum distance,
, which can be integrated in the object cluster. A value of
= 5 mm was empirically determined. The resulting object cluster is therefore composed of the initial 100 points augmented by any other points discovered within the distance threshold,
. The merging condition for the clustering is the Euclidean radius. The algorithm used slightly differs from that available in the PCL library [
30] in that it concentrates on a single cluster located around the user-determined fixation point. Algorithm 1 summarizes the process.
| Algorithm 1. 3D cluster extraction algorithm. |
| |
| Input: |
| Point cloud representing the point cloud after table removal |
| = set of k-nearest-neighbors to the estimated 3D fixation point, (with k = 100) |
| = spatial distance threshold for a point to be considered as a neighbor (set to 5 mm) |
| Output: |
| The object cluster, |
| function ClusterExtraction () |
| if then |
| return |
| else |
| Build k-d tree representation of |
| Set up priority queue of the points that need to be checked, |
| for every do |
| if all the points in have been processed then |
| |
| else |
| search the neighbors set of in a sphere with radius |
| for every ⊂ do |
| if has not been processed then |
| |
| end if |
| end for |
| end if |
| end for |
| end if |
| end function |
Once the object cluster in 3D is identified, the corresponding 2D object cluster in the color image is identified with the inverse 2D-3D mapping in order to initialize the level set contour tracking method. For the case of the yellow object shown in
Figure 2a, the final object cluster is shown in
Figure 2c. The bounding window with which the level set is initialized to process the first RGB-D frame and initiate the contour tracking represents the bounding box of the 2D points (the farthest left, right, up and down locations) enlarged by 50 pixels in all directions. This tolerance of 50 pixels introduces robustness to cases where the object slightly shifts or rotates during manipulation. This initialization also contributes to the acceleration of the contour detection since the initialization area is close to the object of interest.
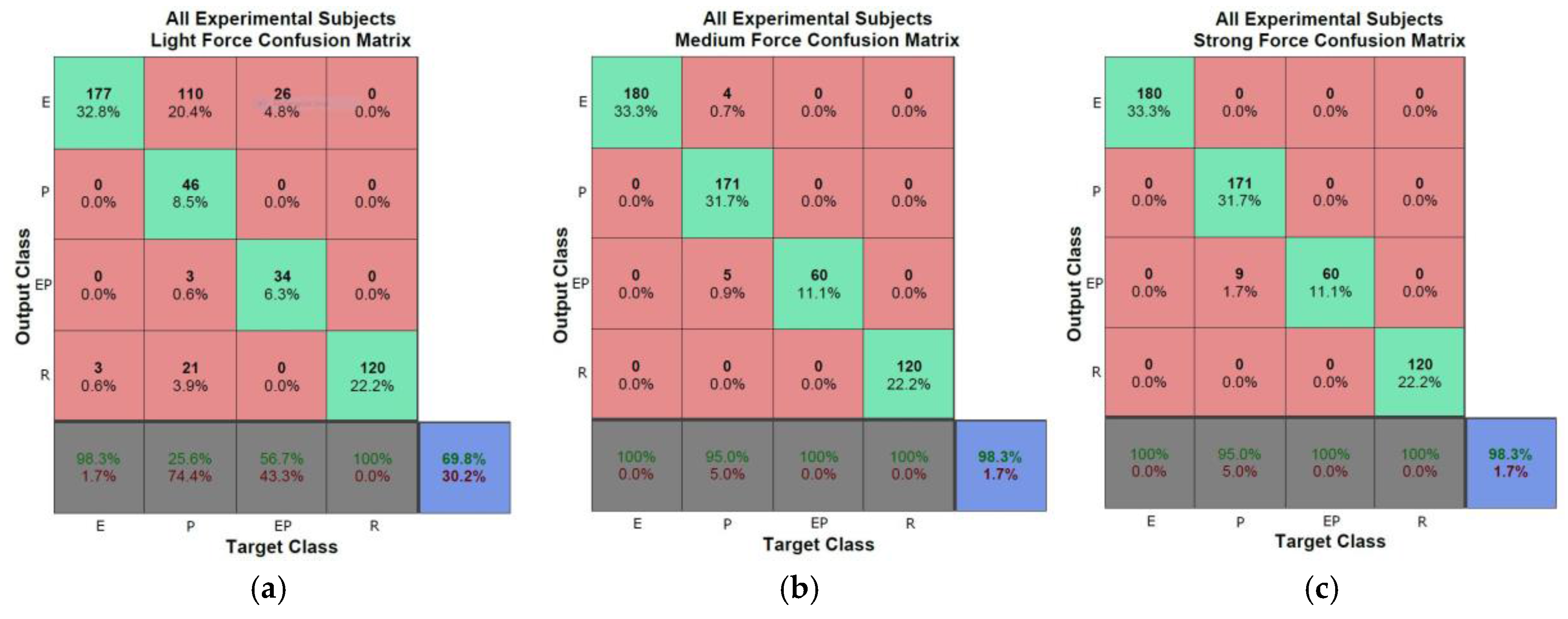
3.3. Object Classification
In order to characterize objects and classify them into different categories related to the material they are made of, and therefore recognize their deformation behavior, an automated measurement procedure is designed that uses a three-finger robotic Barrett hand. The hand applies a series of forces over predefined points distributed all around the object to be characterized, while the contour of the object is visually monitored with the solution described in the previous sections. The object contour obtained at different deformation stages using the fast level set method applied in the log-polar space is remapped into the RGB image coordinates, as shown in
Figure 3d. A subset of the contours is then used to automatically identify the type of object the robot hand is manipulating. The original, not deformed, shape of the object does not influence the classification, and neither the choice of points over which force is applied. This is a benefit of the proposed method that monitors the relative deformation of the object only, while no formal model of the object is involved. Separate methods exist for optimal selection of contact points for the application of force to ensure stable grasp, and this aspect is beyond the scope of the present research.
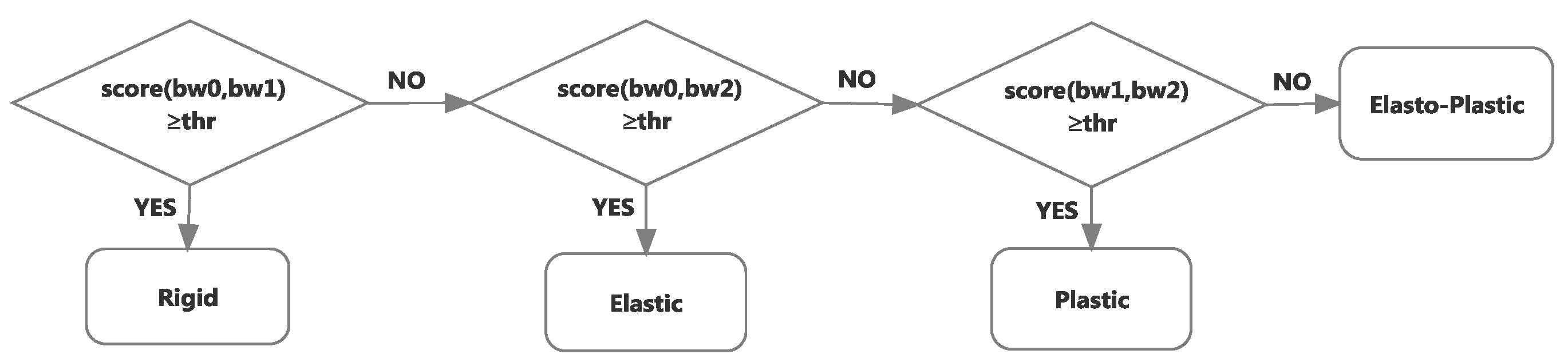
Elastic objects are known to return to their initial shape once the forces applied on them are released. Therefore, in order to detect if the object is elastic, the final deformation contour, after forces are removed, is compared to the initial deformation profile, collected in the beginning of the characterization procedure, that is before any force is applied, as well as to the contour obtained when the largest deformation takes place. If the initial and the final contours are almost identical, within a certain tolerated noise margin, and different from the contour under the largest deformation, the object is classified as elastic (
Figure 5a).
The comparison between the initial, largest deformation and final object contours is also exploited to detect plastic and elasto-plastic deformations. If these three contours are different, beyond a predefined tolerance of a few pixels in order to cope with the noise in the measurements, it means that either a plastic or an elasto-plastic behavior occurred. The differentiation between the plastic and elasto-plastic behaviors is achieved by comparing the final deformation contour with the contour under largest deformation. Given that an object made of plastic material memorizes the largest deformation experienced, if the final contour and the contour under largest deformation are almost identical, as shown in
Figure 5b, it means that a plastic deformation occurred. On the other hand, elasto-plastic material has the property to partially, but not totally, recover from the deformation when the external force is released. This property is recognized by comparing again the final contour with the contour under largest deformation. If they are significantly different, as shown in
Figure 5c, but not identical to the initial contour, then the material is considered to be one exhibiting elasto-plastic properties. Finally, if all three contours are identical, as shown in
Figure 5d, the object is considered rigid, as no deformation is perceived by the contour tracking system under any amount of force.
In the current implementation, the three contours of interest (initial, largest deformation and final) are selected out of the sequence of contours under manual guidance to ensure proper evaluation of the classification algorithm. However, contour tracking also allows automatic extraction of these contours from the sequence. The frame prior to first deformation detection represents the initial contour; the frame in which the deformation changes direction is selected as the contour with largest deformation; and the frame after deformation stops is considered to be the final contour. Continuous contour tracking over the entire manipulation procedure also allows the detection of a special case of rigid objects that would break under the forces applied by the robot hand fingers. Close monitoring of the obtained contours in order to detect any abrupt changes, or definitive loss of contour, can be exploited to identify this sub-category of rigid objects.
In order to perform the classification, the object contours are compared using dynamic time warping (DTW) to detect changes in the various stages of the object deformation. Dynamic time warping is a commonly used technique to align two sequences that may vary in length [
21,
39,
40]. DTW is selected here because the number of pixels forming a contour can significantly vary in between successive frames, as a result of the deformation of the object. As such, DTW does not require extraction of features from the contours. It provides a robust distance-based method to compare contours of variable length, which also eliminates the need for explicit point-to-point matching of contour pixels or subsampling of the contours, and therefore allows full usage of the information available. In particular, starting from a contour, principal component analysis is applied to identify the center pixel of the contour, defined as follows [
41]:
where
represents the center pixel of contour,
, the latter being composed of
K pixels,
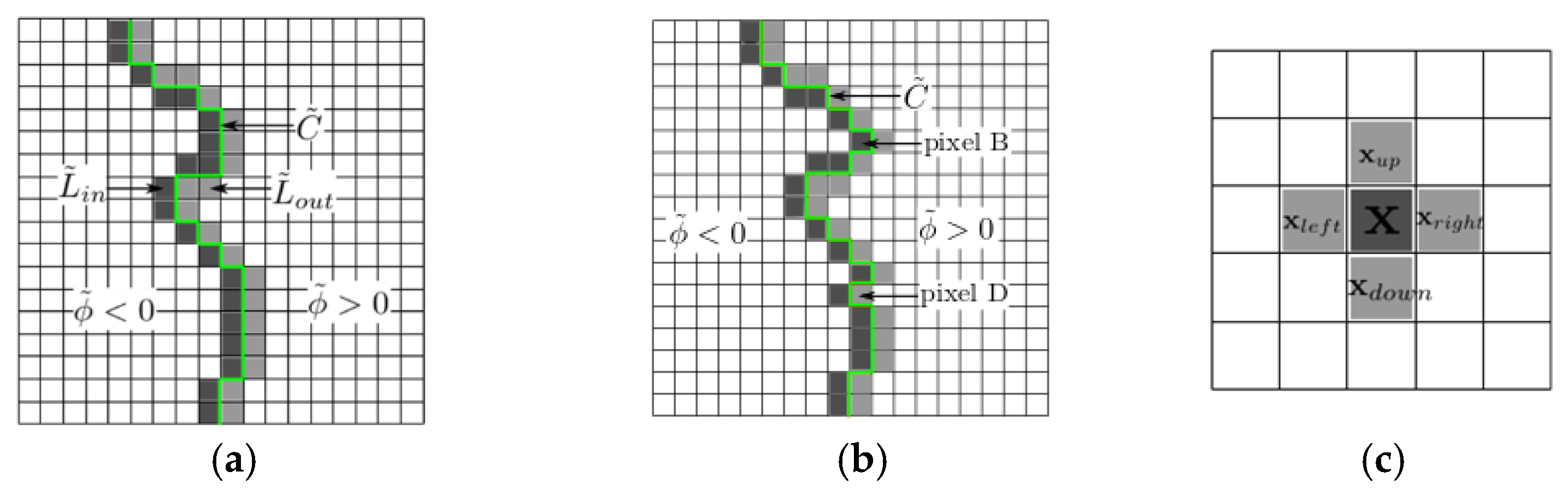
. The first pixel belonging to the contour (
in
Figure 6a) is identified as being the pixel that satisfies the two conditions defined in Listing 4.
Listing 4.
First pixel conditions
Listing 4.
First pixel conditions
| 1: |
| 2: is located on the right side of . |
Once this pixel is identified, the contour sequence is filled up with the remaining contour pixels in the counterclockwise direction (along the arrow in
Figure 6a).
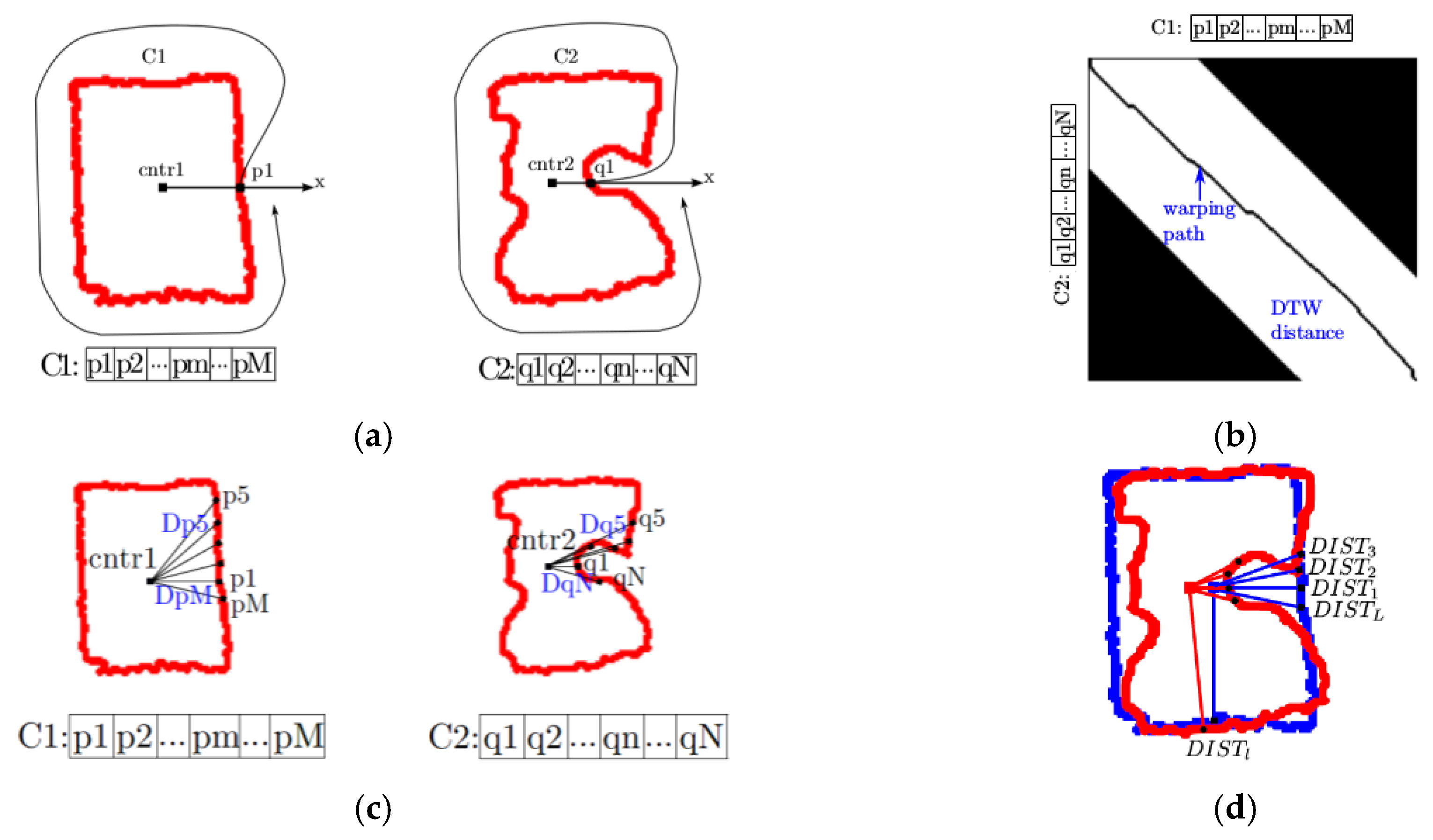
Figure 6a shows an example of two consecutive contours
and
at time
and
, respectively. In order to compare the differences between
and
, the local cost matrix,
, is used to evaluate the similarity of each pair of pixels in the sequences
and
. In this matrix, each element
represents the Euclidean distance between the pixel
from the first contour and the pixel
from the second contour. The value of
d[
m,
n] in the matrix is low (low cost) if
and
are similar to each other in their relative location, or high otherwise. The warping matrix is computed with an additional locality constraint [
42]. This means that for the contour sequences
and
, instead of calculating the DTW distance over all pairs of pixels, the DTW distance is only calculated for the part of warping matrix where the condition
is satisfied. With this locality constraint, the computed DTW distance is restricted to a band (shown in white in
Figure 6b), along the diagonal of the warping matrix, which speeds up the DTW distance calculation. As such, in
Figure 6b, the black areas are eliminated from the calculations in order to accelerate the computation time. The DTW algorithm with locality constraint is summarized in Algorithm 3:
| Algorithm 3. Conditional DTW algorithm with locality constraint. |
| |
| Input: |
| : Sequence of length ; |
| : Sequence of length . |
| Output: |
| DTW matrix |
|
| 1: DTW = matrix [M+1, N+1]; |
| 2: v = 1/5×max(M, N) |
| 3: v = max(v, |M − N |) |
| 4: for m do = 0 : M |
| 5: for n do = 0 : N |
| 6: DTW[m,n] = ∞ |
| 7: end for |
| 8: end for |
| 9: DTW[0, 0] = 0 |
| 10: for m = 1 : M do |
| 11: for n = max(1, m-v) : min(N, m+v) do |
| 12: DTW[m,n] = d[m, n] + min |
| 13: end for |
| 14: end for |
| 15: return DTW[M, N] |
The optimal warping path , with is the one with the minimal overall cost from the DTW matrix, where , and L is the length of the warping path. This warping path must satisfy the three conditions defined in Listing 5.
Listing 5.
Warping path conditions
Listing 5.
Warping path conditions
| 1: Boundary condition: = (1, 1) and = (M, N); |
| 2: Monotonicity condition: and ; |
| 3: Step size condition: for |
It is computed in reverse order of the indices starting with
. Once
is calculated, the next elements are defined using the following equation [
39]:
With the above three warping path conditions, the warping path matches the two contour sequences
and
by assigning the pixel
of
to the pixel
of
so that an element
of the warping path stands for a pair of pixels (
,
). The optimal path is shown as a black line over the white band in
Figure 6b.
In order to compute the differences between the initial contour,
, the contour under largest deformation,
, and the contour after the force is removed,
, we compute a score inspired from [
42]. However, in our case the score is made more robust as it also takes into account shifting and slight rotation movements that the object could exhibit during manipulation. The proposed score is calculated as:
where
L is the length of the warping path, and
with
the Euclidean distance between the pixel
and its contour center
, or
, and
is the Euclidean distance between the pixel
and its contour centre
, or
Figure 6c illustrates the Euclidean distances between a pixel and the center of the contour for the two contours considered previously. However, because it is desired that the method is robust to noise and fast at the same time, we impose two conditions in order to consider that a contour has been deformed. In particular, we verify if a displacement of the contour occurred and that the displacement affects more than three contiguous pixels over the contour. Considering the sequence of
values, if the value of an element in this vector is larger than a threshold (e.g., 4 pixels in our work), it is considered that a movement occurred at that location on the contour, otherwise, the difference is attributed to noise and it is considered that no movement occurred. In case the contour has moved, we also verify the number of contiguous pixels affected by the movement. In particular, if the number of contiguous pixels with movement is larger than 3 pixels, the contour is considered being deformed. An example is shown
Figure 6d. The blue contour represents the contour at time
t, and the red one is the contour at time
t + 1. The pairs of pixels
and
from these two contours, respectively, are matched by the DTW algorithm.
is the distance between two pixels
and
and its value is smaller than 4. Therefore there is no movement at pixel
.
is the distance between pixels
and
and its value is larger than 4 so that pixel
is in movement. The same thing can be noticed for
and
, meaning that the pixels
and
are in movement as well. As four contiguous pixels have movement, it is considered that the contour at the pixels
,
,
and
is deformed. Only the deformed contours are evaluated using Equation (9).
If the contour is deformed, based on the scores computed pairwise between the initial contour,
, the contour under largest deformation,
, and the final contour after the force is removed,
, using Equation (9), the decision process for classifying the object as rigid, elastic, plastic or elasto-plastic is illustrated in
Figure 7. The value of the threshold
thr applied on the score was empirically set to 0.75. Experiments revealed that for larger threshold values (e.g.,
thr = 1.0), the proposed classification approach is over sensitive and noise impacts the classification; on the other hand, for lower threshold values (e.g.,
thr = 0.5), the approach is insufficiently responsive to slightly different contours.